Choosing the Best Members of the Optimal Eighth-Order Petković’s Family by Its Fractal Behavior
Abstract
1. Introduction
- (1)
- If there exists such that , then w is called a fixed point of f;
- (2)
- If there are integers p greater than 1 and such that , then w is called the periodic point of f. The smallest p such that is called the period of w, and is the period p orbit;
- (3)
- Let w be a periodic point with period p, and ;
- If , then w is a superattracting point;
- If , then w is an attractive point;
- If , then w is a neutral point;
- If , then w is a repulsive point.
2. Some Concepts and Properties Related to Riemann Sphere
3. Complex Dynamics Analysis
3.1. Fixed Points and Their Stability
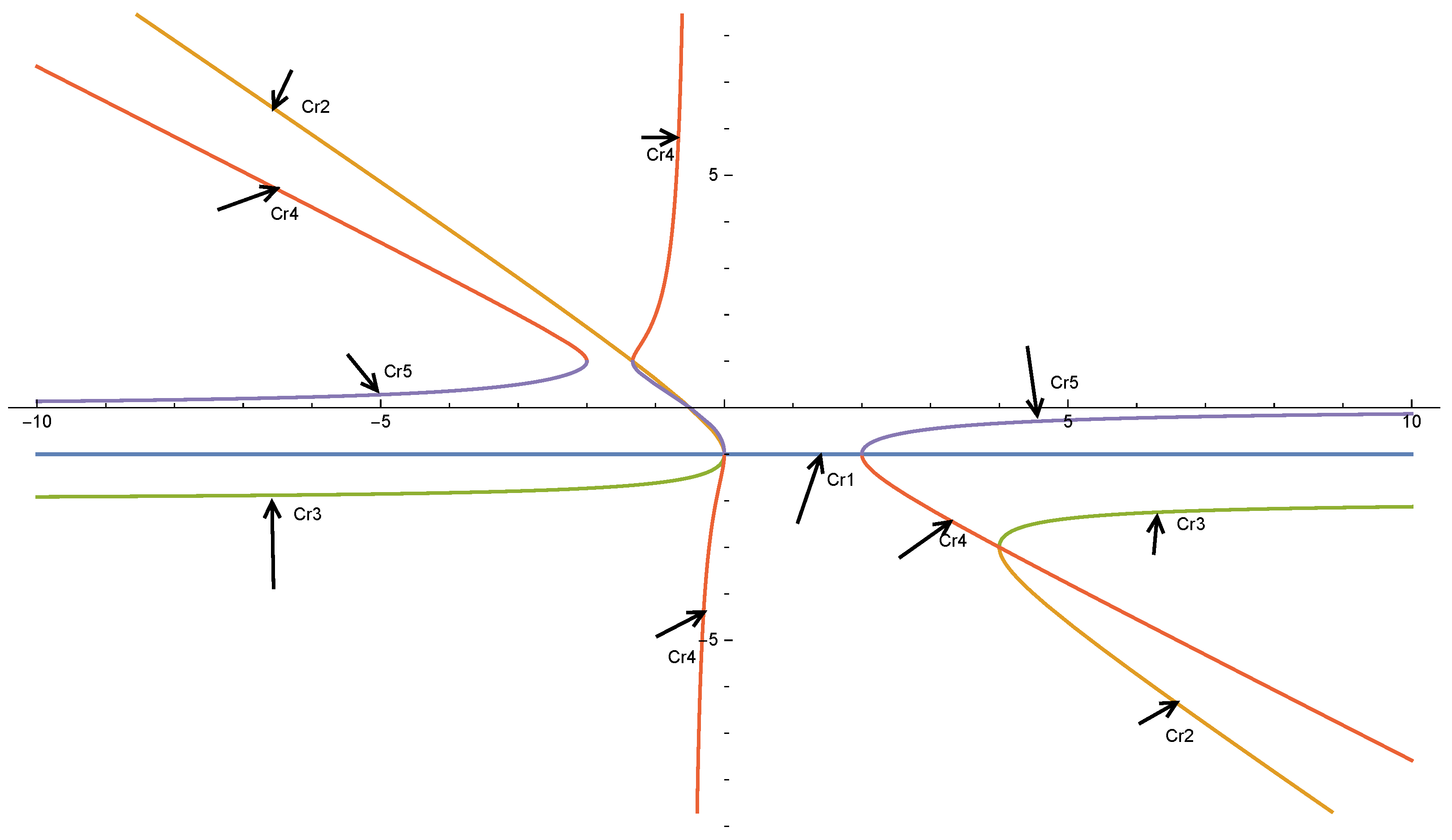
3.2. Analysis of Critical Points
- ;
- ;
- =;
- ;
- = .
- Relation holds when or ;
- Relation holds when , , or ;
- Relation holds when , or ;
- Relation holds when ;
- Relation holds when ;
- Relation holds when or ;
- Relation holds when .
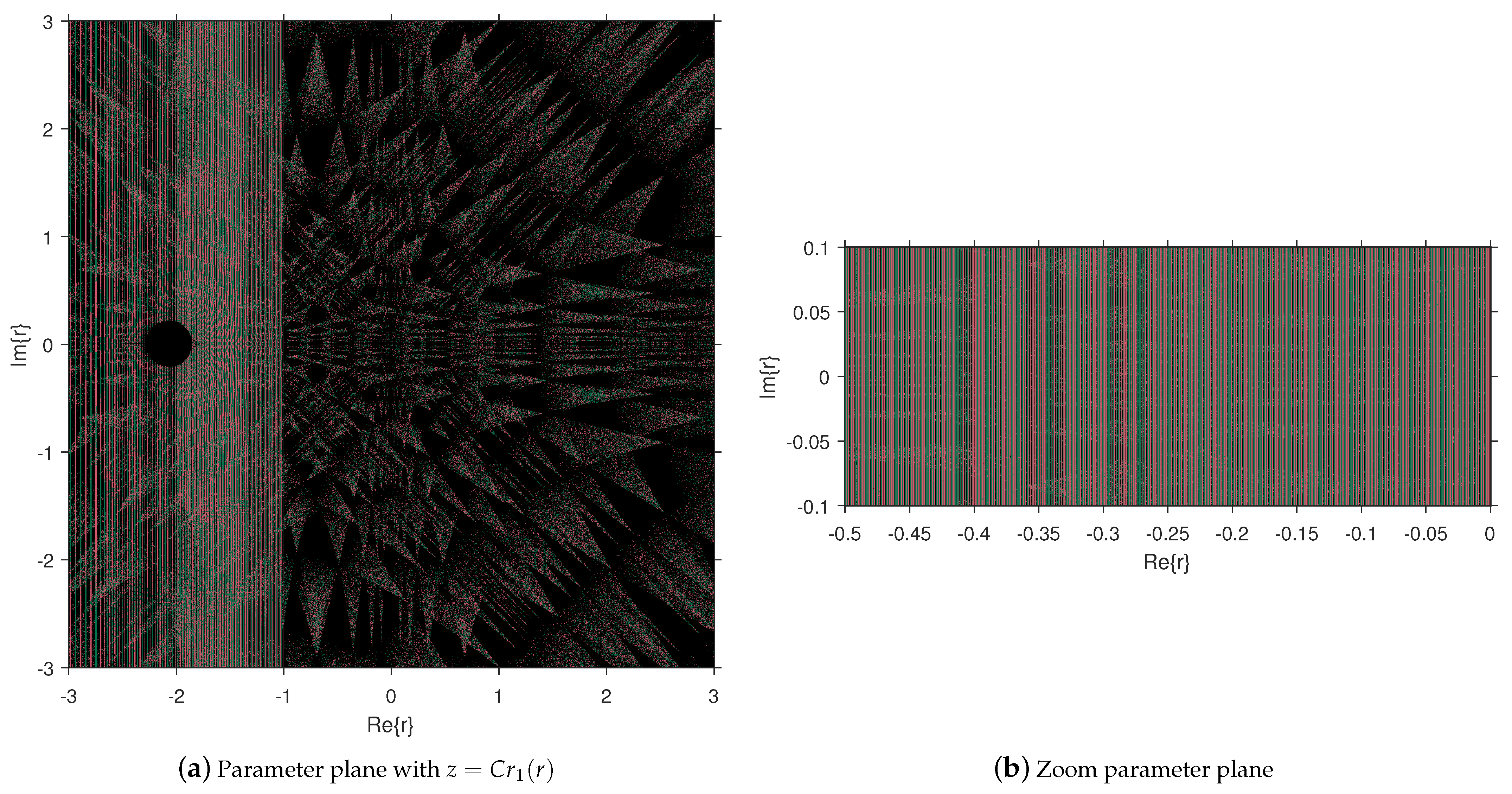
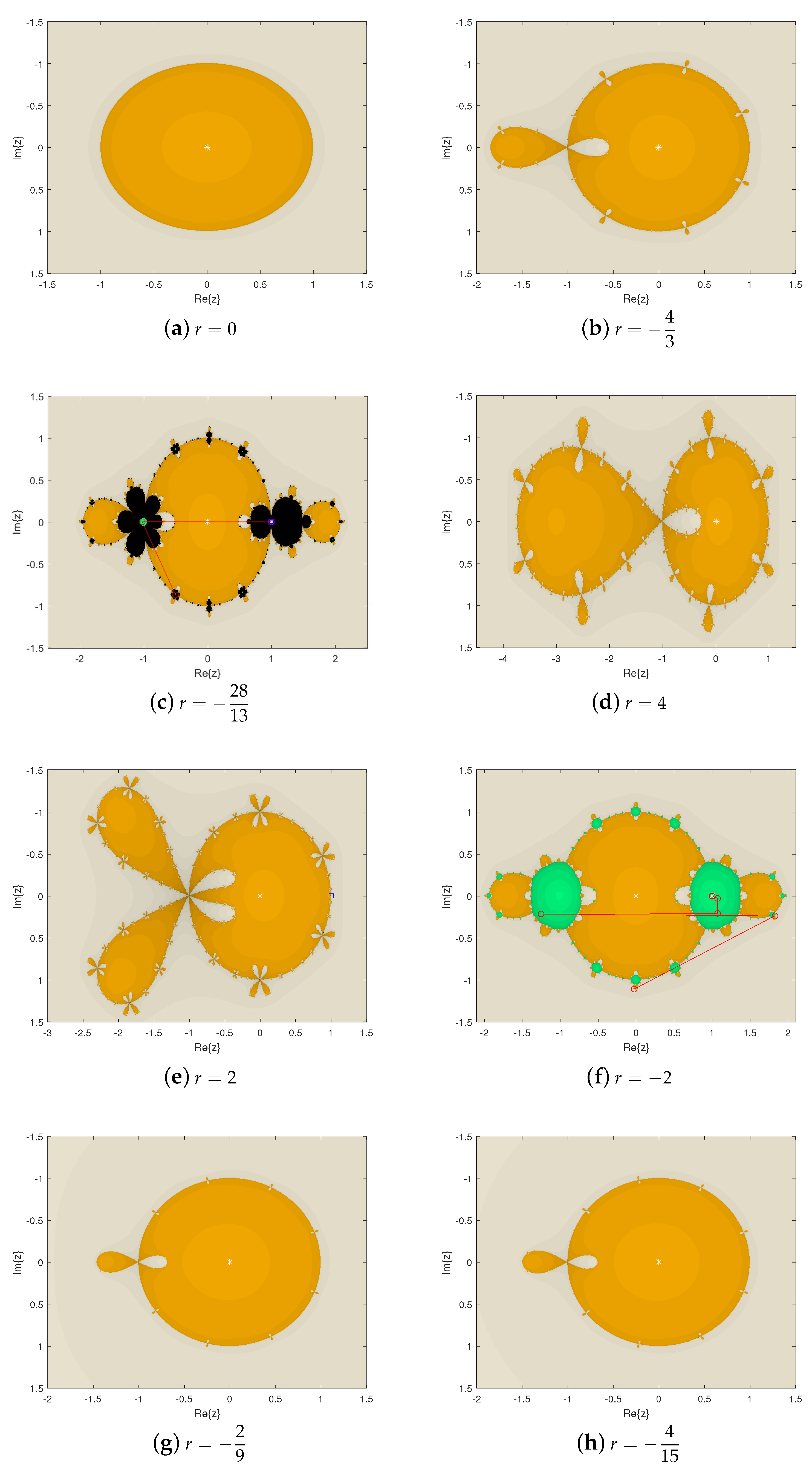
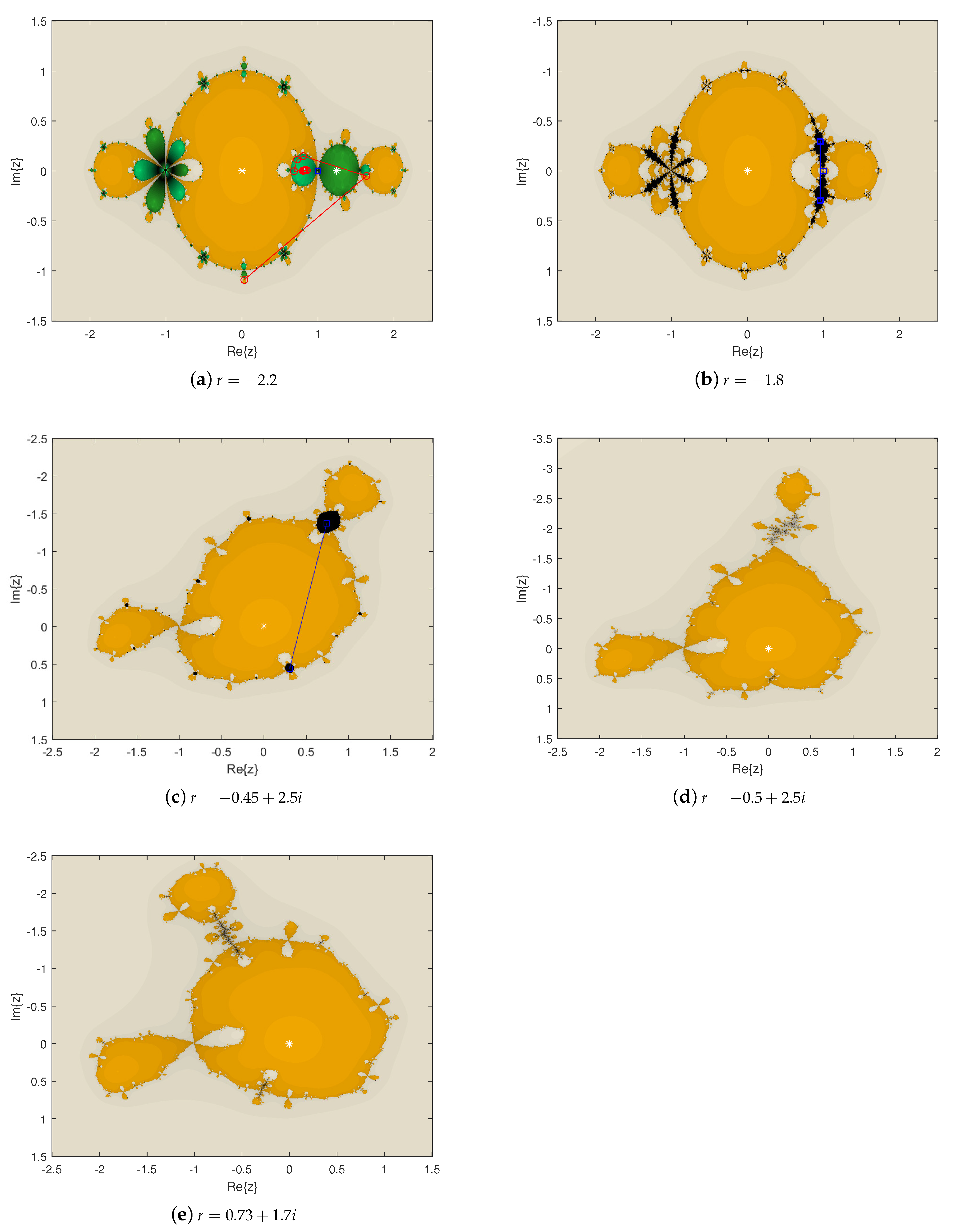
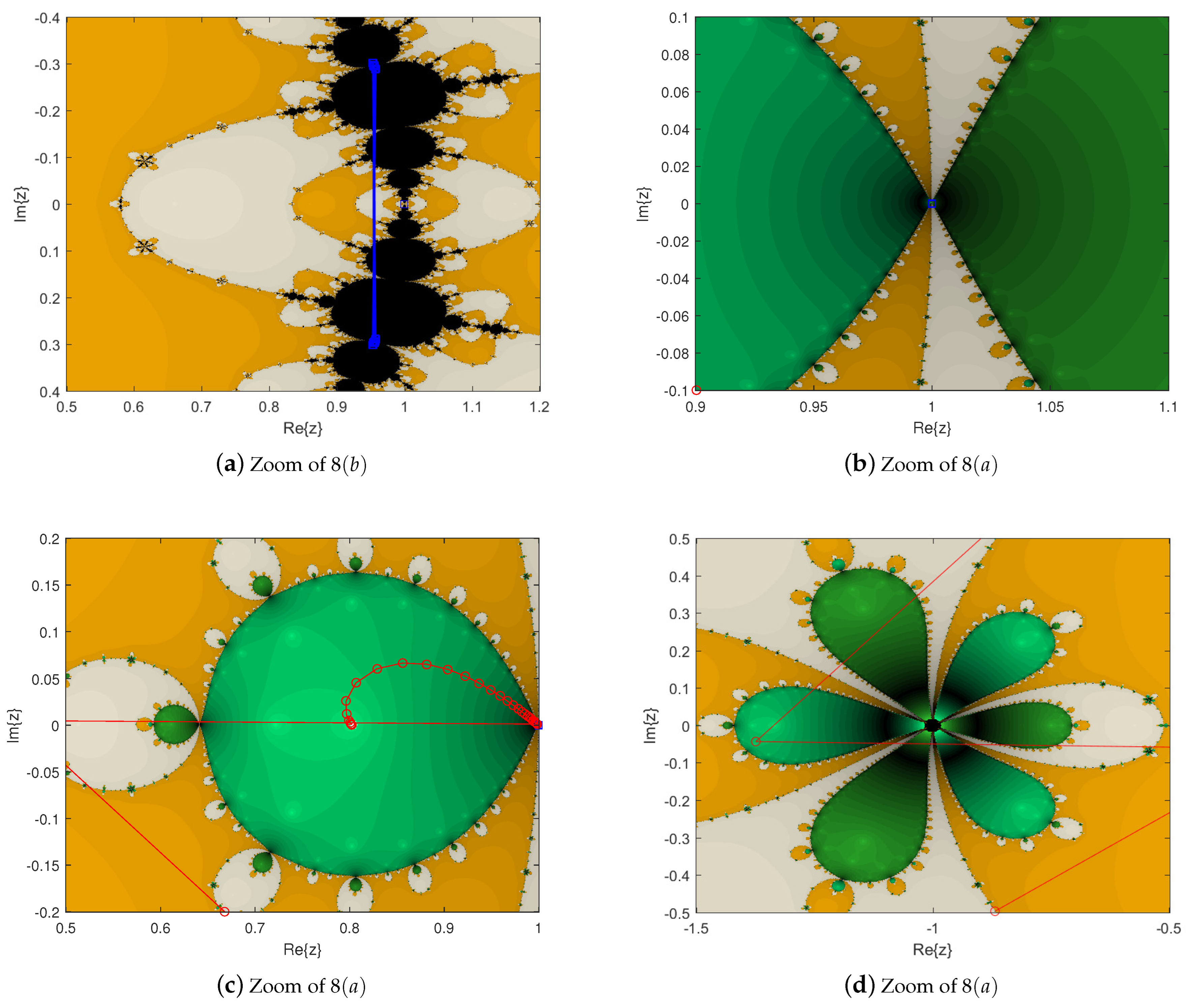
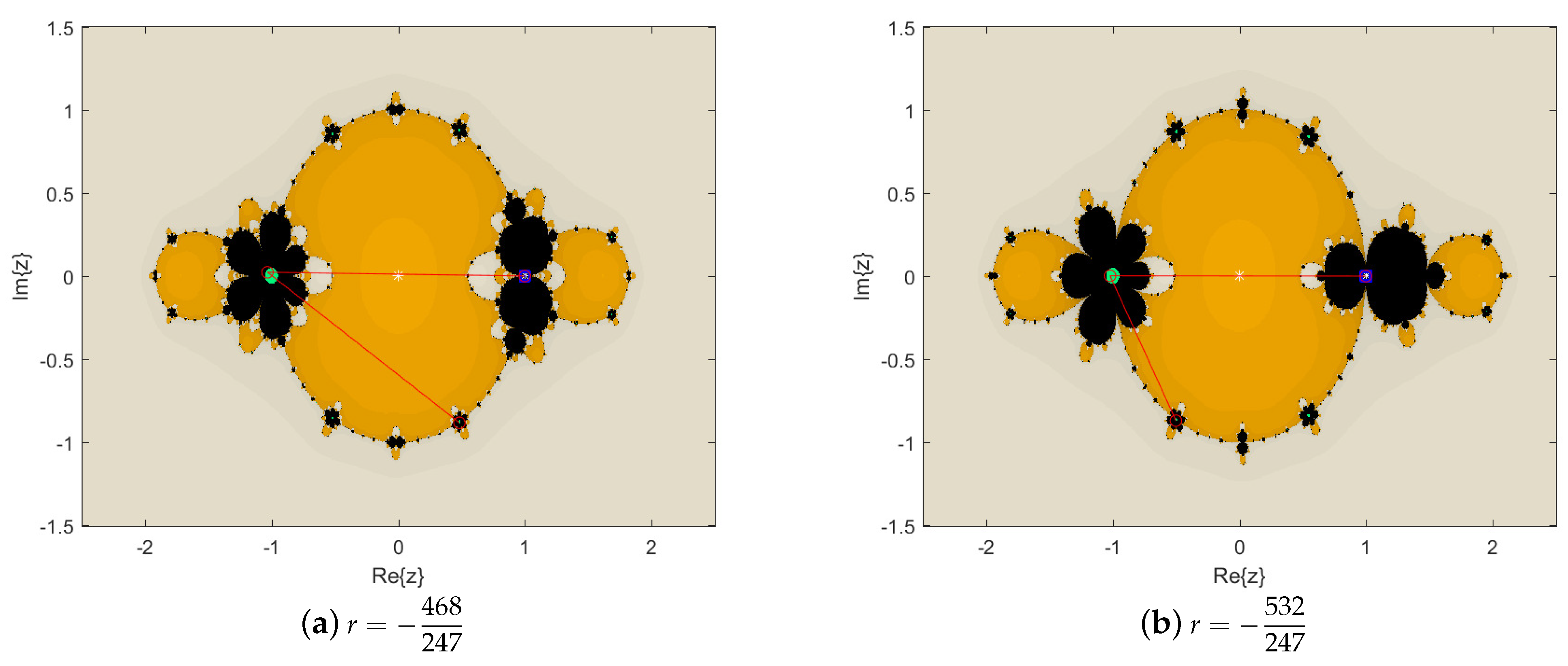
3.3. Parameter Spaces and Dynamical Planes
3.3.1. Parameter Spaces
3.3.2. Dynamical Planes
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mandelbrot, B.B.; Aizenman, M. Fractals: Form, Chance, and Dimension. Phys. Today 1979, 32, 65–66. [Google Scholar] [CrossRef]
- Agop, M.; Gavriluţ, A.; Pǎun, V.P. Fractal Information by Means of Harmonic Mappings and some Physical Implications. Entropy 2016, 18, 160. [Google Scholar] [CrossRef]
- Zhong, X.; Zhu, Y.; Zhou, Y. Spectra of fractal information on Cantor axis. Phys. A 1993, 1711, 349–356. [Google Scholar]
- Shailendra, K.D.; Umesh, D.; Sanyog, R. A Slotted Microstrip Antenna with Fractal Design for Surveillance Based Radar Applications in X-band. Int. J. Eng. Sci. 2018, 7, 64. [Google Scholar]
- Qu, H.; Han, Z.; Chen, Z. Fractal Design Boosts Extrusion-Based 3D Printing of Bone-Mimicking Radial-Gradient Scaffolds. Research 2021, 2021, 9892689. [Google Scholar] [CrossRef]
- Lin, X.; Liu, W. The Application of Fractal Art in Ceramic Product Design. IOP Conf. Ser. Mater. Sci. Eng. 2019, 573, 012003. [Google Scholar] [CrossRef]
- Kumari, S.; Gdawiec, K.; Nandal, A.; Postolache, M.; Chugh, R. A novel approach to generate Mandelbrot sets, Julia sets and biomorphs via viscosity approximation method. Chaos Solitons Fractals 2022, 163, 112540. [Google Scholar] [CrossRef]
- Usurelu, G.I.; Bejenaru, A.; Postolache, M. Newton-like methods and polynomiographic visualization of modified Thakur processes. Int. J. Comput. Math. 2021, 98, 1049–1068. [Google Scholar] [CrossRef]
- Zhang, T.; Guo, Q. The solution theory of the nonlinear q-fractional differential equations. Appl. Math. Lett. 2020, 104, 106282. [Google Scholar] [CrossRef]
- Ryu, K.; Yücesan, E.; Jung, M. Dynamic restructuring process for self-reconfiguration in the fractal manufacturing system. Int. J. Prod. Res. 2011, 44, 3105–3129. [Google Scholar] [CrossRef]
- Yorikawa, H. Energy levels in a self-similar fractal cluster. J. Phys. Commun. 2019, 3, 085004. [Google Scholar] [CrossRef]
- Alexander, T.; Trifce, S. Fractional Diffusion to a Cantor Set in 2D. Fractal Fract. 2020, 4, 52. [Google Scholar]
- Paramanathan, P.; Uthayakumar, R. Fractal interpolation on the Koch Curve. Comput. Math. Appl. 2010, 59, 3229–3233. [Google Scholar] [CrossRef]
- Bock, H. On the dynamics of entire functions on the Julia set. Results Math. 1996, 30, 16–20. [Google Scholar] [CrossRef]
- Peitgen, H.; Richter, P. The Beauty of Fractals; Springer: New York, NY, USA, 1986. [Google Scholar]
- Letherman, S.D.; Wood, R.M.W. A note on the Julia set of a rational function. Math. Proc. Camb. Philos. Soc. 1995, 118, 477–485. [Google Scholar] [CrossRef]
- Hua, X.; Yang, C.C. Fatou Components and a Problem of Bergweiler. Int. J. Bifurc. Chaos Appl. Sci. Eng. 1998, 8, 1613–1616. [Google Scholar] [CrossRef]
- Wang, X.; Chen, X. Derivative-Free Kurchatov-Type Accelerating Iterative Method for Solving Nonlinear Systems: Dynamics and Applications. Fractal Fract. 2022, 6, 59. [Google Scholar] [CrossRef]
- Geum, Y.H.; Kim, Y.I. Computational Bifurcations Occurring on Red Fixed Components in the λ-Parameter Plane for a Family of Optimal Fourth-Order Multiple-Root Finders under the Möbius Conjugacy Map. Mathematics 2020, 8, 763. [Google Scholar] [CrossRef]
- Geum, Y.H.; Kim, Y.I.; Magreñán, Á.A. A biparametric extension of King’s fourth-order methods and their dynamics. Appl. Math Comput. 2016, 282, 254–275. [Google Scholar] [CrossRef]
- Petković, M.S.; Petković, L.D. Families of optimal multipoint methods for solving nonlinear equations: A survey. Appl. Anal. Discr. Math. 2010, 4, 1–22. [Google Scholar] [CrossRef]
- Campos, B.; Cordero, A.; Torregrosa, J.R.; Vindel, P. Orbits of period two in the family of a multipoint variant of Chebyshev-Halley family. Numer. Algorithms 2016, 73, 141–156. [Google Scholar] [CrossRef]
- Lee, M.; Kim, Y.I. The dynamical analysis of a uniparametric family of three-point optimal eighth-order multiple-root finders under the Möbius conjugacy map on the Riemann sphere. Numer. Algorithms 2020, 83, 1063–1090. [Google Scholar] [CrossRef]
- Russen, S.C. Nonlinear dynamics and chaos. Math. Gaz. 2004, 88, 188. [Google Scholar] [CrossRef]
- Takens, F. An introduction to chaotic dynamical systems. Acta Appl. Math. 1988, 13, 221–226. [Google Scholar] [CrossRef]
- Devaney, R.L. The Mandelbrot set, the Farey tree and the Fibonacci sequence. Am. Math. Mon. 1999, 106, 289–302. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Li, W. Choosing the Best Members of the Optimal Eighth-Order Petković’s Family by Its Fractal Behavior. Fractal Fract. 2022, 6, 749. https://doi.org/10.3390/fractalfract6120749
Wang X, Li W. Choosing the Best Members of the Optimal Eighth-Order Petković’s Family by Its Fractal Behavior. Fractal and Fractional. 2022; 6(12):749. https://doi.org/10.3390/fractalfract6120749
Chicago/Turabian StyleWang, Xiaofeng, and Wenshuo Li. 2022. "Choosing the Best Members of the Optimal Eighth-Order Petković’s Family by Its Fractal Behavior" Fractal and Fractional 6, no. 12: 749. https://doi.org/10.3390/fractalfract6120749
APA StyleWang, X., & Li, W. (2022). Choosing the Best Members of the Optimal Eighth-Order Petković’s Family by Its Fractal Behavior. Fractal and Fractional, 6(12), 749. https://doi.org/10.3390/fractalfract6120749





