Approximation by Quantum Meyer-König-Zeller Fractal Functions

Abstract

In this paper, a novel class of quantum fractal functions is introduced based on the Meyer-König-Zeller operator $M_{q,n}$. These quantum Meyer-König-Zeller (MKZ) fractal functions employ $M_{q,n}f$ as the base function in the iterated function system for $\alpha$-fractal functions. For $f\in C\left(I\right)$, I closed interval in $\mathbb{R}$, it is shown that a sequence of quantum MKZ fractal functions ${\{f_n^{(q_n,\alpha )}\}}_{n=0}^{\infty }$ exists which converges uniformly to f without altering the scaling function $\alpha$. The shape of $f_n^{(q_n,\alpha )}$ depends on q as well as the other iterated function system parameters. For $f,g\in C\left(I\right)$, $f\ge g>0$, we show that a sequence ${\{f_n^{(q_n,\alpha )}\}}_{n=0}^{\infty }$ exists with $f_n^{(q_n,\alpha )}\ge g>0$ converging to f. Quantum MKZ fractal versions of some classical Müntz theorems are also presented. For $q=1$, the box dimension and some approximation-theoretic results of MKZ $\alpha$-fractal functions are investigated in $C\left(I\right)$. Finally, MKZ $\alpha$-fractal functions are studied in $L^p$ spaces with $p\ge 1$.

1. Introduction

Quantum calculus or q-calculus is calculus without the use of limits. This theory has been extensively studied in the fields of approximation theory, special functions, combinatorics, number theory, mechanics, quantum physics, and the theory of relativity. In 1987, Lupaş [1] constructed the q-analogue of Bernstein operators and established convergence estimates and shape preserving properties. In the last three decades, q-extensions of various results in classical approximation theory have been proposed by several researchers. For an albeit incomplete list, see, for instance [2,3,4,5,6,7,8,9,10,11].

Since classical approximation theory and q-approximation theory dispense with the approximation of functions using piecewise smooth functions or infinitely differentiable functions, they are not ideal tools to represent non-differentiable functions such as speech signals, bio-electric recordings, time series, financial series, or seismic data, to name a few.

Fractal functions bestow a constructive approximation theory on irregular functions or functions whose derivatives are non-smooth in nature. Fractal functions easily describe functions that have some degree of self-similarity at different scales. Using iterated function systems (IFSs), Barnsley [12] introduced the construction of fractal interpolation functions (FIFs) to obtain a mathematical representation of data sets arising from irregular functions. He conceptualized the idea of approximation of a continuous function f defined on a real compact interval I by a family of $\alpha$-fractal functions $f^{\alpha }$, where $\alpha$ is a set of given or appropriately chosen parameters. We refer the interested reader to the vast literature on fractal functions and fractal interpolation and refer only to [13,14,15,16,17,18,19] as an albeit incomplete list of references as they appertain most closely to the setting considered in this paper.

The choice of a base function b is important in the construction of $f^{\alpha }$, even though it is avoided in its notation. The graph of $f^{\alpha }$ is typically a fractal set and dimension results for classes of such fractal functions can be found in, for instance [13,20,21,22,23,24,25,26,27,28].

Shape preserving interpolants play an important role in engineering and the applied sciences. The question of shape preserving aspects of a function f by its fractal perturbation function $f^{\alpha }$ is answered affirmatively in [29] with a suitable choice for b and $\alpha$.

It is known that an $\alpha$-fractal function $f^{\alpha }$ of f converges to f when the magnitude of the scaling factors of $f^{\alpha }$ goes to zero. Vijender et al. [30] proposed a theory of quantum $\alpha$-fractal functions using Bernstein polynomials associated with f as base function. They showed that the convergence of a sequence of quantum $\alpha$-fractal functions towards the function f follows from the convergence of the q-Bernstein polynomials towards f, even when the scaling parameters are non-null.

In this paper, we propose the use of quantum Meyer-König-Zeller functions as base functions, i.e., we require that $b=M_{q,n}f$, to construct a novel sequence of quantum MKZ fractal functions denoted by $f_{q_n,n}^{\alpha }$. It is proved that $f_{q_n,n}^{\alpha }$ converges to f as $n\to \infty$. However, the magnitude/norm of the scaling functions does not go to 0 when ${\left\{q_n\right\}}_{n=1}^{\infty }$ is a sequence in (0,1] such that $\underset{n\to \infty }{lim}{q}_n=1$. It is also shown that the shape of $f_{q,n}^{\alpha }$ depends on the scaling functions as well as $0<q\le 1$. We study the shape preserving aspects of quantum MKZ fractal functions and consider quantum MKZ analogues of two classical Müntz theorems. The latter approach makes use of so-called quantum MKZ fractal Müntz polynomials.

Setting $q=1$ in the quantum MKZ fractal function $f_n^{(q,\alpha )}$, we obtain a novel MKZ $\alpha$-fractal function. Some approximation-theoretic properties and the box dimension for the graph of such an MKZ $\alpha$-fractal function is investigated. Finally, we study the existence of MKZ $\alpha$-fractal functions in $L^p$ spaces, $p\ge 1$, and investigate their approximation-theoretic properties.

2. Background and Preliminaries

In this section, we present the foundations of IFSs and the construction of $\alpha$-fractal functions from a suitable IFS. For more details, the interested reader may consult the important references [12,15,17,26,31].

Let $N\in \mathbb{N}:=\{1,2,3,\dots \}$ and ${\mathbb{N}}_N:=\{1,\dots ,N\}$ be the initial segment of $\mathbb{N}$ of length N. An IFS $\mathcal{F}:=\{X;w_i:i\in {\mathbb{N}}_N\}$ is a collection of continuous functions on a complete metric space $(X,d)$. $\mathcal{F}$ is called a hyperbolic IFS if each $w_i$ is contractive on X, i.e., its Lipschitz constant

$$s_i:=Lip\left(w_i\right):=\underset{x,y\in X,.x\ne y}{sup}\frac{d(w_i\left(x\right),w_i\left(y\right))}{d(x,y)}<1.$$

Let $\mathcal{H}\left(X\right):=\{A\subseteq X:A \mathrm{is} \mathrm{non}-\mathrm{empty} \mathrm{and} \mathrm{compact}\}$. The Hausdorff-Pompeiu metric h on $\mathcal{H}\left(X\right)$ is defined by

$$h(A,B):=max\left\{d\right(A,B),d(B,A\left)\right\},$$

where $d(A,B):=sup\left\{d\right(x,B):x\in A\}$ and $d(x,B):=inf\left\{d\right(x,y):y\in B\}$. It is known that if $(X,d)$ is a complete metric space then $\left(\mathcal{H}\right(X),h)$ is also a complete metric space, termed the space of fractals in [32].

The Hutchinson map [31] $W:\mathcal{H}\left(X\right)\to \mathcal{H}\left(X\right)$ is defined by

$$W\left(A\right):=\bigcup _{i=1}^N{w}_i\left(A\right),\hspace{1em}\forall A\in \mathcal{H}\left(X\right).$$

If the IFS $\mathcal{F}$ is hyperbolic, then W is a contraction on $\left(\mathcal{H}\right(X),h)$ with contraction factor $s:=\underset{i\in {\mathbb{N}}_N}{max}\left|s_i\right|<1$. Thus, by the Banach fixed point theorem, a unique G in $\mathcal{H}\left(X\right)$ exists such that

$$G=\underset{m\to \infty }{lim}{W}^{\circ m}\left(A\right),\hspace{1em} \mathrm{for} \mathrm{any} A\in \mathcal{H}\left(X\right),$$

where $W^{\circ m}$ denotes the m-fold composition of W with itself. The fixed point G is called the attractor of, or deterministic fractal generated by, the hyperbolic IFS $\mathcal{F}$.

Now, consider a set of interpolation points

$$\{(x_j,y_j)\in [x_1,x_N]\times \mathbb{R}:-\infty <x_1<x_2<\cdots <x_N<+\infty ,j\in {\mathbb{N}}_N\}.$$

Let $u_i,i\in {\mathbb{N}}_{N-1}$, be a set of homeomorphisms from $I:=[x_1,x_N]$ to $I_i:=[x_i,x_{i+1}]$ satisfying

$$u_i\left(x_1\right)=x_i,\hspace{1em}{u}_i\left(x_N\right)=x_{i+1}.$$

(1)

For $i\in {\mathbb{N}}_{N-1}$, let $v_i:I\times K\to K$ be a function, where K is a suitable compact subset of $\mathbb{R}$ that contains all the $y_j$, $j\in {\mathbb{N}}_N$ (the existence of such a set is shown in, i.e., [15]). Assume that each $v_i$ is continuous in the first variable and Lipschitz continuous in the second variable with Lipschitz constant $|{\alpha }_i|<1,i\in {\mathbb{N}}_{N-1}$, i.e.,

$$v_i(x_1,y_1)=y_i,\hspace{1em}{v}_i(x_N,y_N)=y_{i+1},$$

(2)

and

$$|v_i(x,y_1)-v_i(x,y_2)|\le |{\alpha }_i\left|\right|y_1-y_2|,\hspace{1em}\forall i\in {\mathbb{N}}_{N-1}.$$

(3)

Let $C\left(I\right):=\{f:I\to \mathbb{R}:f \mathrm{is} \mathrm{continuous} \mathrm{on} I\}$ and define

$$\mathcal{G}:=\{g\in C\left(I\right):g\left(x_1\right)=y_1\wedge g\left(x_N\right)=y_N\}.$$

Defining a metric on $\mathcal{G}$ by $\rho (h,g):=max\left\{\right|h\left(x\right)-g\left(x\right)|:x\in I\}$ for $g,h\in \mathcal{G}$, makes $(\mathcal{G},\rho )$ into a complete metric space.

Define a Read-Bajraktarević (RB) operator [15] T on $(\mathcal{G},\rho )$ by

$$Tg\left(x\right):=\sum _{i=1}^{N-1}{v}_i(u_i^{-1}\left(x\right),g\circ u_i^{-1}\left(x\right)){\chi }_{u_i\left(I\right)}\left(x\right),\hspace{1em}x\in I,$$

(4)

where ${\chi }_S$ denotes the characteristic or indicator function of a set S.

Using the properties of $u_i$ and $v_i$, it is straight forward to verify that $Tg$ is continuous on I. Also,

$$\rho (Tg,Th)\le {\left|\alpha \right|}_{\infty }\rho (g,h),$$

(5)

where $\alpha :=({\alpha }_1,\dots ,{\alpha }_{N-1})$ and ${\left|\alpha \right|}_{\infty }:=max\left\{\right|{\alpha }_i|:i\in {\mathbb{N}}_{N-1}\}<1$. Hence, T is a contractive map on the complete metric space $(\mathcal{G},\rho )$. Therefore, by the Banach fixed point theorem, T possesses a unique fixed point $f^{*}\in \mathcal{G}$. Consequently, from (4), $f^{*}$ obeys the self-referential functional equation

$$f^{*}=\sum _{i=1}^{N-1}{v}_i(u_i^{-1},f^{*}\circ u_i^{-1}){\chi }_{u_i\left(I\right)}$$

(6)

on I. It can be easily verified that $f^{*}\left(x_j\right)=y_j$, $j\in {\mathbb{N}}_{N-1}$.

Now, define mappings $w_i:I\times K\to I_i\times K$ by

$$w_i(x,y):=(u_i\left(x\right),v_i(x,y)),\hspace{1em}(x,y)\in I\times K,i\in {\mathbb{N}}_{N-1}.$$

The graph of $G\left(f^{*}\right)$ of $f^{*}$ is the attractor of the IFS

$$\mathcal{I}:=\{I\times K;w_i(x,y)=(u_i\left(x\right),v_i(x,y)),i\in {\mathbb{N}}_{N-1}\}$$

and satisfies the self-referential set equation

$$G\left(f^{*}\right)=\bigcup _{i\in {\mathbb{N}}_{N-1}}{w}_i\left(G\left(f^{*}\right)\right).$$

(7)

In this setting, $f^{*}$ is called a fractal interpolation function (FIF) associated with the IFS $\mathcal{I}$.

It was observed in [12,15,17] that the concept of FIF may be used to define a class of fractal functions associated with any function $f\in C\left(I\right)$, as described in the following.

For this purpose, let $I:=[x_1,x_N]\subset \mathbb{R}$. For a given $f\in C\left(I\right)$, consider a partition $\Delta :=\{x_1,x_2,\dots ,x_N\}$ of I satisfying $x_1<x_2<\cdots <x_N$, and a continuous function $b:I\to \mathbb{R}$ with $b\ne f$ that satisfies the endpoint interpolation conditions $b\left(x_1\right)=f\left(x_1\right)$ and $b\left(x_N\right)=f\left(x_N\right)$.

Choose an $\alpha =({\alpha }_1,\dots ,{\alpha }_{N-1})\in {(-1,1)}^{N-1}$. If, for $i\in {\mathbb{N}}_{N-1}$, we set

$$u_i\left(x\right):=a_{i}x+b_i\hspace{1em}\mathrm{and}\hspace{1em}{v}_i(x,y):={\alpha }_{i}y+f\left(u_i\left(x\right)\right)-{\alpha }_{i}b\left(x\right),$$

(8)

and determine the constants $a_i$ and $b_i$ via the conditions (1), then the IFS

$$\{[x_1,x_N]\times \mathbb{R};w_i(x,y)=(u_i\left(x\right),v_i(x,y)),i\in {\mathbb{N}}_{N-1}\}$$

determines an attractor which is the graph of a fractal function $f_{\Delta ,b}^{\alpha }=:f^{\alpha }$. The function $f^{\alpha }$ is referred to as an $\alpha$-fractal function for f and may be considered as the fractalization of f (with respect to the scaling vector $\alpha$, the base function b, and the partition $\Delta$).

The function $f^{\alpha }$ is the fixed point of the RB operator $T:C_f\left(I\right)\to C_f\left(I\right)$ defined by [15]

$$Tg=f+\sum _{i=1}^{N-1}{\alpha }_i(g-b)\circ u_i^{-1}{\chi }_{u_i\left(I\right)}$$

(9)

on I, where $C_f\left(I\right)=\{g\in C\left(I\right):g\left(x_1\right)=f\left(x_1\right)\wedge g\left(x_N\right)=f\left(x_N\right)\}.$ Consequently, $f^{\alpha }$ satisfies the self-referential equation

$$f^{\alpha }\left(x\right)=f\left(x\right)+\sum _{i=1}^{N-1}{\alpha }_i(f^{\alpha }\left(u_i^{-1}\left(x\right)\right)-b\left(u_i^{-1}\left(x\right)\right)){\chi }_{u_i\left(I\right)}\left(x\right),\hspace{1em}x\in I.$$

The fractal dimension of the graph of $f^{\alpha }$ depends on the choice of the scaling vector $\alpha$ and the $a_i$ [20,21].

To obtain more flexibility in the construction of fractal functions, the constant scalings ${\alpha }_i$, $i\in {\mathbb{N}}_{N-1}$, can be replaced by continuous functions ${\alpha }_i\in C\left(I\right)$ with ${\parallel \alpha \parallel }_{\infty }:=max\{\parallel {\alpha }_i{\parallel }_{\infty }:i\in {\mathbb{N}}_{N-1}\}<1$ in the IFS (8). Hence,

$$v_i(x,y)={\alpha }_i\left(x\right)y+f\left(u_i\left(x\right)\right)-{\alpha }_i\left(x\right)b\left(x\right),\hspace{1em}i\in {\mathbb{N}}_{N-1}.$$

(10)

The corresponding $\alpha$-fractal function is then the fixed point of the RB-operator

$$Tg=f+\sum _{i=1}^{N-1}({\alpha }_i\circ u_i^{-1})(g-b)\circ u_i^{-1}{\chi }_{u_i\left(I\right)},$$

(11)

and it satisfies a self-referential equation with location-dependent scalings

$$f^{\alpha }\left(x\right)=f\left(x\right)+\sum _{i=1}^{N-1}{\alpha }_i\left(u_i^{-1}\left(x\right)\right)(f^{\alpha }\left(u_i^{-1}\left(x\right)\right)-b\left(u_i^{-1}\left(x\right)\right)){\chi }_{u_i\left(I\right)}\left(x\right),\hspace{1em}x\in I.$$

(12)

Using (12), it is easy to show that

$$\parallel f^{\alpha }{-f\parallel }_{\infty }\le \frac{{\parallel \alpha \parallel }_{\infty }}{1-{\parallel \alpha \parallel }_{\infty }}{\parallel f-b\parallel }_{\infty }.$$

(13)

The above inequality shows that an $\alpha$-fractal function $f^{\alpha }$ converges uniformly to f if either ${\parallel \alpha \parallel }_{\infty }\to 0$ or ${\parallel f-b\parallel }_{\infty }\to 0$. In particular, if b is taken to be a sequence of MKZ quantum functions, the novel class of MKZ $(q,\alpha )$-fractal functions is obtained.

3. MKZ $(\mathbf{q},\mathbf{\alpha })$-Fractal Functions

We require the following notation from quantum calculus. For $q\in (0,1]$ and $k\in \mathbb{N}$, let

$${\left[k\right]}_q:=\left\{\begin{array}{cc}\frac{1-q^k}{1-q},\hfill & q\ne 1;\hfill \\ k,\hfill & q=1.\hfill \end{array}\right.$$

The q-factorial is defined as

$${\left[k\right]}_q!:=\left\{\begin{array}{cc}{\left[k\right]}_q{[k-1]}_q\dots {\left[2\right]}_q{\left[1\right]}_q,\hfill & k\in \mathbb{N};\hfill \\ 1,\hfill & k=0.\hfill \end{array}\right.$$

By means of the q-factorial, the q-binomial coefficients are then defined by

$${\left(\genfrac{}{}{0pt}{}{n}{k}\right)}_q:=\frac{{\left[n\right]}_q!}{{\left[k\right]}_q!{[n-k]}_q!},$$

for all integers $n\ge k\ge 0$.

Following [33,34,35], we define a sequence of MKZ functions on $I=[x_1,x_N]$ for $f\in C\left(I\right)$ by

$$\begin{array}{c}{M}_{n,q}f\left(x\right):=P_{n,q}\left(x\right)\sum _{k=0}^{\infty }{\left(\genfrac{}{}{0pt}{}{n+k}{k}\right)}_q{\left(\frac{x-x_1}{x_N-x_1}\right)}^{k}f\left(x_1+(x_N-x_1)\frac{{\left[k\right]}_q}{{[k+n]}_q}\right),\hfill \\ M_{n,q}f\left(x_N\right):=f\left(x_N\right),\hfill \end{array}$$

(14)

with

$$P_{n,q}\left(x\right):=\frac{{\displaystyle \prod _{j=0}^n}(x_N-x_1-q^j(x-x_1))}{{(x_N-x_1)}^{n+1}}.$$

It is easy to verify that

$$M_{n,q}f\left(x_1\right)=f\left(x_1\right).$$

If in (10) we take as the base function $b:=M_{n,q}f$, then the corresponding $\alpha$-fractal function

$$f_n^{(q,\alpha )}:={\mathcal{F}}_{\Delta ,b}^{(q,\alpha )}\left(f\right)$$

is termed a $(q,\alpha )$-fractal function or quantum MKZ fractal function associated with $f\in C\left(I\right)$.

Moreover,

$$f_n^{(q,\alpha )}=f+\sum _{i=1}^{N-1}({\alpha }_i\circ u_i^{-1})(f_n^{(q,\alpha )}-M_{n,q}f)\circ u_i^{-1}{\chi }_{u_i\left(I\right)},\hspace{1em}\mathrm{on} I.$$

(15)

It follows from (14) and (15), that the various quantitative and approximation-theoretic properties of $(q,\alpha )$-fractal functions $f_n^{(q,\alpha )}$ depend on the choices for q and the scaling functions ${\alpha }_i$.

The graph of a $(q,\alpha )$-fractal functions $f_n^{(q,\alpha )}$ is constructed via the IFS

$${\mathcal{F}}_{(q,n)}=\{I\times \mathbb{R};w_{n,i}(x,y)=(u_i\left(x\right),v_{n,i}(x,y)),i\in {\mathbb{N}}_{N-1}\},\hspace{1em}n\in \mathbb{N},$$

(16)

where $v_{n,i}(x,y):=f\left(u_i\left(x\right)\right)-{\alpha }_i\left(x\right)(y-M_{n,q}f\left(x\right)).$

The following theorem ensures the convergences of a sequence of quantum MKZ fractal functions to f in the sup-norm.

Theorem 1.

Let $f\in C\left(I\right)$. Then, there exists a sequence of quantum MKZ fractal functions ${\left\{f_n^{(q_n,\alpha )}\right\}}_{n=0}^{\infty }$ that converges uniformly to f on I, where ${\left\{q_n\right\}}_{n=1}^{\infty }$ is a sequence in $(0,1]$ with $\underset{n\to \infty }{lim}{q}_n=1$ and $f_n^{(q_n,\alpha )}$ is the fractal function corresponding to the IFS ${\mathcal{F}}_{(q_n,n)}$ defined in (16). Further, for each integer $n\ge 3$, we have

$$\parallel f_n^{(q_n,\alpha )}{-f\parallel }_{\infty }\le \frac{5}{2}\omega \left(f,\frac{1}{\sqrt{{\left[n\right]}_{q_n}}}\right)\frac{{\parallel \alpha \parallel }_{\infty }}{1-{\parallel \alpha \parallel }_{\infty }},$$

where ω denotes the modulus of continuity of f.

Proof. 

Let $f^{(q_n,\alpha )},n\in \mathbb{N}$, be a quantum MKZ fractal function corresponding to f. From (13), we obtain

$$\parallel f_n^{(q_n,\alpha )}{-f\parallel }_{\infty }\le \frac{{\parallel \alpha \parallel }_{\infty }}{1-{\parallel \alpha \parallel }_{\infty }}{\parallel f-M_{n,q_n}f\parallel }_{\infty }.$$

(17)

By ([33], Theorem 2), it follows that

$$\parallel M_{n,q_n}{f-f\parallel }_{\infty }\to 0 \mathrm{as} n\to \infty ,$$

(18)

which implies uniform convergence of ${\left\{f_n^{(q_n,\alpha )}\right\}}_{n=1}^{\infty }$ to f.

Applying the result

$$\parallel M_{n,q}{f-f\parallel }_{\infty }\le \frac{5}{2}\omega \left(f,\frac{1}{\sqrt{{\left[n\right]}_q}}\right),\hspace{1em}n\ge 3,$$

from ([34], Theorem 2.3) to (17), we obtain the following estimate:

$$\parallel f_n^{(q_n,\alpha )}{-f\parallel }_{\infty }\le \frac{5}{2}\omega \left(f,\frac{1}{\sqrt{{\left[n\right]}_{q_n}}}\right)\frac{{\parallel \alpha \parallel }_{\infty }}{1-{\parallel \alpha \parallel }_{\infty }},\hspace{1em}n\ge 3.$$

(19)

□

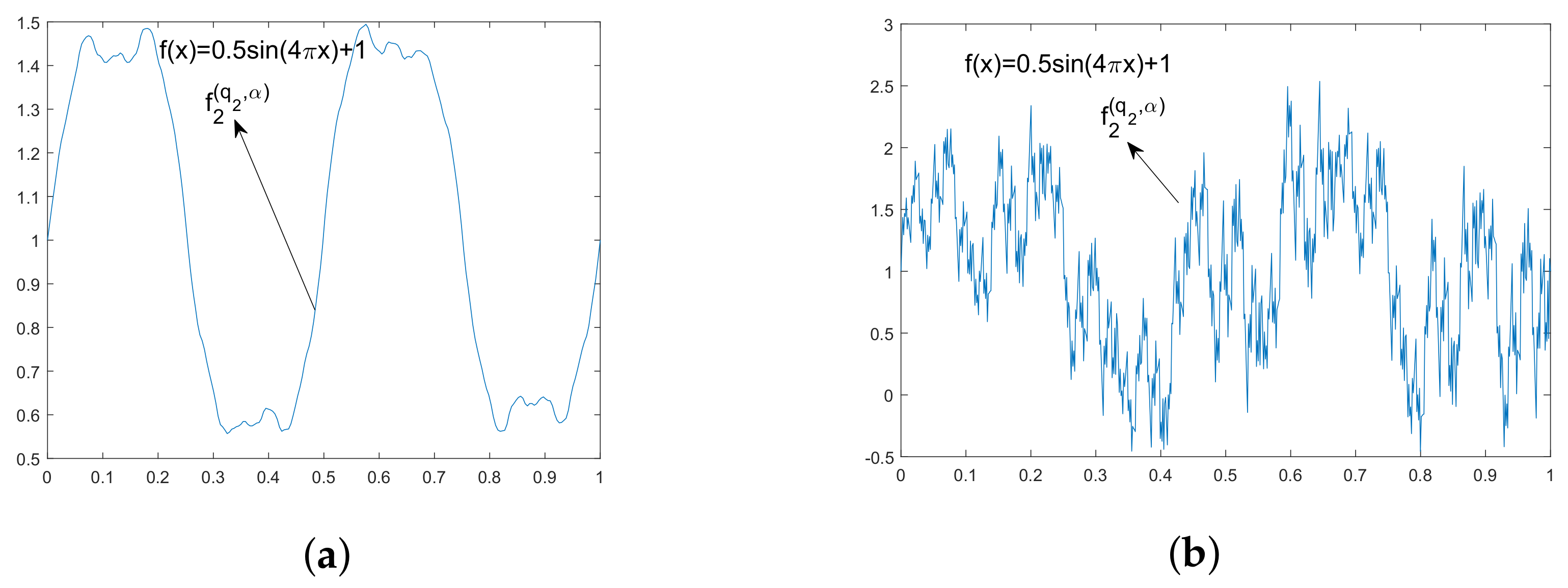
Example 1.

We want to construct a quantum MKZ fractal function associated with $f\left(x\right):=sinx$. Choose $I:=[0,1]$ and consider its partition $\Delta :=\{0,\frac{1}{7},\frac{2}{7},\frac{3}{7},\frac{4}{7},\frac{5}{7},\frac{6}{7},1\}$. Furthermore, let ${\alpha }_i\left(x\right):={(1+e^{-10x})}^{-1}$, $x\in I$, $i\in {\mathbb{N}}_7$. We take ${\left\{M_{n,q_n}f\right\}}_{n=1}^{\infty }$ as a sequence of base functions.

The quantum MKZ fractal functions are depicted in Figure 1a–c and represent the graphs of $f_1^{(0.5,\alpha )}$, $f_{50}^{(0.5,\alpha )}$, and $f_{50}^{(0.9,\alpha )}$, respectively, at the second level of iteration. Figure 1b,c show the effect of q on the quantum MKZ fractal function.

Figure 1. MKZ fractal functions of $sinx$.

Figure 1a,c ensure that the fractal function $f_{50}^{(0.9,\alpha )}$ provides better approximation of $f\left(x\right)=sinx,x\in [0,1]$, than $f_1^{(0.5,\alpha )}$. From $f_1^{(0.5,\alpha )}$ and $f_{50}^{(0.9,\alpha )}$, we observe that these two functions do not have the same irregularity even when their scaling functions are the same. Note that $f_1^{(0.5,\alpha )}$ exhibits irregularities on all scales, whereas $f_{50}^{(0.9,\alpha )}$ exhibits irregularities on small scales. Figure 1d is the blow-up of a small part of $f_{50}^{(0.9,\alpha )}$ showing irregularities of $f_{50}^{(0.9,\alpha )}$ on small scales. One reason for these irregularities is that the scaling functions ${\alpha }_i$ do not satisfy the inequalities $\parallel {\alpha }_i{\parallel }_{\infty }<\frac{a_i}{2},i\in {\mathbb{N}}_7$ ([36], Theorem 3.2).

Theorem 2.

Let $C\left(I\right)$ be endowed with the sup-norm. For every $n\in \mathbb{N}$, the $(q,\alpha )$-operator ${\mathcal{F}}_n^{(q,\alpha )}:C\left(I\right)\to C\left(I\right)$, ${\mathcal{F}}_n^{(q,\alpha )}\left(f\right):=f_n^{(q,\alpha )}$, is bounded and linear.

Proof. 

We know from [34] that $M_{n,q}$ is a positive linear operator. Further, it is known that $M_{n,q}{e}_0\left(x\right)=e_0\left(x\right)$, where $e_0\left(x\right)\equiv 1$. Then,

$$-{\parallel f\parallel }_{\infty }{e}_0\le f\le {\parallel f\parallel }_{\infty }{e}_0\Rightarrow -{\parallel f\parallel }_{\infty }{M}_{n,q}{e}_0\le M_{n,q}f\le {\parallel f\parallel }_{\infty }{M}_{n,q}{e}_0.$$

Thus, $\parallel M_{n,q}{f\parallel }_{\infty }\le {\parallel f\parallel }_{\infty }{M}_{n,q}{e}_0={\parallel f\parallel }_{\infty }.$ Hence $M_{n,q}$ is a bounded operator. By reference [19], we know that ${\mathcal{F}}_n^{(q,\alpha )}$ is a linear and bounded operator. □

4. Constrained Quantum MKZ Fractal Approximation

When we are interested in the computation of energy associated with a wave-function in the time-independent Schrödinger equation, then the energy must be non-negative [37]. Similarly, one may be interested in a non-negative solution of a q-difference equation [38], of q-fractional order differential equations [39], or the q-heat and q-wave equation [40]. As quantum fractal functions are more general than the classical q-functions, one can search for non-negative quantum MKZ fractal function solutions to these problems. For this reason, we study constrained approximation by quantum MKZ fractal functions in the following.

Theorem 3.

Let $f\in C\left(I\right)$ and $f\ge 0$ on I. Let $\Delta :=\{x_1,x_2,\dots ,x_N\}$ be a partition of I satisfying the condition $x_1<x_2<\cdots <x_N$ and let ${\left\{q_n\right\}}_{n=1}^{\infty }$ be a sequence in (0,1] such that $\underset{n\to \infty }{lim}{q}_n=1$. Then, the sequence ${\left\{{\mathcal{F}}_{(q_n,n)}\right\}}_{n=1}^{\infty }$ of IFSs determines a sequence ${\left\{f_n^{(q_n,\alpha )}\right\}}_{n=1}^{\infty }$ of non-negative quantum MKZ fractal functions that converges uniformly to f if the scaling functions ${\alpha }_i\left(x\right)$ are chosen to satisfy the following two conditions:

1. 

${\parallel \alpha \parallel }_{\infty }<1$;

2. 

For all $i\in {\mathbb{N}}_{N-1}$,

$$\begin{array}{ccc}\hfill max\left\{\frac{-\varphi (f,i)}{C_n-{\varphi }_n},\right.& \left.-\frac{C_n-\mathsf{\Phi }(f,i)}{{\mathsf{\Phi }}_n}\right\}\le {\alpha }_i\left(x\right)\hfill & \hfill \\ \hfill \hspace{1em}& \le min\left\{\frac{\varphi (f,i)}{{\mathsf{\Phi }}_n},\frac{C_n-\mathsf{\Phi }(f,i)}{C_n-{\varphi }_n}\right\},\hspace{1em}x\in I.\hfill \end{array}$$

(20)

Here, we set $\varphi (f,i):=\underset{x\in I}{min}f\left(u_i\left(x\right)\right)$, $\mathsf{\Phi }(f,i):=\underset{x\in I}{max}f\left(u_i\left(x\right)\right)$, ${\varphi }_n:=\underset{x\in I}{min}{M}_{n,q_n}f\left(x\right)$, and ${\mathsf{\Phi }}_n:=\underset{x\in I}{max}{M}_{n,q_n}f\left(x\right)$. $C_n$ denotes a positive real number strictly larger than $max\{{\varphi }_n,\parallel f{\parallel }_{\infty }\}$.

Proof. 

By Theorem 1, there exists a sequence ${\left\{f_n^{(q_n,\alpha )}\right\}}_{n=1}^{\infty }$ of quantum MKZ fractal functions that converges to f. Now suppose that $f\in C\left(I\right)$ and $f\ge 0$ on I. It is known (cf. for instance, [34]) that $M_{n,q}$ is a positive linear operator and thus $M_{n,q}f\ge 0$ on I. This implies that ${\mathsf{\Phi }}_n$ is positive. We have that

$$\begin{array}{cc}\hfill f_n^{(q_n,\alpha )}\left(u_i\left(x\right)\right)& =v_{n,i}(x,f_n^{(q_n,\alpha )}\left(x\right))\hfill \\ & =f\left(u_i\left(x\right)\right)+{\alpha }_i\left(x\right)(f_n^{(q_n,\alpha )}\left(x\right)-M_{n,q_n}f\left(x\right)),\hspace{1em}x\in I.\hfill \end{array}$$

(21)

Clearly, $v_{n,i}(x,f_n^{(q_n,\alpha )}\left(x\right))\in [0,C_n],i\in {\mathbb{N}}_{N-1}$, iff $f_n^{(q_n,\alpha )}\left(u_i\left(x\right)\right)\in [0,C_n]$, for all $x\in I$. Note that I is the attractor of the IFS $\{I;u_i\left(x\right),i\in \mathbb{N}\}$. As $f_n^{(q_n,\alpha )}$ is defined recursively, we only need to show that $f_n^{(q_n,\alpha )}\left(u_i\left(x\right)\right)\ge 0$ whenever $f_n^{(q_n,\alpha )}\left(x\right)\ge 0$ using suitable restrictions on the functions ${\alpha }_i$.

To this end, suppose $(x,y)\in I\times [0,C_n]$ and ${\alpha }_i$, $i\in {\mathbb{N}}_{N-1}$, is such that $|{\alpha }_i\left(x\right)|<1$, for all $x\in I$. Now, there are two cases:

Case 1: $0\le {\alpha }_i\left(x\right)<1$, for all $x\in I$.

Then, $0\le y\le C_n$ yields $q_{n,i}\le {\alpha }_i\left(x\right)y+q_{n,i}\le C_n{\alpha }_i\left(x\right)+q_{n,i}$. Therefore,

$$0\le v_{n,i}(x,y)={\alpha }_i\left(x\right)y+q_{n,i}\le C_n,\hspace{1em}i\in {\mathbb{N}}_{N-1},$$

is true for all $(x,y)\in I\times [0,C_n]$ if

$$\left.\begin{array}{c}f\left(u_i\left(x\right)\right)-{\alpha }_i\left(x\right)M_{n,q_n}(f,x)\ge 0,\hfill \\ f\left(u_i\left(x\right)\right)-{\alpha }_i\left(x\right)M_{n,q_n}(f,x)\le C_n(1-{\alpha }_i\left(x\right)),\hspace{1em}x\in I.\hfill \end{array}\right\}$$

(22)

As $f\left(u_i\left(x\right)\right)\ge \varphi (f,i)$ and $M_{n,q_n}(f,x)\le {\mathsf{\Phi }}_n,$ it is easy to verify that

$$f\left(u_i\left(x\right)\right)-{\alpha }_i\left(x\right)M_{n,q_n}(f,x)\ge 0$$

if $\varphi (f,i)-{\alpha }_i\left(x\right){\mathsf{\Phi }}_n\ge 0$, which is equivalent to the condition

$$0\le {\alpha }_i\left(x\right)\le \frac{\varphi (f,i)}{{\mathsf{\Phi }}_n}.$$

Similarly, using $f\left(u_i\left(x\right)\right)\le \mathsf{\Phi }(f,i)$ and $M_{n,q_n}(f,x)\ge {\varphi }_n$, the second inequality in (22) is true, whenever $\mathsf{\Phi }(f,i)-{\alpha }_i\left(x\right){\varphi }_n\le C_n(1-{\alpha }_i\left(x\right))$, which is equivalent to

$$0\le {\alpha }_i\left(x\right)\le \frac{C_n-\mathsf{\Phi }(f,i)}{C_n-{\varphi }_n}.$$

Combining, these two sub-cases, we obtain that $v_{n,i}(x,y)\in [0,C_n]$, $i\in {\mathbb{N}}_{N-1}$, for all $(x,y)\in I\times [0,C_n]$ if

$$0\le {\alpha }_i\left(x\right)\le min\left\{\frac{\varphi (f,i)}{{\mathsf{\Phi }}_n},\frac{C_n-\mathsf{\Phi }(f,i)}{C_n-{\varphi }_n}\right\}.$$

Case 2: $-1<{\alpha }_i\left(x\right)\le 0$, for all $x\in I$.

Then $0\le y\le C_n$ yields $C_n{\alpha }_i\left(x\right)+q_{n,i}\le {\alpha }_i\left(x\right)y+q_{n,i}\le q_{n,i}$. Hence,

$$0\le v_{n,i}(x,y)={\alpha }_i\left(x\right)y+q_{n,i}\le C_n,\hspace{1em}i\in {\mathbb{N}}_{N-1},$$

is valid for all $(x,y)\in I\times [0,C_n]$ whenever

$$\left.\begin{array}{c}f\left(u_i\left(x\right)\right)-{\alpha }_i\left(x\right)M_{n,q_n}f\left(x\right)\le C_n,\hfill \\ C_n{\alpha }_i\left(x\right)+f\left(u_i\left(x\right)\right)-{\alpha }_i\left(x\right)M_{n,q_n}f\left(x\right)\ge 0,\hspace{1em}x\in I.\hfill \end{array}\right\}$$

(23)

As $f\left(u_i\left(x\right)\right)\le \mathsf{\Phi }(f,i)$ and $M_{n,q_n}(f,x)\le {\mathsf{\Phi }}_n$, then, from the first inequality in (23), we obtain $f\left(u_i\left(x\right)\right)-{\alpha }_i\left(x\right)M_{n,q_n}(f,x)\le \mathsf{\Phi }(f,i)-{\alpha }_i\left(x\right){\mathsf{\Phi }}_n\le C_n$. Hence,

$${\alpha }_i\left(x\right)\ge -\frac{C_n-\mathsf{\Phi }(f,i)}{{\mathsf{\Phi }}_n}.$$

Again, due to the fact that $M_{n,q_n}f\left(x\right)\ge {\varphi }_n$ and $f\left(u_i\left(x\right)\right)\ge \varphi (f,i)$, we observe that the second inequality in (23) holds if

$${\alpha }_i\left(x\right)\ge \frac{-\varphi (f,i)}{C_n-{\varphi }_n}.$$

Combining these two results, we conclude that $v_{n,i}(x,y)\in [0,C_n]$, $i\in {\mathbb{N}}_{N-1}$, for all $(x,y)\in I\times [0,C_n]$ if

$$max\left\{\frac{-\varphi (f,i)}{C_n-{\varphi }_n},-\frac{C_n-\mathsf{\Phi }(f,i)}{{\mathsf{\Phi }}_n}\right\}\le {\alpha }_i\left(x\right)\le 0.$$

Both cases yield the desired restrictions on the functions ${\alpha }_i$ in (20). □

By Theorem 3, it is found that for every continuous function f on I with $f\ge 0$ on I, there exists a sequence of non-negative quantum MKZ fractal functions which converges to f in the sup-norm.

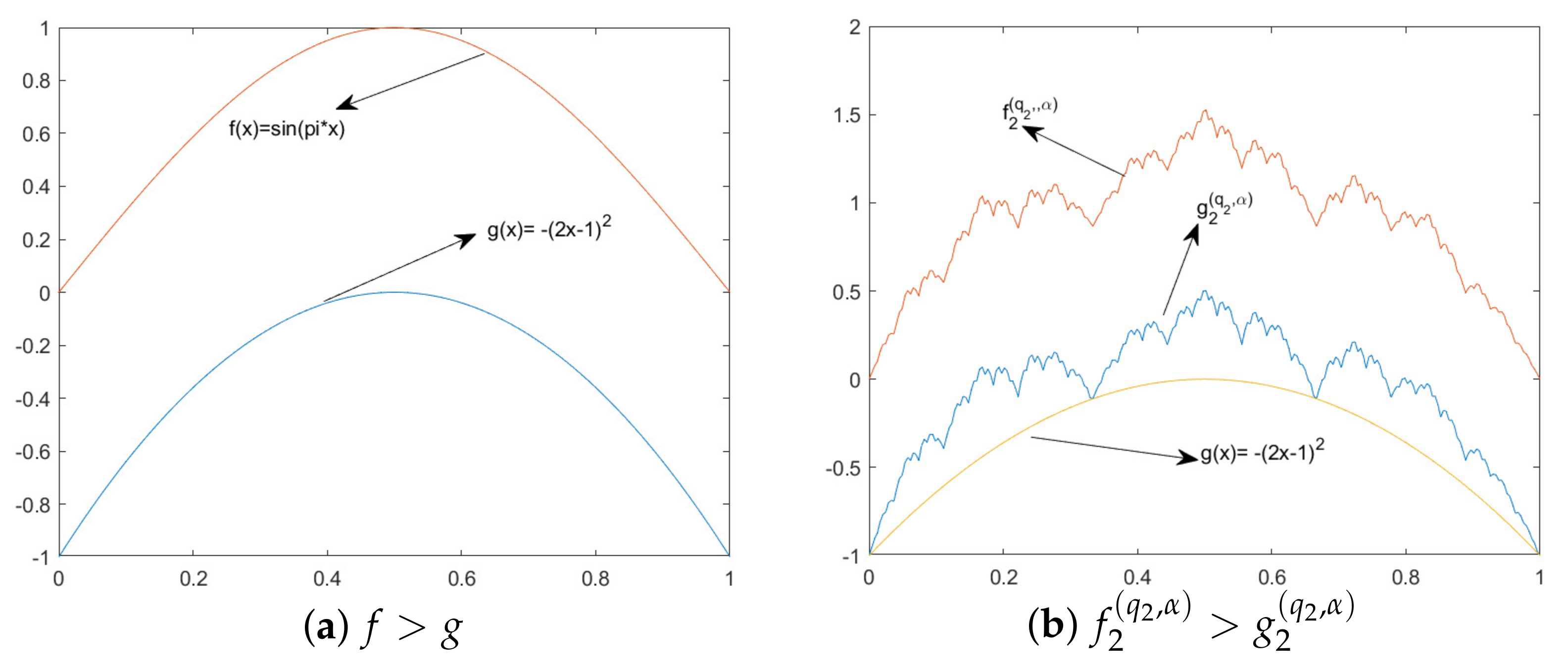
Example 2.

Here, we give an example to illustrate Theorem 3. Let $I:=[0,1]$ and let $f:I\to [0,2]$, $x\mapsto sin\left(\pi x\right)+1$. Further, let $\Delta :=\{0,\frac{1}{3},\frac{2}{3},1\}$ and define ${\alpha }_1\left(x\right):=0.1298/(1+exp(-10x))$, ${\alpha }_2\left(x\right):=0.100/(1+exp(-10x))$, and ${\alpha }_3\left(x\right):=0.2168/(1+exp(-10x))$.

Assume that $q_n:=\frac{2}{\pi }arctan\left(n\right)$, $n\in \mathbb{N}$. Then, the scaling functions ${\alpha }_i$ and the sequence ${\left\{q_n\right\}}_{n=1}^{\infty }$ fulfill the conditions stated in Theorem 3. In Figure 2a, the fractal quantum MKZ fractal function $f_2^{(q_2,\alpha )}$ is shown and provides a positive approximation for f.

Figure 2. Positivity of MKZ fractal function according to Theorem 3. A positive quantum MKZ fractal function (a) and a non−positive quantum MKZ fractal function (b).

If we choose ${\alpha }_1\left(x\right):=0.7$, ${\alpha }_2\left(x\right):=-0.9$, and ${\alpha }_3\left(x\right):=0.9$ instead, then α is not consistent with the conditions given in (20). From Figure 2b, we further observe that the MKZ $(q,\alpha )$-fractal function $f_2^{(q_2,\alpha )}$ is non-positive in nature for this choice of α.

The following theorem gives the existence of a double sequence of positive quantum MKZ fractal functions which converges to f in the sup-norm.

Theorem 4.

Let ${\left\{f_k\right\}}_{k=1}^{\infty }$ be a sequence of positive functions in $C\left(I\right)$ that converges to $f\in C\left(I\right)$. Let $\Delta :=\{x_1,x_2,\dots ,x_N\}$ be a partition of I satisfying the condition $x_1<x_2<\cdots <x_N$ and let ${\left\{q_n\right\}}_{n=1}^{\infty }$ be a sequence in (0,1] such that $\underset{n\to \infty }{lim}{q}_n=1$.

Suppose that $u_i:I\to I_i$, $i\in {\mathbb{N}}_{N-1}$, are affine maps of the form $u_i\left(x\right)=a_{i}x+b_i$ satisfying the conditions $u_i\left(x_1\right)=x_i$, $u_i\left(x_N\right)=x_{i+1}$. Let

$$v_{k,n,i}^{†}(x,y):=f_k\left(u_i\left(x\right)\right)+{\alpha }_i\left(x\right)(y-M_{n,q_n}(f_k,x)),\hspace{1em}i\in {\mathbb{N}}_{N-1}.$$

Let $f_{k,n}^{(q_n,\alpha )}$ be the MKZ fractal function associated with the IFS

$${\mathcal{F}}_{k,(q_n,n)}^{†}:=\{I\times K;(u_i\left(x\right),v_{k,n,i}^{†}(x,y)),i\in {\mathbb{N}}_{N-1}\}.$$

Then, the double sequence of IFSs ${\{{\{{\mathcal{F}}_{k,(q_n,n)}^{†}\}}_{n=1}^{\infty }\}}_{k=1}^{\infty }$ generates a double sequence ${\{{\{f_{k,n}^{(q_n,\alpha )}\}}_{n=1}^{\infty }\}}_{k=1}^{\infty }$ of positive quantum MKZ fractal functions which converges to f in sup-norm provided that all scaling functions ${\alpha }_i$ obey the conditions:

1. 

$\parallel {\alpha }_i{\parallel }_{\infty }<1$;

2. 

For all $i\in {\mathbb{N}}_{N-1}$,

$$\begin{array}{cc}\hfill max& \left\{\frac{-\varphi (f_k,i)}{C_{n,k}^{†}-{\varphi }_{n,k}\left(f_k\right)},-\frac{C_{n,k}^{†}-\mathsf{\Phi }(f_k,i)}{{\mathsf{\Phi }}_{n,k}\left(f_k\right)}\right\}\le {\alpha }_i\left(x\right)\hfill \\ \hfill \hspace{1em}& \le min\left\{\frac{\varphi (f,i)}{{\mathsf{\Phi }}_{n,k}\left(f_k\right)},\frac{C_{n,k}^{†}-\mathsf{\Phi }(f_k,i)}{C_{n,k}^{†}-{\varphi }_{n,k}\left(f_k\right)}\right\},\hspace{1em}x\in I.\hfill \end{array}$$

(24)

where $\varphi (f_k,i):=\underset{x\in I}{min}{f}_k\left(u_i\left(x\right)\right)$, $\mathsf{\Phi }(f_k,i):=\underset{x\in I}{max}{f}_k\left(u_i\left(x\right)\right)$, ${\varphi }_{n,k}\left(f_k\right)$$:=\underset{x\in I}{min}{M}_{n,q}(f_k,x)$, and ${\mathsf{\Phi }}_{n,k}\left(f_k\right):=\underset{x\in I}{max}{M}_{n,q}(f_k,x)$. Here, $C_{n,k}^{†}$ denotes a positive real number strictly greater than $max\{{\varphi }_{n,k}\left(f_k\right),\parallel f_k{\parallel }_{\infty }\}$.

Proof. 

It follows easily from Theorem 3 that the MKZ fractal functions $f_{k,n}^{(q_n,\alpha )}$ are positive on I if the scaling functions ${\alpha }_i$, $i\in {\mathbb{N}}_{N-1}$, obey the inequalities in (24).

Let $ϵ>0$. As ${\left\{f_k\right\}}_{k=1}^{\infty }$ is a sequence of positive functions in $C\left(I\right)$ that converges to f in ${\parallel ·\parallel }_{\infty }$, there exists a natural number $k_1\in \mathbb{N}$ such that

$$\parallel f_k{-f\parallel }_{\infty }<\frac{ϵ}{2},\hspace{1em}\forall k\ge k_1.$$

(25)

Employing Theorem 2 of [33], we can see that for each $k\in \mathbb{N}$, $\parallel M_{n,q_n}{f}_k-f_k{\parallel }_{\infty }\to 0$, as $n\to \infty$. Thus, there exists a $k_2\in \mathbb{N}$ such that

$$\parallel M_{n,q_n}{f}_k-f_k{\parallel }_{\infty }<\frac{ϵ(1-\parallel \alpha {\parallel }_{\infty })}{{2\parallel \alpha \parallel }_{\infty }},\forall n\ge k_2.$$

(26)

Given that $f_{k,n}^{(q_n,\alpha )}$ is the MKZ fractal function obtained from the IFS ${\mathcal{F}}_{k,n}^{†}$, $f_{k,n}^{(q_n,\alpha )}$ satisfies the functional equation

$$\begin{array}{c}\hfill f_{k,n}^{(q_n,\alpha )}=f_k+\sum _{i=1}^{N-1}({\alpha }_i\circ u_i^{-1})(f_{k,n}^{(q_n,\alpha )}\circ u_i^{-1}-M_{n,q_n}{f}_k\circ u_i^{-1}){\chi }_{u_i\left(I\right)}\end{array}$$

(27)

on I. It is easy to derive the following estimate from (27):

$$\parallel f_{k,n}^{(q_n,\alpha )}-f_k{\parallel }_{\infty }\le \frac{{\parallel \alpha \parallel }_{\infty }}{(1-\parallel \alpha {\parallel }_{\infty })}{\parallel f_k-M_{n,q_n}{f}_k\parallel }_{\infty }.$$

(28)

From (26) and (28), we obtain

$$\parallel f_{k,n}^{(q_n,\alpha )}-f_k{\parallel }_{\infty }<\frac{ϵ}{2},\hspace{1em}\forall n\ge k_2.$$

(29)

Combining (25) and (29) shows that for a given $ϵ>0$, there exists a $k_0:=max\{k_1,k_2\}$ such that

$$\parallel f_{k,n}^{(q_n,\alpha )}{-f\parallel }_{\infty }<ϵ,\hspace{1em}\forall k,n\ge k_0,$$

confirming that the sequence ${\{{\{f_{k,n}^{(q_n,\alpha )}\}}_{n=1}^{\infty }\}}_{k=1}^{\infty }$ converges uniformly to f. □

The following theorem gives the existence of a one-sided sequential approximation by MKZ fractal functions.

Theorem 5.

Let $f,g\in C\left(I\right)$ with $f\ge g$ on I. Let $\Delta :=\{x_1,x_2,\dots ,x_N\}$ be a partition of I satisfying the condition $x_1<x_2<\cdots <x_N$ and let ${\left\{q_n\right\}}_{n=1}^{\infty }$ be a sequence in $(0,1]$ such that $\underset{n\to \infty }{lim}{q}_n=1$. For all $n\in \mathbb{N}$, let $f_n^{(q_n,\alpha )}$ denote the MKZ fractal functions associated with the IFS ${\mathcal{F}}_n$.

Then, the sequence of IFSs ${\left\{{\mathcal{F}}_n\right\}}_{n=1}^{\infty }$ determines a sequence of MKZ fractal functions ${\{f_n^{(q_n,\alpha )}\}}_{n=1}^{\infty }$ with $f_n^{(q_n,\alpha )}\ge g$ on I, $n\in \mathbb{N}$, and this sequence converges uniformly to f, provided that the scaling vector α of each $f_n^{(q_n,\alpha )}$ satisfies the following conditions:

1. 

${\parallel \alpha \parallel }_{\infty }<1$;

2. 

For each $i\in {\mathbb{N}}_{N-1}$,

$$0\le {\alpha }_i\left(x\right)\le min\left\{\frac{\varphi (f-g,i)}{{\mathsf{\Phi }}_n\left(f\right)-\varphi \left(g\right)},1\right\},\hspace{1em}x\in I,$$

(30)

where $\varphi (f-g,i):=\underset{x\in I}{min}(f-g)\left(u_i\left(x\right)\right)$, ${\mathsf{\Phi }}_n\left(f\right):=\underset{x\in I}{max}{M}_{n,q_n}f\left(x\right)$, and $\varphi \left(g\right):=\underset{x\in I}{min}g\left(x\right))$.

Proof. 

By the construction of the MKZ fractal function, we observe that $f_n^{(q_n,\alpha )}$ satisfies the following functional equation for $x\in I$:

$$\begin{array}{c}\hfill f_n^{(q_n,\alpha )}\left(x\right)=f\left(x\right)+\sum _{i=1}^{N-1}{\alpha }_i(u_i^{-1}\left(x\right))(f_n^{(q_n,\alpha )}\left(u_i^{-1}\left(x\right)\right)-M_{n,q_n}f\left(u_i^{-1}\left(x\right)\right)){\chi }_{u_i\left(I\right)}\left(x\right).\end{array}$$

(31)

This functional equation is a rule to obtain the values of $f_n^{(q_n,\alpha )}$ at ${(N-1)}^{r+2}+1$ distinct points in I at the $(r+1)$-th iteration using the value of $f_n^{(q_n,\alpha )}$ at ${(N-1)}^{r+1}+1$ points in I at the r-th iteration. Thus, if we can show that the result is true at the first iteration, then it is true for all subsequent iterations.

We begin the iteration process at the nodal points $x_i$, $i\in \mathbb{N}$, where $f_n^{(q_n,\alpha )}\ge$g as $f_n^{(q_n,\alpha )}$ interpolates f at these nodes and $f\ge g$. Now, we want to verify that $f_n^{(q_n,\alpha )}\circ u_i\ge g\circ u_i$ on $u_i\left(I\right)$. By (31), this is equivalent to proving that

$$f\circ u_i+{\alpha }_i{f}_n^{(q_n,\alpha )}-{\alpha }_i{M}_{n,q_n}f-g\circ u_i\ge 0\hspace{1em}\mathrm{on} u_i\left(I\right).$$

(32)

If we choose the functions ${\alpha }_i$ to be positive, then the above inequality is true provided that

$$f\circ u_i+{\alpha }_{i}g-{\alpha }_i{M}_{n,q_n}f-g\circ u_i\ge 0.$$

The sufficient condition for the validity of the above inequality is

$$0\le {\alpha }_i\left(x\right)\le min\left\{\frac{\varphi (f-g,i)}{{\mathsf{\Phi }}_n\left(f\right)-\varphi \left(g\right)}\right\},\hspace{1em}x\in I.$$

Therefore, if the functions ${\alpha }_i$, $i\in {\mathbb{N}}_{N-1}$, are chosen according to (30), then $f_n^{(q_n,\alpha )}\ge g$ on I. □

Example 3.

Let $f\left(x\right):=0.5sin\left(4\pi x\right)+1$ and $g\left(x\right):=-0.5{(2x-1.1)}^2$ be two continuous functions defined on $I:=[0,1]$ and let $\Delta :=\{0,\frac{1}{3},\frac{2}{3},1\}$ be a uniform partition of I. Further, let $q_n:=\frac{2}{\pi }arctan\left(n\right)$, $n\in \mathbb{N}$.

If we take ${\alpha }_1\left(x\right):=0.3950/(1+exp(-10x))$, ${\alpha }_2\left(x\right):=0.3550/(1+exp(-10x))$, and ${\alpha }_3\left(x\right):=0.2774/(1+exp(-10x))$, then the scaling vector α satisfies the required conditions (30) in Theorem 5. Figure 3a shows the MKZ fractal function $f_2^{(q_2,\alpha )}$ and verifies that $f_2^{(q_2,\alpha )}\ge g$ on I.

Figure 3. One−sided approximation by MKZ fractal function according to Theorem 5. $\alpha$ satisfies the sufficient condition (33) (a) and $\alpha$ does not satisfy (33) (b)

Similarly, one can vary n to construct one-sided approximants $f_n^{(q_n,\alpha )}\ge g$ on I. But when ${\alpha }_1\left(x\right):=0.4$, ${\alpha }_2\left(x\right):=0.355$, and ${\alpha }_3\left(x\right):=0.8$, then the scaling vector α does not satisfy condition (33). In Figure 3b, it is shown that for this choice of α, the MKZ fractal function obeys $f_2^{(q_2,\alpha )}\ngeqq g$ on I.

Corollary 1.

Let $f,g\in C\left(I\right)$ with $f\ge g$ on I. Let $\Delta :=\{x_1,x_2,\dots ,x_N\}$ be a partition of I satisfying the condition $x_1<x_2<\cdots <x_N$ and let ${\left\{q_n\right\}}_{n=1}^{\infty }$ be a sequence in $(0,1]$ such that $\underset{n\to \infty }{lim}{q}_n=1$. Then, there exist sequences ${\{f_n^{(q_n,\alpha )}\}}_{n=1}^{\infty }$ and ${\{g_n^{(q_n,\alpha )}\}}_{n=1}^{\infty }$ of $(q,\alpha )$-fractal functions which converge to f and g, respectively, and which satisfy $f_n^{(q_n,\alpha )}\ge g_n^{(q_n,\alpha )}$ on I, whenever the scaling functions ${\alpha }_i$ are chosen according to

$$0\le {\alpha }_i\left(x\right)\le min\left\{\frac{\varphi (f-g,i)}{{\mathsf{\Phi }}_n(f-g)},1\right\},\hspace{1em}i\in {\mathbb{N}}_{N-1}\hspace{1em}x\in I,$$

(33)

where $\varphi (f-g,i):=\underset{x\in I}{min}(f-g)\left(u_i\left(x\right)\right)$ and ${\mathsf{\Phi }}_n(f-g):=\underset{x\in I}{max}{M}_{n,q_n}(f-g)\left(x\right)$.

Proof. 

The corollary follows immediately from Theorem 5 by choosing f as $f-g$ and $g=0$. □

Example 4.

In this example, we illustrate Corollary 1. To this end, let $f\left(x\right):=sin\left(\pi x\right)$ and $g\left(x\right):=-{(2x-1)}^2$, $x\in I:=[0,1]$. Let $\Delta :=\{0,\frac{1}{3},\frac{2}{3},1\}$ and choose ${\alpha }_1\left(x\right):=0.6/(1+exp(-8x))$, ${\alpha }_2\left(x\right):=0.6/(1+exp(-7x))$, and ${\alpha }_3\left(x\right):=0.6/(1+x^2)$. Further, let $q_n=\frac{2}{\pi }arctan\left(n\right)$, $n\in \mathbb{N}$. Then f and g, the scaling functions ${\alpha }_i$, and ${\left\{q_n\right\}}_{n=1}^{\infty }$ satisfy the required conditions in Corollary 1. (See, also Figure 4a). Figure 4b depicts the quantum MKZ fractal functions $f_2^{(q_2,\alpha )}\ge g_2^{(q_2,\alpha )}$ on I.

Figure 4. MKZ fractal functions preserving positivity.

Theorem 6.

Let $f\in C\left(I\right)$ be convex and ${\alpha }_i\left(x\right)\ge 0$, for all $x\in I,$$i\in {\mathbb{N}}_N.$ Then $f_n^{(q,\alpha )}\left(x\right)$$\le f\left(x\right)$ for all $x\in I$ and the sequence ${\{f_n^{(q,\alpha )}\left(x\right)\}}_{n=1}^{\infty }$ is non-increasing for each $x\in I$.

Proof. 

Using the functional Equation (15) of $f_n^{(q,\alpha )}$ and keeping $f\left(x\right)-M_{n}f\left(x\right)\ge 0$ (Theorem 3.2, [34]) in mind, we conclude that for $x\in I$, $i\in {\mathbb{N}}_N$,

$$\begin{array}{cc}\hfill (f_n^{(q,\alpha )}-f)\left(u_i\left(x\right)\right)& ={\alpha }_i\left(x\right)(f_n^{\alpha }\left(x\right)-f\left(x\right))+{\alpha }_i(f\left(x\right)-M_{n}f\left(x\right))\hfill \\ \hfill \hspace{1em}& \le {\alpha }_i\left(x\right)(f_n^{\alpha }\left(x\right)-f\left(x\right)).\hfill \end{array}$$

(34)

By means of (34), we conclude that $f_n^{\alpha }\left(x\right)-f\left(x\right)\le 0$ ensuring that $(f_n^{(q,\alpha )}-f)\left(u_i\left(x\right)\right)\le 0$. As the fractal function $f_n^{(q,\alpha )}$ is constructed iteratively, we obtain $f_n^{(q,\alpha )}\left(x\right)\le f\left(x\right)$ for all $x\in I$.

(15) and the functional equations of $f_{n+1}^{(q,\alpha )}$ and $f_n^{(q,\alpha )}$, respectively, yield

$$\begin{array}{cc}\hfill f_{n+1}^{(q,\alpha )}\left(u_i\left(x\right)\right)& =f\left(u_i\left(x\right)\right)+{\alpha }_i\left(x\right)(f_{n+1}^{(q,\alpha )}\left(x\right)-M_{n+1,q}f\left(x\right)),x\in I,\hfill \\ \hfill f_n^{(q,\alpha )}\left(u_i\left(x\right)\right)& =f\left(u_i\left(x\right)\right)+{\alpha }_i\left(x\right)(f_n^{(q,\alpha )}\left(x\right)-M_{n,q}f\left(x\right)),x\in I.\hfill \end{array}$$

Note that both $f_{n+1}^{(q,\alpha )}$ and $f_n^{(q,\alpha )}$ join up at the interpolation data points and that subsequent values are generated iteratively from the same data. Taking their difference and using the fact that $M_{n+1}f\left(x\right)-M_{n}f\left(x\right)\le 0$ for all $x\in I$ (cf. Theorem 3.3, [34]), we obtain that, for all $x\in I$, and $i\in {\mathbb{N}}_N$,

$$\begin{array}{cc}\hfill (f_{n+1}^{(q,\alpha )}-f_n^{(q,\alpha )})\left(u_i\left(x\right)\right)& \le {\alpha }_i\left(x\right)(f_{n+1}^{(q,\alpha )}-f_n^{(q,\alpha )})\left(x\right)+{\alpha }_i\left(x\right)(M_{n+1}f-M_{n}f)\left(x\right)\hfill \\ \hfill \hspace{1em}& \le {\alpha }_i\left(x\right)(f_{n+1}^{(q,\alpha )}-f_n^{(q,\alpha )})\left(x\right).\hfill \end{array}$$

(35)

As the right hand side of (35) is zero at the first iteration, it is ensured that $f_{n+1}^{(q,\alpha )}\left(x\right)\le f_n^{(q,\alpha )}\left(x\right)$ for all $x\in I$. □

Remark 1.

Using the hypotheses of Theorem 1 and Theorem 6, we can construct a non-increasing sequence of positive quantum MKZ fractal functions converging to $f\in C\left(I\right)$, provided f is convex and non-negative.

5. Approximation with Quantum MKZ Fractal Müntz Polynomials

Let $\Lambda :={\left\{{\lambda }_i\right\}}_{i=1}^{\infty }$, with ${\lambda }_i\ne {\lambda }_j$ if $i\ne j$, ${\lambda }_i>0$, and ${\lambda }_0:=0$. The set of real-valued monomials

$${\Lambda }_m:=\{x^{{\lambda }_0},x^{{\lambda }_1},\dots ,x^{{\lambda }_m}\}$$

is called a finite Müntz system. The linear space

$$M_m(\Lambda ):=\mathrm{span}\left({\Lambda }_m\right)=\mathrm{span}\{x^{{\lambda }_0},x^{{\lambda }_1},\dots ,x^{{\lambda }_m}\}$$

is known as a (finite) Müntz space and

$$M(\Lambda ):=\bigcup _{m=0}^{\infty }{M}_m(\Lambda )$$

is referred to as the Müntz system corresponding to $\Lambda$.

Definition 1.

Let $I:=[0,1]$ and let $\Delta :=\{x_1,x_2,\dots ,x_N\}$ be a partition of I satisfying $0=x_1<x_2<\cdots <x_N=1$. Suppose $\alpha :=({\alpha }_1,\dots ,{\alpha }_{N-1})$, where ${\alpha }_i$ is a bounded function on I with $\parallel {\alpha }_i{\parallel }_{\infty }<1$.

A quantum MKZ fractal Müntz polynomial is a finite linear combination of functions ${\left(x^{{\lambda }_i}\right)}_n^{(q,\alpha )}$, ${\lambda }_i\in \Lambda$, $i\in \mathbb{N}$, where

$${\left(x^{{\lambda }_i}\right)}_n^{(q,\alpha )}:={\mathcal{F}}_{\Delta ,M_{n,q}}^{(q,\alpha )}\left(x^{{\lambda }_i}\right)={\mathcal{F}}_n^{(q,\alpha )}\left(x^{{\lambda }_i}\right)$$

is a quantum MKZ fractal Müntz monomial.

For $x^{{\lambda }_j}\in C[0,1]$, we have that

$$\begin{array}{cc}\hfill {\mathcal{F}}_n^{(q,\alpha )}\left(x^{{\lambda }_j}\right)& =x^{{\lambda }_j}+\sum _{i=1}^{N-1}{\alpha }_i\left(u_i^{-1}\left(x\right)\right)({\mathcal{F}}_n^{(q,\alpha )}{\left(u_i^{-1}\left(x\right)\right)}^{{\lambda }_j})-\hfill \\ & M_{n,q}{(u_i^{-1}\left(x\right))}^{{\lambda }_j}){\chi }_{u_i\left(I\right)}\left(x\right),\hspace{1em}x\in I,n\in {\mathbb{N}}_{N-1}.\hfill \end{array}$$

Let $\tilde{K}:=\{{\left(x^{{\lambda }_i}\right)}_n^{(q,\alpha )}:i,n\in \mathbb{N}\}$. Then, the set $M(\Lambda )=\mathrm{span}(\tilde{K})$ is termed a quantum MKZ fractal Müntz space associated with $\Lambda$.

Theorem 7.

(Fractal version of the full Müntz theorem in $C[0,1])$: Let $\Delta :=\{x_1,x_2,\dots ,x_N\}$ be a partition of $I:=[0,1]$ satisfying $0=x_1<x_2<\cdots <x_N=1$ and let ${\left\{q_n\right\}}_{n=1}^{\infty }$ be a sequence in (0,1] such that $\underset{n\to \infty }{lim}{q}_n=1$. Let $\alpha :=({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_{N-1})$, where ${\alpha }_i$ is a bounded function on I with $\parallel {\alpha }_i{\parallel }_{\infty }<1$, $i\in {\mathbb{N}}_{N-1}$. Further, let $\Lambda ={\left\{{\lambda }_i\right\}}_{i=1}^{\infty }$ be a sequence of distinct positive real numbers. Then, the set

$$S:=\bigcup _{n=1}^{\infty }\bigcup _{m=1}^{\infty }span\{1,{\left(x^{{\lambda }_1}\right)}_n^{(q_n,\alpha )},\cdots ,{\left(x^{{\lambda }_m}\right)}_n^{(q_n,\alpha )}\}$$

is dense in $C[0,1]$ with respect to the sup norm if

$$\sum _{i=1}^{\infty }\frac{{\lambda }_i}{{\lambda }_i^2+1}=\infty .$$

(36)

Proof. 

Let $ϵ>0$ and $f\in C[0,1]$ be given. Then, by the classical Müntz theorem [41], we know that $span{\displaystyle \bigcup _{m=0}^{\infty }}\{1,x^{{\lambda }_1},\cdots ,x^{{\lambda }_m}\}$ is dense in $C[0,1]$ with respect to the sup-norm if ${\displaystyle \sum _{i=1}^{\infty }}\frac{{\lambda }_i}{{\lambda }_i^2+1}$, where ${\left\{{\lambda }_i\right\}}_{i=1}^{\infty }$ is a sequence of distinct positive real numbers. Hence, there exists a Müntz polynomial $p\left(x\right)={\displaystyle \sum _{s=0}^l}{a}_s{x}^{{\lambda }_s},a_s\in \mathbb{R}$, such that

$${\parallel f-p\parallel }_{\infty }<\frac{ϵ}{2}.$$

(37)

Since p is continuous, $\parallel {\mathcal{F}}_n^{(q_n,\alpha )}{\left(p\right)-p\parallel }_{\infty }\to 0$ as $n\to \infty$ by Theorem 1. Therefore, there exists a natural number $n_1$ such that

$$\parallel p_n^{(q_n,\alpha )}{-p\parallel }_{\infty }<\frac{ϵ}{2},\hspace{1em}\forall n\ge n_1,$$

(38)

where ${\mathcal{F}}_n^{(q,\alpha )}\left(p\right)=p_n^{(q,\alpha )}={\displaystyle \sum _{s=0}^l}{a}_s{\left(x^{{\lambda }_s}\right)}_n^{(q,\alpha )}$. Now, by (37) and (38),

$$\parallel p_n^{(q_n,\alpha )}{-f\parallel }_{\infty }\le \parallel p_n^{(q_n,\alpha )}{-f\parallel }_{\infty }+{\parallel f-p\parallel }_{\infty }<\frac{ϵ}{2}+\frac{ϵ}{2}=ϵ,\hspace{1em}\forall n\ge n_1.$$

Hence, there exists a sequence of quantum MKZ fractal Müntz polynomials converging to f in sup-norm; and thus, S is dense in $C[0,1]$. □

Using arguments similar to those in the proof of Theorem 7, we can prove Theorem 8 using the classical Müntz second theorem (see for instance [41,42]).

Theorem 8.

(Fractal version of Müntz second theorem in $C[0,1])$ Let $\Delta :=\{x_1,x_2,\dots ,x_N\}$ be partition of $I:=[0,1]$ satisfying $0=x_1<x_2<\cdots <x_N=1$ and let ${\left\{q_n\right\}}_{n=1}^{\infty }$ be a sequence in $(0,1]$ such that $\underset{n\to \infty }{lim}{q}_n=1$. Let $\alpha :=({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_{N-1})$ be a scaling vector, where each ${\alpha }_i$ is a bounded function on I with $\parallel {\alpha }_i{\parallel }_{\infty }<1$, $i\in {\mathbb{N}}_{N-1}$. Let ${\left\{{\lambda }_i\right\}}_{i=1}^{\infty }$ be a sequence of distinct positive real numbers such that $\underset{i\ge 1}{inf}{\lambda }_i>0$. Then, S is dense in $C[0,1]$ with respect to the sup-norm provided that

$$\sum _{i=1}^{\infty }\frac{1}{{\lambda }_i}=\infty .$$

Proof. 

Let $f\in C[0,1]$ and $ϵ>0$. Then, the classical Müntz theorem [41] ensures the existence of Müntz polynomial $p\left(x\right)$ such that ${\parallel p-f\parallel }_{\infty }<\frac{ϵ}{2}$. By (38), there exists a natural number $n_1$ such that $\parallel p_n^{(q_n,\alpha )}{-p\parallel }_{\infty }<\frac{ϵ}{2},\hspace{1em}\forall n\ge n_1$. These two inequalities imply $\parallel p_n^{(q_n,\alpha )}{-f\parallel }_{\infty }<ϵ,\hspace{1em}\forall n\ge n_1$. Hence, S is dense in $C[0,1]$ with respect to the sup norm. □

Theorem 9.

Let $\Delta :=\{x_1,x_2,\dots ,x_N\}$ where $0=x_1<x_2<\cdots <x_N=1$ be a partition of $I=[0,1]$ and let ${\left\{q_n\right\}}_{n=1}^{\infty }$ be a sequence in $(0,1]$ such that $\underset{n\to \infty }{lim}{q}_n=1$. Let $\alpha :=({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_{N-1})$ be a vector of scaling functions where ${\alpha }_i$ is a bounded function on I with $\parallel {\alpha }_i{\parallel }_{\infty }<1$, $i\in {\mathbb{N}}_{N-1}$. If $S:=\{f_s:s\in \mathbb{N}\}$ is dense in $C[0,1]$, then

$$\bigcup _{n=1}^{\infty }span\{{\mathcal{F}}_n^{(q_n,\alpha )}\left(f_s\right):s\in \mathbb{N}\}$$

is also dense in $C[0,1]$.

Proof. 

Let $f\in C[0,1]$ and $ϵ>0$ be given. By the density of the set S in $C[0,1]$, there exists a polynomial of the form $p\left(x\right)={\displaystyle \sum _{s=0}^l}{a}_s{x}^{{\lambda }_s},a_s\in \mathbb{R}$, such that ${\parallel f-p\parallel }_{\infty }<\frac{ϵ}{2}$. Using Theorem 1, we get $\parallel p_n^{(q_n,\alpha )}{-p\parallel }_{\infty }<\frac{ϵ}{2},\hspace{1em}\forall n\ge n_1$. Finally, these two inequalities result in $\parallel p_n^{(q_n,\alpha )}{-p\parallel }_{\infty }<ϵ,\hspace{1em}\forall n\ge n_1$. Therefore, S is dense in $C[0,1]$. □

6. Approximation by MKZ Fractal Functions

In this section, we investigate some approximation-theoretic properties of MKZ fractal functions and derive conditions for such functions to belong to a Lebesgue space $L^p$, $p\ge 1$.

6.1. MKZ-Fractal Approximation and Integral MKZ Fractal Functions

If we set $q=1$ in (14), then the q-MKZ series $M_{n,q}f$ becomes a classical MKZ series $M_{n}f$, which is also known as the MKZ series of $f\in C\left(I\right)$ (see, for instance, [34,43]). The MKZ series is given by the following expression:

$$\begin{array}{c}{M}_{n}f\left(x\right):=P_n\left(x\right)\sum _{k=0}^{\infty }\left(\genfrac{}{}{0pt}{}{k+n}{k}\right){(x-x_1)}^{k}f(x_1+(x_N-x_1)\frac{k}{k+n});x_1\le x<x_N,\hfill \\ M_{n}f\left(x_N\right):=f\left(x_N\right),\hfill \end{array}$$

(39)

with

$$P_n\left(x\right):={\displaystyle \frac{{(x_N-x)}^{n+1}}{{(x_N-x_1)}^{n+1}}}.$$

$M_{n}f$ satisfies the endpoint interpolation conditions

$$M_{n}f\left(x_1\right)=f\left(x_1\right)\hspace{1em}\mathrm{and}\hspace{1em}{M}_{n}f\left(x_N\right)=f\left(x_N\right).$$

(40)

The IFS with maps given by (10), where the base function is taken to be $b:=M_{n}f$, determines an $\alpha$-fractal function

$$f_n^{\alpha }:={\mathcal{F}}_{\Delta ,b}^{\alpha }\left(f\right),$$

termed an MKZ $\alpha$-fractal function associated with $f\in C\left(I\right)$. Furthermore, this MKZ $\alpha$-fractal function satisfies the functional equation

$$f_n^{\alpha }=f+\sum _{i=1}^{N-1}({\alpha }_i\circ u_i^{-1})(f_n^{\alpha }\circ u_i^{-1})-\left(M_{n}f\right)\circ (u_i^{-1}){\chi }_{u_i\left(I\right)}$$

(41)

on I.

It is easy to obtain the estimate

$$\begin{array}{c}\hfill \parallel f_n^{\alpha }{-f\parallel }_{\infty }\le \frac{{\parallel \alpha \parallel }_{\infty }}{1-{\parallel \alpha \parallel }_{\infty }}{\parallel f-M_{n}f\parallel }_{\infty }.\end{array}$$

(42)

Even if $\alpha \ne 0$, we can get the convergence of $f_n^{\alpha }$ to f as $n\to \infty$ by the following corollaries.

Corollary 2.

Let $f\in C\left(I\right)$ and $\alpha \ne 0$. Then $f_n^{\alpha }$ converges to f as $n\to \infty$, and

$$\begin{array}{c}\hfill \parallel f_n^{\alpha }{-f\parallel }_{\infty }\le \frac{31}{27}\omega \left(f,\frac{1}{\sqrt{n}}\right)\frac{{\parallel \alpha \parallel }_{\infty }}{1-{\parallel \alpha \parallel }_{\infty }},\hspace{1em}n\in \mathbb{N},\end{array}$$

where ω denotes the usual modulus of continuity of a function f.

Proof. 

Using Corollary 2.3 in reference [44],

$$\parallel f-M_n{f\parallel }_{\infty }\le \frac{31}{27}\omega (f,\frac{1}{\sqrt{n}}),$$

in (42), we get the required estimate. □

Corollary 3.

Let $f\in C^1\left(I\right)$ and $\alpha \ne 0$. Then, the uniform error between the MKZ α-fractal functions $f_n^{\alpha }$ and its germ f is given by

$$\begin{array}{c}\hfill \parallel f_n^{\alpha }{-f\parallel }_{\infty }\le \frac{2(2+3\sqrt{3})}{27\sqrt{n}}\omega \left(f,\frac{1}{\sqrt{n}}\right)\frac{{\parallel \alpha \parallel }_{\infty }}{1-{\parallel \alpha \parallel }_{\infty }},\hspace{1em}\forall n\in \mathbb{N},\end{array}$$

(43)

where ω denotes the usual modulus of continuity of f.

Proof. 

Corollary 2.5 in reference [44] yields

$$\parallel M_n{f-f\parallel }_{\infty }\le \frac{2(2+3\sqrt{3})}{27\sqrt{n}}\omega \left(f^{\prime },\frac{1}{\sqrt{n}}\right),\hspace{1em}n\in \mathbb{N}.$$

Using this estimate in (42), we obtain (43). In this case, $f_n^{\alpha }$ converges to f at a faster rate than for an $f\in C\left(I\right)$. □

Definition 2.

Let $A\in \mathbb{R}$, and $0<\beta \le 1$. Then, ${Lip}_A\beta$ is the set of all functions satisfying

$$|f\left(x_2\right)-f\left(x_1\right)|\le A|x_2-x_1{|}^{\beta },\hspace{1em}\forall x_1,x_2\in [x_0,x_N].$$

Such functions are also called uniformly hölderian with exponent β.

Corollary 4.

Let $f\in C^1\left(I\right)$ with $f^{\prime }\in {Lip}_M\beta$ for $0<\beta \le 1$. Further, let $M>0$. Then, the fractal function $f_n^{\alpha }$ defined in (41) satisfies the following estimate:

$$\begin{array}{c}\hfill \parallel f_n^{\alpha }{-f\parallel }_{\infty }\le \frac{2(2+3\sqrt{3})}{27\sqrt{n}}{n}^{\frac{-(\beta +1)}{2}}\frac{{\parallel \alpha \parallel }_{\infty }}{1-{\parallel \alpha \parallel }_{\infty }},\hspace{1em}\forall n\in \mathbb{N}.\end{array}$$

(44)

Proof. 

It is known by Corollary 2.6 of [44] that

$$\parallel M_n{f-f\parallel }_{\infty }\le \frac{2(2+3\sqrt{3})}{27\sqrt{n}}{n}^{\frac{-(\beta +1)}{2}}.$$

Employing the above estimate in (42), we obtain the required inequality. Thus, in this case, the convergence rate of $f_n^{\alpha }$ to the germ function f is faster than that for $f\in C\left(I\right)$ or $f\in C^1\left(I\right)$. □

Proposition 1.

(Cf. [43]). Given a continuous function $f:[x_0,x_N]\to \mathbb{R}$, it holds that

$$f\in {Lip}_A\beta \hspace{1em}⟺\hspace{1em}{M}_{n}f\in {Lip}_A\beta ,\hspace{1em}\forall n\in \mathbb{N},$$

where ${\left(M_n\right)}_{n\ge 1}$ is the sequence of MKZ operators defined in (39).

The computation of the box and Hausdorff dimension of fractal sets and, in particular, of the graph of fractal functions was carried out by several researchers, i.e., [13,21,22,23,24,25,27]. Below, we present a result for the box dimension of MKZ $\alpha$-fractal functions.

Theorem 10.

Let $f\in C\left(I\right)$ be uniformly hölderian with exponent $\beta \in (0,1]$ satisfying $M_{n}f\left(x_1\right)=f\left(x_1\right)$ and $M_{n}f\left(x_N\right)=f\left(x_N\right)$. Suppose $\Delta :=\{x_1,x_2,\dots ,x_N\}$ is a uniform partition of I satisfying $x_{i+1}-x_i=\lambda <1$, for $i\in {\mathbb{N}}_{N-1}$ and $\alpha =({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_{N-1})\in {(-1,1)}^{N-1}$.

Consider the IFS ${\mathcal{I}}_n:=\{I;(u_i\left(x\right),v_i(x,y)),i\in {\mathbb{N}}_{N-1}\}$ where $u_i:I\to I_i$ is an affine map with

$$u_i\left(x\right):=\lambda (x+i-1)$$

and

$$v_i(x,y):={\alpha }_{i}y+f\left(u_i\left(x\right)\right)-{\alpha }_i{M}_{n}f\left(x\right).$$

Further, assume that the set of interpolation points $\{(x_j,f\left(x_j\right)):j\in {\mathbb{N}}_N\}$ is not collinear. Let

$$\gamma :=\sum _{i=1}^{N-1}\left|{\alpha }_i\right|,\hspace{1em}where {\alpha }_i\ne 0 \mathit{for} \mathit{all} i\in {\mathbb{N}}_{N-1}.$$

Then, the box dimension of the graph $G=\{(x,f^{\alpha }\left(x\right)):x\in I\}$ of $f^{\alpha }$ has the following bounds:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}1\le {dim}_{B}G\le 2-\beta ,\hfill & \mathit{for}\gamma \le 1;\hfill \\ 1\le {dim}_{B}G\le 2-\beta +{log}_{N-1}\gamma ,\hfill & \mathit{for} \gamma >1 \mathit{with} \gamma {\left(N-1\right)}^{\beta -1}\le 1;\hfill \\ 1\le {dim}_{B}G\le 1+{log}_{N-1}\gamma ,\hfill & \mathit{for} \gamma >1 \mathit{with} \gamma {\left(N-1\right)}^{\beta -1}>1;\hfill \\ {dim}_{B}G\ge 1+{log}_{N-1}\gamma ,\hfill & \mathit{for} \gamma >1 \mathit{with} \beta =1.\hfill \end{array}\right.\end{array}$$

(45)

Proof. 

By Proposition 1, $f\in {Lip}_A\beta$ implies $M_{n}f\in {Lip}_A\beta$. Therefore, $M_{n}f$ is also hölderian with exponent $\beta$. The statements follow from ([20], Theorem 3.1) for Hölder functions. □

6.2. MKZ $\alpha$-Fractal Functions in $L^p$-Spaces

Given $f\in L^p\left(I\right)$, $p\ge 1$, where $I:=[0,1]$, the integral MKZ operator ${\widehat{M}}_n$ [45] is defined as

$$\begin{array}{c}\hfill {\widehat{M}}_{n}f\left(x\right):={\int }_0^1{H}_n(x,s)f\left(s\right)ds,\end{array}$$

(46)

where

$$H_n(x,s):=\sum _{k=0}^{\infty }{\widehat{m}}_{nk}\left(x\right){\chi }_{I_k}\left(t\right),$$

$${\widehat{m}}_{nk}\left(x\right):=(n+1)\left(\genfrac{}{}{0pt}{}{k+n+1}{k}\right)x^k{(1-x)}^n,$$

(47)

and

$$I_k:=\left[\frac{k}{k+n},\frac{k+1}{k+n+1}\right],$$

(48)

with ${\chi }_{I_k}$ denoting the characteristic function on $I_k$.

In the following theorem, we define MKZ $\alpha$-fractal functions in $L^p$-spaces using as base function ${\widehat{M}}_n$.

Theorem 11.

Let $f\in L^p\left(I\right)$ with $p\ge 1$ and let $I:=[0,1]$. Suppose that $\Delta :=\{0=x_1<x_2<\cdots <x_N=1\}$ is a partition of I. Denote by $I_i:=[x_i,x_{i+1})$, $i\in {\mathbb{N}}_{N-1}$, and $I_N:=[x_{N-1},x_N]$ the subintervals of I induced by Δ.

Define affine maps $u_i:[0,1)\to I_i$ on I by $u_i\left(x\right):=a_{i}x+b_i$. Assume that

$$\begin{array}{c}{u}_i\left(x_1\right)=x_i,\hspace{1em}{u}_i(x_N-)=x_{i+1},\hspace{1em}i\in {\mathbb{N}}_{N-2},\\ u_{N-1}\left(x_1\right)=x_{N-1},\hspace{1em}{u}_{N-1}\left(x_N\right)=x_N.\end{array}$$

Suppose ${\alpha }_i\in L^{\infty }\left(I\right)$ for $i\in {\mathbb{N}}_{N-1}$. Define an RB-operator $T:L^p\left(I\right)\to L^p\left(I\right)$ as follows:

$$\begin{array}{c}\hfill Tg:=f+\sum _{i=1}^{N-1}({\alpha }_i\circ u_i^{-1})(g-{\widehat{M}}_{n}f)\circ u_i^{-1}{\chi }_{I_i}.\end{array}$$

(49)

Assume that the vector of scaling functions $\alpha :=({\alpha }_1,\dots ,{\alpha }_{N-1})\in {\left(L^{\infty }\left(I\right)\right)}^{N-1}$ satisfies

$$\begin{array}{c}\hfill \Lambda :={\left(\sum _{i\in {\mathbb{N}}_{N-1}}{a}_i{\parallel {\alpha }_i\parallel }_{\infty }^p\right)}^{\frac{1}{p}}<1,\mathit{for} 1\le p<\infty .\end{array}$$

(50)

Then T is a contraction map on $L^p\left(I\right)$ with Lipschitz constant Λ and its unique fixed point $f_n^{\alpha }$ satisfies

$$\begin{array}{c}\hfill f_n^{\alpha }=f+\sum _{i=1}^{N-1}({\alpha }_i\circ u_i^{-1})(f_n^{\alpha }-{\widehat{M}}_{n}f)\circ u_i^{-1}{\chi }_{I_i}.\end{array}$$

(51)

Furthermore, the mapping ${\mathcal{F}}_{\Delta ,{\widehat{M}}_n}^{\alpha }:L^p\left(I\right)\to L^p\left(I\right)$ with

$${\mathcal{F}}_{\Delta ,{\widehat{M}}_n}^{\alpha }\left(f\right)=f_n^{\alpha }$$

is a bounded linear operator.

Proof. 

Using the same arguments as in the proof of ([36], Theorem 2.1), we can easily verify that T is contractive. The remaining part follows using Theorem 3.4 in [46]. □

Theorem 12.

Let $f\in L^p\left(I\right)$, $p\in [1,\infty )$. The MKZ fractal functions $f_n^{\alpha }$, $n\in \mathbb{N}$, defined in Theorem 11 converge in $L^p$-norm to f as $n\to \infty$ and satisfy the estimate

$$\begin{array}{c}\hfill \parallel f_n^{\alpha }{-f\parallel }_p\le C\frac{\Lambda }{1-\Lambda }{\omega }_{1,p}\left(f,\frac{1}{\sqrt{n}}\right),\end{array}$$

(52)

with $C>0$ a constant independent of f and p, and

$${\omega }_{1,p}(f,t):=\underset{0<h\le t}{sup}{\parallel f(.+h)-f(.)\parallel }_{p,I_h},$$

where ${\parallel .\parallel }_{p,I_h}$ is the $L^p$ norm taken over the interval $I_h=[0,1-h]$.

Proof. 

From (51), it is easy to compute that

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \parallel f_n^{\alpha }{-f\parallel }_p^p\le & {\Lambda }^p{\parallel f_n^{\alpha }-{\widehat{M}}_{n}f\parallel }_p^p.\hfill \end{array}\end{array}$$

Equivalently,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \parallel f_n^{\alpha }{-f\parallel }_p\le & \Lambda \parallel f_n^{\alpha }-{\widehat{M}}_n{f\parallel }_p\hfill \\ \hfill \le & \Lambda \left\{\parallel f_n^{\alpha }{-f\parallel }_p+{\parallel f-{\widehat{M}}_{n}f\parallel }_p\right\},\hfill \end{array}\end{array}$$

which gives

$$\begin{array}{c}\hfill \parallel f_n^{\alpha }{-f\parallel }_p\le \frac{\Lambda }{1-\Lambda }{\parallel f-{\widehat{M}}_{n}f\parallel }_p.\end{array}$$

(53)

This ensures $\parallel f_n^{\alpha }{-f\parallel }_p\to 0$ as $n\to \infty$.

It is known from Theorem 3 in [45] that $\parallel f-{\widehat{M}}_n{f\parallel }_p\le C{\omega }_{1,p}(f,\frac{1}{\sqrt{n}})$, for some $C>0$. Using this result in (53), we obtain the required estimate. □

Now we give the MKZ-fractal version of the Full Müntz Theorem for $L^p[0,1]$.

Theorem 13.

Let ${\left\{{\lambda }_i\right\}}_{i=0}^{\infty }$ be the sequence of district real numbers such that ${\lambda }_i\ge -\frac{1}{p}$, for all $i\in \mathbb{N}$, where $p\in [1,\infty )$ and ${\left(x^{{\lambda }_i}\right)}_n^{\alpha }$ is defined as in (51). Then, the MKZ Müntz space

$$S:=\bigcup _{n=1}^{\infty }\bigcup _{m=1}^{\infty }span\{{\left(x^{{\lambda }_0}\right)}_n^{\alpha },{\left(x^{{\lambda }_1}\right)}_n^{\alpha },\dots ,{\left(x^{{\lambda }_m}\right)}_n^{\alpha }\}$$

is dense in $L^p\left(I\right)$ if

$$\begin{array}{c}\hfill \sum _{i=0}^{\infty }\frac{{\lambda }_i+\frac{1}{p}}{{({\lambda }_i+\frac{1}{p})}^2+1}=\infty .\end{array}$$

Proof. 

Let $f\in L^p\left(I\right)$ and $ϵ>0$ be given. By [41], it is known that the space

$$\bigcup _{m=1}^{\infty }span\{x^{{\lambda }_0},x^{{\lambda }_1},\cdots ,x^{{\lambda }_m})\}$$

is dense in $L^p\left(I\right)$. Therefore, there exists a Müntz polynomial $r\left(x\right):={\displaystyle \sum _{i=1}^l}{d}_i{x}^{{\lambda }_i}\in L^p\left(I\right)$, $d_i\in \mathbb{R}$, such that

$$\begin{array}{c}\hfill {\parallel f-r\parallel }_p<\frac{ϵ}{2}.\end{array}$$

As $r\in L^p\left(I\right)$, there exists a natural number $n_0$ such that

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \parallel f-r_n^{\alpha }{\parallel }_p<& \frac{ϵ}{2},\hspace{1em}\mathrm{for} \mathrm{all}n\ge n_0.\hfill \end{array}\end{array}$$

(54)

Using the linearity of ${\mathcal{F}}_{\Delta ,{\widehat{M}}_n}^{\alpha }$, we can write $r_n^{\alpha }\left(x\right)={\mathcal{F}}_{\Delta ,{\widehat{M}}_n}^{\alpha }\left(r\right)\left(x\right)={\displaystyle \sum _{i=0}^l}{d}_i{\left(x^{{\lambda }_i}\right)}_n^{\alpha }$ and, thus, the above inequality becomes

$$\begin{array}{c}\hfill {∥f-\sum _{i=0}^l{d}_i{\left(x^{{\lambda }_i}\right)}_n^{\alpha }∥}_p<\frac{ϵ}{2},\hspace{1em}\mathrm{for} \mathrm{all}n\ge n_0.\end{array}$$

(55)

From (54) and (55), we obtain

$${∥f-\sum _{i=0}^l{d}_i{\left(x^{{\lambda }_i}\right)}_n^{\alpha }∥}_p<ϵ,\hspace{1em}\mathrm{for} \mathrm{all} n\ge n_0.$$

Hence S is dense in $L^p\left(I\right)$. □

6.3. A remark about the Case $0<p<1$

Recall that for $0<p<1$, the Lebesgue spaces $L^p\left(I\right)$, $I\subset \mathbb{R}$ a compact interval, are F-spaces whose topology is induced by the complete translation invariant metric

$$d_p(g,h):={∥g-h∥}_p^p={\int }_I{|g\left(x\right)-h\left(x\right)|}^{p}dx,$$

(see, [47], 1.47).

We will show by a counterexample that the above results do not extend to the case $0<p<1$. For this purpose, we need to quote a theorem of Orlicz’s.

Theorem 14.

(Orlicz’s Theorem [48]). Suppose that the kernel $K_n(x,t)$ is measurable in the square $\left\{\right(x,t)\in \mathbb{R}\times \mathbb{R}:a\le x\le b$, $a\le t\le b\}$ and that

$${\int }_a^b\left|K_n(x,t)\right|dt\le M,\hspace{1em}a.e. x\in [a,b],$$

(56)

$${\int }_a^b\left|K_n(x,t)\right|dx\le M,\hspace{1em}a.e. t\in [a,b],$$

(57)

with a constant M and for all $n\in \mathbb{N}$. Then, for $f\in L^p[a,b]$, the singular integral

$$F_n\left(x\right)={\int }_a^b{K}_n(x,t)f\left(t\right)dt$$

(58)

exists for a.e. x and is a function of the class $L^p[a,b]$. If in addition $F_n\to f$ strongly for all elements $f\in H$ of a set $H\subset L^p[a,b]$ which is everywhere dense in $L^p[a,b]$, then this is also true for any $f\in L^p[a,b]$:

$$\parallel f-F_n\parallel ={\left[{\int }_a^b{|f\left(x\right)-F_n\left(x\right)|}^{p}dx\right]}^{\frac{1}{p}}\to 0.$$

(59)

Orlicz theorem is only true for $p\ge 1$. The following example shows that the above theorem does not hold for $0<p<1$:

Example 5.

Let $[a,b]:=I=[0,1]$, $K_n(x,t):=c$, $c\ne 0$, and $f\left(t\right):=t^{-1}$. Then, $f\in L^p\left(I\right)$ for $0<p<1$ and $K_n(x,t)$ satisfy all required conditions of Orlicz’s theorem, but

$$F_n\left(x\right)={\int }_0^1{K}_n(x,t)f\left(t\right)dt={\int }_0^1\frac{c}{t}dt=\left\{\begin{array}{cc}+\infty ,\hfill & c>0;\hfill \\ -\infty ,\hfill & c<0.\hfill \end{array}\right.$$

For $p\ge 1$, Müller [45] proved that the operator ${\widehat{M}}_n$ is well-defined and bounded using Orlicz’s result, see Theorem 14. The above choices for $K_n$ and f imply that Orlicz’s theorem fails to prove the well-definiteness of the operator ${\widehat{M}}_n$ in $L^p$ for $0<p<1$. More precisely, take again $f\left(t\right):=t^{-1}$. As seen above, $f\in L^p$ for $0<p<1$. By the positivity of ${\widehat{m}}_{nk}\left(x\right)$ (i.e., the series given below is a series of positive terms), we have

$$\begin{array}{cc}\hfill {\widehat{M}}_{n}f\left(x\right)& ={\int }_0^1{H}_n(x,t)f\left(t\right)dt=\sum _{k=0}^{\infty }{\widehat{m}}_{nk}\left(x\right){\int }_{I_k}f\left(t\right)dt\ge {\widehat{m}}_{n0}\left(x\right){\int }_{I_0}f\left(t\right)dt\hfill \\ \hfill \hspace{1em}& =(n+1){(1-x)}^n\underset{\epsilon \to 0+}{lim}{\int }_{\epsilon }^1\frac{dt}{t}=\infty ,\hfill \end{array}$$

where ${\widehat{m}}_{nk}$ and $I_k$ are given by (47) and (48), respectively. Hence, the integral MKZ operators ${\widehat{M}}_n$ are not well-defined on $L^p$ for $0<p<1$.

7. Conclusions

In this paper, a novel class of fractal functions is introduced using quantum Meyer-König-Zeller (MKZ) functions as base functions in the $\alpha$-fractal interpolation procedure. For $f\in C\left(I\right)$, we have constructed a sequence of quantum MKZ fractal functions that converges uniformly to f without altering the scaling functions. The convergence and shape of quantum fractal approximants depend on the variable $q\in (0,1]$ as well as the scaling functions. For a given positive function $f\in C\left(I\right)$, we have generated a sequence of positive MKZ fractal functions that converges uniformly to f provided the scaling functions satisfy certain growth restraints. We have shown the existence of one-sided MKZ fractal approximants for a given function and proved MKZ fractal versions of Müntz theorems in $C[0,1]$. Finally, we have investigated some approximation-theoretic properties of MKZ $\alpha$-fractal functions in $C\left(I\right)$ and $L^p$-spaces.