Fractional-Order Impedance Control for Robot Manipulator
Abstract
1. Introduction
2. FO-Impedance Controller Design
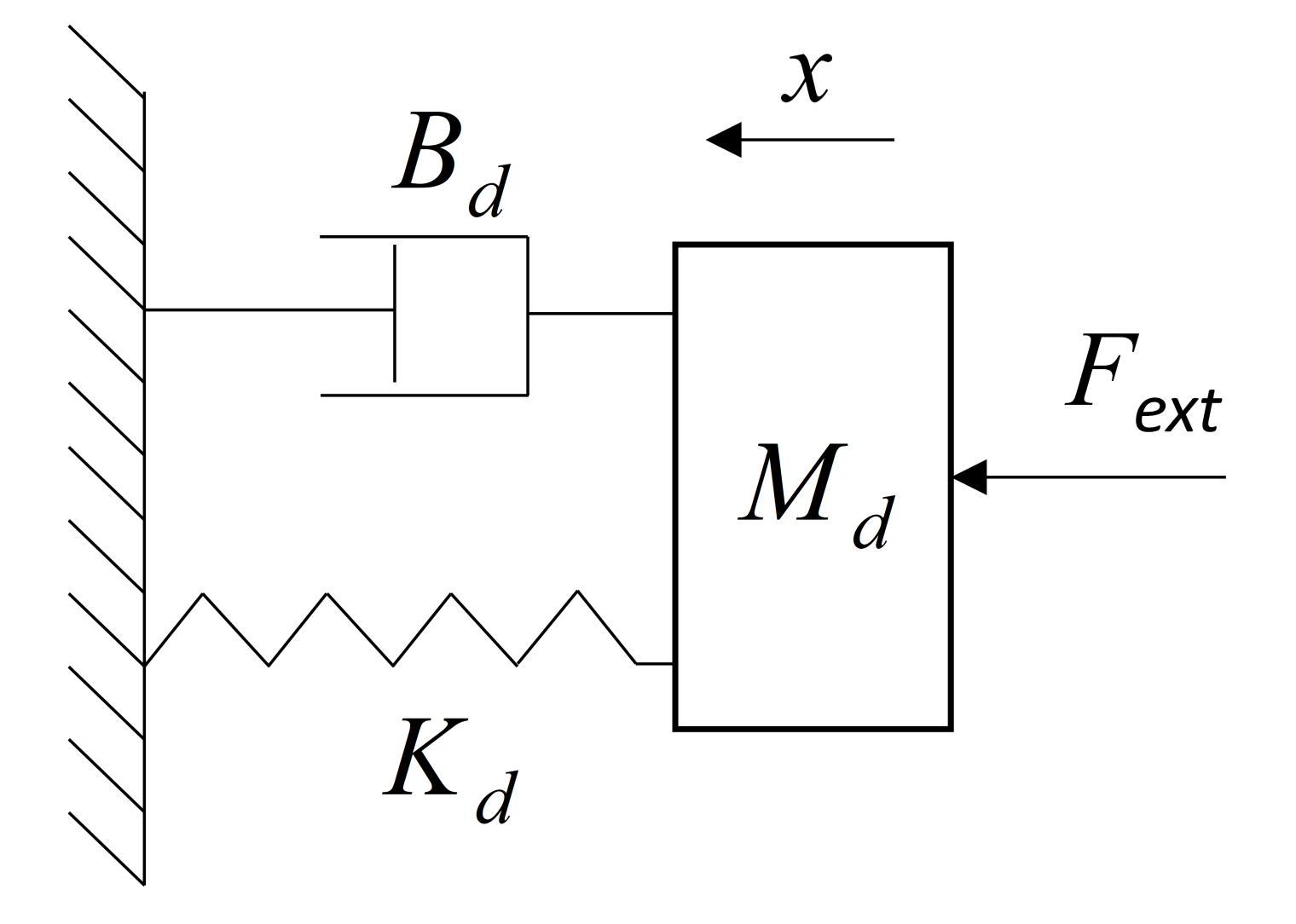
2.1. Impedance Control Methodology
2.2. Controllers Design
2.2.1. Design Specifications
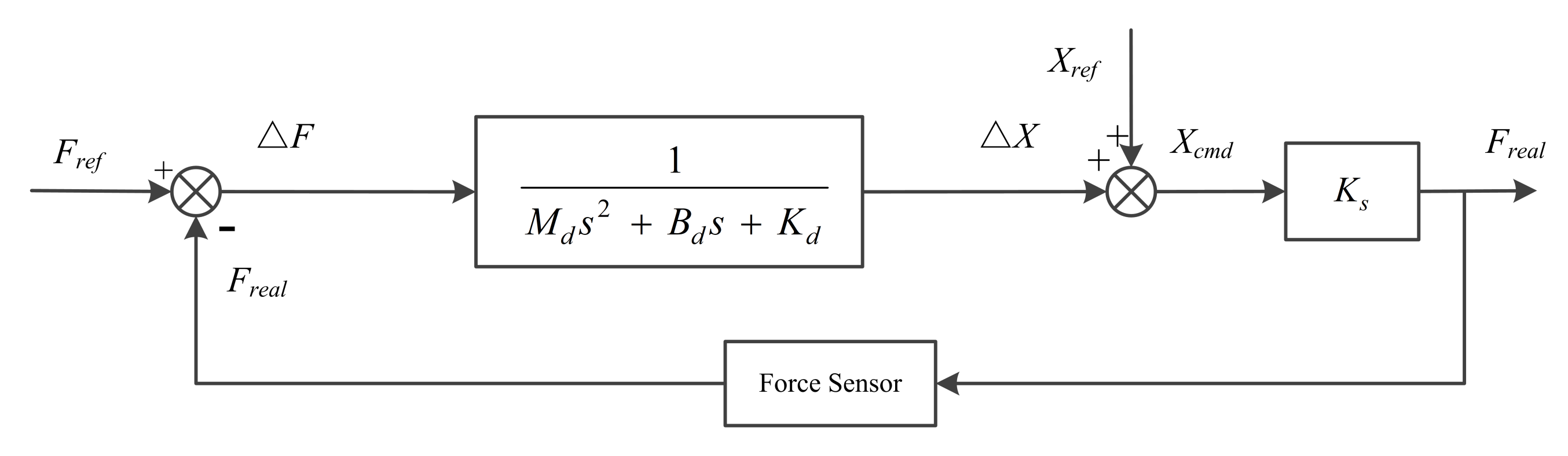
2.2.2. IO-Impedance Controller Design
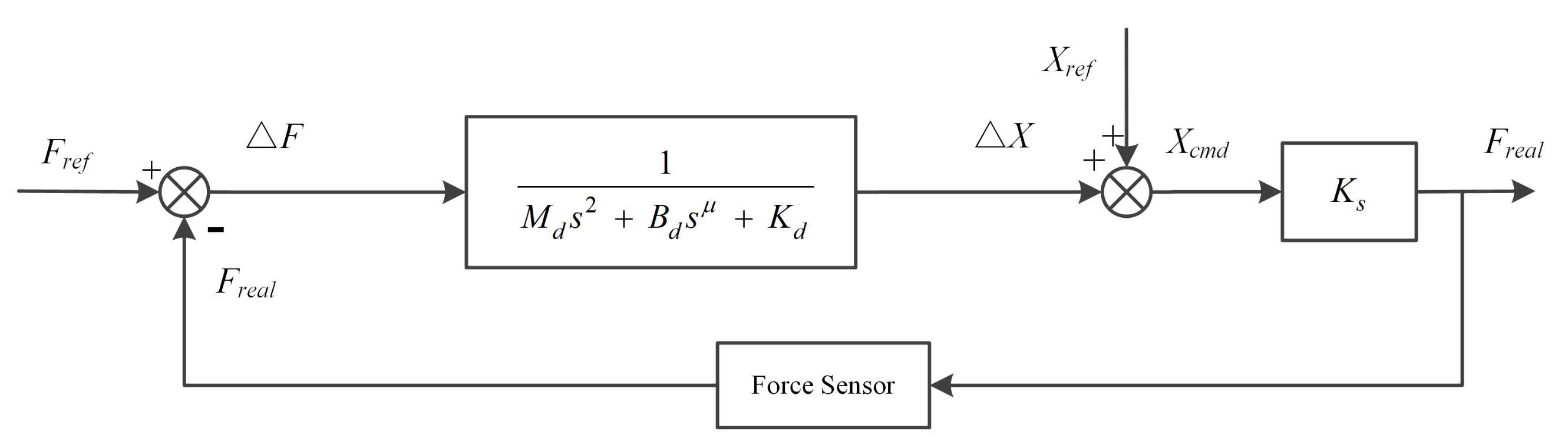
2.2.3. FO-Impedance Controller Design
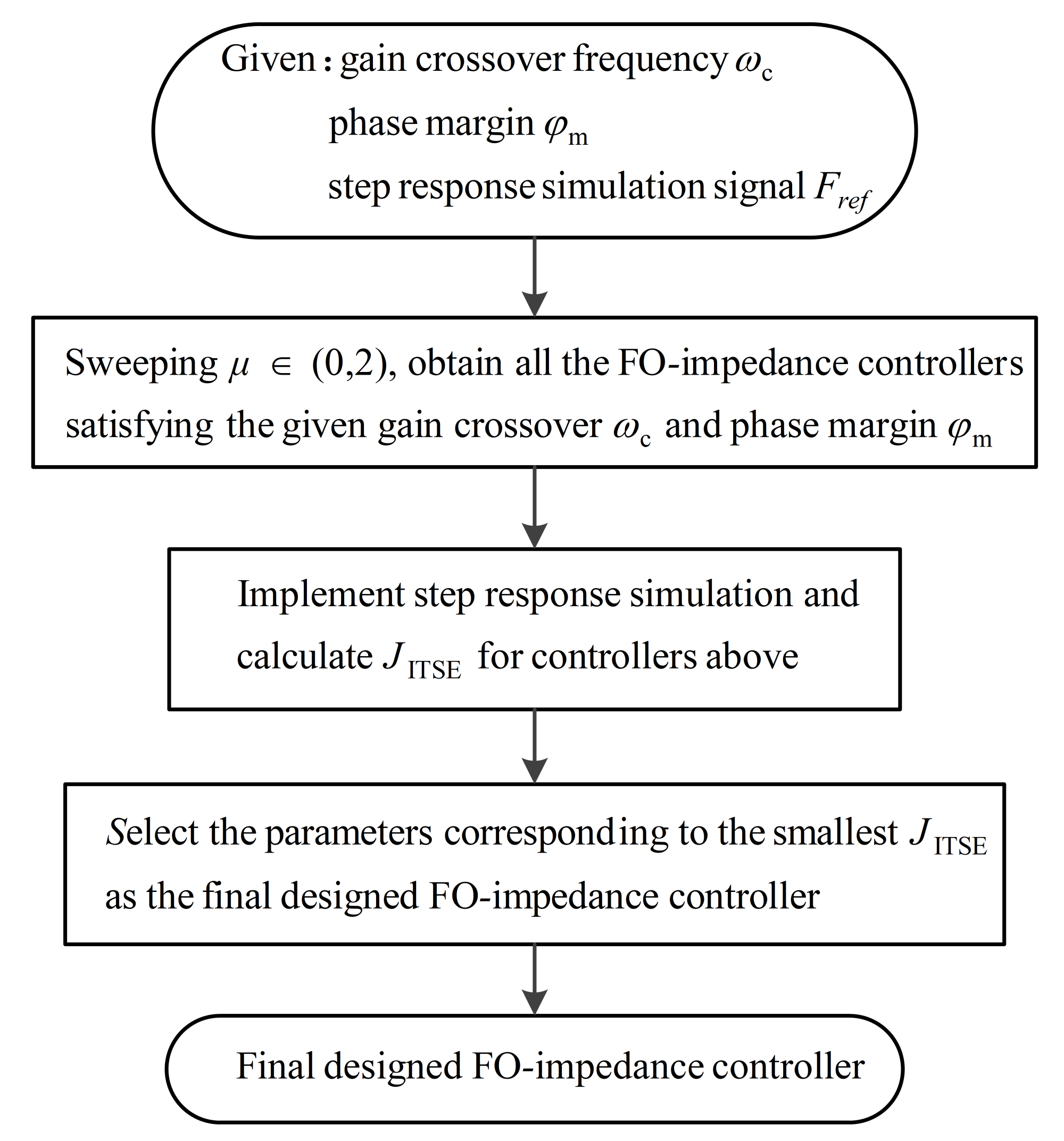
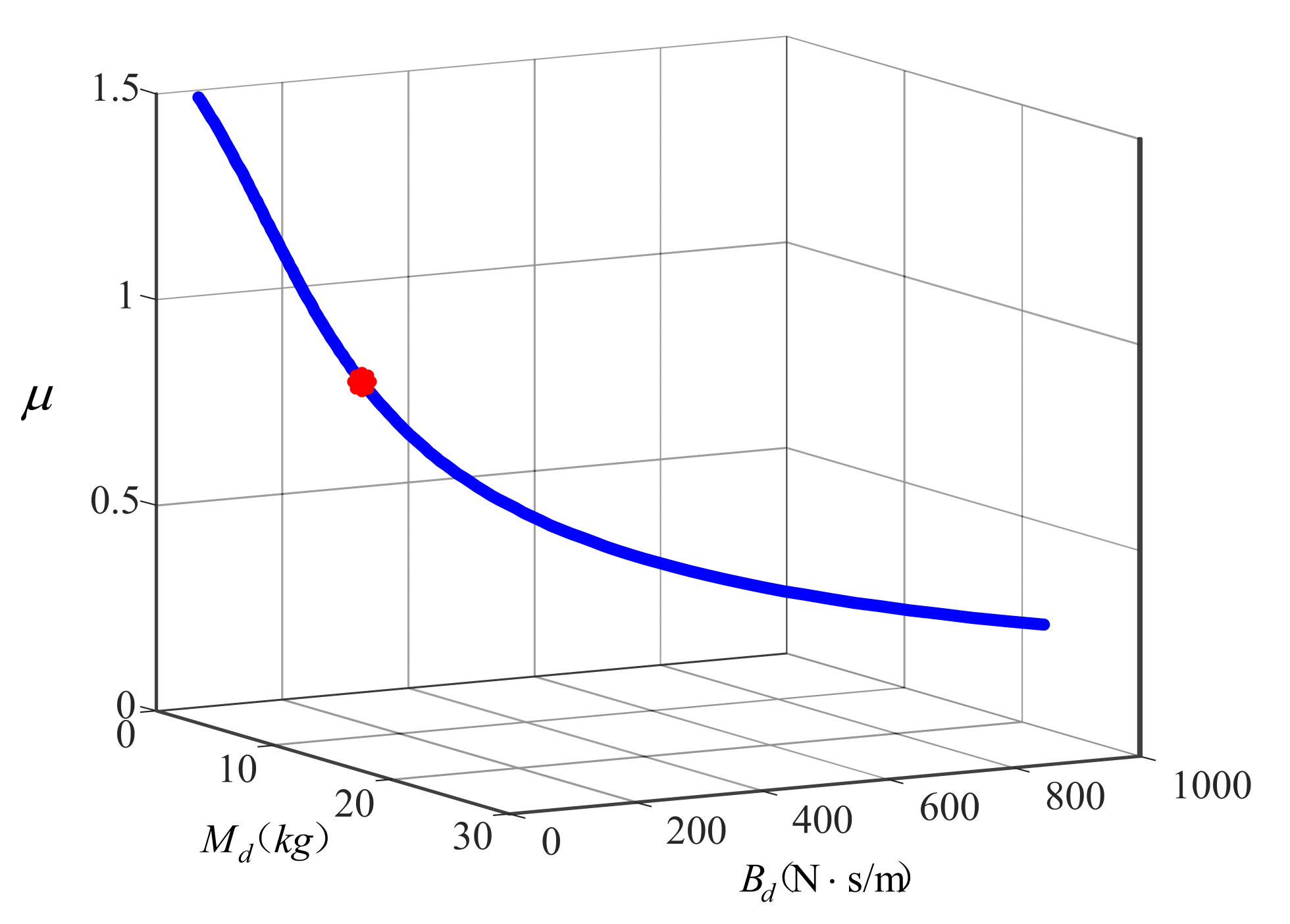
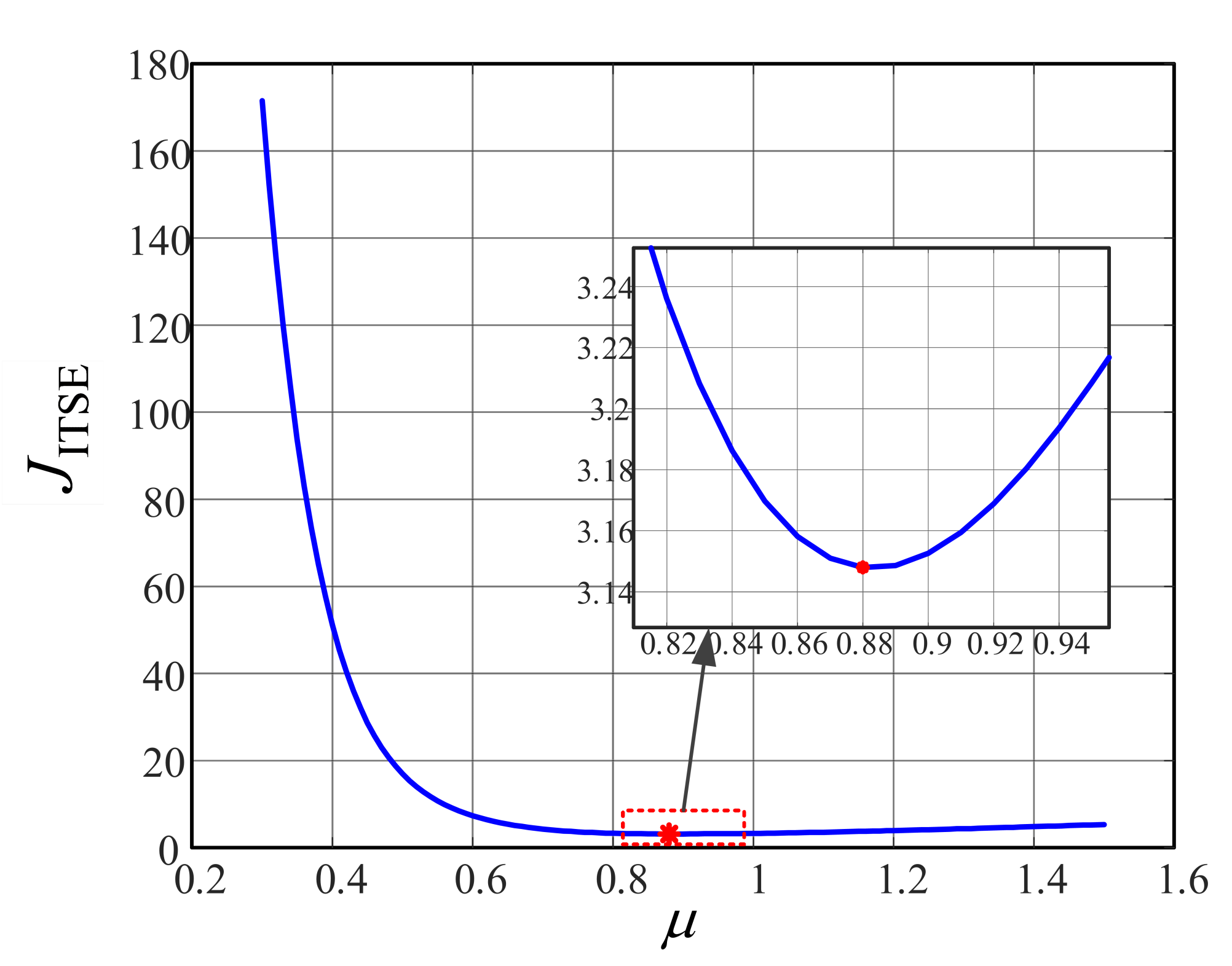
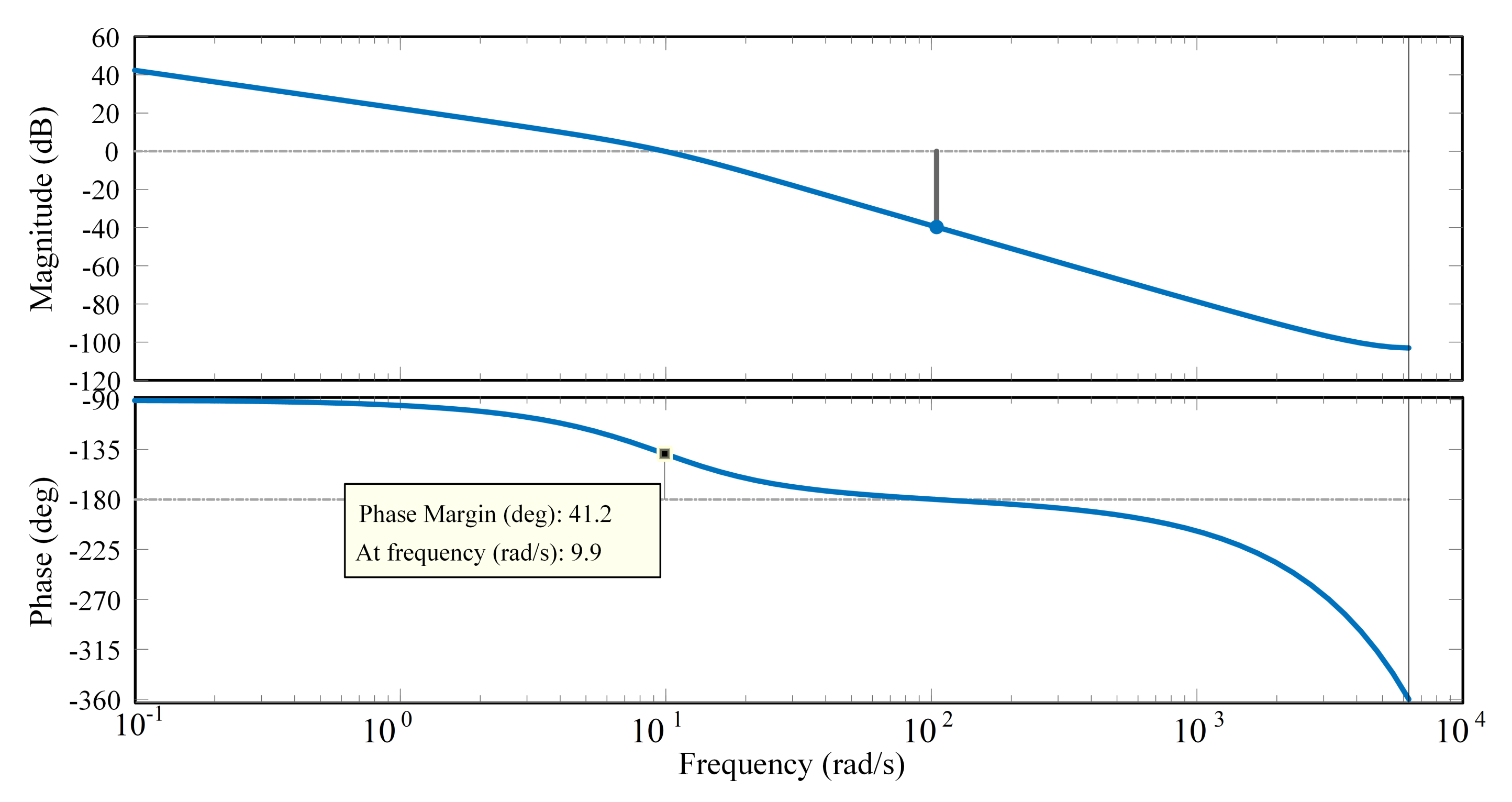
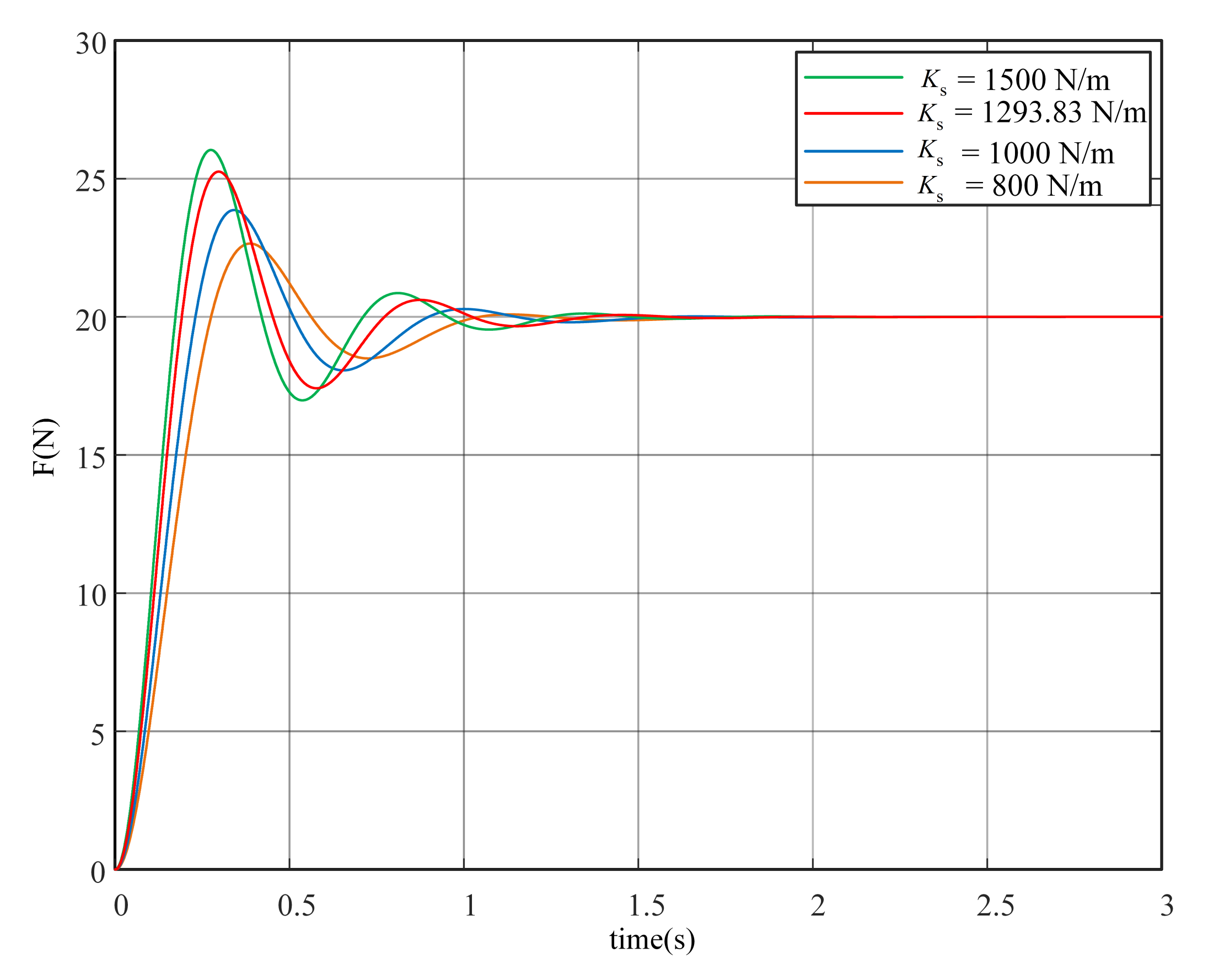
2.2.4. Design Procedure Illustration with an Example
3. Simulation
3.1. Fractional-Order Operator Implementation
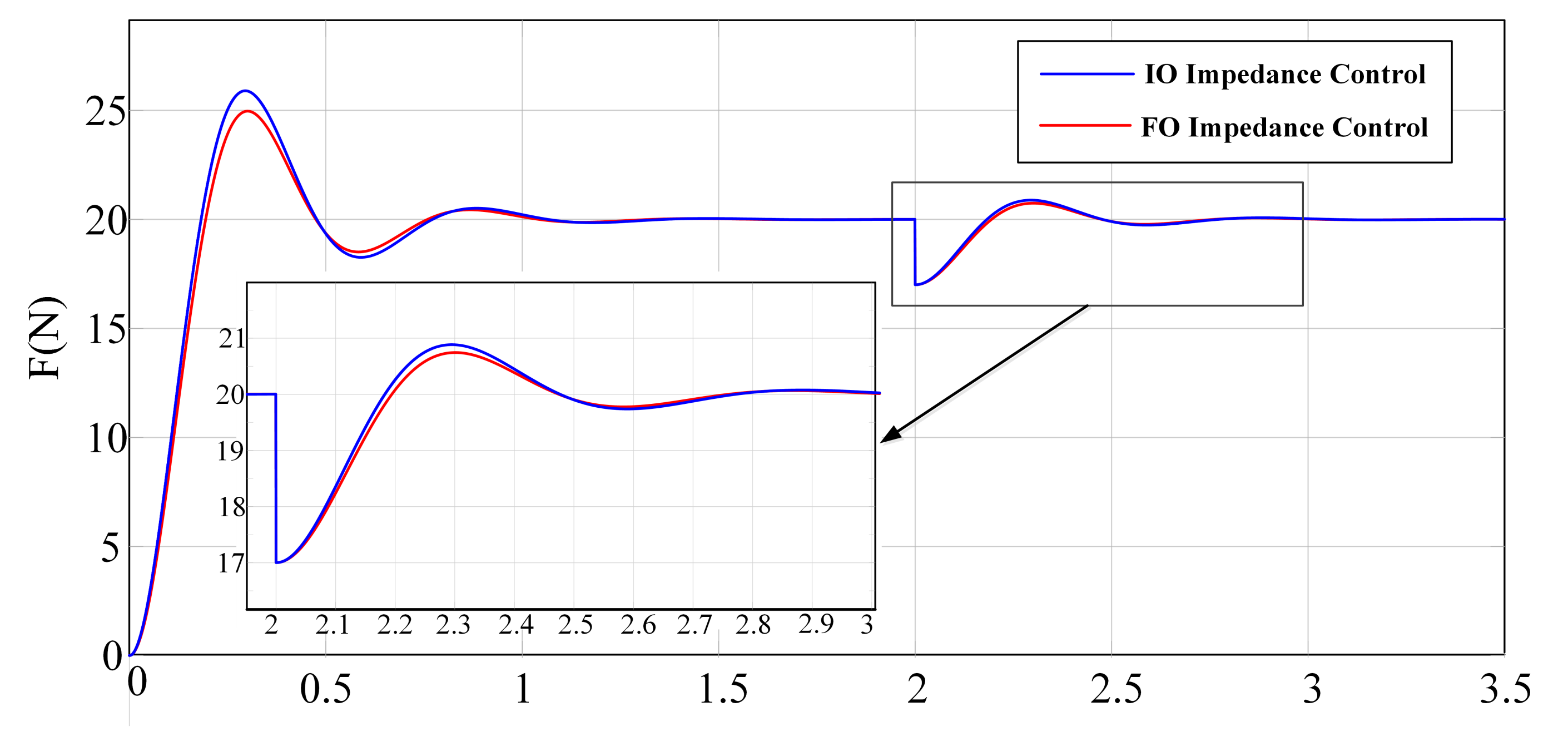
3.2. Step Response and Anti-Disturbance Simulation
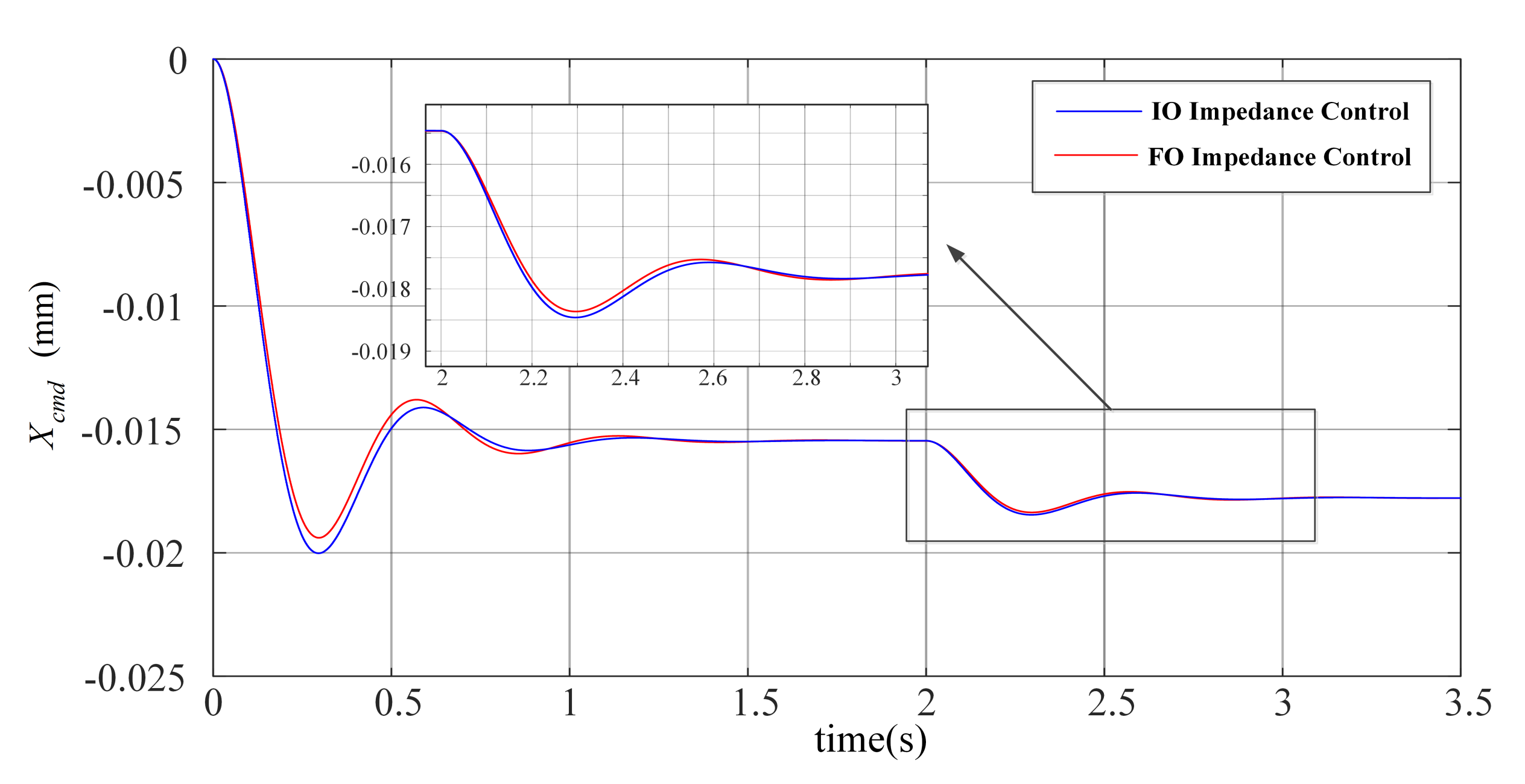
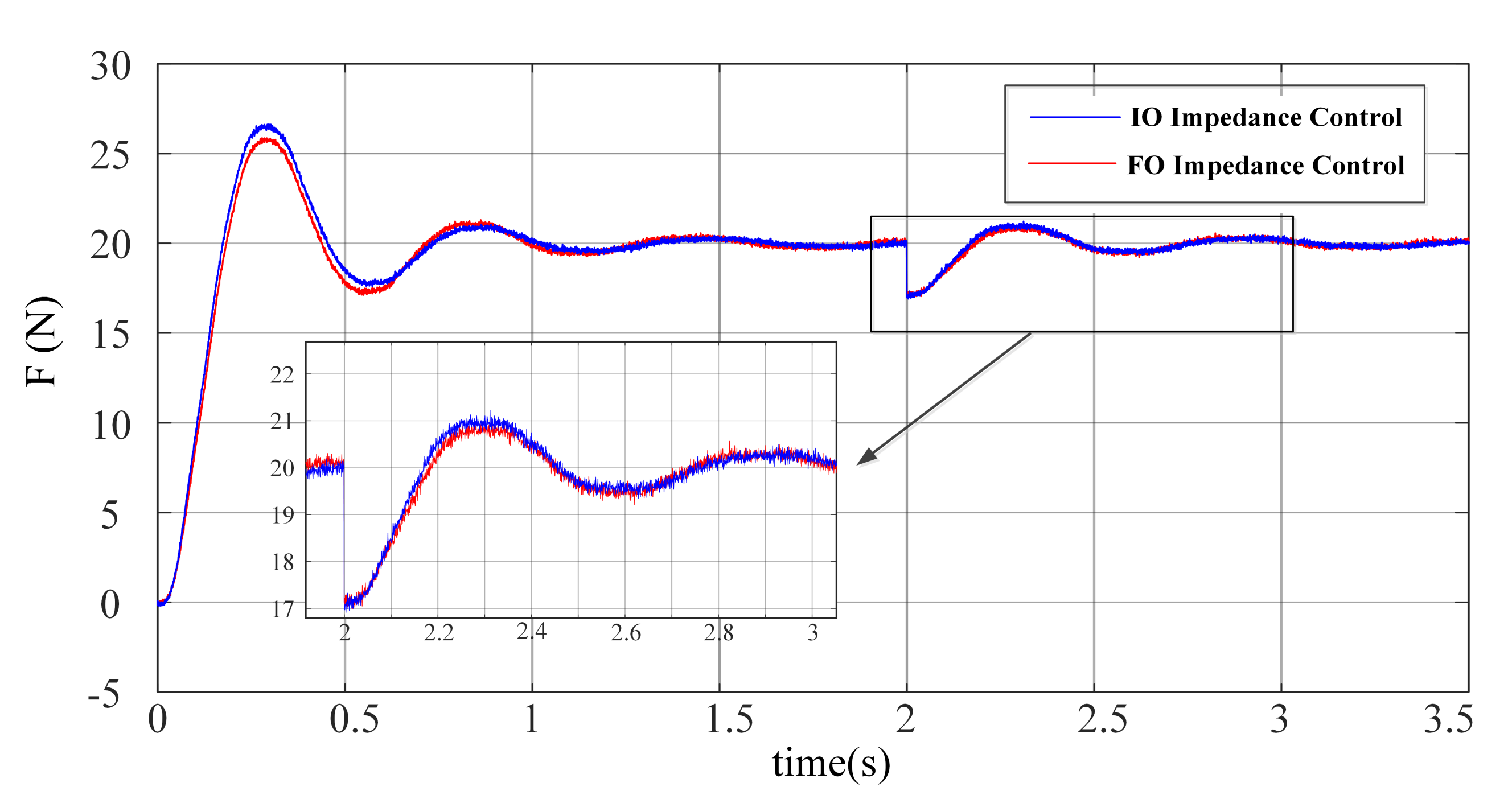
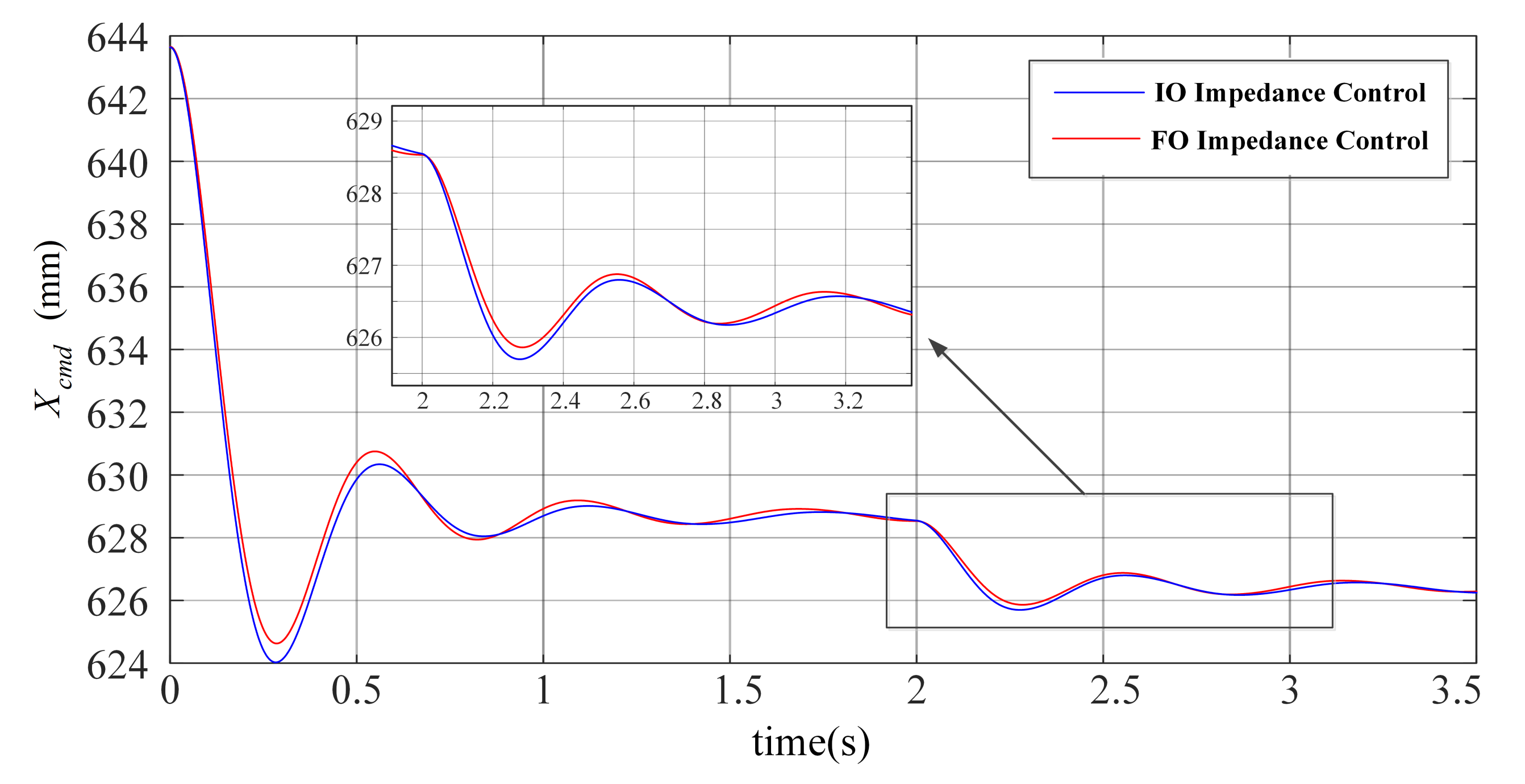
4. Experimental Verification
4.1. Experimental Setup
4.2. Step Response and Anti-Disturbance Test
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, H.; Li, L.; Zhao, J.; Zhao, J. The hybrid force/position anti-disturbance control strategy for robot abrasive belt grinding of aviation blade base on fuzzy PID control. Int. J. Adv. Manuf. Technol. 2021, 114, 3645–3656. [Google Scholar] [CrossRef]
- Zhang, W.; Li, H.; Cui, L.; Li, H.; Zhang, X.; Fang, S.; Zhang, Q. Research progress and development trend of surgical robot and surgical instrument arm. Int. J. Med. Robot. Comput. Assist. Surg. 2021, 17, e2309. [Google Scholar] [CrossRef]
- Junge, K.; Hughes, J.; Thuruthel, T.G.; Iida, F. Improving robotic cooking using batch Bayesian optimization. IEEE Robot. Autom. Lett. 2020, 5, 760–765. [Google Scholar] [CrossRef]
- Zhang, J.; Liao, W.; Bu, Y.; Tian, W.; Hu, J. Stiffness properties analysis and enhancement in robotic drilling application. Int. J. Adv. Manuf. Technol. 2020, 106, 5539–5558. [Google Scholar] [CrossRef]
- Lu, H.; Zhao, X.; Tao, B.; Yin, Z. Online process monitoring based on vibration-surface quality map for robotic grinding. IEEE/ASME Trans. Mechatronics 2020, 25, 2882–2892. [Google Scholar] [CrossRef]
- Abdi, E.; Kulić, D.; Croft, E. Haptics in Teleoperated Medical Interventions: Force Measurement, Haptic Interfaces and Their Influence on User’s Performance. IEEE Trans. Biomed. Eng. 2020, 67, 3438–3451. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Xie, Y.; Liu, S.; Sun, D. Force Modeling, Identification, and Feedback Control of Robot-Assisted Needle Insertion: A Survey of the Literature. Sensors 2018, 18, 561. [Google Scholar] [CrossRef]
- Hogan, N. Impedance Control: An Approach to Manipulation: Part II—Implementation. J. Dyn. Syst. Meas. Control. 1985, 107, 8–16. [Google Scholar] [CrossRef]
- Al-Shuka, H.F.; Leonhardt, S.; Zhu, W.H.; Song, R.; Ding, C.; Li, Y. Active impedance control of bioinspired motion robotic manipulators: An overview. Appl. Bionics Biomech. 2018, 2018, 8203054. [Google Scholar] [CrossRef] [PubMed]
- Tsumugiwa, T.; Yura, M.; Kamiyoshi, A.; Yokogawa, R. Development of mechanical-impedance-varying mechanism in admittance control. J. Robot. Mechatronics 2018, 30, 863–872. [Google Scholar] [CrossRef]
- Li, Z.; Xu, C.; Wei, Q.; Shi, C.; Su, C.Y. Human-inspired control of dual-arm exoskeleton robots with force and impedance adaptation. IEEE Trans. Syst. Man Cybern. Syst. 2018, 50, 5296–5305. [Google Scholar] [CrossRef]
- Duan, J.; Gan, Y.; Chen, M.; Dai, X. Adaptive variable impedance control for dynamic contact force tracking in uncertain environment. Robot. Auton. Syst. 2018, 102, 54–65. [Google Scholar] [CrossRef]
- Abu-Dakka, F.J.; Saveriano, M. Variable Impedance Control and Learning—A Review. Front. Robot. AI 2020, 7, 590681. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Lin, L.; Yang, L.; Fu, Y. Variable impedance control of finger exoskeleton for hand rehabilitation following stroke. Ind. Robot. Int. J. Robot. Res. Appl. 2019, 47, 23–32. [Google Scholar] [CrossRef]
- Liang, L.; Chen, Y.; Liao, L.; Sun, H.; Liu, Y. A novel impedance control method of rubber unstacking robot dealing with unpredictable and time-variable adhesion force. Robot. Comput. Integr. Manuf. 2021, 67, 102038. [Google Scholar] [CrossRef]
- Dong, J.; Xu, J.; Zhou, Q.; Hu, S. Physical human–robot interaction force control method based on adaptive variable impedance. J. Frankl. Inst. 2020, 357, 7864–7878. [Google Scholar] [CrossRef]
- Schmidt, A.; Gaul, L. On a critique of a numerical scheme for the calculation of fractionally damped dynamical systems. Mech. Res. Commun. 2006, 33, 99–107. [Google Scholar] [CrossRef]
- Kobayashi, Y.; Onishi, A.; Hoshi, T.; Kawamura, K.; Hashizume, M.; Fujie, M.G. Validation of viscoelastic and nonlinear liver model for needle insertion from in vivo experiments. In International Workshop on Medical Imaging and Virtual Reality; Springer: Berlin/Heidelberg, Germany, 2008; pp. 50–59. [Google Scholar]
- Sun, H.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Niu, H.; Chen, Y.; West, B.J. Why Do Big Data and Machine Learning Entail the Fractional Dynamics? Entropy 2021, 23, 297. [Google Scholar] [CrossRef]
- Chen, P.; Luo, Y. A Two-Degree-of-Freedom Controller Design Satisfying Separation Principle with Fractional Order PD and Generalized ESO. IEEE/ASME Trans. Mechatron. 2021, 27, 137–148. [Google Scholar] [CrossRef]
- Luo, Y.; Zhang, T.; Lee, B.; Kang, C.; Chen, Y. Fractional-order proportional derivative controller synthesis and implementation for hard-disk-drive servo system. IEEE Trans. Control Syst. Technol. 2013, 22, 281–289. [Google Scholar] [CrossRef]
- Dadkhah Khiabani, E.; Ghaffarzadeh, H.; Shiri, B.; Katebi, J. Spline collocation methods for seismic analysis of multiple degree of freedom systems with visco-elastic dampers using fractional models. J. Vib. Control 2020, 26, 1445–1462. [Google Scholar] [CrossRef]
- Wang, P.; Wang, Q.; Xu, X.; Chen, N. Fractional critical damping theory and its application in active suspension control. Shock Vib. 2017, 2017, 2738976. [Google Scholar] [CrossRef]
- Jung, S.; Hsia, T.C. Stability and convergence analysis of robust adaptive force tracking impedance control of robot manipulators. In Proceedings of the Proceedings 1999 IEEE/RSJ International Conference on Intelligent Robots and Systems. Human and Environment Friendly Robots with High Intelligence and Emotional Quotients, Kyongju, Republic of Korea, 17–21 October 1999; Volume 2, pp. 635–640. [Google Scholar]
- Lee, K.; Buss, M. Force tracking impedance control with variable target stiffness. IFAC Proc. Vol. 2008, 41, 6751–6756. [Google Scholar] [CrossRef]
- Kim, T.; Kim, H.S.; Kim, J. Position-based impedance control for force tracking of a wall-cleaning unit. Int. J. Precis. Eng. Manuf. 2016, 17, 323–329. [Google Scholar] [CrossRef]
- Luo, Y.; Chen, Y. Fractional order [proportional derivative] controller for a class of fractional order systems. Automatica 2009, 45, 2446–2450. [Google Scholar] [CrossRef]
- Impulse Response Invariant Discretization of Fractional Order Integrators/Dierentiators. Available online: http://www.mathworks.com/matlabcentral/fileexchange/21342-impulse-response-invariant-discretization-of-fractional-orderintegrators-dierentiators (accessed on 1 September 2020).



| Step Response Test | Anti-Disturbance Test | ||||
|---|---|---|---|---|---|
| Overshoot (%) | Settling Time (s) | ITSE | Stabilization Time (s) | ITSE | |
| IO-impedance | 29.4820 | 0.9480 | 3.3350 | 0.4070 | 1.7426 |
| FO-impedance | 25.3930 | 0.9425 | 3.1480 | 0.3875 | 1.7411 |
| Performance improvement | 4.0890% | 0.5802% | 5.6072% | 4.7912% | 0.0861% |
| rad/s | rad/s | rad/s | rad/s | |
|---|---|---|---|---|
| delta | 14.6897% | 10.4499% | 7.4661% | 6.3878% |
| ts | 2.6912% | 1.3616% | 0.1577% | 0.8511% |
| ITSE | 3.8581% | 0.9018% | 1.9599% | 1.0003 % |
| Items | Brand and Model | Description |
|---|---|---|
| Robot manipulator mechanical body | EFFORT-ERC20C-C10 | Degree-of-freedom: 6 Maximum load: 20 kg |
| Industrial computer | ADVANTECH | Main board: advantech AIMB-785 Processor: Intel CoreTM i7-7700/3.6 GHz |
| Servo drive | TSINO DYNATRON CoolDrive R6 | Maximum EtherCAT communication frequency: 4 KHz |
| Force sensor | HPS-FT060E | Range in Z-axis: ±1000 N Measurement accuracy: 0.4 N Maximum EtherCAT communication frequency: 2 KHz |
| Spring | Stiffness: 1293.83 N/m |
| Link i | Link Length (mm) | Link Twist (degree) | Joint Offset (mm) | Joint Angle (degree) |
|---|---|---|---|---|
| 1 | 168.46 | 90 | 504 | |
| 2 | 781.55 | 0 | 0 | 90 |
| 3 | 140.34 | 90 | −0.3 | |
| 4 | 0 | −90 | 760.39 | |
| 5 | 0 | 90 | 0 | |
| 6 | 0 | 0 | 125 |
| Step Response Test | Anti-Disturbance Test | ||||
|---|---|---|---|---|---|
| Overshoot (%) | Settling Time (s) | ITSE | Stabilization Time (s) | ITSE | |
| IO-impedance | 33.1100 | 1.8550 | 3.9286 | 1.0080 | 1.8998 |
| FO-impedance | 29.3050 | 1.7030 | 3.8681 | 0.9640 | 1.8601 |
| Performance improvement | 11.4920% | 8.1941% | 1.5400% | 4.3651% | 2.0897% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, Y.; Liu, X.; Chen, P.; Luo, X.; Luo, Y. Fractional-Order Impedance Control for Robot Manipulator. Fractal Fract. 2022, 6, 684. https://doi.org/10.3390/fractalfract6110684
Ding Y, Liu X, Chen P, Luo X, Luo Y. Fractional-Order Impedance Control for Robot Manipulator. Fractal and Fractional. 2022; 6(11):684. https://doi.org/10.3390/fractalfract6110684
Chicago/Turabian StyleDing, Yixiao, Xiaolian Liu, Pengchong Chen, Xin Luo, and Ying Luo. 2022. "Fractional-Order Impedance Control for Robot Manipulator" Fractal and Fractional 6, no. 11: 684. https://doi.org/10.3390/fractalfract6110684
APA StyleDing, Y., Liu, X., Chen, P., Luo, X., & Luo, Y. (2022). Fractional-Order Impedance Control for Robot Manipulator. Fractal and Fractional, 6(11), 684. https://doi.org/10.3390/fractalfract6110684







