Optimal PID Controllers for AVR Systems Using Hybrid Simulated Annealing and Gorilla Troops Optimization
Abstract
1. Introduction
1.1. Literature Review
1.2. Paper Novelty and Idea
1.3. Paper Contribution
- The practical implementation of starting the generator is explained in detail by presenting the experimentally measured output of the generator voltage, excitation voltage, and excitation current.
- A new approach to solving the estimation problem of regulator parameters is presented. It considers the change in the generator voltage within the permitted values of the generator voltage and the change in the excitation voltage in real cases;
- Unlike the literature, the system is modeled as a DISO system rather than the common SISO one;
- The DISO model of the AVR system is presented for both generator and excitation voltage output;
- A novel metaheuristic algorithm named hybrid simulated annealing and gorilla troops optimization is proposed;
- A new fitness function is employed for parameter estimation. It considers the change in the generator voltage triggered by the changes in the reference value of the generator voltage and in the excitation voltage.
1.4. Paper Organization
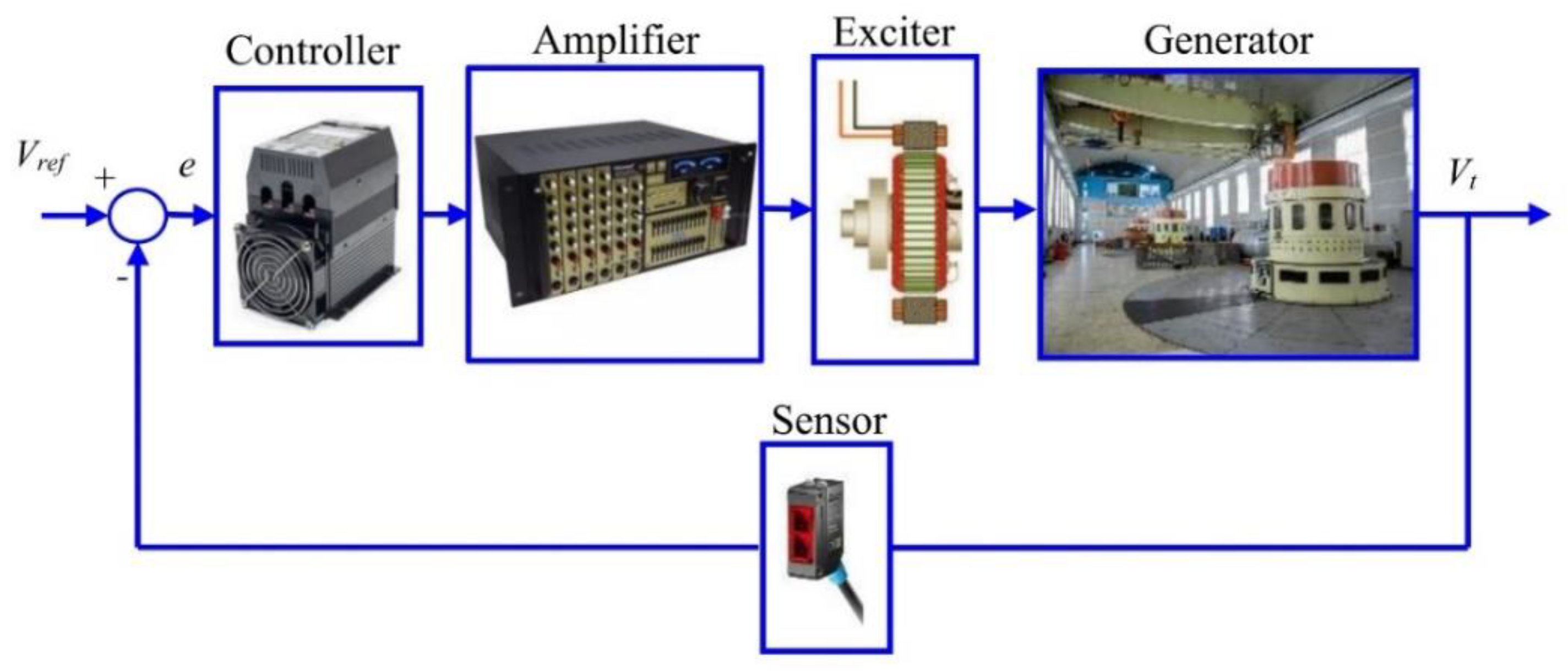
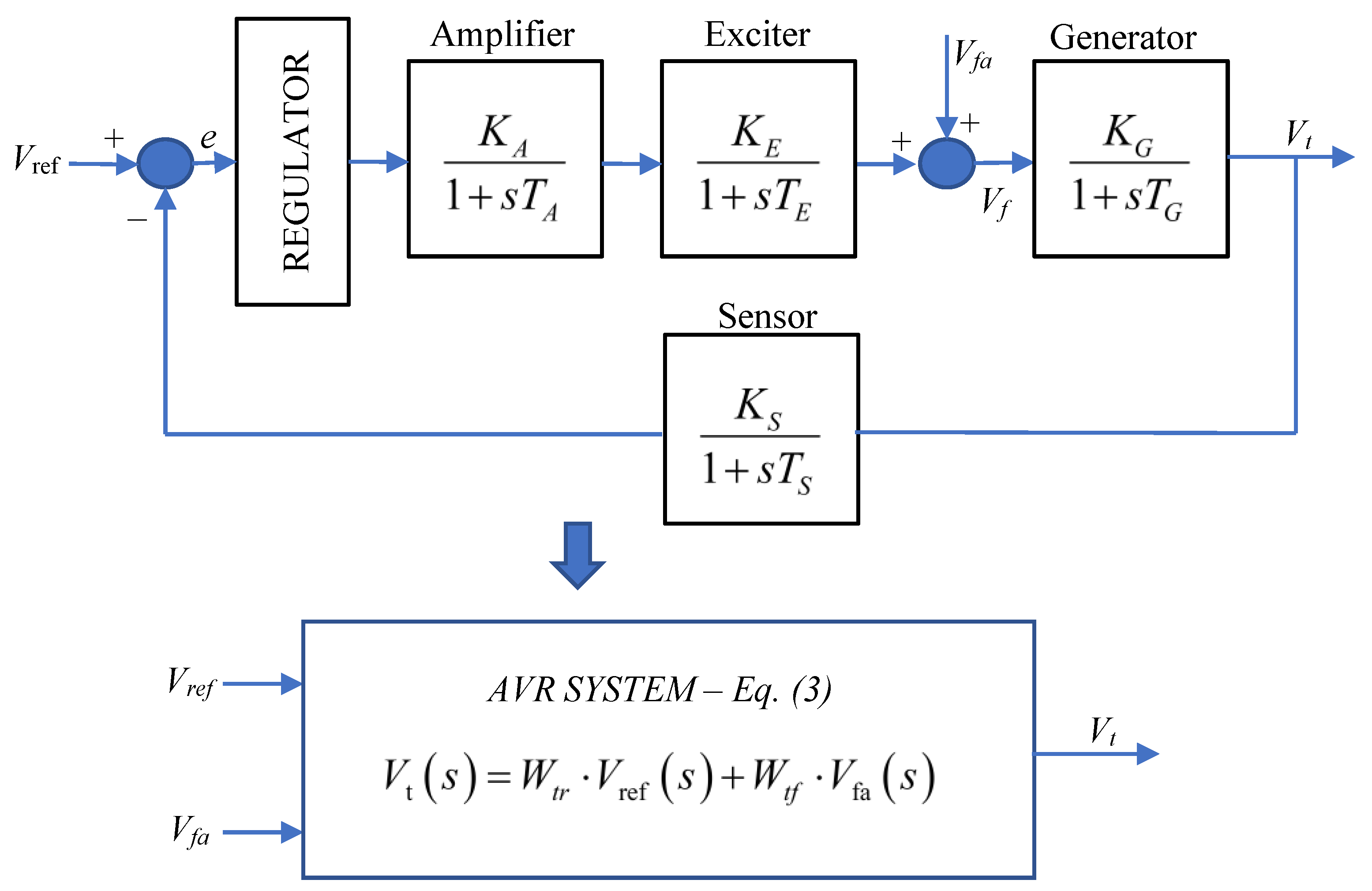
2. Proposed DISO-Model of the AVR
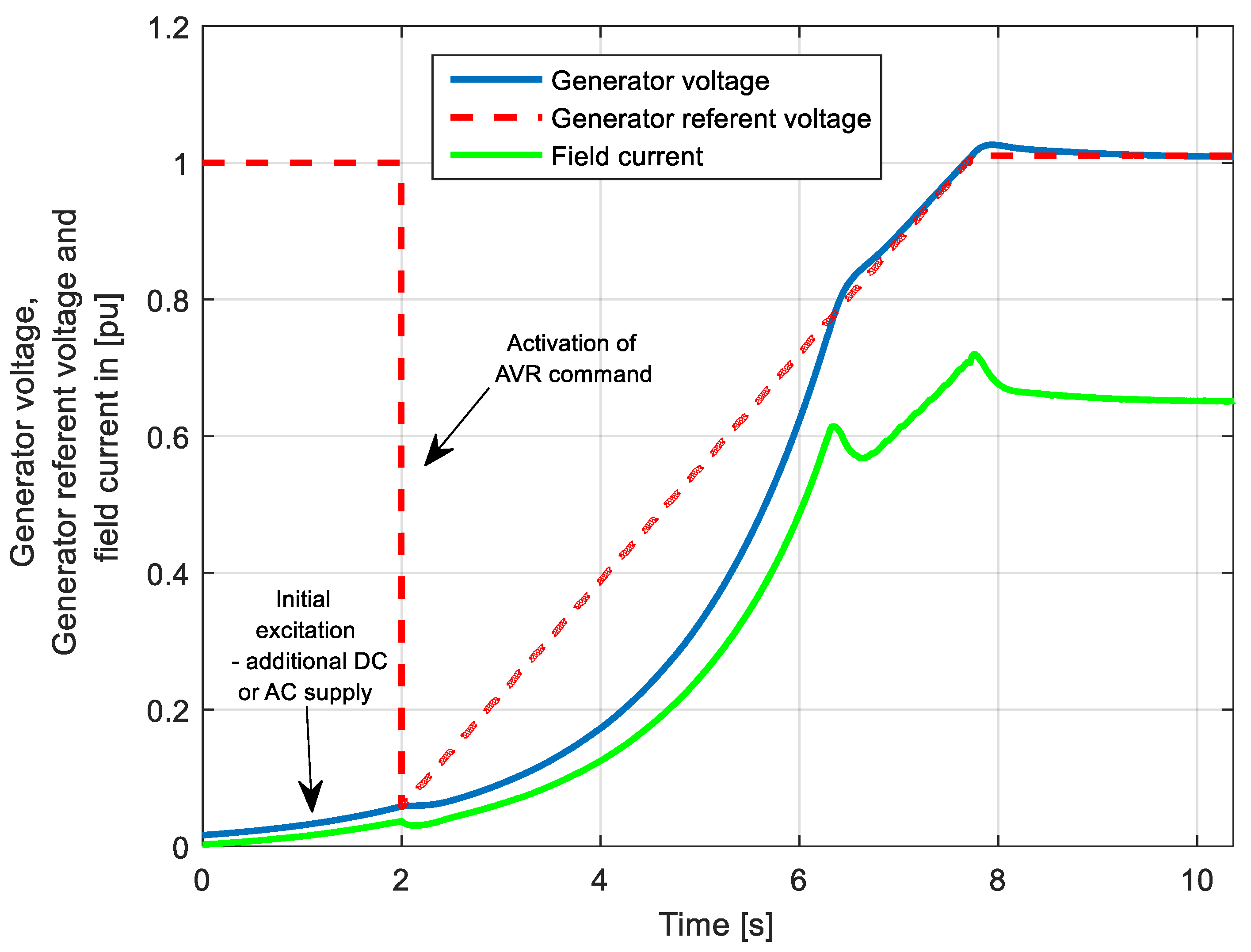
3. Short Notes on Synchronous Generator Starting Excitation
4. Proposed Procedure for Regulator Design in AVRs
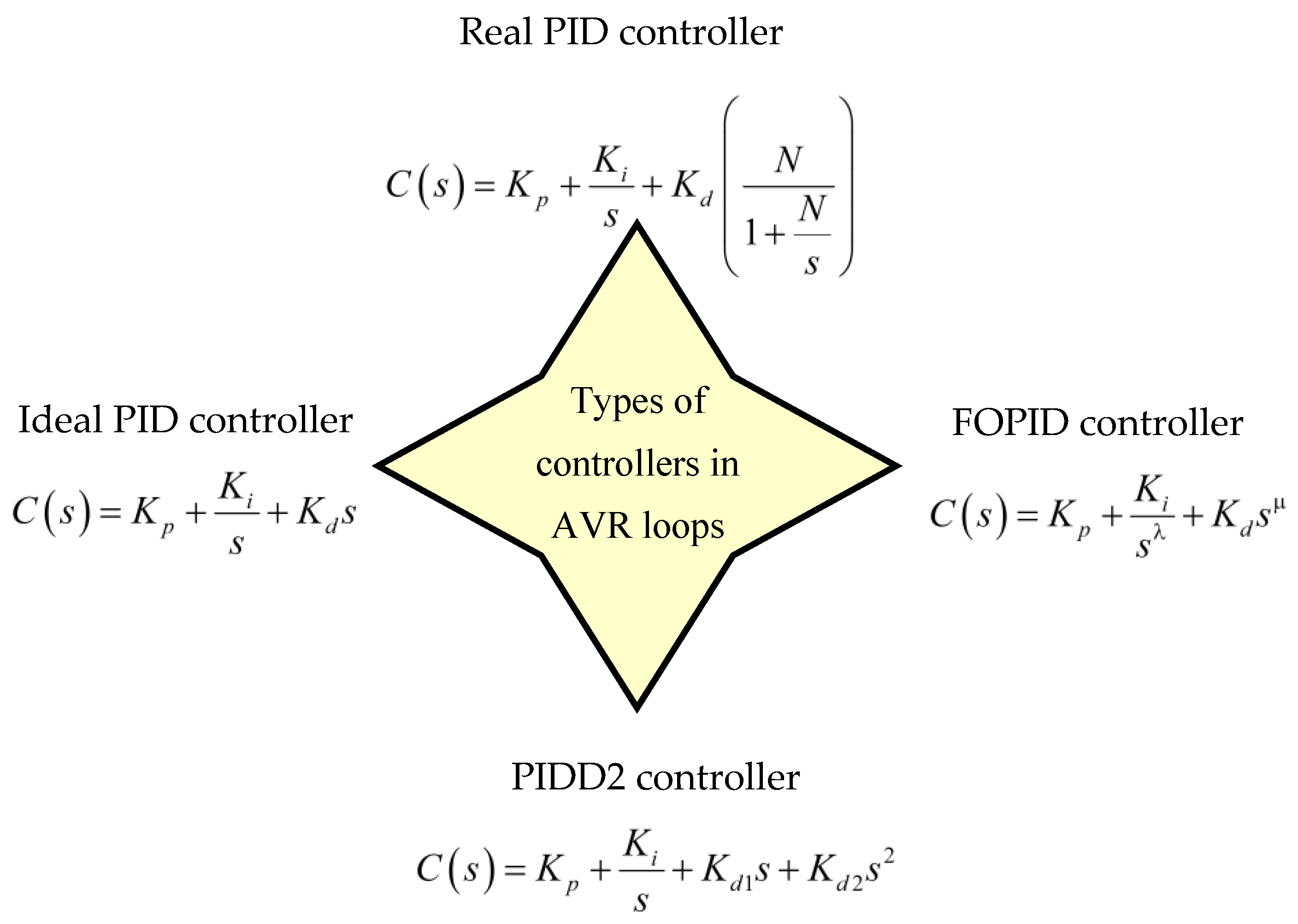
4.1. Novel Procedure for Parameters Design
4.2. Novel Optimization Algorithm for AVR Controllers Design
| Algorithm 1. Pseudo-code of SA (PCSA) |
|
| Algorithm 2 Pseudo-code of SA-GTO algorithm (PCSA-GTO) |
| 1. Set parameters of GTO algorithm: N, N1, N2, p, β, and tmax |
| 2. Apply SA algorithm to initialize the population |
| 3. Assess the fitness of each gorilla |
| 4. for t=1 to tmax |
| 5. Bring up-to-date L and C |
| 6. Conduct EXPr and GX(t) |
| 7. Assess the fitness of each gorilla |
| 8. Update the population X(t) |
| 9. Find Silverback |
| 10. end for |
| 11. Print Xsilverback |
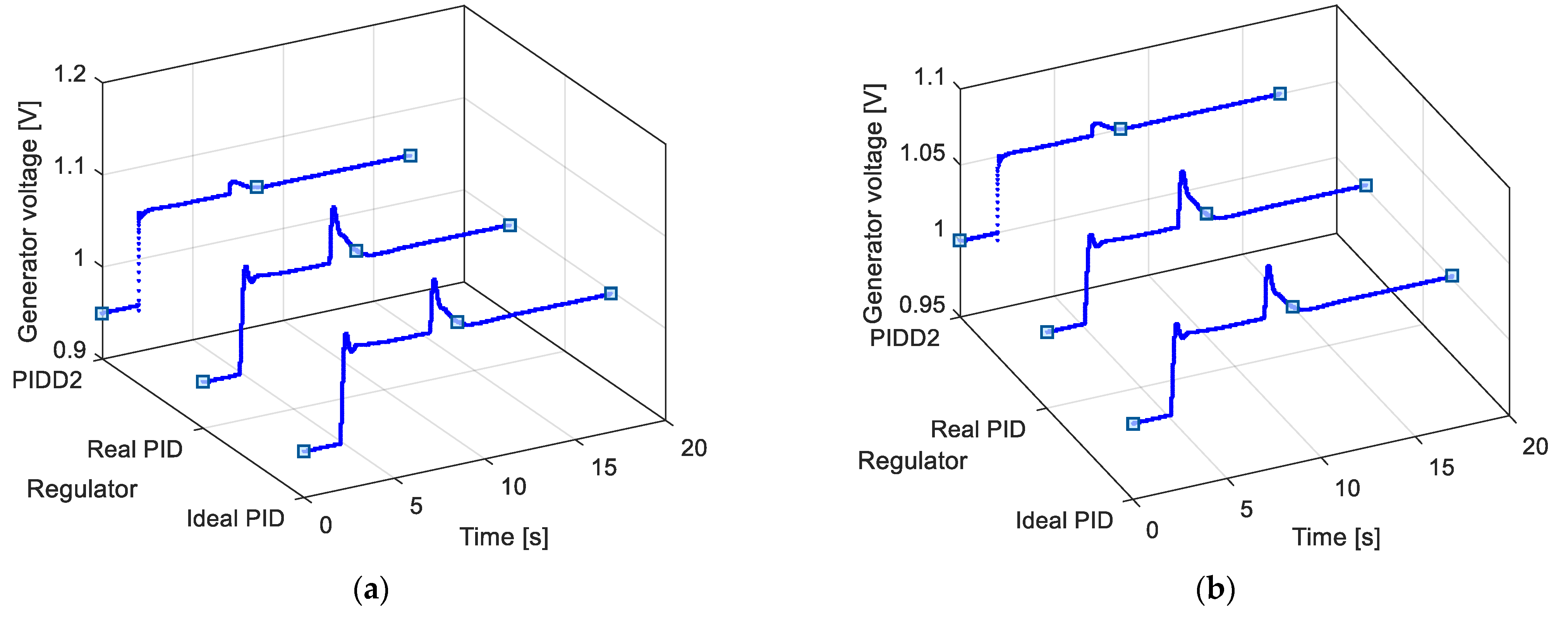
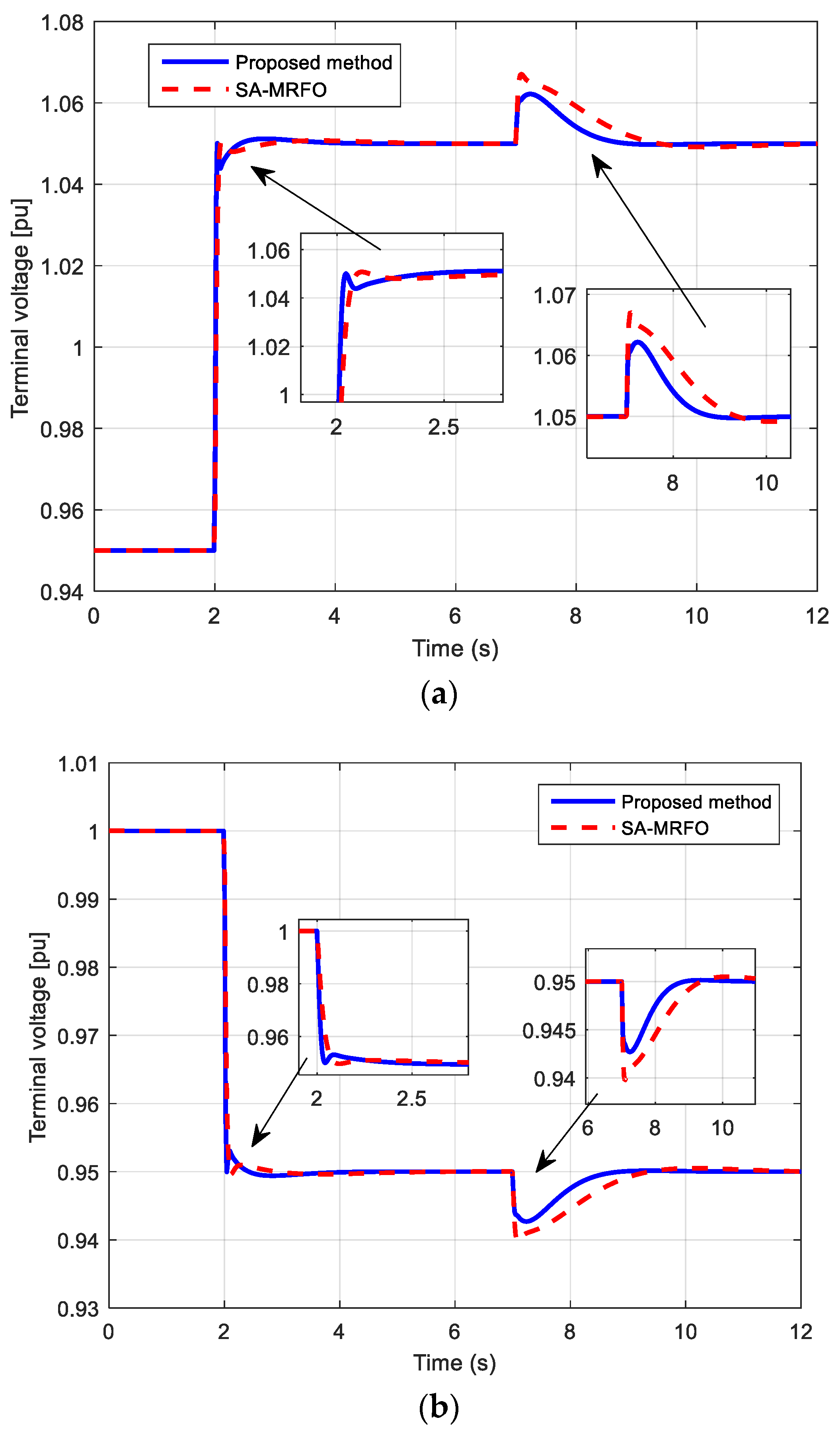
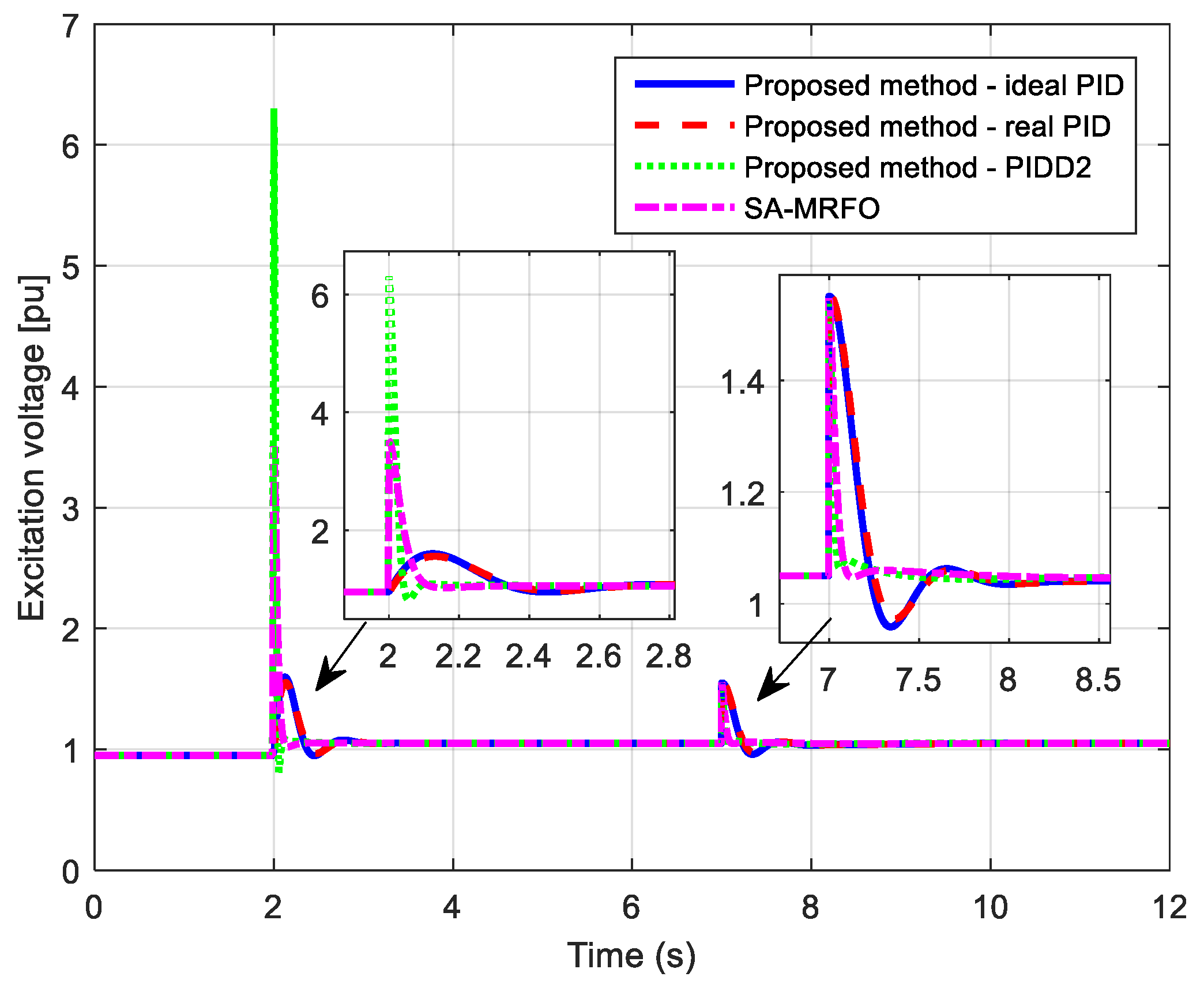
5. Simulation Results with No Limitation of the Excitation Voltage
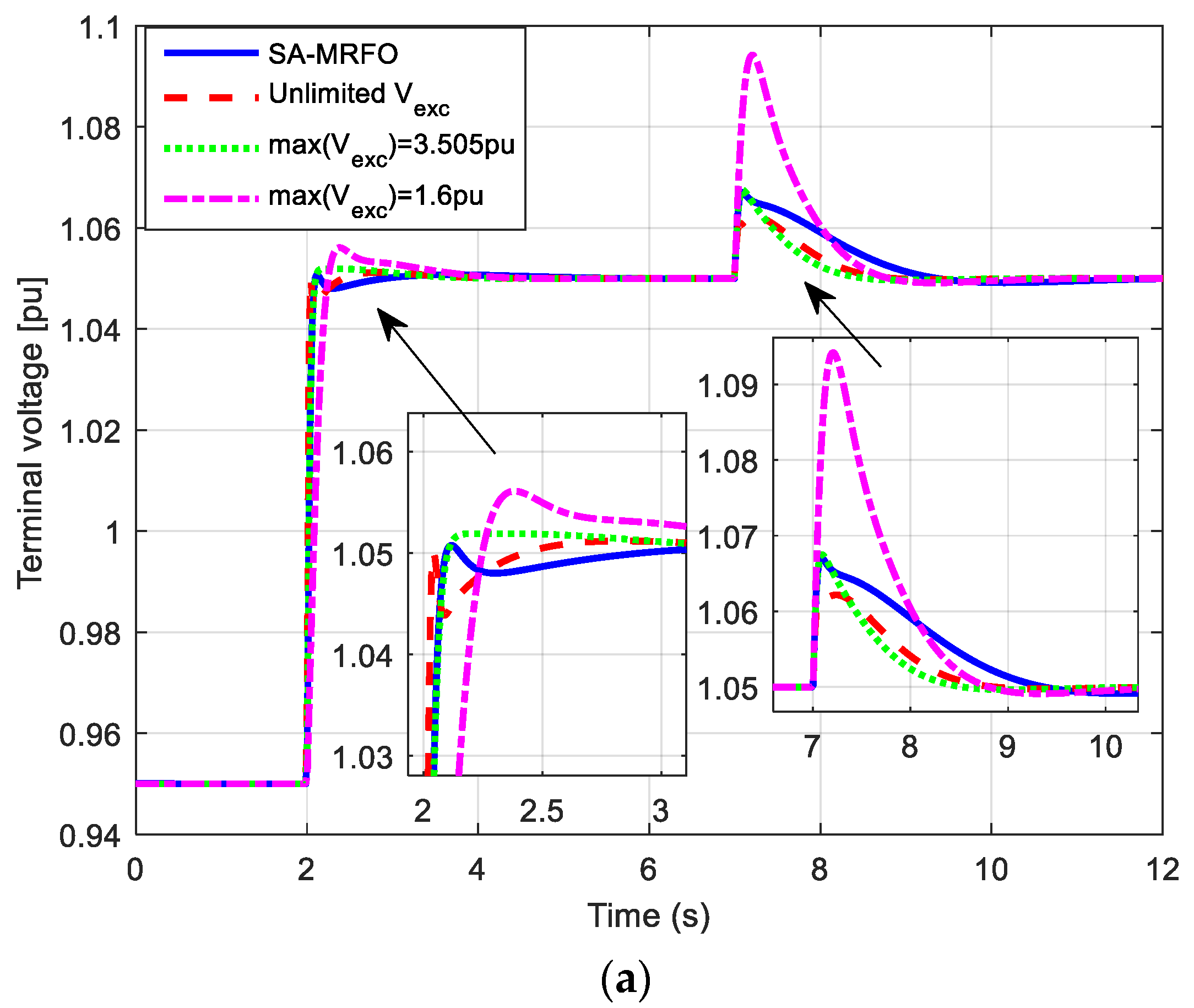
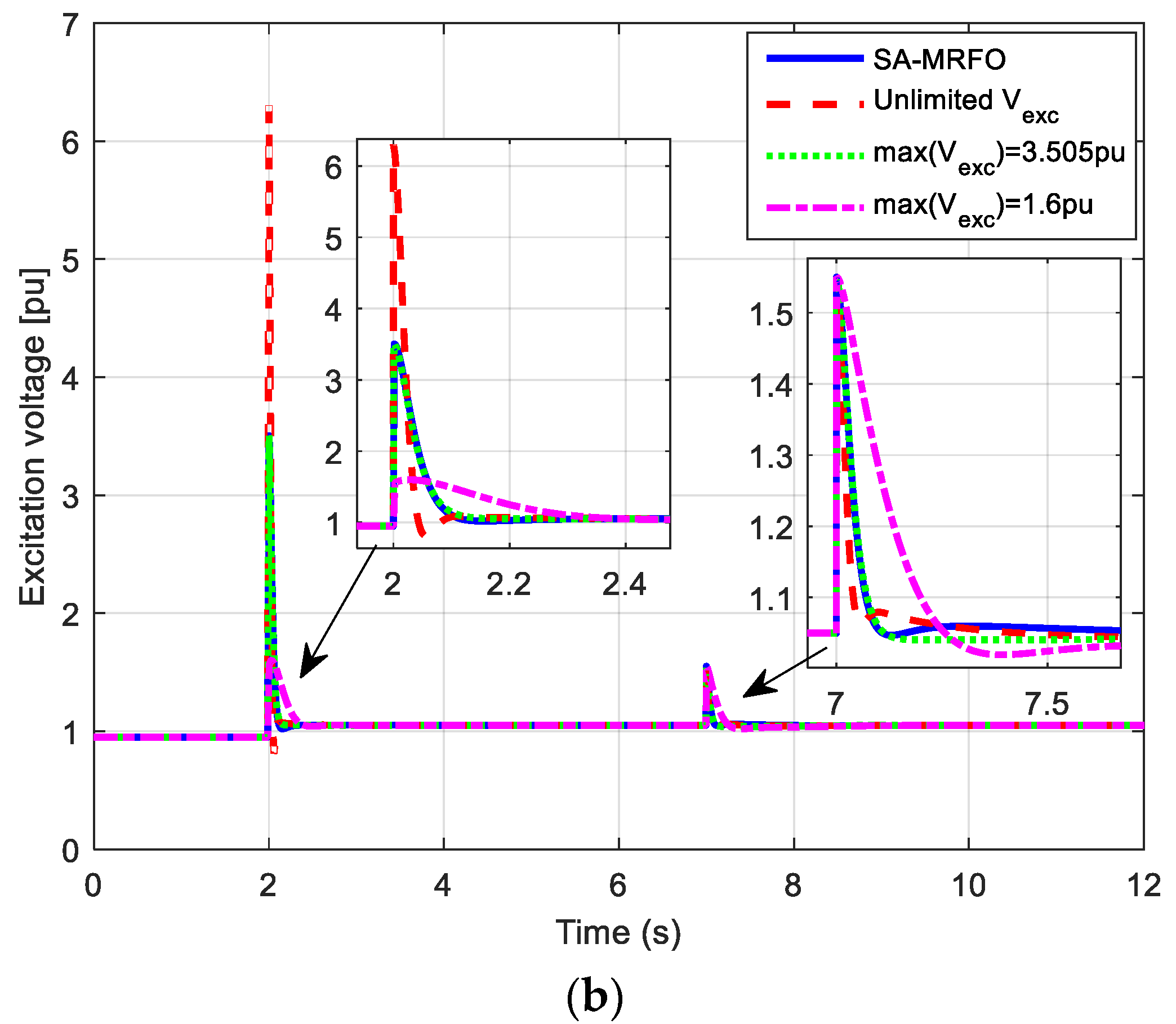
6. Simulation Results with Limitation of the Excitation Voltage
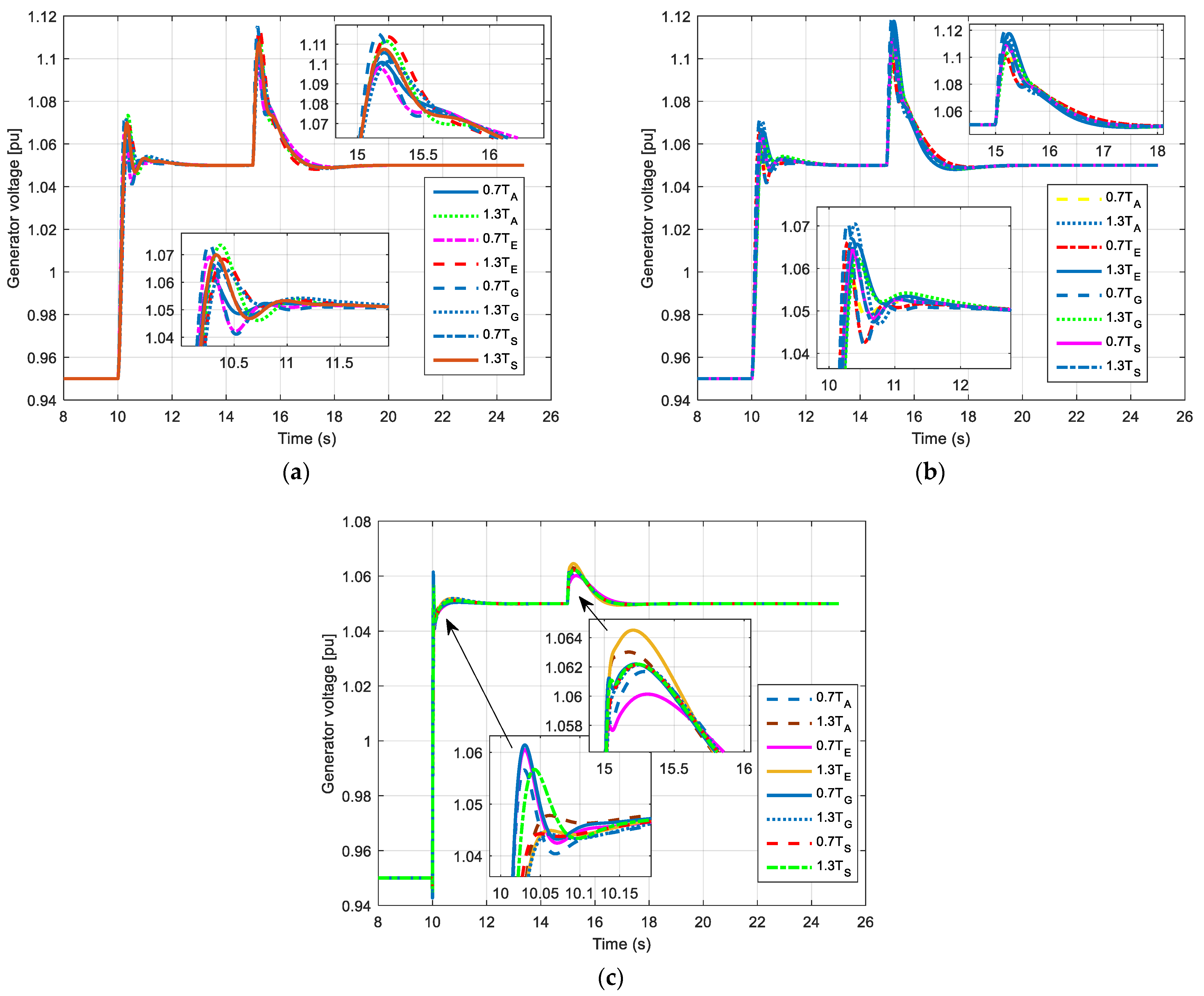
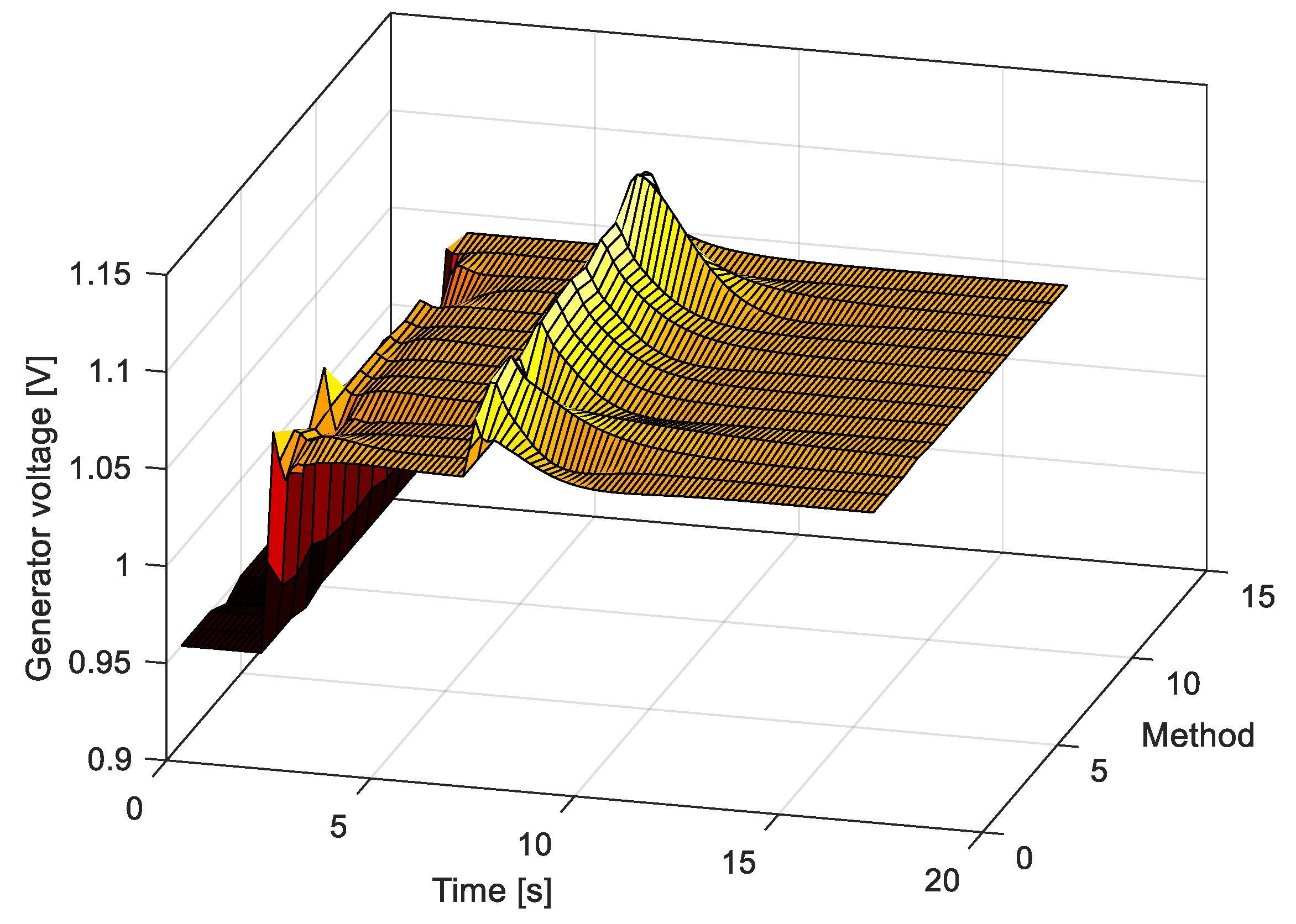
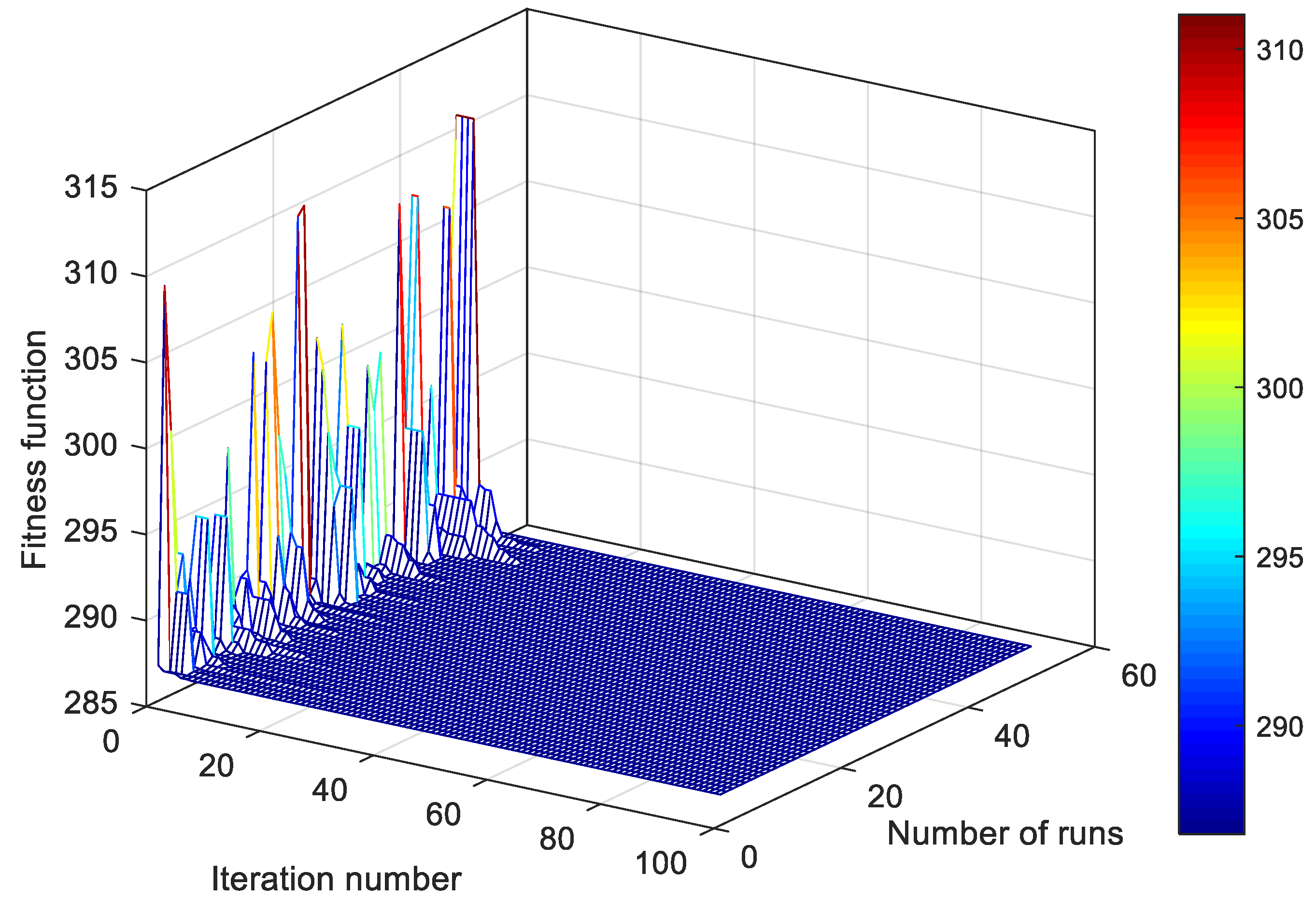
7. Algorithm Testing
8. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A

References
- Glover, J.D.; Sarma, M.S.; Overbye, T.; Birchfield, A. Power System Analysis and Design, 7th ed.; Cengage Learning: Boston, MA, USA, 2022; ISBN 0357676181. [Google Scholar]
- Lipo, T.A. Analysis of Synchronous Machines, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2017; ISBN 9781138073074. [Google Scholar]
- Sikander, A.; Thakur, P. A new control design strategy for automatic voltage regulator in power system. ISA Trans. 2020, 100, 235–243. [Google Scholar] [CrossRef] [PubMed]
- Nøland, J.K.; Nuzzo, S.; Tessarolo, A.; Alves, E.F. Excitation System Technologies for Wound-Field Synchronous Machines: Survey of Solutions and Evolving Trends. IEEE Access 2019, 7, 109699–109718. [Google Scholar] [CrossRef]
- Gaing, Z.-L. A particle swarm optimization approach for optimum design of PID controller in AVR system. IEEE Trans. Energy Convers. 2004, 19, 384–391. [Google Scholar] [CrossRef]
- Micev, M.; Ćalasan, M.; Ali, Z.M.; Hasanien, H.M.; Abdel Aleem, S.H.E. Optimal design of automatic voltage regulation controller using hybrid simulated annealing—Manta ray foraging optimization algorithm. Ain Shams Eng. J. 2021, 12, 641–657. [Google Scholar] [CrossRef]
- Rodriguez, F.J.; García-Martinez, C.; Lozano, M. Hybrid metaheuristics based on evolutionary algorithms and simulated annealing: Taxonomy, comparison, and synergy test. IEEE Trans. Evol. Comput. 2012, 16, 787–800. [Google Scholar] [CrossRef]
- Micev, M.; Ćalasan, M.; Oliva, D. Fractional order PID controller design for an AVR system using Chaotic Yellow Saddle Goatfish Algorithm. Mathematics 2020, 8, 1182. [Google Scholar] [CrossRef]
- Elsisi, M.; Soliman, M. Optimal design of robust resilient automatic voltage regulators. ISA Trans. 2021, 108, 257–268. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.H.; Cho, J.H. Retraction of “A Biologically Inspired Intelligent PID Controller Tuning for AVR Systems”. Int. J. Control. Autom. Syst. 2011, 9, 814. [Google Scholar] [CrossRef]
- Bhullar, A.K.; Kaur, R.; Sondhi, S. Enhanced crow search algorithm for AVR optimization. Soft Comput. 2020, 24, 11957–11987. [Google Scholar] [CrossRef]
- Elsisi, M.; Tran, M.Q.; Hasanien, H.M.; Turky, R.A.; Albalawi, F.; Ghoneim, S.S.M. Robust model predictive control paradigm for automatic voltage regulators against uncertainty based on optimization algorithms. Mathematics 2021, 9, 2885. [Google Scholar] [CrossRef]
- Mosaad, A.M.; Attia, M.A.; Abdelaziz, A.Y. Whale optimization algorithm to tune PID and PIDA controllers on AVR system. Ain Shams Eng. J. 2019, 10, 755–767. [Google Scholar] [CrossRef]
- Blondin, M.J.; Sanchis, J.; Sicard, P.; Herrero, J.M. New optimal controller tuning method for an AVR system using a simplified Ant Colony Optimization with a new constrained Nelder–Mead algorithm. Appl. Soft Comput. 2018, 62, 216–229. [Google Scholar] [CrossRef]
- Tang, Y.; Cui, M.; Hua, C.; Li, L.; Yang, Y. Optimum design of fractional order PIλDμ controller for AVR system using chaotic ant swarm. Expert Syst. Appl. 2012, 39, 6887–6896. [Google Scholar] [CrossRef]
- Sikander, A.; Thakur, P.; Bansal, R.C.; Rajasekar, S. A novel technique to design cuckoo search based FOPID controller for AVR in power systems. Comput. Electr. Eng. 2018, 70, 261–274. [Google Scholar] [CrossRef]
- Mukherjee, V.; Ghoshal, S.P. Intelligent particle swarm optimized fuzzy PID controller for AVR system. Electr. Power Syst. Res. 2007, 77, 1689–1698. [Google Scholar] [CrossRef]
- Wong, C.C.; Li, S.A.; Wang, H.Y. Hybrid evolutionary algorithm for PID controller design of AVR system. J. Chinese Inst. Eng. 2009, 32, 251–264. [Google Scholar] [CrossRef]
- Mohanty, P.K.; Sahu, B.K.; Panda, S. Tuning and Assessment of Proportional–Integral–Derivative Controller for an Automatic Voltage Regulator System Employing Local Unimodal Sampling Algorithm. Electr. Power Components Syst. 2014, 42, 959–969. [Google Scholar] [CrossRef]
- Dos Santos Coelho, L. Tuning of PID controller for an automatic regulator voltage system using chaotic optimization approach. Chaos Solitons Fractals 2009, 39, 1504–1514. [Google Scholar] [CrossRef]
- Gozde, H.; Taplamacioglu, M.C. Comparative performance analysis of artificial bee colony algorithm for automatic voltage regulator (AVR) system. J. Franklin Inst. 2011, 348, 1927–1946. [Google Scholar] [CrossRef]
- Micev, M.; Ćalasan, M.; Oliva, D. Design and robustness analysis of an Automatic Voltage Regulator system controller by using Equilibrium Optimizer algorithm. Comput. Electr. Eng. 2021, 89, 106930. [Google Scholar] [CrossRef]
- Sahib, M.A.; Ahmed, B.S. A new multiobjective performance criterion used in PID tuning optimization algorithms. J. Adv. Res. 2016, 7, 125–134. [Google Scholar] [CrossRef] [PubMed]
- Panda, S.; Sahu, B.K.; Mohanty, P.K. Design and performance analysis of PID controller for an automatic voltage regulator system using simplified particle swarm optimization. J. Franklin Inst. 2012, 349, 2609–2625. [Google Scholar] [CrossRef]
- Zamani, M.; Karimi-Ghartemani, M.; Sadati, N.; Parniani, M. Design of a fractional order PID controller for an AVR using particle swarm optimization. Control Eng. Pract. 2009, 17, 1380–1387. [Google Scholar] [CrossRef]
- Gillard, D.M.; Bollinger, K.E. Neural network identification of power system transfer functions. IEEE Trans. Energy Convers. 1996, 11, 104–110. [Google Scholar] [CrossRef]
- Kim, D.H. Hybrid GA–BF based intelligent PID controller tuning for AVR system. Appl. Soft Comput. 2011, 11, 11–22. [Google Scholar] [CrossRef]
- Ekinci, S.; Hekimoğlu, B. Improved Kidney-Inspired Algorithm Approach for Tuning of PID Controller in AVR System. IEEE Access 2019, 7, 39935–39947. [Google Scholar] [CrossRef]
- Bingul, Z.; Karahan, O. A novel performance criterion approach to optimum design of PID controller using cuckoo search algorithm for AVR system. J. Franklin Inst. 2018, 355, 5534–5559. [Google Scholar] [CrossRef]
- Blondin, M.J.; Sicard, P.; Pardalos, P.M. Controller Tuning Approach with robustness, stability and dynamic criteria for the original AVR System. Math. Comput. Simul. 2019, 163, 168–182. [Google Scholar] [CrossRef]
- Zhang, D.-L.; Tang, Y.-G.; Guan, X.-P. Optimum Design of Fractional Order PID Controller for an AVR System Using an Improved Artificial Bee Colony Algorithm. Acta Autom. Sin. 2014, 40, 973–979. [Google Scholar] [CrossRef]
- Ayas, M.S.; Sahin, E. FOPID controller with fractional filter for an automatic voltage regulator. Comput. Electr. Eng. 2021, 90, 106895. [Google Scholar] [CrossRef]
- Pan, I.; Das, S. Frequency domain design of fractional order PID controller for AVR system using chaotic multi-objective optimization. Int. J. Electr. Power Energy Syst. 2013, 51, 106–118. [Google Scholar] [CrossRef]
- Sahib, M.A. A novel optimal PID plus second order derivative controller for AVR system. Eng. Sci. Technol. Int. J. 2015, 18, 194–206. [Google Scholar] [CrossRef]
- Tabak, A. Maiden application of fractional order PID plus second order derivative controller in automatic voltage regulator. Int. Trans. Electr. Energy Syst. 2021, 31, e13211. [Google Scholar] [CrossRef]
- Chatterjee, S.; Mukherjee, V. PID controller for automatic voltage regulator using teaching–learning based optimization technique. Int. J. Electr. Power Energy Syst. 2016, 77, 418–429. [Google Scholar] [CrossRef]
- Alawad, N.; Rahman, N. Tuning FPID Controller for an AVR System Using Invasive Weed Optimization Algorithm. Jordan J. Electr. Eng. 2020, 6, 1. [Google Scholar] [CrossRef]
- Çelik, E.; Durgut, R. Performance enhancement of automatic voltage regulator by modified cost function and symbiotic organisms search algorithm. Eng. Sci. Technol. Int. J. 2018, 21, 1104–1111. [Google Scholar] [CrossRef]
- Hasanien, H.M. Design Optimization of PID Controller in Automatic Voltage Regulator System Using Taguchi Combined Genetic Algorithm Method. IEEE Syst. J. 2013, 7, 825–831. [Google Scholar] [CrossRef]
- Altbawi SM, A.; Mokhtar AS, B.; Jumani, T.A.; Khan, I.; Hamadneh, N.N.; Khan, A. Optimal design of Fractional order PID controller based Automatic voltage regulator system using gradient-based optimization algorithm. J. King Saud Univ. Eng. Sci. 2021. [Google Scholar] [CrossRef]
- Ćalasan, M.; Micev, M.; Radulović, M.; Zobaa, A.F.; Hasanien, H.M.; Abdel Aleem, S.H.E. Optimal pid controllers for avr system considering excitation voltage limitations using hybrid equilibrium optimizer. Machines 2021, 9, 265. [Google Scholar] [CrossRef]
- Tang, Y.; Zhao, L.; Han, Z.; Bi, X.; Guan, X. Optimal gray PID controller design for automatic voltage regulator system via imperialist competitive algorithm. Int. J. Mach. Learn. Cybern. 2016, 7, 229–240. [Google Scholar] [CrossRef]
- Oziablo, P.; Mozyrska, D.; Wyrwas, M. Fractional-variable-order digital controller design tuned with the chaotic yellow saddle goatfish algorithm for the AVR system. ISA Trans. 2022, 125, 260–267. [Google Scholar] [CrossRef] [PubMed]
- Bakir, H.; Guvenc, U.; Tolga Kahraman, H.; Duman, S. Improved Lévy flight distribution algorithm with FDB-based guiding mechanism for AVR system optimal design. Comput. Ind. Eng. 2022, 168, 108032. [Google Scholar] [CrossRef]
- Mok, R.; Ahmad, M.A. Fast and optimal tuning of fractional order PID controller for AVR system based on memorizable-smoothed functional algorithm. Eng. Sci. Technol. Int. J. 2022, 35, 101264. [Google Scholar] [CrossRef]
- Ekinci, S.; Izci, D.; Abu Zitar, R.; Alsoud, A.R.; Abualigah, L. Development of Lévy flight-based reptile search algorithm with local search ability for power systems engineering design problems. Neural Comput. Appl. 2022, 34, 20263–20283. [Google Scholar] [CrossRef]
- Paliwal, N.; Srivastava, L.; Pandit, M. Rao algorithm based optimal Multi-term FOPID controller for automatic voltage regulator system. Optim. Control Appl. Methods 2022, 43, 1707–1734. [Google Scholar] [CrossRef]
- Furat, M.; Cücü, G.G. Design, Implementation, and Optimization of Sliding Mode Controller for Automatic Voltage Regulator System. IEEE Access 2022, 10, 55650–55674. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Soleimanian Gharehchopogh, F.; Mirjalili, S. Artificial gorilla troops optimizer: A new nature-inspired metaheuristic algorithm for global optimization problems. Int. J. Intell. Syst. 2021, 36, 5887–5958. [Google Scholar] [CrossRef]
- Ćalasan, M.; Micev, M.; Ali, Z.M.; Zobaa, A.F.; Aleem, S.H.E.A. Parameter estimation of induction machine single-cage and double-cage models using a hybrid simulated annealing-evaporation rate water cycle algorithm. Mathematics 2020, 8, 1024. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Hussain, K.; Mabrouk, M.S.; Al-Atabany, W. Honey Badger Algorithm: New metaheuristic algorithm for solving optimization problems. Math. Comput. Simul. 2022, 192, 84–110. [Google Scholar] [CrossRef]



| AVR Mod | FCR Mod | ||
|---|---|---|---|
| Shunt supply | Power supply from sub-distribution of the 0.4 kV power plant (or auxiliary supply) | Shunt supply | Power supply from sub-distribution of the 0.4 kV power plant (or auxiliary supply) |
| Switch for selecting excitation power supply from the generator branch | Switch for power supply from sub-distribution of the 0.4 kV power plant (or auxiliary supply) | Switch for selecting excitation power supply from the generator branch | Switch for power supply from sub-distribution of the 0.4 kV power plant (or auxiliary supply) |
| Start excitation | Start excitation | Start excitation | Start excitation |
| Switch the breaker in the 0.4 kV excitation enclosure | Switch the contactor in the 0.4 kV sub-distribution power plant of the generator | Switch the breaker in the 0.4 kV excitation enclosure | Switch the contactor in the 0.4 kV sub-distribution power plant of the generator |
| Start DC or AC initial excitation | Switch the breaker in the 0.4 kV excitation enclosure | Start DC or AC initial excitation | Switch the breaker in the 0.4 kV excitation enclosure |
| Switch-off initial excitation—filed current reached the predefined value | Raising the voltage of the generator via the ramp function | Switch-off initial excitation—filed current reached the predefined value | Raising the field current via the ramp function |
| Raising the voltage of the generator via the ramp function | Switch network monitoring block that balances the voltage of the generator and the network | Increasing the field current via the ramp function | The excitation current is raised with the manual control buttons until the nominal value of the generator voltage is obtained |
| Switch network monitoring block that balances the voltage of the generator and the network | The generator is ready for synchronization | The excitation current is raised with the manual control buttons until the nominal value of the generator voltage is obtained | The generator is ready for synchronization |
| Regulator | Kp | Ki | Kd | Kd2 | N |
|---|---|---|---|---|---|
| Ideal PID | 1.263847093 | 1.400111255 | 0.4484544985 | -- | -- |
| Real PID | 1.120196097 | 1.200245817 | 0.4066544346 | -- | 895.0548956 |
| PIDD2 | 4.825180395 | 5.000000000 | 1.8100162290 | 0.2140057958 | -- |
| Metrics | Type of Regulator | ||
|---|---|---|---|
| Ideal PID | Real PID | PIDD2 | |
| tr1 | 0.148593626855451 | 0.161054345783414 | 0.023681675214101 |
| ts1 | 1.262884640998164 | 1.412479339684174 | 0.247536364709054 |
| Mp1 | 1.754445571697461 | 1.482506607949641 | 0.112633920529492 |
| ts2 | 1.882946431460990 | 2.005356494034402 | 1.716958369066589 |
| Mp2 | 5.387282031380347 | 5.706993590644194 | 1.159788425071007 |
| Regulator | Time Constant | Change (%) | tr1 | ts1 | Mp1 | ts1 | Mp1 |
|---|---|---|---|---|---|---|---|
| Ideal PID | TA | −30 | 0.1369 | 1.4005 | 1.1208 | 3.0341 | 4.8417 |
| +30 | 0.1602 | 1.3372 | 2.2358 | 1.8253 | 5.8607 | ||
| TE | −30 | 0.1197 | 0.8295 | 1.8230 | 2.1727 | 4.5865 | |
| +30 | 0.1753 | 1.5291 | 1.7515 | 2.9602 | 6.0759 | ||
| TG | −30 | 0.1153 | 0.8434 | 2.2699 | 1.8901 | 6.1944 | |
| +30 | 0.1812 | 1.8210 | 1.4420 | 3.2120 | 4.8892 | ||
| TS | −30 | 0.1511 | 1.2925 | 1.6169 | 2.8189 | 5.3048 | |
| +30 | 0.1463 | 1.2388 | 1.8995 | 1.8759 | 5.4709 | ||
| Real PID | TA | −30 | 0.1497 | 1.5090 | 0.8693 | 3.1855 | 5.1477 |
| +30 | 0.1729 | 1.4280 | 1.9528 | 1.9439 | 6.1944 | ||
| TE | −30 | 0.1293 | 0.6854 | 1.5349 | 2.2991 | 4.8638 | |
| +30 | 0.1904 | 1.6550 | 1.5003 | 3.1108 | 6.4317 | ||
| TG | −30 | 0.1240 | 0.6947 | 1.9898 | 2.0158 | 6.5460 | |
| +30 | 0.1976 | 1.9674 | 1.1880 | 3.3978 | 5.1914 | ||
| TS | −30 | 0.1637 | 1.4500 | 1.3603 | 2.9610 | 5.6259 | |
| +30 | 0.1586 | 1.3656 | 1.6114 | 1.9985 | 5.7893 | ||
| PIDD2 | TA | −30 | 0.0152 | 0.2895 | 0.6256 | 2.4961 | 1.1127 |
| +30 | 0.0333 | 0.1928 | 0.1199 | 1.6599 | 1.2401 | ||
| TE | −30 | 0.0146 | 0.2891 | 1.0001 | 2.0370 | 0.9654 | |
| +30 | 0.0363 | 0.2284 | 0.1765 | 2.6276 | 1.3826 | ||
| TG | −30 | 0.0145 | 0.2384 | 1.0878 | 1.7325 | 1.1621 | |
| +30 | 0.0372 | 0.2581 | 0.1830 | 2.5939 | 1.1568 | ||
| TS | −30 | 0.0291 | 0.2539 | 0.1124 | 2.3695 | 1.1584 | |
| +30 | 0.0215 | 0.2413 | 0.6376 | 1.7132 | 1.1613 |
| Algorithm | Regulator Type | Reference | Gains | |||||
|---|---|---|---|---|---|---|---|---|
| Number | Name | Kp | Ki | Kd | Kd2 | N | ||
| 1 | IKIA | Ideal PID | [28] | 1.0426 | 1.0093 | 0.5999 | - | - |
| 2 | WOA | [13] | 0.7847 | 0.9961 | 0.3061 | - | - | |
| 3 | SA-MRFO | [6] | 0.6778 | 0.3802 | 0.2663. | - | - | |
| 4 | DE | [21] | 1.6524 | 0.4083 | 0.3654 | - | - | |
| 5 | BF–GA | [10] | 0.6823 | 0.6138 | 0.2678 | - | - | |
| 6 | 0.6800 | 0.5221 | 0.2440 | - | - | |||
| 7 | 0.6727 | 0.4786 | 0.2298 | - | - | |||
| 8 | SA-MRFO | Real PID | [6] | 0.6672 | 0.5938 | 0.2599 | - | 863.2453 |
| 9 | CS | [29] | 0.6198 | 0.4165 | 0.2126 | - | 1000.00 | |
| 10 | ACO–NM | [30] | 0.6392 | 0.4757 | 0.2159 | - | 484.09 | |
| 11 | 0.3120 | 0.2567 | 0.1503 | - | 500.00 | |||
| 12 | 0.5463 | 0.3409 | 0.1485 | - | 500.00 | |||
| 13 | CAS | PIDD2 | [6] | 2.9943 | 2.9787 | 1.5882 | 0.102 | - |
| 14 | SA–MRFO | [34] | 2.7784 | 1.8521 | 0.9997 | 0.073 | - | |
| Algorithm Number | Regulator | Reference | tr1 | ts1 | Mp1 | ts1 | Mp1 |
|---|---|---|---|---|---|---|---|
| 1 | Ideal PID | [28] | 0.1274 | 0.7509 | 1.4379 | 4.9617 | 4.7547 |
| 2 | [13] | 0.2149 | 2.1440 | 0.6937 | 3.5659 | 6.6722 | |
| 3 | [6] | 0.2587 | 1.7455 | 0 | 5.7157 | 7.2445 | |
| 4 | [21] | 0.1572 | 2.4050 | 2.3068 | 8.3521 | 5.3198 | |
| 5 | [10] | 0.2521 | 0.3778 | 0.1873 | 2.7347 | 7.2116 | |
| 6 | 0.2686 | 0.9106 | 0.1843 | 3.5329 | 7.5249 | ||
| 7 | 0.2797 | 0.9651 | 0.1850 | 4.0707 | 7.7319 | ||
| 8 | Real PID | [6] | 0.2575 | 0.3880 | 0.1659 | 2.7845 | 7.3442 |
| 9 | [29] | 0.3055 | 1.1777 | 0.0106 | 4.5238 | 8.0943 | |
| 10 | [30] | 0.2926 | 0.4422 | 0.1656 | 3.8047 | 8.0134 | |
| 11 | 1.0319 | 1.8362 | 0.1384 | 5.8342 | 10.5688 | ||
| 12 | 0.3809 | 0.8202 | 0.2010 | 5.2956 | 9.4606 | ||
| 13 | PIDD2 | [6] | 0.0539 | 0.0804 | 0.0756 | 4.2879 | 1.6245 |
| 14 | [34] | 0.0931 | 0.1602 | 0.0032 | 4.0873 | 2.2529 |
| Maximum Excitation Voltage | Kp | Ki | Kd | Kd2 |
|---|---|---|---|---|
| 3.505 | 4.45574152 | 5.401661897 | 1.44405464 | 0.1020983978 |
| 1.600 | 1.541442548 | 1.757814635 | 0.5032448964 | 0.02383454485 |
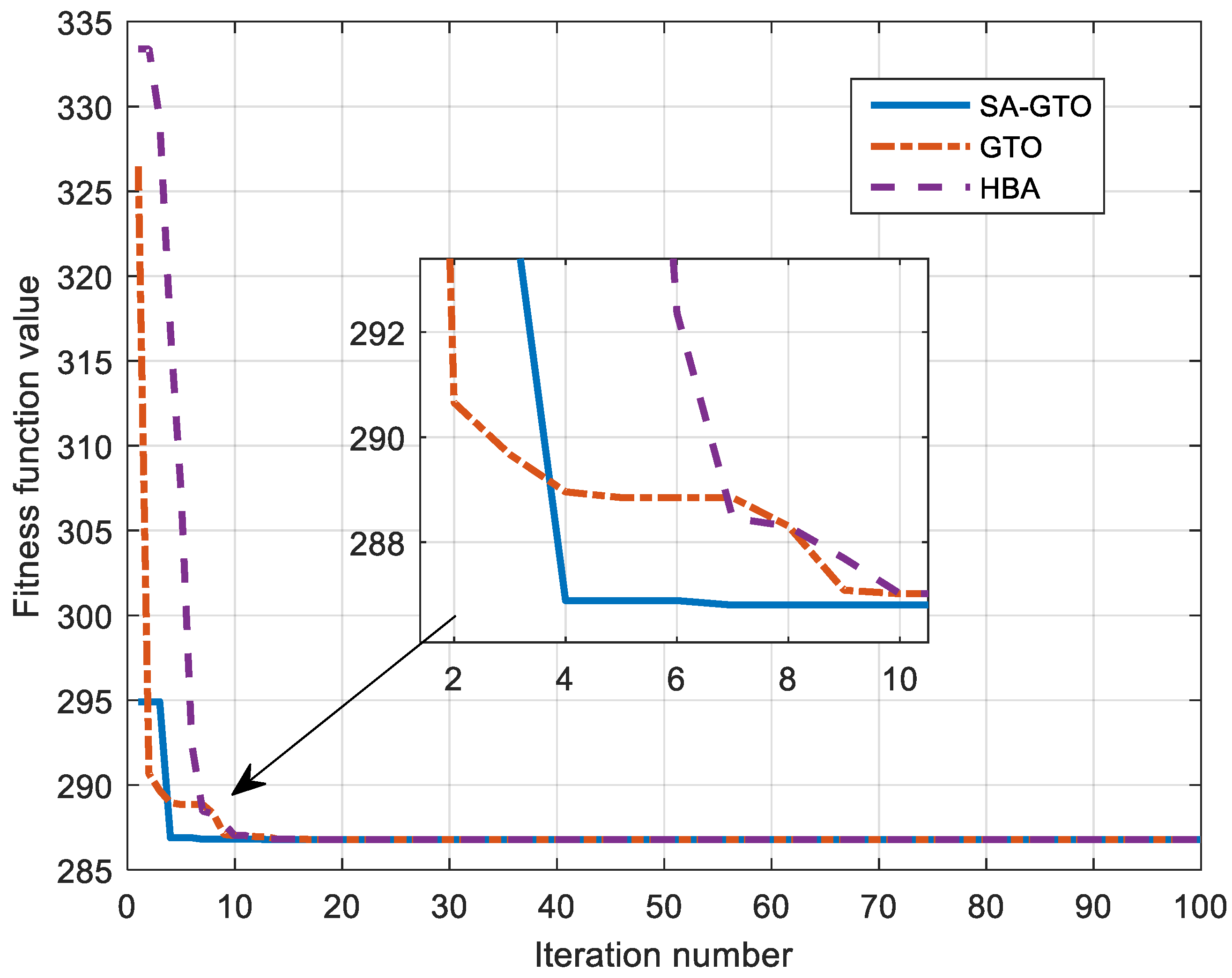
| Metric | SA-GTO | GTO | HBA |
|---|---|---|---|
| Best | 286.792714912089 | 286.792714912101 | 286.792714912099 |
| Worst | 286.792714912148 | 286.792714912125 | 286.792714912130 |
| Mean | 286.792714912103 | 286.792714912110 | 286.792714912112 |
| Median | 286.792714912102 | 286.792714912107 | 286.792714912111 |
| Standard deviation | 8.76202580780095 × 10−12 | 9.07623655038029 × 10−12 | 9.62850632510405 × 10−12 |
| Wilcoxon test results | |||
| SA-GTO versus GTO | SA-GTO versus HBA | ||
| 0.0257 | 0.0091 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alghamdi, S.; Sindi, H.F.; Rawa, M.; Alhussainy, A.A.; Calasan, M.; Micev, M.; Ali, Z.M.; Abdel Aleem, S.H.E. Optimal PID Controllers for AVR Systems Using Hybrid Simulated Annealing and Gorilla Troops Optimization. Fractal Fract. 2022, 6, 682. https://doi.org/10.3390/fractalfract6110682
Alghamdi S, Sindi HF, Rawa M, Alhussainy AA, Calasan M, Micev M, Ali ZM, Abdel Aleem SHE. Optimal PID Controllers for AVR Systems Using Hybrid Simulated Annealing and Gorilla Troops Optimization. Fractal and Fractional. 2022; 6(11):682. https://doi.org/10.3390/fractalfract6110682
Chicago/Turabian StyleAlghamdi, Sultan, Hatem F. Sindi, Muhyaddin Rawa, Abdullah A. Alhussainy, Martin Calasan, Mihailo Micev, Ziad M. Ali, and Shady H. E. Abdel Aleem. 2022. "Optimal PID Controllers for AVR Systems Using Hybrid Simulated Annealing and Gorilla Troops Optimization" Fractal and Fractional 6, no. 11: 682. https://doi.org/10.3390/fractalfract6110682
APA StyleAlghamdi, S., Sindi, H. F., Rawa, M., Alhussainy, A. A., Calasan, M., Micev, M., Ali, Z. M., & Abdel Aleem, S. H. E. (2022). Optimal PID Controllers for AVR Systems Using Hybrid Simulated Annealing and Gorilla Troops Optimization. Fractal and Fractional, 6(11), 682. https://doi.org/10.3390/fractalfract6110682










