Dynamical Analysis of a Novel Fractional-Order Chaotic System Based on Memcapacitor and Meminductor

Abstract

In this paper, a chaotic circuit based on a memcapacitor and meminductor is constructed, and its dynamic equation is obtained. Then, the mathematical model is obtained by normalization, and the system is decomposed and summed by an Adomian decomposition method (ADM) algorithm. So as to study the dynamic behavior in detail, not only the equilibrium stability of the system is analyzed, but also the dynamic characteristics are analyzed by means of a Bifurcation diagram and Lyapunov exponents (Les). By analyzing the dynamic behavior of the system, some special phenomena, such as the coexistence of attractor and state transition, are found in the system. In the end, the circuit implementation of the system is implemented on a Digital Signal Processing (DSP) platform. According to the numerical simulation results of the system, it is found that the system has abundant dynamical characteristics.

1. Introduction

Chaotic systems exist widely in nature; that is to say, chaotic systems are universal, while other systems only exist in a certain range of time and space. In recent years, on account of the rapid development of mathematical science, physical science and instrument science, the research of chaotic systems has made great progress. In 1984, L.O. Chua proposed Chua’s circuit, which first combined chaotic theory with nonlinear circuits [1]. With the in-depth study of chaotic theory, many new chaotic systems have been put forward by some researchers, and the analysis of the dynamic behavior of chaotic systems has improved gradually [2,3,4,5,6]. Not only integer-order chaotic systems but also fractional-order chaotic systems are studied [7,8,9,10,11,12]. It is undeniable that the study of the dynamics of chaotic systems by constructing nonlinear circuits is still the focus of chaos research [13,14,15].

Nonlinear components are important parts of nonlinear circuits, and memristors, memcapacitors and meminductors are more representative of nonlinear components; therefore, the research of memristors, memcapacitors and meminductors is very important. In 1971, Professor Chua proposed a new nonlinear device called a memristor [16]. In 1976, Professor Chua carried out further research on memristors and divided the memristor into charge-controlled memristors and magnetic-controlled memristors [17]. In 2009, on account of the research of memristor, Professor Chua proposed two new nonlinear components: a memcapacitor and a meminductor [18]. Due to the memristive characteristics of memristors, memcapacitors and meminductors, many chaotic oscillators with excellent performance have been made based on memristors, memcapacitors and meminductors, and their dynamic characteristics have been analyzed [19,20,21,22].

Even though scholars have completed a lot of research on integer-order chaotic systems based on memristors, memcapacitors and meminductors, there is still little research on fractional-order chaotic systems based on memristors, memcapacitors and meminductors. At present, with the continuous study of chaotic systems, more and more scholars have begun to explore fractional-order chaotic systems [23,24]. Scholars find that the fractional-order chaotic system, constructed by introducing fractional differential operators into the integer-order chaotic system, still exhibits complex, chaotic behavior [25,26,27]. Because of the rich, dynamic behavior of the fractional chaotic system, it has a good application prospect in neural networks [28,29,30,31,32,33,34], chaotic secure communication [35,36,37,38,39] and image encryption [40,41,42,43,44,45].

At present, the time–frequency conversion method on account of the R-L definition and the predictor–corrector algorithm based on the Caputo definition are widely used in solving fractional chaotic systems [46,47]. However, due to the large step size and limited accuracy of the time–frequency conversion method, many scholars have questioned whether it can accurately represent the dynamic characteristics and change rules of fractional chaotic systems [48]. Although the results of the predictor–corrector algorithm are more accurate than the time–frequency conversion method, and it can study the dynamic behaviors of the system while the order changes continuously, each iteration of the predictor–corrector algorithm requires all the previous historical data, which makes for further iterations of the algorithm, slower solution speed and more memory resources consumed. The Adomian algorithm is a common algorithm for solving the nonlinear time-domain problem [49]. ADM has the advantages of low algorithm consumption and small order required by the system. The Adomian algorithm is one of the mainstream methods of studying fractional systems. In this paper, two theoretical innovations and one experimental contribution are mainly included:

(1)

A novel chaotic system based on a meminductor and memcapacitor is designed, and its unique dynamic characteristics are revealed.

(2)

By introducing the fractional differential operator into the chaotic system based on the memcapacitor and meminductor, a new fractional chaotic system is constructed, and its dynamic characteristics are analyzed.

(3)

The fractional chaotic system based on a meminductor and memcapacitor is implemented and demonstrated on a DSP platform.

The rest of the paper is as follows: In the second part, the model of the meminductor and memcapacitor is given. In the third part, the simple chaotic circuit and dynamic equation are constructed based on the memcapacitor and meminductor, and the fractional differential equation is acquired by introducing the fractional differential operator, which is decomposed by the ADM algorithm. Further, the dynamic behavior is analyzed by a Bifurcation diagram and LEs. In the fourth part, the system is implemented on a DSP platform. Finally, the work in the article is summarized.

2. Model of the Meminductor and Memcapacitor

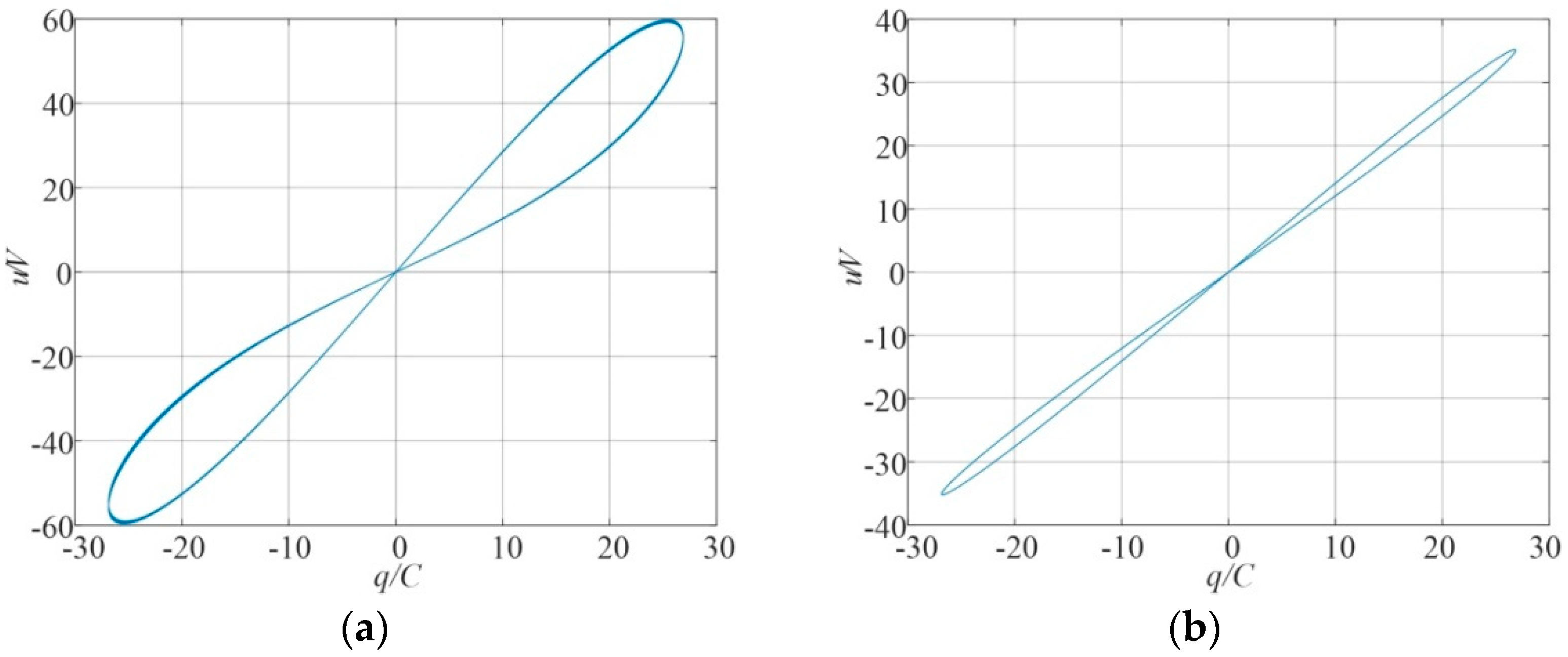
2.1. Model of the Memcapacitor

The memcapacitor is a special kind of nonlinear element. According to Chua’s definition of a memcapacitor, the model of the memcapacitor is shown as:

$$\left\{\begin{array}{l}v\left(t\right)=C_{\mathrm{M}}^{-1}\left(\sigma \right)q\left(t\right)\\ C_{\mathrm{M}}^{-1}\left(\sigma \right)=c+d\cos (\sigma )\\ \sigma ={\displaystyle {\int }_{t_0}^{t}q}\left(\tau \right)\mathrm{d}\tau \\ \theta ={\displaystyle {\int }_{t_0}^{t}i}\left(\tau \right)\mathrm{d}\tau \end{array}\right.,$$

(1)

In order to introduce the memristive characteristics of the memcapacitor more accurately, a sinusoidal current source is added to both ends of the memcapacitor. Denote the inner control parameters of the memcapacitor as c = 2 and d = 1. The relationship between the input q and the related output v with respect to the iteration number is shown in Figure 1a. We obtain a smooth “8” hysteresis curve. When other parameters are kept constant and only the input frequency is changed, the side lobe area of the curve decreases as the frequency increases, which also conforms to the definition of the memcapacitor.

2.2. Model of the Meminductor

The meminductor has very special kinetic properties. According to Professor Chua’s definition, the mathematical model of the meminductor is shown below:

$$\left\{\begin{array}{l}i\left(t\right)=L_{\mathrm{M}}^{-1}\left(\rho \right)\varphi \left(t\right)\\ L_{\mathrm{M}}^{-1}\left(\rho \right)=a+b\cos (\rho )\\ \rho ={\displaystyle {\int }_{t_0}^t\varphi }\left(\tau \right)\mathrm{d}\tau \\ \varphi ={\displaystyle {\int }_{t_0}^{t}v}\left(\tau \right)\mathrm{d}\tau \end{array}\right.,$$

(2)

To further understand the basic properties of the meminductor, let the current through the meminductor be i = Asin(2πft). If a = 1, b = 1 are the internal parameters; the relationship between its output and input is shown in Figure 2a. We obtain a smooth “8” hysteresis curve. 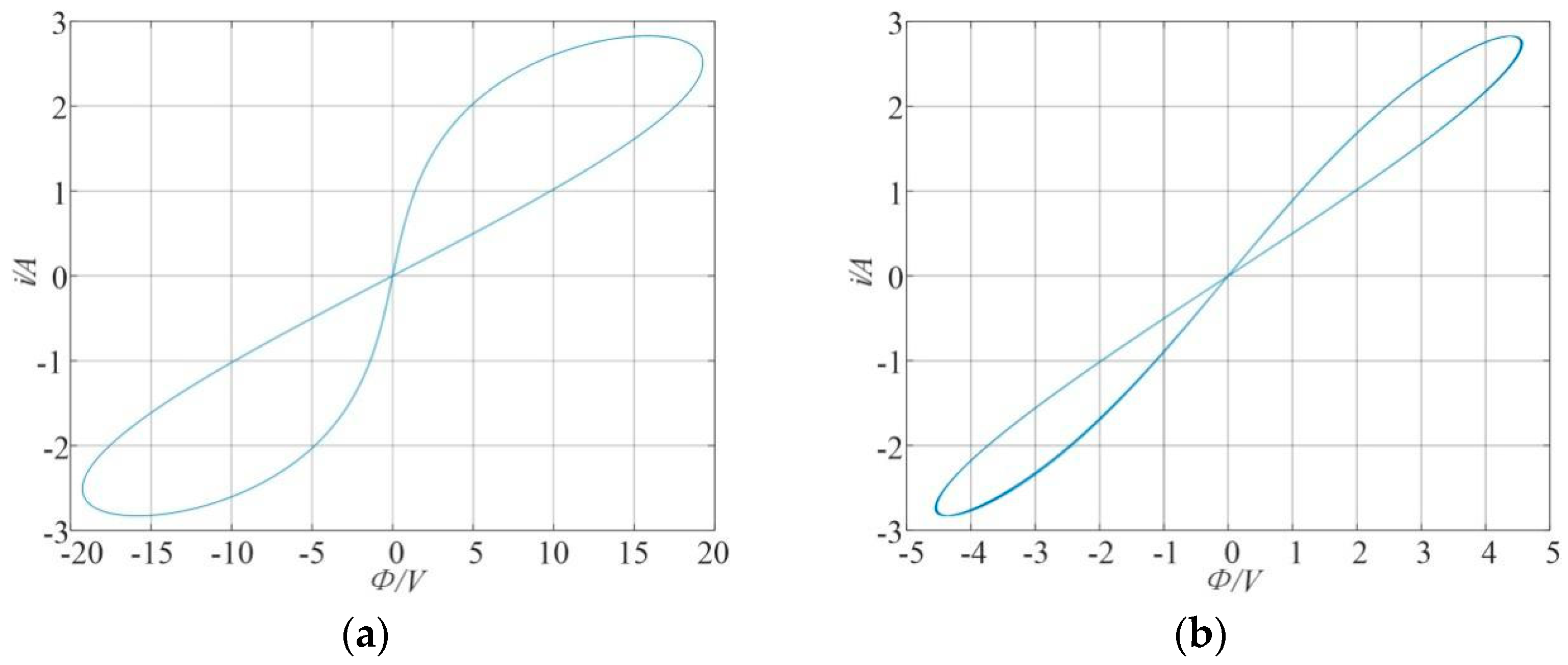While keeping the parameters constant and only changing the input frequency, the sidelobe area of the curve decreases with increasing frequency, which also conforms to the definition of the meminductor.

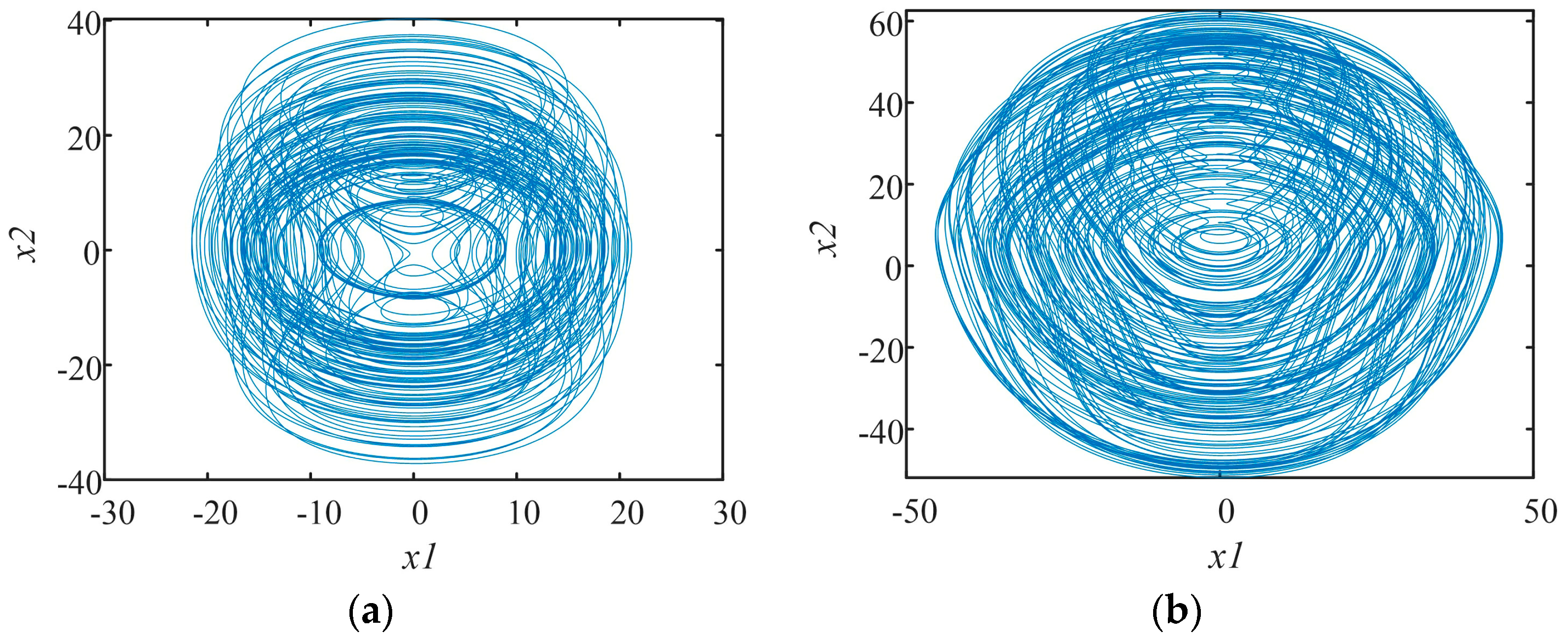
3. Dynamical Analysis of Chaotic Systems

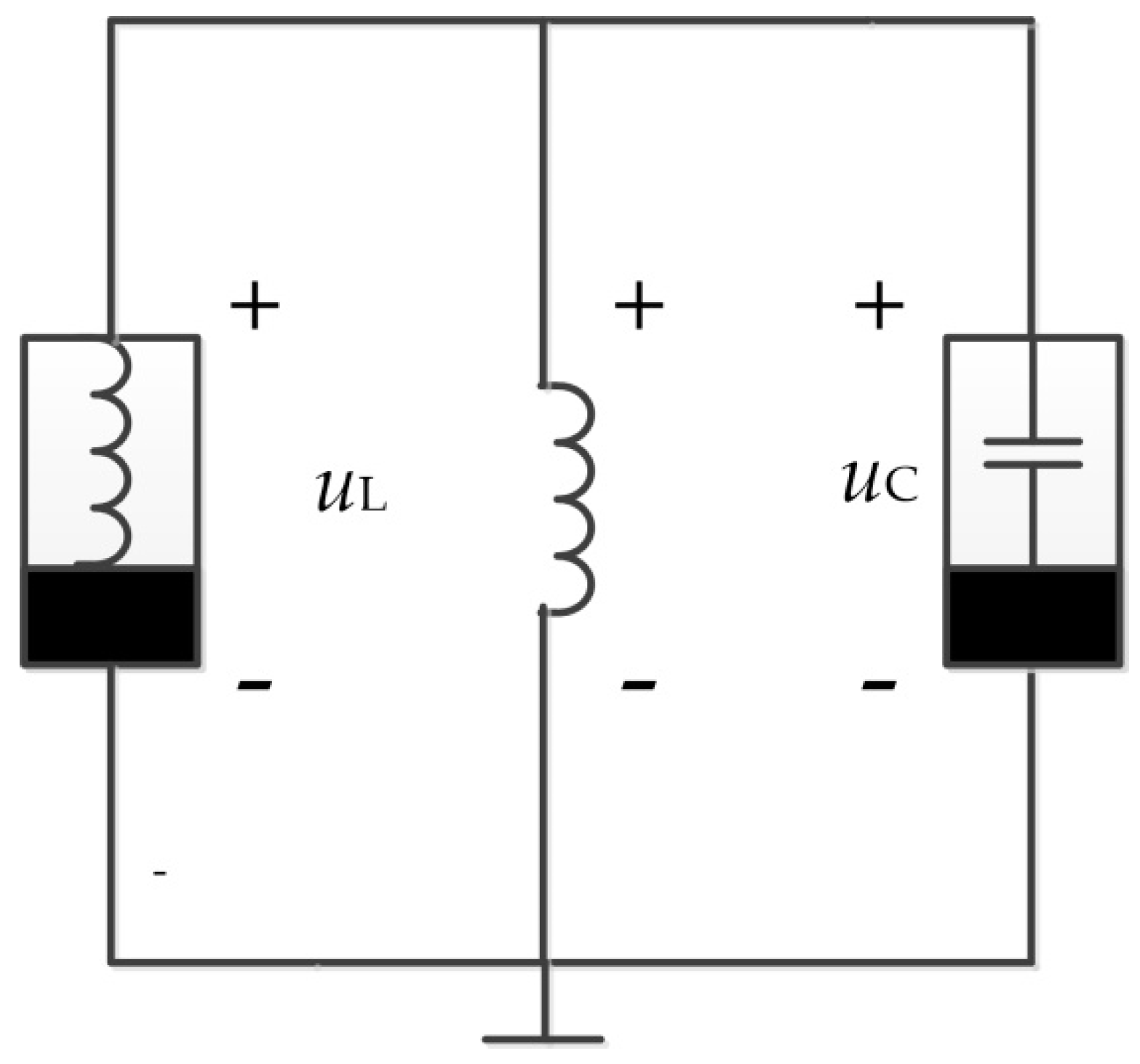
3.1. The Model of a Novel Chaotic Circuit

On the basis of the memcapacitor and meminductor mentioned above, a new type of simple chaotic circuit is involved by connecting the inductor, memcapacitor and meminductor in parallel, and its structure is expressed in Figure 3.

According to the memristive characteristics of the memcapacitor and meminductor and Kirchhoff’s law, the equation of state is expressed as:

$$\left\{\begin{array}{l}\frac{dq}{dt}=-i_{\mathrm{L}}-(a+b\cos (\rho ))\phi \\ \frac{d\phi }{dt}=(c+d\cos (\sigma ))q\\ L\frac{d{i}_{\mathrm{L}}}{dt}=(c+d\cos (\sigma ))q\\ \frac{d\sigma }{dt}=q\\ \frac{d\rho }{dt}=\phi \end{array}\right.,$$

(3)

In Equation (3), q represents the amount of charge collected at both ends of the memcapacitor, Φ represents the magnetic flux passing through the meminductor, i_L represents the current passing through the inductor, δ represents the integration of charge q in the time definition and ρ represents the integration of magnetic flux Φ in the time definition. Set q = x, Φ = y, i_L = z, δ = u and ρ = w by dimensionless processing; the model of the chaotic system is shown as follows:

$$\left\{\begin{array}{l}\dot{x}=-z-(a+b\cos (w))y\\ \dot{y}=(c+d\cos (u))x\\ \dot{z}=e(c+d\cos (u))x\\ \dot{u}=x\\ \dot{w}=y\end{array}\right.,$$

(4)

While the initial condition of the system is (10, 5, 10, 0.1, −1), four different types of chaotic attractors can be obtained under different parameters. The phase diagram is expressed in Figure 4.

3.2. Introduction of the ADM Algorithm

According to the analysis of the fractional differential algorithm, the Caputo definition is used to calculate the fractional differential equation in this paper. The expression is as follows:

$$D_{t_0}^{q}f(t)=\frac{1}{\mathsf{\Gamma }(1-q)}{\displaystyle {\int }_{t_0}^t{(t-\tau )}^{-q}{f}^{\prime }(\tau )}d\tau ,$$

(5)

where $D_{t_0}^q,$ represents the Caputo derivative operator of order q. The inverse operator of $D_{t_0}^q,$ is $J_{t_0}^q,$ and its definition is as follows:

$$J_{t_0}^{q}f(t)=\frac{1}{\mathsf{\Gamma }(q)}{\displaystyle {\int }_{t_0}^t{(t-\tau )}^{q-1}f(\tau )}d\tau ,$$

(6)

On the basis of the ADM decomposition, the fractional differential equation can be obtained as follows: $D_{t_0}^{q}x(t)=f(x(t))$. The f(x(t)) is expressed as:

$$D_{t_0}^{q}x(t)=Lx(t)+Nx(t)+g(t),$$

(7)

where Lx(t) represents the linear part of the equation, Nx(t) represents the nonlinear part of the equation and g(t) shows the constant. Apply the $J_{t_0}^q,$ to both sides of this equation:

$$J_{t_0}^q{D}_{t_0}^{q}x(t)=x(t)-x(t_0),$$

(8)

Then, the ith nonlinear function is expressed as:

$$\left\{\begin{array}{l}{A}_j^i=\frac{1}{i!}{[\frac{d^i}{d{\lambda }^i}N(v_j^i(\lambda ))]}_{\lambda }=0\\ v_j^i(\lambda )={\displaystyle \sum _{k=0}^i{(\lambda )}^k{x}_j^i}\end{array}\right.,$$

(9)

where i = 0, 1, …, ∞; j = 1, 2…, n. The nonlinear function N is denoted as:

$$Nx={\displaystyle \sum _{i=0}^{\infty }{A}^i(x^0,x^1,\dots ,x^1)},$$

(10)

Subsequently, the solution of the equation can be obtained as follows:

$$x={\displaystyle \sum _{i=0}^{\infty }{x}^i}=J_{t_0}^{q}L{\displaystyle \sum _{i=0}^{\infty }{x}^i}+J_{t_0}^q{\displaystyle \sum _{i=0}^{\infty }{A}^i+J_{t_0}^{q}g}+x(t_0),$$

(11)

where x_i can be expressed:

$$\left\{\begin{array}{l}{x}^0=J_{t_0}^{q}g+x(t_0)\\ x^1=J_{t_0}^{q}L{x}^0+J_{t_0}^q{A}^0(x^0)\\ x^2=J_{t_0}^{q}L{x}^1+J_{t_0}^q{A}^1(x^0,x^1)\\ \cdots \\ x^i=J_{t_0}^{q}L{x}^{i-1}+J_{t_0}^q{A}^{i-1}(x^0,x^1,x^2,\dots x^{i-1})\end{array}\right.,$$

(12)

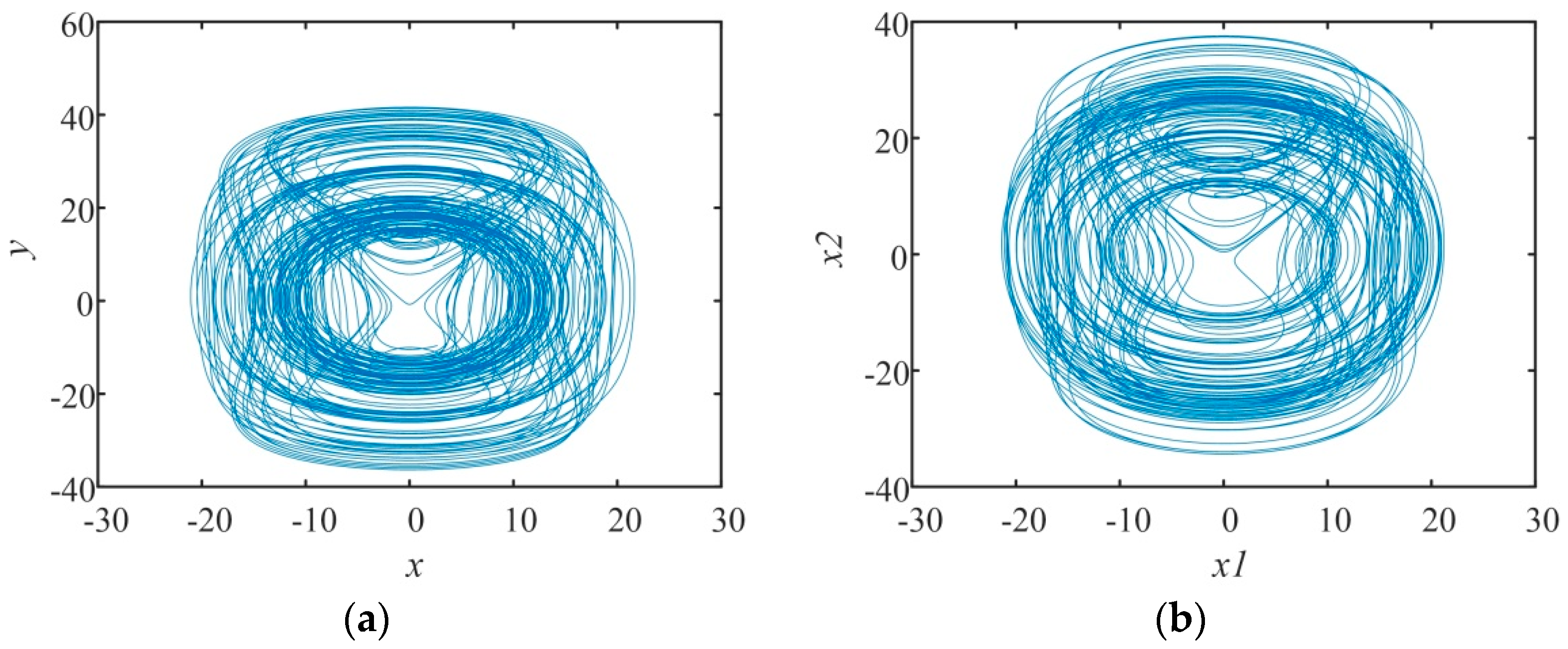
3.3. Analysis of This New Fractional Chaotic System

In this paper, a simple circuit is constructed by a meminductor, memcapacitor and an inductor in parallel. By introducing a fractional differential operator into a chaotic system, we can obtain a five-dimensional fractional chaotic system. The expression of the system can be expressed as follows:

$$\left\{\begin{array}{l}{D}_{t_0}^q{x}_1=-x_3-(a+b\cos (x_5))x_2\\ D_{t_0}^q{x}_2=(c+d\cos (x_4))x_1\\ D_{t_0}^q{x}_3=e(c+d\cos (x_4))x_1\\ D_{t_0}^q{x}_4=x_1\\ D_{t_0}^q{x}_5=x_2\end{array}\right.,$$

(13)

where b, d, e, c and a delegate the parameters; x₁, x₂, x₃, x₄ and x₅ represent the state variables; and there is a nonlinear function f(x) = cos(x) in the system. In order to make the calculation result more accurate, the nonlinear function is decomposed in advance, and the decomposition result is as follows:

$$\left\{\begin{array}{cc}\hfill A_1^0& =\cos x_1^0\hfill \\ \hfill A_1^1& =-x_1^1\sin x_1^0\hfill \\ \hfill A_1^2& =-x_1^2\sin x_1^0-\frac{1}{2!}{x}_1^1{x}_1^1\cos x_1^0\hfill \\ \hfill A_1^3& =-x_1^3\sin x_1^0-x_1^2{x}_1^1\cos x_1^0+\frac{1}{3!}{x}_1^1{x}_1^1{x}_1^1\sin x_1^0\hfill \\ \hfill A_1^4& =-x_1^4\sin x_1^0-x_1^3{x}_1^1\cos x_1^0-\frac{1}{2!}{x}_1^2{x}_1^2\cos x_1^0\hfill \\ & +\frac{1}{2!}{x}_1^1{x}_1^1{x}_1^2\sin x_1^0+\frac{1}{4!}{x}_1^1{x}_1^1{x}_1^1{x}_1^1\cos x_1^0\hfill \end{array}\right.,$$

(14)

On account of ADM decomposition, the iterative formula of this kind of chaotic system is as follows:

$$\left\{\begin{array}{l}{c}_1^0=x_0(1)\\ c_2^0=x_0(2)\\ c_3^0=x_0(3)\\ c_4^0=x_0(4)\\ c_5^0=x_0(5)\end{array}\right.\left\{\begin{array}{l}{c}_1^1=-c_3^0-(a+b\cos c_5^0)c_2^0\\ c_2^1=(c+d\cos c_4^0)c_1^0\\ c_3^1=e(c+d\cos c_4^0)c_1^0\\ c_4^1=c_1^0\\ c_5^1=c_2^0\end{array}\right.,$$

(15)

$$\left\{\begin{array}{l}{c}_1^2=-c_3^1-a{c}_2^1-(b((-c_5^1\sin (c_5^0))c_2^0+\cos (c_5^0)c_2^1))\\ c_2^2=c{c}_1^1+(d((-c_4^1\sin (c_4^0))c_1^0+\cos (c_4^0)c_1^1))\\ c_3^2=ec{c}_1^1+e(d((-c_4^1\sin (c_4^0))c_1^0+\cos (c_4^0)c_1^1))\\ c_4^2=c_1^1\\ c_5^2=c_2^1\end{array}\right.,$$

(16)

$$\left\{\begin{array}{cc}\hfill c_1^3& =-c_3^2-a{c}_2^2-(b((-c_5^2\sin (c_5^0)-0.5c_5^1{c}_5^1\cos (c_5^0)\frac{\mathsf{\Gamma }(2q+1)}{\mathsf{\Gamma }{(q+1)}^2})c_2^0\hfill \\ & +(-c_5^1\sin (c_5^0)c_2^1\frac{\mathsf{\Gamma }(2q+1)}{\mathsf{\Gamma }{(q+1)}^2})+\cos (c_5^0)c_2^2))\hfill \\ \hfill c_2^3& =c{c}_1^2+(d((-c_4^2\sin (c_4^0)-0.5c_4^1{c}_4^1\cos (c_4^0)\frac{\mathsf{\Gamma }(2q+1)}{\mathsf{\Gamma }{(q+1)}^2})c_1^0\hfill \\ & +(-c_4^1\sin (c_4^0)c_1^1\frac{\mathsf{\Gamma }(2q+1)}{\mathsf{\Gamma }{(q+1)}^2})+\cos (c_4^0)c_1^2))\hfill \\ \hfill c_3^3& =ec{c}_1^2+e(d((-c_4^2\sin (c_4^0)-0.5c_4^1{c}_4^1\cos (c_4^0)\frac{\mathsf{\Gamma }(2q+1)}{\mathsf{\Gamma }{(q+1)}^2})c_1^0\hfill \\ & +(-c_4^1\sin (c_4^0)c_1^1\frac{\mathsf{\Gamma }(2q+1)}{\mathsf{\Gamma }{(q+1)}^2})+\cos (c_4^0)c_1^2))\hfill \\ \hfill c_4^3& =c_1^2\hfill \\ \hfill c_5^3& =c_2^2\hfill \end{array}\right.,$$

(17)

$$\left\{\begin{array}{cc}\hfill c_1^4& =-c_3^3-a{c}_2^3-(b((-c_5^3\sin (c_5^0)-c_5^2{c}_5^1\cos (c_5^0)\frac{\mathsf{\Gamma }(3q+1)}{\mathsf{\Gamma }(q+1)\mathsf{\Gamma }(2q+1)}\hfill \\ & +\frac{1}{6}{c}_5^1{c}_5^1{c}_5^1\sin (c_5^0)\frac{\mathsf{\Gamma }(3q+1)}{\mathsf{\Gamma }{(q+1)}^3})c_2^0+(((-c_5^2\sin (c_5^0)\hfill \\ & -0.5c_5^1{c}_5^1\cos (c_5^0)\frac{\mathsf{\Gamma }(2q+1)}{\mathsf{\Gamma }{(q+1)}^2})c_2^1+c_2^2(-c_5^1\sin (c_5^0)))\frac{\mathsf{\Gamma }(3q+1)}{\mathsf{\Gamma }(q+1)\mathsf{\Gamma }(2q+1)})\hfill \\ & +\cos (c_5^0)c_2^3))\hfill \\ \hfill c_2^4& =c{c}_2^3+(d((-c_4^3\sin (c_4^0)-c_4^2{c}_4^1\cos (c_4^0)\frac{\mathsf{\Gamma }(3q+1)}{\mathsf{\Gamma }(q+1)\mathsf{\Gamma }(2q+1)}\hfill \\ & +\frac{1}{6}{c}_4^1{c}_4^1{c}_4^1\sin (c_4^0)\frac{\mathsf{\Gamma }(3q+1)}{\mathsf{\Gamma }{(q+1)}^3})c_1^0+(((-c_4^2\sin (c_4^0)\hfill \\ & -0.5c_4^1{c}_4^1\cos (c_4^0)\frac{\mathsf{\Gamma }(2q+1)}{\mathsf{\Gamma }{(q+1)}^2})c_1^1+c_1^2(-c_4^1\sin (c_4^0)))\frac{\mathsf{\Gamma }(3q+1)}{\mathsf{\Gamma }(q+1)\mathsf{\Gamma }(2q+1)})\hfill \\ & +\cos (c_4^0)c_1^3))\hfill \\ \hfill c_3^4& =ec{c}_2^3+e(d((-c_4^3\sin (c_4^0)-c_4^2{c}_4^1\cos (c_4^0)\frac{\mathsf{\Gamma }(3q+1)}{\mathsf{\Gamma }(q+1)\mathsf{\Gamma }(2q+1)}\hfill \\ & +\frac{1}{6}{c}_4^1{c}_4^1{c}_4^1\sin (c_4^0)\frac{\mathsf{\Gamma }(3q+1)}{\mathsf{\Gamma }{(q+1)}^3})c_1^0+(((-c_4^2\sin (c_4^0)\hfill \\ & -0.5c_4^1{c}_4^1\cos (c_4^0)\frac{\mathsf{\Gamma }(2q+1)}{\mathsf{\Gamma }{(q+1)}^2})c_1^1+c_1^2(-c_4^1\sin (c_4^0)))\frac{\mathsf{\Gamma }(3q+1)}{\mathsf{\Gamma }(q+1)\mathsf{\Gamma }(2q+1)})\hfill \\ & +\cos (c_4^0)c_1^3))\hfill \\ \hfill c_4^4& =c_1^3\hfill \\ \hfill c_5^4& =c_2^3\hfill \end{array}\right.,$$

(18)

$$\left\{\begin{array}{cc}\hfill c_1^5& =-c_3^4-a{c}_2^4-(b((-c_5^4\sin (c_5^0)-c_5^3{c}_5^1\cos (c_5^0)\frac{\mathsf{\Gamma }(4q+1)}{\mathsf{\Gamma }(q+1)\mathsf{\Gamma }(3q+1)}\hfill \\ & -0.5c_5^2{c}_5^2\sin (c_5^0)\frac{\mathsf{\Gamma }(4q+1)}{\mathsf{\Gamma }{(2q+1)}^2}+0.5c_5^1{c}_5^1{c}_5^2\sin (c_5^0)\frac{\mathsf{\Gamma }(4q+1)}{\mathsf{\Gamma }{(q+1)}^2\mathsf{\Gamma }(2q+1)}\hfill \\ & +\frac{1}{24}{c}_5^1{c}_5^1{c}_5^1{c}_5^1\sin (c_5^0)\frac{\mathsf{\Gamma }(4q+1)}{\mathsf{\Gamma }{(q+1)}^4})c_2^0+(((-c_5^3\sin (c_5^0)\hfill \\ & -c_5^2{c}_5^1\cos (c_5^0)\frac{\mathsf{\Gamma }(3q+1)}{\mathsf{\Gamma }(q+1)\mathsf{\Gamma }(2q+1)}+\frac{1}{6}{c}_5^1{c}_5^1{c}_5^1\cos (c_5^0)\frac{\mathsf{\Gamma }(3q+1)}{\mathsf{\Gamma }{(q+1)}^3})c_2^1\hfill \\ & +c_2^3(-c_5^1\sin (c_5^0)))\frac{\mathsf{\Gamma }(4q+1)}{\mathsf{\Gamma }(q+1)\mathsf{\Gamma }(3q+1)})+(-c_5^2\sin (c_5^0)\hfill \\ & -0.5c_5^1{c}_5^1\cos (c_5^0)\frac{\mathsf{\Gamma }(2q+1)}{\mathsf{\Gamma }{(q+1)}^2})c_2^2\frac{\mathsf{\Gamma }(4q+1)}{\mathsf{\Gamma }{(2q+1)}^2}+\cos (c_5^0)c_2^4))\hfill \\ \hfill c_2^5& =c{c}_1^4+(d((-c_4^4\sin (c_4^0)-c_4^3{c}_4^1\cos (c_4^0)\frac{\mathsf{\Gamma }(4q+1)}{\mathsf{\Gamma }(q+1)\mathsf{\Gamma }(3q+1)}\hfill \\ & -0.5c_4^2{c}_4^2\sin (c_4^0)\frac{\mathsf{\Gamma }(4q+1)}{\mathsf{\Gamma }{(2q+1)}^2}+0.5c_4^1{c}_4^1{c}_4^2\sin (c_4^0)\frac{\mathsf{\Gamma }(4q+1)}{\mathsf{\Gamma }{(q+1)}^2\mathsf{\Gamma }(2q+1)}\hfill \\ & +\frac{1}{24}{c}_4^1{c}_4^1{c}_4^1{c}_4^1\sin (c_4^0)\frac{\mathsf{\Gamma }(4q+1)}{\mathsf{\Gamma }{(q+1)}^4})c_1^0+(((-c_4^3\sin (c_4^0)\hfill \\ & -c_4^2{c}_4^1\cos (c_4^0)\frac{\mathsf{\Gamma }(3q+1)}{\mathsf{\Gamma }(q+1)\mathsf{\Gamma }(2q+1)}+\frac{1}{6}{c}_4^1{c}_4^1{c}_4^1\cos (c_4^0)\frac{\mathsf{\Gamma }(3q+1)}{\mathsf{\Gamma }{(q+1)}^3})c_1^1\hfill \\ & +c_1^3(-c_4^1\sin (c_4^0)))\frac{\mathsf{\Gamma }(4q+1)}{\mathsf{\Gamma }(q+1)\mathsf{\Gamma }(3q+1)})\hfill \\ & +(-c_4^2\sin (c_4^0)-0.5c_4^1{c}_4^1\cos (c_4^0)\frac{\mathsf{\Gamma }(2q+1)}{\mathsf{\Gamma }{(q+1)}^2})c_1^2\frac{\mathsf{\Gamma }(4q+1)}{\mathsf{\Gamma }{(2q+1)}^2}+\cos (c_4^0)c_1^4))\hfill \\ \hfill c_3^5& =ec{c}_1^4+e(d((-c_4^4\sin (c_4^0)-c_4^3{c}_4^1\cos (c_4^0)\frac{\mathsf{\Gamma }(4q+1)}{\mathsf{\Gamma }(q+1)\mathsf{\Gamma }(3q+1)}\hfill \\ & -0.5c_4^2{c}_4^2\sin (c_4^0)\frac{\mathsf{\Gamma }(4q+1)}{\mathsf{\Gamma }{(2q+1)}^2}+0.5c_4^1{c}_4^1{c}_4^2\sin (c_4^0)\frac{\mathsf{\Gamma }(4q+1)}{\mathsf{\Gamma }{(q+1)}^2\mathsf{\Gamma }(2q+1)}\hfill \\ & +\frac{1}{24}{c}_4^1{c}_4^1{c}_4^1{c}_4^1\sin (c_4^0)\frac{\mathsf{\Gamma }(4q+1)}{\mathsf{\Gamma }{(q+1)}^4})c_1^0+(((-c_4^3\sin (c_4^0)\hfill \\ & -c_4^2{c}_4^1\cos (c_4^0)\frac{\mathsf{\Gamma }(3q+1)}{\mathsf{\Gamma }(q+1)\mathsf{\Gamma }(2q+1)}+\frac{1}{6}{c}_4^1{c}_4^1{c}_4^1\cos (c_4^0)\frac{\mathsf{\Gamma }(3q+1)}{\mathsf{\Gamma }{(q+1)}^3})c_1^1\hfill \\ & +c_1^3(-c_4^1\sin (c_4^0)))\frac{\mathsf{\Gamma }(4q+1)}{\mathsf{\Gamma }(q+1)\mathsf{\Gamma }(3q+1)})\hfill \\ & +(-c_4^2\sin (c_4^0)-0.5c_4^1{c}_4^1\cos (c_4^0)\frac{\mathsf{\Gamma }(2q+1)}{\mathsf{\Gamma }{(q+1)}^2})c_1^2\frac{\mathsf{\Gamma }(4q+1)}{\mathsf{\Gamma }{(2q+1)}^2}+\cos (c_4^0)c_1^4))\hfill \\ \hfill c_4^5& =c_1^4\hfill \\ \hfill c_5^5& =c_2^5\hfill \end{array}\right.,$$

(19)

Therefore, the solution of the system can be expressed as follows:

$${\tilde{x}}_j(t)={\displaystyle \sum _{i=0}^5{c}_i^j\frac{{(t-t_0)}^{iq}}{\mathsf{\Gamma }(iq+1)}},$$

(20)

To verify the correctness of the ADM algorithm, set the order of the system as q = 1; make the system parameters a = 2, b = 11, c = 20, d = 5 and e = 1; keep the initial value of the system as (1, 10, 1, 0.1, −10); and make the parameters before and after the ADM decomposition and the initial value consistent. The simulation results are shown in Figure 5:

Keep the parameters and initial values of the system unchanged before and after ADM decomposition. By analyzing the phase diagrams of chaotic attractors before and after ADM decomposition, it can be found that the phase diagrams of chaotic attractors before and after ADM decomposition are basically consistent, which also proves the correctness of the ADM algorithm.

When the initial state of the phase diagram is (10, 5, 10, 0.1, −1), the parameters of the system are b = 11, c = 20 and the order q of the system is 0.95; some different types of chaotic attractors can be obtained under different parameters. The phase diagram is expressed in Figure 6:

3.4. Equilibrium Point Set and Stability

So as to study the equilibrium point, the left side of this system of equations represented by Equation (14) is equal to 0, and the result is as follows:

$$\left\{\begin{array}{l}0=-x_3-(a+b\cos (x_5))x_2\\ 0=(c+d\cos (x_4))x_1\\ 0=e(c+d\cos (x_4))x_1\\ 0=x_1\\ 0=x_2\end{array}\right.,$$

(21)

The equilibrium is obtained as a line equilibrium point set, Q (0, 0, 0, m, n), meaning that this system has infinite equilibria. On the basis of Equation (21), the Jacobi matrix J_E at the equilibrium point set is:

$$J_{\mathrm{E}}=\left[\begin{array}{ccccc}0& -(a+b\cos (n))& -1& 0& 0\\ (c+d\cos (m))& 0& 0& 0& 0\\ e(c+d\cos (m))& 0& 0& 0& 0\\ 1& 0& 0& 0& 0\\ 0& 1& 0& 0& 0\end{array}\right],$$

(22)

According to the Jacobi matrix of the system, the characteristic equation is obtained as follows:

$${\lambda }^3({\lambda }^2+(c+d\cos (m))(a+b\cos (n))+e(c+d\cos (m)))=0,$$

(23)

According to Equation (23), it can be seen that there are three zero eigenvalues and two nonzero eigenvalues in the system. For example, Q₁ (0, 0, 0, 10, 10), with parameters as a = 2, b = 11, c = 20, d = 10 and e = 1, we can obtain λ₁ = 0, λ₂ = 0, λ₃ = 0, λ₄ = 12.58 and λ₅ = −12.58. According to the Routh–Hurwitz Stable theorem, the system is unstable at any equilibrium point, and chaos may occur.

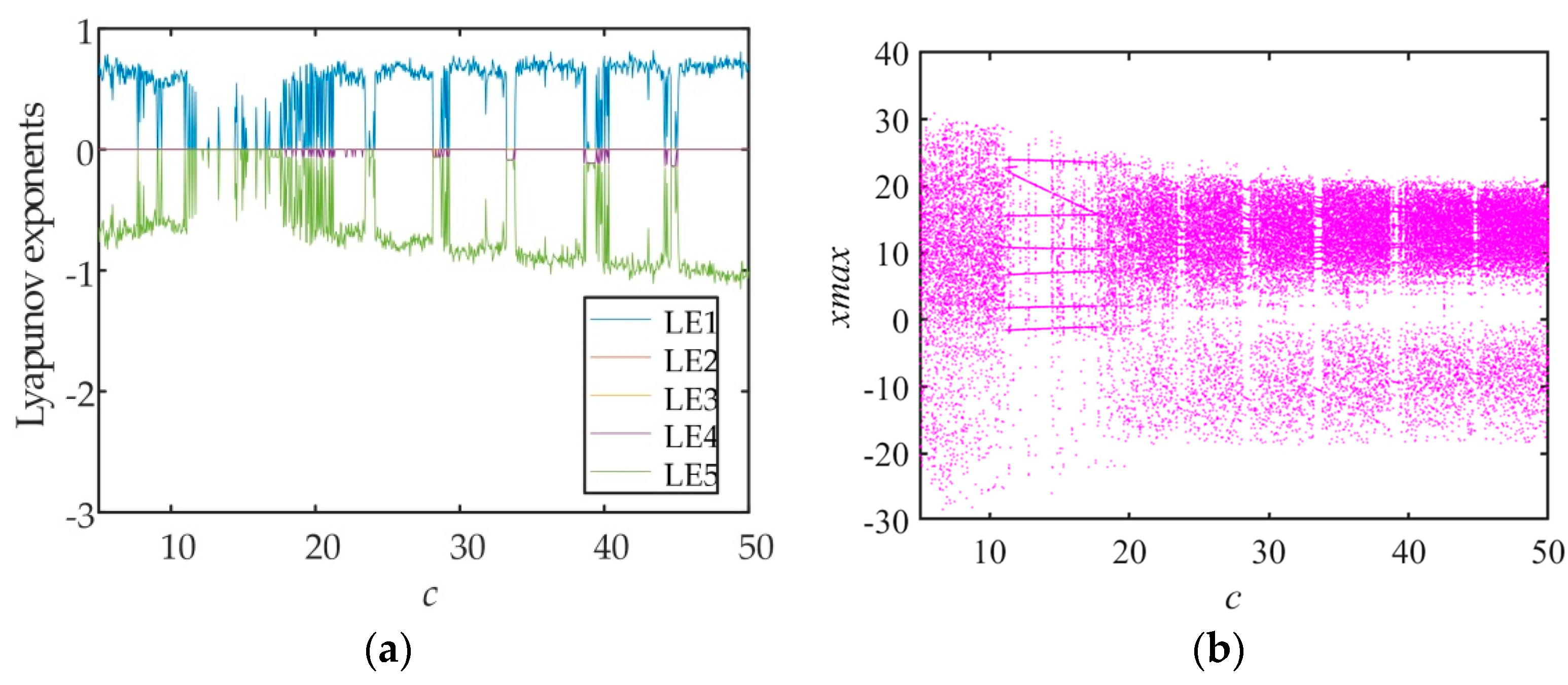
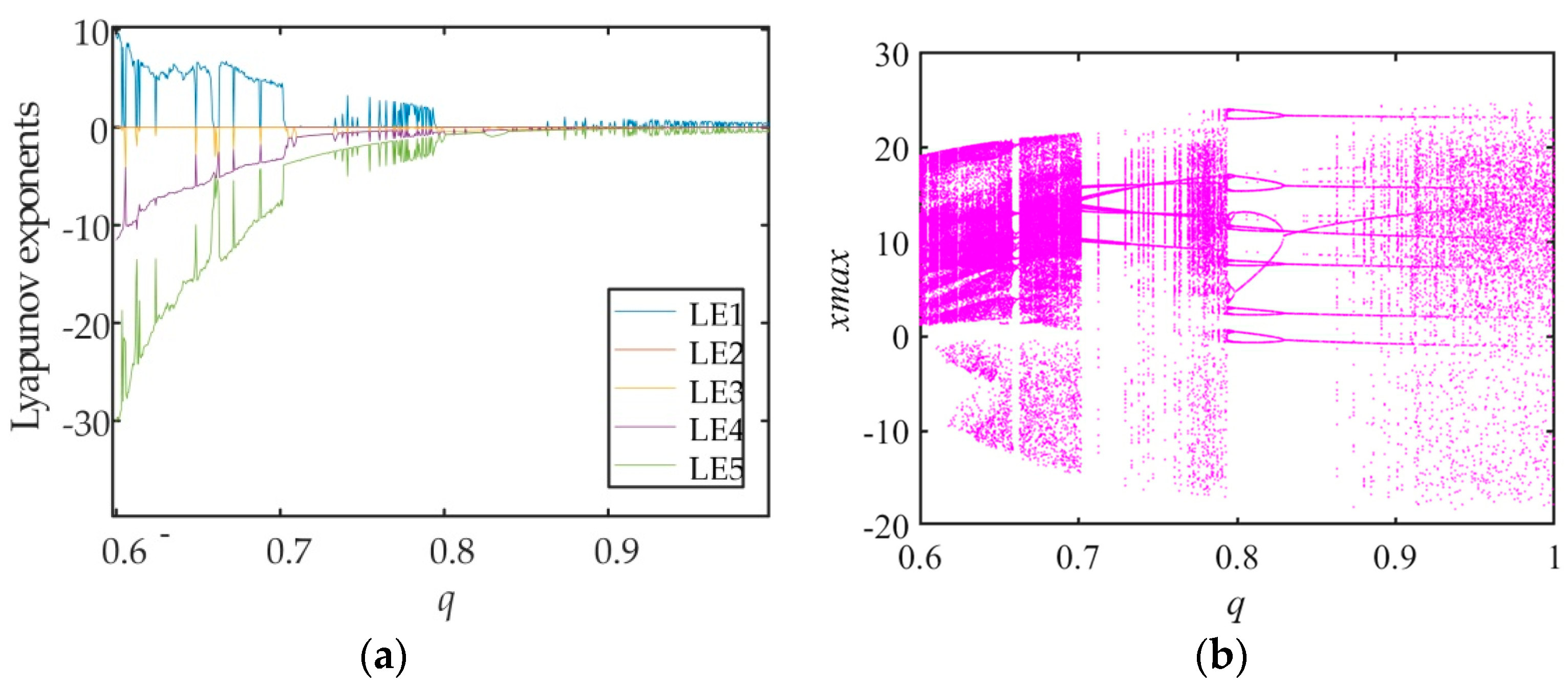
3.5. The Impacts of Parameters

Set the order as q = 0.95; the parameters as a = 2, b = 11, d = 10 and e = 1; and the initial conditions as (10, 5, 10, 0.1, −1). Only the parameter c is changed. Figure 7 shows the LEs of the system and its corresponding bifurcations when the parameter is c = (5, 50).

Different types of chaotic attractors can be found in the bifurcation diagram, and through the LEs, it can be observed that the state changes very frequently. The Lyapunov exponents and bifurcation diagrams can correspond to each other.

The order is kept unchanged; the initial value is set as (10, 5, 10, 0.1, −1); and the parameters are set as a = 2, b = 11, c = 20 and e = 1. When only the parameter d of the system changes, the Lyapunov exponent and its corresponding bifurcations can be obtained through numerical simulation, and the results are expressed in Figure 8.

Through comparing the bifurcation diagram and the LEs, we can see that they completely correspond to each other, and with the change of the parameters, the state of the chaotic system also changes frequently.

So as to show the dynamic characteristics of the chaotic system designed by us more directly, set the parameters as a = 2, b = 11, c = 20, d = 10 and e = 1; the initial condition as (10, 5, 10, 0.1, −1); and the order q of the system as [0.6, 1]. The Bifurcation diagram and the LEs of the state variable x are expressed in Figure 9.

From the LEs, we know that the LEs of this chaotic system are very high, and they change very frequently with the change of order. From the bifurcation diagram of the chaotic system, many different types of chaotic attractors can be observed. This also proves the complex dynamic characteristics of the chaotic system from one side.

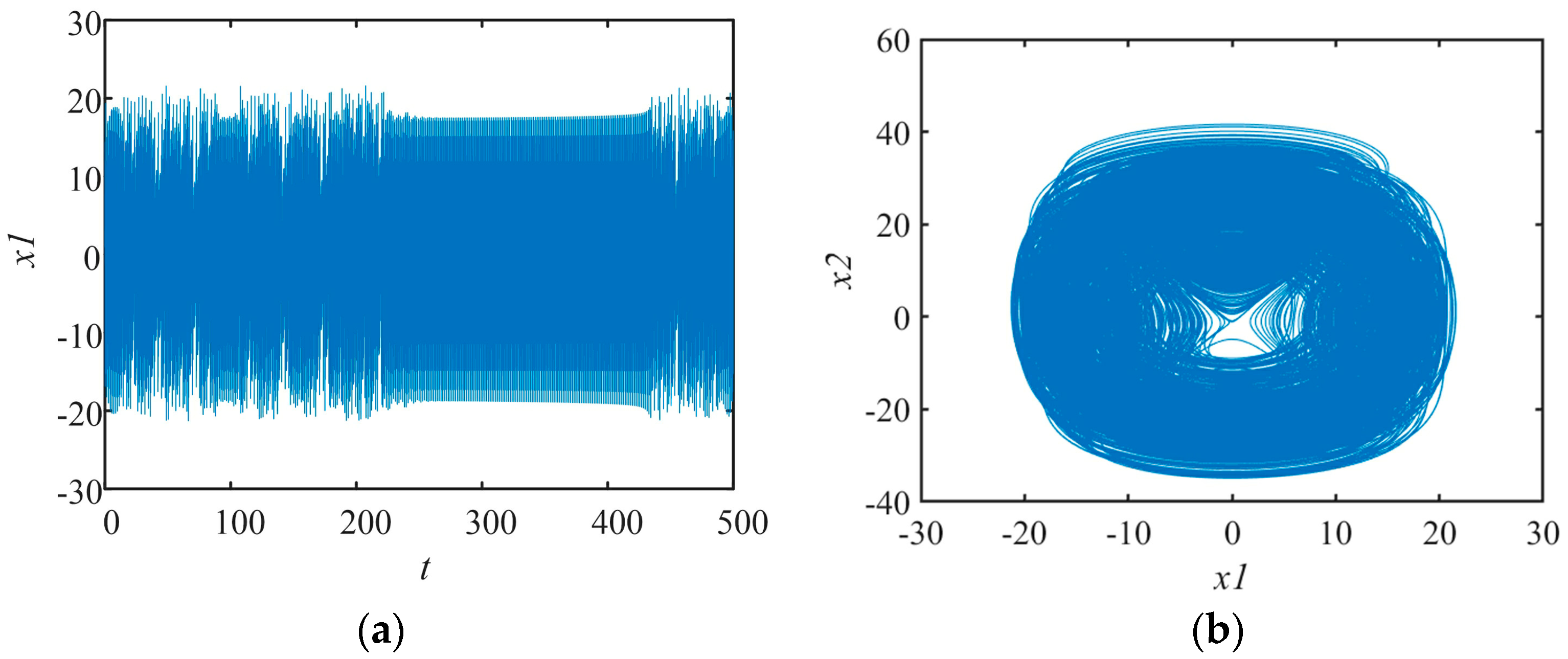
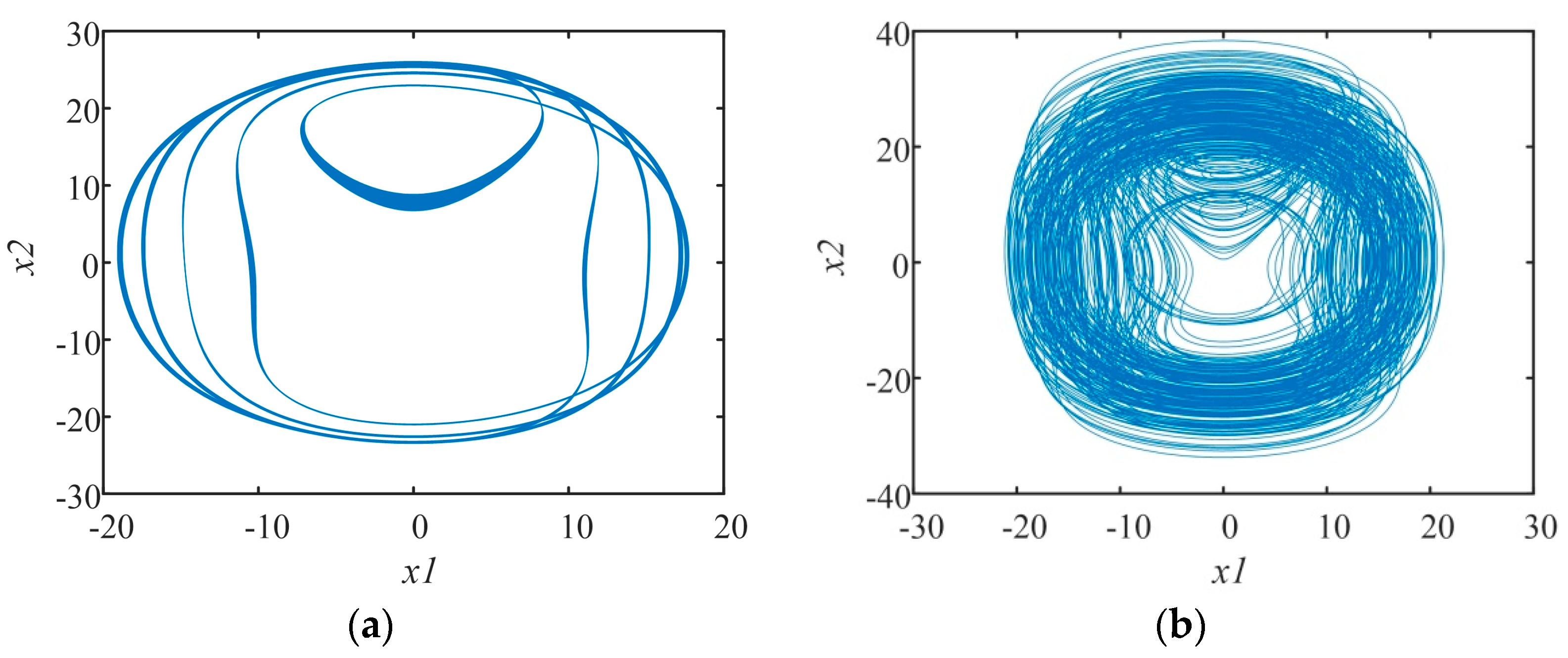
3.6. State Transition

State transition is a special dynamic phenomenon. Some special systems have the phenomenon of an unstable state; that is to say, when the system changes with time, the state will also change, and the system will show different dynamic behaviors. This special phenomenon also exists in the chaotic system constructed in this paper. Set the initial conditions as (10, 5, 10, 0.1, −1); the parameters as a = 2, b = 11, c = 20, d = 10 and e = 1; and the order as q = 0.95. The timing diagram and phase diagram of variable x₁ with t = (0, 500) are expressed in Figure 10. We can observe trajectories going from one state to another.

So as to find the chaotic state more clearly, the timing diagrams of the chaotic system with t = (246, 433) and t = (433, 500) variables x₁ are expressed in Figure 11.

Taking the initial conditions of the system as (10, 5, 10, 0.1, −1); the parameters as b = 11, a = 2, d = 10, e = 1 and c = 20; and the order as q = 0.95, we obtain the phase diagram corresponding to the time sequence diagram, and the results are expressed in Figure 12.

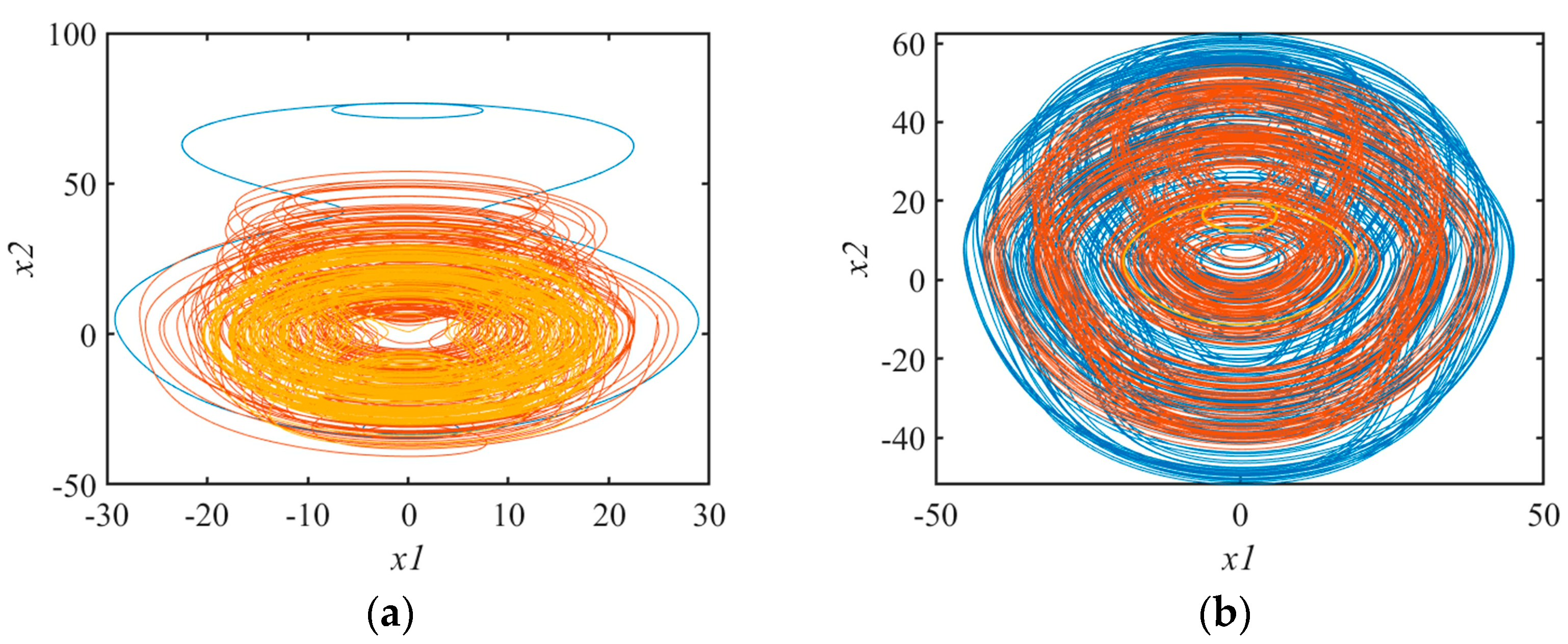
3.7. Coexistence of Attractors

The coexistence of attractors is a special dynamical behavior in chaos research and has become the focus of chaotic system research in recent years. While the parameters are kept constant and only the initial value is changed, the orbit will gradually approach different stable states of point, quasi-periodic, periodic or chaotic. A special phenomenon exists in the chaotic system constructed in this paper; the the parameters of the system is set as b = 11, a = 2, d = 10, e = 1 and c = 20, and the order q of the system is 0.95. When the system changes with the initial state, the state of the system can be observed, where the blue, red and yellow orbits express the states with the initial states of (5, 70, 5, 0.1, −1), (5, 20, 5, 0.1, −1) and (5, 10, 5, 0.1, −1), respectively. The results of the numerical simulation are expressed in Figure 13a.

By keeping the order of the system unchanged and setting the parameters as a = 0.3, b = 11, c = 20, d = 10 and e = 7, chaotic attractors of different orbits are obtained by changing the initial state, in which the blue, red and yellow orbits represent initial values of (5, 10, 5, 0.1, −1), (5, 10, 25, 0.1, −1) and (5, 10, 45, 0.1, −1), respectively. The result is expressed in Figure 13b.

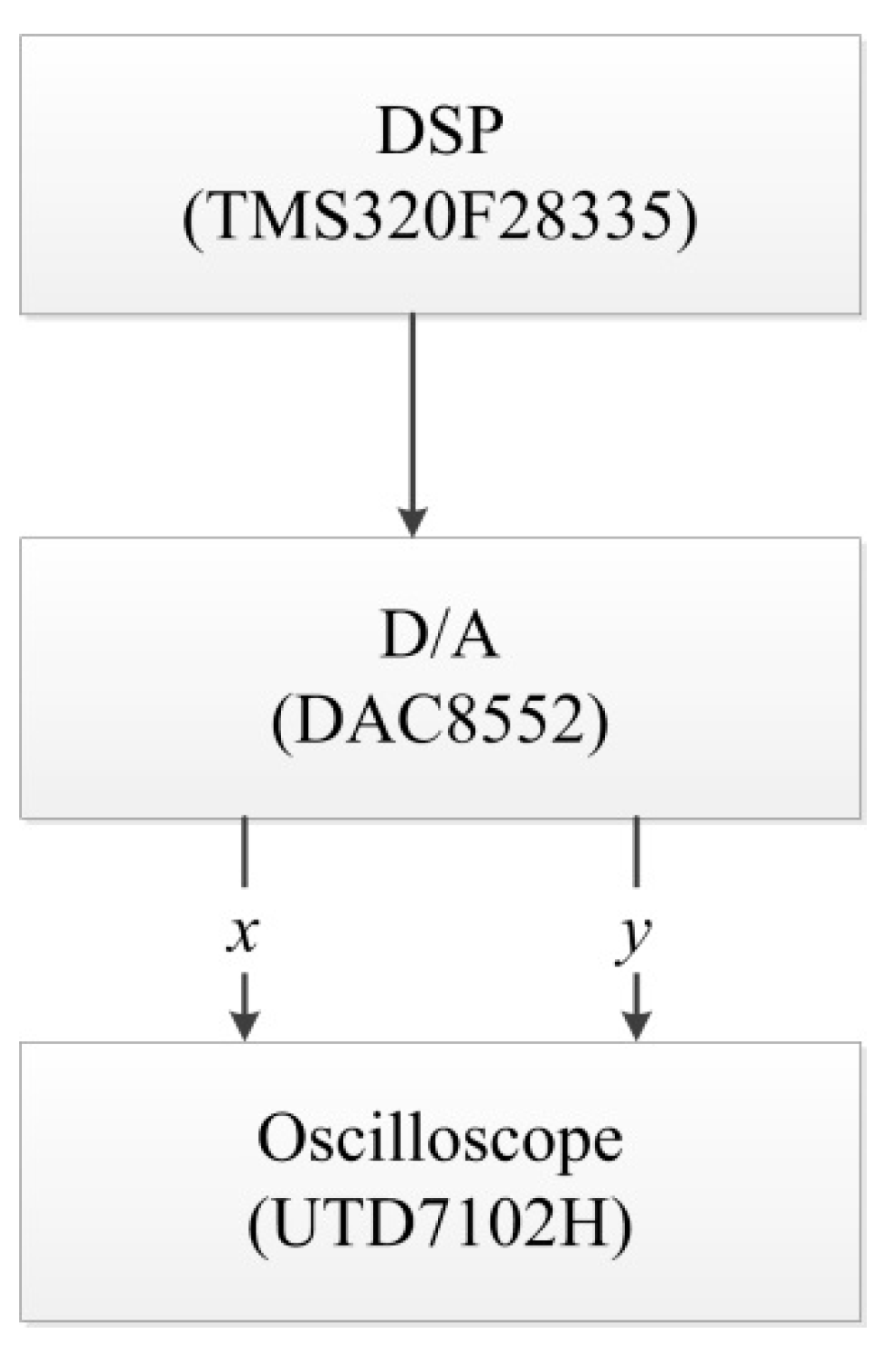
4. Digital Circuit Implementations

In order to prove the effectiveness of the system, a DSP platform is used to implement the system in this paper. DSP is a digital signal processing technology. Due to the DSP implementation having better environmental tolerance ability and the parameters of the system also having better control ability, we chose to implement this chaotic system with DSP. The DSP chip we chose is the TMS320F28335 chip to make it easier for the oscilloscope to capture images. The generated sequence is transformed into an analog sequence through the D/A converter, and then the signal is transmitted to an oscilloscope (EDS102C) by the D/A converter (8552). The implementation process is shown in Figure 14:

In the circuit implementation, DSP is only suitable for processing discrete systems, so if we choose to implement the system on the DSP platform, we need to discretize the continuous chaotic system first. Therefore, we discretize the continuous chaotic system and use an ADM decomposition method to convert it into discrete chaotic sequences. Then, we use C language to write the iteration relationship to the DSP. The stack design is used here to ensure that the data are not corrupted. The programming process is shown in Figure 15.

According to the above process, taking the initial conditions of the system as (10, 5, 10, 0.1, −1); the parameters as d = 10, c = 20; and the order as q = 0.95, the phase diagram of the attractor of DSP can be obtained, and the result are expressed in Figure 16.

In order to verify the correctness of the circuit implementation, we make the initial value of the system (10, 5, 10, 0.1, −1); keep the order of the system as 0.95; and set the parameters of the system as d = 10, c = 20. The numerical simulation results of the chaotic system on the MATLAB platform are shown in Figure 17:

Through comparison, it can be found that the results of the circuit implementation are completely consistent with the results of the numerical simulation, which proves the effectiveness of the circuit simulation. This also provides technical support for our application in practical projects such as chaotic secure communication, chaotic image encryption and neural networks.

Hardware devices such as the D/A converter [USA: Texas Instruments, Dallas, Texas], oscilloscope [China: Uni-Trend Technology, Dongguan, Guangdong] and F28335 chip [USA: Texas Instruments, Dallas, Texas] used in the DSP simulation are shown in Figure 18.

5. Conclusions

In this paper, a simple chaotic circuit on account of a memcapacitor and meminductor is studied. The circuit consists of a meminductor, an inductor and a memcapacitor in parallel. Due to the special dynamical behaviors of the memcapacitor and meminductor, the system has complex, dynamic behavior. Thus, the fractional-order chaotic system is obtained by introducing the fractional differential operator, and the Adomian algorithm is used to solve it. The stability of the equilibrium point of the fractional-order chaotic system is analyzed, and the LEs and bifurcation diagrams based on order q and parameters c and d are studied in detail. As the order changes, the system exhibits a larger Lyapunov exponent. Then, some special phenomena, such as state transition and the coexistence of a chaotic attractor, are found by analyzing the dynamical behavior of the system. In addition, DSP implementation is also carried out to verify the numerical results. Because of its rich dynamical behaviors, the system has good applications in neural networks, chaotic secure communication and image encryption.