Novel Approaches for Solving Fuzzy Fractional Partial Differential Equations

Abstract

In this paper, we present a comparison of several important methods to solve fuzzy partial differential equations (PDEs). These methods include the fuzzy reduced differential transform method (RDTM), fuzzy Adomian decomposition method (ADM), fuzzy Homotopy perturbation method (HPM), and fuzzy Homotopy analysis method (HAM). A distinguishing practical feature of these techniques is administered without the need to use discretion or restricted assumptions. Moreover, we investigate the fuzzy $(n+1)$-dimensional fractional RDTM to obtain the solutions of fuzzy fractional PDEs. The much more distinctive element of this method is that it requires no predetermined assumptions, and reduces the computational effort. We apply the suggested techniques to a set of initial valued problems and get approximate numerical solutions for linear and nonlinear time-fractional PDEs. It is demonstrated that the fuzzy $(n+1)$-dimensional fractional RDTM is both accurate and simple to use. The methods are based on gH-differentiability and fuzzy fractional derivatives. Some illustrative numerical examples are given to demonstrate the effectiveness of our proposed methods. The results show that the methods are powerful mathematical tools for solving fuzzy partial differential equations.

1. Introduction

One of the most important areas of study in the fuzzy analysis is the differential and integral theory of fuzzy valued function, which is grounded in the idea of fuzzy number space. In particular, the fuzzy differential and integral equations, that are extensively used in engineering technology and social science, have piqued the interest of scholars from a variety of disciplines. The study of fuzzy differential equations is mostly based on the following three approaches; the first is based on the H-derivative and the generalized derivative of Bede. The second is considered under Zadeh’s extension principle. The third is predicated on differential inclusion theory and fuzzy differential equations theory. These three explanations are different from one another.

In this work, we consider the H-derivative and the generalized derivative of Bede. We summarize the contributions and novelty as follows:

•

We present the comparison for a fuzzy $(n+1)$-dimensional RDTM, ADM, VIM [1], and fuzzy HPM [2] demonstrates that even though the results of these approaches when implemented to the fuzzy wave-like and heat-like equations are the same. But, the fuzzy $(n+1)$-dimensional RDTM, like fuzzy HPM, does not require specific algorithms and complex calculations such as fuzzy ADM or construction of correction functionals using general Lagranges multipliers in the fuzzy variational iteration method. In particular, the fuzzy RDTM and HPM are simple to apply and represent two successful techniques to obtain the solution of fuzzy PDEs.

•

We investigated the comparison of fuzzy $(n+1)$-dimensional RDTM, ADM, HPM, and fuzzy HAM to obtain the solutions of fuzzy wave-like, heat-like and Zakharov-Kuznetsov equations. Although the results of these methods are the same when applied to problems. Moreover, the fuzzy $(n+1)$-dimensional RDTM, HPM, and HAM don’t require complex techniques and computations as fuzzy ADM. The results recall that the fuzzy RDTM, HPM, and HAM are easy to use for solving fuzzy partial differential equations.

•

We propose the solutions of fuzzy fractional wave-like, heat-like, and Zakharov-Kuznetsov equations using $(n+1)$-dimensional fuzzy fractional RDTM. The method is flexible and can solve problems without calculating complicated Adomian polynomials or making unrealistic assumptions about nonlinear behavior. The provided technique is thus an influential way of solving fuzzy fractional PDEs and fractional order problems in physics, engineering, and other areas.

Fuzzy analysis and fuzzy differential equations have been proposed to deal with uncertainty due to incomplete information that appears in several mathematical or computer models of certain deterministic real-world phenomena. This theory has developed a large number of applications in which fuzzy fractional differential equations and fractional differential equations have emerged as important topics. Stefanini and Bede [3] proposed the generalized Hukuhara differentiation of interval-valued functions and interval differential equations. Also, Bede and Stefanini [4] introduced the generalized differentiation of fuzzy-valued functions. Gomes and Barros [5] discussed the generalized difference and the generalized differentiability. Hong et al. [6] presented an exhaustive review of various modern fractional calculus applications.

The concept of the fuzzy-type Riemann-Liouville differentiability based on Hukuhara differentiability was introduced in [7,8] using the Hausdorff measure of non-compactness, the researchers presented some fuzzy integral equations using appropriate compression-type conditions. In literature various approaches and techniques, based on Hukuhara differentiability or generalized Hukuhara differentiability [4], can be studied for the references introduced in some of the works in the literature; see [9,10,11,12,13,14,15,16,17,18].

The fuzzy partial differential equations (FPDEs) have attracted great interest because of their practical applications in many fields such as physics, social science, and other areas of science and engineering. The FPDEs have been studied by many authors using different methods. Keshavarza et al. [19] presented the fuzzy solution to the mathematical model of a cancer tumor under Caputo-generalized Hukuhara partial differentiability by using fuzzy integral transforms. Keshavarz and Allahviranloo [20] studied the fuzzy fundamental triangular solution of the fractional diffusion equation under Caputo generalized Hukuhara partial differentiability by using the fuzzy Laplace transform and the fuzzy Fourier transform. Furthermore; see [1,21,22,23,24]. The authors [25,26] presented the various transport/diffusion problem and an overview of the corresponding numerical solution approaches.

The differential transform method (DTM) was originally discussed by Zhou [27] in 1986, this technique adopts an analytic solution in polynomial form, which is different from the traditional higher-order Taylor formula technique. After that, many researchers have proposed this method to solve many problems [19,24,28,29,30]. To overcome the demerits of complex computation of DTM, the RDTM was introduced by Keskin et al. [31,32] the method is based on reputable semi-analytical technique and can be applied to find approximate solutions of PDEs, also there are several significant implementations employing RDTM; see [32,33,34,35,36,37,38,39,40,41].

The Adomian decomposition method (ADM) is a well-known and effective approach for solving any type of problem. It is efficient not just for linear but also for nonlinear issues. This technique is famous for fast convergence and achieving the desired appropriate precision in just a few iterations. Several authors have already contributed their works via this technique; for example, see [1,24,42,43,44].

He [45,46,47] is considered as the pioneer of HPM by combining HAM [48,49] and the perturbation method [50]. This method has been used to solve a wide range of problems with forwarding. Kashkari et al. [51] studied dissipative nonplanar solitons in an electronegative complex plasma by using the HPM. The HPM is used to solve both linear and nonlinear higher-order boundary value problems numerically by Kanth and Aruna [52]. This method was used by Biazar et al. [53] to solve nonlinear systems of integro differential equations. Osman et al. [24] compared the fuzzy HPM and other techniques applied to solving the fuzzy $(1+n)$-dimensional Burgers equation. Xu [54] proposed a perturbational approach to construct analytical approximations based on the double-parameter transformation perturbation expansion method. Ahmad et al. [55] studied the nonlinear fractional order KdV and Burger equation with exponential-Decay Kernel using HPM.

The HAM [56,57] was introduced by Liao in 1992. HAM was further developed and improved by Liao in various subjects [58,59,60]. Several researchers have applied the HAM for solving differential equations. Saratha et al. [61] studied the notion of a fractional generalized integral transform under a modified Riemann-Liouville derivative with the Mittag-Leffler function as a kernel. Li et al. [62] presented the time-delay feedback control of a cantilever beam with concentrated mass based on the HAM. Naika et al. [48] studied the estimating an approximate analytical solution of the HIV viral dynamic model via HAM.

This paper is structured as follows. In Section 2, we recall some basic definitions. In Section 3, we applied the fuzzy $(n+1)$-dimensional RDTM, ADM, HPM, and fuzzy HAM to obtain the solutions of fuzzy partial differential equations. In Section 4, we present the solution of fuzzy fractional partial differential equations via fuzzy $(n+1)$-dimensional fractional RDTM. Finally, a conclusion is given in Section 5.

2. Preliminaries

In this paper, we will denote the set of fuzzy numbers by ${\mathbb{E}}^1$, that are, normal, fuzzy convex, upper semi-continuous and compactly supported fuzzy sets defined over the real line. For $0<\lambda \le 1,$ set ${\left[u\right]}_{\lambda }=\{\vartheta \in \mathbb{R}|u\left(\vartheta \right)\ge \lambda \},$ and ${\left[u\right]}_0=cl\{\vartheta \in \mathbb{R}|u\left(\vartheta \right)>0\}.$ We explain ${\left[u\right]}_{\sigma }=[{\underline{u}}_{\sigma },{\overline{u}}_{\sigma }]$, consequently if $u\in {\mathbb{E}}^1,$ the $\sigma$-level set ${\left[u\right]}_{\sigma }$ is a closed interval for all $\sigma \in [0,1]$ (see in [63,64]). Let $u,v\in {\mathbb{E}}^1$ and $k\in \mathbb{R},$ the addition and scalar multiplication are defined as

• ${[u+v]}_{\sigma }={\left[u\right]}_{\sigma }+{\left[v\right]}_{\sigma },$
• ${\left[ku\right]}_{\sigma }=k{\left[u\right]}_{\sigma }.$

The triangular fuzzy number defined as a fuzzy set in ${\mathbb{E}}^1,$ determined by $u=(a,b,c)\in \mathbb{R}$ and $a\le b\le c$ such that ${\underline{u}}_{\sigma }=a+(b-a)\sigma$ and ${\overline{u}}_{\sigma }=c-(c-b)\sigma$ are the endpoints of $\sigma$-level sets for all $\sigma \in [0,1].$ A support of fuzzy number u is given as

$$supp\left(u\right)=cl\{\vartheta \in R|u\left(\vartheta \right)>0\},$$

where $cl$ is the closure of set $\{\vartheta \in \mathbb{R}|u\left(\vartheta \right)>0\}.$

The Hausdorff distance $D:{\mathbb{E}}^1\times {\mathbb{E}}^1⟶{\mathbb{R}}^{+}\cup \left\{0\right\}$ between fuzzy numbers is defined as in [65]

$$D(u,v)=\underset{\sigma \in [0,1]}{sup}\left\{d_H\left({\left[u\right]}_{\sigma },{\left[v\right]}_{\sigma }\right)\right\}=\underset{\sigma \in [0,1]}{sup}max\left\{|{\underline{u}}_{\sigma }-{\underline{v}}_{\sigma }|,|{\overline{u}}_{\sigma }-{\overline{v}}_{\sigma }|\right\},$$

where $d_H$ is the Hausdorff metric.

The metric space $\left({\mathbb{E}}^1,D\right)$ is complete, locally compact and the following properties from [65] for metric D are valid

• $D(u\oplus w,v\oplus w)=D(u,v),\forall u,v,w\in {\mathbb{E}}^1,$
• $D(u\oplus v,w\oplus e)\le D(u,w)+D(v,e),\forall u,v,w,e\in {\mathbb{E}}^1$,
• $D(\tilde{w}\oplus \tilde{v},\tilde{0})\le D(\tilde{w},\tilde{0})+D(\tilde{v},\tilde{0}),\forall \tilde{w},\tilde{v}\in {\mathbb{E}}^1,$
• $D(k\odot u,k\odot v)=\left|k\right|D(u,v),\forall u,v\in {\mathbb{E}}^1,k\in \mathbb{R},$
• $D(k_1\odot u,k_2\odot u)=|k_1-k_2|D(u,0),\forall u\in {\mathbb{E}}^1,k_1,k_2\in \mathbb{R},$ with $k_1·k_2\ge 0$,
• $D(u\ominus v,w\ominus e)\le D(u,w)+D(v,e),aslongasu\ominus v,andw\ominus e\forall u,v,w,e\in {\mathbb{E}}^1$,

where ⊖ is the H-difference, it means that $w\ominus v=u$ if and only if $u\oplus v=w.$

Definition 1 ([4,66]).

The gH-difference between two fuzzy numbers $u,v\in {\mathbb{E}}^1$ is defined as

$$u{\ominus }_{gH}v=e\iff \left\{\begin{array}{c}\left(i\right)u=v\oplus e,\mathrm{or}\hfill \\ \left(ii\right)v=u\oplus (-e).\hfill \end{array}\right.$$

(1)

In terms of $\sigma -$levels, we get $\left[u{\ominus }_{gH}v\right]=[min\{{\underline{w}}_{\sigma }-{\underline{v}}_{\sigma },{\overline{w}}_{\sigma }-{\overline{v}}_{\sigma }\},max\{{\underline{w}}_{\sigma }-{\underline{v}}_{\sigma },{\overline{w}}_{\sigma }-{\overline{v}}_{\sigma }\}]$ and if the H-difference exists, then $u\ominus v=u{\ominus }_{gH}v$; the conditions for the existence of $e=u{\ominus }_{gH}v\in {\mathbb{E}}^1$ are

$$\begin{array}{cc}\hfill Case\left(i\right)& \left\{\begin{array}{c}{\underline{e}}_{\sigma }={\underline{w}}_{\sigma }-{\underline{v}}_{\sigma }and{\overline{e}}_{\sigma }={\overline{w}}_{\sigma }-{\overline{v}}_{\sigma },\forall \lambda \in [0,1],\hfill \\ with{\underline{e}}_{\sigma }increasing,{\overline{e}}_{\sigma }decreasing,{\underline{e}}_{\sigma }\le {\overline{e}}_{\sigma }.\hfill \end{array}\right.\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill Case\left(ii\right)& \left\{\begin{array}{c}{\underline{e}}_{\sigma }={\overline{w}}_{\sigma }-{\overline{v}}_{\sigma }and{\overline{e}}_{\sigma }={\underline{w}}_{\sigma }-{\underline{v}}_{\sigma },\forall \lambda \in [0,1],\hfill \\ with{\underline{e}}_{\sigma }increasing,{\overline{e}}_{\sigma }decreasing,{\underline{e}}_{\sigma }\le {\overline{e}}_{\sigma }.\hfill \end{array}\right.\hfill \end{array}$$

(3)

It is easy to show that (i) and (ii) are both valid if and only if e is a crisp number.

Proposition 1

([67]). Let $u,v\in {\mathbb{E}}^1$ are two fuzzy numbers. Then

• If the $gH$-difference exists, it is unique.
• $u{\ominus }_{gH}v=u\ominus v$ or $u{\ominus }_{gH}v=-(v\ominus u)$ whenever the statement on the right exists, especially, $u{\ominus }_{gH}u=$$u\ominus u=0$.
• If $u{\ominus }_{gH}v$ exists in sense (i), then $v{\ominus }_{gH}u$ exists in sense (ii) and vice versa.
• $(u+v){\ominus }_{gH}v=u$.
• $0{\ominus }_{gH}\left(u{\ominus }_{gH}v\right)=v{\ominus }_{gH}u$.
• $u{\ominus }_{gH}v=v{\ominus }_{gH}u=k$ if and only if $k=-k$; moreover, $k=0$ if and only if $u=v$.

Definition 2 ([4]).

Let $f:[a,b]\to {\mathbb{E}}^1$ and ${\vartheta }_0\in (a,b)$, with $\underline{f}(\vartheta ;\sigma )$ and $\overline{f}(\vartheta ;\sigma )$ both differentiable at ${\vartheta }_0$, then

• f is $[i-gH]$-differentiable at ${\vartheta }_0$ if

  $$\begin{array}{c}\hfill f_{i-gH}^{\prime }\left({\vartheta }_0;\sigma \right)=\left[{\left(\underline{f}\right)}^{\prime }\left({\vartheta }_0;\sigma \right),{\left(\overline{f}\right)}^{\prime }\left({\vartheta }_0;\sigma \right)\right],0\le \sigma \le 1,\end{array}$$

  (4)
• f is $[ii-gH]$-differentiable at ${\vartheta }_0$ if

  $$\begin{array}{c}\hfill f_{ii-gH}^{\prime }\left({\vartheta }_0;\sigma \right)=\left[{\left(\overline{f}\right)}^{\prime }\left({\vartheta }_0;\sigma \right),{\left(\underline{f}\right)}^{\prime }\left({\vartheta }_0;\sigma \right)\right],0\le \sigma \le 1.\end{array}$$

  (5)

Definition 3 ([3]).

We say that a point ${\vartheta }_0\in (a,b)$ is a switching point for the differentiability of a function f if in any neighborhood V of ${\vartheta }_0$ there exist points ${\vartheta }_1<{\vartheta }_0<{\vartheta }_2$ such that

• type I at ${\vartheta }_1$ (4) holds while (5) does not hold and at ${\vartheta }_2$ (5) holds and (4) does not hold, or
• type II at ${\vartheta }_1$ (5) holds while (4) does not hold and at ${\vartheta }_2$ (4) holds and (5) does not hold.

Definition 4 ([63]).

Let $f:[a,b]\to {\mathbb{E}}^1$ and $f_{gH}^{\prime }\left(\vartheta \right)$ be gH-differentiable at ${\vartheta }_0\in (a,b)$ and there is no switching point on $(a,b)$, with ${\left(\underline{f}\right)}^{\prime }(\vartheta ;\sigma )$ and ${\left(\overline{f}\right)}^{\prime }(\vartheta ;\sigma )$ are both differentiable at ${\vartheta }_0$. Then

• $f_{gH}^{\prime }\left(x\right)$ is $[i-gH]$-differentiable whenever the type of $gH$-differentiability $f\left(\vartheta \right)$ and $f_{gH}^{\prime }\left(\vartheta \right)$ is the same:

  $$\begin{array}{c}\hfill f_{i-gH}^{″}\left({\vartheta }_0;\sigma \right)=\left[{\left(\underline{f}\right)}^{\prime \prime }\left({\vartheta }_0;\sigma \right),{\left(\overline{f}\right)}^{\prime \prime }\left({\vartheta }_0;\sigma \right)\right],0\le \sigma \le 1,\end{array}$$

  (6)
• $f_{gH}^{\prime }\left(\vartheta \right)$ is $[ii-gH]$-differentiable if the type of $gH$-differentiability $f\left(\vartheta \right)$ and $f_{gH}^{\prime }\left(\vartheta \right)$ is different:

  $$\begin{array}{c}\hfill f_{ii-gH}^{″}\left({\vartheta }_0;\sigma \right)=\left[{\left(\overline{f}\right)}^{″}\left({\vartheta }_0;\sigma \right),{\left(\underline{f}\right)}^{″}\left({\vartheta }_0;\sigma \right)\right],0\le \sigma \le 1.\end{array}$$

  (7)

Definition 5 ([68]).

Let us suppose a function $f:[a,b]\to {\mathbb{E}}^1$ be fuzzy Riemann integrable in $\mathbb{I}\in {\mathbb{R}}_F$ if for any $\epsilon >0$ there exists $\delta >0$ such that for any division $P=\left\{\right[u,v];\xi \}$ with the norm $\Delta \left(P\right)<\delta$

$$\begin{array}{c}\hfill D\left(\sum _p^{*}(v-u)\odot f\left(\xi \right),\mathbb{I}\right)<\epsilon ,\end{array}$$

where ${\sum }_p^{*}$ denotes the fuzzy summation and $\mathbb{I}$ indicates ${\int }_a^{b}f\left(\vartheta \right)dx$.

Definition 6 ([69]).

A fuzzy-number-valued function $f:[a,b]\to {\mathbb{E}}^1$ is said to be continuous at $t_0\in [a,b]$ if for each $\epsilon >0$ there exist $\delta >0$ such that $D\left(f\left(t\right),f\left(t_0\right)\right)<\epsilon$ whenever $\left|t-t_0\right|<\delta .$ If f is continuous for each $t\in [a,b]$ then we say that f is fuzzy continuous on $[a,b].$

Definition 7 ([70]).

A fuzzy-number-valued function $f:[a,b]\to {\mathbb{E}}^1$ is said to bounded iff there is $M\ge 0$ such that $D\left(f\right(t),0)=\parallel f\left(u\right)\parallel \le M$ for all $t\in [a,b].$

Definition 8 ([63]).

A fuzzy-valued function $\tilde{f}$ of two variables is a rule that assigns to each ordered pair of real numbers, $(\vartheta ,t)$, in a set D a unique fuzzy number denoted by $\tilde{f}(\vartheta ,t)$. The set D is the domain of $\tilde{f}$ and its range is the set of values taken by $\tilde{f}$, i.e., $\left\{\tilde{f}(\vartheta ,t)\right|(\vartheta ,t)\in D\}$.

The fuzzy-valued function $\tilde{f}:D\to {\mathbb{E}}^1$ can also be expressed in the parametric representation as $\tilde{f}(\vartheta ,t;\sigma )=[\underline{f}(\vartheta ,t;\sigma ),\overline{f}(\vartheta ,t;\sigma )]$, for all $(\vartheta ,t)\in D$ and $\sigma \in [0,1]$.

3. Fuzzy Partial Differential Equations

In this section, we present the solution of fuzzy partial differential equations. We considered the following fuzzy $(n+1)$-dimensional reduced differential transform.

3.1. Fuzzy $(n+1)$-Dimensional Reduced Differential Transform

We propose the fuzzy $(n+1)$-dimensional reduced differential transform for solving fuzzy partial q-differential equations, the theory of $(n+1)$-dimensional RDTM with uncertainty represented by using fuzzy concepts is explained as follows.

Definition 9.

Let us consider $\mathcal{X}=({\vartheta }_1,{\vartheta }_2,\dots ,{\vartheta }_n)$ be a vector of $(n+1)$-dimensional reduced differential transformed form of ${\vartheta }_{\varsigma }\left(t\right)=(x_1,x_2,\dots ,x_n)$, respectively, where ${\vartheta }_{\varsigma }\left(t\right)$ be differentiable of order l over time domain T, then

$$\left.\begin{array}{cc}\hfill {\underline{\mathcal{X}}}_{\varsigma }(l;\sigma )& ={\left[\frac{{\partial }^l{\underline{\vartheta }}_{\varsigma }(t;\sigma )}{\partial t^l}\right]}_{t=0},\forall l\in \mathcal{K}=\{0,1,2,3,...\},\hfill \\ \hfill {\overline{\mathcal{X}}}_{\varsigma }(l;\sigma )& ={\left[\frac{{\partial }^l{\overline{\vartheta }}_{\varsigma }(t;\sigma )}{\partial t^l}\right]}_{t=0},\forall l\in \mathcal{K}=\{0,1,2,3,...\},\hfill \end{array}\right\}$$

(8)

when ${\vartheta }_{\varsigma }\left(t\right)$ is (i)-differentiable and

$$\left.\begin{array}{cc}\hfill {\underline{\mathcal{X}}}_{\varsigma }(l;\sigma )& =\frac{{\partial }^l{\overline{\vartheta }}_{\varsigma }(t;\sigma )}{\partial t^l}\left|{}_{t=0}\right.,lis odd,\hfill \\ \hfill {\overline{\mathcal{X}}}_{\varsigma }(l;\sigma )& =\frac{{\partial }^l{\underline{\vartheta }}_{\varsigma }(t;\sigma )}{\partial t^l}\left|{}_{t=0}\right.,lis odd,\hfill \end{array}\right\}$$

(9)

and

$$\left.\begin{array}{cc}\hfill {\underline{\mathcal{X}}}_{\varsigma }(l;\sigma )& =\frac{{\partial }^l{\underline{\vartheta }}_{\varsigma }(t;\sigma )}{\partial t^l}\left|{}_{t=0}\right.,lis even,\hfill \\ \hfill {\overline{\mathcal{X}}}_{\varsigma }(l;\sigma )& =\frac{{\partial }^l{\overline{\vartheta }}_{\varsigma }(t;\sigma )}{\partial t^l}\left|{}_{t=0}\right.,lis even,\hfill \end{array}\right\}$$

(10)

when ${\vartheta }_{\varsigma }\left(t\right)$ is (ii)-differentiable.

Notice that ${\underline{\mathcal{X}}}_{\varsigma }(l;\sigma )$ and ${\overline{\mathcal{X}}}_{\varsigma }(l;\sigma )$ denote the lower and upper spectrum of ${\vartheta }_{\varsigma }\left(t\right)$ at $t=0$, respectively.

Thus, if ${\vartheta }_{\varsigma }\left(t\right)$ be (i)-differentiable, then ${\vartheta }_{\varsigma }\left(t\right)$ can be expressed as:

$$\begin{array}{cc}\hfill {\underline{\vartheta }}_{\varsigma }(t;\sigma )& =\sum _{l=0}^{\infty }\frac{\underline{\mathcal{X}}(l;\sigma )t^l}{l!},l\in \mathcal{K},0\le \sigma \le 1,\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill {\overline{\vartheta }}_{\varsigma }(t;\sigma )& =\sum _{l=0}^{\infty }\frac{\overline{\mathcal{X}}(l;\sigma )t^l}{l!},l\in \mathcal{K},0\le \sigma \le 1,\hfill \end{array}$$

(12)

and if ${\vartheta }_{\varsigma }\left(t\right)$ be (ii)-differentiable, then ${\vartheta }_{\varsigma }\left(t\right)$ can be expressed as:

$$\begin{array}{cc}\hfill {\underline{\vartheta }}_{\varsigma }(t;\sigma )& =\sum _{l=1,odd}^{\infty }\frac{\overline{\mathcal{X}}(l;\sigma )t^l}{l!}+\sum _{l=0,even}^{\infty }\frac{\underline{\mathcal{X}}(l;\sigma )t^l}{l!},0\le \sigma \le 1,\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill {\overline{\vartheta }}_{\varsigma }(t;\sigma )& =\sum _{l=1,odd}^{\infty }\frac{\underline{\mathcal{X}}(l;\sigma )t^l}{l!}+\sum _{l=0,even}^{\infty }\frac{\overline{\mathcal{X}}(l;\sigma )t^l}{l!},0\le \sigma \le 1.\hfill \end{array}$$

(14)

The mentioned equations are known as the inverse transformation of $X(l;\sigma )$, which can be defined as

$$\left.\begin{array}{cc}\hfill \underline{\mathcal{X}}(l;\sigma )& =P\left(l\right){\left[\frac{{\partial }^l\left(\underline{{\vartheta }_{\varsigma }(t;\sigma )}\right)}{\partial t^l}\right]}_{t=0},\forall l\in \mathcal{K},\hfill \\ \hfill \overline{\mathcal{X}}(l;\sigma )& =P\left(l\right){\left[\frac{{\partial }^l\left(\overline{{\vartheta }_{\varsigma }(t;\sigma )}\right)}{\partial t^l}\right]}_{t=0},\forall l\in \mathcal{K},\hfill \end{array}\right\}$$

(15)

when ${\vartheta }_{\varsigma }\left(t\right)$ is (i)-differentiable then, we have

$$\left.\begin{array}{cc}\hfill \underline{\mathcal{X}}(l;\sigma )& =P\left(l\right){\left[\frac{{\partial }^l(\overline{{\vartheta }_{\varsigma }(t;\sigma ))}}{\partial t^l}\right]}_{t=0},lis odd,\hfill \\ \hfill \overline{\mathcal{X}}(l;\sigma )& =P\left(l\right){\left[\frac{{\partial }^l(\underline{{\vartheta }_{\varsigma }(t;\sigma ))}}{\partial t^l}\right]}_{t=0},lis odd,\hfill \end{array}\right\}$$

(16)

and

$$\left.\begin{array}{cc}\hfill \underline{\mathcal{X}}(l;\sigma )& =P\left(l\right){\left[\frac{{\partial }^l(\underline{{\vartheta }_{\varsigma }(t;\sigma ))}}{\partial t^l}\right]}_{t=0},lis even,\hfill \\ \hfill \overline{\mathcal{X}}(l;\sigma )& =P\left(l\right){\left[\frac{{\partial }^l(\overline{{\vartheta }_{\varsigma }(t;\sigma ))}}{\partial t^l}\right]}_{t=0},lis even,\hfill \end{array}\right\}$$

(17)

when ${\vartheta }_{\varsigma }\left(t\right)$ is (ii)-differentiable, then, the function ${\vartheta }_{\varsigma }\left(t\right)$ can be expressed as:

$$\begin{array}{cc}\hfill {\underline{\vartheta }}_{\varsigma }(t;\sigma )& =\sum _{l=0}^{\infty }\frac{t^l}{l!}\frac{\underline{\mathcal{X}}(l;\sigma )}{P\left(l\right)},l\in \mathcal{K},0\le \sigma \le 1,\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill {\overline{\vartheta }}_{\varsigma }(t;\sigma )& =\sum _{l=0}^{\infty }\frac{t^l}{l!}\frac{\overline{\mathcal{X}}(l;\sigma )}{P\left(l\right)},l\in \mathcal{K},0\le \sigma \le 1,\hfill \end{array}$$

(19)

when ${\vartheta }_{\varsigma }\left(t\right)$ are (i)-differentiable, and if ${\vartheta }_{\varsigma }\left(t\right)$ be (ii)-differentiable, we obtain

$$\begin{array}{cc}\hfill {\underline{\vartheta }}_{\varsigma }(t;\sigma )& =\left[\sum _{l=1,odd}^{\infty }\frac{t^l}{l!}\frac{\overline{\mathcal{X}}(l;\sigma )}{P\left(l\right)}+\sum _{l=0,even}^{\infty }\frac{t^l}{l!}\frac{\underline{\mathcal{X}}(l;\sigma )}{P\left(l\right)}\right],0\le \sigma \le 1,\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill {\overline{\vartheta }}_{\varsigma }(t;\sigma )& =\left[\sum _{l=1,odd}^{\infty }\frac{t^l}{l!}\frac{\underline{\mathcal{X}}(l;\sigma )}{P\left(l\right)}+\sum _{l=0,even}^{\infty }\frac{t^l}{l!}\frac{\overline{\mathcal{X}}(l;\sigma )}{P\left(l\right)}\right],0\le \sigma \le 1,\hfill \end{array}$$

(21)

where $P\left(l\right)>0$, $P\left(l\right)$ denoted the weighting factor. In this work $P\left(l\right)=\frac{C^l}{l!}$ is applied, where C is the time horizon on interest. Consequently, if ${\vartheta }_{\varsigma }\left(t\right)$ be (i)-differentiable, then

$$\begin{array}{cc}\hfill \underline{\mathcal{X}}(l;\sigma )& =\frac{C^l}{l!}\frac{{\partial }^l{\underline{\vartheta }}_{\varsigma }(t;\sigma )}{\partial t^l},l\in \mathcal{K},0\le \sigma \le 1,\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill \overline{\mathcal{X}}(l;\sigma )& =\frac{C^l}{l!}\frac{{\partial }^l{\overline{\vartheta }}_{\varsigma }(t;\sigma )}{\partial t^l},l\in \mathcal{K},0\le \sigma \le 1,\hfill \end{array}$$

(23)

and if ${\vartheta }_{\varsigma }\left(t\right)$ be (ii)-differentiable, then

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill \underline{\mathcal{X}}(l;\sigma )& =\frac{C^l}{l!}\frac{{\partial }^l{\overline{\vartheta }}_{\varsigma }(t;\sigma )}{\partial t^l},lis odd,0\le \sigma \le 1,\hfill \\ \hfill \overline{\mathcal{X}}(l;\sigma )& =\frac{C^l}{l!}\frac{{\partial }^l{\underline{\vartheta }}_{\varsigma }(t;\sigma )}{\partial t^l},lis odd,0\le \sigma \le 1,\hfill \end{array}\right\}\end{array}$$

(24)

and

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill \underline{\mathcal{X}}(l;\sigma )& =\frac{C^l}{l!}\frac{{\partial }^l{\underline{\vartheta }}_{\varsigma }(t;\sigma )}{\partial t^l},lis even,0\le \sigma \le 1,\hfill \\ \hfill \overline{\mathcal{X}}(l;\sigma )& =\frac{C^l}{l!}\frac{{\partial }^l{\overline{\vartheta }}_{\varsigma }(t;\sigma )}{\partial t^l},lis even,0\le \sigma \le 1.\hfill \end{array}\right\}\end{array}$$

(25)

Unitizing the fuzzy $(n+1)$-dimensional RDTM, the fuzzy PDEs in the particular domain is transformed into an algebraic equation in the domain $\mathcal{K}$, and ${\vartheta }_{\varsigma }\left(t\right)$ is provided as the finite-term Taylor series plus a reminder as:

$$\begin{array}{cc}\hfill {\underline{\vartheta }}_{\varsigma }(t;\sigma )& =\sum _{l=0}^n\frac{t^l}{l!}\frac{\underline{\mathcal{X}}(l;\sigma )}{P\left(l\right)}+R_{n+1}\left(t\right)=\sum _{l=0}^n{\left(\frac{t}{C}\right)}^l\frac{\underline{\mathcal{X}}(l;\sigma )}{P\left(l\right)}+R_{n+1}\left(t\right),l\in \mathcal{K},0\le \sigma \le 1,\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill {\overline{\vartheta }}_{\varsigma }(t;\sigma )& =\sum _{l=0}^n\frac{t^l}{l!}\frac{\overline{\mathcal{X}}(l;\sigma )}{P\left(l\right)}+R_{n+1}\left(t\right)=\sum _{l=0}^n{\left(\frac{t}{C}\right)}^l\frac{\overline{\mathcal{X}}(l;\sigma )}{P\left(l\right)}+R_{n+1}\left(t\right),l\in \mathcal{K},0\le \sigma \le 1,\hfill \end{array}$$

(27)

when ${\vartheta }_{\varsigma }\left(t\right)$ is (i)-differentiable and

$$\begin{array}{cc}\hfill {\underline{\vartheta }}_{\varsigma }(t;\sigma )=& \sum _{l=0,odd}^n{\left(\frac{t}{C}\right)}^l\frac{\overline{\mathcal{X}}(l;\sigma )}{P\left(l\right)}+R_{n+1}\left(t\right)+\sum _{l=0,even}^{\infty }{\left(\frac{t}{C}\right)}^l\frac{\underline{\mathcal{X}}(l;\sigma )}{P\left(l\right)}+R_{n+1}\left(t\right),0\le \sigma \le 1,\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill {\overline{\vartheta }}_{\varsigma }(t;\sigma )=& \sum _{l=0,odd}^{\infty }{\left(\frac{t}{C}\right)}^l\frac{\underline{\mathcal{X}}(l;\sigma )}{P\left(l\right)}+R_{n+1}\left(t\right)+\sum _{l=0,even}^{\infty }{\left(\frac{t}{C}\right)}^l\frac{\overline{\mathcal{X}}(l;\sigma )}{P\left(l\right)}+R_{n+1}\left(t\right),0\le \sigma \le 1,\hfill \end{array}$$

(29)

when ${\vartheta }_{\varsigma }\left(t\right)$ is (ii)-differentiable.

In this section, we present the solution of fuzzy PDEs at the equally spaced grid points $[t_0,t_1,\dots ,t_n]$ where $t_{\varsigma }=a+\varsigma l^{*}$ for each $(\varsigma =0,1,2,...n)$, and $l^{*}=\frac{b-a}{n}$. That is, the domain of interest are proved to n is sub-domain, and the fuzzy approximation functions in each sub-domain are ${\vartheta }_{\varsigma }(t;\sigma )$ for $\varsigma =0,1,2,\dots ,n-1$, respectively.

Taking the initial conditions, we obtain

$$\begin{array}{cc}\hfill \underline{\mathcal{X}}(0;\sigma )& ={\underline{\vartheta }}_{\varsigma }(0;\sigma ),\overline{\mathcal{X}}(0;\sigma )={\overline{\vartheta }}_{\varsigma }(0;\sigma ),0\le \sigma \le 1.\hfill \end{array}$$

In the first sub-domain, ${\underline{\vartheta }}_{\varsigma }(t;\sigma )$ and ${\overline{\vartheta }}_{\varsigma }(t;\sigma )$ can be described by ${\underline{\vartheta }}_{\varsigma }(0;\sigma )={\underline{\vartheta }}_{\varsigma ,0}\left(\sigma \right)$ and ${\overline{\vartheta }}_{\varsigma }(0;\sigma )={\overline{\vartheta }}_{\varsigma ,0}\left(\sigma \right)$, respectively. They can be expressed in terms of their n-th order bivariate Taylor series with respect to $t_0=0$. That is

$$\begin{array}{cc}\hfill {\underline{\vartheta }}_{\varsigma }(t_0;\sigma )& ={\underline{\mathcal{X}}}_0(0;\sigma )+{\underline{\mathcal{X}}}_0(1;\sigma )t+{\underline{\mathcal{X}}}_0(2;\sigma )t^2+\dots +{\underline{\mathcal{X}}}_0(n;\sigma )t^n,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {\overline{\vartheta }}_{\varsigma }(t_0;\sigma )& ={\overline{\mathcal{X}}}_0(0;\sigma )+{\overline{\mathcal{X}}}_0(1;\sigma )t+{\overline{\mathcal{X}}}_0(2;\sigma )t^2+\dots +{\overline{\mathcal{X}}}_0(n;\sigma )t^n.\hfill \end{array}$$

Additionally, using Taylor series for ${\vartheta }_{\varsigma }(t_{\varsigma };\lambda )$, the solution on the grid points $t_{\varsigma +1}$ can be expressed as:

$$\begin{array}{cc}\hfill {\underline{\vartheta }}_{\varsigma }(t_{\varsigma +1};\sigma )& ={\underline{\mathcal{X}}}_{\varsigma }(t_{\varsigma +1};\sigma )={\underline{\mathcal{X}}}_{\varsigma }(0;\sigma )+{\underline{\mathcal{X}}}_{\varsigma }(1;\sigma )(t_{\varsigma +1}-t_{\varsigma })+{\underline{\mathcal{X}}}_{\varsigma \iota }(2;\sigma ){(t_{\varsigma +1}-t_{\varsigma })}^2\hfill \\ \hfill & +\dots +{\underline{\mathcal{X}}}_{\varsigma }(n;\sigma ){(t_{\varsigma +1}-t_{\varsigma })}^n\hfill \\ \hfill & =\sum _{i=0}^n{\underline{\mathcal{X}}}_{\varsigma }(i;\sigma )h^i,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {\overline{\vartheta }}_{\varsigma }(t_{\varsigma +1};\sigma )& ={\overline{\mathcal{X}}}_{\varsigma }(t_{\varsigma +1};\sigma )={\overline{\mathcal{X}}}_{\varsigma }(0;\sigma )+{\overline{\mathcal{X}}}_{\varsigma }(1;\sigma )(t_{\varsigma +1}-t_{\varsigma })+{\overline{\mathcal{X}}}_{\varsigma \iota }(2;\sigma ){(t_{\varsigma +1}-t_{\varsigma })}^2\hfill \\ \hfill & +\dots +{\overline{\mathcal{X}}}_{\varsigma }(n;\sigma ){(t_{\varsigma +1}-t_{\varsigma })}^n\hfill \\ \hfill & =\sum _{i=0}^n{\overline{\mathcal{X}}}_{\varsigma }(i;\sigma )h^i.\hfill \end{array}$$

3.1.1. The Properties of Fuzzy $(N+1)$-Dimensional Reduced Differential Transform

We present some mathematical operations of fuzzy $(n+1)$-dimensional RDTM as following.

Proposition 2.

Let $u(\mathcal{X},t)$ and $v(\mathcal{X},t)$ are fuzzy-valued functions and their fuzzy $(n+1)$-dimensional reduced differential transformations denoted by $U_l\left(\mathcal{X}\right)$ and $V_l\left(\mathcal{X}\right)$, respectively. Then

• If $f(\mathcal{X},t)=u(\mathcal{X},t)\oplus v(\mathcal{X},t),$ then $F_l\left(\mathcal{X}\right)=U_l\left(\mathcal{X}\right)\oplus V_l\left(\mathcal{X}\right),l\in \mathcal{K}$
• If $f(\mathcal{X},t)=u(\mathcal{X},t){\ominus }_{gH}v(\mathcal{X},t),$ then $F_l\left(\mathcal{X}\right)=U_l\left(\mathcal{X}\right){\ominus }_{gH}{V}_l\left(\mathcal{X}\right),l\in \mathcal{K}$
• If $f(\mathcal{X},t)=c\odot u(\mathcal{X},t),$ then $F_l\left(\mathcal{X}\right)=c\odot U_l\left(\mathcal{X}\right),l\in \mathcal{K},$ where c is a constant.

provided the generalized Hukuhara difference (gH-difference) exists.

Proof. 

By using definition (9), the proof is obvious. □

Proposition 3.

Let us consider the fuzzy-valued function $w\in {\mathbb{E}}^1$ and $f(\mathcal{X},t)=\frac{\partial w(\mathcal{X},t)}{\partial t}$, then we can obtain $F_l\left(\mathcal{X}\right)=\frac{(l+1)!}{l!}{W}_{l+1}\left(\mathcal{X}\right),l\ge 1$ where $F_l\left(\mathcal{X}\right)$ and $W_l\left(\mathcal{X}\right)$ are the fuzzy $(n+1)$-dimensional reduced differential transformations of fuzzy-valued functions f and w, respectively.

Proof. 

Using Definition (9), we obtain for $0\le \sigma \le 1$

$$\begin{array}{cc}\hfill F_l(\mathcal{X};\sigma )& =\frac{1}{l!}{\left[\frac{{\partial }^l}{\partial t^l}\left(\frac{\partial }{\partial t}\underline{w}(\mathcal{X},t;\sigma );\frac{\partial }{\partial t}\overline{w}(\mathcal{X},t;\sigma )\right)\right]}_{t=0}\hfill \\ \hfill & =\frac{1}{l!}{\left[\frac{{\partial }^{l+1}}{\partial t^{l+1}}\underline{w}(\mathcal{X},t;\sigma );\frac{{\partial }^{l+1}}{\partial t^{l+1}}\overline{w}(\mathcal{X},t;\sigma )\right]}_{t=0}\hfill \\ \hfill & =(l+1){\left[\frac{1}{[l+1]!}\left(\frac{{\partial }^{l+1}}{\partial t^{l+1}}\underline{w}(\mathcal{X},t;\sigma );\frac{{\partial }^{l+1}}{\partial t^{l+1}}\overline{w}(\mathcal{X},t;\sigma )\right)\right]}_{t=0}.\hfill \end{array}$$

Using definition of fuzzy $(n+1)$-dimensional RDTM, we have

$$\begin{array}{c}\hfill F_l(\mathcal{X};\sigma )=\frac{(l+1)!}{l!}{W}_{l+1}(\mathcal{X};\sigma ),0\le \sigma \le 1,\end{array}$$

the proof is completed. □

Lemma 1.

Suppose $w\in {\mathbb{E}}^1$ and $f(\mathcal{X},t)=\frac{\partial w(\mathcal{X},t)}{\partial {\vartheta }_{\varsigma }}$, then we can obtain $F_l\left(\mathcal{X}\right)=\frac{\partial W_l\left(\mathcal{X}\right)}{\partial {\vartheta }_{\varsigma }},l\ge 1$ where $F_l\left(\mathcal{X}\right)$ and $W_l\left(\mathcal{X}\right)$ are the fuzzy $(n+1)$-dimensional reduced differential transformations of fuzzy-valued functions f and w, respectively.

Proof. 

Using definition (9), we can obtain the following equation for $\sigma \in [0,1]$

$$\begin{array}{c}\hfill f(\mathcal{X},t;\sigma )=\frac{\partial w(\mathcal{X},t;\sigma )}{\partial {\vartheta }_{\varsigma }}=\left[\frac{\partial \underline{w}(\mathcal{X},t;\sigma )}{\partial {\vartheta }_{\varsigma }},\frac{\partial \overline{w}(\mathcal{X},t;\sigma )}{\partial {\vartheta }_{\varsigma }}\right].\end{array}$$

(30)

Similarly, in view of definition (9) the fuzzy RDTM function can be written as:

$$\begin{array}{c}\hfill F_l(\mathcal{X};\sigma )=\frac{1}{l!}{\left.\left[\frac{{\partial }^l\underline{w}(\mathcal{X},t;\sigma )}{\partial t^l};\frac{{\partial }^l\overline{w}(\mathcal{X},t;\sigma )}{\partial t^l}\right]\right|}_{t=0}.\end{array}$$

(31)

We achieve the result by differentiating the right side of the preceding equality with consideration to ${\vartheta }_{\varsigma },$

$$\begin{array}{cc}\hfill \frac{\partial F_l(\mathcal{X};\sigma )}{\partial {\vartheta }_{\varsigma }}& =\frac{\partial \left(\frac{1}{l!}{\left.\left[\frac{{\partial }^l\underline{w}(\mathcal{X},t;\sigma )}{\partial t^l};\frac{{\partial }^l\overline{w}(\mathcal{X},t;\sigma )}{\partial t^l}\right]\right|}_{t=0}\right)}{\partial {\vartheta }_{\varsigma }}\hfill \\ \hfill & =\frac{1}{l!}{\left.\left[\frac{{\partial }^l\left[\frac{\partial \underline{w}(\mathcal{X},t;\sigma )}{\partial {\vartheta }_{\varsigma }};\frac{\partial \overline{w}(\mathcal{X},t;\sigma )}{\partial {\vartheta }_{\varsigma }}\right]}{\partial t^l}\right]\right|}_{t=0}\hfill \\ \hfill & =F_l(\mathcal{X};\sigma )0\le \sigma \le 1,\hfill \end{array}$$

Hence, the proof is completed by achieving our desired result. □

Lemma 2.

Let us consider $w\in {\mathbb{E}}^1$ and $f(\mathcal{X},t)=\frac{{\partial }^{{\wp }_1+\dots +{\wp }_n+\eta }w(\mathcal{X},t)}{\partial {\vartheta }_1^{{\wp }_1},\dots ,\partial {\vartheta }_n^{{\wp }_n}\partial t^{\eta }}$, then we have

$F_l\left(\mathcal{X}\right)=\frac{\left(l+\eta \right)!}{l!}\frac{{\partial }^{{\wp }_1+\dots +{\wp }_n}{W}_{l+\eta }\left(\mathcal{X}\right)}{\partial {\vartheta }_1^{{\wp }_1},\dots ,\partial {\vartheta }_n^{{\wp }_n}},l\ge n$ where $F_l\left(\mathcal{X}\right)$ and $W_l\left(\mathcal{X}\right)$ are the fuzzy $(n+1)$-dimensional reduced differential transformations of fuzzy-valued functions f and w, respectively.

Proof. 

Using definition (9), we obtain for $0\le \sigma \le 1$

$$\begin{array}{c}\hfill f(\mathcal{X},t;\sigma )=\frac{{\partial }^{{\wp }_1+\dots +{\wp }_n+\eta }w(\mathcal{X},t;\sigma )}{\partial {\vartheta }_1^{{\wp }_1},\dots ,\partial {\vartheta }_n^{{\wp }_n}\partial t^{\eta }}=\left[\frac{{\partial }^{{\wp }_1+\dots +{\wp }_n+\eta }\underline{w}(\mathcal{X},t;\sigma )}{\partial {\vartheta }_1^{{\wp }_1},\dots ,\partial {\vartheta }_n^{{\wp }_n}\partial t^{\eta }},\frac{{\partial }^{{\wp }_1+\dots +{\wp }_n+\eta }\overline{w}(\mathcal{X},t;\sigma )}{\partial {\vartheta }_1^{{\wp }_1},\dots ,\partial {\vartheta }_n^{{\wp }_n}\partial t^{\eta }}\right],\end{array}$$

we have

$$\begin{array}{c}\hfill F_l(\mathcal{X};\sigma )=\frac{1}{l!}\left[\frac{{\partial }^l}{\partial t^l}\left(\frac{{\partial }^{{\wp }_1+\dots +{\wp }_n+\eta }\underline{w}(\mathcal{X},t;\sigma )}{\partial {\vartheta }_1^{{\wp }_1},\dots ,\partial {\vartheta }_n^{{\wp }_n}\partial t^{\eta }},\frac{{\partial }^{{\wp }_1+\dots +{\wp }_n+\eta }\overline{w}(\mathcal{X},t;\sigma )}{\partial {\vartheta }_1^{{\wp }_1},\dots ,\partial {\vartheta }_n^{{\wp }_n}\partial t^{\eta }}\right)\right]{|}_{t=0}.\end{array}$$

From the calculus, one can obtain

$$\begin{array}{c}\hfill F_l(\mathcal{X};\sigma )=\frac{1}{l!}\frac{{\partial }^{{\wp }_1+\dots +{\wp }_n}}{\partial {\vartheta }_1^{{\wp }_1}\dots \partial {\vartheta }_n^{{\wp }_n}}\left[\frac{{\partial }^{l+\eta }\underline{w}(\mathcal{X},t;\sigma )}{\partial t^{l+\eta }},\frac{{\partial }^{l+\eta }\overline{w}(\mathcal{X},t;\sigma )}{\partial t^{l+\eta }}\right]{|}_{t=0}.\end{array}$$

(32)

Consequently, the fuzzy $(n+1)$-dimensional RDTM of fuzzy-valued function $w(\mathcal{X},t;\sigma )=[\underline{w}(\mathcal{X},t;\sigma ),\overline{w}(\mathcal{X},t;\sigma )]$, as follows

$$\begin{array}{c}\hfill F_{l+\eta }(\mathcal{X};\sigma )=\frac{1}{(l+\eta )!}\left[\frac{{\partial }^{l+\eta }\underline{w}(\mathcal{X},t;\sigma )}{\partial t^{l+\eta }},\frac{{\partial }^{l+\eta }\overline{w}(\mathcal{X},t;\sigma )}{\partial t^{l+\eta }}\right]{|}_{t=0},\end{array}$$

thus, we get

$$\begin{array}{c}\hfill F_l(\mathcal{X};\sigma )=\frac{(l+\eta )!}{l!}\frac{{\partial }^{{\wp }_1+\dots +{\wp }_n}{W}_{l+\eta }(\mathcal{X};\sigma )}{\partial {\vartheta }_1^{{\wp }_1},\dots ,\partial {\vartheta }_n^{{\wp }_n}},0\le \sigma \le 1.\end{array}$$

(33)

the proof is completed. □

Theorem 1.

Let $W_l\left(\mathcal{X}\right)$ and $G_l\left(\mathcal{X}\right)$ are the $(n+1)$-dimensional fuzzy RDTM of $w(\mathcal{X},t)$ is a positive real-valued function and $g(\mathcal{X},t)$ is a fuzzy-valued function. Also let us suppose that if $f(\mathcal{X},t)=w(\mathcal{X},t)g(\mathcal{X},t),$ then

$$\begin{array}{cc}\hfill F_l(\mathcal{X};\sigma )& =\sum _{\wp =0}^l{W}_{\wp }\left(\mathcal{X}\right)\odot G_{l-\wp }(\mathcal{X};\sigma ),0\le \sigma \le 1.\hfill \end{array}$$

(34)

Proof. 

Using definition (9), we get

$$\begin{array}{cc}\hfill f(\mathcal{X};\sigma )& \approx \left(\sum _{l=0}^n{W}_l\left(\mathcal{X}\right)t^l\right)\odot \left(\sum _{l=0}^n{G}_l(\mathcal{X};\sigma )t^l\right)\hfill \\ \hfill & =\left[W_0\left(\mathcal{X}\right)+W_1\left(\mathcal{X}\right)t+W_2\left(\mathcal{X}\right)t^2+\dots +W_n\left(\mathcal{X}\right)t^n\right]\odot \left[G_0(\mathcal{X};\sigma )+G_1(\mathcal{X};\sigma )t+G_2(\mathcal{X};\sigma )t^2+\right.\hfill \\ \hfill & \left.\dots +G_n(\mathcal{X};\sigma )t^n\right]\hfill \\ \hfill & =\left[W_0\left(X\right)G_0(\mathcal{X};\sigma )\right]+\left[W_0\left(\mathcal{X}\right)G_1(\mathcal{X};\sigma )+W_1\left(\mathcal{X}\right)G_0(\mathcal{X};\sigma )\right]t\hfill \\ \hfill & +\left[W_0\left(\mathcal{X}\right)G_2(\mathcal{X};\sigma )+W_1\left(\mathcal{X}\right)G_1(\mathcal{X};\sigma )+W_2\left(\mathcal{X}\right)G_0(\mathcal{X};\sigma )\right]t^2+\dots \hfill \\ \hfill & +\left[W_0\left(\mathcal{X}\right)G_n(\mathcal{X};\sigma )+W_1\left(\mathcal{X}\right)G_{n-1}(\mathcal{X};\sigma )+\dots +W_{n-1}\left(\mathcal{X}\right)G_1(\mathcal{X};\sigma )+W_n\left(\mathcal{X}\right)G_0(\mathcal{X};\sigma )\right]t^n.\hfill \end{array}$$

In general, we obtain

$$\begin{array}{c}\hfill f(\mathcal{X};\sigma )\approx \sum _{l=0}^n\sum _{\wp =0}^l{W}_{\wp }\left(\mathcal{X}\right)G_{l-\wp }(\mathcal{X};\sigma )t^l,\end{array}$$

and from the definition of $(n+1)$-dimensional RDTM, we obtain

$$\begin{array}{cc}\hfill F_l(\mathcal{X};\sigma )& =\sum _{\wp =0}^l{W}_{\wp }\left(\mathcal{X}\right)\odot G_{l-\wp }(\mathcal{X};\sigma ),0\le \sigma \le 1.\hfill \end{array}$$

This completes our required proof. □

Lemma 3.

Assume that $f\in {\mathbb{E}}^1,$ if $f(\mathcal{X},t)={\vartheta }_1^{{ı}_1},{\vartheta }_2^{{ı}_2},\dots ,{\vartheta }_n^{{ı}_n}{t}^{\eta }$, then $F_l\left(\mathcal{X}\right)={\vartheta }_1^{{ı}_1},{\vartheta }_2^{{ı}_2},\dots ,{\vartheta }_n^{{ı}_n}\delta (l-\eta ),$ where

$\begin{array}{l}\delta (l-\eta )=\left\{\begin{array}{ccc}& 1,\hfill & \hfill l=\eta ,\\ & 0,\hfill & \hfill otherwise,\end{array}\right.\end{array}$

are the fuzzy $(n+1)$-dimensional reduced differential transformations of f.

Proof. 

From definition (9), for any $\sigma \in [0,1],$ we obtain

$$\begin{array}{cc}\hfill F_l(\mathcal{X};\sigma )& =\frac{1}{l!}{\left.\left[\frac{{\partial }^l\underline{f}(\mathcal{X},t;\sigma )}{\partial t^l},\frac{{\partial }^l\overline{f}(\mathcal{X},t;\sigma )}{\partial t^l}\right]\right|}_{t=0}\hfill \\ \hfill & =\frac{1}{l!}{\left.\left[{\vartheta }_1^{{ı}_1},{\vartheta }_2^{{ı}_2},\dots ,{\vartheta }_n^{{ı}_n}\frac{{\partial }^l{t}^{\eta }}{\partial t^l}\right]\right|}_{t=0}.\hfill \end{array}$$

This means

• If $l<\eta$ or $\eta <l,$ then $F_l(\mathcal{X};\sigma )=\tilde{0}$,
• If $l=\eta$, then $F_l(\mathcal{X};\sigma )={\vartheta }_1^{{ı}_1},{\vartheta }_2^{{ı}_2},\dots ,{\vartheta }_n^{{ı}_n}$,

the required proof is completed. □

Lemma 4.

Let $g\in {\mathbb{E}}^1$ and $f(\mathcal{X},t)={\vartheta }_1^{{ı}_1},{\vartheta }_2^{{ı}_2},\dots ,{\vartheta }_n^{{ı}_n}{t}^{\eta }g(\mathcal{X},t)$, where $\eta \le l,$ then $F_l\left(\mathcal{X}\right)={\vartheta }_1^{{ı}_1},{\vartheta }_2^{{ı}_2},\dots ,{\vartheta }_n^{{ı}_n}{G}_{l-\eta }\left(\mathcal{X}\right),$ are the fuzzy $(n+1)$-dimensional RDTM of fuzzy-valued functions f and g, respectively.

Proof. 

From Definition (9), for any $\sigma \in [0,1].$ Assume that $w(\mathcal{X},t)={\vartheta }_1^{{ı}_1},{\vartheta }_2^{{ı}_2},\dots ,{\vartheta }_n^{{ı}_n}{t}^{\eta },$ i.e., $f(\mathcal{X},t)=w(\mathcal{X},t)g(\mathcal{X},t).$ According to Theorem (1), the RDTM real-valued function of $f(\mathcal{X},t)$ is

$$\begin{array}{c}\hfill {\underline{F}}_l(\mathcal{X};\sigma )=\sum _{\wp =0}^l{W}_{\wp }\left(\mathcal{X}\right)·{\underline{G}}_{l+\wp }(\mathcal{X};\sigma ),0\le \sigma \le 1,\\ \hfill {\overline{F}}_l(\mathcal{X};\sigma )=\sum _{\wp =0}^l{W}_{\wp }\left(\mathcal{X}\right)·{\overline{G}}_{l+\wp }(\mathcal{X};\sigma ),0\le \sigma \le 1.\end{array}$$

Using Lemma (3), it follows

$$\begin{array}{cc}\hfill W_{\wp }\left(\mathcal{X}\right)& ={\vartheta }_1^{{ı}_1},{\vartheta }_2^{{ı}_2},\dots ,{\vartheta }_n^{{ı}_n}{t}^{\eta }\delta (\wp -\eta ).\hfill \end{array}$$

(35)

Since $\eta \le l,$ and using (35), we get

$$\begin{array}{c}\hfill F_l(\mathcal{X};\sigma )=W_{\eta }\left(\mathcal{X}\right)·G_{l+\eta }(\mathcal{X};\sigma )={\vartheta }_1^{{ı}_1},{\vartheta }_2^{{ı}_2},\dots ,{\vartheta }_n^{{ı}_n}{G}_{l-\eta }(\mathcal{X};\sigma ),0\le \sigma \le 1,\end{array}$$

the proof is completed. □

Theorem 2.

Let us consider the real-valued function $w\in \mathbb{R}$ and $f(\mathcal{X},t)=w\left(\mathcal{X}\right)·g(\mathcal{X},t)$, then $F_l\left(\mathcal{X}\right)=w\left(\mathcal{X}\right)·G_l\left(\mathcal{X}\right)$, where $F_l\left(\mathcal{X}\right)$ and $G_l\left(\mathcal{X}\right)$ are $(n+1)$-dimensional RDTM of real-valued functions f and g, respectively.

Proof. 

Using definition (9) for $\sigma \in [0,1]$, we obtain

$$\begin{array}{cc}\hfill F_l(\mathcal{X};\sigma )& =\frac{1}{l!}{\left.\left[\frac{{\partial }^{l}w\left(\mathcal{X}\right)·\underline{g}(X,t;\sigma )}{\partial t^l},\frac{{\partial }^{l}w\left(\mathcal{X}\right)·\overline{g}(\mathcal{X},t;\sigma )}{\partial t^l}\right]\right|}_{t=0}\hfill \\ \hfill & =w\left(\mathcal{X}\right)\frac{1}{l!}{\left.\left[\frac{{\partial }^l\underline{g}(\mathcal{X},t;\sigma )}{\partial t^l},\frac{{\partial }^l\overline{g}(\mathcal{X},t;\sigma )}{\partial t^l}\right]\right|}_{t=0},\hfill \end{array}$$

thus, we obtain

$$\begin{array}{c}\hfill F_l(\mathcal{X};\sigma )=w\left(\mathcal{X}\right)·G_l(\mathcal{X};\sigma ),0\le \sigma \le 1,\end{array}$$

which is our required result. □

3.1.2. Applications

In this section, we propose some examples in [1,2] to illustrate the applicability of the alternative approach of fuzzy $(n+1)$-dimensional RDTM to obtain the solutions of fuzzy heat-like and wave-like equations with variable coefficients.

Example 1.

We consider the following fuzzy $(2+1)$-dimensional heat-like equation [1,2]

$$\begin{array}{c}\hfill \frac{\partial w}{\partial t}=\frac{1}{2}\left({\theta }^2\odot \frac{{\partial }^{2}w}{\partial {\vartheta }^2}\oplus {\vartheta }^2\odot \frac{{\partial }^{2}w}{\partial {\theta }^2}\right),0<\vartheta ,\theta <1,t>0,\end{array}$$

(36)

with the initial condition

$$\begin{array}{c}\hfill w(\vartheta ,\theta ,0)=\left[{(1+2\sigma )}^n,{(5-2\sigma )}^n\right]{\ominus }_{gH}{\theta }^2,\end{array}$$

(37)

where $n=1,2,3,\dots$

Applying the fuzzy reduced differential transform to (36), we get

$$\begin{array}{cc}\hfill (l+1){\underline{W}}_{l+1}\left(\sigma \right)& =\frac{{\theta }^2}{2}\frac{{\partial }^2{\underline{W}}_l\left(\sigma \right)}{\partial {\vartheta }^2}+\frac{{\vartheta }^2}{2}\frac{{\partial }^2{\underline{W}}_l\left(\sigma \right)}{\partial {\theta }^2},0\le \sigma \le 1,\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill (l+1){\overline{W}}_{l+1}\left(\sigma \right)& =\frac{{\theta }^2}{2}\frac{{\partial }^2{\overline{W}}_l\left(\sigma \right)}{\partial {\vartheta }^2}+\frac{{\vartheta }^2}{2}\frac{{\partial }^2{\overline{W}}_l\left(\sigma \right)}{\partial {\theta }^2},0\le \sigma \le 1.\hfill \end{array}$$

(39)

Similarly, applying fuzzy reduced differential transformation on the initial condition (37) to achieve

$$\begin{array}{c}\hfill W_0\left(\sigma \right)=\left[{(1+2\sigma )}^n,{(5-2\sigma )}^n\right]{\ominus }_{gH}{\theta }^2.\end{array}$$

(40)

Putting Equations (40) into (38), we obtain

$$\begin{array}{cc}\hfill \underline{w}(\vartheta ,\theta ,t;\sigma )& =\sum _{l=0}^{\infty }{\underline{W}}_l{t}^l\hfill \\ \hfill & ={(1+2\sigma )}^n-\left[{\theta }^2\left(1+\frac{t^2}{2!}+\frac{t^4}{4!}+\dots \right)+{\vartheta }^2\left(t+\frac{t^3}{3!}+\frac{t^5}{5!}+\dots \right)\right]\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \overline{w}(\vartheta ,\theta ,t;\sigma )& =\sum _{l=0}^{\infty }{\overline{W}}_l{t}^l\hfill \\ \hfill & ={(5-2\sigma )}^n-\left[{\theta }^2\left(1+\frac{t^2}{2!}+\frac{t^4}{4!}+\dots \right)+{\vartheta }^2\left(t+\frac{t^3}{3!}+\frac{t^5}{5!}+\dots \right)\right]\hfill \end{array}$$

thus, we can achieve the solution of $w(\vartheta ,\theta ,t;\sigma )$ as follows:

$$\begin{array}{c}\hfill w(\vartheta ,\theta ,t;\sigma )=\left[{(1+2\sigma )}^n,{(5-2\sigma )}^n\right]{\ominus }_{gH}\left({\theta }^{2}cosh\left(t\right)+{\vartheta }^{2}sinh\left(t\right)\right),0\le \sigma \le 1.\end{array}$$

Example 2.

Consider the following fuzzy $(3+1)$-dimensional heat-like equation [1,2]

$$\begin{array}{c}\hfill \frac{\partial w}{\partial t}=\Psi (\vartheta ,\theta ,\varphi )\oplus \frac{1}{36}\left({\vartheta }^2\odot \frac{{\partial }^{2}w}{\partial {\vartheta }^2}\oplus {\theta }^2\odot \frac{{\partial }^{2}w}{\partial {\theta }^2}\oplus {\varphi }^2\odot \frac{{\partial }^{2}w}{\partial {\varphi }^2}\right),0<\vartheta ,\theta ,\varphi <1,t>0,\end{array}$$

(41)

subject to the initial condition

$$\begin{array}{c}\hfill w(\vartheta ,\theta ,\varphi ,0)=\tilde{0},\end{array}$$

(42)

where

$$\begin{array}{cc}\hfill \Psi (\vartheta ,\theta ,\varphi ;\sigma )& ={(-1,0,1)}^n\odot {\left(\vartheta \theta \varphi \right)}^4\hfill \\ \hfill & =\left[{(\sigma -1)}^n,{(1-\sigma )}^n\right]\odot {\left(\vartheta \theta \varphi \right)}^4,0\le \sigma \le 1,n=1,2,3,\dots ,\tilde{0}\in {\mathbb{E}}^1.\hfill \end{array}$$

Applying the fuzzy $(n+1)$-dimensional reduced differential transform on (41) to get

$$\begin{array}{cc}\hfill (l+1){\underline{W}}_{l+1}\left(\sigma \right)& ={(\sigma -1)}^n{\left(\vartheta \theta \varphi \right)}^4+\frac{1}{36}\left({\vartheta }^2\frac{{\partial }^2\underline{w}}{\partial {\vartheta }^2}+{\theta }^2\frac{{\partial }^2\underline{w}}{\partial {\theta }^2}+{\varphi }^2\frac{{\partial }^2\underline{w}}{\partial {\varphi }^2}\right)\left(\sigma \right),t>0,\hfill \end{array}$$

(43)

$$\begin{array}{cc}\hfill (l+1){\overline{W}}_{l+1}\left(\sigma \right)& ={(1-\sigma )}^n{\left(\vartheta \theta \varphi \right)}^4+\frac{1}{36}\left({\vartheta }^2\frac{{\partial }^2\overline{w}}{\partial {\vartheta }^2}+{\theta }^2\frac{{\partial }^2\overline{w}}{\partial {\theta }^2}+{\varphi }^2\frac{{\partial }^2\overline{w}}{\partial {\varphi }^2}\right)\left(\sigma \right),t>0.\hfill \end{array}$$

(44)

Using the initial condition (42), we obtain

$$\begin{array}{cc}\hfill {\underline{W}}_0\left(\sigma \right)& =\tilde{0},\hfill \end{array}$$

(45)

$$\begin{array}{cc}\hfill {\overline{W}}_0\left(\sigma \right)& =\tilde{0}.\hfill \end{array}$$

(46)

Substituting (46) into (43), we obtain the series solution as

$$\begin{array}{cc}\hfill \underline{w}(\vartheta ,\theta ,\varphi ,t;\sigma )& ={(\sigma -1)}^n{\left(\vartheta \theta \varphi \right)}^4\left(t+\frac{t^2}{2!}+\frac{t^3}{3!}+\frac{t^4}{4!}+\dots \right),\hfill \\ \hfill \overline{w}(\vartheta ,\theta ,\varphi ,t;\sigma )& ={(1-\sigma )}^n{\left(\vartheta \theta \varphi \right)}^4\left(t+\frac{t^2}{2!}+\frac{t^3}{3!}+\frac{t^4}{4!}+\dots \right),\hfill \end{array}$$

we can obtain the exact solution as:

$$\begin{array}{c}\hfill w(\vartheta ,\theta ,\varphi ,t;\sigma )=\left[{(\sigma -1)}^n,{(1-\sigma )}^n\right]\odot {\left(\vartheta \theta \varphi \right)}^4\left(exp\left(t\right)-1\right),0\le \sigma \le 1.\end{array}$$

Example 3.

Consider the following fuzzy $(2+1)$-dimensional wave-like equation [1,2]

$$\begin{array}{c}\hfill \frac{{\partial }^{2}w}{\partial t^2}=\frac{1}{12}\left({\vartheta }^2\odot \frac{{\partial }^{2}w}{\partial {\vartheta }^2}\oplus {\theta }^2\odot \frac{{\partial }^{2}w}{\partial {\theta }^2}\right),0<\vartheta ,\theta <1,t>0,\end{array}$$

(47)

subject to the initial conditions

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & w(\vartheta ,\theta ,0)=\left[{(0.2+0.2\sigma )}^n,{(0.6-0.2\sigma )}^n\right]\odot {\vartheta }^4,\hfill \\ \hfill & {\left.\frac{\partial w}{\partial t}\right|}_{t=0}=\left[{(0.2+0.2\sigma )}^n,{(0.6-0.2\sigma )}^n\right]\odot {\theta }^4,\hfill \end{array}\end{array}$$

(48)

where $n=1,2,3,\dots$

Using the fuzzy RDTM for (47), we get

$$\begin{array}{cc}\hfill (l+1)(l+2){\underline{W}}_{l+2}\left(\sigma \right)& =\frac{1}{12}\left({\vartheta }^2\frac{{\partial }^2{\underline{W}}_l\left(\lambda \right)}{\partial {\vartheta }^2}+{\theta }^2\frac{{\partial }^2{\underline{W}}_l\left(\sigma \right)}{\partial {\theta }^2}\right)\left(\sigma \right),t>0,\hfill \end{array}$$

(49)

$$\begin{array}{cc}\hfill (l+1)(l+2){\overline{W}}_{l+2}\left(\sigma \right)& =\frac{1}{12}\left({\vartheta }^2\frac{{\partial }^2{\overline{W}}_l\left(\sigma \right)}{\partial {\vartheta }^2}+{\theta }^2\frac{{\partial }^2{\overline{W}}_l\left(\sigma \right)}{\partial {\theta }^2}\right)\left(\sigma \right),t>0.\hfill \end{array}$$

(50)

From initial conditions (48), we obtain

$$\begin{array}{cc}\hfill {\underline{W}}_0\left(\sigma \right)& ={(0.2+0.2\lambda )}^n{\vartheta }^4,{\underline{W}}_1\left(\sigma \right)={(0.2+0.2\lambda )}^n{\theta }^4,\hfill \end{array}$$

(51)

$$\begin{array}{cc}\hfill {\overline{W}}_0\left(\sigma \right)& ={(0.6-0.2\lambda )}^n{\vartheta }^4,{\overline{W}}_1\left(\sigma \right)={(0.6-0.2\lambda )}^n{\theta }^4.\hfill \end{array}$$

(52)

Substituting (52) into (49), we get the series solution as:

$$\begin{array}{cc}\hfill \underline{w}(\vartheta ,\theta ,t;\sigma )& ={(0.2+0.2\sigma )}^n\left[{\vartheta }^4\left(1+\frac{t^2}{2!}+\frac{t^4}{4!}+\dots \right)+{\theta }^4\left(t+\frac{t^3}{3!}+\frac{t^5}{5!}+\dots \right)\right],\hfill \\ \hfill \overline{w}(\vartheta ,\theta ,t;\sigma )& ={(0.6-0.2\sigma )}^n\left[{\vartheta }^4\left(1+\frac{t^2}{2!}+\frac{t^4}{4!}+\dots \right)+{\theta }^4\left(t+\frac{t^3}{3!}+\frac{t^5}{5!}+\dots \right)\right],\hfill \end{array}$$

We can obtain the exact solution as:

$$\begin{array}{c}\hfill \tilde{w}(\vartheta ,\theta ,t;\sigma )=\left[{(0.2+0.2\sigma )}^n,{(0.6-0.2\sigma )}^n\right]\odot \left({\vartheta }^{4}cosh\left(t\right)+{\theta }^{4}sinh\left(t\right)\right),0\le \sigma \le 1.\end{array}$$

Example 4.

Consider the following fuzzy $(3+1)$-dimensional wave-like equation [1,2]

$$\begin{array}{c}\hfill \frac{{\partial }^{2}w}{\partial t^2}=\left({\vartheta }^2+{\theta }^2+{\varphi }^2\right)\oplus \frac{1}{2}\left({\vartheta }^2\odot \frac{{\partial }^{2}w}{\partial {\vartheta }^2}\oplus {\theta }^2\odot \frac{{\partial }^{2}w}{\partial {\theta }^2}\oplus {\varphi }^2\odot \frac{{\partial }^{2}w}{\partial {\varphi }^2}\right),0<\vartheta ,\theta ,\varphi <1,t>0,\end{array}$$

(53)

with the initial conditions

$$\begin{array}{c}\hfill w(\vartheta ,\theta ,\varphi ,0)=\tilde{0},{\left.\frac{\partial w}{\partial t}\right|}_{t=0}=\left[{\left(0.5\sigma \right)}^n,{(1-0.5\sigma )}^n\right]\oplus \left({\vartheta }^2+{\theta }^2-{\varphi }^2\right),\end{array}$$

(54)

where $n=1,2,3,\dots$

Applying (53), we get

$$\begin{array}{cc}\hfill (l+1)(l+2){\underline{W}}_{l+2}\left(\sigma \right)& =\left({\vartheta }^2+{\theta }^2+{\varphi }^2\right)+\frac{1}{2}\left({\vartheta }^2\frac{{\partial }^2{\underline{W}}_l}{\partial {\vartheta }^2}+{\theta }^2\frac{{\partial }^2{\underline{W}}_l}{\partial {\theta }^2}+{\varphi }^2\frac{{\partial }^2{\underline{W}}_l}{\partial {\varphi }^2}\right),t>0,\hfill \end{array}$$

(55)

$$\begin{array}{cc}\hfill (l+1)(l+2){\overline{W}}_{l+2}\left(\sigma \right)& =\left({\vartheta }^2+{\theta }^2+{\varphi }^2\right)+\frac{1}{2}\left({\vartheta }^2\frac{{\partial }^2{\overline{W}}_l}{\partial {\vartheta }^2}+{\theta }^2\frac{{\partial }^2{\overline{W}}_l}{\partial {\theta }^2}+{\varphi }^2\frac{{\partial }^2{\overline{W}}_l}{\partial {\varphi }^2}\right),t>0.\hfill \end{array}$$

(56)

Taking Equation (54) yields

$$\begin{array}{ll}\hfill {\underline{W}}_0\left(\sigma \right)& ={\left(0.5\sigma \right)}^n,{\underline{W}}_1\left(\sigma \right)={\left(0.5\sigma \right)}^n+\left({\vartheta }^2+{\theta }^2-{\varphi }^2\right),\hfill \end{array}$$

(57)

$$\begin{array}{ll}\hfill {\overline{W}}_0\left(\sigma \right)& ={(1-0.5\sigma )}^n,{\overline{W}}_1\left(\sigma \right)={(1-0.5\sigma )}^n+\left({\vartheta }^2+{\theta }^2-{\varphi }^2\right).\hfill \end{array}$$

(58)

Using (58) into (55), we get the series solution as:

$$\begin{array}{cc}\hfill \underline{w}(\vartheta ,\theta ,t;\sigma )& ={\left(0.5\sigma \right)}^n+\left[({\vartheta }^2+{\theta }^2)\left(1+t+\frac{t^2}{2!}+\dots \right)+{\varphi }^2\left(1-t+\frac{t^2}{2!}+\dots \right)-\left({\vartheta }^2+{\theta }^2+{\varphi }^2\right)\right]\hfill \\ \hfill \overline{w}(\vartheta ,\theta ,t;\sigma )& ={(1-0.5\sigma )}^n+\left[({\vartheta }^2-{\theta }^2)\left(1+t+\frac{t^2}{2!}+\dots \right)+{\varphi }^2\left(1-t+\frac{t^2}{2!}+\dots \right)-\left({\vartheta }^2+{\theta }^2+{\varphi }^2\right)\right]\hfill \end{array}$$

We can find the exact solution as:

$$\begin{array}{c}\hfill w(\vartheta ,\theta ,t;\sigma )=\left[{\left(0.5\sigma \right)}^n,{(1-0.5\sigma )}^n\right]\oplus \left(\left({\vartheta }^2+{\theta }^2\right)exp\left(t\right)+{\varphi }^{2}exp(-t)-\left({\vartheta }^2+{\theta }^2+{\varphi }^2\right)\right),0\le \sigma \le 1.\end{array}$$

When this method is compared to other methods in [1,2], it shows that when these methods are used to solve fuzzy heat-like and wave-like equations, they all lead to the same proposed solution. In addition, fuzzy $(n+1)$-dimensional RDTM like HPM doesn’t always involve specific algorithms and complex calculations like fuzzy ADM or the development of correction functionals utilizing general Lagranges multipliers in the fuzzy VIM. So, the fuzzy $(n+1)$-dimensional RDTM is a better way to solve fuzzy partial differential equations and is also simple and easy to use.

3.2. Fuzzy Zakharov-Kuznetsov Equations

In this part, we present the nonlinear fuzzy Zakharov-Kuznetsov equations as follows:

$$\begin{array}{c}\hfill w_t\oplus {{\rm Y}}_1\odot {\left(w^m\right)}_{\vartheta }\oplus {{\rm Y}}_2\odot {\left(w^n\right)}_{\vartheta \vartheta \vartheta }\oplus {{\rm Y}}_3\odot {\left(w^l\right)}_{\theta \theta \vartheta }=0,mnl\ne 0,{{\rm Y}}_1,{{\rm Y}}_2,{{\rm Y}}_3\ge 0,\end{array}$$

(59)

subject to the initial condition

$$\begin{array}{c}\hfill w(\vartheta ,\theta ,t)=f(\vartheta ,\theta ,t),\end{array}$$

(60)

where ${{\rm Y}}_1,{{\rm Y}}_2,{{\rm Y}}_3$ are the arbitrary constants and $m,n,l$ are integrals.

3.3. Fuzzy Adomian Decomposition Method

Consider the following formal nonlinear fuzzy differential equation as:

$$\begin{array}{c}\hfill \mathcal{L}w\oplus \mathcal{R}w\oplus \mathcal{N}w=0,\end{array}$$

(61)

where $\mathcal{L}$ is a linear differential operator, $\mathcal{R}$ denotes the linear operator’s remainder, and $\mathcal{N}w$ denotes the nonlinear terms. We can obtain (61) using the inverse operator ${\mathcal{L}}^{-1}$ on both sides

$$\begin{array}{c}\hfill {\mathcal{L}}^{-1}\mathcal{L}w\oplus {\mathcal{L}}^{-1}\left(\mathcal{R}w\right)\oplus {\mathcal{L}}^{-1}\left(\mathcal{N}w\right)=0,\end{array}$$

(62)

Firstly, (59) can be represented as

$$\begin{array}{c}\hfill \mathcal{L}w=\mathcal{N}w,\end{array}$$

(63)

where

$$\begin{array}{c}\hfill \mathcal{L}=\frac{\partial }{\partial t},\end{array}$$

(64)

and

$$\begin{array}{c}\hfill \mathcal{N}w=-{{\rm Y}}_1\odot {\left(w^m\right)}_{\vartheta }{\ominus }_{gH}{{\rm Y}}_2\odot {\left(w^n\right)}_{\vartheta \vartheta \vartheta }{\ominus }_{gH}{{\rm Y}}_3\odot {\left(w^l\right)}_{\theta \theta \vartheta }.\end{array}$$

(65)

Suppose that ${\mathcal{L}}^{-1}$ and an integral operator defined by

$$\begin{array}{c}\hfill {\mathcal{L}}^{-1}(·)={\int }_0^t(·)dt.\end{array}$$

(66)

Using the integral operator ${\mathcal{L}}^{-1}$ on both sides of (59), we get

$$\begin{array}{cc}\hfill w(\vartheta ,\theta ,t;\sigma )& =w(\vartheta ,\theta ,0)\left(\sigma \right){\ominus }_{gH}{\mathcal{L}}^{-1}\left({{\rm Y}}_1\odot {\left(w^m\right)}_{\vartheta }\oplus {{\rm Y}}_2\odot {\left(w^n\right)}_{\vartheta \vartheta \vartheta }\oplus {{\rm Y}}_3\odot {\left(w^l\right)}_{\theta \theta \vartheta }\right).\hfill \end{array}$$

(67)

The fuzzy decomposition method assumes a series solution for $\tilde{w}(\vartheta ,\theta ,t;\sigma )$ given by an infinite sum of components as:

$$\begin{array}{cc}\hfill w(\vartheta ,\theta ,t;\sigma )& =\sum _{l=0}^{\infty }{w}_l(\vartheta ,\theta ,t;\sigma )\hfill \end{array}$$

(68)

where $w_0,w_1,w_2,\dots$ are obtained sequentially.

The nonlinear terms

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill \mathcal{F}\left(w\right(\vartheta ,\theta ,t;\sigma \left)\right)& ={\left(w^m(\vartheta ,\theta ,t;\sigma )\right)}_{\vartheta }\hfill \\ \hfill \mathcal{G}\left(w\right(\vartheta ,\theta ,t;\sigma \left)\right)& ={\left(w^n(\vartheta ,\theta ,t;\sigma )\right)}_{\vartheta \vartheta \vartheta }\hfill \\ \hfill \mathcal{H}\left(w\right(\vartheta ,\theta ,t;\sigma \left)\right)& ={\left(w^l(\vartheta ,\theta ,t;\sigma )\right)}_{\theta \theta \vartheta }\hfill \end{array}\right.\end{array}$$

(69)

are decomposed into three infinite polynomial series

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill \mathcal{F}\left(w\right(\vartheta ,\theta ,t;\sigma \left)\right)& ={\left(w^m(\vartheta ,\theta ,t;\sigma )\right)}_{\vartheta }=\sum _{l=0}^{\infty }{\mathcal{A}}_l\hfill \\ \hfill \mathcal{G}\left(w\right(\vartheta ,\theta ,t;\sigma \left)\right)& ={\left(w^n(\vartheta ,\theta ,t;\sigma )\right)}_{\vartheta \vartheta \vartheta }=\sum _{l=0}^{\infty }{\mathcal{B}}_l\hfill \\ \hfill \mathcal{H}\left(w\right(\vartheta ,\theta ,t;\sigma \left)\right)& ={\left(w^l(\vartheta ,\theta ,t;\sigma )\right)}_{\theta \theta \vartheta }=\sum _{l=0}^{\infty }{\mathcal{C}}_l,\hfill \end{array}\right.\end{array}$$

(70)

where ${\mathcal{A}}_l,{\mathcal{B}}_l$, and ${\mathcal{C}}_l$ are Adomian polynomials, which can be used to determine all types of nonlinearities using fuzzy Adomian’s techniques. The analytical formulae for Adomian polynomials are:

$$\begin{array}{cc}\hfill {\mathcal{A}}_l& =\frac{1}{l!}{\left[\frac{d^l}{d{\mu }^l}\mathcal{F}\left(\sum _{\varsigma =0}^{\infty }{\mu }^{\varsigma }{w}_{\varsigma }(\vartheta ,\theta ,t;\sigma )\right)\right]}_{\mu =0}\hfill \\ \hfill {\mathcal{B}}_l& =\frac{1}{l!}{\left[\frac{d^l}{d{\mu }^l}\mathcal{G}\left(\sum _{\varsigma =0}^{\infty }{\mu }^{\varsigma }{w}_{\varsigma }(\vartheta ,\theta ,t;\sigma )\right)\right]}_{\mu =0}\hfill \\ \hfill {\mathcal{C}}_l& =\frac{1}{l!}{\left[\frac{d^l}{d{\mu }^l}\mathcal{H}\left(\sum _{\varsigma =0}^{\infty }{\mu }^{\varsigma }{w}_{\varsigma }(\vartheta ,\theta ,t;\sigma )\right)\right]}_{\mu =0}.\hfill \end{array}$$

For the nonlinear operators (69), we provide the first few Adomian polynomials

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\mathcal{A}}_0& ={\left(w_0^m\right)}_{\vartheta }\hfill \\ \hfill {\mathcal{A}}_1& ={\left(m{w}_1{w}_0^{m-1}\right)}_{\vartheta }\hfill \\ \hfill ⋮\end{array}\right.\end{array}$$

(71)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\mathcal{B}}_0& ={\left(w_0^n\right)}_{\vartheta \vartheta \vartheta }\hfill \\ \hfill {\mathcal{B}}_1& ={\left(n{w}_1{w}_0^{n-1}\right)}_{\vartheta \vartheta \vartheta }\hfill \\ \hfill ⋮\end{array}\right.\end{array}$$

(72)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\mathcal{C}}_0& ={\left(w_0^l\right)}_{\theta \theta \vartheta }\hfill \\ \hfill {\mathcal{C}}_1& ={\left(l{w}_1{w}_0^{l-1}\right)}_{\theta \theta \vartheta }\hfill \\ \hfill ⋮.\end{array}\right.\end{array}$$

(73)

Using (70) into (68), we obtain

$$\begin{array}{cc}\hfill \sum _{l=0}^{\infty }{w}_l(\vartheta ,\theta ,t;\sigma )& =w(\vartheta ,\theta ,0)\left(\sigma \right){\ominus }_{gH}{\mathcal{L}}^{-1}\left({{\rm Y}}_1\odot \left(\sum _{l=0}^{\infty }{\mathcal{A}}_l\right)\oplus {{\rm Y}}_2\odot \left(\sum _{l=0}^{\infty }{\mathcal{B}}_l\right)\oplus {{\rm Y}}_3\odot \left(\sum _{l=0}^{\infty }{\mathcal{C}}_l\right)\right).\hfill \end{array}$$

(74)

We use the recursive relation to identifying the components $w_l(\vartheta ,\theta ,t),l\ge 0$, as

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill & w_0(\vartheta ,\theta ,t;\sigma )=w(\vartheta ,\theta ,0)\left(\sigma \right),\hfill \\ \hfill & w_{l+1}(\vartheta ,\theta ,t;\sigma )=-{\mathcal{L}}^{-1}\left({{\rm Y}}_1\odot {\mathcal{A}}_l\oplus {{\rm Y}}_2\odot {\mathcal{B}}_l\oplus {{\rm Y}}_3\odot {\mathcal{C}}_l\right),l\ge 0.\hfill \end{array}\right.\end{array}$$

(75)

We assume that all of the components $w_{\varsigma }(\vartheta ,\theta ,t;\sigma )$ are calculated in light of (75) into (71) and

$$\begin{array}{c}\hfill w(\vartheta ,\theta ,t;\sigma )=\sum _{\varsigma =0}^{\infty }{w}_{\varsigma }(\vartheta ,\theta ,t;\sigma ).\end{array}$$

Convergence analysis of the fuzzy ADM can be found in (Theorem 3.3, 24]).

3.4. The Fuzzy Homotopy Perturbation Method

We consider the following general nonlinear fuzzy differential equation

$$\begin{array}{c}\hfill \mathcal{A}\left(w\right)=\tilde{f}(\wp ),\wp \in \Phi ,\end{array}$$

(76)

under the boundary condition

$$\begin{array}{c}\hfill \mathcal{B}\left(w,\frac{\partial w}{\partial \wp }\right)=0,\wp \in \partial \Phi ,\end{array}$$

(77)

where B denotes the boundary operator, $\partial \Phi$ denotes the boundary of the domain $\Phi$, $\tilde{w}(\wp )$ denotes the analytical function, and $\mathcal{A}$ is a general differential operator. The fuzzy operator $\tilde{A}$ can be broken into fuzzy linear $\mathcal{L}$ and nonlinear $\mathcal{N}$ parts. Hence, Equation (76) can be rewritten as:

$$\begin{array}{cc}\hfill \mathcal{L}\left(\underline{w}\right)\left(\sigma \right)+\mathcal{N}\left(\underline{w}\right)\left(\sigma \right)-\underline{f}(\wp ;\sigma )& =\tilde{0},\hfill \end{array}$$

(78)

$$\begin{array}{cc}\hfill \mathcal{L}\left(\overline{w}\right)\left(\sigma \right)+\mathcal{N}\left(\overline{w}\right)\left(\sigma \right)-\overline{f}(\wp ;\sigma )& =\tilde{0}.\hfill \end{array}$$

(79)

We generate a homotopy using the fuzzy homotopy technique:

$$\tilde{v}(\wp ,\varrho ):\Phi \times [0,1]\to R$$

which satisfies

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill H(\underline{v}\left(\sigma \right),\varrho )& =(1-\varrho )\left[\mathcal{L}\left(\underline{v}\right)\left(\sigma \right)-\mathcal{L}\left({\underline{w}}_0\left(\sigma \right)\right)\right]+\varrho [\underline{A\left(v\right)}\left(\sigma \right)-\underline{f}(\wp ;\sigma )]=\tilde{0},\hfill \\ \hfill H(\overline{v}\left(\sigma \right),\varrho )& =(1-\varrho )\left[\mathcal{L}\left(\overline{v}\right)\left(\sigma \right)-\mathcal{L}\left({\overline{w}}_0\left(\sigma \right)\right)\right]+\varrho [\overline{A\left(v\right)}\left(\sigma \right)-\overline{f}(\wp ;\sigma )]=\tilde{0},\hfill \end{array}\end{array}$$

(80)

where $\varrho \in [0,1]$ denote the embedding parameter, and for ${\tilde{w}}_0(\wp )$ denote the initial approximation to (76) which satisfies the boundary conditions. Clearly, from (80), we obtain

$$\begin{array}{cc}\hfill H(\underline{v}\left(\sigma \right),0)& =[\mathcal{L}\left(\underline{v}\right)\left(\sigma \right)-\mathcal{L}\left({\underline{w}}_0\left(\sigma \right)\right)]=\tilde{0},\hfill \end{array}$$

(81)

$$\begin{array}{cc}\hfill H(\underline{v}\left(\sigma \right),1)& =[\underline{A\left(v\right)}\left(\sigma \right)-\underline{f}(\wp ;\sigma )]=\tilde{0},\hfill \end{array}$$

(82)

and

$$\begin{array}{cc}\hfill H(\overline{v}\left(\sigma \right),0)& =[\mathcal{L}\left(\overline{v}\right)\left(\sigma \right)-\mathcal{L}\left({\overline{w}}_0\left(\sigma \right)\right)]=\tilde{0},\hfill \end{array}$$

(83)

$$\begin{array}{cc}\hfill H(\overline{v}\left(\sigma \right),1)& =[\overline{A\left(v\right)}\left(\sigma \right)-\overline{f}(\wp ;\sigma )]=\tilde{0},\hfill \end{array}$$

(84)

and the changing process of $\varrho$ from zero to unity is just that $\tilde{v}(\wp ,\varrho ;\sigma )$ from $w_0(\wp ;\sigma )$ to $w(\wp ;\sigma )$. Applying the Homotopy parameter $\varrho$ as an extending parameter to obtain

$$\begin{array}{cc}\hfill \underline{v}\left(\sigma \right)& =\sum _{n=0}^{\infty }{\varrho }^n{\underline{v}}_n\left(\sigma \right),\hfill \end{array}$$

(85)

$$\begin{array}{cc}\hfill \overline{v}\left(\sigma \right)& =\sum _{n=0}^{\infty }{\varrho }^n{\overline{v}}_n\left(\sigma \right).\hfill \end{array}$$

(86)

As a result of $\varrho \to 1$, the approximate solution of (76) is given as

$$\begin{array}{c}\hfill \underline{w}\left(\sigma \right)=\underset{\varrho \to 1}{lim}\underline{v}\left(\sigma \right)=\sum _{n=0}^{\infty }{\underline{v}}_n\left(\sigma \right),\end{array}$$

(87)

$$\begin{array}{c}\hfill \overline{w}\left(\sigma \right)=\underset{\varrho \to 1}{lim}\overline{v}\left(\sigma \right)=\sum _{n=0}^{\infty }{\overline{v}}_n\left(\sigma \right).\end{array}$$

(88)

Convergence analysis of the fuzzy HPM can be found in (Theorem 3.4, 24]).

3.5. The Fuzzy Homotopy Analysis Method

We consider the following fuzzy differential equation as:

$$\begin{array}{c}\hfill \mathcal{N}\left[\tilde{w}(\wp ,t)\right]=\tilde{0},\end{array}$$

(89)

where $\tilde{0}\in {\mathbb{E}}^1$, $\mathcal{N}$ is a nonlinear operator, ℘ and t were independent variables, and $w(\wp ,t;\sigma )$ denote the unknown fuzzy-valued function, respectively. For simplicity, we disregard all boundary or initial conditions, that can be handled in a similar manner. Constructions for the so-called zero-order deformation equation are made possible through the generalization of the classical homotopy technique.

$$\begin{array}{cc}\hfill (1-\varrho )\mathcal{L}\left[\underline{\phi }(\wp ,t,\varrho ;\sigma )-{\underline{w}}_0(\wp ,t;\sigma )\right]& =p\hslash H(\wp ,t)\mathcal{N}\left[\underline{\phi }(\wp ,t,\varrho ;\sigma )\right],\hfill \end{array}$$

(90)

$$\begin{array}{cc}\hfill (1-\varrho )\mathcal{L}\left[\overline{\phi }(\wp ,t,\varrho ;\sigma )-{\overline{w}}_0(\wp ,t;\sigma )\right]& =p\hslash H(\wp ,t)\mathcal{N}\left[\overline{\phi }(\wp ,t,\varrho ;\sigma )\right],\hfill \end{array}$$

(91)

for $\sigma \in [0,1]$ denotes the fuzzy number, $\varrho \in [0,1]$ denotes the embedding parameter, $\hslash \ne 0$ denotes a non-zero auxiliary parameter, $H(\wp ,t)\ne 0$ denotes the non-zero auxiliary function, and $\mathcal{L}$ denotes the auxiliary linear operator with the follows:

$$\begin{array}{cc}\hfill \mathcal{L}\left[\underline{\phi }(\wp ,t;\sigma )\right]& =\tilde{0},\underline{\phi }(\wp ,t;\sigma )=\tilde{0},\hfill \end{array}$$

(92)

$$\begin{array}{cc}\hfill \mathcal{L}\left[\overline{\phi }(\wp ,t;\sigma )\right]& =\tilde{0},\overline{\phi }(\wp ,t;\sigma )=\tilde{0},\hfill \end{array}$$

(93)

${\tilde{w}}_0(\wp ,t;\sigma )$ shows an initial guess for $\tilde{w}(\wp ,t;\sigma )$, and $\tilde{w}(\wp ,t,\varrho ;\sigma )=[\underline{w}(\wp ,t,\varrho ;\sigma ),\overline{w}(\wp ,t,\varrho ;\sigma )]$ presents an unknown fuzzy-valued function. It the important to note that HAM provides a large amount of flexibility in choosing auxiliary items. Clearly, this is accurate for $\varrho =0$ and $\varrho =1,$

$$\begin{array}{cc}\hfill \underline{\phi }(\wp ,t;0)\left(\sigma \right)& ={\underline{w}}_0(\wp ,t;\sigma ),\underline{\phi }(\wp ,t;1)\left(\sigma \right)=\underline{w}(\wp ,t;\sigma ),\hfill \end{array}$$

(94)

$$\begin{array}{cc}\hfill \overline{\phi }(\wp ,t;0)\left(\sigma \right)& ={\overline{w}}_0(\wp ,t;\sigma ),\overline{\phi }(\wp ,t;1)\left(\sigma \right)=\overline{w}(\wp ,t;\sigma ),\hfill \end{array}$$

(95)

when the quantity $\varrho$ increases from 0 to 1, the solution $\tilde{\phi }(\wp ,t,\varrho )$, changes from the initial guesses, ${\tilde{w}}_0(\wp ,t;\sigma )=[{\underline{w}}_0(\wp ,t;\sigma ),{\overline{w}}_0(\wp ,t;\sigma )]$, to the solution, $\tilde{w}(\wp ,t;\sigma )=[\underline{w}(\wp ,t;\sigma ),\overline{w}(\wp ,t;\sigma )].$ Taylor series can be extended with respect to $\varrho$:

$$\begin{array}{cc}\hfill \underline{\phi }(\wp ,t,\varrho ;\sigma )& ={\underline{w}}_0(\wp ,t;\sigma )+\sum _{\mu =1}^{+\infty }{\underline{w}}_{\mu }(\wp ,t;\sigma ){\varrho }^{\mu },\hfill \end{array}$$

(96)

$$\begin{array}{cc}\hfill \overline{\phi }(\wp ,t,\varrho ;\sigma )& ={\overline{w}}_0(\wp ,t;\sigma )+\sum _{\mu =1}^{+\infty }{\overline{w}}_{\mu }(\wp ,t;\sigma ){\varrho }^{\mu },\hfill \end{array}$$

(97)

where

$$\begin{array}{cc}\hfill {\underline{w}}_{\mu }(\wp ,t;\sigma )& =\frac{1}{\mu !}\frac{{\partial }^{\mu }\underline{\phi }(\wp ,t,\varrho ;\sigma )}{\partial {\varrho }^{\mu }}{|}_{\varrho =0},\hfill \end{array}$$

(98)

$$\begin{array}{cc}\hfill {\overline{w}}_{\mu }(\wp ,t;\sigma )& =\frac{1}{\mu !}\frac{{\partial }^{\mu }\overline{\phi }(\wp ,t,\varrho ;\sigma )}{\partial {\varrho }^{\mu }}{|}_{\varrho =0}.\hfill \end{array}$$

(99)

If such auxiliary linear operator, the initial approximation, the auxiliary parameter ℏ, and the auxiliary fuzzy-valued function are all appropriately determined, and the series (96) and (97) converges at $\varrho =1.$ Then, we obtain the following result:

$$\begin{array}{cc}\hfill {\underline{w}}_{\mu }(\wp ,t;\sigma )& ={\underline{w}}_0(\wp ,t;\sigma )+\sum _{\mu =1}^{+\infty }{\underline{w}}_{\mu }(\wp ,t;\sigma ),\hfill \end{array}$$

(100)

$$\begin{array}{cc}\hfill {\overline{w}}_{\mu }(\wp ,t;\sigma )& ={\overline{w}}_0(\wp ,t;\sigma )+\sum _{\mu =1}^{+\infty }{\overline{w}}_{\mu }(\wp ,t;\sigma ).\hfill \end{array}$$

(101)

As $\hslash =-1$ and $H(\wp ,t;\sigma )=1$ the expression (90) and (91) yields

$$\begin{array}{cc}\hfill (1-\varrho )\mathcal{L}\left[\underline{\phi }(\wp ,t,\varrho ;\sigma )-{\underline{w}}_0(\wp ,t;\sigma )\right]& +\varrho \mathcal{N}\left[\underline{\phi }(\wp ,t,\varrho ;\sigma )\right]=\tilde{0},\hfill \end{array}$$

(102)

$$\begin{array}{cc}\hfill (1-\varrho )\mathcal{L}\left[\overline{\phi }(\wp ,t,\varrho ;\sigma )-{\overline{w}}_0(\wp ,t;\sigma )\right]& +\varrho \mathcal{N}\left[\overline{\phi }(\wp ,t,\varrho ;\sigma )\right]=\tilde{0}.\hfill \end{array}$$

(103)

According to (98) and (99), the governing equation can be deduced from the zero-order deformation Equations (90) and (91). Define the vector

$$\begin{array}{cc}\hfill \overrightarrow{{\underline{w}}_n}\left(\sigma \right)& =\left\{{\underline{w}}_0(\wp ,t,\varrho ;\sigma ),{\underline{w}}_1(\wp ,t,\varrho ;\sigma ),{\underline{w}}_2(\wp ,t,\varrho ;\sigma ),\dots {\underline{w}}_n(\wp ,t,\varrho ;\sigma )\right\},\hfill \end{array}$$

(104)

$$\begin{array}{cc}\hfill \overrightarrow{{\overline{w}}_n}\left(\sigma \right)& =\left\{{\overline{w}}_0(\wp ,t,\varrho ;\sigma ),{\overline{w}}_1(\wp ,t,\varrho ;\sigma ),{\overline{w}}_2(\wp ,t,\varrho ;\sigma ),\dots {\overline{w}}_n(\wp ,t,\varrho ;\sigma )\right\}.\hfill \end{array}$$

(105)

The $m^{th}$ order deformation equation is obtained by differentiating Equations (90) and (91) times with respect to parameter $\varrho$ at $\varrho =0$

$$\begin{array}{c}\hfill \mathcal{L}\left[{\underline{w}}_{\mu }(\wp ,t;\sigma )-{\chi }_{\mu }{\underline{w}}_{\mu -1}(\wp ,t;\sigma )\right]=\hslash H(\wp ,t){\mathcal{R}}_{\mu }\left({\overrightarrow{\underline{w}}}_{\mu -1}(\wp ,t;\sigma )\right),\end{array}$$

(106)

$$\begin{array}{c}\hfill \mathcal{L}\left[{\overline{w}}_{\mu }(\wp ,t;\sigma )-{\chi }_{\mu }{\overline{w}}_{\mu -1}(\wp ,t;\sigma )\right]=\hslash H(\wp ,t){\mathcal{R}}_{\mu }\left({\overrightarrow{\overline{w}}}_{\mu -1}(\wp ,t;\sigma )\right),\end{array}$$

(107)

where

$$\begin{array}{cc}\hfill R_{\mu }\left({\overrightarrow{\underline{w}}}_{\mu -1}(\wp ,t;\sigma )\right)& =\frac{1}{(\mu -1)!}\frac{{\partial }^{\mu -1}\mathcal{N}\left[\underline{\phi }(\wp ,t,\varrho ;\sigma )\right]}{\partial {\varrho }^{\mu -1}}{|}_{\varrho =0}\hfill \end{array}$$

(108)

$$\begin{array}{cc}\hfill R_{\mu }\left({\overrightarrow{\overline{w}}}_{\mu -1}(\wp ,t;\sigma )\right)& =\frac{1}{(\mu -1)!}\frac{{\partial }^{\mu -1}\mathcal{N}\left[\overline{\phi }(\wp ,t,\varrho ;\sigma )\right]}{\partial {\varrho }^{\mu -1}}{|}_{\varrho =0}\hfill \end{array}$$

(109)

and

$${\chi }_{\mu }=\left\{\begin{array}{cc}\hfill & 0,\mu \le 1,\hfill \\ \hfill & 1,\mu >1.\hfill \end{array}\right.$$

(110)

3.6. Applications

In this section, we present examples 5 and 6 to illustrate the discussed methods for effectiveness by solving Zakharov-Kuznetsov equations.

Example 5.

We consider the following fuzzy $ZK(2,2,2)$ equation

$$\begin{array}{c}\hfill w_t\oplus {\left(w^2\right)}_{\vartheta }\oplus \frac{1}{8}\odot {\left(w^2\right)}_{\vartheta \vartheta \vartheta }\oplus \frac{1}{8}\odot {\left(w^2\right)}_{\theta \theta \vartheta }=0,\end{array}$$

(111)

subject to the initial condition

$$\begin{array}{c}\hfill w(\vartheta ,\theta ,0)=[{(2+0.4\sigma )}^n,{(2.8-0.4\sigma )}^n]\odot \frac{4}{3}\rho {sinh}^2(\vartheta +\theta ),\end{array}$$

(112)

where $n=1,2,3,\dots$, for ρ is an arbitrary constant.

Case [A]. Fuzzy Adomian decomposition method.

Applying the fuzzy ADM to (111) and the initial condition (112), we have

$$\begin{array}{cc}\hfill \underline{w}(\vartheta ,\theta ,t;\sigma )& ={(2+0.4\sigma )}^n\frac{4}{3}\rho {sinh}^2(\vartheta +\theta )-{\mathcal{L}}^{-1}\left({\left({\underline{w}}^2\right)}_{\vartheta }+\frac{1}{8}{\left({\underline{w}}^2\right)}_{\vartheta \vartheta \vartheta }+\frac{1}{8}{\left({\underline{w}}^2\right)}_{\theta \theta \theta }\right),\hfill \end{array}$$

(113)

$$\begin{array}{cc}\hfill \overline{w}(\vartheta ,\theta ,t;\sigma )& ={(2.8-0.4\sigma )}^n\frac{4}{3}\rho {sinh}^2(\vartheta +\theta )-{\mathcal{L}}^{-1}\left({\left({\overline{w}}^2\right)}_{\vartheta }+\frac{1}{8}{\left({\overline{w}}^2\right)}_{\vartheta \vartheta \vartheta }+\frac{1}{8}{\left({\overline{w}}^2\right)}_{\theta \theta \vartheta }\right).\hfill \end{array}$$

(114)

The decomposition series (68) is substituted for $w(\vartheta ,\theta ,t;\sigma )$ into (113) and (114) to produce

$$\begin{array}{cc}\hfill \sum _{j=0}^{\infty }{\underline{w}}_j(\vartheta ,\theta ,t;\sigma )& ={(2+0.4\sigma )}^n\frac{4}{3}\rho {sinh}^2(\vartheta +\theta )\hfill \end{array}$$

$$\begin{array}{cc}\hfill & -{\mathcal{L}}^{-1}\left(\left(\sum _{j=0}^{\infty }{\underline{\mathcal{A}}}_j\right)+\frac{1}{8}\left(\sum _{j=0}^{\infty }{\underline{\mathcal{B}}}_j\right)+\frac{1}{8}\left(\sum _{j=0}^{\infty }{\underline{\mathcal{C}}}_j\right)\right),\hfill \\ \hfill \sum _{j=0}^{\infty }{\overline{w}}_j(\vartheta ,\theta ,t;\sigma )& ={(2.8-0.4\sigma )}^n\frac{4}{3}\rho {sinh}^2(\vartheta +\theta ),\hfill \end{array}$$

(115)

$$\begin{array}{cc}\hfill & -{\mathcal{L}}^{-1}\left(\left(\sum _{j=0}^{\infty }{\overline{\mathcal{A}}}_j\right)+\frac{1}{8}\left(\sum _{j=0}^{\infty }{\overline{\mathcal{B}}}_j\right)+\frac{1}{8}\left(\sum _{j=0}^{\infty }{\overline{\mathcal{C}}}_j\right)\right).\hfill \end{array}$$

(116)

The nonlinear terms ${\left(w^2\right)}_{\vartheta },{\left(w^2\right)}_{\vartheta \vartheta \vartheta }$ and ${\left(w^2\right)}_{\theta \theta \vartheta },$ are represented by Adomian polynomials ${\mathcal{A}}_l,{\mathcal{B}}_l$ and ${\mathcal{C}}_l$, respectively. We can derive the recursive relation from (115) as:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill & {\underline{w}}_0(\vartheta ,\theta ,t;\sigma )={(2+0.4\sigma )}^n\frac{4}{3}\rho {sinh}^2(\vartheta +\theta )\hfill \\ \hfill & {\underline{w}}_1(\vartheta ,\theta ,t;\sigma )=-{\mathcal{L}}^{-1}\left({\underline{\mathcal{A}}}_0+\frac{1}{8}{\underline{\mathcal{B}}}_0+\frac{1}{8}{\underline{\mathcal{C}}}_0\right)\hfill \\ \hfill & {\underline{w}}_{j+1}(\vartheta ,\theta ,t;\sigma )=-{\mathcal{L}}^{-1}\left({\underline{\mathcal{A}}}_j+\frac{1}{8}{\underline{\mathcal{B}}}_j+\frac{1}{8}{\underline{\mathcal{C}}}_j\right),j\ge 1.\hfill \end{array}\right.\end{array}$$

(117)

We assume $m=n=j=2$ in (73) into (71) to get Adomian polynomials $A_j,B_j$ and $C_j$, we have

$$\begin{array}{c}\hfill \left\{\begin{array}{cccc}\hfill {\underline{\mathcal{A}}}_0& ={\left({\underline{w}}_0^2\right)}_{\vartheta },\hfill & \hfill {\underline{\mathcal{A}}}_1={\left(2{\underline{w}}_1{\underline{w}}_0\right)}_{\vartheta },{\underline{\mathcal{A}}}_2& ={\left(2{\underline{w}}_2{\underline{w}}_0+{\underline{w}}_1^2\right)}_{\vartheta },\dots ,\hfill \\ \hfill {\underline{\mathcal{B}}}_0& ={\left({\underline{w}}_0^2\right)}_{\vartheta \vartheta \vartheta },\hfill & \hfill {\underline{\mathcal{B}}}_1={\left(2{\underline{w}}_1{\underline{w}}_0\right)}_{\vartheta \vartheta \vartheta },{\underline{\mathcal{B}}}_2& ={\left(2{\underline{w}}_2{\underline{w}}_0+{\underline{w}}_1^2\right)}_{\vartheta \vartheta \vartheta },\dots ,\hfill \\ \hfill {\underline{\mathcal{C}}}_0& ={\left({\underline{w}}_0^2\right)}_{\theta \theta \vartheta },\hfill & \hfill {\underline{C}}_1={\left(2{\underline{w}}_1{\underline{w}}_0\right)}_{\theta \theta \vartheta },{\underline{\mathcal{C}}}_2& ={\left(2{\underline{w}}_2{\underline{w}}_0+{\underline{w}}_1^2\right)}_{\theta \theta \vartheta },\dots ,\hfill \end{array}\right.\end{array}$$

(118)

Substituting (118) into (117), we obtain

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\underline{w}}_0(\vartheta ,\theta ,t;\sigma )& ={(2+0.4\sigma )}^n\frac{4}{3}\rho {sinh}^2(\vartheta +\theta )\hfill \\ \hfill {\underline{w}}_1(\vartheta ,\theta ,t;\sigma )& ={(2+0.4\sigma )}^n\left[-\frac{8}{3}{\rho }^{2}tcosh(\vartheta +\theta )sinh(\vartheta +\theta )\right]\hfill \\ \hfill {\underline{w}}_2(\vartheta ,\theta ,t;\sigma )& ={(2+0.4\sigma )}^n\left[\frac{4}{3}{\rho }^3{t}^2\left[{cosh}^2(\vartheta +\theta )+{sinh}^2(\vartheta +\theta )\right]\right]\hfill \\ \hfill {\underline{w}}_3(\vartheta ,\theta ,t;\sigma )& ={(2+0.4\sigma )}^n\left[-\frac{16}{9}{\rho }^4{t}^{3}cosh(\vartheta +\theta )sinh(\vartheta +\theta )\right]\hfill \\ \hfill ⋮.\end{array}\right.\end{array}$$

(119)

The solution in a series form as

$$\begin{array}{cc}\hfill \underline{w}(\vartheta ,\theta ,t;\sigma )& ={(2+0.4\sigma )}^n\left[\frac{4}{3}\rho {sinh}^2(\vartheta +\theta )-\frac{8}{3}{\rho }^{2}tcosh(\vartheta +\theta )sinh(\vartheta +\theta )\right.\hfill \\ \hfill & \left.+\frac{4}{3}{\rho }^3{t}^2\left[{cosh}^2(\vartheta +\theta )+{sinh}^2(\vartheta +\theta )\right]-\frac{16}{9}{\rho }^4{t}^{3}cosh(\vartheta +\theta )sinh(\vartheta +\theta )+···\right].\hfill \end{array}$$

(120)

Similarly, the series solution of $\overline{w}(\vartheta ,\theta ,t;\sigma )$ on the Formula (116) can be determined as follows:

$$\begin{array}{cc}\hfill \overline{w}(\vartheta ,\theta ,t;\sigma )& ={(2.8-0.4\sigma )}^n\left[\frac{4}{3}\rho {sinh}^2(\vartheta +\theta )-\frac{8}{3}{\rho }^{2}tcosh(\vartheta +\theta )sinh(\vartheta +\theta )\right.\hfill \\ \hfill & \left.+\frac{4}{3}{\rho }^3{t}^2\left[{cosh}^2(\vartheta +\theta )+{sinh}^2(\vartheta +\theta )\right]-\frac{16}{9}{\rho }^4{t}^{3}cosh(\vartheta +\theta )sinh(\vartheta +\theta )+···\right].\hfill \end{array}$$

(121)

Thus, we have obtained the exact solution $w(\vartheta ,\theta ,t;\sigma )$ of (111) as

$$\begin{array}{c}\hfill w(\vartheta ,\theta ,t;\sigma )=[{(2+0.4\sigma )}^n,{(2.8-0.4\sigma )}^n]\odot \frac{4}{3}\rho {sinh}^2(\vartheta +\theta -\rho t),0\le \sigma \le 1.\end{array}$$

Case [B]. Fuzzy Homotopy perturbation method.

Applying the fuzzy HPM, we construct a homotopy as follows

$$\begin{array}{cc}\hfill \underline{\mathcal{H}}(v,p;\sigma )& =(1-p)\left[\frac{\partial \underline{v}}{\partial t}-\frac{\partial {\underline{w}}_0}{\partial t}\right]+p\left[\frac{\partial \underline{v}}{\partial t}+\frac{\partial {\underline{v}}^2}{\partial \vartheta }+\frac{1}{8}\frac{{\partial }^3{\underline{v}}^2}{\partial {\vartheta }^3}+\frac{1}{8}\frac{\partial }{\partial \vartheta }\frac{{\partial }^2{\underline{v}}^2}{\partial {\theta }^2}\right]=\tilde{0},\hfill \end{array}$$

(122)

$$\begin{array}{cc}\hfill \overline{\mathcal{H}}(v,p;\sigma )& =(1-p)\left[\frac{\partial \overline{v}}{\partial t}-\frac{\partial {\overline{w}}_0}{\partial t}\right]+p\left[\frac{\partial \overline{v}}{\partial t}+\frac{\partial {\overline{v}}^2}{\partial \vartheta }+\frac{1}{8}\frac{{\partial }^3{\overline{v}}^2}{\partial {\vartheta }^3}+\frac{1}{8}\frac{\partial }{\partial \vartheta }\frac{{\partial }^2{\overline{v}}^2}{\partial {\theta }^2}\right]=\tilde{0},\hfill \end{array}$$

(123)

We consider the initial approximation that satisfies the initial condition

$$\begin{array}{c}\hfill w(\vartheta ,\theta ,0)=[{(2+0.4\sigma )}^n,{(2.8-0.4\sigma )}^n]\odot \frac{4}{3}\rho {sinh}^2(\vartheta +\theta ).\end{array}$$

(124)

Substituting (85) and (86), with (122), and equating the terms of identical powers of p is

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill & p^0:\frac{\partial {\underline{v}}_0}{\partial t}=\frac{\partial {\underline{w}}_0}{\partial t},{\underline{v}}_0(\vartheta ,\theta ,0)\left(\sigma \right)={(2+0.4\sigma )}^n\frac{4}{3}\rho {sinh}^2(\vartheta +\theta )\hfill \\ \hfill & p^1:\frac{\partial {\underline{v}}_1}{\partial t}=\frac{\partial }{\partial t}{\underline{w}}_0-\frac{\partial }{\partial \vartheta }{\underline{v}}_0^2-\frac{1}{8}\frac{{\partial }^3}{\partial {\vartheta }^3}{\underline{v}}_0^2-\frac{1}{8}\frac{\partial }{\partial \vartheta }\frac{{\partial }^2}{\partial {\theta }^2}{\underline{v}}_0^2,{\underline{v}}_1(\vartheta ,\theta ,0)\left(\sigma \right)=0,\hfill \\ \hfill & p^2:\frac{\partial {\underline{v}}_2}{\partial t}=-2\frac{\partial }{\partial \vartheta }{v}_0{v}_1-\frac{1}{4}\frac{{\partial }^3}{\partial {\vartheta }^3}{v}_0{\underline{v}}_1-\frac{1}{4}\frac{\partial }{\partial \vartheta }\frac{{\partial }^2}{\partial {\theta }^2}{\underline{v}}_0{\underline{v}}_1,{\underline{v}}_2(\vartheta ,\theta ,0)\left(\sigma \right)=0,\hfill \\ \hfill & ⋮.\hfill \end{array}\right.\end{array}$$

(125)

The solution of successively calculating (125) gives

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\underline{v}}_0(\vartheta ,\theta ,t;\sigma )& ={(2+0.4\sigma )}^n\frac{4}{3}\rho {sinh}^2(\vartheta +\theta )\hfill \\ \hfill {\underline{v}}_1(\vartheta ,\theta ,t;\sigma )& ={(2+0.4\sigma )}^n\left[-\frac{224}{9}{\rho }^2{sinh}^3(\vartheta +\theta )cosh(\vartheta +\theta )t\right.\hfill \\ \hfill & \left.-\frac{32}{3}{\rho }^{2}sinh(\vartheta +\theta ){cosh}^3(\vartheta +\theta )t\right]\hfill \\ \hfill {\underline{v}}_2(\vartheta ,\theta ,t;\sigma )& ={(2+0.4\sigma )}^n\left[-\frac{64}{27}{\rho }^3\left(1200{cosh}^6(\vartheta +\theta )\right.\right.\hfill \\ \hfill & \left.\left.-2080{cosh}^4(\vartheta +\theta )+968{cosh}^2(\vartheta +\theta )-79\right)t^2\right]\hfill \\ \hfill & ⋮.\hfill \end{array}\right.\end{array}$$

(126)

Consequently, the solution to (111) for $p\to 1,$ as follows:

$$\begin{array}{cc}\hfill \underline{v}(\vartheta ,\theta ,t;\sigma )& ={(2+0.4\sigma )}^n\left[\frac{4}{3}\rho {sinh}^2(\vartheta +\theta )-\frac{224}{9}{\rho }^2{sinh}^3(\vartheta +\theta )cosh(\vartheta +\theta )t\right.\hfill \\ \hfill & -\frac{32}{3}{\rho }^{2}sinh(\vartheta +\theta ){cosh}^3(\vartheta +\theta )t+\frac{64}{27}{\rho }^3\left(1200{cosh}^6(\vartheta +\theta )\right.\hfill \\ \hfill & \left.\left.-2080{cosh}^4(\vartheta +\theta )+968{cosh}^2(\vartheta +\theta )-79\right)t^2-\dots \right].\hfill \end{array}$$

(127)

Similarly, we can obtain the series solution of $\overline{v}(\vartheta ,\theta ,t;\sigma )$ for Equation (123) as follows:

$$\begin{array}{cc}\hfill \overline{v}(\vartheta ,\theta ,t;\sigma )& ={(2.8-0.4\sigma )}^n\left[\frac{4}{3}\rho {sinh}^2(\vartheta +\theta )-\frac{224}{9}{\rho }^2{sinh}^3(\vartheta +\theta )cosh(\vartheta +\theta )t\right.\hfill \\ \hfill & -\frac{32}{3}{\rho }^{2}sinh(\vartheta +\theta ){cosh}^3(\vartheta +\theta )t+\frac{64}{27}{\rho }^3\left(1200{cosh}^6(\vartheta +\theta )\right.\hfill \\ \hfill & \left.\left.-2080{cosh}^4(\vartheta +\theta )+968{cosh}^2(\vartheta +\theta )-79\right)t^2-\dots \right].\hfill \end{array}$$

(128)

Thus, we have obtained the exact solution $w(\vartheta ,\theta ,t;\sigma )$ of (111) as

$$\begin{array}{c}\hfill w(\vartheta ,\theta ,t;\sigma )=[{(2+0.4\sigma )}^n,{(2.8-0.4\sigma )}^n]\odot \frac{4}{3}\rho {sinh}^2(\vartheta +\theta -\rho t),0\le \sigma \le 1.\end{array}$$

Case [C]. Fuzzy Homotopy analysis method

Using the linear operator to determine the exact solution of (111) as

$$\begin{array}{c}\hfill \mathcal{L}[\Im (\vartheta ,\theta ,t,q)]=\frac{\partial \Im (\vartheta ,\vartheta ,t,q)}{\partial t}\end{array}$$

(129)

with the property

$$\begin{array}{c}\hfill \mathcal{L}[c_1+c_2]=0,\end{array}$$

where $c_1$ and $c_2$ are integral constants. The inverse operator ${\mathcal{L}}^{-1}$ is given by

$$\begin{array}{c}\hfill {\mathcal{L}}^{-1}(·)={\int }_0^t(·)dt,\end{array}$$

(130)

from (111), we define the nonlinear operator as

$$\begin{array}{c}\hfill \mathcal{N}[\Im (\vartheta ,\theta ,t,q)]=\frac{\partial \Im (\vartheta ,\theta ,t,q)}{\partial t}+{(\Im {(\vartheta ,\theta ,t,q)}^2)}_{\vartheta }+\frac{1}{8}{(\Im (\vartheta ,\theta ,t,q))}_{\vartheta \vartheta \vartheta }^2+\frac{1}{8}{(\Im (\vartheta ,\theta ,t,q))}_{\theta \theta \vartheta }^2.\end{array}$$

Using above definition, we construct the zeroth-order deformation equation:

$$\begin{array}{c}\hfill (1-q)\mathcal{L}[\underline{\psi }(\vartheta ,\theta ,t,q;\sigma )-{\underline{w}}_0(\vartheta ,\theta ,t;\sigma )]=q\hslash H(\vartheta ,\theta ,t)\left[\underline{\psi }(\vartheta ,\theta ,t,q;\sigma )\right],\end{array}$$

(131)

$$\begin{array}{c}\hfill (1-q)\mathcal{L}[\overline{\psi }(\vartheta ,\theta ,t,q;\sigma )-{\overline{w}}_0(\vartheta ,\theta ,t;\sigma )]=q\hslash H(\vartheta ,\theta ,t)\left[\overline{\psi }(\vartheta ,\theta ,t,q;\sigma )\right],\end{array}$$

(132)

where ℏ is an auxiliary parameter.

Obviously

$$\begin{array}{cc}\hfill \underline{\psi }(\vartheta ,\theta ,t,0)\left(\sigma \right)& ={\underline{w}}_0(\vartheta ,\theta ,t;\sigma ),\underline{\psi }(\vartheta ,\theta ,t,1)\left(\sigma \right)=\underline{w}(\vartheta ,\theta ,t;\sigma ),\hfill \end{array}$$

(133)

$$\begin{array}{cc}\hfill \overline{\psi }(\vartheta ,\theta ,t,0)\left(\sigma \right)& ={\overline{w}}_0(\vartheta ,\theta ,t;\sigma ),\overline{\psi }(\vartheta ,\theta ,t,1)\left(\sigma \right)=\overline{w}(\vartheta ,\theta ,t;\sigma ),\hfill \end{array}$$

(134)

thus we get the $m^{th}$ order deformation:

$$\begin{array}{c}\hfill \mathcal{L}\left[{\underline{w}}_m(\vartheta ,\theta ,t,q;\sigma )-{\chi }_m{\underline{w}}_{m-1}(\vartheta ,\theta ,t,q;\sigma )\right]=\hslash H(\vartheta ,\theta ,t){\mathcal{R}}_m\left(\overrightarrow{{\underline{w}}_{m-1}}(\vartheta ,\theta ,t,q;\sigma )\right),m\ge 1,\end{array}$$

(135)

$$\begin{array}{c}\hfill \mathcal{L}\left[{\overline{w}}_m(\vartheta ,\theta ,t,q;\sigma )-{\chi }_m{\overline{w}}_{m-1}(\vartheta ,\theta ,t,q;\sigma )\right]=\hslash H(\vartheta ,\theta ,t){\mathcal{R}}_m\left(\overrightarrow{{\overline{w}}_{m-1}}(\vartheta ,\theta ,t,q;\sigma )\right),m\ge 1,\end{array}$$

(136)

where

$$\begin{array}{cc}\hfill \overrightarrow{{\underline{w}}_{m-1}}(\vartheta ,\theta ,t,q;\sigma )& =\left\{{\underline{w}}_0\left(t\right),{\underline{w}}_1\left(t\right),\dots ,{\underline{w}}_n\left(t\right)\right\},\hfill \end{array}$$

(137)

$$\begin{array}{cc}\hfill \overrightarrow{{\overline{w}}_{m-1}}(\vartheta ,\theta ,t,q;\sigma )& =\left\{{\overline{w}}_0\left(t\right),{\overline{w}}_1\left(t\right),\dots ,{\overline{w}}_n\left(t\right)\right\},\hfill \end{array}$$

(138)

and

$$\begin{array}{cc}\hfill \mathcal{R}\left(\overrightarrow{{\underline{w}}_{m-1}}(\vartheta ,\theta ,t,q;\sigma )\right)& ={\underline{w}}_{m-1}^{\prime }(t;\sigma )+\sum _{\wp =0}^{m-1}{\left({\underline{w}}_{\wp }\right)}_{\vartheta }{\left({\underline{w}}_{m-1-\wp }\right)}_{\vartheta }\hfill \end{array}$$

$$\begin{array}{cc}\hfill & +\frac{1}{8}\sum _{\wp =0}^{m-1}{\left({\underline{w}}_{\wp }\right)}_{\vartheta \vartheta \vartheta }{\left({\underline{w}}_{m-1-\wp }\right)}_{\vartheta \vartheta \vartheta }+\frac{1}{8}\sum _{\wp =0}^{m-1}{\left({\underline{w}}_{\wp }\right)}_{\theta \theta \vartheta }{\left({\underline{w}}_{m-1-\wp }\right)}_{\theta \theta \vartheta },\hfill \\ \hfill \mathcal{R}\left(\overrightarrow{{\overline{w}}_{m-1}}(\vartheta ,\theta ,t,q;\sigma )\right)& ={\overline{w}}_{m-1}^{\prime }(t;\sigma )+\sum _{\wp =0}^{m-1}{\left({\overline{w}}_{\wp }\right)}_{\vartheta }{\left({\overline{w}}_{m-1-\wp }\right)}_{\vartheta }\hfill \end{array}$$

(139)

$$\begin{array}{cc}\hfill & +\frac{1}{8}\sum _{\wp =0}^{m-1}{\left({\overline{w}}_{\wp }\right)}_{\vartheta \vartheta \vartheta }{\left({\overline{w}}_{m-1-\wp }\right)}_{\vartheta \vartheta \vartheta }+\frac{1}{8}\sum _{\wp =0}^{m-1}{\left({\overline{w}}_{\wp }\right)}_{\theta \theta \vartheta }{\left({\overline{w}}_{m-1-\wp }\right)}_{\theta \theta \vartheta },\hfill \end{array}$$

(140)

thus the solution of $m^{th}$ order deformation (139) for $m\ge 1$ becomes

$$\begin{array}{c}\hfill {\underline{w}}_m(\vartheta ,\theta ,t;\sigma )={\chi }_m{\underline{w}}_{m-1}(\vartheta ,\theta ,t;\sigma )+\hslash H(\vartheta ,\theta ,t){\mathcal{L}}^{-1}\left[{\mathcal{R}}_m\left(\overrightarrow{{\underline{w}}_{m-1}}(\vartheta ,\theta ,t;\sigma )\right)\right].\end{array}$$

(141)

We choose the initial step $w_0(\vartheta ,\theta ,t;\sigma )=[{(2+0.4\sigma )}^n,{(2.8-0.4\sigma )}^n]\odot \frac{4}{3}\rho {sinh}^2(\vartheta +\theta )$ which makes boundary condition (111). First, we consider the solution of (111) with the boundary condition

$$\begin{array}{c}\hfill {\underline{w}}_0(\vartheta ,\theta ,t;\sigma )={(2+0.4\sigma )}^n\frac{4}{3}\rho {sinh}^2(\vartheta +\theta ).\end{array}$$

(142)

Now, we have

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\underline{w}}_1(\vartheta ,\theta ,t;\sigma )& =-{(2+0.4\sigma )}^n\frac{80}{9}{\rho }^2{sinh}^{2}2(\vartheta +\theta )t\hfill \\ \hfill {\underline{w}}_2(\vartheta ,\theta ,t;\sigma )& ={(2+0.4\sigma )}^n\frac{10880}{27}{\rho }^{3}sinh2(\vartheta +\theta )sinh4(\vartheta +\theta )t^2\hfill \\ \hfill ⋮.\end{array}\right.\end{array}$$

Next, we can achieve the series solutions as

$$\begin{array}{cc}\hfill \underline{w}(\vartheta ,\theta ,t;\sigma )& ={(2+0.4\sigma )}^n\left[\frac{4}{3}\rho {sinh}^2(\vartheta +\theta )-\frac{80}{9}{\rho }^2{sinh}^{2}2(\vartheta +\theta )t\right.\hfill \\ \hfill & \left.+\frac{10880}{27}{\rho }^{3}sinh2(\vartheta +\theta )sinh4(\vartheta +\theta )t^2+\dots \right].\hfill \end{array}$$

(143)

Similarly, the series solution of $\overline{w}(\vartheta ,\theta ,t;\sigma )$ on the Formula (140) can be calculated as follows:

$$\begin{array}{cc}\hfill \overline{w}(\vartheta ,\theta ,t;\sigma )& ={(2.8-0.4\sigma )}^n\left[\frac{4}{3}\rho {sinh}^2(\vartheta +\theta )-\frac{80}{9}{\rho }^2{sinh}^{2}2(\vartheta +\theta )t\right.\hfill \\ \hfill & \left.+\frac{10880}{27}{\rho }^{3}sinh2(\vartheta +\theta )sinh4(\vartheta +\theta )t^2+\dots \right].\hfill \end{array}$$

(144)

Thus, we have obtained the exact solution $w(\vartheta ,\theta ,t;\sigma )$ of (111) as

$$\begin{array}{c}\hfill w(\vartheta ,\theta ,t;\sigma )=[{(2+0.4\sigma )}^n,{(2.8-0.4\sigma )}^n]\odot \frac{4}{3}\rho {sinh}^2(\vartheta +\theta -\rho t),0\le \sigma \le 1.\end{array}$$

Example 6.

We consider the Zakharov-Kuznetsov $\left(ZK\right(3,3,3\left)\right)$ equation

$$\begin{array}{c}\hfill w_t\oplus {\left(w^3\right)}_{\vartheta }\oplus 2\odot {\left(w^3\right)}_{\vartheta \vartheta \vartheta }\oplus 2\odot {\left(w^3\right)}_{\theta \theta \vartheta }=0,\end{array}$$

(145)

subject to the initial condition

$$\begin{array}{c}\hfill w(\vartheta ,\theta ,0)=[{(3.1+0.3\sigma )}^n,{(3.8-0.4\sigma )}^n]\odot \frac{3}{2}\rho sinh\left[\frac{1}{6}(\vartheta +\theta )\right],\end{array}$$

(146)

where $n=1,2,3,\dots$, for ρ is an arbitrary constant.

Case [A]. Fuzzy reduced differential transform method

Applying the fuzzy RDTM to (146) with the initial condition (147), we get

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill & (l+1){\underline{W}}_{l+1}\left(\sigma \right)+\frac{\partial \left({\sum }_{\wp =0}^l{\sum }_{s=0}^{\wp }{\underline{W}}_{l-\wp }{\underline{W}}_{\wp -s}{\underline{W}}_s\right)\left(\sigma \right)}{\partial \vartheta }+2\frac{{\partial }^3\left({\sum }_{\wp =0}^l{\sum }_{s=0}^{\wp }{\underline{W}}_{l-\wp }{\underline{W}}_{\wp -s}{\underline{W}}_s\right)\left(\sigma \right)}{\partial {\vartheta }^3}\hfill \\ \hfill & +2\frac{{\partial }^3\left({\sum }_{\wp =0}^l{\sum }_{s=0}^{\wp }{\underline{W}}_{l-\wp }{\underline{W}}_{\wp -s}{\underline{W}}_s\right)\left(\sigma \right)}{\partial {\theta }^2\partial \vartheta }=0\hfill \\ \hfill & {\underline{W}}_0\left(\sigma \right)={(3.1+0.3\sigma )}^n\frac{3}{2}\rho sinh\left[\frac{1}{6}(\vartheta +\theta )\right],\hfill \end{array}\right.\end{array}$$

(147)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill & (l+1){\overline{W}}_{l+1}\left(\sigma \right)+\frac{\partial \left({\sum }_{\wp =0}^l{\sum }_{s=0}^{\wp }{\overline{W}}_{l-\wp }{\overline{W}}_{\wp -s}{\overline{W}}_s\right)\left(\sigma \right)}{\partial \vartheta }+2\frac{{\partial }^3\left({\sum }_{\wp =0}^l{\sum }_{s=0}^{\wp }{\overline{W}}_{l-\wp }{\overline{W}}_{\wp -s}{\overline{W}}_s\right)\left(\sigma \right)}{\partial {\vartheta }^3}\hfill \\ \hfill & +2\frac{{\partial }^3\left({\sum }_{\wp =0}^l{\sum }_{s=0}^{\wp }{\overline{W}}_{l-\wp }{\overline{W}}_{\wp -s}{\overline{W}}_s\right)\left(\sigma \right)}{\partial {\theta }^2\partial \vartheta }=0\hfill \\ \hfill & {\overline{W}}_0\left(\sigma \right)={(3.8-0.4\sigma )}^n\frac{3}{2}\rho sinh\left[\frac{1}{6}(\vartheta +\theta )\right].\hfill \end{array}\right.\end{array}$$

(148)

Utilizing (147) allows for iteratively obtaining the values of $W_j$ with fewer and simpler computations. Consequently, the $(n+1)$-term numerical solution of (145) can be expressed as follows:

$$\begin{array}{c}\hfill {\underline{w}}_n^{*}(\vartheta ,\theta ,t;\sigma )=\sum _{j=0}^n{\underline{W}}_j{t}^j,\end{array}$$

(149)

and the analytical solution is

$$\begin{array}{c}\hfill \underline{w}(\vartheta ,\theta ,t;\sigma )=\underset{n\to \infty }{lim}{\underline{w}}_n^{*}(\vartheta ,\theta ,t;\sigma )=\sum _{j=0}^n{\underline{W}}_j{t}^j.\end{array}$$

Particularly, the 4-term numerical solution of (145) can be obtained as:

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill {\underline{w}}_3^{*}(\vartheta ,\theta ,t;\sigma )& =\sum _{j=0}^3{\underline{W}}_j{t}^j\left(\sigma \right)\hfill \\ \hfill & ={(3.1+0.3\sigma )}^n\left[\frac{1}{4096}\rho \left(6144{\rho }^{2}tsinh\left(\frac{\vartheta +\theta }{6}\right)-13824{cosh}^3\left(\frac{\vartheta +\theta }{6}\right)\right.\right.\hfill \\ \hfill & +12288{\rho }^{2}tcosh\left(\frac{\vartheta +\theta }{6}\right)+146880{\rho }^4{t}^{2}sinh\left(\frac{\vartheta +\theta }{6}\right){cosh}^4\left(\frac{\vartheta +\theta }{6}\right)\hfill \\ \hfill & \left.-139968{\rho }^4{t}^{2}sinh\left(\frac{\vartheta +\theta }{6}\right){cosh}^2\left(\frac{\vartheta +\theta }{6}\right)\right)+17472{\rho }^4{t}^{2}sinh\left(\frac{\vartheta +\theta }{6}\right)\hfill \\ \hfill & +6116688{\rho }^6{t}^3{cosh}^5\left(\frac{\vartheta +\theta }{6}\right)-3010896{\rho }^6{t}^3{cosh}^7\left(\frac{\vartheta +\theta }{6}\right)\hfill \\ \hfill & \left.-3751488{\rho }^6{t}^3{cosh}^3\left(\frac{\vartheta +\theta }{6}\right)+637616{\rho }^9{t}^{3}cosh\left(\frac{\vartheta +\theta }{6}\right)\right].\hfill \end{array}\right\}\end{array}$$

(150)

Similarly, we can represent the series solution of $\overline{w}(\vartheta ,\theta ,t;\sigma )$ in Equation (148) as:

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill {\overline{w}}_3^{*}(\vartheta ,\theta ,t;\sigma )& =\sum _{j=0}^3{\overline{W}}_j{t}^j\left(\sigma \right)\hfill \\ \hfill & ={(3.8-0.4\sigma )}^n\left[\frac{1}{4096}\rho \left(6144{\rho }^{2}tsinh\left(\frac{\vartheta +\theta }{6}\right)-13824{cosh}^3\left(\frac{\vartheta +\theta }{6}\right)\right.\right.\hfill \\ \hfill & +12288{\rho }^{2}tcosh\left(\frac{\vartheta +\theta }{6}\right)+146880{\rho }^4{t}^{2}sinh\left(\frac{\vartheta +\theta }{6}\right){cosh}^4\left(\frac{\vartheta +\theta }{6}\right)\hfill \\ \hfill & \left.-139968{\rho }^4{t}^{2}sinh\left(\frac{\vartheta +\theta }{6}\right){cosh}^2\left(\frac{\vartheta +\theta }{6}\right)\right)+17472{\rho }^4{t}^{2}sinh\left(\frac{\vartheta +\theta }{6}\right)\hfill \\ \hfill & +6116688{\rho }^6{t}^3{cosh}^5\left(\frac{\vartheta +\theta }{6}\right)-3010896{\rho }^6{t}^3{cosh}^7\left(\frac{\vartheta +\theta }{6}\right)\hfill \\ \hfill & \left.-3751488{\rho }^6{t}^3{cosh}^3\left(\frac{\vartheta +\theta }{6}\right)+637616{\rho }^9{t}^{3}cosh\left(\frac{\vartheta +\theta }{6}\right)\right].\hfill \end{array}\right\}\end{array}$$

(151)

Using Taylor series into (150) and (151), we obtained the closed form solution

$$\begin{array}{c}\hfill w(\vartheta ,\theta ,t;\sigma )=[{(3.1+0.3\sigma )}^n,{(3.8-0.4\sigma )}^n]\odot \frac{3}{2}\rho sinh\left[\frac{1}{6}(\vartheta +\theta -\rho t)\right],0\le \sigma \le 1.\end{array}$$

Case [B]. Fuzzy Adomian decomposition method

Applying to (146) and the initial condition (147), we have

$$\begin{array}{cc}\hfill \underline{w}(\vartheta ,\theta ,t;\sigma )& ={(3.1+0.3\sigma )}^n\left[\frac{3}{2}\rho sinh\left[\frac{1}{6}(\vartheta +\theta )\right]\right]-{\mathcal{L}}^{-1}\left({\left({\underline{w}}^3\right)}_{\vartheta }+2{\left({\underline{w}}^3\right)}_{\vartheta \vartheta \vartheta }+2{\left({\underline{w}}^3\right)}_{\theta \theta \vartheta }\right)\left(\sigma \right),\hfill \end{array}$$

(152)

$$\begin{array}{cc}\hfill \overline{w}(\vartheta ,\theta ,t;\sigma )& ={(3.8-0.4\sigma )}^n\left[\frac{3}{2}\rho sinh\left[\frac{1}{6}(\vartheta +\theta )\right]\right]-{\mathcal{L}}^{-1}\left({\left({\overline{w}}^3\right)}_{\vartheta }+2{\left({\overline{w}}^3\right)}_{\vartheta \vartheta \vartheta }+2{\left({\overline{w}}^3\right)}_{\theta \theta \vartheta }\right)\left(\sigma \right).\hfill \end{array}$$

(153)

From the decomposition series for $\tilde{w}(\vartheta ,\theta ,t;\sigma )$, with (152) and (153), we get

$$\begin{array}{cc}\hfill \sum _{j=0}^{\infty }{\underline{w}}_j(\vartheta ,\theta ,t;\sigma )& ={(3.1+0.3\sigma )}^n\left[\frac{3}{2}\rho sinh\left[\frac{1}{6}(\vartheta +\theta )\right]\right]\hfill \end{array}$$

$$\begin{array}{cc}\hfill & -{\mathcal{L}}^{-1}\left(\left(\sum _{j=0}^{\infty }{\underline{\mathcal{A}}}_j\left(\sigma \right)\right)+2\left(\sum _{j=0}^{\infty }{\underline{\mathcal{B}}}_j\left(\sigma \right)\right)+2\left(\sum _{j=0}^{\infty }{\underline{\mathcal{C}}}_j\left(\sigma \right)\right)\right),\hfill \\ \hfill \sum _{j=0}^{\infty }{\overline{w}}_j(\vartheta ,\theta ,t;\sigma )& ={(3.8-0.4\sigma )}^n\left[\frac{3}{2}\rho sinh\left[\frac{1}{6}(\vartheta +\theta )\right]\right]\hfill \end{array}$$

(154)

$$\begin{array}{cc}\hfill & -{\mathcal{L}}^{-1}\left(\left(\sum _{j=0}^{\infty }{\overline{\mathcal{A}}}_j\left(\sigma \right)\right)+2\left(\sum _{j=0}^{\infty }{\overline{\mathcal{B}}}_j\left(\sigma \right)\right)+2\left(\sum _{j=0}^{\infty }{\overline{\mathcal{C}}}_j\left(\sigma \right)\right)\right).\hfill \end{array}$$

(155)

The nonlinear terms ${\left(w^2\right)}_{\vartheta },{\left(w^2\right)}_{\vartheta \vartheta \vartheta }$ and ${\left(w^2\right)}_{\theta \theta \vartheta },$ are represented by Adomian polynomials ${\mathcal{A}}_j,{\mathcal{B}}_j$ and ${\mathcal{C}}_j$, respectively. We can derive the recursive relation from (154) as follows

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill & {\underline{w}}_0(\vartheta ,\theta ,t;\sigma )={(3.1+0.3\sigma )}^n\left[\frac{3}{2}\rho sinh\left[\frac{1}{6}(\vartheta +\theta )\right]\right]\hfill \\ \hfill & {\underline{w}}_1(\vartheta ,\theta ,t;\sigma )=-{\mathcal{L}}^{-1}\left({\underline{\mathcal{A}}}_0+2{\underline{\mathcal{B}}}_0+2{\underline{\mathcal{C}}}_0\right)\left(\sigma \right),\hfill \\ \hfill & {\underline{w}}_{j+1}(\vartheta ,\theta ,t;\sigma )=-{\mathcal{L}}^{-1}\left({\underline{\mathcal{A}}}_j+2{\underline{\mathcal{B}}}_j+2{\underline{\mathcal{C}}}_j\right)\left(\sigma \right),j⩾1.\hfill \end{array}\right.\end{array}$$

(156)

Assume $m=n=j=2$ and substitute (73) into (71) to get Adomian polynomials ${\mathcal{A}}_j,{\mathcal{B}}_j$ and ${\mathcal{C}}_j,$ as follows

$$\begin{array}{c}\hfill \left\{\begin{array}{cccc}\hfill {\underline{\mathcal{A}}}_0\left(\sigma \right)& ={\left({\underline{w}}_0^3\right)}_{\vartheta },\hfill & \hfill {\underline{\mathcal{A}}}_1\left(\sigma \right)={\left(3{\underline{w}}_1{\underline{w}}_0^2\right)}_{\vartheta },{\underline{\mathcal{A}}}_2\left(\sigma \right)& ={\left(3{\underline{w}}_2{\underline{w}}_0^2+3{\underline{w}}_0{w}_1^2\right)}_{\vartheta },\dots ,\hfill \\ \hfill {\underline{\mathcal{B}}}_0\left(\sigma \right)& ={\left({\underline{w}}_0^3\right)}_{\vartheta \vartheta \vartheta },\hfill & \hfill {\underline{\mathcal{B}}}_1\left(\sigma \right)={\left(3{\underline{w}}_1{\underline{w}}_0^2\right)}_{\vartheta \vartheta \vartheta },{\underline{\mathcal{B}}}_2\left(\sigma \right)& ={\left(3{\underline{w}}_2{\underline{w}}_0^2+3{\underline{w}}_0{w}_1^2\right)}_{\vartheta \vartheta \vartheta },\dots ,\hfill \\ \hfill {\underline{\mathcal{C}}}_0\left(\sigma \right)& ={\left({\underline{w}}_0^3\right)}_{\theta \theta \vartheta },\hfill & \hfill {\underline{\mathcal{C}}}_1\left(\sigma \right)={\left(3{\underline{w}}_1{\underline{w}}_0^2\right)}_{\theta \theta \vartheta },{\underline{\mathcal{C}}}_2\left(\sigma \right)& ={\left(3{\underline{w}}_2{\underline{w}}_0^2+3{\underline{w}}_0{w}_1^2\right)}_{\theta \theta \vartheta },\dots \hfill \end{array}\right.\end{array}$$

(157)

Substituting (157) into (156) gives

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill & {\underline{w}}_0(\vartheta ,\theta ,t;\sigma )={(3.1+0.3\sigma )}^n\left[\frac{3}{2}\rho sinh\left[\frac{\vartheta +\theta }{6}\right]\right]\hfill \\ \hfill & {\underline{w}}_1(\vartheta ,\theta ,t;\sigma )={(3.1+0.3\sigma )}^n\left[-\frac{1}{4}{\rho }^{2}tcosh\left[\frac{\vartheta +\theta }{6}\right]\right]\hfill \\ \hfill & {\underline{w}}_2(\vartheta ,\theta ,t;\sigma )={(3.1+0.3\sigma )}^n\left[\frac{1}{48}{\rho }^3{t}^{2}sinh\left[\frac{\vartheta +\theta }{6}\right]\right]\hfill \\ \hfill & {\underline{w}}_3(\vartheta ,\theta ,t;\sigma )={(3.1+0.3\sigma )}^n\left[\frac{1}{864}{\rho }^4{t}^{3}cosh\left[\frac{\vartheta +\theta }{6}\right]\right]\hfill \\ \hfill & ⋮.\hfill \end{array}\right.\end{array}$$

(158)

Next, we can get the series solutions

$$\begin{array}{cc}\hfill \overline{w}(\vartheta ,\theta ,t;\sigma )& ={(3.1+0.3\sigma )}^n\left[\frac{3}{2}\rho sinh\left[\frac{\vartheta +\theta }{6}\right]-\frac{1}{4}{\rho }^{2}tcosh\left[\frac{\vartheta +\theta }{6}\right]\right.\hfill \\ \hfill & \left.+\frac{1}{48}{\rho }^3{t}^{2}sinh\left[\frac{\vartheta +\theta }{6}\right]-\frac{1}{864}{\rho }^4{t}^{3}cosh\left[\frac{\vartheta +\theta }{6}\right]+\dots \right].\hfill \end{array}$$

(159)

Similarly, the series solution of $\overline{w}(\vartheta ,\theta ,t;\sigma )$ on Formula (155) can be derived as follows:

$$\begin{array}{cc}\hfill \overline{w}(\vartheta ,\theta ,t;\sigma )& ={(3.8-0.4\sigma )}^n\left[\frac{3}{2}\rho sinh\left[\frac{\vartheta +\theta }{6}\right]-\frac{1}{4}{\rho }^{2}tcosh\left[\frac{\vartheta +\theta }{6}\right]\right.\hfill \\ \hfill & \left.+\frac{1}{48}{\rho }^3{t}^{2}sinh\left[\frac{\vartheta +\theta }{6}\right]-\frac{1}{864}{\rho }^4{t}^{3}cosh\left[\frac{\vartheta +\theta }{6}\right]+\dots \right].\hfill \end{array}$$

(160)

According to Taylor series into (158), we obtain

$$\begin{array}{c}\hfill w(\vartheta ,\theta ,t;\sigma )=[{(3.1+0.3\sigma )}^n,{(3.8-0.4\sigma )}^n]\odot \frac{3}{2}\rho sinh\left[\frac{1}{6}(\vartheta +\theta -\rho t)\right],0\le \sigma \le 1.\end{array}$$

Case [C]. Fuzzy Homotopy perturbation method

Taking the fuzzy HPM to (145), we get

$$\begin{array}{cc}\hfill \mathcal{H}(\underline{v}\left(\sigma \right),p)& =(1-p)\left[\frac{\partial \underline{v}\left(\sigma \right)}{\partial t}-\frac{\partial {\underline{w}}_0\left(\sigma \right)}{\partial t}\right]+p\left[\frac{\partial \underline{v}\left(\sigma \right)}{\partial t}+\frac{\partial }{\partial \vartheta }{\underline{v}}^3\left(\sigma \right)+2\frac{{\partial }^3}{\partial {\vartheta }^3}{\underline{v}}^3\left(\sigma \right)+2\frac{\partial }{\partial \vartheta }\frac{{\partial }^2}{\partial {\theta }^2}{\underline{v}}^3\left(\sigma \right)\right]=\tilde{0},\hfill \end{array}$$

(161)

$$\begin{array}{cc}\hfill \mathcal{H}(\overline{v}\left(\sigma \right),p)& =(1-p)\left[\frac{\partial \overline{v}\left(\sigma \right)}{\partial t}-\frac{\partial {\overline{w}}_0\left(\sigma \right)}{\partial t}\right]+p\left[\frac{\partial \overline{v}\left(\sigma \right)}{\partial t}+\frac{\partial }{\partial \vartheta }{\overline{v}}^3\left(\sigma \right)+2\frac{{\partial }^3}{\partial {\vartheta }^3}{\overline{v}}^3\left(\sigma \right)+2\frac{\partial }{\partial \vartheta }\frac{{\partial }^2}{\partial {\theta }^2}{\overline{v}}^3\left(\sigma \right)\right]=\tilde{0}.\hfill \end{array}$$

(162)

Consider the initial approximation that satisfies the initial condition

$$\begin{array}{c}\hfill w(\vartheta ,\theta ,0)\left(\sigma \right)=[{(3.1+0.3\sigma )}^n,{(3.8-0.4\sigma )}^n]\odot \frac{3}{2}\rho sinh\left[\frac{1}{6}(\vartheta +\theta )\right].\end{array}$$

Substituting (85) and (86) into Equations (161) and (162) and equating the terms with identical powers of p, we have

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill & p^0:\frac{\partial {\underline{v}}_0\left(\sigma \right)}{\partial t}=\frac{\partial {\underline{w}}_0\left(\sigma \right)}{\partial t},{\underline{v}}_0(\vartheta ,\theta ,0)\left(\sigma \right)={(3.1+0.3\sigma )}^n\left[\frac{3}{2}\rho sinh\left[\frac{1}{6}(\vartheta +\theta )\right]\right]\hfill \\ \hfill & p^1:\frac{\partial {\underline{v}}_1\left(\sigma \right)}{\partial t}=-\frac{\partial }{\partial \vartheta }{\underline{v}}_0^3\left(\sigma \right)-2\frac{{\partial }^3}{\partial {\vartheta }^3}{\underline{v}}_0^3\left(\sigma \right)-2\frac{\partial }{\partial \vartheta }\frac{{\partial }^2}{\partial {\theta }^2}{\underline{v}}_0^3\left(\sigma \right),{\underline{v}}_1(\vartheta ,\theta ,0)\left(\sigma \right)=\tilde{0}\hfill \\ \hfill & p^2:\frac{\partial {\underline{v}}_2\left(\sigma \right)}{\partial t}=-3\frac{\partial }{\partial \vartheta }{\underline{v}}_0^2{\underline{v}}_1\left(\sigma \right)-6\frac{{\partial }^3}{\partial {\vartheta }^3}{\underline{v}}_0^2{\underline{v}}_1\left(\sigma \right)-6\frac{\partial }{\partial \vartheta }\frac{{\partial }^2}{\partial {\theta }^2}{\underline{v}}_0^2{\underline{v}}_1\left(\sigma \right),{\underline{v}}_2(\vartheta ,\theta ,0)\left(\sigma \right)=\tilde{0}\hfill \\ \hfill & ⋮,\hfill \end{array}\right.\end{array}$$

(163)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill & p^0:\frac{\partial {\overline{v}}_0\left(\sigma \right)}{\partial t}=\frac{\partial {\overline{w}}_0\left(\sigma \right)}{\partial t},{\overline{v}}_0(\vartheta ,\theta ,0)\left(\sigma \right)={(3.8-0.4\sigma )}^n\left[\frac{3}{2}\rho sinh\left[\frac{1}{6}(\vartheta +\theta )\right]\right]\hfill \\ \hfill & p^1:\frac{\partial {\overline{v}}_1\left(\sigma \right)}{\partial t}=-\frac{\partial }{\partial \vartheta }{\overline{v}}_0^3\left(\sigma \right)-2\frac{{\partial }^3}{\partial {\vartheta }^3}{\overline{v}}_0^3\left(\sigma \right)-2\frac{\partial }{\partial \vartheta }\frac{{\partial }^2}{\partial {\theta }^2}{\overline{v}}_0^3\left(\sigma \right),{\overline{v}}_1(\vartheta ,\theta ,0)\left(\sigma \right)=\tilde{0}\hfill \\ \hfill & p^2:\frac{\partial {\overline{v}}_2\left(\sigma \right)}{\partial t}=-3\frac{\partial }{\partial \vartheta }{\overline{v}}_0^2{\overline{v}}_1\left(\sigma \right)-6\frac{{\partial }^3}{\partial {\vartheta }^3}{\overline{v}}_0^2{\overline{v}}_1\left(\sigma \right)-6\frac{\partial }{\partial \vartheta }\frac{{\partial }^2}{\partial {\theta }^2}{\overline{v}}_0^2{\overline{v}}_1\left(\sigma \right),{\overline{v}}_2(\vartheta ,\theta ,0)\left(\sigma \right)=\tilde{0}\hfill \\ \hfill & ⋮.\hfill \end{array}\right.\end{array}$$

(164)

Successive solution of (163) yields

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\underline{v}}_0(\vartheta ,\theta ,t;\sigma )& ={(3.1+0.3\sigma )}^n\left[\frac{3}{2}\rho sinh\left[\frac{1}{6}(\vartheta +\theta )\right]\right],\hfill \\ \hfill {\underline{v}}_1(\vartheta ,\theta ,t;\sigma )& ={(3.1+0.3\sigma )}^n\left[-3{\rho }^3{sinh}^2\left[\frac{1}{6}(\vartheta +\theta )\right]cosh\frac{1}{6}\left[(\vartheta +\theta )\right]t\right.\hfill \\ \hfill & \left.-\frac{3}{8}{\rho }^3{cosh}^3\left[\frac{1}{6}(\vartheta +\theta )\right]t\right],\hfill \\ \hfill {\underline{v}}_2(\vartheta ,\theta ,t;\sigma )& ={(3.1+0.3\sigma )}^n\hfill \\ \hfill & \times \left[\frac{9}{128}t{\rho }^3\left(135t{\rho }^{2}sinh\frac{1}{6}(\vartheta +\theta ){cosh}^4\left[\frac{1}{6}(\vartheta +\theta )\right]\right.\right.\hfill \\ \hfill & -153t{\rho }^{2}sinh\left[\frac{1}{6}(\vartheta +\theta )\right]{cosh}^2\left[\frac{1}{6}(\vartheta +\theta )\right]\hfill \\ \hfill & +24t{\rho }^{2}sinh\left[\frac{1}{6}(\vartheta +\theta )\right]\hfill \\ \hfill & \left.\left.-72{cosh}^3\left[\frac{1}{6}(\vartheta +\theta )\right]+56cosh\left[\frac{1}{6}(\vartheta +\theta )\right]\right)\right],\hfill \\ \hfill & ⋮.\hfill \end{array}\right.\end{array}$$

Consequently, the solution of (145) when $p\to 1,$ yields

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \underline{v}(\vartheta ,\theta ,t;\sigma )& ={(3.1+0.3\sigma )}^n\left[\frac{3}{2}\rho sinh\left[\frac{1}{6}(\vartheta +\theta )\right]-3{\rho }^3{sinh}^2\left[\frac{1}{6}(\vartheta +\theta )\right]cosh\left[\frac{1}{6}(\vartheta +\theta )\right]t\right.\hfill \\ \hfill & -\frac{3}{8}{\rho }^3{cosh}^3\left[\frac{1}{6}(\vartheta +\theta )\right]t+\frac{9}{128}t{\rho }^3\left(135t{\rho }^{2}sinh\left[\frac{1}{6}(\vartheta +\theta )\right]{cosh}^4\left[\frac{1}{6}(\vartheta +\theta )\right]\right.\hfill \\ \hfill & -153t{\rho }^{2}sinh\left[\frac{1}{6}(\vartheta +\theta )\right]{cosh}^2\left[\frac{1}{6}(\vartheta +\theta )\right]+24t{\rho }^{2}sinh\left[\frac{1}{6}(\vartheta +\theta )\right]\hfill \\ \hfill & \left.\left.-72{cosh}^3\left[\frac{1}{6}(\vartheta +\theta )\right]+56cosh\left[\frac{1}{6}(\vartheta +\theta )\right]\right)\right].\hfill \end{array}\end{array}$$

(165)

Similarly, the series solution of $\overline{v}(\vartheta ,\theta ,t;\sigma )$ on equation (164) can be obtained as:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \overline{v}(\vartheta ,\theta ,t;\sigma )& ={(3.8-0.4\sigma )}^n\left[\frac{3}{2}\rho sinh\left[\frac{1}{6}(\vartheta +\theta )\right]-3{\rho }^3{sinh}^2\left[\frac{1}{6}(\vartheta +\theta )\right]cosh\left[\frac{1}{6}(\vartheta +\theta )\right]t\right.\hfill \\ \hfill & -\frac{3}{8}{\rho }^3{cosh}^3\left[\frac{1}{6}(\vartheta +\theta )\right]t+\frac{9}{128}t{\rho }^3\left(135t{\rho }^{2}sinh\left[\frac{1}{6}(\vartheta +\theta )\right]{cosh}^4\left[\frac{1}{6}(\vartheta +\theta )\right]\right.\hfill \\ \hfill & -153t{\rho }^{2}sinh\left[\frac{1}{6}(\vartheta +\theta )\right]{cosh}^2\left[\frac{1}{6}(\vartheta +\theta )\right]+24t{\rho }^{2}sinh\left[\frac{1}{6}(\vartheta +\theta )\right]\hfill \\ \hfill & \left.\left.-72{cosh}^3\left[\frac{1}{6}(\vartheta +\theta )\right]+56cosh\left[\frac{1}{6}(\vartheta +\theta )\right]\right)\right].\hfill \end{array}\end{array}$$

(166)

Thus, we obtained the closed form solution as:

$$\begin{array}{c}\hfill w(\vartheta ,\theta ,t;\sigma )=[{(3.1+0.3\sigma )}^n,{(3.8-0.4\sigma )}^n]\odot \frac{3}{2}\rho sinh\left[\frac{1}{6}(\vartheta +\theta -\rho t)\right],0\le \sigma \le 1.\end{array}$$

Case [D]. Fuzzy Homotopy analysis method

To analyze the exact solution of (145), we use the linear operator

$$\begin{array}{c}\hfill \mathcal{L}[\Im (\vartheta ,\theta ,t,q)]=\frac{\partial \Im (\vartheta ,\theta ,t,q)}{\partial t},\end{array}$$

(167)

with the property

$$\begin{array}{c}\hfill \mathcal{L}[c_1+t{c}_2]=0,\end{array}$$

where $c_1$ and $c_2$ are integral constants. The expression for the inverse operator ${\mathcal{L}}^{-1}$ is defined by

$$\begin{array}{c}\hfill {\mathcal{L}}^{-1}(·)={\int }_0^t(·)dt,\end{array}$$

(168)

depending on (145), we derive the nonlinear operator as

$$\begin{array}{c}\hfill \mathcal{N}[\Im (\vartheta ,\theta ,t,q)]=\frac{\partial \Im (\vartheta ,\theta ,t,q)}{\partial t}\oplus {(\Im {(\vartheta ,\theta ,t,q)}^3)}_{\vartheta }\oplus 2{(\Im {(\vartheta ,\theta ,t,q)}^3)}_{\vartheta \vartheta \vartheta }\oplus 2{(\Im {(\vartheta ,\theta ,t,q)}^3)}_{\theta \theta \vartheta }.\end{array}$$

(169)

To use the preceding formulation, we develop the zeroth-order deformation equation:

$$\begin{array}{c}\hfill (1-q)\mathcal{L}[\underline{\psi }(\vartheta ,\theta ,t,q;\sigma )-{\underline{w}}_0(\vartheta ,\theta ,t;\sigma )]=q\hslash \mathcal{H}(\vartheta ,\theta ,t)\left[\underline{\psi }(\vartheta ,\theta ,t,q;\sigma )\right],\end{array}$$

(170)

$$\begin{array}{c}\hfill (1-q)\mathcal{L}[\overline{\psi }(\vartheta ,\theta ,t,q;\sigma )-{\overline{w}}_0(\vartheta ,\theta ,t;\sigma )]=q\hslash \mathcal{H}(\vartheta ,\theta ,t)\left[\overline{\psi }(\vartheta ,\theta ,t,q;\sigma )\right],\end{array}$$

(171)

Clearly, we have

$$\begin{array}{cc}\hfill \underline{\psi }(\vartheta ,\theta ,t,0)\left(\sigma \right)& ={\underline{w}}_0(\vartheta ,\theta ,t;\sigma ),\underline{\psi }(\vartheta ,\theta ,t,1)\left(\sigma \right)=\underline{w}(\vartheta ,\theta ,t;\sigma ),\hfill \end{array}$$

(172)

$$\begin{array}{cc}\hfill \overline{\psi }(\vartheta ,\theta ,t,0)\left(\sigma \right)& ={\overline{w}}_0(\vartheta ,\theta ,t;\sigma ),\overline{\psi }(\vartheta ,\theta ,t,1)\left(\sigma \right)=\overline{w}(\vartheta ,\theta ,t;\sigma ).\hfill \end{array}$$

(173)

Consequently, we obtain the m-th order deformation:

$$\begin{array}{c}\hfill \mathcal{L}\left[{\underline{w}}_m(\vartheta ,\theta ,t,q;\sigma )-{\mathcal{N}}_m{\underline{w}}_{m-1}(\vartheta ,\theta ,t,q;\sigma )\right]=\hslash \mathcal{H}(\vartheta ,\theta ,t){\mathcal{R}}_m\left(\overrightarrow{{\underline{w}}_{m-1}}(\vartheta ,\theta ,t,q;\sigma )\right),m\ge 1,\end{array}$$

(174)

$$\begin{array}{c}\hfill \mathcal{L}\left[{\overline{w}}_m(\vartheta ,\theta ,t,q;\sigma )-{\mathcal{N}}_m{\overline{w}}_{m-1}(\vartheta ,\theta ,t,q;\sigma )\right]=\hslash \mathcal{H}(\vartheta ,\theta ,t){\mathcal{R}}_m\left(\overrightarrow{{\overline{w}}_{m-1}}(\vartheta ,\theta ,t,q;\sigma )\right),m\ge 1,\end{array}$$

(175)

where

$$\begin{array}{cc}\hfill \overrightarrow{{\underline{w}}_{m-1}}(\vartheta ,\theta ,t,q;\sigma )& =\left\{{\underline{w}}_0\left(t\right),{\underline{w}}_1\left(t\right),\dots ,{\underline{w}}_n\left(t\right)\right\},\hfill \end{array}$$

(176)

$$\begin{array}{cc}\hfill \overrightarrow{{\overline{w}}_{m-1}}(\vartheta ,\theta ,t,q;\sigma )& =\left\{{\overline{w}}_0\left(t\right),{\overline{w}}_1\left(t\right),\dots ,{\overline{w}}_n\left(t\right)\right\},\hfill \end{array}$$

(177)

with

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathcal{R}\left(\overrightarrow{{\underline{w}}_{m-1}}(\vartheta ,\theta ,t,q;\sigma )\right)=& {\underline{w}}_{m-1}^{\prime }(\vartheta ,\theta ,t,q;\sigma )+\sum _{j=0}^{m-1}\left(\sum _{j=0}^{\wp }{\left({\underline{w}}_{\wp }\right)}_{\vartheta }{\left({\underline{w}}_{\wp -j}\right)}_{\vartheta }{\left({\underline{w}}_{m-1-\wp }\right)}_{\vartheta }\left(\sigma \right)\right)\hfill \\ \hfill & +2\sum _{j=0}^{m-1}\left(\sum _{j=0}^{\wp }{\left({\underline{w}}_{\wp }\right)}_{\vartheta \vartheta \vartheta }{\left({\underline{w}}_{\wp -j}\right)}_{\vartheta \vartheta \vartheta }{\left({\underline{w}}_{m-1-\wp }\right)}_{\vartheta \vartheta \vartheta }\left(\sigma \right)\right)\hfill \\ \hfill & +2\sum _{j=0}^{m-1}\left(\sum _{j=0}^{\wp }{\left({\underline{w}}_{\wp }\right)}_{\theta \theta \vartheta }{\left({\underline{w}}_{\wp -j}\right)}_{\theta \theta \vartheta }{\left({\underline{w}}_{m-1-\wp }\right)}_{\theta \theta \vartheta }\left(\sigma \right)\right),\hfill \end{array}\end{array}$$

(178)

and

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathcal{R}\left(\overrightarrow{{\overline{w}}_{m-1}}(\vartheta ,\theta ,t,q;\sigma )\right)=& {\overline{w}}_{m-1}^{\prime }(\vartheta ,\theta ,t,q;\sigma )+\sum _{j=0}^{m-1}\left(\sum _{j=0}^{\wp }{\left({\overline{w}}_c\right)}_{\vartheta }{\left({\overline{w}}_{\wp -j}\right)}_{\vartheta }{\left({\overline{w}}_{m-1-\wp }\right)}_{\vartheta }\left(\sigma \right)\right)\hfill \\ \hfill & +2\sum _{j=0}^{m-1}\left(\sum _{j=0}^{\wp }{\left({\overline{w}}_{\wp }\right)}_{\vartheta \vartheta \vartheta }{\left({\overline{w}}_{\wp -j}\right)}_{\vartheta \vartheta \vartheta }{\left({\overline{w}}_{m-1-\wp }\right)}_{\vartheta \vartheta \vartheta }\left(\sigma \right)\right)\hfill \\ \hfill & +2\sum _{j=0}^{m-1}\left(\sum _{j=0}^{\wp }{\left({\overline{w}}_{\wp }\right)}_{\theta \theta \vartheta }{\left({\overline{w}}_{\wp -j}\right)}_{\theta \theta \vartheta }{\left({\overline{w}}_{m-1-\wp }\right)}_{\theta \theta \vartheta }\left(\sigma \right)\right).\hfill \end{array}\end{array}$$

(179)

Consequently, the solution of $m^{th}$ order deformation (178) for $m\ge 1$, yields

$$\begin{array}{cc}\hfill {\underline{w}}_m(\vartheta ,\theta ,t;\sigma )& ={\chi }_m{\underline{w}}_{m-1}(\vartheta ,\theta ,t;\sigma )+\hslash \mathcal{H}(\vartheta ,\theta ,t){\mathcal{L}}^{-1}\left[{\mathcal{R}}_m\left(\overrightarrow{{\underline{w}}_{m-1}}(\vartheta ,\theta ,t;\sigma )\right)\right],\hfill \end{array}$$

(180)

we choose the initial step $w_0(\vartheta ,\theta ,t;\sigma )=$$[{(3.1+0.3\sigma )}^n,{(3.8-0.4\sigma )}^n]\odot \frac{3}{2}\rho sinh\frac{1}{6}(\vartheta +\theta )$ this causes a specific boundary condition to (145). First, we investigate the solution to (145) with the boundary condition:

$$\begin{array}{c}\hfill w_0(\vartheta ,\theta ,t;\sigma )=[{(3.1+0.3\sigma )}^n,{(3.8-0.4\sigma )}^n]\odot \frac{3}{2}\rho sinh\frac{1}{6}(\vartheta +\theta ).\end{array}$$

(181)

Putting (181) into (180), we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\underline{w}}_1(\vartheta ,\theta ,t;\sigma )& ={(3.1+0.3\sigma )}^n\left[-0.01562547116{\rho }^3{cosh}^3\frac{1}{6}(\vartheta +\theta )t\right]\hfill \\ \hfill {\underline{w}}_2(\vartheta ,\theta ,t;\sigma )& ={(3.1+0.3\sigma )}^n{\rho }^5\left[0.07812735578sinh\frac{1}{6}(\vartheta +\theta ){cosh}^4\frac{1}{6}(\vartheta +\theta )\right.\hfill \\ \hfill & +0.1259803612{sinh}^3\frac{1}{6}(\vartheta +\theta ){cosh}^2\frac{1}{6}(\vartheta +\theta )\hfill \\ \hfill & \left.+0.002929775842{sinh}^5\frac{1}{6}(\vartheta +\theta )\right]\frac{t^2}{2!}\hfill \\ \hfill & ⋮.\hfill \end{array}\end{array}$$

(182)

Next, we can obtain the series solutions as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\underline{w}}_1(\vartheta ,\theta ,t;\sigma )& ={(3.1+0.3\sigma )}^n\left[\frac{3}{2}\rho sinh\frac{1}{6}(\vartheta +\theta )-0.01562547116{\rho }^3{cosh}^3\frac{1}{6}(\vartheta +\theta )t\right.\hfill \\ \hfill & +{\rho }^5\left[0.07812735578sinh\frac{1}{6}(\vartheta +\theta ){cosh}^4\frac{1}{6}(\vartheta +\theta )\right.\hfill \\ \hfill & +0.1259803612{sinh}^3\frac{1}{6}(\vartheta +\theta ){cosh}^2\frac{1}{6}(\vartheta +\theta )\hfill \\ \hfill & \left.\left.+0.002929775842{sinh}^5\frac{1}{6}(\vartheta +\theta )\right]\frac{t^2}{2!}\dots \right].\hfill \end{array}\end{array}$$

(183)

Similarly, we can achieve the series solution of $\overline{w}(\vartheta ,\theta ,t;\sigma )$ on (179) as:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\overline{w}}_1(\vartheta ,\theta ,t;\sigma )& ={(3.8-0.4\sigma )}^n\left[\frac{3}{2}\rho sinh\frac{1}{6}(\vartheta +\theta )-0.01562547116{\rho }^3{cosh}^3\frac{1}{6}(\vartheta +\theta )t\right.\hfill \\ \hfill & +{\rho }^5\left[0.07812735578sinh\frac{1}{6}(\vartheta +\theta ){cosh}^4\frac{1}{6}(\vartheta +\theta )\right.\hfill \\ \hfill & +0.1259803612{sinh}^3\frac{1}{6}(\vartheta +\theta ){cosh}^2\frac{1}{6}(\vartheta +\theta )\hfill \\ \hfill & \left.\left.+0.002929775842{sinh}^5\frac{1}{6}(\vartheta +\theta )\right]\frac{t^2}{2!}\dots \right].\hfill \end{array}\end{array}$$

(184)

Thus, we obtained the closed form solution as follows:

$$\begin{array}{c}\hfill w(\vartheta ,\theta ,t;\sigma )=[{(3.1+0.3\sigma )}^n,{(3.8-0.4\sigma )}^n]\odot \frac{3}{2}\rho sinh\left[\frac{1}{6}(\vartheta +\theta -\rho t)\right],0\le \sigma \le 1.\end{array}$$

The experience of applying ADM, as well as results reported in the literature, indicate that ADM may generate divergent sequences when the time moment is large, so the issue of convergence of the ADM for large t is, in general, rather delicate. In this work, we also get that the solution of example 5 for ADM shows convergence till time $t=414$ but for $t>414$, the solutions tend to infinity and show divergence. Similarly, in example 6, we also get a convergent solution for ADM till t = 4354.

In Figure 1, we plotted $2D$ and $3D$ graphs of the $ZK(2,2,2)$ equation. Figure 1a shows that for $\vartheta =30$, $\theta =45$ and $\rho =1$ using $n=1$ at $t=0.001$ the $ZK(2,2,2)$ equation is bounded and closed. Furthermore, the blue + sign shows increasing functions and red * presents decreasing functions on the $\sigma$-level set of w in example 5. To discuss the concept of the $\sigma$-level set, one can see Figure 2a, which shows that the $\sigma$-level set of ZK(2,2,2) equation is bounded and closed for $\vartheta =30$ and $0<\theta \le 2\pi$. Similarly, in Figure 2, we can observe the same explanation of $\sigma$-level set closedness and boundedness for example 6.

Figure 1. The exact lower and upper solutions of Equation (111) at $\vartheta =30,\theta =45,t=60$, $\rho =1,n=1$ (a) 2D figure for exact solution of fuzzy ZK(2, 2, 2) equation of w in Example 5. (b) 3D figure for exact solution of fuzzy ZK(2,2,2) equation of w in Example 5.

Figure 2. The exact lower and upper solutions of Equation (146) at $\vartheta =60,\theta =90,t=200,\rho =1,n=2$ (a) 2D figure for exact solution of fuzzy ZK(3, 3, 3) equation of w in Example 6. (b) 3D figure for exact solution of fuzzy ZK(3, 3, 3) equation of w in Example 6.

4. Fuzzy Fractional Partial Differential Equations

In this section, we present the solution of fuzzy fractional partial differential equations via fuzzy $(n+1)$-dimensional fractional RDTM.

4.1. Fuzzy Fractional Calculus

We regard to ${\mathcal{C}}^{\mathcal{F}}[a,b]$ as the space of all continuous fuzzy-valued functions on $[a,b]$. Also, we denote the space of all Lebesgue integrable fuzzy-valued functions on the bounded interval $[a,b]\subset \mathbb{R}$ by ${\mathcal{L}}^{\mathcal{F}}[a,b]$, refs. [71].

Definition 10 ([71]).

Let $f\left(\vartheta \right)\in {\mathcal{C}}^{\mathcal{F}}[a,b]\cap {\mathcal{L}}^{\mathcal{F}}[a,b]$. The fuzzy Riemann-Liouville integral of fuzzy function f is defined as:

$$\left(I_{a+}^{\alpha }f\right)\left(\vartheta \right)=\frac{1}{\Gamma \left(\alpha \right)}{\int }_a^{\vartheta }\frac{f\left(t\right)dt}{{(\vartheta -t)}^{1-\alpha }},\vartheta >a,0<\alpha ⩽1.$$

Assume that the σ-level expression of a fuzzy-valued function f as $f(\vartheta ;\sigma )=[\underline{f}(\vartheta ;\sigma ),\overline{f}(\vartheta ;\sigma )]$, for $0⩽\sigma ⩽1$.

Definition 11 ([71]).

Let $f\left(\vartheta \right)\in {\mathcal{C}}^{\mathcal{F}}[a,b]\cap {\mathcal{L}}^{\mathcal{F}}[a,b]$, then the fuzzy Riemann-Liouville integral of fuzzy-valued function f is defined as:

$$\left({\mathcal{I}}_{a+}^{\alpha }f\right)(\vartheta ;\sigma )=[\left({\mathcal{I}}_{a+}^{\alpha }\underline{f}\right)(\vartheta ;\sigma ),\left({\mathcal{I}}_{a+}^{\alpha }\overline{f}\right)(\vartheta ;\sigma )],$$

where $0\le \sigma \le 1$ and

$$\begin{array}{cc}\hfill \left({\mathcal{I}}_{a+}^{\alpha }\underline{f}\right)(\vartheta ;\sigma )& =\frac{1}{\Gamma \left(\alpha \right)}{\int }_a^{\vartheta }\frac{\underline{f}(t;\sigma )\mathrm{d}t}{{(\vartheta -t)}^{1-\alpha }},0\le \sigma \le 1,\hfill \\ \hfill \left({\mathcal{I}}_{a+}^{\alpha }\overline{f}\right)(\vartheta ;\sigma )& =\frac{1}{\Gamma \left(\alpha \right)}{\int }_a^{\vartheta }\frac{\overline{f}(t;\sigma )\mathrm{d}t}{{(\vartheta -t)}^{1-\alpha }},0\le \sigma \le 1.\hfill \end{array}$$

Definition 12 ([28,71]).

Let $\tilde{f}\in C^1[a,b]$ be fuzzy-valued function and $0<\alpha \le 1$. Then $\tilde{f}$ is said to be Caputo’s gH-differentiable at ϑ when

$${}^{\mathcal{C}}{\mathcal{D}}_a^{\alpha }\tilde{f}(\vartheta ;\sigma )=\frac{1}{\Gamma (1-\alpha )}{\int }_{{\vartheta }_0}^{\vartheta }{(\vartheta -t)}^{-\alpha }{\tilde{f}}^{\prime }(t;\sigma )dt.$$

Note that later we indicate ${}^{\mathcal{C}}{\mathcal{D}}_0^{\alpha }\tilde{f}(t;\sigma )$ using ${}^{\mathcal{C}}{\mathcal{D}}^{\alpha }\tilde{f}(t;\sigma ).$

Theorem 3

([28]). Let $\tilde{f}\in C^{\mathcal{F}}[a,b]\cap L^{\mathcal{F}}[a,b],{\vartheta }_0\in (a,b)$ and $0<\alpha \le 1.$ Then

(i)

if $\tilde{f}$ is (i)-differentiable fuzzy-valued function, then

$$\left({}_i^{\mathcal{C}}{\mathcal{D}}_{{\vartheta }_0}^{\alpha }\right)f(\vartheta ;\sigma )=\left[\left({}^{\mathcal{C}}{D}_{{\vartheta }_0}^{\alpha }\right)\underline{f}(\vartheta ;\sigma ),\left({}^{\mathcal{C}}{\mathcal{D}}_{{\vartheta }_0}^{\alpha }\right)\overline{f}(\vartheta ;\sigma )\right],0\le \sigma \le 1,$$

(ii)

if $\tilde{f}$ is (ii)-differentiable fuzzy-valued function, then

$$\left({}_{ii}^{\mathcal{C}}{\mathcal{D}}_{{\vartheta }_0}^{\alpha }\right)f(\vartheta ;\sigma )=\left[\left({}^{\mathcal{C}}{\mathcal{D}}_{{\vartheta }_0}^{\alpha }\right)\overline{f}(\vartheta ;\sigma ),\left({}^{\mathcal{C}}{\mathcal{D}}_{{\vartheta }_0}^{\alpha }\right)\underline{f}(\vartheta ;\sigma )\right],0\le \sigma \le 1.$$

4.2. Fuzzy $(N+1)$-Dimensional Fractional Reduced Differential Transform

We consider the theory of fuzzy $(n+1)$-dimensional fractional RDTM, at which uncertainty can be expressed by fuzzy concepts.

Definition 13.

Let us consider $\mathcal{X}=({\vartheta }_1,{\vartheta }_2,\dots ,{\vartheta }_n)$ be a vector of fuzzy $(n+1)$-dimensional fractional reduced differential transformed form of ${\vartheta }_{\varsigma }\left(t\right)=(x_1,x_2,\dots ,x_n)$, respectively, where ${\vartheta }_{\varsigma }\left(t\right)$ be differentiable of order $\alpha l$ over time domain T, then

$$\left.\begin{array}{cc}\hfill {\underline{\mathcal{X}}}_{\varsigma }(l;\sigma )& ={\left[\frac{{\partial }^{\alpha l}{\underline{\vartheta }}_{\varsigma }(t;\sigma )}{\partial t^{\alpha l}}\right]}_{t=0},\forall \alpha l\in \mathcal{K}=\{0,1,2,3,...\},\hfill \\ \hfill {\overline{\mathcal{X}}}_{\varsigma }(l;\sigma )& ={\left[\frac{{\partial }^{\alpha l}{\overline{\vartheta }}_{\varsigma }(t;\sigma )}{\partial t^{\alpha l}}\right]}_{t=0},\forall \alpha l\in \mathcal{K}=\{0,1,2,3,...\},\hfill \end{array}\right\}$$

(185)

when $x\left(t\right)$ is (i)-differentiable with

$$\left.\begin{array}{cc}\hfill {\underline{\mathcal{X}}}_{\varsigma }(l;\sigma )& ={\left.\frac{{\partial }^{\alpha l}{\overline{\vartheta }}_{\varsigma }(t;\sigma )}{\partial t^{\alpha l}}\right|}_{t=0},\alpha lis odd,\hfill \\ \hfill {\overline{\mathcal{X}}}_{\varsigma }(l;\sigma )& ={\left.\frac{{\partial }^{\alpha l}{\underline{\vartheta }}_{\varsigma }(t;\sigma )}{\partial t^{\alpha l}}\right|}_{t=0},\alpha lis odd,\hfill \end{array}\right\}$$

(186)

and

$$\left.\begin{array}{cc}\hfill {\underline{\mathcal{X}}}_{\varsigma }(l;\sigma )& ={\left.\frac{{\partial }^{\alpha l}{\underline{\vartheta }}_{\varsigma }(t;\sigma )}{\partial t^{\alpha l}}\right|}_{t=0},\alpha lis even,\hfill \\ \hfill {\overline{\mathcal{X}}}_{\varsigma }(l;\sigma )& ={\left.\frac{{\partial }^{\alpha l}{\overline{\vartheta }}_{\varsigma }(t;\sigma )}{\partial t^{\alpha l}}\right|}_{t=0},\alpha lis even,\hfill \end{array}\right\}$$

(187)

when ${\vartheta }_{\varsigma }\left(t\right)$ is (ii)-differentiable.

Notice that ${\underline{\mathcal{X}}}_{\varsigma }(l;\sigma )$ and ${\overline{\mathcal{X}}}_{\varsigma }(l;\sigma )$ denote the lower and upper spectrum of ${\vartheta }_{\varsigma }\left(t\right)$ at $t=0$, respectively.

Thus, if ${\vartheta }_{\varsigma }\left(t\right)$ be (i)-differentiable, then ${\vartheta }_{\varsigma }\left(t\right)$ can be expressed as:

$$\begin{array}{cc}\hfill {\underline{\vartheta }}_{\varsigma }(t;\sigma )& =\sum _{l=0}^{\infty }\frac{\underline{\mathcal{X}}(l;\sigma )t^{\alpha l}}{\Gamma (\alpha l+1)},\alpha l\in \mathcal{K},0\le \sigma \le 1,\hfill \end{array}$$

(188)

$$\begin{array}{cc}\hfill {\overline{\vartheta }}_{\varsigma }(t;\sigma )& =\sum _{l=0}^{\infty }\frac{\overline{\mathcal{X}}(l;\sigma )t^{\alpha l}}{\Gamma (\alpha l+1)},\alpha l\in \mathcal{K},0\le \sigma \le 1,\hfill \end{array}$$

(189)

and if ${\vartheta }_{\varsigma }\left(t\right)$ be (ii)-differentiable, then ${\vartheta }_{\varsigma }\left(t\right)$ can be expressed as:

$$\begin{array}{cc}\hfill {\underline{\vartheta }}_{\varsigma }(t;\sigma )& =\sum _{l=1,odd}^{\infty }\frac{\overline{\mathcal{X}}(l;\sigma )t^{\alpha l}}{\Gamma (\alpha l+1)}+\sum _{l=0,even}^{\infty }\frac{\underline{\mathcal{X}}(l;\sigma )t^{\alpha l}}{\Gamma (\alpha l+1)},0\le \sigma \le 1,\hfill \end{array}$$

(190)

$$\begin{array}{cc}\hfill {\overline{\vartheta }}_{\varsigma }(t;\sigma )& =\sum _{l=1,odd}^{\infty }\frac{\underline{\mathcal{X}}(l;\sigma )t^{\alpha l}}{\Gamma (\alpha l+1)}+\sum _{l=0,even}^{\infty }\frac{\overline{\mathcal{X}}(l;\sigma )t^{\alpha l}}{\Gamma (\alpha l+1)},0\le \sigma \le 1.\hfill \end{array}$$

(191)

The mentioned equations are considered as the inverse transformation of $\mathcal{X}(l;\sigma )$. If $\mathcal{X}(l;\sigma )$ is defined as

$$\left.\begin{array}{cc}\hfill \underline{\mathcal{X}}(l;\sigma )& =P\left(l\right){\left[\frac{{\partial }^{\alpha l}\left(\underline{{\vartheta }_{\varsigma }(t;\sigma )}\right)}{\partial t^{\alpha l}}\right]}_{t=0},\forall \alpha l\in \mathcal{K},\hfill \\ \hfill \overline{\mathcal{X}}(l;\sigma )& =P\left(l\right){\left[\frac{{\partial }^{\alpha l}\left(\overline{{\vartheta }_{\varsigma }(t;\sigma )}\right)}{\partial t^{\alpha l}}\right]}_{t=0},\forall \alpha l\in \mathcal{K},\hfill \end{array}\right\}$$

(192)

when ${\vartheta }_{\varsigma }\left(t\right)$ (i)-differentiable with

$$\left.\begin{array}{cc}\hfill \underline{\mathcal{X}}(l;\sigma )& =P\left(l\right){\left[\frac{{\partial }^{\alpha l}\left(\overline{{\vartheta }_{\varsigma }(t;\sigma )}\right)}{\partial t^{\alpha l}}\right]}_{t=0},\alpha lis odd\hfill \\ \hfill \overline{\mathcal{X}}(l;\sigma )& =P\left(l\right){\left[\frac{{\partial }^{\alpha l}\left(\underline{{\vartheta }_{\varsigma }(t;\sigma )}\right)}{\partial t^{\alpha l}}\right]}_{t=0},\alpha lis odd\hfill \end{array}\right\}$$

(193)

and

$$\left.\begin{array}{cc}\hfill \underline{\mathcal{X}}(l;\sigma )& =P\left(l\right){\left[\frac{{\partial }^{\alpha l}\left(\underline{{\vartheta }_{\varsigma }(t;\sigma )}\right)}{\partial t^{\alpha l}}\right]}_{t=0},\alpha lis even\hfill \\ \hfill \overline{\mathcal{X}}(l;\sigma )& =P\left(l\right){\left[\frac{{\partial }^{\alpha l}\left(\overline{{\vartheta }_{\varsigma }(t;\sigma )}\right)}{\partial t^{\alpha l}}\right]}_{t=0},\alpha lis even\hfill \end{array}\right\}$$

(194)

then ${\vartheta }_{\varsigma }\left(t\right)$ is (ii)-differentiable.

The function ${\vartheta }_{\varsigma }\left(t\right)$ can be expressed as:

$$\begin{array}{cc}\hfill {\underline{\vartheta }}_{\varsigma }(t;\sigma )& =\sum _{l=0}^{\infty }\frac{t^{\alpha l}}{\Gamma (\alpha l+1)}\frac{\underline{\mathcal{X}}(l;\sigma )}{P\left(l\right)},\alpha l\in \mathcal{K},0\le \sigma \le 1,\hfill \end{array}$$

(195)

$$\begin{array}{cc}\hfill {\overline{\vartheta }}_{\varsigma }(t;\sigma )& =\sum _{l=0}^{\infty }\frac{t^{\alpha l}}{\Gamma (\alpha l+1)}\frac{\overline{\mathcal{X}}(l;\sigma )}{P\left(l\right)},\alpha l\in \mathcal{K},0\le \sigma \le 1,\hfill \end{array}$$

(196)

moreover if ${\vartheta }_{\varsigma }\left(t\right)$ is (i)-differentiable then, the function ${\vartheta }_{\varsigma }\left(t\right)$ can be (ii)-differentiable. Hence we get

$$\begin{array}{cc}\hfill {\underline{\vartheta }}_{\varsigma }(t;\sigma )& =\left[\sum _{l=1,odd}^{\infty }\frac{t^{\alpha l}}{\Gamma (\alpha l+1)}\frac{\overline{\mathcal{X}}(l;\sigma )}{P\left(l\right)}+\sum _{l=0,even}^{\infty }\frac{t^{\alpha l}}{\Gamma (\alpha l+1)}\frac{\underline{\mathcal{X}}(l;\sigma )}{P\left(l\right)}\right],0\le \sigma \le 1,\hfill \end{array}$$

(197)

$$\begin{array}{cc}\hfill {\overline{\vartheta }}_{\varsigma }(t;\sigma )& =\left[\sum _{l=1,odd}^{\infty }\frac{t^{\alpha l}}{\Gamma (\alpha l+1)}\frac{\underline{\mathcal{X}}(l;\sigma )}{P\left(l\right)}+\sum _{l=0,even}^{\infty }\frac{t^{\alpha l}}{\Gamma (\alpha l+1)}\frac{\overline{\mathcal{X}}(l;\sigma )}{P\left(l\right)}\right],0\le \sigma \le 1,\hfill \end{array}$$

(198)

where $P\left(l\right)>0$, $P\left(l\right)$ denote the weighting factor. In this work $P\left(l\right)=\frac{C^{\alpha l}}{\Gamma (\alpha l+1)}$ is implemented where C is the time horizon on interest. Consequently, if ${\vartheta }_{\varsigma }\left(t\right)$ be (i)-differentiable, then

$$\begin{array}{cc}\hfill \underline{\mathcal{X}}(l;\sigma )& =\frac{C^{\alpha l}}{\Gamma (\alpha l+1)}\frac{{\partial }^{\alpha l}{\underline{\vartheta }}_{\varsigma }(t;\sigma )}{\partial t^{\alpha l}},\alpha l\in \mathcal{K},0\le \sigma \le 1,\hfill \end{array}$$

(199)

$$\begin{array}{cc}\hfill \overline{\mathcal{X}}(l;\sigma )& =\frac{C^{\alpha l}}{\Gamma (\alpha l+1)}\frac{{\partial }^{\alpha l}{\overline{\vartheta }}_{\varsigma }(t;\sigma )}{\partial t^{\alpha l}},\alpha l\in \mathcal{K},0\le \sigma \le 1,\hfill \end{array}$$

(200)

and if ${\vartheta }_{\varsigma }\left(t\right)$ be (ii)-differentiable, then

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill \underline{\mathcal{X}}(l;\sigma )& =\frac{C^{\alpha l}}{\Gamma (\alpha l+1)}\frac{{\partial }^{\alpha l}{\overline{\vartheta }}_{\varsigma }(t;\sigma )}{\partial t^{\alpha l}},\alpha lisodd,0\le \sigma \le 1,\hfill \\ \hfill \overline{\mathcal{X}}(l;\sigma )& =\frac{C^{\alpha l}}{\Gamma (\alpha l+1)}\frac{{\partial }^{\alpha l}{\underline{\vartheta }}_{\varsigma }(t;\sigma )}{\partial t^{\alpha l}},\alpha lisodd,0\le \sigma \le 1,\hfill \end{array}\right\}\end{array}$$

(201)

and

$$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill \underline{\mathcal{X}}(l;\sigma )& =\frac{C^{\alpha l}}{\Gamma (\alpha l+1)}\frac{{\partial }^{\alpha l}{\underline{\vartheta }}_{\varsigma }(t;\sigma )}{\partial t^l},\alpha lisodd,0\le \sigma \le 1,\hfill \\ \hfill \overline{\mathcal{X}}(l;\sigma )& =\frac{C^{\alpha l}}{\Gamma (\alpha l+1)}\frac{{\partial }^{\alpha l}{\overline{\vartheta }}_{\varsigma }(t;\sigma )}{\partial t^l},\alpha lisodd,0\le \sigma \le 1.\hfill \end{array}\right\}\end{array}$$

(202)

Unitizing the fuzzy $(n+1)$-dimensional fractional RDTM, a fuzzy fractional PDEs within the domain of interest can be transformed to an algebraic equation in the domain $\mathcal{K}$ and ${\vartheta }_{\varsigma }\left(t\right)$ can be expressed as the finite-term Taylor series plus a reminder as:

$$\begin{array}{cc}\hfill {\underline{\vartheta }}_{\varsigma }(t;\sigma )& =\sum _{l=0}^n\frac{t^{\alpha l}}{\Gamma (\alpha l+1)}\frac{\underline{\mathcal{X}}(l;\sigma )}{P\left(l\right)}+R_{n+1}\left(t\right)=\sum _{l=0}^n{\left(\frac{t}{C}\right)}^{\alpha l}\frac{\underline{\mathcal{X}}(l;\sigma )}{P\left(l\right)}+R_{n+1}\left(t\right),\alpha l\in \mathcal{K},0\le \sigma \le 1,\hfill \end{array}$$

(203)

$$\begin{array}{cc}\hfill {\overline{\vartheta }}_{\varsigma }(t;\sigma )& =\sum _{l=0}^n\frac{t^{\alpha l}}{\Gamma (\alpha l+1)}\frac{\overline{\mathcal{X}}(l;\sigma )}{P\left(l\right)}+R_{n+1}\left(t\right)=\sum _{l=0}^n{\left(\frac{t}{C}\right)}^{\alpha l}\frac{\overline{\mathcal{X}}(l;\sigma )}{P\left(l\right)}+R_{n+1}\left(t\right),\alpha l\in \mathcal{K},0\le \sigma \le 1,\hfill \end{array}$$

(204)

when ${\vartheta }_{\varsigma }\left(t\right)$ is (i)-differentiable and

$$\begin{array}{cc}\hfill {\underline{\vartheta }}_{\varsigma }(t;\sigma )=& \sum _{l=0,odd}^{\infty }{\left(\frac{t}{C}\right)}^{\alpha l}\frac{\overline{\mathcal{X}}(l;\sigma )}{P\left(l\right)}+R_{n+1}\left(t\right)+\sum _{l=0,even}^{\infty }{\left(\frac{t}{C}\right)}^{\alpha l}\frac{\underline{\mathcal{X}}(l;\sigma )}{P\left(l\right)}+R_{n+1}\left(t\right),0\le \sigma \le 1,\hfill \end{array}$$

(205)

$$\begin{array}{cc}\hfill {\overline{\vartheta }}_{\varsigma }(t;\sigma )=& \sum _{l=0,odd}^{\infty }{\left(\frac{t}{C}\right)}^{\alpha l}\frac{\underline{\mathcal{X}}(l;\sigma )}{P\left(l\right)}+R_{n+1}\left(t\right)+\sum _{l=0,even}^{\infty }{\left(\frac{t}{C}\right)}^{\alpha l}\frac{\overline{\mathcal{X}}(l;\sigma )}{P\left(l\right)}+R_{n+1}\left(t\right),0\le \sigma \le 1,\hfill \end{array}$$

(206)

when ${\vartheta }_{\varsigma }\left(t\right)$ is (ii)-differentiable.

In this section, we will give the solution of fuzzy fractional PDEs at the equally spaced grid points $[t_0,t_1,\dots ,t_n]$ where $t_{\varsigma }=a+\varsigma l^{*}$ for each $(\varsigma =0,1,2,...n)$, and $l^{*}=\frac{b-a}{n}$. That is, the domain of interest are divided to n is sub-domain, and the fuzzy approximation functions in each sub-domain are ${\vartheta }_{\varsigma }(t;\sigma )$ for $\varsigma =0,1,2,\dots ,n-1$, respectively. Taking the initial conditions, we obtain

$$\begin{array}{cc}\hfill \underline{\mathcal{X}}(0;\sigma )& ={\underline{\vartheta }}_{\varsigma }(0;\sigma ),\overline{\mathcal{X}}(0;\sigma )={\overline{\vartheta }}_{\varsigma }(0;\sigma ),0\le \sigma \le 1.\hfill \end{array}$$

In the first sub-domain, ${\underline{\vartheta }}_{\varsigma }(t;\sigma )$ and ${\overline{\vartheta }}_{\varsigma }(t;\sigma )$ can be described by ${\underline{\vartheta }}_{\varsigma }(0;\sigma )={\underline{\vartheta }}_0\left(\sigma \right)$ and ${\overline{\vartheta }}_{\varsigma }(0;\sigma )={\overline{\vartheta }}_0\left(\sigma \right)$, respectively. They can be expressed in terms of their n-th order bivariate Taylor series with respect to $t_0=0$. That is

$$\begin{array}{cc}\hfill {\underline{\vartheta }}_{\varsigma }(t_0;\sigma )& ={\underline{\mathcal{X}}}_0(0;\sigma )+{\underline{\mathcal{X}}}_0(1;\sigma )t+{\underline{\mathcal{X}}}_0(2;\sigma )t^2+\dots +{\underline{\mathcal{X}}}_0(n;\sigma )t^n,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {\overline{\vartheta }}_{\varsigma }(t_0;\sigma )& ={\overline{\mathcal{X}}}_0(0;\sigma )+{\overline{\mathcal{X}}}_0(1;\sigma )t+{\overline{\mathcal{X}}}_0(2;\sigma )t^2+\dots +{\overline{\mathcal{X}}}_0(n;\sigma )t^n.\hfill \end{array}$$

Additionally, using Taylor series for ${\vartheta }_{\varsigma }(t_{\varsigma };\sigma )$, the solution on the grid points $t_{\varsigma +1}$ can be obtained as:

$$\begin{array}{cc}\hfill {\underline{\vartheta }}_{\varsigma }(t_{\varsigma +1};\sigma )& ={\underline{\mathcal{X}}}_{\varsigma }(t_{\varsigma +1};\sigma )={\underline{\mathcal{X}}}_{\varsigma }(0;\sigma )+{\underline{\mathcal{X}}}_{\varsigma }(1;\sigma )(t_{\varsigma +1}-t_{\varsigma })+{\underline{\mathcal{X}}}_{\varsigma \iota }(2;\sigma ){(t_{\varsigma +1}-t_{\varsigma })}^2\hfill \\ \hfill & +\dots +{\underline{\mathcal{X}}}_{\varsigma }(n;\sigma ){(t_{\varsigma +1}-t_{\varsigma })}^n\hfill \\ \hfill & =\sum _{i=0}^n{\underline{\mathcal{X}}}_{\varsigma }(i;\sigma )h^i,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {\overline{\vartheta }}_{\varsigma }(t_{\varsigma +1};\sigma )& ={\overline{\mathcal{X}}}_{\varsigma }(t_{\varsigma +1};\sigma )={\overline{\mathcal{X}}}_{\varsigma }(0;\sigma )+{\overline{\mathcal{X}}}_{\varsigma }(1;\sigma )(t_{\varsigma +1}-t_{\varsigma })+{\overline{\mathcal{X}}}_{\varsigma \iota }(2;\sigma ){(t_{\varsigma +1}-t_{\varsigma })}^2\hfill \\ \hfill & +\dots +{\overline{\mathcal{X}}}_{\varsigma }(n;\sigma ){(t_{\varsigma +1}-t_{\varsigma })}^n\hfill \\ \hfill & =\sum _{i=0}^n{\overline{\mathcal{X}}}_{\varsigma }(i;\sigma )h^i.\hfill \end{array}$$

The Properties of Fuzzy $(N+1)$-Dimensional Fractional Reduced Differential Transform

We investigate some mathematical operations of fuzzy $(n+1)$-dimensional fractional reduced differential transform.

Lemma 5.

Let us consider $u(\mathcal{X},t)$ and $v(\mathcal{X},t)$ are fuzzy-valued functions and their fuzzy $(n+1)$-dimensional fractional RDTM denoted by $U_{\alpha l}\left(\mathcal{X}\right)$ and $V_{\alpha l}\left(\mathcal{X}\right)$, respectively. Then

• If $f(\mathcal{X},t)=u(\mathcal{X},t)\oplus v(\mathcal{X},t),$ then $F_{\alpha l}\left(\mathcal{X}\right)=U_{\alpha l}\left(\mathcal{X}\right)\oplus V_{\alpha l}\left(\mathcal{X}\right),\alpha l\in \mathcal{K}$
• If $f(\mathcal{X},t)=u(\mathcal{X},t){\ominus }_{gH}v(\mathcal{X},t),$ then $F_{\alpha l}\left(\mathcal{X}\right)=U_{\alpha l}\left(\mathcal{X}\right){\ominus }_{gH}{V}_{\alpha l}\left(\mathcal{X}\right),\alpha l\in \mathcal{K}$
• If $f(\mathcal{X},t)=c\odot u(\mathcal{X},t),$ then $F_{\alpha l}\left(\mathcal{X}\right)=c\odot U_{\alpha l}\left(\mathcal{X}\right),\alpha l\in \mathcal{K},$ where c is a constant,

proposed the generalized Hukuhara difference (gH-difference) exists.

Proof. 

According to Definition (13), the proof is obvious. □

Lemma 6.

Let $w\in {\mathbb{E}}^1$ and $f(\mathcal{X},t)=\frac{{\partial }^{\alpha }w(\mathcal{X},t)}{\partial t^{\alpha }}$, then we obtain $F_{\alpha l}\left(\mathcal{X}\right)=\frac{\Gamma \left(\alpha \right(l+1)+1)}{\Gamma (\alpha l+1)}{W}_{\alpha l}\left(\mathcal{X}\right),l\ge 1$ where $F_{\alpha l}\left(\mathcal{X}\right)$ and $W_{\alpha l}\left(\mathcal{X}\right)$ are the fuzzy $(n+1)$-dimensional fractional reduced differential transformations of fuzzy-valued functions f and w, respectively.

Proof. 

Using Definition (13), we obtain for $0\le \sigma \le 1$

$$\begin{array}{cc}\hfill F_{\alpha l}(\mathcal{X};\sigma )& =\frac{1}{\Gamma (\alpha +1)}{\left[\frac{{\partial }^{\alpha l}}{\partial t^{\alpha l}}\left(\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}\underline{w}(\mathcal{X},t;\sigma );\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}\overline{w}(\mathcal{X},t;\sigma )\right)\right]}_{t=0}\hfill \\ \hfill & =\frac{1}{\Gamma (\alpha +1)}{\left[\frac{{\partial }^{\alpha (l+1)}}{\partial t^{\alpha (l+1)}}\underline{w}(\mathcal{X},t;\sigma );\frac{{\partial }^{\alpha (l+1)}}{\partial t^{\alpha (l+1)}}\overline{w}(\mathcal{X},t;\sigma )\right]}_{t=0}\hfill \\ \hfill & =\frac{\Gamma \left(\alpha \right(l+1)+1)}{\Gamma (\alpha l+1)\Gamma \left(\alpha \right(l+1)+1)}{\left[\frac{{\partial }^{\alpha (l+1)}}{\partial t^{\alpha (l+1)}}\underline{w}(\mathcal{X},t;\sigma );\frac{{\partial }^{\alpha (l+1)}}{\partial t^{\alpha (l+1)}}\overline{w}(\mathcal{X},t;\sigma )\right]}_{t=0}.\hfill \end{array}$$

Using definition of fuzzy fractional RDTM, we obtain

$$\begin{array}{c}\hfill F_{\alpha l}(\mathcal{X};\sigma )=\frac{\Gamma \left(\alpha \right(l+1)+1)}{\Gamma (\alpha l+1)}{W}_{\alpha l}(\mathcal{X};\sigma ),0\le \sigma \le 1,\end{array}$$

the proof is completed. □

Theorem 4.

Let us consider $f(\mathcal{X},t)={\vartheta }_1^{{\wp }_1}.{\vartheta }_2^{{\wp }_2}\dots {\vartheta }_n^{{\wp }_n}.t^s$, then $F_{\alpha l}\left(\mathcal{X}\right)={\vartheta }_1^{{\wp }_1}.{\vartheta }_2^{{\wp }_2}\dots {\vartheta }_n^{{\wp }_n}.\delta (\alpha l-s)$ where

$\delta (\alpha l-s)=\left\{\begin{array}{ccc}& 1,if\hfill & \hfill \alpha l=s,\\ & 0,if\hfill & \hfill \alpha l\ne s,\end{array}\right.$

is the $(n+1)$-dimensional fuzzy fractional RDTM of f.

Proof. 

According to definition of $(n+1)$-dimensional fuzzy fractional RDTM, for any $\sigma \in [0,1],$

$$\begin{array}{cc}\hfill F_{\alpha l}(\mathcal{X};\sigma )& =\frac{1}{\Gamma (\alpha l+1)}{\left[D^{\alpha l}\underline{f}(\mathcal{X},t;\sigma ),D^{\alpha l}\overline{f}(\mathcal{X},t;\sigma )\right]}_{t=0}\hfill \\ \hfill & =\frac{1}{\Gamma (\alpha l+1)}{\left[{\vartheta }_1^{{\wp }_1}.{\vartheta }_2^{{\wp }_2}\dots {\vartheta }_n^{{\wp }_n}{t}^s\frac{{\partial }^{\alpha l}}{\partial t^{\alpha l}}\right]}_{t=0},\hfill \end{array}$$

this implies that

• If $\alpha l>s$ or $\alpha l<s$, then $F_{\alpha l}(\mathcal{X};\sigma )=0$.
• If $\alpha l=s$, then $F_{\alpha l}(\mathcal{X};\sigma )=({\vartheta }_1^{{\wp }_1}.{\vartheta }_2^{{\wp }_2}\dots {\vartheta }_n^{{\wp }_n})\left(\sigma \right).$

This implies $F_{\alpha l}(\mathcal{X};\sigma )={\vartheta }_1^{{\wp }_1}.{\vartheta }_2^{{\wp }_2}\dots {\vartheta }_n^{{\wp }_n}\delta (\alpha l-s)\left(\sigma \right).$ □

Lemma 7.

Let us consider $g\in {\mathbb{E}}^1$ and $f(\mathcal{X},t)=\frac{\partial g(\mathcal{X},t)}{\partial {\vartheta }_{\varsigma }}$, then we obtain $F_{\alpha l}\left(\mathcal{X}\right)=\frac{\partial G_{\alpha l}\left(\mathcal{X}\right)}{\partial {\vartheta }_{\varsigma }},l\ge 1$ where $F_{\alpha l}\left(\mathcal{X}\right)$ and $G_{\alpha l}\left(\mathcal{X}\right)$ are $(n+1)$-dimensional fuzzy fractional reduced differential transformations of fuzzy-valued functions f and g, respectively.

Proof. 

From definition (13), we obtain for $0\le \sigma \le 1$

$$\begin{array}{c}\hfill f(\mathcal{X},t;\sigma )=\frac{\partial g(\mathcal{X},t;\sigma )}{\partial {\vartheta }_{\varsigma }}=\left[\frac{\partial \underline{g}(\mathcal{X},t;\sigma )}{\partial {\vartheta }_{\varsigma }},\frac{\partial \overline{g}(\mathcal{X},t;\sigma )}{\partial {\vartheta }_{\varsigma }}\right].\end{array}$$

(207)

The $(n+1)$-dimensional fuzzy fractional RDTM function is written as:

$$\begin{array}{c}\hfill G_{\alpha l}(\mathcal{X};\sigma )=\frac{1}{\Gamma (\alpha l+1)}{\left.\left[\frac{{\partial }^{\alpha l}\underline{g}(\mathcal{X},t;\sigma )}{\partial t^{\alpha l}},\frac{{\partial }^{\alpha l}\overline{g}(\mathcal{X},t;\sigma )}{\partial t^{\alpha l}}\right]\right|}_{t=0}.\end{array}$$

(208)

Using differentiating the right side of the mentioned equality with respect to ${\vartheta }_{\varsigma },$ we obtain

$$\begin{array}{cc}\hfill \frac{\partial G_{\alpha l}(\mathcal{X};\sigma )}{\partial {\vartheta }_{\varsigma }}& =\frac{\partial \left(\frac{1}{\Gamma (\alpha l+1)}{\left.\left[\frac{{\partial }^{\alpha l}\underline{g}(\mathcal{X},t;\sigma )}{\partial t^{\alpha l}},\frac{{\partial }^{\alpha l}\overline{g}(\mathcal{X},t;\sigma )}{\partial t^{\alpha l}}\right]\right|}_{t=0}\right)}{\partial {\vartheta }_{\varsigma }}\hfill \\ \hfill & =\frac{1}{\Gamma (\alpha l+1)}{\left.\left[\frac{{\partial }^{\alpha l}\left[\frac{\partial \underline{g}(\mathcal{X},t;\sigma )}{\partial t},\frac{\partial \overline{g}(\mathcal{X},t;\sigma )}{\partial t}\right]}{\partial {\vartheta }_{\varsigma }}\right]\right|}_{t=0}\hfill \\ \hfill & =F_{\alpha l}(\mathcal{X};\sigma ),0\le \sigma \le 1,\hfill \end{array}$$

the proof is completed. □

Lemma 8.

Let us consider $g\in {\mathbb{E}}^1$ and $f(\mathcal{X},t)=\frac{{\partial }^{{\wp }_1+{\wp }_2+\dots +{\wp }_n+\eta }g(\mathcal{X},t)}{\partial {\vartheta }_1^{{\wp }_1},\partial {\vartheta }_2^{{\wp }_2},\dots ,\partial {\vartheta }_n^{{\wp }_n}\partial t^{\eta }}$, $s-1<\eta \le s$ then we obtain $F_{\alpha l}\left(\mathcal{X}\right)=\frac{\Gamma (\alpha l+\eta +1)}{\Gamma (\alpha l+1)}\frac{{\partial }^{{\wp }_1+{\wp }_2+\dots +{\wp }_n}{G}_{\alpha l+\eta }\left(\mathcal{X}\right)}{\partial {\vartheta }_1^{{\wp }_1},\partial {\vartheta }_2^{{\wp }_2},\dots ,\partial {\vartheta }_n^{{\wp }_n}}$, $l\ge n$ where $F_{\alpha l}\left(\mathcal{X}\right)$ and $G_{\alpha l}\left(\mathcal{X}\right)$ are the fuzzy $(n+1)$-dimensional fractional reduced differential transformations of fuzzy-valued functions f and g, respectively.

Proof. 

Using definition (13), we obtain for $0\le \sigma \le 1$

$$\begin{array}{c}\hfill F_{\alpha l}(X;\sigma )=\frac{1}{\Gamma (\alpha l+1)}{\left[\frac{{\partial }^{\alpha l}}{\partial t^{\alpha l}}\left(\frac{{\partial }^{{\wp }_1+{\wp }_2+\dots +{\wp }_n+\eta }\underline{g}(\mathcal{X},t;\sigma )}{\partial {\vartheta }_1^{{\wp }_1},\partial {\vartheta }_2^{{\wp }_2},\dots ,\partial {\vartheta }_n^{{\wp }_n}\partial t^{\eta }},\frac{{\partial }^{{\wp }_1+{\wp }_2+\dots +{\wp }_n+\eta }\overline{g}(\mathcal{X},t;\sigma )}{\partial {\vartheta }_1^{{\wp }_1},\partial {\vartheta }_2^{{\wp }_2},\dots ,\partial {\vartheta }_n^{{\wp }_n}\partial t^{\eta }}\right)\right]}_{t=0}.\end{array}$$

Applying the calculus, we derive

$$\begin{array}{c}\hfill F_{\alpha l}(\mathcal{X};\sigma )=\frac{1}{\Gamma (\alpha l+1)}\frac{{\partial }^{{\wp }_1+{\wp }_2+\dots +{\wp }_n}}{\partial {\vartheta }_1^{{\wp }_1}\partial {\vartheta }_1^{{\wp }_1}\dots \partial {\vartheta }_n^{{\wp }_n}}{\left[\frac{{\partial }^{\alpha l+\eta }\underline{g}(\mathcal{X},t;\sigma )}{\partial t^{\alpha l+\eta }},\frac{{\partial }^{\alpha l+\eta }\overline{g}(\mathcal{X},t;\sigma )}{\partial t^{\alpha l+\eta }}\right]}_{t=0}.\end{array}$$

Using definition of fuzzy fractional RDTM on $\frac{{\partial }^{\eta }}{\partial t^{\eta }}\underline{g}(\mathcal{X},t;\sigma )$ and $\frac{{\partial }^{\eta }}{\partial t^{\eta }}\overline{g}(\mathcal{X},t;\sigma )$ are

$$\begin{array}{c}\hfill F_{\alpha l}(\mathcal{X};\sigma )=\frac{1}{\Gamma (\alpha l+\eta +1)}{\left[\frac{{\partial }^{\alpha l+\eta }\underline{g}(\mathcal{X},t;\sigma )}{\partial t^{\alpha l+\eta }},\frac{{\partial }^{\alpha l+\eta }\overline{g}(\mathcal{X},t;\sigma )}{\partial t^{\alpha l+\eta }}\right]}_{t=0},\end{array}$$

thus, we obtain

$$\begin{array}{c}\hfill F_{\alpha l}(\mathcal{X};\sigma )=\frac{\Gamma (\alpha l+\eta +1)}{\Gamma (\alpha l+1)}\frac{{\partial }^{{\wp }_1+{\wp }_2+\dots +{\wp }_n}{G}_{\alpha l+\eta }(\mathcal{X};\sigma )}{\partial {\vartheta }_1^{{\wp }_1},\partial {\vartheta }_2^{{\wp }_2},\dots ,\partial {\vartheta }_n^{{\wp }_n}},0\le \sigma \le 1.\end{array}$$

the proof is completed. □

Note: Assuming $\eta =n\alpha ,$ then the expression above can be represented as follows:

$$\begin{array}{c}\hfill F_{\alpha l}(\mathcal{X};\sigma )=\frac{\Gamma \left(\alpha \right(l+n)+1)}{\Gamma (\alpha l+1)}\frac{{\partial }^{{\wp }_1+{\wp }_2+\dots +{\wp }_n}{G}_{\alpha (l+n)}(\mathcal{X};\sigma )}{\partial {\vartheta }_1^{{\wp }_1},\partial {\vartheta }_2^{{\wp }_2},\dots ,\partial {\vartheta }_n^{{\wp }_n}},0\le \sigma \le 1.\end{array}$$

Lemma 9.

Let $g\in {\mathbb{E}}^1$ and $f(\mathcal{X},t)={\vartheta }_1^{{\wp }_1},{\vartheta }_2^{{\wp }_2},\dots ,{\vartheta }_n^{{\wp }_n}{t}^{\eta }g(\mathcal{X};t)$, then $F_{\alpha l}\left(\mathcal{X}\right)={\vartheta }_1^{{\wp }_1},{\vartheta }_2^{{\wp }_2},\dots ,{\vartheta }_n^{{\wp }_n}{\sum }_{\wp =0}^l\delta (\alpha \wp -\eta )G_{\alpha (l-\wp )}\left(\mathcal{X}\right),$ where $F_{\alpha l}\left(\mathcal{X}\right)$ and $G_{\alpha l}\left(\mathcal{X}\right)$ are the fuzzy $(n+1)$-dimensional fractional RDTM of f and g, respectively.

Proof. 

Suppose that $w(\mathcal{X},t)={\vartheta }_1^{{\wp }_1},{\vartheta }_2^{{\wp }_2},\dots ,{\vartheta }_n^{{\wp }_n}{t}^{\eta },i.e.,f(\mathcal{X},t)=w(\mathcal{X},t)g(\mathcal{X},t)$ then by Definition (13) of $f(\mathcal{X},t)$, we have

$$\begin{array}{cc}\hfill {\underline{F}}_{\alpha l}(\mathcal{X};\sigma )& =\sum _{\wp =0}^l{W}_{\alpha \wp }\left(\mathcal{X}\right)·{\underline{G}}_{\alpha (l-\wp )}(\mathcal{X};\sigma ),\hfill \\ \hfill {\overline{F}}_{\alpha l}(\mathcal{X};\sigma )& =\sum _{\wp =0}^l{W}_{\alpha \wp }\left(\mathcal{X}\right)·{\overline{G}}_{\alpha (l-\wp )}(\mathcal{X};\sigma ),\hfill \end{array}$$

Hence, using Theorem (4), we get

$$\begin{array}{cc}\hfill W_{\alpha l}\left(\mathcal{X}\right)& ={\vartheta }_1^{{\wp }_1},{\vartheta }_2^{{\wp }_2},\dots ,{\vartheta }_n^{{\wp }_n}\delta (\alpha \wp -\eta ),\hfill \end{array}$$

where

$$\begin{array}{c}\hfill \delta (\alpha c-\eta )=\left\{\begin{array}{ccc}\hfill & 1,if\hfill & \hfill \alpha \wp =\eta ,\\ \hfill & 0,if\hfill & \hfill \alpha \wp \ne \eta ,\end{array}\right.\end{array}$$

so, we obtain

$$\begin{array}{c}\hfill F_{\alpha l}(\mathcal{X};\sigma )={\vartheta }_1^{{\wp }_1},{\vartheta }_2^{{\wp }_2},\dots ,{\vartheta }_n^{{\wp }_n}\sum _{\wp =0}^l\delta (\alpha \wp -\eta )G_{\alpha (l-\wp )}(\mathcal{X};\sigma ),\end{array}$$

This completes our desired result. □

Theorem 5.

Let us consider $u\in \mathbb{R}$ and $f(\mathcal{X},t)=u\left(\mathcal{X}\right)g(\mathcal{X},t)$, then $F_{\alpha l}\left(\mathcal{X}\right)=u\left(\mathcal{X}\right)G_{\alpha l}\left(\mathcal{X}\right)$, where $F_{\alpha l}\left(\mathcal{X}\right)$ and $G_{\alpha l}\left(\mathcal{X}\right)$ are the fuzzy $(n+1)$-dimensional fractional reduced differential transformations of real-valued functions f and g, respectively.

Proof. 

Using definition (13), we obtain for $0\le \sigma \le 1$

$$\begin{array}{cc}\hfill F_{\alpha l}(\mathcal{X};\sigma )& =\frac{1}{\Gamma (\alpha l+1)}{\left.\left[\frac{{\partial }^{\alpha l}u\left(\mathcal{X}\right)·\underline{g}(\mathcal{X},t;\sigma )}{\partial t^{\alpha l}},\frac{{\partial }^{\alpha l}u\left(\mathcal{X}\right)·\overline{g}(\mathcal{X},t;\sigma )}{\partial t^{\alpha l}}\right]\right|}_{t=0}\hfill \\ \hfill & =u\left(\mathcal{X}\right)\frac{1}{\Gamma (\alpha l+1)}{\left.\left[\frac{{\partial }^{\alpha l}\underline{g}(\mathcal{X},t;\sigma )}{\partial t^{\alpha l}},\frac{{\partial }^{\alpha l}\overline{g}(\mathcal{X},t;\sigma )}{\partial t^{\alpha l}}\right]\right|}_{t=0}\hfill \end{array}$$

thus, we obtain

$$\begin{array}{c}\hfill F_{\alpha l}(\mathcal{X};\sigma )=u\left(\mathcal{X}\right)·G_{\alpha l}(\mathcal{X};\sigma ),0\le \sigma \le 1,\end{array}$$

the proof is accomplished. □

4.3. Examples

We propose some examples to illustrate this method is a powerful mathematical tool for solving fuzzy fractional partial differential equations.

Example 7.

We take into account the fuzzy $(3+1)$-dimensional time-fractional wave-like equations [1,2]

$$\begin{array}{c}\hfill \frac{{\partial }^{\beta }w}{\partial t^{\beta }}=({\vartheta }^2+{\theta }^2+{\varphi }^2)\oplus \frac{1}{2}\left({\vartheta }^2\odot w_{\vartheta \vartheta }\oplus {\theta }^2\odot w_{\theta \theta }\oplus {\varphi }^2\odot w_{\varphi \varphi }\right),t>0,1<\beta \le 2,\end{array}$$

(209)

with the initial conditions

$$\begin{array}{c}\hfill w(\vartheta ,\theta ,\varphi ,0)=\tilde{0},w_t(\vartheta ,\theta ,\varphi ,0)=\left[{\left(0.5\sigma \right)}^n,{(1-0.5\sigma )}^n\right]\oplus ({\vartheta }^2+{\theta }^2-{\varphi }^2),\end{array}$$

(210)

where $n=1,2,3,\dots ,$$\beta =n\alpha$, and $\tilde{0}\in {\mathbb{E}}^1.$

Using the properties of fuzzy $(n+1)$-dimensional fractional RDTM, we have

$$\begin{array}{cc}\hfill {\underline{W}}_{\alpha (l+n)}(\vartheta ,\theta ,\varphi ;\sigma )& =\frac{\Gamma (\alpha l+1)}{\Gamma \left(\alpha \right(l+n)+1)}\left(\left({\vartheta }^2+{\theta }^2+{\varphi }^2\right)\delta \left(\alpha l\right)\right.\hfill \\ \hfill & \left.+\frac{1}{2}\left({\vartheta }^2\frac{{\partial }^2{\underline{W}}_{\alpha l}}{\partial {\vartheta }^2}+{\theta }^2\frac{{\partial }^2{\underline{W}}_{\alpha l}}{\partial {\theta }^2}+{\varphi }^2\frac{{\partial }^2{\underline{W}}_{\alpha l}}{\partial {\varphi }^2}\right)\right),\hfill \end{array}$$

(211)

and

$$\begin{array}{cc}\hfill {\overline{W}}_{\alpha (l+n)}(\vartheta ,\theta ,\varphi ;\sigma )& =\frac{\Gamma (\alpha l+1)}{\Gamma \left(\alpha \right(l+n)+1)}\left(\left({\vartheta }^2+{\theta }^2+{\varphi }^2\right)\delta \left(\alpha l\right)\right.\hfill \\ \hfill & \left.+\frac{1}{2}\left({\vartheta }^2\frac{{\partial }^2{\overline{W}}_{\alpha l}}{\partial {\vartheta }^2}+{\theta }^2\frac{{\partial }^2{\overline{W}}_{\alpha l}}{\partial {\theta }^2}+{\varphi }^2\frac{{\partial }^2{\overline{W}}_{\alpha l}}{\partial {\varphi }^2}\right)\right).\hfill \end{array}$$

(212)

Taking the initial conditions (213), we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & {\underline{W}}_0=\tilde{0},\hfill \\ \hfill & {\underline{W}}_{\alpha l}=\left\{\begin{array}{cc}{\left(0.5\sigma \right)}^n+\left({\vartheta }^2+{\theta }^2-{\varphi }^2\right),\hfill & \mathrm{if}\alpha l=1\hfill \\ 0,\hfill & \mathrm{if}\alpha l\ne 1,l=0,1,2,\dots ,n-1,\hfill \end{array}\right.\hfill \end{array}\end{array}$$

(213)

and

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & {\overline{W}}_0=\tilde{0},\hfill \\ \hfill & {\overline{W}}_{\alpha l}=\left\{\begin{array}{cc}{(1-0.5\sigma )}^n+\left({\vartheta }^2+{\theta }^2-{\varphi }^2\right),\hfill & \mathrm{if}\alpha l=1\hfill \\ 0,\hfill & \mathrm{if}\alpha l\ne 1,l=0,1,2,\dots ,n-1,\hfill \end{array}\right.\hfill \end{array}\end{array}$$

(214)

for $\beta =1.5,$ i.e., $n=3,\alpha =\frac{1}{2},$ and $l=0,1,2,3,\dots$ (214) into (211), we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \underline{w}(\vartheta ,\theta ,\varphi ,t;\sigma )& ={\left(0.5\sigma \right)}^n+\left[\left({\vartheta }^2+{\theta }^2\right)\left(t+\frac{t^{3/2}}{\Gamma \left(\right(3/2)+1)}+\frac{\Gamma \left(2\right)t^{5/2}}{\Gamma \left(\right(5/2)+1)}+\frac{t^3}{\Gamma \left(4\right)}+\dots \right)\right.\hfill \\ \hfill & \left.+{\varphi }^2\left(t+\frac{t^{3/2}}{\Gamma \left(\right(3/2)+1)}+\frac{\Gamma \left(2\right)t^{5/2}}{\Gamma \left(\right(5/2)+1)}+\frac{t^3}{\Gamma \left(4\right)}+\dots \right)\right],\hfill \end{array}\end{array}$$

(215)

and

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \overline{w}(\vartheta ,\theta ,\varphi ,t;\sigma )& ={(1-0.5\sigma )}^n+\left[\left({\vartheta }^2+{\theta }^2\right)\left(t+\frac{t^{3/2}}{\Gamma \left(\right(3/2)+1)}+\frac{\Gamma \left(2\right)t^{5/2}}{\Gamma \left(\right(5/2)+1)}+\frac{t^3}{\Gamma \left(4\right)}+\dots \right)\right.\hfill \\ \hfill & \left.+{\varphi }^2\left(t+\frac{t^{3/2}}{\Gamma \left(\right(3/2)+1)}+\frac{\Gamma \left(2\right)t^{5/2}}{\Gamma \left(\right(5/2)+1)}+\frac{t^3}{\Gamma \left(4\right)}+\dots \right)\right].\hfill \end{array}\end{array}$$

(216)

For $\beta =2,$ i.e., $n=2,\alpha =1,$ and $l=0,1,2,3,\dots$ (217) into (214), we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & \underline{w}(\vartheta ,\theta ,\varphi ,t;\sigma )={\left(0.5\sigma \right)}^n+\left[\left({\vartheta }^2+{\theta }^2\right)\left(t+\frac{t^2}{\Gamma \left(3\right)}+\frac{\Gamma \left(2\right)t^3}{\Gamma \left(4\right)}+\frac{t^4}{\Gamma \left(5\right)}+\dots \right)\right.\hfill \\ \hfill & \left.+{\varphi }^2\left(-t+\frac{t^2}{\Gamma \left(3\right)}-\frac{\Gamma \left(2\right)t^3}{\Gamma \left(4\right)}+\frac{t^4}{\Gamma \left(5\right)}+\dots \right)\right],\hfill \end{array}\end{array}$$

and

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & \overline{w}(\vartheta ,\theta ,\varphi ,t;\sigma )={(1-0.5\sigma )}^n+\left[\left({\vartheta }^2+{\theta }^2\right)\left(t+\frac{t^2}{\Gamma \left(3\right)}+\frac{\Gamma \left(2\right)t^3}{\Gamma \left(4\right)}+\frac{t^4}{\Gamma \left(5\right)}+\dots \right)\right.\hfill \\ \hfill & \left.+{\varphi }^2\left(-t+\frac{t^2}{\Gamma \left(3\right)}-\frac{\Gamma \left(2\right)t^3}{\Gamma \left(4\right)}+\frac{t^4}{\Gamma \left(5\right)}+\dots \right)\right].\hfill \end{array}\end{array}$$

thus, we can obtained the exact solution as:

$$w(\vartheta ,\theta ,\varphi ,t;\sigma )=\left[{\left(0.5\sigma \right)}^n,{(1-0.5\sigma )}^n\right]\oplus \left(-\left({\vartheta }^2+{\theta }^2+{\varphi }^2\right)+\left({\vartheta }^2+{\theta }^2\right)e^t+{\varphi }^2{e}^{-t}\right),0\le \sigma \le 1.$$

The results corresponding to example 7 are shown in Figure 3 at different values of β. But, if we compare it with others methods in [1,2] shows that although the result of these methods implemented the same at $\beta =2$. But, unlike fuzzy ADM or the generation of correction functionals using general Lagranges multiplication in fuzzy VIM. The fuzzy $(n+1)$-dimensional fractional RDTM does not call for additional algorithms and complicated calculations.

Figure 3. Comparison of exact and approximate solution of fuzzy fractional wave-like equation for $\vartheta =0.02,\theta =0.002$, $\varphi =0.03$, $t=0.007$, $n=5$. (a) $2D$ figure for the comparison of exact and approximate solutions of w in Example 7. (b) $3D$ figure for the comparison of exact and approximate solutions of w in Example 7.

Table 1 shows the error term between exact and approximate solutions of example 7 for σ between 0 and 1. We have also checked and verified the convergence for time t in this example, which shows that example 7 exhibit convergent solutions till time $t=709$ and as the value of t exceeds 709, the solutions tend to infinity and show divergence.

Table 1. Table for the error term between exact solutions (ES) and approximate solutions (AS).

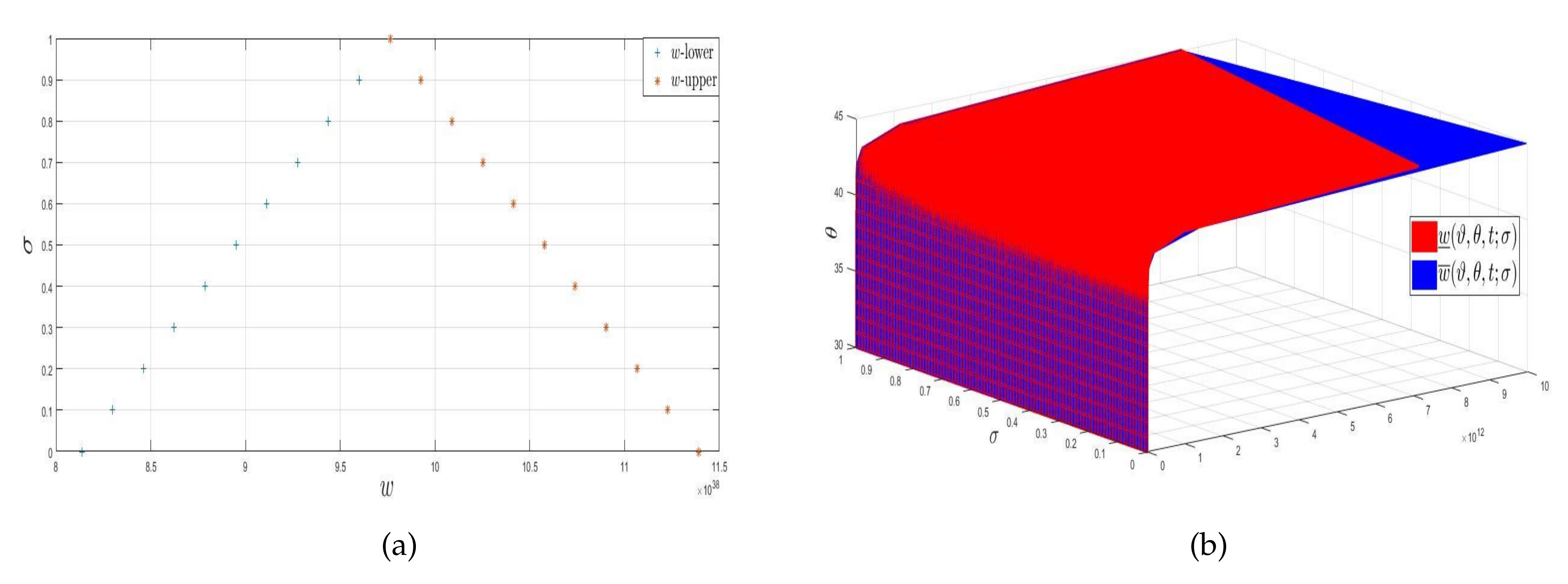
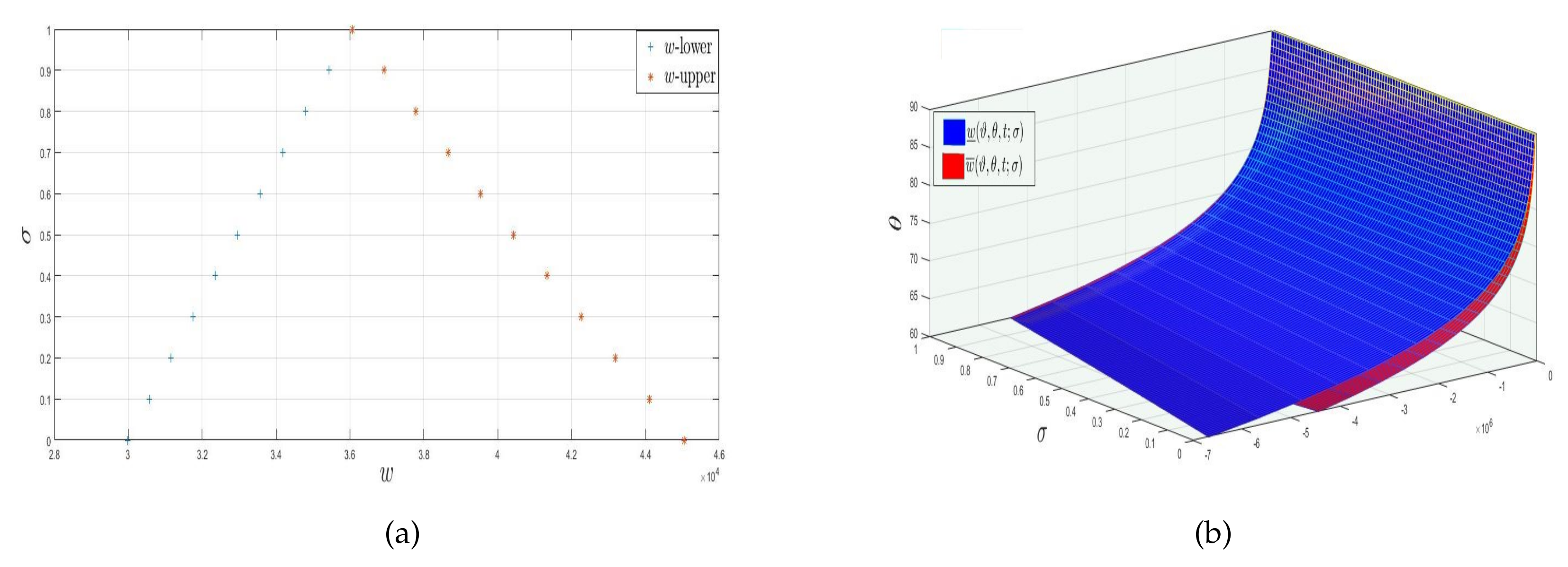
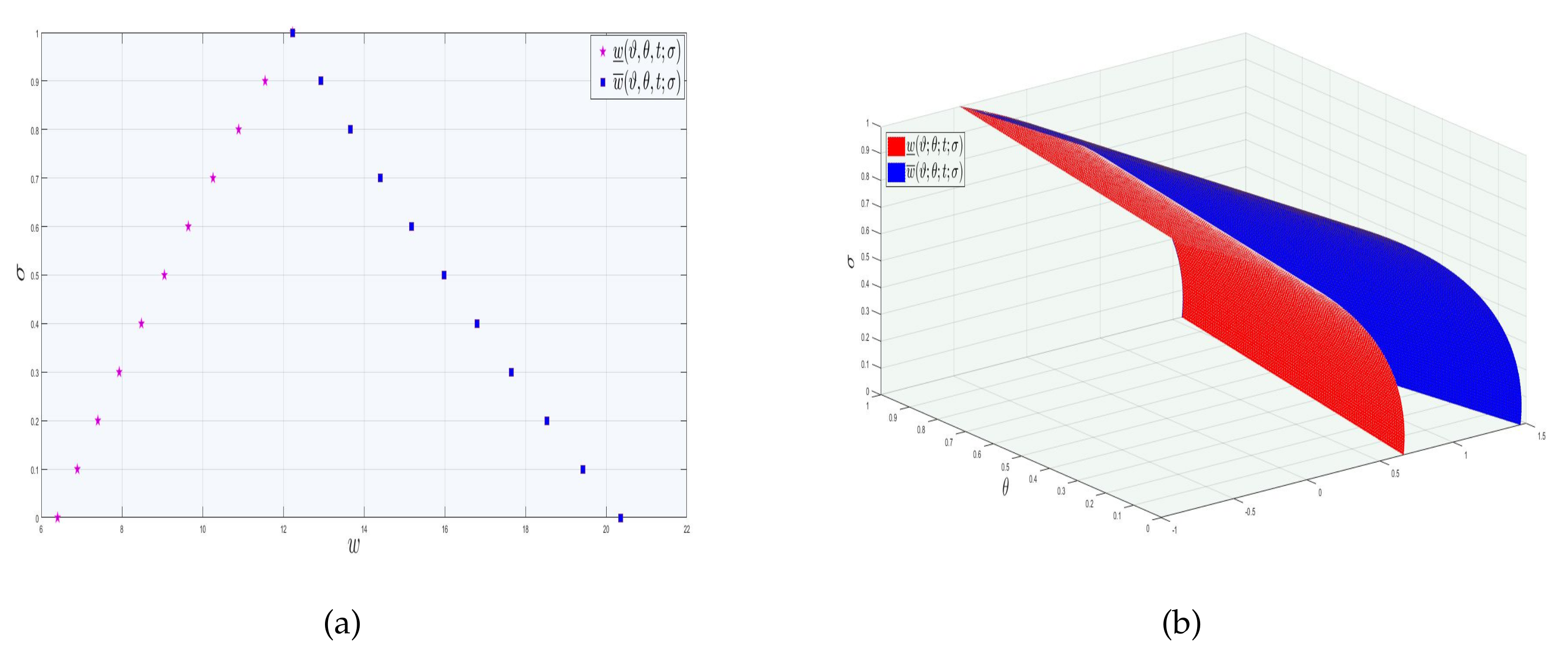
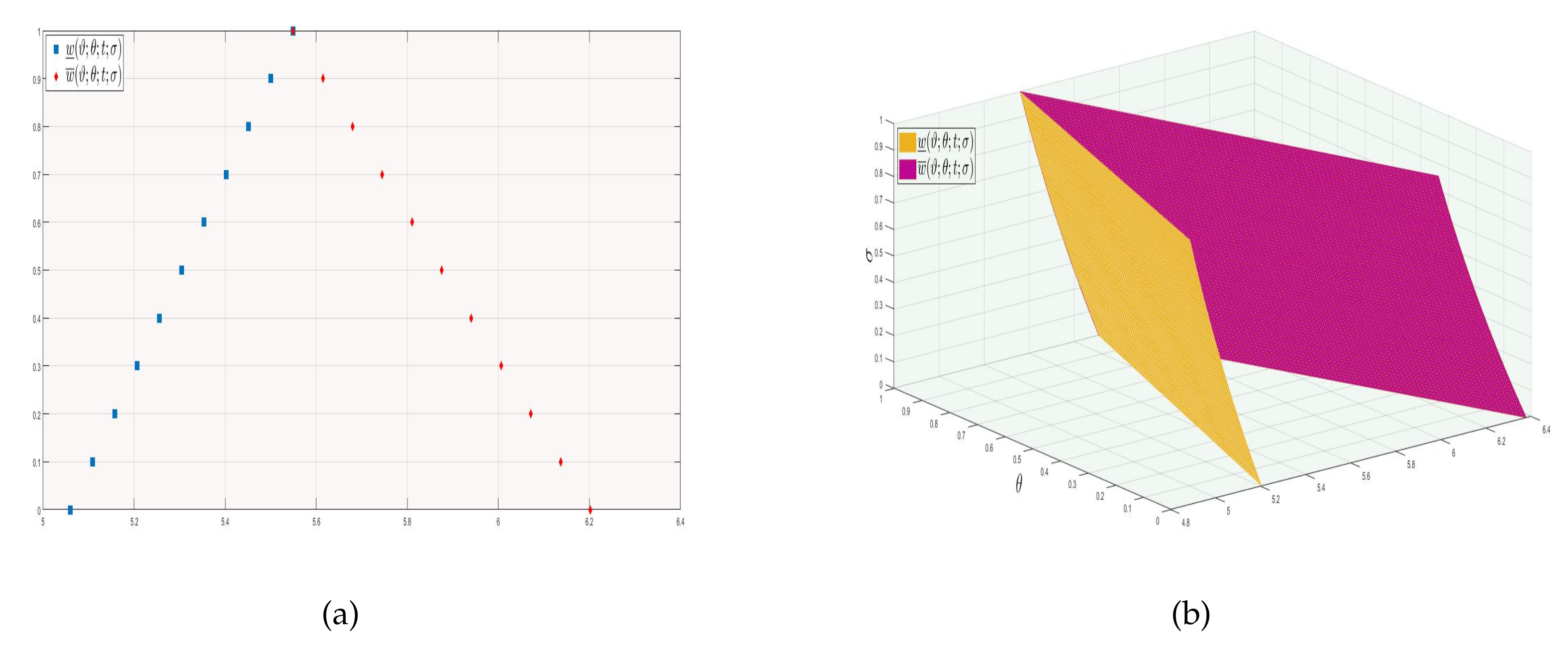
$\mathit{\sigma }$	Lower ES	Lower AS	Lower Error	Upper ES	Upper AS	Upper Error
0	−3.1552 ×${10}^{-5}$	0.00011003	−0.00014158	0.99997	1.0001	−0.00014158
0.1	−3.124 ×${10}^{-5}$	0.00011034	−0.00014158	0.77375	0.77389	−0.00014158
0.2	−2.1552 ×${10}^{-5}$	0.00012003	−0.00014158	0.59046	0.5906	−0.00014158
0.3	4.4385 × ${10}^{-5}$	0.00018597	−0.00014158	0.44367	0.44382	−0.00014158
0.4	0.00028845	0.00043003	−0.00014158	0.32765	0.32779	−0.00014158
0.5	0.00094501	0.0010866	−0.00014158	0.23727	0.23741	−0.00014158
0.6	0.0023984	0.00254	−0.00014158	0.16804	0.16818	−0.00014158
0.7	0.0052206	0.0053622	−0.00014158	0.116	0.11614	−0.00014158
0.8	0.010208	0.01035	−0.00014158	0.077728	0.07787	−0.00014158
0.9	0.018421	0.018563	−0.00014158	0.050297	0.050438	−0.00014158
1	0.031218	0.03136	−0.00014158	0.031218	0.03136	−0.00014158

In Figure 3a, we have compared solutions of fuzzy wave-like equations based on integer as well as fractional order derivatives. It can be seen that red ⋆ and blue colored ■ are for exact solution using $\beta =2$, while orange and purple colored dashed-dotted lines are for fractional order at $\beta =1.5$. For specific values of $\vartheta =0.02,\theta =0.002$, $\varphi =0.03$ the solution of fuzzy fractional wave-like equations at $\beta =1.5$ and 2 are same. Therefore, for a detailed study, we plot a three-dimensional Figure 3b in which we fix all the parameters except θ. Here, one can observe in detail that at the start there exists an error in the exact and approximate solution which reduces time and finally the approximate solution overlaps the exact solution.

Example 8.

Consider the following fuzzy time-fractional $ZK(2,2,2)$ equation

$$\begin{array}{c}\hfill \frac{{\partial }^{\alpha }w}{\partial t^{\alpha }}\oplus {\left(w^2\right)}_{\vartheta }\oplus \frac{1}{8}\odot {\left(w^2\right)}_{\vartheta \vartheta \vartheta }\oplus \frac{1}{8}\odot {\left(w^2\right)}_{\theta \theta \vartheta }=0,0<\alpha \le 1,\end{array}$$

(217)

subject to the initial condition

$$\begin{array}{c}\hfill w(\vartheta ,\theta ,0)=[{(2+0.4\sigma )}^n,{(2.8-0.4\sigma )}^n]{\ominus }_{gH}\frac{4}{3}\rho {cosh}^2(\vartheta +\theta ),\end{array}$$

(218)

where $n=1,2,3,\dots$, and ρ is an arbitrary constant.

Using the properties of fuzzy $(n+1)$-dimensional fractional RDTM, we have

$$\begin{array}{cc}\hfill {\underline{W}}_{\alpha (l+1)}(\vartheta ,\theta ;\sigma )& =-\frac{\Gamma (\alpha l+1)}{\Gamma \left(\alpha \right(l+1)+1)}\left(\sum _{\wp =0}^l\frac{\partial \left({\underline{W}}_{\alpha \wp }{\underline{W}}_{\alpha (l-\wp )}(\vartheta ,\theta ;\sigma )\right)}{\partial \vartheta }\right.\hfill \\ \hfill & \left.+\frac{1}{8}\sum _{\wp =0}^l\frac{{\partial }^3\left({\underline{W}}_{\alpha \wp }{\underline{W}}_{\alpha (l-\wp )}(\vartheta ,\theta ;\sigma )\right)}{\partial {\vartheta }^3}+\frac{1}{8}\sum _{\wp =0}^l\frac{{\partial }^3\left({\underline{W}}_{\alpha \wp }{\underline{W}}_{\alpha (l-\wp )}(\vartheta ,\theta ;\sigma )\right)}{\partial {\theta }^2\partial \vartheta }\right),\hfill \end{array}$$

(219)

and

$$\begin{array}{cc}\hfill {\overline{W}}_{\alpha (l+1)}(\vartheta ,\theta ;\sigma )& =-\frac{\Gamma (\alpha l+1)}{\Gamma \left(\alpha \right(l+1)+1)}\left(\sum _{\wp =0}^l\frac{\partial \left({\overline{W}}_{\alpha \wp }{\overline{W}}_{\alpha (l-\wp )}(\vartheta ,\theta ;\sigma )\right)}{\partial \vartheta }\right.\hfill \\ \hfill & \left.+\frac{1}{8}\sum _{\wp =0}^l\frac{{\partial }^3\left({\overline{W}}_{\alpha \wp }{\overline{W}}_{\alpha (l-\wp )}(\vartheta ,\theta ;\sigma )\right)}{\partial {\vartheta }^3}+\frac{1}{8}\sum _{\wp =0}^l\frac{{\partial }^3\left({\overline{W}}_{\alpha \wp }{\overline{W}}_{\alpha (l-\wp )}(\vartheta ,\theta ;\sigma )\right)}{\partial {\theta }^2\partial \vartheta }\right).\hfill \end{array}$$

(220)

From the initial condition (218), we obtain

$$\begin{array}{c}\hfill W_0(\vartheta ,\theta ,0)\left(\sigma \right)=[{(2+0.4\sigma )}^n,{(2.8-0.4\sigma )}^n]{\ominus }_{gH}\frac{4}{3}\rho {cosh}^2(\vartheta +\theta ),\end{array}$$

(221)

for $l=0,1,2,...$ to using (221) into (219), we get

$$\begin{array}{c}\hfill w_m^{*}(\vartheta ,\theta ,t;\sigma )=\sum _{l=0}^{m-1}{W}_{\alpha l}{t}^{\alpha l},\end{array}$$

(222)

and the exact solution can be obtain as

$$\begin{array}{c}\hfill w(\vartheta ,\theta ,t;\sigma )=\underset{m\to \infty }{lim}{w}_m^{*}(\vartheta ,\theta ,t;\sigma )=\sum _{l=0}^{\infty }{W}_{\alpha l}{t}^{\alpha l},\end{array}$$

(223)

i.e., the 3-term approximate result to (217) can obtain as:

$$\begin{array}{c}\hfill w(\vartheta ,\theta ,t;\sigma )\approx \sum _{l=0}^2{W}_{\alpha l}{t}^{\alpha l}.\end{array}$$

(224)

The solution of Equation (217) is represented as follows:

$$\begin{array}{c}\hfill w(\vartheta ,\theta ,t;\sigma )=[{(2+0.4\sigma )}^n,{(2.8-0.4\sigma )}^n]{\ominus }_{gH}\frac{4}{3}\rho {cosh}^2(\vartheta +\theta -\rho t),0\le \sigma \le 1.\end{array}$$

Similar to previous examples, here we have also checked the convergence for time t, which shows that example 8 exhibit convergent solutions till time $t=355$ and as the value of t exceeds 355, the solutions tend to infinity and show divergence.

In Figure 4, we plotted $2D$ and $3D$ graphs of the $ZK(2,2,2)$ equation but with different initial condition. Figure 4a shows that for $\vartheta =0.0001$, $\theta =0.05$, $\varphi =0.6$ and $\rho =1$ using $n=1$ at $t=0.07$ the $ZK(2,2,2)$ equation become bounded and closed. Furthermore, the pink colored ■ sign shows increasing functions and blue colored ■ presents decreasing functions on the σ-level set of w. To discuss the concept of the σ-level set, one can see Figure 4b, which shows that the σ-level set of ZK(2,2,2) equation is bounded and closed for $\vartheta =0.0001$, $0<\theta <1$ and $\varphi =0.6$.

Figure 4. The exact lower and upper solutions of Equation (222) at $\vartheta =0.0001,\theta =0.05,t=0.07,n=1$ (a) 2D figure for the exact solutions of fuzzy time-fractional ZK(2, 2, 2) equation of w in Example 8. (b) 3D figure for the exact solutions of w in Example 8.

Example 9.

We take into account the following fuzzy fractional $ZK(3,3,3)$ equation

$$\begin{array}{c}\hfill \frac{{\partial }^{\alpha }w}{\partial t^{\alpha }}\oplus {\left(w^3\right)}_{\vartheta }\oplus \frac{1}{8}\odot {\left(w^3\right)}_{\vartheta \vartheta \vartheta }\oplus \frac{1}{8}\odot {\left(w^3\right)}_{\theta \theta \vartheta }=0,0<\alpha \le 1,\end{array}$$

(225)

subject to the initial condition

$$\begin{array}{c}\hfill w(\vartheta ,\theta ,0)=[{(3.1+0.3\sigma )}^n,{(3.8-0.4\sigma )}^n]\odot \frac{3}{2}\rho cosh\left(\frac{\vartheta +\theta }{6}\right),\end{array}$$

(226)

where $n=1,2,3,\dots$, for ρ is an arbitrary constant.

Using the properties of fuzzy $(n+1)$-dimensional fractional RDTM, we have

$$\begin{array}{cc}\hfill & {\underline{W}}_{\alpha (l+1)}(\vartheta ,\theta ;\sigma )=-\frac{\Gamma (\alpha l+1)}{\Gamma \left(\alpha \right(l+1)+1)}\left(\sum _{\wp =0}^l\sum _{s=0}^{\wp }\frac{\partial \left({\underline{W}}_{\alpha s}{\underline{W}}_{\alpha (\wp -s)}{\underline{W}}_{\alpha (l-\wp )}(\vartheta ,\theta ;\sigma )\right)}{\partial \vartheta }\right.\hfill \\ \hfill & \left.+\frac{1}{8}\sum _{\wp =0}^l\sum _{s=0}^{\wp }\frac{{\partial }^3\left({\underline{W}}_{\alpha s}{\underline{W}}_{\alpha (\wp -s)}{W}_{\alpha (l-\wp )}(\vartheta ,\theta ;\sigma )\right)}{\partial {\vartheta }^3}+\frac{1}{8}\sum _{\wp =0}^l\sum _{s=0}^{\wp }\frac{{\partial }^3\left({\underline{W}}_{\alpha s}{\underline{W}}_{\alpha (\wp -s)}{\underline{W}}_{\alpha (l-\wp )}(\vartheta ,\theta ;\sigma )\right)}{\partial {\theta }^2\partial \vartheta }\right),\hfill \end{array}$$

(227)

and

$$\begin{array}{cc}\hfill & {\overline{W}}_{\alpha (l+1)}(\vartheta ,\theta ;\sigma )=-\frac{\Gamma (\alpha l+1)}{\Gamma \left(\alpha \right(l+1)+1)}\left(\sum _{\wp =0}^l\sum _{s=0}^{\wp }\frac{\partial \left({\overline{W}}_{\alpha s}{\overline{W}}_{\alpha (\wp -s)}{\overline{W}}_{\alpha (l-\wp )}(\vartheta ,\theta ;\sigma )\right)}{\partial \vartheta }\right.\hfill \\ \hfill & \left.+\frac{1}{8}\sum _{\wp =0}^l\sum _{s=0}^{\wp }\frac{{\partial }^3\left({\overline{W}}_{\alpha s}{\overline{W}}_{\alpha (\wp -s)}{\overline{W}}_{\alpha (l-\wp )}(\vartheta ,\theta ;\sigma )\right)}{\partial {\vartheta }^3}+\frac{1}{8}\sum _{\wp =0}^l\sum _{s=0}^{\wp }\frac{{\partial }^3\left({\overline{W}}_{\alpha s}{\overline{W}}_{\alpha (\wp -s)}{\overline{W}}_{\alpha (l-\wp )}(\vartheta ,\theta ;\sigma )\right)}{\partial {\theta }^2\partial \vartheta }\right).\hfill \end{array}$$

(228)

From the initial condition (226), we obtain

$$\begin{array}{c}\hfill W_0(\vartheta ,\theta ;\sigma )=[{(3.1+0.3\sigma )}^n,{(3.8-0.4\sigma )}^n]\odot \frac{3}{2}\rho cosh\left(\frac{\vartheta +\theta }{6}\right),\end{array}$$

(229)

for $l=0,1$ in (229) into (227), and using (226), yields

$$\begin{array}{c}\hfill w(\vartheta ,\theta ,t;\sigma )\approx \sum _{l=0}^2{W}_{\alpha l}{t}^{\alpha l}\left(\sigma \right).\end{array}$$

(230)

The solution of Equation (225) is obtained as follows:

$$\begin{array}{c}\hfill w(\vartheta ,\theta ,t;\sigma )=[{(3.1+0.3\sigma )}^n,{(3.8-0.4\sigma )}^n]\odot \frac{3}{2}\rho cosh\left[\frac{1}{6}(\vartheta +\theta -\rho t)\right],0\le \sigma \le 1.\end{array}$$

Finally, the convergence for example 9 shows that their solutions are convergent till time $t=4254$.

Figure 5 also satisfies the condition of σ-level set in both (two and three dimensional) cases for example 9.

Figure 5. The exact lower and upper solutions of Equation (230) at $\vartheta =0.1,\theta =0.4,\varphi =0.9,t=3,n=1$ (a) 2D figure for the exact solutions of fuzzy fractional ZK(3, 3, 3) equation of w in Example 9. (b) 3D figure for the exact solutions of w in Example 9.

5. Conclusions

In this paper, we have successfully compared $(n+1)$-dimensional fuzzy RDTM, ADM, HPM, and fuzzy HAM to obtain the solutions of fuzzy heat-like and wave-like equations, and fuzzy Zakharov-Kuznetsov equations. Furthermore, we investigated the fuzzy $(n+1)$-dimensional fractional RDTM to apply the solution of fuzzy fractional heat-like and wave-like equations, and fuzzy Zakharov-Kuznetsov equations. The RDTM is applied in an uncomplicated approach, without discretization or limiting assumptions. Previous numerical studies demonstrated that the RDTM is occasionally more effective than other techniques. We demonstrated that the suggested methods are highly accurate and efficient by applying them to some of the initial value problems. Hence, we have obtained several new results to solve the above problems when these methods have been applied. Moreover, we observed that our methods are strong mathematical tools for solving PDEs and issues in physics, engineering, and other fields. In future, we are trying our best to present new techniques for solving fuzzy fractional diffusion equations, and the numerical technique for solving fuzzy fractional Cauchy reaction-diffusion equations as well.