Exact Fractional Solution by Nucci’s Reduction Approach and New Analytical Propagating Optical Soliton Structures in Fiber-Optics
Abstract
1. Introduction
2. Construction of Analytical Solutions
2.1. New Extended Direct Algebraic Method
2.2. Application to the Equation (3)
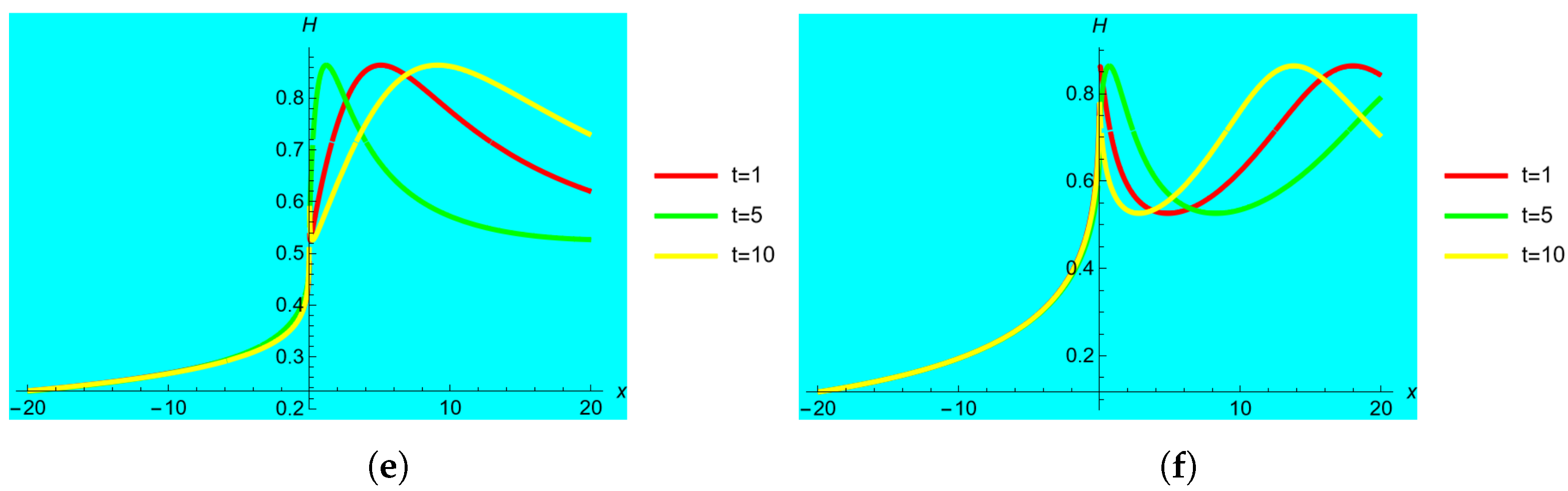
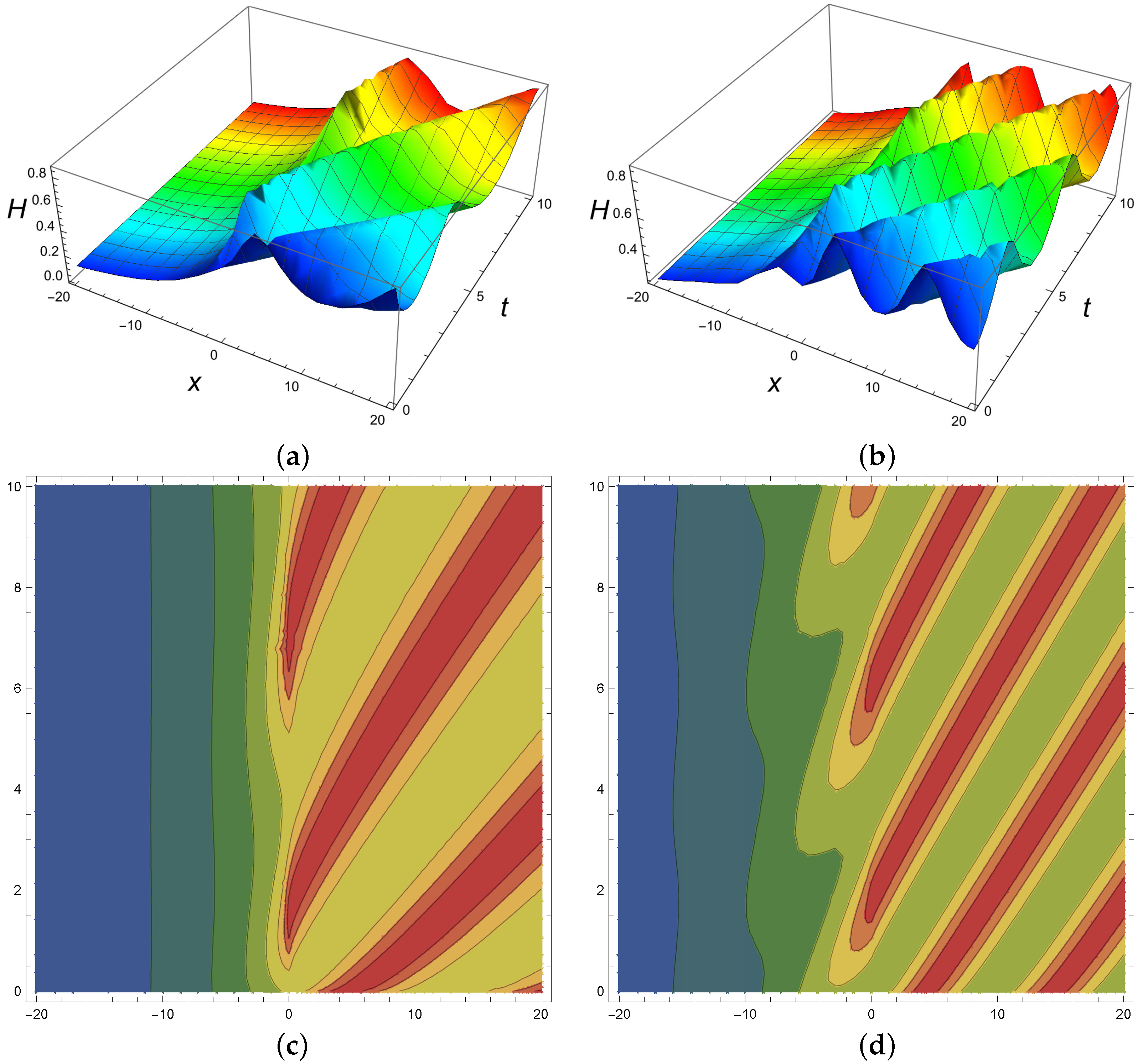
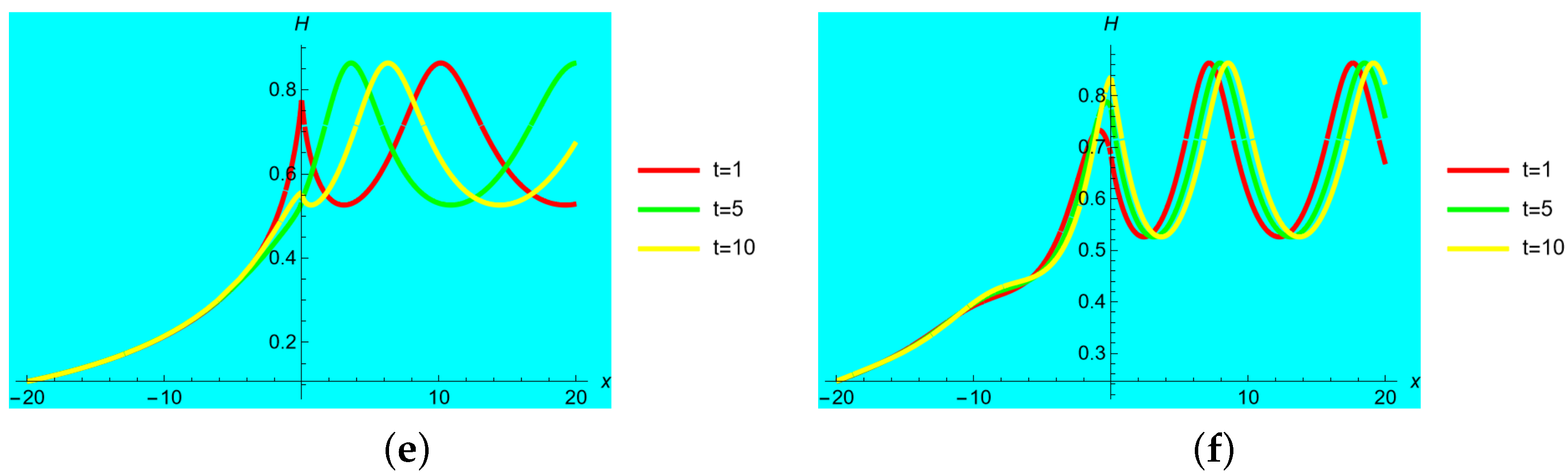
3. Graphical Study
4. Nucci’s Reduction Approach
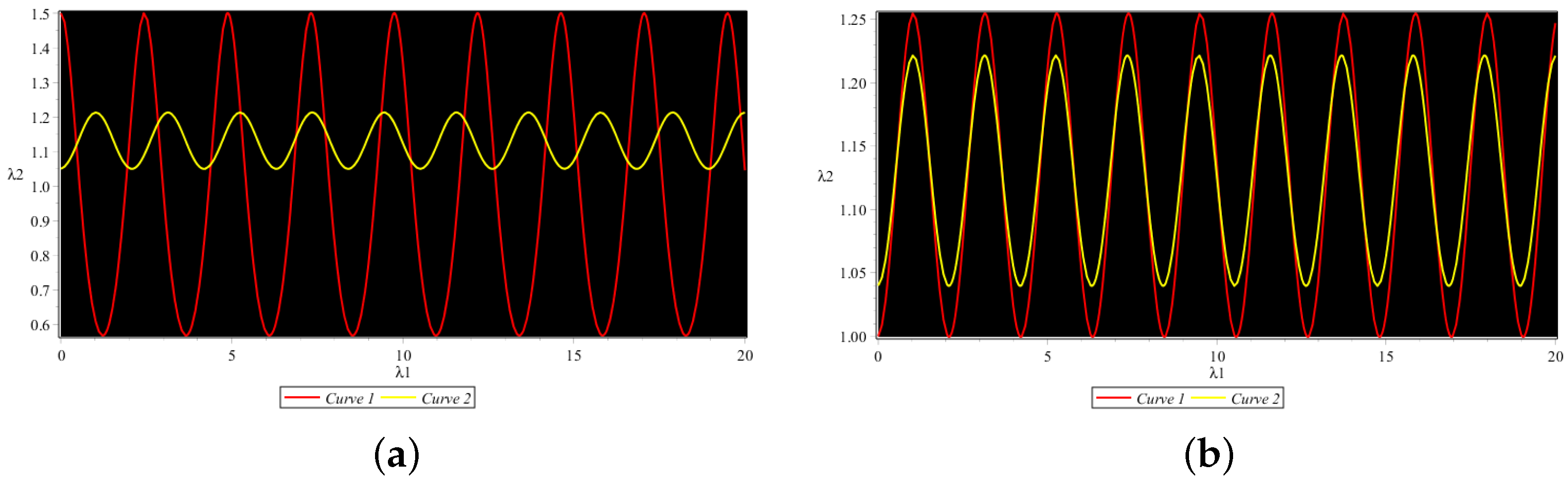
Sensitivity Assessment
5. Conclusions
- The acquired types of soliton include exponential, plane wave solution, shock wave solution, rational, mixed-shock wave, trigonometric, complex shock wave solution, hyperbolic trigonometric, periodic, singular, singular shock wave solution, dark-singular, brilliant singular, and dark-bright solitons.
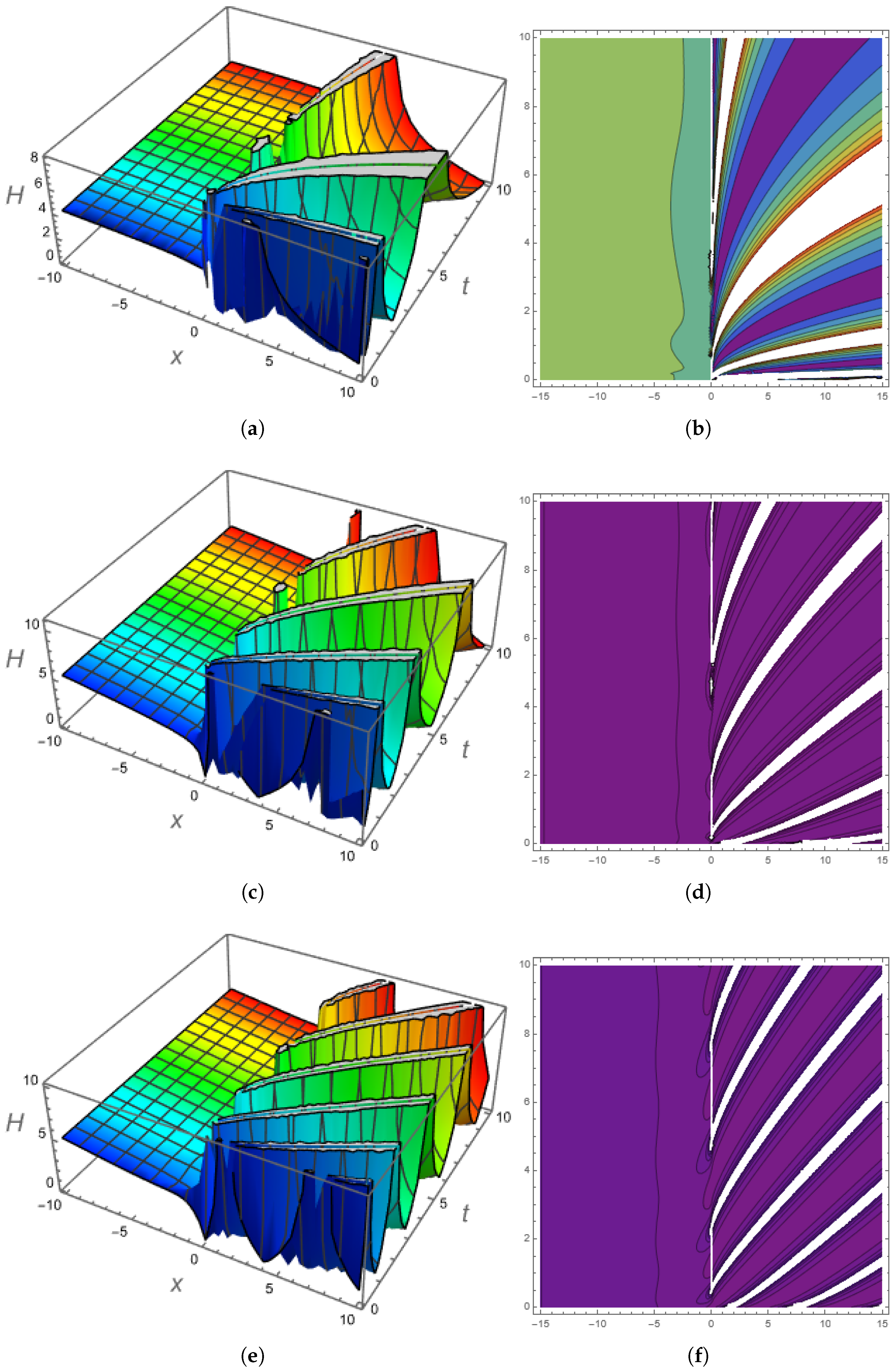
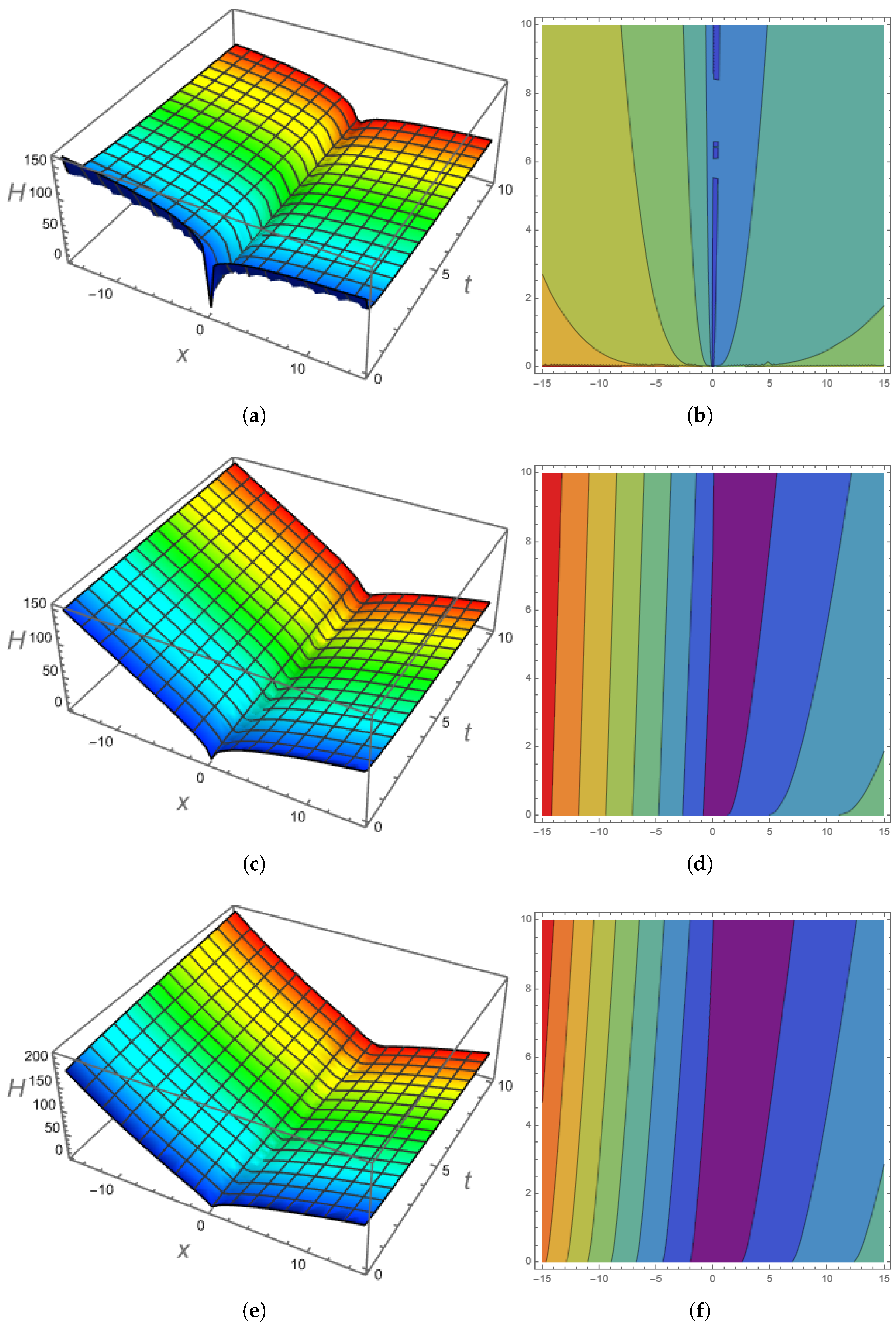
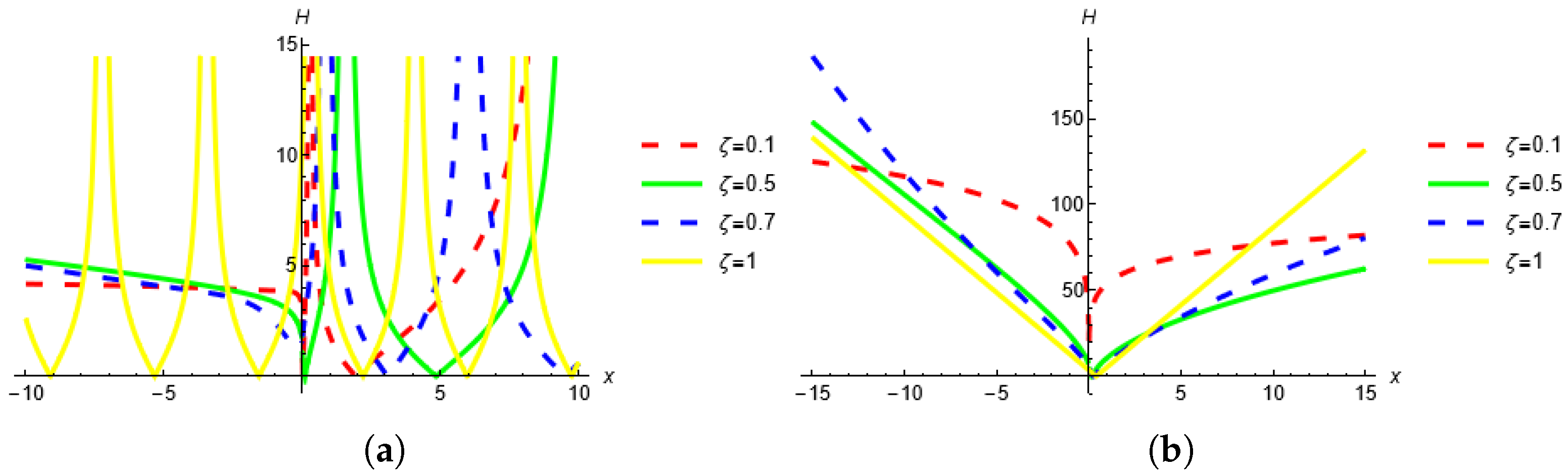
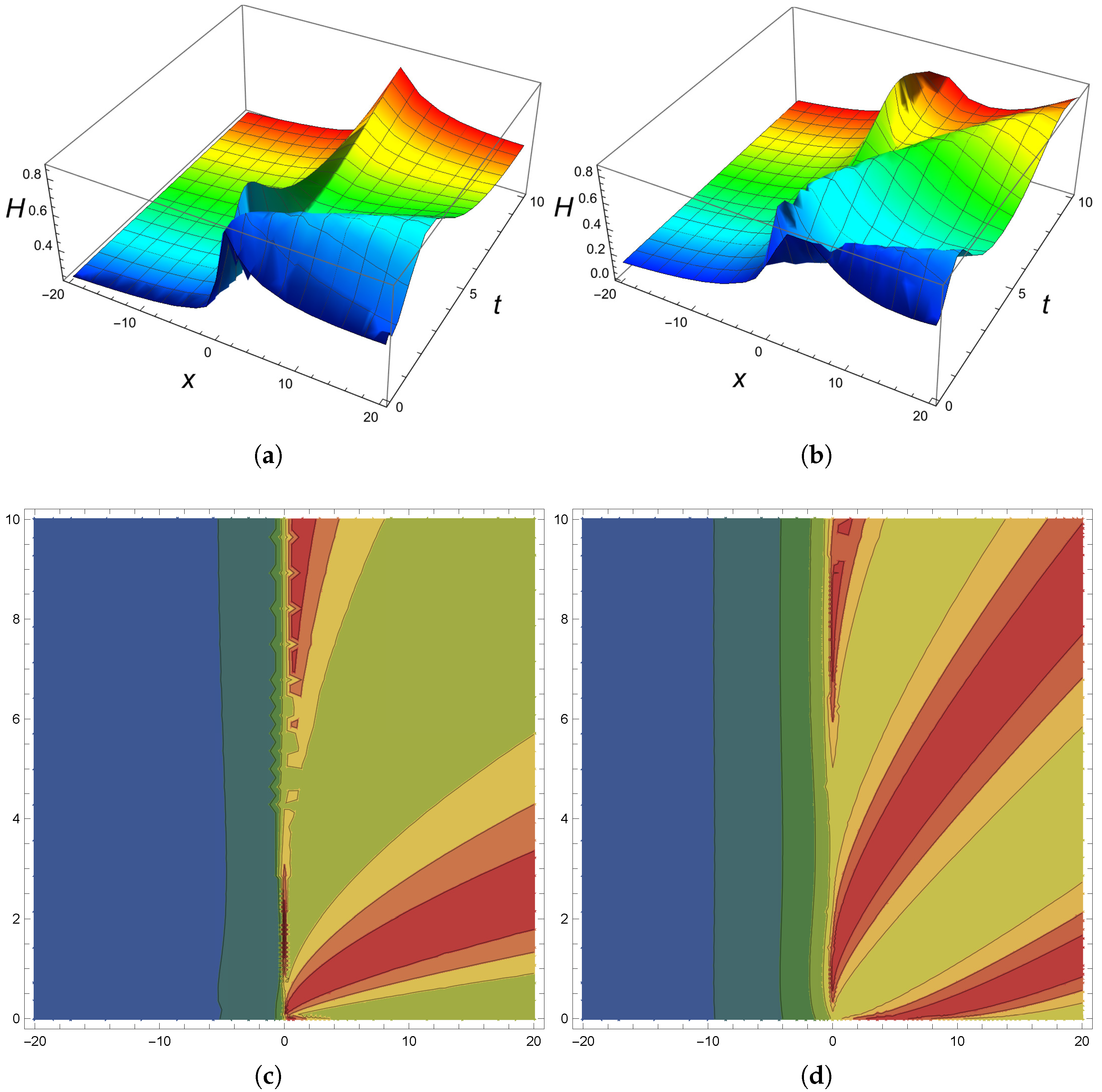
- The solutions are presented in 2-D, 3-D and contour profiles.
- A new fractional exact solution is obtained by utilizing Nucci’s reduction method.
- The governing model is very sensitive with respect to the initial conditions.
- For solution , the fractional-order shows more exciting behaviour, such as a larger singularity as moves to the classical order and bright solution behaviour is produced when the fractional-order moves to the classical order for solution .
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gao, W.; Ismael, H.F.; Bulut, H.; Baskonus, H.M. Instability modulation for the (2+1)-dimension paraxial wave equation and its new optical soliton solutions in Kerr media. Phys. Scr. 2020, 95, 035207. [Google Scholar] [CrossRef]
- Gao, W.; Ismael, H.F.; Husien, A.M.; Bulut, H.; Baskonus, H.M. Optical soliton solutions of the cubicquartic nonlinear Schrödinger and resonant nonlinear Schrödinger equation with the parabolic law. Appl. Sci. 2020, 10, 219. [Google Scholar] [CrossRef]
- Ali, K.K.; Yilmazer, R.; Yokus, A.; Bulut, H. Analytical solutions for the (3+1)-dimensional nonlinear extended quantum Zakharov-Kuznetsov equation in plasma physics. Phys. A Stat. Mech. Appl. 2020, 548, 124327. [Google Scholar] [CrossRef]
- Du, Q.; Zhang, J.; Zheng, C. Nonlocal wave propagation in unbounded multi-scale media. Commun. Comput. Phys. 2018, 24, 4. [Google Scholar] [CrossRef]
- Xie, J.; Zhang, Z. An effective dissipation-preserving fourth-order difference solver for fractional-in-space nonlinear wave equations. J. Sci. Comput. 2019, 79, 1753–1776. [Google Scholar] [CrossRef]
- Tian, X.; Engquist, B. Fast algorithm for computing nonlocal operators with finite interaction distance. arXiv 2019, arXiv:1905.08375. [Google Scholar] [CrossRef]
- Zafar, A.; Shakeel, M.; Ali, A.; Akinyemi, L.; Rezazadeh, H. Optical solitons of nonlinear complex Ginzburg-Landau equation via two modified expansion schemes. Opt. Quantum. Electron. 2022, 54, 5. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Baleanu, D.; Machado, J.A.T.; Osman, M.S.; Rezazadeh, H.; Arshed, S.; Günerhan, H. Traveling wave solutions to nonlinear directional couplers by modified Kudryashov method. Phys. Scr. 2020, 95, 075217. [Google Scholar] [CrossRef]
- Fahim, M.R.A.; Kundu, P.R.; Islam, M.E.; Akbar, M.A.; Osman, M.S. Wave profile analysis of a couple of (3+1)-dimensional nonlinear evolution equations by sine-Gordon expansion approach. J. Ocean Eng. Sci. 2022, 7, 272–279. [Google Scholar] [CrossRef]
- Abdul Kayum, M.; Ali Akbar, M.; Osman, M.S. Stable soliton solutions to the shallow water waves and ion-acoustic waves in a plasma. Waves Random Complex Media 2020, 32, 1672–1693. [Google Scholar] [CrossRef]
- Zhang, R.; Bilige, S.; Chaolu, T. Fractal solitons, arbitrary function solutions, exact periodic wave and breathers for a nonlinear partial differential equation by using bilinear neural network method. J. Syst. Sci. Complex. 2021, 34, 122–139. [Google Scholar] [CrossRef]
- Zhang, R.F.; Bilige, S. Bilinear neural network method to obtain the exact analytical solutions of nonlinear partial differential equations and its application to p-gBKP equation. Nonlinear Dyn. 2019, 95, 3041–3048. [Google Scholar] [CrossRef]
- Khater, M.; Jhangeer, A.; Rezazadeh, H.; Akinyemi, L.; Akbar, M.A.; Inc, M.; Ahmad, H. New kinds of analytical solitary wave solutions for ionic currents on microtubules equation via two different techniques. Opt. Quantum Electron. 2021, 53, 609. [Google Scholar] [CrossRef]
- Karaman, B. The use of improved-F expansion method for the time-fractional Benjamin-Ono equation. Rev. Real Acad. Cienc. Exactas Físicas Nat. Ser. A Matemáticas 2021, 115, 128. [Google Scholar] [CrossRef]
- Yıldırım, Y. Optical solitons with Biswas-Arshed equation by F-expansion method. Optik 2021, 227, 165788. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Shohib, R.M.A. Solitons and Other Solutions for Two Higher-Order Nonlinear Wave Equations of KdV Type Using the Unified Auxiliary Equation Method. Acta Phys. Pol. A 2019, 136, 33–41. [Google Scholar] [CrossRef]
- Zayed, E.M.; Gepreel, K.A.; Shohib, R.M.; Alngar, M.E.; Yıldırım, Y. Optical solitons for the perturbed Biswas-Milovic equation with Kudryashov’s law of refractive index by the unified auxiliary equation method. Optik 2021, 230, 166286. [Google Scholar] [CrossRef]
- Ismael, H.F.; Bulut, H.; Baskonus, H.M. Optical soliton solutions to the Fokas-Lenells equation via sine-Gordon expansion method and ()-expansion method. Pramana 2020, 94, 35. [Google Scholar] [CrossRef]
- Abdulkadir Sulaiman, T.; Yusuf, A. Dynamics of lump-periodic and breather waves solutions with variable coefficients in liquid with gas bubbles. Waves Random Complex Media 2021, 1–14. [Google Scholar] [CrossRef]
- Khodadad, F.S.; Mirhosseini-Alizamini, S.M.; Günay, B.; Akinyemi, L.; Rezazadeh, H.; Inc, M. Abundant optical solitons to the Sasa-Satsuma higher-order nonlinear Schröinger equation. Opt. Quantum Electron. 2021, 53, 702. [Google Scholar] [CrossRef]
- Ghanbari, B.; Kumar, S.; Niwas, M.; Baleanu, D. The Lie symmetry analysis and exact Jacobi elliptic solutions for the Kawahara-KdV type equations. Results Phys. 2021, 23, 104006. [Google Scholar] [CrossRef]
- Lü, D. Jacobi elliptic function solutions for two variant Boussinesq equations. Chaos Solitons Fractals 2005, 24, 1373–1385. [Google Scholar] [CrossRef]
- Baskonus, H.M.; Sulaiman, T.A.; Bulut, H. On the exact solitary wave solutions to the long-short wave interaction system. ITM Web Conf. 2018, 22, 01063. [Google Scholar] [CrossRef][Green Version]
- Rehman, S.U.; Yusuf, A.; Bilal, M.; Younas, U.; Younis, M.; Sulaiman, T.A. Application of ()-expansion method to microstructured solids, magneto-electro-elastic circular rod and (2+1)-dimensional nonlinear electrical lines. Math. Eng. Sci. Aerosp. 2020, 11, 789–803. [Google Scholar]
- Zhang, R.F.; Li, M.C.; Yin, H.M. Rogue wave solutions and the bright and dark solitons of the (3+1)-dimensional Jimbo-Miwa equation. Nonlinear Dyn. 2021, 103, 1071–1079. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Liu, Z.H.; Miao, X.J.; Chen, Y.Z. Qualitative analysis and traveling wave solutions for the perturbed nonlinear Schrödinger’s equation with Kerr law nonlinearity. Phys. Letts. A 2011, 375, 1275–1280. [Google Scholar] [CrossRef]
- Biswas, A. Chirp-free bright optical soliton perturbation with Chen-Lee-Liu equation by traveling wave hypothesis and semi-inverse variational principle. Optik 2018, 172, 772–776. [Google Scholar] [CrossRef]
- Biswas, A.; Ekici, M.; Sonmezoglu, A.; Alshomrani, A.S.; Zhou, Q.; Moshokoa, S.P.; Belic, M. Chirped optical solitons of Chen-Lee-Liu equation by extended trial equation scheme. Optik 2018, 156, 999–1006. [Google Scholar] [CrossRef]
- Kudryashov, N.A. General solution of the traveling wave reduction for the perturbed Chen-Lee-Liu equation. Optik 2019, 186, 339–349. [Google Scholar] [CrossRef]
- Yıldırım, Y.; Biswas, A.; Asma, M.; Ekici, M.; Ntsime, B.P.; Zayed, E.M.; Moshokoa, S.P.; Alzahrani, A.K.; Belic, M.R. Optical soliton perturbation with Chen-Lee-Liu equation. Optik 2020, 220, 165177. [Google Scholar] [CrossRef]
- Esen, H.; Ozdemir, N.; Secer, A.; Bayram, M. On solitary wave solutions for the perturbed Chen-Lee-Liu equation via an analytical approach. Optik 2021, 245, 167641. [Google Scholar] [CrossRef]
- Tarla, S.; Karmina, K.A.; Yilmazer, R.; Osman, M.S. New optical solitons based on the perturbed Chen-Lee-Liu model through Jacobi elliptic function method. Opt. Quantum Electron. 2022, 54, 131. [Google Scholar] [CrossRef]
- Adil, J.; Faridi, W.A.; Asjad, M.I.; Inc, M. A comparative study about the propagation of water waves with fractional operators. J. Ocean Eng. Sci. 2022. [Google Scholar] [CrossRef]
- Xia, F.L.; Jarad, F.; Hashemi, M.S.; Riaz, M.B. A reduction technique to solve the generalized nonlinear dispersive mK (m, n) equation with new local derivative. Results Phys. 2022, 38, 105512. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Faridi, W.A.; Asjad, M.I.; Eldin, S.M. Exact Fractional Solution by Nucci’s Reduction Approach and New Analytical Propagating Optical Soliton Structures in Fiber-Optics. Fractal Fract. 2022, 6, 654. https://doi.org/10.3390/fractalfract6110654
Faridi WA, Asjad MI, Eldin SM. Exact Fractional Solution by Nucci’s Reduction Approach and New Analytical Propagating Optical Soliton Structures in Fiber-Optics. Fractal and Fractional. 2022; 6(11):654. https://doi.org/10.3390/fractalfract6110654
Chicago/Turabian StyleFaridi, Waqas Ali, Muhammad Imran Asjad, and Sayed M. Eldin. 2022. "Exact Fractional Solution by Nucci’s Reduction Approach and New Analytical Propagating Optical Soliton Structures in Fiber-Optics" Fractal and Fractional 6, no. 11: 654. https://doi.org/10.3390/fractalfract6110654
APA StyleFaridi, W. A., Asjad, M. I., & Eldin, S. M. (2022). Exact Fractional Solution by Nucci’s Reduction Approach and New Analytical Propagating Optical Soliton Structures in Fiber-Optics. Fractal and Fractional, 6(11), 654. https://doi.org/10.3390/fractalfract6110654






