Abstract
A pseudorandom sequence is a repeatable sequence with random statistical properties that is widely used in communication encryption, authentication and channel coding. The pseudorandom sequence generator based on the linear feedback shift register has the problem of a fixed sequence, which is easily tracked. Existing methods use the secret linear feedback shift register (LFSR) and built-in multiple LFSRs and is difficult to prevent cracking based on the hardware analysis. Since the plaintext depends on a specific language to be generated, using pseudo-random sequence encryption, it faces the problem that the encryptor cannot hide the characteristics of the plaintext data. Fractal functions have the following properties: chaotic, unpredictable and random. We propose a novel pseudorandom sequence generator based on the nonlinear chaotic systems, which is constructed by the fractal function. Furthermore, we design a data processing matrix to hide the data characteristics of the sequence and enhance the randomness. In the experiment, the pseudo-random sequences generator passed 16 rigorous test items from the National Institute of Standards and Technology (NIST), which means that the nonlinear pseudorandom sequence generator for the fractal function is effective and efficient.
1. Introduction
Pseudorandom sequences are generated by deterministic algorithms and used to simulate truly random sequences [1], which are reproducible, traceable and predictable sequences with random statistical properties. Initially, research was conducted on pseudorandom sequences owing to their unique mathematical structure; for example, the De Bruijn sequence was studied as a combinatorial problem. In 1948, Shannon systematically proposed the concept of information theory [2]. A secure cryptosystem requires the amount of key data used for secure communication to be greater than the amount of encrypted plaintext data, and Shannon proved the security of the one-time pad encryption method [3]. Since then, researchers have focused on generating the longest possible pseudorandom sequences [4,5,6,7,8,9], which is convenient for encryption but difficult for attackers to crack.
The m-sequence is the longest sequence of an n-stage linear feedback shift register, with a length of up to . It satisfies the random properties of Golomb’s randomness assumption [10]. Massey proposed that if the linear complexity of the sequence is k, the attacker only needs to track consecutive bits to recover the entire sequence [11]. This means that m-sequences with low linear complexity are easy to recover; thus, nonlinear pseudorandom generators have become a new research direction [12,13,14,15]. Some classical nonlinear pseudorandom sequence generators are widely used and studied, such as the Geffe generator [16,17,18,19,20], JK flip-flop [21,22,23] and clock-control generator [24,25,26].
A chaotic system refers to the existence of irregular motion in a deterministic system, and its dynamic properties lead it to a secure cryptosystem design, such as unpredictability, randomness, sensitivity to the minute change in its initial value, ergodicity and complex structure [27]. Chaos may be realized by analog circuitry or finite precision computing in the design of algorithms and digital devices, which are termed analog chaotic systems or discrete chaotic maps, respectively [28].
Over the past few decades, designing ciphers based on the chaotic systems has attracted the attention of researchers and a huge number of papers published in the field of chaos-based cryptography [29,30,31,32,33,34]. Kocarev proposed that there are some deficiencies in the existing research:
- All chaotic-based cryptographic algorithms use dynamic systems defined on the set of real numbers and are therefore difficult to implement;
- The security and performance of chaos-based methods are rarely tested by researchers using standard tools of cryptography.
Hence, the impact of this research on conventional cryptography was not as far-reaching as expected [35]. Je Sen Teh et al. proposed that the realization problem of chaotic system exists until now [28].
A pseudo-random sequence generator (hereinafter referred to as PRSG) based on the nonlinear chaotic systems and the fractal functions is a research direction that has attracted attention and achieved practical results. Shafali proposed the pseudorandom sequence generator based on the cascaded fractal function [27]. Shouliang Li et al. proposed an implementation based on the discrete hyper-chaotic system [36]. The impact of finite precision in different hardware and software setups has received little attention. Even a cryptosystem based on the chaotic system will generate different key streams on different devices, which is caused by the calculation accuracy error of different devices. In order to overcome this problem, Lucas et al. introduced an efficient cryptosystem in which the chaotic logistic map and the Galois field theory are applied [37]. This technical path solves the problem of errors caused by computational precision. Computing binary sequences can yield the same and accurate results on different devices.
We propose a novel pseudorandom sequence generator based on the non-linear chaotic systems with the lambda fractal function. Furthermore, we design the data processor to hide the data characteristics of the ciphertext. The main contributions of this work are as follows:
- We propose a pseudo-random sequence generator based on the non-linear chaotic systems with the lambda fractal function.
- Sequences generated by PRSG pass 16 rigorous tests from the National Institute of Standards and Technology (NIST), which has developed the most authoritative pseudo-random sequence standard detection tool [38].
- We propose a data processor based on the matrix operations for the secondary encryption, which reduces the data characteristics of the ciphertext sequences, producing a more balanced distribution of 0 s and 1 s.
The rest of this paper is organized as follows. In Section 2, we introduce the theoretical foundation of the pseudo-random sequence generator and its typical solutions. In Section 3, we elaborate the design of the novel non-linear pseudo-random sequence generator and describe the mathematical foundations and effects of data processors. In Section 4, we demonstrate the random properties of pseudorandom sequences and test the performance of the data processor. In Section 5, we conclude the work of this paper.
2. Related Work
In this section, we describe the related work of this paper in three aspects: the concept and properties of sequences generators, an introduction to three typical non-linear sequence generators and an introduction to the PRSG based on the non-linear chaotic systems.
2.1. Random Sequence Generator
Random sequence generators can be divided into two categories based on the generating methods: physically implemented true random generators and computationally implemented pseudorandom generators. The true random sequence generator realized by physics is mainly based on components including electronic component noise [39,40], nuclear radiation [41,42] and vacuum energy fluctuation [43,44]. Such components have the disadvantages of inconvenient use and high manufacturing, testing and use costs, which limit their wide application.
Pseudorandom sequences are repeatable and have random statistical properties. Common pseudorandom generators mainly include m-sequence generators and nonlinear sequence generators. Formula (1) is the characteristic polynomial of the linear feedback shift register:
where represents the corresponding position of the elements, and represents the feedback state of the i-stage [45]. The m-sequence represents the longest linear feedback shift register sequence. An n-stage linear feedback shift register has a maximum of states, and except for the all 0 state, the m sequence has a maximum period of [45]. The primitive polynomial is the generator polynomial corresponding to the m sequence, which is only a minority among the polynomials. The linear complexity of the m-sequence is low, and the ciphertext encrypted by the m-sequence is easily recovered. Researchers have developed many nonlinear pseudorandom sequence generators based on LFSR, and we introduce the typical generators in detail in the next two sections.
2.2. Typical Nonlinear Sequence Generators
In this section, we mainly introduce the Geffe generator, the JK flip-flop and the clock-control generator.
Geffe generators and the JK flip-flop are filter generators, which are generally composed of one or more LFSRs and filter functions, wherein the filter functions are required to have better nonlinear properties. We show the Geffe generator and JK flip-flop generator in the Figure 1 and Figure 2.
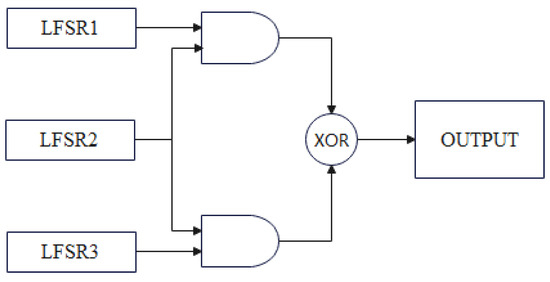
Figure 1.
Geffe generator, which use three LFSRs and three logic gates.
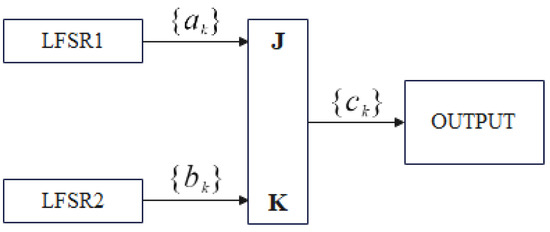
Figure 2.
J-K flip-flop, which use two LFSRs and one flip-flop.
The sequence from is directly input to the J terminal of the J-K flip-flop and the sequence from is input to the K terminal. When the gates of the two LFSRs are and , the period of the output sequence is .
The clock-control generator uses the sequence generated by one LFSR to control the shift of another LFSR [26], with the maximum period being . We show the clock-control generator in the Figure 3.

Figure 3.
Clock-control generator, which use two LFSRs and one logic gate.
2.3. Generators Based on the Non-Linear Chaotic Systems
Shafali proposed the pseudorandom sequence generator based on the cascaded fractal function [27], which is proposed by considering the phoenix and lambda fractal functions. Shafali performed several analyses on the generator, such as key sensitivity using NBCR analysis, entropy analysis, correlation analysis and autocorrelation analysis, proving that the generator has a large key space, fast key generation speed, high key sensitivity and strong randomness.
Shouliang Li et al. proposed the implementation based on the discrete hyper-chaotic system with an embedded cross-coupled topological structure, which exhibit a high level of the complexity of chaotic dynamics [36]. Shouliang Li et al. used the tool of the NIST SP800.22 and TestU01 to test the generator and proved that it has good randomness.
3. Method
In this section, we elaborate the implementation of the non-linear pseudo-random sequence generator, which mainly includes three aspects: generator design, data processor design and discussion of security.
3.1. Nonlinear Generator
In this section, we elaborate the implementation of the non-linear generator, which mainly includes three aspects: theoretical foundations, implementation and period estimation.
3.1.1. Theoretical Foundations
In general, the characteristic polynomial of LFSR is fixed and determined by the hardware design:
We hope that tap of the ith stage is random; that is, some data are randomly selected for calculating the feedback value. We obtain the formulas of AND operations:
where takes the values 0 and 1:
, and represent the entries involved in the AND operation. Hence, we can use AND operations to simulate tap functions and form generators of dynamic polynomials. We obtain the polynomial of the generator as:
where represents the feedback state of the i-stage and represents the state sequence of the register. We show the structure and data flow of the nonlinear pseudorandom sequence generator in Figure 5. Furthermore, we obtain:
The Lambda function is an alternative version of the equation for Julia fractals. While it is capable of creating the same Julia sets, the corresponding Mandelbrot version looks different. Julia sets are closely related to the well-known Mandelbrot set. Tan discusses the similarities between the Julia sets and the Mandelbrot sets [46]. The mathematical definition of the lambda fractal function is as follows [47]:
where , and we take for convenient implementation. We assume the use of 32-bit data, and the fractal function is as follows:
We convert to a binary number, and by default, the decimal point is at the far left and not displayed, which means that the value range of is from to . We use inverters to implement and perform the shift operations on the result of , leaving only the upper bits for the next calculation. Therefore, Formula (8) is not equivalent to . We show the lambda fractal function in Figure 4.
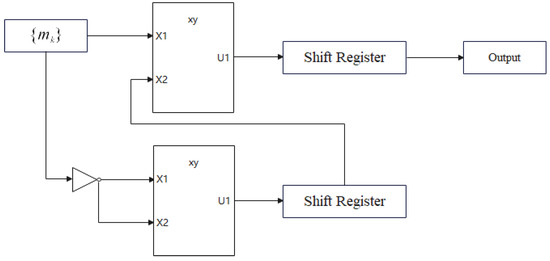
Figure 4.
Lambda fractal function, which use two multipliers, one inverter and two shift registers.
The output sequence is also reserved for high bits, which is consistent with the length of sequence . We use Algorithm A1 to describe the fractal function in the Appendix A.
3.1.2. Implementation
When the generator finishes running, record the state sequence of m-LFSR and shift the register at this time, as and , for the input of the next process. The process of the generator is as follows:
- The m-LFSR reads the and generates the new state sequence ;
- Input the to the lambda fractal function and output sequence ;
- The shift register reads and generates the new state sequence ;
- Output the state sequence and perform bitwise AND operation ; then, store in the register;
- Read the register state sequence and perform a bit-by-bit XOR operation to generate the new element ;
- The shift register is shifted to the left by one bit, and is used as the return value of the feedback function to enter the rightmost end;
- Output as the pseudorandom number.
The decryptor needs to know the and ; otherwise, it cannot decrypt, which means that and become the keys for valid communication. In Section 3.3, we will discuss how to use and . In Section 3.2.2, we will introduce how to securely synchronize and via the data processor. We used Algorithm A2 to describe the process of pseudorandom sequence generation in the Appendix A. We show the structure and data flow of the nonlinear pseudorandom sequence generator in Figure 5.
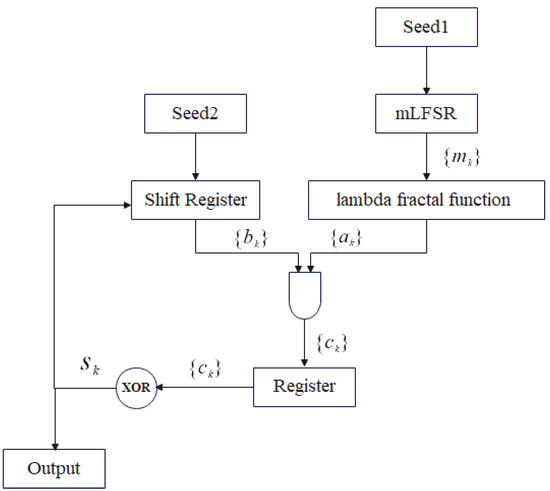
Figure 5.
Nonlinear pseudorandom sequence generator, which uses one m-sequence LFSR, two logic gates and two registers.
3.1.3. Period Estimation
We estimate the average period of the generator. The formula for the mathematical expectation of discrete variables is:
where represents the number of polynomials, represents the number of primitive polynomials, represents the number of nonprimitive polynomials and and are independent of each other. The m-sequence contains all states of the LFSR; thus, the variable X is uniformly distributed. We obtain:
and the length of the m-sequence is the constant , which represents the mathematical expectation . Therefore, we obtain the following formula:
We count the proportion of primitive polynomials in all polynomials within the 64th degree and plot them on the scatter plot shown in Figure 6.
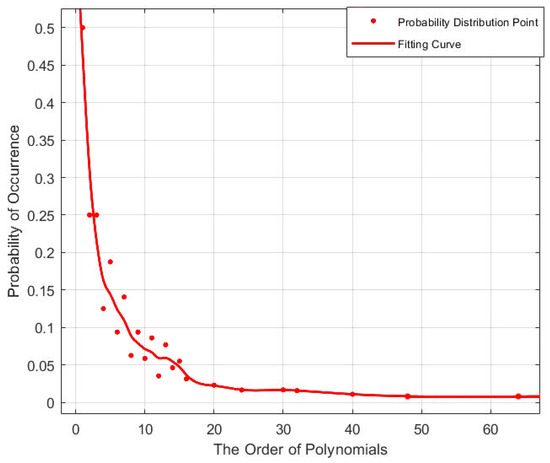
Figure 6.
Proportion of primitive polynomials in all polynomials within the 64th degree, used a curve for fitting.
We calculate the fitting function and draw a fitting curve as:
and obtain the expectation formula:
The approximation of Formula (13) is:
and the right side of the inequality is mono-increasing. In summary, we have proved the feasibility of the dynamic polynomials.
3.2. Data Processor
In this section, we describe the data processor from two aspects: the theoretical foundations and implementation.
3.2.1. Theoretical Foundations
At present, the one-way trapdoor function is a common encryption method. After the attacker obtains the ciphertext, it is difficult to recover the plaintext through data characteristics. For example, RSA is based on the difficulty of factoring large integers in number theory to ensure security [48,49]. Kocher et al. conducted security tests on the RSA cryptosystem [50,51].
Because the plaintext depends on a specific language to be generated, using pseudorandom sequence encryption, we face the problem that the encryptor cannot hide the characteristics of the plaintext data. We hope to use the data processor to prevent the attacker from deducing the plaintext from the data characteristics until the encryption method is broken. We elaborate on the rationale for this method below.
First, the plaintext suspicion degree formula is [52]:
where M is the plaintext space, m is the plaintext, C is the ciphertext space and c is the ciphertext.
Formula (16) expresses the degree of doubt about the corresponding plaintext space M while determining the ciphertext space C. When the ciphertext and plaintext distributions are independent of each other, and are the same. At this time, M is entirely untrustworthy, and the cryptographic system has perfect secrecy [53]. When the value of is 0, M is fully trusted and the ciphertext can determine the plaintext. Simplify the Formula (16) to obtain:
and we suppose that , where . Entry m and c obey uniform distribution; thus, we obtain:
where q is the number of plaintexts in the plaintext space. is 0, if . After determining all the mapping relations between the plaintext space and the ciphertext space, we can obtain ; however, this is almost impossible for attackers. As X approaches 0, the limit exists and is 0. When the attacker has obtained enough ciphertext, plaintext and ciphertext information is accumulated, the uncertainty of the plaintext is reduced and the plaintext can be determined by the ciphertext.
We classify the sequences in the ciphertext space and define the offset sequences in which the probability of an occurrence of 0 or 1 is lower than 25% or higher than 75%. The rest are represented as uniform sequences. We hope to map the offset sequences in C to the uniform sequence through a matrix algorithm to form the ciphertext space . C is invisible to the attacker and keeps as a subset of C so that the attacker is unable to establish a complete mapping from the plaintext space (M) to .
Information entropy is used to describe the uncertainty of information. The greater the information entropy, the higher the tension. The formula is as follows:
and if the same probability of 0 and 1 appears in the space, information entropy is the same, which is meaningless. Whether it is the decryptor or the attacker, a series of continuous data is obtained. Therefore, we use sequence information entropy to evaluate the uncertainty of information. For example, we set a sequence space consisting of 6-bit sequences, and the mathematical expectation of traversing the sequence entropy is:
If the sequence of the sum of the bit values of the sequence space of 3 is retained (for example, 111,000), there are only 20 sequences left in the sequence space, and the sequence entropy is as follows:
which shows the information entropy increasing for the sequence space. We extend this feature to the general situation. For a q-bit traversal sequence space, the mathematical expectation of its entropy is as follows:
When the offset sequences is mapped to a uniform sequence, the mathematical expectation of sequence entropy in the new space is:
Sequence information entropy has increased, which means that some information is added to the sequences.
3.2.2. Implementation
We used the Algorithm A3 to simulate the operation of the data processor in the Appendix A. We encrypted the plaintext using a pseudorandom sequence to form the initial ciphertext and then fill the matrix A with the ciphertext bits in order. The array controls the times of the left shift for the rows in matrix A, which can be used as the keys.
In the algorithm, we use the formula:
which changes the ratio of 0 s and 1 s in the matrix A. The proportion of the offset sequences gradually increases as the algorithm loops, if without the Formula (24).
Figure 7 shows matrix A of dimensions , which uses Algorithm A3 without the Formula (24). The horizontal axis is the value of the input sequence, traversing all sequences from 0x0001 to 0xffff; the vertical axis is the mathematical expectation of the offset sequences in matrix A in the 2000 left-shift operations.
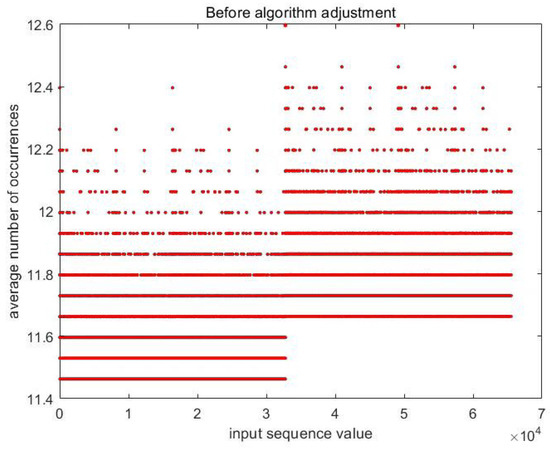
Figure 7.
Mathematical expectation of the offset sequences in matrix A in the 2000 left-shift operations without Formula (24). The horizontal axis is the value of the input sequence; the vertical axis is the mathematical expectation of the offset sequences.
In Figure 7, the average value of the offset sequences exceeds 11, which indicates that most of the sequences in the matrix are offset sequences at each iteration. After adding the Formula (24) to the algorithm, we show the result in Figure 8. The proportion of offset sequences drops from 74.375% to 16.5625%. The experiment simply demonstrated the importance of the feasibility of the method. In Section 4, we discuss extended experiments to further demonstrate the effectiveness and efficiency of the data processor.
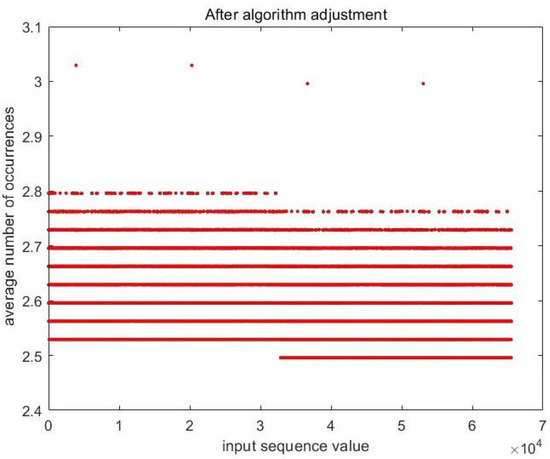
Figure 8.
Mathematical expectation of the offset sequences in matrix A, in the 2000 left-shift operations. The horizontal axis is the value of the input sequence; the vertical axis is the mathematical expectation of the offset sequences.
The communicating parties can agree on a special sequence, such as , to regard the number of required operations as the . The number of required operations refers to the number of shift and XOR operations required to make the ciphertext sequence completely coincide with the agreed sequence.
3.3. Security
and can be used as dynamic keys, which need the receiver and sender to synchronize before the communication starts. is a fixed value and the process of synchronizing and by communication parties needs to be encrypted by a data processor that is controlled by . After the communication ends, the receiver and the sender can agree on the for the next communication and update the existing communication.
Ensuring that authorized keys are not copied has been a recent concern of researchers. We set up the memory for the data as follows:
- Record the identifier of the communication object;
- Record the state of the nonlinear generator at the beginning and end of the communication, which are the seeds of this and the next loop, respectively;
- The nonlinear generator starts to work when it receives the communication requests and if the verification of the communication object fails, record the state of the linear generator and the object identifier sending the communication request.
We used the following example to reveal what the data do. We assumed that an attacker wants to use device R to illegally copy an access control card S. The process is as follows:
- S records the device identifier of the device requesting communication and then checks whether the device is legal;
- If R is not in the list of objects that are allowed to communicate, S does not respond to the communication request and then records the state of the nonlinear generator and the identifier of R;
- If R is in the list of objects allowed to communicate, S responds to the communication request and then updates the seeds with F (we cannot rule out that R is masquerading as the legitimate device F).
This is under the condition that R has obtained ; otherwise communication cannot be established. In the access control card S, the seeds related to F have been updated. If the attacker uses R and S to verify the identity on a legitimate device, the access control system do not pass the key verification of F. To re-enable this card, we need to delete the data in the card and distribute a new set of seeds.
A pseudorandom sequence generator based on m-sequence linear feedback shift registers (m-LFSR) is a common solution. There is mature research on the cracking of such pseudo-random generators, such as algebraic attacks [54,55], fast correlation attacks [56,57], known-plaintext attacks [58], etc. m-LFSR is also weak against rational approximation algorithms and Berlekamp–Massey algorithm attacks [59,60,61,62].
Siswanto et al. studied the randomness of m-sequence primitive polynomials [63]. They tested four m-sequence primitive polynomials using NIST tools, and only one m-sequence passed the test. The m-sequence has a large key space, but does not have good randomness. The nonlinear chaotic system has unpredictability, randomness, sensitivity to the minute change in its initial value, ergodicity and complex structure, which makes the above attack methods to be ineffective. Lucas et al. proposed that the pseudorandom sequence generator based on nonlinear chaotic system presents an astonishing key space of up to [37].
We briefly discuss the key distribution process ahead and use an example to explain the need to record this data. A secure and efficient key distribution process could be the direction of future work. In the next section, we will show the advantages of nonlinear chaotic systems in terms of randomness, and the generator can pass 16 rigorous NIST test items.
4. Results
We truncated three sequences with 125 MB from the data stream generated by the 128-bit nonlinear PRNG and ran all NIST test items. The NIST tools and specific content of the test items can be found at https://csrc.nist.gov/projects/random-bit-generation (accessed on 29 September 2022). We show the results of the NIST test items in Table 1. We need to declare that the generator was simulated by the computing system and the sequences were not from a real 128-bit generator. If the p-value was more than 0.001, it could be considered as passing the test.

Table 1.
The results of the NITST test, where we used three sequences with 125 MB from the data stream generated by the 128-bit nonlinear PRNG and ran all NIST test items.
The experimental results show that the nonlinear pseudorandom sequence generator based on the dynamic polynomials is effective and efficient and the generated sequences pass 16 rigorous NIST test items.
In Section 3.2.2, we preliminarily demonstrated the effectiveness of Algorithm A3 through the experiment based on a 16-order matrix. We extensively tested the effectiveness of the data processor on the range of 3000-order matrices, and the results are shown in Figure 9 and Figure 10. The input is the sequences of all 1 s, the horizontal axis is the order of the matrices and the vertical axis is the occurrence probability of the offset sequence in 5000 loops.
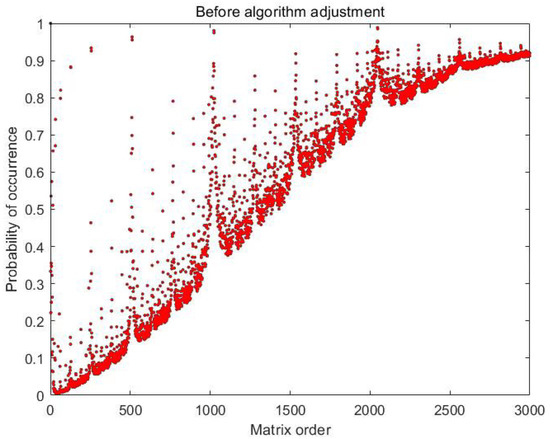
Figure 9.
Occurrence probability of the offset sequence in the range of 3000-order matrices, where the horizontal axis is the order of the matrices and the vertical axis is the occurrence probability of the offset sequence in 5000 loops, without Formula (24).
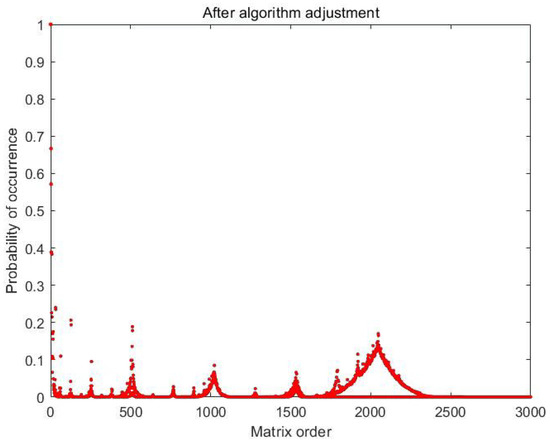
Figure 10.
Occurrence probability of the offset sequences in the range of 3000-order matrices, where the horizontal axis is the order of the matrices and the vertical axis is the occurrence probability of the offset sequences in 5000 loops.
In Figure 9, the occurrence probability of the offset sequence has peaks, which can be represented as:
where , represents the operation of round down and represents the position of the peak. We added Formula (24) to Algorithm A3 and obtained the result in Figure 10.
In Figure 9, there is a vague relationship between the peak width and order of matrices:
if and only if . Otherwise, we obtain the formula as follows:
which means that the peak width is not monotonically increasing.
Thus, in the extended experiments, we found that the 16-order matrix did not have good data processing capabilities, which almost made us miss the important results of this paper. The proportion of offset sequences in the matrix with better performance was less than 3‰. We show the result in Figure 10. A limitation of this study is the lack of clarity behind the reason for this phenomenon.
5. Conclusions
In this study, we proposed a novel nonlinear pseudorandom sequence generator based on the nonlinear chaotic systems, which is constructed by the fractal function. Furthermore, we design a data processing matrix to hide the data characteristics of the sequence and enhance the randomness. We experimentally verified the effectiveness and efficiency of the generator of the nonlinear chaotic systems, which passed 16 rigorous test items from NIST. Furthermore, we briefly discussed how to ensure the security of the system through dynamic data and provided an example of access control card replication to facilitate understanding of the method. In extended experiments, we further demonstrated the better performance of the data processor in reducing offset sequences, which laid a solid foundation for subsequent research.
Despite the limitations of this study, the safety of the generator is not affected. The generator had a wide range of application directions, such as identity authentication, secret sharing, data anti-counterfeiting, information interaction and data transmission. We will focus on the adaptation of the method to usage scenarios and operating devices in the future.
Author Contributions
Methodology, C.W.; Resources, C.C.; Validation, F.Y.; Writing—original draft, Y.F.; Writing—review and editing, H.W. and H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research is partially supported by the Hong Kong Scholars Program with No. 2021-101, in part by the National Natural Science Foundation of China under Grant No. 62002377, 62072424.
Data Availability Statement
The code of this paper can be found at https://github.com/lxrzlyr/Nonlinear-pseudo-random-sequence-generator.git (accessed on 28 August 2022). Not applicable of data.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| Initial input to the generator, which are the sequences of booleans | |
| Characteristic polynomial of the linear feedback shift register | |
| The feedback state of i-stage | |
| The greatest common factor of a and b | |
| Complex parameters | |
| Sequence | |
| Mathematical expectations for X | |
| The plaintext suspicion degree | |
| Space of plaintext and ciphertext | |
| Sequences of plaintext and ciphertext | |
| The mathematical expectation of traversing the sequence entropy | |
| The position and width of the peak |
Appendix A. Algorithm
| Algorithm A1: The Fractal Function |
 |
| Algorithm A2: The Nonlinear Pseudorandom Sequence Generator |
 |
| Algorithm A3: Data Processor |
 |
Appendix B. Code
The code of this paper can be found at https://github.com/lxrzlyr/Nonlinear-pseudo-random-sequence-generator.git accessed on 29 September 2022.
References
- Topuzoğlu, A.; Winterhof, A. Pseudorandom sequences. In Topics in Geometry, Coding Theory and Cryptography; Springer: Berlin/Heidelberg, Germany, 2006; pp. 135–166. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Shannon, C.E. Communication theory of secrecy systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Sarwate, D.V.; Pursley, M.B. Crosscorrelation properties of pseudorandom and related sequences. Proc. IEEE 1980, 68, 593–619. [Google Scholar] [CrossRef]
- Shamir, A. On the generation of cryptographically strong pseudorandom sequences. ACM Trans. Comput. Syst. (TOCS) 1983, 1, 38–44. [Google Scholar] [CrossRef]
- Blum, M.; Micali, S. How to generate cryptographically strong sequences of pseudorandom bits. SIAM J. Comput. 1984, 13, 850–864. [Google Scholar] [CrossRef]
- Ko, K.I. On the notion of infinite pseudorandom sequences. Theor. Comput. Sci. 1986, 48, 9–33. [Google Scholar] [CrossRef]
- Bardell, P.H. Analysis of cellular automata used as pseudorandom pattern generators. In Proceedings of the International Test Conference, Washington, DC, USA, 10–14 September 1990; pp. 762–768. [Google Scholar]
- Gong, G.; Berson, T.A.; Stinson, D.R. Elliptic curve pseudorandom sequence generators. In Proceedings of the International Workshop on Selected Areas in Cryptography, Kingston, ON, Canada, 9–10 August 1999; pp. 34–48. [Google Scholar]
- Zierler, N. Linear recurring sequences. J. Soc. Ind. Appl. Math. 1959, 7, 31–48. [Google Scholar] [CrossRef]
- Massey, J. Shift-register synthesis and BCH decoding. IEEE Trans. Inf. Theory 1969, 15, 122–127. [Google Scholar] [CrossRef]
- Key, E. An analysis of the structure and complexity of nonlinear binary sequence generators. IEEE Trans. Inf. Theory 1976, 22, 732–736. [Google Scholar] [CrossRef]
- Persons, C.; Brandon, M. Linear and Nonlinear Correlators for Pseudorandom Signal Detection: A Theoretical and Experimental Study of the Output Characteristics of Correlators for Active Sonar Systems; Technical Report; Navy Electronics Lab: San Diego, CA, USA, 1963. [Google Scholar]
- Simpson, H. A sampled-data nonlinear filter. In Proceedings of the Institution of Electrical Engineers; IET Digital Library: London, UK, 1965; Volume 112, pp. 1187–1196. [Google Scholar]
- Lewis, T.G.; Payne, W.H. Generalized feedback shift register pseudorandom number algorithm. J. ACM 1973, 20, 456–468. [Google Scholar] [CrossRef]
- Zeng, K.; Yang, C.H.; Wei, D.Y.; Rao, T. Pseudorandom bit generators in stream-cipher cryptography. Computer 1991, 24, 8–17. [Google Scholar] [CrossRef]
- Bensikaddour, E.H.; Bentoutou, Y.; Taleb, N. Satellite image encryption method based on AES-CTR algorithm and GEFFE generator. In Proceedings of the 2017 8th International Conference on Recent Advances in Space Technologies (RAST), Istanbul, Turkey, 19–22 June 2017; pp. 247–252. [Google Scholar]
- Salman, Z.I. Attacking of Geffe Generator by Solving Linear Equations System of the Generated Sequence. J. Univ. Babylon 2014, 22, 1516–1524. [Google Scholar]
- Din, M.; Bhateja, A.K.; Ratan, R. Cryptanalysis of geffe generator using genetic algorithm. In Proceedings of the Third International Conference on Soft Computing for Problem Solving, New Delhi, India, 17–24 October 2014; pp. 509–515. [Google Scholar]
- Khader, A.S.; Lai, D. Preventing man-in-the-middle attack in Diffie-Hellman key exchange protocol. In Proceedings of the 2015 22nd International Conference on Telecommunications (ICT), Sydney, Australia, 27–29 April 2015; pp. 204–208. [Google Scholar]
- Elineau, G.; Wiesbeck, W. A new JK flip-flop for synchronizers. IEEE Trans. Comput. 1977, 26, 1277–1279. [Google Scholar] [CrossRef]
- Hirota, K.; Pedrycz, W. Designing sequential systems with fuzzy JK flip-flops. Fuzzy Sets Syst. 1991, 39, 261–278. [Google Scholar] [CrossRef]
- Law, F.K.; Uddin, M.R.; Chen, A.T.C.; Nakarmi, B. Positive edge-triggered JK flip-flop using silicon-based micro-ring resonator. Opt. Quantum Electron. 2020, 52, 1–12. [Google Scholar] [CrossRef]
- Zenner, E. On the efficiency of the clock control guessing attack. In Proceedings of the International Conference on Information Security and Cryptology, Melbourne, Australia, 3–5 July 2002; pp. 200–212. [Google Scholar]
- Sadkhan, S.B.; Hamza, R.M. A study of Algebraic Attack and proposed developed clock control stream cipher. J. Babylon Univ. Appl. Sci. 2014, 22, 622–633. [Google Scholar]
- Sadkhan, S.B. A proposed Development of Clock Control Stream Cipher based on Suitable Attack. In Proceedings of the 2020 1st. Information Technology to Enhance e-Learning and Other Application (IT-ELA), Baghdad, Iraq, 12–13 July 2020; pp. 165–170. [Google Scholar]
- Agarwal, S. Designing a pseudo-random bit generator using generalized cascade fractal function. Chaos Theory Appl. 2021, 3, 11–19. [Google Scholar] [CrossRef]
- Teh, J.S.; Alawida, M.; Sii, Y.C. Implementation and practical problems of chaos-based cryptography revisited. J. Inf. Secur. Appl. 2020, 50, 102421. [Google Scholar] [CrossRef]
- Yang, T.; Wu, C.W.; Chua, L.O. Cryptography based on chaotic systems. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1997, 44, 469–472. [Google Scholar] [CrossRef]
- Baptista, M. Cryptography with chaos. Phys. Lett. A 1998, 240, 50–54. [Google Scholar] [CrossRef]
- Dachselt, F.; Schwarz, W. Chaos and cryptography. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2001, 48, 1498–1509. [Google Scholar] [CrossRef]
- Muthukumar, P.; Balasubramaniam, P. Feedback synchronization of the fractional order reverse butterfly-shaped chaotic system and its application to digital cryptography. Nonlinear Dyn. 2013, 74, 1169–1181. [Google Scholar] [CrossRef]
- Hsiao, H.I.; Lee, J. Fingerprint image cryptography based on multiple chaotic systems. Signal Process. 2015, 113, 169–181. [Google Scholar] [CrossRef]
- Akgul, A.; Arslan, C.; Aricioglu, B. Design of an interface for random number generators based on integer and fractional order chaotic systems. Chaos Theory Appl. 2019, 1, 1–18. [Google Scholar]
- Kocarev, L. Chaos-based cryptography: A brief overview. IEEE Circuits Syst. Mag. 2001, 1, 6–21. [Google Scholar] [CrossRef]
- Li, S.; Liu, Y.; Ren, F.; Yang, Z. Design of a high throughput pseudo-random number generator based on discrete hyper-chaotic system. IEEE Trans. Circuits Syst. II Express Briefs 2022. [Google Scholar] [CrossRef]
- Nardo, L.G.; Nepomuceno, E.G.; Bastos, G.T.; Santos, T.A.; Butusov, D.N.; Arias-Garcia, J. A reliable chaos-based cryptography using Galois field. Chaos Interdiscip. J. Nonlinear Sci. 2021, 31, 091101. [Google Scholar] [CrossRef]
- Olver, F.W.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. NIST Handbook of Mathematical Functions Hardback and CD-ROM; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Fischer, V.; Drutarovskỳ, M. True random number generator embedded in reconfigurable hardware. In Proceedings of the International Workshop on Cryptographic Hardware and Embedded Systems, Redwood Shores, CA, USA, 13–15 August 2002; pp. 415–430. [Google Scholar]
- Holman, W.T.; Connelly, J.A.; Dowlatabadi, A.B. An integrated analog/digital random noise source. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1997, 44, 521–528. [Google Scholar] [CrossRef]
- Park, K.H.; Park, S.M.; Choi, B.G.; Kim, J.B.; Son, K.J. High rate true random number generator using beta radiation. AIP Conf. Proc. 2020, 2295, 020020. [Google Scholar]
- Huo, J.; Xu, Y.; Chen, Y.; Cui, W.; Li, W.; Zhang, Z.; Han, D.; Wang, Y.; Wang, J. An X-ray CCD signal generator with true random arrival time. Nucl. Electron. Detect. Technol. 2011, 31, 174–177. [Google Scholar]
- Zheng, Z.; Zhang, Y.; Huang, W.; Yu, S.; Guo, H. 6 Gbps real-time optical quantum random number generator based on vacuum fluctuation. Rev. Sci. Instrum. 2019, 90, 043105. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Chng, B.; Kurtsiefer, C. Random numbers from vacuum fluctuations. Appl. Phys. Lett. 2016, 109, 041101. [Google Scholar] [CrossRef]
- Cusick, T.W.; Stanica, P. Chapter 2—Fourier Analysis of Boolean Functions. In Cryptographic Boolean Functions and Applications, 2nd ed.; Cusick, T.W., Stanica, P., Eds.; Academic Press: Cambridge, MA, USA, 2017; pp. 7–29. [Google Scholar] [CrossRef]
- Lei, T. Similarity between the Mandelbrot set and Julia sets. Commun. Math. Phys. 1990, 134, 587–617. [Google Scholar] [CrossRef]
- Peitgen, H.O.; Jürgens, H.; Saupe, D. Chaos and Fractals: New Frontiers of Science; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Shand, M.; Vuillemin, J. Fast implementations of RSA cryptography. In Proceedings of the IEEE 11th Symposium on Computer Arithmetic, Windsor, ON, Canada, 29 June–2 July 1993; pp. 252–259. [Google Scholar]
- Wiener, M.J. Cryptanalysis of short RSA secret exponents. IEEE Trans. Inf. Theory 1990, 36, 553–558. [Google Scholar] [CrossRef]
- Boneh, D. Twenty years of attacks on the RSA cryptosystem. Not. AMS 1999, 46, 203–213. [Google Scholar]
- Kocher, P.C. Timing attacks on implementations of Diffie-Hellman, RSA, DSS, and other systems. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 18–22 August 1996; pp. 104–113. [Google Scholar]
- Zhang, Z. Fundamentals of Modern Cryptography; Beijing University of Posts and Telecommunications Press: Beijing, China, 2004. [Google Scholar]
- Yan, S.Y. Computational Number Theory and Modern Cryptography; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Courtois, N.T.; Meier, W. Algebraic attacks on stream ciphers with linear feedback. In Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, Warsaw, Poland, 4–8 May 2003; pp. 345–359. [Google Scholar]
- Courtois, N.T.; O’Neil, S.; Quisquater, J.J. Practical algebraic attacks on the Hitag2 stream cipher. In Proceedings of the International Conference on Information Security, Orlando, FL, USA, 13–16 July 2009; pp. 167–176. [Google Scholar]
- Meier, W.; Staffelbach, O. Fast correlation attacks on certain stream ciphers. J. Cryptol. 1989, 1, 159–176. [Google Scholar] [CrossRef]
- Chose, P.; Joux, A.; Mitton, M. Fast correlation attacks: An algorithmic point of view. In Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, Amsterdam, The Netherlands, 28 April–2 May 2002; pp. 209–221. [Google Scholar]
- Biham, E.; Kocher, P.C. A known plaintext attack on the PKZIP stream cipher. In Proceedings of the International Workshop on Fast Software Encryption, Leuven, Belgium, 14–16 December 1994; pp. 144–153. [Google Scholar]
- Klapper, A.; Goresky, M. Cryptanalysis based on 2-adic rational approximation. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 27–31 August 1995; pp. 262–273. [Google Scholar]
- Carlet, C.; Feng, K. An infinite class of balanced functions with optimal algebraic immunity, good immunity to fast algebraic attacks and good nonlinearity. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Melbourne, Australia, 7–11 December 2008; pp. 425–440. [Google Scholar]
- Aqel, M.J.; Alqadi, Z.A.; El Emary, I.M. Analysis of stream cipher security algorithm. J. Inf. Comput. Sci. 2007, 2, 288–298. [Google Scholar]
- Jiang, H.; Li, C.; Fan, J. Research on Pseudo-Random Characteristics of New Random Components. In Proceedings of the 2019 International Conference on Artificial Intelligence and Advanced Manufacturing (AIAM), Dublin, Ireland, 17–19 October 2019; pp. 163–167. [Google Scholar] [CrossRef]
- Siswanto, M.; Witjaksono, G.; Soeheila, M.; Hamdan, Z. Study on the effects of characteristic polynomial in LFSR for randomness quality. In Proceedings of the International Conference on Advanced Science, Engineering and Information Technology (ICASEIT 2011), Daegu, Korea, 20–22 April 2011. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).