Soliton Solution of the Peyrard–Bishop–Dauxois Model of DNA Dynamics with M-Truncated and β-Fractional Derivatives Using Kudryashov’s R Function Method

Abstract

In this paper, the Peyrard–Bishop–Dauxois model of DNA dynamics is discussed along with the fractional effects of the M-truncated derivative and $\beta$-derivative. The Kudryashov’s R method was applied to the model in order to obtain a solitary wave solution. The obtained solution is explained graphically and the fractional effects of the $\beta$ and M-truncated derivatives are also shown for a better understanding of the model.

1. Introduction

The study of DNA structures is essential in various fields of science. The main purpose of this paper is to investigate the soliton oscillations for the fractional dynamical Peyrard–Bishop–Dauxois (PBD) model of DNA dynamics. The governing equation of the PBD model is a nonlinear evolution equation. The Peyrard–Bishop (PB) model for DNA denaturation was presented in 1989 [1]. DNA denaturation is the process of breaking down the DNA in such a way that the hydrogen bonds in the DNA break to unwind the double strands. The proposed model was a simple yet useful extension of the Ising models, which were previously being used to investigate DNA denaturation. Peyrard and Bishop further developed and improved the PB model along with Dauxois [2,3,4,5].

The Peyrard–Bishop–Dauxois model (PBD) model has been successfully used in many fruitful studies. Theodorakopoulos [6] used the PBD model in his study of bubble formation during the denaturation process. Hillebrand et al. [7] used numerical simulations to present a study on the bubbles’ lifetime using the PBD model. Ares et al. [8] applied the same model to present a theoretical investigation of bubbles formed during DNA melting. They showed that the theoretical results matched with the previously reported experimental results. Some analytic results concerning the lengths of the thermal openings in the DNA structure were presented by Ares and Kalosakas in [9]. The simple yet effective PBD nonlinear model was found to be helpful in investigating the influence of heterogeneity on the DNA structure [10,11]. More results on the dynamical and statistical properties of the DNA structure were presented in [12,13,14,15,16,17,18].

The complex helical double-stranded structure of DNA molecules has been an interest of research for biologists, physicists and mathematicians for many years. In recent years, different useful extensions and modifications of the PBD dynamical model have been proposed, owing to its applicability and effectiveness in explaining many physical processes [19,20,21]. The thermal excitations in DNA molecules give rise to solitonic vibrations. The solitons for the nonlinear vibrations of the DNA molecules were computed in [22,23] in order to have a deeper insight into the dynamical properties. The PBD model has also been explored using the ansatz technique [24], improved tan($\frac{\varphi }{2}$)-expansion technique, exp$(-\varphi (\eta \left)\right)$-expansion technique, generalized $\left(\frac{G^{\prime }}{G}\right)$-expansion technique and the exp-function technique [25].

At the same time, fractional calculus has become very popular during the last two decades. The fractional differential equations are the generalized form of the standard integer order differential equations. Over the years, different definitions of the fractional order derivatives have been proposed, which have been successfully utilized in several applications. The most widely used definitions include the definitions in Captuto’s sense and Riemann–Liouville’s sense. However, various studies have shown that the these previously well-accepted definitions have some limitations. The Caputo derivative is not able to deal with the problems with a singular kernel, whereas the Riemann–Liouville derivative has a seemingly more serious problem, i.e., it is unable to yield the derivative of a constant equal to zero. Such limitations have prompted researchers for more generalized definitions with a non-integer order.

Atangana et al. [26] introduced a fractional derivative that exhibits many useful mathematical properties. The definition is now commonly referred to as the $\beta$-derivative. Another recent attempt to define the fractional derivative was made by using the definition of the Mittag–Leffler function [27]. Both of these definitions have been proven to satisfy the basic mathematical laws of differential calculus, which encourages further explorations using these newly defined concepts. Recently, the fractional order PBD model was investigated [28] considering the definition of the $\beta$-derivative. The authors computed the traveling wave solutions of the considered model using different methods, keeping the fractional derivative as the $\beta$-derivative.

The M-truncated and $\beta$-fractional derivatives are recently developed definitions of fractional derivatives. Both proposed definitions are generalized forms of the classical integer order derivative and satisfy many useful mathematical properties exhibited by the classical integer order derivative. For example, the fractional derivative of a constant is zero according to these two definitions, which is in line with results of the classical calculus. The definition of the $\beta$-fractional derivative is simple and easily applicable. The M-truncated derivative involves the use of an extra parameter due to the involvement of Mittag–Leffler expansion, but it has been established as a good version of the fractional derivative because it unifies the fractional derivatives proposed by Katugampola, Khalil et al. and Sousa et al.

The aim of this work is to present a comparison of the solution of the fractional order PBD model for the M-truncated derivative and the $\beta$-derivative. The solution was computed using a recent effective technique, namely, the Kudryashov’s R function method. The main objective of the work was then achieved by presenting a graphical comparison of the evolution in the shape of the constructed soliton for both definitions of the fractional derivative. It is observed that the conservations laws for the fractional PBD model have not been discussed in the literature to the best of our knowledge. Although this topic is beyond the scope of the current work, it will be useful to present theoretical investigations on the conservations laws of the considered model in future work.

The paper is organized as follows: in Section 2, the governing model is explained, while in Section 3, the definitions of the $\beta$-derivative and M-truncated derivative are given. Kudryashov’s R function method is described in Section 4. The application of the method is presented in Section 5. The fractional effects on the obtained solution are graphically illustrated in Section 6. The whole work is concluded in Section 7.

2. Governing Model

The Hamiltonian for the PBD model is considered by using the Morse’s potential, which can be expressed as

$$V_p(U_q-{\mu }_q)=r{[exp(-u(U_q-{\mu }_q))-1]}^2.$$

(1)

The right side of Equation (1) is Morse’s potential, where u and r denote the width and depth of Morse’s potential, respectively. $U_q$, ${\mu }_q$ denote the nucleotides’ displacements. The expression for the Hamiltonian for hydrogen links can be expressed [23] as

$$G\left(U\right)=\frac{1}{2n}{u}_q^2+\frac{{\psi }_1}{2}{\Delta }^2{U}_q+\frac{{\psi }_2}{4}{\Delta }^4{U}_q+\tau {(e^{-u\sqrt{2}{U}_q}-1)}^2,$$

(2)

where ${\psi }_1$ is the strength of linear coupling, ${\psi }_2$ is the strength of nonlinear coupling and $u_q=n\frac{\partial U_q}{\partial t}$ denotes the momentum corresponding to the displacement $U_q$.

Equation (2) expresses the Hamiltonian for the description of the stretch in the hydrogen bonds of the DNA. This relation is essential for the derivation of a nonlinear evolution equation for the dynamical behavior of DNA. Initiating with Equation (2), the standard continuum approximation is used to derive an equation of motion, where the independent variable U denotes the displacement. As a result, the nonlinear evolution equation for DNA dynamics [23] can be written as

$$U_{tt}-({\mathsf{\Psi }}_1+3{\mathsf{\Psi }}_2{\left(U_x\right)}^2{U}_{xx}-2pr{e}^{-pU}(e^{-pU}-1)=0,$$

(3)

where ${\mathsf{\Psi }}_1=\frac{{\psi }_1}{n}{s}^2$, ${\mathsf{\Psi }}_2=\frac{{\psi }_2}{n}{s}^4$, $r=\frac{\tau }{n}$, $p=\sqrt{2}u$ and $s=$ the inter-site nucleotide distance.

The fractional order model corresponding to Equation (3) is discussed in [28] using the $\beta$-derivative. In this research work, the following forms of the PBD model are to be studied.

The PBD model with the $\beta$-derivative is considered as

$$D_t^{2\beta }\left(U\right)-({\mathsf{\Psi }}_1+3{\mathsf{\Psi }}_2{\left(D_x^{\beta }\left(U\right)\right)}^2)D_x^{2\beta }\left(U\right)-2pr{e}^{-pU}(e^{-pU}-1)=0.$$

(4)

The PBD model with the M-truncated derivative is considered as

$$D_{M,t}^{2\beta ,\alpha }\left(U\right)-({\mathsf{\Psi }}_1+3{\mathsf{\Psi }}_2{\left(D_{M,x}^{\beta ,\alpha }\left(U\right)\right)}^2)D_{M,x}^{2\beta ,\alpha }\left(U\right)-2pr{e}^{-pU}(e^{-pU}-1)=0.$$

(5)

Both derivatives are explained in the next section.

3. Important Definitions

3.1. $\beta$-Derivative

The $\beta$-derivative [26] of a function l, where $l\left(t\right):[a,\infty ]\to R$, is given as

$$D_t^{\beta }\left(l\left(t\right)\right)=\underset{\sigma \to 0}{lim}\frac{l(t+\sigma {(t+\frac{1}{\mathsf{\Gamma }\left(\beta \right)})}^{1-\beta })-l\left(t\right)}{\sigma },\beta \in (0,1].$$

(6)

The following properties are satisfied for $\beta$-differentiable functions $l\left(t\right)$ and $m\left(t\right)$, with $\beta \in (0,1]$ [26,29].

$$\begin{array}{ccc}\hfill D_t^{\beta }(cl\left(t\right)+dm\left(t\right))& =& c{D}_t^{\beta }\left(l\left(t\right)\right)+d{D}_t^{\beta }\left(m\left(t\right)\right),\forall c,d\in R,\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill D_t^{\beta }(l\left(t\right)\times m\left(t\right))& =& m\left(t\right)D_t^{\beta }\left(l\left(t\right)\right)+l\left(t\right)D_t^{\beta }\left(m\left(t\right)\right),\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill D_t^{\beta }\left(\frac{l\left(t\right)}{m\left(t\right)}\right)& =& \frac{m\left(t\right)D_t^{\beta }\left(l\left(t\right)\right)-l\left(t\right)D_t^{\beta }\left(m\left(t\right)\right)}{{\left(m\left(t\right)\right)}^2},\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill D_t^{\beta }\left(l\left(t\right)\right)& =& \frac{d\left(l\right(t\left)\right)}{dt}{\left(t+\frac{1}{\mathsf{\Gamma }\left(\beta \right)}\right)}^{1-\beta }.\hfill \end{array}$$

(10)

The $\beta$-fractional integral can be expressed by the relation [26]

$$I_t^{\beta }h\left(t\right)={\int }_0^t{\left(y+\frac{1}{\mathsf{\Gamma }\left(\beta \right)}\right)}^{\beta -1}h\left(y\right)dy.$$

(11)

3.2. M-Truncated Derivative

The M-truncated derivative [27] of a function l, where $l\left(t\right):[0,\infty ]\to R$, is given as

$$D_{M,t}^{\beta ,\alpha }\left(l\left(t\right)\right)=\underset{\sigma \to 0}{lim}\frac{l\left(t{}_j{E}_{\alpha }\left(\sigma t^{-\beta }\right)\right)-l\left(t\right)}{\sigma },t>0,\beta \in (0,1],\alpha >0,$$

(12)

where ${}_j{E}_{\alpha }(.)$, $\alpha >0$ is a truncated one-parameter Mittag–Leffler function.

The following properties are satisfied for functions $l\left(t\right)$ and $m\left(t\right)$, which are $\beta$-derivable, with $\beta \in (0,1]$ and $\alpha >0$ [30].

$$\begin{array}{ccc}\hfill D_{M,t}^{\beta ,\alpha }(cl\left(t\right)+dm\left(t\right))& =& c{D}_{M,t}^{\beta ,\alpha }\left(l\left(t\right)\right)+d{D}_{M,t}^{\beta ,\alpha }\left(m\left(t\right)\right),\forall c,d\in R,\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill D_{M,t}^{\beta ,\alpha }(l\left(t\right)\times m\left(t\right))& =& m\left(t\right)D_{M,t}^{\beta ,\alpha }\left(l\left(t\right)\right)+l\left(t\right)D_{M,t}^{\beta ,\alpha }\left(m\left(t\right)\right),\hfill \end{array}$$

(14)

$$\begin{array}{ccc}\hfill D_{M,t}^{\beta ,\alpha }\left(\frac{l}{m}\right)\left(t\right)& =& \frac{m\left(t\right)D_{M,t}^{\beta ,\alpha }\left(l\left(t\right)\right)-l\left(t\right)D_{M,t}^{\beta ,\alpha }\left(m\left(t\right)\right)}{{\left(m\left(t\right)\right)}^2},\hfill \end{array}$$

(15)

$$\begin{array}{ccc}\hfill D_{M,t}^{\beta ,\alpha }(l\circ m)\left(t\right)& =& l^{\prime }\left(m\left(t\right)\right)D_{M,t}^{\beta ,\alpha }m\left(t\right),\hfill \end{array}$$

(16)

$$\begin{array}{ccc}\hfill D_{M,t}^{\beta ,\alpha }\left(t^{\psi }\right)& =& \psi t^{\psi -\alpha },\psi \in R.\hfill \end{array}$$

(17)

Let h be a function that is defined in $(c,\infty ]$, where $c\ge 0$, and fix some $0<\beta \le 1$.

The left M-truncated integral can be expressed by the relation [27]

$${}_M{I}_c^{\beta ,\alpha }h\left(t\right)={\int }_c^{t}h\left(y\right)d_{\gamma }(y,c)=\mathsf{\Gamma }(\alpha +1){\int }_c^{t}h\left(y\right){(y-c)}^{\beta -1}dy,$$

(18)

with $d_{\gamma }(y,c)=\mathsf{\Gamma }(\alpha +1){(y-c)}^{\beta -1}$.

The right M-truncated integral is expressed by the relation

$${}_d^{\beta ,\alpha }{I}_{M}h\left(t\right)={\int }_t^{d}h\left(y\right)d_{\gamma }(d,y)=\mathsf{\Gamma }(\alpha +1){\int }_t^{d}h\left(y\right){(d-y)}^{\beta -1}dy.$$

(19)

4. Description of Kudryashov’s R Function Method [31]

Kudryashov’s R function method [31] is a recently developed mathematical technique for the construction of traveling wave solutions of partial differential equations.

The R function can be written as

$$R\left(\xi \right)=\frac{1}{f{e}^{\left(\delta \xi \right)}+g{e}^{(-\delta \xi )}},$$

(20)

which satisfies the differential equation

$$R_{\xi }^2=\delta R^2(1-\omega R^2),\mathrm{where}\omega =4fg.$$

(21)

Here, f, g and $\delta$ are parameters of the R function. The value of $\omega$ depends on the parameters f and g in the definition of the R function. This definition of the R function allows us to express the nonlinear differential equation in terms of R and $R_{\xi }$, thus simplifying the equation to a great extent to obtain the exact solution. This is applicable to a large class of integrable nonlinear differential equations. Without losing generality, $\omega$ can be taken as 1.

In this study, this method is applied due to its novelty, generality and simplicity in solving the governing nonlinear model.

According to the Kudryashov’s R function method [31], firstly, a suitable wave transformation is used to reduce a nonlinear partial differential of the form

$$P(U,U_x,U_{xt},U_t,\dots )=0,$$

(22)

to an ODE as

$$D(v,v_{\xi },v_{\xi \xi },v_{\xi \xi \xi },\dots )=0.$$

(23)

The value of N is determined using the homogeneous balance, and then a solution is assumed in the form

$$v={\Sigma }_{l=0}^N{C}_{l}R{\left(\xi \right)}^l.$$

(24)

In order to obtain a polynomial in R or in R and $R_{\xi }$, Equation (24) and the derivatives of R are put into Equation (23).

When the polynomial involves R, the powers of R are collected, whereas, in the case of R and $R_{\xi }$, the collection of powers is carried out accordingly. The resulting system of equations can be solved to determine the values of the unknown parameters and $C_l$’s parameter, which can be used to determine the solution of Equation (22).

5. Mathematical Analysis

The fractional model PBD model is considered, as described by Equations (1) and (4). In order to solve these nonlinear equations, the transformation $U(x,t)=v\left(\xi \right)$ is considered, where

$$\begin{array}{ccc}\hfill \xi & =& \frac{1}{\beta }{\left(x+\frac{1}{\mathsf{\Gamma }\left(\beta \right)}\right)}^{\beta }-\frac{\eta }{\beta }{\left(t+\frac{1}{\mathsf{\Gamma }\left(\beta \right)}\right)}^{\beta },(\mathrm{for}\beta -\mathrm{derivative}),\hfill \end{array}$$

(25)

$$\begin{array}{ccc}\hfill \xi & =& \frac{\mathsf{\Gamma }(\alpha +1)}{\beta }(x^{\beta }-\eta t^{\beta }),(\mathrm{for}\mathrm{M}-\mathrm{truncated}\mathrm{derivative}).\hfill \end{array}$$

(26)

Using these transformations, Equations (1) and (4) are reduced to the following ODE.

$${\eta }^2{v}^{″}-({\mathsf{\Psi }}_1+3{\mathsf{\Psi }}_2{\left(v^{\prime }\right)}^2)v^{″}-2pr{e}^{-pv}(e^{-pv}-1)=0.$$

(27)

Multiplication of Equation (27) with $v^{\prime }$ and then integration with regard to $\xi$ gives

$$\frac{({\eta }^2-{\mathsf{\Psi }}_1)}{2}{\left(v^{\prime }\right)}^2-\frac{3}{4}{\mathsf{\Psi }}_2{\left(v^{\prime }\right)}^4+r{e}^{-pv}(e^{-pv}-2)+a=0.$$

(28)

Here, a is an integration constant. Using the transformation

$$\mathsf{\Omega }\left(\xi \right)=e^{-pv\left(\xi \right)},$$

(29)

the following nonlinear ODE is retrieved.

$$\frac{({\eta }^2-{\mathsf{\Psi }}_1)}{2p^2}{\mathsf{\Omega }}^2{\left({\mathsf{\Omega }}^{\prime }\right)}^2-\frac{3}{4p^4}{\mathsf{\Psi }}_2{\left({\mathsf{\Omega }}^{\prime }\right)}^4+r{\mathsf{\Omega }}^5(\mathsf{\Omega }-2)+a{\mathsf{\Omega }}^4=0.$$

(30)

The degree of nonlinear term is balanced with the degree of the highest order derivative in Equation (30) using the homogeneous balance principle described in [32], which provides the value $N=2$. Hence, the proposed method suggests that the solution can be assumed in the form

$$\mathsf{\Omega }\left(\xi \right)=C_0+C_{1}R\left(\xi \right)+C_{2}R{\left(\xi \right)}^2.$$

(31)

The function $\mathsf{\Omega }\left(\xi \right)$ is substituted from Equation (31) into Equation (30), and (21) is used for simplification. As a result, a polynomial is obtained in terms of R. This can be achieved with the help of Maple or Mathematica. Equating the coefficients of powers of R to 0 yields a system of algebraic equations.

The following values of the unknowns are obtained by solving the system of equations simultaneously.

• $\eta =\eta$, $C_0=0$, $C_1=0$, $C_2=\pm \frac{(\pm r+\sqrt{-ar+r^2})\omega }{r}$, ${\mathsf{\Psi }}_1=\mp (\pm r+\sqrt{-ar+r^2})p^2+a{p}^2+{\eta }^2$, ${\mathsf{\Psi }}_2=\frac{1}{12}{p}^4(2r\pm 2\sqrt{-ar+r^2}-a)$.

Substituting these values into Equation (31) yields

$$\begin{array}{ccc}\hfill \mathsf{\Omega }\left(\xi \right)& =& \left(\frac{(r+\sqrt{-ar+r^2})\omega }{r}\right){\left(\frac{1}{f{e}^{\xi }+g{e}^{-\xi }}\right)}^2,\hfill \end{array}$$

(32)

or

$$\begin{array}{ccc}\hfill \mathsf{\Omega }\left(\xi \right)& =& \left(\frac{(r+\sqrt{-ar+r^2})\omega }{r}\right){\left(\frac{4f}{4f^2{e}^{\xi }+\omega e^{-\xi }}\right)}^2,\hfill \end{array}$$

(33)

which is substituted into Equation (29).

Since

$$\begin{array}{ccc}\hfill \mathsf{\Omega }\left(\xi \right)& =& e^{-pv\left(\xi \right)},\hfill \\ \hfill ln\left(\mathsf{\Omega }\right(\xi \left)\right)& =& -pv\left(\xi \right),\hfill \\ \hfill v\left(\xi \right)& =& -\frac{1}{p}ln\left(\mathsf{\Omega }\left(\xi \right)\right),\hfill \end{array}$$

therefore, $v\left(\xi \right)$ can be written as

$$\begin{array}{ccc}\hfill v\left(\xi \right)& =& -\frac{1}{p}ln\left(\left(\frac{(r+\sqrt{-ar+r^2})\omega }{r}\right){\left(\frac{4f}{4f^2{e}^{\xi }+\omega e^{-\xi }}\right)}^2\right).\hfill \end{array}$$

(34)

The resulting relation can be expressed as

$$U(x,t)=-\frac{1}{p}ln\left(\left(\frac{(r+\sqrt{-ar+r^2})\omega }{r}\right){\left(\frac{4f}{4f^2{e}^{\xi }+\omega e^{-\xi }}\right)}^2\right),$$

(35)

where $\omega =4fg$ and $\delta =1$ in the value of R.

Considering the $\beta$-derivative, the solution (35) can be written as

$$\begin{array}{ccc}\hfill U(x,t)& =& -\frac{1}{p}ln(\left(\frac{(r+\sqrt{-ar+r^2})\omega }{r}\right)\hfill \\ & & {\left(\frac{4f}{4f^2{e}^{\frac{1}{\beta }{\left(x+\frac{1}{\mathsf{\Gamma }\left(\beta \right)}\right)}^{\beta }-\frac{\eta }{\beta }{\left(t+\frac{1}{\mathsf{\Gamma }\left(\beta \right)}\right)}^{\beta }}+\omega e^{-\left(\frac{1}{\beta }{\left(x+\frac{1}{\mathsf{\Gamma }\left(\beta \right)}\right)}^{\beta }-\frac{\eta }{\beta }{\left(t+\frac{1}{\mathsf{\Gamma }\left(\beta \right)}\right)}^{\beta }\right)}}\right)}^2),\hfill \end{array}$$

(36)

where $p=\sqrt{2}u$ and $\omega =4fg$. The symbols u and r denote the width and depth of Morse’s potential, whereas f and g are the parameters of the R function, respectively. Moreover, $\beta$ is the fractional order of the derivative, $\eta$ is the speed of the soliton and a is a constant of integration.

Considering the M-truncated derivative, solution (35) can be written as

$$\begin{array}{ccc}\hfill U(x,t)& =& -\frac{1}{p}ln(\left(\frac{(r+\sqrt{-ar+r^2})\omega }{r}\right)\hfill \\ & & {\left(\frac{4f}{4f^2{e}^{\frac{\mathsf{\Gamma }(\alpha +1)}{\beta }(x^{\beta }-\eta t^{\beta })}+\omega e^{-\left(\frac{\mathsf{\Gamma }(\alpha +1)}{\beta }(x^{\beta }-\eta t^{\beta })\right)}}\right)}^2),\hfill \end{array}$$

(37)

where $p=\sqrt{2}u$ and $\omega =4fg$. The symbols u and r denote the width and depth of Morse’s potential, whereas f and g are the parameters of the R function, respectively. Moreover, $\beta$ is the fractional order of the derivative, $\eta$ is the speed of the soliton and a is a constant of integration. The parameter $\alpha >0$ appears to be due to the truncated one-parameter Mittag–Leffler function in the definition of the M-truncated derivative.

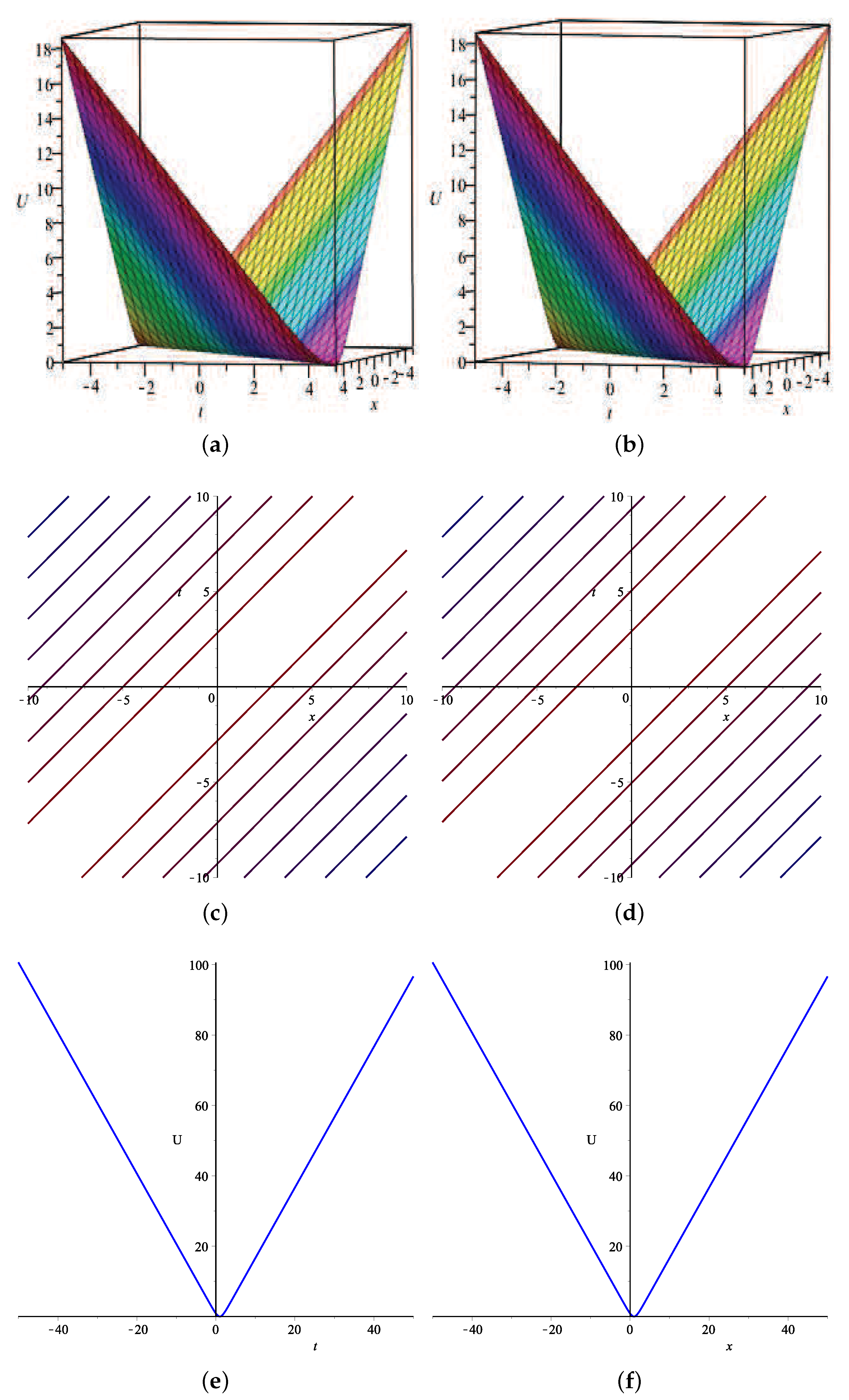
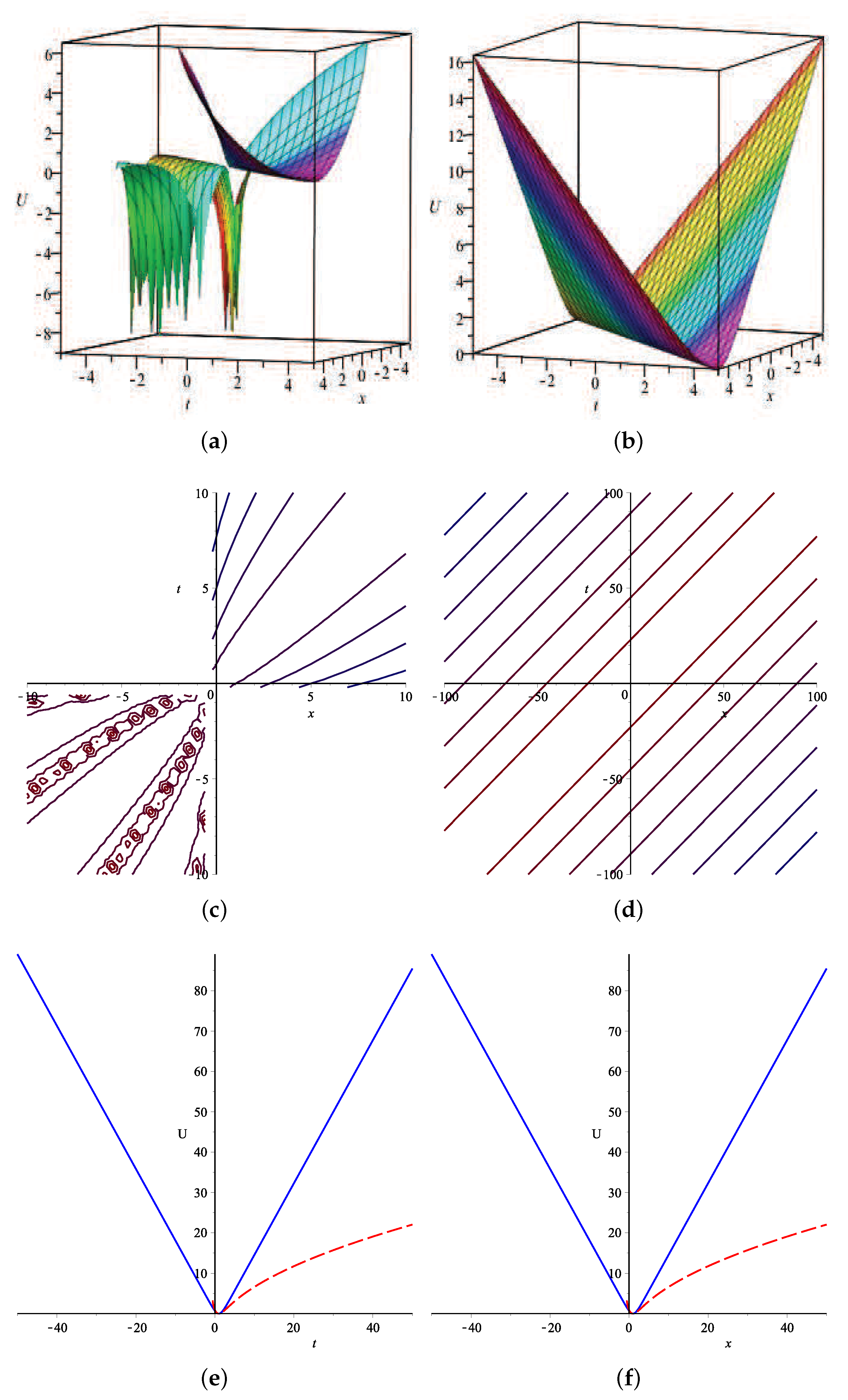
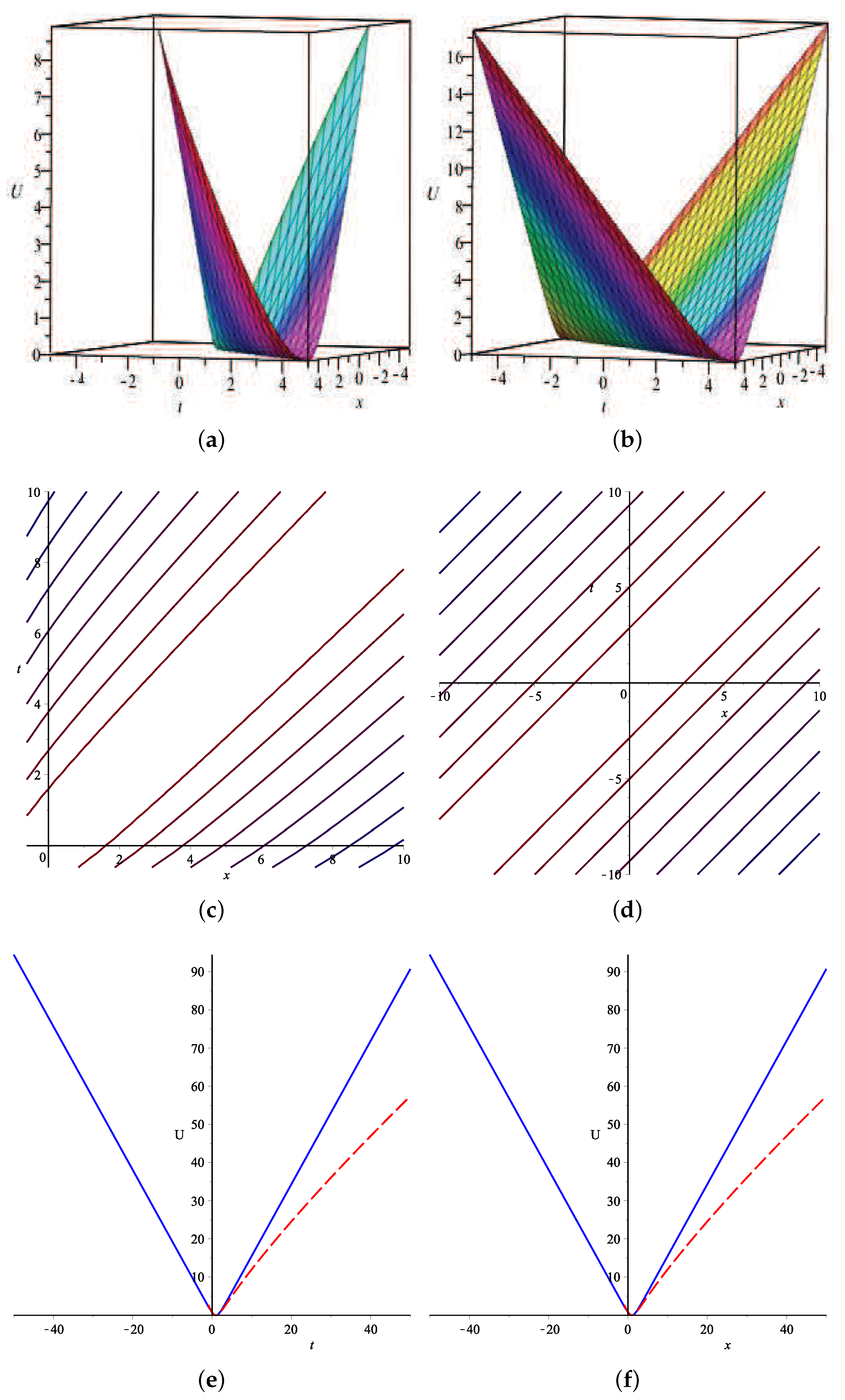
6. Graphical Illustrations

The obtained solution for the $\beta$-derivative and M-truncated derivative is graphically plotted to compare the influence of the change in the fractional order of both kinds of derivatives. Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5 have been plotted to demonstrate the evolution of the wave profile corresponding to the obtained solution, as the fractional order is gradually increased by taking the values $\beta =0.5$, $\beta =0.75$, $\beta =0.83$, $\beta =0.9$ and $\beta =1$, respectively. The graphs for Equation (36) are presented in Figure 1a, Figure 2a, Figure 3a, Figure 4a and Figure 5a, which show the evolution of the wave profile using the definition of the $\beta$-derivative. For a better visualization of the physical structure of the soliton corresponding to the obtained solution, two-dimensional contour plots have been plotted as well. The contour plots corresponding to $\beta =0.5$, $\beta =0.75$, $\beta =0.83$, $\beta =0.9$ and $\beta =1$ are shown in Figure 1c, Figure 2c, Figure 3c, Figure 4c and Figure 5c respectively.

The graphs for Equation (37) are presented in Figure 1b, Figure 2b, Figure 3b, Figure 4b and Figure 5b, which show the evolution of the wave profile using the definition of the M-truncated derivative. The corresponding contours are shown in Figure 1d, Figure 2d, Figure 3d, Figure 4d and Figure 5d.

It is clear from the graphical demonstration that the shape of the wave appears as different for different values of the fractional order $\beta$ using the $\beta$-derivative and M-truncated derivative. However, it is observed that the wave profile tends to become increasingly similar with an increase in the value of $\beta$. Ultimately, at $\beta =1$, the soliton converges to the unique form, as depicted by Figure 5. Hence, it can be concluded that both definitions provide a solution that is in agreement with the usual Hamiltonian and the standard integer order equation of motion for the PBD model when $\beta$ converges to unity.

Further confirmation of this observation is provided by the comparison of the line graphs of the obtained solution expressions for both definitions of the derivative. Figure 1e, Figure 2e, Figure 3e, Figure 4e and Figure 5e show the comparison of 2D line graphs corresponding to the $\beta$-derivative and M-truncated derivative for different values of $\beta$ at $x=1$. It is evident from Figure 5e that the wave profiles for both definitions of the derivative become coincident with each other. A similar confirmation is provided by the 2D line graphs at $t=1$, as depicted by Figure 1f, Figure 2f, Figure 3f, Figure 4f and Figure 5f. For sake of convenience, the values of $\eta$, f and a are taken as unity.

7. Conclusions

In this paper, the fractional PBD model was examined with the M-truncated derivative and $\beta$-derivative using Kudryashov’s R technique. The obtained soliton solution was graphically illustrated to depict the effects of the fractional order of the derivative for both the M-truncated derivative and $\beta$-derivative, as shown in Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5. The obtained solution represents a dark soliton. It is evident that the wave profile has a localized decrease in the wave amplitude. The changes in the shape of the soliton solution have been observed by making variations in the value of fractional order $\beta$. The graphical interpretation of the obtained solution reveals that the graphs for both definitions are different for the same value of the fractional order $\beta$. However, as the value of $\beta$ is increased, the wave profile corresponding to both definitions of the fractional derivative becomes increasingly similar. These observations show that both M-truncated and $\beta$ derivatives provide results that are in good agreement if the fractional order is nearly one. Ultimately, the graphs related to the M-truncated derivative and the $\beta$-derivative tend to become the same as the value of $\beta$ approaches unity. The reported results are novel and Kudryashov’s R technique has been utilized to explore the considered model for the first time in this work to provide a comparison of the soliton solutions for $\beta$-fractional and M-truncated derivatives. The proposed research may be helpful for providing a deeper insight into fractional order nonlinear models and the related physical phenomena.