1. Introduction
Concerning various applications of the “classical” Riemann–Liouville and Caputo fractional derivatives in various problems of physics and mechanics, there exists a very large amount of literature (see for example [
1,
2,
3,
4,
5] and references therein). On the other hand, the concept of general fractional calculus (GFC) has recently gained an increasing interest from a theoretical point of view. We mention the review article of V. E. Tarasov [
6], where a development of ideas concerning the generalization of the Riemann–Liouville and Caputo fractional integrals and derivatives are presented. The idea of GFC may be traced to the work of A. N. Kochubei [
7]. Further developments may be found in the papers of Y. Luchko [
8,
9], as well as in [
1,
2].
The main idea of the GFC concept is to describe dynamical systems with the nonlocality in time and space.
The following definitions of GFC are introduced; see [
6,
8,
10] and references given therein:
where
and
denotes convolution. Equation (
1)
defines the integral in GFC, whereas (
1)
and (
1)
define the generalized fractional derivative in the Riemann–Liouville sense, and generalized fractional derivative in the Caputo sense, respectively. Kernels
M and
K in (
1) belong to the class of Sonin kernels, defined as follows. Let
. Then,
where
is the space of continuous functions on
. Then, the
set of Sonin kernels
is defined as a set of pairs of functions
, such that
which satisfies the so-called Sonin condition
is called a Sonin pair. By [
11], if
and
, we have locally integrable derivatives (that belong to
) that satisfy
Then,
for all
, where
and
exist. Moreover, (
2) implies
see [
7,
12]. Then, (
2) implies
where
denotes the Laplace transform. This is used in [
7] for the construction of
M when
K is given.
We note that, in the frame of the Riemann–Liouville fractional calculus, one has
so that (
2), (
3) and (
5) hold true.
Our aim in this work is to analyze the Zener model of a viscoelastic body with specific
K and
M satisfying (
2). Moreover, we will derive the thermodynamical admissibility conditions that guarantee the dissipation.
We consider kernels
M and
K in two forms, called cases. The first one is proposed by Hanyga [
12] as
Case H
where
is a two-parameter Mittag–Lefler function [
13]. Conditions
and
imply that
K is a singular, locally integrable completely monotone function; see [
14], p.144. It was shown in [
12], Theorem 4.1, that any singular, unbounded in a neighborhood of zero, locally integrable, completely monotone function is a Sonin kernel, i.e., satisfies (
5). Thus, functions (
6) make a pair that belongs to
. The Laplace transforms of
and
are
The second Sonin pair, proposed by Zacher [
15], is
Case Z
where
. The Laplace transforms of
and
are
Our goal is to investigate mechanical models with constitutive equations in the framework of GFC.
More precisely, we consider the one-dimensional generalized Zener model [
16] given as
where
and
denotes the stress
, which is the strain in a body at time
t and position
x, and
are constants. The case
is trivial; the results are well known, so we do not consider it.
As in our earlier papers, Refs [
17,
18,
19], we consider a generalized Zener constitutive equation for a viscoelastic body. We point out that our intention in this paper is to present that fractional derivatives with kernels
and
given above (Cases
H and
Z) require a completely different implementation in solving the wave equation in relation to the method of solving the same equation with the Riemann–Louvile fractional derivatives in the constitutive equation.
Concerning our previous paper [
19], we have two remarks. The first one is that the obtained sufficient conditions for the thermodynamical admissibility of the constitutive equation (
10) for both cases were obtained by our original approach given in the quoted paper, with the aim of analyzing the dissipations inequality. The second remark is that one can assume, as in [
19], that the body force
f and the initial conditions
are random since they may incorporate trough epistemic randomness or errors in the measuring devices. Such an analysis will be considered in our future work since it involves additional extensive analysis. Moreover, the environmental noise in random fluctuations in transient dynamics of interdisciplinary physical models is an important issue that deserves further investigations; see [
20,
21,
22,
23,
24] for the “classical” fractional derivatives in various applications. In several papers, the authors of [
21,
25]—see also references therein—use a memristor (elements of electric circuits) in the analysis of fluctuations of various nonlinear models of nanoelectronics. Their stochastic approach gives a new insight concerning physical models through the prediction of memristor behaviour.
We comment on the possible applicability of our constitutive equation (
10). In the case of the Caputo derivative, in [
26], the description of experimental data for certain dental materials was successful. Since we have one additional parameter
in (
8) and (
10), the modeling of experimental results within the new framework is expected to be even more precise.
Let us briefly present the content of the paper. After a short introduction concerning the generalized functions framework, we analyze in
Section 2 the thermodynamical restrictions for the Zener constitutive equation in cases
H and
Z. Starting with
Section 3, up to the end of the paper, we will consider case
Z with kernels (
8).
Section 3 is devoted to the stress relaxation and the spatially one-dimensional wave equation in a viscoelastic material when the coefficients satisfy the thermo-dynamical restriction; that is, condition
This condition implies the existence and the unicity of a solution of this equation. Moreover, in
Section 3, we analyze the regularity of a solution and give an example confirming the numerical evidence of the properties of a solution.
Notation and Notions
We use the usual notation; for example,
,
is the space of functions with continuous
k derivatives. We refer to the classical distribution theory (cf. [
27] or any other one about distributions) for the mathematical preliminaries related to the space of tempered distributions
, the Fourier and the Laplace transforms. Recall that the space of smooth functions, where all derivatives rapidly decrease as
—that is, are bounded by any power
—is denoted by
. Its dual is the space of tempered distributions
. Elements
supported by
(
have the form
, where
F is a continuous polynomially bounded function supported by
(equal to zero in
). The Laplace transform will be considered for the so-called exponentially bounded distributions, the linear combination of the distributions of the form
, where
. Recall that, for the exponentially bounded function
f (
),
The Fourier transform is an isomorphism of
onto
and of
onto
. It is given by
Recall that Heaviside’s function H is the characteristic function of . Its derivative over is the delta distribution . Also in , its derivative is Let us recall that , where .
We denote the dual pairing of a test function and a distribution through the integral sign, explaining such an integral when it exists in the sense of classical functions or in the sense of distribution pairing.
In order to simplify the exposition, we will assume in the main theorem of
Section 3 that a function
, the initial data
, and their derivatives up to an imposed order belong to the space of integrable continuous functions with a suitable decay property, in order to have the existence of a convolution in
x of these functions with a fundamental solution
P, for which, we show that it is a distribution.
2. Thermodynamical Restrictions
We consider the constitutive Equation (
10) with kernel
K of both cases. Our intention is to derive the restrictions on the coefficients in (
10) that follow from the second law of thermodynamics under isothermal conditions. We assume that
and
for each
, and
. Further on, we assume that
. The second law of thermodynamics, under appropriate isothermal conditions, requires that, for any cycle of duration
, where cycle here means
, there exists
such that the dissipation inequality
holds for every
. Because of that, in the analysis that follows, we shall write (
11) without
x. Inequality (
11) is used for
, which does not satisfy the conditions of a cycle. For example, in [
28], the use of (
11) for any sufficiently smooth
is proposed, which also satisfies
. We follow [
28] since it does not require a definition of a cycle. Note that the cycles are differently defined in various papers. In [
29], it is required that the entropy inequality holds (
11) is just a special case of it) for a specially defined D-cyclic process. We refer to [
17,
30,
31,
32] for a more detailed analysis of a dissipativity condition.
Applying the Fourier transform now on a function (or a distribution) depending on
(those supported by
with respect to variable
t) to (
10)
, we obtain the Fourier transform of
as
2.1. Restrictions on the Coefficients for Case Z
In this subsection, we use notation
and
. Applying the Fourier transform (on a function or distribution depending on
t), we obtain
Let
so that
. This leads to
Then, we have
with
and
given by (
14). Now, it is easy to prove the next proposition.
Proposition 1. Condition is a sufficient one for the components and of the complex dynamic modulus E defined by (12) to satisfyfor some . Proof. Relations (
13)–(
15) imply that
Since
and
and
have the same sign + for
and sign − for
, we can easily conclude that
Now, we simply conclude that
The last part is clear. □
2.2. Restrictions for H
In this subsection,
. We present the restrictions for (
10) with the assumptions
In fact, we have the same formulation as in the case of Proposition 2,but now in a quite different context:
Proposition 2. Condition is a sufficient one for the components and of the complex dynamic modulus E, defined by (12), to satisfyfor some . Proof. Applying the Fourier transform to (
10) and using (
7), we obtain
so that, instead of (
13), we have
It will be clear from the proof that is to follow that the converse assumption does not imply the claims of the proposition. We will consider the case when since the case of is quite similar.
Let
and
. Then, we have
which implies that
Thus,
implies that
lies in the first quadrant. Rewrite (
16) in the form
Since
we again have that
belongs to the first quadrant.
Then, using simple geometric arguments (sum of three terms, each having an argument in
), we conclude that
In the case of
, we obtain
. Rewriting
E as
we obtain
.
Therefore, looking at the real and imaginary part of
E in (
17), we easily conclude that
For the last part, we note that , and it is differentiable in a neighborhood of zero so that . □
2.3. Dissipation Inequality
Our main theorem of this section is to follow. Since the condition for cases H and Z are the same (), the next theorem holds in both cases.
For simplicity, we assume that and belong to .
Theorem 1. With the quoted assumptions on σ and ε, and the constitutive Equation (13), condition implies the dissipation inequality (10). Proof. The basic idea is the Bochner–Schwartz theorem for non-negative measures; see [
33], p. 331.
We will rewrite (
10) in another form.
Now,
is even and
, whereas
is odd. Since
is odd, as in our previous paper [
19], we can show that
Thus, we have to prove that the non-negativity of
implies
This will complete the proof of (
11).
Let
. Then, by Theorem IX.10 in [
33], the positivity of
implies that
is positive definite; that is, for every
and
,
where we also use the assumption that
is even.
Finally, since any function in
is a pointwise limit of a real-valued sequence
in
, let
pointwisely on open set
as
. For such
,
The last expression is simply
, i.e., (
11) holds. □
Remark 1. Conditions stated in Theorem 1 are obtained by a different approach in relation to the one used by Bagley and Torvik; see [34,35]. Their approach is based on the assumption that a sinusoidal stress, imposed on a viscoelastic body, after a transition period, implies that the strain has the same form but with a phase shift. The energy dissipation condition has to be satisfied during a deformation process starting from a virginal state and it is not required for this deformation to constitute a cycle. The approach used here is also used in [18,31,36]. 3. Stress Relaxation and Wave Equation
We will show how condition , which follows from the dissipation inequality, implies the solvability and the unicity of a solution for a real model, which will be described below. As we already noted, in the sequel, we consider only case Z.
The next lemma is needed.
Lemma 1. (a) Let . Then,(b) If , then there exists such that Proof. (a) The proof will be given in several simple steps. Let
. Then, using simple geometry, one can conclude that
The same reasoning shows that, for
and
, there holds
Thus, for , in both cases, we have .
Again, we conclude by elementary observation that
implies
since
. In addition, in a similar way, we conclude that
implies
because
.
Now, we will determine the location of points of
, where
We will decompose mapping A in several simple mappings, having in mind that .
1. transforms into ;
2.
transforms
into the interior of the circle
that is, to the set of points
belonging to the interior of the circle
;
3.
transforms the interior of the circle to the translated one,
With this analysis, we conclude that
is transformed by the mapping
A into the interior of
C given by (
18).
We conclude:
If and , then we know that z has the real part and the imaginary part . Thus, has a positive real part and negative imaginary part. With this, we conclude that must belong to . The same arguments show that the assumption imply that must belong to . This proves assertion (a).
(b) The first quadrant in the
z-plane goes by the mapping
A into the lower half of
C in (
18), whereas the fourth quadrant in the
z-plane goes to the upper half of
C. Thus, by the first part, we have that
A maps points
into points
of the complex plane so that
belongs to the set of points
Now, the first part of the proof implies that, after the multiplication of s and , one must have . This proves assertion (b). □
Remark 2. Previous proof shows that, for , the circle lies in the left side of and intersects both the left and right half of the complex plane. This contradicts a). Thus, the conclusion that we have obtained from the dissipation inequality appears as the essential one for the existence and the uniqueness of a solution of a wave equation in Theorem 2.
3.1. Stress Relaxation for Z in Case
We treat the creep problem. Applying the Laplace transform to (
10), we obtain
For the stress relaxation test, we take
, where
is the characteristic function of
(
). Since
, we have
Proposition 3. Let be the strain in (10). Then, the stress σ has the formwhere, for any , which means that the integral does not depend on ,is a continuous function. Proof. By Lemma 1, part (b), the integrand does not have zeros in the right half of
. Moreover,
so that, using the Cauchy formula, the complex integral below does not depend on the choice of
. Thus,
where
. Thus,
where
is a continuous function because of (
20). □
The result of the numerical inversion of (
19) is shown in
Figure 1.
In
Figure 1,
. The stress relaxation curve for the case of a “classical” fractional Zener model is given in [
16], p. 64.
3.2. Wave Equation for Z
We present a wave equation for case
Z. Note that the waves in the Zener model of the viscoelastic body with the Riemann–Liouville and Caputo derivative have been studied in many papers. We refer to the review articles [
19,
37]. The one-dimensional equation of motion, constitutive equation, and geometrical conditions in the dimensionless form are
where
denotes the body force. We associate to (
21)–(23) the following initial conditions:
where
and
are functions with properties that will be discussed in the main theorem of this section. The use of the Laplace transform, (
1)
and (
9), give, for
,
Note that, for
,we recover the result presented in [
38], p. 98. Applying the Laplace transform to (22), we obtain
where we used
. Let
so that
In order not to go into cumbersome detail, we will say that a continuous function rapidly decreases enough as if it is convolvable with a given function b; that is, is a continuous function. Thus, we assume:
- (i)
and the first three derivatives , , and rapidly decrease enough with respect to so that their convolutions in x with a bounded continuous function are continuous on .
- (ii)
and and their derivatives up to the third order rapidly decrease enough with respect to so that their convolutions in x with a bounded continuous function are continuous on .
Theorem 2. Assume that f, , and satisfy assumptions and given above. Equations (21)–(24) have a unique solution given bywhereis a solution of the equationand is a distribution so that it is a smooth bounded function out of a set of points for any . The singularity is the point so that, in a neighbourhood of this point, , one has that P is the third derivative with respect to x of a bounded continuous function over to .
The solution is a continuous function.
Proof. The Laplace transform
applied to (
25), with
and
, gives
Applying the Fourier transform
to (
27), we obtain
The next step is to apply the inverse Fourier transform. We note that
if
. In order to use this result, we need to check that
is positive if
. This follows from Lemma 1, part (a). Thus, for
, the function
is smooth. Thus,
P is smooth over
.
Next, (
28) becomes
for
, and, thus,
Lemma 1 implies that we can take any
in the integrals below since we will perform the use of te Cauchy formula in the analysis of these integrals. Thus, for
,
,
we conclude that the point
is singular. Thus, the integral (
31) must be understood in the sense of dual pairing (it does not exist in the classical sense). We have to enter into the space of the distribution and rewrite
P into the form
so that
is integrable in a neighbourhood of
. We have that
is a bounded continuous function.
Regarding the behavior of the integrand, we conclude that it is a bounded continuous function on
. Since (
26) holds for
B, we obtain
This, with the assumptions on and , implies that is a continuous function. This completes the proof of the theorem. □
Corollary 1. If and f and and their derivatives up to order 5 satisfy assumptions and , then the solution u is a classical one.
Proof. The assumptions imply that the second derivative of is continuous in x.We note that the member with disappears and that the second derivative of is . Thus, in the convolution of B with respect to t with , one obtains for the solution that the second derivative is continuous for . □
Corollary 2. If and and their derivatives up to order 6 satisfy assumptions and , then the solution u is a classical one.
Proof. Note that
gives an additional member on the right hand side of
. Thus, in order to improve the properties of
with respect to
t, one should put in the definition of
P,
. Then,
u given by (
32) will have a new form: a convolution of a new
and the fourth derivatives of
and
With this, one has that
is also continuous with respect to
and
. This completes the proof. □
Example
As a specific example, we consider Equations (
21)–(
24) with
The solution is given by (
30). It has the form
It has a strong singularity at
for any
, so, in our numerical experiment, we consider it for
. In
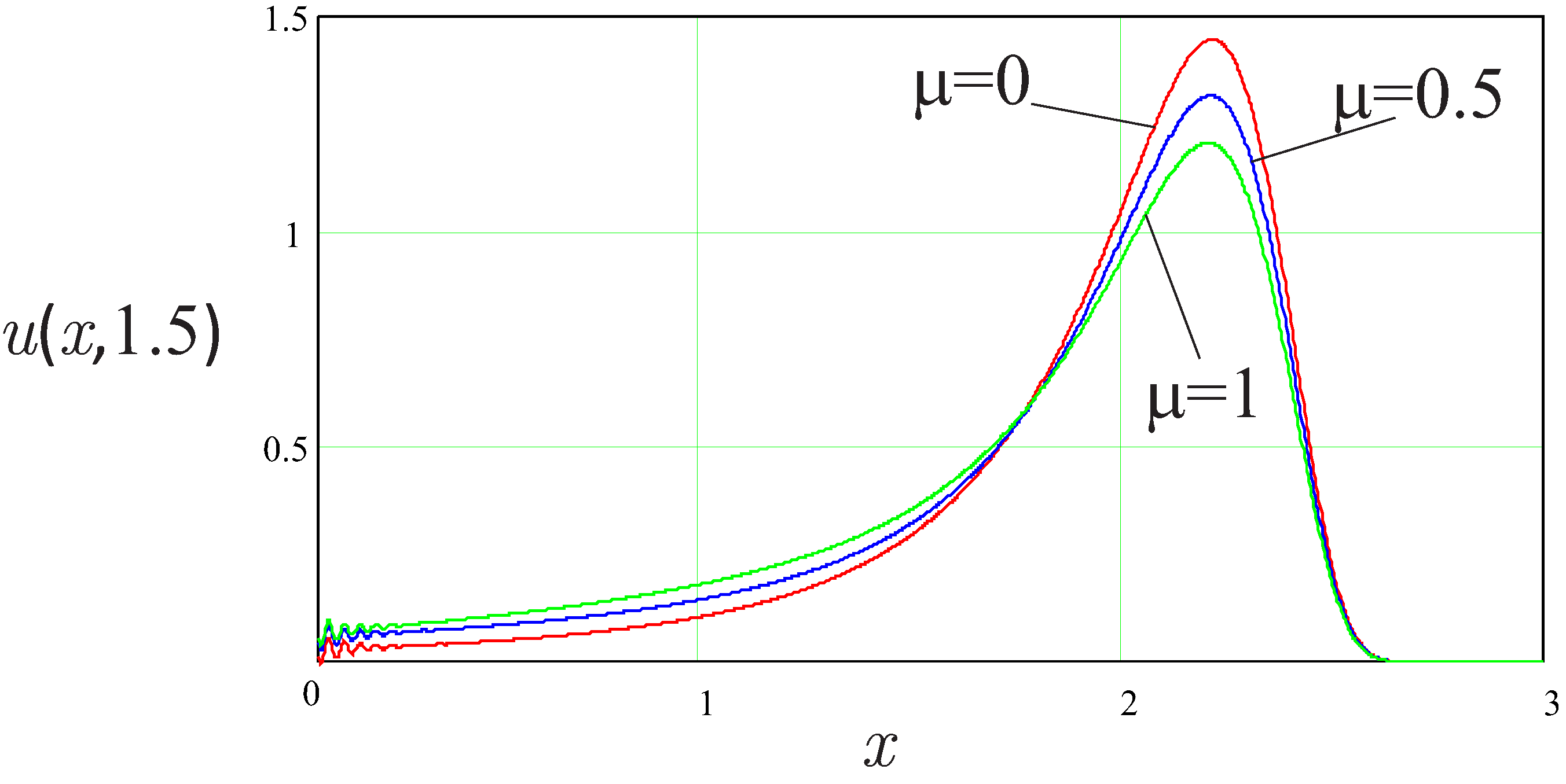
Figure 2, we show (
33) for several values of parameters. The results presented in
Figure 2 show that, for selected values of
, by increasing the parameter
, the speed of the propagation of the maximum decreases and the amplitude of the maximum decreases.
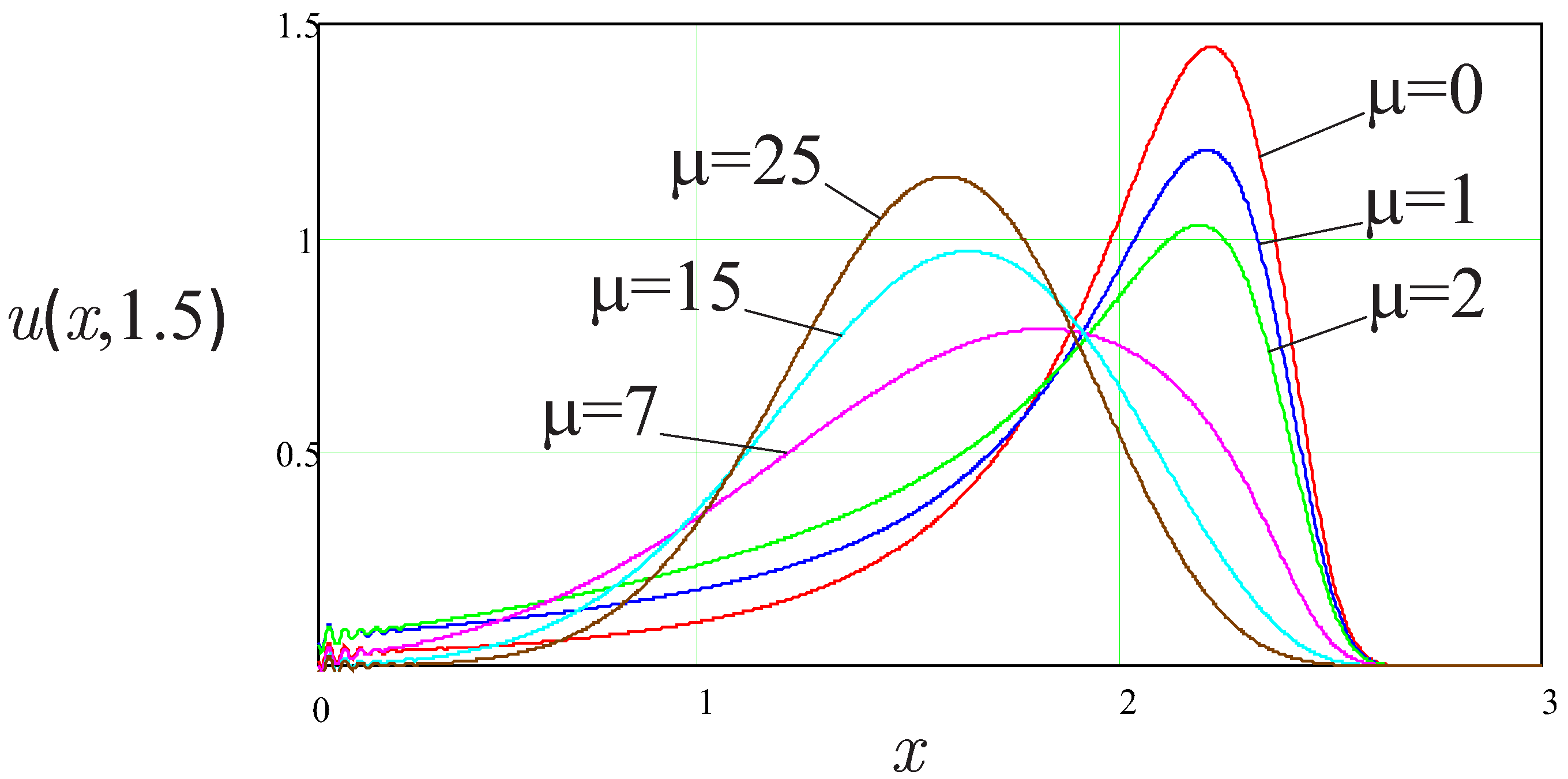
Figure 3 shows the solution when
increases further. It is seen that the speed of the propagation of the maximum decreases further, whereas the amplitude of the maximum increases. This interesting property needs to be studied further.
4. Conclusions
We considered a general form of a fractional derivation and fractional integral, suggested by several leading experts in the field. Two Sonin pairs, called cases
of Hanyga and
of Zacher, were analyzed through the dissipation inequality for the Zener-type constitutive equation. Our approach for the proof of the dissipation inequality was based on the Bochner–Schwartz theorem as in our recent papers [
18,
36]. The limitation of our approach is that it can only be applied to linear constitutive equations.
Our framework includes the space of generalized functions. This enables us to use the strong results of the Schwartz theory. However, our results are closely connected with the formulations of classical analysis.
In the case , we present results related to a stress relaxation and a wave propagation for a Zener-type viscoelastic body for which the proposed thermodynamical restriction for coefficients in the constitutive equation guarantee the existence and uniqueness.
The analysis of a solution for a wave propagation is the main part of our analysis. It appears that some estimates based on the condition , followed from the dissipation inequality, are necessary for the use of the Fourier and Laplace transforms and their inverses. Additional assumptions on initial data and the perturbation f imply the existence of the classical solution given in the integral form.
It is shown in examples that a parameter appearing in the definition of the generalized derivative in a Sonin pair proposed by Zacher allows for a better fit of experimental results. The numerical results show the properties of a solution out of a neighbourhood of .
Finally, we comment the possible extension of the present work. The introduction of stochastic terms in the constitutive equation for the case
Z when
(cf. (
8)) seems possible. However, the first step in such an analysis is the restriction on the coefficients that are obtained in this paper.