Legendre Spectral Collocation Technique for Advection Dispersion Equations Included Riesz Fractional
Abstract
:1. Introduction
2. Riemann–Liouville Fractional Derivative
3. Fully Spectral Collocation Treatment
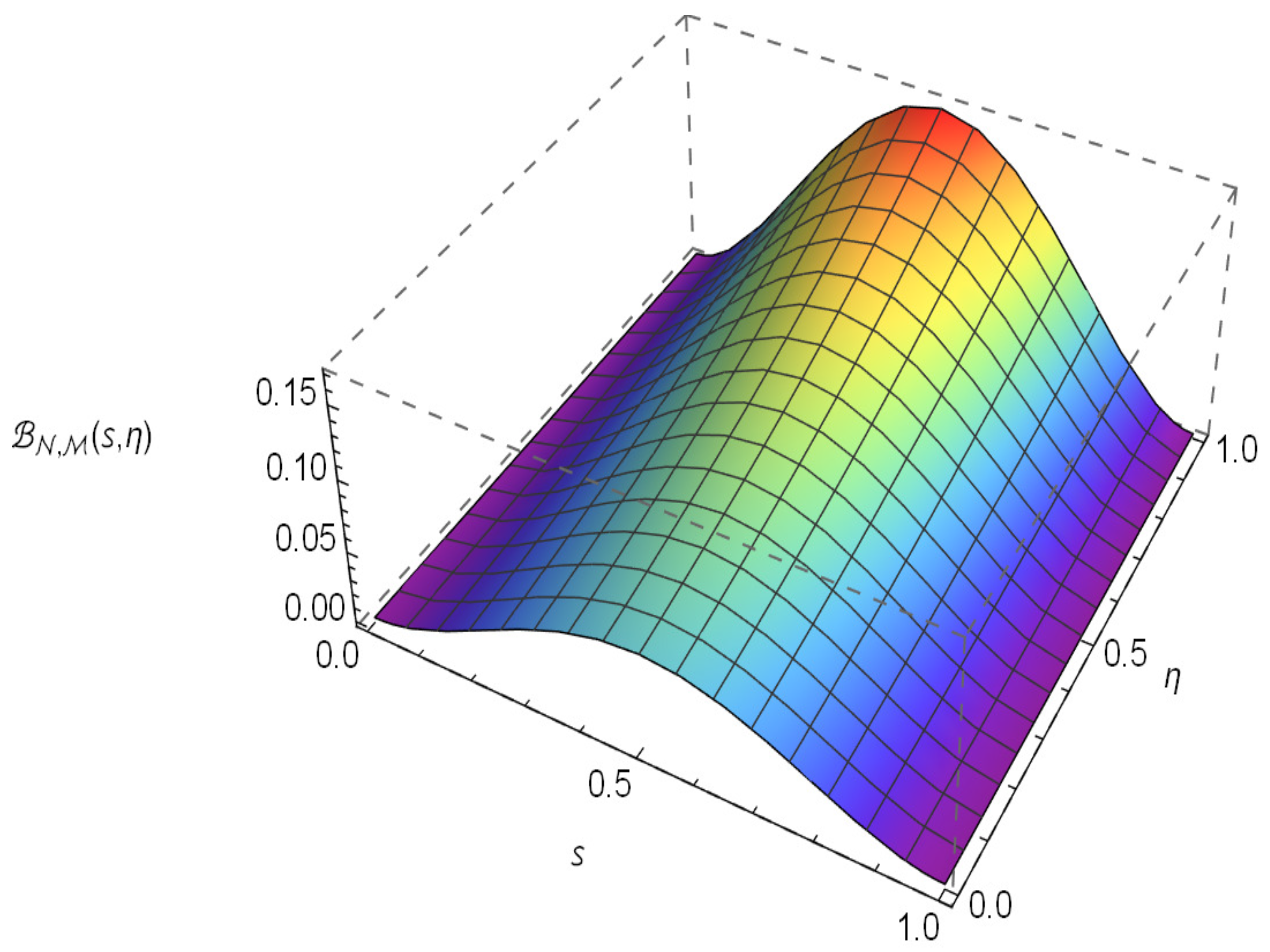
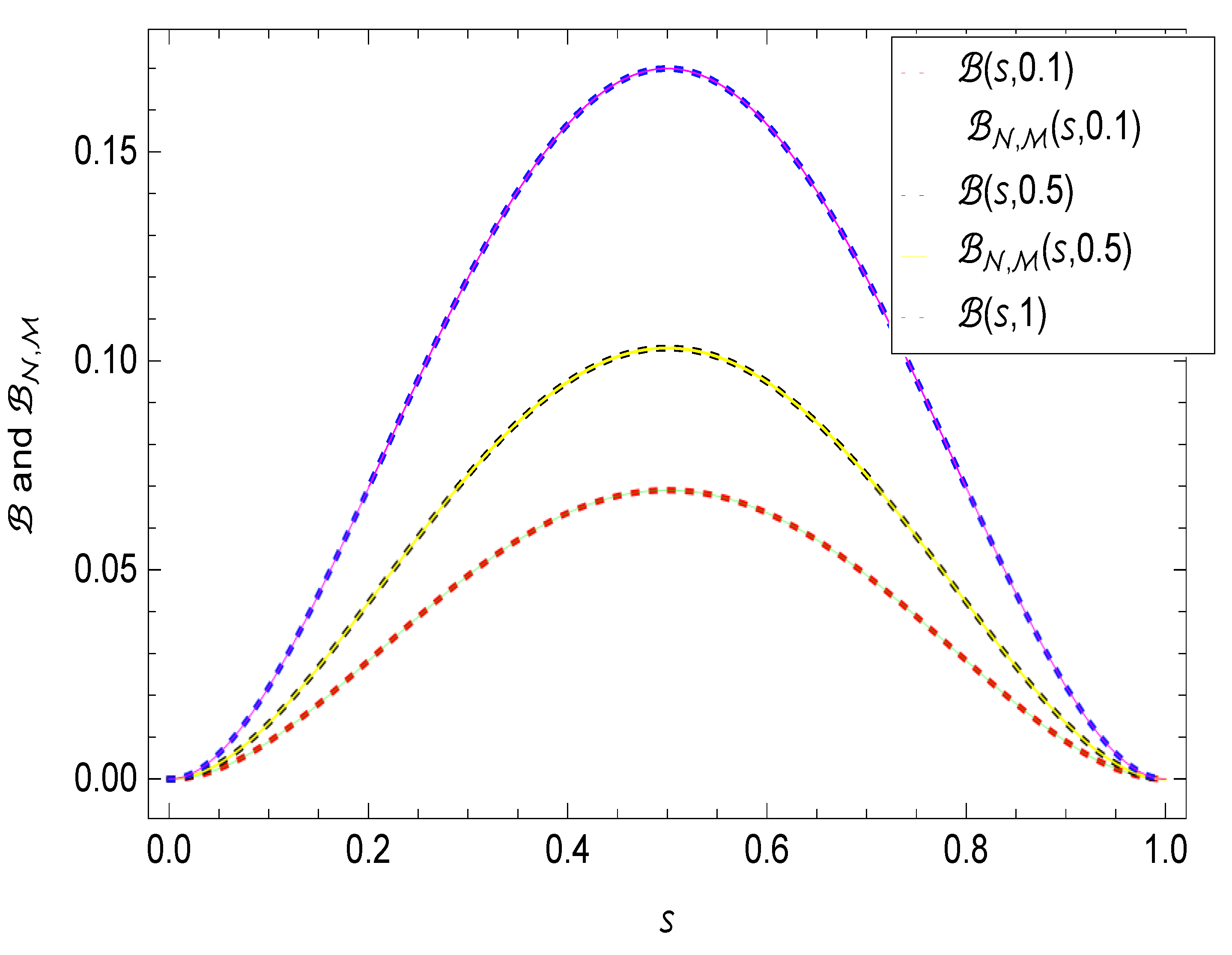
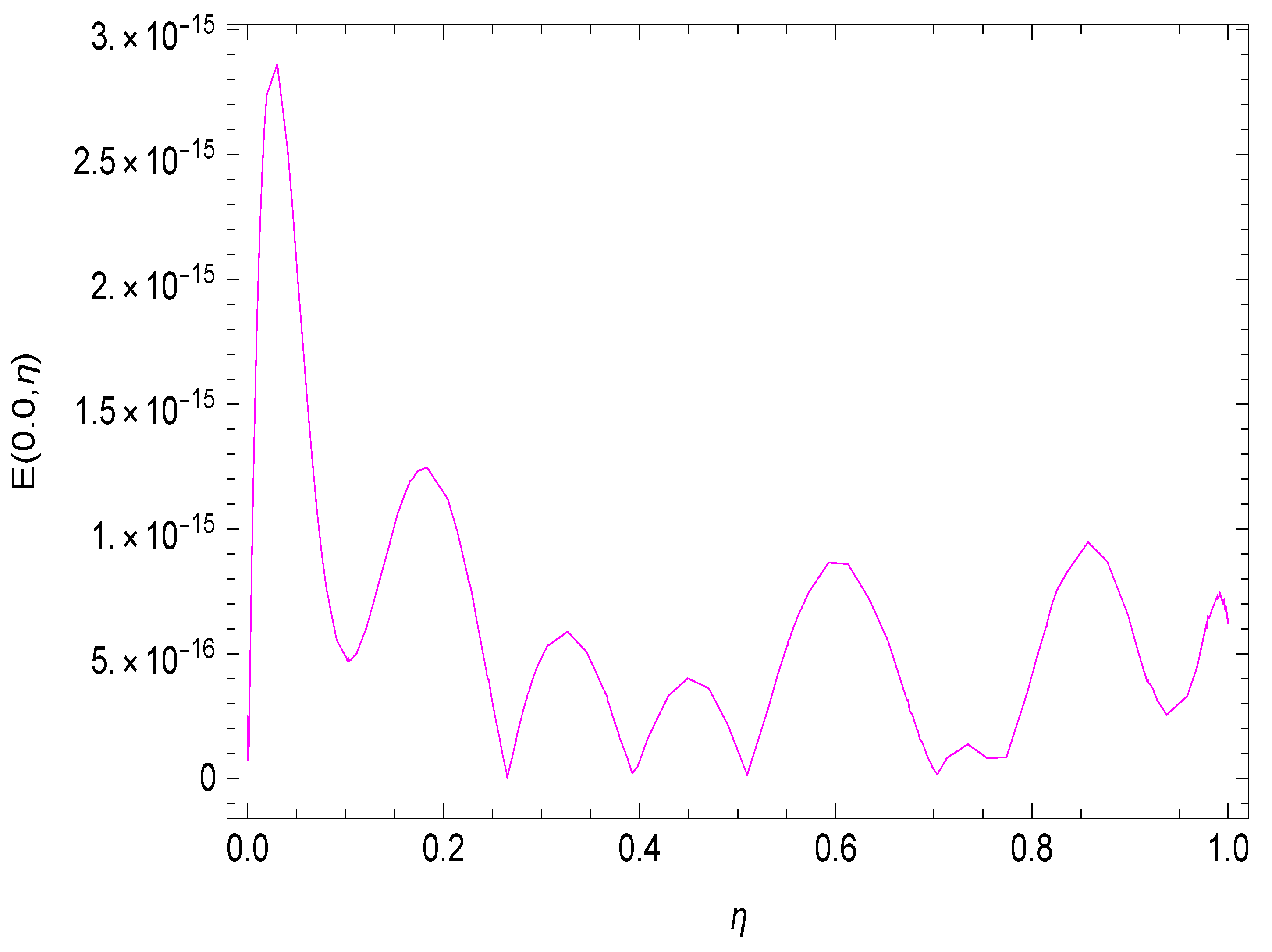
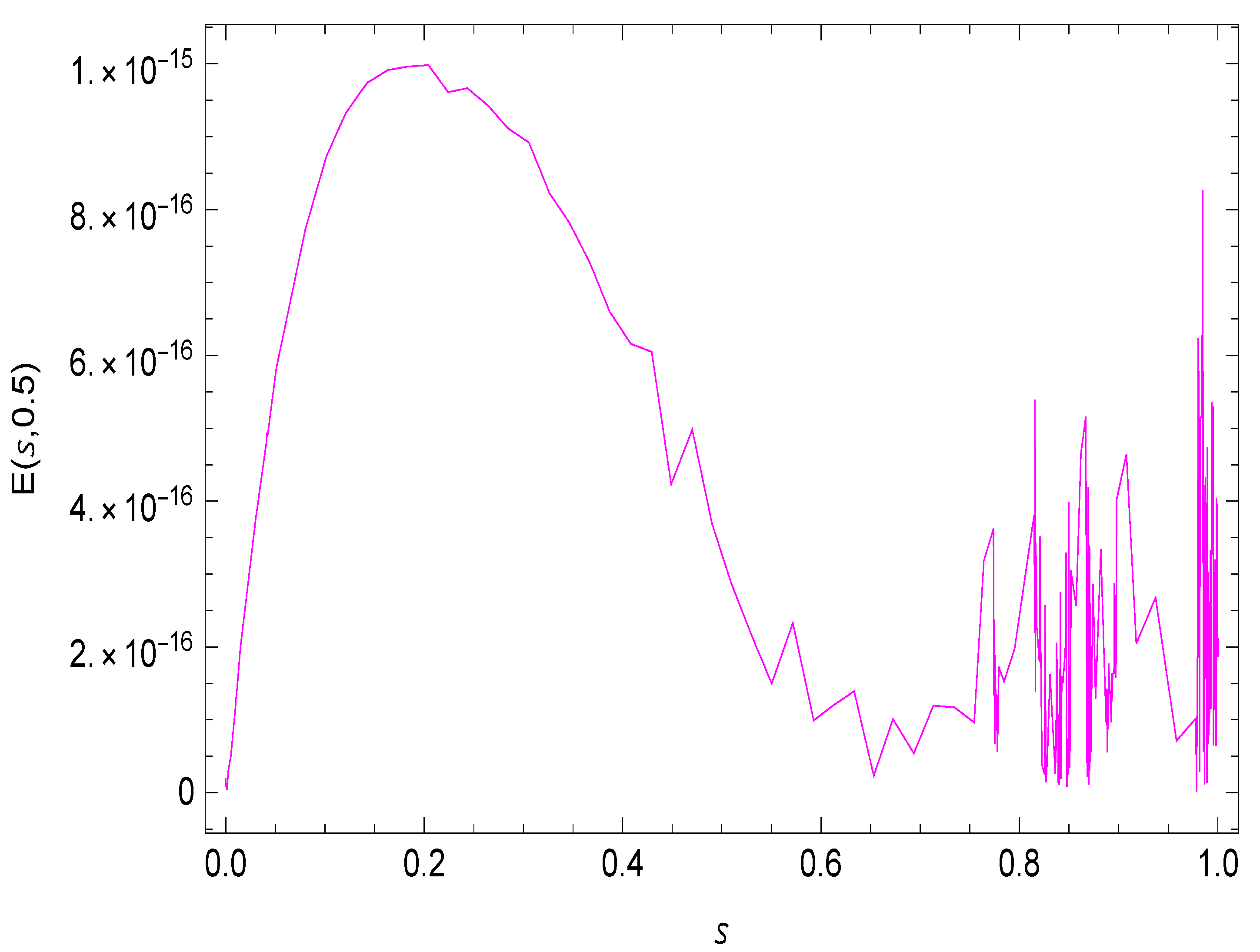
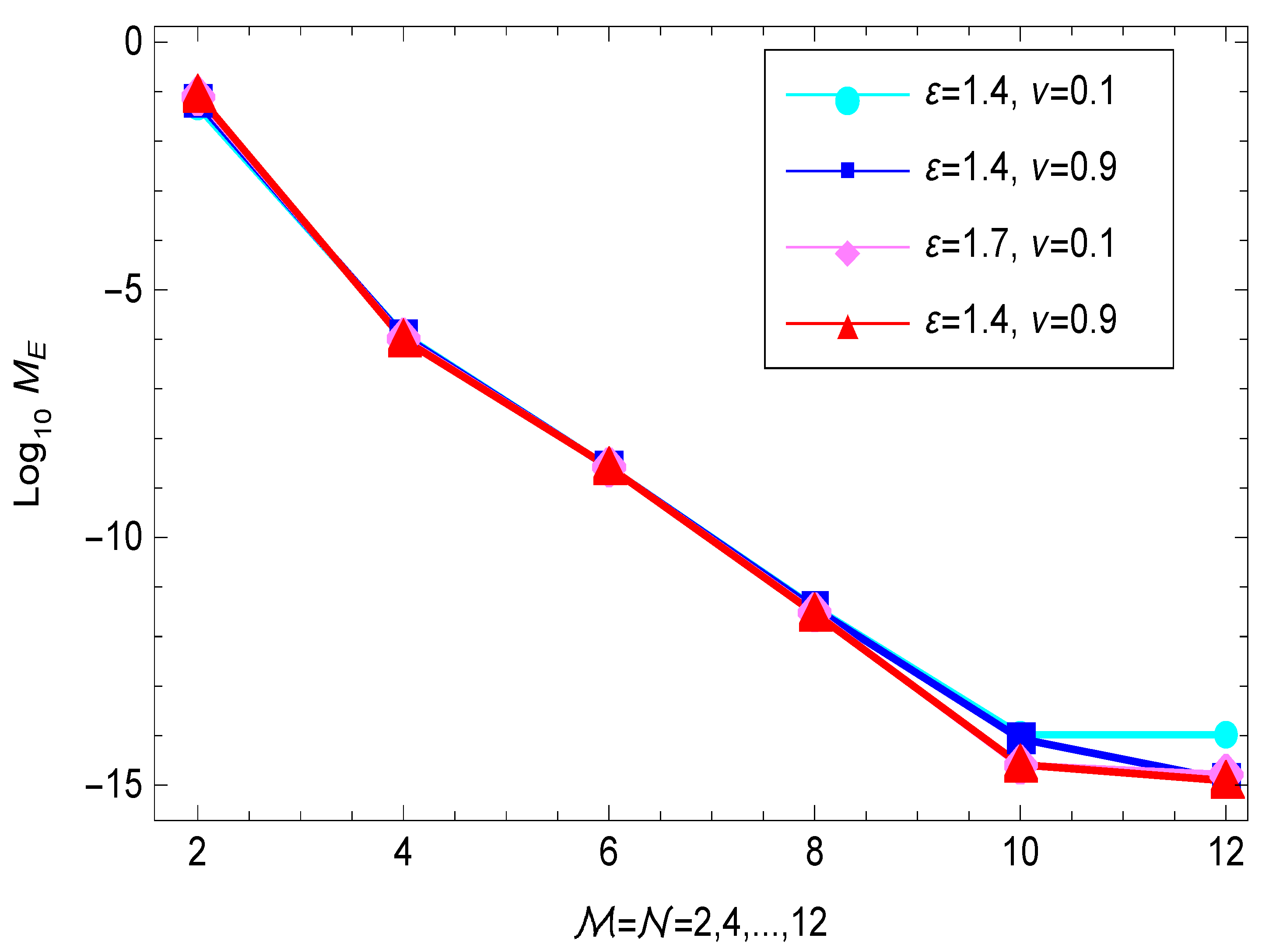
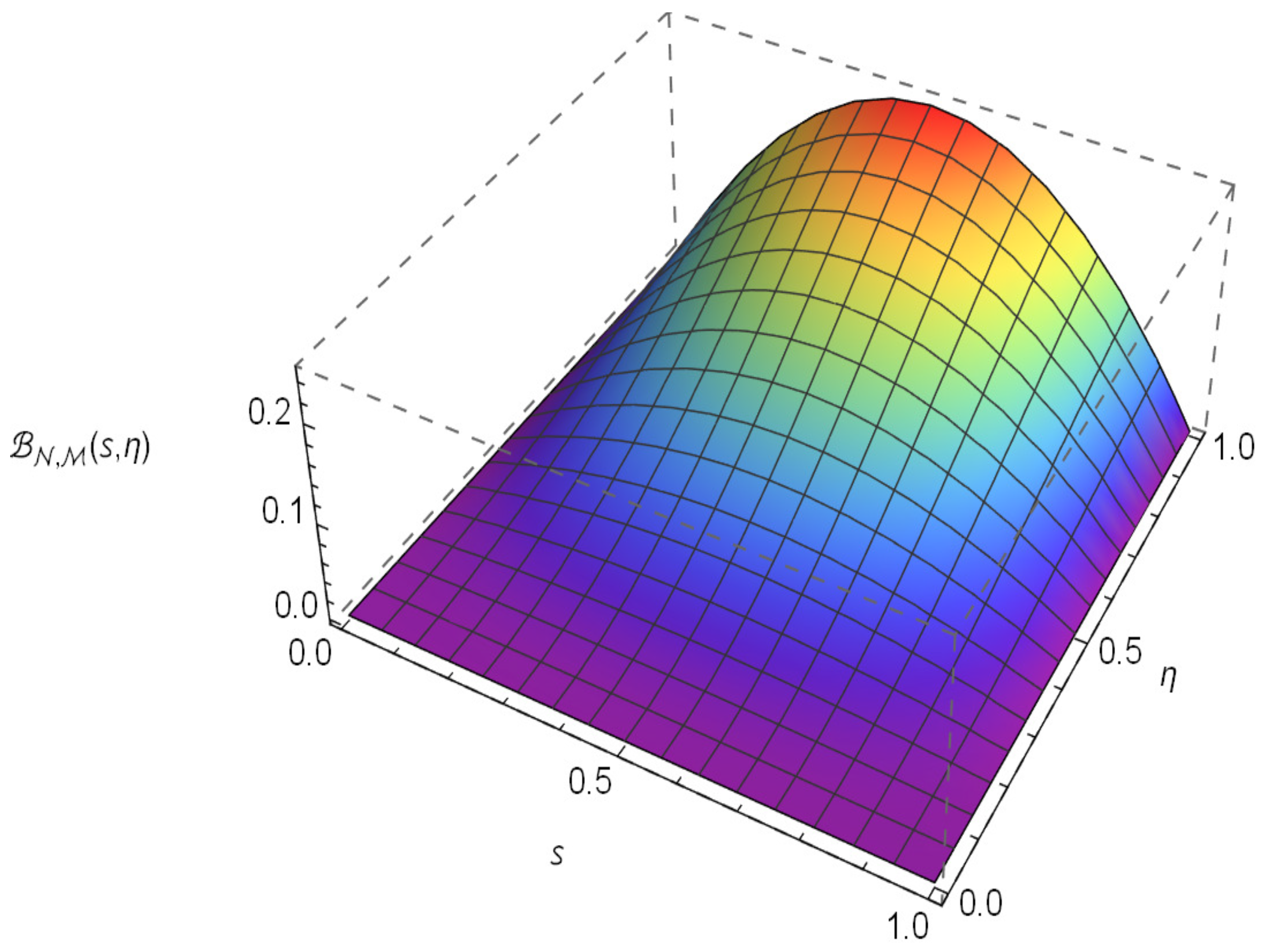
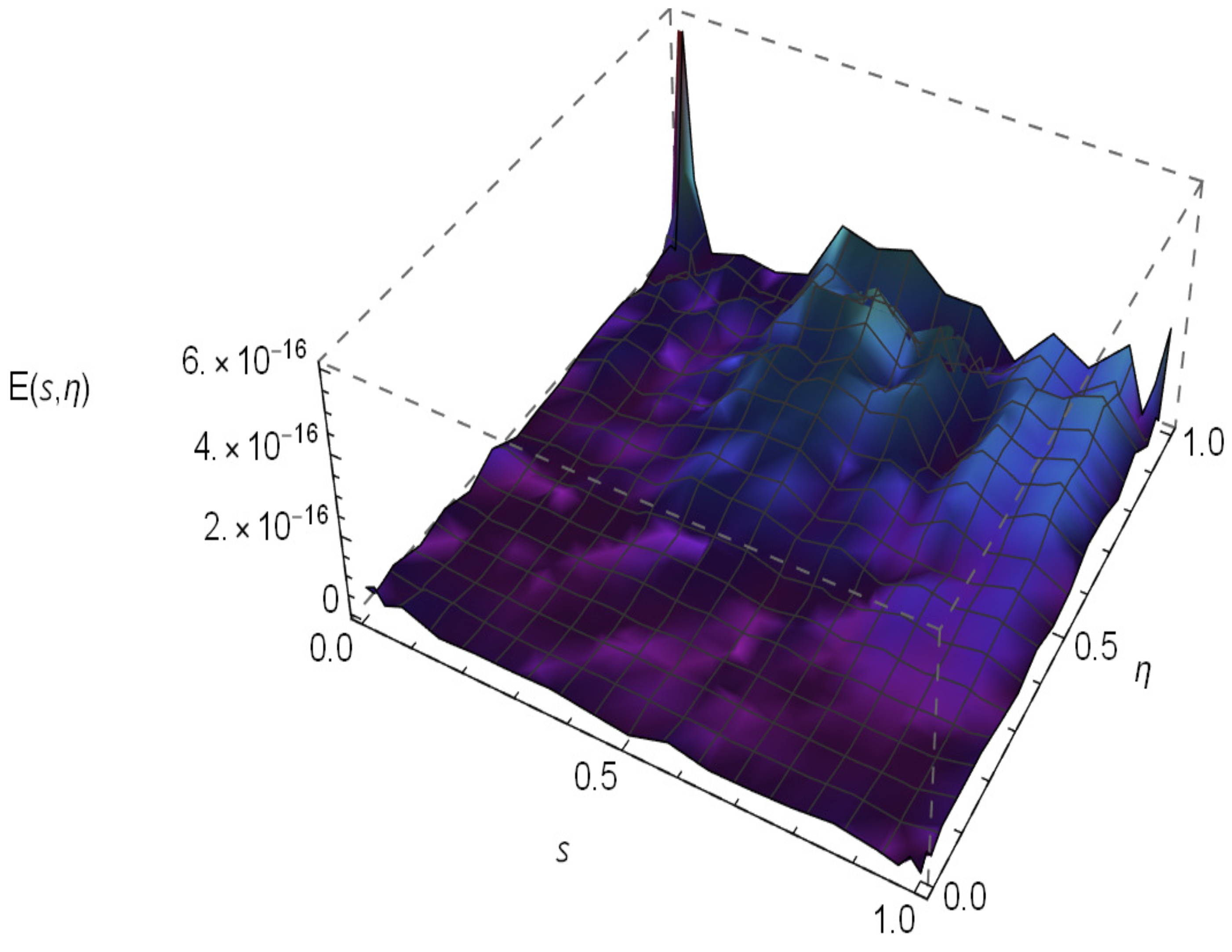
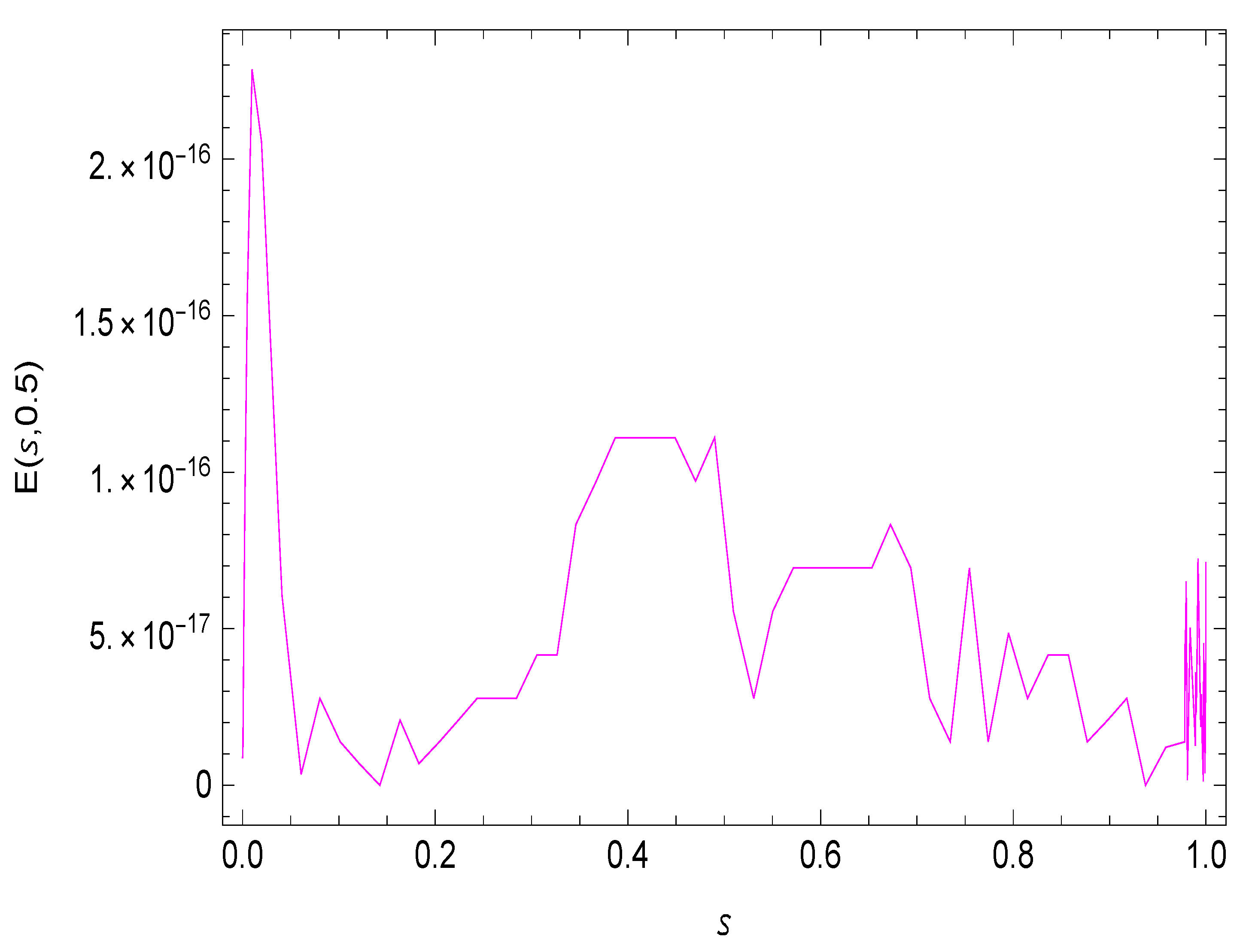
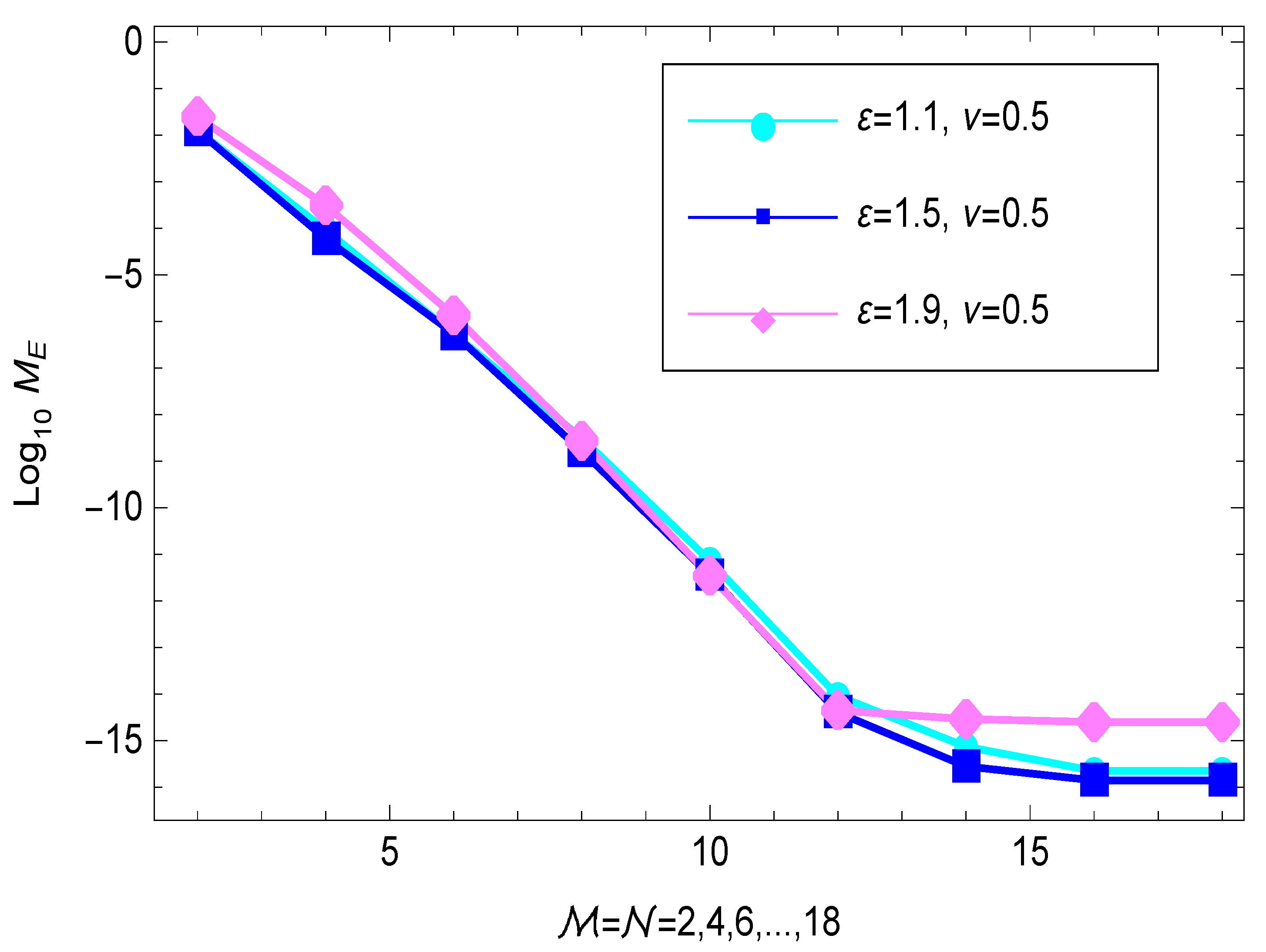
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sousa, F.S.; Lages, C.; Ansoni, J.L.; Castelo, A.; Simao, A. A finite difference method with meshless interpolation for incompressible flows in non-graded tree-based grids. J. Comput. Phys. 2019, 396, 848–866. [Google Scholar] [CrossRef]
- Mbroh, N.A.; Munyakazi, J.B. A fitted operator finite difference method of lines for singularly perturbed parabolic convection–diffusion problems. Math. Comput. Simul. 2019, 165, 156–171. [Google Scholar] [CrossRef]
- Patil, H.M.; Maniyeri, R. Finite difference method based analysis of bio-heat transfer in human breast cyst. Therm. Sci. Eng. Prog. 2019, 10, 42–47. [Google Scholar] [CrossRef]
- Li, P.W.; Fu, Z.J.; Gu, Y.; Song, L. The generalized finite difference method for the inverse Cauchy problem in two-dimensional isotropic linear elasticity. Int. J. Solids Struct. 2019, 174, 69–84. [Google Scholar] [CrossRef]
- Shu, Y.; Li, J.; Zhang, C. A local and parallel Uzawa finite element method for the generalized Navier–Stokes equations. Appl. Math. Comput. 2020, 387, 124671. [Google Scholar] [CrossRef]
- Wang, C.; Wang, J. Primal–dual weak Galerkin finite element methods for elliptic Cauchy problems. Comput. Math. Appl. 2020, 79, 746–763. [Google Scholar] [CrossRef] [Green Version]
- Xiao, X.; Dai, Z.; Feng, X. A positivity preserving characteristic finite element method for solving the transport and convection–diffusion–reaction equations on general surfaces. Comput. Phys. Commun. 2020, 247, 106941. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Taha, T.M.; Machado, J.A.T. A review of operational matrices and spectral techniques for fractional calculus. Nonlinear Dyn. 2015, 81, 1023–1052. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Zaky, M.A. A method based on the Jacobi tau approximation for solving multi-term time–space fractional partial differential equations. J. Comput. Phys. 2015, 281, 876–895. [Google Scholar] [CrossRef]
- Doha, E.; Abdelkawy, M.; Amin, A.; Lopes, A.M. Shifted Jacobi–Gauss-collocation with convergence analysis for fractional integro-differential equations. Commun. Nonlinear Sci. Numer. Simul. 2019, 72, 342–359. [Google Scholar] [CrossRef]
- Doha, E.H.; Bhrawy, A.H.; Ezz-Eldien, S.S. A Chebyshev spectral method based on operational matrix for initial and boundary value problems of fractional order. Comput. Math. Appl. 2011, 62, 2364–2373. [Google Scholar] [CrossRef] [Green Version]
- Doha, E.H.; Abdelkawy, M.A.; Amin, A.; Baleanu, D. Shifted Jacobi spectral collocation method with convergence analysis for solving integro-differential equations and system of integro-differential equations. Nonlinear Anal. Model. Control 2019, 24, 332–352. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Abdelkawy, M.A. A fully spectral collocation approximation for multi-dimensional fractional Schrödinger equations. J. Comput. Phys. 2015, 294, 462–483. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Doha, E.H.; Baleanu, D.; Ezz-Eldien, S.S. A spectral tau algorithm based on Jacobi operational matrix for numerical solution of time fractional diffusion-wave equations. J. Comput. Phys. 2015, 293, 142–156. [Google Scholar] [CrossRef]
- Hafez, R.M.; Zaky, M.A.; Abdelkawy, M.A. Jacobi Spectral Galerkin method for Distributed-Order Fractional Rayleigh-Stokes problem for a Generalized Second Grade Fluid. Front. Phys. 2020, 7, 240. [Google Scholar] [CrossRef]
- Doha, E.H.; Abd-Elhameed, W.M. Efficient spectral ultraspherical-dual-Petrov–Galerkin algorithms for the direct solution of (2n+ 1) th-order linear differential equations. Math. Comput. Simul. 2009, 79, 3221–3242. [Google Scholar] [CrossRef]
- Bologna, M.; Tsallis, C.; Grigolini, P. Anomalous diffusion associated with nonlinear fractional derivative Fokker-Planck-like equation: Exact time-dependent solutions. Phys. Rev. E 2000, 62, 2213. [Google Scholar] [CrossRef] [Green Version]
- Tsallis, C.; Lenzi, E. Anomalous diffusion: Nonlinear fractional Fokker–Planck equation. Chem. Phys. 2002, 284, 341–347. [Google Scholar] [CrossRef]
- Saichev, A.I.; Zaslavsky, G.M. Fractional kinetic equations: Solutions and applications. Chaos Interdiscip. J. Nonlinear Sci. 1997, 7, 753–764. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Xiao, A.; Yang, W. Crank–Nicolson difference scheme for the coupled nonlinear Schrödinger equations with the Riesz space fractional derivative. J. Comput. Phys. 2013, 242, 670–681. [Google Scholar] [CrossRef]
- Wang, P.; Huang, C. An efficient fourth-order in space difference scheme for the nonlinear fractional Ginzburg–Landau equation. BIT Numer. Math. 2018, 58, 783–805. [Google Scholar] [CrossRef]
- Liao, H.l.; Lyu, P.; Vong, S. Second-order BDF time approximation for Riesz space-fractional diffusion equations. Int. J. Comput. Math. 2018, 95, 144–158. [Google Scholar] [CrossRef]
- Cheng, X.; Duan, J.; Li, D. A novel compact ADI scheme for two-dimensional Riesz space fractional nonlinear reaction–diffusion equations. Appl. Math. Comput. 2019, 346, 452–464. [Google Scholar] [CrossRef]
- Liu, F.; Zhuang, P.; Turner, I.; Burrage, K.; Anh, V. A new fractional finite volume method for solving the fractional diffusion equation. Appl. Math. Model. 2014, 38, 3871–3878. [Google Scholar] [CrossRef]
- Ervin, V.J.; Heuer, N.; Roop, J.P. Numerical approximation of a time dependent, nonlinear, space-fractional diffusion equation. SIAM J. Numer. Anal. 2007, 45, 572–591. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Z.; Li, C. A numerical approach to the generalized nonlinear fractional Fokker–Planck equation. Comput. Math. Appl. 2012, 64, 3075–3089. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Huang, C.; Wang, P. Galerkin finite element method for nonlinear fractional Schrödinger equations. Numer. Algorithms 2017, 74, 499–525. [Google Scholar] [CrossRef]
- Lai, J.; Liu, H. On a novel numerical scheme for Riesz fractional partial differential equations. Mathematics 2021, 9, 2014. [Google Scholar] [CrossRef]
- Yang, S.; Liu, Y.; Liu, H.; Wang, C. Numerical Methods for Semilinear Fractional Diffusion Equations with Time Delay. Adv. Appl. Math. Mech. 2022, 14, 56–78. [Google Scholar]
- Zhao, X.; Sun, Z.z.; Hao, Z.p. A fourth-order compact ADI scheme for two-dimensional nonlinear space fractional Schrodinger equation. SIAM J. Sci. Comput. 2014, 36, A2865–A2886. [Google Scholar] [CrossRef]
- Yang, Q.; Turner, I.; Moroney, T.; Liu, F. A finite volume scheme with preconditioned Lanczos method for two-dimensional space-fractional reaction–diffusion equations. Appl. Math. Model. 2014, 38, 3755–3762. [Google Scholar] [CrossRef] [Green Version]
- Liu, F.; Zhuang, P.; Turner, I.; Anh, V.; Burrage, K. A semi-alternating direction method for a 2-D fractional FitzHugh–Nagumo monodomain model on an approximate irregular domain. J. Comput. Phys. 2015, 293, 252–263. [Google Scholar] [CrossRef] [Green Version]
- Bu, W.; Tang, Y.; Wu, Y.; Yang, J. Crank–Nicolson ADI Galerkin finite element method for two-dimensional fractional FitzHugh–Nagumo monodomain model. Appl. Math. Comput. 2015, 257, 355–364. [Google Scholar] [CrossRef]
- Yang, Z.; Yuan, Z.; Nie, Y.; Wang, J.; Zhu, X.; Liu, F. Finite element method for nonlinear Riesz space fractional diffusion equations on irregular domains. J. Comput. Phys. 2017, 330, 863–883. [Google Scholar] [CrossRef] [Green Version]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: Hoboken, NJ, USA, 1993. [Google Scholar]
- Zhuang, P.; Liu, F.; Anh, V.; Turner, I. Numerical methods for the variable-order fractional advection-diffusion equation with a nonlinear source term. SIAM J. Numer. Anal. 2009, 47, 1760–1781. [Google Scholar] [CrossRef] [Green Version]
- Bhrawy, A.; Abdelkawy, M.; Ezz-Eldien, S. Efficient spectral collocation algorithm for a two-sided space fractional Boussinesq equation with non-local conditions. Mediterr. J. Math. 2016, 13, 2483–2506. [Google Scholar] [CrossRef]
- Zhang, J. A stable explicitly solvable numerical method for the Riesz fractional advection–dispersion equations. Appl. Math. Comput. 2018, 332, 209–227. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Shomrani, M.M.; Abdelkawy, M.A. Legendre Spectral Collocation Technique for Advection Dispersion Equations Included Riesz Fractional. Fractal Fract. 2022, 6, 9. https://doi.org/10.3390/fractalfract6010009
Al-Shomrani MM, Abdelkawy MA. Legendre Spectral Collocation Technique for Advection Dispersion Equations Included Riesz Fractional. Fractal and Fractional. 2022; 6(1):9. https://doi.org/10.3390/fractalfract6010009
Chicago/Turabian StyleAl-Shomrani, Mohamed M., and Mohamed A. Abdelkawy. 2022. "Legendre Spectral Collocation Technique for Advection Dispersion Equations Included Riesz Fractional" Fractal and Fractional 6, no. 1: 9. https://doi.org/10.3390/fractalfract6010009
APA StyleAl-Shomrani, M. M., & Abdelkawy, M. A. (2022). Legendre Spectral Collocation Technique for Advection Dispersion Equations Included Riesz Fractional. Fractal and Fractional, 6(1), 9. https://doi.org/10.3390/fractalfract6010009






