Solutions of General Fractional-Order Differential Equations by Using the Spectral Tau Method
Abstract
:1. Introduction
2. Mathematical Formulation for the Main Results
2.1. Liouville–Caputo Type Fractional Derivatives
- for each constant and ;
- ;
- For , we havewhere
2.2. Second Kind Chebyshev Polynomial
2.3. Linear Fractional Arguments
3. Theoretical Analysis Applied to FODDE
4. Methodology and the Error Estimation
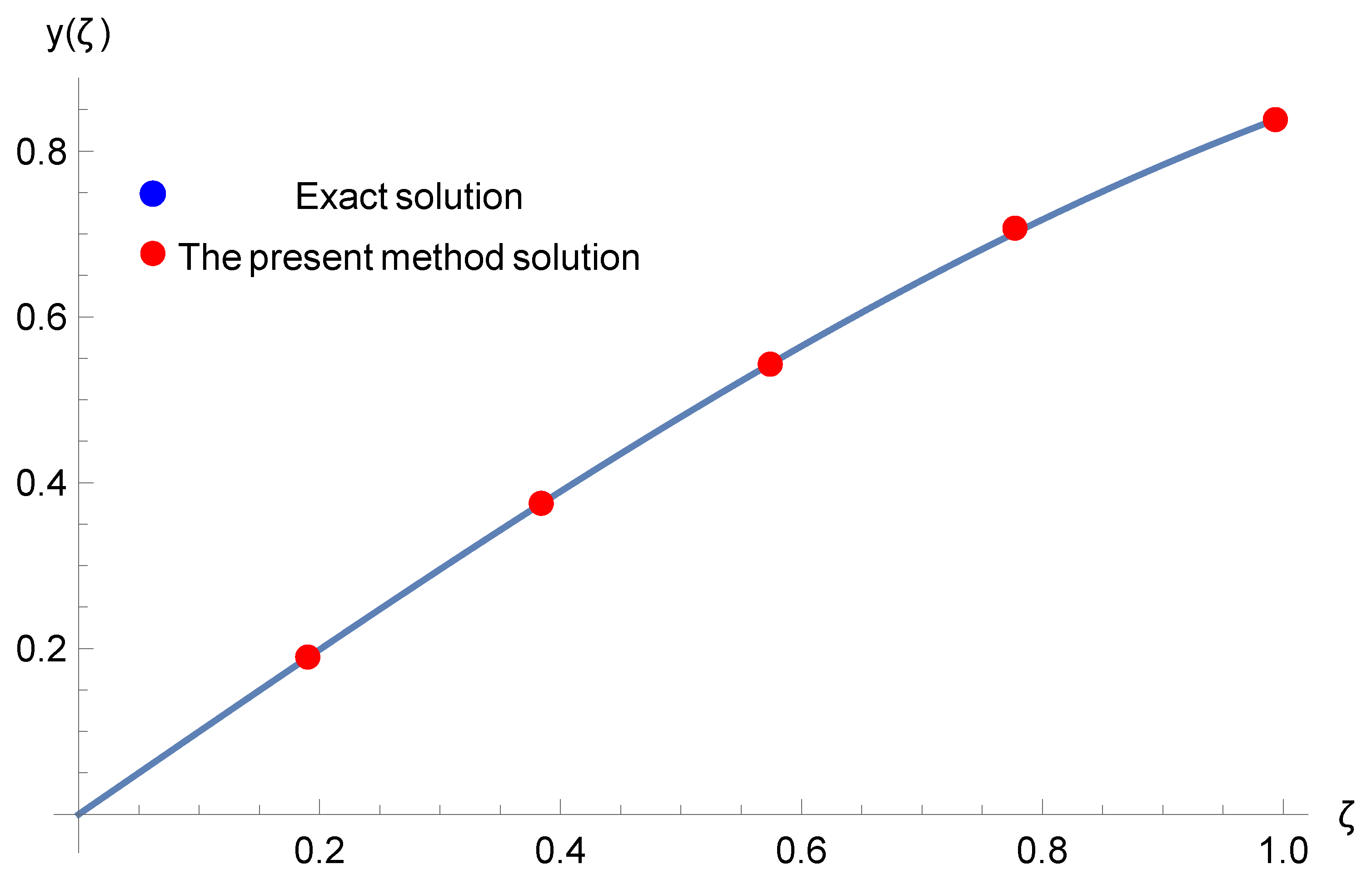
5. Illustrative Examples
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vanani, S.K.; Aminataei, A. Tau approximate solution of fractional partial differential equations. Comput. Math. Appl. 2011, 62, 1075–1083. [Google Scholar] [CrossRef] [Green Version]
- Ghoreishi, F.; Yazdani, S. An extension of the spectral Tau method for numerical solution of multi-order fractional differential equations with convergence analysis. Comput. Math. Appl. 2011, 61, 30–43. [Google Scholar] [CrossRef] [Green Version]
- Ren, R.-F.; Li, H.-B.; Jiang, W.; Song, M.-Y. An efficient Chebyshev-Tau method for solving the space fractional diffusion equations. Appl. Math. Comput. 2013, 224, 259–267. [Google Scholar] [CrossRef]
- Eslahchi, M.R.; Dehghan, M.; Parvizi, M. Application of the collocation method for solving nonlinear fractional integro-differential equations. J. Comput. Appl. Math. 2014, 257, 105–128. [Google Scholar] [CrossRef]
- Tohidi, E.; Bhrawy, A.H.; Erfani, K. A collocation method based on Bernoulli operational matrix for numerical solution of generalized pantograph equation. Appl. Math. Model. 2013, 37, 4283–4294. [Google Scholar] [CrossRef]
- Sedaghat, S.; Ordokhani, Y.; Dehghan, M. Numerical solution of the delay differential equations of pantograph type via Chebyshev polynomials. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 4815–4830. [Google Scholar] [CrossRef]
- Izadi, M.; Srivastava, H.M. A novel matrix technique for multi-order pantograph differential equations of fractional order. Proc. R. Soc. Lond. Ser. A 2021, 477, 2021031. [Google Scholar] [CrossRef]
- Hafshejani, M.S.; Vanani, S.K.; Hafshejani, J.S. Numerical solution of delay differential equations using Legendre wavelet method. World Appl. Sci. J. 2011, 13, 27–33. [Google Scholar]
- Marzban, H.R.; Razzaghi, M. Solution of multi-delay systems using hybrid of block-pulse functions and Taylor series. J. Sound Vib. 2006, 292, 954–963. [Google Scholar] [CrossRef]
- Tang, X.; Shi, Y.; Xu, H. Well conditioned pseudospectral schemes with tunable basis for fractional delay differential equations. J. Sci. Comput. 2018, 74, 920–936. [Google Scholar] [CrossRef]
- Khader, M.M.; Hendy, A.S. The approximate and exact solutions of the fractional-order delay differential equations using Legendre pseudospectral method. Int. J. Pure Appl. Math. 2012, 74, 287–297. [Google Scholar]
- Wang, Z. A numerical method for delayed fractional-order differential equations. J. Appl. Math. 2013, 2013, 256071. [Google Scholar] [CrossRef]
- Moghaddam, B.P.; Mostaghim, Z.S. A numerical method based on finite difference for solving fractional delay differential equations. J. Taibah Univ. Sci. 2013, 7, 120–127. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.-L.; Zhao, W.-W. Haar wavelet operational matrix of fractional order integration and its applications in solving the fractional order differential equations. Appl. Math. Comput. 2010, 216, 2276–2285. [Google Scholar] [CrossRef]
- Iqbal, M.A.; Ali, A.; Mohyud-Din, S.T. Chebyshev wavelets method for fractional delay differential equations. Int. J. Mod. Appl. Phys. 2013, 4, 49–61. [Google Scholar]
- Keshavarz, E.; Ordokhani, Y.; Razzaghi, M. Bernoulli wavelet operational matrix of fractional order integration and its applications in solving the fractional order differential equations. Appl. Math. Model. 2014, 38, 6038–6051. [Google Scholar] [CrossRef]
- Dehghan, M.; Manafian, J.; Saadatmandi, A. Solving nonlinear fractional partial differential equations using the homotopy analysis method. Numer. Methods Partial Differ. Equ. 2010, 26, 448–479. [Google Scholar] [CrossRef]
- Saadatmandi, A.; Dehghan, M. A Tau approach for solution of the space fractional diffusion equation. Comput. Math. Appl. 2011, 62, 1135–1142. [Google Scholar] [CrossRef] [Green Version]
- Azizi, M.R.; Saadatmandi, A.; Dehghan, M. The Sinc Legendre collocation method for a class of fractional convection diffusion equations with variable coefficients. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 4125–4136. [Google Scholar]
- Manafian, J.; Dehghan, M.; Saadatmandi, A. The solution of the linear fractional partial differential equations using the homotopy analysis method. Z. Naturforsh. A 2010, 65, 935. [Google Scholar]
- Iakovleva, V.; Vanegas, C.J. On the solution of differential equations with delayed and advanced arguments. Electron. J. Differ. Equ. Conf. 2005, 13, 57–63. [Google Scholar]
- Rus, A.I.; Dârzu-Ilea, V.A. First order functional-differential equations with both advanced and retarded arguments. Fixed Point Theory 2004, 5, 103–115. [Google Scholar]
- Mohammed, P.O.; Machado, J.A.T.; Guirao, J.L.G.; Agarwal, R.P. Adomian decomposition and fractional power series solution of a class of nonlinear fractional differential equations. Mathematics 2021, 9, 1070. [Google Scholar] [CrossRef]
- Sana, G.; Mohammed, P.O.; Shin, D.Y.; Noor, M.A.; Oudat, M.S. On iterative methods for solving nonlinear equations in quantum calculus. Fractal Fract. 2021, 5, 60. [Google Scholar] [CrossRef]
- Grbz, F.; Ding, S.; Han, H.; Long, P. A characterization of rough fractional type integral operators and Campanato estimates for their commutators on the variable exponent vanishing generalized Morrey spaces. arXiv 2018, arXiv:1811.06702. [Google Scholar]
- Reutskiy, S.Y. The backward substitution method for multipoint problems with linear Volterra-Fredholm integro-differential equations of the neutral type. J. Comput. Appl. Math. 2016, 296, 724–738. [Google Scholar] [CrossRef]
- Ramadan, M.A.; Raslan, K.R.; El-Danaf, T.S.; Abd-El-Salam, M.A. An exponential Chebyshev second kind approximation for solving high-order ordinary differential equations in unbounded domains, with application to Dawson’s integral. J. Egypt. Math. Soc. 2017, 25, 197–205. [Google Scholar] [CrossRef] [Green Version]
- Raslan, K.R.; Khalid, K.A.; Emad, M. Spectral Tau method for solving general fractional order differential equation with linear functional argument. J. Egypt. Math. Soc. 2019, 27, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Lazarević, M.P.; Rapaić, M.R.; Šekara, T.B. Introduction to Fractional Calculus with Brief Historical Background. In Advanced Topics on Applications of Fractional Calculus on Control Problems, System Stability and Modelin; Mladenov, V., Mastorakis, N., Eds.; WSEAS Press: New York, NY, USA, 2014; pp. 3–16. [Google Scholar]
- Mohammed, P.O.; Abdeljawad, T.; Hamasalh, F.K. On Discrete delta Caputo-Fabrizio fractional operators and monotonicity analysis. Fractal Fract. 2021, 5, 116. [Google Scholar] [CrossRef]
- Diethelm, K. The Analysis of Fractional Differential Equations; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Molliq, R.Y.; Noorani, M.S.M.; Hashim, I. Variational iteration method for fractional heat- and wave-like equations. Nonlinear Anal. Real World Appl. 2009, 10, 1854–1869. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; North-Holland Mathematics Studies; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Baleanu, D.; Fernandez, A. On fractional operators and their classifications. Mathematics 2019, 7, 830. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, H.M. Fractional-order derivatives and integrals: Introductory overview and recent developments. Kyungpook Math. J. 2020, 60, 73–116. [Google Scholar]
- Srivastava, H.M. Some parametric and argument variations of the operators of fractional calculus and related special functions and integral transformations. J. Nonlinear Convex Anal. 2021, 22, 1501–1520. [Google Scholar]
- Srivastava, H.M. An introductory overview of fractional-calculus operators based upon the Fox-Wright and related higher transcendental functions. J. Adv. Eng. Comput. 2021, 5, 135–166. [Google Scholar]
- Saeed, U. Hermite wavelet method for fractional delay differential equations. J. Differ. Equ. 2014, 2014, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Rahimkhani, P.; Ordokhani, Y.; Babolian, E. A new operational matrix based on Bernoulli wavelets for solving fractional delay differential equations. Numer. Algorithms 2017, 74, 223–245. [Google Scholar] [CrossRef]
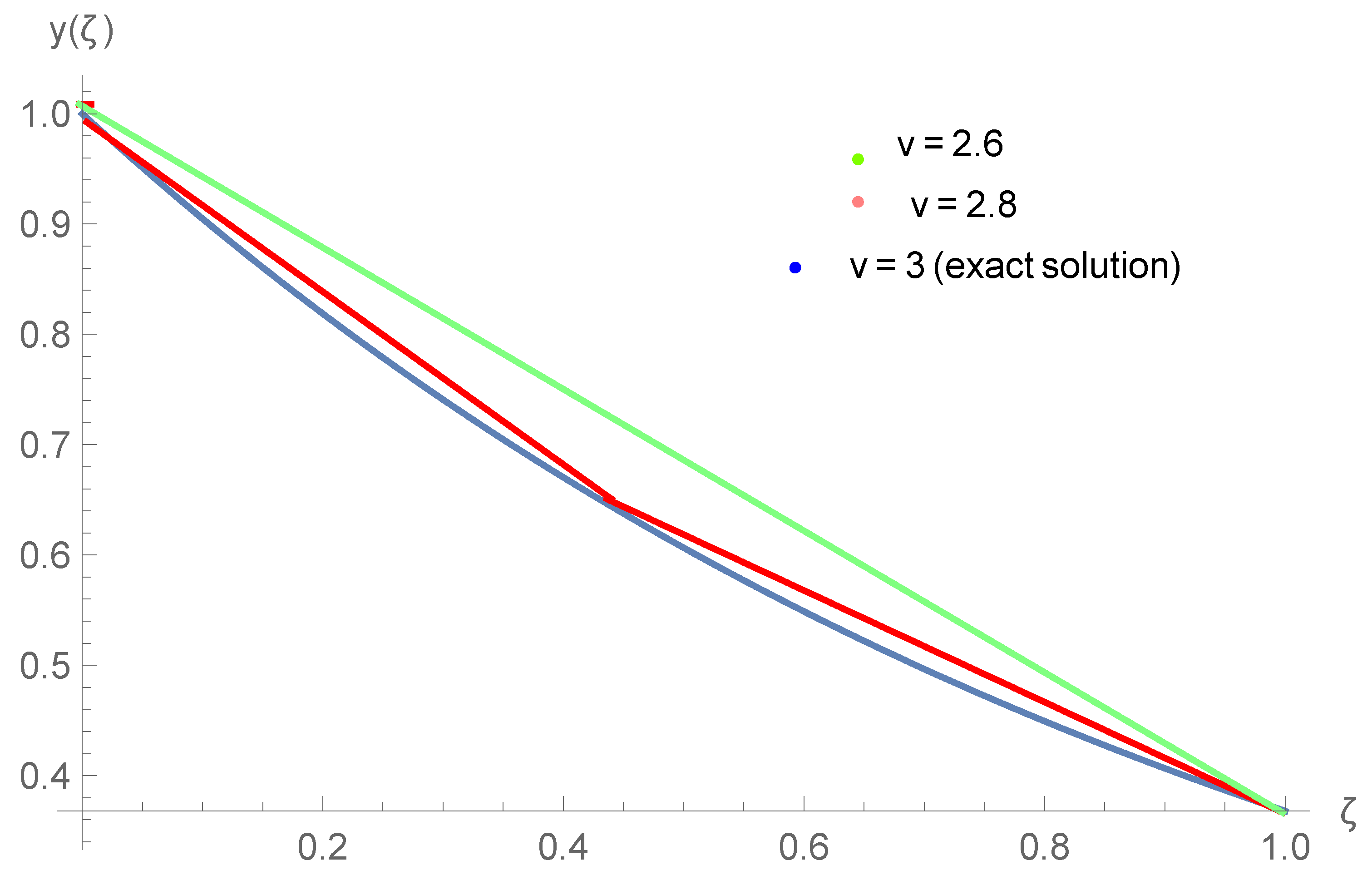
| Exact | Present Method | [39] | [38] | Presented Method | Presented Method | |
|---|---|---|---|---|---|---|
| Solution | () () | () | () () | |||
| 0 | 1.00000 | 1.00000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 0.2 | 0.8187 | 0.8187 | 0.8187 | 0.8187 | 0.8185 | 0.8185 |
| 0.4 | 0.6703 | 0.6703 | 0.6703 | 0.6703 | 0.6685 | 0.6682 |
| 0.6 | 0.5488 | 0.5488 | 0.5488 | 0.5488 | 0.5480 | 0.5488 |
| 0.8 | 0.4493 | 0.4493 | 0.4494 | 0.4493 | 0.4366 | 0.4281 |
| 1 | 0.3679 | 0.3679 | 0.3679 | 0.3680 | 0.3679 | 0.3652 |
| Exact | Present Method | |
|---|---|---|
| Solution | (), | |
| 0.2 | 0.1975 | 0.1985 |
| 0.4 | 0.3894 | 0.3892 |
| 0.6 | 0.5646 | 0.5645 |
| 0.8 | 0.7173 | 0.7173 |
| 1 | 0.8414 | 0.8414 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Srivastava, H.M.; Gusu, D.M.; Mohammed, P.O.; Wedajo, G.; Nonlaopon, K.; Hamed, Y.S. Solutions of General Fractional-Order Differential Equations by Using the Spectral Tau Method. Fractal Fract. 2022, 6, 7. https://doi.org/10.3390/fractalfract6010007
Srivastava HM, Gusu DM, Mohammed PO, Wedajo G, Nonlaopon K, Hamed YS. Solutions of General Fractional-Order Differential Equations by Using the Spectral Tau Method. Fractal and Fractional. 2022; 6(1):7. https://doi.org/10.3390/fractalfract6010007
Chicago/Turabian StyleSrivastava, Hari Mohan, Daba Meshesha Gusu, Pshtiwan Othman Mohammed, Gidisa Wedajo, Kamsing Nonlaopon, and Y. S. Hamed. 2022. "Solutions of General Fractional-Order Differential Equations by Using the Spectral Tau Method" Fractal and Fractional 6, no. 1: 7. https://doi.org/10.3390/fractalfract6010007
APA StyleSrivastava, H. M., Gusu, D. M., Mohammed, P. O., Wedajo, G., Nonlaopon, K., & Hamed, Y. S. (2022). Solutions of General Fractional-Order Differential Equations by Using the Spectral Tau Method. Fractal and Fractional, 6(1), 7. https://doi.org/10.3390/fractalfract6010007










