Investigation of Finite-Difference Schemes for the Numerical Solution of a Fractional Nonlinear Equation
Abstract
1. Introduction
- little information about numerical methods based on finite difference schemes;
- no or little comparison of simulation results with real experimental data of processes with saturation;
- mostly the order of the fractional derivative, is constant, which may produce unacceptable results when describing experimental data;
- approaches to the numerical solution of the Riccati equation with a fractional variable order derivative are poorly studied.
2. The Concept of Heredity and Memory
3. Elements of Fractional Calculus
4. Relationship between Heredity and Fractional Calculus
5. Statement of the Problem for a Nonlinear Fractional Equation
- 1.
- , moreover, the function is monotone if the function is monotone on the interval ;
- 2.
- ;
- 3.
- .
6. Nonlocal Implicit Finite Difference Scheme (IFDS)
7. Modified Newton’s Method (MNM)
8. Mnm Method for Numerical Solution of Fractional Riccati Equation
9. Explicit Finite Difference Scheme (EFDS) for Fractional Riccati Equation
10. Computational Accuracy and Test Cases
11. Software Package for Maple 2021 Environment
- implementation of a non-local explicit finite difference scheme (EFDS);
- implementation of a non-local implicit finite difference scheme (IFDS);
- implementation of the modified Newton’s method (MNM), for solving the IFDS scheme;
- implementation of modifications of the Gerasimov-Caputo fractional operator of the form and , considered in [50];
- the ability to set the coefficients of functions from t;
- the ability to set non-constant as a function of t.
- —clears the transmitted data from the specified elements;
- —create a name for a custom file;
- —display the path to the file where the function is called;
- —extract a column from a file;
- —cubic spline data smoothing;
- —normalization of the transmitted data to the maximum;
- —periodic function ;
- —displaying the chart based on the transmitted data;
- —investigation of the solution for computational accuracy and maximum error;
- —extract a column from a file;
- —output the results to a file;
- —output the results to a file.
12. Some Applications of the Fractional Riccati Equation
13. Conclusions
- A mathematical model is proposed for describing processes with saturation based on the fractional Riccati equation with variable coefficients and the derivative of a fractional variable order of the Gerasimov-Caputo type;
- Numerical methods for solving the Cauchy problem for a mathematical model are proposed: non-local EFDS, non-local IFDS, and also MNM for solving IFDS;
- The questions of approximation, stability and convergence of methods are investigated. It is shown that the EFDS converge conditionally with the first order of accuracy . IFDS is stable and has convergence order ;
- This theoretical result is confirmed by specific test examples and estimates of the computational accuracy according to Runge’s rule. It is important to note that, as a test case, the case of comparing a numerical solution using the IFDS and EFDS schemes with an exact solution is also considered. It is shown that the order of computational accuracy of numerical methods approaches the theoretical order of accuracy with an increase in the nodes of the computational grid;
- A library in the environment of symbolic mathematics Maple 2021 has been developed, which contains procedures for the numerical analysis of the fractional Riccati equation with a variable fractional order derivative of the Gerasimov-Caputo type and non-constant coefficients with the ability to visualize the simulation results.
14. Patents
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MNM | modified Newton method |
| EFDS | Explicit Finite-difference Method |
| IFDS | Implicit Finite-difference Method |
References
- Nazarov, V.E.; Kiyashko, S.B. Wave processes in media with inelastic hysteresis with saturation of nonlinear losses. Radiophysics 2016, 59, 124–136. (In Russian) [Google Scholar]
- Kurkin, A.A.; Kurkina, O.E.; Pelenovskij, E.N. Logistic models for the spread of epidemics. Proc. NSTU Im. R.E. Alekseeva 2020, 129, 9–18. (In Russian) [Google Scholar]
- Volterra, V. Theory of Functionals and of Integral and Integro-Differential Equations; Dover Publications: Mineola, NY, USA, 2005; p. 288. [Google Scholar]
- Volterra, V. Sur les ´equations int´egro-differentielles et leurs applications. Acta Math. 1912, 35, 295–356. [Google Scholar] [CrossRef]
- Uchajkin, V.V. Fractional Derivatives Method; Artichoke: Ulyanovsk, Russia, 2008; p. 510. (In Russian) [Google Scholar]
- Nakhushev, A.M. Fractional Calculus and Its Applications; Fizmatlit: Moscow, Russia, 2003; p. 272. (In Russian) [Google Scholar]
- Ortigueira, M.D.; Machado, J.T. What is a fractional derivative? J. Comput. Phys. 2015, 321, 4–13. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier Science Limited: Amsterdam, The Netherland, 2006; Volume 204, p. 523. [Google Scholar]
- Uchaikin, V.V. Fractional Derivatives for Physicists and Engineers; Vol. I. Background and Theory; Springer: Berlin/Heidelberg, Germany, 2013; p. 373. [Google Scholar]
- Ortigueira, M.D.; Valerio, D.; Machado, J.T. Variable order fractional systems. In Communications in Nonlinear Science and Numerical Simulation; Elsevier: Amsterdam, The Netherland, 2019; Volume 71, pp. 231–243. [Google Scholar] [CrossRef]
- Parovik, R.I. Mathematical Modeling of Linear Hereditary Oscillators; Kamchatka State University Named after Vitus Bering: Petropavlovsk-Kamchatsky, Russia, 2015; p. 187. (In Russian) [Google Scholar]
- Pskhu, A.V. Uravneniya v Chastnyh Proizvodnyh Drobnogo Poryadka; Science: Moscow, Russia, 2005; p. 199. (In Russian) [Google Scholar]
- Mamchuev, M.O. Boundary Value Problems for Equations and Systems of Partial Differential Equations of Fractional Order; Publishing House KBSC RAS: Nalchik, Russia, 2015; p. 200, (In Russian). [Google Scholar] [CrossRef]
- Shogenov, V.K.; Akhkubekov, A.A.; Akhkubekov, R.A. Fractional differentiation method in the theory of Brownian motion. Izv Vyssh. Uchebn. Zaved. Severo-Kavkaz. Reg. Estestv. Nauki. 2004, 1, 46–50. [Google Scholar]
- Méhauté, A.L.; Nigmatullin, R.R.; Nivanen, L. Flèches du Temps et Géométrie Fractale; Hermes: Paris, France, 1998; p. 348. [Google Scholar]
- Kobelev, Y.L. Phenomenological Models for Describing Large Systems with Fractal Structures. In Abstract of the Dissertation of the Candidate of Physical and Mathematical Sciences; Ural State University A.M. Gorky: Yekaterinburg, Russia, 2001. (In Russian) [Google Scholar]
- Sun, H.; Chen, W.; Wei, H.; Chen, Y.Q. A comparative study of constant-order and variable-order fractional models in characterizing memory property of systems. Eur. Phys. J.-Spec. Top. 2011, 193, 185–192. [Google Scholar] [CrossRef]
- Sun, H.; Chen, W.; Li, C.; Chen, Y. Finite difference schemes for variable-order time fractional diffusion equation. Int. J. Bifurc. Chaos 2012, 22, 1250085. [Google Scholar] [CrossRef]
- Momani, S.; Shawagfeh, N. Decomposition method for solving fractional Riccati differential equations. Appl. Math. Comput. 2006, 182, 1083–1092. [Google Scholar] [CrossRef]
- Tan, Y.; Abbasbandy, S. Homotopy analysis method for quadratic Riccati differential equation. Commun. Nonlinear Sci. Numer. Simul. 2008, 13, 539–546. [Google Scholar] [CrossRef]
- Jafari, H.; Tajadodi, H. He’s variational iteration method for solving fractional Riccati differential equation. Int. J. Differ. Equ. 2010, 2010, 1–8. [Google Scholar] [CrossRef]
- Khan, N.A.; Ara, A.; Jamil, M. An efficient approach for solving the Riccati equation with fractional orders. Comput. Math. Appl. 2011, 61, 2683–2689. [Google Scholar] [CrossRef]
- Sweilam, N.H.; Khader, M.M.; Mahdy, A.M.S. Numerical studies for solving fractional Riccati differential equation. Appl. Appl. Math. 2012, 7, 595–608. [Google Scholar]
- Merdan, M. On the solutions fractional Riccati differential equation with modified Riemann–Liouville derivative. Int. J. Differ. Equ. 2012, 2012, 1–17. [Google Scholar] [CrossRef]
- Khader, M.M. Numerical treatment for solving fractional Riccati differential equation. J. Egypt. Math. Soc. 2013, 21, 32–37. [Google Scholar] [CrossRef]
- Khader, M.M.; Mahdy, A.M.S.; Mohamed, E.S. On approximate solutions for fractional Riccati differential equation. Int. J. Eng. Appl. Sci. 2014, 4, 1–10. Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.682.4526&rep=rep1&type=pdf (accessed on 15 November 2021).
- Ezz-Eldien, S.S. On solving fractional logistic population models with applications. Comput. Appl. Math. 2018, 37, 6392–6409. [Google Scholar] [CrossRef]
- Khan, N.A.; Ara, A.; Khan, N.A. Fractional-order Riccati differential equation: analytical approximation and numerical results. Adv. Differ. Equ. 2013, 185. [Google Scholar] [CrossRef][Green Version]
- Salehi, Y.; Darvishi, M.T. An investigation of fractional Riccati differential equation. Int. J. Light Electron Opt. 2016, 127, 11505–11521. [Google Scholar] [CrossRef]
- Aminikhah, H.; Sheikhani, A.H.R.; Rezazadeh, H. Approximate analytical solutions of distributed order fractional Riccati differential equation. Ain Shams Eng. J. 2018, 9, 581–588. [Google Scholar] [CrossRef]
- Syam, M.I.; Alsuwaidi, A.; Alneyadi, A.; Al Refai, S.; Al Khaldi, S. Implicit hybrid methods for solving fractional Riccati equation. J. Nonlinear Sci. Appl. 2019, 12, 124–134. [Google Scholar] [CrossRef][Green Version]
- Khader, M.M.; Sweilam, N.H.; Kharrat, B.N. Numerical Simulation for Solving Fractional Riccati and Logistic Differential Equations as a Difference Equation. Appl. Appl. Math. Int. J. 2020, 15, 37. Available online: https://digitalcommons.pvamu.edu/aam/vol15/iss1/37/ (accessed on 21 December 2021).
- Cai, M.; Li, C. Numerical approaches to fractional integrals and derivatives: A review. Mathematics 2020, 8, 43. [Google Scholar] [CrossRef]
- Volterra, V. Mathematical Theory of the Struggle for Existence; Nauka: Moscow, Russia, 1976; p. 286. [Google Scholar]
- Gerasimov, A.N. Generalization of linear deformation laws and their application to internal friction problems. AS USSR. Appl. Math. Mech. 1948, 12, 529–539. [Google Scholar]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent—II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Caputo, M. Elasticita e Dissipazione; Zanichelli: Bologna, Italy, 1969; p. 150. [Google Scholar]
- Oldham, K.; Spanier, J. The Fractional Calculus Theory and Applications of Differentiation and Integration to Arbitrary Order; Academic Press: London, UK, 1974; p. 240. [Google Scholar]
- Parovik, R.I. Mathematical models of oscillators with memory. Oscil.-Recent Dev. 2019, 3–21. [Google Scholar] [CrossRef]
- Parovik, R.I. On a finite-difference scheme for an hereditary oscillatory equation. J. Math. Sci. 2021, 253, 547–557. [Google Scholar] [CrossRef]
- Parovik, R.I. Explicit finite-difference scheme for the numerical solution of the model equation of nonlinear hereditary oscillator with variable-order fractional derivatives. Arch. Control. Sci. 2016, 26, 429–435. [Google Scholar] [CrossRef]
- Parovik, R.I. Mathematical modeling of linear fractional oscillators. Math. Model. Linear Fract. Oscil. 2020, 8, 1879. [Google Scholar] [CrossRef]
- Parovik, R.I.; Tverdyi, D.A. Some Aspects of Numerical Analysis for a Model Nonlinear Fractional Variable Order Equation. Math. Comput. Appl. 2021, 26, 55. [Google Scholar] [CrossRef]
- Cai, M.; Li, C. Theory and Numerical Approximations of Fractional Integrals and Derivatives; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2020; p. 317. [Google Scholar] [CrossRef]
- Torres-Hernandez, A.; Brambila-Paz, F.; Iturrarán-Viveros, U.; Caballero-Cruz, R. Fractional Newton–Raphson Method Accelerated with Aitken’s Method. Axioms 2021, 10, 47. [Google Scholar] [CrossRef]
- Tvyordyj, D.A. Hereditary Riccati equation with fractional derivative of variable order. J. Math. Sci. 2021, 253, 564–572. [Google Scholar] [CrossRef]
- Garrappa, R. Numerical Solution of Fractional Differential Equations: A Survey and a Software Tutorial. Mathematics 2018, 6, 16. [Google Scholar] [CrossRef]
- Tverdyi, D.A. Investigation of numerical methods for solving the Riccati equation with a fractional derivative of variable order. Probl. Comput. Appl. Math. 2021, 23, 5–18. (In Russian) [Google Scholar]
- Korotayev, A.V.; Grinin, L.E. Kondratieff waves in the world system perspective. In Kondratieff Waves. Dimensions and Prospects at the Dawn of the 21st Century; Uchitel: Volgograd, Russia, 2012; pp. 23–64. [Google Scholar]
- Tverdyi, D.A.; Parovik, R.I. Research of the Hereditary Dynamic Riccati System with Modification Fractional Differential Operator of Gerasimov-Caputo. AIP Conf. Proc. 2021, 2365, 020011. [Google Scholar] [CrossRef]
- Tverdyi, D.A.; Parovik, R.I. Mathematical modeling of the dynamics of solar activity using the fractional Riccati equation with variable heredity. In Proceedings of the VI International Scientific Conference IAMA KBSC RAS, Nalchik, Russia, 5–9 December 2021; p. 155. (In Russian). [Google Scholar]
- Tverdyi, D.A.; Parovik, R.I.; Makarov, E.O.; Firstov, P.P. Application of the Riccati hereditary mathematical model to the study of the dynamics of radon accumulation in the storage chamber. In EPJ Web of Conferences; EDP Sciences: Paris, France, 2021; Volume 254, pp. 1–5. [Google Scholar] [CrossRef]
- Tverdyi, D.A.; Parovik, R.I. Fractional Riccati equation to model the dynamics of COVID-19 coronovirus infection. J. Physics Conf. Ser. 2021, 2094, 032042. [Google Scholar] [CrossRef]
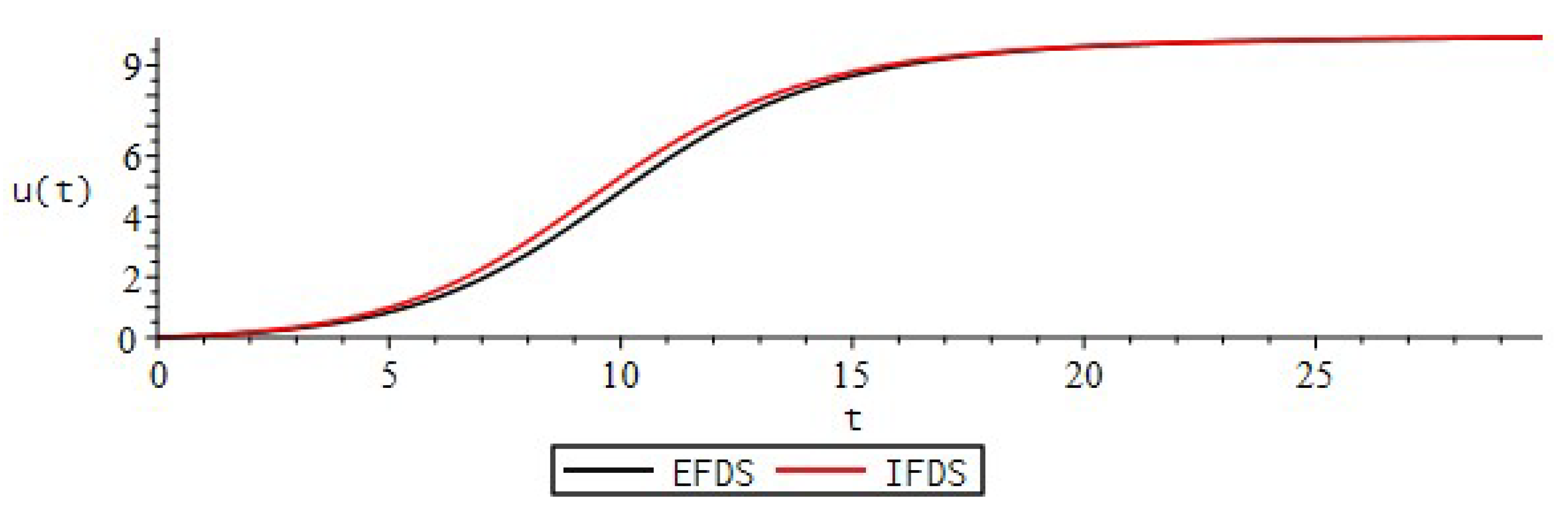
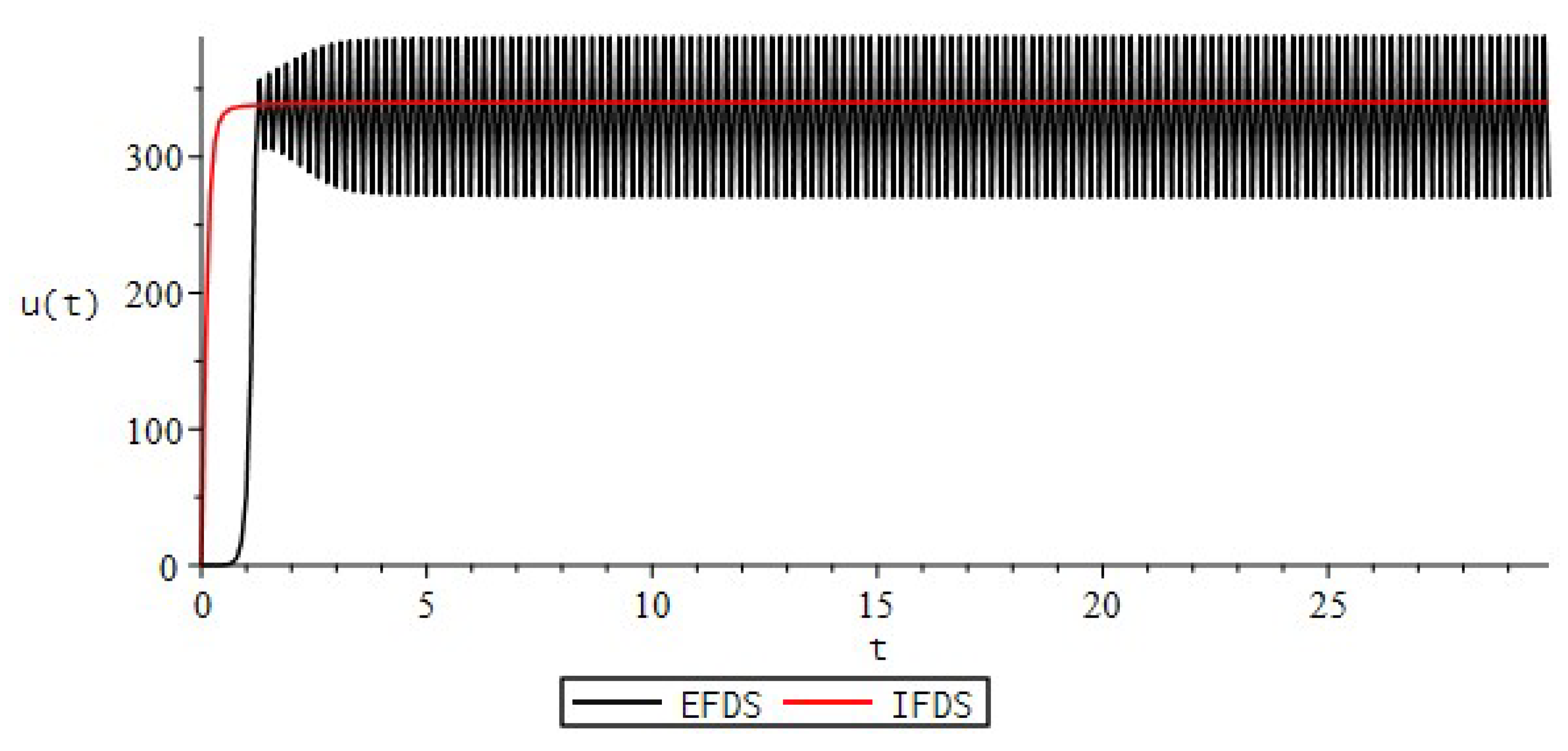
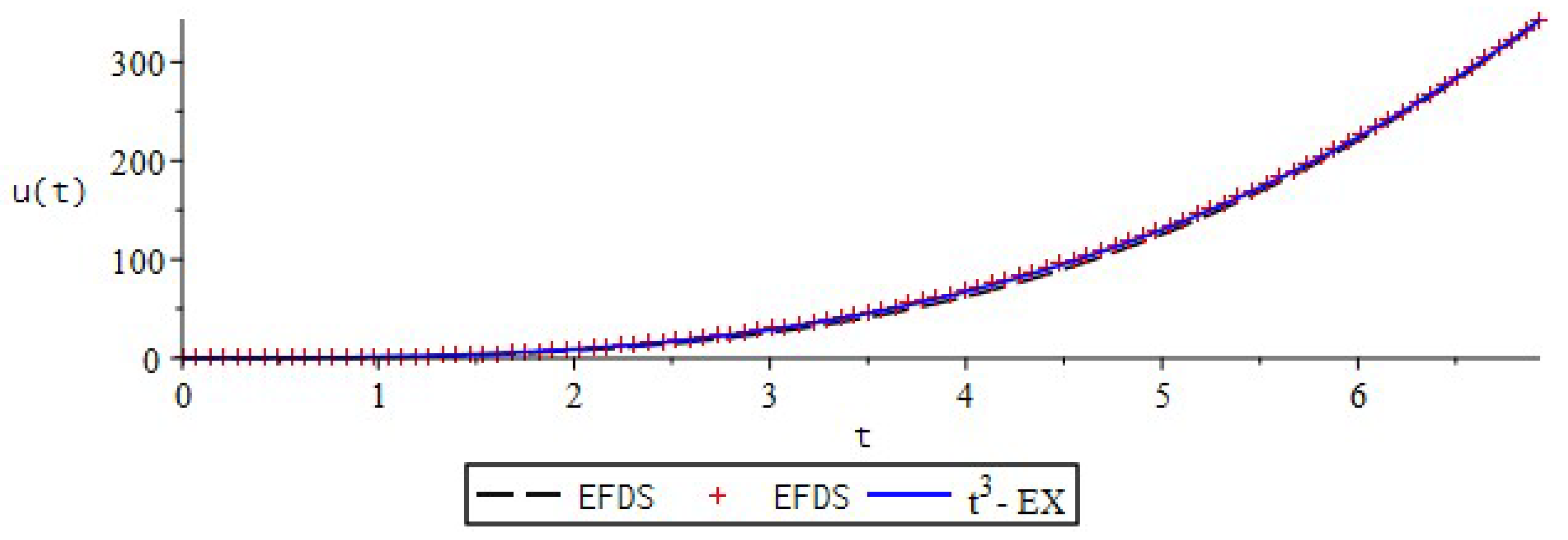
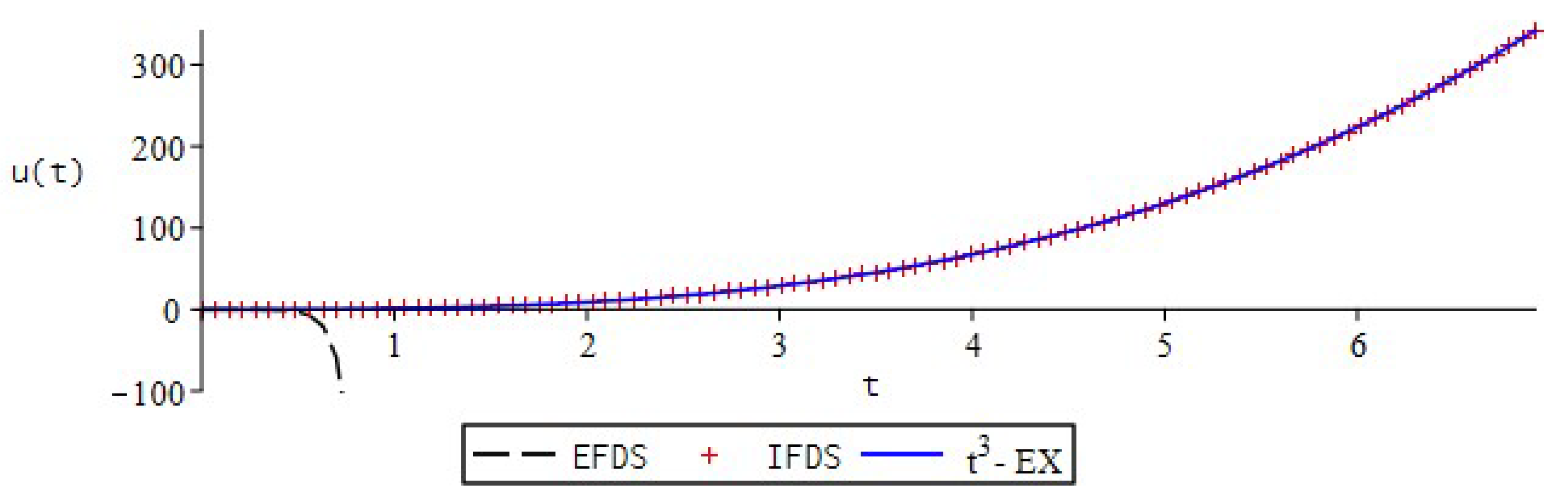
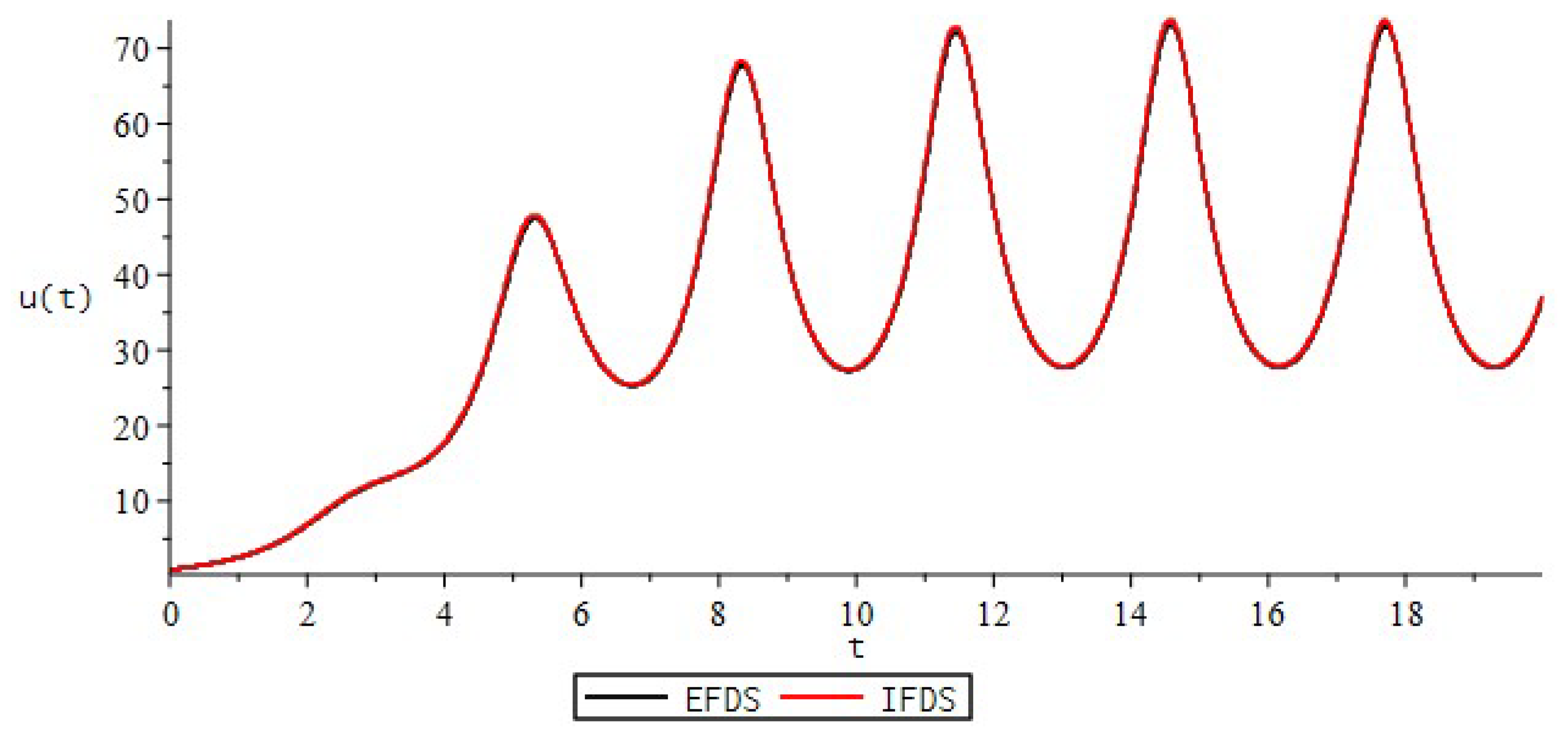
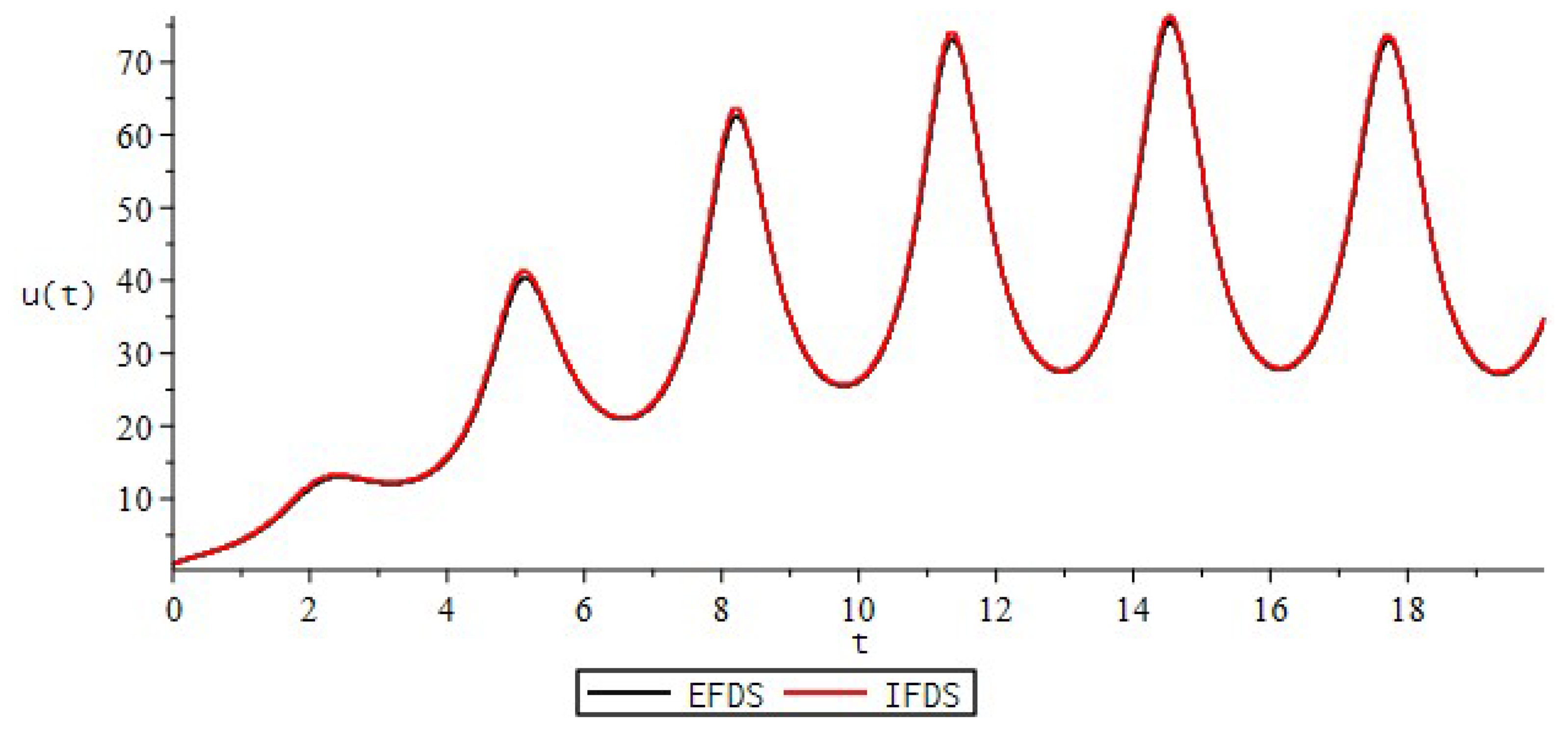


| EFDS | IFDS | |||||
|---|---|---|---|---|---|---|
| i | N | |||||
| 1 | 20 | 3/2 | 3.84086 | - | 2.17611 | - |
| 2 | 40 | 3/4 | 2.25311 | 0.76951 | 1.10581 | 0.97664 |
| 3 | 80 | 3/8 | 1.21857 | 0.88671 | 0.48416 | 1.19153 |
| 4 | 160 | 3/16 | 0.64976 | 0.90720 | 0.22022 | 1.13650 |
| 5 | 320 | 3/32 | 0.34048 | 0.93231 | 0.10018 | 1.13630 |
| 6 | 640 | 3/64 | 0.17676 | 0.94577 | 0.04548 | 1.13917 |
| 7 | 1280 | 3/128 | 0.09126 | 0.95368 | 0.02056 | 1.14522 |
| EX – EFDS | EX – IFDS | |||||
|---|---|---|---|---|---|---|
| i | N | |||||
| 1 | 20 | 1/20 | 0.14430 | - | 0.05206 | - |
| 2 | 40 | 1/40 | 0.07790 | 0.88928 | 0.02274 | 1.19515 |
| 3 | 80 | 1/80 | 0.04112 | 0.92166 | 0.00993 | 1.19410 |
| 4 | 160 | 1/160 | 0.02140 | 0.94215 | 0.00434 | 1.19527 |
| 5 | 320 | 1/320 | 0.01103 | 0.95550 | 0.00189 | 1.19671 |
| 6 | 640 | 1/640 | 0.00565 | 0.96457 | 0.00082 | 1.19788 |
| 7 | 1280 | 1/1280 | 0.00288 | 0.97105 | 0.00035 | 1.19870 |
| EFDS | IFDS | |||||
|---|---|---|---|---|---|---|
| i | N | |||||
| 1 | 20 | 1/2 | 16.9716 | - | 21.8875 | - |
| 2 | 40 | 1/4 | 4.10786 | 2.04666 | 5.21343 | 2.06980 |
| 3 | 80 | 1/8 | 2.83581 | 0.53462 | 2.14741 | 1.27963 |
| 4 | 160 | 1/16 | 1.70580 | 0.73330 | 0.90911 | 1.24006 |
| 5 | 320 | 1/32 | 0.95277 | 0.84024 | 0.39496 | 1.20272 |
| 6 | 640 | 1/64 | 0.51645 | 0.88350 | 0.17357 | 1.18613 |
| 7 | 1280 | 1/128 | 0.27275 | 0.92105 | 0.07673 | 1.17768 |
| EFDS | IFDS | |||||
|---|---|---|---|---|---|---|
| i | N | |||||
| 1 | 20 | 1/2 | 4.62978 | - | 18.3955 | - |
| 2 | 40 | 1/4 | 3.95342 | 0.22784 | 4.11895 | 2.15900 |
| 3 | 80 | 1/8 | 3.04877 | 0.37487 | 1.65080 | 1.31910 |
| 4 | 160 | 1/16 | 1.93859 | 0.65321 | 0.66586 | 1.30986 |
| 5 | 320 | 1/32 | 1.16042 | 0.74036 | 0.27601 | 1.27050 |
| 6 | 640 | 1/64 | 0.64893 | 0.83850 | 0.11415 | 1.27376 |
| 7 | 1280 | 1/128 | 0.34560 | 0.90893 | 0.04734 | 1.26961 |
| EFDS | IFDS | |||||
|---|---|---|---|---|---|---|
| i | N | |||||
| 1 | 20 | 1/2 | 4.53506 | - | 23.0946 | - |
| 2 | 40 | 1/4 | 3.23887 | 0.48562 | 4.58889 | 2.33133 |
| 3 | 80 | 1/8 | 2.65104 | 0.28893 | 1.64571 | 1.47942 |
| 4 | 160 | 1/16 | 1.71817 | 0.62568 | 0.64363 | 1.35441 |
| 5 | 320 | 1/32 | 1.01576 | 0.75831 | 0.26495 | 1.28046 |
| 6 | 640 | 1/64 | 0.56034 | 0.85818 | 0.11185 | 1.24414 |
| 7 | 1280 | 1/128 | 0.29775 | 0.91215 | 0.04785 | 1.22502 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tverdyi, D.; Parovik, R. Investigation of Finite-Difference Schemes for the Numerical Solution of a Fractional Nonlinear Equation. Fractal Fract. 2022, 6, 23. https://doi.org/10.3390/fractalfract6010023
Tverdyi D, Parovik R. Investigation of Finite-Difference Schemes for the Numerical Solution of a Fractional Nonlinear Equation. Fractal and Fractional. 2022; 6(1):23. https://doi.org/10.3390/fractalfract6010023
Chicago/Turabian StyleTverdyi, Dmitriy, and Roman Parovik. 2022. "Investigation of Finite-Difference Schemes for the Numerical Solution of a Fractional Nonlinear Equation" Fractal and Fractional 6, no. 1: 23. https://doi.org/10.3390/fractalfract6010023
APA StyleTverdyi, D., & Parovik, R. (2022). Investigation of Finite-Difference Schemes for the Numerical Solution of a Fractional Nonlinear Equation. Fractal and Fractional, 6(1), 23. https://doi.org/10.3390/fractalfract6010023







