Scaling in Anti-Plane Elasticity on Random Shear Modulus Fields with Fractal and Hurst Effects
Abstract
1. Introduction
2. Theory
2.1. Governing Equations
2.2. Scale-Dependent Homogenization
2.2.1. Hill–Mandel Macrohomogeneity Condition
- Uniform displacement (Dirichlet):
- Uniform traction (Neumann):
- Uniform displacement-traction (mixed-orthogonal):
2.2.2. Apparent and Effective Properties
2.2.3. Scaling
2.3. Random Fields
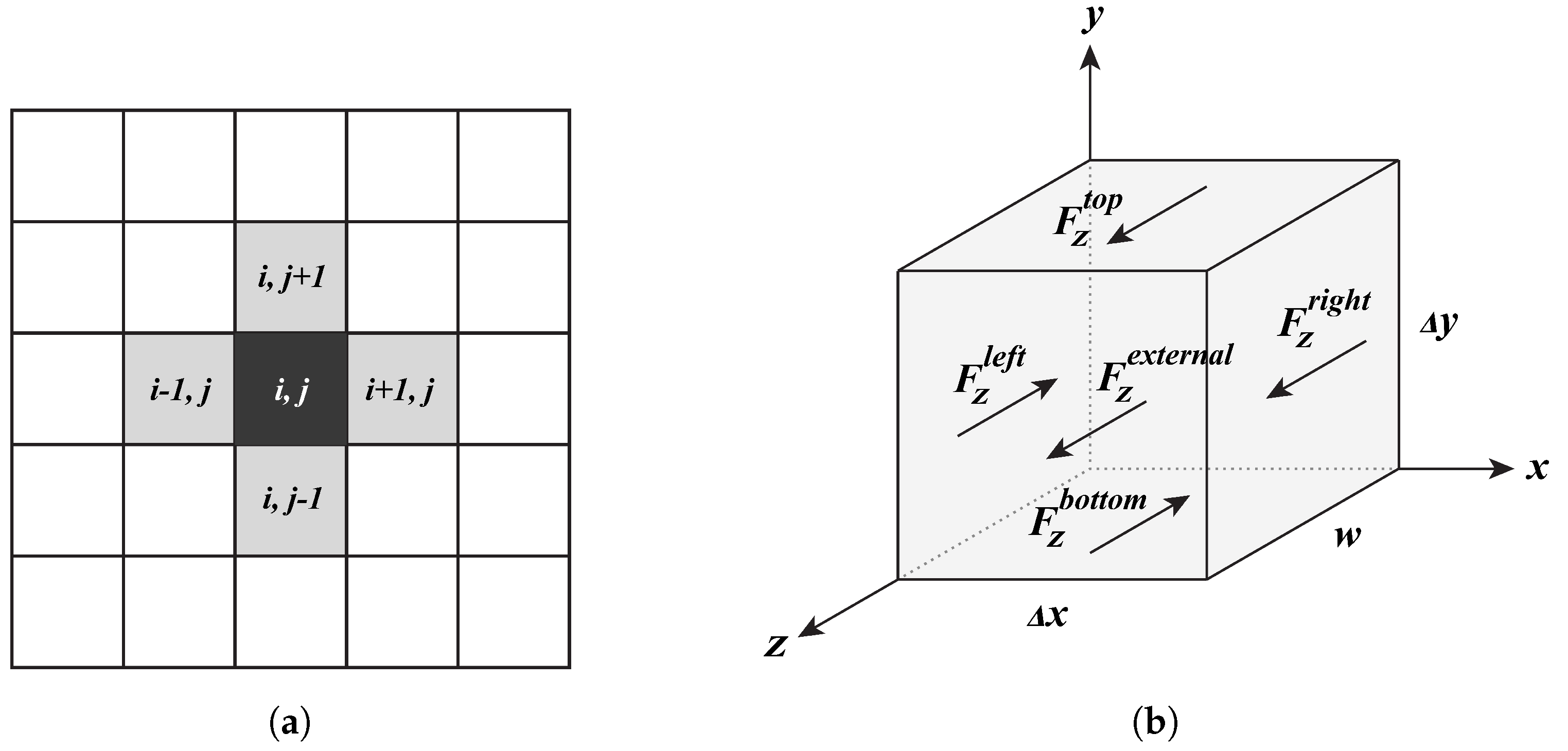
2.4. Cellular Automata
3. Numerical Results and Discussion
3.1. Cauchy Random Field Responses
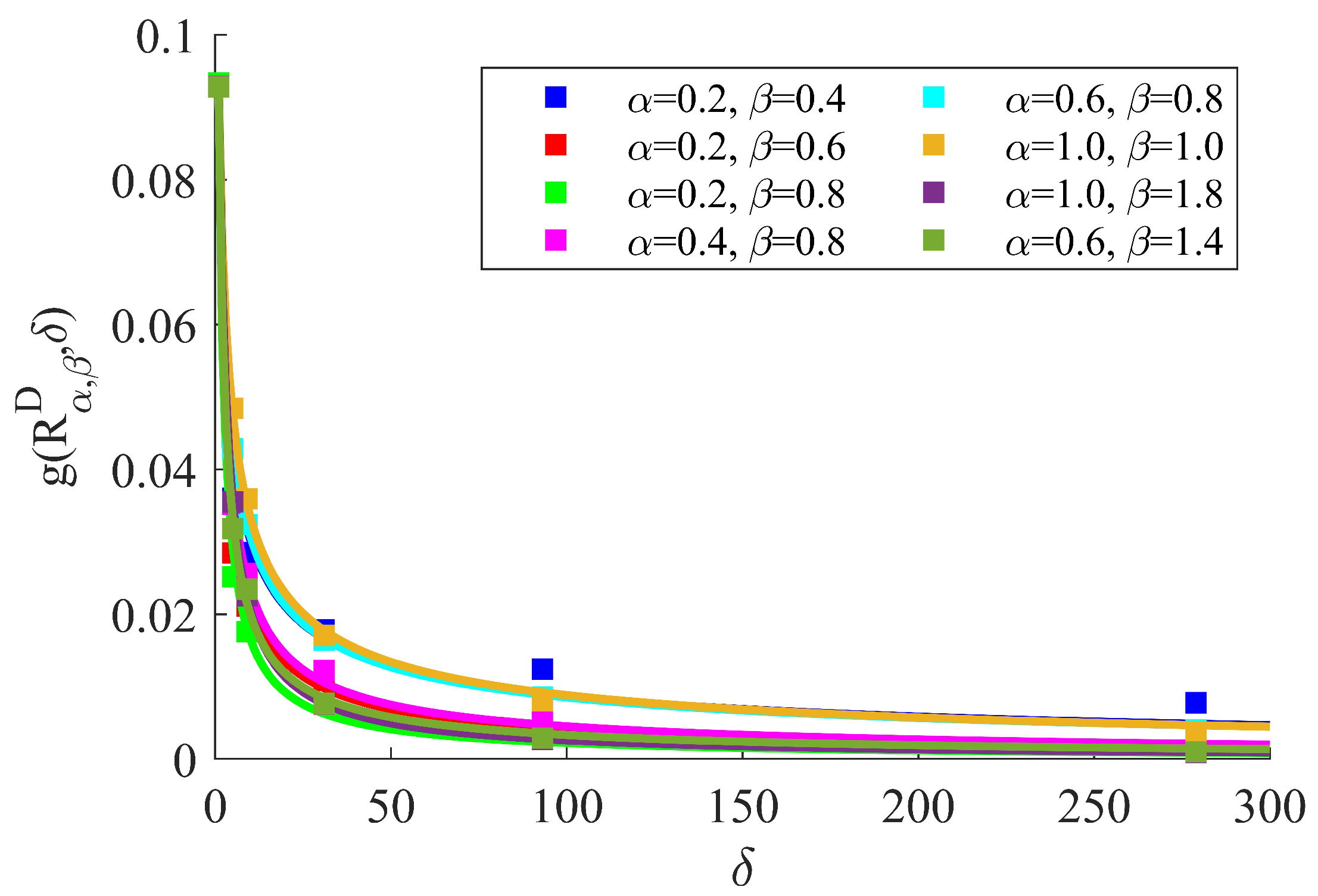
3.2. Dagum Random Field Responses
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ostoja-Starzewski, M. Microstructural Randomness and Scaling in Mechanics of Materials; Chapman and Hall/CRC: Boca Raton, FL, USA, 2007. [Google Scholar]
- Ostoja-Starzewski, M.; Kale, S.; Karimi, P.; Malyarenko, A.; Raghavan, B.; Ranganathan, S.; Zhang, J. Scaling to RVE in random media. Adv. Appl. Mech. 2016, 49, 111–211. [Google Scholar]
- Huet, C. Application of variational concepts to size effects in elastic heterogeneous bodies. J. Mech. Phys. Solids 1990, 38, 813–841. [Google Scholar] [CrossRef]
- Sab, K. On the homogenization and the simulation of random materials. Eur. J. Mech. Solids 1992, 11, 585–607. [Google Scholar]
- Ranganathan, S.I.; Ostoja-Starzewski, M. Scaling function, anisotropy and the size of RVE in elastic random polycrystals. J. Mech. Phys. Solids 2008, 56, 2773–2791. [Google Scholar] [CrossRef]
- Ranganathan, S.I.; Ostoja-Starzewski, M. Towards scaling laws in random polycrystals. Int. J. Eng. Sci. 2009, 47, 1322–1330. [Google Scholar] [CrossRef]
- Murshed, M.R.; Ranganathan, S.I. Hill–Mandel condition and bounds on lower symmetry elastic crystals. Mech. Res. Commun. 2017, 81, 7–10. [Google Scholar] [CrossRef]
- Dalaq, A.S.; Ranganathan, S.I. Invariants of mesoscale thermal conductivity and resistivity tensors in random checkerboards. Eng. Comput. 2015, 32, 1601–1618. [Google Scholar] [CrossRef]
- Kale, S.; Saharan, A.; Koric, S.; Ostoja-Starzewski, M. Scaling and bounds in thermal conductivity of planar Gaussian correlated microstructures. J. Appl. Phys. 2015, 117, 104301. [Google Scholar] [CrossRef]
- Ostoja-Starzewski, M.; Schulte, J. Bounding of effective thermal conductivities of multiscale materials by essential and natural boundary conditions. Phys. Rev. B 1996, 54, 278. [Google Scholar] [CrossRef]
- Ghossein, E.; Lévesque, M. Homogenization models for predicting local field statistics in ellipsoidal particles reinforced composites: Comparisons and validations. Int. J. Solids Struct. 2015, 58, 91–105. [Google Scholar] [CrossRef]
- Savvas, D.; Stefanou, G.; Papadrakakis, M. Determination of RVE size for random composites with local volume fraction variation. Comput. Methods Appl. Mech. Eng. 2016, 305, 340–358. [Google Scholar] [CrossRef]
- Raghavan, B.V.; Ranganathan, S.I.; Ostoja-Starzewski, M. Electrical properties of random checkerboards at finite scales. AIP Adv. 2015, 5, 017131. [Google Scholar] [CrossRef]
- Karimi, P.; Zhang, X.; Yan, S.; Ostoja-Starzewski, M.; Jin, J.M. Electrostatic and magnetostatic properties of random materials. Phys. Rev. E 2019, 99, 022120. [Google Scholar] [CrossRef]
- Mandelbrot, B. The Fractal Geometry of Nature; W.H. Freeman & Co.: New York, NY, USA, 1982. [Google Scholar]
- Malyarenko, A.; Ostoja-Starzewski, M. Tensor-Valued Random Fields for Continuum Physics; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Hill, R. Elastic properties of reinforced solids: Some theoretical principles. J. Mech. Phys. Solids 1963, 11, 357–372. [Google Scholar] [CrossRef]
- Mandel, J.; Dantu, P. Contribution à l’étude théorique et expérimentale du coefficient d’élastcité d’un milieu hétérogène, mais statistiquement homogène. Annales des Ponts et Chaussées Paris 1963, 6, 115–145. [Google Scholar]
- Hill, R. The Mathematical Theory of Plasticity; Oxford University Press: Oxford, UK, 1998; Volume 11. [Google Scholar]
- Gneiting, T.; Schlather, M. Stochastic models that separate fractal dimension and the Hurst effect. SIAM Rev. 2004, 46, 269–282. [Google Scholar] [CrossRef]
- Porcu, E. Spatio-Temporal Geostatistics: New Classes of Covariance, Variogram and Spectral Densities. Ph.D. Thesis, University of Milano, Milano, Italy, 2004. [Google Scholar]
- Chiles, J.P.; Delfiner, P. Geostatistics: Modeling Spatial Uncertainty; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Porcu, E.; Mateu, J.; Zini, A.; Pini, R. Modelling spatio-temporal data: A new variogram and covariance structure proposal. Stat. Probab. Lett. 2007, 77, 83–89. [Google Scholar] [CrossRef]
- Lim, S.; Teo, L. Analytic and asymptotic properties of multivariate generalized Linnik’s probability densities. J. Fourier Anal. Appl. 2010, 16, 715–747. [Google Scholar] [CrossRef]
- Laudani, R.; Zhang, D.; Faouzi, T.; Porcu, E.; Ostoja-Starzewski, M.; Chamorro, L.P. On streamwise velocity spectra models with fractal and long-memory effects. Phys. Fluids 2021, 33, 035116. [Google Scholar] [CrossRef]
- Davies, T.M.; Bryant, D. On circulant embedding for Gaussian random fields in R. J. Stat. Softw. 2013, 55, 1–21. [Google Scholar] [CrossRef]
- von Neumann, J.; Burks, A.W. Theory of Self-Reproducing Automata; University of Illinois Press Urbana: Champaign, IL, USA, 1966; Volume 1102024. [Google Scholar]
- Leamy, M.J. Application of cellular automata modeling to seismic elastodynamics. Int. J. Solids Struct. 2008, 45, 4835–4849. [Google Scholar] [CrossRef][Green Version]
- Hopman, R.K.; Leamy, M.J. Arbitrary geometry cellular automata for elastodynamics. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Lake Buena Vista, FL, USA, 13–19 November 2009; Volume 43888, pp. 535–547. [Google Scholar]
- Zhang, X.; Nishawala, V.; Ostoja-Starzewski, M. Anti-plane shear Lamb’s problem on random mass density fields with fractal and Hurst effects. Evol. Equ. Control Theory 2019, 8, 231. [Google Scholar] [CrossRef]

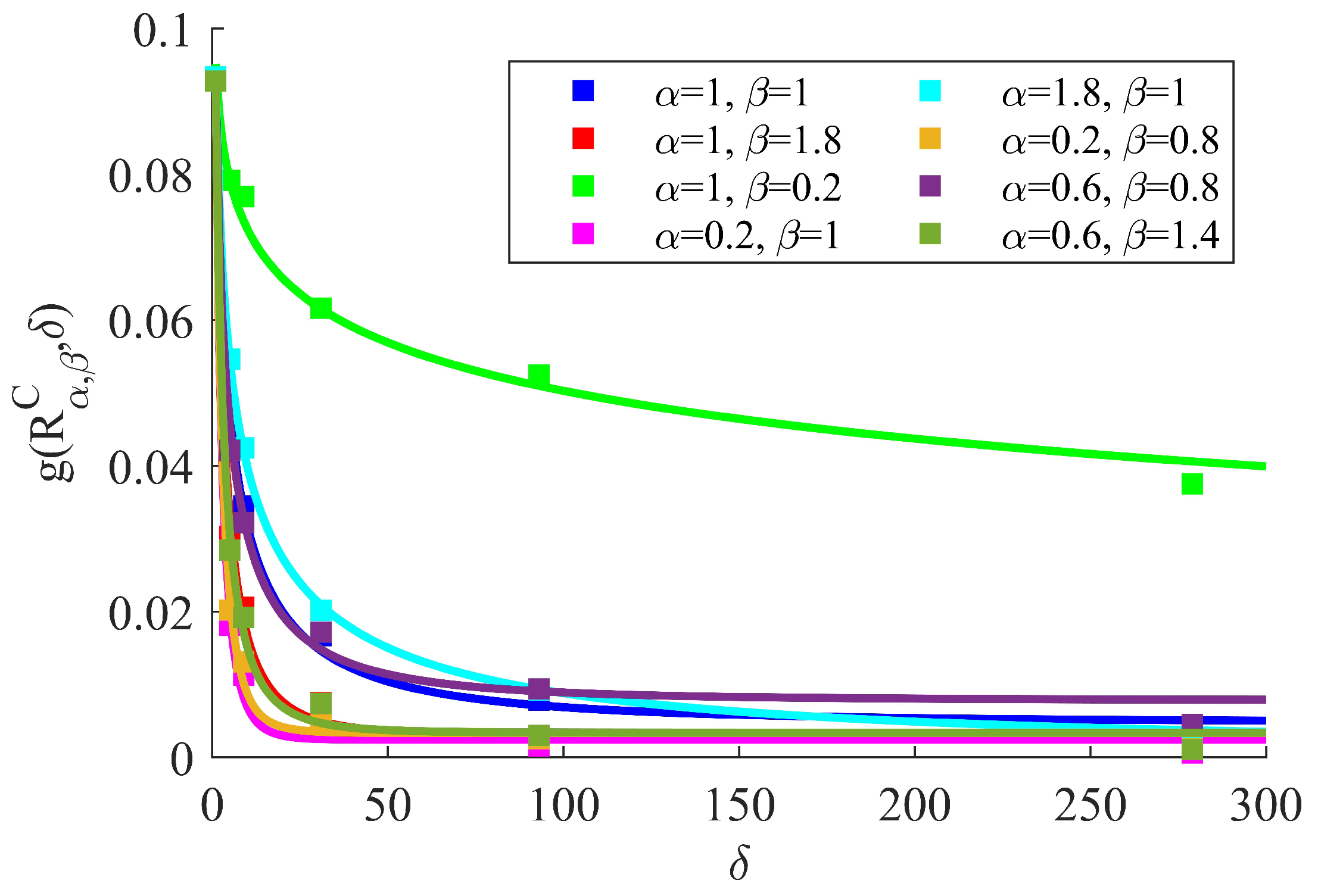
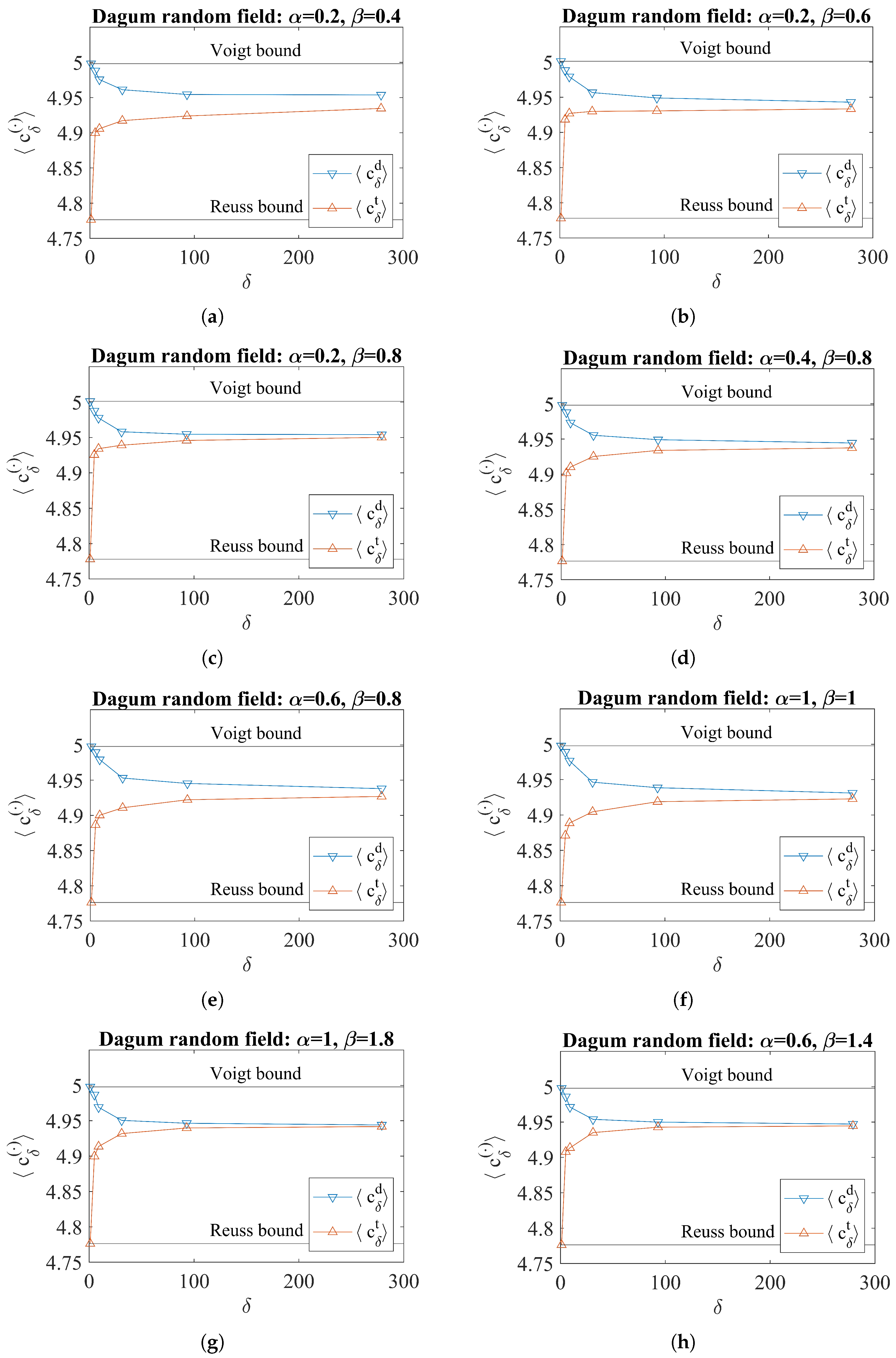

| D | H | A | B | C | |||||||
| 1 | 1 | 2.5 | 0.5 | 0.24 | 0.34 | 0.005 | 2.5 × 10 | 0.46 | 0.34 | 2.3 | 2.1 × 10 |
| 1 | 1.8 | 2.5 | 0.1 | 0.24 | 0.46 | 0.003 | 2.2 × 10 | 0.11 | 4.60 | 0.16 | 1 × 10 |
| 1 | 0.2 | 2.5 | 0.9 | 0.50 | 0.05 | −0.090 | 2.7 × 10 | 0.12 | 0.53 | 0.35 | 3.9 × 10 |
| 0.2 | 1 | 2.9 | 0.5 | 0.25 | 0.60 | 0.002 | 3.7 × 10 | 25.36 | 0.22 | 8.11 | 7.5 × 10 |
| 1.8 | 1 | 2.1 | 0.5 | 0.25 | 0.27 | 0.001 | 9.4 × 10 | 0.17 | 0.69 | 0.82 | 2.7 × 10 |
| 0.2 | 0.8 | 2.9 | 0.6 | 0.24 | 0.58 | 0.003 | 2.2 × 10 | 14.88 | 0.23 | 7.33 | 1.2 × 10 |
| 0.6 | 0.8 | 2.7 | 0.6 | 0.23 | 0.37 | 0.008 | 2.8 × 10 | 1.11 | 0.23 | 3.59 | 5.6 × 10 |
| 0.6 | 1.4 | 2.7 | 0.3 | 0.24 | 0.48 | 0.004 | 2.4 × 10 | 1.90 | 0.29 | 4.36 | 1.4 × 10 |
| (a) Cauchy random fields | |||||||||||
| D | H | A | B | C | |||||||
| 0.2 | 0.4 | 2.9 | 0.8 | 0.22 | 0.45 | 0.012 | 4.9 × 10 | 2.35 | 0.58 | 0.056 | 8.5 × 10 |
| 0.2 | 0.6 | 2.9 | 0.7 | 0.23 | 0.51 | 0.007 | 3.7 × 10 | 2.43 | 0.75 | 0.055 | 6.5 × 10 |
| 0.2 | 0.8 | 2.9 | 0.6 | 0.24 | 0.52 | 0.004 | 3.3 × 10 | 0.76 | 0.90 | 0.187 | 2.3 × 10 |
| 0.4 | 0.8 | 2.8 | 0.6 | 0.24 | 0.42 | 0.006 | 3.1 × 10 | 0.54 | 0.75 | 0.273 | 8.7 × 10 |
| 0.6 | 0.8 | 2.7 | 0.6 | 0.23 | 0.36 | 0.006 | 2.1 × 10 | 0.66 | 0.60 | 0.215 | 4.5 × 10 |
| 1 | 1 | 2.5 | 0.5 | 0.24 | 0.32 | 0.004 | 3.3 × 10 | 0.22 | 0.64 | 0.821 | 4.9 × 10 |
| 1 | 1.8 | 2.5 | 0.1 | 0.25 | 0.42 | 0.002 | 6.4 × 10 | 0.15 | 0.95 | 1.33 | 5.8 × 10 |
| 0.6 | 1.4 | 2.7 | 0.3 | 0.24 | 0.44 | 0.003 | 2.6 × 10 | 1.18 | 0.81 | 0.119 | 6.3 × 10 |
| (b) Dagum random fields | |||||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jetti, Y.S.; Ostoja-Starzewski, M. Scaling in Anti-Plane Elasticity on Random Shear Modulus Fields with Fractal and Hurst Effects. Fractal Fract. 2021, 5, 255. https://doi.org/10.3390/fractalfract5040255
Jetti YS, Ostoja-Starzewski M. Scaling in Anti-Plane Elasticity on Random Shear Modulus Fields with Fractal and Hurst Effects. Fractal and Fractional. 2021; 5(4):255. https://doi.org/10.3390/fractalfract5040255
Chicago/Turabian StyleJetti, Yaswanth Sai, and Martin Ostoja-Starzewski. 2021. "Scaling in Anti-Plane Elasticity on Random Shear Modulus Fields with Fractal and Hurst Effects" Fractal and Fractional 5, no. 4: 255. https://doi.org/10.3390/fractalfract5040255
APA StyleJetti, Y. S., & Ostoja-Starzewski, M. (2021). Scaling in Anti-Plane Elasticity on Random Shear Modulus Fields with Fractal and Hurst Effects. Fractal and Fractional, 5(4), 255. https://doi.org/10.3390/fractalfract5040255







