Sets of Fractional Operators and Numerical Estimation of the Order of Convergence of a Family of Fractional Fixed-Point Methods

Abstract

Considering the large number of fractional operators that exist, and since it does not seem that their number will stop increasing soon at the time of writing this paper, it is presented for the first time, as far as the authors know, a simple and compact method to work the fractional calculus through the classification of fractional operators using sets. This new method of working with fractional operators, which may be called fractional calculus of sets, allows generalizing objects of conventional calculus, such as tensor operators, the Taylor series of a vector-valued function, and the fixed-point method, in several variables, which allows generating the method known as the fractional fixed-point method. Furthermore, it is also shown that each fractional fixed-point method that generates a convergent sequence has the ability to generate an uncountable family of fractional fixed-point methods that generate convergent sequences. So, it is presented a method to estimate numerically in a region $\mathsf{\Omega }$ the mean order of convergence of any fractional fixed-point method, and it is shown how to construct a hybrid fractional iterative method to determine the critical points of a scalar function. Finally, considering that the proposed method to classify fractional operators through sets allows generalizing the existing results of the fractional calculus, some examples are shown of how to define families of fractional operators that satisfy some property to ensure the validity of the results to be generalized.

1. Introduction

A fractional derivative is an operator that generalizes the ordinary derivative, in the sense that if

$$\begin{array}{c}\hfill {\displaystyle \frac{d^{\alpha }}{d{x}^{\alpha }}}\end{array}$$

denotes the differential of order $\alpha \in \mathbb{R}$, then $\alpha$ may be considered a parameter such that the first derivative corresponds to the particular case $\alpha =1$. On the other hand, a fractional differential equation is an equation that involves at least one differential operator of order $\alpha$, with $(n-1)<\alpha \le n$ for some positive integer n, and it is said to be a differential equation of order $\alpha$ if this operator is the highest order in the equation. Analogously, a fractional partial differential equation is an equation that involves at least one differential operator of order $\alpha$, which in general are usually partial derivatives of order $\alpha$, that is,

$$\begin{array}{ccc}\hfill {\displaystyle \frac{{\partial }^{\alpha }}{\partial t^{\alpha }}},& {\displaystyle \frac{{\partial }^{\alpha }}{\partial x^{\alpha }}},& {\displaystyle \frac{{\partial }^{\alpha }}{\partial y^{\alpha }}}.\hfill \end{array}$$

The fractional operators have many representations, but one of their fundamental properties is that they allow retrieving the results of conventional calculus when $\alpha \to n$. So, considering a scalar function $h:{\mathbb{R}}^m\to \mathbb{R}$ and the canonical basis of ${\mathbb{R}}^m$ denoted by ${\left\{{\widehat{e}}_k\right\}}_{k\ge 1}$, it is possible to define the following fractional operator of order $\alpha$, using Einstein notation as follows:

$$\begin{array}{c}\hfill o_x^{\alpha }h\left(x\right):={\widehat{e}}_k{o}_k^{\alpha }h\left(x\right),\end{array}$$

(1)

and then, denoting by ${\partial }_k^n$ the partial derivative of order n applied with respect to the k-th component of the vector x and using the previous operator, it is possible to define the following set of fractional operators as follows:

$$\begin{array}{c}\hfill O_{x,\alpha }^n\left(h\right):= \left\{o_x^{\alpha }:\exists o_k^{\alpha }h\left(x\right)\text{and}\underset{\alpha \to n}{lim}{o}_k^{\alpha }h\left(x\right)={\partial }_k^{n}h\left(x\right)\forall k\ge 1\right\},\end{array}$$

(2)

which may be proved to be a nonempty set through the following sets of fractional operators:

$$\begin{array}{c}\begin{array}{c}{\displaystyle O_{0,x,\alpha }^n\left(h\right):= \left\{o_x^{\alpha }:\exists o_k^{\alpha }h\left(x\right)= \left({\partial }_k^n+\left(n-\alpha \right){\partial }_k^{\alpha }\right)h\left(x\right)\text{and}\underset{\alpha \to n}{lim}{\partial }_k^{\alpha }h\left(x\right)\ne {\partial }_k^{n}h\left(x\right)\forall k\ge 1\right\},}\end{array}\end{array}$$

(3)

$$\begin{array}{c}\begin{array}{c}{\displaystyle O_{1,x,\alpha }^n\left(h\right):= \left\{o_x^{\alpha }:\exists o_k^{\alpha }h\left(x\right)={\displaystyle \frac{1}{2}}\left({\partial }_k^n+{\partial }_k^{\alpha }\right)h\left(x\right)\text{and}\underset{\alpha \to n}{lim}{\partial }_k^{\alpha }h\left(x\right)={\partial }_k^{n}h\left(x\right)\forall k\ge 1\right\},}\end{array}\end{array}$$

(4)

$$\begin{array}{c}{O}_{2,x,\alpha }^n\left(h\right):= \left\{o_x^{\alpha }:\exists o_k^{\alpha }h\left(x\right)={\partial }_k^{\alpha }h\left(x\right)-{\left(\left({\partial }_k^n-{\partial }_k^{\alpha }\right)h\left(x\right)\right)}^n\text{and}\underset{\alpha \to n}{lim}{\partial }_k^{\alpha }h\left(x\right)={\partial }_k^{n}h\left(x\right)\forall k\ge 1\right\},\end{array}$$

(5)

whose complement may be defined as follows:

$$\begin{array}{c}\hfill O_{x,\alpha }^{n,c}\left(h\right):= \left\{o_x^{\alpha }:\exists o_k^{\alpha }h\left(x\right)\forall k\ge 1\text{and}\underset{\alpha \to n}{lim}{o}_k^{\alpha }h\left(x\right)\ne {\partial }_k^{n}h\left(x\right)\mathrm{i}\mathrm{n} \mathrm{a}\mathrm{t} \mathrm{l}\mathrm{e}\mathrm{a}\mathrm{s}\mathrm{t} \mathrm{o}\mathrm{n}\mathrm{e} \mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e} k\ge 1\right\},\end{array}$$

(6)

and which may be considered as a generating set of sets of fractional tensor operators. For example, considering $\alpha ,n\in {\mathbb{R}}^d$ with $\alpha ={\widehat{e}}_k{\left[\alpha \right]}_k$ and $n={\widehat{e}}_k{\left[n\right]}_k$, it is possible to define the following set of fractional tensor operators:

$$\begin{array}{c}\hfill O_{x,\alpha }^n\left(h\right):= \left\{o_x^{\alpha }:o_x^{\alpha }\in O_{x,{\left[\alpha \right]}_1}^{{\left[n\right]}_1}\left(h\right)\times O_{x,{\left[\alpha \right]}_2}^{{\left[n\right]}_2}\left(h\right)\times \cdots \times O_{x,{\left[\alpha \right]}_d}^{{\left[n\right]}_d}\left(h\right)\right\}.\end{array}$$

(7)

Therefore, considering a function $h:{\mathbb{R}}^m\times {\mathbb{R}}_{\ge 0}\to \mathbb{R}$, as well as the vectors $\alpha ,n\in {\mathbb{R}}^3$ with $\alpha ={\widehat{e}}_k{\left[\alpha \right]}_k$ and $n={\widehat{e}}_k{\left[n\right]}_k$, it is possible to combine the sets (2) and (7) to define new sets of fractional operators related to the theory of differential equations, as shown with the following set:

$$\begin{array}{c}\hfill W_{t,x,\alpha }^n\left(h\right):= \left\{w_{t,x}^{\alpha }=o_t^{{\left[\alpha \right]}_1}-tr\left(o_x^{({\left[\alpha \right]}_2,{\left[\alpha \right]}_3)}\right):o_t^{{\left[\alpha \right]}_1}\in O_{t,{\left[\alpha \right]}_1}^{{\left[n\right]}_1}\left(h\right)and{o}_x^{({\left[\alpha \right]}_2,{\left[\alpha \right]}_3)}\in O_{0,x,({\left[\alpha \right]}_2,{\left[\alpha \right]}_3)}^{({\left[n\right]}_2,{\left[n\right]}_3)}\left(h\right)\right\},\end{array}$$

(8)

where $tr(·)$ denotes the trace of a matrix. So, denoting the Laplacian operator by ${\nabla }^2$, it is possible to obtain the following results:

$$\begin{array}{c}\begin{array}{c}{\displaystyle \mathrm{If}{w}_{t,x}^{\alpha }\in W_{t,x,\alpha }^n\left(h\right)\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h} n=(1,1,1)\Rightarrow \underset{\alpha \to n}{lim}{w}_{t,x}^{\alpha }h(x,t)=\left({\partial }_t-{\nabla }^2\right)h(x,t),}\end{array}\end{array}$$

(9)

$$\begin{array}{c}\mathrm{If}{w}_{t,x}^{\alpha }\in W_{t,x,\alpha }^n\left(h\right)\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h} n=(2,1,1)\Rightarrow \underset{\alpha \to n}{lim}{w}_{t,x}^{\alpha }h(x,t)=\left({\partial }_t^2-{\nabla }^2\right)h(x,t),\end{array}$$

(10)

which may generalize the diffusion equation and the wave equation, respectively. To finish this section, it is necessary to mention that the applications of fractional operators have spread to different fields of science, such as finance [1,2], economics [3], number theory through the Riemann zeta function [4,5] and in engineering with the study of the manufacture of hybrid solar receivers [6,7]. It should be mentioned that there is also a growing interest in fractional operators and their properties for the solution of nonlinear algebraic systems [7,8,9,10,11,12,13,14,15,16,17,18], which is a classical problem in mathematics, physics and engineering that consists of finding the set of zeros of a function $f:\mathsf{\Omega }\subset {\mathbb{R}}^n\to {\mathbb{R}}^n$, that is,

$$\begin{array}{c}\hfill \left\{\xi \in \mathsf{\Omega }:∥f\left(\xi \right)∥=0\right\},\end{array}$$

(11)

where $∥·∥ :{\mathbb{R}}^n\to \mathbb{R}$ denotes any vector norm, or equivalently,

$$\begin{array}{c}\hfill \left\{\xi \in \mathsf{\Omega }:{\left[f\right]}_k\left(\xi \right)=0\forall k\ge 1\right\},\end{array}$$

(12)

where ${\left[f\right]}_k:{\mathbb{R}}^n\to \mathbb{R}$ denotes the k-th component of the function f. This paper presents a simple and compact method to work the fractional calculus through the classification of fractional operators using sets. This new method of working with fractional operators allows generalizing objects of the conventional calculus, such as tensor operators, the Taylor series of a vector-valued function, and the fixed-point method in several variables, which allows generating the method known as the fractional fixed-point method. It is also shown that each fractional fixed-point method that generates a convergent sequence has the ability to generate an uncountable family of fractional fixed-point methods that generate convergent sequences. It is presented one method to estimate numerically in a region $\mathsf{\Omega }$ the mean order of convergence of any fractional fixed-point method through the problem of determining the critical points of a scalar function, and it is shown how to construct a hybrid fractional iterative method to determine the critical points of a scalar function.

2. Fixed-Point Method

Let $\Phi :{\mathbb{R}}^n\to {\mathbb{R}}^n$ be a function. It is possible to build a sequence ${\left\{x_i\right\}}_{i\ge 1}$ by defining the following iterative method:

$$\begin{array}{cc}\hfill x_{i+1}:=\Phi \left(x_i\right),& i=0,1,2,\cdots .\end{array}$$

(13)

If it is fulfilled that $x_i\to \xi \in {\mathbb{R}}^n$ and if the function $\Phi$ is continuous around $\xi$, we obtain the following:

$$\begin{array}{c}\hfill {\displaystyle \xi =\underset{i\to \infty }{lim}{x}_{i+1}=\underset{i\to \infty }{lim}\Phi \left(x_i\right)=\Phi \left(\underset{i\to \infty }{lim}{x}_i\right)=\Phi \left(\xi \right).}\end{array}$$

(14)

The above result is the reason by which the method (13) is known as the fixed-point method. Furthermore, the function $\Phi$ is called an iteration function. Before continuing, it is necessary to define the order of convergence of an iteration function $\Phi$ [18,19]:

Definition 1.

Let $\Phi :\mathsf{\Omega }\subset {\mathbb{R}}^n\to {\mathbb{R}}^n$ be an iteration function with a fixed point $\xi \in \mathsf{\Omega }$. So, the method (13) is called (locally) convergent, with an order of convergence of order (at least) p (with $p\ge 1$), if there exist $\delta >0$ and a non-negative constant C (with $C<1$ if $p=1$) such that for any initial value $x_0\in B(\xi ;\delta )$, it is fulfilled that

$$\begin{array}{cc}\hfill ∥x_{i+1}-\xi ∥ \le C{∥x_i-\xi ∥}^p,& i=0,1,2,\cdots ,\end{array}$$

(15)

where C is called the convergence factor.

The order of convergence is usually related to the speed at which the sequence generated by an iteration function $\Phi$ converges. It is necessary to mention that for the case $p=1$, it is said that the function $\Phi$ has an order of convergence that is (at least) linear, and for the case $p=2$, it is said that the function $\Phi$ has an order of convergence that is (at least) quadratic. From the previous definition, the following proposition is obtained.

Proposition 1.

Let $\Phi :{\mathbb{R}}^n\to {\mathbb{R}}^n$ be an iteration function that defines a sequence ${\left\{x_i\right\}}_{i\ge 1}$ such that $x_i\to \xi \in {\mathbb{R}}^n$. So, if Φ has an order of convergence of order (at least) p in $B(\xi ;\delta )$, there exists a non-negative constant $K=K\left(C\right)$, such that for all values of the sequence ${\left\{x_i\right\}}_{i\ge 1}$, it is fulfilled that

$$\begin{array}{cc}\hfill ∥x_{i+1}-x_i∥ \le K{∥x_i-x_{i-1}∥}^p,& i=0,1,2,\cdots ,\end{array}$$

(16)

where $∥x_{-1}∥ :=0$.

Proof. 

Considering that Φ defines a sequence ${\left\{x_i\right\}}_{i\ge 1}$ and that it has an order of convergence of order (at least) p, it is possible to obtain the following inequality:

$$\begin{array}{c}\hfill ∥x_{i+1}-x_i∥ \le C({∥x_i-\xi ∥}^p+{\left(∥x_i--\xi ∥ + ∥x_i-x_{i-1}∥\right)}^p).\end{array}$$

As a consequence,

$$\begin{array}{c}\hfill ∥x_{i+1}-x_i∥ \le 2C{\left(∥x_i-\xi ∥ + ∥x_i-x_{i-1}∥\right)}^p,\end{array}$$

and since $x_i\to \xi$, there exists a positive constant c such that

$$\begin{array}{c}\hfill ∥x_{i+1}-x_i∥ \le 2cC{∥x_i-x_{i-1}∥}^p=K{∥x_i-x_{i-1}∥}^p.\end{array}$$

□

From the previous proposition, the following theorem is obtained the following.

Theorem 1.

Let $\Phi :{\mathbb{R}}^n\to {\mathbb{R}}^n$ be an iteration function that defines a sequence ${\left\{x_i\right\}}_{i\ge 1}$ such that $x_i\to \xi \in {\mathbb{R}}^n$. So, if Φ has an order of convergence of order (at least) p in $B(\xi ;\delta )$, there exists a value $m\in \mathbb{N}$ such that for all subsequence ${\left\{x_i\right\}}_{i\ge m}\in B(\xi ;1/2)$ that fulfills the following condition

$$\begin{array}{cc}\hfill ∥x_{i+2}-x_{i+1}∥ \le K{∥x_{i+1}-x_i∥}^p,& \forall i\ge m,\end{array}$$

there exist ${\delta }_K={\delta }_K\left(C\right)>0$ and a sequence of values $P_i$ given by the following expression

$$\begin{array}{c}\hfill P_i:={\displaystyle \frac{log\left(∥x_i-x_{i-1}∥\right)}{log\left(∥x_{i-1}-x_{i-2}∥\right)}},\end{array}$$

(17)

such that ${\left\{P_i\right\}}_{i\ge m+2}\in B(p;{\delta }_K)$.

Proof. 

Considering that Φ defines a sequence ${\left\{x_i\right\}}_{i\ge 1}$ and that it has an order of convergence of order (at least) p, from Proposition 1, it is possible to obtain the following inequality:

$$\begin{array}{c}\hfill log\left(∥x_{i+2}-x_{i+1}∥\right) - plog\left(∥x_{i+1}-x_i∥\right) \le log\left(K\right),\end{array}$$

assuming that there exists a subsequence ${\left\{x_i\right\}}_{i\ge m}\in B(\xi ;1/2)$; then

$$\begin{array}{cc}\hfill log\left(∥x_{i+1}-x_i∥\right) <0,& \forall i\ge m.\end{array}$$

So, if the subsequence ${\left\{x_i\right\}}_{i\ge m}$ fulfills the above inequality

$$\begin{array}{c}\hfill {\displaystyle \frac{log\left(K\right)}{log\left(∥x_{i+1}-x_i∥\right)}}\le {\displaystyle \frac{log\left(∥x_{i+2}-x_{i+1}∥\right)}{log\left(∥x_{i+1}-x_i∥\right)}}-p,\end{array}$$

then considering that $x\le \left|x\right|\forall x\in \mathbb{R}$, there exists a positive constant c such that

$$\begin{array}{c}\hfill {\displaystyle \frac{log\left(K\right)}{log\left(∥x_{i+1}-x_i∥\right)}}\le |{\displaystyle \frac{log\left(∥x_{i+2}-x_{i+1}∥\right)}{log\left(∥x_{i+1}-x_i∥\right)}}-p| \le c|{\displaystyle \frac{log\left(K\right)}{log\left(∥x_{i+1}-x_i∥\right)}}|,\end{array}$$

and since $K=K\left(C\right)$, there exists a positive value ${\delta }_K={\delta }_K\left(C\right)$ such that the sequence ${\left\{P_i\right\}}_{i\ge m+2}\in B(p;{\delta }_K)$. □

From the previous theorem, the following corollary is obtained.

Corollary 1.

Let $\Phi :{\mathbb{R}}^n\to {\mathbb{R}}^n$ be an iteration function that defines a sequence ${\left\{x_i\right\}}_{i\ge 1}$ such that $x_i\to \xi \in {\mathbb{R}}^n$. So, if Φ has an order of convergence of order (at least) p in $B(\xi ;1/2)$, for some $m\in \mathbb{N}$, there exists a sequence ${\left\{P_i\right\}}_{i\ge m}\in B(p;{\delta }_K)$ that fulfills the following condition:

$$\begin{array}{c}\hfill \underset{i\to \infty }{lim}{P}_i\to p,\end{array}$$

and therefore, there exists at least one value $k\ge m$ such that

$$\begin{array}{c}\hfill |P_k-p|\le ϵ.\end{array}$$

(18)

The previous corollary allows estimating numerically the order of convergence of an iteration function $\Phi$ that generates at least one convergent sequence ${\left\{x_i\right\}}_{i\ge 1}$. On the other hand, the following corollary allows characterizing the order of convergence of an iteration function $\Phi$ through its Jacobian matrix ${\Phi }^{\left(1\right)}$ [18]:

Corollary 2.

Let $\Phi :{\mathbb{R}}^n\to {\mathbb{R}}^n$ be an iteration function. If Φ defines a sequence, ${\left\{x_i\right\}}_{i\ge 1}$ such that $x_i\to \xi \in {\mathbb{R}}^n$. So, Φ has an order of convergence of order (at least) p in $B(\xi ;\delta )$, where it is fulfilled that:

$$\begin{array}{c}\hfill p:=\left\{\begin{array}{cc}1,& {\displaystyle if \underset{x\to \xi }{lim}∥{\Phi }^{\left(1\right)}\left(x\right)∥\ne 0}\\ 2,& {\displaystyle if \underset{x\to \xi }{lim}∥{\Phi }^{\left(1\right)}\left(x\right)∥=0}\end{array}\right..\end{array}$$

(19)

3. Riemann–Liouville Fractional Operators

Let $f:\mathsf{\Omega }\subset \mathbb{R}\to \mathbb{R}$ be a function. One of the fundamental operators of fractional calculus is the operator Riemann–Liouville fractional integral, which is defined as follows: follows [20,21]

$$\begin{array}{c}\hfill {}_a^{}{I}_x^{\alpha }f\left(x\right):={\displaystyle \frac{1}{\mathrm{\Gamma }\left(\alpha \right)}}{\int }_a^x{(x-t)}^{\alpha -1}f\left(t\right)dt,\end{array}$$

(20)

which is a fundamental piece to construct the operator Riemann-Liouville fractional derivative, which is defined as follows [20,22]:

$$\begin{array}{c}\hfill {}_a^{}{D}_x^{\alpha }f\left(x\right):= \left\{\begin{array}{cc}{\displaystyle {}_a^{}{I}_x^{-\alpha }f\left(x\right),}& \text{if} \alpha <0\\ {\displaystyle {\displaystyle \frac{d^n}{d{x}^n}}\left({}_a^{}{I}_x^{n-\alpha }f\left(x\right)\right),}& \text{if} \alpha \ge 0\end{array}\right.,\end{array}$$

(21)

where $n=\lceil \alpha \rceil$ and ${}_a^{}{I}_x^{0}f\left(x\right):=f\left(x\right)$. Applying the operator (21) with $a=0$ to the function $x^{\mu }$, with $\mu >-1$, we obtain the following result [18]:

$$\begin{array}{cc}\hfill {}_0^{}{D}_x^{\alpha }{x}^{\mu }={\displaystyle \frac{\mathrm{\Gamma }\left(\mu +1\right)}{\mathrm{\Gamma }\left(\mu -\alpha +1\right)}}{x}^{\mu -\alpha },& \alpha \in \mathbb{R}\backslash \mathbb{Z}.\end{array}$$

(22)

4. Fractional Fixed-Point Method

Let ${\mathbb{N}}_0$ be the set $\mathbb{N}\cup \left\{0\right\}$ if $\gamma \in {\mathbb{N}}_0^m$ and $x\in {\mathbb{R}}^m$. Then it is possible to define the following multi-index notation:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\begin{array}{ccc}{\displaystyle \gamma !:=\prod _{k=1}^m{\left[\gamma \right]}_k!,}& {\displaystyle \left|\gamma \right|:=\sum _{k=1}^m{\left[\gamma \right]}_k,}& {\displaystyle x^{\gamma }:=\prod _{k=1}^m{\left[x\right]}_k^{{\left[\gamma \right]}_k}}\end{array}\\ {\displaystyle \frac{{\partial }^{\gamma }}{\partial x^{\gamma }}}:={\displaystyle \frac{{\partial }^{{\left[\gamma \right]}_1}}{\partial {\left[x\right]}_1^{{\left[\gamma \right]}_1}}}{\displaystyle \frac{{\partial }^{{\left[\gamma \right]}_2}}{\partial {\left[x\right]}_2^{{\left[\gamma \right]}_2}}}\cdots {\displaystyle \frac{{\partial }^{{\left[\gamma \right]}_m}}{\partial {\left[x\right]}_m^{{\left[\gamma \right]}_m}}}\end{array}\right..\end{array}$$

(23)

So, considering a function $h:\mathsf{\Omega }\subset {\mathbb{R}}^m\to \mathbb{R}$, it is possible to define the following set of fractional operators:

$$\begin{array}{c}\hfill S_{x,\alpha }^{n,\gamma }\left(h\right):=\left\{s_x^{\alpha \gamma }=s_x^{\alpha \gamma }\left(o_x^{\alpha }\right):o_x^{\alpha }\in O_{x,\alpha }^s\left(h\right)\forall s\le n^2\mathrm{a}\mathrm{n}\mathrm{d}{s}_x^{\alpha \gamma }h\left(x\right):=o_1^{\alpha {\left[\gamma \right]}_1}{o}_2^{\alpha {\left[\gamma \right]}_2}\cdots o_m^{\alpha {\left[\gamma \right]}_m}h\left(x\right)\forall \alpha ,\left|\gamma \right|\le n\right\},\end{array}$$

(24)

from which it is possible to obtain the following results:

$$\begin{array}{c}\hfill \mathrm{If}{s}_x^{\alpha \gamma }\in S_{x,\alpha }^{n,\gamma }\left(h\right)\Rightarrow \left\{\begin{array}{c}{\displaystyle \underset{\alpha \to 0}{lim}{s}_x^{\alpha \gamma }h\left(x\right)=o_1^0{o}_2^0\cdots o_m^{0}h\left(x\right)=h\left(x\right)}\hfill \\ {\displaystyle \underset{\alpha \to 1}{lim}{s}_x^{\alpha \gamma }h\left(x\right)=o_1^{{\left[\gamma \right]}_1}{o}_2^{{\left[\gamma \right]}_2}\cdots o_m^{{\left[\gamma \right]}_m}h\left(x\right)={\displaystyle \frac{{\partial }^{\gamma }}{\partial x^{\gamma }}}h\left(x\right)\forall \left|\gamma \right|\le n}\hfill \\ {\displaystyle \underset{\alpha \to k}{lim}{s}_x^{\alpha \gamma }h\left(x\right)=o_1^{k{\left[\gamma \right]}_1}{o}_2^{k{\left[\gamma \right]}_2}\cdots o_m^{k{\left[\gamma \right]}_m}h\left(x\right)={\displaystyle \frac{{\partial }^{k\gamma }}{\partial x^{k\gamma }}}h\left(x\right)\forall k\left|\gamma \right|\le kn}\hfill \\ {\displaystyle \underset{\alpha \to n}{lim}{s}_x^{\alpha \gamma }h\left(x\right)=o_1^{n{\left[\gamma \right]}_1}{o}_2^{n{\left[\gamma \right]}_2}\cdots o_m^{n{\left[\gamma \right]}_m}h\left(x\right)={\displaystyle \frac{{\partial }^{n\gamma }}{\partial x^{n\gamma }}}h\left(x\right)\forall n\left|\gamma \right|\le n^2}\hfill \end{array}\right..\end{array}$$

(25)

As a consequence, considering a function $h:\mathsf{\Omega }\subset {\mathbb{R}}^m\to {\mathbb{R}}^m$, it is possible to define the following set of fractional operators:

$$\begin{array}{c}\hfill {}_m{S}_{x,\alpha }^{n,\gamma }\left(h\right):=\left\{s_x^{\alpha \gamma }:s_x^{\alpha \gamma }\in S_{x,\alpha }^{n,\gamma }\left({\left[h\right]}_k\right)\forall k\le m\right\}.\end{array}$$

(26)

On the other hand, using little-O notation, it is possible to obtain the following result:

$$\begin{array}{c}\hfill \mathrm{I}\mathrm{f} x\in B(a;\delta )\Rightarrow \underset{x\to a}{lim}{\displaystyle \frac{o\left({(x-a)}^{\gamma }\right)}{{(x-a)}^{\gamma }}}\to 0\forall \left|\gamma \right|\ge 1,\end{array}$$

(27)

with which it is possible to define the following set of functions:

$$\begin{array}{c}\hfill R_{\alpha \gamma }^n\left(a\right):=\left\{r_{\alpha \gamma }^n:\underset{x\to a}{lim}∥r_{\alpha \gamma }^n\left(x\right)∥=0\forall \left|\gamma \right|\ge nand∥r_{\alpha \gamma }^n\left(x\right)∥\le o\left({∥x-a∥}^n\right)\forall x\in B(a;\delta )\right\},\end{array}$$

(28)

where $r_{\alpha \gamma }^n:B(a;\delta )\subset \mathsf{\Omega }\to {\mathbb{R}}^m$. So, considering the previous set and some $B(a;\delta )\subset \mathsf{\Omega }$, it is possible to define the following set of fractional operators:

$$\begin{array}{c}\begin{array}{c}{\displaystyle {}_m{T}_{x,\alpha ,p}^{n,q,\gamma }(a,h):= \left\{t_x^{\alpha ,p}=t_x^{\alpha ,p}\left(s_x^{\alpha \gamma }\right):s_x^{\alpha \gamma }\in {}_m{S}_{x,\alpha }^{M,\gamma }\left(h\right)\mathrm{a}\mathrm{n}\mathrm{d}{t}_x^{\alpha ,p}h\left(x\right):=\sum _{\left|\gamma \right|=0}^p{\displaystyle \frac{1}{\gamma !}}{\widehat{e}}_j{s}_x^{\alpha \gamma }{\left[h\right]}_j\left(a\right){(x-a)}^{\gamma }+r_{\alpha \gamma }^p\left(x\right)\begin{array}{c}\forall \alpha \le n\\ \forall p\le q\end{array}\right\},}\end{array}\end{array}$$

(29)

$$\begin{array}{c}\begin{array}{c}{\displaystyle {}_m{T}_{x,\alpha }^{\infty ,\gamma }(a,h):= \left\{t_x^{\alpha ,\infty }=t_x^{\alpha ,\infty }\left(s_x^{\alpha \gamma }\right):s_x^{\alpha \gamma }\in {}_m{S}_{x,\alpha }^{\infty ,\gamma }\left(h\right)\mathrm{a}\mathrm{n}\mathrm{d}{t}_x^{\alpha ,\infty }h\left(x\right):=\sum _{\left|\gamma \right|=0}^{\infty }{\displaystyle \frac{1}{\gamma !}}{\widehat{e}}_j{s}_x^{\alpha \gamma }{\left[h\right]}_j\left(a\right){(x-a)}^{\gamma }\right\},}\end{array}\end{array}$$

(30)

which allow generalizing the Taylor series expansion of a vector-valued function in multi-index notation [18], where $M=max\left\{n,q\right\}$. As a consequence, it is possible to obtain the following results:

$$\begin{array}{c}\begin{array}{c}{\displaystyle \mathrm{If} t_x^{\alpha ,p}\in {}_m{T}_{x,\alpha ,p}^{1,q,\gamma }(a,h)\mathrm{a}\mathrm{n}\mathrm{d} \alpha \to 1\Rightarrow t_x^{1,p}h\left(x\right)=h\left(a\right)+\sum _{\left|\gamma \right|=1}^p{\displaystyle \frac{1}{\gamma !}}{\widehat{e}}_j{\displaystyle \frac{{\partial }^{\gamma }}{\partial x^{\gamma }}}{\left[h\right]}_j\left(a\right){(x-a)}^{\gamma }+r_{\gamma }^p\left(x\right),}\end{array}\end{array}$$

(31)

$$\begin{array}{c}\mathrm{If}{t}_x^{\alpha ,p}\in {}_m{T}_{x,\alpha ,p}^{n,1,\gamma }(a,h)\mathrm{a}\mathrm{n}\mathrm{d} p\to 1\Rightarrow t_x^{\alpha ,1}h\left(x\right)=h\left(a\right)+\sum _{k=1}^m{\widehat{e}}_j{o}_k^{\alpha }{\left[h\right]}_j\left(a\right){\left[(x-a)\right]}_k+r_{\alpha \gamma }^1\left(x\right).\end{array}$$

(32)

Let $f:\mathsf{\Omega }\subset {\mathbb{R}}^n\to {\mathbb{R}}^n$ be a function with a point $\xi \in \mathsf{\Omega }$ such that $∥f\left(\xi \right)∥=0$. So, for some $x_i\in B(\xi ;\delta )\subset \mathsf{\Omega }$ and for some fractional operator $t_x^{\alpha ,\infty }\in {}_n{T}_{x,\alpha }^{\infty ,\gamma }(x_i,f)$, it is possible to define a type of linear approximation of the function f around the value $x_i$ as follows:

$$\begin{array}{c}\hfill t_x^{\alpha ,\infty }f\left(x\right)\approx f\left(x_i\right)+\sum _{k=1}^n{\hat{e}}_j{o}_k^{\alpha }{\left[f\right]}_j\left(x_i\right){\left[(x-x_i)\right]}_k,\end{array}$$

which may be rewritten more compactly as follows:

$$\begin{array}{c}\hfill t_x^{\alpha ,\infty }f\left(x\right)\approx f\left(x_i\right)+\left(o_k^{\alpha }{\left[f\right]}_j\left(x_i\right)\right)(x-x_i),\end{array}$$

(33)

where $\left(o_k^{\alpha }{\left[f\right]}_j\left(x_i\right)\right)$ denotes a square matrix. On the other hand, if $x\to \xi$ since $∥f\left(\xi \right)∥=0$, it follows that

$$\begin{array}{ccc}\hfill 0\approx f\left(x_i\right)+\left(o_k^{\alpha }{\left[f\right]}_j\left(x_i\right)\right)(\xi -x_i)& \Rightarrow & \xi \approx x_i-{\left(o_k^{\alpha }{\left[f\right]}_j\left(x_i\right)\right)}^{-1}f\left(x_i\right).\hfill \end{array}$$

Then, defining the following matrix,

$$\begin{array}{c}\hfill A_{f,\alpha }\left(x\right)=\left({\left[A_{f,\alpha }\right]}_{jk}\left(x\right)\right):={\left(o_k^{\alpha }{\left[f\right]}_j\left(x\right)\right)}^{-1},\end{array}$$

(34)

it is possible to define the following fractional iterative method

$$\begin{array}{cc}\hfill x_{i+1}:=\Phi (\alpha ,x_i)=x_i-A_{f,\alpha }\left(x_i\right)f\left(x_i\right),& i=0,1,2,\cdots ,\end{array}$$

(35)

which corresponds to the more general case of the fractional Newton–Raphson method [7,16,17,18]. As a consequence, considering an iteration function $\Phi :(\mathbb{R}\backslash \mathbb{Z})\times {\mathbb{R}}^n\to {\mathbb{R}}^n$, the iteration function of a fractional iterative method may be written in general form as follows

$$\begin{array}{cc}\hfill \Phi (\alpha ,x):=x-A_{g,\alpha }\left(x\right)f\left(x\right),& \alpha \in \mathbb{R}\backslash \mathbb{Z},\end{array}$$

(36)

where $A_{g,\alpha }$ is a matrix that depends, in at least one of its entries, on fractional operators of order $\alpha$ applied to some function $g:{\mathbb{R}}^n\to {\mathbb{R}}^n$, whose particular case occurs when $g=f$. So, it is possible to define the following sets of fractional operators:

$$\begin{array}{c}\begin{array}{c}{\displaystyle {}_n{O}_{x,\alpha }^m\left(g\right):= \left\{o_x^{\alpha }:o_x^{\alpha }\in O_{x,\alpha }^m\left({\left[g\right]}_k\right)\forall k\le n\right\},}\end{array}\end{array}$$

(37)

$$\begin{array}{c}\begin{array}{c}{\displaystyle {}_n{O}_{x,\alpha }^{m,c}\left(g\right):= \left\{o_x^{\alpha }:o_x^{\alpha }\in O_{x,\alpha }^{m,c}\left({\left[g\right]}_k\right)\forall k\le n\right\},}\end{array}\end{array}$$

(38)

$$\begin{array}{c}{}_n{O}_{x,\alpha }^{m,u}\left(g\right):={}_n{O}_{x,\alpha }^m\left(g\right)\cup {}_n{O}_{x,\alpha }^{m,c}\left(g\right),\end{array}$$

(39)

which allow defining the following sets of matrices:

$$\begin{array}{c}\begin{array}{c}{\displaystyle {}_n{M}_{x,\alpha }^m\left(g\right):= \left\{A_{g,\alpha }=A_{g,\alpha }\left(o_x^{\alpha }\right):o_x^{\alpha }\in {}_n{O}_{x,\alpha }^{s,u}\left(g\right)\forall s\in {\mathbb{Z}}_{\le m}\mathrm{a}\mathrm{n}\mathrm{d}{A}_{g,\alpha }\left(x\right)=\left({\left[A_{g,\alpha }\right]}_{jk}\left(x\right)\right) := \left(o_k^{\alpha }{\left[g\right]}_j\left(x\right)\right)\right\},}\end{array}\end{array}$$

(40)

$$\begin{array}{c}{}_n{IM}_{x,\alpha }^m\left(g\right):= \left\{A_{g,\alpha }\in {}_n{M}_{x,\alpha }^m\left(g\right):\exists A_{g,\alpha }^{-1}\right\}.\end{array}$$

(41)

Therefore, the fractional Newton–Raphson method may be defined and classified through the set of matrices ${}_n{IM}_{x,\alpha }^{\infty }\left(g\right)$, using the following set:

$$\begin{array}{c}\hfill \left\{A_{g,\alpha }:\exists A_{g,\alpha }^{-1}\in {}_n{IM}_{x,\alpha }^{\infty }\left(g\right)\text{and}{A}_{g,\alpha }\left(x\right)=\left({\left[A_{g,\alpha }\right]}_{jk}\left(x\right)\right) :={\left(o_k^{\alpha }{\left[g\right]}_j\left(x\right)\right)}^{-1}\right\}.\end{array}$$

(42)

Furthermore, considering that when using the classical Hadamard product in general $o_x^{p\alpha }\circ o_x^{q\alpha }\ne o_x^{(p+q)\alpha }$, assuming the existence of a fixed set of matrices ${}_n{IM}_{x,\alpha }^{\infty }\left(g\right)$, joined with a modified Hadamard product that fulfills the following property

$$\begin{array}{c}\hfill o_{i,x}^{p\alpha }\circ o_{j,x}^{q\alpha }:=\left\{\begin{array}{cc}{o}_{i,x}^{p\alpha }\circ o_{j,x}^{q\alpha },& \text{if} i\ne j\left(\text{Hadamard product of type horizontal}\right)\hfill \\ o_{i,x}^{(p+q)\alpha },& \text{if} i=j\left(\text{Hadamard product of type vertical}\right)\hfill \end{array}\right.,\end{array}$$

(43)

by omitting the function g it has the ability to generate a group of fractional matrix operators$A_{\alpha }$ that fulfill the following equation

$$\begin{array}{c}\hfill A_{\alpha }\left(o_{i,x}^{p\alpha }\right)\circ A_{\alpha }\left(o_{j,x}^{q\alpha }\right) := \left\{\begin{array}{cc}{A}_{\alpha }\left(o_{i,x}^{p\alpha }\circ o_{j,x}^{q\alpha }\right),& \text{if} i\ne j\hfill \\ A_{\alpha }\left(o_{i,x}^{(p+q)\alpha }\right),& \text{if} i=j\hfill \end{array}\right.,\end{array}$$

(44)

through the following set

$$\begin{array}{c}\hfill {}_n{G}_{FNR}\left(\alpha \right):= \left\{A_{\alpha }^{\circ m}=A_{\alpha }\left(o_x^{m\alpha }\right):\exists A_{\alpha }^{\circ m}\in {}_n{IM}_{x,\alpha }^{\infty }(·)\forall m\in \mathbb{Z}and{A}_{\alpha }^{\circ m}=\left({\left[A_{\alpha }^{\circ m}\right]}_{jk}\right) := \left(o_k^{m\alpha }\right)\right\}.\end{array}$$

(45)

where $\forall A_{i,\alpha }^{\circ m}\in {}_n{G}_{FNR}\left(\alpha \right)$, the following properties are defined

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{A}_{i,\alpha }^{\circ 0}\circ A_{i,\alpha }^{\circ p}=A_{i,\alpha }^{\circ p}:=A_{i,\alpha }\left(o_{i,x}^{p\alpha }\right)\hfill \\ A_{i,\alpha }^{\circ p}\circ A_{i,\alpha }^{\circ q}=A_{i,\alpha }^{\circ (p+q)}:=A_{i,\alpha }\left(o_{i,x}^{(p+q)\alpha }\right)\hfill \\ A_{i,\alpha }^{\circ p}\circ A_{j,\alpha }^{\circ q}=A_{k,\alpha }^{\circ 1}:=A_{k,\alpha }\left(o_{i,x}^{p\alpha }\circ o_{j,x}^{q\alpha }\right)\hfill \end{array}\right.,\end{array}$$

(46)

as a consequence

$$\begin{array}{c}\hfill \forall A_{k,\alpha }^{\circ 1}\in {}_n{G}_{FNR}\left(\alpha \right)\text{such that}{A}_{k,\alpha }\left(o_{k,x}^{\alpha }\right)=A_{k,\alpha }\left(o_{i,x}^{p\alpha }\circ o_{j,x}^{q\alpha }\right)\exists A_{k,\alpha }^{\circ r}=A_{k,\alpha }^{\circ (r-1)}\circ A_{k,\alpha }^{\circ 1}=A_{k,\alpha }\left(o_{i,x}^{rp\alpha }\circ o_{j,x}^{rq\alpha }\right).\end{array}$$

(47)

Therefore, it is possible to obtain the following corollary:

Corollary 3.

Let $g:{\mathbb{R}}^n\to {\mathbb{R}}^n$ be a function such that $\exists {}_n{O}_{x,\alpha }^{k,u}\left(g\right)\forall k\in \mathbb{Z}$, then it is fulfilled that

$$\begin{array}{c}\hfill \forall o_x^{\alpha }\in {}_n{MO}_{x,\alpha }^{\infty ,u}\left(g\right):=\bigcap _{k\in \mathbb{Z}}{}_n{O}_{x,\alpha }^{k,u}\left(g\right)\exists {}_{n}G\left(A_{\alpha }\left(o_x^{\alpha }\right)\right) \subset {}_n{G}_{FNR}\left(\alpha \right),\end{array}$$

(48)

such that ${}_{n}G\left(A_{\alpha }\left(o_x^{\alpha }\right)\right)$ is a group. As a consequence

$$\begin{array}{c}\hfill {}_n{G}_{FNR}\left(\alpha \right)=\bigcup _{o_x^{\alpha }\in {}_n{MO}_{x,\alpha }^{\infty ,u}\left(g\right)}{}_{n}G\left(A_{\alpha }\left(o_x^{\alpha }\right)\right).\end{array}$$

(49)

Furthermore, defining $A_{\alpha }\left(g\right)=\left({\left[A_{\alpha }\left(g\right)\right]}_{jk}\right) := \left({\left[g\right]}_k^{}\right)$, it is possible to obtain the following result:

$$\begin{array}{c}\hfill \forall A_{\alpha }^{\circ m}\in {}_n{G}_{FNR}\left(\alpha \right)\exists A_{g,m\alpha }\in {}_n{IM}_{x,\alpha }^{\infty }\left(g\right)\text{such that}{A}_{g,m\alpha }:=A_{\alpha }\left(o_x^{m\alpha }\right)\circ A_{\alpha }^T\left(g\right).\end{array}$$

(50)

As a consequence, the fractional Newton–Raphson method may also be defined through the set of fractional matrix operators ${}_n{G}_{FNR}\left(\alpha \right)$ using the following set:

$$\begin{array}{c}\hfill \left\{A_{\alpha }^{\circ 1}\in {}_n{G}_{FNR}\left(\alpha \right):\exists A_{g,\alpha }^{-1}=A_{\alpha }\left(o_x^{\alpha }\right)\circ A_{\alpha }^T\left(g\right)\text{and}{A}_{g,\alpha }^{-1}\in {}_n{IM}_{x,\alpha }^{\infty }\left(g\right)\right\}.\end{array}$$

(51)

Therefore, if ${\Phi }_{FNR}$ denotes the iteration function of the fractional Newton–Raphson method, it is possible to obtain the following results:

$$\begin{array}{cc}\hfill \mathrm{Let}{\alpha }_0\in \mathbb{R}\backslash \mathbb{Z}\Rightarrow \forall A_{g,{\alpha }_0}^{-1}\in {}_n{IM}_{x,\alpha }^{\infty }\left(g\right)\exists {\Phi }_{FNR}={\Phi }_{FNR}\left(A_{g,{\alpha }_0}\right)& \therefore \forall A_{g,{\alpha }_0}\exists \left\{{\Phi }_{FNR}\left(A_{g,\alpha }\right):\alpha \in \mathbb{R}\backslash \mathbb{Z}\right\},\hfill \end{array}$$

(52)

$$\begin{array}{cc}\hfill \mathrm{Let}{\alpha }_0\in \mathbb{R}\backslash \mathbb{Z}\Rightarrow \forall A_{{\alpha }_0}^{\circ 1}\in {}_n{G}_{FNR}\left(\alpha \right)\exists {\Phi }_{FNR}={\Phi }_{FNR}\left(A_{{\alpha }_0}\right)& \therefore \forall A_{{\alpha }_0}\exists \left\{{\Phi }_{FNR}\left(A_{\alpha }\right):\alpha \in \mathbb{R}\backslash \mathbb{Z}\right\}.\hfill \end{array}$$

(53)

On the other hand, it is possible to define in a general way a fractional fixed-point method as follows:

$$\begin{array}{cc}\hfill x_{i+1}:=\Phi (\alpha ,x_i),& i=0,1,2,\cdots .\end{array}$$

(54)

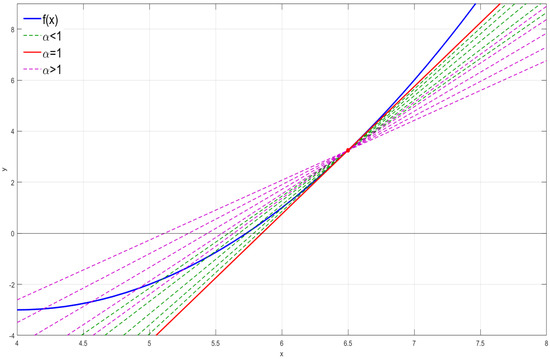
Figure 1. Illustration of some lines generated by the fractional Newton–Raphson method for the same initial condition $x_0$ but with different orders $\alpha$ of the fractional operator implemented [16]. The fractional Newton–Raphson method usually generates lines that are not tangent to the function f whose zeros are sought, unlike the classical Newton–Raphson method.

Before continuing, it is necessary to mention that one of the main advantages of fractional iterative methods is that the initial condition $x_0$ can remain fixed, with which it is enough to vary the order $\alpha$ of the fractional operators involved until generating a sequence convergent ${\left\{x_i\right\}}_{i\ge 1}$ to the value $\xi \in \mathsf{\Omega }$. Since the order $\alpha$ of the fractional operators is varied, different values of $\alpha$ can generate different convergent sequences to the same value $\xi$ but with a different number of iterations (see Figure 1). So, it is possible to define the following set

$$\begin{array}{c}\hfill {Conv}_{\delta }\left(\xi \right):= \left\{\Phi :\underset{x\to \xi }{lim}\Phi (\alpha ,x)={\xi }_{\alpha }\in B(\xi ;\delta )\right\},\end{array}$$

(55)

which may be interpreted as the set of fractional fixed-point methods that define a convergent sequence ${\left\{x_i\right\}}_{i\ge 1}$ to some value ${\xi }_{\alpha }\in B(\xi ;\delta )$. So, denoting by $card\left(·\right)$ the cardinality of a set, it is possible to define the following theorem:

Theorem 2.

Let $\Phi :(\mathbb{R}\backslash \mathbb{Z})\times {\mathbb{R}}^n\to {\mathbb{R}}^n$ be an iteration function with a value $\alpha \in \mathbb{R}\backslash \mathbb{Z}$ such that $\Phi (\alpha ,x)\in {Conv}_{\delta }\left(\xi \right)$ in a region Ω. So, if there exists $ϵ>0$ small enough to ensure that there exists a non-integer value $\beta \in B(\alpha ;ϵ)$ such that

$$\begin{array}{ccc}\hfill \Phi (\beta ,x)\in B\left(\Phi (\alpha ,x);{\delta }_{\beta }\right)\forall x\in \mathsf{\Omega }& and& \Phi (\beta ,x)\in {Conv}_{\delta }\left(\xi \right),\hfill \end{array}$$

then the following is fulfilled:

$$\begin{array}{c}\hfill card\left({Conv}_{\delta }\left(\xi \right)\right)=card\left(\mathbb{R}\right).\end{array}$$

(56)

Proof. 

The proof of the theorem is carried out by contradiction, assuming the following:

$$\begin{array}{c}\hfill card\left({Conv}_{\delta }\left(\xi \right)\right) <card\left(\mathbb{R}\right).\end{array}$$

So, considering that

$$\begin{array}{ccc}\hfill \Phi (\beta ,x)\in B\left(\Phi (\alpha ,x);{\delta }_{\beta }\right)\forall x\in \mathsf{\Omega }& and& \left\{\Phi (\alpha ,x),\Phi (\beta ,x)\right\}\subset {Conv}_{\delta }\left(\xi \right),\hfill \end{array}$$

(57)

there exists at least one value $x_k\in B(\xi ;\delta )$ such that

$$\begin{array}{c}\hfill \Phi (\beta ,x_k)\in B\left(\Phi (\alpha ,x_k);{\delta }_{\beta }\right) =B(x_{k+1};{\delta }_{\beta })\subset B(\xi ;\delta ).\end{array}$$

(58)

Since $\beta \in B(\alpha ;ϵ)$ for some ϵ small enough, without loss of generality if $\alpha <\beta <m$ with $m=\lceil \alpha \rceil$, it follows that

$$\begin{array}{c}\hfill \Phi (a,x_k)\in B\left(\Phi (\alpha ,x_k);{\delta }_a\right) \subset B\left(x_{k+1};{\delta }_{\beta }\right)\forall a\in [\alpha ,\beta ].\end{array}$$

(59)

As a consequence, the following holds:

$$\begin{array}{ccc}\hfill {Conv}_{\delta }\left(\xi \right)\supset \left\{\Phi (a,x):a\in [\alpha ,\beta ]\right\}& \Rightarrow & card\left({Conv}_{\delta }\left(\xi \right)\right) \ge card\left([\alpha ,\beta ]\right).\hfill \end{array}$$

Then, considering the following function

$$\begin{array}{c}\hfill h\left(x\right)={\displaystyle \frac{x-\alpha }{\beta -\alpha }},\end{array}$$

it is fulfilled that

$$\begin{array}{ccc}\hfill h:[\alpha ,\beta ]\to [0,1]& \Rightarrow & card\left([\alpha ,\beta ]\right)=card\left([0,1]\right)=card\left(\mathbb{R}\right),\hfill \end{array}$$

and therefore,

$$\begin{array}{c}\hfill card\left({Conv}_{\delta }\left(\xi \right)\right) \ge card\left(\mathbb{R}\right).\end{array}$$

□

Finally, it is necesssary to mention that fsractional iterative methods may be defined in the complex space [18], that is,

$$\begin{array}{c}\hfill \left\{\Phi (\alpha ,x):\alpha \in \mathbb{R}\backslash \mathbb{Z}\text{and}x\in {\mathbb{C}}^n\right\}.\end{array}$$

(60)

However, due to the part of the integral operator that fractional operators usually have, it may be considered that in matrix $A_{g,\alpha }$, each fractional operator $o_k^{\alpha }$ is obtained for a real variable ${\left[x\right]}_k$, and if the result allows it, this variable is subsequently substituted by a complex variable ${\left[x_i\right]}_k$, that is, the following:

$$\begin{array}{ccc}\hfill A_{g,\alpha }\left(x_i\right):=A_{g,\alpha }\left(x\right){|}_{x⟶x_i},& x\in {\mathbb{R}}^n,& x_i\in {\mathbb{C}}^n.\hfill \end{array}$$

(61)

So, considering the above as well as the Theorem 1 and the Theorem 2, the following corollary is obtained:

Corollary 4.

Let $\Phi :(\mathbb{R}\backslash \mathbb{Z})\times {\mathbb{C}}^n\to {\mathbb{C}}^n$ be an interaction function with a sequence of different values ${\left\{{\alpha }_i\right\}}_{i\ge 1}\in \mathbb{R}\backslash \mathbb{Z}$ that define the following set:

$$\begin{array}{c}\hfill Conv\left(\mathsf{\Omega },{\left\{{\alpha }_i\right\}}_{i\ge 1}\right):=\left\{\Phi (\alpha ,x)\in {Conv}_{\delta }\left({\xi }_{\alpha }\right)forsome {\xi }_{\alpha }\in \mathsf{\Omega }:\alpha \in {\left\{{\alpha }_i\right\}}_{i\ge 1}\right\}.\end{array}$$

So, if $card\left(Conv\left(\mathsf{\Omega },{\left\{{\alpha }_i\right\}}_{i\ge 1}\right)\right)=M$ with $1<M<\infty$, then Φ has a mean order of convergence of order (at least) $\overline{p}$ in Ω, and there exists a sequence ${\left\{P_i\right\}}_{i\ge 1}^M\in B(\overline{p};{\delta }_K)$ with $P_i=P_i\left({\alpha }_i\right)$ that allows defining the following value:

$$\begin{array}{c}\hfill \overline{P}:={\displaystyle \frac{1}{M}}\sum _{i=1}^M{P}_i,\end{array}$$

Therefore, for M large enough, it is fulfilled the following:

$$\begin{array}{c}\hfill |\overline{P}-\overline{p}|<ϵ.\end{array}$$

(62)

5. Approximation to the Critical Points of a Function

Let $C^s\left(\mathsf{\Omega }\right)$ be a set of functions defined as follows

$$\begin{array}{c}\hfill C^s\left(\mathsf{\Omega }\right):= \left\{f:\exists {\displaystyle \frac{{\partial }^{\gamma }}{\partial x^{\gamma }}}f\left(x\right)\forall \left|\gamma \right|\le s\text{and}\forall x\in \mathsf{\Omega }\right\}.\end{array}$$

(63)

So, it is possible to obtain the following result:

$$\begin{array}{c}\hfill \mathrm{Let}f:\mathsf{\Omega }\subset {\mathbb{R}}^n\to \mathbb{R} \text{a function such that} f\in C^2\left(\mathsf{\Omega }\right)\Rightarrow \exists \nabla f\left(x\right) \text{and} \exists Hf\left(x\right)\forall x\in \mathsf{\Omega },\end{array}$$

(64)

where $\nabla f$ and $Hf$ denote the gradient of f and the Hessian matrix of f, respectively. So in general, for every scalar function $f:\mathsf{\Omega }\subset {\mathbb{C}}^n\to \mathbb{C}$ that belongs to the set $C^2\left(\mathsf{\Omega }\right)$, it is possible to define the following set:

$$\begin{array}{c}\hfill \mathfrak{C}(\mathsf{\Omega },f):=\left\{\xi \in \mathsf{\Omega }:∥\nabla f\left(\xi \right)∥ =0\right\},\end{array}$$

(65)

which corresponds to the set of critical points of the function f in the region $\mathsf{\Omega }$. On the other hand, denoting by Re$(·)$ the real part of a complex, by $det(·)$ the determinant of a matrix and by $sgn(·)$ the sign function such that for a square matrix A,

$$\begin{array}{c}\hfill sgn\left(A\right):=\left(sgn\left({\left[A\right]}_{jk}\right)\right),\end{array}$$

it is possible to define the following functions

$$\begin{array}{ccc}\hfill {\mathsf{\Delta }}_d\left(\xi \right):=sgn\left(det\left(\text{Re}\left(Hf\right(\xi \left)\right)\right)\right)& \text{and}& {\mathsf{\Delta }}_t\left(\xi \right):=tr\left(sgn\left(\text{Re}\left(Hf\right(\xi \left)\right)\right)\right),\hfill \end{array}$$

(66)

which allow defining the following sets

$$\begin{array}{c}\begin{array}{c}{\displaystyle {\mathfrak{C}}_M(\mathsf{\Omega },f):= \left\{\xi \in \mathfrak{C}(\mathsf{\Omega },f):{\mathsf{\Delta }}_d\left(\xi \right)=1\text{and}{\mathsf{\Delta }}_t\left(\xi \right)=-n\right\},}\end{array}\end{array}$$

(67)

$$\begin{array}{c}\begin{array}{c}{\displaystyle {\mathfrak{C}}_m(\mathsf{\Omega },f):= \left\{\xi \in \mathfrak{C}(\mathsf{\Omega },f):{\mathsf{\Delta }}_d\left(\xi \right)=1\text{and}{\mathsf{\Delta }}_t\left(\xi \right)=n\right\},}\end{array}\end{array}$$

(68)

$$\begin{array}{c}{\mathfrak{C}}_S(\mathsf{\Omega },f):= \left\{\xi \in \mathfrak{C}(\mathsf{\Omega },f):{\mathsf{\Delta }}_d\left(\xi \right)=-1\text{and}{\mathsf{\Delta }}_t\left(\xi \right)\in [-n,n]\right\},\end{array}$$

(69)

which correspond respectively to the sets of local maxima, local minima, and local saddle points of the function f in the region $\mathsf{\Omega }$. So, defining the following set of functions

$$\begin{array}{c}\hfill C_H^2\left(\mathsf{\Omega }\right):= \left\{f\in C^2\left(\mathsf{\Omega }\right):\exists {\left(Hf\left(x\right)\right)}^{-1}\forall x\in \mathsf{\Omega }\right\},\end{array}$$

(70)

and considering a function $f:\mathsf{\Omega }\subset {\mathbb{C}}^n\to \mathbb{C}$ such that $f\in C_H^2\left(\mathsf{\Omega }\right)$, it is possible to construct an iteration function ${\Phi }_{H,\delta }:(\mathbb{R}\backslash \mathbb{Z})\times {\mathbb{C}}^n\to {\mathbb{C}}^n$ defined as follows:

$$\begin{array}{c}\hfill {\Phi }_{H,\delta }(\alpha ,x):=x-{\mathcal{H}}_{g,\alpha }\left(x\right)\nabla f\left(x\right),\end{array}$$

(71)

which corresponds to the iteration function of a hybrid fractional iterative method, where

$$\begin{array}{c}\hfill {\mathcal{H}}_{g,\alpha }\left(x\right):= \left\{\begin{array}{cc}{A}_{g,\alpha }\left(x\right),& \text{if} ∥\nabla f\left(x\right)∥>\delta \\ {\left(Hf\left(x\right)\right)}^{-1},& \text{if} ∥\nabla f\left(x\right)∥\le \delta \end{array}\right.,\end{array}$$

(72)

and $A_{g,\alpha }$ is a matrix of some fractional iterative method.

Examples

Let $f:\mathsf{\Omega }\subset {\mathbb{C}}^2\to \mathbb{C}$ be a function given by the following expression:

$$\begin{array}{c}\hfill \begin{array}{c}f\left(x\right)=\left(2-{\left[x\right]}_1^2+{\left[x\right]}_1^3{\left[x\right]}_2\right)cos\left({\left[x\right]}_1\right)-\left(2-{\left[x\right]}_2^2\right)cos\left({\left[x\right]}_2\right)-{\left[x\right]}_1\left(5-{\left[x\right]}_2^{3}cos\left({\left[x\right]}_2\right)-2sin\left({\left[x\right]}_1\right)\right)-{\left[x\right]}_2\left(7+2sin\left({\left[x\right]}_2\right)\right).\end{array}\end{array}$$

Then,

$$\begin{array}{c}\hfill \begin{array}{c}\nabla f\left(x\right)=\left(\begin{array}{c}3{\left[x\right]}_1^2{\left[x\right]}_{2}cos\left({\left[x\right]}_1\right)+{\left[x\right]}_2^{3}cos\left({\left[x\right]}_2\right)+{\left[x\right]}_1^2\left(1-{\left[x\right]}_1{\left[x\right]}_2\right)sin\left({\left[x\right]}_1\right)-5\\ {}_1^{3}cos\left({\left[x\right]}_1\right)+3{\left[x\right]}_1{\left[x\right]}_2^{2}cos\left({\left[x\right]}_2\right)-{\left[x\right]}_2^2\left(1+{\left[x\right]}_1{\left[x\right]}_2\right)sin\left({\left[x\right]}_2\right)-7\end{array}\right),\end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{c}Hf\left(x\right)=\left(\begin{array}{cc}{\left[x\right]}_1\left(\left({\left[x\right]}_1+6{\left[x\right]}_2-{\left[x\right]}_1^2{\left[x\right]}_2\right)cos\left({\left[x\right]}_1\right)+2\left(1-3{\left[x\right]}_1{\left[x\right]}_2\right)sin\left({\left[x\right]}_1\right)\right)& {\left[x\right]}_1^2\left(3cos\left({\left[x\right]}_1\right)-{\left[x\right]}_{1}sin\left({\left[x\right]}_1\right)\right)+{\left[x\right]}_2^2\left(3cos\left({\left[x\right]}_2\right)-{\left[x\right]}_{2}sin\left({\left[x\right]}_2\right)\right)\\ {}_1^2\left(3cos\left({\left[x\right]}_1\right)-{\left[x\right]}_{1}sin\left({\left[x\right]}_1\right)\right)+{\left[x\right]}_2^2\left(3cos\left({\left[x\right]}_2\right)-{\left[x\right]}_{2}sin\left({\left[x\right]}_2\right)\right)& -{\left[x\right]}_2\left(\left({\left[x\right]}_2-{\left[x\right]}_1\left(6-{\left[x\right]}_2^2\right)\right)cos\left({\left[x\right]}_2\right)+2\left(1+3{\left[x\right]}_1{\left[x\right]}_2\right)sin\left({\left[x\right]}_2\right)\right)\end{array}\right).\end{array}\end{array}$$

So, considering the following function

$$\begin{array}{c}\hfill {Rnd}_m\left(x\right) := \left\{\begin{array}{cc}\text{Re}\left(x\right),& \text{if} \left|Im\left(x\right)\right|\le {10}^{-m}\\ x,& \text{if} \left|Im\left(x\right)\right|>{10}^{-m}\end{array}\right.,\end{array}$$

(73)

it is possible to define the following iteration function:

$$\begin{array}{c}\hfill {Rnd}_5\left({\Phi }_{H,\delta }(\alpha ,x)\right) :={\widehat{e}}_j{Rnd}_5\left({\left[{\Phi }_{H,\delta }\right]}_j(\alpha ,x)\right).\end{array}$$

(74)

Before continuing, it is necessary to mention that a description of the algorithm that must be implemented when working with a fractional iterative method given by Equation (54) may be found in Ref. [17]. Simplified examples of how a fractional iterative method given by a matrix $A_{g,\alpha }$ should be programmed may be found in Refs. [23,24].

Example 1.

Using the function (73), the Riemann–Liouville fractional derivative (22) and $\nabla f$, it is possible to construct an iteration function analogous to Equation (36), using the following matrix:

$$\begin{array}{cc}\hfill A_{g_f,\beta }\left(x_i\right)=\left({\left[A_{g_f,\beta }\right]}_{jk}\left(x_i\right)\right):={\left({\partial }_k^{\beta (\alpha ,{\left[x_i\right]}_k)}{\left[g_f\right]}_j\left(x\right)\right)}_{x_i}^{-1},& \alpha \in \mathbb{R}\backslash \mathbb{Z},\end{array}$$

(75)

which generates a particular case of the fractional quasi-Newton method [7,17], where $g_f\left(x\right)$ and $\beta (\alpha ,{\left[x_i\right]}_k)$ are functions defined as follows:

$$\begin{array}{ccc}\hfill g_f\left(x\right):=\nabla f\left(x_i\right)+Hf\left(x_i\right)x& and& \beta (\alpha ,{\left[x_i\right]}_k):= \left\{\begin{array}{cc}\alpha ,& if |{\left[x_i\right]}_k|\ne 0\\ 1,& if |{\left[x_i\right]}_k|=0\end{array}\right..\hfill \end{array}$$

(76)

So, considering following initial condition

$$\begin{array}{ccc}\hfill x_0={(5.21,5.21)}^T& with& {∥\nabla f\left(x_0\right)∥}_2\approx 1,289.4083,\hfill \end{array}$$

the results shown in Table 1 are obtained.

Table 1. Results obtained using the fractional quasi-Newton method [7].

	$\mathit{\alpha }$	${\left[{\mathit{x}}_{\mathit{k}}\right]}_1$	${\left[{\mathit{x}}_{\mathit{k}}\right]}_2$	${∥{\mathit{x}}_{\mathit{k}}-{\mathit{x}}_{\mathit{k}-1}∥}_2$	${∥\mathit{\nabla }\mathit{f}\left({\mathit{x}}_{\mathit{k}}\right)∥}_2$	${\mathit{P}}_{\mathit{k}}$	${\mathbf{\Delta }}_{\mathit{d}}\left({\mathit{x}}_{\mathit{k}}\right)$	${\mathbf{\Delta }}_{\mathit{t}}\left({\mathit{x}}_{\mathit{k}}\right)$	k
1	−0.530515	6.6771554 − 0.02130862i	−0.014023 + 1.72836829i	1.41E-08	9.24E-05	0.9812	−1	2	167
2	−0.516037	0.01499973 − 1.73190718i	6.6757499 − 0.04157569i	1.41E-08	9.86E-05	1.0260	−1	−2	165
3	−0.472867	0.01499966 + 1.73190711i	6.67574974 + 0.04157578i	2.45E-08	9.54E-05	1.0000	−1	−2	180
4	−0.440017	6.67715551 + 0.02130861i	−0.014023 − 1.72836833i	1.41E-08	9.47E-05	1.0113	−1	2	180
5	−0.372536	−1.12922862 + 1.02480512i	3.7817693 + 0.02894647i	3.22E-07	8.23E-05	0.9960	1	−2	92
6	−0.359168	−1.12922793 − 1.02480539i	3.78176969 − 0.02894643i	1.36E-06	7.78E-05	1.0255	1	−2	92
7	−0.317767	3.68514423 − 0.05398726i	−1.20114465 + 1.03004598i	4.35E-07	7.98E-05	1.0095	1	−2	89
8	−0.175657	6.66385192 + 0.00958153i	−3.05535188 + 0.51526774i	1.66E-07	9.98E-05	1.0145	1	2	129
9	−0.174937	9.69844564 − 0.00485976i	− 1.49692201 + 1.85490018i	1.41E-08	8.99E-05	0.9812	1	−2	180
10	−0.167409	9.69844566 + 0.00485981i	−1.49692201 − 1.85490019i	1.00E-08	8.76E-05	1.0000	1	−2	178
11	−0.165538	3.68514454 + 0.0539876i	−1.20114479 − 1.0300467i	8.66E-07	8.57E-05	1.0144	1	−2	117
12	−0.162111	−1.47430587 + 1.85378122i	9.71215809 + 0.012692i	1.41E-08	8.26E-05	1.0313	1	−2	178
13	−0.148486	12.78190313 − 0.00664448i	−3.36083258 − 1.47015693i	1.00E-08	8.71E-05	1.0192	1	2	195
14	−0.141354	−1.47430585 − 1.85378123i	9.71215813 − 0.01269197i	3.00E-08	5.73E-05	0.9966	1	−2	179
15	−0.140788	−3.01831349 + 0.5058919i	6.69924174 + 0.01613682i	3.16E-08	9.57E-05	1.0285	1	2	146
16	−0.125015	19.0075656	−7.54961078	1.41E-08	8.38E-05	1.0000	1	2	197
17	−0.119655	−4.59285859	9.73129666	3.61E-08	4.16E-05	1.0195	1	−2	111
18	−0.092015	6.66385199 − 0.00958166i	−3.05535203 − 0.51526774i	2.45E-08	8.85E-05	1.0044	1	2	85
19	−0.081244	12.81002482	−7.10966547	1.41E-08	8.10E-05	1.0399	1	2	190
20	−0.075076	9.71878342	−4.62771758	2.24E-08	9.26E-05	1.0000	1	−2	97
21	−0.073120	−3.01831348 − 0.50589194i	6.69924174 − 0.01613673i	4.58E-08	7.95E-05	1.0187	1	2	82
22	−0.056190	18.99311678	−9.30049381	1.41E-08	9.76E-05	0.9812	−1	0	145
23	−0.052492	−6.39937485	9.68519629	2.24E-08	9.90E-05	0.9563	−1	0	161
24	−0.052490	−7.09665187	12.81542466	2.24E-08	7.76E-05	1.0377	1	2	113
25	−0.037197	−5.68870793 − 0.65962195i	15.8889979 − 0.00516137i	1.41E-08	2.87E-05	0.9812	1	−2	183
26	−0.030387	−9.30202535	18.99474019	1.41E-08	7.22E-05	0.9812	−1	0	162

Therefore,

$$\begin{array}{c}\hfill \overline{P}\approx 1.0060\in B\left(\overline{p};{\delta }_K\right),\end{array}$$

which is consistent with the Corollary 2 since, in general, if $\xi \in \mathfrak{C}(\mathsf{\Omega },f)$, then it is fulfilled the following (see [18], proof of Proposition 1):

$$\begin{array}{c}\hfill \underset{x\to \xi }{lim}∥{\Phi }^{\left(1\right)}(\alpha ,x)∥\ne 0.\end{array}$$

Example 2.

Using the iteration function (74) and the matrix $A_{g_f,\beta }$ given by Equation (75), considering following values

$$\begin{array}{ccc}\hfill \delta =7& and& x_0={(4.78,4.78)}^{T}with{∥\nabla f\left(x_0\right)∥}_2\approx 770.4734,\hfill \end{array}$$

the results shown in Table 2 are obtained.

Table 2. Results obtained using the iteration function (74) with the fractional quasi-Newton method [7].

	$\mathit{\alpha }$	${\left[{\mathit{x}}_{\mathit{k}}\right]}_1$	${\left[{\mathit{x}}_{\mathit{k}}\right]}_2$	${∥{\mathit{x}}_{\mathit{k}}-{\mathit{x}}_{\mathit{k}-1}∥}_2$	${∥\mathit{\nabla }\mathit{f}\left({\mathit{x}}_{\mathit{k}}\right)∥}_2$	${\mathit{P}}_{\mathit{k}}$	${\mathbf{\Delta }}_{\mathit{d}}\left({\mathit{x}}_{\mathit{k}}\right)$	${\mathbf{\Delta }}_{\mathit{t}}\left({\mathit{x}}_{\mathit{k}}\right)$	k
1	−0.991504	3.98115471	3.92170125	1.00E-08	1.50E-06	2.1162	1	2	55
2	−0.985320	−0.20172521	−2.13862013	1.00E-08	3.55E-08	2.0096	−1	0	184
3	−0.977534	4.76944744	0.24682585	5.21E-06	4.75E-07	2.0536	−1	2	115
4	−0.957378	−0.14249533	7.84459109	2.32E-06	1.71E-06	2.1574	−1	0	44
5	−0.931674	1.52183063 + 0.04852431i	−1.07285283 + 0.62177498i	1.64E-05	6.40E-08	1.9728	−1	0	147
6	−0.910766	−0.1411895	4.75629836	5.06E-07	4.42E-07	2.0939	−1	−2	99
7	−0.902424	−1.66983169	−1.47843397	3.51E-05	6.06E-08	2.0210	1	−2	141
8	−0.796926	7.84012182	0.11780088	5.96E-05	2.18E-06	2.2020	−1	0	32
9	−0.747172	−1.47430586 − 1.85378123i	9.71215811 − 0.01269197i	5.21E-06	1.45E-05	2.0987	1	−2	193
10	−0.739854	9.69844563 − 0.0048598i	−1.496922 + 1.85490017i	4.57E-06	1.59E-05	2.1076	1	−2	190
11	−0.734400	9.69844563 + 0.0048598i	−1.496922 − 1.85490017i	4.77E-06	1.59E-05	2.1051	1	−2	194
12	−0.718024	−1.47430586 + 1.85378123i	9.71215811 + 0.01269197i	5.09E-06	1.45E-05	2.1055	1	−2	172
13	−0.691512	−1.12922847 − 1.02480556i	3.78176946 − 0.02894603i	4.21E-06	5.54E-07	2.0281	1	−2	166
14	−0.654774	−0.9615658 + 0.5828065i	1.85727226 + 0.22306481i	2.46E-06	1.41E-07	1.9957	−1	0	99
15	−0.639046	0.72967089 + 0.94166299i	0.62407461 − 0.91988663i	7.18E-07	1.54E-07	2.0484	1	2	128
16	−0.616404	3.68514466 + 0.05398708i	−1.20114498 − 1.03004629i	6.54E-06	6.96E-07	1.9881	1	−2	150
17	−0.598098	−1.12922847 + 1.02480556i	3.78176946 + 0.02894603i	3.10E-06	5.54E-07	2.0471	1	−2	62
18	−0.591784	3.68514466 − 0.05398708i	−1.20114498 + 1.03004629i	8.24E-06	6.96E-07	2.0008	1	−2	67
19	−0.531176	6.67715546 − 0.02130875i	−0.01402295 + 1.7283683i	1.41E-08	4.70E-06	1.9773	−1	2	52
20	−0.527738	12.78275364 − 0.00603578i	−0.00730626 + 2.36240058i	8.25E-07	2.69E-05	2.1144	−1	2	193
21	−0.511182	1.59511265 + 0.92462709i	0.28169602 − 0.00845802i	3.61E-08	9.30E-08	1.9993	−1	2	70
22	−0.503186	0.01499973 − 1.73190712i	6.67574976 − 0.04157565i	3.33E-05	3.96E-06	2.1931	−1	−2	57
23	−0.490941	−3.34309333 + 1.46646036i	12.79048871 + 0.01073275i	7.06E-07	4.43E-05	2.1248	1	2	194
24	−0.490753	0.00737884 − 2.36289538i	12.78266688 − 0.00836806i	8.19E-07	3.00E-05	2.1172	−1	−2	199
25	−0.470183	12.78275364 + 0.00603578i	−0.00730626 − 2.36240058i	8.35E-07	2.69E-05	2.1169	−1	2	200
26	−0.468001	−3.34309333 − 1.46646036i	12.79048871 − 0.01073275i	9.49E-07	4.43E-05	2.0622	1	2	186
27	−0.463959	12.78190312 − 0.00664448i	−3.36083257 − 1.47015693i	3.42E-07	3.36E-05	2.1539	1	2	200
28	−0.458777	1.30993837 − 0.36023537i	0.99738945 − 0.66890573i	1.16E-06	8.98E-08	1.9828	−1	2	53
29	−0.437585	0.01499973 + 1.73190712i	6.67574975 + 0.04157565i	8.14E-05	5.27E-06	2.0388	−1	−2	57
30	−0.429119	12.78190312 + 0.00664448i	−3.36083257 + 1.47015693i	2.80E-07	3.36E-05	2.1486	1	2	184
31	−0.417531	6.67715546 + 0.02130875i	−0.01402295 − 1.72836831i	8.14E-05	5.37E-06	2.0768	−1	2	49
32	−0.321303	15.88192661 + 0.00033296i	−1.64153442 − 2.37001819i	1.37E-07	4.16E-05	2.1186	1	−2	192
33	−0.295259	15.88518055 + 0.00474592i	−5.70013516 + 0.67487422i	4.69E-08	5.96E-05	2.1502	1	−2	195
34	−0.287905	−5.68870793 + 0.65962195i	15.8889979 + 0.00516137i	7.23E-07	2.87E-05	2.0120	1	−2	177
35	−0.278601	15.88518055 − 0.00474592i	−5.70013516 − 0.67487422i	1.15E-07	5.96E-05	2.0524	1	−2	197
36	−0.264047	−5.68870793 − 0.65962195i	15.8889979 − 0.00516137i	3.32E-08	2.87E-05	2.1731	1	−2	194
37	−0.263797	6.66385192 − 0.00958162i	−3.05535199 − 0.51526776i	3.78E-05	5.76E-06	2.0466	1	2	110
38	−0.242447	−4.59285856	9.73129667	1.34E-07	2.16E-05	2.7985	1	−2	199
39	−0.240107	9.71878344	−4.6277176	5.48E-07	7.22E-06	2.6624	1	−2	173
40	−0.235095	−3.01831353 + 0.50589193i	6.69924181 + 0.01613676i	3.61E-08	1.43E-06	1.9762	1	2	77
41	−0.212867	6.66385192 + 0.00958162i	−3.05535199 + 0.51526775i	8.78E-05	6.78E-06	1.9815	1	2	57
42	−0.211725	19.0075656	−7.54961079	1.61E-04	4.83E-05	0.7767	1	2	197
43	−0.209337	−3.01831353 − 0.50589194i	6.69924181 − 0.01613676i	7.73E-05	3.05E-06	1.9919	1	2	64
44	−0.204931	−7.53686364	19.00985885	1.00E-08	3.66E-05	2.0867	1	2	158
45	−0.181783	12.81002482	−7.10966546	1.32E-07	3.93E-05	2.2517	1	2	196
46	−0.181407	−9.30202535	18.99474019	1.00E-08	7.22E-05	2.1044	−1	0	197
47	−0.178655	−7.09665188	12.81542466	1.00E-08	4.79E-05	2.6959	1	2	188
48	−0.175623	18.99311678	−9.3004938	1.00E-08	6.54E-05	2.1290	−1	0	187
49	−0.125919	−6.39937487	9.6851963	1.81E-06	2.11E-05	2.0664	−1	0	195
50	−0.092457	9.67778512	−6.40235748	5.02E-07	2.22E-05	2.2493	−1	0	183
51	−0.076797	19.02754978	−12.95559618	1.29E-04	4.95E-05	0.9503	1	2	156

Therefore, the following holds:

$$\begin{array}{c}\hfill \overline{P}\approx 2.0692\in B\left(\overline{p};{\delta }_K\right),\end{array}$$

which is consistent with Corollary 2 since, in general, if $\xi \in \mathfrak{C}(\mathsf{\Omega },f)$, then it is fulfilled the following (see [18], proof of Proposition 1):

$$\begin{array}{c}\hfill \underset{x\to \xi }{lim}∥{\Phi }_{H,\delta }^{\left(1\right)}(\alpha ,x)∥=0.\end{array}$$

Example 3.

Using the Riemann–Liouville fractional derivative (22), it is possible to construct the following matrix:

$$\begin{array}{cc}\hfill A_{ϵ,\beta }\left(x_i\right)=\left({\left[A_{ϵ,\beta }\right]}_{jk}\left(x_i\right)\right) :={\left({\partial }_k^{\beta (\alpha ,{\left[x_i\right]}_k)}{\delta }_{jk}+ϵ{\delta }_{jk}\right)}_{x_i},& \alpha \in \mathbb{R}\backslash \mathbb{Z},\end{array}$$

(77)

which generates a particular case of thefractional pseudo-Newton method[5], where ${\delta }_{jk}$ is the Kronecker delta, ϵ is a positive constant $\ll 1$, and $\beta (\alpha ,{\left[x_i\right]}_k)$ is a function defined by the Equation (76). So, using the iteration function (74) and the matrix $A_{ϵ,\beta }$ given by the Equation (77), considering the following values,

$$\begin{array}{c}\hfill \begin{array}{cccc}ϵ={10}^{-4},& \delta =13& and& x_0={(14.55,14.55)}^{T}with{∥\nabla f\left(x_0\right)∥}_2\approx 65,057.2221,\end{array}\end{array}$$

the results shown in Table 3 are obtained.

Table 3. Results obtained using the iteration function (74) with the fractional pseudo-Newton method [5].

	$\mathit{\alpha }$	${\left[{\mathit{x}}_{\mathit{k}}\right]}_1$	${\left[{\mathit{x}}_{\mathit{k}}\right]}_2$	${∥{\mathit{x}}_{\mathit{k}}-{\mathit{x}}_{\mathit{k}-1}∥}_2$	${∥\mathit{\nabla }\mathit{f}\left({\mathit{x}}_{\mathit{k}}\right)∥}_2$	${\mathit{P}}_{\mathit{k}}$	${\mathbf{\Delta }}_{\mathit{d}}\left({\mathit{x}}_{\mathit{k}}\right)$	${\mathbf{\Delta }}_{\mathit{t}}\left({\mathit{x}}_{\mathit{k}}\right)$	k
1	0.997025	6.40346174	−9.68745629	7.48E-06	2.99E-05	2.0712	−1	0	11
2	0.997053	−6.8254374	−6.80736533	1.34E-06	1.17E-05	2.1970	1	−2	37
3	0.997061	9.73394944	4.59418309	3.34E-06	1.33E-05	2.1262	1	2	33
4	0.998113	4.62598971	9.72138809	2.20E-07	1.78E-05	2.8079	1	2	13
5	0.998133	−9.67933962	6.40821255	3.58E-07	3.16E-05	2.1427	−1	0	19
6	0.998185	−3.75670368 + 0.00677324i	1.14479461 − 0.90835133i	6.32E-08	8.42E-07	1.9860	1	−2	184
7	0.998189	−3.75670368 − 0.00677324i	1.14479461 + 0.90835133i	2.47E-06	8.42E-07	1.9809	1	−2	126
8	0.998229	−12.81526848	−7.09878784	3.61E-08	3.00E-05	2.1703	1	−2	22
9	0.998469	−12.6804252	−15.85472455	1.00E-08	4.54E-05	2.2093	−1	0	49
10	0.999045	1.52183063 − 0.04852431i	−1.07285283 − 0.62177498i	8.25E-06	6.40E-08	1.9673	−1	0	161
11	0.999065	7.09845974	−12.81449874	7.07E-08	2.76E-05	2.2122	1	2	33
12	0.999909	9.81602358	9.80895121	2.24E-08	4.07E-05	2.1124	1	2	25
13	0.999917	−7.09665188	12.81542466	1.06E-07	4.79E-05	2.1726	1	2	26
14	0.999921	−6.80274842	6.8263687	7.69E-06	1.15E-05	2.2126	1	2	28
15	0.999925	−12.80936242	7.11220453	1.30E-07	5.55E-05	2.2710	1	2	28
16	0.999929	−9.73194065	−4.58368411	2.72E-06	5.55E-06	2.7275	1	2	62
17	0.999937	−9.81505776	−9.80760476	1.13E-04	2.80E-05	1.4237	1	2	18
18	0.999941	−4.61844557	−9.71852806	1.53E-06	1.39E-05	2.8405	1	2	61
19	0.999945	6.80674644	−6.820744	4.50E-06	1.44E-05	2.1855	1	2	176
20	0.999953	12.81002482	−7.10966546	3.41E-07	3.93E-05	2.2868	1	2	44
21	1.003393	6.82167482	6.80212518	8.31E-06	1.48E-05	2.1795	1	−2	5
22	1.004893	−0.55742729 − 0.65679566i	−0.20882106 − 1.14800938i	3.11E-07	1.41E-07	2.0709	−1	0	64
23	1.004925	3.68514466 + 0.05398708i	−1.20114498 − 1.03004629i	5.10E-08	6.96E-07	1.9686	1	−2	119
24	1.004969	−1.12922847 + 1.02480556i	3.78176946 + 0.02894603i	4.58E-08	5.54E-07	1.9971	1	−2	137
25	1.005025	0.72967089 − 0.94166299i	0.62407461 + 0.91988663i	2.37E-05	1.54E-07	1.9983	1	2	84
26	1.005549	0.29601303	−4.65165906	1.49E-05	4.30E-07	2.1087	−1	−2	15
27	1.005849	3.68514466 − 0.05398708i	−1.20114498 + 1.03004629i	6.25E-08	6.96E-07	1.9890	1	−2	184
28	1.005937	−1.12922847 − 1.02480556i	3.78176946 − 0.02894603i	1.41E-08	5.54E-07	1.9735	1	−2	82
29	1.006421	−1.3914151 − 0.70003547i	0.17621271 + 1.00035774i	1.02E-04	1.46E-07	2.0270	−1	0	50
30	1.006437	1.30993837 − 0.36023537i	0.99738945 − 0.66890573i	4.91E-06	8.98E-08	1.9863	−1	2	44
31	1.006465	−0.55742729 + 0.65679566i	−0.20882106 + 1.14800938i	6.32E-08	1.41E-07	2.1428	−1	0	38
32	1.007481	−3.95538299	−3.88543329	9.14E-05	3.64E-06	2.3031	1	2	5
33	1.008713	1.59511265 − 0.92462709i	0.28169602 + 0.00845802i	1.63E-06	9.30E-08	2.1184	−1	2	20
34	1.009697	−2.30034423	−0.45950443	4.99E-06	7.08E-08	2.1235	−1	0	6
35	1.009817	0.09238517 + 0.91135195i	−1.48626899 − 0.45588717i	5.70E-07	1.37E-07	1.9727	1	−2	28
36	1.009821	0.09238517 − 0.91135195i	−1.48626899 + 0.45588717i	1.41E-08	1.37E-07	2.0053	1	−2	34
37	1.009861	−1.3914151 + 0.70003546i	0.17621271 − 1.00035774i	9.45E-05	2.55E-07	2.0119	−1	0	22
38	1.010385	1.30993837 + 0.36023537i	0.99738945 + 0.66890573i	4.13E-05	8.98E-08	1.9803	−1	2	38
39	1.908362	0.72967089 + 0.94166298i	0.62407461 − 0.91988663i	8.45E-05	1.83E-07	1.9642	1	2	14
40	1.913438	1.52183063 + 0.04852431i	−1.07285283 + 0.62177498i	1.10E-07	6.40E-08	1.9787	−1	0	13
41	1.918790	−1.66983169	−1.47843397	1.14E-04	6.06E-08	2.2493	1	−2	5
42	1.920778	1.59511265 + 0.92462709i	0.28169602 − 0.00845802i	4.58E-08	9.30E-08	1.9835	−1	2	17
43	1.922506	3.8890101	−3.98878888	1.22E-07	1.48E-06	2.1461	1	−2	19
44	1.928090	−3.91843903	3.94777085	1.97E-07	2.03E-06	2.0974	1	−2	75
45	1.928198	4.76944744	0.24682585	4.45E-05	4.75E-07	2.0605	−1	2	19
46	1.938338	−0.1411895	4.75629836	6.65E-06	4.42E-07	2.0695	−1	−2	12
47	2.027490	−4.63811516	−0.17366027	3.50E-07	5.12E-07	2.4473	−1	2	6
48	2.027714	−0.9615658 − 0.5828065i	1.85727226 − 0.22306481i	1.22E-06	1.41E-07	2.0016	−1	0	80
49	2.027802	−0.9615658 + 0.5828065i	1.85727226 + 0.22306481i	8.66E-07	1.41E-07	2.0016	−1	0	23
50	2.028082	3.98115471	3.92170125	4.47E-08	1.50E-06	2.0806	1	2	9
51	2.050222	0.10127937 − 0.65790456i	−0.69552033 − 1.28219351i	4.24E-08	2.55E-08	1.9278	1	−2	9
52	2.892915	−0.2017252	−2.13862013	8.96E-05	1.79E-07	2.0069	−1	0	5
53	2.979539	−9.68548222	−6.40422387	1.48E-05	6.43E-06	2.0748	−1	0	43
54	2.979543	−6.40734755	−9.67742959	1.68E-05	7.33E-06	2.0878	−1	0	43
55	2.983015	6.66385192 − 0.00958162i	−3.05535199 − 0.51526776i	4.88E-06	5.76E-06	1.9701	1	2	65
56	2.983279	1.07448447 + 0.94219835i	−3.88986554 + 0.11532861i	7.72E-05	9.22E-07	2.0229	1	−2	92
57	2.989991	−3.01831353 + 0.50589193i	6.69924181 + 0.01613676i	5.64E-06	1.43E-06	1.9676	1	2	101
58	2.990235	12.78190312 + 0.00664448i	−3.36083257 + 1.47015693i	3.33E-06	3.36E-05	2.0443	1	2	27
59	2.990955	−3.34309333 − 1.46646036i	12.79048871 − 0.01073275i	2.29E-06	4.43E-05	2.0444	1	2	26
60	3.002283	−12.78071432 + 0.00620911i	3.36250229 + 1.47445201i	7.91E-06	1.73E-05	2.0486	1	2	38
61	3.004719	9.55477471	12.75308268	3.30E-07	1.49E-05	2.1260	−1	0	9
62	3.013455	−6.65415389 + 0.00918318i	3.06649242 + 0.56418379i	5.49E-06	4.40E-06	1.9795	1	2	90
63	3.013911	9.68717241	6.39860852	1.86E-05	7.26E-06	2.0743	−1	0	199
64	3.014343	6.40322967	9.6796959	2.04E-05	1.09E-05	2.0718	−1	0	189
65	3.982916	6.66385192 + 0.00958162i	−3.05535199 + 0.51526776i	8.57E-05	5.76E-06	2.1002	1	2	87
66	3.982992	12.78190312 − 0.00664448i	−3.36083257 − 1.47015693i	1.25E-05	3.36E-05	2.0505	1	2	35
67	3.983884	3.02691487 + 0.54276524i	−6.68492207 + 0.01504716i	1.41E-08	5.46E-06	1.9751	1	2	117
68	3.990568	3.34433054 + 1.46955548i	−12.78880218 + 0.01004339i	7.60E-07	3.97E-05	2.1391	1	2	20
69	3.990580	3.34433054 − 1.46955548i	−12.78880218 − 0.01004339i	9.72E-07	3.97E-05	2.1398	1	2	23
70	3.991060	−3.01831353 − 0.50589193i	6.69924181 − 0.01613676i	9.65E-06	1.43E-06	1.9672	1	2	81

Therefore

$$\begin{array}{c}\hfill \overline{P}\approx 2.0994\in B\left(\overline{p};{\delta }_K\right),\end{array}$$

which is consistent with Corollary 2 since in general if $\xi \in \mathfrak{C}(\mathsf{\Omega },f)$, then it is fulfilled the following (see Ref. [18], proof of Proposition 1):

$$\begin{array}{c}\hfill \underset{x\to \xi }{lim}∥{\Phi }_{H,\delta }^{\left(1\right)}(\alpha ,x)∥=0.\end{array}$$

Finally, it is necessary to mention that the fractional iterative methods, such as the fractional Newton–Raphson method, can find multiple zeros of a function using a single initial condition. This partially solves the intrinsic problem of classical iterative methods, which is that in general, to find N zeros of a function, N initial conditions must be provided. Due to the fractional operators implemented, which are usually non-local operators, these methods may be considered non-local parametric iterative methods, so they have two important characteristics for both real and complex variables:

(i)

The initial condition does not necessarily have to be close to the sought values due to the non-local nature of fractional operators [5].

(ii)

When working in a space of N dimensions, in the case that it is necessary to change the initial condition, unlike the classical iterative methods, where in the worst case, it is necessary to vary the N components of the initial condition until a suitable value is obtained; in the fractional fixed-point methods, it is enough to vary the parameter $\alpha$ of the fractional operators until an adequate value is found that allows generating a sequence that converges to a sought value [16].

It is necessary to mention that, although there exist theories such as theorems, prepositions, and corollaries of classical iterative methods that can be transferred to fractional iterative methods, most of these results are for local iterative methods, so it is necessary to continue developing theories with results of a non-local nature, such as Corollary 4.

6. Conclusions

Considering the large number of fractional operators that exist [25,26], and since it does not seem that their number will stop increasing soon at the time of writing this paper [27,28,29], the most simple and compact method to work the fractional calculus is through the classification of fractional operators using sets, which, as shown in the previous sections, allows generalizing objects of the conventional calculus, such as the fixed-point method in several variables, which allows generating the method known as the fractional fixed-point method, which in turn allows generating a new type of numerical analysis using sets [7]. It is necessary to mention that the use of sets to classify fractional operators allows generalizing the existing results of the fractional calculus to families of operators that fulfill some property to ensure the validity of the results to be generalized, as shown by defining the following sets of fractional operators:

$$\begin{array}{c}\begin{array}{c}{\displaystyle {}_m{O}_{x,\alpha }^n\left(g\right)\cap \left\{o_x^{\alpha }:o_k^{\alpha }c=0\forall c\in \mathbb{R}\text{and}\forall k\ge 1\right\},}\end{array}\end{array}$$

(78)

$$\begin{array}{c}\begin{array}{c}{\displaystyle {}_m{O}_{x,\alpha }^n\left(g\right)\cap \left\{o_x^{\alpha }:o_k^{\alpha }c\ne 0\forall c\in \mathbb{R}\backslash \left\{0\right\}\text{and}\forall k\ge 1\right\},}\end{array}\end{array}$$

(79)

$$\begin{array}{c}\begin{array}{c}{\displaystyle {}_m{O}_{x,\alpha }^n\left(g\right)\cap \left\{o_x^{\alpha }:o_k^{\alpha }\text{is a local operator} \forall k\ge 1\right\},}\end{array}\end{array}$$

(80)

$$\begin{array}{c}\begin{array}{c}{\displaystyle {}_m{O}_{x,\alpha }^n\left(g\right)\cap \left\{o_x^{\alpha }:o_k^{\alpha }\text{is a non-local operator} \forall k\ge 1\right\},}\end{array}\end{array}$$

(81)

$$\begin{array}{c}\begin{array}{c}{\displaystyle {}_m{O}_{x,\alpha }^n\left(g\right)\cap \left\{o_x^{\alpha }:o_k^{\alpha }\text{is a linear operator} \forall k\ge 1\right\},}\end{array}\end{array}$$

(82)

$$\begin{array}{c}\begin{array}{c}{\displaystyle {}_m{O}_{x,\alpha }^n\left(g\right)\cap \left\{o_x^{\alpha }:o_k^{\alpha }\text{is a non-linear operator} \forall k\ge 1\right\},}\end{array}\end{array}$$

(83)

$$\begin{array}{c}{}_m{O}_{x,\alpha }^n\left(g\right)\cap \left\{o_x^{\alpha }:\exists o_k^{-\alpha }\text{and}{o}_k^{\alpha }{o}_k^{-\alpha }\ne o_k^{-\alpha }{o}_k^{\alpha }=o_k^0\forall k\ge 1\right\}.\end{array}$$

(84)

Furthermore, it is possible to define elements of the fractional calculus that fulfill some property, such as the following set of matrices:

$$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle \left\{A_{g,\alpha }:\exists A_{g,\alpha }^{-1}\in {}_m{IM}_{x,\alpha }^{\infty }\left(g\right)\text{and}{A}_{g,\alpha }\left(x\right)=\left({\left[A_{g,\alpha }\right]}_{jk}\left(x\right)\right) :={\left(o_k^{\alpha }{\left[g\right]}_j\left(x\right)\right)}^{-1}\right\} \cap \left\{o_x^{\alpha }:o_k^{\alpha }c\ne 0\forall c\in \mathbb{R}\backslash \left\{0\right\}\text{and}\forall k\ge 1\right\},}\end{array}\end{array}$$

(85)

which allows defining the fractional quasi-Newton method. On the other hand since each fractional fixed-point method that generates a convergent sequence has the ability to generate an uncountable family of fractional fixed-point methods that generate convergent sequences as shown by the Theorem 2, and considering that determining the critical points of a scalar function is usually one of the most recurrent problems in physics, mathematics and engineering, it becomes almost natural to estimate numerically in a region $\mathsf{\Omega }$ the mean order of convergence of any fractional fixed-point method by determining the critical points of a scalar function. Finally, it should be mentioned that the result of the Theorem 2 may be transferred to the theory of fractional differential equations, resulting in a new type of theory of differential equations using sets, which allows defining the following sets of functions for some operator $s_x^{\alpha \gamma }\in S_{x,\alpha }^{s,\gamma }\left(f\right)$

$$\begin{array}{c}\begin{array}{c}{\displaystyle C_{\alpha }^s\left(s_x^{\alpha \gamma },\mathsf{\Omega }\right) := \left\{f:\exists s_x^{\alpha \gamma }f\left(x\right)\forall \alpha \left|\gamma \right|\le s\text{and}\forall x\in \mathsf{\Omega }\right\},}\end{array}\end{array}$$

(86)

$$\begin{array}{c}{H}_{\alpha }^s\left(s_x^{\alpha \gamma },\mathsf{\Omega }\right) := \left\{f\in C_{\alpha }^s\left(s_x^{\alpha \gamma },\mathsf{\Omega }\right):s_x^{\alpha \gamma }f\left(x\right)\in L^2\left(\mathsf{\Omega }\right)\forall \alpha \left|\gamma \right|\le s\right\},\end{array}$$

(87)

and which allows defining multidimensional fractional partial differential equations [2]. Therefore, working with fractional operators through sets opens the possibility that fractional calculus becomes a more extensive theory, which should be renamed fractional calculus of sets.