Applications of a Fixed Point Result for Solving Nonlinear Fractional and Integral Differential Equations
Abstract
1. Introduction and Preliminaries
- (1)
- New conditions were introduced in the given contractive relation using new relations (Kannan, Chatterje, Reich, Hardy-Rogers, Ćirić, …).
- (2)
- The axioms of metric space have been changed.
- (F1)
- whenever ;
- (F2)
- If then if and only if ;
- (F3)
- as for some
- (dbl1)
- yields
- (dbl2)
- (dbl3)
- (i)
- The sequence is said to be convergent to if
- (ii)
- The sequence is said to be Cauchy in if exists and is finite. If then is called Cauchy sequence.
- (iii)
- One says that a b-metric-like space is complete (resp. complete) if for every Cauchy (resp. Cauchy) sequence in it there exists an such that
- (iv)
- A mapping is called continuous if the sequence tends to whenever the sequence tends to as that is, if yields
2. Fixed Point Remarks
3. Main Results
- (i)
- there exists such that for all where is defined by
- (ii)
- there exists such that for allfor all , wherewith and
- (iii)
- for all and yields
- (iv)
- for all if is a sequence in such that in and for all then for allThen problem (21) has a solution.
- (i)
- the function is a continuous function;
- (ii)
- there exists such that, for all , we have:for all and , wherewith and
- (iii)
- for all and ,
4. Numerical Example
5. Conclusions
- One type of Caputo fractional differential equation has at least one solution.
- A special integral equation created in mechanical engineering has a solution.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alghmandi, M.A.; Hussain, N.; Salimi, P. Fixed point and coupled fixed point theorems on b-metric-like spaces. J. Inequal. Appl. 2013, 2013, 402. [Google Scholar] [CrossRef]
- Alsulami, H.H.; Karapınar, E.; Piri, H. Fixed point of generalized F-Suzuki type contraction in complete b-metric spaces. Discret. Dyn. Nat. Soc. 2015, 2015, 969726. [Google Scholar]
- Banach, S. Sur les opérations dans les ensembles abstraits et leur application aux équations integrales. Fundam. Math. 1922, 3, 133–181. [Google Scholar] [CrossRef]
- Kadelburg, Z.; Radenović, S. Notes on some recent papers concerning F-contractions in b-metric spaces. Constr. Math. Anal. 2018, 2, 108–112. [Google Scholar] [CrossRef]
- Mitrović, Z.D. A note on the result of Suzuki, Miculescku and Mihail. J. Fixed Point Theory Appl. 2019, 21, 24. [Google Scholar] [CrossRef]
- Padhan, S.K.; Rao, G.V.V.J.; Al-Rawashdeh, A.; Nashine, H.K.; Agarwal, R.P. Existence of fixed points for γ-FG-contractive condition via cyclic (α,β)-admissible mappings in b-metric spaces. J. Nonlinear Sci. Appl. 2017, 10, 5495–5508. [Google Scholar] [CrossRef][Green Version]
- Parvaneh, V.; Hussain, N.; Kadelburg, Z. Generalized Wardowski type fixed point theorems via α-admissible FG-contractions in b-metric spaces. Acta Math. Sci. 2016, 36, 1445–1456. [Google Scholar] [CrossRef]
- Popescu, O.; Stan, G. Two fixed point theorems concerning F-contraction in complete metric spaces. Symmetry 2020, 12, 58. [Google Scholar] [CrossRef]
- Saleem, N.; Iqbal, I.; Iqbal, B.; Radenović, S. Coincidence and fixed points of multivalued F-contractions in generalized metric space with application. J. Fixed Point Theory Appl. 2020, 22, 81. [Google Scholar] [CrossRef]
- Shukla, S.; Radenović, S.; Rajić, V.Ć. Some common fixed point theorems in 0-σ-complete metric-like spaces. Vietnam J. Math. 2013, 41, 341–352. [Google Scholar] [CrossRef]
- Wardowski, D. Fixed points of a new type of contractive mappings in complete metric space. Fixed Point Theory Appl. 2012, 2012, 94. [Google Scholar] [CrossRef]
- Cosentino, M.; Vetro, P. Fixed point result for F-contractive mappings of Hardy-Rogers-Type. Filomat 2014, 28, 715–722. [Google Scholar] [CrossRef]
- Hammad, H.A.; la Sen, M.D. Fixed-point results for a generalized almost (s, q)-Jaggi F-contraction-type on b-metric-like spaces. Mathematics 2020, 8, 63. [Google Scholar] [CrossRef]
- Karapınar, E.; Fulga, A.; Agarwal, R.P. A survey: F-contractions with related fixed point results. J. Fixed Point Theory Appl. 2020, 22, 69. [Google Scholar] [CrossRef]
- Lukacs, A.; Kajanto, S. Fixed point theorems for various types of F-contractions in complete b-metric spaces. Fixed Point Theory 2018, 19, 321–334. [Google Scholar] [CrossRef]
- Nazam, M.; Arshad, M.; Postolache, M. Coincidence and common fixed point theorems for four mappings satisfying (αS-F)-contraction. Nonlinear Anal. Model. Control 2018, 23, 664–690. [Google Scholar] [CrossRef]
- Paesano, D.; Vetro, C. Multi-valued F-contractions in 0-complete partial metric spaces with application to Voltera type integral equation. Rev. Real Acad. Cienc. Exactas Fis. Nat. Ser. Mat. 2014, 108, 1005–1020. [Google Scholar] [CrossRef]
- Piri, H.; Kumam, P. Some fixed point theorems concerning F-contraction in complete metric spaces. Fixed Point Theory Appl. 2014, 2014, 210. [Google Scholar] [CrossRef]
- Shukla, S.; Radenović, S.; Kadelburg, Z. Some fixed point theorems for ordered F-generalized contractions in O-f-orbitally complete partial metric spaces. Theory Appl. Math. Comput. Sci. 2014, 4, 87–98. [Google Scholar]
- Mirkov, N.; Radenović, S.; Radojević, S. Some new observations for F-contractions in vector-valued metric spaces of Perov’s type. Axioms 2021, 10, 127. [Google Scholar] [CrossRef]
- Radenović, S.; Mirkov, N.; Paunović, L.J. Some new results on F-contractions in 0-complete partial metric spaces and 0-complete metric-like spaces. Fractal Fract. 2021, 5, 34. [Google Scholar] [CrossRef]
- Vujaković, J.; Ljajko, E.; Radojević, S.; Radenović, S. On some new Jungck-Fisher-Wardowski type fixed point results. Symmetry 2020, 12, 2048. [Google Scholar] [CrossRef]
- Harandi, A.A. Metric-like spaces, partial metric spaces and fixed points. Fixed Point Theory Appl. 2012, 2012, 204. [Google Scholar] [CrossRef]
- De la Sen, M.; Nikolić, N.; Došenović, T.; Pavlović, M.; Radenović, S. Some results on (s-q)-graphic contraction mappings in b-metric-like spaces. Mathematics 2019, 7, 1190. [Google Scholar] [CrossRef]
- Jovanović, M.; Kadelburg, Z.; Radenović, S. Common fixed point results in metric-type spaces. Fixed Point Theory Appl. 2010, 2010, 978121. [Google Scholar] [CrossRef]
- Aleksić, S.; Mitrović, Z.D.; Radenović, S. Picard sequences in b-metric spaces. Fixed Point Theory 2020, 21, 35–46. [Google Scholar] [CrossRef]
- Sing, S.L.; Czerwik, S.; Krol, K.; Singh, A. Coincidences and fixed points of hybrid contractions. Tamsui Oxf. J. Math. Sci. 2008, 24, 401–416. [Google Scholar]
- Vujaković, J.; Aydi, H.; Radenović, S.; Mukheimer, A. Some remarks and new reults in ordered partial b-metric spaces. Mathematics 2019, 7, 334. [Google Scholar] [CrossRef]
- Rudin, W. Principles of Mathematical Analysis; McGraw Book Company: New York, NY, USA, 1964. [Google Scholar]
- Collaco, P.; Silva, J.C. A complete comparison of 23 contraction conditions. Nonlinear Anal. Theory Methods Appl. 1997, 30, 471–476. [Google Scholar] [CrossRef]
- Rhoades, B.E. A comparison of various definitions of contractive mappings. Trans. Amer. Math. Soc. 1997, 226, 257–290. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; North-Holland Mathematics Studies; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integral and Derivative; Gordon and Breach: London, UK, 1993. [Google Scholar]
- Chandok, S.; Sharma, R.K.; Radenović, S. Multivalued problems via orthogonal contraction mappings with application to fractional differential equation. J. Fixed Point Theory Appl. 2021, 23, 14. [Google Scholar] [CrossRef]
- Baleanu, D.; Rezapour, S.; Mohammadi, M. Some existence results on nonlinear fractional differential equations. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2013, 371, 20120144. [Google Scholar] [CrossRef]
- Zhu, H.; Han, S.; Shen, J. Some Results on Fractional m-Point Boundary Value Problems. J. Funct. Spaces 2021, 2021, 3152688. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
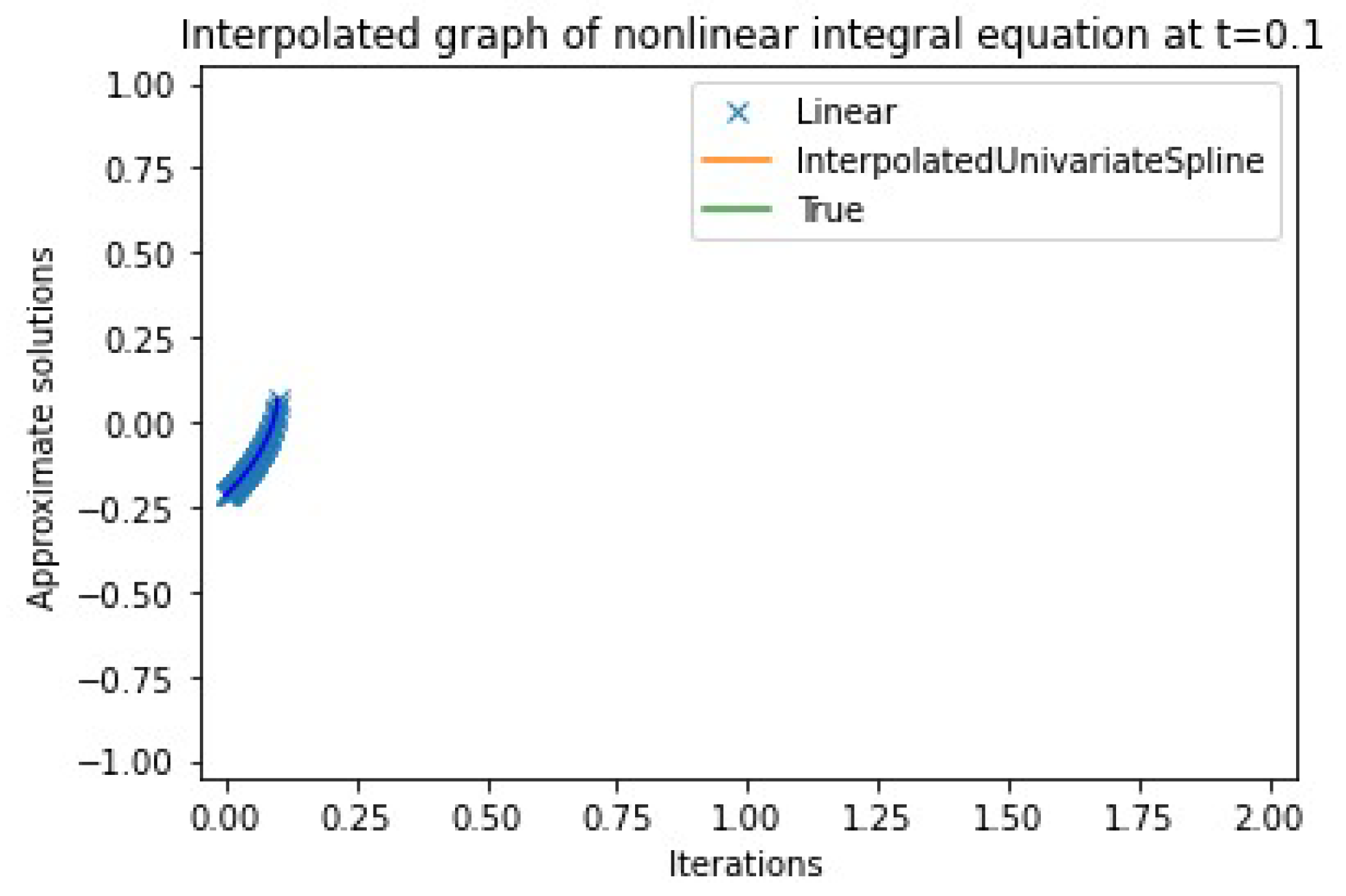
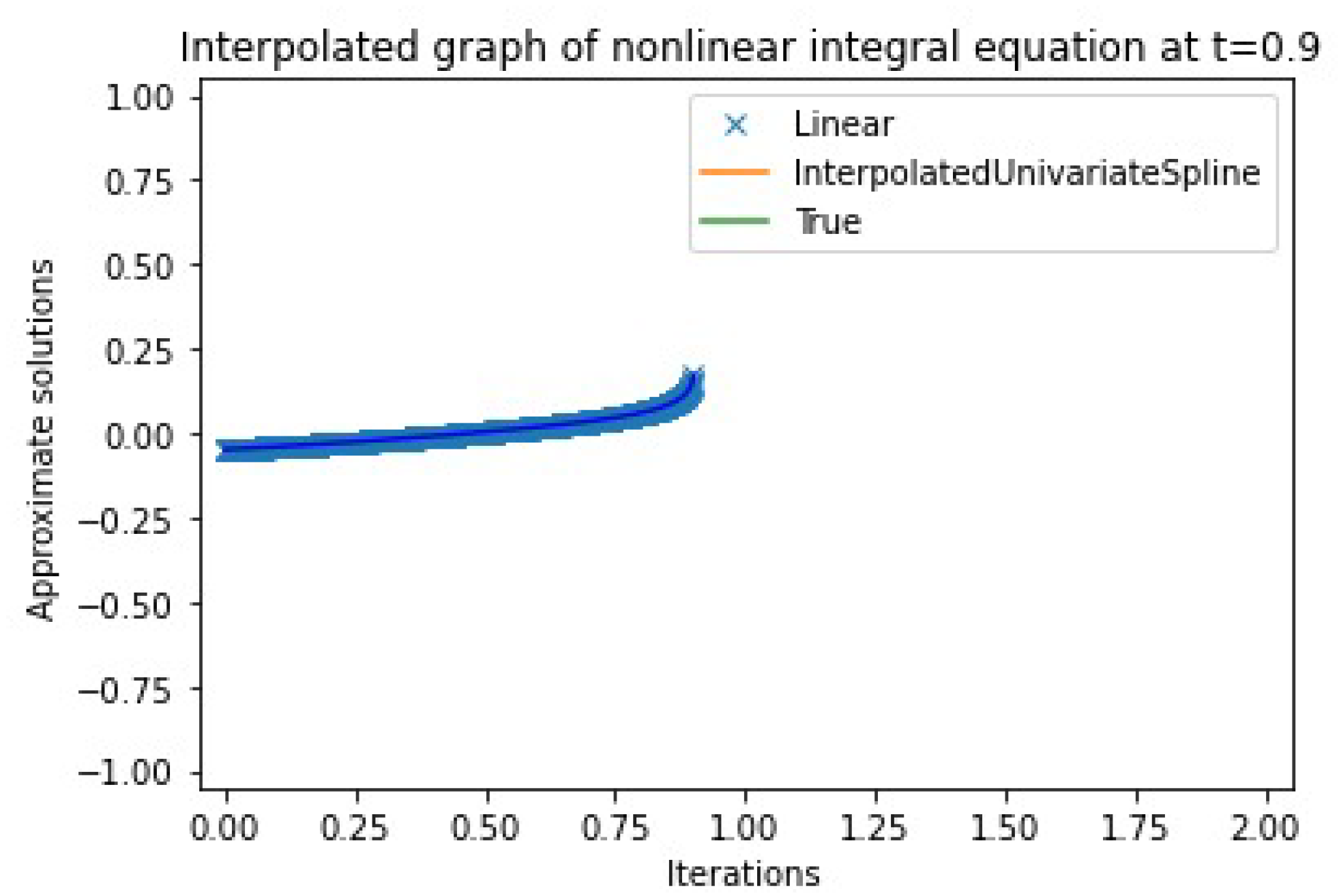
| n | Approximate Solution | Absolute Error | |
|---|---|---|---|
| 0 | 0.0308 | ||
| 1 | 0.0307 | ||
| 2 | 0.0307 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guran, L.; Mitrović, Z.D.; Reddy, G.S.M.; Belhenniche, A.; Radenović, S. Applications of a Fixed Point Result for Solving Nonlinear Fractional and Integral Differential Equations. Fractal Fract. 2021, 5, 211. https://doi.org/10.3390/fractalfract5040211
Guran L, Mitrović ZD, Reddy GSM, Belhenniche A, Radenović S. Applications of a Fixed Point Result for Solving Nonlinear Fractional and Integral Differential Equations. Fractal and Fractional. 2021; 5(4):211. https://doi.org/10.3390/fractalfract5040211
Chicago/Turabian StyleGuran, Liliana, Zoran D. Mitrović, G. Sudhaamsh Mohan Reddy, Abdelkader Belhenniche, and Stojan Radenović. 2021. "Applications of a Fixed Point Result for Solving Nonlinear Fractional and Integral Differential Equations" Fractal and Fractional 5, no. 4: 211. https://doi.org/10.3390/fractalfract5040211
APA StyleGuran, L., Mitrović, Z. D., Reddy, G. S. M., Belhenniche, A., & Radenović, S. (2021). Applications of a Fixed Point Result for Solving Nonlinear Fractional and Integral Differential Equations. Fractal and Fractional, 5(4), 211. https://doi.org/10.3390/fractalfract5040211








