Abstract
We investigate particle diffusion in a heterogeneous medium limited by a surface where sorption–desorption processes are governed by a kinetic equation. We consider that the dynamics of the particles present in the medium are governed by a diffusion equation with a spatial dependence on the diffusion coefficient, i.e., K(x) = D|x|−η, with −1 < η and D = const, respectively. This system is analyzed in a semi-infinity region, i.e., the system is defined in the interval [0,∞) for an arbitrary initial condition. The solutions are obtained and display anomalous spreading, that is, the dynamics may be viewed as anomalous diffusion, which in turn is related, and hence, the model can be directly applied to several complex systems ranging from biological fluids to electrolytic cells.
1. Introduction
Separation is a transformation process of a mixture into two or more distinct products [1]. It is widely used in modern society, from the petrochemical [2] to biotechnology industries [3]. Among several ways of promoting the separation process, adsorption phenomena stands out due to its simple design and low investment required, finding applications in removing a substance from fluid (liquid or gas) in several areas [1,4,5]. In a few words, adsorption is an adhesion of some chemical species from a fluid (adsorbate) on a surface (absorbent) [6,7]. While adsorption may occur by two distinctive mechanisms [6], that is, chemisorption (particles chemically bonded to the substrate) or physisorption (particles adhere to the substrate by falling into potential wells) [7], the process in which particles reach the adsorbing substrates often takes place by diffusion [8]. Hence, adsorption and diffusion are two coupled phenomena since, as particles exit the volume to the surface, the gradient of concentration changes toward the surface and diffusion takes place to equalize the concentration. Similarly, during the desorption process (substance is released to the bulk), diffusion compensates for the increase in concentration near the substrate. Therefore, understanding how these two phenomena work together is crucial not only in separation process but in several other systems where diffusion and adsorption occur together, such as biochemical reactions in living systems [9,10], in the electrical response of weak electrolytes [11], in cancer [12] and population dynamics [13,14], and many others [15,16,17,18,19,20,21].
Recently, several works have been devoted to study systems where diffusion and adsorption simultaneously occur. In particular, it is important to understand how the diffusion process is affected by the adsorbing surfaces, which is often calculated by measuring how the distribution of particles spread over time, that is, by following how the mean square displacement (MSD) changes over time [11]. In fact, such measurements are important because they probe, for example, memory effects [22], diffusion in membranes [23,24] and diffusion in porous media [25,26], which in turn helps to describe the morphology of these materials. Indeed, by studying the MSD’s dependence in time, one can classify diffusion as being normal or anomalous, that is, MSD, so it is either normal if , or anomalous if . Different behaviors for the MSD are also possible, such as MSD , which are related to an ultra-slow diffusion [27,28,29]. Indeed, it is often observed that the diffusion regime is heavily affected by surface adsorption [30,31,32,33,34]. Another important phenomenon that affects diffusivity is by space variations of the diffusion coefficient [8]. In this case, since the diffusion coefficient alters how fast diffusion happens, the overall spreading of particles changes. This may happen due to several factors, including molecular crowding [35,36,37], bulk modulation [38] and porous media or traps [39,40]. Indeed, it has been shown that the above facts have a great deal of influence on the diffusive regime on the bulk, so probing diffusion can provide insights about surface and bulk phenomena [41,42,43,44,45]. In this work, in order to provide a general framework and model to study systems where both spatial variation on the diffusion coefficient and adsorption phenomena occur, we investigate a heterogeneous system, which is governed by the diffusion equation
where is the bulk particle distribution, with the diffusion coefficient given by , where is a constant and . This spatial dependence for the diffusion coefficient has been used to model several situations and is usually associated with stretched exponential distributions, which are typical in different systems, including diffusion on fractals [46,47], turbulence [48,49], diffusion and reaction on fractals [50], solute transport in fractal porous media [51], and atom deposition in a porous substrate [52]. This feature shows that this choice for the diffusion coefficient connects our results with these heterogeneous structures. We consider this system subjected to boundary conditions:
where stands for the surface coverage and
with the initial condition . These equations lead us the following conservation equation:
This result implies that the number of particles of the system is constant, i.e., when we consider the contribution of the surface and the bulk. In this scenario, , which is related to the surface effects, may represent the particle flow injected into the system by a source or a desorption process and removal rate of particles from the system by a sorption process.
For the sorption–desorption processes on the surface, we may assume that they are modeled by the following balance equation:
In Equation (5), is the subsurface density. The kernel may be connected to the adsorption phenomena and the second term on the right side of Equation (5), i.e., , is related to a desorption process. In other words, this equation is a modified version, with fractional derivatives, of a balance equation stating that the time variation on the surface density is equal to the amount available to be adsorbed from the bulk minus the amount desorbed back to the bulk [45]. This equation, on the other hand, is a simplification of the classical Langmuir dynamics for a system where the number of particles is much smaller than the number of available adsorption sites. The presence of the kernel represents the importance of the previous state of a given particle in the bulk to the adsorption process, while the fractional derivative can be used to interpret any anomalous behavior during the dynamics of the surface. The fractional derivative used in Equation (5) is the Caputo one, defined as follows:
for , where corresponds to the time derivative, respectively. In particular, in our analysis, we consider . Equation (5) may be considered an extension of the usual kinetic equations (Langmuir approximation) to situations characterized by non-usual relaxations, i.e., non-Debye relaxations for which a non-exponential behavior of the densities can be obtained, depending on the choice of the and the kernel [41,43]. From a phenomenological point of view, the choice of the kernel of the Equations (5) can be related to surface irregularities, which are important in adsorption–desorption, to diffusion, to catalysis processes, and to microscopic parameters representing the van der Waals interaction between the particles and the surfaces. It is also interesting to mention that Equation (1) is coupled with Equation (5) in such a way that processes occurring for each part of the system (surface and bulk) modify the dynamic of the other.
This work is organized as follows. Next, Section 2 is devoted to investigate the solutions and the processes related to Equation (1) when considering the set of Equations (1) to (6). We show the behavior of the adsorption process for different scenarios and, in particular, consider two different adsorption processes in order to illustrate the influence on the bulk processes. In Section 3, we present a summary of the results, discussion and our conclusions.
2. Diffusion Equation and Solutions
Let us start our discussion about the time-dependent solutions of Equation (1) by considering it subjected to the boundary conditions previously discussed, in particular the Equation (5), which represents an adsorption–desorption process at the surface located in . To face this problem, we consider the eigenfunctions that emerge from the Sturm–Liouville theory related to the equation
with the boundary conditions, and , which implies
where is the Bessel function [53] and . In order to solve Equation (7) and obtain Equation (8), we use the result presented in Reference [54] related to the differential equations satisfied by the Bessel functions. By using these results, it is possible to show that
which may be related to a generalized Hankel transform. By using the previous equations, it is possible to obtain from Equations (1)–(3) that
and, consequently,
By substituting Equation (11) into Equation (9) and performing some calculations, we obtain that
with
( is a Bessel function of modified argument [53]) where
From Equations (5) and (12), it is possible to obtain the equation that governs the adsorption–desorption process on the surface under the influence of the diffusion process. In particular, we have that
with
It is worth mentioning that Equation (15) is an integro–differential equation with two terms. One of them represents an exponential relaxation and the second one relies on the time dependence of the diffusion coefficient. It can be related with a fractional time derivative yielding,
which is essentially a fractional time derivative in the Caputo sense, where defines the order of the fractional time derivative. This feature implies that Equation (15) can be written as
for and where ,
and
Consequently, when subjected to the diffusion of the particles in the bulk, the adsorption-desorption process on the surface presents two different diffusion regimes. One of them is governed by the usual differential operator, and a fractional time derivative controls another. The fractional time derivative present in Equation (18) is directly related to the bulk effects and, in particular, depends on the heterogeneity of the substrate, where the particles diffuse. The solution for Equation (18) by considering , i.e., the particles are initially in bulk may be obtained by considering the Laplace transform and , yielding
By performing the inverse of Laplace transform, we obtain that the solution is given by
with
Note that Equation (23) was obtained by using the integration on the complex plane to perform the inverse Laplace transform as discussed in Reference [55] by taking the Bromwich’s contour into account (see Figure 1).
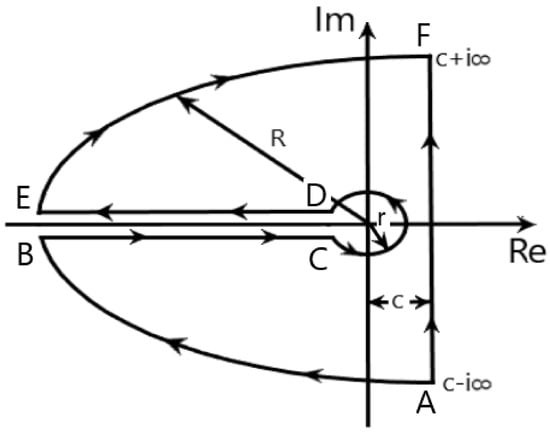
Figure 1.
The contour used to invert the Laplace transform given in Equation (23), see Reference [55] for more details.
Figure 2 shows the time behavior of for different values of . We may also observe from this figure that the diffusive behavior has a direct influence on the adsorption process of the particles by the surface. In fact, the heterogeneity of the media, which is measured by the parameter , may promote a faster spreading of the system by allowing a large amount of particles, in comparison with other regimes, to reach the surface where the adsorption process is present.
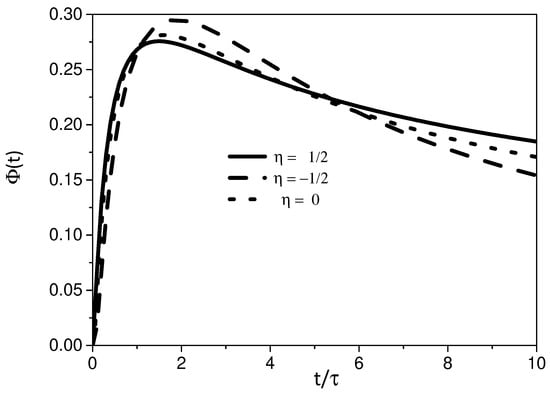
For the case , the previous result obtained for changes to
with
Similar to the previous case, Equation (25) was also obtained by performing the inverse Laplace transform with the Bromwich’s contour [55], as performed for Equation (23). Figure 3 shows the behavior of the adsorption process for the case and . In this case, we have an interplay between two different phenomena, one related to the heterogeneity of the bulk, and the other is related to the factional nature of the kinetic equation. In the three curves, a general behavior where a rapid adsorption process followed by a slow desorption is observed. However, it is quite interesting how this dynamic process is altered by the heterogeneity of the bulk and by the processes taking place at the surface, which in turn could be applied in the phenomenological approach of several systems as previously discussed.
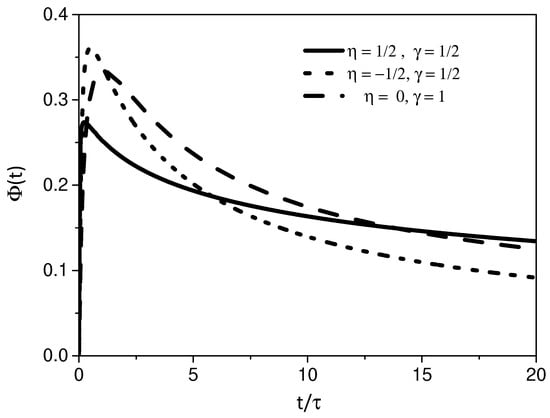
Figure 3.
This figure shows the behavior of the Equation (24) for different values of and , where and . It is possible to verify that the choice of may be directly related to the asymptotic behavior of . We consider, for simplicity, , , and .
For an arbitrary adsorption process, i.e., for a general kernel, it is possible to obtain a formal expression, which can be used to obtain particular cases. In this sense, we start by expanding the solution obtained from Equation (15), for the initial condition , in the Laplace space as follows
where . By applying the inverse of Laplace transform in Equation (26), we obtain that
with
and
Figure 4 shows the behavior of the mean square displacement for the cases related to the super-, usual and subdiffusive cases. Figure 5, Figure 6 and Figure 7 show the behavior of the system for , where an exponential is considered for the kernel related to the adsorption process. We observe a similar behavior for the mean square displacement in the asymptotic limits of short and long times. For intermediate times, a different behavior is observed. The feature is connected to the different processes of adsorption present in each case.
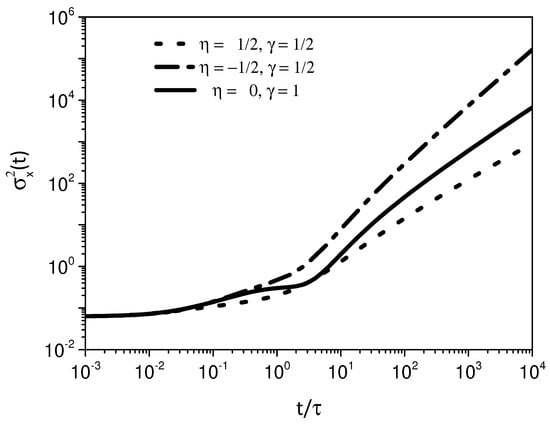
Figure 4.
Behavior of the mean square displacement for different values of and , where and . It is possible to verify that the choice of may be directly related to the asymptotic behavior of . We consider, for simplicity, , , and .
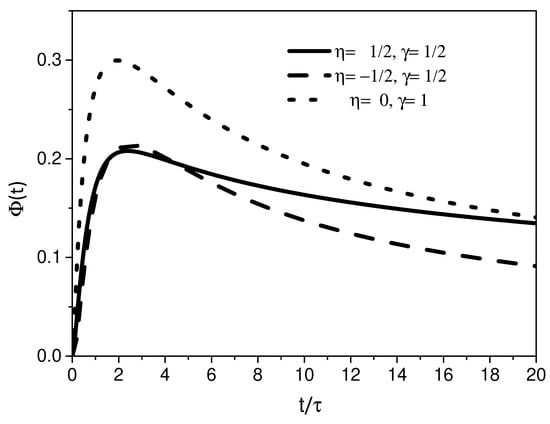
Figure 5.
This figure shows the behavior of the distribution for different values of and , with . We consider, for simplicity, , , , and .
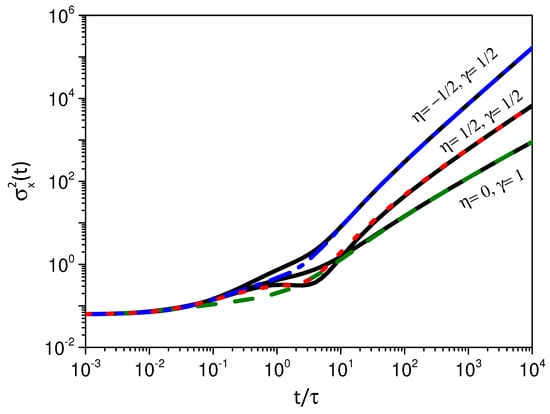
Figure 6.
This figure shows the behavior of the mean square displacement for different values of and , for the initial condition . The colored lines were obtained by considering and the black lines were obtained for . We consider, for simplicity, , , , and .
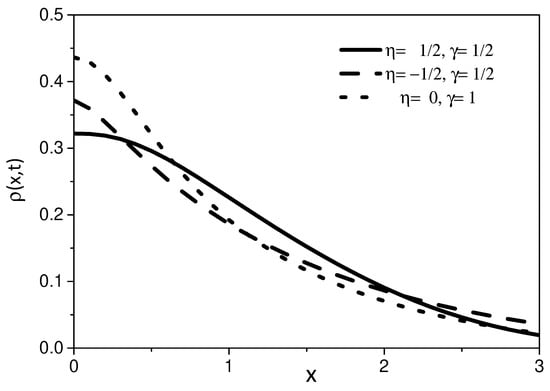
Figure 7.
This figure shows the behavior of the Equation (27) for different values of and , with . We consider, for simplicity, , , , and .
3. Discussion and Conclusions
We have investigated the adsorption–desorption process of a system governed by a diffusion equation with a spatial dependence on the diffusion coefficient. The spatial dependence present on the diffusion coefficient given by has been related to several physical contexts as mentioned before. In particular, an interesting point about this spatial dependence concerns the shape of the solution. It is given in terms of a stretched exponential, characteristic of a system subjected to a heterogeneous process. For the processes on the surface, we consider a fractional kinetic equation by taking memory effects into account on the adsorption term. This kinetic equation may cover different scenarios and related to non-Debye relaxations. The boundary conditions couple the processes present in the bulk and surface so that one modifies the other with the time evolution. For this system, we have found a general solution and analyzed particular cases for different scenarios. The first one considers the effect of heterogeneity on the adsorption–desorption process. In this sense, Figure 2 shows the influence of the different regimes on the effects of the surface related to the parameter . Following, we consider in the previous scenario, and an interplay between two different effects may be present while the particles diffuse (see Figure 3 and Figure 4). One of them is related to the heterogeneity and the other to the connected kinetic process, which determines the interaction between the surface and bulk. In this scenario, we also consider the case , (see Figure 5, Figure 6 and Figure 7). In particular, the mean square displacement has shown a wide range of behaviors related to anomalous diffusion.
Author Contributions
Conceptualization, E.K.L., M.K.L. and R.S.Z.; methodology, A.P.S.K., E.K.L., M.K.L. and R.S.Z.; writing—original draft preparation, A.P.S.K., E.K.L., M.K.L. and R.S.Z.; writing—review and editing, A.P.S.K., E.K.L., M.K.L. and R.S.Z. All authors have read and agreed to the published version of the manuscript.
Funding
E.K.L. is thankful for the partial financial support of the CNPq under grant No. 302983/2018-0. R.S.Z. is thankful to CNPq (304634/2020-4).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We thank the National Institutes of Science and Technology of Complex Fluids—INCT-FCx and Complex Systems—INCT-SC. Research developed with the support of LAMAP-UTFPR.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yang, R. Gas Separation by Adsorption Processes; Elsevier Science: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Council, N.; Sciences, D.; Board, N.; Systems, C.; Assessments, C.; Recycling, P. Separation Technologies for the Industries of the Future; Publication NMAB, National Academies Press: Washington, DC, USA, 1999. [Google Scholar]
- Grandison, A.; Grandison, A.; Lewis, M. Separation Processes in the Food and Biotechnology Industries: Principles and Applications; Woodhead Publishing Series in Food Science, Technology and Nutrition; Elsevier Science: Amsterdam, The Netherlands, 1996. [Google Scholar]
- Worch, E. Adsorption Technology in Water Treatment: Fundamentals, Processes, and Modeling; De Gruyter: Berlin, Germany, 2012. [Google Scholar]
- Yiacoumi, S.; Tien, C. Kinetics of Metal Ion Adsorption from Aqueous Solutions: Models, Algorithms, and Applications; Springer: New York, NY, USA, 2013. [Google Scholar]
- Adamson, A.; Gast, A. Physical Chemistry of Surfaces; Wiley: New York, NY, USA, 1997. [Google Scholar]
- Barbero, G.; Evangelista, L. Adsorption Phenomena and Anchoring Energy in Nematic Liquid Crystals; Liquid Crystals Book Series; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Crank, J. The Mathematics of Diffusion; Oxford Science Publications; Clarendon Press: Oxford, UK, 1979. [Google Scholar]
- Weiss, M.; Hashimoto, H.; Nilsson, T. Anomalous Protein Diffusion in Living Cells as Seen by Fluorescence Correlation Spectroscopy. Biophys. J. 2003, 84, P4043–P4052. [Google Scholar] [CrossRef] [Green Version]
- Gal, N.; Weihs, D. Experimental evidence of strong anomalous diffusion in living cells. Phys. Rev. E 2010, 81, 020903. [Google Scholar] [CrossRef]
- Evangelista, L.R.; Lenzi, E.K. Fractional Diffusion Equations and Anomalous Diffusion; Cambridge University Press: Cambridge, UK, 2018; p. 395. [Google Scholar]
- Gatenby, R.A.; Gawlinski, E.T. A Reaction-Diffusion Model of Cancer Invasion. Cancer Res. 1996, 56, 5745–5753. [Google Scholar]
- Cohen, D.S.; Murray, J.D. A generalized diffusion model for growth and dispersal in a population. J. Math. Biol. 1981, 12, 237–249. [Google Scholar] [CrossRef]
- Cantrell, R.S.; Cosner, C. Diffusion models for population dynamics incorporating individual behavior at boundaries: Applications to refuge design. Theor. Popul. Biol. 1999, 55, 189–207. [Google Scholar] [CrossRef] [PubMed]
- Sonetaka, N.; Fan, H.J.; Kobayashi, S.; Chang, H.N.; Furuya, E. Simultaneous determination of intraparticle diffusivity and liquid film mass transfer coefficient from a single-component adsorption uptake curve. J. Hazard. Mater. 2009, 164, 1447–1451. [Google Scholar] [CrossRef] [PubMed]
- Bouzid, M.; Torkia, Y.B.; Wjihi, S.; Lamine, A.B. Kinetic adsorption modeling of ethanol molecules onto three types of activated carbons: Microscopic interpretation of adsorption and diffusion parameters. J. Mol. Liq. 2017, 242, 98–108. [Google Scholar] [CrossRef]
- Fontana, K.B.; Lenzi, G.G.; Watanabe, E.R.; Lenzi, E.K.; Pietrobelli, J.A.; Chaves, E.S. Biosorption and Diffusion Modeling of Pb(II) by Malt Bagasse. Int. J. Chem. Eng. 2016, 2016. [Google Scholar] [CrossRef]
- Song, J.J.; Bhattacharya, R.; Kim, H.; Chang, J.; Tang, T.Y.; Guo, H.; Ghosh, S.K.; Yang, Y.; Jiang, Z.; Kim, H.; et al. One-Dimensional Anomalous Diffusion of Gold Nanoparticles in a Polymer Melt. Phys. Rev. Lett. 2019, 122, 107802. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Berland, K.M. Propagators and Time-Dependent Diffusion Coefficients for Anomalous Diffusion. Biophys. J. 2008, 95, 2049–2052. [Google Scholar] [CrossRef] [Green Version]
- Alcázar-Cano, N.; Delgado-Buscalioni, R. A general phenomenological relation for the subdiffusive exponent of anomalous diffusion in disordered media. Soft Matter 2018, 14, 9937–9949. [Google Scholar] [CrossRef]
- Yurchenko, I.; Basso, J.M.V.; Syrotenko, V.S.; Staii, C. One-Dimensional Anomalous Diffusion of Gold Nanoparticles in a Polymer Melt. PLoS ONE 2019, 14, e021618. [Google Scholar]
- Naumov, S.; Valiullin, R.; Monson, P.A.; Kärger, J. Probing Memory Effects in Confined Fluids via Diffusion Measurements. Langmuir 2008, 24, 6429–6432. [Google Scholar] [CrossRef]
- Murase, K.; Fujiwara, T.; Umemura, Y.; Suzuki, K.; Iino, R.; Yamashita, H.; Saito, M.; Murakoshi, H.; Ritchie, K.; Kusumi, A. Ultrafine Membrane Compartments for Molecular Diffusion as Revealed by Single Molecule Techniques. Biophys. J. 2004, 86, 4075–4093. [Google Scholar] [CrossRef] [Green Version]
- Berrod, Q.; Hanot, S.; Guillermo, A.; Mossa, S.; Lyonnard, S. Water sub-diffusion in membranes for fuel cells. Sci. Rep. 2017, 7, 8326. [Google Scholar] [CrossRef] [Green Version]
- Dudko, O.K.; Berezhkovskii, A.M.; Weiss, G.H. Time-Dependent Diffusion Coefficients in Periodic Porous Materials. J. Phys. Chem. B 2005, 109, 21296–21299. [Google Scholar] [CrossRef] [PubMed]
- Gerber, G.; Bensouda, M.; Weitz, D.A.; Coussot, P. Self-Limited Accumulation of Colloids in Porous Media. Phys. Rev. Lett. 2019, 123, 158005. [Google Scholar] [CrossRef] [PubMed]
- Sandev, T.; Metzler, R.; Chechkin, A. From continuous time random walks to the generalized diffusion equation. Fract. Calc. Appl. Anal. 2018, 21, 10–28. [Google Scholar] [CrossRef] [Green Version]
- Sandev, T.; Tomovski, Z. Fractional Equations and Models; Springer International Publishing: Zurich, Switwerland, 2019. [Google Scholar]
- Liang, Y.; Wang, S.; Chen, W.; Zhou, Z.; Magin, R.L. A Survey of Models of Ultraslow Diffusion in Heterogeneous Materials. Appl. Mech. Rev. 2019, 71, 040802. [Google Scholar] [CrossRef]
- Yang, Q.H.; Yang, X.; Luo, M.B. Adsorption of polymer chains on heterogeneous surfaces with random adsorption sites. Polymer 2019, 180, 121677. [Google Scholar] [CrossRef]
- Morrin, G.T.; Schwartz, D.K. Three Regimes of Polymer Surface Dynamics under Crowded Conditions. Macromolecule 2018, 51, 1207–1214. [Google Scholar] [CrossRef]
- Dumazer, G.; Flekkøy, E.; Renard, F.M.C.; Angheluta, L. Transient anomalous diffusion regimes in reversible adsorbing systems. Phys. Rev. E 2017, 96, 042106. [Google Scholar] [CrossRef]
- Recanello, M.; Lenzi, E.K.; Martins, A.; Li, Q.; Zola, R. Extended adsorbing surface reach and memory effects on the diffusive behavior of particles in confined systems. Int. J. Heat Mass Transf. 2020, 151, 119433. [Google Scholar] [CrossRef]
- Guimarães, V.G.; Ribeiro, H.V.; Li, Q.; Evangelista, L.R.; Lenzi, E.K.; Zola, R.S. Unusual diffusing regimes caused by different adsorbing surfaces. Soft Matter 2015, 11, 1658–1666. [Google Scholar] [CrossRef]
- Höfling, F.; Franosch, T. Anomalous transport in the crowded world of biological cells. Rep. Prog. Phys. 2013, 76, 046602. [Google Scholar] [CrossRef] [Green Version]
- Saxton, M.J. A Biological Interpretation of Transient Anomalous Subdiffusion. I. Qualitative Model. Biophys. J. 2007, 92, 1178–1191. [Google Scholar] [CrossRef] [Green Version]
- Banks, D.S.; Fradin, C. Anomalous Diffusion of Proteins Due to Molecular Crowding. Biophys. J. 2005, 89, 2960–2971. [Google Scholar] [CrossRef] [Green Version]
- Fermandes, M.; Lenzi, E.K.; Evangelista, L.R.; Li, Q.; Zola, R.S.; de Souza, R. Diffusion and adsorption-deserntion phenomena in confined systems with periodically varying medium. Chem. Eng. Sci. 2021, 233, 116386. [Google Scholar] [CrossRef]
- Ribeiro, H.V.; Tateishi, A.A.; Alves, L.G.A.; Zola, R.S.; Lenzi, E.K. Investigating the interplay between mechanisms of anomalous diffusion via fractional Brownian walks on a comb-like structure. New J. Phys. 2014, 16, 093050. [Google Scholar] [CrossRef] [Green Version]
- Torquato, S. Diffusion and reaction among traps: Some theoretical and simulation results. J. Stat. Phys. 1991, 65, 1173–1206. [Google Scholar] [CrossRef]
- Lenzi, E.K.; Yednak, C.A.R.; Evangelista, L.R. Non-Markovian diffusion and the adsorption-desorption process. Phys. Rev. E 2010, 81, 011116. [Google Scholar] [CrossRef] [Green Version]
- Lenzi, E.K.; Evangelista, L.R.; Barbero, G.; Mantegazza, F. Anomalous diffusion and the adsorption-desorption process in anisotropic media. EPL (Europhys. Lett.) 2009, 85, 28004. [Google Scholar] [CrossRef]
- de Paula, J.L.; Santoro, P.A.; Zola, R.S.; Lenzi, E.K.; Evangelista, L.R.; Ciuchi, F.; Mazzulla, A.; Scaramuzza, N. Non-Debye relaxation in the dielectric response of nematic liquid crystals: Surface and memory effects in the adsorption-desorption process of ionic impurities. Phys. Rev. E 2012, 86, 051705. [Google Scholar] [CrossRef] [PubMed]
- Lenzi, E.K.; Lenzi, M.K.; Zola, R.; Ribeiro, H.; Zola, F.; Evangelista, L.; Gonçalves, G. Reaction on a solid surface supplied by an anomalous mass transfer source. Phys. A 2014, 410, 399–406. [Google Scholar] [CrossRef]
- Zola, R.S.; Lenzi, E.K.; Evangelista, L.R.; Barbero, G. Memory effect in the adsorption phenomena of neutral particles. Phys. Rev. E 2007, 75, 042601. [Google Scholar] [CrossRef] [PubMed]
- O’Shaughnessy, B.; Procaccia, I. Diffusion on fractals. Phys. Rev. A 1985, 32, 3073–3083. [Google Scholar] [CrossRef] [PubMed]
- O’Shaughnessy, B.; Procaccia, I. Analytical Solutions for Diffusion on Fractal Objects. Phys. Rev. Lett. 1985, 54, 455–458. [Google Scholar] [CrossRef] [PubMed]
- Richardson, L.F. Atmospheric diffusion shown on a distance-neighbour graph. Proc. Math. Phys. Eng. Sci. 1926, 110, 709–737. [Google Scholar]
- Boffetta, G.; Sokolov, I.M. Relative Dispersion in Fully Developed Turbulence: The Richardson’s Law and Intermittency Corrections. Phys. Rev. Lett. 2002, 88, 094501. [Google Scholar] [CrossRef] [Green Version]
- Daniel ben Avraham, S.H. Diffusion and Reactions in Fractals and Disordered Systems; CUP: Cambridge, UK, 2000. [Google Scholar]
- Su, N.; Sander, G.; Liu, F.; Anh, V.; Barry, D. Similarity solutions for solute transport in fractal porous media using a time- and scale-dependent dispersivity. App. Math. Model. 2005, 29, 852–870. [Google Scholar] [CrossRef] [Green Version]
- Brault, P.; Josserand, C.; Bauchire, J.M.; Caillard, A.; Charles, C.; Boswell, R.W. Anomalous Diffusion Mediated by Atom Deposition into a Porous Substrate. Phys. Rev. Lett. 2009, 102, 045901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wyld, H.W. Mathematical Methods for Physics, Advanced Book Program; Perseus Books: Reading, MA, USA, 1976. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products; Academic Press: Washington, DC, USA, 2007. [Google Scholar]
- Duffy, D.G. Transform Methods for Solving Partial Differential Equations; Chapman & Hall/CRC: Boca Raton, FL, USA, 2004. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).