Multivariate Fractal Functions in Some Complete Function Spaces and Fractional Integral of Continuous Fractal Functions

Abstract

There has been a considerable evolution of the theory of fractal interpolation function (FIF) over the last three decades. Recently, we introduced a multivariate analogue of a special class of FIFs, which is referred to as $\alpha$-fractal functions, from the viewpoint of approximation theory. In the current note, we continue our study on multivariate $\alpha$-fractal functions, but in the context of a few complete function spaces. For a class of fractal functions defined on a hyperrectangle $\mathsf{\Omega }$ in the Euclidean space ${\mathbb{R}}^n$, we derive conditions on the defining parameters so that the fractal functions are elements of some standard function spaces such as the Lebesgue spaces ${\mathcal{L}}^p\left(\mathsf{\Omega }\right)$, Sobolev spaces ${\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right)$, and Hölder spaces ${\mathcal{C}}^{m,\sigma }\left(\mathsf{\Omega }\right)$, which are Banach spaces. As a simple consequence, for some special choices of the parameters, we provide bounds for the Hausdorff dimension of the graph of the corresponding multivariate $\alpha$-fractal function. We shall also hint at an associated notion of fractal operator that maps each multivariate function in one of these function spaces to its fractal counterpart. The latter part of this note establishes that the Riemann–Liouville fractional integral of a continuous multivariate $\alpha$-fractal function is a fractal function of similar kind.

1. Preamble

This note aims to offer a modest contribution to the field of fractal interpolation. In particular, we consider a special class of fractal interpolation functions referred to as the $\alpha$-fractal function, which has played a considerable role in the theory of univariate fractal approximation. Our work in the current note seeks to show that a few results on the construction of univariate $\alpha$-fractal functions in various function spaces and associated fractal operator (see, for instance, [1]) carry over to higher dimensions.

For a prescribed data set $D=\{(x_0,y_0),(x_1,y_1),\cdots ,(x_k,y_k)\}$ in ${\mathbb{R}}^2$ with increasing abscissae, there are multitude of methods to construct a continuous function that maps each $x_i$ to $y_i$—generally known as interpolation methods—available in the field of classical numerical analysis and approximation theory. Roughly speaking, the fractal interpolation function (FIF for short), as introduced by Barnsley in the original version [2], is a continuous function $g:[x_0,x_k]\to \mathbb{R}$ that interpolates D such that the graph of g, denoted by $\mathrm{Gr}\left(g\right)$, is a self-referential set (fractal set). Here the word fractal or self-referential is used to indicate that $\mathrm{Gr}\left(g\right)$ is the attractor of an iterated function system [3]. That is, roughly, $\mathrm{Gr}\left(g\right)$ is a finite union of tranformed copies of itself. For a compendium of the theory of FIF and its applications in interpolation and approximation, the reader is referred to the book and monograph [4,5]; the recent articles [6,7,8] may also be of interest.

In her research works on fractal interpolation, Navascués emphasized a special class of univariate FIFs, named $\alpha$-fractal functions, (see, for instance, [9,10]) which garnered a significant amount of research attention in fractal approximation theory. It is our opinion that the notion of $\alpha$-fractal functions assisted the field of fractal interpolation to find connections and consequences in other branches of mathematics such as approximation theory, harmonic analysis, functional analysis and the theory of bases and frames; see, for instance, [11,12]. In the research works reported in [13,14], authors utilized $\alpha$-fractal functions to demonstrate that FIFs can be applied in various constrained approximation problems.

Several extensions of FIF to higher dimensions, in particular, bivariate FIFs or fractal surfaces, have been studied in the literature; see, for example, [4,15,16,17,18,19]. Despite that the $\alpha$-fractal function facilitated the theory of univariate FIF to merge seamlessly with various fields in mathematics, a similar approach to multivariate FIFs was not attempted except for a few research works on bivariate $\alpha$-fractal functions reported lately in [20,21,22]. The aforementioned works on bivariate $\alpha$-fractal functions find their origin, perhaps implicitly, in the general framework for the construction of fractal surfaces introduced in [23].

While an increasing amount of literature is being published in the field of univariate FIFs and fractal surfaces, the research in multivariate FIFs are still inadequate, especially in the framework of $\alpha$-fractal functions. In the context of multivariate FIFs, the ingenious constructions appeared in [24,25], though worth mentioning, do not seem to be suitable for the implementation of the $\alpha$-fractal function formalism. On the other hand, our acquaintance with the univariate and bivariate $\alpha$-fractal functions revealed that the development of multivariate analogue of $\alpha$-fractal function could be highly beneficial for the expansion of multivariate fractal approximation theory. Stimulated by the construction of fractal surface in [23], recently we put forward a satisfactory extension of the Barnsley’s theory of univariate FIF to the multivariate case [26].

In this note, we continue to explore the notion of multivariate $\alpha$-fractal functions. In the first part, we define multivariate $\alpha$-fractal functions in various function spaces such as the Lebesgue spaces ${\mathcal{L}}^p$, Sobolev spaces ${\mathcal{W}}^{m,p}$, and Hölder spaces ${\mathcal{C}}^{m,\sigma }$. We also hint at some elementary properties of the fractal operator associated with the notion of multivariate $\alpha$-fractal functions.

Fractal dimension is an important parameter of fractal geometry providing information about the geometric structure of the objects that it deals with. There are different notions of fractal dimension, the two most commonly used being the Hausdorff dimension and box dimension [27]. In particular, the Hausdorff dimension and box dimension of the graphs of fractal interpolation functions have been investigated; see, for instance, [2,4,15,28]. Since the aforementioned fractal dimensions are scale-independent, they may not be useful for describing scale-dependent laws and more complicated phenomena in nature. To this end, a new definition of fractal dimension, referred to as the two-scale dimension, is broached in [29], and it is perhaps more akin to physics than mathematics. However, we are forced to settle for less in the framework of multivariate $\alpha$-fractal functions considered herein, because the analysis for the fractal dimension of the general nonaffine case is subtle. We shall just mention bounds for the Hausdorff dimension of the graph of the multivariate $\alpha$-fractal function as an immediate consequence of its Hölder continuity for suitable choice of parameters.

On the other hand, fractional calculus, which broadly deals with derivatives and integrals of fractional order, is rather an old subject. During the last decades, fractional calculus has opened its wings wider to cover several real world applications in science and engineering. Despite being an old subject, fractional calculus continues to be a hot topic of research, resulting in a substantial body of literature; we refer the reader to the informative surveys [30,31]. Some recent developments made in the direction of fractional PDEs and their applications deserve a special mention; see, for instance, [32,33,34,35]. Studies on the interconnection between fractional calculus and fractal geometry have gained significant attention in recent years. For some links between the two-scale problem mentioned previously and fractional calculus, the reader may consult [36]. In the second part of this note, our modest aim is to show that the fractional integral of the multivariate fractal function considered herein is again a fractal function of a similar kind.

Overall, this note discusses how some results in univariate fractal interpolation, to be specific $\alpha$-fractal functions, fractal operator and fractional calculus of fractal functions, carry over to higher dimensions. We strongly believe that these research findings may assist efforts to find interesting interconnections between multivariate FIFs and the theory of PDEs.

2. Preparatory Facts

To begin with, we list pertinent definitions and notation for use throughout the remainder of this note.

The set of first n natural numbers shall be denoted by ${\mathsf{\Sigma }}_n$. For $l=(l_1,\dots ,l_n)\in {(\mathbb{N}\cup \left\{0\right\})}^n,$ called a multi-index, let $\left|l\right|={\sum }_{k=1}^n{l}_k.$ Given two multi-indices $l=(l_1,\dots ,l_n)$ and $l^{\prime }=(l_1^{{}^{\prime }},\dots ,l_n^{{}^{\prime }}),$ we say that $l^{\prime }\le l$ if $l_k^{{}^{\prime }}\le l_k$ for all $k\in {\mathsf{\Sigma }}_n.$ For $l^{\prime }\le l$, we define:

$$\left(\genfrac{}{}{0pt}{}{l}{l^{\prime }}\right)=\prod _{k=1}^n\left(\genfrac{}{}{0pt}{}{l_k}{l_k^{{}^{\prime }}}\right).$$

Let $n\ge 2$ and $\mathsf{\Omega }={\prod }_{k=1}^n{I}_k$ be an n-dimensional hyperrectangle, where each $I_k=[a_k,b_k]$ is a closed and bounded interval in $\mathbb{R}.$ For a function $g:\mathsf{\Omega }\to \mathbb{R}$ and $X_0=(x_1^0,\dots ,x_n^0)\in \mathsf{\Omega }$, denoted by

$$D^l\left(g\right)\left(X_0\right)=\frac{{\partial }^{l_1+\dots +l_n}g}{{\partial x_1}^{l_1}\dots {\partial x_n}^{l_n}}\left(X_0\right),$$

provided the right-hand side exists.

2.1. Function Spaces

The purpose here is to provide a short presentation of various function spaces that are used in this note. We refer to Triebel [37] for more information.

Let $\mathcal{C}\left(\mathsf{\Omega }\right)$ denote the Banach space of all real-valued continuous functions defined on $\mathsf{\Omega }$, endowed with the sup-norm ${\parallel .\parallel }_{\infty }$. For a positive integer m, we consider the linear space ${\mathcal{C}}^m\left(\mathsf{\Omega }\right)$ defined by

$$\begin{array}{cc}\hfill {\mathcal{C}}^m\left(\mathsf{\Omega }\right)=& \{g\in \mathcal{C}\left(\mathsf{\Omega }\right):D^l\left(g\right)\mathrm{exists}\mathrm{and}\mathrm{it}\mathrm{is}\mathrm{continuous}\mathrm{for}\mathrm{each}\mathrm{multi}-\mathrm{index}l\hfill \\ & \mathrm{with}\left|l\right|\le m\}.\hfill \end{array}$$

For any $g\in {\mathcal{C}}^m\left(\mathsf{\Omega }\right)$, we define

$${\parallel g\parallel }_{{\mathcal{C}}^m\left(\mathsf{\Omega }\right)}=\sum _{\left|l\right|\le m}{\parallel D^l\left(g\right)\parallel }_{\infty }.$$

It is well-known that ${\mathcal{C}}^m\left(\mathsf{\Omega }\right)$ equipped with ${\parallel .\parallel }_{{\mathcal{C}}^m\left(\mathsf{\Omega }\right)}$ is a Banach space. Next, we recall the Lebesgue spaces. For $0<p\le \infty ,$ let

$${\mathcal{L}}^p\left(\mathsf{\Omega }\right)=\left\{g:\mathsf{\Omega }\to {\mathbb{R}\mathrm{such}\mathrm{that}g\mathrm{is}\mathrm{measurable}\mathrm{and}\parallel g\parallel }_p<\infty \right\},$$

where ${\parallel g\parallel }_p$ is defined as

$${\parallel g\parallel }_p=\left\{\begin{array}{cc}{\left({\int }_{\mathsf{\Omega }}{\left|g\left(X\right)\right|}^p\mathrm{d}X\right)}^{\frac{1}{p}},\hfill & \mathrm{for}0<p<\infty .\hfill \\ \mathrm{ess}\underset{X\in \mathsf{\Omega }}{sup}\left|g\left(X\right)\right|,\hfill & \mathrm{for}p=\infty .\hfill \end{array}\right.$$

It is a standard result in functional analysis that $\left({\mathcal{L}}^p\left(\mathsf{\Omega }\right),{\parallel .\parallel }_p\right)$ is a Banach space for $1\le p\le \infty$. For $0<p<1,$${\parallel .\parallel }_p$ is a quasi-norm, that is, in place of the triangle inequality one has

$${\parallel g+h\parallel }_p\le 2^{\frac{1}{p}}\left({\parallel g\parallel }_p+{\parallel h\parallel }_p\right),$$

and ${\mathcal{L}}^p\left(\mathsf{\Omega }\right)$ is a quasi-Banach space.

Let $g\in {\mathcal{L}}^p\left(\mathsf{\Omega }\right).$ For a multi-index $l,$ a function $h:\mathsf{\Omega }\to \mathbb{R}$ is called the $l^{th}$-weak derivative of g if it satisfies

$${\int }_{\mathsf{\Omega }}g\left(X\right)D^l\varphi \left(X\right)\mathrm{d}X={(-1)}^{\left|l\right|}{\int }_{\mathsf{\Omega }}h\left(X\right)\varphi \left(X\right)\mathrm{d}X,$$

for all infinitely differentiable functions $\varphi$ with compact support contained in $\mathsf{\Omega }.$ By a slight abuse of notation, we write $l^{th}$-weak derivative of g as $D^l\left(g\right)=h.$

For $1\le p\le \infty$ and a non-negative integer $m,$${\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right)$ denotes the Sobolev space with smoothness m and integrability p defined by

$${\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right)=\left\{g:\mathsf{\Omega }\to \mathbb{R}\mathrm{such}\mathrm{that}{D}^l\left(g\right)\in {\mathcal{L}}^p\left(\mathsf{\Omega }\right)\mathrm{for}\mathrm{all}\mathrm{multi}-\mathrm{index}l\mathrm{with}\left|l\right|\le m\right\}.$$

The linear space ${\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right)$ endowed with the norm

$${\parallel g\parallel }_{{\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right)}=\left\{\begin{array}{cc}{\left(\sum _{\left|l\right|\le m}{\parallel D^l\left(g\right)\parallel }_p^p\right)}^{\frac{1}{p}},\hfill & \mathrm{for}1\le p<\infty .\hfill \\ \underset{\left|l\right|\le m}{max}{\parallel D^l\left(g\right)\parallel }_{\infty },\hfill & \mathrm{for}p=\infty .\hfill \end{array}\right.$$

is a Banach space. For $p=2$, it is a Hilbert space, which shall be denoted by ${\mathcal{H}}^m\left(\mathsf{\Omega }\right).$

A function $g:\mathsf{\Omega }\to \mathbb{R}$ is Hölder continuous with exponent $\sigma \in (0,1]$ (or $\sigma$- Hölder continuous) if

$$|g\left(X\right)-g\left(Y\right)|\le C_g{\parallel X-Y\parallel }^{\sigma },$$

for all $X,Y\in \mathsf{\Omega }$ and some $C_g>0$, called a Hölder constant of g. Given a Hölder continuous $g:\mathsf{\Omega }\to \mathbb{R}$ with exponent $\sigma ,$ the $\sigma$-Hölder semi-norm of g is defined by

$${\left[g\right]}_{\sigma }=\underset{X,Y\in \mathsf{\Omega },X\ne Y}{sup}\frac{\left|g\right(X)-g(Y\left)\right|}{{\parallel X-Y\parallel }^{\sigma }}.$$

If m is a positive integer, then the Hölder space ${\mathcal{C}}^{m,\sigma }\left(\mathsf{\Omega }\right)$ is defined as

$$\begin{array}{cc}\hfill {\mathcal{C}}^{m,\sigma }\left(\mathsf{\Omega }\right)=& \{g\in {\mathcal{C}}^m\left(\mathsf{\Omega }\right):D^l\left(g\right)\mathrm{is}\sigma -\mathrm{Hölder}\mathrm{continuous}\hfill \\ & \mathrm{for}\mathrm{all}\mathrm{multi}-\mathrm{index}l\mathrm{with}\left|l\right|=m\}.\hfill \end{array}$$

The space ${\mathcal{C}}^{m,\sigma }\left(\mathsf{\Omega }\right)$ equipped with the norm

$${\parallel g\parallel }_{{\mathcal{C}}^{m,\sigma }\left(\mathsf{\Omega }\right)}={\parallel g\parallel }_{{\mathcal{C}}^m\left(\mathsf{\Omega }\right)}+\sum _{\left|l\right|=m}{\left[D^l\left(g\right)\right]}_{\sigma }$$

is a Banach space. Note that ${\mathcal{C}}^{0,\sigma }\left(\mathsf{\Omega }\right)$ coincides with the space of all Hölder continuous functions with exponent $\sigma$.

2.2. Towards Multivariate FIF

Here we shall equip ourselves with a few rudiments needed for multivariate fractal functions that concern us. As mentioned previously, let $I_k=[a_k,b_k]$, $k=1,2,\cdots ,n$ be compact intervals in $\mathbb{R}$ and $\mathsf{\Omega }={\prod }_{k=1}^n{I}_k$ be an n-dimensional hyperrectangle.

Let $n\ge 2$ be an integer and $\mathsf{\Delta }=\{(x_{1,i_1},x_{2,i_2},\dots ,x_{n,i_n})\in {\mathbb{R}}^n:i_k=0,1,\cdots ,N_k$; $k=1,\cdots ,n\}$ be such that $a_k=x_{k,0}<x_{k,1}<\cdots <x_{k,N_k}=b_k$ for each $k=1,2,\dots ,n$. Note that $a_k=x_{k,0}<x_{k,1}<\cdots <x_{k,N_k}=b_k$ determines a partition of $I_k$ into subintervals $I_{k,i_k}=\left[x_{k,i_{k-1}},x_{k,i_k}\right)$ for $i_k=1,2,\cdots ,N_{k-1}$ and $I_{k,N_k}=\left[x_{k,N_{k-1}},x_{k,N_k}\right]$. It is worth to note that $I_k={\cup }_{i_k=1}^{N_k}{I}_{k,i_k}$ and each knot point in the partition of $I_k$ is exactly in one of the subintervals $I_{k,i_k}$, $i_k=1,2\cdots ,N_k$ mentioned above. We call such a set $\mathsf{\Delta }$ as a partition of $\mathsf{\Omega }$ for an obvious reason.

For convenience, let us introduce the following notation. For a positive integer $N,$

$$\begin{array}{cc}\hfill & {\mathsf{\Sigma }}_N=\{1,2,\cdots ,N\},{\mathsf{\Sigma }}_{N,0}=\{0,1,\cdots N\},\hfill \\ \hfill & \partial {\mathsf{\Sigma }}_{N,0}=\{0,N\},\mathrm{int}{\mathsf{\Sigma }}_{N,0}=\{1,2,\cdots ,N-1\}.\hfill \end{array}$$

For each $i_k\in {\mathsf{\Sigma }}_{N_k},$ let $u_{k,i_k}:I_k\to I_{k,i_k}$ be an affine map of the form

$$u_{k,i_k}\left(x\right)=a_{k,i_k}x+b_{k,i_k},$$

satisfying

$$\left\{\begin{array}{cc}\hfill & u_{k,i_k}\left(x_{k,0}\right)=x_{k,i_k-1}\mathrm{and}{u}_{k,i_k}\left(x_{k,N_k}\right)=x_{k,i_k}\mathrm{if}{i}_k\mathrm{is}\mathrm{odd},\hfill \\ \hfill & u_{k,i_k}\left(x_{k,0}\right)=x_{k,i_k}\mathrm{and}{u}_{k,i_k}\left(x_{k,N_k}\right)=x_{k,i_k-1}\mathrm{if}{i}_k\mathrm{is}\mathrm{even}.\hfill \end{array}\right.$$

(1)

When the interval $I_{k,i_k}$ involved in the definition of the affine map is half-open, the above equation needs to be interpreted in terms of the one-sided limit. For instance, when $i_k\in \{1,2,\cdots ,N_{k-1}\}$ is odd, $u_{k,i_k}\left(x_{k,N_k}\right)=x_{k,i_k}$ in (1) actually means ${lim}_{x\to x_{k,N_k}^{-}}{u}_{k,i_k}\left(x\right)=x_{k,i_k}$.

Note that

$$\begin{array}{c}\hfill |u_{k,i_k}\left(x\right)-u_{k,i_k}\left(x^{\prime }\right)|\le {\gamma }_{k,i_k}|x-x^{\prime }|,\forall x,x^{\prime }\in I_k,\end{array}$$

(2)

for $0\le {\gamma }_{k,i_k}=\left|a_{k,i_k}\right|<1$. Using the definition of the map $u_{k,i_k}$, one can verify that

$$\begin{array}{c}\hfill u_{k,i_k}^{-1}\left(x_{k,i_k}\right)=u_{k,i_k+1}^{-1}\left(x_{k,i_k}\right),\end{array}$$

(3)

for all $i_k\in \mathrm{int}{\mathsf{\Sigma }}_{N_k,0}.$

Let $\tau :\mathbb{Z}\times \{0,N_1,N_2,\dots ,N_n\}\to \mathbb{Z}$ be defined by

$$\left\{\begin{array}{cc}\tau (i,0)=i-1,\tau (i,N_k)=i,\hfill & \mathrm{if}i\mathrm{is}\mathrm{odd},\hfill \\ \tau (i,0)=i,\tau (i,N_k)=i-1,\hfill & \mathrm{if}i\mathrm{is}\mathrm{even}.\hfill \end{array}\right.$$

(4)

Using the above notation, we see that $u_{k,i_k}\left(x_{k,j_k}\right)=x_{k,\tau (i_k,j_k)}$ for all $i_k\in {\mathsf{\Sigma }}_{N_k},j_k\in \partial {\mathsf{\Sigma }}_{N_k,0}$ and $k\in {\mathsf{\Sigma }}_n.$

It is easy to observe that the boundary of $\mathsf{\Omega }$ in the usual metric of ${\mathbb{R}}^n$ is

$$\partial \mathsf{\Omega }=\left\{X=(x_1,\dots ,x_{k,j_k},\dots x_n)\in \mathsf{\Omega }:j_k\in \partial {\mathsf{\Sigma }}_{N_k,0},k\in {\mathsf{\Sigma }}_n\right\}.$$

3. Multivariate $\mathbf{\alpha }$-Fractal Functions in Some Complete Function Spaces

This section targets to construct fractal functions (self-referential functions) in the complete function spaces ${\mathcal{C}}^m\left(\mathsf{\Omega }\right)$, ${\mathcal{L}}^p\left(\mathsf{\Omega }\right)$, ${\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right)$ and ${\mathcal{C}}^{m,\sigma }\left(\mathsf{\Omega }\right)$, which we recalled in the previous section. To this end, let $\mathbb{X}$ be any of the function space from the list $\{{\mathcal{C}}^m\left(\mathsf{\Omega }\right),{\mathcal{L}}^p\left(\mathsf{\Omega }\right)$, ${\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right),{\mathcal{C}}^{m,\sigma }\left(\mathsf{\Omega }\right)\}$ and $f\in \mathbb{X},$ be a fixed function, which we shall refer to as the germ function. Let $b\in \mathbb{X}$ be a fixed function, called the base function.

For each $g\in \mathbb{X}$, and $X=(x_1,\dots ,x_n)\in {\prod }_{k=1}^n{I}_{k,i_k},$$(i_1,\dots ,i_n)\in {\prod }_{k=1}^n{\mathsf{\Sigma }}_{N_k},$ we define $T_f\left(g\right)$ as

$$T_f\left(g\right)\left(X\right)=f\left(X\right)+{\alpha }_{i_1\dots i_n}(g-b)\left(u_{i_1\dots i_n}^{-1}\left(X\right)\right),$$

(5)

where $u_{i_1\dots i_n}^{-1}\left(X\right)=\left(u_{1,i_1}^{-1}\left(x_1\right),\dots ,u_{1,i_1}^{-1}\left(x_n\right)\right)$ and ${\alpha }_{i_1\dots i_n}$ are real numbers such that

$$max\{|{\alpha }_{i_1\dots i_n}|:(i_1,\dots ,i_n)\in \prod _{k=1}^n{\mathsf{\Sigma }}_{N_k}\}<1.$$

The ${\prod }_{k=1}^n{N}_k$-tuple comprised of the real numbers ${\alpha }_{i_1\dots i_n}$ is called the scaling vector and it is denoted by $\alpha$. We define

$${\parallel \alpha \parallel }_{\infty }=max\{|{\alpha }_{i_1\dots i_n}|:(i_1,\dots ,i_n)\in \prod _{k=1}^n{\mathsf{\Sigma }}_{N_k}\}.$$

The main objective in this section is to choose the scale vector $\alpha$ and base function b in (5) so that the Read-Bajraktarević (RB) operator $T_f$ is a well-defined map, and, in fact, $T_f$ is a contraction map on the function $\mathbb{X}$ or a suitable subspace of $\mathbb{X}$. It is worth to emphasize that throughout the current note, a partition $\mathsf{\Delta }$ of the hyperrectangle $\mathsf{\Omega }$ is chosen as mentioned in the previous section.

Theorem 1.

Let $f\in {\mathcal{C}}^m\left(\mathsf{\Omega }\right)$ and define

$${\mathcal{C}}_f^m\left(\mathsf{\Omega }\right):=\left\{g\in {\mathcal{C}}^m\left(\mathsf{\Omega }\right):g\left(X\right)=f\left(X\right)\forall X\in \partial \mathsf{\Omega }\right\}.$$

Suppose that the scaling vector α is so chosen that

$$\underset{(i_1,\dots ,i_n)\in {\prod }_{k=1}^n{\mathsf{\Sigma }}_{N_k}}{max}\left\{\frac{|{\alpha }_{i_1\dots i_n}|}{{\prod }_{k=1}^n{\left|a_{k,i_k}\right|}^m}\right\}<1$$

and $b\in {\mathcal{C}}_f^m\left(\mathsf{\Omega }\right)$.

Then the following hold.

• The map $T_f$ given in (5) is well-defined on ${\mathcal{C}}_f^m\left(\mathsf{\Omega }\right)$.
• In fact, $T_f:{\mathcal{C}}_f^m\left(\mathsf{\Omega }\right)\to {\mathcal{C}}_f^m\left(\mathsf{\Omega }\right)\subset {\mathcal{C}}^m\left(\mathsf{\Omega }\right)$ is a contraction map.
• As a consequence, by the Banach fixed point theorem, there exists a unique function $f_{\mathsf{\Delta },b}^{\alpha }\in {\mathcal{C}}_f^m\left(\mathsf{\Omega }\right)$ such that

  $$D^l\left(f_{\mathsf{\Delta },b}^{\alpha }\right)(x_{1,i_1},x_{2,i_2},\dots ,x_{n,i_n})=D^l\left(f\right)(x_{1,i_1},x_{2,i_2},\dots ,x_{n,i_n}),$$
  for all $(i_1,\dots ,i_n)\in {\prod }_{k=1}^n{\mathsf{\Sigma }}_{N_k,0}$ and multi-index l with $\left|l\right|\le m.$ Moreover, the function $f_{\mathsf{\Delta },b}^{\alpha }$ and its derivatives satisfy the self-referential equations given by

  $$\begin{array}{cc}\hfill D^l\left(f_{\mathsf{\Delta },b}^{\alpha }\right)\left(X\right)& =D^l\left(f\right)\left(X\right)+\frac{{\alpha }_{i_1\dots i_n}}{{\prod }_{k=1}^n{a}_{k,i_k}^{l_k}}\left(D^l(f_{\mathsf{\Delta },b}^{\alpha }-b)\right)\left(u_{i_1\dots i_n}^{-1}\left(X\right)\right),\hfill \end{array}$$

  (6)
  for all $X\in {\prod }_{k=1}^n{I}_{k,i_k}$, $(i_1,\dots ,i_n)\in {\prod }_{k=1}^n{\mathsf{\Sigma }}_{N_k}$ and multi-index l with $\left|l\right|\le m.$

Proof. 

We shall first show that $T_f$ is well-defined on ${\mathcal{C}}_f^m\left(\mathsf{\Omega }\right)$, that is, we show that $T_f\left(g\right)\in {\mathcal{C}}_f^m\left(\mathsf{\Omega }\right)$ for all $g\in {\mathcal{C}}_f^m\left(\mathsf{\Omega }\right).$

Let $g\in {\mathcal{C}}_f^m\left(\mathsf{\Omega }\right)$ and $X=(x_1,\dots ,x_r,\dots ,x_n)\in {\prod }_{k=1}^n{I}_{k,i_k}$ be such that $x_r\in I_{r,i_r}\cap I_{r,i_r+1}$ for some $r\in {\mathsf{\Sigma }}_n$ and $i_r\in \mathrm{int}{\mathsf{\Sigma }}_{N_r,0}.$

Note that this is possible only when $x_r=x_{r,i_r}$ and in that case, by (3), we have

$$\left(u_{1,i_1}^{-1}\left(x_1\right),\dots ,u_{r,i_r}^{-1}\left(x_{r,i_r}\right),\dots ,u_{n,i_n}^{-1}\left(x_n\right)\right)=\left(u_{1,i_1}^{-1}\left(x_1\right),\dots ,u_{r,i_r+1}^{-1}\left(x_{r,i_r}\right),\dots ,u_{n,i_n}^{-1}\left(x_n\right)\right),$$

and $u_{i_1\dots i_n}^{-1}\left(X\right)\in \partial \mathsf{\Omega }.$ So, by the specified choice of b, we have

$$D^l(g-b)\left(u_{1,i_1}^{-1}\left(x_1\right),\dots ,u_{r,i_r}^{-1}\left(x_{r,i_r}\right),\dots ,u_{1,i_1}^{-1}\left(x_n\right)\right)=0,$$

for all multi-index l with $\left|l\right|\le m.$ Thus,

$$\begin{array}{cc}\hfill & D^l\left(T_f\left(g\right)\right)(x_1,\dots ,x_r,\dots ,x_n)\hfill \\ & =D^l\left(f\right)(x_1,\dots ,x_r,\dots ,x_n)\hfill \\ \hfill & +\frac{{\alpha }_{i_1\dots i_n}}{{\prod }_{k=1}^n{a}_{k,i_k}^{l_k}}\left[D^l(g-b)\right]\left(u_{1,i_1}^{-1}\left(x_1\right),\dots ,u_{r,i_r}^{-1}\left(x_{r,i_r}\right),\dots ,u_{1,i_1}^{-1}\left(x_n\right)\right)\hfill \\ \hfill & =D^l\left(f\right)(x_1,\dots ,x_r,\dots ,x_n)\hfill \\ \hfill & +\frac{{\alpha }_{i_1\dots i_n}}{{\prod }_{k=1}^n{a}_{k,i_k}^{l_k}}\left[D^l(g-b)\right]\left(u_{1,i_1}^{-1}\left(x_1\right),\dots ,u_{r,i_r}^{-1}\left(x_{r,i_r+1}\right),\dots ,u_{1,i_1}^{-1}\left(x_n\right)\right)\hfill \\ \hfill & =D^l\left(f\right)(x_1,\dots ,x_r,\dots ,x_n).\hfill \end{array}$$

That is, $D^l\left(T_f\left(g\right)\right)\left(X\right)=D^l\left(f\right)\left(X\right)$ irrespective of whether $x_r$ is considered as a point in $I_{r,i_r}$ or as a point in $I_{r,i_r+1}.$ The above observation also yields the following:

• $D^l\left(T_f\left(g\right)\right)\left(X\right)=D^l\left(f\right)\left(X\right)$ for all $X\in \partial \mathsf{\Omega }$ and $\left|l\right|\le m.$
• $D^l\left(T_f\left(g\right)\right)(x_{1,i_1},\dots ,x_{n,i_n})=D^l\left(f\right)(x_{1,i_1},\dots ,x_{n,i_n})$ for all $(i_1,\dots ,i_n)\in {\prod }_{k=1}^n{\mathsf{\Sigma }}_{N_k}$ and $\left|l\right|\le m.$

In particular, $T_f\left(g\right)\in {\mathcal{C}}_f^m\left(\mathsf{\Omega }\right)$.

Next, let $g,h\in {\mathcal{C}}_f^m\left(\mathsf{\Omega }\right)$ and l be a multi-index with $\left|l\right|\le m.$ Then

$$\begin{array}{cc}\hfill \left|D^l[T_f\left(g\right)-T_f\left(h\right)]\left(X\right)\right|& =\left|\frac{{\alpha }_{i_1\dots i_n}}{{\prod }_{k=1}^n{a}_{k,i_k}^{l_k}}{D}^l(g-h)\left(u_{i_1\dots i_n}^{-1}\left(X\right)\right)\right|\hfill \\ \hfill & \le \underset{(i_1,\dots ,i_n)\in {\prod }_{k=1}^n{\mathsf{\Sigma }}_{N_k}}{max}\left\{\frac{|{\alpha }_{i_1\dots i_n}|}{{\prod }_{k=1}^n{\left|a_{k,i_k}\right|}^m}\right\}{\parallel D^l(g-h)\parallel }_{\infty }.\hfill \end{array}$$

Taking sum over all $\left|l\right|\le m$, we get

$${\parallel T_f\left(g\right)-T_f\left(h\right)\parallel }_{{\mathcal{C}}^m\left(\mathsf{\Omega }\right)}\le \underset{(i_1,\dots ,i_n)\in {\prod }_{k=1}^n{\mathsf{\Sigma }}_{N_k}}{max}\left\{\frac{|{\alpha }_{i_1\dots i_n}|}{{\prod }_{k=1}^n{\left|a_{k,i_k}\right|}^m}\right\}{\parallel g-h\parallel }_{{\mathcal{C}}^m\left(\mathsf{\Omega }\right)}.$$

Since, ${max}_{(i_1,\dots ,i_n)\in {\prod }_{k=1}^n{\mathsf{\Sigma }}_{N_k}}\left\{\frac{|{\alpha }_{i_1\dots i_n}|}{{\prod }_{k=1}^n{\left|a_{k,i_k}\right|}^m}\right\}<1,$ the map $T_f:{\mathcal{C}}_f^m\left(\mathsf{\Omega }\right)\to {\mathcal{C}}_f^m\left(\mathsf{\Omega }\right)$ is a contraction. Rest of the claim follows by a simple application of the Banach fixed point theorem. □

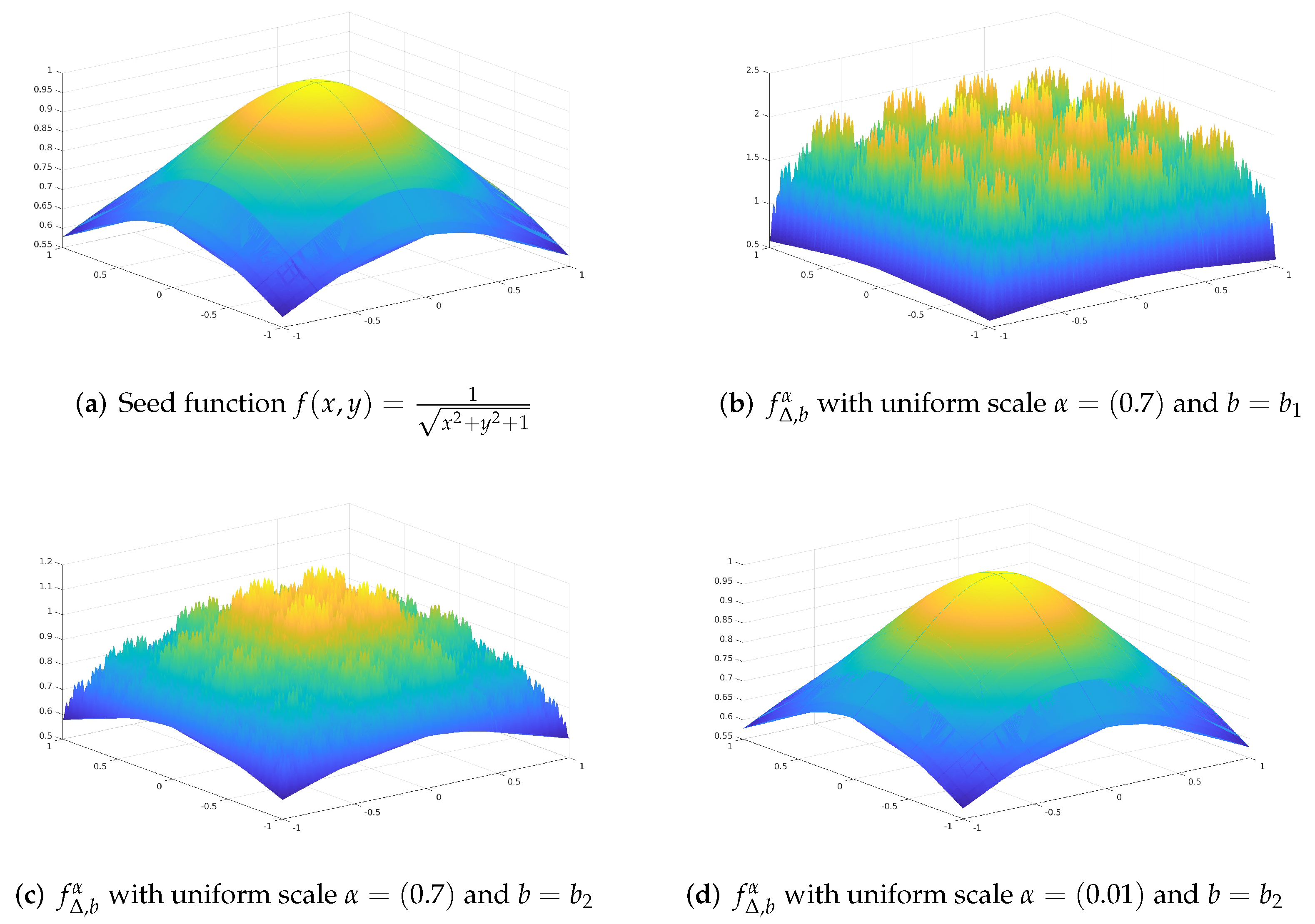
Example 1.

Let us consider the surface in${\mathbb{R}}^3$defined by the bivariate function$f(x,y)=\frac{1}{\sqrt{x^2+y^2+1}}$for all$(x,y)\in [-1,1]\times [-1,1]$and a mesh partition$\mathsf{\Delta }=\{-1,-0.5,0,0.5,1\}\times \{-1,-0.5,0,0.5,1\}$of the square$[-1,1]\times [-1,1].$Fractal functions$f_{\mathsf{\Delta },b}^{\alpha }$corresponding tofassociated with different choices of scale vector$\alpha$and base function b are shown below.

Let us consider two base functions as follows:

$$b_1(x,y)=1-(x-1)(x+1)(y-1)(y+1)f(x,y),$$

and

$$\begin{array}{cc}\hfill b_2(x,y)=& \frac{1}{2}\left((x+1)f(1,y)-(x-1)f(-1,y)+(y+1)f(x,1)-(y-1)f(x,-1)\right)\hfill \\ \hfill & -\frac{1}{4}\left((x+1)(y+1)f(1,1)-(x-1)(y+1)f(-1,1)\right)\hfill \\ \hfill & -\frac{1}{4}\left((x-1)(y-1)f(-1,-1)-(x+1)(y-1)f(1,-1)\right).\hfill \end{array}$$

Figure 1a is the graph of the germ function $f(x,y)=\frac{1}{\sqrt{x^2+y^2+1}}.$Figure 1b is the graph of fractal perturbation $f_{\mathsf{\Delta },b}^{\alpha }$ with base function $b=b_1$ and uniform scale vector $\alpha$, where ${\alpha }_{i_1{i}_2}=0.7$ for all $i_k\in {\mathsf{\Sigma }}_4$ for $k=1,2$. Figure 1c depicts the graph of $f_{\mathsf{\Delta },b}^{\alpha }$ with base function $b=b_2$ and uniform scale vector $\alpha$ as taken previously. Finally, Figure 1d displays the graph of $f_{\mathsf{\Delta },b}^{\alpha }$ with base function $b=b_2$ and uniform scale vector $\alpha$, where ${\alpha }_{i_1{i}_2}=0.01$. In this case, the parameters satisfy the conditions prescribed in Theorem 1, for $m=1$. Thus, Figure 1a,b corroborate the technique demonstrated for the construction of smoothness preserving fractal functions in Theorem 1.

Theorem 2.

Let $f\in {\mathcal{C}}^{m,\sigma }\left(\mathsf{\Omega }\right)$ and define

$${\mathcal{C}}_f^{m,\sigma }\left(\mathsf{\Omega }\right):=\left\{g\in {\mathcal{C}}^{m,\sigma }\left(\mathsf{\Omega }\right):g\left(X\right)=f\left(X\right)\forall X\in \partial \mathsf{\Omega }\right\}.$$

Choose the scale vector satisfying

$$\underset{(i_1,\dots ,i_n)\in {\prod }_{k=1}^n{\mathsf{\Sigma }}_{N_k}}{max}\left\{\frac{|{\alpha }_{i_1\dots i_n}|}{{\prod }_{k=1}^n{\left|a_{k,i_k}\right|}^{m+\sigma }}\right\}<1$$

(7)

and the base function $b\in {\mathcal{C}}_f^{m,\sigma }\left(\mathsf{\Omega }\right)$. Then the RB operator $T_f$ defined in (5) is a contraction on ${\mathcal{C}}_f^{m,\sigma }\left(\mathsf{\Omega }\right)$, and its unique fixed point $f_{\mathsf{\Delta },b}^{\alpha }$ satisfies the self-referential Equation (6).

Proof. 

Using Theorem 1 we see that $T_f\left(g\right)\in {\mathcal{C}}_f^m\left(\mathsf{\Omega }\right)$ for all $g\in {\mathcal{C}}_f^{m,\sigma }\left(\mathsf{\Omega }\right)$. We shall show that for all multi-index l with $\left|l\right|=m$, $D^l\left(T_f\left(g\right)\right)$ is Hölder continuous with exponent $\sigma$. Towards this, let $X,Y\in {\prod }_{k=1}^n{I}_{k,i_k}$ be two points in the same rectangular mesh. We have

$$\begin{array}{cc}\hfill & |D^l\left(T_f\left(g\right)\right)\left(X\right)-D^l\left(T_f\left(g\right)\right)\left(Y\right)|\hfill \\ & =\left|\frac{{\alpha }_{i_1\dots i_n}}{{\prod }_{k=1}^n{a}_{k,i_k}^{l_k}}\left[D^l(g-b)\left(u_{i_1\dots i_n}^{-1}\left(X\right)\right)-D^l(g-b)\left(u_{i_1\dots i_n}^{-1}\left(Y\right)\right)\right]\right|\hfill \\ \hfill & \le \frac{|{\alpha }_{i_1\dots i_n}|}{{\prod }_{k=1}^n{\left|a_{k,i_k}\right|}^{l_k}}|D^l\left(g\right)\left(u_{i_1\dots i_n}^{-1}\left(X\right)\right)-D^l\left(g\right)\left(u_{i_1\dots i_n}^{-1}\left(Y\right)\right)|\hfill \\ \hfill & +\frac{|{\alpha }_{i_1\dots i_n}|}{{\prod }_{k=1}^n{\left|a_{k,i_k}\right|}^{l_k}}|D^l\left(b\right)\left(u_{i_1\dots i_n}^{-1}\left(X\right)\right)-D^l\left(b\right)\left(u_{i_1\dots i_n}^{-1}\left(Y\right)\right)|\hfill \\ \hfill & \le \frac{C_{D^l\left(g\right)}\left|{\alpha }_{i_1\dots i_n}\right|}{{\prod }_{k=1}^n{\left|a_{k,i_k}\right|}^{l_k}}{\parallel u_{i_1\dots i_n}^{-1}\left(X\right)-u_{i_1\dots i_n}^{-1}\left(Y\right)\parallel }^{\sigma }\hfill \\ \hfill & +\frac{C_{D^l\left(b\right)}\left|{\alpha }_{i_1\dots i_n}\right|}{{\prod }_{k=1}^n{\left|a_{k,i_k}\right|}^{l_k}}{\parallel u_{i_1\dots i_n}^{-1}\left(X\right)-u_{i_1\dots i_n}^{-1}\left(Y\right)\parallel }^{\sigma }\hfill \\ \hfill & =\left[\frac{C_{D^l\left(g\right)}\left|{\alpha }_{i_1\dots i_n}\right|}{{\prod }_{k=1}^n{\left|a_{k,i_k}\right|}^{l_k}}+\frac{C_{D^l\left(b\right)}\left|{\alpha }_{i_1\dots i_n}\right|}{{\prod }_{k=1}^n{\left|a_{k,i_k}\right|}^{l_k}}\right]{\parallel u_{i_1\dots i_n}^{-1}\left(X\right)-u_{i_1\dots i_n}^{-1}\left(Y\right)\parallel }^{\sigma }\hfill \\ \hfill & \le \underset{(i_1,\dots ,i_n)\in {\prod }_{k=1}^n{\mathsf{\Sigma }}_{N_k}}{max}\frac{|{\alpha }_{i_1\dots i_n}|}{{\prod }_{k=1}^n{\left|a_{k,i_k}\right|}^{m+\sigma }}\left[C_{D^l\left(g\right)}+C_{D^l\left(b\right)}\right]{\parallel X-Y\parallel }^{\sigma },\hfill \end{array}$$

where $C_{D^l\left(g\right)}$ and $C_{D^l\left(b\right)}$ denote the Hölder constants of $D^l\left(g\right)$ and $D^l\left(b\right)$, respectively. If X and Y lie in two distinct but in adjacent meshes, then by taking point on their common boundary and repeating the above steps we get

$$\begin{array}{cc}\hfill & |D^l\left(T_f\left(g\right)\right)\left(X\right)-D^l\left(T_f\left(g\right)\right)\left(Y\right)|\hfill \\ & \le 2\underset{(i_1,\dots ,i_n)\in {\prod }_{k=1}^n{\mathsf{\Sigma }}_{N_k}}{max}\frac{|{\alpha }_{i_1\dots i_n}|}{{\prod }_{k=1}^n{\left|a_{k,i_k}\right|}^{m+\sigma }}[C_{D^l\left(g\right)}+C_{D^l\left(b\right)}]{\parallel X-Y\parallel }^{\sigma }.\hfill \end{array}$$

Since the total number of rectangular meshes is ${\prod }_{k=1}^n{N}_k,$ for any $X,Y\in \mathsf{\Omega }$, we have

$$\begin{array}{cc}\hfill & |D^l\left(T_f\left(g\right)\right)\left(X\right)-D^l\left(T_f\left(g\right)\right)\left(Y\right)|\hfill \\ & \le \left(\prod _{k=1}^n{N}_k\right)\underset{(i_1,\dots ,i_n)\in {\prod }_{k=1}^n{\mathsf{\Sigma }}_{N_k}}{max}\frac{|{\alpha }_{i_1\dots i_n}|}{{\prod }_{k=1}^n{\left|a_{k,i_k}\right|}^{m+\sigma }}[C_{D^l\left(g\right)}+C_{D^l\left(b\right)}]{\parallel X-Y\parallel }^{\sigma },\hfill \end{array}$$

which shows that $T_f\left({\mathcal{C}}_f^{m,\sigma }\left(\mathsf{\Omega }\right)\right)\subseteq {\mathcal{C}}_f^{m,\sigma }\left(\mathsf{\Omega }\right)$.

A similar computation reveals also that the map $T_f:{\mathcal{C}}_f^{m,\sigma }\left(\mathsf{\Omega }\right)\to {\mathcal{C}}_f^{m,\sigma }\left(\mathsf{\Omega }\right)$ is a contraction map, completing the proof. □

Corollary 1.

Let$f:\mathsf{\Omega }\to \mathbb{R}$be a Hölder continuous function with exponent$\sigma$. Assume that a scaling vector$\alpha$is so chosen that

$$\underset{(i_1,\dots ,i_n)\in {\prod }_{k=1}^n{\mathsf{\Sigma }}_{N_k}}{max}\left\{\frac{|{\alpha }_{i_1\dots i_n}|}{{\prod }_{k=1}^n{\left|a_{k,i_k}\right|}^{\sigma }}\right\}<1$$

and the parameter mapbis a Hölder continuous function with exponent$\sigma$and$b\left(X\right)=f\left(X\right)$for all$X\in \partial \mathsf{\Omega }$. Then the Hausdorff dimension of the graph of the corresponding self-referential function$f_{\mathsf{\Delta },b}^{\alpha }$satisfies

$$n\le {dim}_H\left(\mathrm{Gr}\left(f_{\mathsf{\Delta },b}^{\alpha }\right)\right)\le n+1-\sigma .$$

Proof. 

With the stated hypotheses on $\alpha$ and b, it follows from the previous theorem (with $m=0$) that the self-referential counterpart $f_{\mathsf{\Delta },b}^{\alpha }$ of f is a Hölder continuous function with exponent $\sigma$. Define a map $A:\mathrm{Gr}\left(f_{\mathsf{\Delta },b}^{\alpha }\right)\to \mathsf{\Omega }$ by

$$A\left(x,f_{\mathsf{\Delta },b}^{\alpha }\left(x\right)\right)=x,$$

where we endow $\mathrm{Gr}\left(f_{\mathsf{\Delta },b}^{\alpha }\right)\subseteq {\mathbb{R}}^{n+1}$ and $\mathsf{\Omega }\subseteq {\mathbb{R}}^n$ with the usual Euclidean norm. It is plain to see that A is a surjective Lipschitz map. From fundamental properties of the Hausdorff dimension given in ([38], Theorem 2, Items (5), (8)) we have

$$n={dim}_H\left(\mathsf{\Omega }\right)={dim}_H\left(A\left(\mathrm{Gr}(f_{\mathsf{\Delta },b}^{\alpha }\right)\right))\le {dim}_H\left(\mathrm{Gr}\left(f_{\mathsf{\Delta },b}^{\alpha }\right)\right).$$

For the desired upper bound, let us recall that the Hausdorff dimension of the graph of a Hölder continuous function with Hölder exponent $s\in (0,1]$ whose domain is a compact subset of ${\mathbb{R}}^n$ with the Hausdorff dimension equal to d is less than or equal to $min\{d+1-s,\frac{d}{s}\}$([39], Chapter 10). Therefore,

$${dim}_H\left(\mathrm{Gr}\left(f_{\mathsf{\Delta },b}^{\alpha }\right)\right)\le n+1-\sigma ,$$

completing the proof. □

Theorem 3.

Let $f\in {\mathcal{L}}^p\left(\mathsf{\Omega }\right)$ for $0<p\le \infty .$ Suppose the scaling vector α is so chosen that

$$\left\{\begin{array}{cc}{\left[\sum _{i_n=1}^{N_n}\dots \sum _{i_1=1}^{N_1}(\prod _{k=1}^n|a_{k,i_k}\left|\right)|{\alpha }_{i_1\dots i_n}{|}^p\right]}^{1/p}<1,\hfill & \mathrm{for}1\le p<\infty .\hfill \\ {\parallel \alpha \parallel }_{\infty }<1,\hfill & \mathrm{for}p=\infty .\hfill \\ \left[\sum _{i_n=1}^{N_n}\dots \sum _{i_1=1}^{N_1}(\prod _{k=1}^n|a_{k,i_k}\left|\right)|{\alpha }_{i_1\dots i_n}{|}^p\right]<1,\hfill & \mathrm{for}0<p<1.\hfill \end{array}\right.$$

(8)

Then $T_f$ defined in (5) maps ${\mathcal{L}}^p\left(\mathsf{\Omega }\right)$ to ${\mathcal{L}}^p\left(\mathsf{\Omega }\right)$. Further, $T_f$ is a contraction map and hence by the Banach fixed point theorem, there exists a unique $f_{\mathsf{\Delta },b}^{\alpha }\in {\mathcal{L}}^p\left(\mathsf{\Omega }\right)$ such that

$$f_{\mathsf{\Delta },b}^{\alpha }\left(X\right)=f\left(X\right)+{\alpha }_{i_1\dots i_n}(f_{\mathsf{\Delta },b}^{\alpha }-b)\left(u_{i_1\dots i_n}^{-1}\left(X\right)\right),$$

for $X\in {\prod }_{k=1}^n{I}_{k,i_k},$ and $(i_1,\dots ,i_n)\in {\prod }_{k=1}^n{\mathsf{\Sigma }}_{N_k}.$

Proof. 

Using the stated hypotheses, it is easy to verify that the operator $T_f:{\mathcal{L}}^p\left(\mathsf{\Omega }\right)\to {\mathcal{L}}^p\left(\mathsf{\Omega }\right)$ is well-defined. What remains is to show that $T_f$ is a contraction map. To this end, let $g,h\in {\mathcal{L}}^p\left(\mathsf{\Omega }\right),$$1\le p<\infty .$ We have

$$\begin{array}{cc}\hfill \parallel T_f\left(g\right)-T_f{\left(h\right)\parallel }_p^p& ={\int }_{\mathsf{\Omega }}{\left|(T_f\left(g\right)-T_f\left(h\right))\left(X\right)\right|}^p\mathrm{d}X\hfill \\ \hfill & =\sum _{i_n=1}^{N_n}\dots \sum _{i_1=1}^{N_1}{\int }_{X\in {\prod }_{k=1}^n{I}_{k,i_k}}|{\alpha }_{i_1\dots i_n}(g-h)\left(u_{i_1\dots i_n}^{-1}\left(X\right)\right){|}^p\mathrm{d}X\hfill \\ \hfill & =\sum _{i_n=1}^{N_n}\dots \sum _{i_1=1}^{N_1}\left(\prod _{k=1}^n\left|a_{k,i_k}\right|\right){\left|{\alpha }_{i_1\dots i_n}\right|}^p{\int }_{\mathsf{\Omega }}{\left|(g-h)\left(\tilde{X}\right)\right|}^p\mathrm{d}\tilde{X}\hfill \\ \hfill & =\left[\sum _{i_n=1}^{N_n}\dots \sum _{i_1=1}^{N_1}\left(\prod _{k=1}^n\left|a_{k,i_k}\right|\right){|{\alpha }_{i_1\dots i_n}|}^p\right]{\parallel g-h\parallel }_p^p\hfill \end{array}$$

Thus,

$${\parallel T_f\left(g\right)-T_f\left(h\right)\parallel }_p={\left[\sum _{i_n=1}^{N_n}\dots \sum _{i_1=1}^{N_1}\left(\prod _{k=1}^n\left|a_{k,i_k}\right|\right)\left|{\alpha }_{i_1\dots i_n}\right|{}^p\right]}^{1/p}{\parallel g-h\parallel }_p,$$

proving the claim for the case $1\le p<\infty$. The other cases can be dealt similarly. □

Next, let us construct self-referential functions associated with a function $f\in {\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right).$ First, let us recall the following result, popularly known as the Leibniz theorem.

If $f\in {\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right)$ and $\varphi$ is infinitely differentiable on $\mathsf{\Omega }$, then $\varphi f\in {\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right)$ and

$$D^l\left(\varphi f\right)=\sum _{q=0}^l\left(\genfrac{}{}{0pt}{}{l}{p}\right)D^p\left(\varphi \right)D^{l-q}\left(f\right),\forall \left|l\right|\le m.$$

Theorem 4.

Let $f\in {\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right)$ for $1\le p\le \infty$. Suppose that the base function $b\in {\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right)$ and the scaling vector is chosen so that

$$\left\{\begin{array}{cc}{\left[\sum _{i_n=1}^{N_n}\dots \sum _{i_1=1}^{N_1}\frac{|{\alpha }_{i_1\dots i_n}{|}^p}{{\prod }_{k=1}^n{\left|a_{k,i_k}\right|}^{mp-1}}\right]}^{1/p}<1,\hfill & \mathrm{for}1\le p<\infty .\hfill \\ max\{\frac{|{\alpha }_{i_1\dots i_n}|}{{\prod }_{k=1}^n{\left|a_{k,i_k}\right|}^m}:(i_1,\dots ,i_n)\in \prod _{k=1}^n{\mathsf{\Sigma }}_{N_k}\}<1,\hfill & \mathrm{for}p=\infty .\hfill \end{array}\right.$$

(9)

Then the RB operator $T_f$ given in (5) is a contraction map on ${\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right).$ Consequently, $T_f$ has a unique fixed point $f_{\mathsf{\Delta },b}^{\alpha }$.

Proof. 

A routine computation yields that the RB operator is well-defined and it maps the space ${\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right)$ into itself. We shall just show that it is a contraction on ${\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right).$ To this end, let $1\le p<\infty$ and l be a multi-index with $\left|l\right|\le m.$ We note that

$$\begin{array}{cc}\hfill & \parallel D^l\left[T_f\left(g\right)-T_f\left(h\right)\right]{\parallel }_p^p\hfill \\ & ={\int }_{\mathsf{\Omega }}|D^l[T_f\left(g\right)-T_f\left(h\right)]\left(X\right){|}^p\mathrm{d}X\hfill \\ \hfill & ={\int }_{\mathsf{\Omega }}|D^l[T_f\left(g\right)-T_f\left(h\right)]\left(X\right){|}^p\mathrm{d}X\hfill \\ \hfill & =\sum _{i_n=1}^{N_n}\dots \sum _{i_1=1}^{N_1}{\int }_{{\prod }_{k=1}^n{I}_{k,i_k}}|D^l[T_f\left(g\right)-T_f\left(h\right)]\left(X\right){|}^p\mathrm{d}X\hfill \\ \hfill & =\sum _{i_n=1}^{N_n}\dots \sum _{i_1=1}^{N_1}{\int }_{{\prod }_{k=1}^n{I}_{k,i_k}}|D^l\left[{\alpha }_{i_1\dots i_n}(g-h)\left(u_{i_1\dots i_n}^{-1}\left(X\right)\right)\right]{|}^p\mathrm{d}X\hfill \\ \hfill & =\sum _{i_n=1}^{N_n}\dots \sum _{i_1=1}^{N_1}{\left|{\alpha }_{i_1\dots i_n}\right|}^p{\int }_{{\prod }_{k=1}^n{I}_{k,i_k}}|\left[\frac{1}{{\prod }_{k=1}^n{a}_{k,i_k}^{l_k}}{D}^l(g-h)\left(u_{i_1\dots i_n}^{-1}\left(X\right)\right)\right]{|}^p\mathrm{d}X\hfill \\ \hfill & =\sum _{i_n=1}^{N_n}\dots \sum _{i_1=1}^{N_1}\frac{|{\alpha }_{i_1\dots i_n}{|}^p}{{\prod }_{k=1}^n{\left|a_{k,i_k}\right|}^{p{l}_k-1}}{\int }_{\mathsf{\Omega }}|D^l(g-h)\left(X^{\prime }\right){|}^p\mathrm{d}{X}^{\prime }\hfill \\ \hfill & =\left(\sum _{i_n=1}^{N_n}\dots \sum _{i_1=1}^{N_1}\frac{|{\alpha }_{i_1\dots i_n}{|}^p}{{\prod }_{k=1}^n{\left|a_{k,i_k}\right|}^{p{l}_k-1}}\right){\parallel D^l(g-h)\parallel }_p^p.\hfill \end{array}$$

Thus, for a multi-index l with $\left|l\right|\le m$ we have

$${\parallel D^l[T_f\left(g\right)-T_f\left(h\right)]\parallel }_p={\left(\sum _{i_n=1}^{N_n}\dots \sum _{i_1=1}^{N_1}\frac{|{\alpha }_{i_1\dots i_n}{|}^p}{{\prod }_{k=1}^n{\left|a_{k,i_k}\right|}^{p{l}_k-1}}\right)}^{\frac{1}{p}}\parallel D^l(g-h){\parallel }_p.$$

Hence,

$$\begin{array}{cc}\hfill \parallel T_f\left(g\right)-T_f\left(h\right){\parallel }_{{\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right)}& =\sum _{\left|l\right|\le m}{\left(\sum _{i_n=1}^{N_n}\dots \sum _{i_1=1}^{N_1}\frac{|{\alpha }_{i_1\dots i_n}{|}^p}{{\prod }_{k=1}^n{\left|a_{k,i_k}\right|}^{p{l}_k-1}}\right)}^{\frac{1}{p}}{\parallel D^l(g-h)\parallel }_p\hfill \\ \hfill & \le {\left(\sum _{i_n=1}^{N_n}\dots \sum _{i_1=1}^{N_1}\frac{|{\alpha }_{i_1\dots i_n}{|}^p}{{\prod }_{k=1}^n{\left|a_{k,i_k}\right|}^{pm-1}}\right)}^{\frac{1}{p}}\sum _{\left|l\right|\le m}{\parallel D^l(g-h)\parallel }_p\hfill \\ \hfill & \le {\left(\sum _{i_n=1}^{N_n}\dots \sum _{i_1=1}^{N_1}\frac{|{\alpha }_{i_1\dots i_n}{|}^p}{{\prod }_{k=1}^n{\left|a_{k,i_k}\right|}^{pm-1}}\right)}^{\frac{1}{p}}{\parallel g-h\parallel }_{{\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right)}\hfill \end{array}$$

The rest of the theorem follows from the Banach fixed point theorem and the assumption on the scale vector. The case $p=\infty$ can be worked out similarly. □

4. Fractal Operator on Function Spaces

Let $f\in \mathbb{X}$, where $\mathbb{X}$ is a fixed function space from the list

$$\left\{{\mathcal{C}}^m\left(\mathsf{\Omega }\right),{\mathcal{L}}^p\left(\mathsf{\Omega }\right),{\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right),{\mathcal{C}}^{m,\sigma }\left(\mathsf{\Omega }\right)\right\}.$$

The results established in the previous section provide a self-referential counterpart to each $f\in \mathbb{X}$, and consequently provide an operator. That is, for a prescribed set of parameters such as the partition, scale vector and the base function, there exists a fractal operator ${\mathcal{F}}_{\mathsf{\Delta },b}^{\alpha }:\mathbb{X}\to \mathbb{X}$ defined by ${\mathcal{F}}_{\mathsf{\Delta },b}^{\alpha }\left(f\right)=f_{\mathsf{\Delta },b}^{\alpha }.$ This section intends to record a few elementary properties of the operator ${\mathcal{F}}_{\mathsf{\Delta },b}^{\alpha }:\mathbb{X}\to \mathbb{X}$, what we call a multivariate self-referential operator (fractal operator); see also [1]. We shall provide the details only for $\mathbb{X}={\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right)$, as the other spaces can be similarly dealt with. For future reference, we introduce the notation

$$K_{\alpha ,m,p}=\left\{\begin{array}{cc}\hfill & {\displaystyle {\left[\sum _{i_n=1}^{N_n}\dots \sum _{i_1=1}^{N_1}\frac{|{\alpha }_{i_1\dots i_n}{|}^p}{{\prod }_{k=1}^n{\left|a_{k,i_k}\right|}^{mp-1}}\right]}^{1/p},\mathrm{for}1\le p<\infty .}\hfill \\ \hfill & max\left\{\frac{|{\alpha }_{i_1\dots i_n}|}{{\prod }_{k=1}^n{\left|a_{k,i_k}\right|}^m}:i_k\in {\mathsf{\Sigma }}_{N_k},k\in {\mathsf{\Sigma }}_n\right\},\mathrm{for}p=\infty .\hfill \end{array}\right.$$

Proposition 1.

(Perturbation Error) Let$f\in {\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right)$. Suppose that a partition$\mathsf{\Delta }$of the hyperrectangle$\mathsf{\Omega }$, base function$b\in {\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right)$, and scale vector$\alpha$be chosen as in Theorem 4. Then

$${\parallel f_{\mathsf{\Delta },b}^{\alpha }-f\parallel }_{{\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right)}\le K_{\alpha ,m,p}{\parallel f_{\mathsf{\Delta },b}^{\alpha }-b\parallel }_{{\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right)}.$$

(10)

Proof. 

Let us recall the self-referential equations satisfied by the fractal counterpart $f_{\mathsf{\Delta },b}^{\alpha }\in {\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right)$ and its derivatives

$$\begin{array}{cc}\hfill D^l\left(f_{\mathsf{\Delta },b}^{\alpha }\right)\left(X\right)& =D^l\left(f\right)\left(X\right)+\frac{{\alpha }_{i_1\dots i_n}}{{\prod }_{k=1}^n{a}_{k,i_k}^{l_k}}{D}^l(f_{\mathsf{\Delta },b}^{\alpha }-b)\left(u_{i_1\dots i_n}^{-1}\left(X\right)\right),\hfill \end{array}$$

(11)

for all $X\in {\prod }_{k=1}^n{I}_{k,i_k}$, $(i_1,\dots ,i_n)\in {\prod }_{k=1}^n{\mathsf{\Sigma }}_{N_k}$ and multi-index l with $\left|l\right|\le m.$ Assume that $1\le p<\infty$. By simple calculations

$${\parallel D^l\left(f_{\mathsf{\Delta },b}^{\alpha }-f\right)\parallel }_p={\left(\sum _{i_n=1}^{N_n}\dots \sum _{i_1=1}^{N_1}\frac{|{\alpha }_{i_1\dots i_n}{|}^p}{{\prod }_{k=1}^n{\left|a_{k,i_k}\right|}^{p{l}_k-1}}\right)}^{\frac{1}{p}}\parallel D^l(f_{\mathsf{\Delta },b}^{\alpha }-b){\parallel }_p.$$

Therefore,

$$\begin{array}{cc}\hfill {\parallel f_{\mathsf{\Delta },b}^{\alpha }-f\parallel }_{{\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right)}=& {\left(\sum _{\left|l\right|\le m}{\parallel D^l(f_{\mathsf{\Delta },b}^{\alpha }-f)\parallel }_p^p\right)}^{\frac{1}{p}}\hfill \\ \hfill \le & {\displaystyle {\left[\sum _{i_n=1}^{N_n}\dots \sum _{i_1=1}^{N_1}\frac{|{\alpha }_{i_1\dots i_n}{|}^p}{{\prod }_{k=1}^n{\left|a_{k,i_k}\right|}^{mp-1}}\right]}^{1/p}{\parallel f_{\mathsf{\Delta },b}^{\alpha }-b\parallel }_{{\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right)}.}\hfill \end{array}$$

Similar analysis for $p=\infty$. □

Now, let us take the multivariate base function $b:\mathsf{\Omega }\to \mathbb{R}$ used in the construction of the self-referential function $f_{\mathsf{\Delta },b}^{\alpha }$ through a suitable operator $L:\mathbb{X}\to \mathbb{X}$. That is, we take $b=L\left(f\right)$ so that the conditions required for b are satisfied. In this case, the multivariate fractal operator will be denoted by ${\mathcal{F}}_{\mathsf{\Delta },L}^{\alpha }:\mathbb{X}\to \mathbb{X}.$ In what follows, we intend to record some elementary properties of the multivariate fractal operator ${\mathcal{F}}_{\mathsf{\Delta },L}^{\alpha }$.

The following proposition provides a counterpart to the linearity property of the fractal operator well explored in the setting of univariate $\alpha$-fractal functions on various function spaces; see, for instance, [11]. The proof follows almost verbatim, and hence omitted.

Proposition 2.

Let$\mathbb{X}={\mathcal{W}}^{m.p}\left(\mathsf{\Omega }\right)$and$L:\mathbb{X}\to \mathbb{X}$be a linear operator. Choose the base functionbin the construction of fractal function$f_{\mathsf{\Delta },b}^{\alpha }$via this operatorLso that$b=L\left(f\right)$. Then the corresponding fractal operator, which shall be denoted by${\mathcal{F}}_{\mathsf{\Delta },L}^{\alpha }:\mathbb{X}\to \mathbb{X}$, defined by${\mathcal{F}}_{\mathsf{\Delta },L}^{\alpha }\left(f\right)=f_{\mathsf{\Delta },L\left(f\right)}^{\alpha }$is linear.

Let X be a Banach space and $A:X\to X$ be a bounded linear operator such that $\parallel I-A\parallel <1$, where I is the identity operator on X. Then, it is well-known that A is bijective and $A^{-1}$ is bounded; see, for instance, [40]. The following result available in [41] is a generalization of the aforementioned Neumann’s lemma.

Lemma 1.

([41], Lemma 1) Let $A:X\to X$ be a linear operator on a Banach space X such that

$$\parallel A\left(x\right)-x\parallel \le {\lambda }_1\parallel x\parallel +{\lambda }_2\parallel A\left(x\right)\parallel \forall x\in X,$$

for some ${\lambda }_1$ and ${\lambda }_2\in [0,1).$ Then A is a topological automorphism (a bounded, invertible map that possesses a bounded inverse). Furthermore,

$$\begin{array}{cc}\hfill & \frac{1-{\lambda }_1}{1+{\lambda }_2}\parallel x\parallel \le \parallel A\left(x\right)\parallel \le \frac{1+{\lambda }_1}{1-{\lambda }_2}\parallel x\parallel ,\hfill \\ & \frac{1-{\lambda }_2}{1+{\lambda }_1}\parallel x\parallel \le \parallel A^{-1}\left(x\right)\parallel \le \frac{1+{\lambda }_2}{1-{\lambda }_1}\parallel x\parallel ,\forall x\in X.\hfill \end{array}$$

Proposition 3.

Let$L:{\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right)\to {\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right)$be a bounded linear operator and the scale vector$\alpha$be chosen such that$max\left\{K_{\alpha ,m,p},\parallel L\parallel K_{\alpha ,m,p}\right\}<1$. Then the linear operator${\mathcal{F}}_{\mathsf{\Delta },L}^{\alpha }:{\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right)\to {\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right)$is a topological automorphism.

Proof. 

Recall that here the base function $b=L\left(f\right)$ so that by Proposition 1 we have

$$\begin{array}{cc}\hfill \parallel {\mathcal{F}}_{\mathsf{\Delta },L}^{\alpha }\left(f\right)-f{\parallel }_{{\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right)}=& \parallel f_{\mathsf{\Delta },L\left(f\right)}^{\alpha }{-f\parallel }_{{\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right)}\hfill \\ & \le K_{\alpha ,m,p}{\parallel f_{\mathsf{\Delta },L\left(f\right)}^{\alpha }-L\left(f\right)\parallel }_{{\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right)}\hfill \\ \hfill & \le K_{\alpha ,m,p}\parallel f_{\mathsf{\Delta },L\left(f\right)}^{\alpha }{\parallel }_{{\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right)}+K_{\alpha ,m,p}{\parallel L\parallel \parallel f\parallel }_{{\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right)}\hfill \\ \hfill & =K_{\alpha ,m,p}\parallel {\mathcal{F}}_{\mathsf{\Delta },L}^{\alpha }{\left(f\right)\parallel }_{{\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right)}+K_{\alpha ,m,p}{\parallel L\parallel \parallel f\parallel }_{{\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right)}.\hfill \end{array}$$

The assertion is now immediate from the previous proposition. □

The existence of Schauder bases consisting of appropriate functions for the Sobolev spaces is quite desirable in analysis of PDEs, for instance, for demonstrating the existence of solutions of various non-linear boundary value problems. We have the following result giving a Schauder basis consisting of self-referential functions for the Sobolev space ${\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right)$. The heart of the matter is an elementary result in the theory of bases, which states that a topological isomorphism preserves Schauder bases; see, for instance, [37].

Corollary 2.

The Banach space${\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right)$has a Schauder basis consisting of multivariate self-referential functions.

Proof. 

Let ${\left\{f_m\right\}}_{m\in \mathbb{N}}$ be a Schauder basis of ${\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right)$ whose existence is established and reported, for instance, in [42,43,44]. Choose the scale function $\alpha$ and operator L as in the previous proposition so that the fractal operator ${\mathcal{F}}_{\mathsf{\Delta },L}^{\alpha }$ is a topological automorphism. As an isomorphism, in particular, an automorphism, preserves Schauder bases, we conclude that ${\left\{{\left(f_m\right)}_{\mathsf{\Delta },L}^{\alpha }\right\}}_{m\in \mathbb{N}}$, where ${\left(f_m\right)}_{\mathsf{\Delta },L}^{\alpha }={\mathcal{F}}_{\mathsf{\Delta },L}^{\alpha }\left(f_m\right)$ is a Schauder basis consisting of self-referential functions for the Banach space ${\mathcal{W}}^{m,p}\left(\mathsf{\Omega }\right)$. □

5. Fractional Integral of Continuous Multivariate $\alpha$-Fractal Function

As mentioned in the introductory section, exploration of interconnection between fractional calculus and fractal geometry has always been of interest. Our purpose in this section is limited; we shall observe that the Riemann–Liouville fractional integral of the continuous multivariate $\alpha$-fractal function is also a fractal function. A similar result regarding univariate FIF can be found in [28].

Definition 1.

[45] Let f be a continuous function on the closed and bounded hyperrectangle$\mathsf{\Omega }$in${\mathbb{R}}^n$. The left-hand-sided mixed Riemann–Liouville fractional integral of f of order$\gamma$is defined as

$$\begin{array}{cc}\hfill {\mathcal{I}}_a^{\gamma }f\left(X\right)=& \frac{1}{{\prod }_{k=1}^n\mathsf{\Gamma }\left({\gamma }_k\right)}{\int }_{a_1}^{x_1}\dots {\int }_{a_n}^{x_n}{(x_1-s_1)}^{{\gamma }_1-1}\dots {(x_n-s_n)}^{{\gamma }_n-1}\hfill \\ & .f(s_1,s_2,\cdots ,s_n)\mathrm{d}{s}_1\mathrm{d}{s}_2\cdots \mathrm{d}{s}_n,\hfill \end{array}$$

where$a=(a_1,\dots ,a_n)$is a fixed point,$X=(x_1,x_2\cdots ,x_n)$and$\gamma =({\gamma }_1,\dots ,{\gamma }_n)$with$a_k\le x_k$,${\gamma }_k>0$for each$k\in {\mathsf{\Sigma }}_n.$

Let $f\in \mathcal{C}\left(\mathsf{\Omega }\right)$. We write $f\left(X\right)=f(x_1,x_2,\cdots ,x_n)$. From Theorem 1 it follows that by choosing $b\in {\mathcal{C}}_f\left(\mathsf{\Omega }\right)$ and scaling vector $\alpha$ such that

$${\parallel \alpha \parallel }_{\infty }:=\underset{(i_1,\dots ,i_n)\in {\prod }_{k=1}^n{\mathsf{\Sigma }}_{N_k}}{max}\left|{\alpha }_{i_1\dots i_n}\right|<1,$$

the fractal counterpart $f_{\mathsf{\Delta },b}^{\alpha }$ of f belongs to $\mathcal{C}\left(\mathsf{\Omega }\right)$. Furthermore, since $f_{\mathsf{\Delta },b}^{\alpha }$ is the fixed point of the RB operator $T_f:\mathcal{C}\left(\mathsf{\Omega }\right)\to \mathcal{C}\left(\mathsf{\Omega }\right)$ defined by

$$T_f\left(g\right)\left(X\right)=f\left(X\right)+{\alpha }_{i_1\dots i_n}(g-b)\left(u_{i_1\dots i_n}^{-1}\left(X\right)\right),$$

for all $X\in {\prod }_{k=1}^n{I}_{k,i_k}$, $(i_1,\dots ,i_n)\in {\prod }_{k=1}^n{\mathsf{\Sigma }}_{N_k}$. Consequently, $f_{\mathsf{\Delta },b}^{\alpha }$ satisfies the functional equation

$$\begin{array}{cc}\hfill f_{\mathsf{\Delta },b}^{\alpha }\left(u_{i_1\dots i_n}\left(X\right)\right)& =f\left(u_{i_1\dots i_n}\left(X\right)\right)+{\alpha }_{i_1\dots i_n}(f_{\mathsf{\Delta },b}^{\alpha }-b)\left(X\right)\hfill \\ \hfill & ={\alpha }_{i_1\dots i_n}{f}_{\mathsf{\Delta },b}^{\alpha }\left(X\right)+f\left(u_{i_1\dots i_n}\left(X\right)\right)-{\alpha }_{i_1\dots i_n}b\left(X\right).\hfill \end{array}$$

Let us define

$$q_{i_1\dots i_n}\left(X\right)=f\left(u_{i_1\dots i_n}\left(X\right)\right)-{\alpha }_{i_1\dots i_n}b\left(X\right)$$

so that the self-referential equation for $f_{\mathsf{\Delta },b}^{\alpha }$ becomes

$$f_{\mathsf{\Delta },b}^{\alpha }\left(u_{i_1\dots i_n}\left(X\right)\right)={\alpha }_{i_1\dots i_n}{f}_{\mathsf{\Delta },b}^{\alpha }\left(X\right)+q_{i_1\dots i_n}\left(X\right).$$

Since the multivariate fractal function $f_{\mathsf{\Delta },b}^{\alpha }$ is continuous, we can talk about its Riemann–Liouville fractional integral. In what follows, we establish that the Riemann–Liouville fractional integral of $f_{\mathsf{\Delta },b}^{\alpha }$ is again a fractal function.

For the sake of convenience, we shall deal with the uniform scaling factor, that is, ${\alpha }_{i_1\dots i_n}=\alpha$ for all $(i_1,\dots ,i_n)\in {\prod }_{k=1}^n{\mathsf{\Sigma }}_{N_k}.$ Then, with a slight abuse of notation, the above equation reduces to

$$f_{\mathsf{\Delta },b}^{\alpha }\left(u_{i_1\dots i_n}\left(X\right)\right)=\alpha f_{\mathsf{\Delta },b}^{\alpha }\left(X\right)+q_{i_1\dots i_n}\left(X\right).$$

(12)

Theorem 5.

Let Δ be a partition of the hyperrectangle Ω in ${\mathbb{R}}^n$ and $f\in \mathcal{C}\left(\mathsf{\Omega }\right)$. Assume that $b:\mathsf{\Omega }\to \mathbb{R}$ is continuous and $b\left(X\right)=f\left(X\right)$ for all $X\in \partial \mathsf{\Omega }$, the boundary of Ω. Choose a scaling vector α such that ${\parallel \alpha \parallel }_{\infty }<1.$ Then ${\mathcal{I}}_a^{\gamma }{f}_{\mathsf{\Delta },b}^{\alpha }$, the left-hand-sided mixed Riemann–Liouville fractional integral of order γ of the self-referential function $f_{\mathsf{\Delta },b}^{\alpha }$, satisfies the following equation:

$$\begin{array}{c}\hfill {\mathcal{I}}_a^{\gamma }{f}_{\mathsf{\Delta },b}^{\alpha }\left(u_{i_1\dots i_n}\left(X\right)\right)=\left(\alpha \prod _{k=1}^n{a}_{k,i_k}^{{\gamma }_k}\right){\mathcal{I}}_a^{\gamma }{f}_{\mathsf{\Delta },b}^{\alpha }\left(X\right)+{\widehat{q}}_{i_1\dots i_n}\left(X\right),\end{array}$$

where

$$\begin{array}{cc}\hfill & {\widehat{q}}_{i_1\dots ,i_n}\left(X\right)\hfill \\ \hfill =& \frac{1}{{\prod }_{k=1}^n\mathsf{\Gamma }\left({\gamma }_k\right)}\sum _{k=0}^{n-1}\left(\prod _{j=0}^k{a}_{n-j,i_{n-j}}^{{\gamma }_{n-j}}\right){\int }_{a_1}^{u_{1,i_1}\left(x_1\right)}\dots {\int }_{a_{n-k}}^{u_{n-k,i_{n-k}}\left(x_{n-k}\right)}{\int }_{a_{n-k+1}}^{x_{n-k+1}}\dots {\int }_{a_n}^{x_n}\hfill \\ \hfill & {\left(u_{1,i_1}\left(x_1\right)-s_1\right)}^{{\gamma }_1-1}\dots {\left(u_{n-k,i_{n-k}}\left(x_{n-k}\right)-s_{n-k}\right)}^{{\gamma }_{n-k}-1}{(x_{n-k+1}-s_{n-k+1})}^{{\gamma }_{n-k+1}-1}\hfill \\ \hfill & \dots {(x_n-s_n)}^{{\gamma }_n-1}{f}_{\mathsf{\Delta },b}^{\alpha }\left(s_1,\dots ,s_{n-k},u_{n-k+1,i_{n-k+1}}\left(s_{n-k+1}\right),\dots ,u_{n,i_n}\left(s_n\right)\right)\mathrm{d}{s}_1\dots \mathrm{d}{s}_n+\hfill \\ \hfill & \left(\prod _{k=1}^n{a}_{k,i_k}^{{\gamma }_k}\right){\mathcal{I}}_a^{\gamma }{q}_{i_1\dots i_n}\left(X\right).\hfill \end{array}$$

Proof. 

According to Theorem 1, it follows that $f_{\mathsf{\Delta },b}^{\alpha }$ is continuous on $\mathsf{\Omega }$ and satisfies the equation

$$f_{\mathsf{\Delta },b}^{\alpha }\left(u_{i_1\dots i_n}\left(X\right)\right)=\alpha f_{\mathsf{\Delta },b}^{\alpha }\left(X\right)+q_{i_1\dots i_n}\left(X\right),\forall X\in \mathsf{\Omega }.$$

Hence,

$$\begin{array}{cc}\hfill {\mathcal{I}}_a^{\gamma }{f}_{\mathsf{\Delta },b}^{\alpha }\left(u_{i_1\dots i_n}\left(X\right)\right)=& \frac{1}{{\prod }_{k=1}^n\mathsf{\Gamma }\left({\gamma }_k\right)}{\int }_{a_1}^{u_{1,i_1}\left(x_1\right)}\dots {\int }_{a_n}^{u_{n,i_n}\left(x_n\right)}{\left(u_{1,i_1}\left(x_1\right)-s_1\right)}^{{\gamma }_1-1}\hfill \\ \hfill & \dots {\left(u_{n,i_n}\left(x_n\right)-s_n\right)}^{{\gamma }_n-1}{f}_{\mathsf{\Delta },b}^{\alpha }(s_1,\dots ,s_n)\mathrm{d}{s}_1\dots \mathrm{d}{s}_n\hfill \\ \hfill =& \frac{1}{{\prod }_{k=1}^n\mathsf{\Gamma }\left({\gamma }_k\right)}{\int }_{a_1}^{u_{1,i_1}\left(x_1\right)}\dots {\int }_{a_n}^{u_{n,i_n}\left(a_n\right)}{(u_{1,i_1}\left(x_1\right)-s_1)}^{{\gamma }_1-1}\hfill \\ \hfill & \dots {(u_{n,i_n}\left(x_n\right)-s_n)}^{{\gamma }_n-1}{f}_{\mathsf{\Delta },b}^{\alpha }(s_1,\dots ,s_n)\mathrm{d}{s}_1\dots \mathrm{d}{s}_n\hfill \\ \hfill & +\frac{1}{{\prod }_{k=1}^n\mathsf{\Gamma }\left({\gamma }_k\right)}{\int }_{a_1}^{u_{1,i_1}\left(x_1\right)}\dots {\int }_{u_{n,i_n}\left(a_n\right)}^{u_{n,i_n}\left(x_n\right)}{\left(u_{1,i_1}\left(x_1\right)-s_1\right)}^{{\gamma }_1-1}\hfill \\ \hfill & \dots {\left(u_{n,i_n}\left(x_n\right)-s_n\right)}^{{\gamma }_n-1}{f}_{\mathsf{\Delta },b}^{\alpha }(s_1,\dots ,s_n)\mathrm{d}{s}_1\dots \mathrm{d}{s}_n.\hfill \end{array}$$

Let us write

$$\begin{array}{cc}\hfill E_0=& \frac{1}{{\prod }_{k=1}^n\mathsf{\Gamma }\left({\gamma }_k\right)}{\int }_{a_1}^{u_{1,i_1}\left(x_1\right)}\dots {\int }_{a_n}^{u_{n,i_n}\left(a_n\right)}{\left(u_{1,i_1}\left(x_1\right)-s_1\right)}^{{\gamma }_1-1}\hfill \\ & \dots {\left(u_{n,i_n}\left(x_n\right)-s_n\right)}^{{\gamma }_n-1}{f}_{\mathsf{\Delta },b}^{\alpha }(s_1,\dots ,s_n)\mathrm{d}{s}_1\dots \mathrm{d}{s}_n,\hfill \\ \hfill {\mathcal{J}}_1=& \frac{1}{{\prod }_{k=1}^n\mathsf{\Gamma }\left({\gamma }_k\right)}{\int }_{a_1}^{u_{1,i_1}\left(x_1\right)}\dots {\int }_{u_{n,i_n}\left(a_n\right)}^{u_{n,i_n}\left(x_n\right)}{\left(u_{1,i_1}\left(x_1\right)-s_1\right)}^{{\gamma }_1-1}\hfill \\ \hfill & \dots {\left(u_{n,i_n}\left(x_n\right)-s_n\right)}^{{\gamma }_n-1}{f}_{\mathsf{\Delta },b}^{\alpha }(s_1,\dots ,s_n)\mathrm{d}{s}_1\dots \mathrm{d}{s}_n.\hfill \end{array}$$

so that

$${\mathcal{I}}_a^{\gamma }{f}_{\mathsf{\Delta },b}^{\alpha }\left(u_{i_1\dots i_n}\left(X\right)\right)=E_0+{\mathcal{J}}_1.$$

Turning our attention to ${\mathcal{J}}_1$, let us change the variable $s_n$ using the transformation $s_n=u_{n,i_n}\left(t_n\right)$. We have

$$\begin{array}{cc}\hfill {\mathcal{J}}_1=& \frac{a_{n,i_n}^{{\gamma }_n}}{{\prod }_{k=1}^n\mathsf{\Gamma }\left({\gamma }_k\right)}{\int }_{a_1}^{u_{1,i_1}\left(x_1\right)}\dots {\int }_{a_n}^{x_n}{\left(u_{1,i_1}\left(x_1\right)-s_1\right)}^{{\gamma }_1-1}\hfill \\ \hfill & \dots {(x_n-t_n)}^{{\gamma }_n-1}{f}_{\mathsf{\Delta },b}^{\alpha }\left(s_1,\dots ,u_{n,i_n}\left(t_n\right)\right)\mathrm{d}{s}_1\dots \mathrm{d}{t}_n\hfill \\ \hfill =& \frac{a_{n,i_n}^{{\gamma }_n}}{{\prod }_{k=1}^n\mathsf{\Gamma }\left({\gamma }_k\right)}{\int }_{a_1}^{u_{1,i_1}\left(x_1\right)}\dots {\int }_{a_{n-1}}^{u_{n-1,i_{n-1}}\left(x_{n-1}\right)}{\int }_{a_n}^{x_n}{\left(u_{1,i_1}\left(x_1\right)-s_1\right)}^{{\gamma }_1-1}\hfill \\ \hfill & \dots {(x_n-s_n)}^{{\gamma }_n-1}{f}_{\mathsf{\Delta },b}^{\alpha }\left(s_1,\dots ,u_{n,i_n}\left(s_n\right)\right)\mathrm{d}{s}_1\dots \mathrm{d}{s}_n.\hfill \end{array}$$

Applying similar process to the variable $s_{n-1}$ we get

$$\begin{array}{cc}\hfill {\mathcal{J}}_1=& \frac{a_{n,i_n}^{{\gamma }_n}}{{\prod }_{k=1}^n\mathsf{\Gamma }\left({\gamma }_k\right)}{\int }_{a_1}^{u_{1,i_1}\left(x_1\right)}\dots {\int }_{a_{n-1}}^{u_{n-1,i_{n-1}}\left(a_{n-1}\right)}{\int }_{a_n}^{x_n}{(u_{1,i_1}\left(x_1\right)-s_1)}^{{\gamma }_1-1}\hfill \\ \hfill & \dots {(x_n-s_n)}^{{\gamma }_n-1}{f}_{\mathsf{\Delta },b}^{\alpha }\left(s_1,\dots ,u_{n,i_n}\left(s_n\right)\right)\mathrm{d}{s}_1\dots \mathrm{d}{s}_n\hfill \\ \hfill & +\frac{a_{n,i_n}^{{\gamma }_n}}{{\prod }_{k=1}^n\mathsf{\Gamma }\left({\gamma }_k\right)}{\int }_{a_1}^{u_{1,i_1}\left(x_1\right)}\dots {\int }_{u_{n-1,i_{n-1}}\left(a_{n-1}\right)}^{u_{n-1,i_{n-1}}\left(x_{n-1}\right)}{\int }_{a_n}^{x_n}{(u_{1,i_1}\left(x_1\right)-s_1)}^{{\gamma }_1-1}\hfill \\ \hfill & \dots {(x_n-s_n)}^{{\gamma }_n-1}{f}_{\mathsf{\Delta },b}^{\alpha }\left(s_1,\dots ,u_{n,i_n}\left(s_n\right)\right)\mathrm{d}{s}_1\dots \mathrm{d}{s}_n\hfill \\ \hfill & =:E_1+{\mathcal{J}}_2.\hfill \end{array}$$

In ${\mathcal{J}}_2$, let us perform a change of variable using $s_{n-1}=u_{n-1,i_{n-1}}\left(t_{n-1}\right)$ so that

$$\begin{array}{cc}\hfill {\mathcal{J}}_2& =\frac{a_{n-1,i_{n-1}}^{{\gamma }_{n-1}}{a}_{n,i_n}^{{\gamma }_n}}{{\prod }_{k=1}^n\mathsf{\Gamma }\left({\gamma }_k\right)}{\int }_{a_1}^{u_{1,i_1}\left(x_1\right)}\dots {\int }_{a_{n-1}}^{x_{n-1}}{\int }_{a_n}^{x_n}{(u_{1,i_1}\left(x_1\right)-s_1)}^{{\gamma }_1-1}\hfill \\ \hfill & \dots {(x_{n-1}-s_{n-1})}^{{\gamma }_{n-1}-1}{(x_n-s_n)}^{{\gamma }_n-1}{f}_{\mathsf{\Delta },b}^{\alpha }\left(s_1,\dots ,u_{n-1,i_n-1}\left(s_{n-1}\right),u_{n,i_n}\left(s_n\right)\right)\mathrm{d}{s}_1\dots \mathrm{d}{s}_n.\hfill \end{array}$$

Consequently,

$${\mathcal{I}}_a^{\gamma }{f}_{\mathsf{\Delta },b}^{\alpha }\left(u_{i_1\dots i_n}\left(X\right)\right)=E_0+E_1+{\mathcal{J}}_2.$$

Proceeding in the same fashion, at the $n^{th}$ step we get

$$\begin{array}{cc}\hfill I_a^{\gamma }{f}_{\mathsf{\Delta },b}^{\alpha }\left(u_{i_1\dots i_n}\left(X\right)\right)=& \sum _{k=0}^{n-1}{E}_k+\frac{{\prod }_{k=1}^n{a}_{k,i_k}^{{\gamma }_k}}{{\prod }_{k=1}^n\mathsf{\Gamma }\left({\gamma }_k\right)}{\int }_{a_1}^{x_1}\dots {\int }_{a_{n-1}}^{x_{n-1}}{\int }_{a_n}^{x_n}{(x_1-s_1)}^{{\gamma }_1-1}\hfill \\ \hfill & \dots {(x_{n-1}-s_{n-1})}^{{\gamma }_{n-1}-1}{(x_n-s_n)}^{{\gamma }_n-1}{f}_{\mathsf{\Delta },b}^{\alpha }\left(u_{i_1\dots i_n}\left(S\right)\right)\mathrm{d}{s}_1\dots \mathrm{d}{s}_n,\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill E_k=& \frac{{\prod }_{j=0}^k{a}_{n-j,i_{n-j}}^{{\gamma }_{n-j}}}{{\prod }_{k=1}^n\mathsf{\Gamma }\left({\gamma }_k\right)}{\int }_{a_1}^{u_{1,i_1}\left(x_1\right)}\dots {\int }_{a_{n-k}}^{u_{n-k,i_{n-k}}\left(x_{n-k}\right)}{\int }_{a_{n-k+1}}^{x_{n-k+1}}\dots {\int }_{a_n}^{x_n}\hfill \\ \hfill & {\left(u_{1,i_1}\left(x_1\right)-s_1\right)}^{{\gamma }_1-1}\dots {\left(u_{n-k,i_{n-k}}\left(x_{n-k}\right)-s_{n-k}\right)}^{{\gamma }_{n-k}-1}{(x_{n-k+1}-s_{n-k+1})}^{{\gamma }_{n-k+1}-1}\hfill \\ \hfill & \dots {(x_n-s_n)}^{{\gamma }_n-1}{f}_{\mathsf{\Delta },b}^{\alpha }\left(s_1,\dots ,s_{n-k},u_{n-k+1,i_{n-k+1}}\left(s_{n-k+1}\right),\dots ,u_{n,i_n}\left(s_n\right)\right)\mathrm{d}{s}_1\dots \mathrm{d}{s}_n\hfill \end{array}$$

for $k=0,1,\dots ,n-1$, with the assumption that ${\prod }_{j=0}^0{a}_{n-j,i_{n-j}}^{{\gamma }_{n-j}}=1.$

Finally, using the functional equation

$$f_{\mathsf{\Delta },b}^{\alpha }\left(u_{i_1\dots i_n}\left(S\right)\right)=\alpha f_{\mathsf{\Delta },b}^{\alpha }\left(S\right)+q_{i_1\dots i_n}\left(S\right),$$

for all $S\in \mathsf{\Omega }$, we get

$$\begin{array}{cc}\hfill & {\mathcal{I}}_a^{\gamma }{f}_{\mathsf{\Delta },b}^{\alpha }\left(u_{i_1\dots i_n}\left(X\right)\right)\hfill \\ \hfill =& \sum _{k=0}^{n-1}{E}_k+\frac{{\prod }_{k=1}^n{a}_{k,i_k}^{{\gamma }_k}}{{\prod }_{k=1}^n\mathsf{\Gamma }\left({\gamma }_k\right)}{\int }_{a_1}^{x_1}\dots {\int }_{a_{n-1}}^{x_{n-1}}{\int }_{a_n}^{x_n}{(x_1-s_1)}^{{\gamma }_1-1}\hfill \\ \hfill & \dots {(x_{n-1}-s_{n-1})}^{{\gamma }_{n-1}-1}{(x_n-s_n)}^{{\gamma }_n-1}\left(\alpha f_{\mathsf{\Delta },b}^{\alpha }\left(S\right)+q_{i_1\dots i_n}\left(S\right)\right)\mathrm{d}{s}_1\dots \mathrm{d}{s}_n\hfill \\ \hfill =& \frac{\alpha {\prod }_{k=1}^n{a}_{k,i_k}^{{\gamma }_k}}{{\prod }_{k=1}^n\mathsf{\Gamma }\left({\gamma }_k\right)}{\int }_{a_1}^{x_1}\dots {\int }_{a_{n-1}}^{x_{n-1}}{\int }_{a_n}^{x_n}{(x_1-s_1)}^{{\gamma }_1-1}\hfill \\ \hfill & \dots {(x_{n-1}-s_{n-1})}^{{\gamma }_{n-1}-1}{(x_n-s_n)}^{{\gamma }_n-1}{f}_{\mathsf{\Delta },b}^{\alpha }\left(S\right)\mathrm{d}{s}_1\dots \mathrm{d}{s}_n\hfill \\ \hfill & +(\sum _{k=0}^{n-1}{E}_k+\frac{{\prod }_{k=1}^n{a}_{k,i_k}^{{\gamma }_k}}{{\prod }_{k=1}^n\mathsf{\Gamma }\left({\gamma }_k\right)}{\int }_{a_1}^{x_1}\dots {\int }_{a_{n-1}}^{x_{n-1}}{\int }_{a_n}^{x_n}{(x_1-s_1)}^{{\gamma }_1-1}\hfill \\ \hfill & \dots {(x_{n-1}-s_{n-1})}^{{\gamma }_{n-1}-1}{(x_n-s_n)}^{{\gamma }_n-1}{q}_{i_1\dots i_n}\left(S\right)\mathrm{d}{s}_1\dots \mathrm{d}{s}_n)\hfill \\ \hfill =& \left(\alpha \prod _{k=1}^n{a}_{k,i_k}^{{\gamma }_k}\right){\mathcal{I}}_a^{\gamma }{f}_{\mathsf{\Delta },b}^{\alpha }\left(X\right)+{\widehat{q}}_{i_1\dots i_n}\left(X\right),\hfill \end{array}$$

as desired. □

6. Conclusions

The $\alpha$-fractal formalism of fractal interpolation function is proved to be beneficial in expanding the applications of univariate fractal approximation theory. Through the construction of multivariate $\alpha$-fractal functions on a few complete function spaces which are ubiquitous in the theory of partial differential equations and harmonic analysis, the present work intends to be a step forward in the theory of multivariate fractal approximation. The construction of self-referential analogue for each germ function in a complete function space under consideration leads naturally to an operator, referred to as the multivariate fractal operator. We have studied a few elementary properties of the fractal operator. The multivariate fractal operator introduced and studied here enabled us, in particular, to construct Schauder bases consisting of self-referential functions for the function spaces. Further, taking a slight detour from the main theme, it is shown that the Riemann–Liouville fractional integral of a self-referential counterpart of the given multivariate germ function will also be a self-referential function under some suitable conditions.