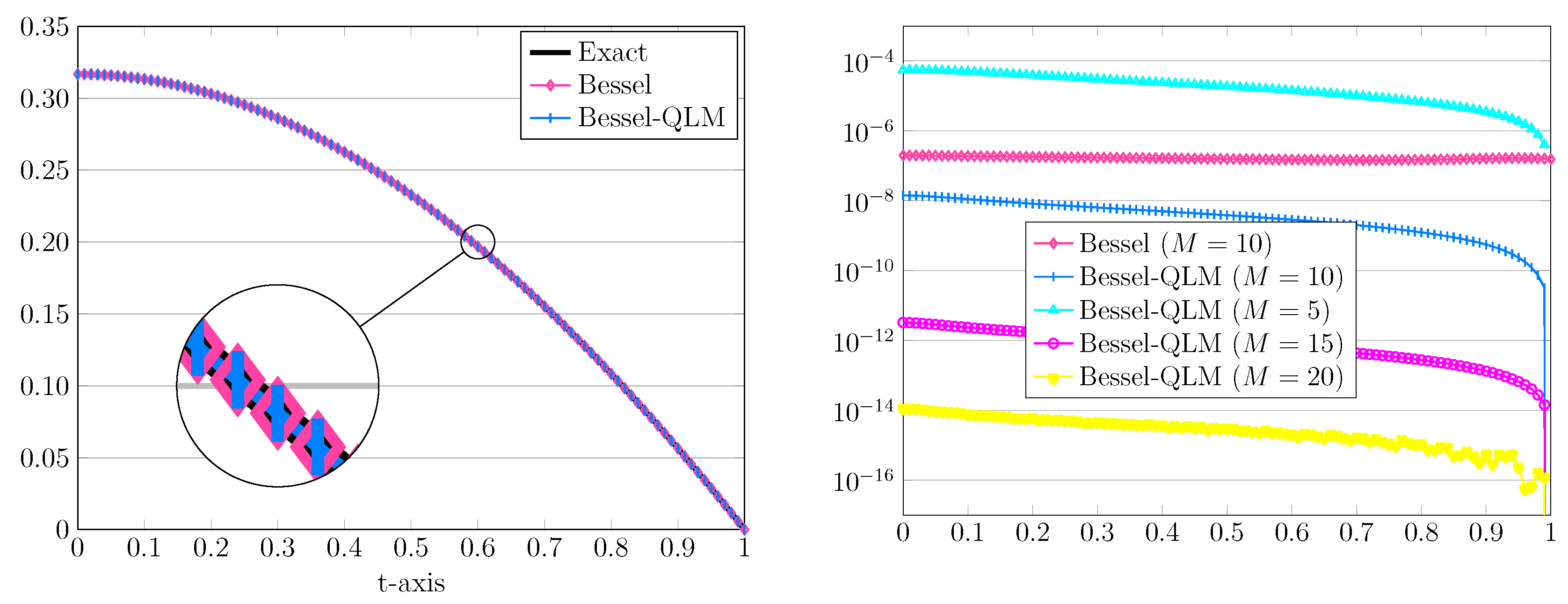
Figure 1.
The graphs of approximated and exact solutions (left) and the related absolute errors (right) for , , and in Example 1.
Figure 1.
The graphs of approximated and exact solutions (left) and the related absolute errors (right) for , , and in Example 1.
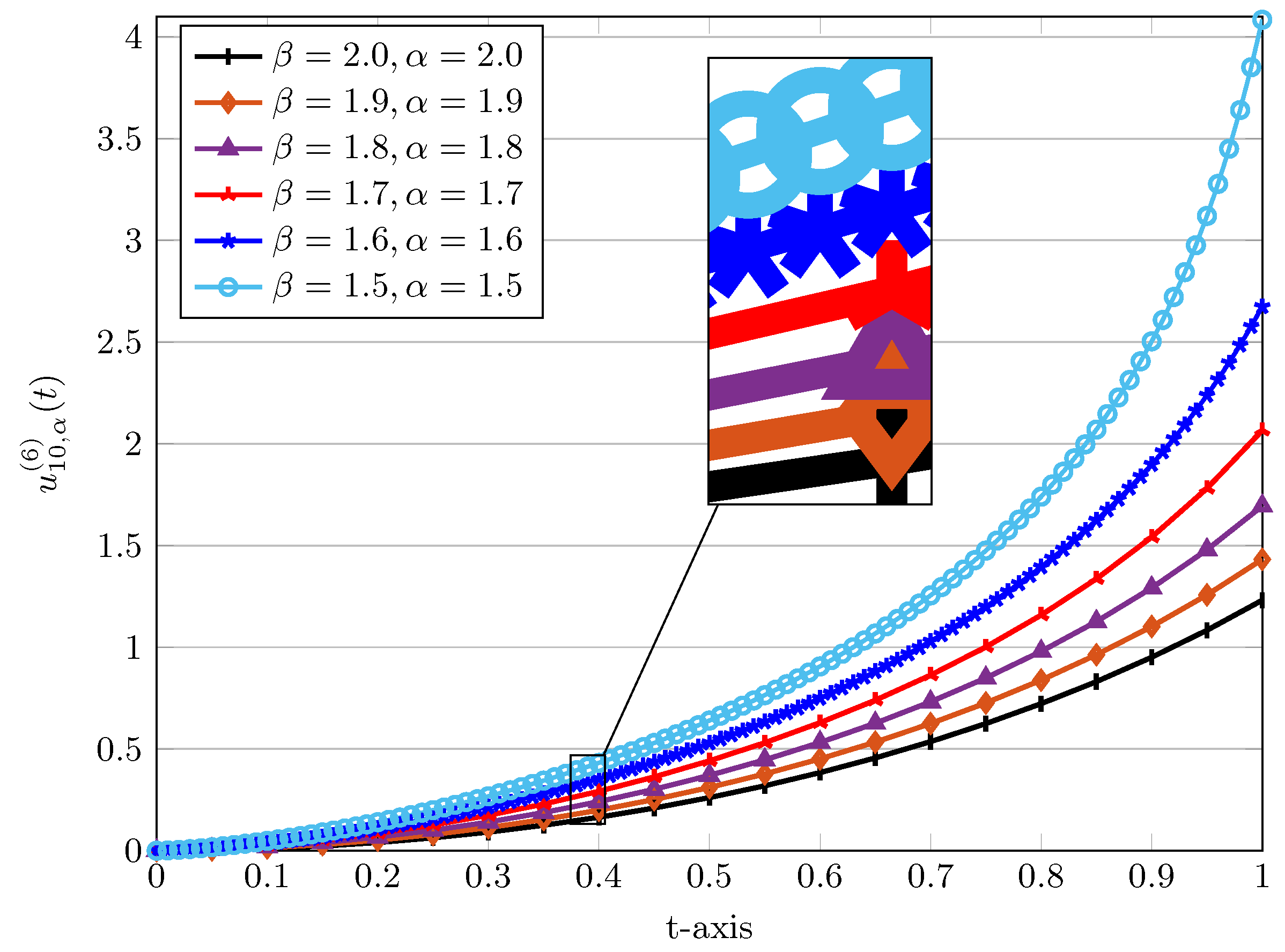
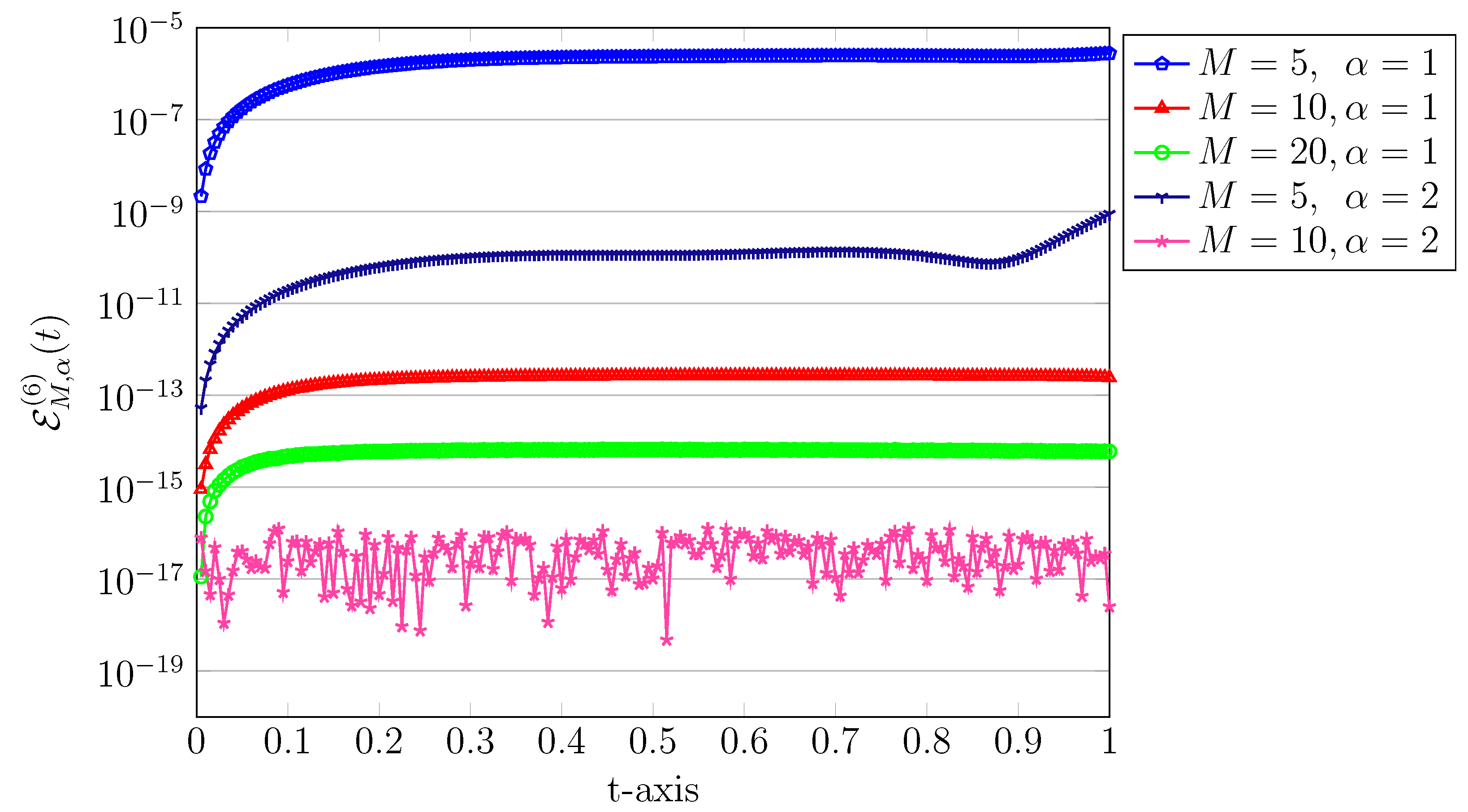
Figure 2.
The approximated Bessel-QLM series solutions for Example 1 using various , 1.6, for , .
Figure 2.
The approximated Bessel-QLM series solutions for Example 1 using various , 1.6, for , .
Figure 3.
The graphs of numerical and exact solutions for (left) and the resulting absolute errors for (right) for , , and in Example 2.
Figure 3.
The graphs of numerical and exact solutions for (left) and the resulting absolute errors for (right) for , , and in Example 2.
Figure 4.
Numerical approximations in Bessel-QLM for various , , , and in Example 2.
Figure 4.
Numerical approximations in Bessel-QLM for various , , , and in Example 2.
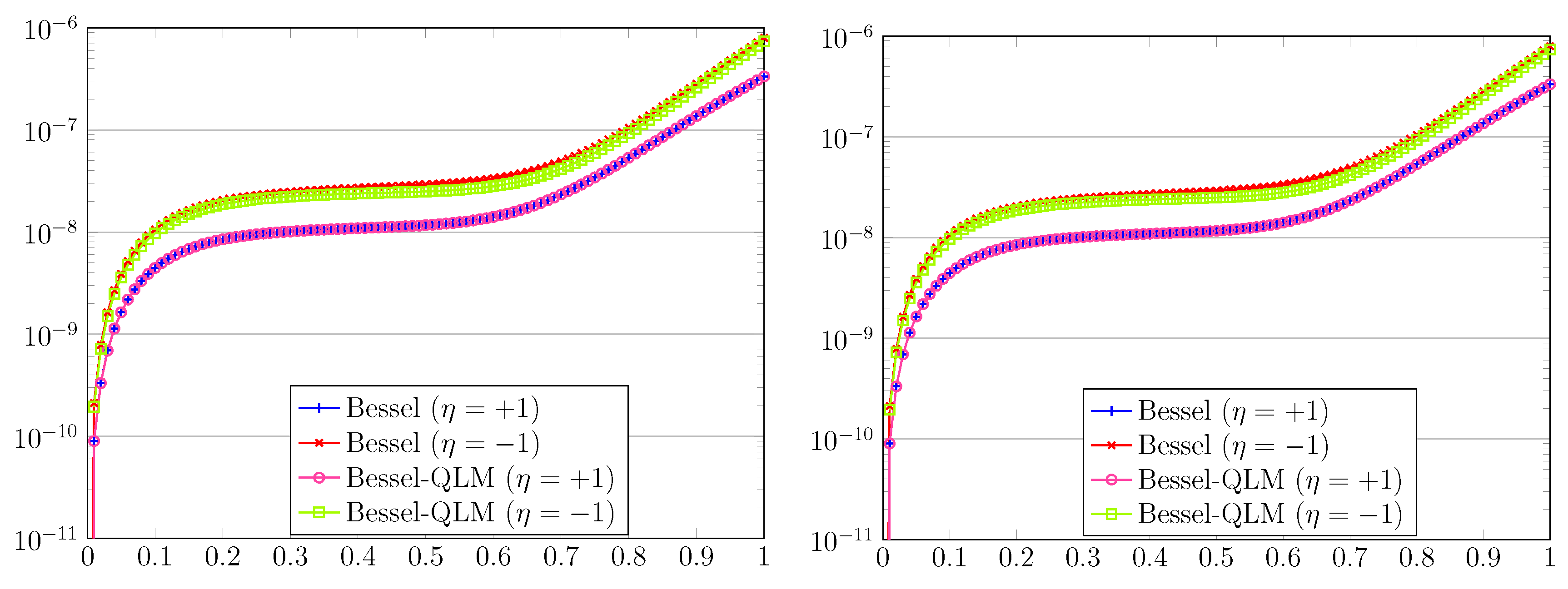
Figure 5.
The graphs of of errors (left) and the resulting residual errors (right) for , , and in Example 3.
Figure 5.
The graphs of of errors (left) and the resulting residual errors (right) for , , and in Example 3.
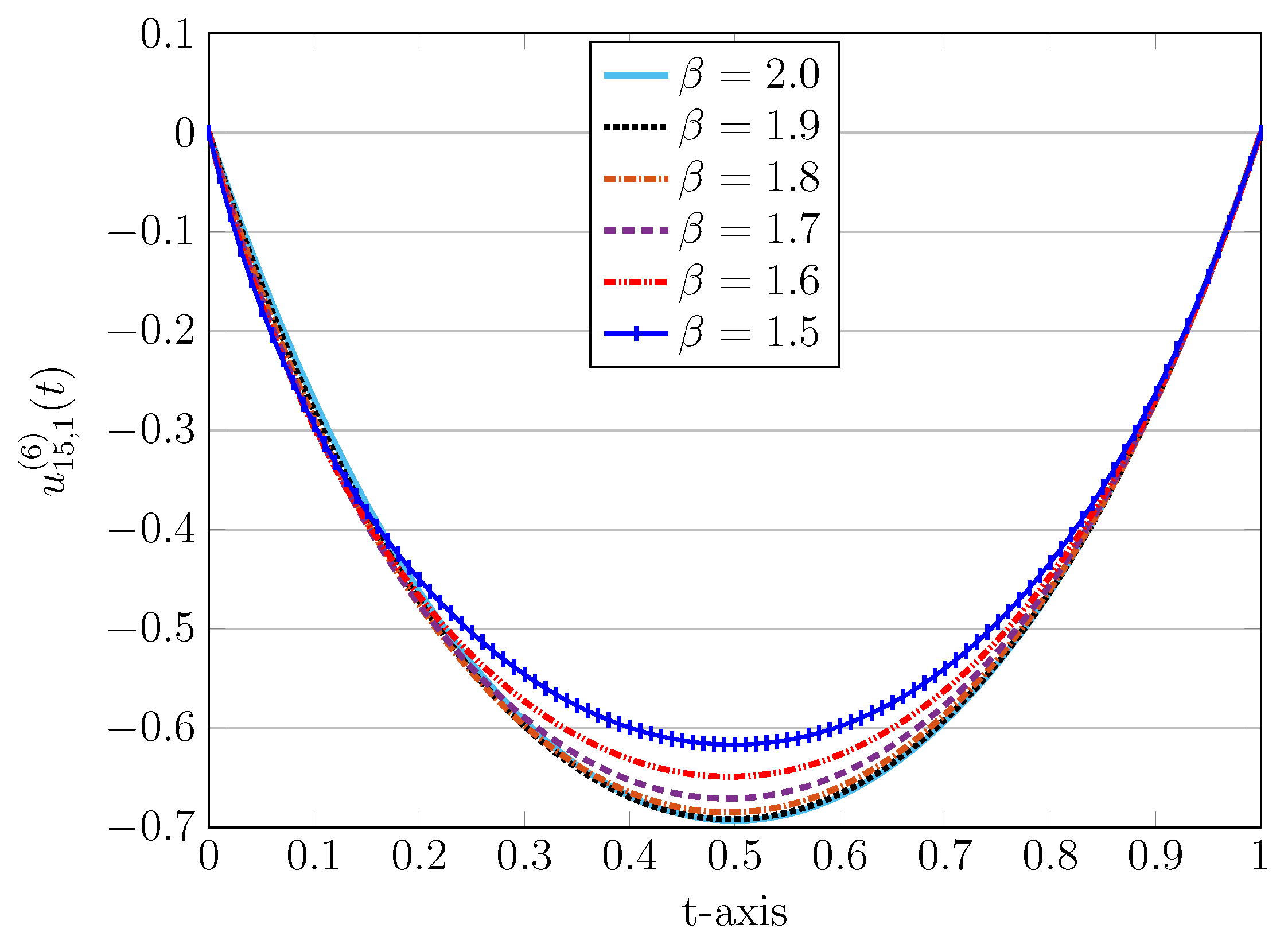
Figure 6.
Approximated solutions with (left) and (right) in Bessel-QLM for , , and various in Example 3.
Figure 6.
Approximated solutions with (left) and (right) in Bessel-QLM for , , and various in Example 3.
Figure 7.
The graphs of numerical and exact solutions for (left) and the resulting absolute errors for (right) for , and in Example 4.
Figure 7.
The graphs of numerical and exact solutions for (left) and the resulting absolute errors for (right) for , and in Example 4.
Figure 8.
Numerical approximations in Bessel-QLM for various , , and in Example 4.
Figure 8.
Numerical approximations in Bessel-QLM for various , , and in Example 4.
Figure 9.
Absolute errors in Bessel-QLM for , and various in Example 5.
Figure 9.
Absolute errors in Bessel-QLM for , and various in Example 5.
Figure 10.
A comparison of numerical solutions in Bessel-QLM for and various in Example 5.
Figure 10.
A comparison of numerical solutions in Bessel-QLM for and various in Example 5.
Table 1.
The comparison of absolute errors using Bessel-QLM in Example 1 for , , and various .
Table 1.
The comparison of absolute errors using Bessel-QLM in Example 1 for , , and various .
| t | | | | | |
|---|
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
Table 2.
Comparison of absolute errors in Bessel-QLM for Example 1 using , , and various .
Table 2.
Comparison of absolute errors in Bessel-QLM for Example 1 using , , and various .
| t | Bessel-QLM | LSM () [23] | TWM [36] | RKM [10] |
|---|
| | Method (a) | Method (b) | | |
|---|
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
Table 3.
The comparison of numerical results using Bessel-QLM in Example 1 for and various equal to .
Table 3.
The comparison of numerical results using Bessel-QLM in Example 1 for and various equal to .
| t | Bessel-QLM | RKM () [10] |
|---|
| | | | | | | | | |
|---|
| | | | | | | | | | |
| | | | | | | | | | |
| | | | | | | | | | |
| | | | | | | | | | |
| | | | | | | | | | |
| | | | | | | | | | |
| | | | | | | | | | |
| | | | | | | | | | |
| | | | | | | | | | |
| | | | | | | | | | |
Table 4.
The comparison of the numerical results using Bessel-QLM in Example 1 for and various equal to at .
Table 4.
The comparison of the numerical results using Bessel-QLM in Example 1 for and various equal to at .
| Bessel-QLM | RKM () [10] | FDTM () [20] |
|---|
| | | |
| | | |
| | | |
| | | |
| | | |
Table 5.
The comparison of the numerical results using Bessel-QLM in Example 2 with , , and , . Numbers in bold show that the correct digits are obtained by the Bessel-QLM.
Table 5.
The comparison of the numerical results using Bessel-QLM in Example 2 with , , and , . Numbers in bold show that the correct digits are obtained by the Bessel-QLM.
| t | Bessel-QLM | TWM [36] |
|---|
| | | | |
|---|
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
Table 6.
Numerical solutions in Bessel-QLM for in Example 2 for , , and .
Table 6.
Numerical solutions in Bessel-QLM for in Example 2 for , , and .
| t | | | |
|---|
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
Table 7.
The comparison of the numerical results using Bessel-QLM in Example 2 with , , , and .
Table 7.
The comparison of the numerical results using Bessel-QLM in Example 2 with , , , and .
| t | Bessel-QLM | L-RKM [21] |
|---|
| | | | | |
|---|
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
Table 8.
The comparison of various numerical results with Bessel-QLM for Example 3 for , , , and .
Table 8.
The comparison of various numerical results with Bessel-QLM for Example 3 for , , , and .
| t | Bessel-QLM () | ADM [9] | LOMMs () [34] |
|---|
| | | Scheme-I | Scheme-II |
|---|
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
Table 9.
The comparison of (residual) error functions using Bessel-QLM in Example 3 with , and .
Table 9.
The comparison of (residual) error functions using Bessel-QLM in Example 3 with , and .
| t | Bessel-QLM () | LOMMs [34] | Bessel-QLM () | JOMMs [37] |
|---|
| | Scheme-I | Scheme-II | | | | |
|---|
| | | | | | | − | − |
| | | | | | | | |
| | | | | | | | |
| | | | | | | | |
| | | | | | | | |
Table 10.
Comparison of numerical results in Bessel-QLM for and in Example 3.
Table 10.
Comparison of numerical results in Bessel-QLM for and in Example 3.
| t | | |
|---|
| Bessel-QLM | HPMADM [25] | Bessel-QLM |
|---|
| | | | | | | | |
|---|
| | | | | | | | | |
| | | | | | | | | |
| | | | | | | | | |
| | | | | | | | | |
| | | | | | | | | |
| | | | | | | | | |
| | | | | | | | | |
| | | | | | | | | |
| | | | | | | | | |
| | | | | | | | | |
Table 11.
The comparison of numerical solutions using Bessel-QLM with , , and in Example 3. Numbers in bold show that the correct digits are obtained by the Bessel-QLM.
Table 11.
The comparison of numerical solutions using Bessel-QLM with , , and in Example 3. Numbers in bold show that the correct digits are obtained by the Bessel-QLM.
| t | Bessel-QLM | LWOMM [36] |
|---|
| | | | |
|---|
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
Table 12.
Numerical solutions in Bessel-QLM for in Example 4 for and .
Table 12.
Numerical solutions in Bessel-QLM for in Example 4 for and .
| t | | | |
|---|
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
Table 13.
The weighted error norms and the related EOCs in Bessel-QLM for Examples 1–4 for , , and diverse M.
Table 13.
The weighted error norms and the related EOCs in Bessel-QLM for Examples 1–4 for , , and diverse M.
| M | Example 1 | Example 2 | Example 3 | Example 4 |
|---|
| EOC | | EOC | | EOC | | EOC |
|---|
| 1 | | − | | − | | − | | − |
| 2 | | | | | | | | |
| 4 | | | | | | | | |
| 8 | | | | | | | | |
| 16 | | | | | | | | |
Table 14.
Residual errors in Bessel-QLM for in Example 5 for and .
Table 14.
Residual errors in Bessel-QLM for in Example 5 for and .
| t | | | | | | |
|---|
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
Table 15.
The weighted error norms and the related EOCs in Bessel-QLM for Example 5 for , and diverse M.
Table 15.
The weighted error norms and the related EOCs in Bessel-QLM for Example 5 for , and diverse M.
| M | | | | | |
|---|
| EOC | | EOC | | EOC | | EOC | | EOC |
|---|
| 1 | | − | | − | | − | | − | | − |
| 2 | | | | | | | | | | |
| 4 | | | | | | | | | | |
| 8 | | | | | | | | | | |