Numerical Solutions of Fractional Differential Equations by Using Laplace Transformation Method and Quadrature Rule
Abstract
1. Introduction
- -
- Good accuracy and simple implementation.
- -
- Exponential convergence.
- -
- Provide a global approach in
- -
- Provide the possibility of error analysis and convergence of method due to the clear and strong theoretical structure.
- -
- It can be a basis for solving problems with higher complexity.
2. Laplace Transform Method and Quadrature Rule
3. Special Cases and Their Examples
3.1. First Order FDE
3.2. FDE with Delay Term
3.3. Second Order FDE
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ren, H.P.; Wang, X.; Fan, J.T.; Kaynak, O. Fractional order sliding mode control of a pneumatic position servo system. J. Frankl. Inst. 2019, 356, 6160–6174. [Google Scholar] [CrossRef]
- Zhang, J.; Jin, Z.; Zhao, Y.; Tang, Y.; Liu, F.; Lu, Y.; Liu, P. Design and implementation of novel fractional-order controllers for stabilized platforms. IEEE Access 2020, 8, 93133–93144. [Google Scholar] [CrossRef]
- Vashisht, R.K.; Peng, Q. Efficient active chatter mitigation for boring operation by electromagnetic actuator using optimal fractional order PDλ controller. J. Mater. Process. Technol. 2020, 276, 116423. [Google Scholar] [CrossRef]
- Sidhardh, S.; Patnaik, S.; Semperlotti, F. Geometrically nonlinear response of a fractional-order nonlocal model of elasticity. Int. J. Non-Linear Mech. 2020, 125, 103529. [Google Scholar] [CrossRef]
- Sánchez-López, C. An experimental synthesis methodology of fractional-order chaotic attractors. Nonlinear Dyn. 2020, 100, 3907–3923. [Google Scholar] [CrossRef]
- Khan, A.; Nigar, U. Sliding mode disturbance observer control based on adaptive hybrid projective compound combination synchronization in fractional-order chaotic systems. J. Control Autom. Electr. Syst. 2020, 31, 885–899. [Google Scholar] [CrossRef]
- Mahto, T.; Malik, H.; Mukherjee, V.; Alotaibi, M.A.; Almutairi, A. Renewable generation based hybrid power system control using fractional order-fuzzy controller. Energy Rep. 2021, 7, 641–653. [Google Scholar]
- Lv, X.; Sun, Y.; Hu, W.; Dinavahi, V. Robust load frequency control for networked power system with renewable energy via fractional-order global sliding mode control. IET Renew. Power Gener. 2021, 15, 1046–1057. [Google Scholar] [CrossRef]
- Farman, M.; Akgül, A.; Ahmad, A.; Imtiaz, S. Analysis and dynamical behavior of fractional-order cancer model with vaccine strategy. Math. Methods Appl. Sci. 2020, 43, 4871–4882. [Google Scholar] [CrossRef]
- Owusu-Mensah, I.; Akinyemi, L.; Oduro, B.; Iyiola, O.S. A fractional order approach to modeling and simulations of the novel COVID-19. Adv. Differ. Equ. 2020, 2020, 1–21. [Google Scholar]
- Zeid, S.S. Approximation methods for solving fractional equations. Chaos Solitons Fractals 2019, 125, 171–193. [Google Scholar] [CrossRef]
- Lloyd, N.G. Remarks on generalising Rouché’s theorem. J. Lond. Math. Soc. 1979, 2, 259–272. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Wiora, J.; Wiora, A. Influence of methods approximating fractional-order differentiation on the output signal illustrated by three variants of Oustaloup filter. Symmetry 2020, 12, 1898. [Google Scholar] [CrossRef]
- Kapoulea, S.; Psychalinos, C.; Elwakil, A.S. Minimization of spread of time-constants and scaling factors in fractional-order differentiator and integrator realizations. Circuits Syst. Signal Process. 2018, 37, 5647–5663. [Google Scholar] [CrossRef]
- Jia, Z.; Liu, C. Fractional-order modeling and simulation of magnetic coupled boost converter in continuous conduction mode. Int. J. Bifurc. Chaos 2018, 28, 1850061. [Google Scholar] [CrossRef]
- Kartci, A.; Agambayev, A.; Farhat, M.; Herencsar, N.; Brancik, L.; Bagci, H.; Salama, K.N. Synthesis and optimization of fractional-order elements using a genetic algorithm. IEEE Access 2019, 7, 80233–80246. [Google Scholar] [CrossRef]
- Sheen, D.; Sloan, I.H.; Thomée, V. A parallel method for time discretization of parabolic equations based on Laplace transformation and quadrature. IMA J. Numer. Anal. 2003, 23, 269–299. [Google Scholar] [CrossRef][Green Version]
- Uddin, M.; Taufiq, M. On the approximation of Volterra integral equations with highly oscillatory Bessel kernels via Laplace transform and quadrature. Alex. Eng. J. 2018, 58, 413–417. [Google Scholar] [CrossRef]
- Uddin, M.; Khan, S. On the numerical solution of fractional order differential equations using transforms and quadrature. TWMS J. Appl. Eng. Math. 2019, 8, 267–274. [Google Scholar]
- McLean, W.; Thomée, V. Maximum-norm error analysis of a numerical solution via Laplace transformation and quadrature of a fractional-order evolution equation. IMA J. Numer. Anal. 2010, 30, 208–230. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Baleanu, D.; Assas, L.M. Efficient generalized Laguerre-spectral methods for solving multi-term fractional differential equations on the half line. J. Vib. Control 2014, 20, 973–985. [Google Scholar] [CrossRef]
- Carothers, D.; Ingham, W.; Liu, J.; Lyons, C.; Marafino, J.; Parker, G.E.; Wilk, D. An Overview of the Modified Picard Method; Department of Mathematics and Statistics, Physics, James Madison University: Harrisonburg, VA, USA, 2004. [Google Scholar]
- Solanki, C.; Thapliyal, P.; Tomar, K. Role of bisection method. Int. J. Comput. Appl. Technol. Res. 2014, 3, 535. [Google Scholar] [CrossRef]
- Ford, N.J.; Connolly, J.A. Systems-based decomposition schemes for the approximate solution of multi-term fractional differential equations. J. Comput. Appl. Math. 2009, 229, 382–391. [Google Scholar] [CrossRef]
- Ahmad, S. On the Numerical Solution of Linear Multi-Term Fractional Order Differential Equations Using Laplace Transform and Quadrature. PJCIS 2017, 2, 43–49. [Google Scholar]
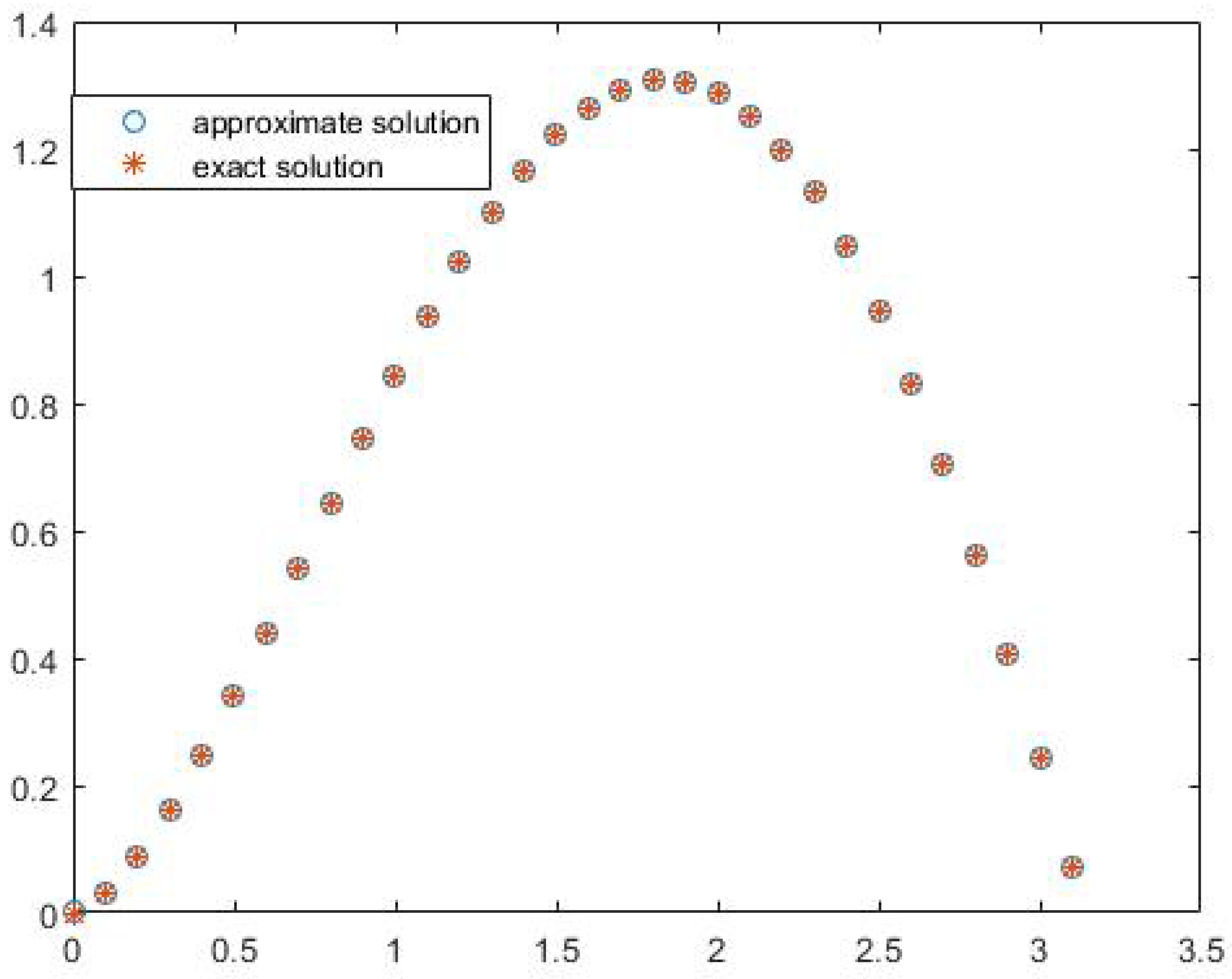
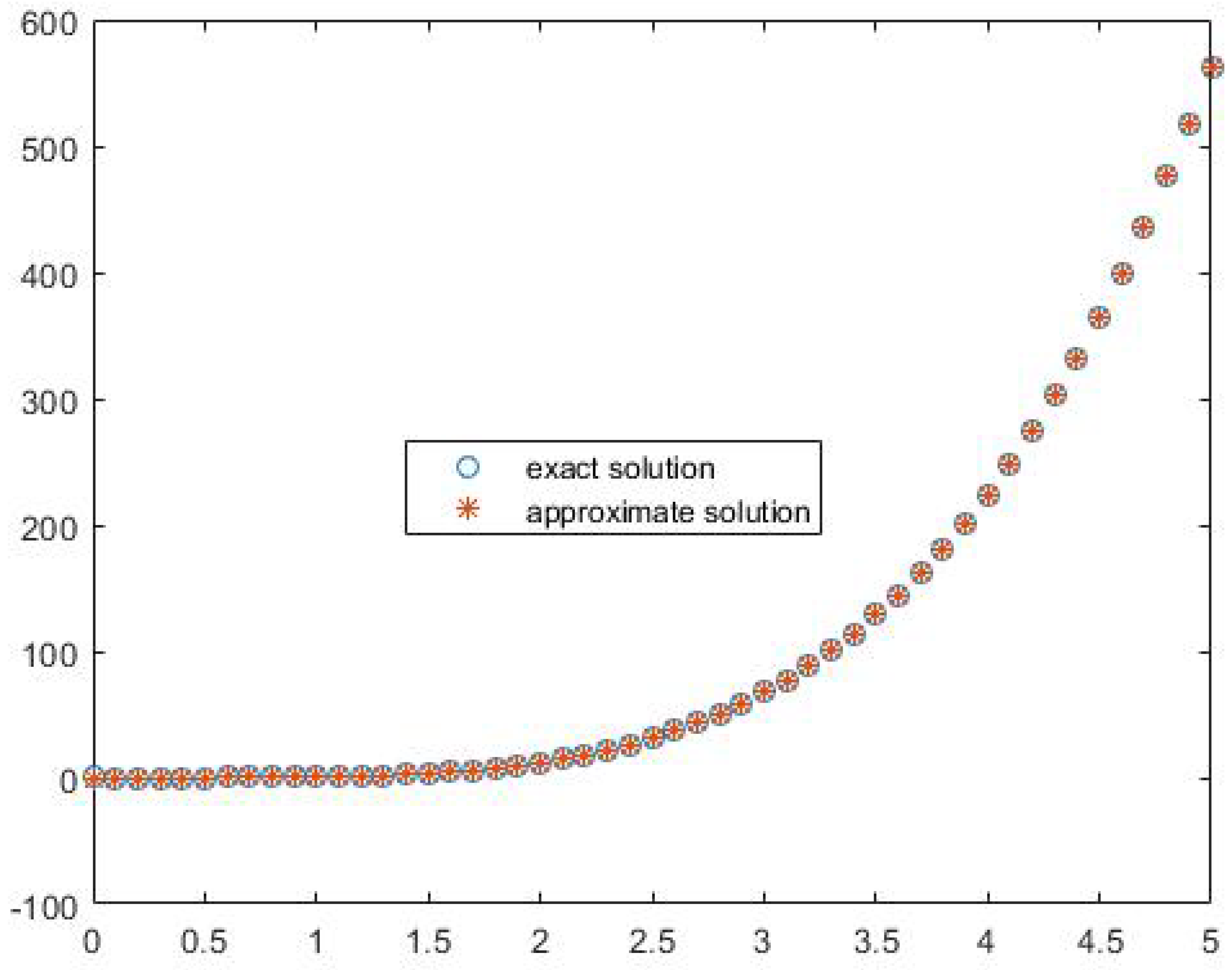
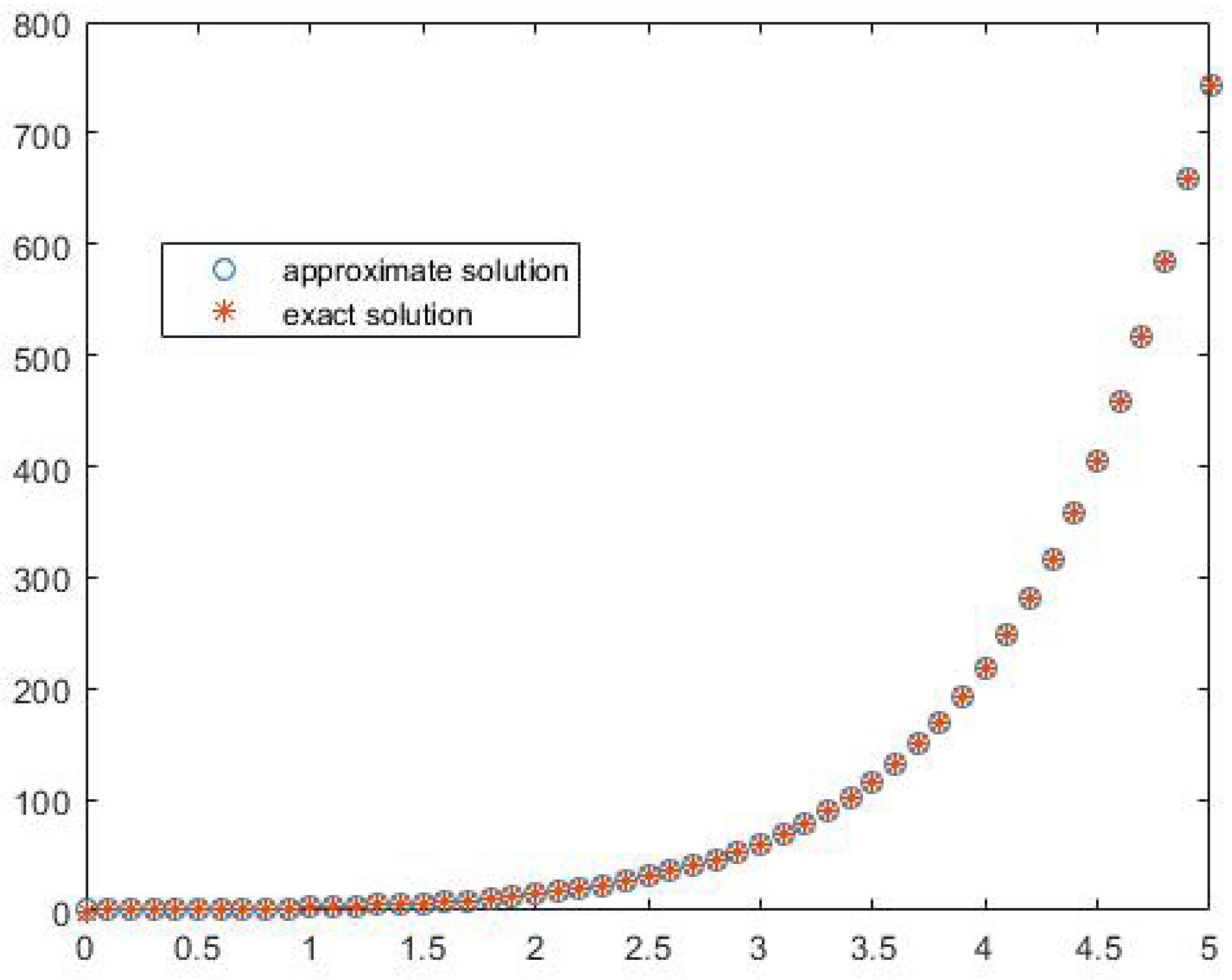
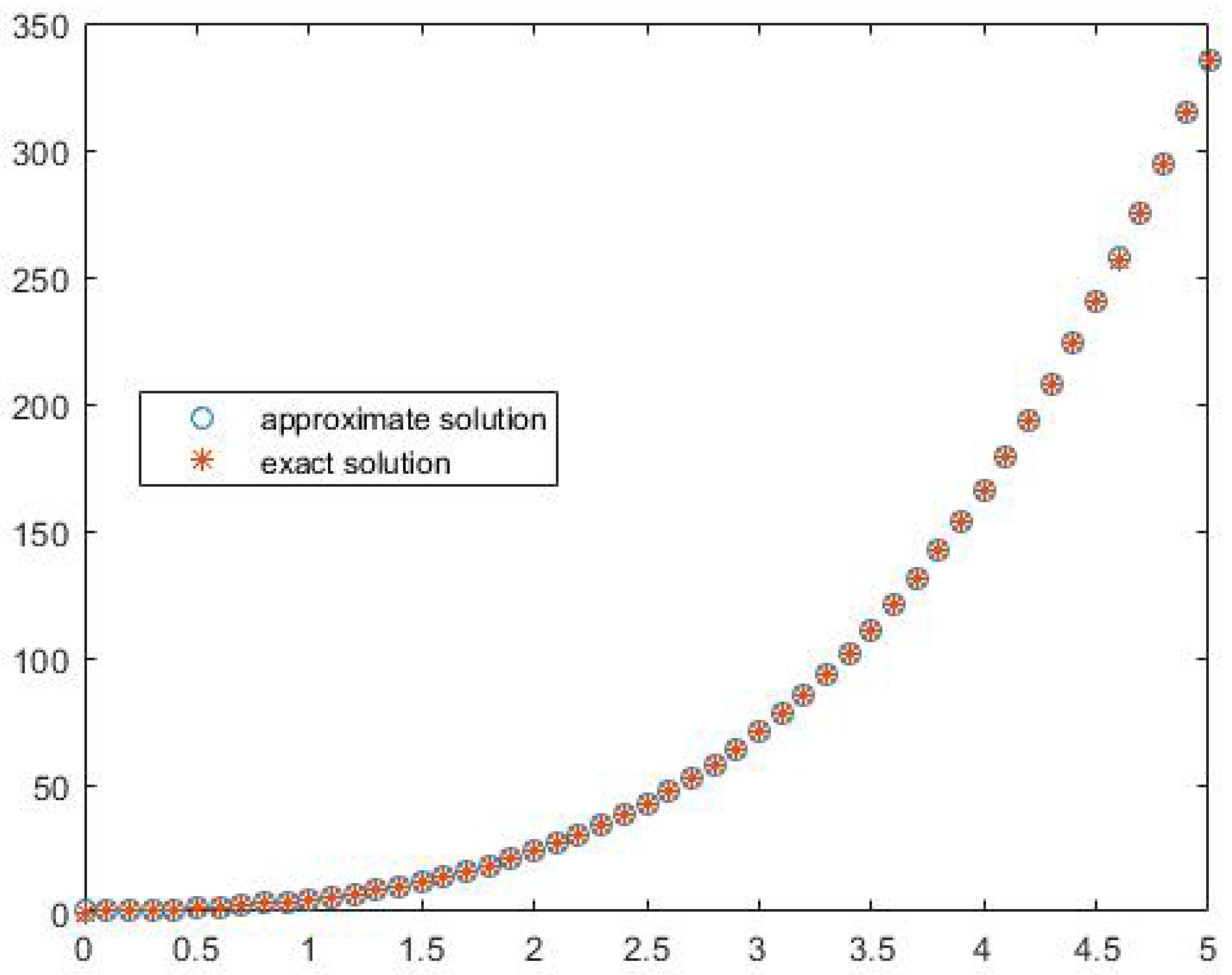
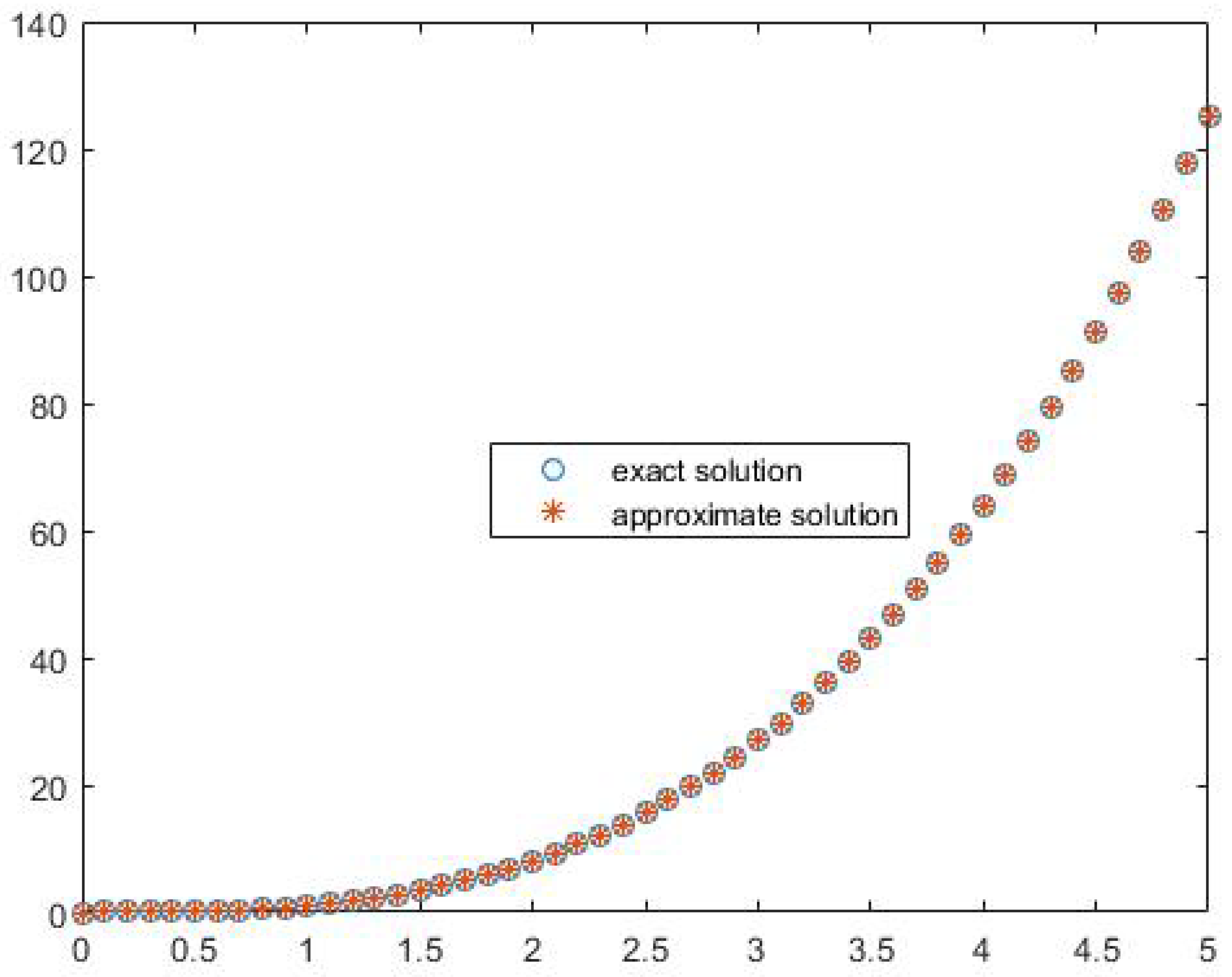
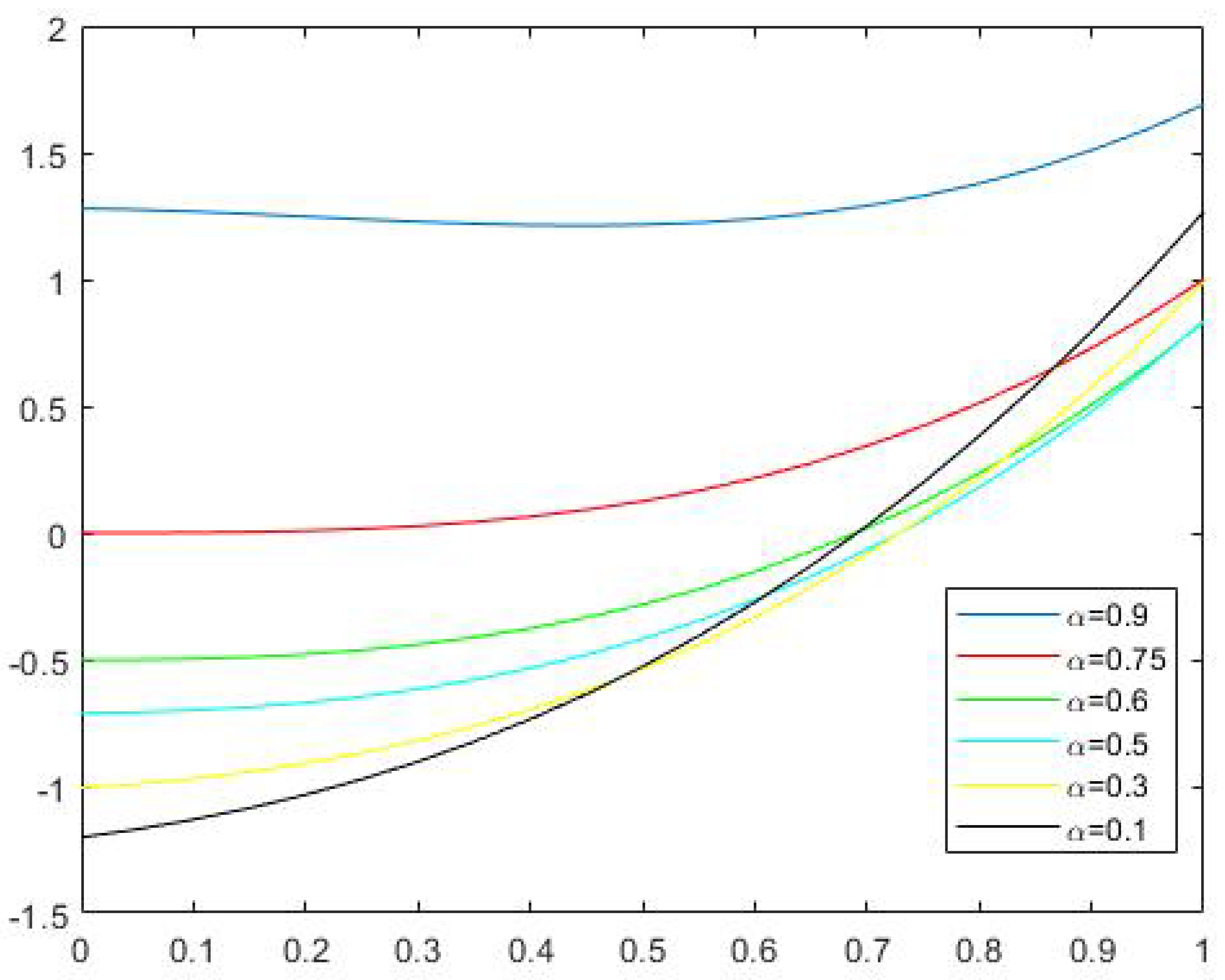
| t | Error | ||
|---|---|---|---|
| t | ||
|---|---|---|
| Error of the Approximate Solution | ||||
|---|---|---|---|---|
| t | |||
|---|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soradi-Zeid, S.; Mesrizadeh, M.; Cattani, C. Numerical Solutions of Fractional Differential Equations by Using Laplace Transformation Method and Quadrature Rule. Fractal Fract. 2021, 5, 111. https://doi.org/10.3390/fractalfract5030111
Soradi-Zeid S, Mesrizadeh M, Cattani C. Numerical Solutions of Fractional Differential Equations by Using Laplace Transformation Method and Quadrature Rule. Fractal and Fractional. 2021; 5(3):111. https://doi.org/10.3390/fractalfract5030111
Chicago/Turabian StyleSoradi-Zeid, Samaneh, Mehdi Mesrizadeh, and Carlo Cattani. 2021. "Numerical Solutions of Fractional Differential Equations by Using Laplace Transformation Method and Quadrature Rule" Fractal and Fractional 5, no. 3: 111. https://doi.org/10.3390/fractalfract5030111
APA StyleSoradi-Zeid, S., Mesrizadeh, M., & Cattani, C. (2021). Numerical Solutions of Fractional Differential Equations by Using Laplace Transformation Method and Quadrature Rule. Fractal and Fractional, 5(3), 111. https://doi.org/10.3390/fractalfract5030111







