Numerical Exploration via Least Squares Estimation on Three Dimensional MHD Yield Exhibiting Nanofluid Model with Porous Stretching Boundaries
Abstract
1. Introduction
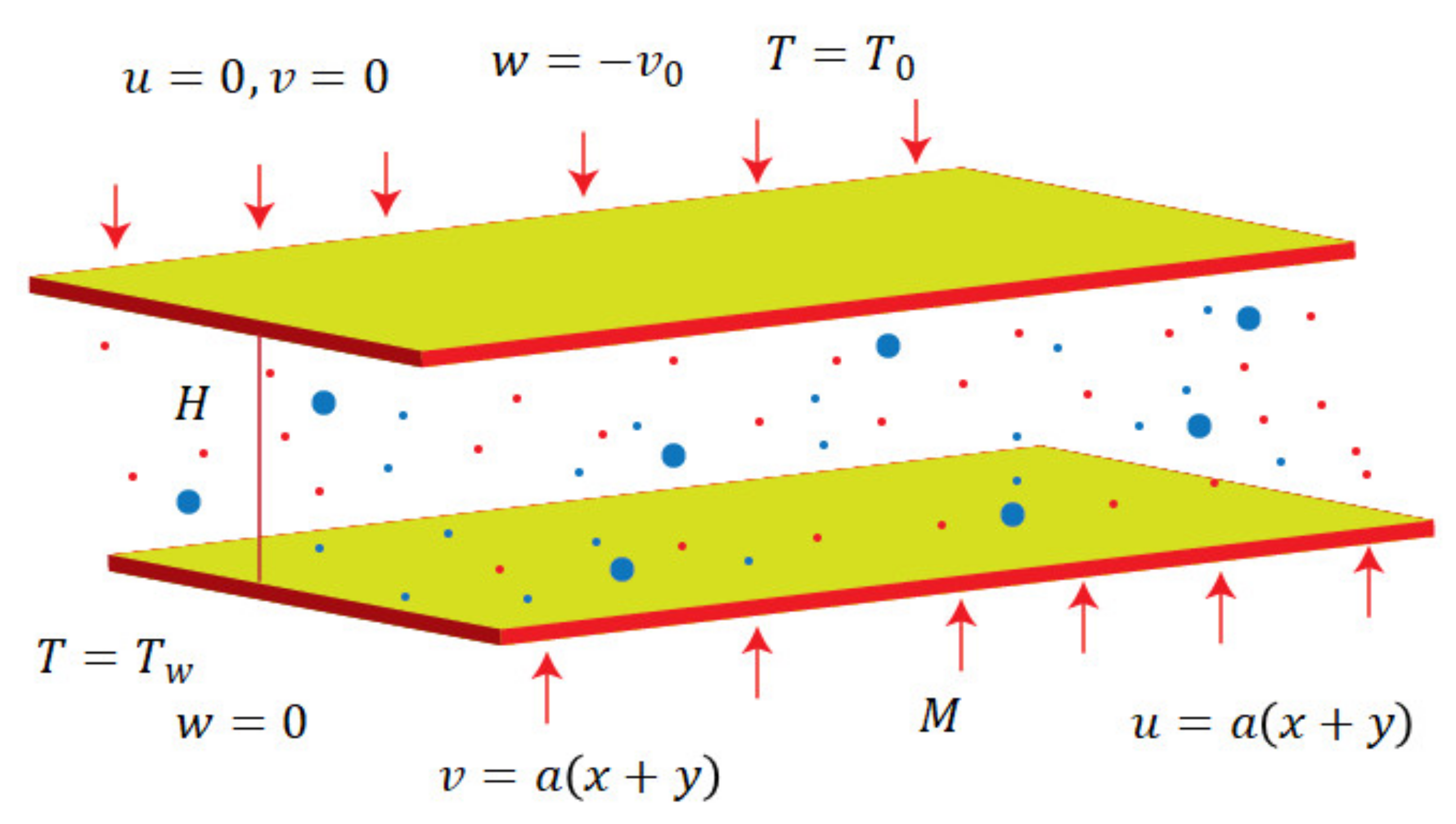
2. Mathematical and Geometrical Analysis
3. Methodology and Solution Procedure
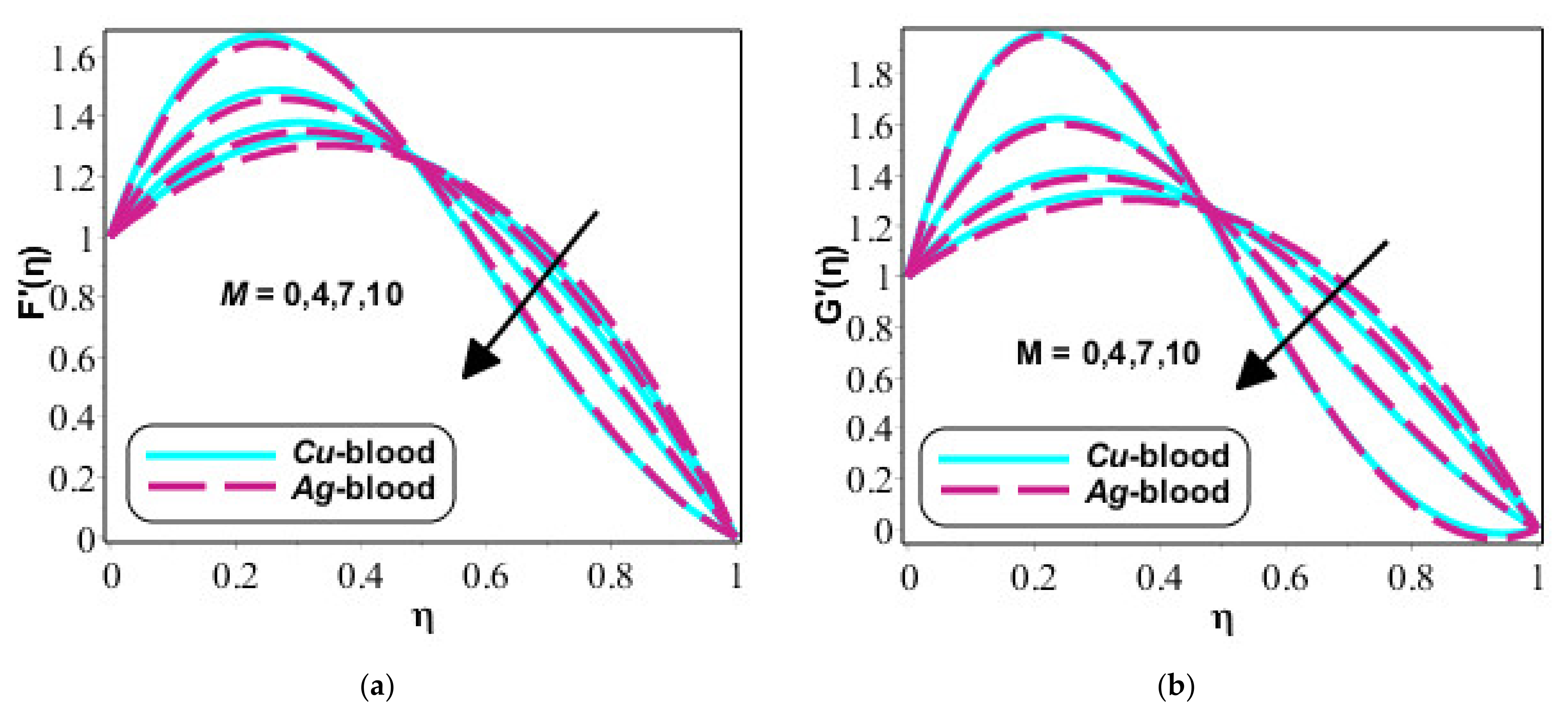
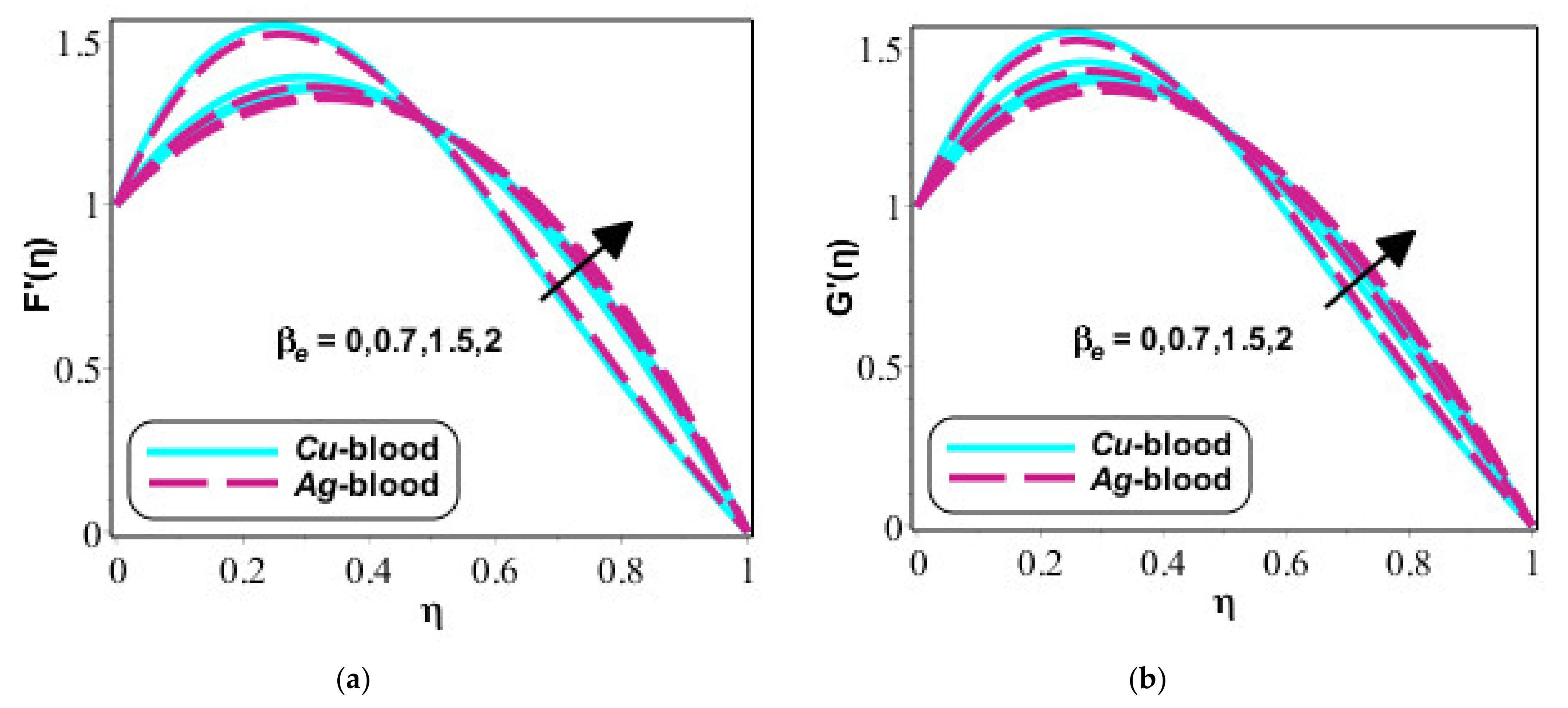
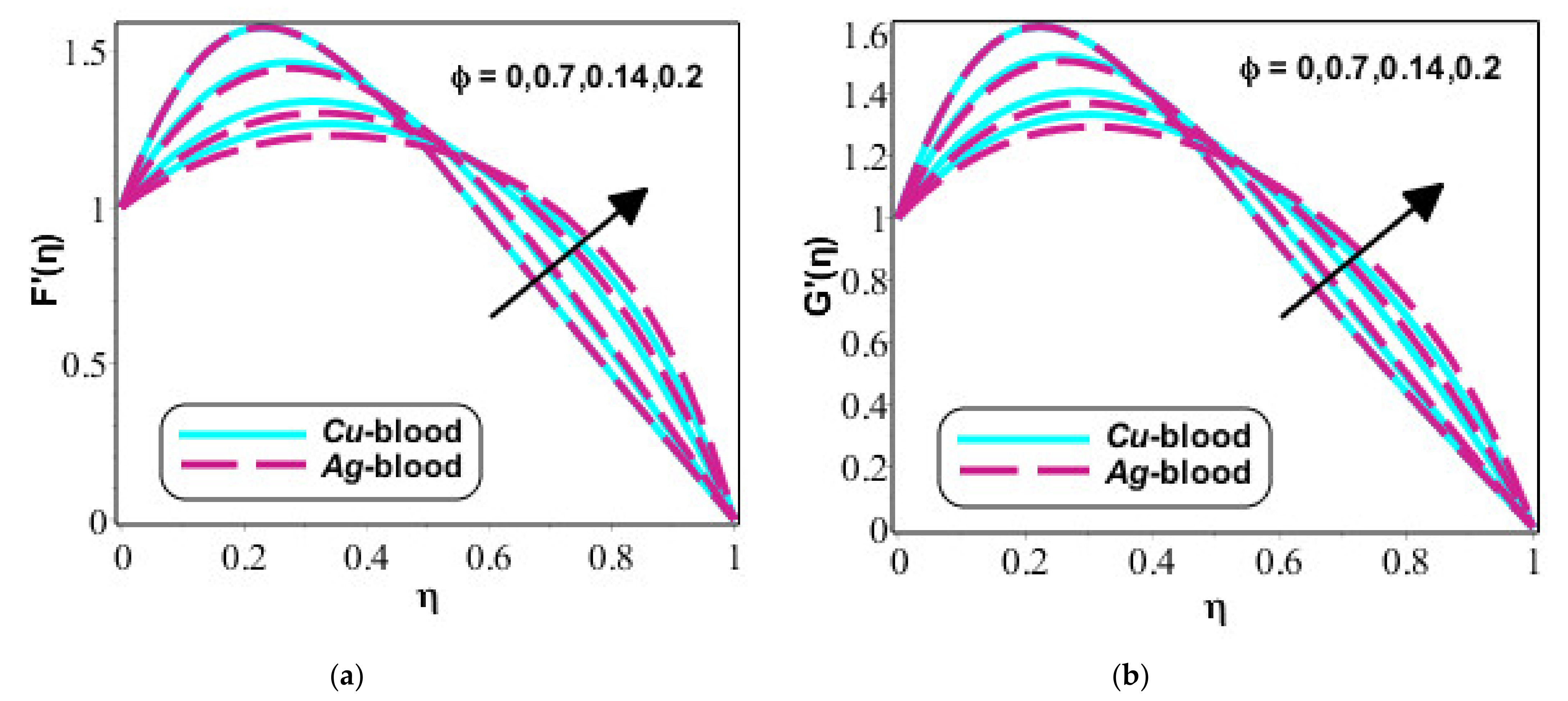
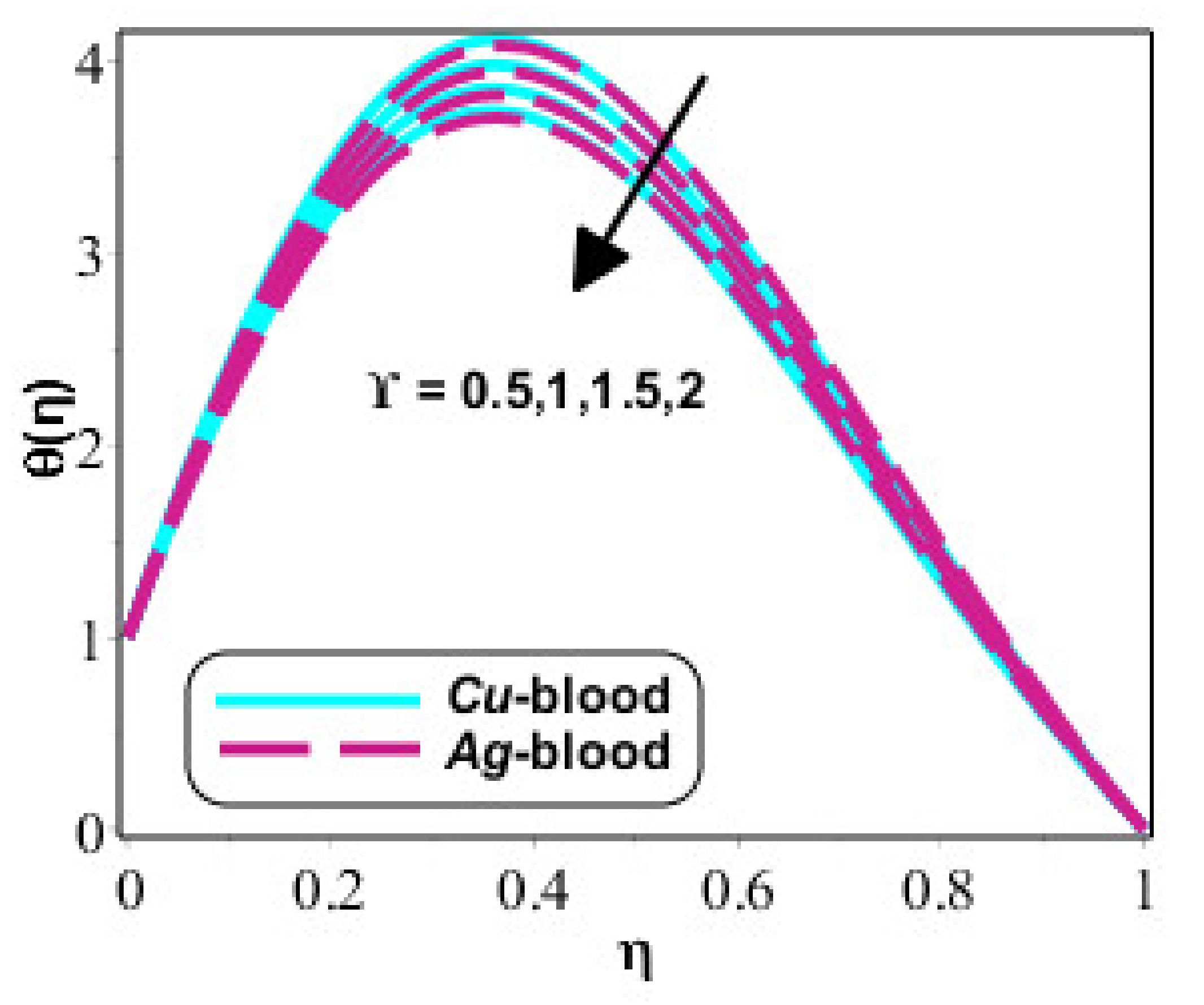
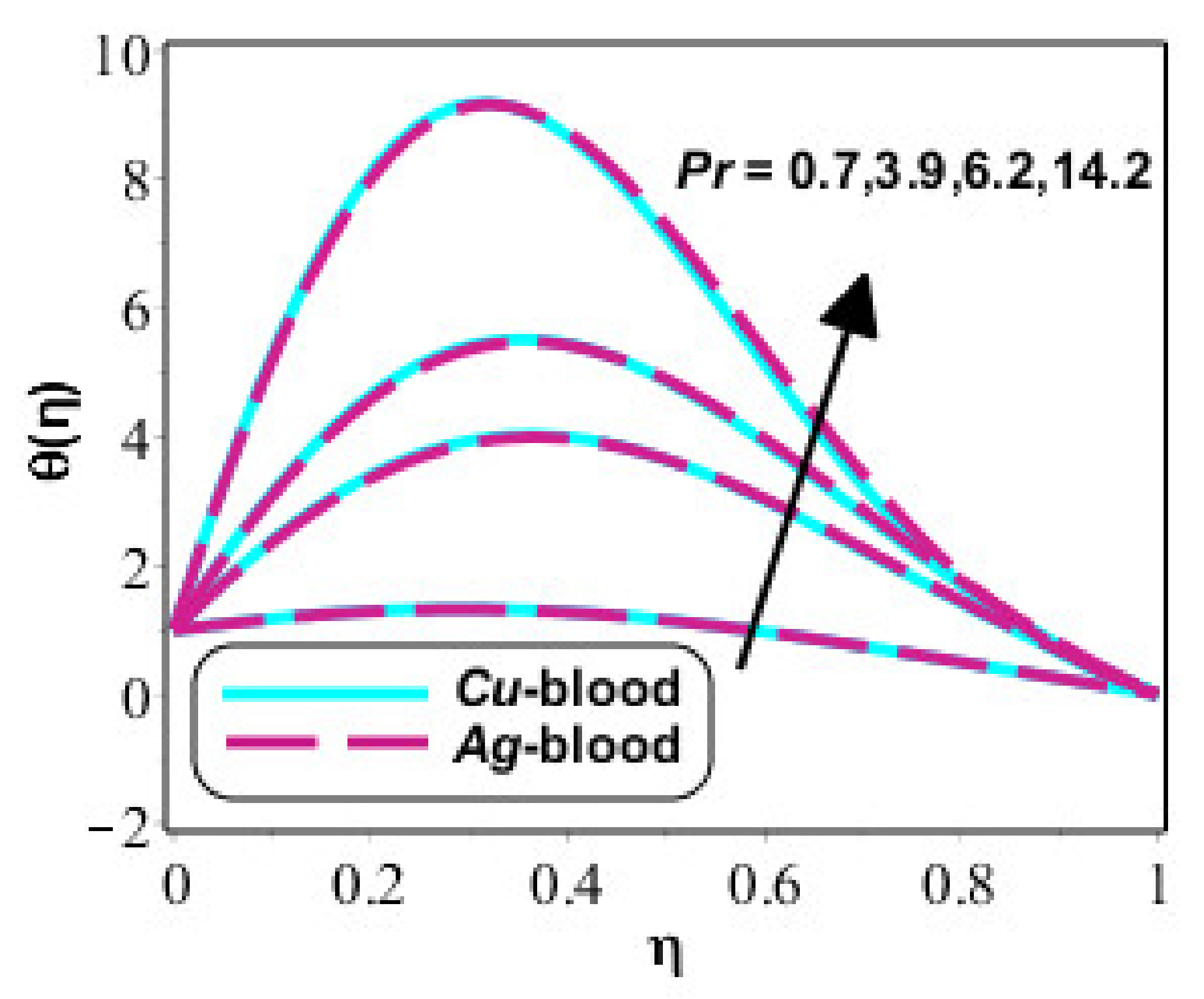
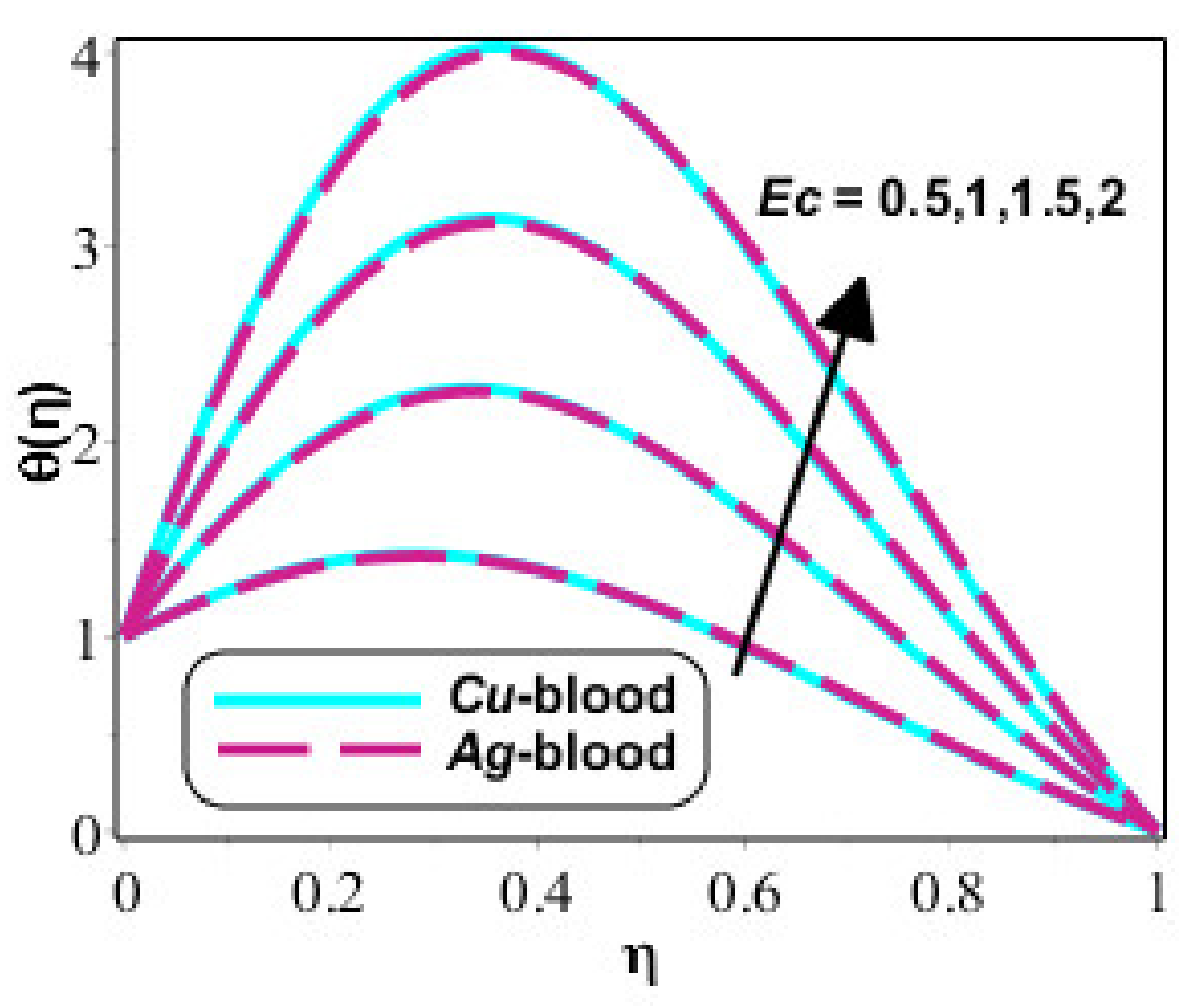
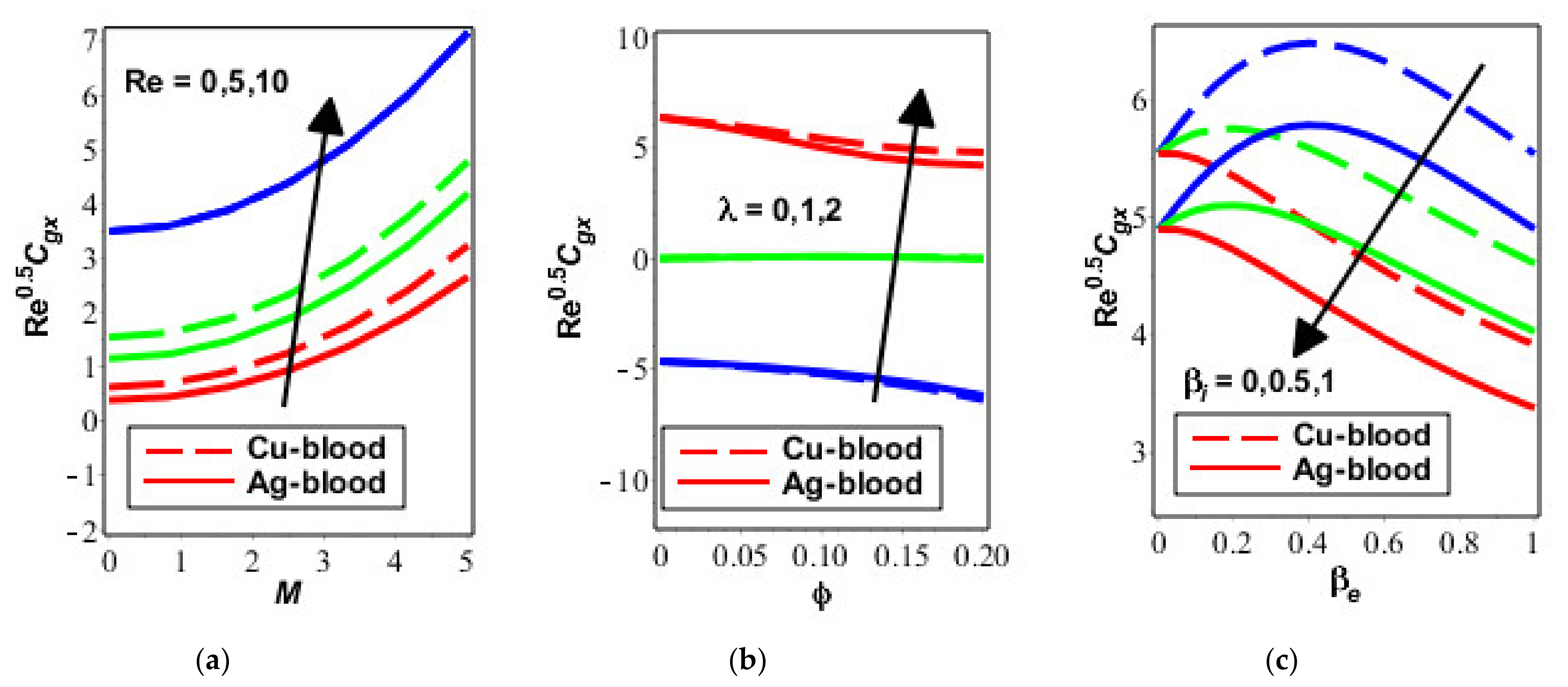
4. Results and Discussion
5. Conclusions
- ⮚
- Flow and thermal energy into particles is inclined for rather than flow and thermal energy into particles for case of ;
- ⮚
- Reduction into flow analysis is noticed versus change in Hartmann and volume fraction numbers;
- ⮚
- Thermal energy boosts for variation in Eckert number while flow is declined when Hall number is boosted;
- ⮚
- Rate of heat flux is decayed versus change in Prandtl, ion slip, Eckert and thermal radiation numbers whereas rate of heat flux is boosted against higher values of Reynolds and ion slip numbers;
- ⮚
- Error analysis is computed within help of least square approach.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Esfahani, M.A.; Toghraie, D. Experimental investigation for developing a new model for the thermal conductivity of silica/water-ethylene glycol (40%–60%) nano-fluid at different temperatures and solid volume fractions. J. Mol. Liq. 2017, 232, 105–120. [Google Scholar] [CrossRef]
- Das, R.S.; Makindco, J. Magnetohydrodynamic-free convective flow of nano-fluid past a oscillating porous flat plate in a rotating system with thermal radiation and Hall effects. J. Mech. 2015, 32, 1593–1610. [Google Scholar]
- Usman, M.; Hamid, M.; Khan, U.; Mohyud-Din, S.T.; Iqbal, M.A.; Wang, W. Differential transform method for un-steady nano-fluid flow and heat transfer. Alex. Eng. J. 2017, 57, 1867–1875. [Google Scholar] [CrossRef]
- Anoop, K.; Sudararajan, T.; Das, S. Effects of particles size on the convective heat transfer in nano-fluid in the developing region. Int. J. Heat Transf. 2009, 52, 2189–2195. [Google Scholar] [CrossRef]
- Sheikholeslami, M. Influence of Lorentz forces on nano-fluid flow in a porous cylinder considering Darcy model. J. Mol. Liq. 2017, 225, 903–912. [Google Scholar] [CrossRef]
- Ali, F.M.; Nazar, R.; Arifin, N.M.; Pop, I. Unsteady flow and heat transfer past an axisymmetric permeable shrinking sheet with radiation effect. Int. J. Numer. Methods Fluids 2011, 67, 1310–1320. [Google Scholar] [CrossRef]
- Bhattacharyya, K.; Layek, G. Effects os suction/blowing on steady boundary layer stagnation-point flow heat transfer towards a shrinking sheet with thermal radiation. Int. J. Heat Mass Transf. 2011, 54, 302–307. [Google Scholar] [CrossRef]
- Nadeem, S.; Zaheer, S.; Fang, T. Effects of thermal radiation on the boundary layer flow of jaffery fluid over an exponentially stretching surface. Number Algorithms 2011, 57, 187–205. [Google Scholar] [CrossRef]
- Ishaq, A. Thermal boundary layer flow over a stretching sheet in micropolar fluid with radiation effect. Meccanica 2010, 73, 367–373. [Google Scholar] [CrossRef]
- Usman, M.; Zubair, T.; Hamid, M.; Haq, R.U.; Wang, W. Wavelets solution of MHD three-dimensional fluid flow in the presence of slip and thermal radiation effects. Phys. Fluids 2018, 30, 5016946. [Google Scholar] [CrossRef]
- Aoyagi, M.; Ito, S.; Hashizume, H. Numerical study of the MHD flow characteristics in a three-surface-multi-layered channel with different inlet conditions. Fusion Eng. Des. 2014, 89, 1227–1231. [Google Scholar] [CrossRef]
- Borrelli, A.; Giantesio, G.; Patria, M.; Roşca, N.; Roşca, A.; Pop, I. Buoyancy effects on the 3D MHD stagnation-point flow of a Newtonian fluid. Commun. Nonlinear Sci. Numer. Simul. 2017, 43, 1–13. [Google Scholar] [CrossRef]
- Akbar, N.S.; Nadeem, S.; Haq, R.U.; Khan, Z. Radiation effects on MHD stagnation point flow of nano fluid towards a stretching surface with convective boundary condition. Chin. J. Aeronaut. 2013, 26, 1389–1397. [Google Scholar] [CrossRef]
- Motsa, S.; Shateyi, S. The effects of chemical reaction, Hall and ion-slip currents on MHD micropolar flu-id flow with thermal diffusivity using a novel numerical technical. J. Appl. Math 2012, 2012, 1–30. [Google Scholar]
- Sohail, M.; Naz, R.; Abdelsalam, S. Application of non-Fourier double diffusions theories to the boundary-layer flow of a yield stress exhibiting fluid model. Phys. A Stat. Mech. Appl. 2020, 537, 122753. [Google Scholar] [CrossRef]
- Nayak, M. MHD 3D flow and heat transfer analysis of nano-fluid by shrinking surface inspired by thermal radiation and viscous dissipation. Int. J. Mech. Sci. 2017, 124, 185–193. [Google Scholar] [CrossRef]
- Kumaran, G.; Sandeep, N. Thermophoresis and Brownian moment effects on parabolic flow of MHD Casson and Williamson fluids with cross diffusion. J. Mol. Liq. 2017, 233, 262–269. [Google Scholar] [CrossRef]
- Nayak, M.; Akbar, N.; Pandey, V.S.; Khan, Z.H.; Tripathi, D. 3D free convective MHD flow of nano-fluid over permeable linear stretching sheet with thermal radiation. Powder Technol. 2017, 315, 205–215. [Google Scholar] [CrossRef]
- Nazir, U.; Sohail, M.; Ali, U.; Sherif, E.S.M.; Park, C.; Lee, J.R.; Selim, M.M.; Thounthong, P. Applications of Cattaneo–Christov fluxes on modelling the boundary value problem of Prandtl fluid comprising variable properties. Sci. Rep. 2021, 11, 1–13. [Google Scholar] [CrossRef]
- Toghraie, D.; Mahmoudi, M.; Akbari, O.A.; Pourfattah, F.; Heydari, M. The effect of using water/CuO nano-fluid and L-shaped porous ribs on the performance evaluation criterion of microchannels. J. Therm. Anal. Calorim. 2019, 135, 145–159. [Google Scholar] [CrossRef]
- Arasteh, H.; Mashayekhi, R.; Toghraie, D.; Karimipour, A.; Bahiraei, M.; Rahbari, A. Optimal arrangements of a heat sink partially filled with multilayered porous media employing hybrid nano-fluid. J. Therm. Anal. Calorim. 2019, 137, 1045–1058. [Google Scholar] [CrossRef]
- Gheynani, R.A.; Akbari, O.A.; Zarringhalam, M.; Ahmadi, G.; Shabani, S.; Abdulwahab, S.; Alnaqi, A.; Goodarzi, M.; Toghraie, D. Investigating the effect of nano-particles diameter on turbulent flow and heat transfer properties of non-Newtonian carboxymethyl cellulose/CuO fluid in a microtube. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 1699–1723. [Google Scholar] [CrossRef]
- Shahsavar, A.; Sardari, P.T.; Toghraie, D.; Salehipour, H. Impact of variable fluid properties on forced convection of Fe3O4/CNT/water hybrid nano-fluid in a double-pipe mini-channel heat exchanger. J. Therm. Anal. Calorim. 2019, 137, 1031–1043. [Google Scholar] [CrossRef]
- Newman, J.C., Jr. An Improved Method of Collocation for the Stress Analysis of Cracked Plates with Various Shaped Boundaries; Lungley Research Center: Hampton, VA, USA, 1971. [Google Scholar]
- Zhu, T.; Atluri, S.N. A modified collocation method and a penalty formulation for enforcing the essential boundary conditions in the element free Galerkin method. Comp. Mech. 1998, 21, 211–222. [Google Scholar] [CrossRef]
- Babuska, I.; Nobile, F.; Tempone, R. A stochastic collocation method for elliptic partial differential equations with random input data. SIAM J. Numer. Anal. 2007, 45, 1005–1034. [Google Scholar] [CrossRef]
- Zubair, T.; Sajjad, M.; Madni, R.; Shabir, A. Hermite Solution of Bagley-Torvik Equation of Fractional Order. Int. J. Mod. Nonlinear Theory Appl. 2017, 6, 104–118. [Google Scholar] [CrossRef][Green Version]
- Schneider, K.; Vasilyev, O. Wavelet Methods in Computational Fluid Dynamics. Annu. Rev. Fluid Mech. 2010, 42, 473–503. [Google Scholar] [CrossRef]
- Nawaz, M.; Zubair, T. Finite element study of three dimensional radiative nano-plasma flow subject to Hall and ion slip currents. Results Phys. 2017, 7, 4111–4122. [Google Scholar] [CrossRef]
- Khan, J.; Mustafa, M.; Hayat, T.; Alsaedi, A. Three-dimensional flow of nano fluid over a nonlinearly stretching sheet, An application to solar energy. Int. J. Heat Mass Transf. 2015, 8, 158–164. [Google Scholar] [CrossRef]
- Zubair, T.; Usman, M.; Hamid, M.; Sohail, M.; Nazir, U.; Nisar, K.; Vijayakumar, V. Computational analysis of radiative Williamson hybrid nano-fluid comprising variable thermal conductivity. Jpn. J. Appl. Phys. 2021, 60, 087004. [Google Scholar] [CrossRef]





| TP | Σ | |||
|---|---|---|---|---|
| Water | 0.613 | 997.1 | 4179 | 1.19 |
| Ag | 429 | 10,500 | 235 | 6.63 × 107 |
| Cu | 400 | 8933 | 385 | 5.96 × 107 |
| 5 | 1.1337 × 10−11 | 2.3403 × 10−09 | 2.3140 × 10−05 |
| 8 | 8.8110 × 10−19 | 1.5896 × 10−17 | 3.7655 × 10−13 |
| 12 | 1.0671 × 10−28 | 1.2267 × 10−26 | 2.7063 × 10−22 |
| 16 | 8.0748 × 10−38 | 1.4473 × 10−36 | 7.1356 × 10−29 |
| 21 | 2.4514 × 10−49 | 2.7840 × 10−48 | 2.3603 × 10−38 |
| n | λ | Obtained F″ | [30] | Obtained G″ | [30] | |
|---|---|---|---|---|---|---|
| 1 | 0:5 | 1.22391 | 1.22475 | 0.61245 | 0.61237 | |
| 1 | 1.41540 | 1.41421 | 1.41434 | 1.41421 | ||
| 3 | 0:5 | 1.98814 | 1.98942 | 0.99357 | 0.99471 | |
| 1 | 2.29704 | 2.29719 | 2.29704 | 2.29719 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zubair, T.; Usman, M.; Nazir, U.; Kumam, P.; Sohail, M. Numerical Exploration via Least Squares Estimation on Three Dimensional MHD Yield Exhibiting Nanofluid Model with Porous Stretching Boundaries. Fractal Fract. 2021, 5, 167. https://doi.org/10.3390/fractalfract5040167
Zubair T, Usman M, Nazir U, Kumam P, Sohail M. Numerical Exploration via Least Squares Estimation on Three Dimensional MHD Yield Exhibiting Nanofluid Model with Porous Stretching Boundaries. Fractal and Fractional. 2021; 5(4):167. https://doi.org/10.3390/fractalfract5040167
Chicago/Turabian StyleZubair, Tamour, Muhammad Usman, Umar Nazir, Poom Kumam, and Muhammad Sohail. 2021. "Numerical Exploration via Least Squares Estimation on Three Dimensional MHD Yield Exhibiting Nanofluid Model with Porous Stretching Boundaries" Fractal and Fractional 5, no. 4: 167. https://doi.org/10.3390/fractalfract5040167
APA StyleZubair, T., Usman, M., Nazir, U., Kumam, P., & Sohail, M. (2021). Numerical Exploration via Least Squares Estimation on Three Dimensional MHD Yield Exhibiting Nanofluid Model with Porous Stretching Boundaries. Fractal and Fractional, 5(4), 167. https://doi.org/10.3390/fractalfract5040167








