1. Introduction
Fractional differential equations (FDEs) are considered an important area of research in the direction of the applications of fractional calculus. Regarding applications of FDEs, one can observe some fields including aerodynamics, biochemistry, electro-chemistry, bioengineering, physics, viscoelasticity, mathematical biology, and so on (see [
1,
2]). In the last few years, a large number of studies regarding the existence theory for different FDEs have received much attentions from researchers and some examples include [
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18]. Since we can model some of applied phenomena in the framework of the fractional coupled systems, a large number of researchers have conducted many research studies on the existence of solution for such a type of systems (for instances, see [
19,
20,
21,
22,
23]).
Stability analysis along with numerical techniques are the most important components of research in this regard. Usually, obtaining the exact solutions of a non-linear boundary problem in the fractional settings is time-consuming wor,k and it is a task full of challenges. Therefore, these items motivated mathematicians to find the best approximate solutions for existing boundary value problems (BVPs). To perform this, various procedures were introduced, including decomposition methods [
24,
25], HATM [
26],
q-HATM [
27], and integral transforms [
28].
The generalized differential transform method (GDT-method) is considered as one of the most accurate and strongest techniques for finding approximate solutions of nonlinear or linear FDEs. This transform can be observed in some papers such as [
29,
30] in which the authors have used it to analyze approximate solutions of the given BVPs. Notice that there is no specified method to study nonlinear FDEs for obtaining explicit solutions. Therefore, a reliable method is required to find approximate solutions in the framework of finite/infinite series regarding the given FBVPs.
In 2018, Shah et al. [
31] established the existence results and obtained approximate solutions with the help of GDT-method for the system of coupled FDEs with movable integral conditions:
by assuming
,
,
, and
. In 2020, Alrabaiah, Ahmad, Shah, and Rahman [
32] conducted qualitative research regarding H-U-type stability of solutions to a system of coupled nonlinear integral delay pantograph BVPs:
with
.
,
, and
are nonlinear, and
is bounded.
In this paper, inspired by [
33] and the above papers, we focus on the intention in which some qualitative aspects of possible solutions for a system of the coupled fractional sequential Navier model are investigated. In more precise words, we consider the following structure of a coupled sequential Navier FBVPs as follows:
where
,
and
. Moreover, the operator
denotes the Caputo fractional derivative of different orders. Furthermore, two continuous single-valued functions
are assumed to be arbitrary equipped with some needed properties, which are explained in the sequel.
Notice that the novelty of our paper is that the above suggested structure for the Navier problem is unique and novel, and one can consider it as a generalized fractional model of standard Navier problem in the context of Caputo operators. Indeed, by taking
and
, we obtain the standard system of Navier BVPs of the fourth orders formulated by the following.
For deriving the needed conditions implying the uniqueness and existence of solutions to a given coupled system of sequential Navier FBVPs, fixed point theory is used in this paper. In this direction, the Krasnoselskii’s fixed point theorem and Banach’s contraction principle have the key role for proving the existence and uniqueness of solution. To study the H-U-type stability criterion, we first define the relevant notions for the given system (Equation (
1)) and then prove the results with respect to this qualitative property. Along with these, in the sequel, the approximate solutions of Equation (
1) are obtained by applying numerical algorithms arising in the GDT-method. All these approximate solutions are plotted in two illustrative examples. We emphasize that the main motivation is that we conduct our research based on numerical methods of differential transform type to search for approximate solutions of a new fractional model of Navier BVP, which is more applicable in fourth-order models arising in engineering, and this renders our theoretical findings as useful results. In other words, for the first time, we apply the generalized differential transform method for a real model of boundary value problems to investigate the qualitative behaviors of the given system. Until now, the existing limited works regarding the Navier problem studied the existence results for integer-order systems, while we not only generalize the supposed system to a fractional structure but we also try to use an accurate algorithm for finding the approximate solution. These results show the novelty of our research. By the accuracy of this method, we can analyze other models in this direction.
The rest of the contents are as follows: Preliminaries are collected in the next section. The results in relation to the existence of solution and its uniqueness are presented in
Section 3. In
Section 4, the results regarding H-U-type stability criterion are proved.
Section 5 introduces numerical algorithms of the GDT-method for a given sequential system (
1). Different cases of the sequential Navier system are analyzed in two examples (with graphs) in
Section 6. The last section is devoted to presenting conclusive remarks.
3. Results for Existence
It is an evident notion that is a space of the Banach type subject to the norm . Consequently, is a product Banach space that is equipped with norm .
Proposition 2. Let , , , and . Then the solution of the nonlinear sequential fractional Navier BVP defined by the following:is given by Proof. We consider the function
as a solution for the nonlinear sequential Navier BVP (
3). Then, we obtain the following:
. By virtue of
and by taking the fractional integral in the Riemann-Liouville settings of order
on both sides of the latter equation, we get
so that
are some constants that we need to find. Now, by the third condition
, we obtain
. Thus, the following is the case.
On the other hand, by considering Equation (
5) and the fourth condition
, we obtain the following.
Thus, the following is the case.
In the sequel, in view of Equation (
6), relation (
5) becomes the following.
Again, by virtue of
and by taking the fractional integral in the Riemann–Liouville settings of order
on both sides of the latter equation, we obtain the following:
in which
and
are some constants that we have to find. Immediately, the first condition
gives us
. Consequently, we have the following.
Lastly, the second condition
implies that the following is the case.
Consequently, the constant
is obtained as follows.
We insert
into Equation (
8) and obtain the following.
This yields the result that
satisfies the integral Equation (
4), and the proof is completed. □
In view of above proposition, we here present an equivalent version of the coupled system of integral equations in relation to the given system of coupled sequential Navier BVPs (
1) by the following proposition.
Proposition 3. Let , and and . Then, an equivalent version of the coupled BVPs of fractional Navier differential equations is as follows: This is given by the following coupled integral equations. Based on Proposition 3 and because of our further proofs, we here define
and
by the following:
and
Thus, the following system of operator equations is produced as follows.
Now, we introduce defined by , and we find its fixed points. To perform this, we try to use the theory of fixed points due to the Banach and Krasnoselskii. Let us now remember these two fixed point theorems.
Theorem 1 (Banach, [
35])
. Let be a complete metric space and be a contraction. Then, there is a unique such that Theorem 2 (Krasnoselskii, [
35])
. Assume that is a bounded, closed, and convex set in the Banach space and are two operators satisfying the following: (a) for each ; (b) is a contraction; (c) is compact and continuous. Then, there is such that To continue the proof of our main results, we focus on the following hypotheses that are required.
Hypothese 1 (H1). forand
Hypothese 2 (H2). There issatisfying the following. Hypothese 3 (H3). There issatisfying the following.forand Now, for more convenience in computations, we set the following.
At this time, we can establish the following existence theorem.
Theorem 3. Suppose that Hypotheses ()–() are valid together with and . Then, the coupled sequential FBVPs of the Navier model (1) possess a unique solution. Proof. First, we choose
where
and
. We consider the bounded, closed, and convex set
defined by
From Hypotheses (H1) and (H2), we can write, for each
and
that the following is the case.
By some simple calculations, we obtain the following.
Then, by Definition 3, we obtain the following.
Thus, Equations (
14) and (
15) provide the following.
By following the same procedure, we can obtain the following.
Consequently, Equations (
16) and (
17) result in
Therefore
.
We prove that
is a contraction. For this aim, let us consider
, and
arbitrarily. Then, we have the following.
On the other hand, since the following is the case:
by using (
19), we obtain the following.
From Equations (
18) and (
20), we obtain the following.
By the same arguments, we obtain the following.
Therefore, Equations (
21) and (
22) together with the assumptions
and
result in
This means that
is a contraction. Hence, Theorem 1 ensured that the coupled sequential FBVPs of Navier model (
1) possess a unique solution; thus, the proof is now completed. □
In order to continue the establishment of the main existence result, we need to decompose the operators
and
as follows:
and
, where the following is the case.
In this case, the operator
can be expressed as
where
and
are given by the following.
In addition, suppose that the functions K and M satisfy the following assumption.
Hypothese 4 (H4). There existssuch that the following is the case:andfor alland for each Theorem 4. Suppose that the assumptions Hypotheses ()–() hold. Furthermore, the conditionsandare valid. Then, the coupled sequential FBVPs of Navier model (1) has at least one solution. Proof. First of all, the continuity property of the operator
is obtained from that of the functions
K and
M. Let the set
D be bounded in
. Then, in view of the assumption (H4), we have the following for any
and all
.
On the other hand, by
and by Definition 3, we obtain the following.
Thus, Equations (
26) and (
27) provide the following.
In a similar manner, we have the following.
Therefore, Equations (
28) and (
29) provide the boundedness of
In the sequel, we shall investigate that
is equicontinuous. Let
with
and
We have the following.
In a similar manner, we obtain the following.
We also have the following.
By using the same arguments, we obtain the following.
From inequalities (Equations (
30)–(
33)), we conclude
and
The obtained inequalities (
34)–(
35) provide
and
if
Therefore, by Arzela–Ascoli’s theorem, it follows that
is continuous and compact.
Finally, we prove the last part of the theorem regarding the operator
. For each
we have the following.
Similarly, we have the following.
We also have the following:
and
Then, the following is the case:
and
Consequently, in view of Equations (
36), (
37), (
40), and (
41), we obtain
and
Therefore, from Equations (
42) and (
43) together with the conditions (
24) and (
25), it follows that
is a contraction. Hence, by the conclusion of Theorem 2, we conclude
has at least one fixed point which is the solution of the coupled sequential FBVPs of Navier model (
1). □
4. Results for H-U-Type Stability
In the present section, we investigate some sufficient conditions to obtain H-U-stability results of the solutions to the coupled sequential FBVPs of Navier model (
1). Before starting work in this regard, we present some auxiliary definitions.
Definition 4 ([
36,
37])
. Let . Then, the operator equation of the following:is said to be H-U-stable, if for the given inequalitythere is some such that for each solution of the Equation (44), we can find some satisfying (44) such that the following is the case. Now, based on above definition, we define two operators
The coupled system of the following:
is called H-U-stable if, for the system, the following is the case.
Two constants
can be found provided that for each
satisfying (
45), a unique solution
exists for the system (
45) such that the following is the case.
Remark 1. There are two functions with respect to μ and ν, respectively, and that satisfy the following:and Lemma 1. Suppose that is a solution of (46) with the following. Then, the following system of inequalities holds:where , and and are defined by Equations (11) and (12), respectively. Proof. In view of the condition
(Remark 1), we have the following.
By Proposition (3), the solution of Equation (
47) is given by the following.
Since
then from the last system, we have the following:
which provides the following.
With the same computation techniques, we obtain the following.
On the other hand, we have the following.
With the same arguments, we obtain the following.
Therefore, from Equations (
48)–(
51), it follows that the following is the case.
The proof is completed. □
Theorem 5. Consider the assumptions (H2) and (H3). If the following is the case: where then the solution of the coupled BVPs of fractional Navier DEs (9) is H-U-stable. Proof. Let
be a solution of the following system of inequalities:
and
be a unique solution of the following.
Then, by Proposition (3) together with Equation (
9), the solution of Equation (
52) is given by
and
Then, from the last system, we can write the following.
From the last inequalities and Lemma (1) with some modifications, we obtain the following.
In an analogous manner, we find the following.
Since we have assumed that
then from Equations (
53) and (
54), we obtain
and
Consequently, Equations (
55) and (
56) result in the following.
Consequently, the solution of the coupled BVPs of fractional Navier differential Equations (
9) is H-U-stable. □
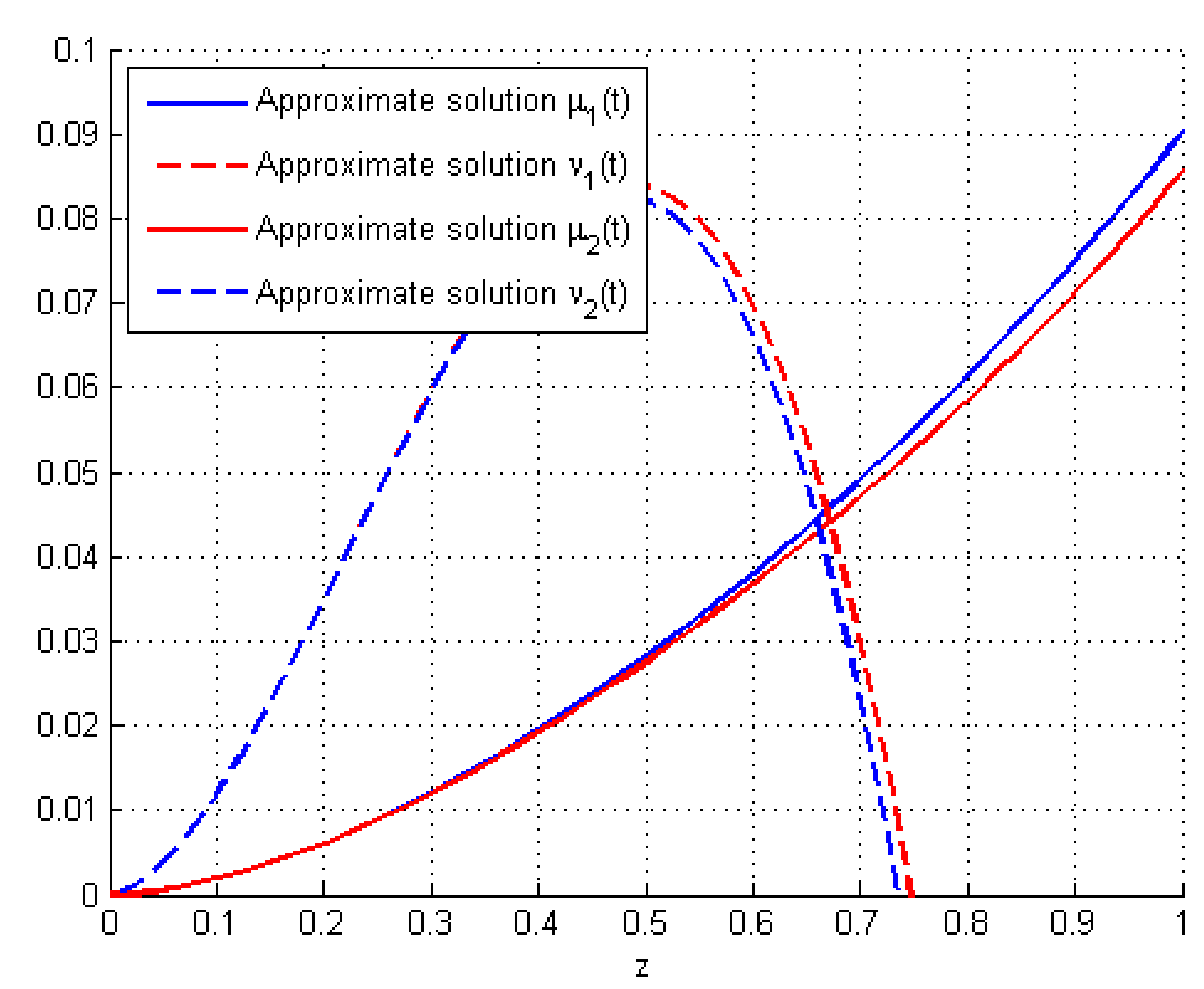
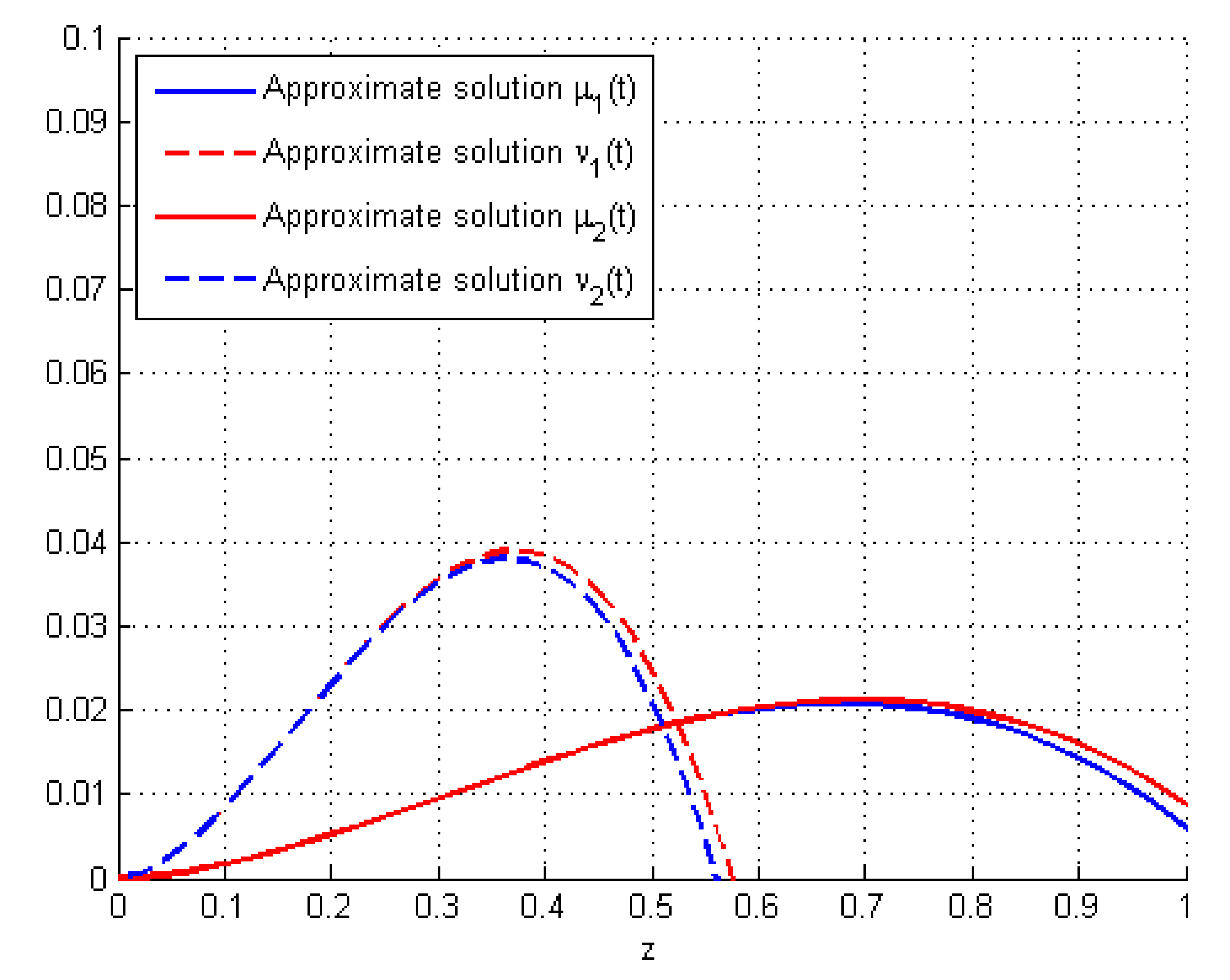
5. Numerical Solutions via GDT-Method
Due to the complexity of the nonlinear FDEs, it would be time consuming to obtain the exact solutions of given boundary problems with complicated nonlinear boundary conditions. Hence, we need to try deriving new approximate techniques and methods to solve these nonlinear problems. In the existing techniques, there exist some numerical methods that are applicable in finding the approximate solutions for nonlinear BVPs of non-integer orders. In the present study, we aim to apply one of these methods called the differential transformation method, which Zhou has presented in [
38] and Odibat et al. had later extended it to the generalized version called GDT-Method in [
39]. It is an iterative technique that yields analytical solutions of the Taylor series to FDEs with arbitrary boundary or initial conditions. In fact, it is with respect to the generalized Taylor’s formulas. For this reason, we shall use the GDT-Method to obtain approximate solutions of our coupled Navier FBVPs (
1).
The generalized differential transform for the
-derivative of
and
in terms of one variable is introduced by
in which
[
40]. The inverses are given as follows.
Therefore, the approximate solutions of the Navier model (
1) are found in the form of a finite series of the analytical polynomials:
where
stands for the order of the mentioned transformation and must be taken so that
, and
with
and
are the generalized differential transforms of
and
, respectively, and they are given as
in which
and
are the generalized
-differential transforms of
and
, respectively.
Since
, and
so their GDTs provide
,
, and
,
for all
satisfying
or
,
for all
satisfying
or
, where
and
are unknowns that can be computed by applying other initial conditions of the Navier model (
1).
By recursive Equation (
59), the solution
of Navier problem (
1) can be represented via the following series:
where
, and
are coefficients in terms of
and
, which can be obtained by invoking other initial conditions of given Navier problem (
1).
From (
60), we have the following.
Therefore, Equation (
61) yields the following system.
Finally, by solving Equation (
62) in terms of
and
and replacing them in Equation (
60), we find the approximate solutions of Navier model (
1).
Estimation of Error
The base of the GDT-method consists in finding a development in fractional series for solutions of nonlinear models containing fractional derivatives around the initial value
.
For estimation of error, the following theorems are useful.
Theorem 6 ([
41])
. Let . Then, the series solution converges if there exists such that the following is the case. Theorem 7 ([
41])
. Suppose that the series solution with converges to the solution . If the truncated series is an approximation to the solution , then the maximum absolute truncated error is estimated as follows. In conclusion, in view of Theorem 6, we find that the fractional power series solution converges to the exact solution if there exists such that
In other words, if for each
, we have the folllowing:
where
then, the series solution
converges to the exact solution
, when
, for all
. In addition, the conclusion of Theorem 7 confirms that the maximum absolute truncation error is estimated to be the following:
where
Consequently, if the trucated series
is an approximation to the solution
defined by Equation (
63), then the maximum absolute truncated error is estimated as follows:
where
and
.