Homotopy Perturbation Method for the Fractal Toda Oscillator
Abstract
:1. Introduction
2. Fractal Toda Oscillator and Fractal Weierstrass Theorem
3. A Simplified Model for the Fractal Toda Oscillator
Application of the HPM
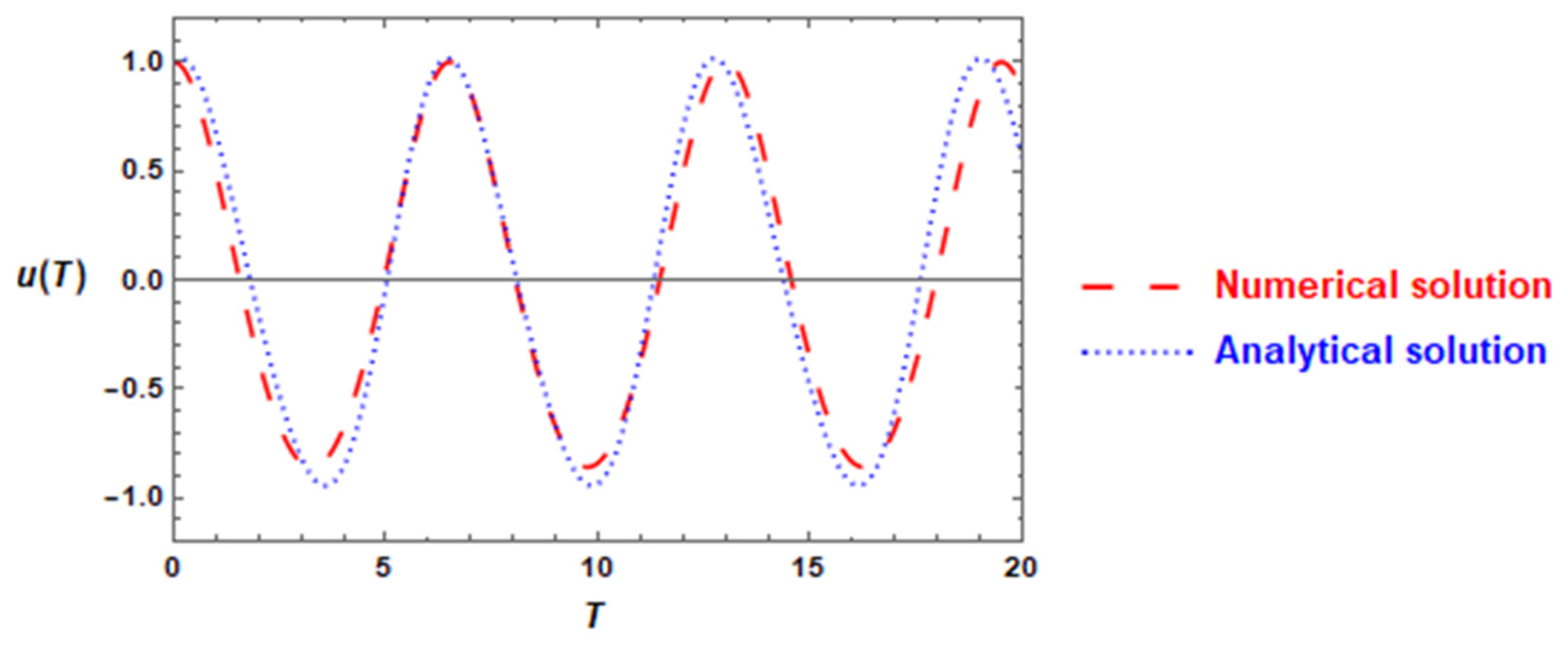
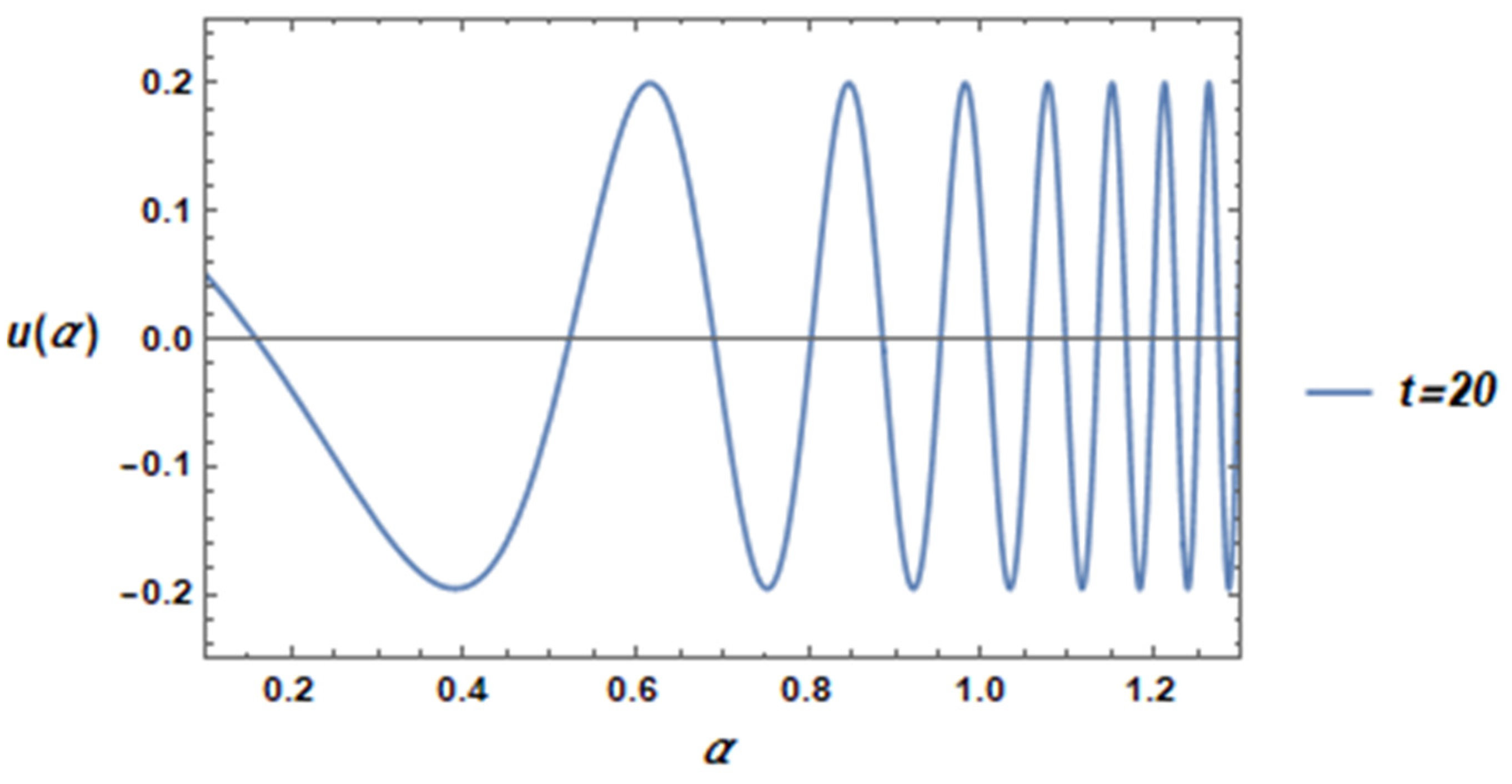
4. Numerical Illustration
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- He, J.H. Variational principle and periodic solution of the Kundu–Mukherjee–Naskar equation. Results Phys. 2020, 17, 103031. [Google Scholar] [CrossRef]
- He, J.H.; Anjum, N.; Skrzypacz, P.S. A Variational Principle for a Nonlinear Oscillator Arising in Microelectromechanical System. J. Appl. Comput. Mech. 2021, 7, 78–83. [Google Scholar] [CrossRef]
- Liu, H.Y.; Li, Z.M.; Yao, S.W.; Yao, Y.J.; Liu, J. A variational principle for the photocatalytic NOx abatement. Therm. Sci. 2020, 24, 2515–2518. [Google Scholar] [CrossRef]
- He, J.-H.; Hou, W.-F.; Qie, N.; Gepreel, K.A.; Shirazi, A.H.; Sedighi, H.M. Hamiltonian-based frequency-amplitude formulation for nonlinear oscillators. Facta Univ. Ser. Mech. Eng. 2021, 19, 199–208. [Google Scholar] [CrossRef]
- He, J.H. The simpler, the better: Analytical methods for nonlinear oscillators and fractional oscillators. J. Low Freq. Noise Vib. Act. Control 2019, 38, 1252–1260. [Google Scholar] [CrossRef] [Green Version]
- He, J.H. The simplest approach to nonlinear oscillators. Results Phys. 2019, 15, 102546. [Google Scholar] [CrossRef]
- Cialdi, S.; Castelli, F.; Prati, F. Lasers as Toda oscillators: An experimental confirmation. Opt. Commun. 2013, 287, 76–179. [Google Scholar] [CrossRef]
- Elías-Zúñiga, A.; Palacios-Pineda, L.M.; Jiménez-Cedeño, I.H.; Martínez-Romero, O.; Trejo, D.O. Equivalent power-form representation of the fractal Toda oscillator. Fractals 2021, 29, 2150034. [Google Scholar] [CrossRef]
- Mboupda Pone, J.R.; Kingni, S.T.; Kol, G.R.; Pham, V.T. Hopf bifurcation, antimonotonicity and amplitude controls in the chotic Toda jerk oscillator: Analysis, circuit realization and combination synchronization in its fractional-order form. Automatika 2019, 60, 149–161. [Google Scholar] [CrossRef]
- Takahashi, D.A. Newton’s equation of motion with quadratic drag force and Toda’s potential as a solvable one. Phys. Scr. 2018, 93, 075204. [Google Scholar] [CrossRef] [Green Version]
- Tian, D.; Ain, Q.T.; Anjum, N. Fractal N/MEMS: From pull-in instability to pull-in stability. Fractals 2021, 29, 2050030. [Google Scholar] [CrossRef]
- Tian, D.; He, C.H. A fractal micro-electromechanical system and its pull-in stability. J. Low Freq. Noise Vib. Act. Control 2021. [Google Scholar] [CrossRef]
- Tian, D.; He, C.H.; He, J.H. Fractal Pull-in Stability Theory for Microelectromechanical Systems. Front. Phys.-Math. Stat. Phys. 2021, 9, 606011. [Google Scholar]
- Ji, F.Y.; He, C.H.; Zhang, J.J.; He, J.H. A fractal Boussinesq equation for nonlinear transverse vibration of a nanofiber-reinforced concrete pillar. Appl. Math. Model. 2020, 82, 437–448. [Google Scholar] [CrossRef]
- He, C.-H.; He, J.-H.; Sedighi, H.M. Fangzhu: An ancient Chinese nanotechnology for water collection from air: History, mathematical insight, promises, and challenges. Math. Methods Appl. Sci. 2021. [Google Scholar] [CrossRef]
- Wang, K.L. Effect of Fangzhu’s nano-scale surface morphology on water collection. Math. Methods Appl. Sci. 2021. [Google Scholar] [CrossRef]
- He, J.-H.; El-Dib, Y.O. Homotopy perturbation method for Fangzhu oscillator. J. Math. Chem. 2020, 58, 2245–2253. [Google Scholar] [CrossRef]
- He, C.H.; Liu, C.; He, J.H.; Shirazi, A.H.; Mohammad-Sedighi, H. Passive Atmospheric water harvesting utilizing an ancient Chinese ink slab and its possible applications in modern architecture. Facta Univ. Mech. Eng. 2021, 19, 229–239. [Google Scholar] [CrossRef]
- Wang, K.L. A new fractal model for the soliton motion in a microgravity space. Int. J. Numer. Methods Heat Fluid Flow. 2020. [Google Scholar] [CrossRef]
- Zuo, Y.-T. A gecko-like fractal receptor of a three-dimensional printing technology: A fractal oscillator. J. Math. Chem. 2021, 59, 735–744. [Google Scholar] [CrossRef]
- Elias-Zuniga, A.; Palacios-Pineda, L.M.; Jiménez-Cedeño, I.H.; Martínez-Romero, O.; Olvera-Trejo, D. A fractal model for current generation in porous electrodes. J. Electroanal. Chem. 2021, 880, 114883. [Google Scholar] [CrossRef]
- Elias-Zuniga, A.; Palacios-Pineda, L.M.; Jimenez-Cedeno, I.H.; Martínez-Romeroa, O.; Olvera-Trejo, D. Analytical solution of the fractal Cubic-Quintic Duffing equation. Fractals 2021, 29, 2150080. [Google Scholar] [CrossRef]
- He, C.H.; Liu, C.; Gepreel, K.A. Low frequency property of a fractal vibration model for a concrete beam. Fractals 2021, 29, 2150117. [Google Scholar] [CrossRef]
- He, C.H.; Liu, C.; He, J.H.; Mohammad-Sedighi, H.; Shokri, A.; Gepreel, K.A. A fractal model for the internal temperature response of a porous concrete. Appl. Comput. Math. 2021, 20, 1871–1875. [Google Scholar]
- Wang, K.L.; Wei, C.F. A powerful and simple frequency formula to nonlinear fractal oscillators. J. Low Freq. Noise Vib. Act. Control 2020. [Google Scholar] [CrossRef]
- Elías-Zúñiga, A.; Palacios-Pineda, L.M.; Jiménez-Cedeño, I.H.; Martínez-Romero, O.; Trejo, D.O. He’s frequency–amplitude formulation for nonlinear oscillators using Jacobi elliptic functions. J. Low Freq. Noise Vib. Act. Control 2020, 39, 1216–1223. [Google Scholar] [CrossRef]
- He, J.H.; Kou, S.J.; He, C.H.; Zhang, Z.W.; Gepreel, K.A. Fractal oscillation and its frequency-amplitude property. Fractals 2021, 29, 2150105. [Google Scholar] [CrossRef]
- Feng, G.Q. He’s frequency formula to fractal undamped Duffing equation. J. Low Freq. Noise Vib. Act. Control 2021. [Google Scholar] [CrossRef]
- He, J.H.; Qie, N.; He, C.H.; Saeed, T. On a strong minimum condition of a fractal variational principle. Appl. Math. Lett. 2021, 119, 107199. [Google Scholar] [CrossRef]
- He, J.H.; Ain, Q.T. New promises and future challenges of fractal calculus: From two-scale thermodynamics to fractal variational principle. Therm. Sci. 2020, 24, 659–681. [Google Scholar] [CrossRef]
- He, J.H. A fractal variational theory for one-dimensional compressible flow in a microgravity space. Fractals 2020, 28, 2050024. [Google Scholar] [CrossRef]
- He, J.H. On the fractal variational principle for the Telegraph equation. Fractals 2021, 29, 2150022. [Google Scholar] [CrossRef]
- Wang, K.L.; Yao, S.W. Fractal variational theory for Chaplygin-He Gas in a microgravity condition. Comput. Methods Appl. Mech. Eng. 2020, 6, 1606–1612. [Google Scholar]
- Wang, K.L.; He, C.H. A remark on Wang’s fractal variational principle. Fractals 2019, 27, 1950134. [Google Scholar] [CrossRef]
- Khan, Y. A novel soliton solutions for the fractal Radhakrishnan-Kundu-Lakshmanan model arising in birefringent fibers. Opt. Quantum Electron. 2021, 53, 127. [Google Scholar] [CrossRef]
- Khan, Y. Fractal modification of complex Ginzburg-Landau model arising in the oscillating phenomena. Results Phys. 2020, 18, 103324. [Google Scholar] [CrossRef]
- Khan, Y. A variational approach for novel solitary solutions of FitzHugh-Nagumo equation arising in the nonlinear reac-tion-diffusion equation. Int. J. Numer. Methods Heat Fluid Flow 2020, 31. [Google Scholar] [CrossRef]
- Cao, X.Q.; Hou, S.C.; Guo, Y.N.; Zhang, C.Z.; Peng, K.C. Variational principle for 2+1 dimensional Broer-Kaup equations with fractal derivatives. Fractals 2020, 28, 2050107. [Google Scholar] [CrossRef]
- He, J.H.; El-Dib, Y.O. The reducing rank method to solve third-order Duffing equation with the homotopy perturbation. Numer. Methods Partial. Differ. Equ. 2020, 37, 1800–1808. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation technique. Comput. Methods Appl. Mech. Eng. 1999, 178, 257–262. [Google Scholar] [CrossRef]
- He, J.H.; El-Dib, Y.O. Homotopy perturbation method with three expansions. J. Math. Chem. 2021, 59, 1139–1150. [Google Scholar] [CrossRef]
- He, J.H.; El-Dib, Y.O. Periodic property of the time-fractional Kundu–Mukherjee–Naskar equation. Results Phys. 2020, 19, 103345. [Google Scholar] [CrossRef]
- Li, X.X.; He, C.H. Homotopy perturbation method coupled with the enhanced perturbation method. J. Low Freq. Noise Vib. Act. Control 2019, 38, 1399–1403. [Google Scholar] [CrossRef]
- Ji, Q.P.; Wang, J.; Lu, L.X.; Ge, C.F. Li-He’s modified homotopy perturbation method coupled with the energy method for the dropping shock response of a tangent nonlinear packaging system. J. Low Freq. Noise Vib. Act. Control 2020, 40, 675–682. [Google Scholar] [CrossRef]
- Shen, Y.; El-Dib, Y.O. A periodic solution of the fractional sine-Gordon equation arising in architectural engineering. J. Low-Freq. Noise. Vib. Act. Control 2020. [Google Scholar] [CrossRef] [Green Version]
- El-Dib, Y.O.; Elgazery, N. Effect of fractional derivative properties on the periodic solution of the nonlinear oscillators. Fractals 2020, 28, 2050095. [Google Scholar] [CrossRef]
- El-Dib, Y.O. Homotopy perturbation method with rank upgrading technique for the superior nonlinear oscillation. Math. Comput. Simul. 2021, 182, 555–565. [Google Scholar] [CrossRef]
- El-Dib, Y.O.; Matoog, R.T. The Rank Upgrading Technique for a Harmonic Restoring Force of Nonlinear oscillators. Appl. Comput. Mech. 2021, 7, 782–789. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, J.-H.; El-Dib, Y.O.; Mady, A.A. Homotopy Perturbation Method for the Fractal Toda Oscillator. Fractal Fract. 2021, 5, 93. https://doi.org/10.3390/fractalfract5030093
He J-H, El-Dib YO, Mady AA. Homotopy Perturbation Method for the Fractal Toda Oscillator. Fractal and Fractional. 2021; 5(3):93. https://doi.org/10.3390/fractalfract5030093
Chicago/Turabian StyleHe, Ji-Huan, Yusry O. El-Dib, and Amal A. Mady. 2021. "Homotopy Perturbation Method for the Fractal Toda Oscillator" Fractal and Fractional 5, no. 3: 93. https://doi.org/10.3390/fractalfract5030093
APA StyleHe, J.-H., El-Dib, Y. O., & Mady, A. A. (2021). Homotopy Perturbation Method for the Fractal Toda Oscillator. Fractal and Fractional, 5(3), 93. https://doi.org/10.3390/fractalfract5030093






