Abstract
We considered forced harmonic vibration systems with the Liouville–Weyl fractional derivative where the order is between 1 and 2 and with a distributed-order derivative where the Liouville–Weyl fractional derivatives are integrated on the interval [1, 2] with respect to the order. Both types of derivatives enhance the viscosity and inertia of the system and contribute to damping and mass, respectively. Hence, such types of derivatives characterize the viscoinertia and represent an “inerter-pot” element. For such vibration systems, we derived the equivalent damping and equivalent mass and gave the equivalent integer-order vibration systems. Particularly, for the distributed-order vibration model where the weight function was taken as an exponential function that involved a parameter, we gave detailed analyses for the weight function, the damping contribution, and the mass contribution. Frequency–amplitude curves and frequency-phase curves were plotted for various coefficients and parameters for the comparison of the two types of vibration models. In the distributed-order vibration system, the weight function of the order enables us to simultaneously involve different orders, whilst the fractional-order model has a single order. Thus, the distributed-order vibration model is more general and flexible than the fractional vibration system.
1. Introduction
Fractional calculus has undergone rapid developments in its theory, methods, and applications in recent decades due to its capability of modeling memory phenomena and hereditary properties. Its application range includes viscoelastic mechanics [1,2,3], anomalous diffusion-related problems [2,3], control theory [4,5], vibration theory [6], signal processing [7], bioengineering [8], data fitting [9], and so on. Interpretations that use physics and geometry for fractional calculus have been developed [10,11]. Torbati and Hammond [10] applied fractional calculus to research on fractals to model self-similarity, hereditary effects, and partial dissipation. Podlubny [11] introduced two kinds of time—the equably flowing homogeneous individual time and the cosmic inhomogeneous time—to show that the fractional derivative describes the relationship between the real distance and the individual speed of a moving object.
Fractional calculus has been applied to viscoelasticity theory since the middle of the last century. Its wide uses and the importance of viscoelastic materials have promoted the theoretical development of fractional calculus. Scott-Blair [1] suggested a fractional constitutive relation for viscoelastic bodies with a fractional derivative of order , which represents the mechanical properties between elastic solids and viscous fluids. The fractional model is referred to as the Scott-Blair model [2] and represents a “spring-pot" element [12], which is homologous with the dashpot element. In [2], fractional constitutive models describing viscoelastic behavior, including the fractional Kelvin–Voigt, Maxwell, and Zener models, were considered. In [13], a fractional Maxwell relation was used to model the flow of a superpolymer. In [14], a fractional constitutive relation with five parameters was investigated for high-frequency polymeric materials. In addition, a six-parameter fractional constitutive model was proposed and analyzed [15].
Fractional oscillation or vibration problems have attracted the interest of many scholars, such as Caputo [16], Bagley and Torvik [17], Beyer and Kempfle [18], and more [19,20,21,22]. Li et al. [20] considered impulse response and stability for fractional oscillation. In [21], equivalent integer-order equations were presented for three types of fractional oscillators. In [22], fractional vibration and Brownian motion were compared. In [23], steady-state responses to harmonic and periodic excitations in a fractional vibration system were given. Shen et al. [24], Li et al. [25], and Wang and Hu [26] explored the dynamics and stability of a fractional-order system.
In research on dissipation mechanisms, Caputo [16,27] generalized fractional derivatives to a situation where the fractional-order derivatives are integrated with respect to the order of differentiation, which is currently called the distributed-order derivative. In [28], the distributed-order derivative was used in the constitutive relation of dielectric media with model diffusion. In [29], solutions of distributed-order differential equations were considered. In [30], mechanical models of a viscoelastic body with distributed-order derivatives were analyzed. In [31], the properties of the solutions for a distributed-order oscillator system were investigated. In [32], the steady-state periodic responses of a distributed-order vibration system were considered.
For a piecewise continuous function on , the Riemann–Liouville fractional integral is defined as
and where is the Gamma function,
There exist different definitions for fractional derivatives. The th-order Riemann–Liouville fractional derivative is defined, when it exists, as
The th-order Caputo fractional derivative is defined as
In this article, we employ fractional integrals and derivatives with support in the real set . That is, the lower limit in the fractional integral is taken as . In this case, the two fractional derivatives in Equations (2) and (3) are consistent [4]. We denote them uniformly as . Such cases are also called the Liouville–Weyl fractional integral and derivative [2]. With such definitions, the steady-state solutions of a vibration system can be directly obtained. We note that the steady-state solutions are more significant than the transient solution in the vibration mechanics. Moreover, the solution can be considered within the field of elementary functions.
If is a non-negative integer, will be used to represent the integer-order derivative . We notice the convenient formula [2,4]:
For comparison, we review the classical vibration system with the harmonic excitation
where i is the imaginary unit and are all positive constants. The steady-state response is
where is the phase difference between the excitation and the response within the range , and it satisfies
The phase difference may be explicitly given in the following equation:
where is the principal value of the inverse tangent function with the range .
In fractional constitutive relations and their simulations of the oscillations of viscoelastic bodies, the order of the fractional derivative is usually taken between 0 and 1 to characterize both the viscosity and the elasticity (e.g., in [32,33]). In [34], a fractional vibration equation was considered, and it was found that if the order satisfies , the fractional derivative contributes to both the viscosity and the inertia, i.e., the viscoinertia, corresponding to the terminology of viscoelasticity. We will continue this research on the subject of the fractional calculus and the viscoinertia and will include both the case of the fractional order and the case of the distributed order in this paper.
We note that there is a mechanical element, the inerter [35,36,37]—analogous to the spring or dashpot—which has two endpoints, one of which can shift relative to the other end. However, the magnitude of the external force depends on the relative acceleration of the two ends. Inerters have been applied to vehicle suspension, motorcycle steering damping systems, and other structures [38,39]. In [40], effects of inerter-based isolators were shown to have some advantages over the effects of traditional dynamic absorbers if the same mass ratio was applied. In [41], multichannel inertial absorbers were distributed on a panel to implement vibration control in a wide frequency range. In [42], Wang et al. presented a hydraulic inerter with an external helical tube and found that in high-frequency stimulation, the hydraulic inerter could be treated as a component with a damper and an inerter in parallel.
In this article, a fractional derivative model of these dampers with inertia is presented. We focus on the effects of the fractional derivative and the distributed-order derivative on the viscosity and the inertia in a vibration system. Both the fractional and distributed-order derivatives play the role of a damper and an inerter in parallel. In the next section, we consider a forced harmonic vibration system with the fractional-order derivative , where . We derive the equivalent integer-order vibration system and discuss the contribution of damping and that of mass, as well as the frequency–amplitude response and frequency-phase response.
In Section 3, we further investigate the harmonic vibration system with the distributed-order derivative , where is a weight function of the order . The distributed-order derivative enhances the viscosity and inertia of the system, contributes to the damping and mass, and thus represents an “inerter-pot” element. The equivalent damping, the equivalent mass, and the steady-state response are expressed with the general weight function . Compared with the fractional case, the weight function influences the viscosity and inertia of the system instead of the order in Section 2.
In Section 4, we explore a distributed-order vibration model where the weight function is taken as an exponential function involving the parameter p, . Detailed analyses of the weight function, the contribution of damping, and the contribution of mass are given. Frequency–amplitude curves and the frequency-phase curves are plotted for various coefficients and parameters for comparison with the fractional case in Section 2. Section 5 presents our conclusions.
2. Fractional-Order Vibration Characterizing Viscoinertia
Consider a fractional-order vibration system with a complex harmonic excitation
where are positive real constants, i is the imaginary unit, the order is restricted on the interval , and is the system response to be determined.
Similarly to the case of integer orders, the form of the response is assumed to be
where X is independent of t and is called the complex amplitude. Substituting the integer-order derivatives and the fractional derivative into Equation (9) and eliminating the nonzero factor , we solve for the amplitude X as
Using the equality , we rewrite the complex amplitude as
Since , and the equality in the first expression holds only for , while the equality in the second expression holds only for . Thus, the two terms generated from the fractional derivative enhance the viscosity and inertia, i.e., they contribute to the damping and mass, respectively. In view of this, we introduce the following equivalent damping and equivalent mass as
Using the equivalent damping and equivalent mass, Equation (12) has the form
Further, we denote the denominator as the exponential form
where the phase difference between the excitation and the response is determined as
Thus, substituting Equation (15) into Equation (10), we obtain the response of the system to complex harmonic excitation:
As regards the steady-state response, the fractional-order vibration system (9) is equivalent to the integer-order system
where the coefficients and are frequency-dependent. We refer to
as the damping contribution and the mass contribution, respectively. In Figure 1 and Figure 2, the curves of the damping contribution and the mass contribution versus the order are shown for and different values of .
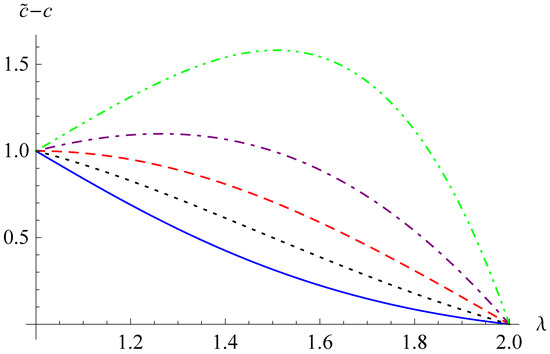
Figure 1.
The curves of versus for and for 0.2 (solid line), 0.5 (dotted line), 1 (dashed line), 2 (dot-dashed line), and 5 (dot-dot-dashed line).
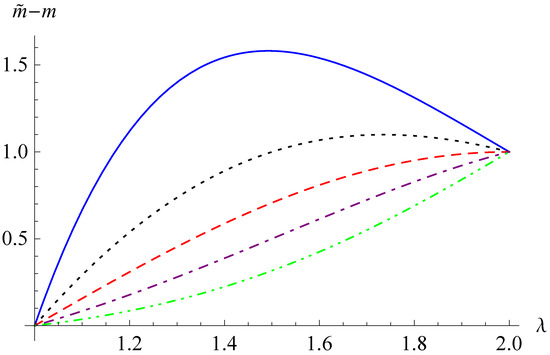
Figure 2.
The curves of versus for and for 0.2 (solid line), 0.5 (dotted line), 1 (dashed line), 2 (dot-dashed line), 5 (dot-dot-dashed line).
At the two endpoints of , the equivalent damping and equivalent mass satisfy the properties
From the derivatives
we obtain the following conclusions.
Proposition 1.
(i) When the damping contribution is a strictly decreasing function of λ; when , reaches a peak within the interval . (ii) When the mass contribution reaches a peak within the interval ; when , is a strictly increasing function of λ.
From Equation (17), the magnification factor of the amplitude is derived as a function of ,
where denotes the static elongation of the spring for the applied force . Equations (24) and (16) are also called the frequency–amplitude response and frequency-phase response, respectively. They completely determine the response features of the system.
We take , , and and 5 to explore the frequency–amplitude response and the frequency-phase response. In Figure 3 and Figure 4, the frequency–amplitude curves are shown for and 5, respectively, and for different values of . In Figure 5 and Figure 6, the frequency-phase curves are displayed for and 5, respectively, and for different values of . From Figure 3, Figure 4, Figure 5 and Figure 6, the increase in the order enhances the values of the resonance humps and makes the changes in the phase differences following more sensitive. In addition, the resonance humps in Figure 4 are shifted to the left compared with those in Figure 3, and the growth spurts of the phase differences appear for smaller values of in Figure 6 than in Figure 5.
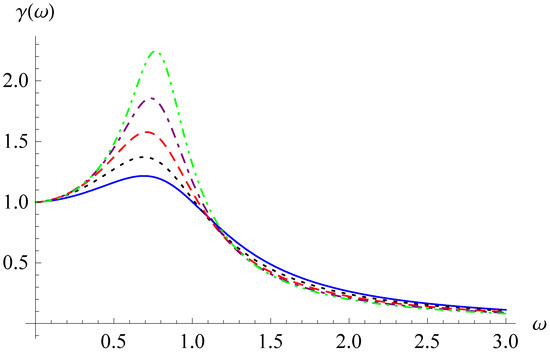
Figure 3.
Frequency–amplitude curves for , , , and (solid line), 1.3 (dotted line), 1.5 (dashed line), 1.7 (dot-dashed line), or 1.9 (dot-dot-dashed line).
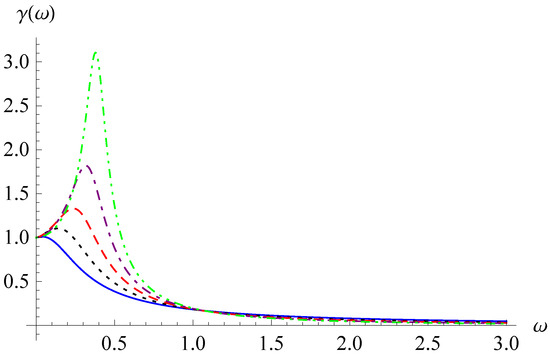
Figure 4.
Frequency–amplitude curves for , , , and (solid line), 1.3 (dotted line), 1.5 (dashed line), 1.7 (dot-dashed line), or 1.9 (dot-dot-dashed line).
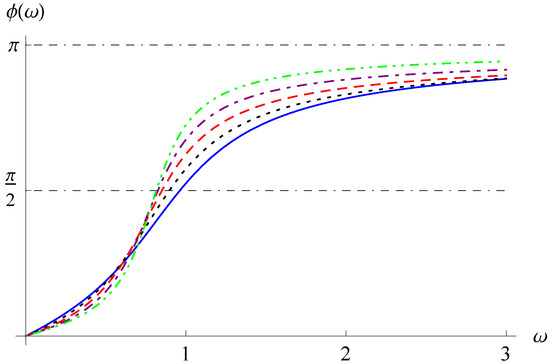
Figure 5.
Frequency–phase curves for , , , and (solid line), 1.3 (dotted line), 1.5 (dashed line), 1.7 (dot-dashed line), or 1.9 (dot-dot-dashed line).
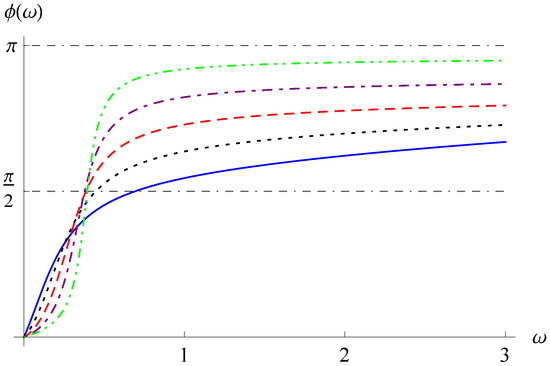
Figure 6.
Frequency–phase curves for , , , and (solid line), 1.3 (dotted line), 1.5 (dashed line), 1.7 (dot-dashed line), or 1.9 (dot-dot-dashed line).
3. Distributed-Order Vibration Characterizing Viscoinertia
Consider a forced harmonic vibration system equipped with the distributed-order derivative:
where are positive real constants, and is the weight function of the order that satisfies
We note that the constraint (27) is not a prerequisite for a distributed-order derivative. Here, is regarded as a weight function of the order . It includes the special case of the Dirac -function
In this case, Equation (25) degenerates to the fractional case in the last section.
Similarly to the last section, we suppose that the response is Substituting it into Equation (25) and eliminating the common factor , we obtain the complex amplitude as
The integration in Equation (28) may be decomposed into
where the imaginary part and the real part satisfy
Therefore, the distributed-order derivative enhances the viscosity and inertia and contributes to the damping and mass as well. We introduce the equivalent damping and equivalent mass as
That is, and are the damping contribution and mass contribution, respectively. Then, Equation (28) has the equivalent expression
and the equivalent integer-order system of (25) is
Therefore, we obtain the system response to complex harmonic excitation:
where the phase difference between the excitation and the response satisfies
From (35), the magnification factor of the amplitude is
In next section, the weight function is specified to analyze these results.
4. Results for the Weight Function in the Form of a Parametrized Exponential Function
The weight function can be specified in infinitely many ways. In this section, we consider the weight function in the form of an exponential involving the parameter p as
where the coefficient is
It is easy to verify that satisfies the conditions for a weight function in Equations (26) and (27). Choosing such a weight function can adequately express the shift of the order on the interval . Meanwhile, this weight function is easy to deal with in the following calculations. In Figure 7, we plot the curve of versus p on the interval . In Figure 8, we display the curves of versus on the interval for the values 0.01, 0.1, 1, 10, and 100. For , the weight function is the constant unity function.
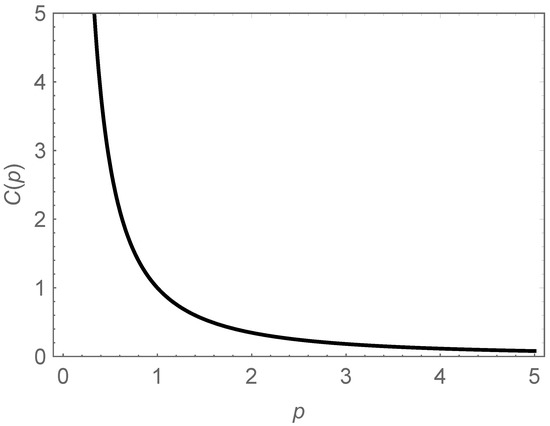
Figure 7.
Curves of versus p on the interval .
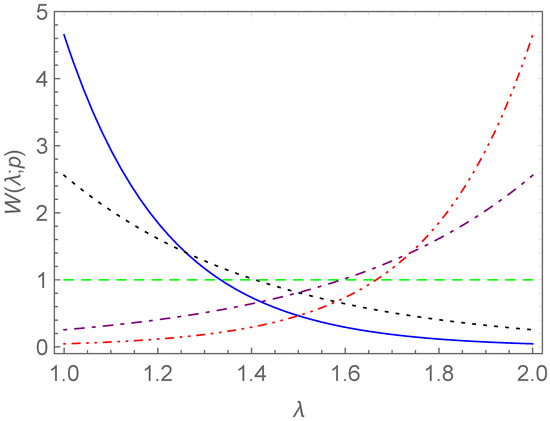
Figure 8.
Curves of versus on when p takes different values: (solid line), (dotted line), (dashed line), (dot-dashed line), and (dot-dot-dashed line).
In order to gain further understanding of the coefficient and the parametrized weight , we give the following two propositions.
Proposition 2.
is positive, monotonically decreasing, and differentiable on the interval
Proof.
It is direct that whenever and is continuous on the interval . By calculating the first-order derivative, we have
By the L’Hospital’s rule, we obtain the limitation Thus, we have , so is differentiable on the interval
In order to show that is monotonically decreasing, we let , the numerator in Equation (40). Then, It is clear that has a unique zero at , and reaches the minimum at as Thus, we have for . Therefore, we derive that for all This means that is monotonically decreasing. □
Proposition 3.
(i) The curves of versus λ and versus λ are symmetrical about the vertical line .
(ii) For , decreases monotonically on , while for , increases monotonically on .
(iii) decreases monotonically on , while increases monotonically on .
Proof .
(i) The relation
may be verified via direct substitution. (ii) From the sign of the derivative , we can obtain the monotonicity of the weight function on the interval . (iii) First, from
we calculate the derivative as
It is easy to verify that for and . Thus, ensures that is monotonically decreasing on . The monotonic increase in follows from the symmetry property in (i). The proof is complete. □
Considering the symmetry property stated in Proposition 3 (i) and shown in Figure 8, we will use the logarithmic scale of the parameter p whenever plotting the p axis. Substituting the weight function in Equation (38) into (31) and (32) and calculating the integrals, we obtain the damping contribution and the mass contribution for the case of the distributed-order derivative:
It is easy to verify that the equivalent damping and equivalent mass satisfy the following initial value and final value with respect to the parameter p:
In Figure 9, the curves of the damping contribution versus p are depicted for and different values of . In Figure 10, the curves of the mass contribution versus p for and different values of are shown. Here, logarithmic scales are used for the p axes with the range Compared with the single fractional case in Section 2, there are similar properties between the fractional order and the distributed order as far as the damping contribution and mass contribution.
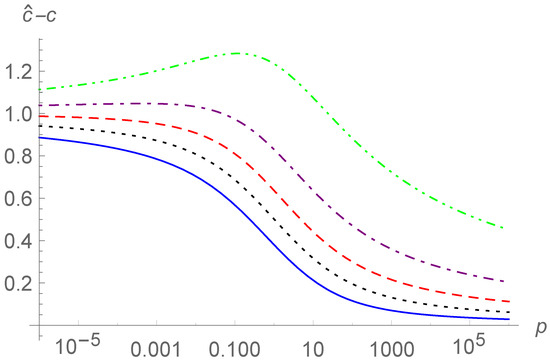
Figure 9.
The damping contribution versus p for and for (solid line), 0.5 (dotted line), 1 (dashed line), 2 (dot-dashed line), and 5 (dot-dot-dashed line).
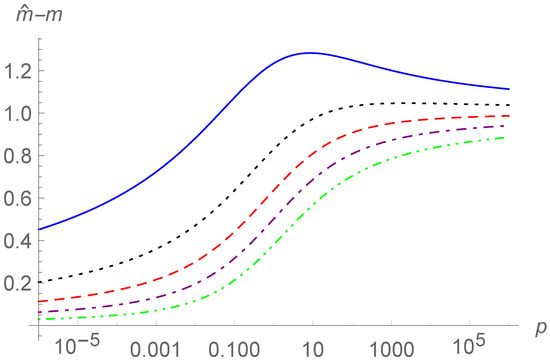
Figure 10.
The mass contribution versus p for and for (solid line), 0.5 (dotted line), 1 (dashed line), 2 (dot-dashed line), and 5 (dot-dot-dashed line).
By using the equivalent damping and the equivalent mass in Equations (43) and (44), the system response , the frequency–amplitude response , and the frequency-phase response can be calculated from Equations (35)–(37). We take , , and and 5 to examine the frequency–amplitude response and frequency-phase response for different values of the parameter p. In Figure 11 and Figure 12, the frequency–amplitude curves are shown for and 5, respectively. In Figure 13 and Figure 14, the frequency-phase curves are displayed for and 5, respectively.
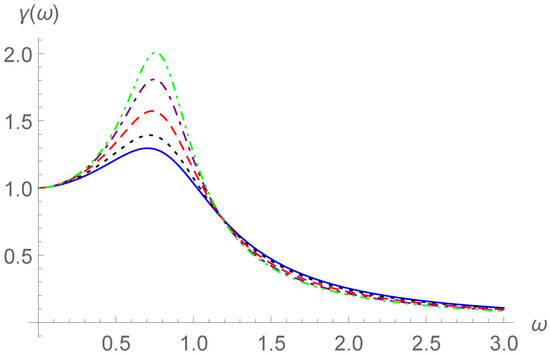
Figure 11.
Frequency–amplitude curves for , , , and (solid line), (dotted line), (dashed line), (dot-dashed line), or (dot-dot-dashed line).
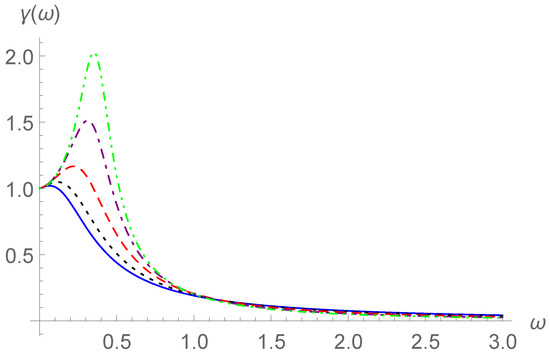
Figure 12.
Frequency–amplitude curves for , , , and (solid line), (dotted line), (dashed line), (dot-dashed line), or (dot-dot-dashed line).
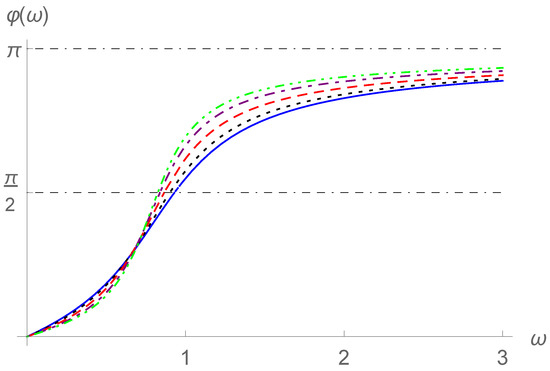
Figure 13.
Frequency–phase curves for , , , and (solid line), (dotted line), (dashed line), (dot-dashed line), or (dot-dot-dashed line).
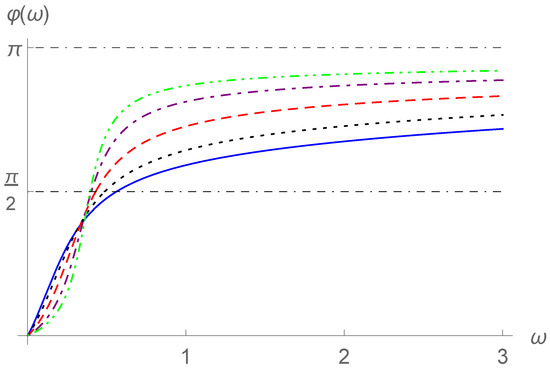
Figure 14.
Frequency–phase curves for , , , and (solid line), (dotted line), (dashed line), (dot-dashed line), or (dot-dot-dashed line).
Comparing Figure 11, Figure 12, Figure 13 and Figure 14 with Figure 3, Figure 4, Figure 5 and Figure 6, some similar characteristics can be observed. For example, similarly to the effects of increasing the order in Section 2, the growth of the parameter p heightens the resonance humps in Figure 11 and Figure 12 and makes the changes in the phase differences with more sensitive. Comparing Figure 11 and Figure 13 with Figure 12 and Figure 14, we find that the increase in brings forward the resonance humps and growth spurts of phase differences.
5. Conclusions
We considered forced harmonic vibration systems with a fractional-order derivative where and a distributed-order derivative where is a weight function of the order . Both of the two types of derivatives enhance the viscosity and inertia of the system, contribute to damping and mass, and play the role of a damper and an inerter in parallel. Hence, such types of derivatives characterize the viscoinertia and represent an “inerter-pot”, corresponding to a “spring-pot" in viscoelasticity.
In the distributed-order vibration system, the weight function of the order defined by Equations (26) and (27) can be given in infinitely many ways. Instead of the order in the fractional-order vibration model, we discuss the effects of the weight function on the system. The distributed-order vibration model is more self-directed and flexible than the fractional vibration system. In particular, the fractional vibration system is a special case of the distributed-order vibration if the weight function is the Dirac -function , .
For the fractional-order and the distributed-order vibration systems characterizing viscoinertia, we derived the equivalent damping and equivalent mass and gave the equivalent integer-order vibration systems. Further, we considered the damping contribution and the mass contribution of the fractional-order derivative and the distributed-order derivative, the frequency–amplitude response, and the frequency-phase response. Particularly, for the distributed-order vibration model where the weight function was taken as an exponential function involving the parameter p, , we gave detailed analyses for the weight function, the damping contribution, and the mass contribution. The frequency–amplitude curves and the frequency-phase curves were plotted for the two types of vibration models, and the various model coefficients and parameters were used for the comparison of the two vibration models.
Author Contributions
Conceptualization, J.-S.D. and D.-C.H.; Data curation, D.-C.H.; Formal analysis, J.-S.D. and D.-C.H.; Funding acquisition, J.-S.D.; Methodology, J.-S.D.; Software, J.-S.D. and D.-C.H.; Validation, J.-S.D. and D.-C.H.; Visualization, D.-C.H.; Writing—original draft, J.-S.D. and D.-C.H.; Writing—review and editing, J.-S.D. and D.-C.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (No. 11772203).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors show their appreciation for the valuable comments from the reviewers on the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Scott-Blair, G.W. A Survey of General and Applied Rheology; Pitman: London, UK, 1949. [Google Scholar]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity; Imperial College: London, UK, 2010. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic: San Diego, CA, USA, 1999. [Google Scholar]
- Jiao, Z.; Chen, Y.; Podlubn, Y.I. Distributed-Order Dynamic Systems–Stability, Simulation, Applications and Perspectives; Springer: London, UK, 2012. [Google Scholar]
- Li, M. Theory of Fractional Engineering Vibrations; De Gruyter: Berlin, Germany; Boston, UK, 2021. [Google Scholar]
- Sheng, H.; Chen, Y.; Qiu, T. Fractional Processes and Fractional—Order Signal Processing–Techniques and Applications; Springer: London, UK, 2012. [Google Scholar]
- Magin, R.L. Fractional Calculus in Bioengineering; Begell House: Danbury, CT, USA, 2006. [Google Scholar]
- Can, N.H.; Jafari, H.; Ncube, M.N. Fractional calculus in data fitting. Alex. Eng. J. 2020, 59, 3269–3274. [Google Scholar] [CrossRef]
- Torbati, M.M.; Hammond, J.K. Physical and geometrical interpretation of fractional operators. J. Frankl. Inst. 1998, 335, 1077–1086. [Google Scholar] [CrossRef]
- Podlubny, I. Geometric and physical interpretation of fractional integration and fractional differentiation. Fract. Calc. Appl. Anal. 2002, 5, 367–386. [Google Scholar]
- Koeller, R.C. Applications of fractional calculus to the theory of viscoelasticity. J. Appl. Mech. 1984, 51, 299–307. [Google Scholar] [CrossRef]
- Palade, L.I.; Verney, V.; Attané, P. A modified fractional model to describe the entire viscoelastic behavior of polybutadienes from flow to glassy regime. Rheol. Acta 1996, 35, 265–273. [Google Scholar] [CrossRef]
- Pritz, T. Five-parameter fractional derivative model for polymeric dampling materials. J. Sound Vib. 2003, 265, 935–952. [Google Scholar] [CrossRef]
- Duan, J.S.; Hu, D.C.; Chen, Y.Q. Simultaneous characterization of relaxation, creep, dissipation, and hysteresis by fractional-order constitutive models. Fractal Fract. 2021, 5, 36. [Google Scholar] [CrossRef]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent. Ann. Geophys. 1966, 19, 383–393. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P.J. A generalized derivative model for an elastomer damper. Shock Vib. 1979, 49, 135–143. [Google Scholar]
- Beyer, H.; Kempfle, S. Definition of physically consistent damping laws with fractional derivatives. ZAMM Z. Fur Angew. Math. Und Mech. 1995, 75, 623–635. [Google Scholar] [CrossRef]
- Achar, B.N.N.; Hanneken, J.W.; Clarke, T. Response characteristics of a fractional oscillator. Phys. Stat. Mech. Appl. 2002, 309, 275–288. [Google Scholar] [CrossRef]
- Li, M.; Lim, S.C.; Chen, S. Exact solution of impulse response to a class of fractional oscillators and its stability. Math. Probl. Eng. 2011, 2011, 657839. [Google Scholar] [CrossRef] [Green Version]
- Li, M. Three classes of fractional oscillators. Symmetry 2018, 10, 40. [Google Scholar] [CrossRef] [Green Version]
- Lim, S.C.; Li, M.; Teo, L.P. Locally self-similar fractional oscillator processes. Fluct. Noise Lett. 2007, 7, L169–L179. [Google Scholar] [CrossRef]
- Huang, C.; Duan, J.S. Steady-state response to periodic excitation in fractional vibration system. J. Mech. 2016, 32, 25–33. [Google Scholar] [CrossRef]
- Shen, Y.J.; Yang, S.P.; Xing, H.J. Dynamical analysis of linear single degree-of-freedom oscillator with fractional-order derivative. Acta Phys. Sin. 2012, 61, 110505. [Google Scholar]
- Li, C.P.; Deng, W.H.; Xu, D. Chaos synchronization of the Chua system with a fractional order. Phys. Stat. Mech. Appl. 2006, 360, 171–185. [Google Scholar] [CrossRef]
- Wang, Z.H.; Hu, H.Y. Stability of a linear oscillator with damping force of the fractional-order derivative. Sci. China Ser. 2010, 53, 345–352. [Google Scholar] [CrossRef]
- Caputo, M. Mean fractional-order-derivatives differential equations and filters. Ann. Dell’Univ. Ferrara 1995, 41, 73–84. [Google Scholar]
- Caputo, M. Distributed order differential equations modelling dielectric induction and diffusion. Fract. Calc. Appl. Anal. 2001, 4, 421–442. [Google Scholar]
- Bagley, R.L.; Torvik, P.J. On the existence of the order domain and the solution of distributed order equations—Part I. Int. J. Appl. Math. 2000, 2, 865–882. [Google Scholar]
- Atanackovic, T.M. A generalized model for the uniaxial isothermal deformation of a viscoelastic body. Acta Mech. 2002, 159, 77–86. [Google Scholar] [CrossRef]
- Atanackovic, T.M.; Budincevic, M.; Pilipovic, S. On a fractional distributed-order oscillator. J. Phys. Math. Gen. 2005, 38, 6703–6713. [Google Scholar] [CrossRef]
- Duan, J.S.; Baleanu, D. Steady periodic response for a vibration system with distributed-order derivatives to periodic excitation. J. Vib. Control 2018, 24, 3124–3131. [Google Scholar] [CrossRef]
- Duan, J.S.; Chen, Y.Q. Mechanical response and simulation for constitutive equations with distributed order derivatives. Int. J. Model. Simul. Sci. Comput. 2017, 8, 1750040. [Google Scholar] [CrossRef] [Green Version]
- Duan, J.S.; Xu, Y.Y. Vibration equation of fractional order describing viscoelasticity and viscous inertia. Open Phys. 2019, 17, 850–856. [Google Scholar] [CrossRef]
- Smith, M.C. Synthesis of mechanical networks: The inerter. IEEE Trans. Autom. Control 2002, 47, 1648–1662. [Google Scholar] [CrossRef] [Green Version]
- Chen, M.Z.Q.; Hu, Y.; Huang, L.; Chen, G. Influence of inerter on natural frequencies of vibration systems. J. Sound Vib. 2014, 333, 1874–1887. [Google Scholar] [CrossRef] [Green Version]
- Chen, M.Z.; Hu, Y. Inerter and Its Application in Vibration Control Systems; Springer: Singapore, 2019. [Google Scholar]
- Papageorgiou, C.; Smith, M.C. Positive real synthesis using matrix inequalities for mechanical networks: Application to vehicle suspension. IEEE Trans. Control Syst. Technol. 2006, 14, 423–435. [Google Scholar] [CrossRef] [Green Version]
- Evangelou, S.; Limebeer, D.J.N.; Sharp, R.S.; Smith, M.C. Control of motorcycle steering instabilities. IEEE Control Syst. Mag. 2006, 26, 78–88. [Google Scholar]
- Hu, Y.; Chen, M.Z.Q.; Shu, Z.; Huang, L. Analysis and optimisation for inerter-based isolators via fixed-point theory and algebraic solution. J. Sound Vib. 2015, 346, 17–36. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.B.; Wang, Z.; Zhang, W. Active absorption measurement of panels using multichannel inertial absorbers in wideband frequencies. Noise Vib. Control 2015, 35, 213–216. [Google Scholar]
- Wang, L.; Mao, M.; Lei, Q.; Chen, Y.; Zhang, X. Modeling and testing for a hydraulic inerter. J. Vib. Shock 2018, 37, 146–152. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).