Pseudo-Likelihood Estimation for Parameters of Stochastic Time-Fractional Diffusion Equations
Abstract
:1. Introduction
2. Parameter Estimation Problem
3. Pseudo-Likelihood Approach
3.1. Pseudo-Likelihood Estimation for Stochastic ODEs
3.2. Pseudo-Likelihood Estimation for Stochastic PDEs
3.2.1. Spatio-Temporal Discretization Scheme
- (i)
- Full observation. We denote by for integers the discrete observation of concentration in the computational domain . A full observation is defined as the case where the spatial sampling step and temporal sampling step are taken to be the smallest values that are allowed in practice. Due to the limitation of economic cost of placing concentration sensors and restriction of measurement precision of sensors, in reality, the spatial and temporal steps cannot be arbitrarily small. We denote by and the smallest steps that are allowed in practice. The full observation is the most ideal case for parameter estimation, as we can extract most information from an observation. We assume that usually one can accurately estimate parameters from such an observation.
- (ii)
- Partial observation. Sometimes we cannot achieve a full observation due to shrinking budget and geological constraints for placing sensors. For example, when monitoring wells have to be digged for measuring contaminant concentration in groundwater, the budget for placing sensors has been halved for certain reason and the remaining budget only allows a less dense spatial distribution of monitoring wells. We suppose that there exists a full observation , from which we can accurately estimate model parameters. Then, the partial observation is defined as a subset of , namely, for sampling ratios . When the sampling ratios , the partial observation is the same as the full observation.
3.2.2. Pseudo-Likelihood Estimation for Full Observation
3.2.3. Pseudo-Likelihood Estimation for Partial Observation
4. Numerical Results
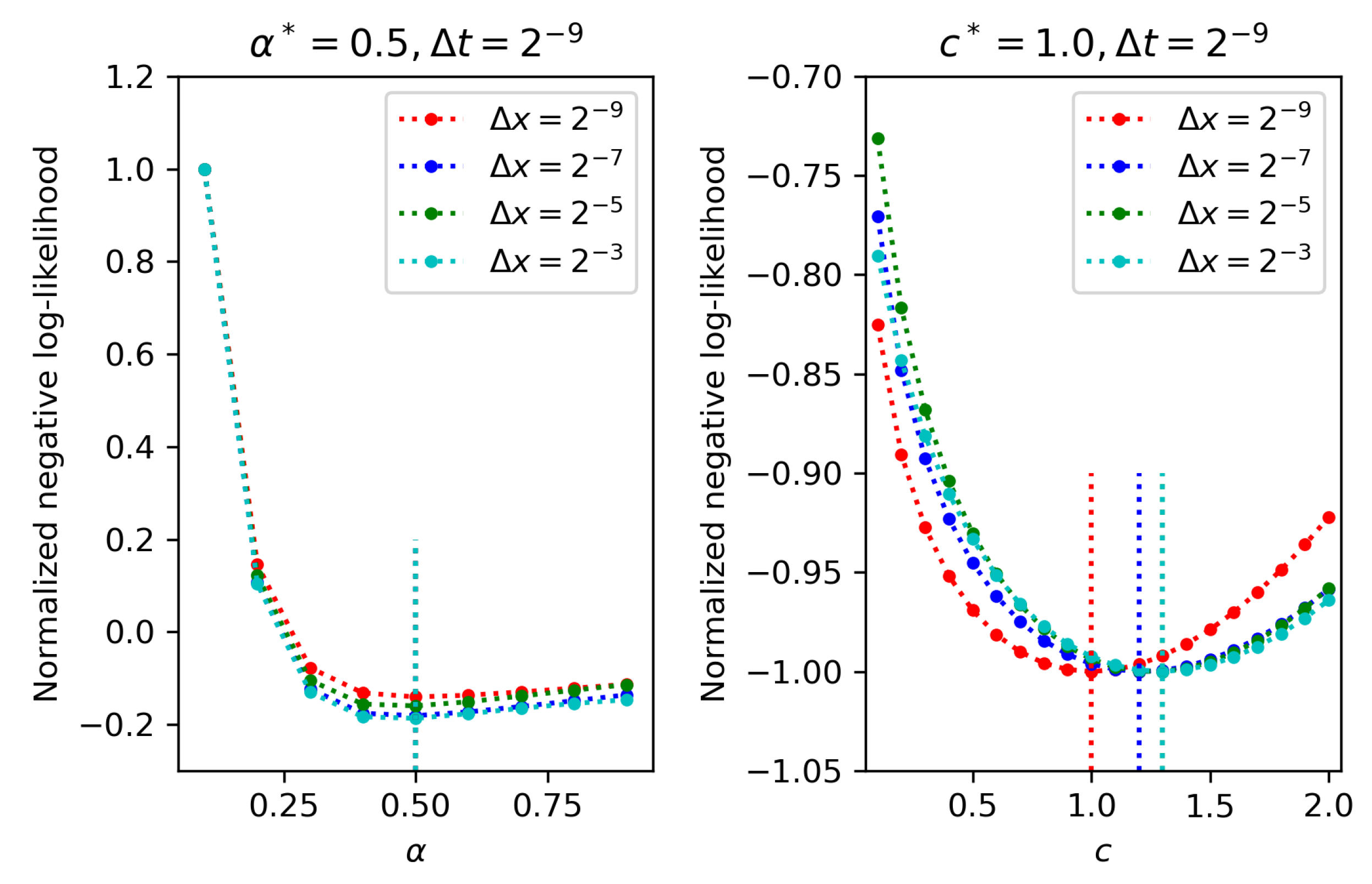
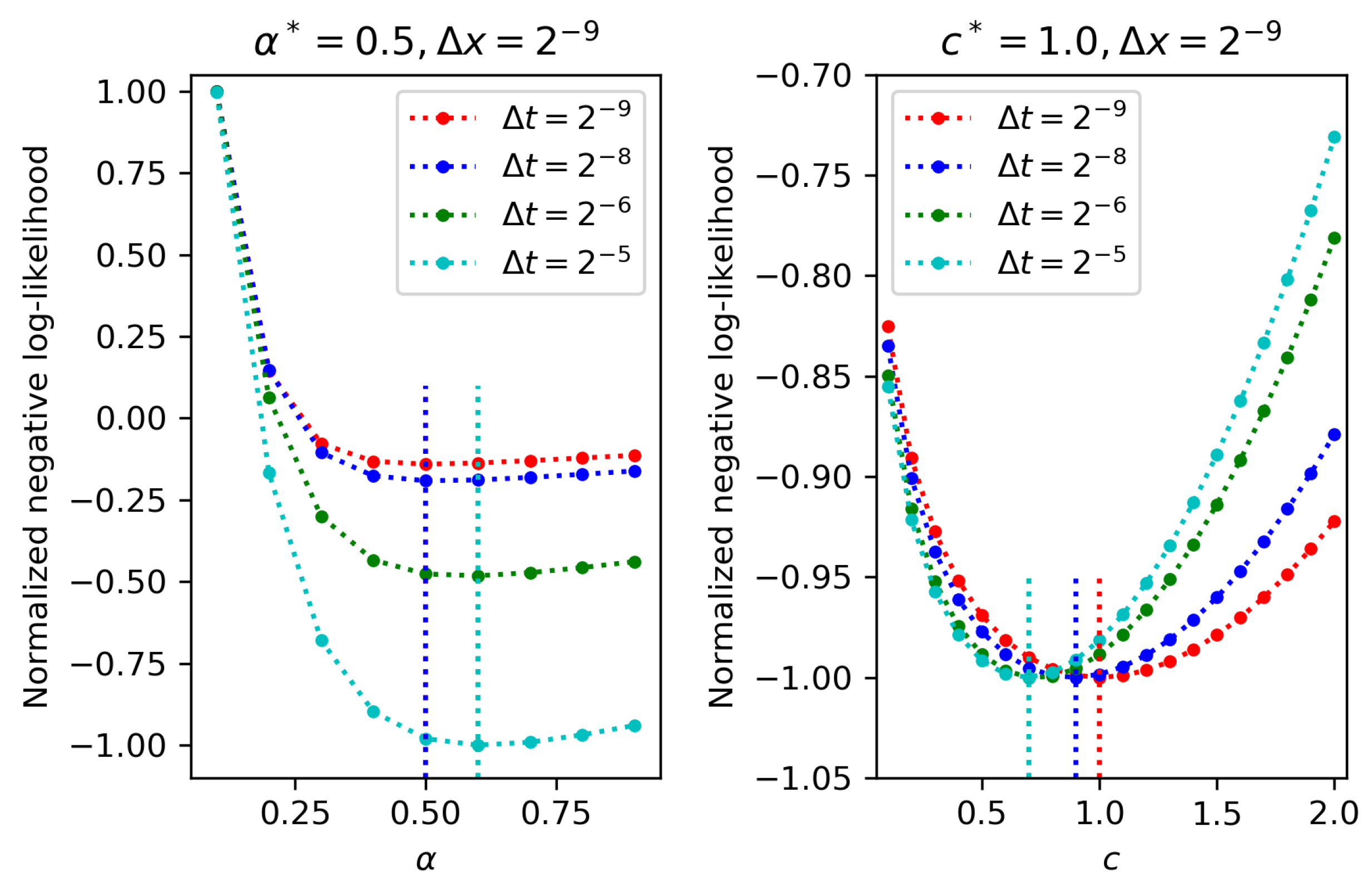
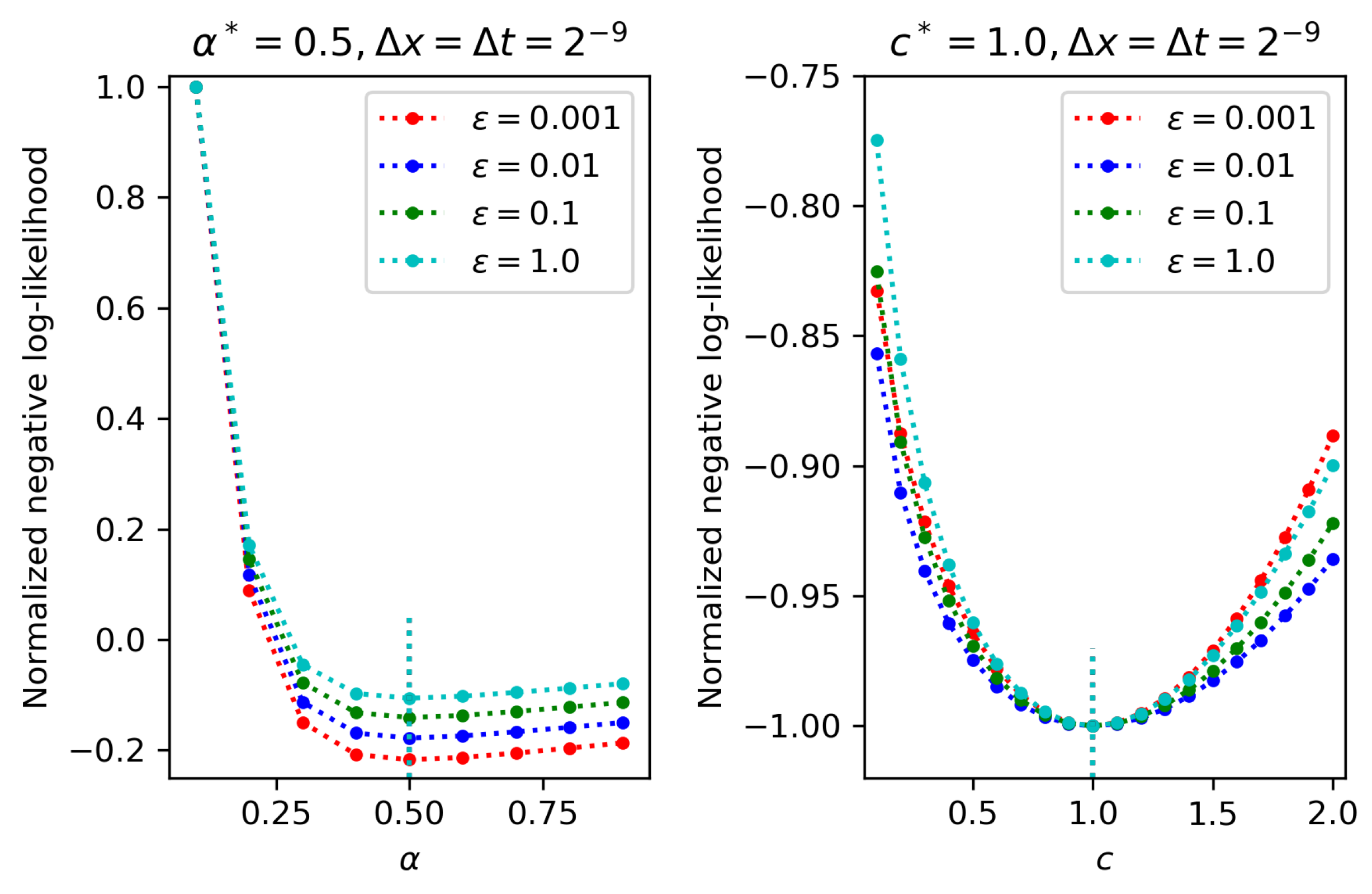
4.1. One-Parameter Estimation
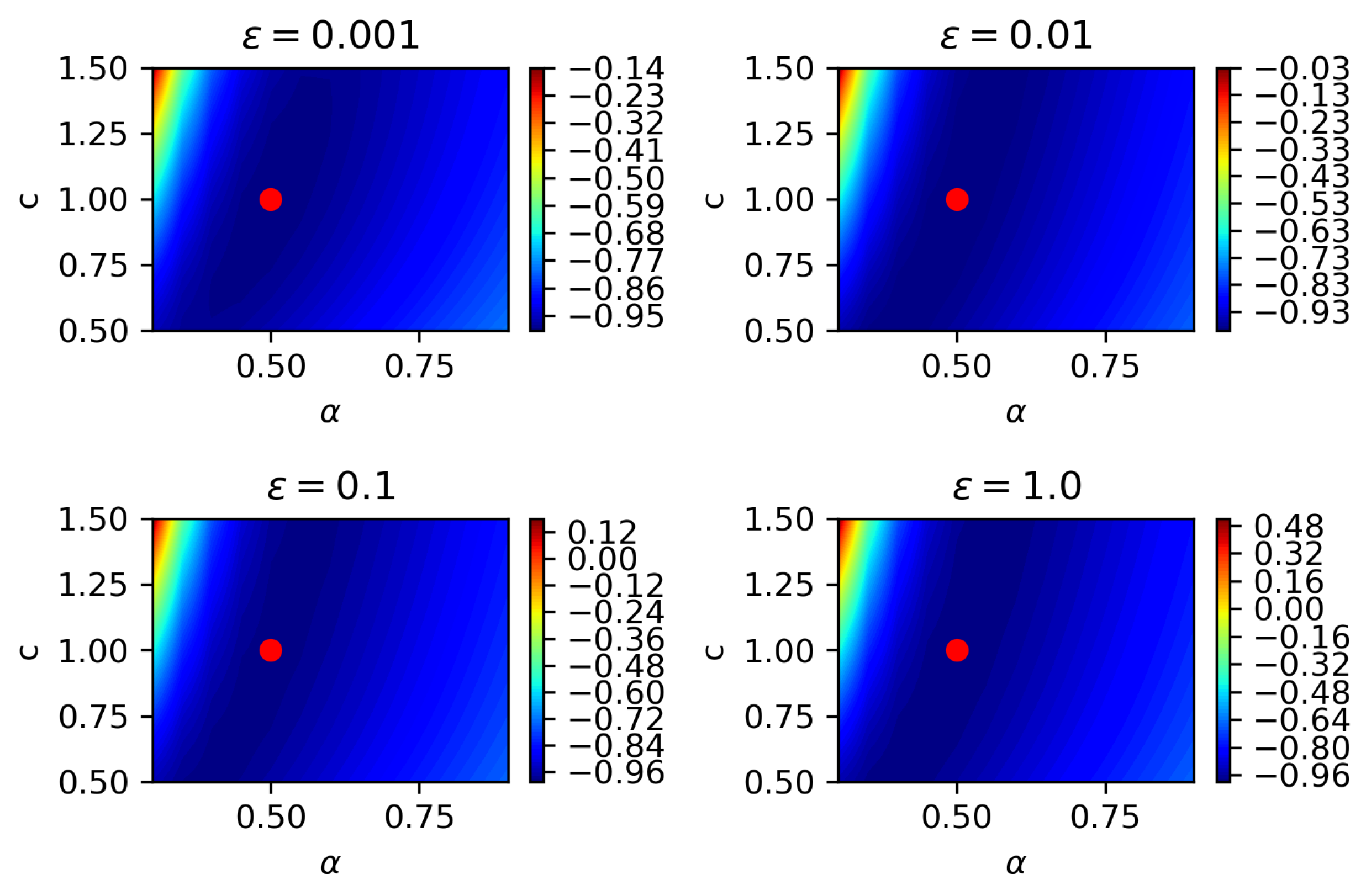
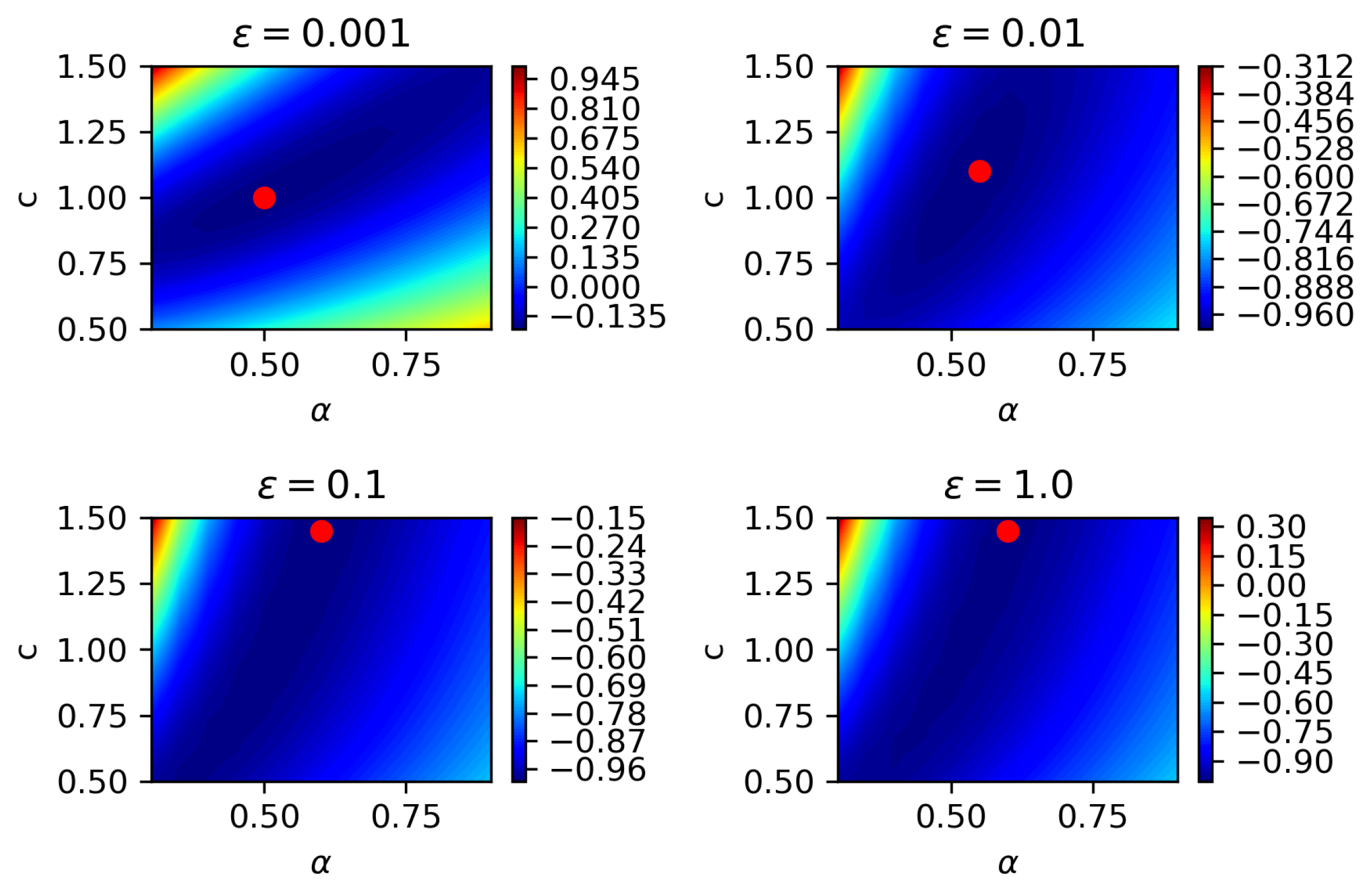
4.2. Two-Parameter Estimation
4.3. Three-Parameter Estimation
5. Concluding Remarks
- i
- The larger the spatio-temporal sampling steps are, the lower the accuracy of estimated parameters is, which is intuitive.
- ii
- Keeping temporal sampling step small is more important than keeping spatial step small in terms of increasing the parameter estimation accuracy for partial observation.
- iii
- Among the three parameters being estimated, namely, fractional order, diffusion coefficient, and noise magnitude, the diffusion coefficient is most difficult to be estimated, since it is most sensitive to varying spatio-temporal steps in partial observation.
- iv
- The high accuracy of mean of estimated parameters is usually related to the low standard deviation of estimated parameters, when we fortunately have multiple observations, corresponding to different realizations of driving noise, to obtain multiple groups of estimated parameters.
- v
- Estimating more parameters jointly leads to larger variability of estimated parameters when spatio-temporal steps increase. Making spatio-temporal steps as small as possible is suggested for a joint estimation of a large number of parameters.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
| TLA | Three letter acronym |
| LD | Linear dichroism |
Appendix A. Proof of Proposition 1
Appendix B. Numerical Solution to Forward Problem

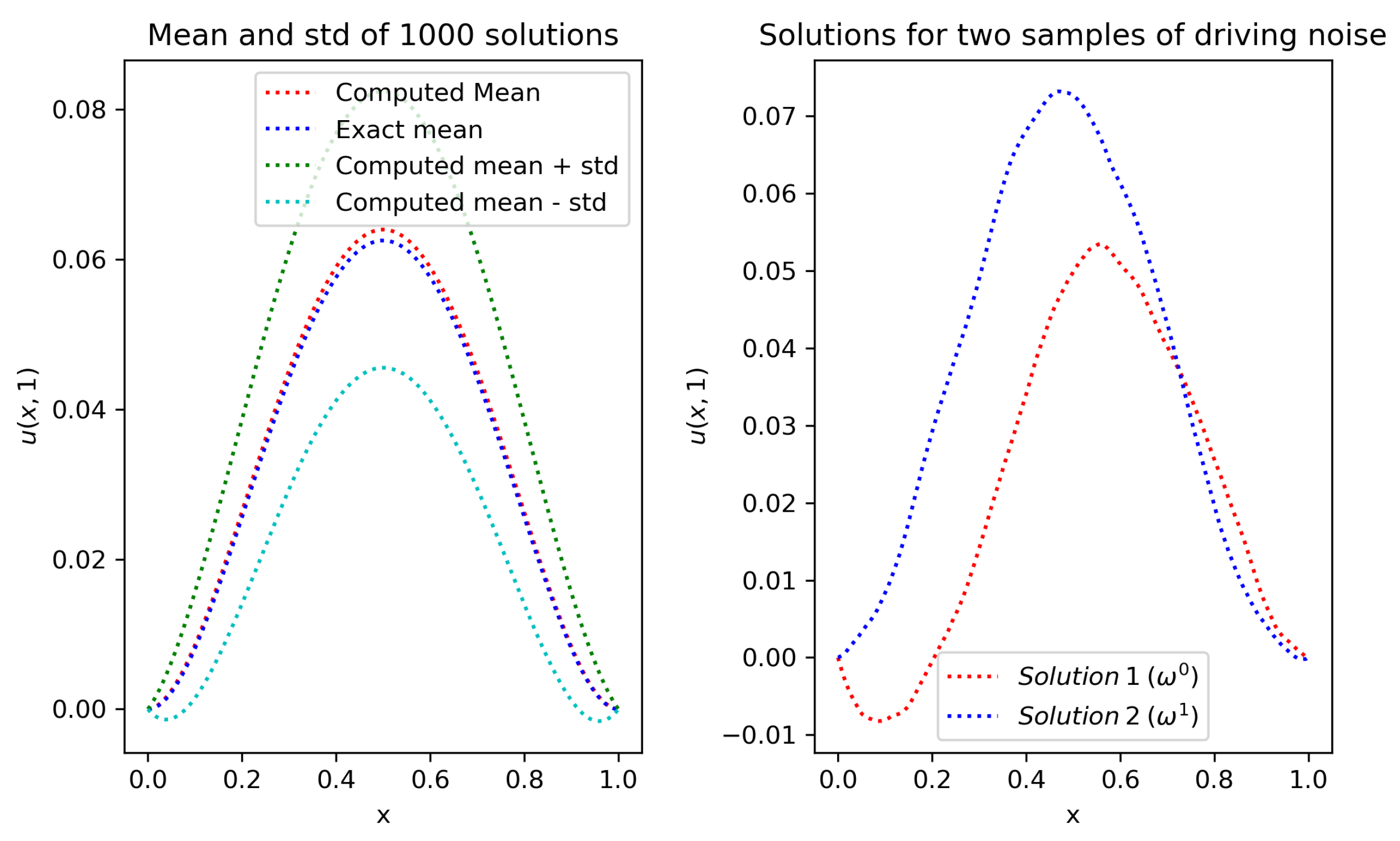
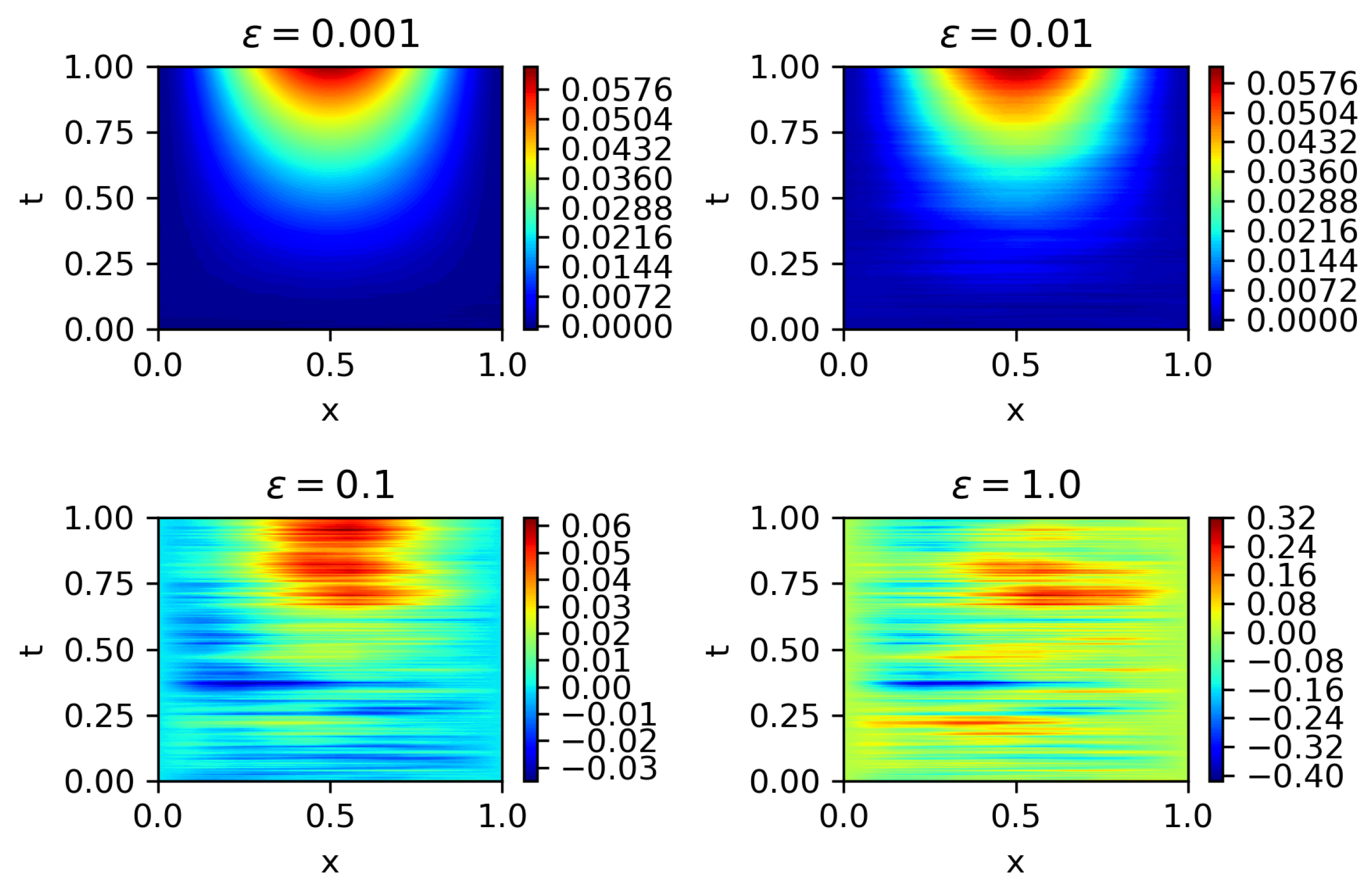
References
- Mijena, J.B.; Nane, E. Space–time fractional stochastic partial differential equations. J. Stoch. Process Their Appl. 2015, 125, 3301–3326. [Google Scholar] [CrossRef]
- Anh, V.V.; Leonenko, N.N.; Ruiz-Medina, M.D. Fractional-in-time and multifractional-in-space stochastic partial differential equations. Fract. Calc. Appl. Anal. 2016, 19, 1434–1459. [Google Scholar] [CrossRef] [Green Version]
- Gunzburger, M.; Li, B.Y.; Wang, J.L. Sharp convergence rates of time discretization for stochastic time-fractional PDEs subject to additive space-time white noise. Math. Comput. 2019, 88, 1715–1741. [Google Scholar] [CrossRef]
- Bolin, D.; Kirchner, K.; Kovács, M. Fractional-in-time and multifractional-in-space stochastic partial differential equations. IMA J. Numer. Anal. 2020, 40, 1051–1073. [Google Scholar] [CrossRef]
- Anh, V.V.; Olenko, A.; Wang, Y.G. Fractional stochastic partial differential equation for random tangent fields on the sphere. arXiv 2021, arXiv:2107.03717. [Google Scholar]
- Mohammed, W.W. Approximate solutions for stochastic time-fractional reaction–diffusion equations with multiplicative noise. Math. Methods Appl. Sci. 2021, 44, 2140–2157. [Google Scholar] [CrossRef]
- Xia, D.F.; Yan, L.T. Some properties of the solution to fractional heat equation with a fractional Brownian noise. Adv. Differ. Equ. 2017, 107, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Huebner, M.; Rozovskii, B.L. AOn asymptotic properties of maximum likelihood estimators for parabolic stochastic PDE’s. Probab. Theory Relat. Fields 1995, 103, 143–163. [Google Scholar] [CrossRef]
- Bishwal, J.P.N. Parameter Estimation in Stochastic Differential Equations; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Rao, B.L.S.P. Statistical Inference for Fractional Diffusion Processes; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Huebner, M.; Khasminskii, R.; Rozovskii, B.L. Two examples of parameter estimation for stochastic partial differential equations. In Stochastic Processes: A Festschrift in Honour of Gopinath Kallianpur; Cambanis, S., Ghosh, J.K., Karandikar, R.L., Sen, P.K., Eds.; Springer: New York, NY, USA, 1993; pp. 149–160. [Google Scholar]
- Cialenco, I.; Lototsky, S.V.; Pospíšil, J. Asymptotic properties of the maximum likelihood estimator for stochastic parabolic equations with additive fractional Brownian motion. Stoch. Dyn. 2009, 9, 169–185. [Google Scholar] [CrossRef]
- Cialenco, I. Parameter estimation for SPDEs with multiplicative fractional noise. Stoch. Dyn. 2010, 10, 561–576. [Google Scholar] [CrossRef]
- Geldhauser, C.; Valdinoci, E. Optimizing the fractional power in a model with stochastic PDE constraints. Adv. Nonlinear Stud. 2018, 18, 649–669. [Google Scholar] [CrossRef] [Green Version]
- Aster, R.C.; Borchers, B.; Thurber, C.H. Parameter Estimation and Inverse Problems; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Pang, G.F.; Perdikaris, P.; Cai, W.; Karniadakis, G.E. Discovering variable fractional orders of advection–dispersion equations from field data using multi-fidelity Bayesian optimization. J. Comput. 2017, 348, 694–714. [Google Scholar] [CrossRef]
- Yan, L.; Guo, L. Stochastic Collocation Algorithms Using l1-Minimization for Bayesian Solution of Inverse Problems. SIAM J. Sci. Comput. 2015, 37, A1410–A1435. [Google Scholar] [CrossRef]
- Garcia, L.A.; Shigidi, A. Using neural networks for parameter estimation in ground water. J. Hydrol. 2006, 318, 215–231. [Google Scholar] [CrossRef]
- Pang, G.F.; Lu, L.; Karniadakis, G.E. fPINNs: Fractional physics-informed neural networks. SIAM J. Sci. Comput. 2019, 41, A2603–A2626. [Google Scholar] [CrossRef]
- Da, P.G.; Zabczyk, J. Stochastic Equations in Infinite Dimensions; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Iacus, S.M. Simulation and Inference for Stochastic Differential Equations: With R Examples; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Yoshida, N. Estimation for diffusion processes from discrete observation. J. Multivar. Anal. 1992, 41, 220–242. [Google Scholar] [CrossRef] [Green Version]
- Lubich, C. Convolution quadrature and discretized operational calculus. I. Numer. Math. 1988, 52, 129–145. [Google Scholar] [CrossRef]
- Lubich, C. Convolution quadrature and discretized operational calculus. II. Numer. Math. 1988, 52, 413–425. [Google Scholar] [CrossRef]
- Byrd, R.H.; Lu, P.H.; Nocedal, J.; Zhu, C.Y. A limited memory algorithm for bound constrained optimization. SIAM J. Sci. Comput. 1995, 16, 1190–1208. [Google Scholar] [CrossRef]
- Zheng, X.C.; Wang, H. An error estimate of a numerical approximation to a hidden-memory variable-order space-time fractional diffusion equation. SIAM J. Numer. Anal. 2020, 58, 2492–2514. [Google Scholar] [CrossRef]
- Zheng, X.C.; Wang, H. Wellposedness and regularity of a variable-order space-time fractional diffusion equation. Anal. Appl. 2020, 18, 615–638. [Google Scholar] [CrossRef]
- Hogg, R.V.; McKean, J.; Craig, A.T. Introduction to Mathematical Statistics; Pearson Education: London, UK, 2005. [Google Scholar]
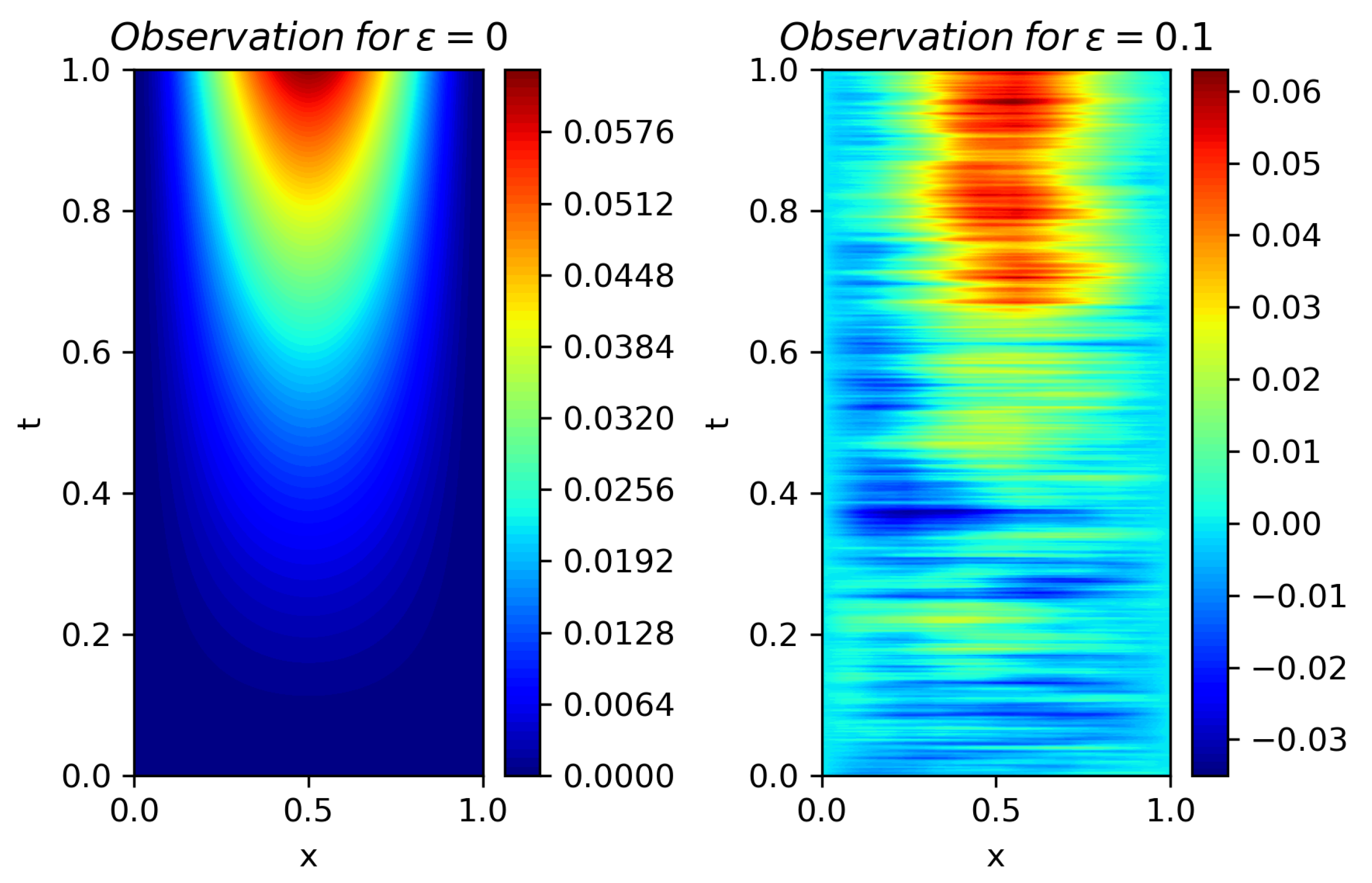
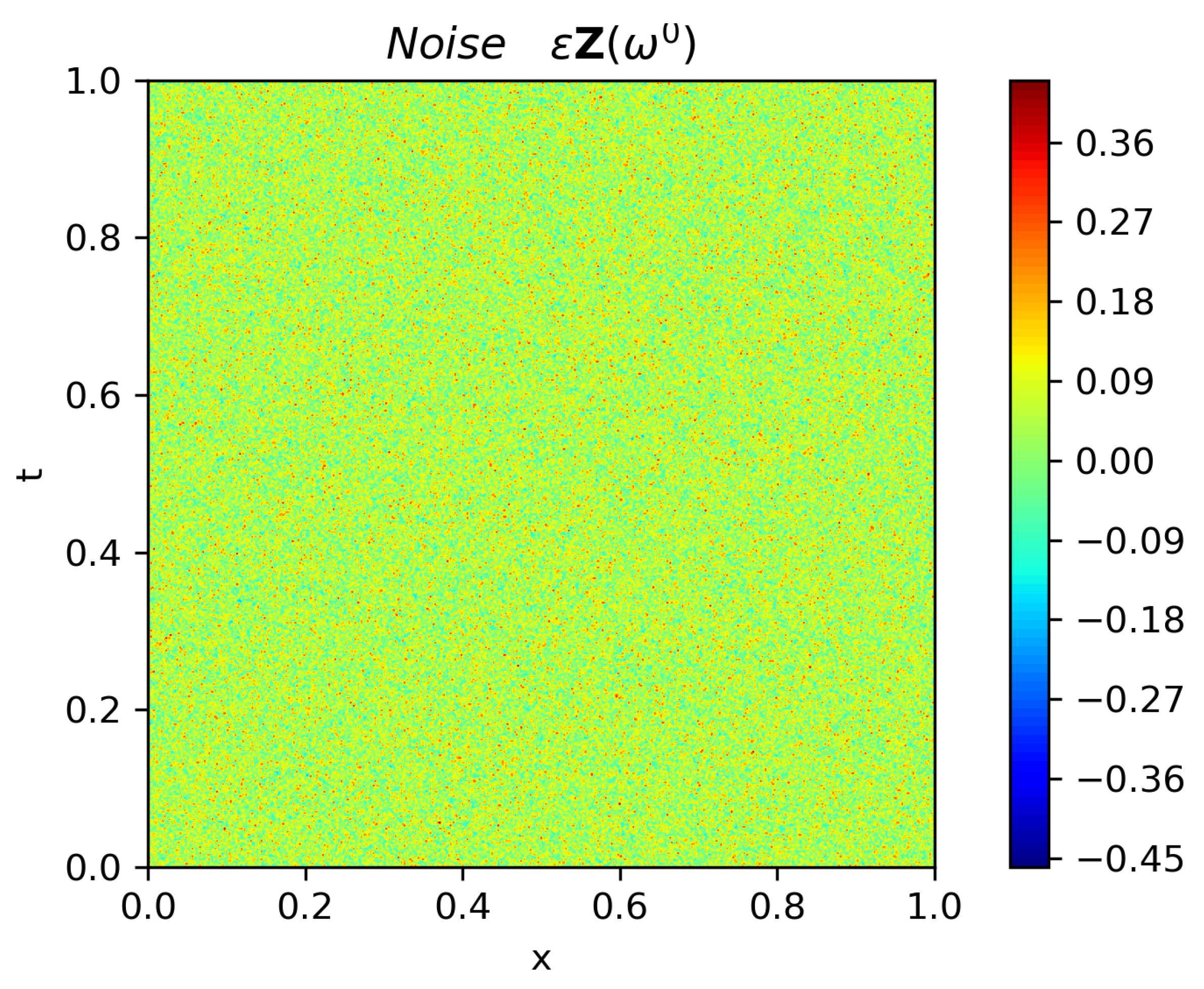



| Mean | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
|---|---|---|---|---|---|---|---|---|
| 0.673 | 0.634 | 0.649 | 0.664 | 0.673 | 0.682 | 0.682 | 0.683 | |
| 0.621 | 0.603 | 0.612 | 0.628 | 0.637 | 0.645 | 0.648 | 0.651 | |
| 0.581 | 0.573 | 0.589 | 0.603 | 0.611 | 0.617 | 0.620 | 0.621 | |
| 0.555 | 0.557 | 0.569 | 0.579 | 0.582 | 0.586 | 0.588 | 0.590 | |
| 0.528 | 0.26 | 0.536 | 0.544 | 0.546 | 0.548 | 0.550 | 0.551 | |
| 0.491 | 0.485 | 0.492 | 0.497 | 0.498 | 0.499 | 0.500 | 0.500 | |
| Mean | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
| 1.455 | 1.259 | 1.277 | 1.307 | 1.314 | 1.324 | 1.264 | 1.100 | |
| 1.428 | 1.297 | 1.317 | 1.365 | 1.386 | 1.400 | 1.351 | 1.183 | |
| 1.409 | 1.316 | 1.379 | 1.438 | 1.466 | 1.478 | 1.423 | 1.238 | |
| 1.400 | 1.371 | 1.424 | 1.473 | 1.485 | 1.487 | 1.432 | 1.248 | |
| 1.361 | 1.326 | 1.375 | 1.410 | 1.411 | 1.408 | 1.355 | 1.177 | |
| 1.233 | 1.186 | 1.211 | 1.223 | 1.219 | 1.205 | 1.155 | 1.000 |
| Std | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
|---|---|---|---|---|---|---|---|---|
| 0.094 | 0.062 | 0.044 | 0.032 | 0.023 | 0.019 | 0.014 | 0.009 | |
| 0.071 | 0.045 | 0.035 | 0.025 | 0.016 | 0.012 | 0.009 | 0.007 | |
| 0.056 | 0.033 | 0.024 | 0.017 | 0.013 | 0.010 | 0.007 | 0.005 | |
| 0.035 | 0.023 | 0.016 | 0.011 | 0.007 | 0.006 | 0.004 | 0.003 | |
| 0.027 | 0.017 | 0.011 | 0.008 | 0.007 | 0.005 | 0.003 | 0.002 | |
| 0.021 | 0.010 | 0.007 | 0.006 | 0.005 | 0.004 | 0.003 | 0.002 | |
| Std | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
| 0.392 | 0.225 | 0.167 | 0.121 | 0.088 | 0.072 | 0.049 | 0.278 | |
| 0.350 | 0.211 | 0.173 | 0.123 | 0.077 | 0.062 | 0.045 | 0.028 | |
| 0.327 | 0.182 | 0.140 | 0.102 | 0.081 | 0.066 | 0.046 | 0.027 | |
| 0.254 | 0.151 | 0.112 | 0.080 | 0.060 | 0.050 | 0.032 | 0.020 | |
| 0.215 | 0.122 | 0.084 | 0.065 | 0.055 | 0.038 | 0.027 | 0.015 | |
| 0.161 | 0.075 | 0.054 | 0.046 | 0.041 | 0.028 | 0.019 | 0.011 |
| 64 | 32 | 16 | 8 | 4 | 2 | 1 | ||
|---|---|---|---|---|---|---|---|---|
| 0.495 | 0.596 | 0.661 | 0.668 | 0.665 | 0.694 | 0.683 | 0.691 | |
| 0.518 | 0.583 | 0.609 | 0.607 | 0.614 | 0.650 | 0.651 | 0.662 | |
| 0.518 | 0.558 | 0.576 | 0.586 | 0.597 | 0.624 | 0.627 | 0.632 | |
| 0.505 | 0.515 | 0.548 | 0.565 | 0.569 | 0.586 | 0.587 | 0.590 | |
| 0.498 | 0.497 | 0.512 | 0.533 | 0.536 | 0.547 | 0.549 | 0.553 | |
| 0.456 | 0.456 | 0.473 | 0.487 | 0.491 | 0.496 | 0.500 | 0.500 | |
| 64 | 32 | 16 | 8 | 4 | 2 | 1 | ||
| 1.382 | 1.152 | 1.137 | 1.170 | 1.162 | 1.174 | 1.155 | 1.101 | |
| 1.281 | 1.192 | 1.190 | 1.252 | 1.246 | 1.260 | 1.217 | 1.096 | |
| 1.246 | 1.211 | 1.272 | 1.378 | 1.391 | 1.376 | 1.448 | 1.079 | |
| 1.720 | 1.686 | 1.845 | 2.000 | 1.980 | 1.950 | 1.496 | 1.360 | |
| 1.5000 | 1.554 | 1.726 | 1.880 | 1.862 | 1.857 | 1.441 | 1.337 | |
| 1.369 | 1.463 | 1.622 | 1.744 | 1.730 | 1.709 | 1.523 | 1.038 | |
| 64 | 32 | 16 | 8 | 4 | 2 | 1 | ||
| 0.162 | 0.109 | 0.091 | 0.091 | 0.093 | 0.085 | 0.091 | 0.098 | |
| 0.130 | 0.102 | 0.094 | 0.078 | 0.096 | 0.087 | 0.088 | 0.089 | |
| 0.109 | 0.099 | 0.098 | 0.101 | 0.100 | 0.090 | 0.099 | 0.084 | |
| 0.146 | 0.146 | 0.141 | 0.142 | 0.140 | 0.131 | 0.105 | 0.108 | |
| 0.122 | 0.132 | 0.139 | 0.139 | 0.138 | 0.132 | 0.107 | 0.112 | |
| 0.126 | 0.140 | 0.146 | 0.148 | 0.147 | 0.143 | 0.131 | 0.104 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pang, G.; Cao, W. Pseudo-Likelihood Estimation for Parameters of Stochastic Time-Fractional Diffusion Equations. Fractal Fract. 2021, 5, 129. https://doi.org/10.3390/fractalfract5030129
Pang G, Cao W. Pseudo-Likelihood Estimation for Parameters of Stochastic Time-Fractional Diffusion Equations. Fractal and Fractional. 2021; 5(3):129. https://doi.org/10.3390/fractalfract5030129
Chicago/Turabian StylePang, Guofei, and Wanrong Cao. 2021. "Pseudo-Likelihood Estimation for Parameters of Stochastic Time-Fractional Diffusion Equations" Fractal and Fractional 5, no. 3: 129. https://doi.org/10.3390/fractalfract5030129
APA StylePang, G., & Cao, W. (2021). Pseudo-Likelihood Estimation for Parameters of Stochastic Time-Fractional Diffusion Equations. Fractal and Fractional, 5(3), 129. https://doi.org/10.3390/fractalfract5030129







