Analytic Fuzzy Formulation of a Time-Fractional Fornberg–Whitham Model with Power and Mittag–Leffler Kernels

Abstract

This manuscript assesses a semi-analytical method in connection with a new hybrid fuzzy integral transform and the Adomian decomposition method via the notion of fuzziness known as the Elzaki Adomian decomposition method (briefly, EADM). Moreover, we use the aforesaid strategy to address the time-fractional Fornberg–Whitham equation (FWE) under $g\mathcal{H}$-differentiability by employing different initial conditions (IC). Several algebraic aspects of the fuzzy Caputo fractional derivative (CFD) and fuzzy Atangana–Baleanu (AB) fractional derivative operator in the Caputo sense, with respect to the Elzaki transform, are presented to validate their utilities. Apart from that, a general algorithm for fuzzy Caputo and AB fractional derivatives in the Caputo sense is proposed. Some illustrative cases are demonstrated to understand the algorithmic approach of FWE. Taking into consideration the uncertainty parameter $\zeta \in [0,1]$ and various fractional orders, the convergence and error analysis are reported by graphical representations of FWE that have close harmony with the closed form solutions. It is worth mentioning that the projected approach to fuzziness is to verify the supremacy and reliability of configuring numerical solutions to nonlinear fuzzy fractional partial differential equations arising in physical and complex structures.

1. Introduction

Recently, fractional calculus (FC) theory has shown incredible capabilities for describing the dynamical behavior and memory-related properties of scientific structures and procedures. Fractional differential equations (FDEs) have been developed by researchers to investigate and interpret natural phenomena in a variety of domains. FC theory comprises numerous generalizations in terms of non-local properties of fractional operators, expanded degree of independence, and maximum information application, and these features only arise in fractional order processes, not in integer-order mechanisms. Some scholars have recently investigated a series of innovative mathematical models using distinct local and non-local fractional derivative operators (see, [1,2,3,4,5,6,7,8,9,10,11,12]).

Recently, many innovative fractional derivative operators beyond the singular kernel have been explored, such as the Mittag–Leffler function [13] and exponential function [14]. In particular, researchers who would like to develop and address a real-life problem have recommended fractional operators, see [15]. Problems involving these operators can be solved quickly and reliably because they include a non-singular kernel. Numerical algorithms can also be conducted conveniently regarding the integral transforms of these fractional formulations. Many authors have investigated fractional operators, as evidenced by the references [16,17] and those cited therein.

Modeling uncertain problems with fuzzy set theory is a useful method. As a consequence, fuzzy notions have been employed to model a wide range of natural processes. Specifically, fuzzy partial differential equations (PDEs) have been exploited in a wide range of scientific domains, including patteren formation theory, engineering, population dynamics, control systems, knowledge-based systems, image processing, power engineering, industrial automation, robotics, consumer electronics, artificial intelligence/expert systems, management, and operations research. However, the notion of fuzzy set theory has a strong connection with fractional calculus, due to its crucial aspects in various scientific disciplines [18]. In 1978, Kandel and Byatt [19] contemplated the idea of fuzzy DEs, then Agarwal et al. [20] were the first to address fuzziness and the Riemann–Liouville differentiability notion under the Hukuhara differentiability. Fuzzy set theory and FC incorporate several numerical approaches that enable a more in-depth understanding of complicated systems while also reducing the amount of computational cost involved in the solution process. In the case of FPDEs, finding accurate analytical solutions is a difficult task. To cope with this challenge, several numerical methods have been expounded to obtain the analytical solutions of PDES and ODEs, such as the Adomian decomposition method (ADM) [21], q-homotopy analysis method (q-HAM) [22], pseudo spectral method (PSM) [23], Laguerre wavelets collocation method (LWCM) [24], new Legendre-Wavelets decomposition method (NLWDM) [25], etc. Fuzzy FPDEs have expanded in prominence over the last decade as a result of their vast applicability and significance in analyzing the behavior of complex geometries. Recently, Hoa et al. [26,27] investigated the gH-differentiability with a Katugampola fractional derivative in the Caputo sense and employed fuzzy FDEs. Salahshour et al. [28] expounded the H-differentiability with the Laplace transform to solve the FDEs. Ahmad et al. [29] studied the third order fuzzy dispersive PDEs in the Caputo, Caputo–Fabrizio, and Atangana–Baleanu fractional operator frameworks. Shah et al. [30] presented the evolution of one dimensional fuzzy fractional PDEs. For more details, see [31,32,33,34] and the references cited therein.

Accessing the influence of PDEs for external potential has been extensively applied as a model for the evaluation of multiple challenges. The Fornberg–Whitham (FW) model is an important complex formulation in mathematical physics. The FWE [35,36] is presented as

$$\begin{array}{c}\hfill \frac{\partial \mathbf{f}}{\partial \vartheta }-\frac{{\partial }^3\mathbf{f}}{\partial \vartheta \partial {\ell }_1^2}+\frac{\partial \mathbf{f}}{\partial {\ell }_1}=\mathbf{f}\frac{{\partial }^3\mathbf{f}}{\partial {\ell }_1^3}-\mathbf{f}\frac{\partial \mathbf{f}}{\partial {\ell }_1}+3\frac{\partial \mathbf{f}}{\partial {\ell }_1}\frac{{\partial }^2\mathbf{f}}{\partial {\ell }_1^2},\end{array}$$

(1)

where the fluid velocity is expressed by $\mathbf{f}({\ell }_1,\vartheta )$ along with ${\ell }_1$ as the spatial co-ordinate and $\vartheta$ denoting time. In 1978, Fornberg and Whitham [35,36] contemplated a solution $\mathbf{f}({\ell }_1,\vartheta )=\delta exp\left(\frac{{\ell }_1}{2}-\frac{4\vartheta }{3}\right)$ with an arbitrarily defined constant of $\alpha .$ The FWE has been discovered to need peakon outcomes as a model for controlling wave heights and wave break frequency. Recently, various sorts of FWE models in physics have been investigated by Abidi and Omrani [37], Gupta and Singh [38], Lu [39], Sakar et al. [40], Chen et al. [41], Yin et al. [42], Zhou and Tian [43], He et al. [44], Fan et al. [45], Jiang and Bi [46].

This research creates a modified fuzzy EADM framework to assess the fuzzy time fractional FWE. The approximate analytical solutions for various fractional Brownian movements, as well as standard motion, are derived using the uncertainty parameter in ICs. Graphically, the diversity of approximate results is illustrated, and the error estimate demonstrates the validity of the approximate analytical solutions. In the time fractional operator form, this equation can be expressed as

$$\begin{array}{c}\hfill \frac{{\partial }^{\alpha }\mathbf{f}}{\partial {\vartheta }^{\alpha }}-\frac{{\partial }^3\mathbf{f}}{\partial \vartheta \partial {\ell }_1^2}+\frac{\partial \mathbf{f}}{\partial {\ell }_1}=\mathbf{f}\frac{{\partial }^3\mathbf{f}}{\partial {\ell }_1^3}-\mathbf{f}\frac{\partial \mathbf{f}}{\partial {\ell }_1}+3\frac{\partial \mathbf{f}}{\partial {\ell }_1}\frac{{\partial }^2\mathbf{f}}{\partial {\ell }_1^2},\end{array}$$

(2)

subject to ICs $\mathbf{f}({\ell }_1,0)=exp\left(\frac{{\ell }_1}{2}\right)$ and ${cosh}^2\left(\frac{{\ell }_1}{4}\right),$ and $\alpha \in (0,1]$ is the order of the time fractional derivative. It is remarkable that the exact traveling wave solution of FWE subject to IC $\mathbf{f}({\ell }_1,\vartheta )=0.75exp\left(\frac{3{\ell }_1-2\vartheta }{6}\right)$ has been investigated in [38].

In order to simplify the approach to solving ODEs and PDEs in the time domain, Tarig Elzaki [47] introduced a new transform known as ET in 2001. This innovative transform is a refinement of existing transforms (Laplace and Sumudu) that can help determine the analytical solutions of PDEs in a similar fashion to the Laplace and Sumudu transformations.

The ADM is a semi-analytical approach to solving linear-nonlinear FDEs by advantageously creating a functional series solution, initially presented by Adomian [48]. Later, this approach was used with numerous transformations (such as the Sumudu, Aboodh, Laplace, and Mohand transforms), as shown in [49,50,51,52,53,54,55,56,57,58].

Owing to the above propensity, configuring the exact solution of nonlinear fuzzy fractional PDEs is an ever challenging task. In this paper, our intention is to establish an efficacious algorithm for generating estimated solutions of fuzzy fractional FWE, the general FWE arising in wave breaking subject to uncertainty in IC by EADM that models the dynamics of the system being analyzed. The EADM is merged with the Elzaki transform (ET), and the ADM is known as the Elzaki Adomian decomposition method (EADM). This novel method is applied to examining fractional-order FW models. The findings of a particular test case are evaluated in terms of showing that the proposed technique is viable. The findings of the fractional-order with an uncertainty factor are determined by advanced tools and methods. The convergence analysis for EADM was also briefly discussed. The FW model was leveraged to generate synthesized trajectories. In a simulation study, we illustrate the applicability and effectiveness of the offered algorithmic strategies for determining numerical solutions. Several fuzzy fractional orders of linear and non-linear PDEs can be addressed using the proposed method.

2. Preliminaries

This section clearly exhibits some major features connected to the stream of fuzzy ($\mathbf{F}$) set theory and FC, as well as certain key findings about ET. For more details, we refer to [59].

Definition 1

([60,61]). We say that $\mathsf{\Omega }:\mathbb{R}\mapsto [0,1]$ is a $\mathbf{F}$ number, if it holds the subsequent assumptions:

1. 

Ω is normal (for some ${{\ell }_1}_0\in \mathbb{R};\mathsf{\Omega }\left({{\ell }_1}_0\right)=1$);

2. 

Ω is upper semi continuous;

3. 

$\mathsf{\Omega }({\ell }_1\vartheta +(1-\vartheta ){\ell }_2)\ge \left(\mathsf{\Omega }\left({\ell }_1\right)\wedge \mathsf{\Omega }\left({\ell }_2\right)\right)\forall \vartheta \in [0,1],{\ell }_1,{\ell }_2\in \mathbb{R},$, i.e., Ω is convex;

4. 

$cl\left\{{\ell }_1\in \mathbb{R},\mathsf{\Omega }\left({\ell }_1\right)>0\right\}$ is compact.

Definition 2

([60]). We say that a $\mathbf{F}$ number Ω is a ζ-level set described as

$$\begin{array}{c}\hfill {\left[\mathsf{\Omega }\right]}^{\zeta }=\left\{\mathbf{f}\in \mathbb{R}:\mathsf{\Omega }\left(\mathbf{f}\right)\ge \zeta \right\},\end{array}$$

(3)

where $\zeta \in [0,1]$ and $\mathbf{f}\in \mathbb{R}.$

Definition 3

([60]). The parameterized version of a $\mathbf{F}$ number is denoted by $\left[\underline{\mathsf{\Omega }}\left(\zeta \right),\overline{\mathsf{\Omega }}\left(\zeta \right)\right]$ such that $\zeta \in [0,1]$ satisfies the subsequent assumptions:

1. 

$\underline{\mathsf{\Omega }}\left(\zeta \right)$ is non-decreasing, left continuous, bounded over $(0,1]$ and left continuous at $0.$

2. 

$\overline{\mathsf{\Omega }}\left(\zeta \right)$ is non-increasing, right continuous, bounded over $(0,1]$ and right continuous at $0.$

3. 

$\underline{\mathsf{\Omega }}\left(\zeta \right)\le \overline{\mathsf{\Omega }}\left(\zeta \right).$

Moreover, ζ is known to be a crisp number if $\underline{\mathsf{\Omega }}\left(\zeta \right)=\overline{\mathsf{\Omega }}\left(\zeta \right)=\zeta .$

Definition 4. 

([59]). For $\zeta \in [0,1]$ and χ to be a scalar, assume that there are two $\mathbf{F}$ numbers $\tilde{\mathbf{f}}=(\underline{\mathbf{f}},\overline{\mathbf{f}}),\tilde{\varphi }=(\underline{\varphi },\overline{\varphi }),$ then the addition, subtraction and scalar multiplication, respectively, are stated as

1. 

$\tilde{\mathbf{f}}\oplus \tilde{\varphi }=\left(\underline{\mathbf{f}}\left(\zeta \right)\oplus \underline{\varphi }\left(\zeta \right),\overline{\mathbf{f}}\left(\zeta \right)\oplus \overline{\varphi }\left(\zeta \right)\right);$

2. 

$\tilde{\mathbf{f}}\ominus \tilde{\varphi }=\left(\underline{\mathbf{f}}\left(\zeta \right)\ominus \underline{\varphi }\left(\zeta \right),\overline{\mathbf{f}}\left(\zeta \right)\ominus \overline{\varphi }\left(\zeta \right)\right);$

3. 

$\chi \odot \tilde{\mathbf{f}}=\left\{\begin{array}{c}(\chi \odot \underline{\mathbf{f}},\chi \odot \overline{\mathbf{f}})\chi \ge 0,\hfill \\ (\chi \odot \overline{\mathbf{f}},\chi \odot \underline{\mathbf{f}})\chi <0.\hfill \end{array}\right.$

Suppose the set $\tilde{D}$ is a domain of $\mathbf{F}$-valued mapping $\mathsf{\Theta }$. Let us introduce the mappings $\underline{\mathsf{\Theta }}(.,.,\zeta ),$$\overline{\mathsf{\Theta }}(.,.,\zeta )$: $\tilde{D}\mapsto \mathbb{R},\forall zeta\in [0,1].$ These mappings are said to be the left and right ℘-level mappings of the map $\mathsf{\Theta }.$

Definition 5

([28]). Suppose a $\mathbf{F}$ mapping $\mathsf{\Theta }:\tilde{E}\times \tilde{E}\mapsto \mathbb{R}$ with two $\mathbf{F}$ numbers $\tilde{\mathbf{f}}=(\underline{\mathbf{f}},\overline{\mathbf{f}}),\tilde{\varphi }=(\underline{\varphi },\overline{\varphi }),$ then the Θ-distance between $\tilde{\mathbf{f}}$ and $\tilde{\varphi }$ is represented as

$$\begin{array}{c}\hfill \mathsf{\Theta }(\tilde{\mathbf{f}},\tilde{\varphi })=\underset{\zeta \in [0,1]}{sup}\left[max\left\{|\underline{\mathbf{f}}\left(\zeta \right)-\underline{\varphi }\left(\zeta \right)|,|\overline{\mathbf{f}}\left(\zeta \right)-\overline{\varphi }\left(\zeta \right)|\right\}\right].\end{array}$$

(4)

Definition 6

([28]). Consider a $\mathbf{F}$ mapping $\mathsf{\Theta }:\tilde{D}\mapsto \tilde{E},$ is said to be continuous at $(a_0,b_0)\in \tilde{D}$ if for every $ϵ>0$ and there is $\delta >0$ such that

$$\begin{array}{c}\hfill d(\mathsf{\Theta }(a,b),\mathsf{\Theta }(a_0,b_0))<ϵ;whenever|a-a_0|+|b-b_0|<\delta .\end{array}$$

(5)

If Θ is continuous for each $(a,b)\in \tilde{D},$ we say that Θ is continuous on $\tilde{D}.$

Definition 7

([62]). Let ${\beta }_1,{\beta }_2\in \tilde{E},$ if ${\beta }_3\in \tilde{E}$ and ${\beta }_1={\beta }_2+{\beta }_3.$ The $\mathcal{H}$-difference ${\beta }_3$ of ${\beta }_1$ and ${\beta }_2$ is denoted as ${\beta }_1{\ominus }^{\mathcal{H}}{\beta }_2.$ Observe that ${\beta }_1{\ominus }^{\mathcal{H}}{\beta }_2\ne {\beta }_1+(-1){\beta }_2.$

Now suppose ${\beta }_1,{\beta }_2\in \tilde{E},$ then ${\beta }_1\ominus \_g\mathcal{H}{\beta }_2={\beta }_3\iff$

(i) 

${\beta }_3=(\underline{{\beta }_1}\left(\zeta \right)-{\underline{\beta }}_2\left(\zeta \right),\overline{{\beta }_1}\left(\zeta \right)-{\overline{\beta }}_2\left(\zeta \right))$.

or

(ii) 

${\beta }_3=(\overline{{\beta }_1}\left(\zeta \right)-{\overline{\beta }}_2\left(\zeta \right),\underline{{\beta }_1}\left(\zeta \right)-{\underline{\beta }}_2\left(\zeta \right)).$

The following Lemma demonstrates the link between the $g\mathcal{H}$-difference and the Housdroff distance.

Lemma 1

([63]). For all ${\beta }_1,{\beta }_2\in \tilde{E}$, then

$$\begin{array}{c}\hfill d({\beta }_1,{\beta }_2)=\underset{\zeta \in [0,1]}{sup}\parallel {\left[{\beta }_1\right]}^{\zeta }\ominus {}_{g\mathcal{H}}{\left[{\beta }_2\right]}^{\zeta }\parallel ,\end{array}$$

(6)

where, for an interval $[a,b],$ the norm is $\parallel [a,b]\parallel =max\left\{\left|a\right|,\left|b\right|\right\}.$

Definition 8

([64]). Suppose $\mathsf{\Theta }:\tilde{D}\mapsto \tilde{E}$ and $({\ell }_0,\vartheta )\in \tilde{D}.$ Then Θ is said to be strongly generalized Hukuhara differentiable on $({\zeta }_0,\vartheta )$ ($g\mathcal{H}$-differentiable) if ∃ an element $\frac{\partial \theta ({\ell }_0,\vartheta )}{\partial \ell }\in \tilde{E}$ such that the following holds:

(i) 

For all $\hslash >0$ of sufficiently small size, the subsequent $g\mathcal{H}$-differences exist:

$$\begin{array}{c}\hfill \mathsf{\Theta }({\ell }_0+\hslash ,\vartheta )\ominus {}_{g\mathcal{H}}\mathsf{\Theta }({\ell }_0,\vartheta ),\mathsf{\Theta }({\ell }_0,\vartheta )\ominus {}_{g\mathcal{H}}\mathsf{\Theta }({\ell }_0-\hslash ,\vartheta )\end{array}$$

and the following limits hold:

$$\begin{array}{c}\hfill \underset{\hslash \mapsto 0}{lim}\frac{\mathsf{\Theta }({\ell }_0+\hslash ,\vartheta )\ominus {}_{g\mathcal{H}}\mathsf{\Theta }({\ell }_0,\vartheta )}{\hslash }=\underset{\hslash \mapsto 0}{lim}\frac{\mathsf{\Theta }({\ell }_0,\vartheta )\ominus {}_{g\mathcal{H}}\mathsf{\Theta }({\ell }_0-\hslash ,\vartheta )}{\hslash }=\frac{\partial \theta ({\ell }_0,\vartheta )}{\partial \ell }.\end{array}$$

(ii) 

For all $\hslash >0$ of sufficiently small size, the subsequent $g\mathcal{H}$-differences exist:

$$\begin{array}{c}\hfill \mathsf{\Theta }({\ell }_0,\vartheta )\ominus {}_{g\mathcal{H}}\mathsf{\Theta }({\ell }_0+\hslash ,\vartheta ),\mathsf{\Theta }({\ell }_0-\hslash ,\vartheta )\ominus {}_{g\mathcal{H}}\mathsf{\Theta }({\ell }_0,\vartheta )\end{array}$$

and the following limits hold:

$$\begin{array}{c}\hfill \underset{\hslash \mapsto 0}{lim}\frac{\mathsf{\Theta }({\ell }_0,\vartheta )\ominus {}_{g\mathcal{H}}\mathsf{\Theta }({\ell }_0+\hslash ,\vartheta )}{-\hslash }=\underset{\hslash \mapsto 0}{lim}\frac{\mathsf{\Theta }({\ell }_0-\hslash ,\vartheta )\ominus {}_{g\mathcal{H}}\mathsf{\Theta }({\ell }_0,\vartheta )}{-\hslash }=\frac{\partial \theta ({\ell }_0,\vartheta )}{\partial \ell }.\end{array}$$

Lemma 2

([65]). Consider that Θ:$\tilde{D}\mapsto \tilde{E}$ is a continuous $\mathbf{F}$ -valued mapping and $\mathsf{\Theta }(\ell ,\vartheta )=(\underline{\mathsf{\Theta }}(\ell ,\vartheta ,\zeta ),\overline{\mathsf{\Theta }}(\ell ,\vartheta ,\zeta )),\forall \zeta \in [0,1].$ Then

(i) 

If $\mathsf{\Theta }(\ell ,\vartheta )$ is $\left(\mathit{i}\right)$-partial differentiable for ℓ (i.e., Θ is partial differentiable for ℓ under the meaning of Definition 8(i)), then

$$\begin{array}{c}\hfill \frac{\partial \mathsf{\Theta }(\ell ,\vartheta )}{\partial \ell }=\left(\frac{\partial \underline{\mathsf{\Theta }}(\ell ,\vartheta )}{\partial \ell },\frac{\partial \overline{\mathsf{\Theta }}(\ell ,\vartheta )}{\partial \ell }\right),\end{array}$$

(7)

(ii) 

If $\mathsf{\Theta }(\ell ,\vartheta )$ is $\left(\mathit{i}\right)$-partial differentiable for ℓ (i.e., Θ is partial differentiable for ℓ under the meaning of Definition 8(ii)), then

$$\begin{array}{c}\hfill \frac{\partial \mathsf{\Theta }(\ell ,\vartheta )}{\partial \ell }=\left(\frac{\partial \overline{\mathsf{\Theta }}(\ell ,\vartheta )}{\partial \ell },\frac{\partial \underline{\mathsf{\Theta }}(\ell ,\vartheta )}{\partial \ell }\right).\end{array}$$

(8)

Definition 9

([28]). Assume that a $\mathbf{F}$ mapping $\mathbf{f}\in {\mathbb{C}}^F[0,d_1]\bigcap {\mathbb{L}}^F[0,d_1]$ is represented in parameterized version as $\mathbf{f}=\left[{\underline{\mathbf{f}}}_{\zeta }\left(\vartheta \right),{\overline{\mathbf{f}}}_{\zeta }\left(\vartheta \right)\right],\zeta \in [0,1]$ and ${\vartheta }_0\in (0,d_1),$ then CFD in the $\mathbf{F}$ sense is stated as

$$\begin{array}{c}\hfill {\left[{\mathcal{D}}^{\alpha }\mathbf{f}\left({\vartheta }_0\right)\right]}_{\zeta }=\left[{\mathcal{D}}^{\alpha }\underline{\mathbf{f}}\left({\vartheta }_0\right),{\mathcal{D}}^{\alpha }\overline{\mathbf{f}}\left({\vartheta }_0\right)\right],\zeta \in (0,\zeta ],\end{array}$$

(9)

where $q=\left[\zeta \right].$

$$\begin{array}{ccc}\hfill \left[{\mathcal{D}}^{\alpha }\underline{\mathbf{f}}\left({\vartheta }_0\right)\right]& & =\frac{1}{\Gamma (q-\alpha )}{\left[\underset{0}{\overset{\vartheta }{\int }}{(\vartheta -{\ell }_1)}^{q-\alpha -1}\frac{d^q}{d{\ell }_1^q}\underline{\mathbf{f}}\left({\ell }_1\right)d{\ell }_1\right]}_{\vartheta ={\vartheta }_0},\hfill \\ \hfill \left[{\mathcal{D}}^{\alpha }\overline{\mathbf{f}}\left({\vartheta }_0\right)\right]& & =\frac{1}{\Gamma (q-\alpha )}{\left[\underset{0}{\overset{\vartheta }{\int }}{(\vartheta -{\ell }_1)}^{q-\alpha -1}\frac{d^q}{d{\ell }_1^q}\overline{\mathbf{f}}\left({\ell }_1\right)d{\ell }_1\right]}_{\vartheta ={\vartheta }_0}.\hfill \end{array}$$

(10)

2.1. A Fuzzy Elzaki Transform for Fuzzy Caputo Fractional Derivative and a Fuzzy Atangana–Baleanu Fractional Derivative Operator

Definition 10.

Consider $\tilde{\mathbf{f}}$ to be continuous $\mathbf{F}$-valued mapping and assume that $exp\left(\frac{-\vartheta }{\omega }\right)\odot \tilde{\mathbf{f}}\left(\vartheta \right)$ is an improper fuzzy Riemann-integrable on $[0,\infty )$ and then $\underset{0}{\overset{\infty }{\int }}exp\left(\frac{-\vartheta }{\omega }\right)\odot \tilde{\mathbf{f}}\left(\vartheta \right)d\vartheta$ is said to be the fuzzy Elzaki transform and is described over the set of mappings:

$$\begin{array}{c}\hfill \mathcal{M}=\left\{\mathbf{f}\left(\vartheta \right):\exists z,p_1,p_2>0,\left|\mathbf{f}\left(\vartheta \right)\right|<z{e}^{\frac{\left|\vartheta \right|}{p_i}},if\vartheta \in {(-1)}^i\times [0,\infty )|\right\}.\end{array}$$

(11)

where z is a finite number, but $p_1,p_2$ may be finite or infinite, then the fuzzy Elzaki transform is described as

$$\begin{array}{c}\hfill \mathbb{E}\left\{\tilde{\mathbf{f}}\left(\vartheta \right)\right\}=\mathbf{Q}\left(\omega \right)=\omega \underset{0}{\overset{\infty }{\int }}{e}^{-\frac{\vartheta }{\omega }}\odot \tilde{\mathbf{f}}\left(\vartheta \right)d\vartheta ,\vartheta \ge 0,\omega \in [p_1,p_2].\end{array}$$

(12)

Remark 1.

In (12), $\tilde{\mathbf{f}}$ hold the cases of the decreasing diameter $\underline{\mathbf{f}}$ and the increasing diameter $\overline{\mathbf{f}}$ of a fuzzy mapping $\mathbf{f}.$ Moreover, when $\omega =1,$ then the fuzzy Elzaki transform reduces to a Laplace transform.

The parameterized version of $\tilde{\mathbf{f}}\left(\vartheta \right)$ is defined as

$$\begin{array}{c}\hfill \omega \underset{0}{\overset{\infty }{\int }}{e}^{-\frac{\vartheta }{\omega }}\tilde{\mathbf{f}}\left(\vartheta \right)d\vartheta =\left[\omega \underset{0}{\overset{\infty }{\int }}{e}^{-\frac{\vartheta }{\omega }}\underline{\mathbf{f}}\left(\vartheta \right)d\vartheta ,\omega \underset{0}{\overset{\infty }{\int }}{e}^{-\frac{\vartheta }{\omega }}\overline{\mathbf{f}}\left(\vartheta \right)d\vartheta \right].\end{array}$$

(13)

Thus,

$$\begin{array}{c}\hfill \mathbb{E}\left[\mathbf{f}(\vartheta ,\zeta )\right]=\left[\mathbb{E}\left[\underline{\mathbf{f}}(\vartheta ,\zeta )\right],\mathbb{E}\left[\overline{\mathbf{f}}(\vartheta ,\zeta )\right]\right].\end{array}$$

(14)

2.2. Some Algebraic Properties of Fuzzy Elzaki Transform

Here, our first result is the following theorem.

Theorem 1.

Assume that an integrable fuzzy valued mapping ${\tilde{\mathbf{f}}}^{\left(q\right)}\left(\vartheta \right)$ and $\tilde{\mathbf{f}}\left(\vartheta \right)$ is the primitive of ${\tilde{\mathbf{f}}}^{\left(q\right)}\left(\vartheta \right)$ on $[0,\infty ),$ then

$$\begin{array}{c}\hfill \mathbb{E}\left[{\tilde{\mathbf{f}}}^{\left(q\right)}\left(\vartheta \right)\right]={\left(\frac{1}{\omega }\right)}^q\odot \mathbb{E}\left[\tilde{\mathbf{f}}\left(\vartheta \right)\right]\ominus \sum _{\kappa =0}^{q-1}{\omega }^{2-q+\kappa }\odot {\tilde{\mathbf{f}}}^{\left(\kappa \right)}\left(0\right).\end{array}$$

(15)

The first few terms of (15) are represented as follows:

$$\begin{array}{ccc}& & \mathbb{E}\left[{\tilde{\mathbf{f}}}^{\prime }\left(\vartheta \right)\right]=\left(\frac{1}{\omega }\right)\odot \mathbf{Q}\left(\omega \right)\ominus \omega \odot \tilde{\mathbf{f}}\left(0\right),\hfill \\ & & \mathbb{E}\left[{\tilde{\mathbf{f}}}^{\prime \prime }\left(\vartheta \right)\right]={\left(\frac{1}{\omega }\right)}^2\odot \mathbf{Q}\left(\omega \right)-\omega \odot {\tilde{\mathbf{f}}}^{\prime }\left(0\right)\ominus \tilde{\mathbf{f}}\left(0\right).\hfill \end{array}$$

(16)

Proof. 

Assume that $\zeta \in [0,1]$ is arbitrary, and then we deduce

$$\begin{array}{ccc}\hfill & & {\left(\frac{1}{\omega }\right)}^q\odot \mathbb{E}\left[\tilde{\mathbf{f}}\left(\vartheta \right)\right]\ominus \sum _{\kappa =0}^{q-1}{\omega }^{2-q+\kappa }\odot {\tilde{\mathbf{f}}}^{\left(\kappa \right)}\left(0\right)\hfill \\ & & =\left({\left(\frac{1}{\omega }\right)}^q\odot \mathbb{E}\left[\overline{\mathbf{f}}(\vartheta ;\zeta )\right]\ominus \sum _{\kappa =0}^{q-1}{\omega }^{2-q+\kappa }\odot {\overline{\mathbf{f}}}^{\left(\kappa \right)}(0;\zeta ),{\left(\frac{1}{\omega }\right)}^q\odot \mathbb{E}\left[\underline{\mathbf{f}}(\vartheta ;\zeta )\right]\ominus \sum _{\kappa =0}^{q-1}{\omega }^{2-q+\kappa }\odot {\underline{\mathbf{f}}}^{\left(\kappa \right)}(0;\zeta )\right).\hfill \end{array}$$

(17)

In view of (14), we have

$$\begin{array}{ccc}\hfill & & {\left(\frac{1}{\omega }\right)}^n\odot \mathbb{E}\left[\tilde{\mathbf{f}}\left(\vartheta \right)\right]\ominus \sum _{\kappa =0}^{q-1}{\omega }^{2-q+\kappa }\odot {\tilde{\mathbf{f}}}^{\left(\kappa \right)}\left(0\right)\hfill \\ & & =\left(\mathbb{E}\left[{\overline{\mathbf{f}}}^{\left(q\right)}(\vartheta ;\zeta )\right],\mathbb{E}\left[{\underline{\mathbf{f}}}^{\left(q\right)}(\vartheta ;\zeta )\right]\right).\hfill \end{array}$$

(18)

By mathematical induction, (15) holds for $q=\kappa$ and, utilizing (18), we have

$$\begin{array}{ccc}\hfill \mathbb{E}\left[{\left({\tilde{\mathbf{f}}}^{\kappa }\left(\vartheta \right)\right)}^{\prime }\right]& & =\frac{1}{\omega }\odot \mathbb{E}\left[{\tilde{\mathbf{f}}}^{\kappa }\left(\vartheta \right)\right]\ominus {\tilde{\mathbf{f}}}^{\kappa }\left(0\right)\hfill \\ & & =\frac{1}{\omega }\odot \left[{\left(\frac{1}{\omega }\right)}^{\kappa }\odot \mathbb{E}\left[\tilde{\mathbf{f}}\left(\vartheta \right)\right]\ominus \sum _{j=0}^{\kappa -1}{\omega }^{2-\kappa +j}\odot {\tilde{\mathbf{f}}}^{(j)}\left(0\right)\right]\ominus \widetilde{{\mathbf{f}}^{\left(\kappa \right)}}\left(0\right)\hfill \\ & & ={\left(\frac{1}{\omega }\right)}^{\kappa +1}\odot \mathbb{E}\left[\tilde{\mathbf{f}}\left(\vartheta \right)\right]\ominus \sum _{j=0}^{\kappa }{\omega }^{1-j+\kappa }\odot {\tilde{\mathbf{f}}}^{\left(j\right)}\left(0\right).\hfill \end{array}$$

(19)

Consequently, (15) is truewhen $q=\kappa +1.$ This completes the proof. □

Our next result is the convolution property of the fuzzy Elzaki transform.

Theorem 2.

Assume that two integrable fuzzy-valued mappings ${\tilde{\mathbf{f}}}_1\left(\vartheta \right)$ and ${\tilde{\mathbf{f}}}_2\left(\vartheta \right),$ with their respective fuzzy Elzaki transforms ${\mathbf{Q}}_1\left(\omega \right)$ and ${\mathbf{Q}}_2\left(\omega \right),$ respectively, then

$$\begin{array}{c}\hfill \mathbb{E}\left[\left({\tilde{\mathbf{f}}}_1\ast {\tilde{\mathbf{f}}}_2\right)\left(\vartheta \right)\right]={\omega }^{-1}\odot {\mathbf{Q}}_1\left(\omega \right)\odot {\mathbf{Q}}_2\left(\omega \right),\end{array}$$

(20)

where the convolution of ${\tilde{\mathbf{f}}}_1\ast {\tilde{\mathbf{f}}}_2$ is defined as

$$\begin{array}{c}\hfill \underset{0}{\overset{\vartheta }{\int }}{\tilde{\mathbf{f}}}_1\left(\tau \right)\odot {\tilde{\mathbf{f}}}_2(\vartheta -\tau )d\tau =\underset{0}{\overset{\vartheta }{\int }}{\tilde{\mathbf{f}}}_1(\vartheta -\tau )\odot {\tilde{\mathbf{f}}}_2\left(\tau \right)d\tau .\end{array}$$

(21)

Proof. 

Utilizing (13), (20) and (21), we have

$$\begin{array}{c}\hfill \mathbb{E}\left[\underset{0}{\overset{\vartheta }{\int }}{\tilde{\mathbf{f}}}_1\left(\tau \right)\odot {\tilde{\mathbf{f}}}_2(\vartheta -\tau )d\tau \right]=\omega \underset{0}{\overset{\infty }{\int }}exp\left(-\frac{\vartheta }{\omega }\right)\odot \left(\underset{0}{\overset{\vartheta }{\int }}{\tilde{\mathbf{f}}}_1\left(\tau \right)\odot {\tilde{\mathbf{f}}}_2(\vartheta -\tau )d\tau \right)d\tau .\end{array}$$

(22)

Exchanging the order and limit of the integrals, we have

$$\begin{array}{c}\hfill \mathbb{E}\left[\underset{0}{\overset{\vartheta }{\int }}{\tilde{\mathbf{f}}}_1\left(\tau \right)\odot {\tilde{\mathbf{f}}}_2(\vartheta -\tau )d\tau \right]=\omega \underset{0}{\overset{\infty }{\int }}\left(\tilde{\mathbf{f}}\left(\tau \right)\odot \underset{\tau }{\overset{\infty }{\int }}exp\left(-\frac{\vartheta }{\omega }\right)\odot {\tilde{\mathbf{f}}}_2(\vartheta -\tau )d\vartheta \right)d\tau .\end{array}$$

(23)

Substituting $\theta =\vartheta -\tau ,$ we have

$$\begin{array}{ccc}\hfill \underset{\tau }{\overset{\infty }{\int }}exp\left(\frac{-\vartheta }{\omega }\right)\odot {\tilde{\mathbf{f}}}_2(\vartheta -\tau )d\vartheta & & =\underset{0}{\overset{\infty }{\int }}exp\left(\frac{-(\theta +\tau )}{\omega }\right)\odot {\tilde{\mathbf{f}}}_2\left(\theta \right)d\theta \hfill \\ & & =exp\left(-\frac{\tau }{\omega }\right)\odot \underset{0}{\overset{\infty }{\int }}exp\left(-\frac{\theta }{\omega }\right)\odot {\tilde{\mathbf{f}}}_2\left(\theta \right)d\theta \hfill \\ & & =exp\left(-\frac{\tau }{\omega }\right)\odot \frac{1}{\omega }\odot {\mathbf{Q}}_2\left(\omega \right).\hfill \end{array}$$

(24)

Thus, we conclude

$$\begin{array}{ccc}\hfill \mathbb{E}\left[\underset{0}{\overset{\vartheta }{\int }}{\tilde{\mathbf{f}}}_1\left(\tau \right)\odot {\tilde{\mathbf{f}}}_2(\vartheta -\tau )d\tau \right]& & =\underset{0}{\overset{\infty }{\int }}{\tilde{\mathbf{f}}}_1\left(\tau \right)\odot exp\left(-\frac{\tau }{\omega }\right)\odot {\mathbf{Q}}_2\left(\omega \right)d\tau \hfill \\ & & ={\omega }^{-1}\odot {\mathbf{Q}}_1\left(\omega \right)\odot \left[\underset{0}{\overset{\infty }{\int }}{\tilde{\mathbf{f}}}_1\left(\tau \right)\odot exp\left(-\frac{\tau }{\omega }\right)d\tau \right]\hfill \\ & & ={\omega }^{-1}\odot {\mathbf{Q}}_2\left(\omega \right)\odot {\mathbf{Q}}_1\left(\omega \right).\hfill \end{array}$$

(25)

□

Theorem 3.

(Inverse fuzzy Elzaki transform.) Consider the mapping $\mathbf{f}\left(\vartheta \right)\in \mathcal{M}$ and $\mathbf{Q}\left(\omega \right)$ to be the fuzzy Elzaki transform of the mapping $\mathbf{f}\left(\vartheta \right),$ then the inverse transforms ${\mathbb{E}}^{-1}$ are presented as follows:

$$\begin{array}{ccc}\hfill {\mathbb{E}}^{-1}\left[\mathbf{Q}\left(\omega \right)\right]& & =\underset{b_1\mapsto \infty }{lim}\frac{1}{2\pi \iota }\odot \underset{a_1-\iota b_1}{\overset{a_1+\iota b_1}{\int }}\mathbf{Q}\left(\frac{1}{\omega }\right)\odot exp\left(\vartheta \omega \right)\odot \omega d\omega \hfill \\ & & =\sum residuesof\left[\mathbf{Q}\left(\frac{1}{\omega }\right)\odot exp\left(\vartheta \omega \right)\odot \omega \right].\hfill \end{array}$$

(26)

Adopting the idea of Allahviranloo et al. [66], here, we illustrate the fuzzy Elzaki transform of Caputo and generalize the Hukuhara derivative ${}_{g\mathcal{H}}{\mathcal{D}}_{\vartheta }^{\alpha }\mathbf{f}\left(\vartheta \right).$

Theorem 4.

Consider an integrable fuzzy-valued mapping ${}_{g\mathcal{H}}{\mathcal{D}}_{\vartheta }^{\alpha }\tilde{\mathbf{f}}\left(\vartheta \right)$ and $\mathbf{f}\left(\vartheta \right)$ is the primitive of ${}_{g\mathcal{H}}{\mathcal{D}}_{\vartheta }^{\alpha }\tilde{\mathbf{f}}\left(\vartheta \right)$ defined on $[0,\infty ),$ then the CFD operator of order α satisfies

$$\begin{array}{c}\hfill \mathbb{E}\left[{}_{g\mathcal{H}}{\mathcal{D}}_{\vartheta }^{\alpha }\tilde{\mathbf{f}}\left(\vartheta \right)\right]={\left(\frac{1}{\omega }\right)}^{\alpha }\odot \mathbb{E}\left[\tilde{\mathbf{f}}\left(\vartheta \right)\right]\ominus \sum _{\kappa =0}^{q-1}{\omega }^{2-\alpha +\kappa }\odot {\tilde{\mathbf{f}}}^{\left(\kappa \right)}\left(0\right),q-1<\alpha \le 1.\end{array}$$

(27)

Proof. 

By means of Definition 10 and Theorem 2, we have

$$\begin{array}{ccc}\hfill {}_{g\mathcal{H}}{\mathcal{D}}_{\vartheta }^{\alpha }\tilde{\mathbf{f}}\left(\vartheta \right)& & =\frac{1}{\Gamma (q-\alpha )}\odot \underset{0}{\overset{\vartheta }{\int }}{(\vartheta -\tau )}^{q-\alpha -1}\odot \frac{{\partial }^q\tilde{f}\left(\tau \right)}{\partial {\tau }^q}d\tau \hfill \\ & & =\frac{1}{\Gamma (q-\alpha )}\odot {\tilde{\mathbf{f}}}^{\left(q\right)}\odot {\vartheta }^{q-\alpha -1}.\hfill \end{array}$$

(28)

Again, in view of Definition 10 and Theorem 1, we obtain

$$\begin{array}{ccc}\hfill {}_{g\mathcal{H}}{\mathcal{D}}_{\vartheta }^{\alpha }\tilde{\mathbf{f}}\left(\vartheta \right)& & =\frac{1}{\Gamma (q-\alpha )}\odot \mathbb{E}\left[{\vartheta }^{q-\alpha -1}\odot \widetilde{{\mathbf{f}}^{\left(q\right)}}\left(\vartheta \right)\right]\hfill \\ & & ={\left(\frac{1}{\omega }\right)}^{\alpha }\odot \mathbb{E}\left[\tilde{\mathbf{f}}\left(\vartheta \right)\right]\ominus \sum _{\kappa =0}^{q-1}{\omega }^{2-\alpha +\kappa }\odot {\tilde{\mathbf{f}}}^{\left(\kappa \right)}\left(0\right).\hfill \end{array}$$

(29)

Using the fact that $\zeta \in [0,1]$, and the result provided by Salahhshour et al. [67], we have

$$\begin{array}{ccc}& & {\left(\frac{1}{\omega }\right)}^{\alpha }\odot \mathbb{E}\left[\tilde{\mathbf{f}}\left(\vartheta \right)\right]\ominus \sum _{\kappa =0}^{q-1}{\omega }^{2-\alpha +\kappa }\odot {\tilde{\mathbf{f}}}^{\left(\kappa \right)}\left(0\right)\hfill \\ & & =\left({\left(\frac{1}{\omega }\right)}^{\alpha }\mathbb{E}\left[\underline{\mathbf{f}}(\vartheta ;\zeta )\right]-\sum _{\kappa =0}^{q-1}{\omega }^{2-\alpha +\kappa }{\underline{\mathbf{f}}}^{\left(\kappa \right)}(0;\zeta ),{\left(\frac{1}{\omega }\right)}^{\alpha }\mathbb{E}\left[\overline{\mathbf{f}}\left(\vartheta wp\right)\right]-\sum _{\kappa =0}^{q-1}{\omega }^{2-\alpha +\kappa }{\overline{\mathbf{f}}}^{\left(\kappa \right)}(0;\zeta )\right).\hfill \end{array}$$

(30)

This completes the proof. □

Next we illustrate the linearity property of yjr fuzzy Elzaki transform.

Theorem 5.

Assume that there are two continuous fuzzy valued-mappings ${\tilde{\mathbf{f}}}_1\left(\vartheta \right)$ and ${\tilde{\mathbf{f}}}_2\left(\vartheta \right)$ with real constants $c_1$ and $c_2,$, then

$$\begin{array}{c}\hfill \mathbb{E}\left[c_1\odot {\tilde{\mathbf{f}}}_1\left(\vartheta \right)\oplus c_2\odot {\tilde{\mathbf{f}}}_2\left(\vartheta \right)\right]=c_1\odot \mathbb{E}\left[{\tilde{\mathbf{f}}}_1\left(\vartheta \right)\right]+c_2\odot \mathbb{E}\left[{\tilde{\mathbf{f}}}_2\left(\vartheta \right)\right].\end{array}$$

(31)

Proof. 

Consider $\zeta \in [0,1]$ to be arbitrarily fixed. Then, by means of (13), we have

$$\begin{array}{ccc}\hfill \mathbb{E}\left[c_1\odot {\tilde{\mathbf{f}}}_1\left(\vartheta \right)\oplus c_2\odot {\tilde{\mathbf{f}}}_1\left(\vartheta \right)\right]& & =\omega \underset{0}{\overset{\infty }{\int }}\left(a_1\odot {\tilde{\mathbf{f}}}_1\left(\vartheta \right)\oplus c_2\odot {\tilde{\mathbf{f}}}_2\left(\vartheta \right)\right)\odot exp\left(\frac{-\vartheta }{\omega }\right)d\vartheta \hfill \\ & & =\omega \underset{0}{\overset{\infty }{\int }}{c}_1\odot {\tilde{\mathbf{f}}}_1\left(\vartheta \right)\odot exp\left(\frac{-\vartheta }{\omega }\right)d\vartheta \oplus \omega \underset{0}{\overset{\infty }{\int }}{c}_2\odot {\tilde{\mathbf{f}}}_2\left(\vartheta \right)\odot exp\left(\frac{-\vartheta }{\omega }\right)d\vartheta \hfill \\ & & =\left(c_1\odot \omega \underset{0}{\overset{\infty }{\int }}{\tilde{\mathbf{f}}}_1\left(\vartheta \right)\odot exp\left(\frac{-\vartheta }{\omega }\right)d\vartheta \right)\oplus \left(c_2\odot \omega \underset{0}{\overset{\infty }{\int }}{\tilde{\mathbf{f}}}_1\left(\vartheta \right)\odot exp\left(\frac{-\vartheta }{\omega }\right)d\vartheta \right)\hfill \\ & & =c_1\odot \left(\omega \underset{0}{\overset{\infty }{\int }}{\underline{\mathbf{f}}}_1(\vartheta ;\zeta )\odot exp\left(\frac{-\vartheta }{\omega }\right)d\vartheta ,\omega \underset{0}{\overset{\infty }{\int }}{\overline{\mathbf{f}}}_1(\vartheta ;\zeta )\odot exp\left(\frac{-\vartheta }{\omega }\right)d\vartheta \right)\hfill \\ & & \oplus c_2\odot \left(\omega \underset{0}{\overset{\infty }{\int }}{\underline{\mathbf{f}}}_2(\vartheta ;\zeta )\odot exp\left(\frac{-\vartheta }{\omega }\right)d\vartheta ,\omega \underset{0}{\overset{\infty }{\int }}{\overline{\mathbf{f}}}_2(\vartheta ;\zeta )\odot exp\left(\frac{-\vartheta }{\omega }\right)d\vartheta \right)\hfill \\ & & =c_1\odot \mathbb{E}\left[{\tilde{\mathbf{f}}}_1\left(\vartheta \right)\right]+c_2\odot \mathbb{E}\left[{\tilde{\mathbf{f}}}_2\left(\vartheta \right)\right],\hfill \end{array}$$

(32)

This completes the proof. □

Definition 11.

Consider $\mathbf{f}\in {\mathbb{C}}^F[0,\overline{d_1}]\bigcap {\mathbb{L}}^F[0,\overline{d_1}]$ such that $\mathbf{f}\left(\vartheta \right)=\left[\underline{\mathbf{f}}(\vartheta ,\zeta ),\overline{\mathbf{f}}(\vartheta ,\zeta )\right],\zeta \in [0,1],$ then the Elzaki transform of fuzzy CFD of order $\alpha \in (0,1]$ is described as follows:

$$\begin{array}{c}\hfill \mathbb{E}\left[{\left({\mathcal{D}}^{\alpha }\mathbf{f}\left(\vartheta \right)\right)}_{\zeta }\right]=\left[\mathbb{E}\left[{\mathcal{D}}^{\alpha }\underline{\mathbf{f}}(\vartheta ,\zeta )\right],\mathbb{E}\left[{\mathcal{D}}^{\alpha }\overline{\mathbf{f}}(\vartheta ,\zeta )\right]\right],\end{array}$$

(33)

where

$$\begin{array}{ccc}\hfill \mathbb{E}\left[{\mathcal{D}}^{\alpha }\underline{\mathbf{f}}(\vartheta ,\zeta )\right]& & =\frac{1}{{\omega }^{\alpha }}\mathbb{E}\left[\underline{\mathbf{f}}(\vartheta ,\zeta )\right]-\sum _{\kappa =0}^{q-1}{\underline{\mathbf{f}}}_{\left(\kappa \right)}({\ell }_1;\zeta ){\omega }^{2-\alpha +\kappa },\alpha \in (q-1,q],\hfill \\ \hfill \mathbb{E}\left[{\mathcal{D}}^{\alpha }\overline{\mathbf{f}}(\vartheta ,\zeta )\right]& & =\frac{1}{{\omega }^{\alpha }}\mathbb{E}\left[\overline{\mathbf{f}}(\vartheta ,\zeta )\right]-\sum _{\kappa =0}^{q-1}{\overline{\mathbf{f}}}_{\left(\kappa \right)}({\ell }_1;\zeta ){\omega }^{2-\alpha +\kappa },\alpha \in (q-1,q].\hfill \end{array}$$

(34)

Definition 12.

Consider $\tilde{\mathbf{f}}\left(\vartheta \right)\in {\tilde{\mathbb{H}}}^1(0,T)$ and $\alpha \in [0,1],$ then the $\alpha th$-order variable Atangana–Baleanu derivative under (i)—$g\mathcal{H}$ differentiability of $\tilde{\mathbf{f}}$ in the Caputo sense is stated as

$$\begin{array}{c}\hfill \left[{}^{ABC}{\mathcal{D}}_{\left(i\right)-g\mathcal{H}}^{\alpha }\tilde{\mathbf{f}}({\vartheta }_0;\zeta )\right]=\left[{}^{ABC}{\mathcal{D}}_{\left(i\right)-g\mathcal{H}}^{\alpha }\underline{\mathbf{f}}({\vartheta }_0;\zeta ),{}^{ABC}{\mathcal{D}}_{\left(i\right)-g\mathcal{H}}^{\alpha }\overline{\mathbf{f}}({\vartheta }_0;\zeta )\right],\zeta \in [0,1],\end{array}$$

(35)

where

$$\begin{array}{ccc}& & {}^{ABC}{\mathcal{D}}_{\left(i\right)-g\mathcal{H}}^{\alpha }\underline{\mathbf{f}}({\vartheta }_0;\zeta )=\frac{\mathcal{N}\left(\alpha \right)}{1-\alpha }{\left[\underset{0}{\overset{\vartheta }{\int }}{\underline{\mathbf{f}}}_{\left(i\right)-g\mathcal{H}}^{\prime }\left({\ell }_1\right)E_{\alpha }\left[\frac{-\alpha {(\vartheta -{\ell }_1)}^{\alpha }}{1-\alpha }\right]d{\ell }_1\right]}_{\vartheta ={\vartheta }_0},\hfill \\ & & {}^{ABC}{\mathcal{D}}_{\left(i\right)-g\mathcal{H}}^{\alpha }\overline{\mathbf{f}}({\vartheta }_0;\zeta )=\frac{\mathcal{N}\left(\alpha \right)}{1-\alpha }{\left[\underset{0}{\overset{\vartheta }{\int }}{\overline{\mathbf{f}}}_{\left(i\right)-g\mathcal{H}}^{\prime }\left({\ell }_1\right)E_{\alpha }\left[\frac{-\alpha {(\vartheta -{\ell }_1)}^{\alpha }}{1-\alpha }\right]d{\ell }_1\right]}_{\vartheta ={\vartheta }_0},\hfill \end{array}$$

(36)

where $\mathcal{N}\left(\alpha \right)$ denotes the normalize function that equals 1 when α is assumed to be 0 and 1. Furthermore, we suppose that type $\left(i\right)$—$g\mathcal{H}$ exists. So here is no need to consider $\left(ii\right)$—$g\mathcal{H}$ differentiability.

Yauvaz and Abdeljawad [68] defined the ABC fractional derivative operator in the Elzaki sense. Furthermore, we extend the idea of a fuzzy ABC fractional derivative in the Elzaki transform sense as follows:

Definition 13.

Consider $\mathbf{f}\in {\mathbb{C}}^F[0,\overline{d_1}]\bigcap {\mathbb{L}}^F[0,\overline{d_1}]$ such that $\mathbf{f}\left(\vartheta \right)=\left[\underline{\mathbf{f}}(\vartheta ,\zeta ),\overline{\mathbf{f}}(\vartheta ,\zeta )\right],\zeta \in [0,1],$ then the Elzaki transform of fuzzy ABC of order $\alpha \in [0,1]$ is described as follows:

$$\begin{array}{c}\hfill \mathbb{E}\left[{\left({}^{ABC}{\mathcal{D}}^{\alpha }\mathbf{f}\left(\vartheta \right)\right)}_{\zeta }\right]=\left[\mathbb{E}\left[{}^{ABC}{\mathcal{D}}^{\alpha }\underline{\mathbf{f}}(\vartheta ,\zeta )\right],\mathbb{E}\left[{}^{ABC}{\mathcal{D}}^{\alpha }\overline{\mathbf{f}}(\vartheta ,\zeta )\right]\right],\end{array}$$

(37)

where

$$\begin{array}{ccc}\hfill \mathbb{E}\left[{}^{ABC}{\mathcal{D}}^{\alpha }\underline{\mathbf{f}}(\vartheta ,\zeta )\right]& & =\frac{\omega \mathcal{N}\left(\alpha \right)}{\alpha {\omega }^{\alpha }+1-\alpha }\left[\frac{\mathbb{E}\left[\underline{\mathbf{f}}(\vartheta ,\zeta )\right]}{\omega }-\omega \underline{\mathbf{f}}\left(0\right)\right],\hfill \\ \hfill \mathbb{E}\left[{}^{ABC}{\mathcal{D}}^{\alpha }\overline{\mathbf{f}}(\vartheta ,\zeta )\right]& & =\frac{\omega \mathcal{N}\left(\alpha \right)}{\alpha {\omega }^{\alpha }+1-\alpha }\left[\frac{\mathbb{E}\left[\overline{\mathbf{f}}(\vartheta ,\zeta )\right]}{\omega }-\omega \overline{\mathbf{f}}\left(0\right)\right].\hfill \end{array}$$

(38)

3. Proposed Algorithm

Here, the general methodology of obtaining the numerical results of one-dimensional fractional FWE involving the CFD and ABC fractional derivative operator in the fuzzy ET is investigated.

The parameterized version of (2) is presented as

$$\left\{\begin{array}{c}\begin{array}{c}\frac{{\partial }^{\alpha }}{\partial {\vartheta }^{\alpha }}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )=\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )-\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )+\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{{\partial }^3}{\partial {\ell }_1^3}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\hfill \\ -\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )+3\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{{\partial }^2}{\partial {\ell }_1^2}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta ),\hfill \\ \underline{\mathbf{f}}({\ell }_1,0)=\underline{g}({\ell }_1;\zeta ),\hfill \\ \frac{{\partial }^{\alpha }}{\partial {\vartheta }^{\alpha }}\overline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )=\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\overline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )-\frac{\partial }{\partial {\ell }_1}\overline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )+\overline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{{\partial }^3}{\partial {\ell }_1^3}\overline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\hfill \\ -\overline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{\partial }{\partial {\ell }_1}\overline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )+3\frac{\partial }{\partial {\ell }_1}\overline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{{\partial }^2}{\partial {\ell }_1^2}\overline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta ),\hfill \\ \overline{\mathbf{f}}({\ell }_1,0)=\overline{g}({\ell }_1;\zeta ).\hfill \end{array}\hfill \end{array}\right.$$

(39)

Employing ET on both sides of the first preceding case of (39) by utilizing the fuzzy CFD, we have

$$\begin{array}{c}\hfill \mathbb{E}\left[\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right]=\mathbb{E}[\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )-\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )+\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{{\partial }^3}{\partial {\ell }_1^3}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\\ \hfill -\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )+3\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{{\partial }^2}{\partial {\ell }_1^2}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )]\end{array}$$

(40)

subject to the IC $\underline{\mathbf{f}}({\ell }_1,0)=\underline{g}\left({\ell }_1\right),$ we have

$$\begin{array}{c}\hfill \frac{1}{{\omega }^{\alpha }}\mathbb{E}\left[\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right]-\sum _{\kappa =0}^{q-1}{\underline{\mathbf{f}}}_{\left(\kappa \right)}({\ell }_1;\zeta ){\omega }^{2-\alpha +\kappa }=\mathbb{E}[\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )-\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )+\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{{\partial }^3}{\partial {\ell }_1^3}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\\ \hfill -\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )+3\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{{\partial }^2}{\partial {\ell }_1^2}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )],\end{array}$$

or, accordingly, we have

$$\begin{array}{c}\hfill \mathbb{E}\left[\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right]={\omega }^2\underline{g}({\ell }_1;\zeta )+{\omega }^{\alpha }\mathbb{E}[\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )-\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )+\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{{\partial }^3}{\partial {\ell }_1^3}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\\ \hfill -\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )+3\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{{\partial }^2}{\partial {\ell }_1^2}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )].\end{array}$$

(41)

Again, applying ET on both sides of the first preceding case of (39) by utilizing the fuzzy ABC fractional derivative, we have

$$\begin{array}{ccc}\hfill \mathbb{E}\left[\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right]& & ={\omega }^2\underline{g}({\ell }_1;\zeta )+\left(\frac{\alpha {\omega }^{\alpha }+1-\alpha }{\mathcal{N}\left(\alpha \right)}\right)\mathbb{E}[\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )-\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\hfill \\ & & +\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{{\partial }^3}{\partial {\ell }_1^3}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )-\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )+3\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{{\partial }^2}{\partial {\ell }_1^2}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )].\hfill \end{array}$$

(42)

The unknown series solution is expressed as

$$\begin{array}{c}\hfill \underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )=\sum _{q=0}^{\infty }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta ),\end{array}$$

(43)

and the nonlinear terms are decomposed as

$$\begin{array}{ccc}\hfill {\underline{\mathcal{N}}}_1({\ell }_1,\vartheta ;\zeta )& & =\sum _{q=0}^{\infty }{\underline{\mathcal{A}}}_q({\ell }_1,\vartheta ;\zeta )=\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{{\partial }^3}{\partial {\ell }_1^3}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta ),\hfill \\ \hfill {\underline{\mathcal{N}}}_2({\ell }_1,\vartheta ;\zeta )& & =\sum _{q=0}^{\infty }{\underline{\mathcal{B}}}_q({\ell }_1,\vartheta ;\zeta )=\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta ),\hfill \\ \hfill {\underline{\mathcal{N}}}_3({\ell }_1,\vartheta ;\zeta )& & =\sum _{q=0}^{\infty }{\underline{\mathcal{C}}}_q({\ell }_1,\vartheta ;\zeta )=\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{{\partial }^2}{\partial {\ell }_1^2}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta ),\hfill \end{array}$$

(44)

where ${\underline{\mathcal{A}}}_q,{\underline{\mathcal{B}}}_q$ and ${\underline{\mathcal{C}}}_q$ are known to be the Adomian polynomial are presented as

$$\begin{array}{ccc}\hfill & & {\underline{\mathcal{A}}}_q=\frac{1}{q!}\frac{d^q}{d{\lambda }^q}{\left[{\underline{\mathcal{N}}}_1\left(\sum _{q=0}^{\infty }{\lambda }^q{\underline{\mathbf{f}}}_q({\ell }_1,\vartheta ;\zeta )\right)\right]}_{\lambda =0},\hfill \\ & & {\underline{\mathcal{B}}}_q=\frac{1}{q!}\frac{d^q}{d{\lambda }^q}{\left[{\underline{\mathcal{N}}}_2\left(\sum _{q=0}^{\infty }{\lambda }^q{\underline{\mathbf{f}}}_q({\ell }_1,\vartheta ;\zeta )\right)\right]}_{\lambda =0},\hfill \\ & & {\underline{\mathcal{C}}}_q=\frac{1}{q!}\frac{d^q}{d{\lambda }^q}{\left[{\underline{\mathcal{N}}}_3\left(\sum _{q=0}^{\infty }{\lambda }^q{\underline{\mathbf{f}}}_q({\ell }_1,\vartheta ;\zeta )\right)\right]}_{\lambda =0}.\hfill \end{array}$$

(45)

Now, (41) and (42), respectively, can be expressed as

$$\begin{array}{ccc}\hfill & & \mathbb{E}\left[\sum _{q=0}^{\infty }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right]={\omega }^2\underline{g}({\ell }_1;\zeta )+{\omega }^{\alpha }\mathbb{E}[\sum _{q=0}^{\infty }{\left(\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_q-\sum _{q=0}^{\infty }{\left(\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_q\hfill \\ & & +\sum _{q=0}^{\infty }{\underline{\mathcal{A}}}_q({\ell }_1,\vartheta ;\zeta )-\sum _{q=0}^{\infty }{\underline{\mathcal{B}}}_q({\ell }_1,\vartheta ;\zeta )+3\sum _{q=0}^{\infty }{\underline{\mathcal{C}}}_q({\ell }_1,\vartheta ;\zeta )]\hfill \end{array}$$

(46)

and

$$\begin{array}{ccc}\hfill \mathbb{E}\left[\sum _{q=0}^{\infty }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right]& & ={\omega }^2\underline{g}({\ell }_1;\zeta )+\left(\frac{\alpha {\omega }^{\alpha }+1-\alpha }{\mathcal{N}\left(\alpha \right)}\right)\mathbb{E}[\sum _{q=0}^{\infty }{\left(\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_q-\sum _{q=0}^{\infty }{\left(\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_q\hfill \\ & & +\sum _{q=0}^{\infty }{\underline{\mathcal{A}}}_q({\ell }_1,\vartheta ;\zeta )-\sum _{q=0}^{\infty }{\underline{\mathcal{B}}}_q({\ell }_1,\vartheta ;\zeta )+3\sum _{q=0}^{\infty }{\underline{\mathcal{C}}}_q({\ell }_1,\vartheta ;\zeta )].\hfill \end{array}$$

(47)

Applying the inverse ET on [46] and comparing terms by terms on both sides, we have

$$\begin{array}{ccc}\hfill {\underline{\mathbf{f}}}_0({\ell }_1,\vartheta ;\zeta )& & ={\mathbb{E}}^{-1}\left[{\omega }^2\underline{g}({\ell }_1;\zeta )\right],\hfill \\ \hfill {\underline{\mathbf{f}}}_1({\ell }_1,\vartheta ;\zeta )& & ={\mathbb{E}}^{-1}\left[{\omega }^{\alpha }\mathbb{E}\right[{\left(\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_1-{\left(\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_1+{\underline{\mathcal{A}}}_1({\ell }_1,\vartheta ;\zeta )-{\underline{\mathcal{B}}}_1({\ell }_1,\vartheta ;\zeta )\hfill \\ & & +3{\underline{\mathcal{C}}}_1({\ell }_1,\vartheta ;\zeta )\left]\right],\hfill \\ \hfill {\underline{\mathbf{f}}}_2({\ell }_1,\vartheta ;\zeta )& & ={\mathbb{E}}^{-1}\left[{\omega }^{\alpha }\mathbb{E}\right[{\left(\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_2-{\left(\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_2+{\underline{\mathcal{A}}}_2({\ell }_1,\vartheta ;\zeta )-{\underline{\mathcal{B}}}_2({\ell }_1,\vartheta ;\zeta )\hfill \\ & & +3{\underline{\mathcal{C}}}_2({\ell }_1,\vartheta ;\zeta )\left]\right],\hfill \\ \hfill ⋮\\ \hfill {\underline{\mathbf{f}}}_{q+1}({\ell }_1,\vartheta ;\zeta )& & ={\mathbb{E}}^{-1}\left[{\omega }^{\alpha }\mathbb{E}\right[{\left(\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_q-{\left(\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_q+{\underline{\mathcal{A}}}_q({\ell }_1,\vartheta ;\zeta )-{\underline{\mathcal{B}}}_q({\ell }_1,\vartheta ;\zeta )\hfill \\ & & +3{\underline{\mathcal{C}}}_q({\ell }_1,\vartheta ;\zeta )\left]\right].\hfill \end{array}$$

Again, applying the inverse ET on (47) and comparing terms by terms on both sides, we have

$$\begin{array}{ccc}\hfill {\underline{\mathbf{f}}}_0({\ell }_1,\vartheta ;\zeta )& & ={\mathbb{E}}^{-1}\left[{\omega }^2\underline{g}({\ell }_1;\zeta )\right],\hfill \\ \hfill {\underline{\mathbf{f}}}_1({\ell }_1,\vartheta ;\zeta )& & ={\mathbb{E}}^{-1}\left[\left(\frac{\alpha {\omega }^{\alpha }+1-\alpha }{\mathcal{N}\left(\alpha \right)}\right)\mathbb{E}\right[{\left(\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_0-{\left(\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_0+{\underline{\mathcal{A}}}_0({\ell }_1,\vartheta ;\zeta )\hfill \\ & & -{\underline{\mathcal{B}}}_0({\ell }_1,\vartheta ;\zeta )+3{\underline{\mathcal{C}}}_0({\ell }_1,\vartheta ;\zeta )\left]\right],\hfill \\ \hfill {\underline{\mathbf{f}}}_2({\ell }_1,\vartheta ;\zeta )& & ={\mathbb{E}}^{-1}\left[\left(\frac{\alpha {\omega }^{\alpha }+1-\alpha }{\mathcal{N}\left(\alpha \right)}\right)\mathbb{E}\right[{\left(\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_1-{\left(\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_1+{\underline{\mathcal{A}}}_1({\ell }_1,\vartheta ;\zeta )\hfill \\ & & -{\underline{\mathcal{B}}}_1({\ell }_1,\vartheta ;\zeta )+3{\underline{\mathcal{C}}}_1({\ell }_1,\vartheta ;\zeta )\left]\right],\hfill \\ \hfill ⋮\\ \hfill {\underline{\mathbf{f}}}_{q+1}({\ell }_1,\vartheta ;\zeta )& & ={\mathbb{E}}^{-1}\left[\left(\frac{\alpha {\omega }^{\alpha }+1-\alpha }{\mathcal{N}\left(\alpha \right)}\right)\mathbb{E}\right[{\left(\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_q-{\left(\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_q+{\underline{\mathcal{A}}}_q({\ell }_1,\vartheta ;\zeta )\hfill \\ & & -{\underline{\mathcal{B}}}_q({\ell }_1,\vartheta ;\zeta )+3{\underline{\mathcal{C}}}_q({\ell }_1,\vartheta ;\zeta )\left]\right].\hfill \end{array}$$

Hence, the required series solution is expressed as

$$\begin{array}{c}\hfill \underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )={\underline{\mathbf{f}}}_0({\ell }_1,\vartheta ;\zeta )+{\underline{\mathbf{f}}}_1({\ell }_1,\vartheta ;\zeta )+....\end{array}$$

(48)

Repeating the same procedure for the upper case of (39). Therefore, we mention the solution in the parameterized version as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )={\underline{\mathbf{f}}}_0({\ell }_1,\vartheta ;\zeta )+{\underline{\mathbf{f}}}_1({\ell }_1,\vartheta ;\zeta )+...,\hfill \\ \overline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )={\overline{\mathbf{f}}}_0({\ell }_1,\vartheta ;\zeta )+{\overline{\mathbf{f}}}_1({\ell }_1,\vartheta ;\zeta )+....\hfill \end{array}\right.\end{array}$$

(49)

4. Test Examples and Their Physical Interpretation

In this note, we demonstrate the series solutions with the aid of EADM concerning different initial conditions by employing fuzzy Caputo and ABC fractional derivative operators, respectively.

Firstly, we surmise the FW model (2) by considering EADM.

Problem 1.

Assume the one-dimension fuzzy fractional FW model with fuzzy ICs is represented as follows:

$$\begin{array}{ccc}\hfill \frac{{\partial }^{\alpha }}{\partial {\vartheta }^{\alpha }}\tilde{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )& & =\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\tilde{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\ominus \frac{\partial }{\partial {\ell }_1}\tilde{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\oplus \tilde{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\odot \frac{{\partial }^3}{\partial {\ell }_1^3}\tilde{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\hfill \\ & & \ominus \tilde{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\odot \frac{\partial }{\partial {\ell }_1}\tilde{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\oplus \frac{\partial }{\partial {\ell }_1}\tilde{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\odot \frac{{\partial }^2}{\partial {\ell }_1^2}\tilde{\mathbf{f}}({\ell }_1,\vartheta ;\zeta ),\hfill \\ & & \tilde{\mathbf{f}}({\ell }_1,0)=\tilde{\chi }\left(\zeta \right)\odot exp\left(\frac{{\ell }_1}{2}\right),\hfill \end{array}$$

(50)

where $\tilde{\chi }\left(\zeta \right)=[\underline{\chi }\left(\zeta \right),\overline{\chi }\left(\zeta \right)]=[\zeta -1,1-\zeta ]$ for $\zeta \in [0,1]$ is a fuzzy number.

Proof. 

The parameterized version of the problem (50) is expressed as follows

$$\left\{\begin{array}{c}\begin{array}{c}\frac{{\partial }^{\alpha }}{\partial {\vartheta }^{\alpha }}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )=\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )-\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )+\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{{\partial }^3}{\partial {\ell }_1^3}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\hfill \\ -\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )+\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{{\partial }^2}{\partial {\ell }_1^2}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta ),\hfill \\ \underline{\mathbf{f}}({\ell }_1,0)=\underline{\chi }\left(\zeta \right)exp\left(\frac{{\ell }_1}{2}\right),\hfill \\ \frac{{\partial }^{\alpha }}{\partial {\vartheta }^{\alpha }}\overline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )=\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\overline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )-\frac{\partial }{\partial {\ell }_1}\overline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )+\overline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{{\partial }^3}{\partial {\ell }_1^3}\overline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\hfill \\ -\overline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{\partial }{\partial {\ell }_1}\overline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )+\frac{\partial }{\partial {\ell }_1}\overline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{{\partial }^2}{\partial {\ell }_1^2}\overline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta ),\hfill \\ \overline{\mathbf{f}}({\ell }_1,0)=\overline{\chi }\left(\zeta \right)exp\left(\frac{{\ell }_1}{2}\right).\hfill \end{array}\hfill \end{array}\right.$$

(51)

Case I. (For the fuzzy Caputo fractional derivative)

Here, we obtain the EADM solution for the first case of (51) by using the fuzzy Caputo fractional derivative operator.

Taking into consideration the procedure described in Section 3, we have

$$\begin{array}{ccc}& & \frac{1}{{\omega }^{\alpha }}\mathbb{E}\left[\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right]-\sum _{\kappa =0}^{q-1}{\underline{\mathbf{f}}}_{\left(\kappa \right)}({\ell }_1;\zeta ){\omega }^{2-\alpha +\kappa }\hfill \\ & & =\mathbb{E}[\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )-\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )+\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{{\partial }^3}{\partial {\ell }_1^3}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\hfill \\ & & -\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )+\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{{\partial }^2}{\partial {\ell }_1^2}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )].\hfill \end{array}$$

Simple computations result in

$$\begin{array}{c}\hfill \underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )=(\zeta -1)exp\left(\frac{{\ell }_1}{2}\right)+{\mathbb{E}}^{-1}\left[{\omega }^{\alpha }\mathbb{E}\right[\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )-\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )+\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{{\partial }^3}{\partial {\ell }_1^3}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\\ \hfill -\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )+\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{{\partial }^2}{\partial {\ell }_1^2}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\left]\right].\end{array}$$

(52)

Let us surmise the infinite sum $\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )=\sum _{q=0}^{\infty }{\underline{\mathbf{f}}}_q({\ell }_1,\vartheta ;\zeta ),(q=0,1,2,...)$ accompanying it with (45) and affirming the non-linearity. Therefore, (52) takes the form

$$\begin{array}{ccc}\hfill \sum _{q=0}^{\infty }{\underline{\mathbf{f}}}_q({\ell }_1,\vartheta ;\zeta )& & =(\zeta -1)exp\left(\frac{{\ell }_1}{2}\right)+{\mathbb{E}}^{-1}\left[{\omega }^{\alpha }\mathbb{E}\right[\sum _{q=0}^{\infty }{\left(\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_q-\sum _{q=0}^{\infty }{\left(\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_q\hfill \\ & & +\sum _{q=0}^{\infty }{\underline{\mathcal{A}}}_q-\sum _{q=0}^{\infty }{\underline{\mathcal{B}}}_q+3\sum _{q=0}^{\infty }{\underline{\mathcal{C}}}_q\left]\right].\hfill \end{array}$$

(53)

The first few Adomian polynomials are

$$\begin{array}{ccc}\hfill & & {\underline{\mathcal{A}}}_q\left(\underline{\mathbf{f}}\frac{{\partial }^3}{\partial {\ell }_1^3}\underline{\mathbf{f}}\right)=\left\{\begin{array}{c}{\underline{\mathbf{f}}}_0\frac{{\partial }^3}{\partial {\ell }_1^3}{\underline{\mathbf{f}}}_0,q=0,\hfill \\ {\underline{\mathbf{f}}}_0\frac{{\partial }^3}{\partial {\ell }_1^3}{\underline{\mathbf{f}}}_1+{\underline{\mathbf{f}}}_1\frac{{\partial }^3}{\partial {\ell }_1^3}{\underline{\mathbf{f}}}_0,q=1,\hfill \\ {\underline{\mathbf{f}}}_1\frac{{\partial }^3}{\partial {\ell }_1^3}{\underline{\mathbf{f}}}_2+{\underline{\mathbf{f}}}_1\frac{{\partial }^3}{\partial {\ell }_1^3}{\underline{\mathbf{f}}}_1+{\underline{\mathbf{f}}}_2\frac{{\partial }^3}{\partial {\ell }_1^3}{\underline{\mathbf{f}}}_0,q=2,\hfill \end{array}\right.\hfill \\ & & {\underline{\mathcal{B}}}_q\left(\underline{\mathbf{f}}\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}\right)=\left\{\begin{array}{c}{\underline{\mathbf{f}}}_0\frac{\partial }{\partial {\ell }_1}{\underline{\mathbf{f}}}_0,q=0,\hfill \\ {\underline{\mathbf{f}}}_0\frac{\partial }{\partial {\ell }_1}{\underline{\mathbf{f}}}_1+{\underline{\mathbf{f}}}_1\frac{\partial }{\partial {\ell }_1}{\underline{\mathbf{f}}}_0,q=1,\hfill \\ {\underline{\mathbf{f}}}_1\frac{\partial }{\partial {\ell }_1}{\underline{\mathbf{f}}}_2+{\underline{\mathbf{f}}}_1\frac{\partial }{\partial {\ell }_1}{\underline{\mathbf{f}}}_1+{\underline{\mathbf{f}}}_2\frac{\partial }{\partial {\ell }_1}{\underline{\mathbf{f}}}_0,q=2,\hfill \end{array}\right.\hfill \\ & & {\underline{\mathcal{C}}}_q\left(\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}\frac{{\partial }^2}{\partial {\ell }_1^2}\underline{\mathbf{f}}\right)=\left\{\begin{array}{c}\frac{\partial }{\partial {\ell }_1}{\underline{\mathbf{f}}}_0\frac{{\partial }^2}{\partial {\ell }_1^2}{\underline{\mathbf{f}}}_0,q=0,\hfill \\ \frac{\partial }{\partial {\ell }_1}{\underline{\mathbf{f}}}_0\frac{{\partial }^2}{\partial {\ell }_1^2}{\underline{\mathbf{f}}}_1+\frac{\partial }{\partial {\ell }_1}{\underline{\mathbf{f}}}_1\frac{{\partial }^2}{\partial {\ell }_1^2}{\underline{\mathbf{f}}}_0,q=1,\hfill \\ \frac{\partial }{\partial {\ell }_1}{\underline{\mathbf{f}}}_1\frac{{\partial }^2}{\partial {\ell }_1^2}{\underline{\mathbf{f}}}_2+\frac{\partial }{\partial {\ell }_1}{\underline{\mathbf{f}}}_1\frac{{\partial }^2}{\partial {\ell }_1^2}{\underline{\mathbf{f}}}_1+\frac{\partial }{\partial {\ell }_1}{\underline{\mathbf{f}}}_2\frac{{\partial }^2}{\partial {\ell }_1^2}{\underline{\mathbf{f}}}_0,q=2.\hfill \end{array}\right.\hfill \end{array}$$

(54)

then (53) simplifies to

$$\begin{array}{ccc}\hfill \underline{{\mathbf{f}}_0}({\ell }_1,\vartheta ;\zeta )& & =(\zeta -1)exp\left(\frac{{\ell }_1}{2}\right),\hfill \\ \hfill \underline{{\mathbf{f}}_1}({\ell }_1,\vartheta ;\zeta )& & ={\mathbb{E}}^{-1}\left[{\omega }^{\alpha }\mathbb{E}\left[{\left(\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_0-{\left(\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_0+{\underline{\mathcal{A}}}_0-{\underline{\mathcal{B}}}_0+3{\underline{\mathcal{C}}}_0\right]\right]\hfill \\ & & =-\frac{\zeta -1}{2}exp\left(\frac{{\ell }_1}{2}\right)\frac{{\vartheta }^{\alpha }}{\Gamma (\alpha +1)},\hfill \\ \hfill \underline{{\mathbf{f}}_2}({\ell }_1,\vartheta ;\zeta )& & ={\mathbb{E}}^{-1}\left[{\omega }^{\alpha }\mathbb{E}\left[{\left(\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_1-{\left(\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_1+{\underline{\mathcal{A}}}_1-{\underline{\mathcal{B}}}_1+3{\underline{\mathcal{C}}}_1\right]\right]\hfill \\ & & =\frac{-(\zeta -1)}{8}exp\left(\frac{{\ell }_1}{2}\right)\frac{{\vartheta }^{2\alpha -1}}{\Gamma \left(2\alpha \right)}+\frac{(\zeta -1)}{4}exp\left(\frac{{\ell }_1}{2}\right)\frac{{\vartheta }^{2\alpha }}{\Gamma (2\alpha +1)},\hfill \\ \hfill \underline{{\mathbf{f}}_3}({\ell }_1,\vartheta ;\zeta )& & ={\mathbb{E}}^{-1}\left[{\omega }^{\alpha }\mathbb{E}\left[{\left(\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_2-{\left(\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_2+{\underline{\mathcal{A}}}_2-{\underline{\mathcal{B}}}_2+3{\underline{\mathcal{C}}}_2\right]\right]\hfill \\ & & =\frac{-(\zeta -1)}{32}exp\left(\frac{{\ell }_1}{2}\right)\frac{{\vartheta }^{3\alpha -2}}{\Gamma (3\alpha -1)}+\frac{(\zeta -1)}{8}exp\left(\frac{{\ell }_1}{2}\right)\frac{{\vartheta }^{3\alpha -1}}{\Gamma \left(3\alpha \right)}-\frac{(\zeta -1)}{8}exp\left(\frac{{\ell }_1}{2}\right)\frac{{\vartheta }^{3\alpha }}{\Gamma (3\alpha +1)},\hfill \\ & & ⋮.\hfill \end{array}$$

By implementing a similar technique, the remaining terms of ${\underline{\mathbf{f}}}_q(q\ge 4)$ of the EADM solution can be simply determined. Furthermore, when the iterative process expands, the accuracy of the obtained solution improves dramatically, and the deduced solution moves closer to the precise result. Finally, we have come up with the following answers in a series form

$$\begin{array}{c}\hfill \underline{\mathbf{f}}({\ell }_1,\vartheta ,\zeta )={\underline{\mathbf{f}}}_0({\ell }_1,\vartheta ,\zeta )+{\underline{\mathbf{f}}}_1({\ell }_1,\vartheta ,\zeta )+{\underline{\mathbf{f}}}_1({\ell }_1,\vartheta ,\zeta )+...,\end{array}$$

such that

$$\begin{array}{ccc}\hfill \underline{\mathbf{f}}({\ell }_1,\vartheta ,\zeta )& & ={\underline{\mathbf{f}}}_0({\ell }_1,\vartheta ,\zeta )+{\underline{\mathbf{f}}}_1({\ell }_1,\vartheta ,\zeta )+{\underline{\mathbf{f}}}_1({\ell }_1,\vartheta ,\zeta )+...,\hfill \\ \hfill \overline{\mathbf{f}}({\ell }_1,\vartheta ,\zeta )& & ={\overline{\mathbf{f}}}_0({\ell }_1,\vartheta ,\zeta )+{\overline{\mathbf{f}}}_1({\ell }_1,\vartheta ,\zeta )+{\overline{\mathbf{f}}}_1({\ell }_1,\vartheta ,\zeta )+....\hfill \end{array}$$

Consequently, we have

$$\begin{array}{ccc}\hfill \underline{\mathbf{f}}({\ell }_1,\vartheta ,\zeta )& & =(\zeta -1)exp\left(\frac{{\ell }_1}{2}\right)-\frac{\zeta -1}{2}exp\left(\frac{{\ell }_1}{2}\right)\frac{{\vartheta }^{\alpha }}{\Gamma (\alpha +1)}\hfill \\ & & -\frac{(\zeta -1)}{8}exp\left(\frac{{\ell }_1}{2}\right)\frac{{\vartheta }^{2\alpha -1}}{\Gamma \left(2\alpha \right)}+\frac{(\zeta -1)}{4}exp\left(\frac{{\ell }_1}{2}\right)\frac{{\vartheta }^{2\alpha }}{\Gamma (2\alpha +1)}\hfill \\ & & -\frac{(\zeta -1)}{32}exp\left(\frac{{\ell }_1}{2}\right)\frac{{\vartheta }^{3\alpha -2}}{\Gamma (3\alpha -1)}+\frac{(\zeta -1)}{8}exp\left(\frac{{\ell }_1}{2}\right)\frac{{\vartheta }^{3\alpha -1}}{\Gamma \left(3\alpha \right)}-\frac{(\zeta -1)}{8}exp\left(\frac{{\ell }_1}{2}\right)\frac{{\vartheta }^{3\alpha }}{\Gamma (3\alpha +1)}...,\hfill \\ \hfill \overline{\mathbf{f}}({\ell }_1,\vartheta ,\zeta )& & =(1-\zeta )exp\left(\frac{{\ell }_1}{2}\right)-\frac{1-\zeta }{2}exp\left(\frac{{\ell }_1}{2}\right)\frac{{\vartheta }^{\alpha }}{\Gamma (\alpha +1)}\hfill \\ & & -\frac{(1-\zeta )}{8}exp\left(\frac{{\ell }_1}{2}\right)\frac{{\vartheta }^{2\alpha -1}}{\Gamma \left(2\alpha \right)}+\frac{(1-\zeta )}{4}exp\left(\frac{{\ell }_1}{2}\right)\frac{{\vartheta }^{2\alpha }}{\Gamma (2\alpha +1)}\hfill \\ & & -\frac{(1-\zeta )}{32}exp\left(\frac{{\ell }_1}{2}\right)\frac{{\vartheta }^{3\alpha -2}}{\Gamma (3\alpha -1)}+\frac{(1-\zeta )}{8}exp\left(\frac{{\ell }_1}{2}\right)\frac{{\vartheta }^{3\alpha -1}}{\Gamma \left(3\alpha \right)}-\frac{(1-\zeta )}{8}exp\left(\frac{{\ell }_1}{2}\right)\frac{{\vartheta }^{3\alpha }}{\Gamma (3\alpha +1)}....\hfill \end{array}$$

(55)

Case II. (For the fuzzy Atangana–Baleanu Caputo fractional derivative)

Here, we obtain the EADM solution for the first case of (51) by the using fuzzy ABC fractional derivative operator.

Taking into consideration the procedure described in Section 3, we have

$$\begin{array}{ccc}& & \mathbb{E}\left[\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right]={\omega }^2{\underline{\mathbf{f}}}_{\left(\kappa \right)}({\ell }_1;\zeta )+\left(\frac{\alpha {\omega }^{\alpha }+1-\alpha }{\mathcal{N}\left(\alpha \right)}\right)\mathbb{E}[\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )-\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\hfill \\ & & +\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{{\partial }^3}{\partial {\ell }_1^3}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )-\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )+\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{{\partial }^2}{\partial {\ell }_1^2}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )].\hfill \end{array}$$

Simple computations result in

$$\begin{array}{ccc}\hfill \underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )& & =(\zeta -1)exp\left(\frac{{\ell }_1}{2}\right)+{\mathbb{E}}^{-1}\left[\left(\frac{\alpha {\omega }^{\alpha }+1-\alpha }{\mathcal{N}\left(\alpha \right)}\right)\mathbb{E}\right[\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )-\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\hfill \\ & & +\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{{\partial }^3}{\partial {\ell }_1^3}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )-\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )+\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{{\partial }^2}{\partial {\ell }_1^2}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\left]\right].\hfill \end{array}$$

(56)

Let us surmise the infinite sum $\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )=\sum _{q=0}^{\infty }{\underline{\mathbf{f}}}_q({\ell }_1,\vartheta ;\zeta ),(q=0,1,2,...)$ accompanying it with (45) and affirming the non-linearity. Therefore, (52) takes the form

$$\begin{array}{ccc}\hfill \sum _{q=0}^{\infty }{\underline{\mathbf{f}}}_q({\ell }_1,\vartheta ;\zeta )& & =(\zeta -1)exp\left(\frac{{\ell }_1}{2}\right)\hfill \\ & & +{\mathbb{E}}^{-1}\left[\left(\frac{\alpha {\omega }^{\alpha }+1-\alpha }{\mathcal{N}\left(\alpha \right)}\right)\mathbb{E}\right[\sum _{q=0}^{\infty }{\left(\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_q-\sum _{q=0}^{\infty }{\left(\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_q\hfill \\ & & +\sum _{q=0}^{\infty }{\underline{\mathcal{A}}}_q-\sum _{q=0}^{\infty }{\underline{\mathcal{B}}}_q+3\sum _{q=0}^{\infty }{\underline{\mathcal{C}}}_q\left]\right].\hfill \end{array}$$

(57)

Utilizing the Adomian polynomials described in (54), then (57) simplifies to

$$\begin{array}{ccc}\hfill \underline{{\mathbf{f}}_0}({\ell }_1,\vartheta ;\zeta )& & =(\zeta -1)exp\left(\frac{{\ell }_1}{2}\right),\hfill \\ \hfill \underline{{\mathbf{f}}_1}({\ell }_1,\vartheta ;\zeta )& & ={\mathbb{E}}^{-1}\left[\left(\frac{\alpha {\omega }^{\alpha }+1-\alpha }{\mathcal{N}\left(\alpha \right)}\right)\mathbb{E}\left[{\left(\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_0-{\left(\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_0+{\underline{\mathcal{A}}}_0-{\underline{\mathcal{B}}}_0+3{\underline{\mathcal{C}}}_0\right]\right]\hfill \\ & & =-\frac{\zeta -1}{2\mathcal{N}\left(\alpha \right)}exp\left(\frac{{\ell }_1}{2}\right)\left[\frac{\alpha {\vartheta }^{\alpha }}{\Gamma (\alpha +1)}+(1-\alpha )\right],\hfill \\ \hfill \underline{{\mathbf{f}}_2}({\ell }_1,\vartheta ;\zeta )& & ={\mathbb{E}}^{-1}\left[\left(\frac{\alpha {\omega }^{\alpha }+1-\alpha }{\mathcal{N}\left(\alpha \right)}\right)\mathbb{E}\left[{\left(\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_1-{\left(\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_1+{\underline{\mathcal{A}}}_1-{\underline{\mathcal{B}}}_1+3{\underline{\mathcal{C}}}_1\right]\right]\hfill \\ & & =\frac{-(\zeta -1)}{8{\mathcal{N}}^2\left(\alpha \right)}exp\left(\frac{{\ell }_1}{2}\right)\left[\frac{{\alpha }^2{\vartheta }^{2\alpha -1}}{\Gamma \left(2\alpha \right)}+\alpha (\alpha -1)\frac{{\vartheta }^{\alpha -1}}{\Gamma \left(\alpha \right)}+\alpha \frac{{\vartheta }^{\alpha }}{\Gamma (\alpha +1)}+(1-\alpha )\right]\hfill \\ & & +\frac{(\zeta -1)}{4{\mathcal{N}}^2\left(\alpha \right)}exp\left(\frac{{\ell }_1}{2}\right)\left[\frac{{\alpha }^2{\vartheta }^{2\alpha }}{\Gamma (2\alpha +1)}+2\alpha (1-\alpha )\frac{{\vartheta }^{\alpha }}{\Gamma (\alpha +1)}+{(1-\alpha )}^2\right],\hfill \\ \hfill \underline{{\mathbf{f}}_3}({\ell }_1,\vartheta ;\zeta )& & ={\mathbb{E}}^{-1}\left[\left(\frac{\alpha {\omega }^{\alpha }+1-\alpha }{\mathcal{N}\left(\alpha \right)}\right)\mathbb{E}\left[{\left(\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_2-{\left(\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_2+{\underline{\mathcal{A}}}_2-{\underline{\mathcal{B}}}_2+3{\underline{\mathcal{C}}}_2\right]\right]\hfill \\ & & =\frac{-(\zeta -1)}{32{\mathcal{N}}^3\left(\alpha \right)}exp\left(\frac{{\ell }_1}{2}\right)\left\{\begin{array}{c}\frac{4{\alpha }^3{\vartheta }^{3\alpha }}{\Gamma (3\alpha +1)}-\frac{2{\alpha }^3{\vartheta }^{3\alpha -1}}{\Gamma \left(3\alpha \right)}-\frac{{\alpha }^3{\vartheta }^{3\alpha -2}}{\Gamma (3\alpha -1)}+2{\alpha }^2(5-2\alpha )\frac{{\vartheta }^{2\alpha }}{\Gamma (2\alpha +1)}\hfill \\ -2{\alpha }^2(1-\alpha )\frac{{\vartheta }^{2\alpha -1}}{\Gamma \left(2\alpha \right)}-{\alpha }^2(1-\alpha )\frac{{\vartheta }^{2\alpha -2}}{\Gamma (2\alpha -1)}+\alpha (1-\alpha )(7-6\alpha )\frac{{\vartheta }^{\alpha -1}}{\Gamma \left(\alpha \right)}\hfill \\ +2(1-\alpha )(1-2\alpha ),\hfill \end{array}\right.\hfill \\ & & ⋮\hfill \end{array}$$

By implementing a similar technique, the remaining terms of ${\underline{\mathbf{f}}}_q(q\ge 3)$ of the EADM solution can be simply determined. Furthermore, when the iterative process expands, the accuracy of the obtained solution improves dramatically, and the deduced solution moves closer to the precise result. Finally, we have come up with the following answers in a series form

$$\begin{array}{c}\hfill \underline{\mathbf{f}}({\ell }_1,\vartheta ,\zeta )={\underline{\mathbf{f}}}_0({\ell }_1,\vartheta ,\zeta )+{\underline{\mathbf{f}}}_1({\ell }_1,\vartheta ,\zeta )+{\underline{\mathbf{f}}}_1({\ell }_1,\vartheta ,\zeta )+...,\end{array}$$

such that

$$\begin{array}{ccc}\hfill \underline{\mathbf{f}}({\ell }_1,\vartheta ,\zeta )& & ={\underline{\mathbf{f}}}_0({\ell }_1,\vartheta ,\zeta )+{\underline{\mathbf{f}}}_1({\ell }_1,\vartheta ,\zeta )+{\underline{\mathbf{f}}}_1({\ell }_1,\vartheta ,\zeta )+...,\hfill \\ \hfill \overline{\mathbf{f}}({\ell }_1,\vartheta ,\zeta )& & ={\overline{\mathbf{f}}}_0({\ell }_1,\vartheta ,\zeta )+{\overline{\mathbf{f}}}_1({\ell }_1,\vartheta ,\zeta )+{\overline{\mathbf{f}}}_1({\ell }_1,\vartheta ,\zeta )+....\hfill \end{array}$$

Consequently, we have

$$\begin{array}{ccc}\hfill \underline{\mathbf{f}}({\ell }_1,\vartheta ,\zeta )& & =(\zeta -1)exp\left(\frac{{\ell }_1}{2}\right)-\frac{\zeta -1}{2\mathcal{N}\left(\alpha \right)}exp\left(\frac{{\ell }_1}{2}\right)\left[\frac{\alpha {\vartheta }^{\alpha }}{\Gamma (\alpha +1)}+(1-\alpha )\right]\hfill \\ & & -\frac{(\zeta -1)}{8{\mathcal{N}}^2\left(\alpha \right)}exp\left(\frac{{\ell }_1}{2}\right)\left[\frac{{\alpha }^2{\vartheta }^{2\alpha -1}}{\Gamma \left(2\alpha \right)}+\alpha (\alpha -1)\frac{{\vartheta }^{\alpha -1}}{\Gamma \left(\alpha \right)}+\alpha \frac{{\vartheta }^{\alpha }}{\Gamma (\alpha +1)}+(1-\alpha )\right]\hfill \\ & & +\frac{(\zeta -1)}{4{\mathcal{N}}^2\left(\alpha \right)}exp\left(\frac{{\ell }_1}{2}\right)\left[\frac{{\alpha }^2{\vartheta }^{2\alpha }}{\Gamma (2\alpha +1)}+2\alpha (1-\alpha )\frac{{\vartheta }^{\alpha }}{\Gamma (\alpha +1)}+{(1-\alpha )}^2\right]\hfill \\ & & -\frac{(\zeta -1)}{32{\mathcal{N}}^3\left(\alpha \right)}exp\left(\frac{{\ell }_1}{2}\right)\times \left\{\begin{array}{c}\frac{4{\alpha }^3{\vartheta }^{3\alpha }}{\Gamma (3\alpha +1)}-\frac{2{\alpha }^3{\vartheta }^{3\alpha -1}}{\Gamma \left(3\alpha \right)}-\frac{{\alpha }^3{\vartheta }^{3\alpha -2}}{\Gamma (3\alpha -1)}+2{\alpha }^2(5-2\alpha )\frac{{\vartheta }^{2\alpha }}{\Gamma (2\alpha +1)}\hfill \\ -2{\alpha }^2(1-\alpha )\frac{{\vartheta }^{2\alpha -1}}{\Gamma \left(2\alpha \right)}-{\alpha }^2(1-\alpha )\frac{{\vartheta }^{2\alpha -2}}{\Gamma (2\alpha -1)}+\alpha (1-\alpha )(7-6\alpha )\frac{{\vartheta }^{\alpha -1}}{\Gamma \left(\alpha \right)}\hfill \\ +2(1-\alpha )(1-2\alpha )\hfill \end{array}\right.+...,\hfill \\ \hfill \overline{\mathbf{f}}({\ell }_1,\vartheta ,\zeta )& & =(1-\zeta )exp\left(\frac{{\ell }_1}{2}\right)-\frac{1-\zeta }{2\mathcal{N}\left(\alpha \right)}exp\left(\frac{{\ell }_1}{2}\right)\left[\frac{\alpha {\vartheta }^{\alpha }}{\Gamma (\alpha +1)}+(1-\alpha )\right]\hfill \\ & & -\frac{(1-\zeta )}{8{\mathcal{N}}^2\left(\alpha \right)}exp\left(\frac{{\ell }_1}{2}\right)\left[\frac{{\alpha }^2{\vartheta }^{2\alpha -1}}{\Gamma \left(2\alpha \right)}+\alpha (\alpha -1)\frac{{\vartheta }^{\alpha -1}}{\Gamma \left(\alpha \right)}+\alpha \frac{{\vartheta }^{\alpha }}{\Gamma (\alpha +1)}+(1-\alpha )\right]\hfill \\ & & +\frac{(1-\zeta )}{4{\mathcal{N}}^2\left(\alpha \right)}exp\left(\frac{{\ell }_1}{2}\right)\left[\frac{{\alpha }^2{\vartheta }^{2\alpha }}{\Gamma (2\alpha +1)}+2\alpha (1-\alpha )\frac{{\vartheta }^{\alpha }}{\Gamma (\alpha +1)}+{(1-\alpha )}^2\right]\hfill \\ & & -\frac{(1-\zeta )}{32{\mathcal{N}}^3\left(\alpha \right)}exp\left(\frac{{\ell }_1}{2}\right)\times \left\{\begin{array}{c}\frac{4{\alpha }^3{\vartheta }^{3\alpha }}{\Gamma (3\alpha +1)}-\frac{2{\alpha }^3{\vartheta }^{3\alpha -1}}{\Gamma \left(3\alpha \right)}-\frac{{\alpha }^3{\vartheta }^{3\alpha -2}}{\Gamma (3\alpha -1)}+2{\alpha }^2(5-2\alpha )\frac{{\vartheta }^{2\alpha }}{\Gamma (2\alpha +1)}\hfill \\ -2{\alpha }^2(1-\alpha )\frac{{\vartheta }^{2\alpha -1}}{\Gamma \left(2\alpha \right)}-{\alpha }^2(1-\alpha )\frac{{\vartheta }^{2\alpha -2}}{\Gamma (2\alpha -1)}+\alpha (1-\alpha )(7-6\alpha )\frac{{\vartheta }^{\alpha -1}}{\Gamma \left(\alpha \right)}\hfill \\ +2(1-\alpha )(1-2\alpha )\hfill \end{array}\right.+....\hfill \end{array}$$

(58)

In this analysis, Figure 1 demonstrates the insight into the influence of multiple layer surface plots for Problem 1 correlated with the CFD and Elzaki transform in the fuzzy sense. It is worth mentioning that the profile identifies the variation in the mapping $\mathbf{f}({\ell }_1,\vartheta ;\zeta )$ on space co-ordinate ${\ell }_1$ with respect to $\vartheta$ and uncertainty parameter $\zeta \in [0,1]$.

The graph illustrates that as, time progresses, the mapping $\mathbf{f}({\ell }_1,\vartheta ;\zeta )$ will also increase.

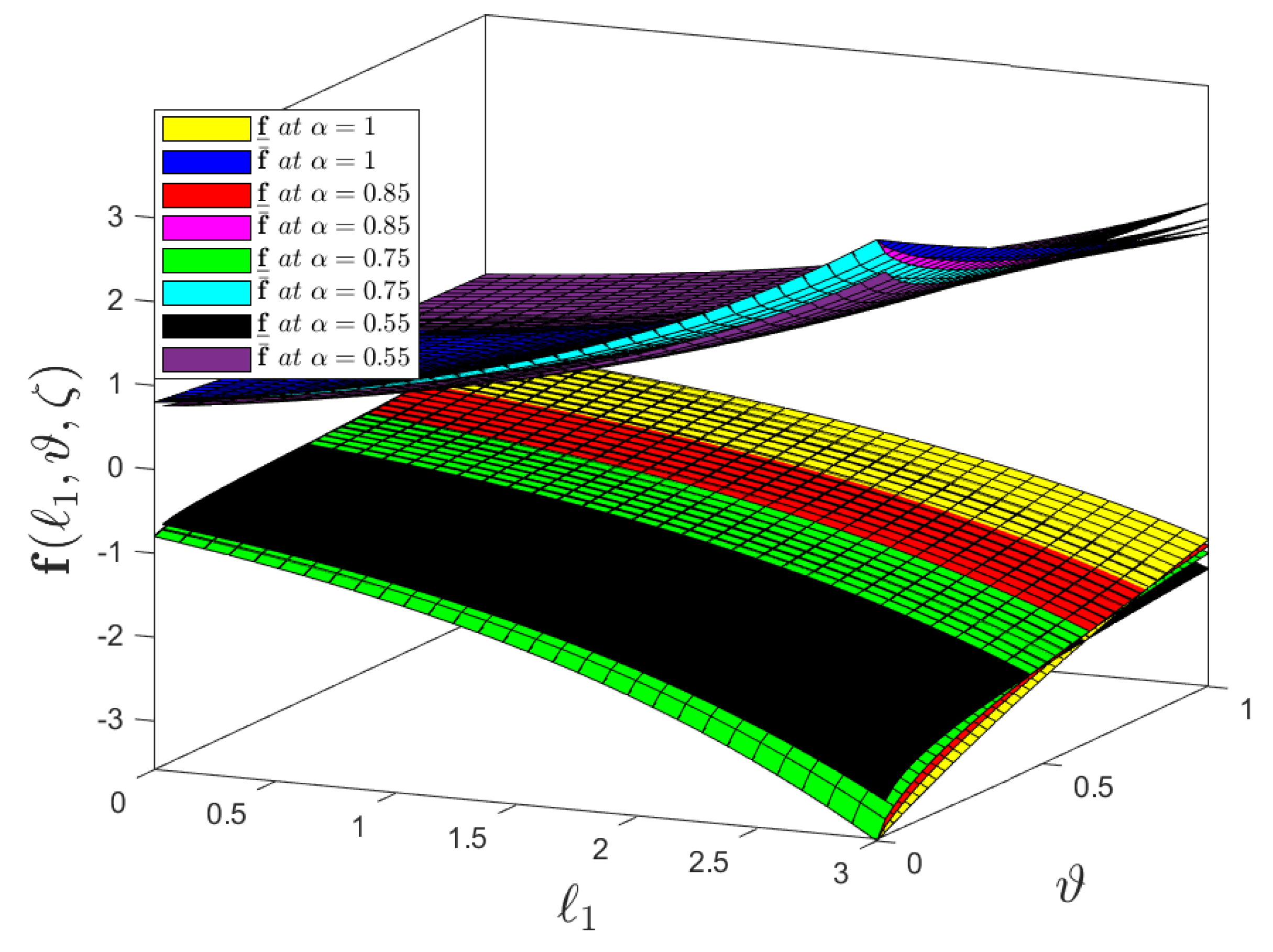
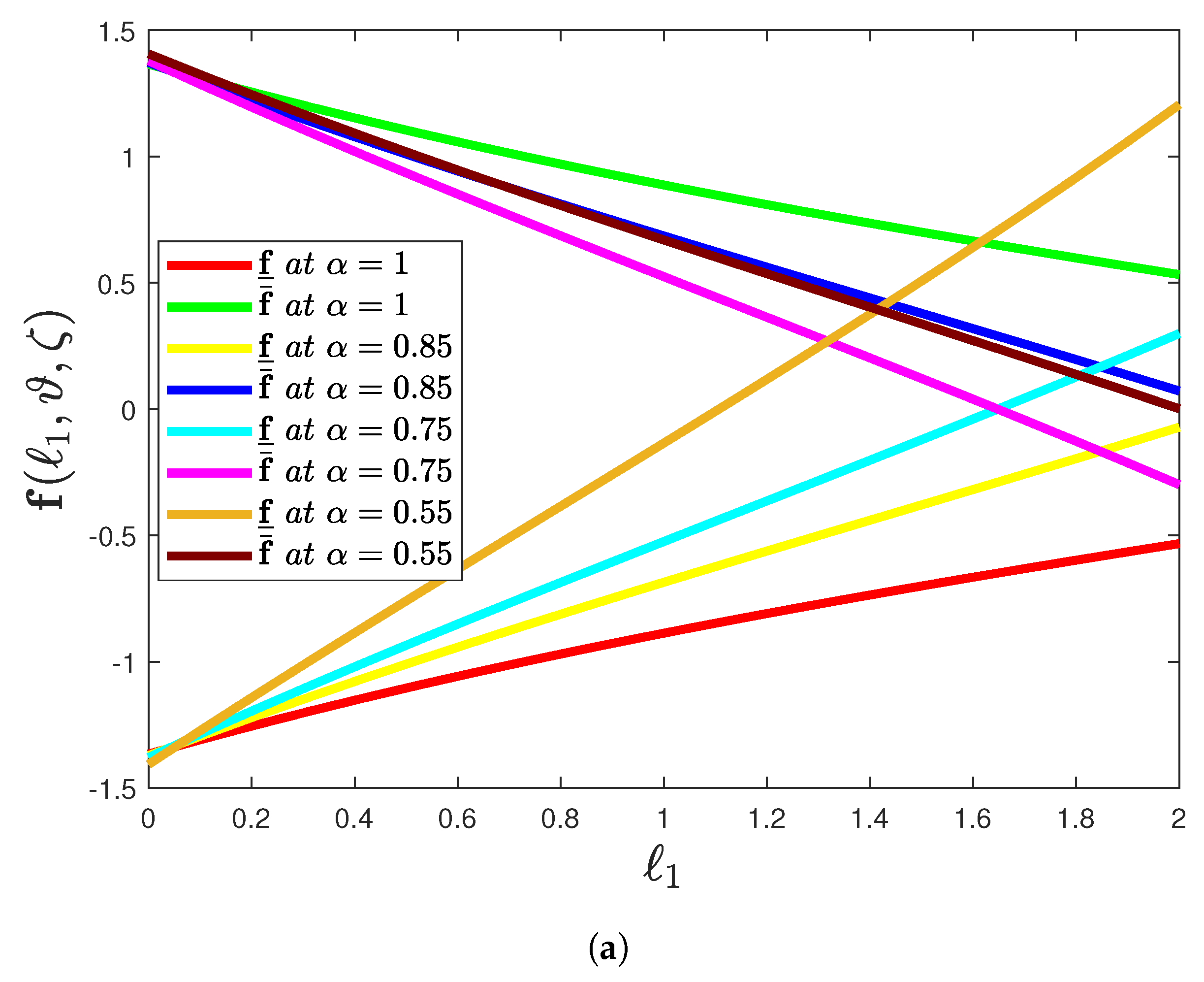
• The effect of the proposed methodology on the mapping $\mathbf{f}({\ell }_1,\vartheta ;\zeta )$ is displayed in Figure 2a for the varying fractional orders $\alpha =1,0.85,0.75,0.55$ by considering CFD operator. It exhibits a relatively small increase in the mapping $\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )$ with the decrease in $\overline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )$.
• The profile graph of Figure 2b demonstrates the lower and upper solution of varying uncertainty when the fractional order is assumed to be $\alpha =0.2$ by proposing CFD operator. It emphasizes a relatively small variation in the mapping $\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )$ with the increase in $\overline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )$.
• The effect of the proposed methodology on the mapping $\mathbf{f}({\ell }_1,\vartheta ;\zeta )$ is displayed in Figure 3a for the varying fractional orders $\alpha =1,0.85,0.75,0.55$ by considering the ABC fractional derivative operator. It exhibits a relatively small increase in the mapping $\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )$ with the decrease in $\overline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )$.
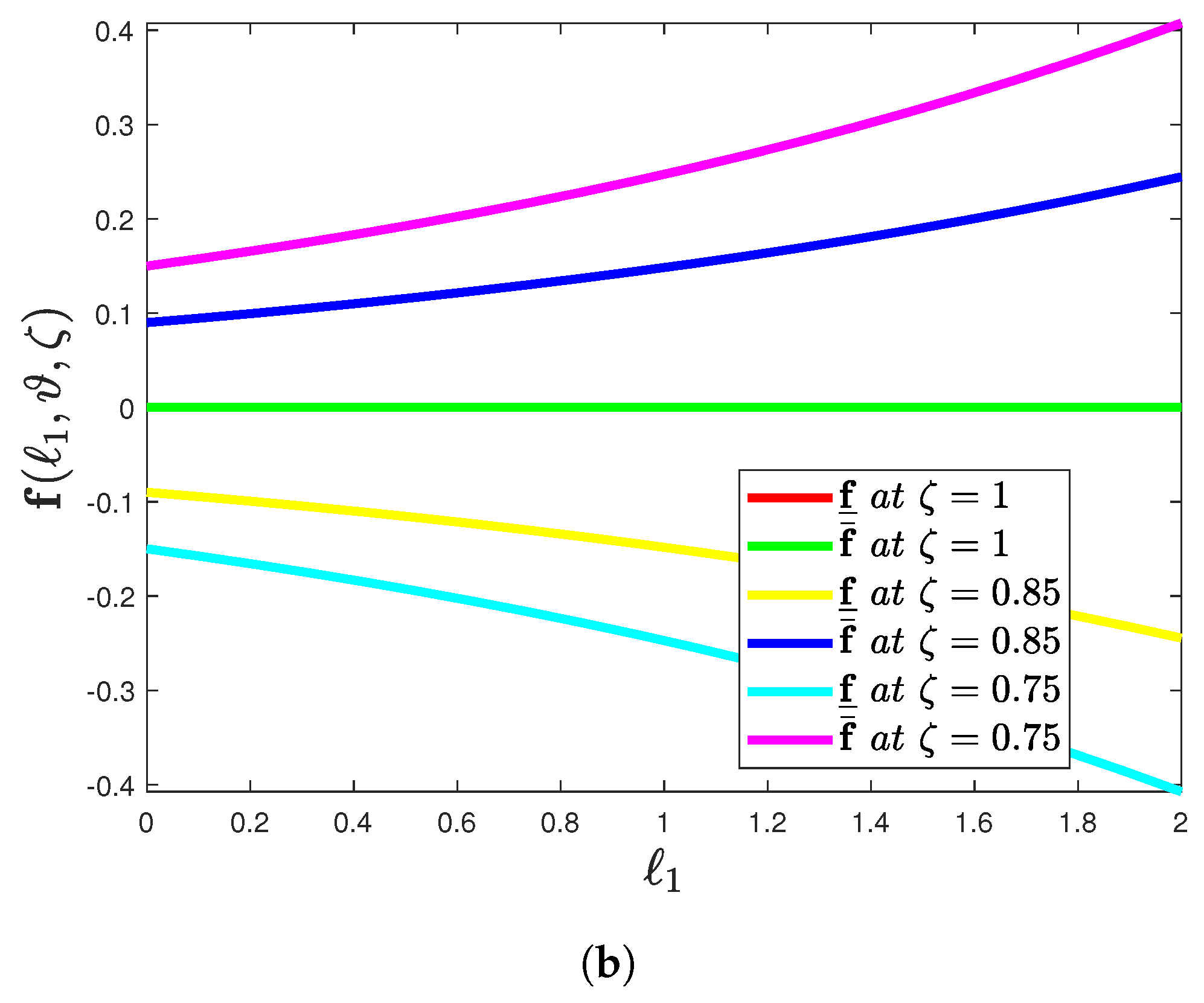
• The Profile graph of Figure 3b demonstrates the lower and upper solutions of varying uncertainty when the fractional order is assumed to be $\alpha =0.2$ by proposing the ABC fractional derivative operator. It emphasizes a relatively small variation in the mapping $\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )$ with the increase in $\overline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )$.
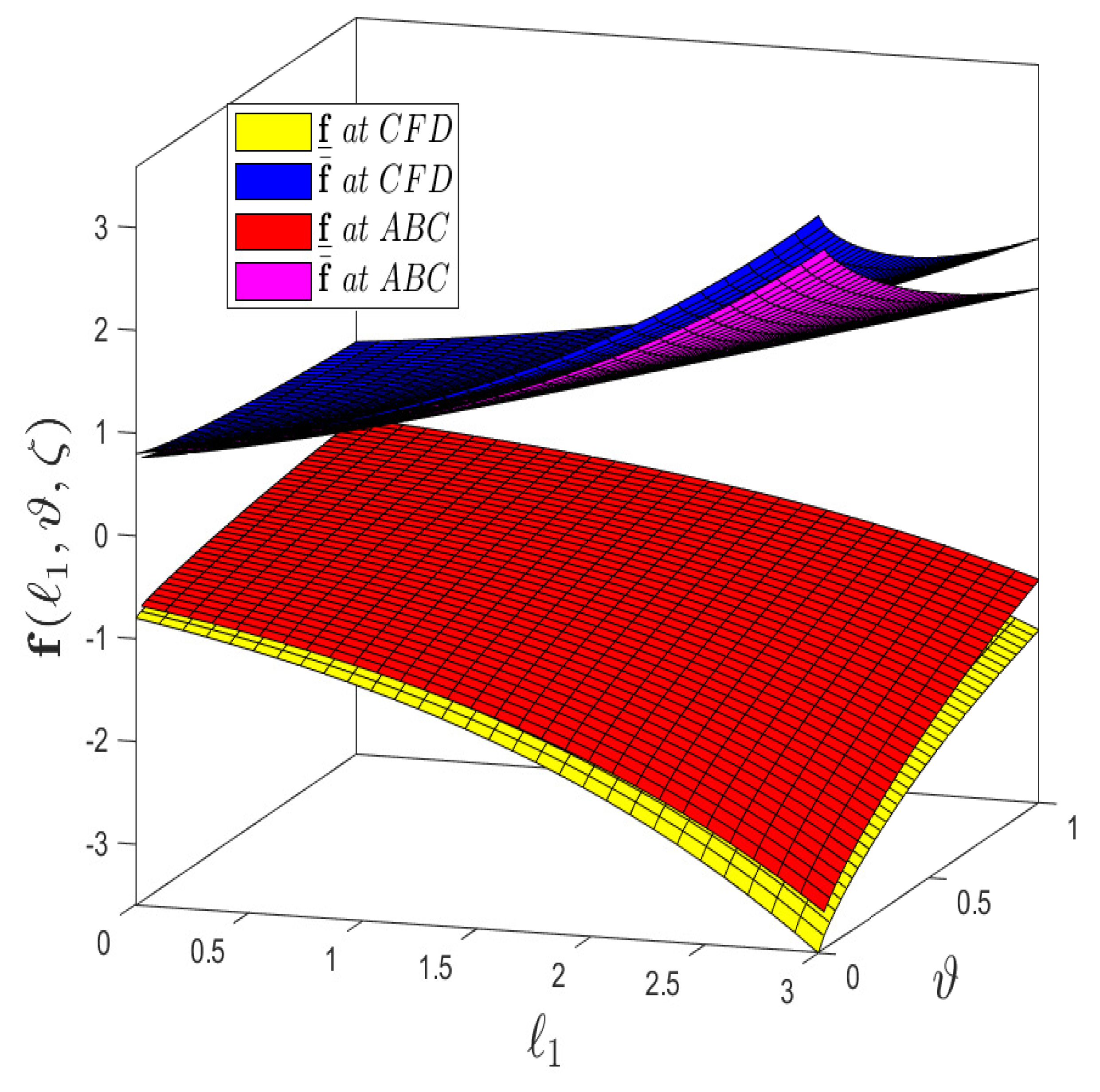
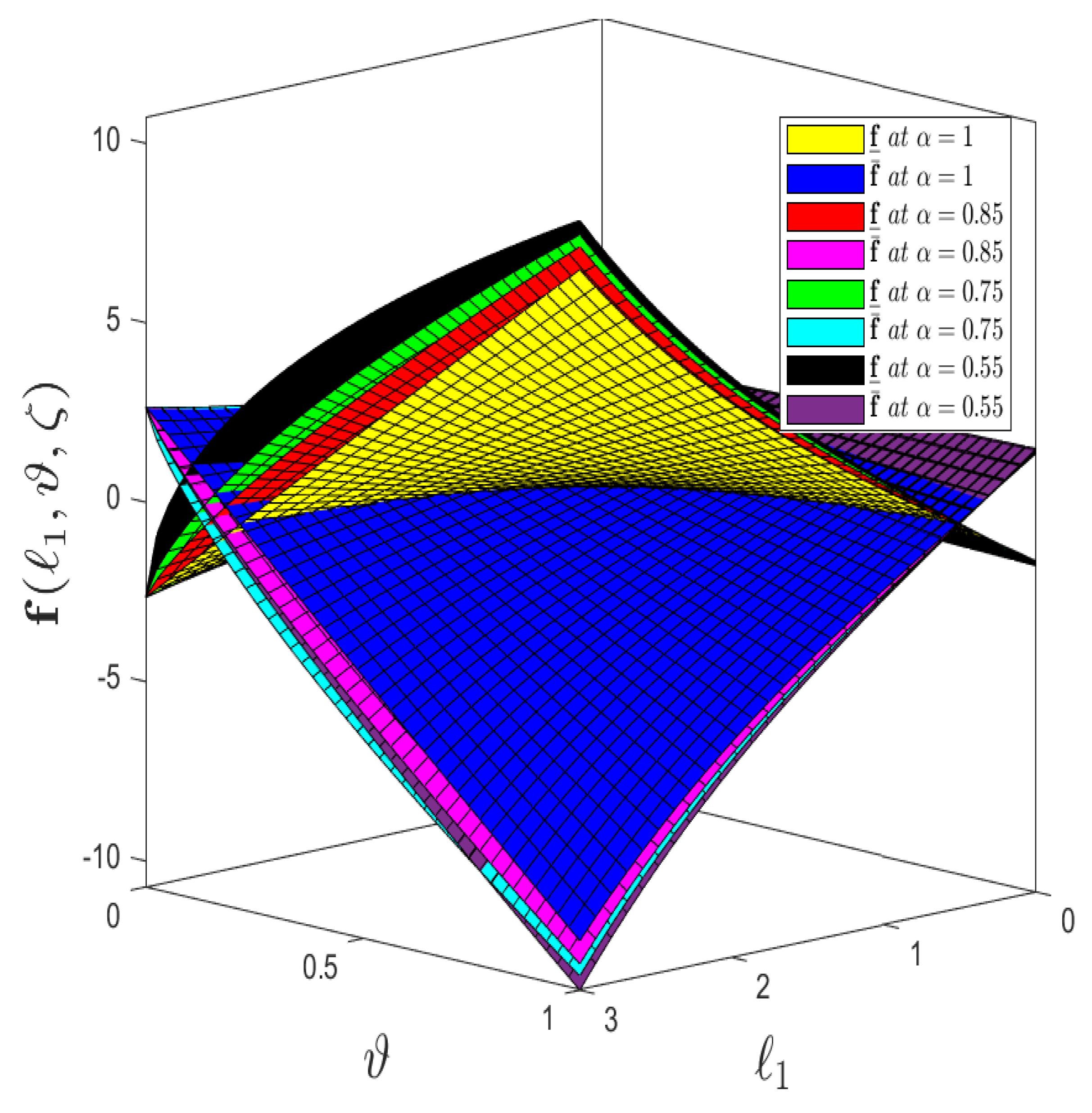
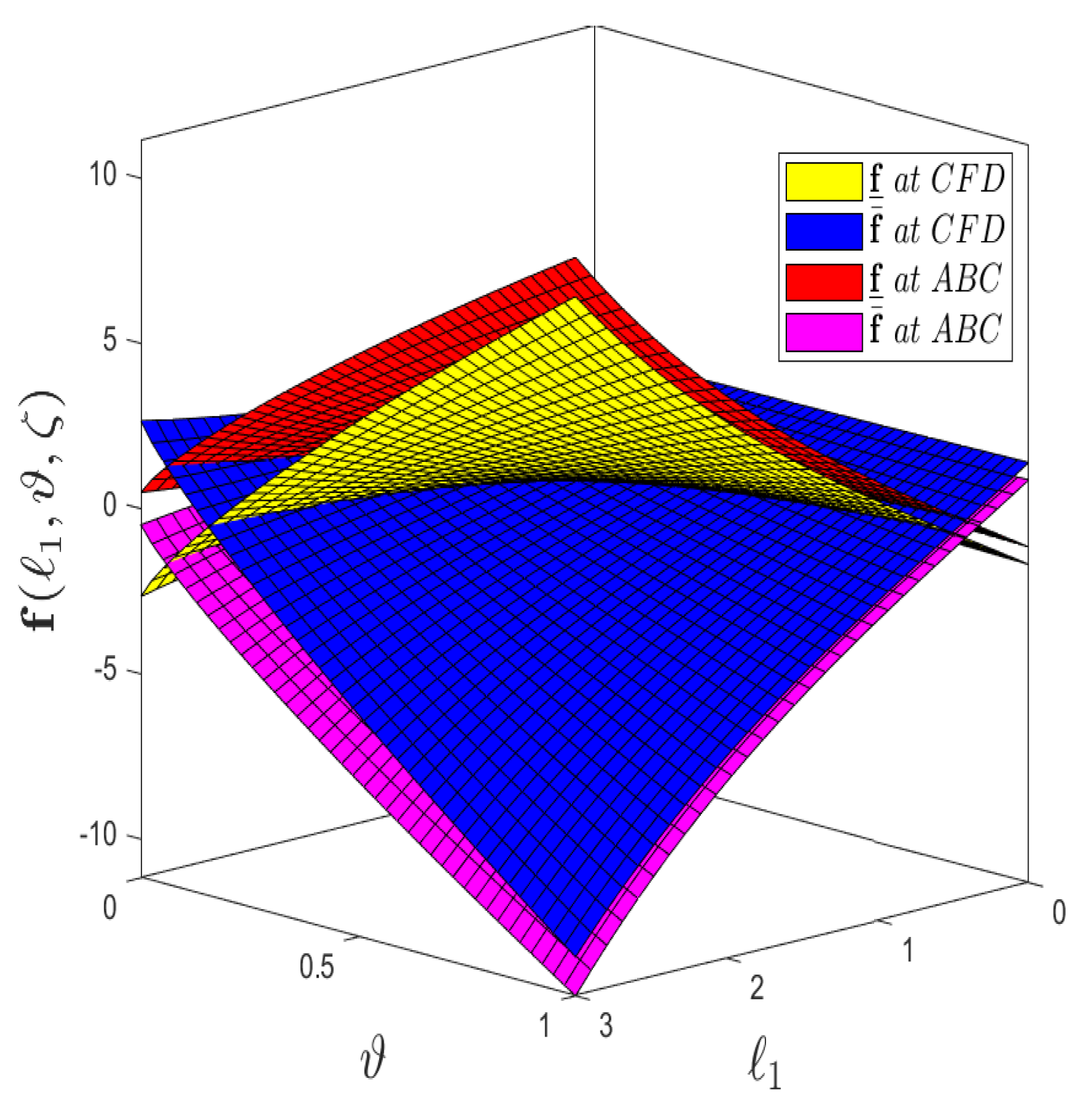
• Figure 4 demonstrates the comparison analysis between the CFD operator and the ABC fractional derivative operator for varying fractional order with uncertainty $\kappa \in [0,1],$ exhibits that lower the solution profile for the ABC fractional operator has strong ties with the upper solution as compared to the CFD operator.
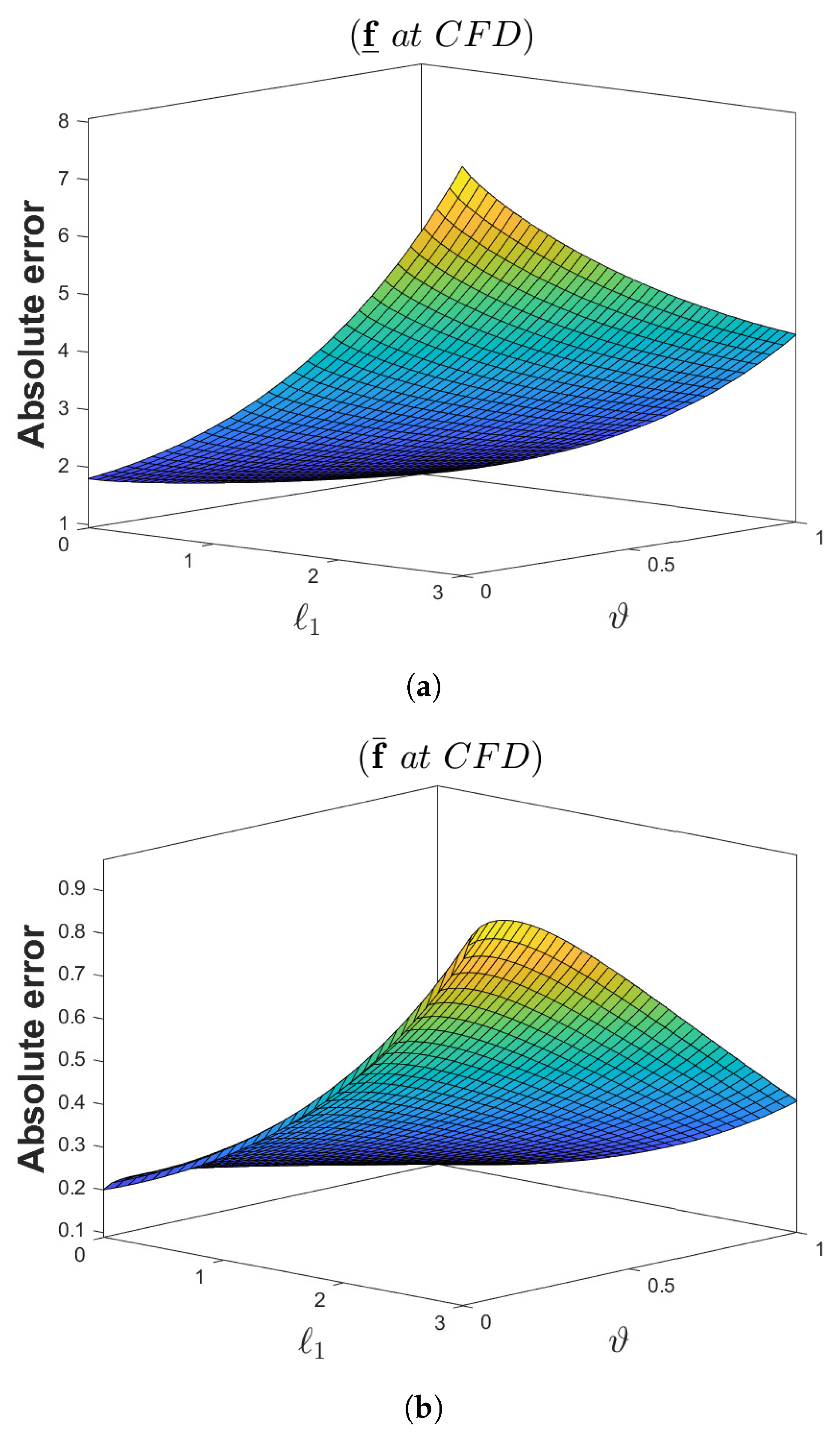
• Figure 5 shows the comparison analysis between ($\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )$ and the exact solution), ($\overline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )$ and exact solution), respectively, for three dimensional error plots by considering the CFD operator.

Furthermore, the offered approach does not provide a unique solution but will aid scientists in selecting the best approximate solution. It is remarkable that the fuzzy ABC fractional derivative operator has better performance than the CFD operators, because the curves have a strong harmony with the integer-order graph in the ABC operator case.

□

Remark 2.

When $\underline{\chi }\left(\zeta \right)=\overline{\chi }\left(\zeta \right)=1$ along with $\alpha =1,$ then both solutions of Problem 1 converge to the integer-order solution $\mathbf{f}({\ell }_1,\vartheta )=exp\left(\frac{{\ell }_1}{2}-\frac{2\vartheta }{3}\right).$

Problem 2.

Assume the one-dimension fuzzy fractional FW model with fuzzy ICs is represented as follows:

$$\begin{array}{ccc}\hfill \frac{{\partial }^{\alpha }}{\partial {\vartheta }^{\alpha }}\tilde{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )& & =\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\tilde{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\ominus \frac{\partial }{\partial {\ell }_1}\tilde{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\oplus \tilde{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\odot \frac{{\partial }^3}{\partial {\ell }_1^3}\tilde{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\hfill \\ & & \ominus \tilde{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\odot \frac{\partial }{\partial {\ell }_1}\tilde{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\oplus \frac{\partial }{\partial {\ell }_1}\tilde{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\odot \frac{{\partial }^2}{\partial {\ell }_1^2}\tilde{\mathbf{f}}({\ell }_1,\vartheta ;\zeta ),\hfill \\ & & \tilde{\mathbf{f}}({\ell }_1,0)=\tilde{\chi }\left(\zeta \right)\odot {cosh}^2\left(\frac{{\ell }_1}{4}\right),\hfill \end{array}$$

(59)

where $\tilde{\chi }\left(\zeta \right)=[\underline{\chi }\left(\zeta \right),\overline{\chi }\left(\zeta \right)]=[\zeta -1,1-\zeta ]$ for $\zeta \in [0,1]$ is a fuzzy number.

Proof. 

The parameterized version of the problem (50) is expressed as follows

$$\left\{\begin{array}{c}\begin{array}{c}\frac{{\partial }^{\alpha }}{\partial {\vartheta }^{\alpha }}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )=\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )-\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )+\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{{\partial }^3}{\partial {\ell }_1^3}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\hfill \\ -\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )+\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{{\partial }^2}{\partial {\ell }_1^2}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta ),\hfill \\ \underline{\mathbf{f}}({\ell }_1,0)=\underline{\chi }\left(\zeta \right){cosh}^2\left(\frac{{\ell }_1}{4}\right),\hfill \\ \frac{{\partial }^{\alpha }}{\partial {\vartheta }^{\alpha }}\overline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )=\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\overline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )-\frac{\partial }{\partial {\ell }_1}\overline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )+\overline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{{\partial }^3}{\partial {\ell }_1^3}\overline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\hfill \\ -\overline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{\partial }{\partial {\ell }_1}\overline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )+\frac{\partial }{\partial {\ell }_1}\overline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{{\partial }^2}{\partial {\ell }_1^2}\overline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta ),\hfill \\ \overline{\mathbf{f}}({\ell }_1,0)=\overline{\chi }\left(\zeta \right){cosh}^2\left(\frac{{\ell }_1}{4}\right).\hfill \end{array}\hfill \end{array}\right.$$

(60)

Case I. (For the fuzzy Caputo fractional derivative)

Here, we obtain the EADM solution for the first case of (51) by using the fuzzy CFD operator.

Taking into consideration the procedure described in Section 3, we have

$$\begin{array}{ccc}& & \frac{1}{{\omega }^{\alpha }}\mathbb{E}\left[\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right]-\sum _{\kappa =0}^{q-1}{\underline{\mathbf{f}}}_{\left(\kappa \right)}({\ell }_1;\zeta ){\omega }^{2-\alpha +\kappa }\hfill \\ & & =\mathbb{E}[\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )-\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )+\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{{\partial }^3}{\partial {\ell }_1^3}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\hfill \\ & & -\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )+\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{{\partial }^2}{\partial {\ell }_1^2}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )].\hfill \end{array}$$

Simple computations result in

$$\begin{array}{c}\hfill \underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )=(\zeta -1){cosh}^2\left(\frac{{\ell }_1}{4}\right)+{\mathbb{E}}^{-1}\left[{\omega }^{\alpha }\mathbb{E}\right[\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )-\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )+\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{{\partial }^3}{\partial {\ell }_1^3}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\\ \hfill -\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )+\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{{\partial }^2}{\partial {\ell }_1^2}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\left]\right].\end{array}$$

(61)

Let us surmise the infinite sum $\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )=\sum _{q=0}^{\infty }{\underline{\mathbf{f}}}_q({\ell }_1,\vartheta ;\zeta )$ accompanying it with (45) and affirming the non-linearity. Therefore, (63) takes the form

$$\begin{array}{ccc}\hfill \sum _{q=0}^{\infty }{\underline{\mathbf{f}}}_q({\ell }_1,\vartheta ;\zeta )& & =(\zeta -1){cosh}^2\left(\frac{{\ell }_1}{4}\right)+{\mathbb{E}}^{-1}\left[{\omega }^{\alpha }\mathbb{E}\right[\sum _{q=0}^{\infty }{\left(\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_q-\sum _{q=0}^{\infty }{\left(\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_q\hfill \\ & & +\sum _{q=0}^{\infty }{\underline{\mathcal{A}}}_q-\sum _{q=0}^{\infty }{\underline{\mathcal{B}}}_q+3\sum _{q=0}^{\infty }{\underline{\mathcal{C}}}_q\left]\right].\hfill \end{array}$$

(62)

Utilizing the Adomian polynomials described in (54), then (64) simplifies to

$$\begin{array}{ccc}\hfill \underline{{\mathbf{f}}_0}({\ell }_1,\vartheta ;\zeta )& & =(\zeta -1)\left(\frac{1}{2}+\frac{1}{2}cosh\left(\frac{{\ell }_1}{2}\right)\right),\hfill \\ \hfill \underline{{\mathbf{f}}_1}({\ell }_1,\vartheta ;\zeta )& & ={\mathbb{E}}^{-1}\left[{\omega }^{\alpha }\mathbb{E}\left[{\left(\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_0-{\left(\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_0+{\underline{\mathcal{A}}}_0-{\underline{\mathcal{B}}}_0+3{\underline{\mathcal{C}}}_0\right]\right]\hfill \\ & & =-\frac{11}{32}(\zeta -1)sinh\left(\frac{{\ell }_1}{2}\right)\frac{{\vartheta }^{\alpha }}{\Gamma (\alpha +1)},\hfill \\ \hfill \underline{{\mathbf{f}}_2}({\ell }_1,\vartheta ;\zeta )& & ={\mathbb{E}}^{-1}\left[{\omega }^{\alpha }\mathbb{E}\left[{\left(\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_1-{\left(\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_1+{\underline{\mathcal{A}}}_1-{\underline{\mathcal{B}}}_1+3{\underline{\mathcal{C}}}_1\right]\right]\hfill \\ & & =\frac{-11}{128}(\zeta -1)sinh\left(\frac{{\ell }_1}{2}\right)\frac{{\vartheta }^{\alpha }}{\Gamma (\alpha +1)}+\frac{242(\zeta -1)}{1024}cosh\left(\frac{{\ell }_1}{2}\right)\frac{{\vartheta }^{2\alpha }}{\Gamma (2\alpha +1)},\hfill \\ \hfill \underline{{\mathbf{f}}_3}({\ell }_1,\vartheta ;\zeta )& & ={\mathbb{E}}^{-1}\left[{\omega }^{\alpha }\mathbb{E}\left[{\left(\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_2-{\left(\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_2+{\underline{\mathcal{A}}}_2-{\underline{\mathcal{B}}}_2+3{\underline{\mathcal{C}}}_2\right]\right]\hfill \\ & & =\frac{-11(\zeta -1)}{512}sinh\left(\frac{{\ell }_1}{2}\right)\frac{{\vartheta }^{\alpha }}{\Gamma (\alpha +1)}+\frac{242(\zeta -1)}{2048}cosh\left(\frac{{\ell }_1}{2}\right)\frac{{\vartheta }^{2\alpha }}{\Gamma (2\alpha +1)}\hfill \\ & & -\frac{7986(\zeta -1)}{49152}sinh\left(\frac{{\ell }_1}{2}\right)\frac{{\vartheta }^{3\alpha }}{\Gamma (3\alpha +1)},\hfill \\ & & ⋮.\hfill \end{array}$$

By implementing a similar technique, the remaining terms of ${\underline{\mathbf{f}}}_q(q\ge 4)$ of EADM solution can be simply determined. Furthermore, when the iterative process expands, the accuracy of the obtained solution improves dramatically, and the deduced solution moves closer to the precise result. Finally, we have come up with the following answers in a series form

$$\begin{array}{c}\hfill \underline{\mathbf{f}}({\ell }_1,\vartheta ,\zeta )={\underline{\mathbf{f}}}_0({\ell }_1,\vartheta ,\zeta )+{\underline{\mathbf{f}}}_1({\ell }_1,\vartheta ,\zeta )+{\underline{\mathbf{f}}}_1({\ell }_1,\vartheta ,\zeta )+...,\end{array}$$

such that

$$\begin{array}{ccc}\hfill \underline{\mathbf{f}}({\ell }_1,\vartheta ,\zeta )& & ={\underline{\mathbf{f}}}_0({\ell }_1,\vartheta ,\zeta )+{\underline{\mathbf{f}}}_1({\ell }_1,\vartheta ,\zeta )+{\underline{\mathbf{f}}}_1({\ell }_1,\vartheta ,\zeta )+...,\hfill \\ \hfill \overline{\mathbf{f}}({\ell }_1,\vartheta ,\zeta )& & ={\overline{\mathbf{f}}}_0({\ell }_1,\vartheta ,\zeta )+{\overline{\mathbf{f}}}_1({\ell }_1,\vartheta ,\zeta )+{\overline{\mathbf{f}}}_1({\ell }_1,\vartheta ,\zeta )+....\hfill \end{array}$$

Consequently, we have

$$\begin{array}{ccc}\hfill \underline{\mathbf{f}}({\ell }_1,\vartheta ,\zeta )& & =(\zeta -1)\left(\frac{1}{2}+\frac{1}{2}cosh\left(\frac{{\ell }_1}{2}\right)\right)-\frac{231}{32}(\zeta -1)sinh\left(\frac{{\ell }_1}{2}\right)\frac{{\vartheta }^{\alpha }}{\Gamma (\alpha +1)}\hfill \\ & & +\frac{363(\zeta -1)}{1024}cosh\left(\frac{{\ell }_1}{2}\right)\frac{{\vartheta }^{2\alpha }}{\Gamma (2\alpha +1)}-\frac{7986(\zeta -1)}{49152}sinh\left(\frac{{\ell }_1}{2}\right)\frac{{\vartheta }^{3\alpha }}{\Gamma (3\alpha +1)}+...,\hfill \\ \hfill \overline{\mathbf{f}}({\ell }_1,\vartheta ,\zeta )& & =(1-\zeta )\left(\frac{1}{2}+\frac{1}{2}cosh\left(\frac{{\ell }_1}{2}\right)\right)-\frac{231}{32}(1-\zeta )sinh\left(\frac{{\ell }_1}{2}\right)\frac{{\vartheta }^{\alpha }}{\Gamma (\alpha +1)}\hfill \\ & & +\frac{363(1-\zeta )}{1024}cosh\left(\frac{{\ell }_1}{2}\right)\frac{{\vartheta }^{2\alpha }}{\Gamma (2\alpha +1)}-\frac{7986(1-\zeta )}{49152}sinh\left(\frac{{\ell }_1}{2}\right)\frac{{\vartheta }^{3\alpha }}{\Gamma (3\alpha +1)}+....\hfill \end{array}$$

Case II. (For the fuzzy Atangana–Baleanu Caputo fractional derivative)

Here, we obtain the EADM solution for the first case of (51) by using the fuzzy ABC fractional derivative operator.

Taking into consideration the procedure described in Section 3, we have

$$\begin{array}{ccc}\hfill \mathbb{E}\left[\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right]& & ={\omega }^2{\underline{\mathbf{f}}}_{\left(\kappa \right)}({\ell }_1;\zeta )+\left(\frac{\alpha {\omega }^{\alpha }+1-\alpha }{\mathcal{N}\left(\alpha \right)}\right)\mathbb{E}[\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )-\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\hfill \\ & & +\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{{\partial }^3}{\partial {\ell }_1^3}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )-\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )+\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{{\partial }^2}{\partial {\ell }_1^2}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )].\hfill \end{array}$$

Simple computations result in

$$\begin{array}{ccc}\hfill \underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )& & =(\zeta -1){cosh}^2\left(\frac{{\ell }_1}{4}\right)+{\mathbb{E}}^{-1}\left[\left(\frac{\alpha {\omega }^{\alpha }+1-\alpha }{\mathcal{N}\left(\alpha \right)}\right)\mathbb{E}\right[\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )-\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\hfill \\ & & +\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{{\partial }^3}{\partial {\ell }_1^3}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )-\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )+\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\frac{{\partial }^2}{\partial {\ell }_1^2}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\left]\right].\hfill \end{array}$$

(63)

Let us surmise the infinite sum $\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )=\sum _{q=0}^{\infty }{\underline{\mathbf{f}}}_q({\ell }_1,\vartheta ;\zeta )$ accompanying it with (45) and affirming the non-linearity. Therefore, (63) takes the form

$$\begin{array}{ccc}\hfill \sum _{q=0}^{\infty }{\underline{\mathbf{f}}}_q({\ell }_1,\vartheta ;\zeta )& & =(\zeta -1){cosh}^2\left(\frac{{\ell }_1}{4}\right)+{\mathbb{E}}^{-1}\left[\left(\frac{\alpha {\omega }^{\alpha }+1-\alpha }{\mathcal{N}\left(\alpha \right)}\right)\mathbb{E}\right[\sum _{q=0}^{\infty }{\left(\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_q\hfill \\ & & -\sum _{q=0}^{\infty }{\left(\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_q+\sum _{q=0}^{\infty }{\underline{\mathcal{A}}}_q-\sum _{q=0}^{\infty }{\underline{\mathcal{B}}}_q+3\sum _{q=0}^{\infty }{\underline{\mathcal{C}}}_q\left]\right].\hfill \end{array}$$

(64)

Utilizing the Adomian polynomials described in (54), then (64) simplifies to

$$\begin{array}{ccc}\hfill \underline{{\mathbf{f}}_0}({\ell }_1,\vartheta ;\zeta )& & =(\zeta -1)\left(\frac{1}{2}+\frac{1}{2}cosh\left(\frac{{\ell }_1}{2}\right)\right),\hfill \\ \hfill \underline{{\mathbf{f}}_1}({\ell }_1,\vartheta ;\zeta )& & ={\mathbb{E}}^{-1}\left[\left(\frac{\alpha {\omega }^{\alpha }+1-\alpha }{\mathcal{N}\left(\alpha \right)}\right)\mathbb{E}\left[{\left(\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_0-{\left(\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_0+{\underline{\mathcal{A}}}_0-{\underline{\mathcal{B}}}_0+3{\underline{\mathcal{C}}}_0\right]\right]\hfill \\ & & =-\frac{11}{32}(\zeta -1)sinh\left(\frac{{\ell }_1}{2}\right)\left[\frac{\alpha {\vartheta }^{\alpha }}{\Gamma (\alpha +1)}+(1-\alpha )\right],\hfill \\ \hfill \underline{{\mathbf{f}}_2}({\ell }_1,\vartheta ;\zeta )& & ={\mathbb{E}}^{-1}\left[\left(\frac{\alpha {\omega }^{\alpha }+1-\alpha }{\mathcal{N}\left(\alpha \right)}\right)\mathbb{E}\left[{\left(\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_1-{\left(\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_1+{\underline{\mathcal{A}}}_1-{\underline{\mathcal{B}}}_1+3{\underline{\mathcal{C}}}_1\right]\right]\hfill \\ & & =\frac{-11}{128}(\zeta -1)sinh\left(\frac{{\ell }_1}{2}\right)\left[\frac{\alpha {\vartheta }^{\alpha }}{\Gamma (\alpha +1)}+(1-\alpha )\right]\hfill \\ & & +\frac{242(\zeta -1)}{1024}cosh\left(\frac{{\ell }_1}{2}\right)\left[\frac{{\alpha }^2{\vartheta }^{2\alpha }}{\Gamma (2\alpha +1)}+2\alpha (1-\alpha )\frac{{\vartheta }^{\alpha }}{\Gamma (\alpha +1)}+{(1-\alpha )}^2\right],\hfill \\ \hfill \underline{{\mathbf{f}}_3}({\ell }_1,\vartheta ;\zeta )& & ={\mathbb{E}}^{-1}\left[\left(\frac{\alpha {\omega }^{\alpha }+1-\alpha }{\mathcal{N}\left(\alpha \right)}\right)\mathbb{E}\left[{\left(\frac{{\partial }^3}{\partial {\ell }_1^2\partial \vartheta }\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_2-{\left(\frac{\partial }{\partial {\ell }_1}\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )\right)}_2+{\underline{\mathcal{A}}}_2-{\underline{\mathcal{B}}}_2+3{\underline{\mathcal{C}}}_2\right]\right]\hfill \\ & & =\frac{-11(\zeta -1)}{512}sinh\left(\frac{{\ell }_1}{2}\right)\left[\frac{\alpha {\vartheta }^{\alpha }}{\Gamma (\alpha +1)}+(1-\alpha )\right]\hfill \\ & & +\frac{242(\zeta -1)}{2048}cosh\left(\frac{{\ell }_1}{2}\right)\left[\frac{{\alpha }^2{\vartheta }^{2\alpha }}{\Gamma (2\alpha +1)}+2\alpha (1-\alpha )\frac{{\vartheta }^{\alpha }}{\Gamma (\alpha +1)}+{(1-\alpha )}^2\right]\hfill \\ & & -\frac{7986(\zeta -1)}{49152}sinh\left(\frac{{\ell }_1}{2}\right)\left[\frac{{\alpha }^3{\vartheta }^{3\alpha }}{\Gamma (3\alpha +1)}+3{\alpha }^2(1-\alpha )\frac{{\vartheta }^{2\alpha }}{\Gamma (2\alpha +1)}+3\alpha {(1-\alpha )}^2\frac{{\vartheta }^{\alpha }}{\Gamma (\alpha +1)}+{(1-\alpha )}^3\right],\hfill \\ & & ⋮.\hfill \end{array}$$

By implementing a similar technique, the remaining terms of ${\underline{\mathbf{f}}}_q(q\ge 4)$ of the EADM solution can be simply determined. Furthermore, when the iterative process expands, the accuracy of the obtained solution improves dramatically, and the deduced solution moves closer to the precise result. Finally, we have come up with the following answers in a series form

$$\begin{array}{c}\hfill \underline{\mathbf{f}}({\ell }_1,\vartheta ,\zeta )={\underline{\mathbf{f}}}_0({\ell }_1,\vartheta ,\zeta )+{\underline{\mathbf{f}}}_1({\ell }_1,\vartheta ,\zeta )+{\underline{\mathbf{f}}}_1({\ell }_1,\vartheta ,\zeta )+...,\end{array}$$

such that

$$\begin{array}{ccc}\hfill \underline{\mathbf{f}}({\ell }_1,\vartheta ,\zeta )& & ={\underline{\mathbf{f}}}_0({\ell }_1,\vartheta ,\zeta )+{\underline{\mathbf{f}}}_1({\ell }_1,\vartheta ,\zeta )+{\underline{\mathbf{f}}}_1({\ell }_1,\vartheta ,\zeta )+...,\hfill \\ \hfill \overline{\mathbf{f}}({\ell }_1,\vartheta ,\zeta )& & ={\overline{\mathbf{f}}}_0({\ell }_1,\vartheta ,\zeta )+{\overline{\mathbf{f}}}_1({\ell }_1,\vartheta ,\zeta )+{\overline{\mathbf{f}}}_1({\ell }_1,\vartheta ,\zeta )+....\hfill \end{array}$$

Consequently, we have

$$\begin{array}{ccc}\hfill \underline{\mathbf{f}}({\ell }_1,\vartheta ,\zeta )& & =(\zeta -1)\left(\frac{1}{2}+\frac{1}{2}cosh\left(\frac{{\ell }_1}{2}\right)\right)-\frac{231}{32}(\zeta -1)sinh\left(\frac{{\ell }_1}{2}\right)\left[\frac{\alpha {\vartheta }^{\alpha }}{\Gamma (\alpha +1)}+(1-\alpha )\right]\hfill \\ & & +\frac{363(\zeta -1)}{1024}cosh\left(\frac{{\ell }_1}{2}\right)\left[\frac{{\alpha }^2{\vartheta }^{2\alpha }}{\Gamma (2\alpha +1)}+2\alpha (1-\alpha )\frac{{\vartheta }^{\alpha }}{\Gamma (\alpha +1)}+{(1-\alpha )}^2\right]\hfill \\ & & -\frac{7986(\zeta -1)}{49152}sinh\left(\frac{{\ell }_1}{2}\right)[\frac{{\alpha }^3{\vartheta }^{3\alpha }}{\Gamma (3\alpha +1)}+3{\alpha }^2(1-\alpha )\frac{{\vartheta }^{2\alpha }}{\Gamma (2\alpha +1)}+3\alpha {(1-\alpha )}^2\frac{{\vartheta }^{\alpha }}{\Gamma (\alpha +1)}\hfill \\ & & +{(1-\alpha )}^3]+...,\hfill \\ \hfill \overline{\mathbf{f}}({\ell }_1,\vartheta ,\zeta )& & =(1-\zeta )\left(\frac{1}{2}+\frac{1}{2}cosh\left(\frac{{\ell }_1}{2}\right)\right)-\frac{231}{32}(1-\zeta )sinh\left(\frac{{\ell }_1}{2}\right)\left[\frac{\alpha {\vartheta }^{\alpha }}{\Gamma (\alpha +1)}+(1-\alpha )\right]\hfill \\ & & +\frac{363(1-\zeta )}{1024}cosh\left(\frac{{\ell }_1}{2}\right)\left[\frac{{\alpha }^2{\vartheta }^{2\alpha }}{\Gamma (2\alpha +1)}+2\alpha (1-\alpha )\frac{{\vartheta }^{\alpha }}{\Gamma (\alpha +1)}+{(1-\alpha )}^2\right]\hfill \\ & & -\frac{7986(1-\zeta )}{49152}sinh\left(\frac{{\ell }_1}{2}\right)[\frac{{\alpha }^3{\vartheta }^{3\alpha }}{\Gamma (3\alpha +1)}+3{\alpha }^2(1-\alpha )\frac{{\vartheta }^{2\alpha }}{\Gamma (2\alpha +1)}+3\alpha {(1-\alpha )}^2\frac{{\vartheta }^{\alpha }}{\Gamma (\alpha +1)}\hfill \\ & & +{(1-\alpha )}^3]+....\hfill \end{array}$$

In this analysis, Figure 6 demonstrates the insight into the influence of multiple-layer surface plots for Problem 2 correlated with the CFD and Elzaki transform in the fuzzy sense. It is worth mentioning that the profile identifies the variation in the mapping $\mathbf{f}({\ell }_1,\vartheta ;\zeta )$ on space co-ordinate ${\ell }_1$ with respect to $\vartheta$ and the uncertainty parameter $\zeta \in [0,1]$.

The graph illustrates that, as time progresses, the mapping $\mathbf{f}({\ell }_1,\vartheta ;\zeta )$ will also increase.

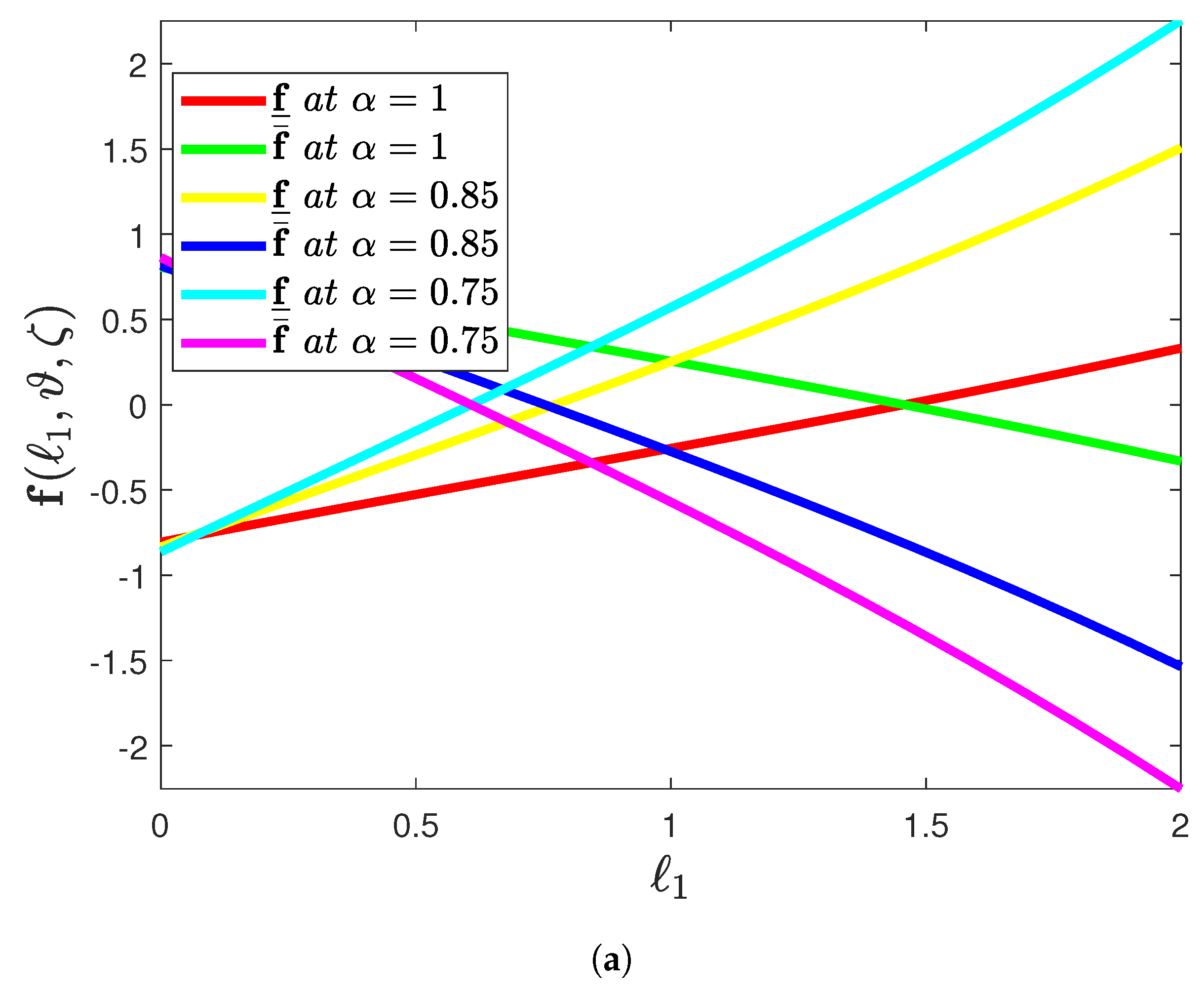
• The effect of the proposed methodology on the mapping $\mathbf{f}({\ell }_1,\vartheta ;\zeta )$ is displayed in Figure 7a for the varying fractional-orders $\alpha =1,0.85,0.75,0.55$ by the considering CFD operator. It exhibits a relatively small increase in the mapping $\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )$ with the decrease in $\overline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )$.
• The profile graph of Figure 7b demonstrates the lower and upper solution of varying uncertainty when the fractional order is assumed to be $\alpha =0.2$ by proposing the CFD operator. It emphasizes a relatively small variation in the mapping $\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )$ with the increase in $\overline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )$.
• The effect of the proposed methodology on the mapping $\mathbf{f}({\ell }_1,\vartheta ;\zeta )$ is displayed in Figure 8a for the varying fractional orders $\alpha =1,0.85,0.75,0.55$ by considering ABC fractional derivative operator. It exhibits a relatively small increase in the mapping $\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )$ with the decrease in $\overline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )$.
• The profile graph of Figure 8b demonstrates the lower and upper solutions of varying uncertainty when the fractional order is assumed to be $\alpha =0.2$ by proposing the ABC fractional derivative operator. It emphasizes a relatively small variation in the mapping $\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )$ with the increase in $\overline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )$.
• Figure 9 demonstrates the comparison analysis between CFD operator and ABC fractional derivative operator for varying fractional order with uncertainty $\kappa \in [0,1],$ exhibits that the lower solution profile for ABC fractional operator has strong ties with the upper solution as compared to the CFD operator.
• Figure 10 shows the comparison analysis between ($\underline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )$ and the exact solution), ($\overline{\mathbf{f}}({\ell }_1,\vartheta ;\zeta )$ and the exact solution), respectively, for three dimensional error plots by considering the CFD operator.

Furthermore, the offered approach does not provide a unique solution but will aid scientists in selecting the best approximate solution. It is remarkable that the fuzzy ABC fractional derivative operator has better performance than the CFD operators, because the curves have a strong harmony with the integer-order graph in the ABC operator case.

□

Remark 3.

When $\underline{\chi }\left(\zeta \right)=\overline{\chi }\left(\zeta \right)=1$ along with $\alpha =1,$ then both solutions of Problem 2 converge to the integer-order solution $\mathbf{f}({\ell }_1,\vartheta )={cosh}^2\left(\frac{{\ell }_1}{4}-\frac{11\vartheta }{24}\right).$

5. Conclusions

The paper has demonstrated families of approximate solutions to the FWE under $g\mathcal{H}-\left(i\right)$ differentiability taking into consideration the Elzaki and ADM. Fractional operators (Caputo and ABC) describing fuzzy characteristics have been separately discussed. The fuzzy solutions of FWE proposed for such flows are characterized by EADM. Nevertheless, the crisp operators are unable to simulate any physical mechanism in an unpredictable setting. Therefore, fuzzy operators are a preferable means to describe the physical phenomenon in such a scenario. Specifically, we illustrated two test examples of the evolutionary method to gain deeper insight into the exact–approximate solutions to validate the projected technique to attain a parametric solution for each case of the fuzzy (Caputo and ABC) fractional derivative operator. It has been demonstrated that the solution graphs predict the fuzzy solution since they satisfy the fuzzy number conditions. As for applications of this framework, the convergence and error analysis can be predicated by the simulation study that specified that fractional-order plots have a strong correlation with the evolutionary trajectories of FWE. It has also been shown that fuzzy EADM represents two solutions, which often leads to an advantage in selecting the best one possible for a governing model. As a consequence, the fuzzy theory connected with FC allows a model to improve performance in an uncertain domain. In the future, we will investigate a similar problem by defining the Henstock integrals (fuzzy integrals in the sense of Lebesgue) at infinite intervals [69,70].