Abstract
Herein, we developed and analyzed a new fractal–fractional (FF) operational matrix for orthonormal normalized ultraspherical polynomials. We used this matrix to handle the FF Riccati differential equation with the new generalized Caputo FF derivative. Based on the developed operational matrix and the spectral Tau method, the nonlinear differential problem was reduced to a system of algebraic equations in the unknown expansion coefficients. Accordingly, the resulting system was solved by Newton’s solver with a small initial guess. The efficiency, accuracy, and applicability of the developed numerical method were checked by exhibiting various test problems. The obtained results were also compared with other recent methods, based on the available literature.
1. Introduction
Since a few years ago and to this day, some researchers have started focusing on old stable methodologies such as finite difference and finite element [1,2,3,4,5]. The main drawback of these methods is their limited accuracy, which has motivated some researchers to dedicated significant effort to develop new numerical techniques which can reduce their difficulties, such as the time consumed and the convergence rate and obtain reasonably high accuracy. These advantages can be achieved via using spectral methods [6,7,8,9,10,11].
Spectral algorithms are a category of schemes used in mathematics and physics to handle numerically specific types of differential equations. The main idea behind these algorithms is to expand the exact unknown solution of the differential equation as a truncated series of basis functions—most probably orthogonal functions—for example: the Fourier basis, Chebyshev polynomials, Jacobi polynomials or others, and then to choose the expansion coefficients in the sum to satisfy both the differential equation as well as its initial and/or boundary conditions [12,13].
Gegenbauer (ultraspherical) polynomials have generated significant attention due to their rudimentary properties as well as their heavy use in mathematics and physics. The presence of the parameter enriches their implementation in spectral and pseudo-spectral methods to solve many types of differential problems. Gegenbauer polynomials provide a convenient basis functions for polynomial approximations of many models involving differential, integral and integro-differential equations [14,15,16,17,18].
The fractional calculus theory is a study of the differential/integral operators of arbitrary order, as the fractional calculus was initially considered a purely mathematical idea with no applications; nevertheless, in recent decades, a noteworthy evolution has been achieved from both theoretical and applied points of views. Most of the fractional differential problems are difficult—sometimes impossible—to solve analytically; for this reason, there is a brawny need to handle them numerically [19,20,21].
The omnipresence of fractional derivative/integral operators inspired by the value of the parameters included in the definition of the operator, studying the effect of these parameters on the nature of the resulted function is one of the trends in the fractional calculation. The generalized Caputo type fractional derivative [22] has the same properties as the Caputo derivative. It also dispenses a useful method for superintending and constructing fractional measured mathematical models.
In this research, we developed the operational matrix of the new generalized Caputo FF derivative for the orthonormal normalized ultraspherical polynomials, we built an efficient Tau algorithm to handle the nonlinear FF Riccati equation, and we used the linearization formula of the product of two ultraspherical polynomials to deal with the quadratic term, resulting in a system of nonlinear algebraic equations. We then used Newton’s iterative method to solve this system and finally obtain the needed approximate solution.
The manuscript is organized as follows. In Section 2, we report the essential definitions of the generalized as well as the new generalized Caputo derivatives and the relevant properties of the orthonormal normalized ultraspherical polynomials; in Section 3, we build the operational matrices of the FF derivative of the ultraspherical vector; in Section 4, we construct a spectral Tau algorithm for the FF Riccati equation; in Section 5, we report the truncation error estimate of the approximate solution; in Section 6, we exhibit some numerical test problems; and some concluding remarks are reported in Section 7.
2. Preliminaries
In this section, we report the essential definitions of the generalized as well as the new generalized Caputo derivatives and some relevant properties of the orthonormal normalized ultraspherical polynomials, which will subsequently be of important use.
2.1. New Generalized Caputo FF Derivative
Definition 1
([23]). Let ρ be a positive constant, the generalized fractional integral of a continuous function of order is defined by
Definition 2
([23]). Let , and , the generalized Caputo fractional derivative of order α of a function is defined as
The generalized Caputo fractional derivative satisfies:
if , then
Definition 3
([19]). Let be continuous and fractal differentiable of order β on , and as the new generalized Caputo FF derivative of order is defined as
where, and .
It should be noted here that, in Definition 3, if we set , we directly obtain the usual Caputo derivative.
2.2. Orthonormal Normalized Shifted Ultraspherical Polynomials
The analytic form of the orthonormal normalized shifted ultraspherical polynomials [24], , of degree k, is given by
where:
the following special values are important:
satisfy the following orthonormality relation:
where , and is the well-known Kronecker delta symbol.
The following linearization formula [25] is needed:
where:
2.3. Function Approximation
If , then can be expanded as a series of as
where:
If we truncate the above series and only keep the first -terms, we have:
where, and are given by
3. Different Derivatives of the Orthonormal Normalized Ultraspherical Vector
The first derivative of can be expressed as
where is the operational matrix of the first-order derivative [26], with entries:
We also have:
Lemma 1.
For and , we have:
Theorem 1.
The new generalized Caputo FF derivative of is given by
where:
where is given by
Proof.
From (1), we have:
Now, we can approximate as
and:
again with the aid of (1), we have:
which completes the proof of the theorem. □
As a direct special case of Theorem 1, we have the following theorem.
Theorem 2.
The generalized Caputo FF derivative of is given by
where:
where is given by
4. Tau Algorithm for FF Riccati Equation
Usually, the Tau method was used for linear problems, whereas in this section, we adopt it to handle the following nonlinear Riccati equation:
subject to the initial condition:
where are known constants, and is a known continuous source term.
We start with the following approximation:
by Theorem 1, we have:
and we have:
where:
thanks to the linearization formula (3), can be simplified as
where is defined in (3), and the source term can be approximated as
where is given by
and:
now the residual of Equation (5) is given by
in other words:
the application of the Tau method:
the use of the initial condition (6), and thanks to (2), we have
Finally, Equations (7) and (8) generate a system of algebraic equations in the unknown expansion coefficients, with quadratic nonlinearity, which can be perfectly solved by Newton’s iterative procedure, with the vanishing initial guess of the form , and consequently, we obtain the desired approximate solution.
5. Truncation Error Estimate
In this section, we report an upper estimate for the truncation error of the suggested approximate solution. Based on the detailed analysis in [16], we have the following theorem.
Theorem 3.
If , for some , then the expansion coefficients in (4) satisfy the following estimate
where ⪅ means that there exists a generic constant d such that .
Based on the result of Theorem 3, we the following truncation error estimate.
Theorem 4.
If satisfies the hypothesis of Theorem 3 is approximated by , and then the following truncation error estimate is valid:
Proof.
We start with:
hence:
now, by the application of Theorem 3 and noting that , we have
which completes the proof of the theorem. □
6. Test Problems
In this section, we handle three Riccati problems with the new generalized FF derivative.
Example 1.


Consider the following FF Riccati initial value problem (see [19,22,27,28,29]):
subject to the homogeneous initial condition:
The exact smooth solution for the classical model (when ) is .In Table 1 and Table 2, we compare our results for and with:

Table 1.
Comparison between our method [19,22], methods for of Example 1, with and .

Table 2.
Comparison between our method [19,27,28,29], methods for of Example 1, with .
- Legendre operational matrix method [19];
- Variation of parameters method [27];
- Modified homotopy perturbation method [28];
- Trigonometric basic functions [22];
- Fractional generalized homotopy analysis method [29].
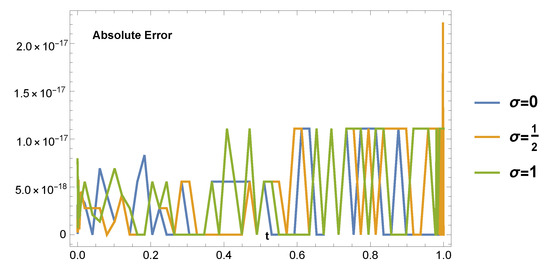
In Figure 1, we depict the best absolute errors for Example 1, with and .

Figure 1.
The absolute error graph of Example 1, for and .
Based on the CPU time reported in seconds in Table 1, it is worth mentioning here that we obtained the numerical approximate solutions in a few seconds, which emphasizes the effectiveness of the method.
In Figure 2, we study the effect of changing and on the approximate solution for a fixed value of .
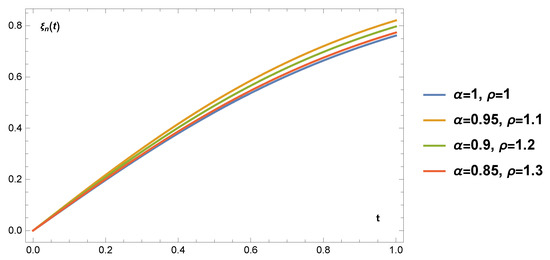
Figure 2.
Different solutions of Example 1, for and .
Example 2.


Consider the following FF Riccati initial value problem (see [22,28,30,31]):
subject to the homogeneous initial condition:
The exact smooth solution for the classical model is:
In Table 3, we compare our results for , we take with:

Table 3.
Comparison of absolute errors for some methods for Example 2, with .
- Modified homotopy perturbation method [28];
- Trigonometric basic functions [22];
- Variational iteration method [30];
- Optimal homotopy asympytotic method [31].
In Table 4, we list the maximum absolute residual error MAR for this problem for the case , where is defined by

Table 4.
MAR for Example 2, with .
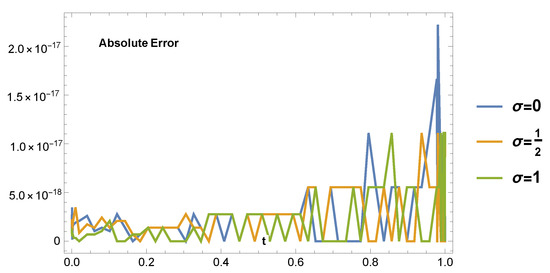
In Figure 3, we depict the absolute error graph of Example 2, for and .

Figure 3.
The absolute error graph of Example 2, for and .
Example 3.
Consider the FF simple Riccati equation:
subject to the homogeneous initial condition:
The exact smooth solution for this model is .
Application of the proposed method for will yield the following system of equations:
thanks to Newton’s method, we obtain:
and consequently:
which is the exact solution.
7. Conclusions
In this research, the spectral Tau method was adopted for numerically solving the nonlinear Riccati initial value problem with a new generalized Caputo FF derivative. The FF operational matrix of the orthonormal normalized ultraspherical polynomials was constructed and then used to discretize the problem to a system of algebraic equations with quadratic nonlinearity. We then applied Newton’s method with the vanishing initial guess to obtain the desired approximate solution. The Tau method is characterized by its efficiency, accuracy, and fine applicability. The validity of the presented method was verified through three numerical simulations.
Funding
The author received no funding for this study.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The author would like to thank the anonymous referees for critically reading the manuscript and also for their insightful comments, which helped substantially to improve the manuscript.
Conflicts of Interest
The author declares no conflict of interest.
References
- Strikwerda, J. Finite Difference Schemes and Partial Differential Equations; SIAM: Philadelphia, PA, USA, 2004. [Google Scholar]
- Leveque, R. Finite Difference Methods for Ordinary and Partial Differential Equations: Steady-State and Time-Dependent Problems; SIAM: Philadelphia, PA, USA, 2007. [Google Scholar]
- Ciarlet, P.G. The Finite Element Method for Elliptic Problems; SIAM: Philadelphia, PA, USA, 2002. [Google Scholar]
- Stynes, M.; O’Riordan, E.; Gracia, J. Error analysis of a finite difference method on graded meshes for a time-fractional diffusion equation. SIAM J. Numer. Anal. 2017, 55, 1057–1079. [Google Scholar] [CrossRef]
- Deng, W. Finite element method for the space and time fractional Fokker–Planck equation. SIAM J. Numer. Anal. 2009, 47, 204–226. [Google Scholar] [CrossRef]
- Hesthaven, J.; Gottlieb, S.; Gottlieb, D. Spectral Methods for Time-Dependent Problems; Cambridge University Press: Cambridge, UK, 2007; Volume 21. [Google Scholar]
- Shen, J.; Tang, T.; Wang, L.L. Spectral Methods: Algorithms, Analysis and Applications; Springer Science & Business Media: Hoboken, NJ, USA, 2011; Volume 41. [Google Scholar]
- Sheng, C.; Cao, D.; Shen, J. Efficient spectral methods for PDEs with spectral fractional Laplacian. J. Sci. Comput. 2021, 88, 4. [Google Scholar] [CrossRef]
- Atta, A.; Abd-Elhameed, W.; Moatimid, G.; Youssri, Y. Shifted fifth-kind Chebyshev Galerkin treatment for linear hyperbolic first-order partial differential equations. Appl. Numer. Math. 2021, 167, 237–256. [Google Scholar] [CrossRef]
- Abd-Elhameed, W.M.; Machado, J.A.T.; Youssri, Y.H. Hypergeometric fractional derivatives formula of shifted Chebyshev polynomials: Tau algorithm for a type of fractional delay differential equations. Int. J. Nonlinear Sci. Numer. Simul. 2021. [Google Scholar] [CrossRef]
- Lui, S.; Nataj, S. Spectral collocation in space and time for linear PDEs. J. Comput. Phys. 2021, 424, 109843. [Google Scholar] [CrossRef]
- Canuto, C.; Hussaini, M.; Quarteroni, A.; Thomas, A., Jr. Spectral Methods in Fluid Dynamics; Springer Science & Business Media: Hoboken, NJ, USA, 2012. [Google Scholar]
- Canuto, C.; Hussaini, M.; Quarteroni, A.; Zang, T. Spectral Methods: Fundamentals in Single Domains; Springer Science & Business Media: Hoboken, NJ, USA, 2007. [Google Scholar]
- Faheem, M.; Raza, A.; Khan, A. Collocation methods based on Gegenbauer and Bernoulli wavelets for solving neutral delay differential equations. Math. Comput. Simul. 2021, 180, 72–92. [Google Scholar] [CrossRef]
- Usman, M.; Hamid, M.; Zubair, T.; Haq, R.; Wang, W.; Liu, M. Novel operational matrices-based method for solving fractional-order delay differential equations via shifted Gegenbauer polynomials. Appl. Math. Comput. 2020, 372, 124985. [Google Scholar] [CrossRef]
- Taghian, H.; Abd-Elhameed, W.; Moatimid, G.; Youssri, Y. Shifted Gegenbauer—Galerkin algorithm for hyperbolic telegraph type equation. Int. J. Mod. Phys. C 2021, 2150118. [Google Scholar] [CrossRef]
- Dahy, S.; Elgindy, K. High-order numerical solution of viscous Burgers’ equation using an extended Cole–Hopf barycentric Gegenbauer integral pseudospectral method. Int. J. Comput. Math. 2021. [Google Scholar] [CrossRef]
- Elgindy, K.; Refat, H. High-order Gegenbauer integral spectral element method integrated with an adaptive Chebyshev optimization strategy for solving linear singularly perturbed differential equations. J. Comput. Appl. Math. 2020, 372, 112722. [Google Scholar] [CrossRef]
- Shloof, A.; Senu, N.; Ahmadian, A.; Salahshour, S. An efficient operation matrix method for solving fractal–fractional differential equations with generalized Caputo-type fractional–fractal derivative. Math. Comput. Simul. 2021, 188, 415–435. [Google Scholar] [CrossRef]
- Gorenflo, R.; Mainardi, F. Fractional calculus. In Fractals and Fractional Calculus in Continuum Mechanics; Springer: Berlin/Heidelberg, Germany, 1997; pp. 223–276. [Google Scholar]
- Li, C.; Zeng, F. Numerical Methods for Fractional Calculus; Chapman and Hall/CRC: London, UK, 2019. [Google Scholar]
- Sakar, M.; Akgül, A.; Baleanu, D. On solutions of fractional Riccati differential equations. Adv. Differ. Equ. 2017, 2017, 39. [Google Scholar] [CrossRef]
- Odibat, Z.; Baleanu, D. Numerical simulation of initial value problems with generalized Caputo-type fractional derivatives. Appl. Numer. Math. 2020, 156, 94–105. [Google Scholar] [CrossRef]
- Hafez, R.; Youssri, Y. Shifted Gegenbauer–Gauss collocation method for solving fractional neutral functional-differential equations with proportional delays. Kragujev. J. Math. 2022, 46, 2022. [Google Scholar]
- Carlitz, L. The product of two ultraspherical polynomials. Glasg. Math. J. 1961, 5, 76–79. [Google Scholar] [CrossRef] [Green Version]
- Abd-Elhameed, W.M.; Youssri, Y.; Doha, E.H. New solutions for singular Lane-Emden equations arising in astrophysics based on shifted ultraspherical operational matrices of derivatives. Comput. Methods Differ. Equ. 2014, 2, 171–185. [Google Scholar]
- Haq, E.; Ali, M.; Khan, A. On the solution of fractional Riccati differential equations with variation of parameters method. Eng. Appl. Sci. Lett. 2020, 3, 41. [Google Scholar]
- Odibat, Z.; Momani, S. Modified homotopy perturbation method: Application to quadratic Riccati differential equation of fractional order. Chaos Solitons Fractals 2008, 36, 167–174. [Google Scholar] [CrossRef]
- Saratha, S.; Bagyalakshmi, M.; Krishnan, G. Fractional generalised homotopy analysis method for solving nonlinear fractional differential equations. Comput. Appl. Math. 2020, 39, 112. [Google Scholar] [CrossRef]
- Batiha, B.; Noorani, M.; Hashim, I. Application of variational iteration method to a general Riccati equation. Int. Math. Forum 2007, 56, 2759–2770. [Google Scholar] [CrossRef] [Green Version]
- Riccati, H.; Mabood, F.; Izani, A.; Isami, M.; Hashim, I. Application of optimal homotopy asymptotic method for the approximate solution of Riccati equation. Sains Malays. 2013, 42, 863–867. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).