1. Introduction
Recently, fractional differential equations have attracted considerable attention because of their extensive use in various problems in science and engineering (see the monographs [
1,
2,
3] and the references therein). There are various types of fractional derivatives known in the literature. The main advantage of fractional derivatives is that they can describe the property of heredity and memory of many materials. The stability property in solutions of any type of differential equation is one of the most practically applicable qualitative properties. The application of a fractional derivative leads to the particular initial conditions to the studied equations. Some of them are totally different than the classical initial conditions for ordinary differential equations, such as Riemann–Liouville (RL) fractional differential equations. It requires a change in the definitions of the initial condition. In this paper, following the ideas developed in the classical book [
2], we define in the appropriate way the initial value problem for RL fractional differential equations.
There are various types of stability that describe different properties of the solutions. One of them is the Lipschitz stability, introduced in [
4] and later studied for nonlinear differential equations [
5,
6], for functional differential equations [
7,
8], for impulsive functional differential equations [
9], for Caputo fractional differential equations [
10], for partial differential equations [
11,
12], and applied to some models such as neural networks [
13], electrical impedance tomography [
14], and the radiate transport problem [
15].
In this paper, we study a nonlinear system of RL fractional differential equations (RLFrDE). The solution of the studied FrDE has a singularity at the initial point 0 (see Example 1). Therefore, the stability properties of the solutions could not be defined for
(such as it is done in Definition 2.3 [
16]). In connection with this phenomenon, in this paper, the stability properties for the RLFrDE have to be studied on appropriate intervals excluding the initial time point. The stability and uniform stability for RLFrDE is appropriately defined and studied recently in [
17]. According to our knowledge, Lipschitz stability is not studied for RLFrDE. In this paper, we generalize this type of stability of the zero solution of the initial value problem (IVP) for a nonlinear system of RLFrDE called Lipschitz stability in time. This type of stability is connected with the singularity of the solution at the initial time point. In connection with this, we consider an interval excluding this initial time point. We use Lyapunov functions and two types of their derivatives among the studied fractional equation. Several sufficient conditions for Lipschitz stability in time are obtained by the application of both derivatives. Some examples illustrate the results and use the application of both fractional derivatives of Lyapunov functions.
In this paper, we consider the following system of nonlinear Riemann–Liouville fractional differential equations (FrDE) of fractional order
with initial condition
where
and
is the Riemann–Liouville fractional derivative.
The main contributions of the paper could be summarized as follows:
- -
The Lipschitz stability in time of zero solution of a system of nonlinear RL fractional differential equations is defined;
- -
Two types of derivatives of Lyapunov functions among the RL fractional differential equations are applied;
- -
Comparison results by Lyapunov functions, a scalar RL fractional equation, and both types of derivatives of Lyapunov functions are proved;
- -
Several sufficient conditions for Lipschitz stability in time are obtained by the application of both types of derivatives of Lyapunov functions. These conditions are deeply connected with the type of initial condition as an RL fractional integral.
2. Preliminaries
We will provide the definition of the main fractional derivatives of order
(see, for example, Refs. [
1,
2,
3]).
- -
Riemann–Liouville (RL) fractional derivative:
where Γ (.) denotes the Gamma function.
- -
The Grünwald–Letnikov fractional derivative is given by
and the Grünwald–Letnikov fractional Dini derivative by
where
and
denote the integer part of the fraction
.
Remark 1. If , then hold (see Theorem 2.25 [2]). The above defined fractional derivatives for scalar functions are generalized to the vector case by taking fractional derivatives component-wise.
Proposition 1. (Lemma 2.3 [18]) Let . Suppose that for an arbitrary , we have and for . Then, it follows that . Remark 2. From Remark 1, it follows that in Proposition 1, the fractional derivative could be replaced by .
We will define the initial condition of RL fractional differential equations based on the following result:
Proposition 2. ([2]) Let and , be a Lebesgue measurable function. - (a)
If there exists a.e. a limit,
then there also exists a limit - (b)
If there exists a.e. a limitand if there exists the limit,
then
Remark 3. According to Proposition 2, the initial condition (2) could be replaced by . We introduce the assumption:
A1. The function, , for .
Let
,
. Define the classes
and
Remark 4. The function and . Further, , is from the class with . The function is from the class with for .
We will generalize Lipschitz stability [
4] to systems of nonlinear RL fractional differential equations. In our further considerations below, we will assume the existence of the solution of the IVP for FrDE (
1), (
2) and we will denote it by
.
The solution of (
1), (
2) has a singularity at the initial point 0. We will illustrate it on a simple linear scalar RL fractional equation:
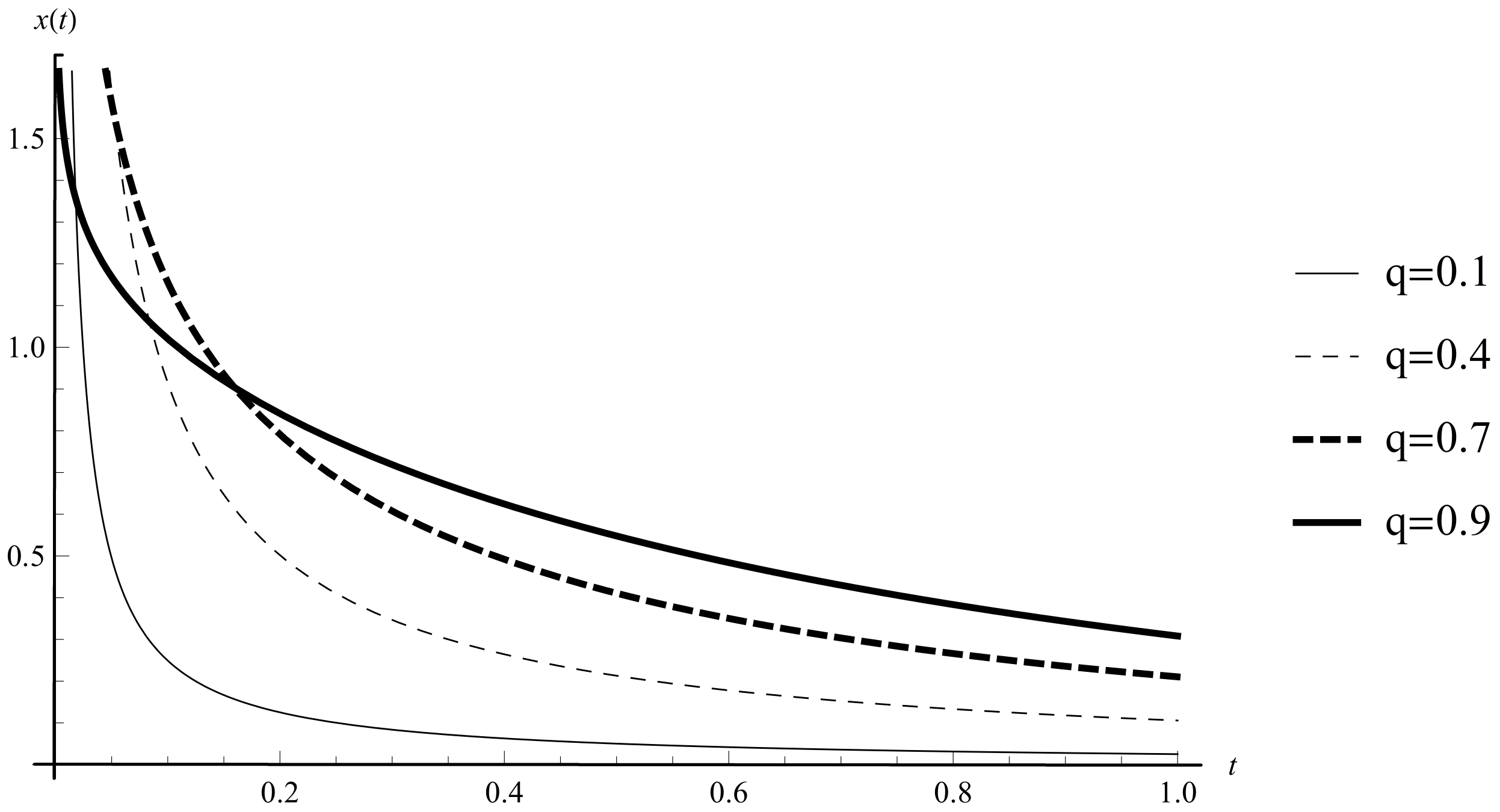
Example 1. Consider the initial value problem for the scalar linear FrDE The function is a solution of (4). It is not defined at the initial time 0. (see Figure 1 for and various fractional orders. Example 1 illustrates that the stability of the solution in the case of RL fractional derivative could not be defined for
(such as it is done in Definition 2.3 [
16]). In connection with this phenomenon, we will define a new type of stability:
Definition 1. The zero solution of the IVP for FrDE (1), (2) is Lipschitz stable in time if there exist constants and such that for any , the inequality holds for 3. Lyapunov Functions and Comparison Results
We will use Lyapunov-like functions from the class .
Definition 2. The function belongs to the class if it is locally Lipschitz with respect to its second argument, where and .
We will use the two following types of derivatives of Lyapunov functions
to study the Lipschitz stability properties of FrDE (
1):
- -
First type—
RL fractional derivative of
is defined by
where
is a solution of (
1), (
2).
- -
Second type—
Dini fractional derivative of
among (
1):
Remark 5. Let be a solution of (1), then Remark 6. Dini fractional derivative of a Lyapunov function is less restrictive than its RL fractional derivative.
We will use the following IVP for the scalar comparison RL fractional differential equation:
where
.
Consider the following condition:
A2. The function is decreasing with respect to its second argument and for .
In our study, we will use comparison results by Lyapunov functions.
3.1. Comparison Result with RL Fractional Derivative of Lyapunov Functions
Lemma 1. Assume:
- 1.
Conditions (A1), (A2) are satisfied.
- 2.
The function is a solution of (1), (2). - 3.
The function , is a solution of (7). - 4.
The function is such that the inequalityholds.
If then the inequality for holds.
Proof. Define , .
Let
be an arbitrary number. We will prove
From the choice of the initial point
, we get
From inequality (
9), there exists a number
such that
for
, i.e., inequality
holds, i.e., (
8) is satisfied on
.
Assume the inequality (
8) is not true. Then, there exists a point
such that
.
From condition (A2), equalities
,
, and Proposition 1 with
and
, we obtain the inequality
Inequality (
10) contradicts condition 4.
Therefore, inequality (
8) is true for any arbitrary number
and thus,
, which proves the claim of Lemma 1. □
3.2. Comparison Result with Dini Fractional Derivative (6) of Lyapunov Functions
Lemma 2. Assume:
- 1.
Conditions 1, 2, and 3 of Lemma 1 are satisfied.
- 2.
The function is such that the inequalityholds.
If then the inequality for holds.
Proof. The proof is similar to the one of Lemma 1, where the Dini fractional derivative is applied instead of RL fractional derivative of the Lyapunov function. The main difference between the proofs of both Lemma 1 and Lemma 2 is connected with the proof of inequality (
8). Assume it is not true. Then, there exists a point
such that
. According to Remark 2 with
, we get the inequality
For any fixed
, we have
From Equation (
1), it follows
. Therefore,
, where
.
Therefore, for any
and
, we get
Thus, by
, i.e.,
, we obtain
From inequalities (
12)–(
14) and condition 2 of Lemma 2, we get
Inequality (
15) contradicts (
11). The contradiction proves the validity of (
8). □
4. Main Results
We will obtain some sufficient conditions for Lipschitz stability in time by Lyapunov functions and their two fractional derivatives defined above.
4.1. RL Fractional Derivative of Lyapunov Functions among Solutions of (1) and (2)
Theorem 1. Assume the following:
- 1.
Conditions (A1), (A2) are satisfied.
- 2.
There exists a function such that:
- (i)
there exists a number such that the inequalityholds, where , ; - (ii)
for any function , the inequalityholds with ; - (iii)
for any and the corresponding solution of (1), (2), the inequalityholds.
- 3.
The zero solution of (7) is Lipschitz stable in time. Then, the zero solution of (1), (2) is Lipschitz stable in time.
Proof. Let the zero solution of (
7) be Lipschitz stable in time. Therefore, there exist constants
such that for any
, the inequality
holds, where
is a solution of (
7) with the initial value
.
From the conditions of the functions
a and
b (
), there exist a function
for
and
such that
and
Without loss of generality, we can assume .
Choose the constant such that and . Therefore, .
Let . Choose the initial value , thus, .
Consider the solution
of (
1), (
2) for the chosen initial value
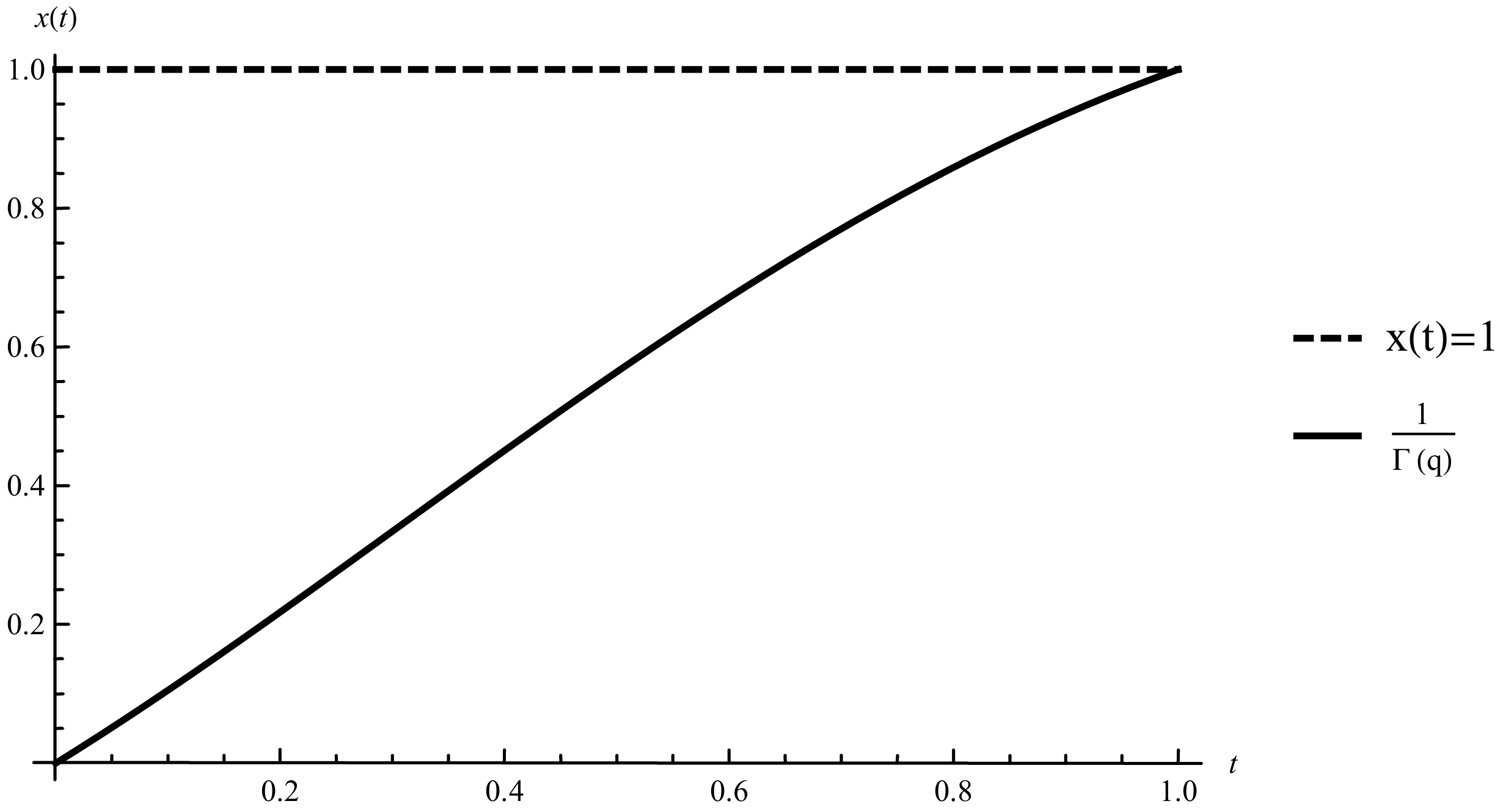
. Then, applying
(see
Figure 2), we get
, i.e.,
and, according to condition 2(ii), the inequality
holds. From inequality (
20), it follows that there exists
such that
for
.
Let
be a solution of (
7) with
. From the choice of
, the initial condition (
2), inequality (
20), and condition
, we obtain
. Therefore, the function
satisfies (
17) for
with
.
Let
. Then, from conditions 2(i), 2(ii); inequalities (
17)–(
19); with
,
, and (
20), (
21), we obtain
Inequality (
22) proves the claim of Theorem 1. □
Theorem 2. Let the conditions of Theorem 1 be satisfied where the conditions 2(i) and 2(ii) are replaced by the following
2* (i) there exist numbers such that the inequalityholds, where , is a constant; 2* (ii) for any function , the inequalityholds with . Then, the zero solution of (1) and (2) is Lipschitz stable in time. Proof. The proof is similar to the one of Theorem 1, where and . □
4.2. Dini Fractional Derivative of Lyapunov Functions among Solutions of (1) and (2)
Theorem 3. Let the conditions of Theorem 1 be satisfied where condition 2(iii) is replaced by the following:
2(iii*) for any point , the inequalityholds. Then, the zero solution of (1) is Lipschitz stable in time. The proof of Theorem 3 is similar to the one of Theorem 1, where Lemma 2 is applied instead of Lemma 1.
Remark 7. Note condition 2(iii) of Theorem 1 is harder than condition 2(iii*) of Theorem 3. It is practically easier to check the validity of condition 2(iii*) of Theorem 3 since we do not use the solution of (1), (2). Theorem 4. Let the conditions 1, 3 of Theorem 1 be satisfied and
- 2(i)
there exist numbers such that the inequalityholds, where , is a constant; - 2(ii)
for any function , the inequalityholds with ; - 2(iii)
Then, the zero solution of (1) and (2) is Lipschitz stable in time.
The proof of Theorem 4 is similar to the one of Theorem 2 with the application of Lemma 2 and we omit it.
Example 2. Consider the following IVP for the system of RL fractional differential equations: Let , . Then, for any and any solution of (25), we get Thus, the comparison scalar RL fractional equation is The solution of (26) is . According to Theorem 1, the zero solution of (25) is Lipschitz stable is time. Example 3. Consider the following IVP for the system of RL fractional differential equations: Choose the Lyapunov function , .
Thus, the inequality for holds, i.e., condition 2(i) of Theorem 2 (Theorem 4) is satisfied with .
Let the function , be such that . Then, Therefore, the condition 2(ii) of Theorem 2 (Theorem 4) is satisfied with .
The RL fractional derivative of the function with , being of solution of (27), is very difficult to be obtained, so the results with the RL fractional derivative of Lyapunov functions are not applicable. We will apply the Dini fractional derivative of V.
For , we get Therefore, the condition 2(ii) of Theorem 4 is satisfied with . According to Theorem 4, the zero solution of (27) is Lipschitz stable in time. 5. Conclusions
In this paper, a system of nonlinear RL fractional differential equations is studied. The appropriate initial condition is applied and, in connection with the singularity of the corresponding solutions at the initial time, a new type of stability is defined. This stability is a generalization of the classical Lipschitz stability with appropriate changes connected with the type of the initial condition and RL fractional derivative. Two types of derivatives of the applied Lyapunov functions are used to obtain sufficient conditions for the defined stability. The conditions are deeply connected with the type of initial condition required for RL fractional differential equations.
Note the ideas about this type of stability and that the conditions of Lyapunov functions could be applied to study another types of stability properties of RL fractional differential equations.
Author Contributions
Conceptualization, S.H., S.T., and R.T.; methodology, S.H., S.T., and R.T.; validation, S.H., S.T., and R.T.; formal analysis, S.H., S.T., and R.T.; writing—original draft preparation, S.H., S.T., and R.T.; funding acquisition, S.H., S.T., and R.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Bulgarian National Science Fund under Project KP-06-N32/7.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Das, S. Functional Fractional Calculus; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Diethelm, K. The Analysis of Fractional Differential Equations; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Dannan, F.M.; Elaydi, S. Lipschitz stability of nonlinear systems of differential equations. J. Math. Anal. Appl. 1986, 113, 562–577. [Google Scholar] [CrossRef]
- Choia, S.I.; Goob, Y.H. Uniformly Lipschitz stability and asymptotic property in perturbed nonlinear differential systems. Pure Appl. Math. 2016, 23, 1–12. [Google Scholar] [CrossRef]
- Soliman, A.A. On Lipschitz stability for comparison systems of differential equations via limiting equation. Appl. Math. Comput. 2005, 163, 3. [Google Scholar] [CrossRef]
- Fu, Y.L. On Lipschitz stability for F.D.E. Pac. J. Math. 1991, 151, 229–235. [Google Scholar] [CrossRef][Green Version]
- Stamova, I.; Stamov, G. Lipschitz stability criteria for functional differential systems of fractional order. J. Math. Phys. 2013, 54, 043502. [Google Scholar] [CrossRef]
- Bainov, D.D.; Stamova, I.M. Lipschitz stability of impulsive functional-differential equations. ANZIAM J. 2001, 42, 504–514. [Google Scholar] [CrossRef]
- Agarwal, R.; Hristova, S.; O’Regan, D. Lipschitz stability for non-instantaneous impulsive Caputo fractional differential equations with state dependent delays. Axioms 2019, 8, 4. [Google Scholar] [CrossRef]
- Alessandrini, G.; de Hoop, M.V.; Gaburro, R.; Sincich, E. Lipschitz stability for a piecewise linear Schrödinger potential from local Cauchy data. Asymptot. Anal. 2018, 108, 115–149. [Google Scholar] [CrossRef]
- Bellassoued, M.; Jellali, D.; Yamamoto, M. Lipschitz stability for a hyperbolic inverse problem by finite local boundary data. Appl. Anal. 2006, 85, 1219–1243. [Google Scholar] [CrossRef]
- Agarwal, R.; Hristova, S.; O’Regan, D.; Terzieva, R. Stability properties of neural networks with non-instantaneous impulses. Math. Biosci. Eng. 2019, 16, 1210–1227. [Google Scholar] [CrossRef] [PubMed]
- Beretta, E.; Francini, E. Lipschitz Stability for the Electrical Impedance Tomography Problem: The Complex Case. Commun. Partial Diff. Eq. 2011, 36, 1723–1749. [Google Scholar] [CrossRef]
- Machida, M.; Yamamoto, M. Global Lipschitz stability in determining coefficients of the radiative transport equation. Inverse Probl. 2014, 30, 035010. [Google Scholar] [CrossRef]
- Qian, D.; Li, C.; Agarwal, R.P.; Wong, P.J. Stability analysis of fractional differential system with Rieman–Liouville derivative. Math. Comput. Modell. 2010, 52, 862–874. [Google Scholar] [CrossRef]
- Agarwal, R.; Hristova, S.; O’Regan, D. Stability Concepts of Riemann-Liouville Fractional-Order Delay Nonlinear Systems. Mathematics 2021, 9, 435. [Google Scholar] [CrossRef]
- Devi, J.V.; Mc Rae, F.A.; Drici, Z. Variational Lyapunov method for fractional differential equations. Comput. Math. Appl. 2012, 64, 2982–2989. [Google Scholar] [CrossRef]
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).