Simultaneous Characterization of Relaxation, Creep, Dissipation, and Hysteresis by Fractional-Order Constitutive Models
Abstract
1. Introduction
2. Fractional Models and Thermodynamic Requirements
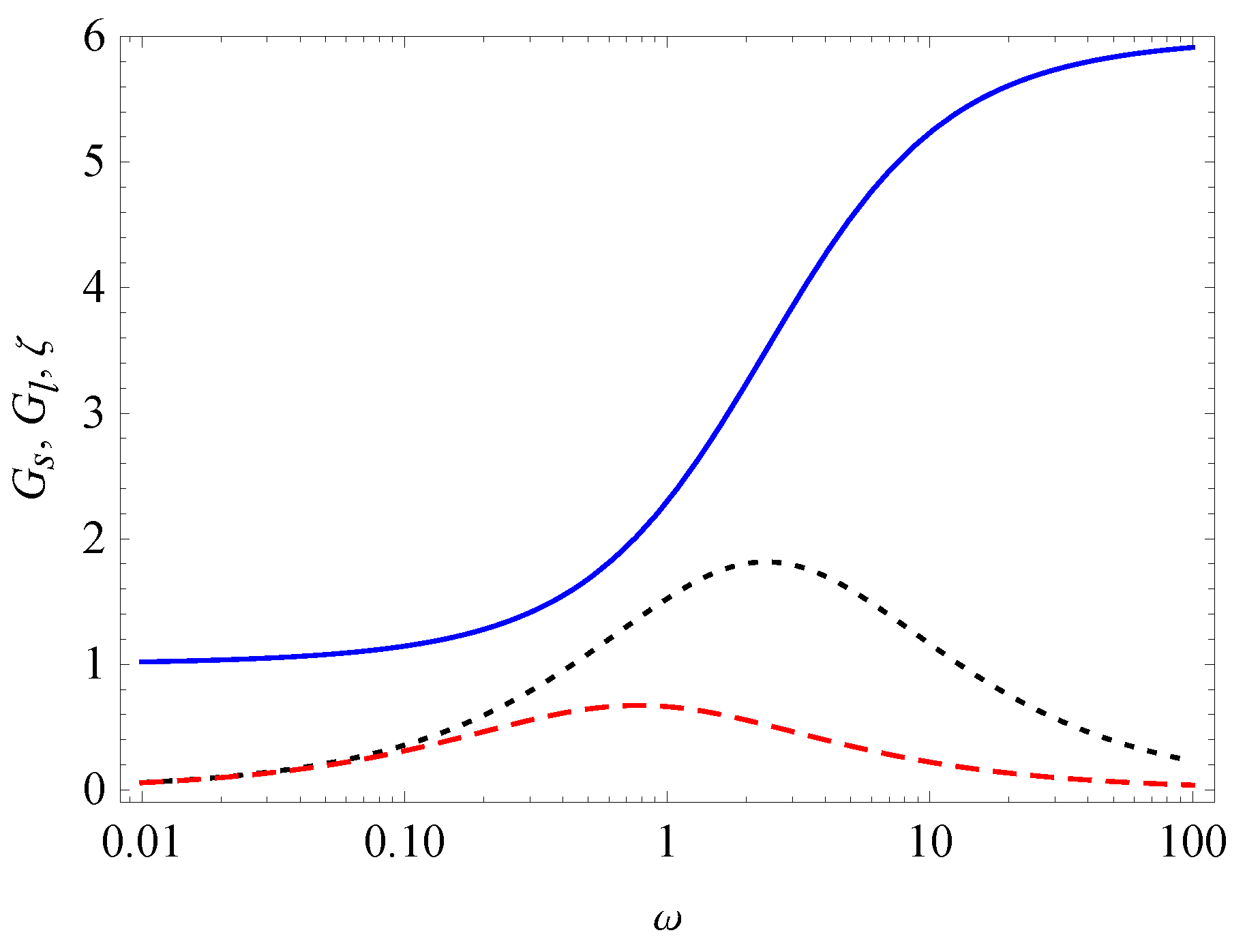
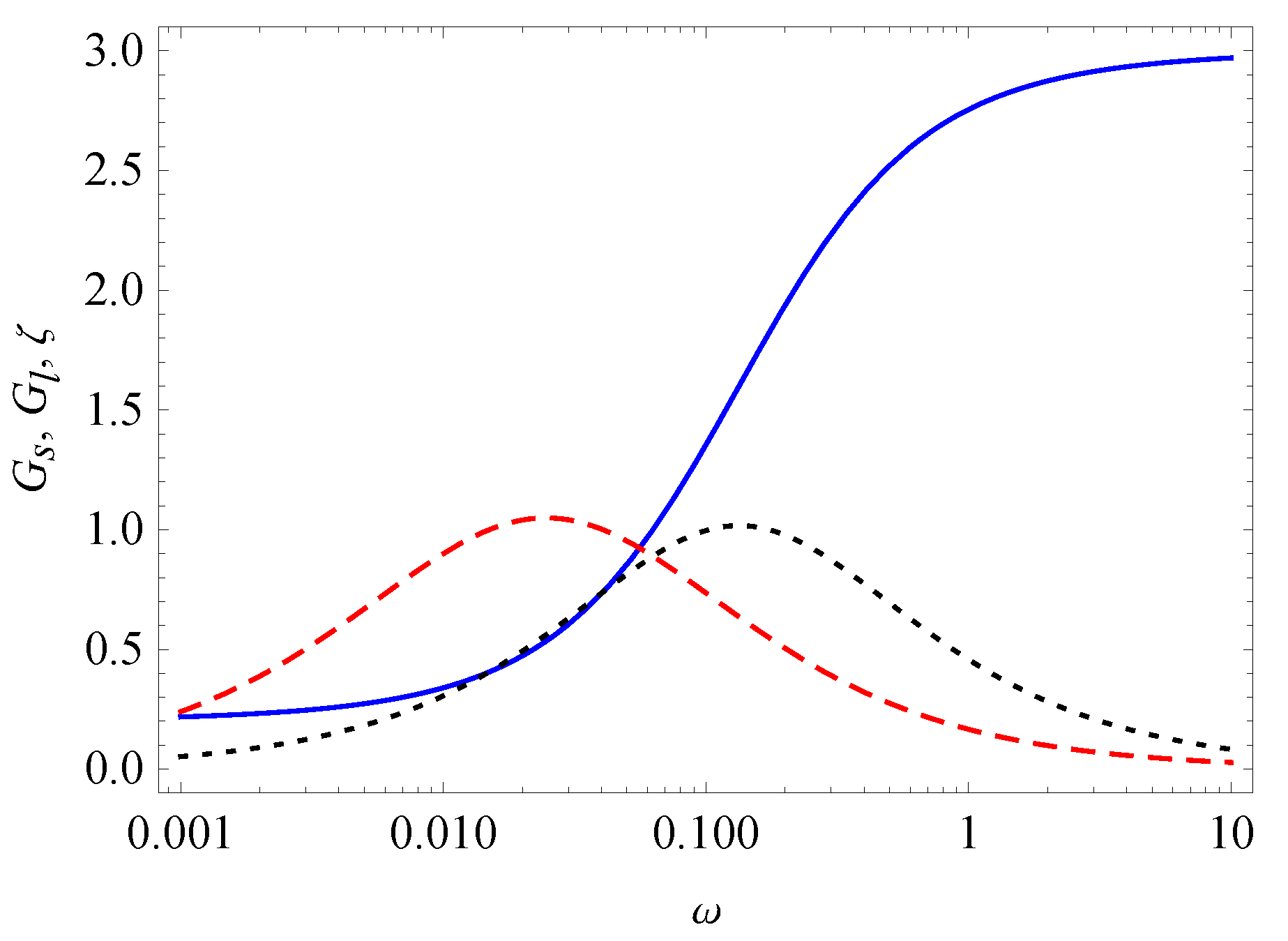
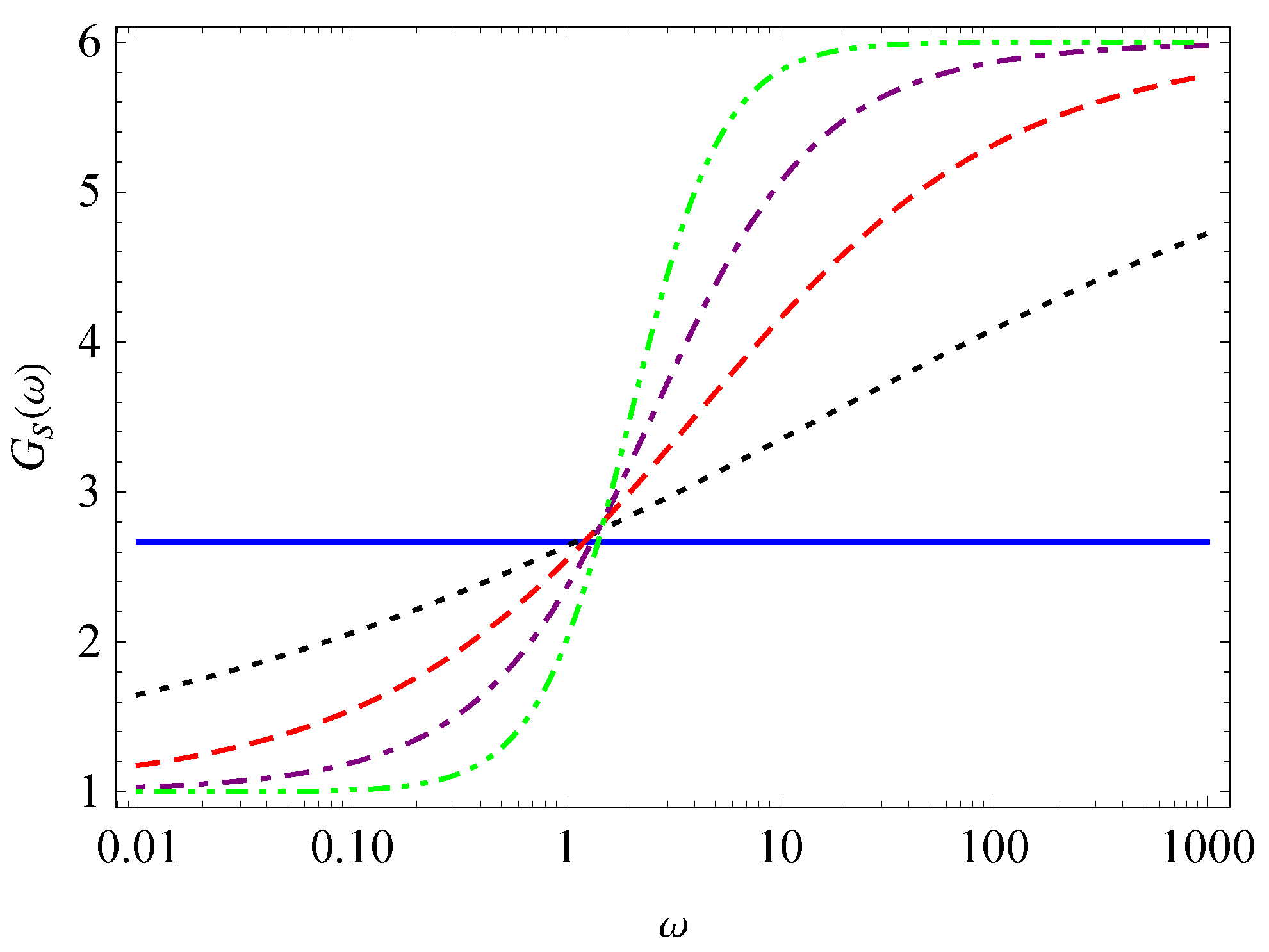
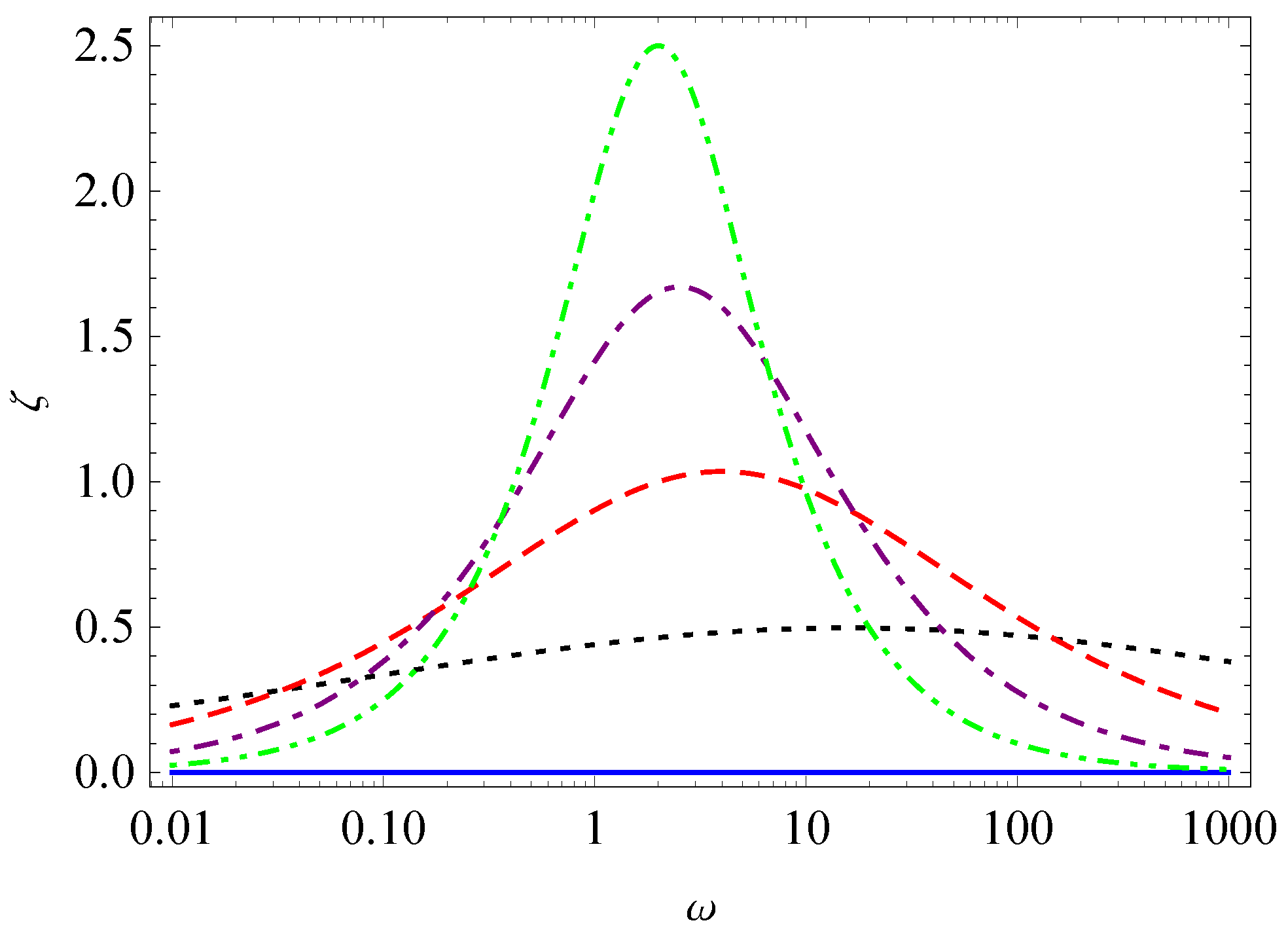
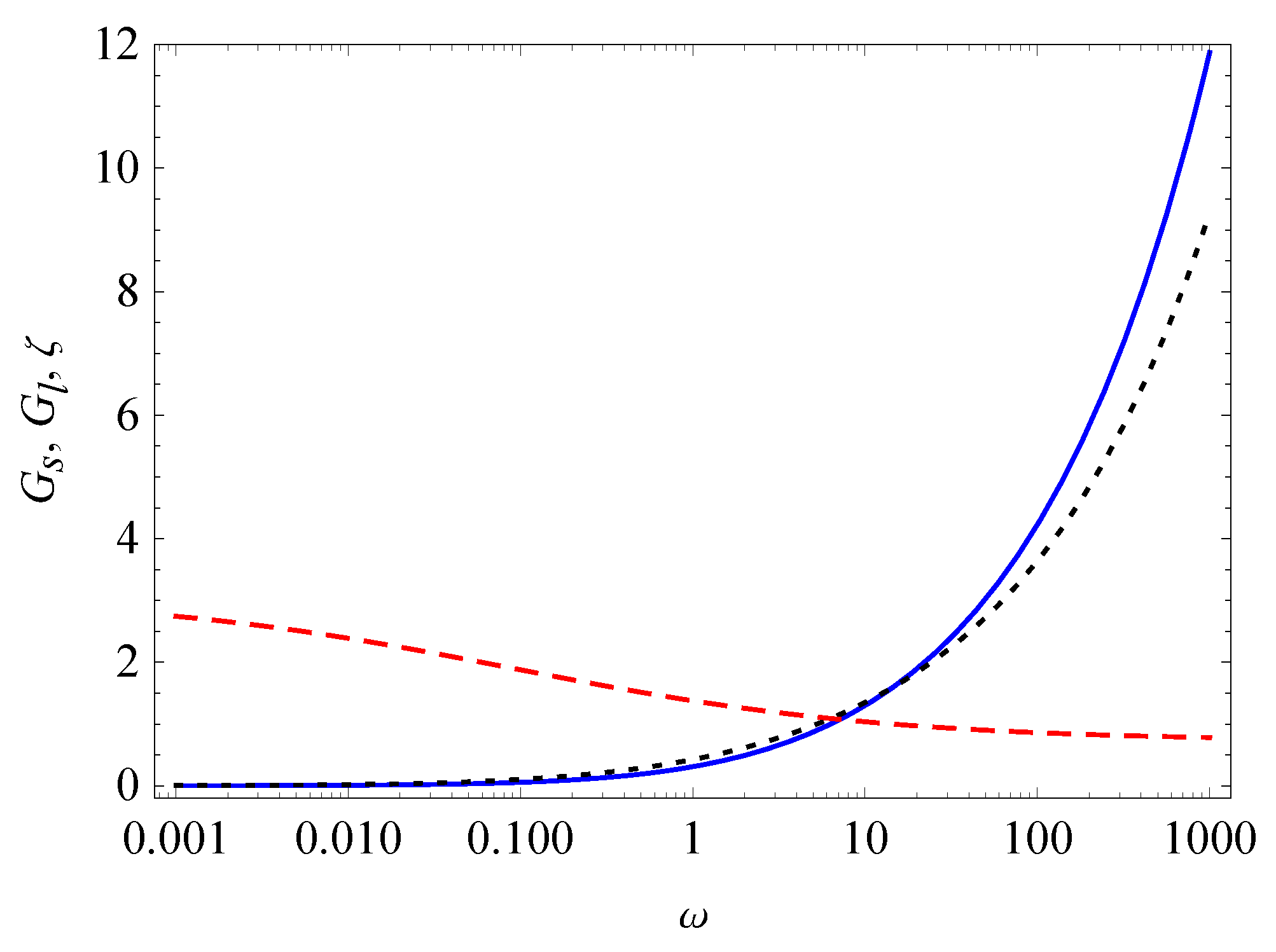
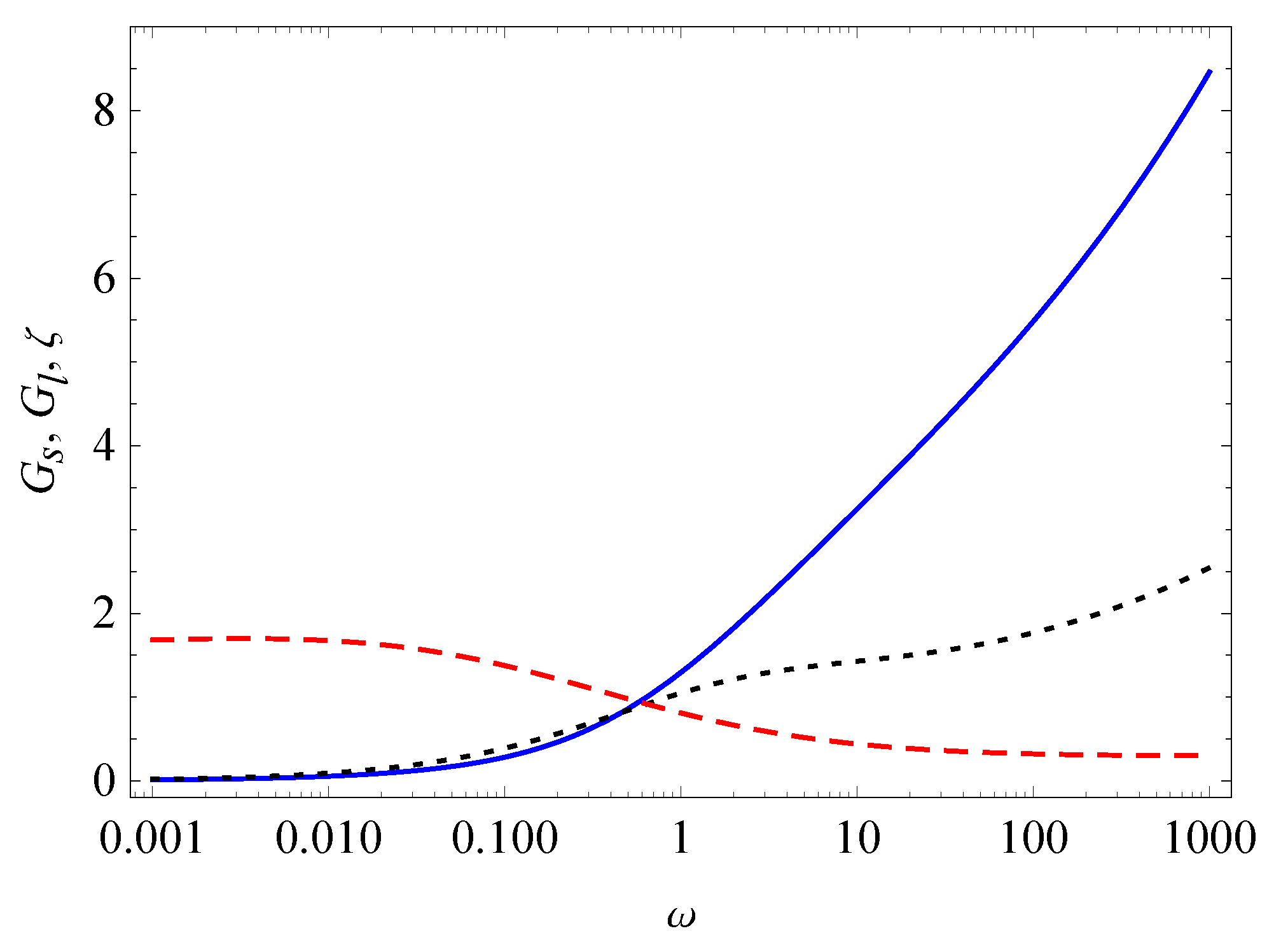
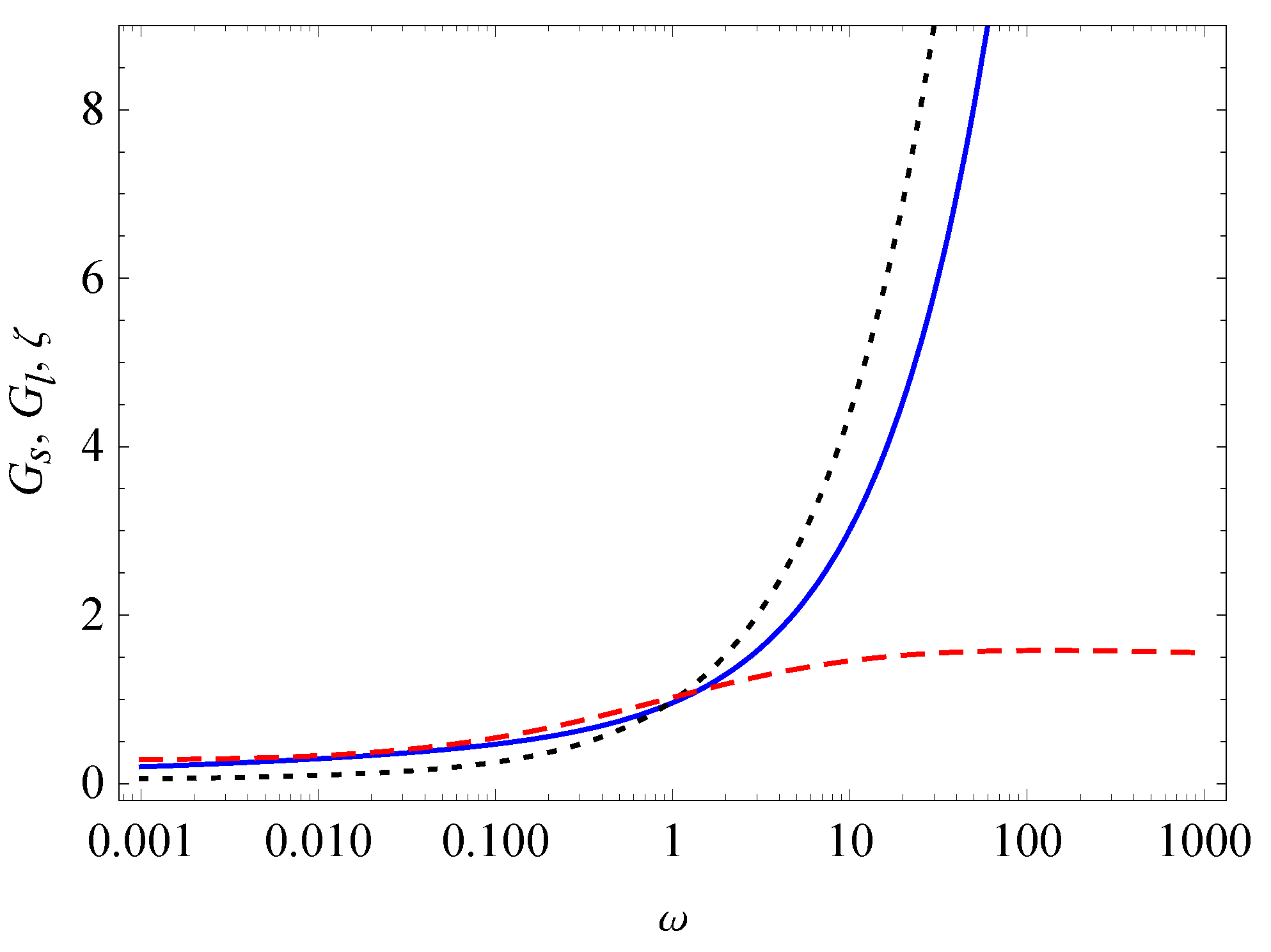
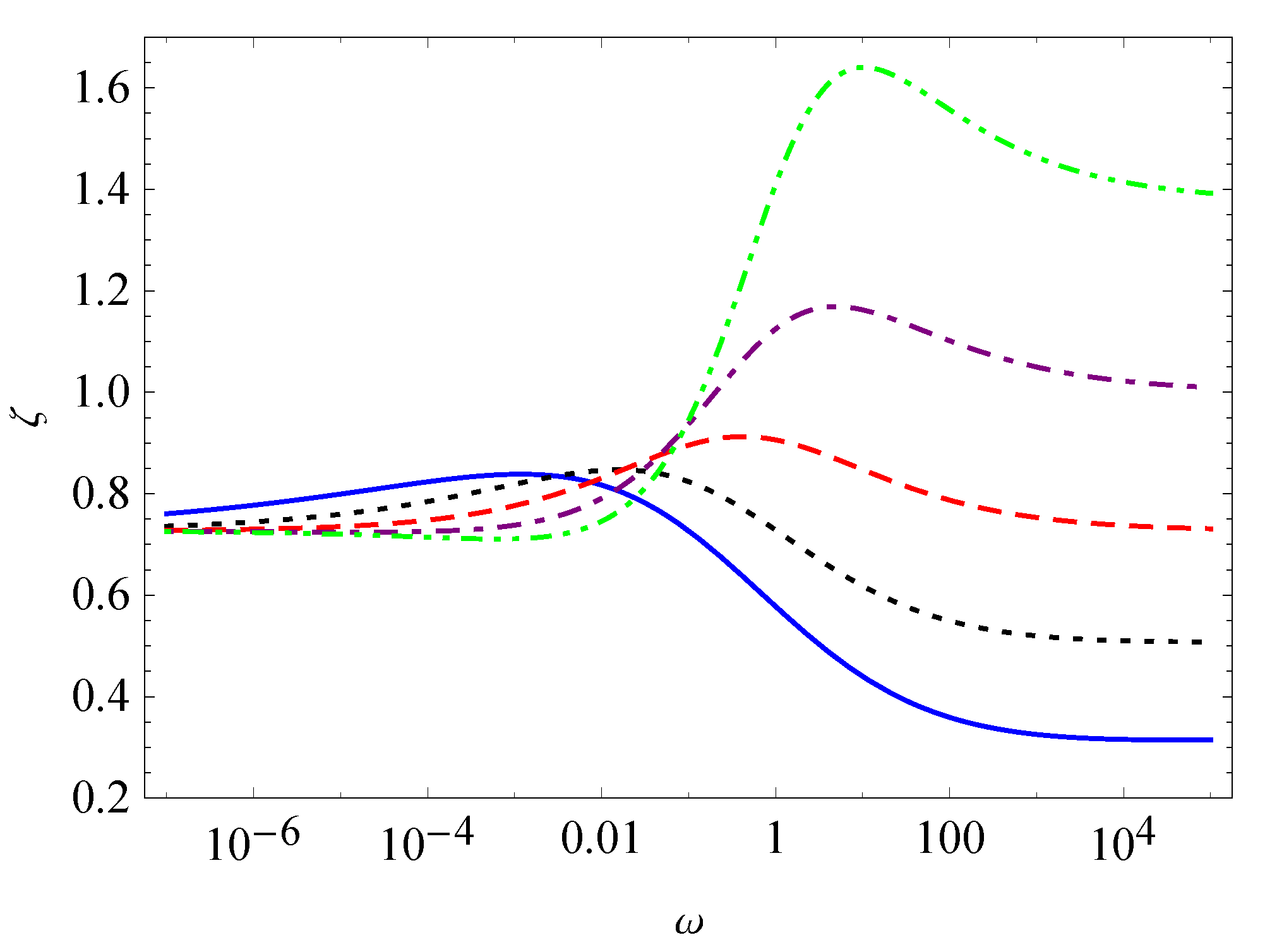
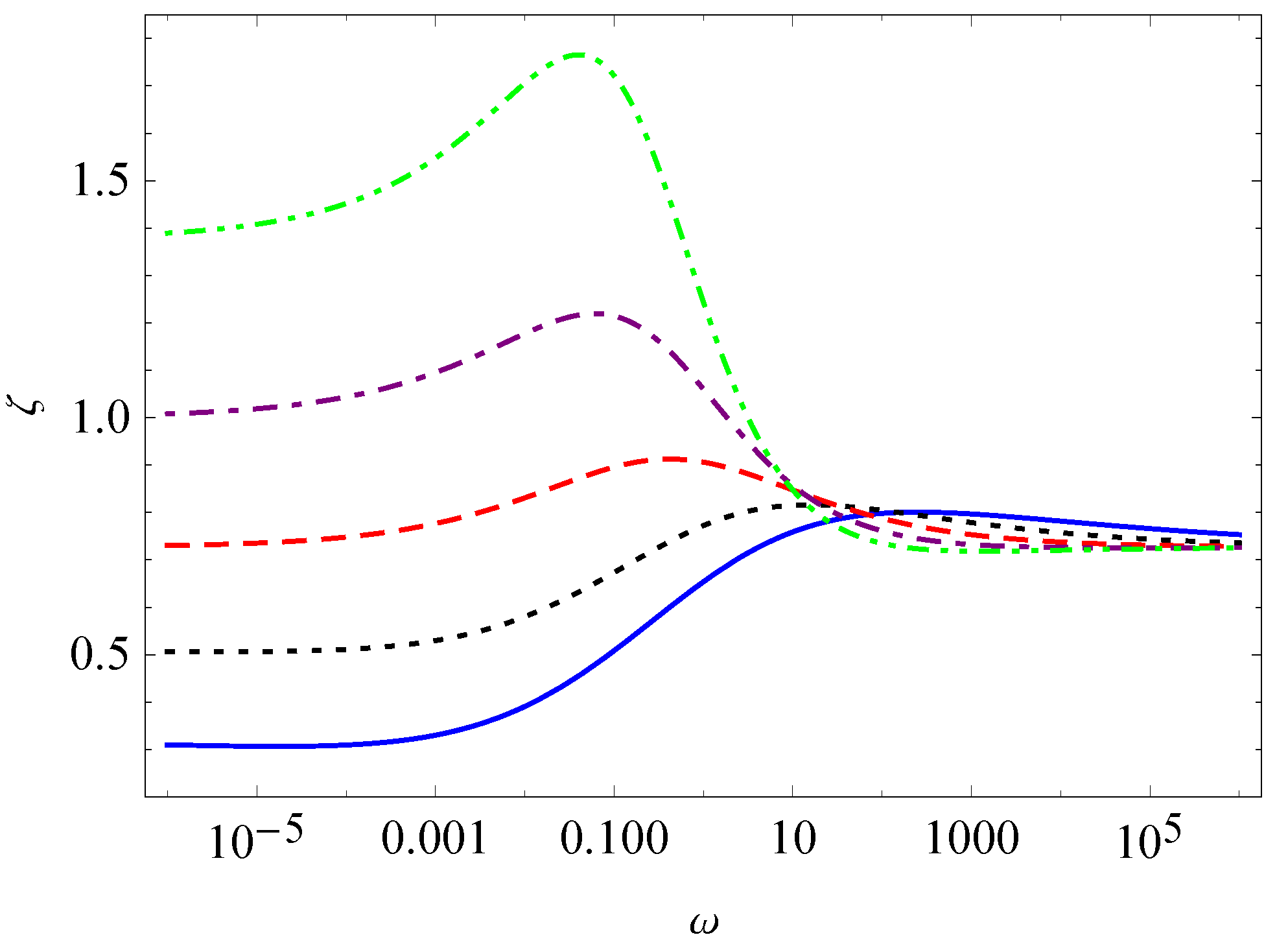
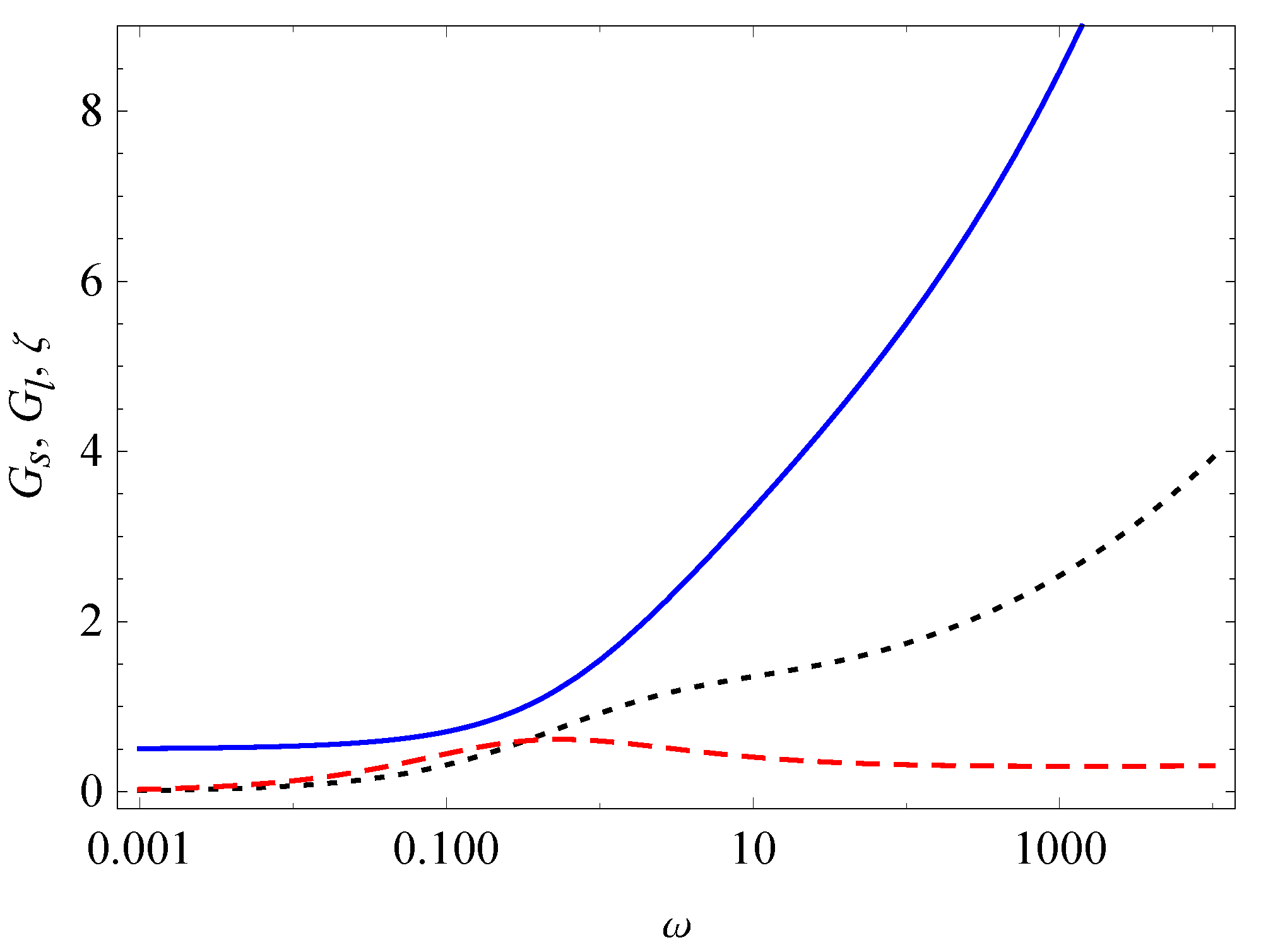
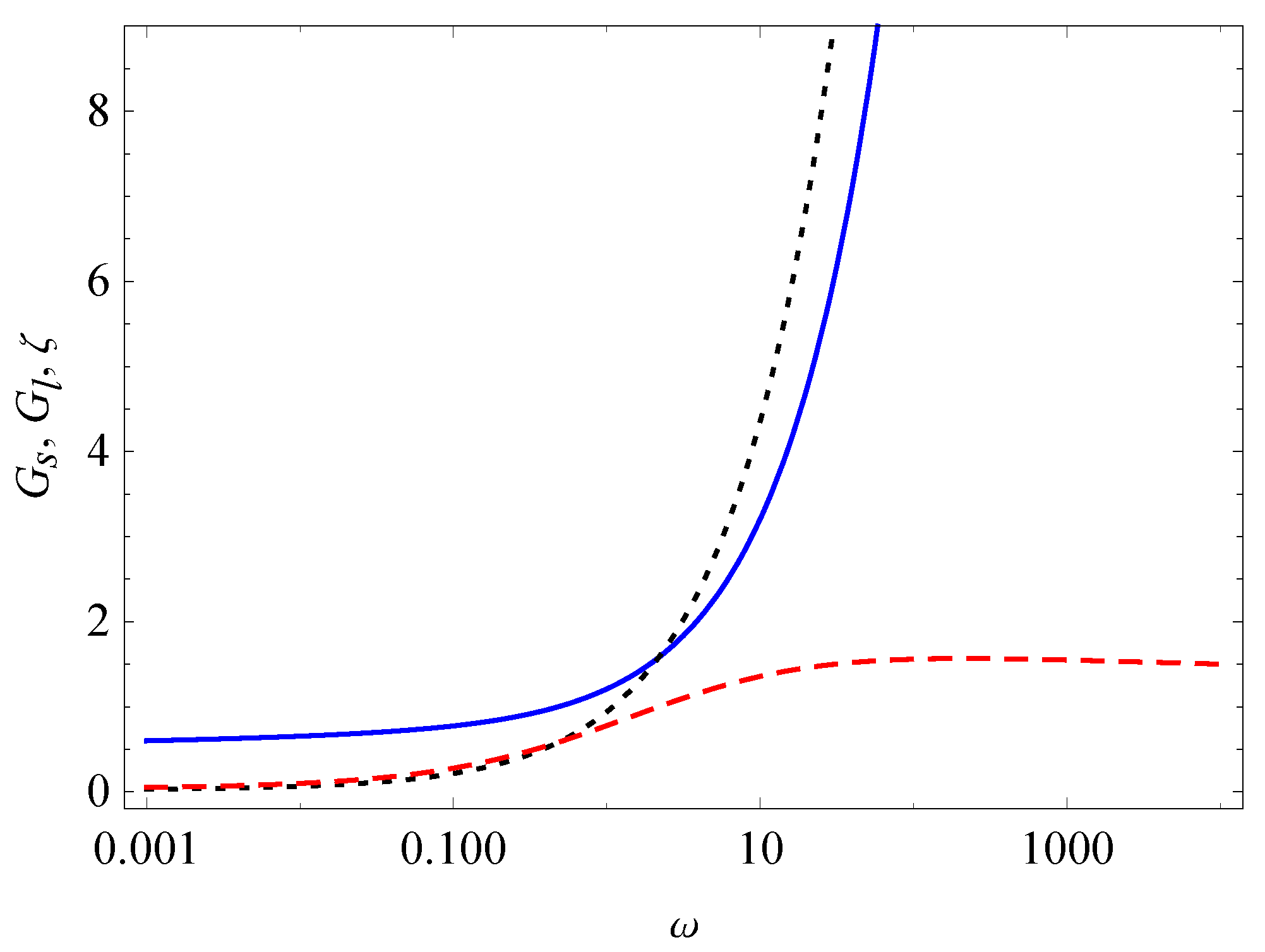
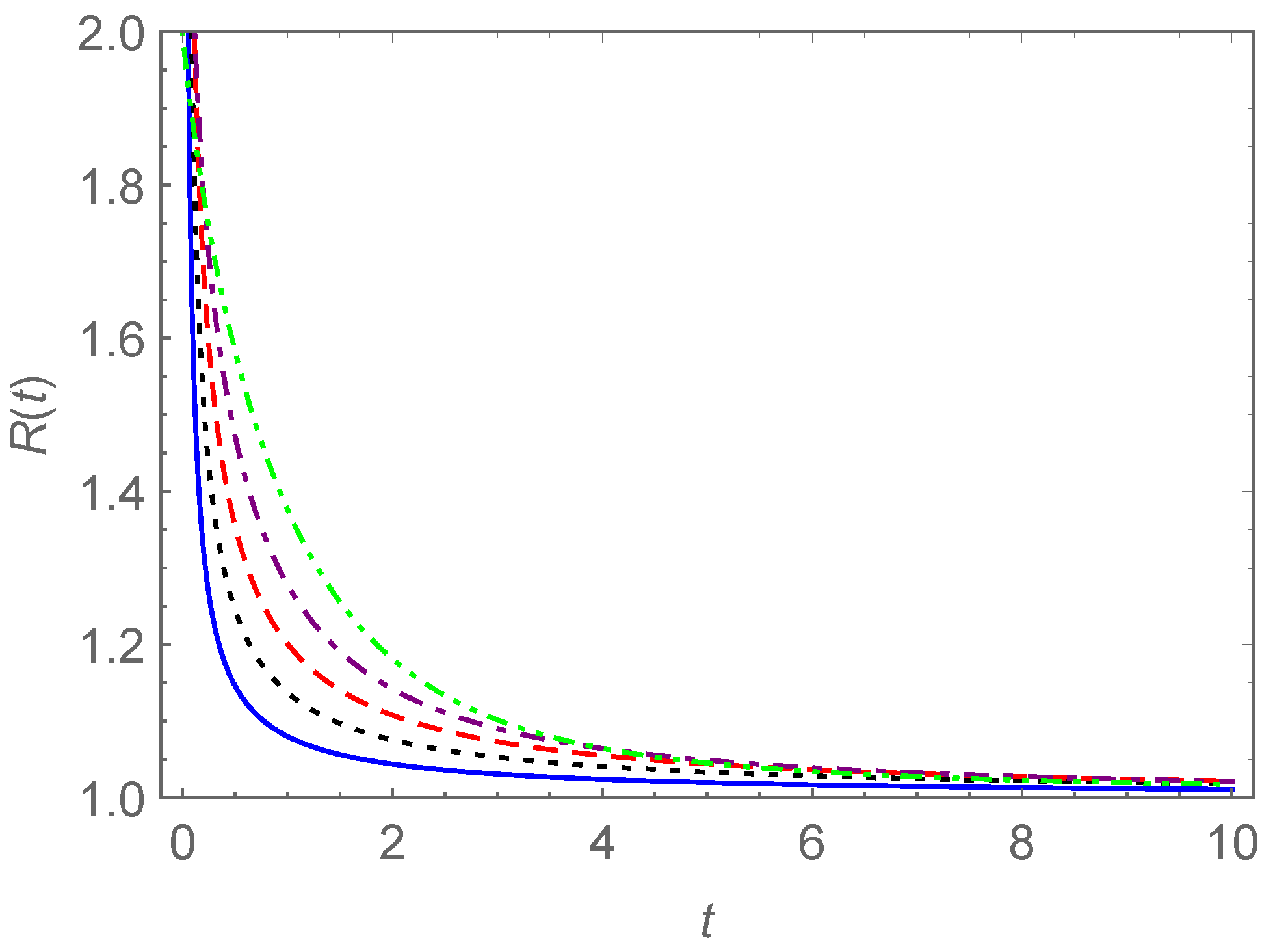
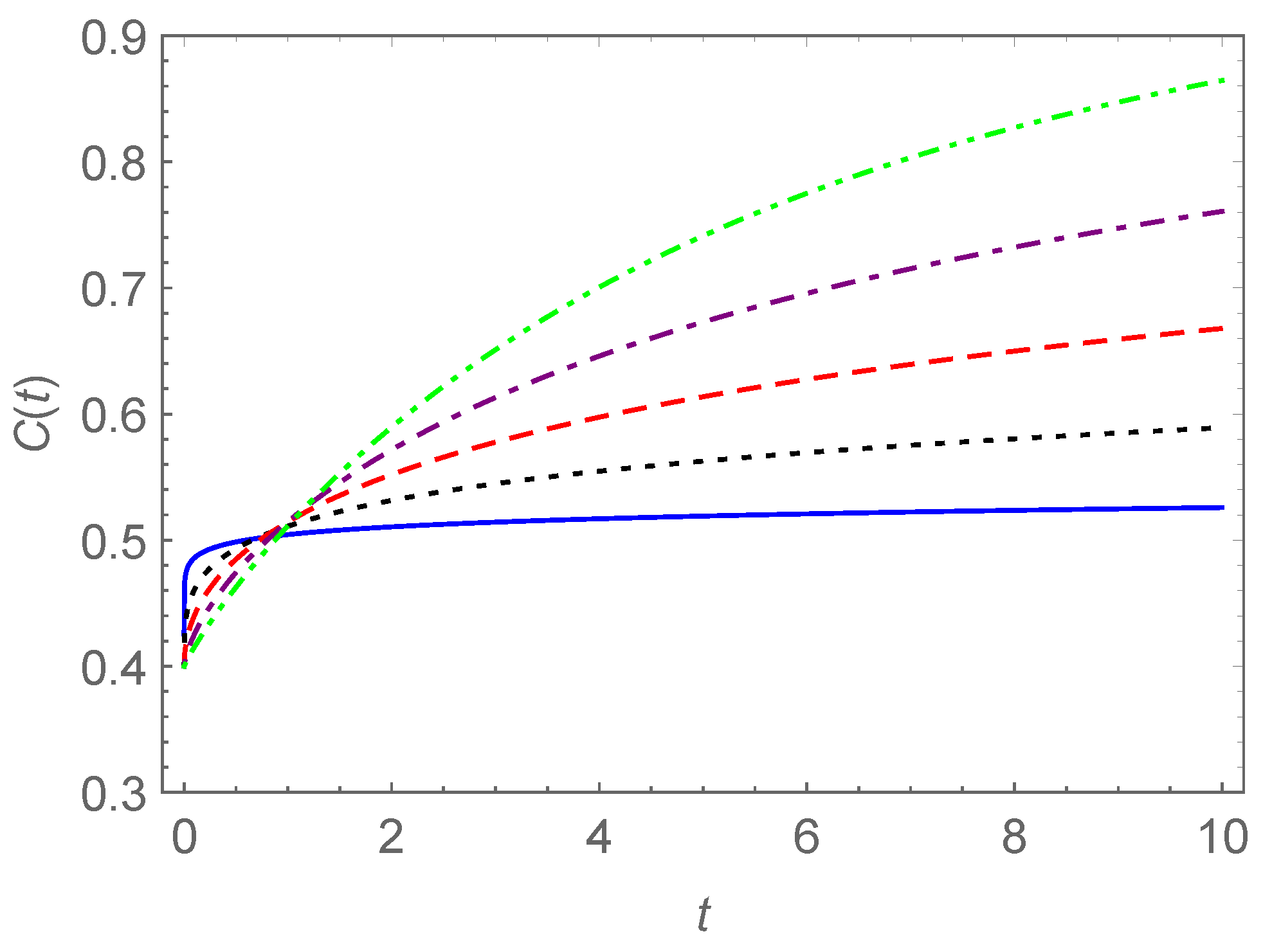
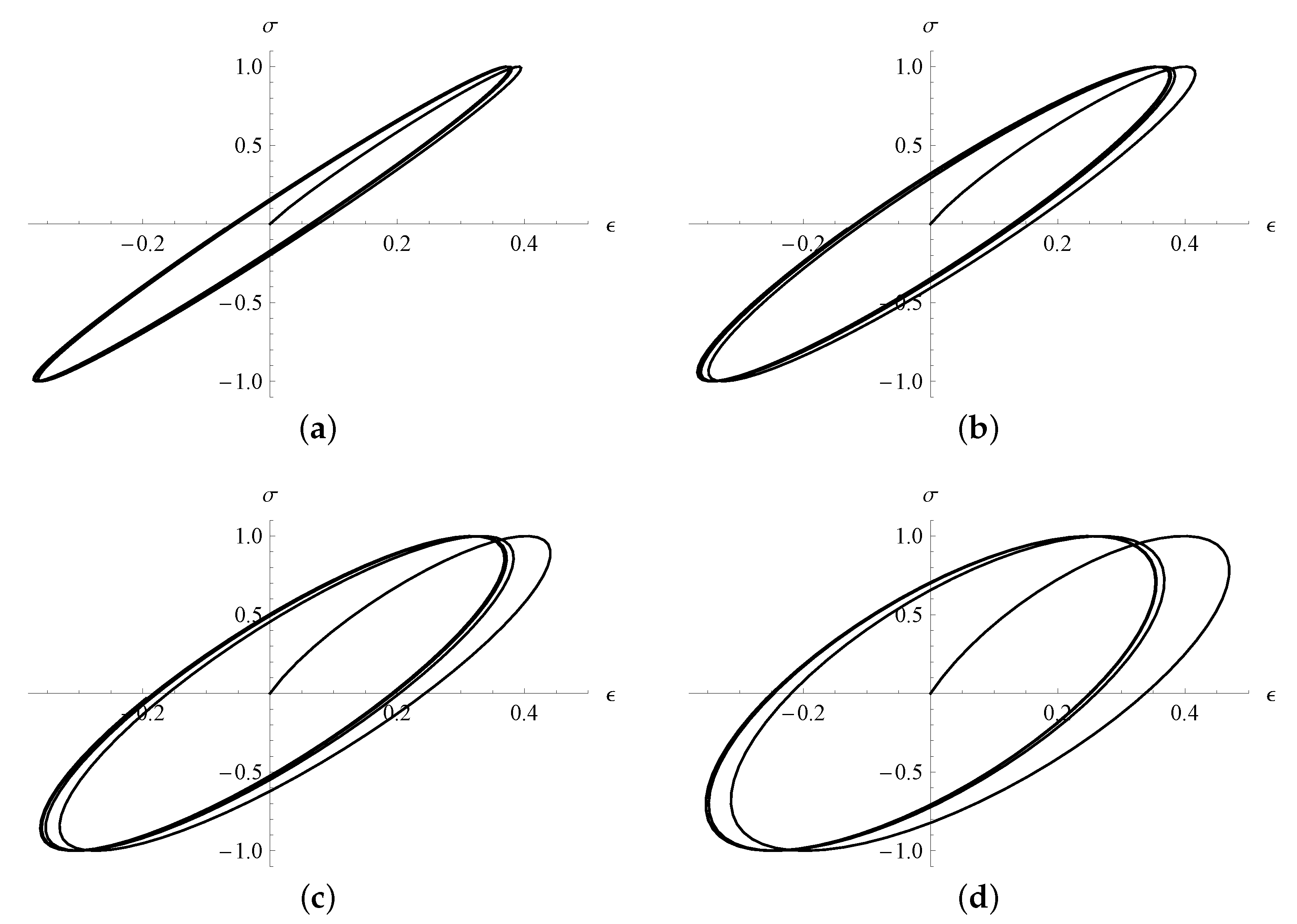
3. Relaxation, Creep, and Hysteresis
- Case I.
- Case II.
- and
- Case III.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Oldham, K.B.; Spanier, J. The Fractional Calculus; Academic: New York, NY, USA, 1974. [Google Scholar]
- Ross, B. (Ed.) Fractional Calculus and Its Applications (Lecture Notes in Mathematics 457); Springer: Berlin/Heidelberg, Germany, 1975. [Google Scholar]
- Gorenflo, R.; Vessella, S. Abel Integral Equations; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Kiryakova, V. Generalized Fractional Calculus and Applications (Pitman Res. Notes in Math. Ser., Vol. 301); Longman Scientific & Technical and John Wiley & Sons, Inc.: Harlow, UK; New York, NY, USA, 1994. [Google Scholar]
- Carpinteri, A.; Mainardi, F. (Eds.) Fractals and Fractional Calculus in Continuum Mechanics; Springer: Wien, Austria; New York, NY, USA, 1997. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic: San Diego, CA, USA, 1999. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity; Imperial College: London, UK, 2010. [Google Scholar]
- Diethelm, K. The Analysis of Fractional Differential Equations; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Monje, C.A.; Chen, Y.Q.; Vinagre, B.M.; Xue, D.; Feliu, V. Fractional-Order Systems and Controls, Fundamentals and Applications; Springer: London, UK, 2010. [Google Scholar]
- Klafter, J.; Lim, S.C.; Metzler, R. (Eds.) Fractional Dynamics: Recent Advances; World Scientific: Singapore, 2011. [Google Scholar]
- Băleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus Models and Numerical Methods. Series on Complexity, Nonlinearity and Chaos; World Scientific: Boston, MA, USA, 2012. [Google Scholar]
- Jiao, Z.; Chen, Y.; Podlubny, I. Distributed-Order Dynamic Systems–Stability, Simulation, Applications and Perspectives; Springer: London, UK, 2012. [Google Scholar]
- Li, C.; Zeng, F. Numerical Methods for Fractional Calculus; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Scott-Blair, G.W. The role of psychophysics in rheology. J. Colloid Sci. 1947, 2, 21–32. [Google Scholar] [CrossRef]
- Tan, W.; Xu, M. Plane surface suddenly set in motion in a viscoelastic fluid with fractional Maxwell model. Acta Mech. Sin. 2002, 18, 342–349. [Google Scholar]
- Yang, P.; Lam, Y.C.; Zhu, K.Q. Constitutive equation with fractional derivatives for the generalized UCM model. J. Non-Newton. Fluid Mech. 2010, 165, 88–97. [Google Scholar] [CrossRef]
- Wang, X.; Xu, H.; Qi, H. Numerical analysis for rotating electro-osmotic flow of fractional Maxwell fluids. Appl. Math. Lett. 2020, 103, No. 106179. [Google Scholar] [CrossRef]
- Gerasimov, A.N. A generalization of linear laws of deformation and its application to inner friction problems. Prikl. Mat. Mekh. 1948, 12, 251–259. [Google Scholar]
- Koeller, R.C. Applications of fractional calculus to the theory of viscoelasticity. J. Appl. Mech. 1984, 51, 299–307. [Google Scholar] [CrossRef]
- Koeller, R.C. Polynomial operators, Stieltjes convolution, and fractional calculus in hereditary mechanics. Acta Mech. 1986, 58, 251–264. [Google Scholar] [CrossRef]
- Schiessel, H.; Metzler, R.; Blumen, A.; Nonnenmacher, T.F. Generalized viscoelastic models: Their fractional equations with solutions. J. Phys. A Math. Gen. 1995, 28, 6567–6584. [Google Scholar] [CrossRef]
- Nigmatullin, R.R. The realization of the generalized transfer equation in a medium with fractal geometry. Phys. Stat. Sol. B 1986, 133, 425–430. [Google Scholar] [CrossRef]
- Schneider, W.R.; Wyss, W. Fractional diffusion and wave equations. J. Math. Phys. 1989, 30, 134–144. [Google Scholar] [CrossRef]
- Metzler, R.; Glockle, W.G.; Nonnenmacher, T.F. Fractional model equation for anomalous diffusion. Physica A 1994, 211, 13–24. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Duan, J.S.; Xu, M.Y. Concentration distribution of fractional anomalous diffusion caused by an instantaneous point source. Appl. Math. Mech. (Engl. Ed.) 2003, 24, 1302–1308. [Google Scholar]
- Jiang, X.; Xu, M.; Qi, H. The fractional diffusion model with an absorption term and modified Fick’s law for non-local transport processes. Nonlinear Anal. Real World Appl. 2010, 11, 262–269. [Google Scholar] [CrossRef]
- Qi, H.; Jiang, X. Solutions of the space-time fractional Cattaneo diffusion equation. Physica A 2011, 390, 1876–1883. [Google Scholar] [CrossRef]
- Bagley, R.L.; Calico, R.A. Fractional order state equations for the control of viscoelastically damped structures. J. Guid. Control Dyn. 1991, 14, 304–311. [Google Scholar] [CrossRef]
- Makroglou, A.; Miller, R.K.; Skaar, S. Computational results for a feedback control for a rotating viscoelastic beam. J. Guid. Control Dyn. 1994, 17, 84–90. [Google Scholar] [CrossRef]
- Chen, Y.; Moore, K.L. Analytical stability bound for a class of delayed fractional-order dynamic systems. Nonlinear Dyn. 2002, 29, 191–200. [Google Scholar] [CrossRef]
- Chen, Y.Q.; Xue, D.; Dou, H. Fractional calculus and biomimetic control. In Proceedings of the 2004 IEEE International Conference on Robotics and Biomimetics, Shengyang, China, 22–25 August 2004; pp. 901–906. [Google Scholar]
- Li, Y.; Chen, Y.Q.; Podlubny, I. Mittag-Leffler stability of fractional order nonlinear dynamic systems. Automatica 2009, 45, 1965–1969. [Google Scholar] [CrossRef]
- Ding, C.; Cao, J.; Chen, Y.Q. Fractional-order model and experimental verification for broadband hysteresis in piezoelectric actuators. Nonlinear Dyn. 2019, 98, 3143–3153. [Google Scholar] [CrossRef]
- Sokolov, I.M.; Klafter, J.; Blumen, A. Fractional kinetics. Phys. Today 2002, 55, 48–54. [Google Scholar] [CrossRef]
- Li, C.P.; Deng, W.H.; Xu, D. Chaos synchronization of the Chua system with a fractional order. Physica A 2006, 360, 171–185. [Google Scholar] [CrossRef]
- Wang, Z.H.; Hu, H.Y. Stability of a linear oscillator with damping force of the fractional-order derivative. Sci. China Ser. G 2010, 53, 345–352. [Google Scholar] [CrossRef]
- Li, C.; Ma, Y. Fractional dynamical system and its linearization theorem. Nonlinear Dyn. 2013, 71, 621–633. [Google Scholar] [CrossRef]
- Wu, G.C.; Baleanu, D.; Xie, H.P.; Chen, F.L. Chaos synchronization of fractional chaotic maps based on the stability condition. Physica A 2016, 460, 374–383. [Google Scholar] [CrossRef]
- Scott-Blair, G.W. Analytical and integrative aspects of the stress-strain-time problem. J. Sci. Instrum. 1944, 21, 80–84. [Google Scholar] [CrossRef]
- Scott-Blair, G.W. Survey of General and Applied Rheology; Pitman: London, UK, 1949. [Google Scholar]
- Bland, D.R. The Theory of Linear Viscoelasticity; Pergamon: Oxford, UK, 1960. [Google Scholar]
- Bagley, R.L.; Torvik, P.J. A theoretical basis for the application of fractional calculus to viscoelasticity. J. Rheol. 1983, 27, 201–210. [Google Scholar] [CrossRef]
- Rogers, L. Operators and fractiorial derivatives for viscoelastic constituitive equations. J. Rheol. 1983, 27, 351–372. [Google Scholar] [CrossRef]
- Pritz, T. Analysis of four-parameter fractional derivative model of real solid materials. J. Sound Vib. 1996, 195, 103–115. [Google Scholar] [CrossRef]
- Mainardi, F.; Spada, G. Creep, relaxation and viscosity properties for basic fractional models in rheology. Eur. Phys. J. Spec. Top. 2011, 193, 133–160. [Google Scholar] [CrossRef]
- Atanacković, T.M.; Pilipović, S.; Stanković, B.; Zorica, D. Fractional Calculus with Applications in Mechanics; Wiley: New York, NY, USA, 2014. [Google Scholar]
- Duan, J.S.; Qiu, X. The periodic solution of Stokes’ second problem for viscoelastic fluids as characterized by a fractional constitutive equation. J. Non-Newton. Fluid Mech. 2014, 205, 11–15. [Google Scholar] [CrossRef]
- Lewandowski, R.; Chorazyczewski, B. Identification of the parameters of the Kelvin-Voigt and the Maxwell fractional models, used to modeling of viscoelastic dampers. Comput. Struct. 2010, 88, 1–17. [Google Scholar] [CrossRef]
- Friedrich, C. Mechanical stress relaxation in polymers: Fractional integral model versus fractional differential model. J. Non-Newton. Fluid Mech. 1993, 46, 307–314. [Google Scholar] [CrossRef]
- Pritz, T. Five-parameter fractional derivative model for polymeric dampling materials. J. Sound Vib. 2003, 265, 935–952. [Google Scholar] [CrossRef]
- Yang, S.M.; Duan, J.S. Response analysis of six-parameter fractional constitutive model. Phys. Scr. 2021, 96, 025220. [Google Scholar] [CrossRef]
- Colombaro, I.; Giusti, A.; Vitali, S. Storage and dissipation of energy in Prabhakar viscoelasticity. Mathematics 2018, 6, 15. [Google Scholar] [CrossRef]
- Caputo, M. Distributed order differential equations modelling dielectric induction and diffusion. Fract. Calc. Appl. Anal. 2001, 4, 421–442. [Google Scholar]
- Duan, J.S.; Chen, Y.Q. Mechanical response and simulation for constitutive equations with distributed order derivatives. Int. J. Model. Simul. Sci. Comput. 2017, 8, 1750040. [Google Scholar] [CrossRef]
- Duan, J.S.; Qiu, X. Stokes’ second problem of viscoelastic fluids with constitutive equation of distributed-order derivative. Appl. Math. Comput. 2018, 331, 130–139. [Google Scholar] [CrossRef]
- Duan, J.S.; Chen, L. Oscillatory shear flow between two parallel plates for viscoelastic constitutive model of distributed-order derivative. Int. J. Numer. Methods Heat Fluid Flow 2020, 30, 1137–1148. [Google Scholar] [CrossRef]
- Mainardi, F.; Gorenflo, R. On Mittag-Leffler-type functions in fractional evolution processes. J. Comput. Appl. Math. 2000, 118, 283–299. [Google Scholar] [CrossRef]
- Gorenflo, R.; Kilbas, A.A.; Mainardi, F.; Rogosin, S. Mittag-Leffler Functions, Related Topics and Applications, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Deng, L.; Seethaler, R.J.; Chen, Y.Q.; Yang, P.; Cheng, Q. Modified Elman neural network based neural adaptive inverse control of rate-dependent hysteresis. In Proceedings of the 2016 International Joint Conference on Neural Networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016; pp. 2366–2373. [Google Scholar]
- Li, Z.; Zeng, J.; Chen, Y.; Ma, G.; Liu, G. Adaptive control of a piezo-positioning mechanism with hysteresis and input saturation using time delay estimation. IEEE Access 2020, 8, 176062–176072. [Google Scholar] [CrossRef]
- Pei, J.S.; Carboni, B.; Lacarbonara, W. Mem-models as building blocks for simulation and identification of hysteretic systems. Nonlinear Dyn. 2020, 100, 973–998. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P.J. On the fractional calculus model of viscoelastic behavior. J. Rheol. 1986, 30, 133–155. [Google Scholar] [CrossRef]
- Palade, L.I.; Verney, V.; Attané, P. A modified fractional model to describe the entire viscoelastic behavior of polybutadienes from flow to glassy regime. Rheol. Acta 1996, 35, 265–273. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, J.-S.; Hu, D.-C.; Chen, Y.-Q. Simultaneous Characterization of Relaxation, Creep, Dissipation, and Hysteresis by Fractional-Order Constitutive Models. Fractal Fract. 2021, 5, 36. https://doi.org/10.3390/fractalfract5020036
Duan J-S, Hu D-C, Chen Y-Q. Simultaneous Characterization of Relaxation, Creep, Dissipation, and Hysteresis by Fractional-Order Constitutive Models. Fractal and Fractional. 2021; 5(2):36. https://doi.org/10.3390/fractalfract5020036
Chicago/Turabian StyleDuan, Jun-Sheng, Di-Chen Hu, and Yang-Quan Chen. 2021. "Simultaneous Characterization of Relaxation, Creep, Dissipation, and Hysteresis by Fractional-Order Constitutive Models" Fractal and Fractional 5, no. 2: 36. https://doi.org/10.3390/fractalfract5020036
APA StyleDuan, J.-S., Hu, D.-C., & Chen, Y.-Q. (2021). Simultaneous Characterization of Relaxation, Creep, Dissipation, and Hysteresis by Fractional-Order Constitutive Models. Fractal and Fractional, 5(2), 36. https://doi.org/10.3390/fractalfract5020036







