Generalized Cauchy Process: Difference Iterative Forecasting Model
Abstract
1. Introduction
2. GC Process: Properties
2.1. Preliminary Knowledge
2.2. GC Process
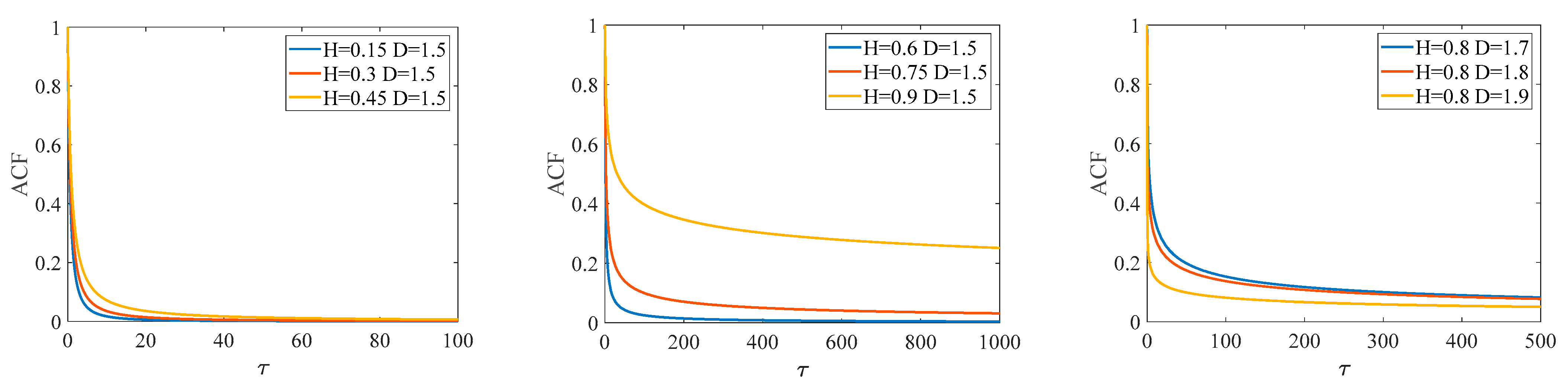
2.2.1. The LRD Characteristics of the GC Process
2.2.2. Self-Similarity Properties of the GC Process
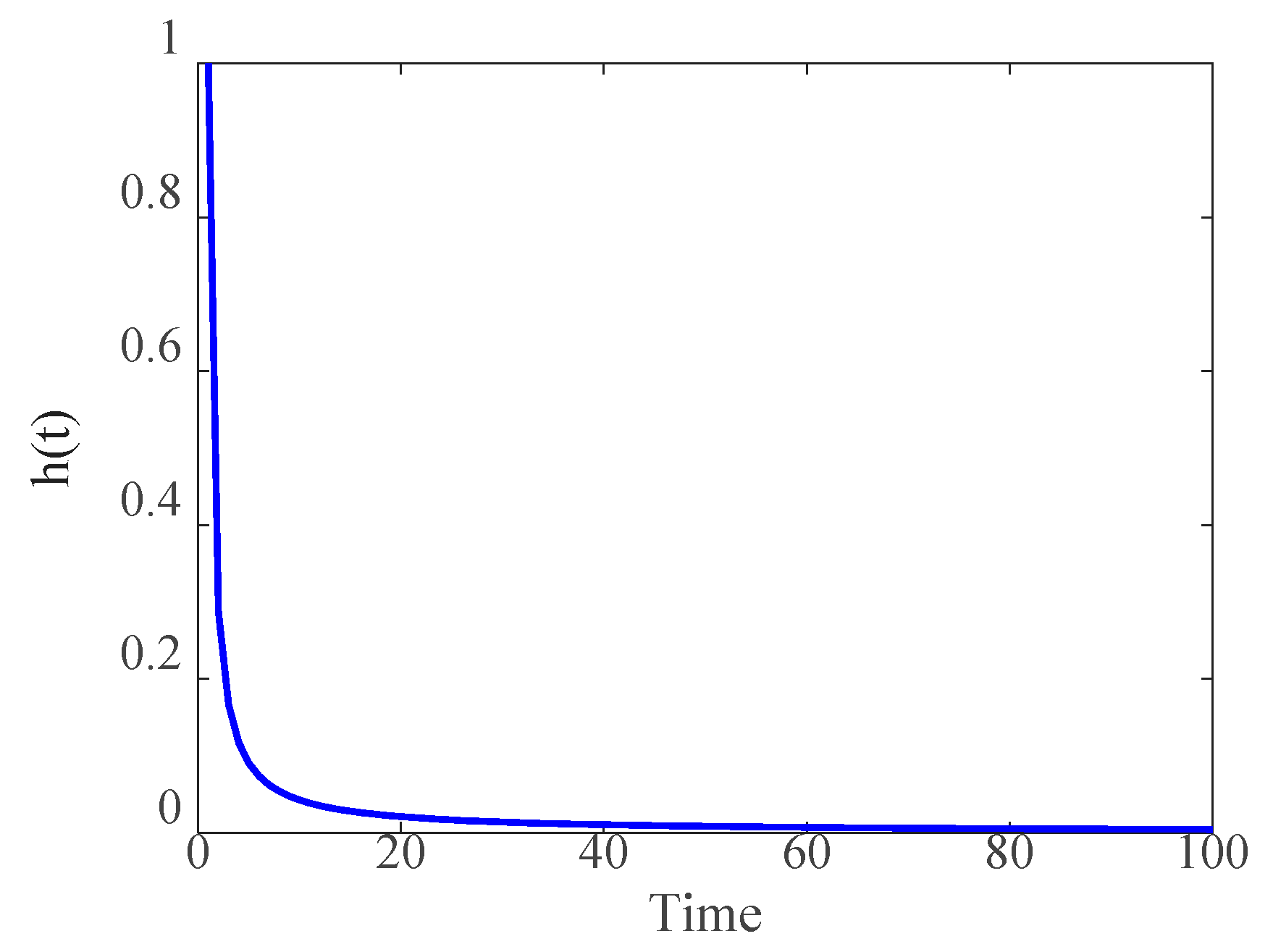
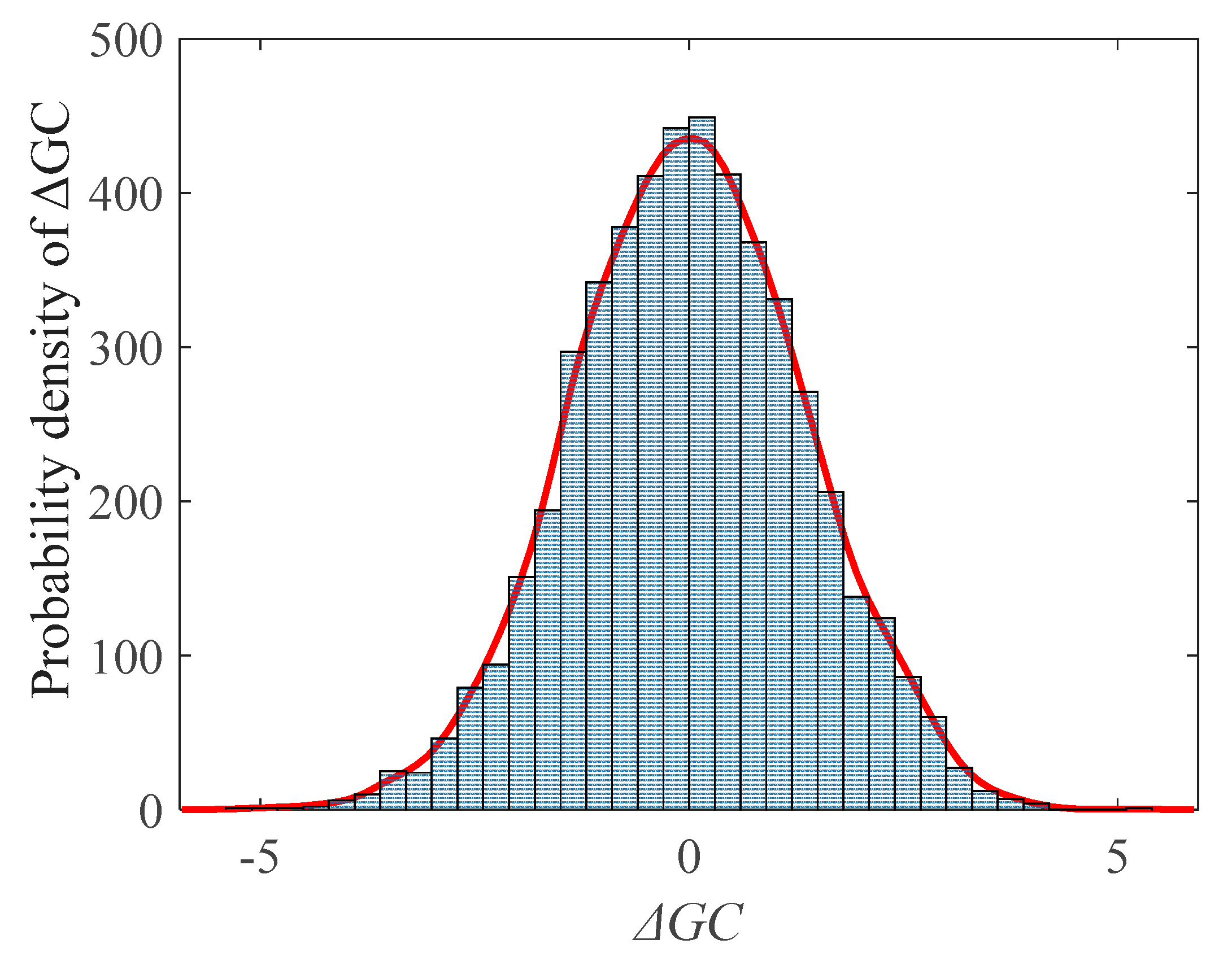
2.3. The Generation of the GC Sequence
3. The Difference Iterative Forecasting Model Based on the GC Process
4. Parameter Estimation of Difference Iterative Forecasting Model
4.1. Estimated Hurst Parameter H
4.2. Estimated Fractal Dimension D
4.3. Estimated Drift and Diffusion Coefficients
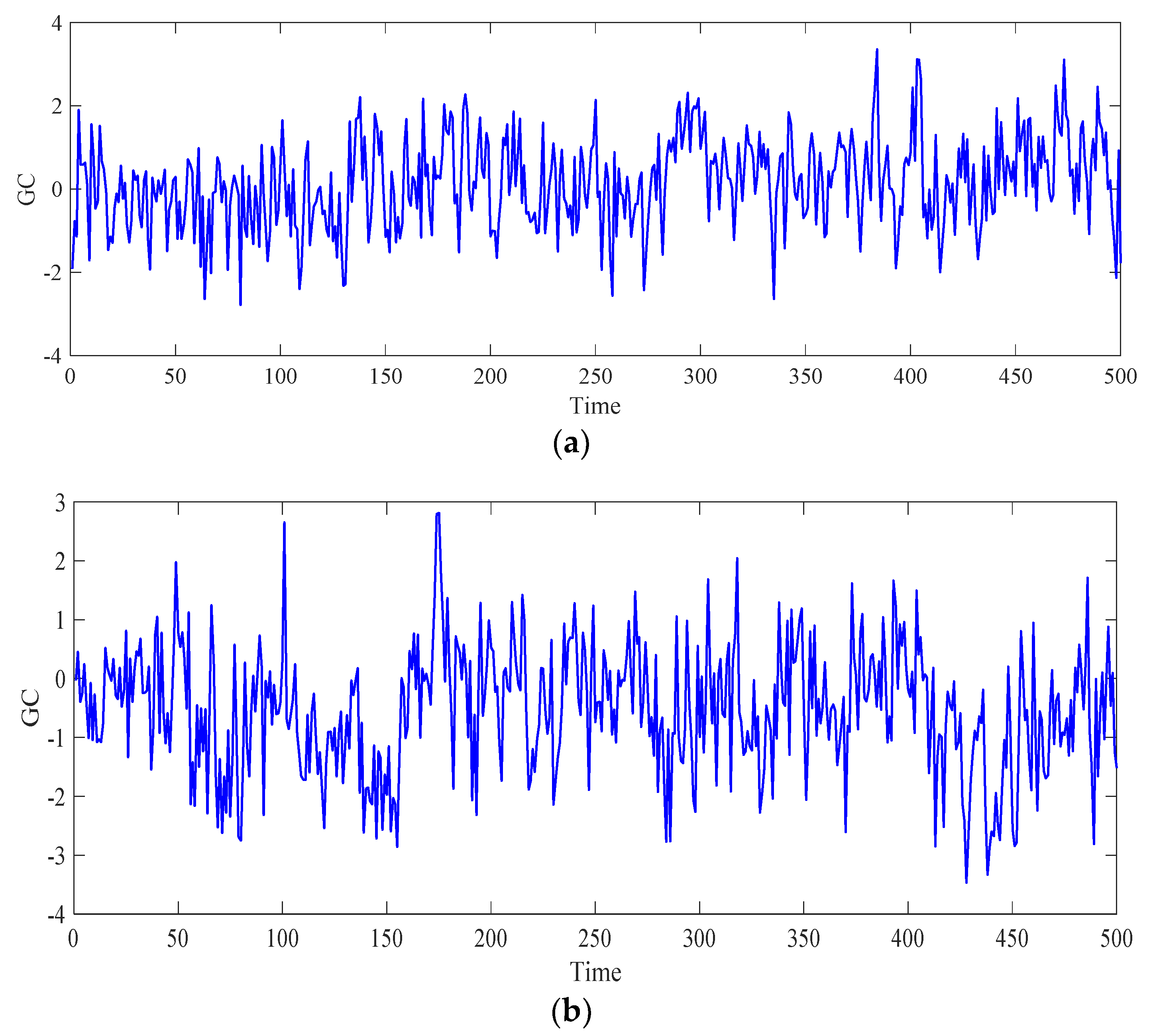
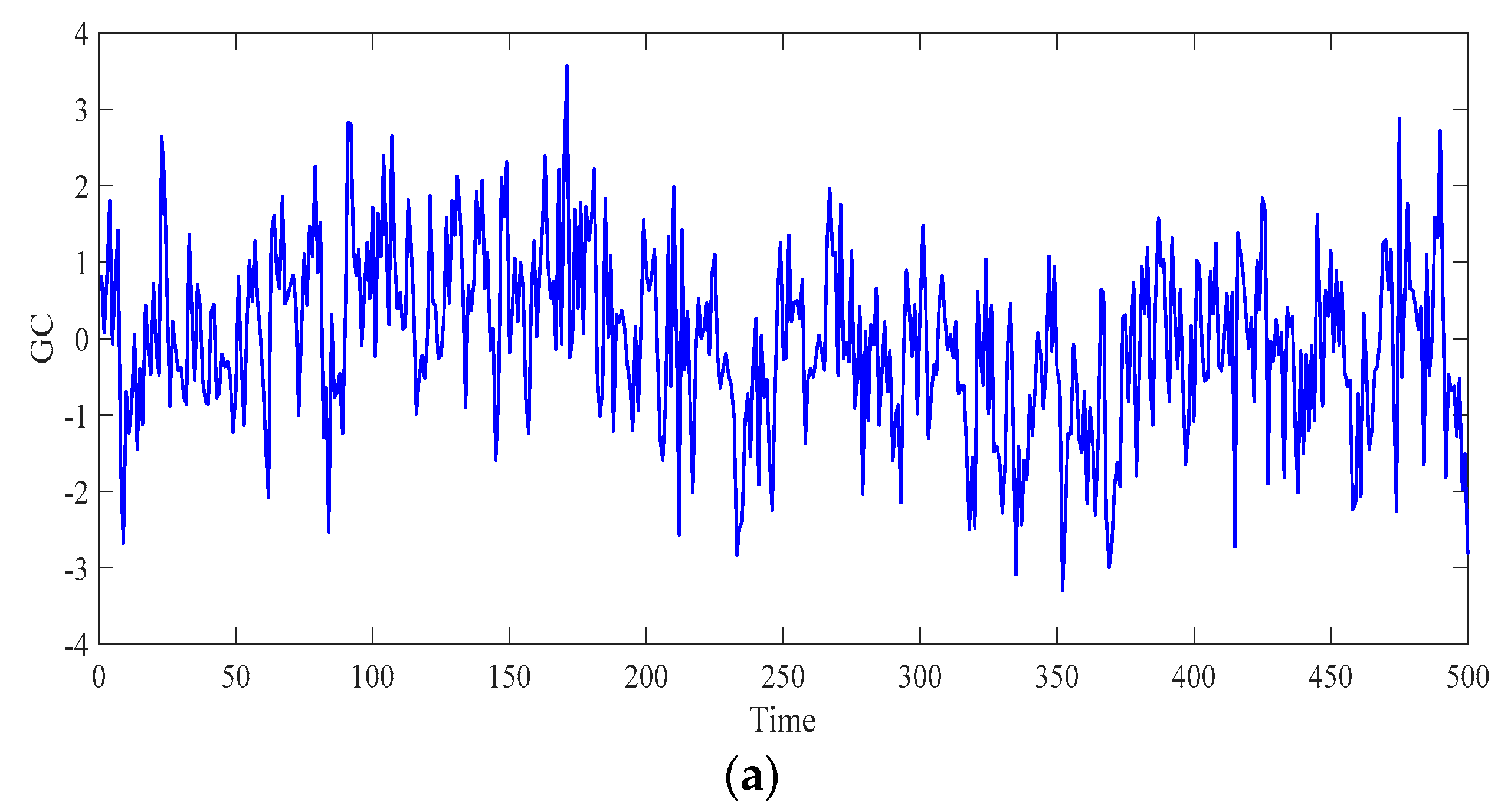
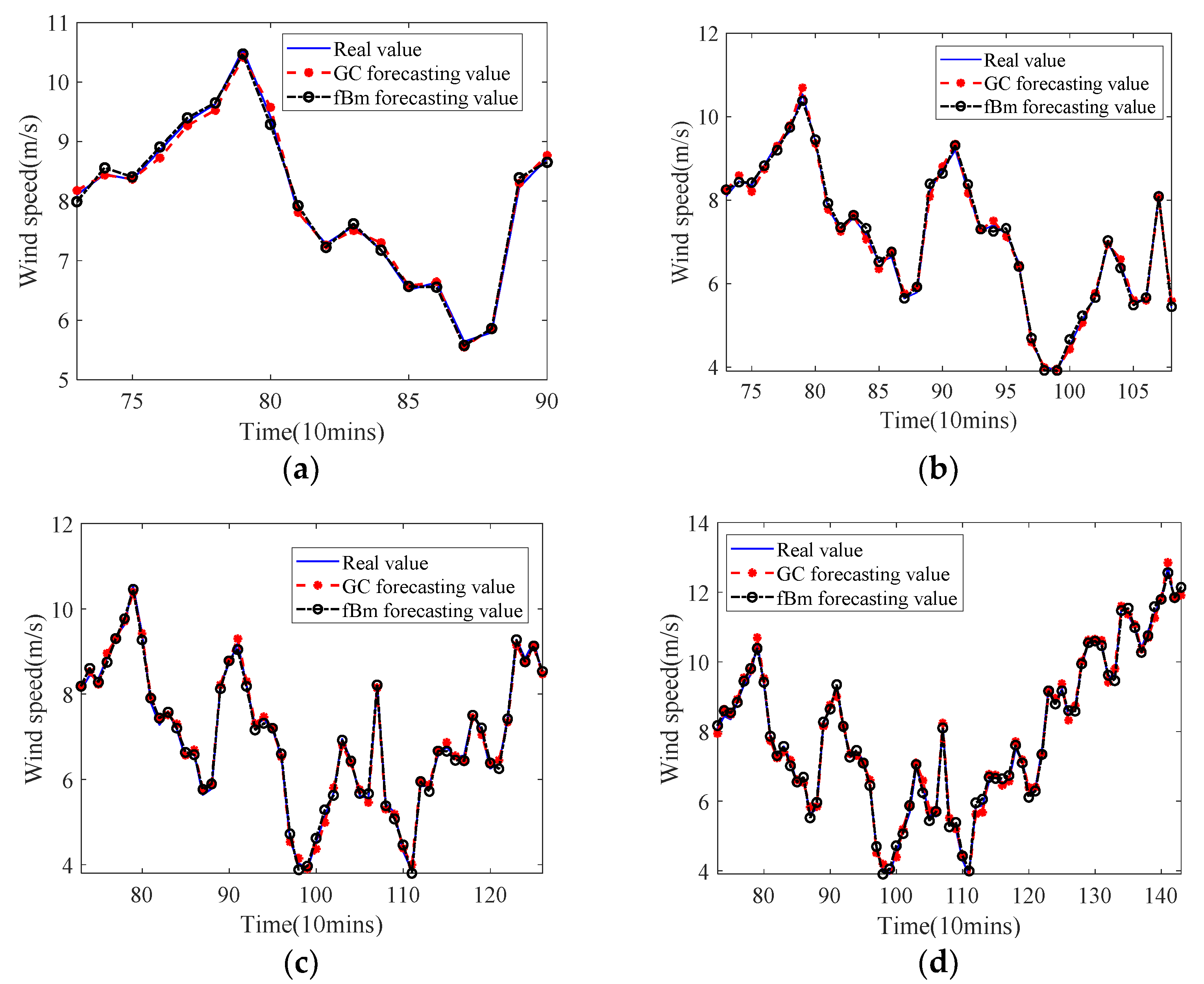
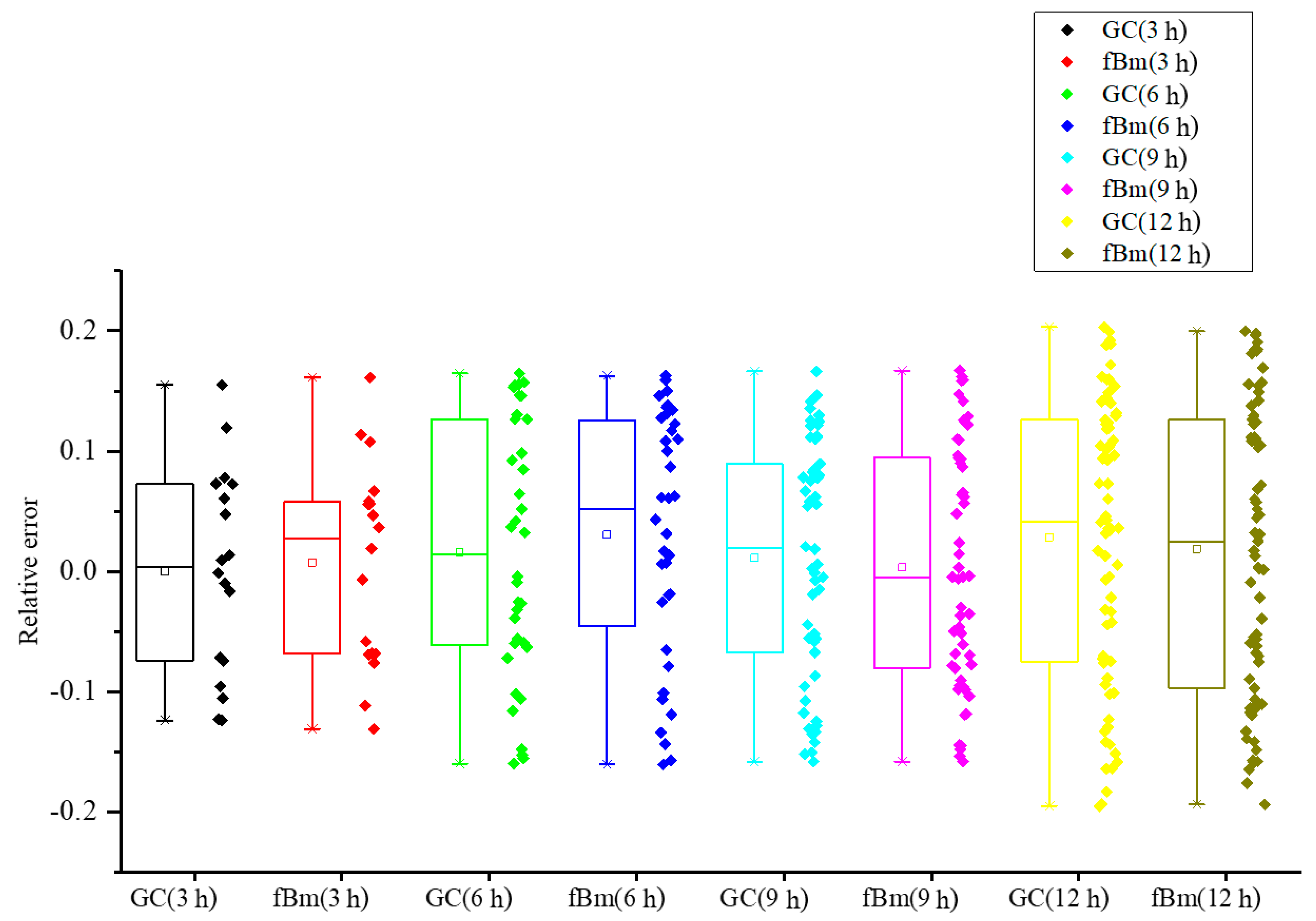
5. Case Study
6. Conclusions
- The properties of the Hurst parameter and fractal dimension of the generalized Cauchy process are analyzed by the ACF, which describes the global and local properties of stochastic sequences, that is, long-range dependent characteristics and local irregularities, respectively;
- The simulation sequence of the generalized Cauchy process is generated by the white noise through the impulse function, and the incremental distribution of the generalized Cauchy process is obtained by statistical reasoning;
- The Ito process of the generalized Cauchy process is derived through the fractional Black–Schole model; then, the difference iterative forecasting model is established;
- The analysis of the relative error of forecasting results obtained in the wind speed case study considered that the difference iterative forecasting model based on the generalized Cauchy process has good forecasting performance.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Konar, A.; Bhattacharya, D. Time-Series Prediction and Applications. In Intelligent Systems Reference Library; Springer Nature Switzerland AG: Cham, Switzerland, 2017; Volume 127. [Google Scholar]
- Fontes, X.; Silva, D. Hybrid Approaches for Time Series Prediction. In Hybrid Intelligent Systems. HIS 2018. Advances in Intelligent Systems and Computing; Springer: Cham, Switzerland, 2018; Volume 923, pp. 146–155. [Google Scholar]
- Safari, N.; Chung, C.Y.; Price, G.C.D. Novel Multi-Step Short-Term Wind Power Prediction Framework Based on Chaotic Time Series Analysis and Singular Spectrum Analysis. IEEE Trans. Power Syst. 2018, 33, 590–601. [Google Scholar] [CrossRef]
- Song, W.; Li, M.; Liang, J.-K. Prediction of Bearing Fault Using Fractional Brownian Motion and Minimum Entropy Deconvolution. Entropy 2016, 18, 418. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, Y.; Kong, C.; Chen, B. A new prediction method based on VMD-PRBF-ARMA-E model considering wind speed characteristic. Energy Convers. Manag. 2020, 203, 112254. [Google Scholar] [CrossRef]
- Xu, W.; Peng, H.; Zeng, X.; Zhou, F.; Tian, X.; Peng, X. Deep belief network-based AR model for nonlinear time series forecasting. Appl. Soft Comput. 2019, 77, 605–621. [Google Scholar] [CrossRef]
- Yang, X.; Fang, Z.; Yang, Y.; Mba, D.; Li, X. A novel multi-information fusion grey model and its application in wear trend prediction of wind turbines. Appl. Math. Model. 2019, 71, 543–557. [Google Scholar] [CrossRef]
- Ding, S.; Hipel, K.W.; Dang, Y.-G. Forecasting China’s electricity consumption using a new grey prediction model. Energy 2018, 149, 314–328. [Google Scholar] [CrossRef]
- Kayacan, E.; Ulutas, B.; Kaynak, O. Grey System Theory-Based Models in Time Series Prediction. Expert Syst. Appl. 2010, 37, 1784–1789. [Google Scholar] [CrossRef]
- Wang, X.; Balakrishnan, N.; Guo, B. Residual life estimation based on a generalized Wiener degradation process. Reliab. Eng. Syst. Saf. 2014, 124, 13–23. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhu, H.; Hu, K.; Wu, J.; Shao, X.; Wang, Y. Reliability prediction of machinery with multiple degradation characteristics using double-Wiener process and Monte Carlo algorithm. Mech. Syst. Signal Process. 2019, 134, 106333. [Google Scholar] [CrossRef]
- Sheng, L.; Cheng, W.; Xia, H.; Wu, X.; Zhang, X. Prediction of annual precipitation based on fuzzy and grey Markov process. In Proceedings of the 2010 International Conference on Machine Learning and Cybernetics, Qingdao, China, 11–14 July 2010; Volume 3, pp. 1136–1140. [Google Scholar]
- Manoj, J. Application of Markov Process for Prediction of Stock Market Performance. Int. J. Recent Technol. Eng. 2020, 8, 2277–3878. [Google Scholar]
- Zaki, J.F.; Ali-Eldin, A.; Hussein, S.E.; Saraya, S.F.; Areed, F.F. Traffic congestion prediction based on Hidden Markov Models and contrast measure. Ain Shams Eng. J. 2019, 11, 535–551. [Google Scholar] [CrossRef]
- Feng, Z.K.; Niu, W.J.; Tang, Z.Y.; Jiang, Z.Q.; Xu, Y.; Liu, Y.; Zhang, H.R. Monthly runoff time series prediction by variational mode decomposition and support vector machine based on quantum-behaved particle swarm optimization. J. Hydrol. 2020, 583, 124627. [Google Scholar] [CrossRef]
- Li, C.; Lin, S.; Xu, F.; Liu, D.; Liu, J. Short-term wind power prediction based on data mining technology and improved support vector machine method: A case study in Northwest China. J. Clean. Prod. 2018, 205, 909–922. [Google Scholar] [CrossRef]
- Han, M.; Zhong, K.; Qiu, T.; Han, B. Interval Type-2 Fuzzy Neural Networks for Chaotic Time Series Prediction: A Concise Overview. IEEE Trans. Cybern. 2018, 49, 2720–2731. [Google Scholar] [CrossRef]
- Ho, D.T.; Garibaldi, J.M. Context-Dependent Fuzzy Systems with Application to Time-Series Prediction. IEEE Trans. Fuzzy Syst. 2014, 22, 778–790. [Google Scholar] [CrossRef]
- Quan, H.; Srinivasan, D.; Khosravi, A. Short-Term Load and Wind Power Forecasting Using Neural Network-Based Prediction Intervals. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 303–315. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, B.; Zhao, Y.; Pan, G. Wind Speed Prediction of IPSO-BP Neural Network Based on Lorenz Disturbance. IEEE Access 2018, 6, 53168–53179. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; van Ness, J.W. Fractional Brownian Motions, Fractional Noises and Applications. SIAM Rev. 1968, 10, 422–437. [Google Scholar] [CrossRef]
- Samorodnitsky, G.; Taqqu, M. Stable Non-Gaussian Random Processes: Stochastic Models with Infinite Variance. J. Am. Stat. Assoc. 1996, 90, 123–138. [Google Scholar]
- Li, M. Fractal Time Series—A Tutorial Review. Math. Probl. Eng. 2010, 2010, 1–26. [Google Scholar] [CrossRef]
- Sottinen, T.; Viitasaari, L. Prediction Law of fractional Brownian Motion. Stat. Probab. Lett. 2017, 129, 155–166. [Google Scholar] [CrossRef]
- Li, Q.; Liang, S.; Yang, J.; Li, B. Long Range Dependence Prognostics for Bearing Vibration Intensity Chaotic Time Series. Entropy 2016, 18, 23. [Google Scholar] [CrossRef]
- Liu, H.; Song, W.; Li, M.; Kudreyko, A.; Zio, E. Fractional Levy stable motion: Finite difference iterative forecasting model. Chaos Solitons Fract. 2020, 133, 109632. [Google Scholar] [CrossRef]
- Li, M.; Jia-Yue, L. On the Predictability of Long-Range Dependent Series. Math. Probl. Eng. 2010, 2010, 1–9. [Google Scholar] [CrossRef]
- Song, W.; Li, M.; Li, Y.; Cattani, C.; Chi, C.-H. Fractional Brownian motion: Difference iterative forecasting models. Chaos Solitons Fract. 2019, 123, 347–355. [Google Scholar] [CrossRef]
- Wan-Qing, S.; Cheng, X.; Cattani, C.; Zio, E. Multi-Fractional Brownian Motion and Quantum-Behaved Partial Swarm Optimization for Bearing Degradation Forecasting. Complexity 2019, 2020, 1–9. [Google Scholar]
- Zhang, H.; Chen, M.; Xi, X.; Zhou, D. Remaining Useful Life Prediction for Degradation Processes with Long-Range Dependence. IEEE Trans. Reliab. 2017, 66, 1–12. [Google Scholar] [CrossRef]
- Wang, H.; Song, W.; Zio, E.; Kudreyko, A.; Zhang, Y. Remaining useful life prediction for Lithium-ion batteries using fractional Brownian motion and Fruit-fly Optimization Algorithm. Measurement 2020, 161, 107904. [Google Scholar] [CrossRef]
- Duan, S.; Wanqing, S.; Cattani, C.; Yasen, Y.; Liu, H. Fractional Levy Stable and Maximum Lyapunov Exponent for Wind Speed Prediction. Symmetry 2020, 2020, 605. [Google Scholar] [CrossRef]
- Yadav, A.; Jha, C.K.; Sharan, A. Optimizing LSTM for time series prediction in Indian stock market. Proc. Comput. Sci. 2020, 167, 2091–2100. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, Z.; Kong, D.; Han, H.; Zhao, Y. EA-LSTM: Evolutionary attention-based LSTM for time series prediction. Knowl. Based Syst. 2019, 181, 104785. [Google Scholar] [CrossRef]
- Karevan, Z.; Suykens, J.A.K. Transductive LSTM for time-series prediction: An application to weather forecasting. Neural Netw. 2020, 125, 1–9. [Google Scholar] [CrossRef]
- Song, W.; Cattani, C.; Chi, C.-H. Multifractional Brownian motion and quantum-behaved particle swarm optimization for short term power load forecasting: An integrated approach. Energy 2020, 194, 116847. [Google Scholar] [CrossRef]
- Schlager, W. Fractal nature of stratigraphic sequences. Geology 2004, 32, 185–188. [Google Scholar] [CrossRef]
- Li, M.; Li, J.-Y. Generalized Cauchy model of sea level fluctuations with long-range dependence. Phys. A Stat. Mech. Appl. 2017, 484, 309–335. [Google Scholar] [CrossRef]
- Liu, H.; Song, W.-Q.; Zio, E. Generalized Cauchy difference iterative forecasting model for wind speed based on fractal time series. Nonlinear Dyn. 2021, 103, 759–773. [Google Scholar] [CrossRef]
- Li, M. Multi-fractional generalized Cauchy process and its application to teletraffic. Phys. A Stat. Mech. Appl. 2020, 550, 123982. [Google Scholar] [CrossRef]
- Lim, S.; Li, M. A generalized Cauchy process and its application to relaxation phenomena. J. Phys. A Math. Gen. 2006, 39, 2935. [Google Scholar] [CrossRef]
- Carrillo, R.; Aysal, T.; Barner, K. A Generalized Cauchy Distribution Framework for Problems Requiring Robust Behavior. EURASIP J. Adv. Signal Process. 2010, 2010, 312989. [Google Scholar] [CrossRef]
- Dai, W.; Heyde, C.C. Itô’s formula with respect to fractional Brownian motion and its application. J. Appl. Math. Stoch. Anal. 1996, 9, 439–448. [Google Scholar] [CrossRef]
- Scholes, M.; Black, F. The Pricing of Options and Corporate Liabilities. J. Polit. Econ. 1973, 81, 637–654. [Google Scholar]
- Wang, X.-T.; Qiu, W.-Y.; Ren, F.-Y. Option pricing of fractional version of the Black–Scholes model with Hurst exponent H being in (1/3,1/2). Chaos Solitons Fract. 2001, 12, 599–608. [Google Scholar] [CrossRef]
- Ortigueira, M.D. Introduction to fractional linear systems. Part 2. Discrete-time case. In IEE Proceedings—Vision, Image and Signal Processing; IET—Institution of Engineering and Technology: Karnataka, India, 2000; Volume 147, pp. 71–78. [Google Scholar]
- Ortigueira, M.C. Introduction to fractional linear systems. Part 1. Continuous-time case. In IEE Proceedings—Vision, Image and Signal Processing; IET—Institution of Engineering and Technology: Karnataka, India, 2000; Volume 147, pp. 62–70. [Google Scholar]
- Yan, L.; Shen, G.; He, K. Itô’s formula for a sub-fractional Brownian motion. Commun. Stoch. Anal. 2011, 5, 135–159. [Google Scholar] [CrossRef]
- Li, M.; Lim, S.; Feng, H. Generating Traffic Time Series Based on Generalized Cauchy Process. In Proceedings of the International Conference on Computational Science, Beijing, China, 27–30 May 2007; Springer: Berlin/Heidelberg, Germany, 2007; pp. 374–381. [Google Scholar]
- Panigrahy, C.; Seal, A.; Mahato, N.K.; Bhattacharjee, D. Differential box counting methods for estimating fractal dimension of gray-scale images: A survey. Chaos Solitons Fract. 2019, 126, 178–202. [Google Scholar] [CrossRef]
- Silva, P.M.; Florindo, J.B. A statistical descriptor for texture images based on the box counting fractal dimension. Phys. A Stat. Mech. Appl. 2019, 528, 121469. [Google Scholar] [CrossRef]
- Konno, H.; Watanabe, F. Maximum likelihood estimators for generalized Cauchy processes. J. Math. Phys. 2007, 48, 1–19. [Google Scholar] [CrossRef]
- Sotavento. Sotavento Technical Area Real Time Data Historical. Available online: http://www.sotaventogalicia.com/en/technical-area/real-time-data/historical/ (accessed on 25 March 2021).




| GC | 0.8293 | 1.3650 | 0.0025 | 0.0143 | 0.0103 |
| fBm | 0.8293 | / | −0.3702 | 0.5793 | / |
| MAX | MIN | Mean | Median | Mode | SID | MAPE (%) | |
|---|---|---|---|---|---|---|---|
| GC (3h) | 0.0169 | 0.0002 | 0.0087 | 0.0005 | 0.0169 | 0.0106 | 0.87 |
| fBm (3h) | 0.0196 | 0.0010 | 0.0093 | 0.0034 | 0.0139 | 0.106 | 0.93 |
| GC (6h) | 0.0287 | 0.0006 | 0.0133 | 0.0019 | 0.0239 | 0.0151 | 1.33 |
| fBm (6h) | 0.0303 | 0.0011 | 0.0136 | 0.0067 | 0.0264 | 0.0154 | 1.36 |
| GC (9h) | 0.0350 | 0.0002 | 0.0133 | 0.0030 | 0.0349 | 0.0158 | 1.33 |
| fBm (9h) | 0.0366 | 0.0004 | 0.0146 | 0.0060 | 0.0358 | 0.0169 | 1.37 |
| GC (12h) | 0.0427 | 0.0006 | 0.0146 | 0.0053 | 0.0332 | 0.0169 | 1.46 |
| fBm(12h) | 0.0434 | 0.0002 | 0.0153 | 0.0025 | 0.0313 | 0.0184 | 1.53 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, J.; Song, W.; Villecco, F. Generalized Cauchy Process: Difference Iterative Forecasting Model. Fractal Fract. 2021, 5, 38. https://doi.org/10.3390/fractalfract5020038
Xing J, Song W, Villecco F. Generalized Cauchy Process: Difference Iterative Forecasting Model. Fractal and Fractional. 2021; 5(2):38. https://doi.org/10.3390/fractalfract5020038
Chicago/Turabian StyleXing, Jie, Wanqing Song, and Francesco Villecco. 2021. "Generalized Cauchy Process: Difference Iterative Forecasting Model" Fractal and Fractional 5, no. 2: 38. https://doi.org/10.3390/fractalfract5020038
APA StyleXing, J., Song, W., & Villecco, F. (2021). Generalized Cauchy Process: Difference Iterative Forecasting Model. Fractal and Fractional, 5(2), 38. https://doi.org/10.3390/fractalfract5020038








