Fractal, Scale Free Electromagnetic Resonance of a Single Brain Extracted Microtubule Nanowire, a Single Tubulin Protein and a Single Neuron
Abstract
1. Introduction
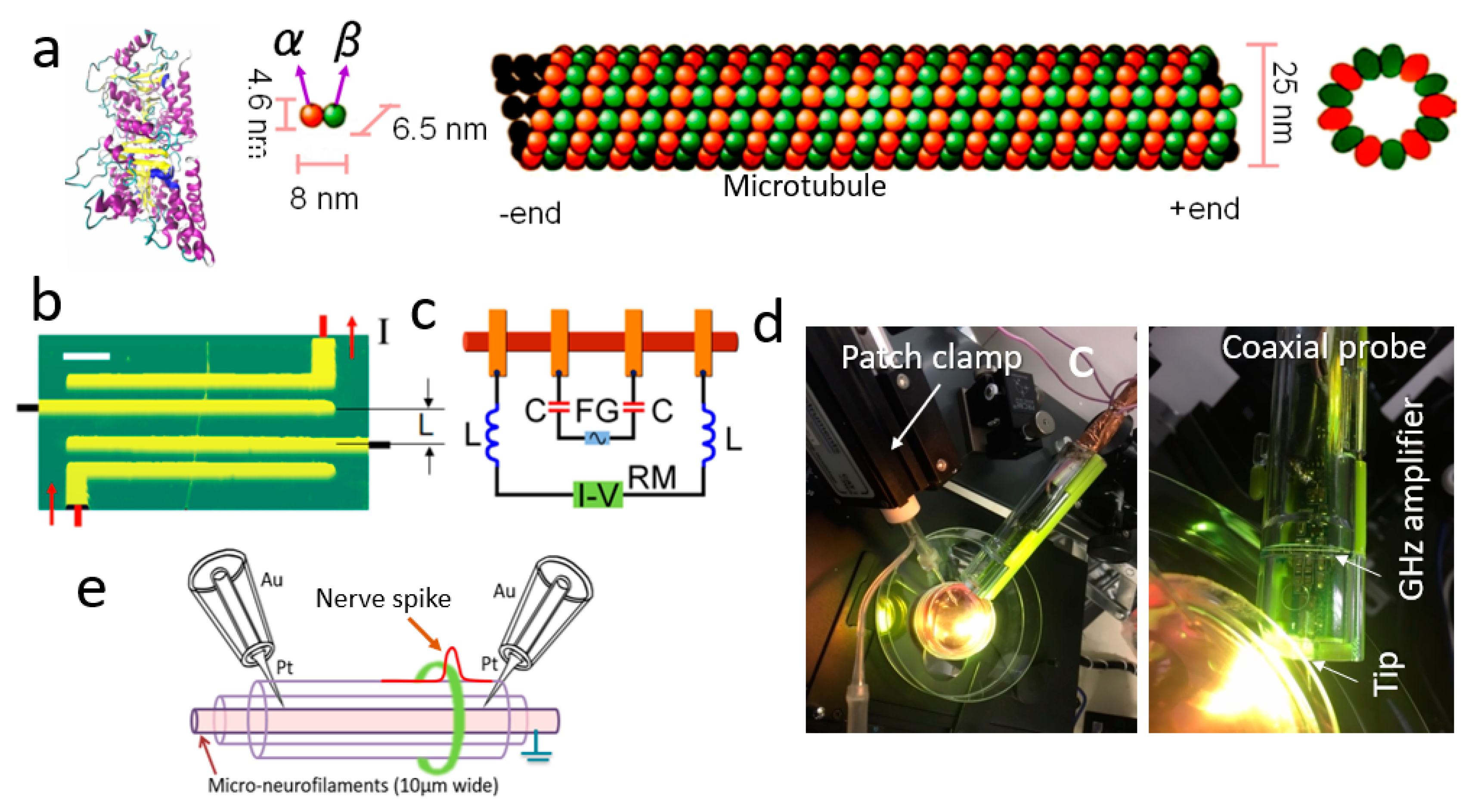
2. Experimental Section
2.1. Neuron Culture on Pre-grown Electrodes for Simultaneous Patch-Clamp and Wireless Axon Initial Segment (AIS) Experiment
2.2. Reconstitution of Microtubule
2.3. Preparation of Protein Sample
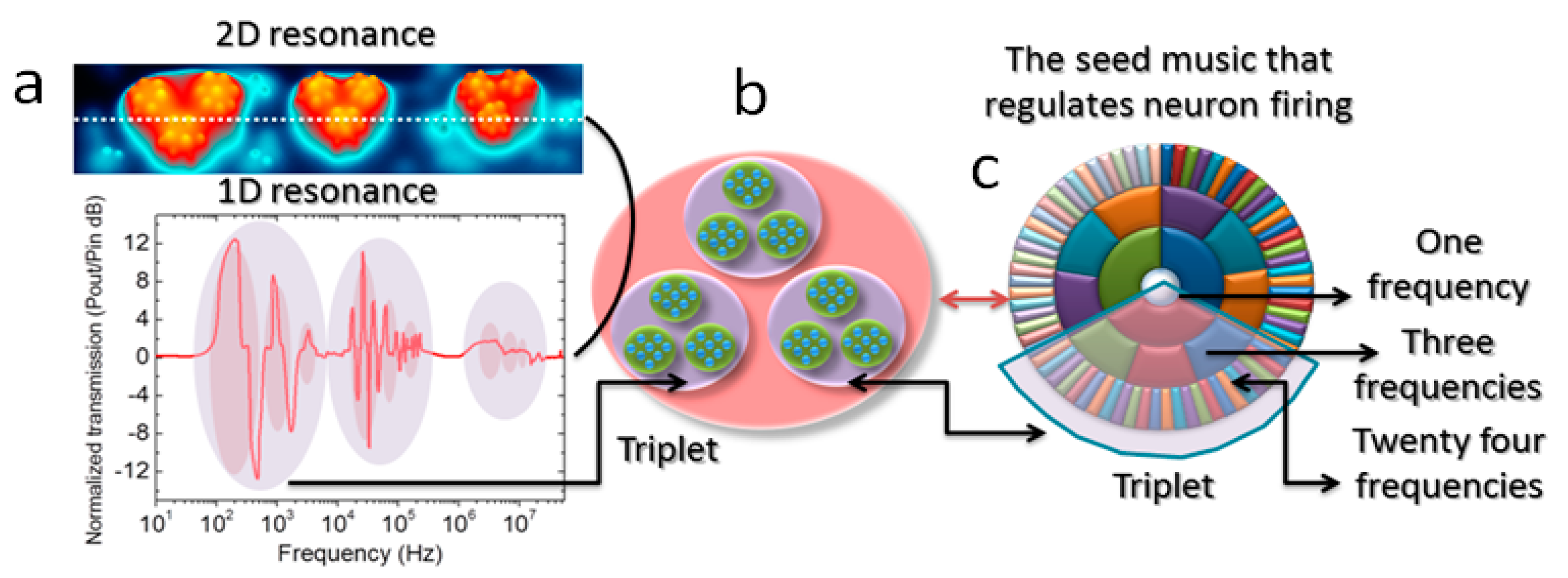
3. Results and Discussion
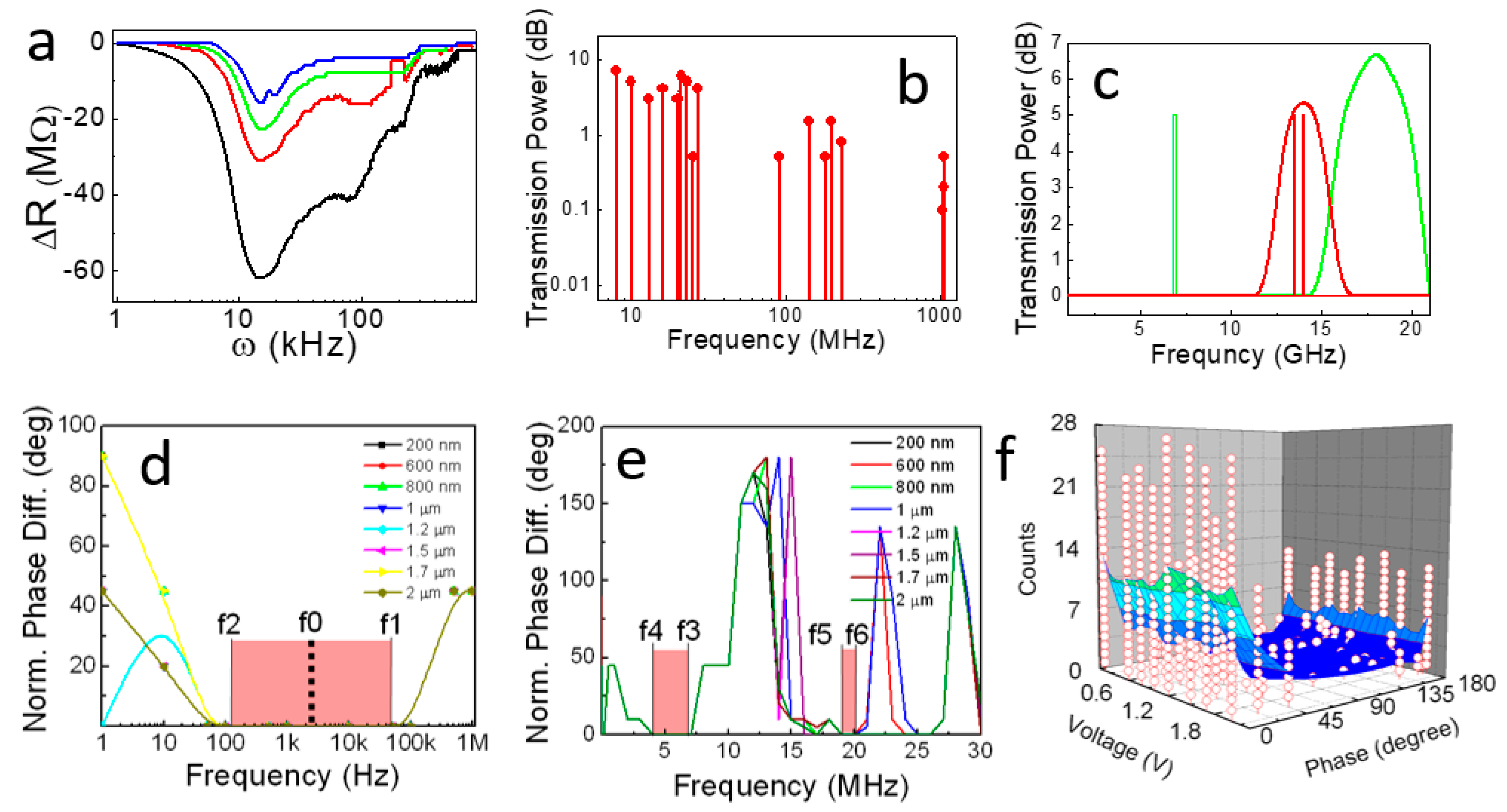
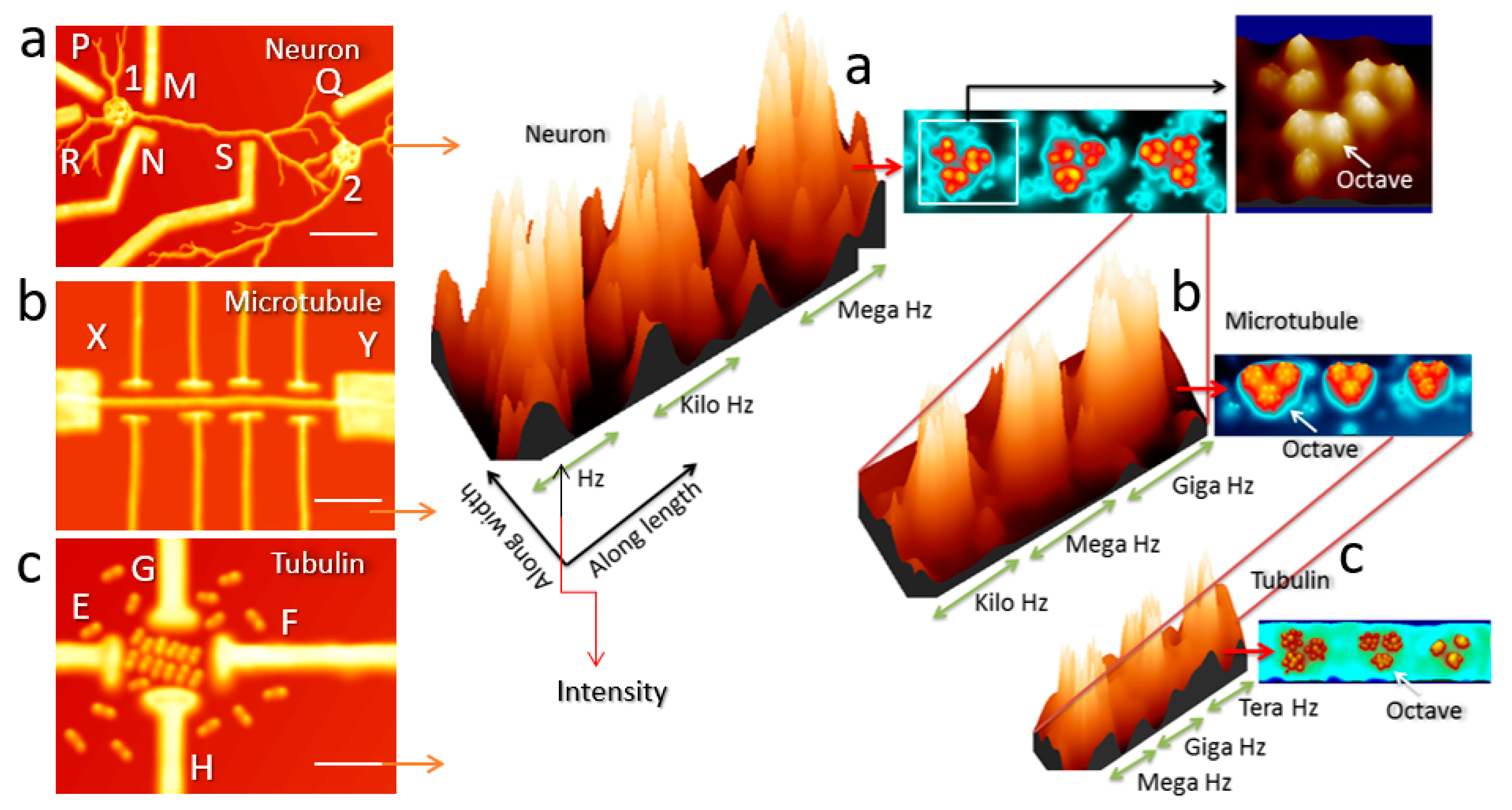
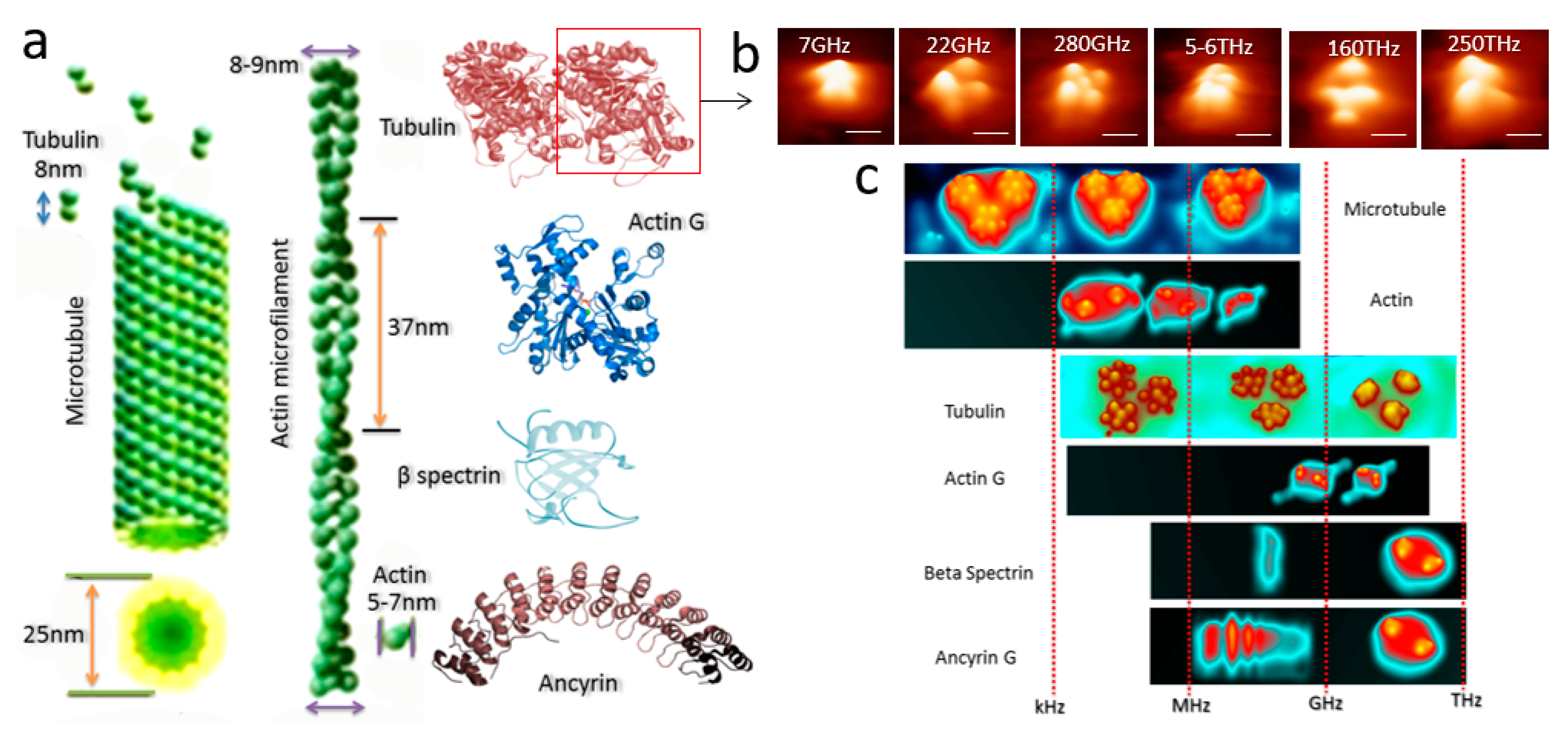
3.1. Triplet of Triplet Fractal Electromagnetic Resonance Band of Single Brain Extracted Microtubule
3.2. Triplet of Triplet Fractal Ionic Resonance Band of a Single Neuron
4. Conclusion and Future
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- He, B. Scale-free properties of the functional magnetic resonance imaging signal during rest and task. J. Neurosci. 2011, 31, 13786–13795. [Google Scholar] [CrossRef] [PubMed]
- Hudetz, A.G. General Anesthesia and Human Brain Connectivity. Brain Connect. 2012, 2, 291–302. [Google Scholar] [CrossRef] [PubMed]
- Singh, P.; Ray, K.; Fujita, D.; Bandyopadhyay, A. Complete Dielectric Resonator Model of Human Brain from MRI Data: A Journey from Connectome Neural Branching to Single Protein. In Lecture Notes in Electrical Engineering; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2018; Volume 478, pp. 717–733. [Google Scholar]
- Ghosh, S.; Sahu, S.; Fujita, D.; Bandyopadhyay, A. Design and operation of a brain like computer: A new class of frequency-fractal computing using wireless communication in a supramolecular organic, inorganic systems. Information 2014, 5, 28–99. [Google Scholar] [CrossRef]
- Singh, P.; Ocampo, M.; Lugo, J.E.; Doti, R.; Faubert, J.; Rawat, S.; Ghosh, S.; Ray, K.; Bandyopadhyay, A. Fractal and periodic biological antennas: Hidden topologies in DNA, Wasps, and retina in the eye. Stud. Comput. Intell. 2018, 761, 113–130. [Google Scholar]
- Anguera, J.; Andújar, A.; Jayasinghe, J.; Chakravarthy, V.S.S.S.S.; Chowdary, P.S.R.; Ali, T.; Pijoan, J.L.; Cattani, C. Fractal Antennas: An Historic Perspective. Fractal Fract. 2020, 4, 3. [Google Scholar] [CrossRef]
- Ghosh, S.; Sahu, S.; Agrawal, L.; Shiga, T.; Bandyopadhyay, A. Inventing a co-axial atomic resolution patch clamp to study a single resonating protein complex and ultra-low power communication deep inside a living neuron cell. J. Integr. Neurosci. 2016, 15, 403–433. [Google Scholar] [CrossRef]
- Whittier, J.E.; Goddard, G.R. Microtubule Structural Dynamics Measured with Impedance Spectroscopy. FASEB J. 2006, 20, A492. [Google Scholar]
- Agrawal, L.; Sahu, S.; Ghosh, S.; Shiga, T.; Fujita, D.; Bandyopadhyay, A. Inventing atomic resolution scanning dielectric microscopy to see a single protein complex operation live at resonance in a neuron without touching or adulterating the cell. J. Integr. Neurosci. 2016, 15, 435–462. [Google Scholar] [CrossRef]
- Jelinek, F.; Pokorný, J. Microtubules in Biological Cells as Circular Waveguides and Resonators. Electro Magn. 2001, 20, 75–80. [Google Scholar] [CrossRef]
- Hameroff, S.R.; Watt, R.C. Information processing in microtubules. J. Theor. Boil. 1982, 98, 549–561. [Google Scholar] [CrossRef]
- Sahu, S.; Ghosh, S.; Hirata, K.; Fujita, D.; Bandyopadhyay, A. Multi-level memory-switching properties of a single brain microtubule. Appl. Phys. Lett. 2013, 102, 123701. [Google Scholar] [CrossRef]
- Cosic, I.; Cosic, D.; Lazar, K. Is it possible to predict electromagnetic resonances in proteins, DNA and RNA? Nonlinear Biomed. Phys. 2015, 3. [Google Scholar] [CrossRef]
- Sahu, S.; Ghosh, S.; Ghosh, B.; Aswani, K.; Hirata, K.; Fujita, D.; Bandyopadhyay, A. Atomic water channel controlling remarkable properties of a single brain microtubule: Correlating single protein to its supramolecular assembly. Biosens. Bioelectron. 2013, 47, 141–148. [Google Scholar] [CrossRef] [PubMed]
- Tuszynski, J.A.; Friesen, D.; Freedman, H.; Sbitnev, V.I.; Kim, H.; Santelices, I.; Kalra, A.P.; Patel, S.D.; Shankar, K.; Chua, L.O. Microtubules as Sub-Cellular Memristors. Sci. Rep. 2020, 10, 2108. [Google Scholar] [CrossRef]
- Kalra, A.P.; Patel, S.D.; Bhuiyan, A.F.; Preto, J.; Scheuer, K.G.; Mohammed, U.; Lewis, J.D.; Rezania, V.; Shankar, K.; Tuszynski, J.A. Investigation of the Electrical Properties of Microtubule Ensembles under Cell-Like Conditions. Nanomaterials 2020, 10, 265. [Google Scholar] [CrossRef]
- Priel, A.; Ramos, A.J.; Tuszynski, J.A.; Cantiello, H.F. A Biopolymer Transistor: Electrical Amplification by Microtubules. Biophys. J. 2006, 90, 4639–4643. [Google Scholar] [CrossRef]
- Sahu, S.; Ghosh, S.; Fujita, D.; Bandyopadhyay, A. Live visualizations of single isolated tubulin protein self-assembly via tunneling current: Effect of electromagnetic pumping during spontaneous growth of microtubule. Sci. Rep. 2014, 4, 7303. [Google Scholar] [CrossRef]
- Minoura, I.; Muto, E. Dielectric Measurement of Individual Microtubules Using the Electroorientation Method. Biophys. J. 2006, 90, 3739–3748. [Google Scholar] [CrossRef]
- Umnov, M.; Palusinski, O.A.; Deymier, P.A.; Guzman, R.; Hoying, J.; Barnaby, H.; Yang, Y.; Raghavan, S. Experimental evaluation of electrical conductivity of microtubules. J. Mater. Sci. 2006, 42, 373–378. [Google Scholar] [CrossRef]
- Langmuir, I. The Role of Attractive and Repulsive Forces in the Formation of Tactoids, Thixotropic Gels, Protein Crystals and Coacervates. J. Chem. Phys. 1938, 6, 873. [Google Scholar] [CrossRef]
- Ebbinghaus, S.; Kim, S.J.; Heyden, M.; Yu, X.; Heugen, U.; Gruebele, M.; Leitner, D.M.; Havenith, M. An extended dynamical hydration shell around proteins. Proc. Natl. Acad. Sci. USA 2007, 104, 20749–20752. [Google Scholar] [CrossRef] [PubMed]
- Mershin, A.; Kolomenski, A.; Schuessler, H.; Nanopoulos, D. Tubulin dipole moment, dielectric constant and quantum behavior: Computer simulations, experimental results and suggestions. Biosystems 2004, 77, 73–85. [Google Scholar] [CrossRef] [PubMed]
- Otting, G.; Liepinsh, E.; Wüthrich, K. Protein hydration in aqueous solution. Science 1991, 254, 974–980. [Google Scholar] [CrossRef] [PubMed]
- Denisov, V.P.; Peters, J.; Hörlein, H.D.; Halle, B. Using buried water molecules to explore the energy landscape of proteins. Nat. Struct. Mol. Boil. 1996, 3, 505–509. [Google Scholar] [CrossRef]
- Satyajit, S.; Daisuke, F.; Anirban, B. Helical symmetries observed in proteins: An inductor made of arrayed capacitors (2010) Japanese patent has been issued on 20th August 2015 JP-511630 (world patent filed, this is the invention of fourth circuit element). U.S. Patent 9019685B2, 28 April 2015. [Google Scholar]
- Borisy, G.G.; Marcum, J.M.; Olmsted, J.B.; Murphy, D.B.; Johnson, K.A. Purification of Tubulin and Associated High Molecular Weight Proteins from Porcine Brain and Characterization of Microtubule Assembly in Vitro. Ann. N. Y. Acad. Sci. 1975, 253, 107–132. [Google Scholar] [CrossRef]
- Fygenson, D.K.; Braun, E.; Libchaber, A. Phase diagram of microtubules. Phys. Rev. E 1994, 50, 1579–1588. [Google Scholar] [CrossRef]
- Pizzi, R.; Strini, G.; Fiorentini, S.; Pappalardo, V.; Pregnolatio, M. Evidences of new biophysical properties of microtubule. In Artificial Neural Networks; Kwon, S.J., Ed.; Nova Science Publications: New York, NY, USA, 2010; pp. 1–17. [Google Scholar]
- Attiya, A. Lower Frequency Limit of Carbon Nanotube Antenna. Prog. Electromagn. Res. 2009, 94, 419–433. [Google Scholar] [CrossRef]
- Sanabria, H.; Miller, J.H., Jr.; Mershin, A. Impedance spectroscopy of alpha-beta tubulin heterodimer suspensions. Biophys. J. 2006, 90, 4644–4650. [Google Scholar] [CrossRef][Green Version]
- Hanson, G. Fundamental transmitting properties of carbon nanotube antennas. IEEE Trans. Antennas Propag. 2005, 53, 3426–3435. [Google Scholar] [CrossRef]
- Pokorny, J.; Jelenek, F.; Trkval, V.; Lamprecht, I.; Holtzel, R. Vibrations in microtubules. J. Biol. Phys. 1997, 48, 261–266. [Google Scholar]
- Daneshmand, F.; Amabili, M. Coupled oscillations of a protein microtubule immersed in cytoplasm: An orthotropic elastic shell modeling. J. Boil. Phys. 2012, 38, 429–448. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Hirokawa, N. Cross-linker system between neurofilaments, microtubules and membranous organelles in frog axons revealed by the quick-freeze, deep-etching method. J. Cell Boil. 1982, 94, 129–142. [Google Scholar] [CrossRef] [PubMed]
- Heidemann, S.R.; Landers, J.M.; Hamborg, M.A. Polarity orientation of axonal microtubules. J. Cell Boil. 1981, 91, 661–665. [Google Scholar] [CrossRef] [PubMed]
- Baas, P.W.; Deitch, J.S.; Black, M.M.; Banker, G.A. Polarity orientation of microtubules in hippocampal neurons: Uniformity in the axon and nonuniformity in the dendrite. Proc. Natl. Acad. Sci. USA 1988, 85, 8335–8339. [Google Scholar] [CrossRef]
- Heidemann, S.R.; Hamborg, M.A.; Thomas, S.J.; Song, B.; Lindley, S.; Chu, D. Spatial organization of axonal microtubules. J. Cell Boil. 1984, 99, 1289–1295. [Google Scholar] [CrossRef]
- Craig, E.M.; Yeung, H.T.; Rao, A.; Baas, P.W. Polarity sorting of axonal microtubules: A computational study. Mol. Boil. Cell 2017, 28, 3271–3285. [Google Scholar] [CrossRef]
- Sahu, S.; Fujita, D.; Bandyopadhyay, A. Helical Symmetries Observed in Proteins: An Inductor Made of Arrayed Capacitors. Japanese Patent JP-511630, 20 August 2015. [Google Scholar]
- Leterrier, C.; Vacher, H.; Fache, M.P.; d’Ortoli, S.A.; Castets, F.; Autillo-Touati, A.; Dargent, B. End-binding protiens EB3 and EB1 link microtubules to ankyrin G in the axon initial segment. Proc. Natl. Acad. Sci. USA 2011, 108, 8826–8831. [Google Scholar] [CrossRef]
- Xu, K.; Zhong, G.; Zhuang, X. Actin, Spectrin, and Associated Proteins Form a Periodic Cytoskeletal Structure in Axons. Science 2012, 339, 452–456. [Google Scholar] [CrossRef]
- Lee, G.; Abdi, K.; Jiang, Y.; Michaely, P.; Bennett, V.; Marszalek, P.E. Nanospring behavior of ankyrin repeats. Nature 2006, 440, 246–249. [Google Scholar] [CrossRef]
- Buzsaki, G.; Moser, E.I. Memory, navigation and theta rhythm in the hippocampal-entorhinal system. Nat. Neurosci. 2013, 16, 130–138. [Google Scholar] [CrossRef]
- Reddy, S.; Sonker, D.; Singh, P.; Saxena, K.; Singh, S.; Chhajed, R.; Tiwari, S.; Karthik, K.V.; Ghosh, S.; Ray, K.; et al. A Brain-like Computer Made of Time Crystal: Could a Metric of Prime Alone Replace a User and Alleviate Programming Forever? Stud. Comput. Intell. 2018, 761, 1–43. [Google Scholar]
- Bandyopadhyay, A. Nanobrain: The Making of an Artificial Brain from a Time Crystal, 1st ed.; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saxena, K.; Singh, P.; Sahoo, P.; Sahu, S.; Ghosh, S.; Ray, K.; Fujita, D.; Bandyopadhyay, A. Fractal, Scale Free Electromagnetic Resonance of a Single Brain Extracted Microtubule Nanowire, a Single Tubulin Protein and a Single Neuron. Fractal Fract. 2020, 4, 11. https://doi.org/10.3390/fractalfract4020011
Saxena K, Singh P, Sahoo P, Sahu S, Ghosh S, Ray K, Fujita D, Bandyopadhyay A. Fractal, Scale Free Electromagnetic Resonance of a Single Brain Extracted Microtubule Nanowire, a Single Tubulin Protein and a Single Neuron. Fractal and Fractional. 2020; 4(2):11. https://doi.org/10.3390/fractalfract4020011
Chicago/Turabian StyleSaxena, Komal, Pushpendra Singh, Pathik Sahoo, Satyajit Sahu, Subrata Ghosh, Kanad Ray, Daisuke Fujita, and Anirban Bandyopadhyay. 2020. "Fractal, Scale Free Electromagnetic Resonance of a Single Brain Extracted Microtubule Nanowire, a Single Tubulin Protein and a Single Neuron" Fractal and Fractional 4, no. 2: 11. https://doi.org/10.3390/fractalfract4020011
APA StyleSaxena, K., Singh, P., Sahoo, P., Sahu, S., Ghosh, S., Ray, K., Fujita, D., & Bandyopadhyay, A. (2020). Fractal, Scale Free Electromagnetic Resonance of a Single Brain Extracted Microtubule Nanowire, a Single Tubulin Protein and a Single Neuron. Fractal and Fractional, 4(2), 11. https://doi.org/10.3390/fractalfract4020011









