Abstract
The manuscript surveys the special functions of the Fox-Wright type. These functions are generalizations of the hypergeometric functions. Notable representatives of the type are the Mittag-Leffler functions and the Wright function. The integral representations of such functions are given and the conditions under which these function can be represented by simpler functions are demonstrated. The connection with generalized Erdélyi-Kober fractional differential and integral operators is demonstrated and discussed.
Keywords:
Wright function; Gamma function; Beta function; fractional calculus; Erdélyi-Kober operators MSC:
Primary: 33C20; Secondary: 33C60, 33C99, 26A33, 33B15
1. Introduction
This paper is concerned with integral representations of the Fox-Wright functions and their relationship to fractional calculus. The first characteristic exemplar of this function family has been introduced by E. M. Wright, who generalized the concept in a series of papers in 1930s. The Fox-Wright special functions are very general mathematical objects, which have broad applications in mathematical physics, notably in descriptions of wave phenomena, heat and mass transfer. They encompass the generalized hypergeometric functions and are related to the family of the Bessel functions.
The conditions for existence of the generalized Wright function together with its representation in terms of the Mellin-Barnes integral and of the H-function can be found in [1]. Fox-Wright functions encompass other important families of functions, such as the the Mittag-Leffler functions (surveys in [2,3]). The Mittag-Leffler function in turn expresses the solution of fractional order integral or fractional order differential equations. It has applications in the theory of random walks, Levy flights, superdiffusive transport, among others. Another important example is the M-Wright function, which expresses the fundamental solution of the time-fractional diffusion-wave equation [4]. A recent survey about the properties of the function can be found in [5].
The objective of the present paper is to give a self-contained treatment of the generalized fractional calculus Erdélyi-Kober operators, which appear as re-parametrizations of the Euler integrals. The actions of the Erdélyi-Kober operators are thus expressed in a natural way as adding or removing parameters of multi-parameter Fox-Wright functions.
Many authors introduce the Fox-Wright functions from their representation as H-functions, which are in turn defined as Mellin transforms pairs. Such presentation tends to obfuscate the utility of Fox-Wright functions. In this paper, the Fox-Wright functions are represented as generalized hypergeoemtric series (GHG) and related to the theory of the Euler Gamma and Beta functions. This provides some advantages, as for example Theorem 3, which to the present author’s knowledge has not been stated in such form before.
2. Preliminaries and Notation
The generalized hypergeometric functions are defined by the infinite hypergeometric (HG) series
The defining property fo HG series is that the coefficients are rational functions of the index variable (i.e., k).
In the following sections, we will use the parametric notation similar to the one adopted by Oldham and Spanier [6].
The classical hypergeometric series obey the differential identities
and
which entails the differential equation
These relationships can be suitably generalized for fractional operators.
The Fox-Wright functions are further generalizations of the hypergeometric (HG) functions of the form
For this generalization, one can not expect that in general the coefficients are rational functions of the index variable.
For convergence of the series the condition
will be assumed everywhere [7,8]. At this point we introduce some extended notation under the convention
In this notation, the hypergeometric indices of the function are written first while the non-simplified indices are left second. The non-simplified indices result in factors of the form
or their reciprocals, respectively, and follow the usual convention established in literature. The order in the parametric convention for the arguments of the Gamma function follows the usual convention, used for example in [9,10]. This is unfortunately converse to the order of the more conventional Wright function and Mittag-Leffler type of functions.
The following simplifying convention will be used further:
and
This example shows different ways to write a hypergeometric function.
3. Algebraic Decomposition
The coefficients of the GHG series can be identified by means of the following Lemma:
Lemma 1
(HG Recurrence). Suppose that
where is a linear expression in the index k or
under the same convention. Then
or
respectively, where
and
Proof.
We prove the first case only since the second one follows identical reasoning. By hypothesis for some unknown A and a. Let’s form the ratio
Then and . □
The generalized hypergeometric series can be decomposed in symmetric (even) and anti-symmetric (odd) series as follows:
Theorem 1
(GH Series Parity Decomposition). Suppose that the generalized hypergeometric series is absolutely convergent at z. Denote as the even part while as the odd part.
If S is of the form
then
If S is of the form
then
Proof.
Let the even part and odd series be and , respectively. We prove only the first statement because the second one can be proved in an identical way. For simplicity of calculations suppose that S is of the form
For the even part:
so that the ratio of the coefficients is
Therefore,
For the odd part starting from
so the the ratio of the coefficients is
Therefore, after an index shift
□
Remark 1.
From this result, it can be seen that the hypergeometric (HG) series are not closed with regard to the parity decomposition. In contrast, the GHG series of the Wright type are closed with regard to this decomposition.
The simplest example illustrating the Theorem is given by the exponential series.
Example 1
(The Exponential Function Decomposition).
and
as expected.
A non-trivial example of the present Theorem is the following
Example 2
(The Mittag-Leffler Function Decomposition).
Then
For the first part by the Gamma duplication formula for the argument :
For the second part by the Gamma duplication formula for the argument :
so that finally
The negative multiplicative parameters can be raised to the numerator by the application of the following Theorem:
Theorem 2.
Suppose that z , and . Then
where , .
Proof.
Consider the monomial
By the reflection formula
This can be embedded in the complex monomial expression
Assuming that z is real, the original expression is the imaginary part of . Further, has modulus
so that the infinite series for converges and so does its imaginary part. Finally the GHG parameters can be read off from the arguments of the Gamma functions. □
Corollary 1.
Under the same hypothesis
4. Integral Representations
4.1. Integral Representations by Beta Integrals
The main result of this section is given by the theorem below. The result allows for the representation of a GHG function of order in terms of an integral of a GHG function of order or in special cases . In this section everywhere the argument of a GHG function will be considered real-valued.
Theorem 3
(Beta integral representation). For and the following representation holds
By change of variables
Proof.
The proof follows from the hypothesis of absolute convergence of the series. Therefore, the order of integration and summation can be switched.
Let and suppose that . Observe that by Equation (A3)
Therefore,
Therefore, by absolute convergence of the series
Therefore,
Furthermore, let now . It can be further observed that for the monomial term
Therefore,
□
This representation step reduces a GHG series into a GHG series. It can be seen that the reduction via Beta integral is not complete except if . Therefore, it can be instructive to distinguish homogeneous GHG series with indices and different multiplicies. This is the subject of the following results:
Corollary 2
(Homogeneous Euler Reduction). For and
Furthermore, for the usual Euler reduction for hypergeometric functions holds
By change of variables the reduced representation can be expressed as an improper integral:
Corollary 3.
By change of variables for
and for
4.2. Integral Representations by Gamma Integrals
Theorem 4
(Complex GH Series Representation). Suppose that all indices and are real. Then for real z and
where Hankel path starts at infinity on the real axis, encircling 0 in a positive sense, and returns to infinity along the real axis, respecting the cut along the positive real axis, while is its reflection.
Proof.
From the Heine’s formula for the reciprocal Gamma function representation
It follows that
Therefore,
and
by extension. □
Corollary 4.
For the following representation holds
Remark 2.
This theorem can be interpreted as the inverse Laplace transform of a simpler Fox-Wright function. Moreover, the complex integral can be converted to a real integral for suitable functions [11].
Theorem 5
(Real GH Series Representation). Suppose that all indices and are real. Then for some real and and
Proof.
From the Gamma function representation
it follows that
Therefore,
provided that all parameters are real.
Corollary 5.
Remark 3.
The last Theorem can be interpreted as the Laplace transform of a simpler Fox-Wright function. Pogany et al. give essentially the same result as Corrollary 5 as Equation (7) in page 128 [12].
In summary, the section shows that a GHG series can be reduced to a multiple integrals of the Euler type.
5. Applications
5.1. Mittag-Leffler Functions
The 2 parameter Mittag-Leffler function [13,14] under the present convention will be denoted as
This immediately gives the complex integral representation according to Corollary 4
However, in this case the contour encloses the curve .
Another example is the 3-parameter Mittag-Leffler function generalization, that is the Prabhakar function [15] defined as
In this case
which leads to an integral involving the Wright function.
An interesting special case is the function which is a confluent Kummer () hypergeometric function. In this case for
as expected.
5.2. The Kummer-Wright Function
In particular, the following representation can be stated for the basic GH function (the Kummer-Wright function)
And also
This Wright function in turn can be represented as (see Equation (A4)):
For the homogeneous case then
according to the representation of the reciprocal Gamma function. Therefore, according to the Homogeneous Reduction Corollary:
which is a generalization of the Kummer function.
5.3. Generalized Fractional Erdélyi-Kober Operations
The theory of GHG series has an interesting relationship with the generalized fractional calculus. The right Erdélyi-Kober (E-K) fractional integrals are defined as [10]:
while another equivalent form is [16] [Ch. 18]:
The two forms are related by the change of variables . Therefore, from the preceding presentation it follows that
This corresponds to the findings of Kiryakova [17].
The E-K operator reduces to the Riemann-Liouville fractional integral for and as
Conversely,
It is interesting to note further that the EK operators map the functions of the Dimovski space into one another [18]:
where the function space is given by the following:
Definition 1
(Dimovski Space [19]). The space of functions consists of all functions , that can be represented in the form with and .
The corresponding generalized Erdélyi-Kober fractional derivative is defined by a composition product as
where is the fractional part and is the integral part of the number.
For the E-K fractional derivative operator reduces to the Riemann-Liouville fractional derivative of order as
The E-K fractional derivative operator is the left-inverse of E-K integral for suitable functions from :
Therefore,
and
The last equation can be used for index reduction.
6. Discussion
These results demonstrate that the homogeneous class of GHG series are closed with respect to the (generalized) fractional calculus operations. One can, therefore, expect that the solutions of fractional differential equations could be expressed in terms of Fox-Wright functions. Therefore, the Fox-Wright functions are the most general functions of the mathematical physics.
Furthermore, the results demonstrate a strong link between the special function theory and the theory of the Euler Beta and Gamma functions. It appears that the E-K operators can be thought of Euler’s Beta integrals in disguise. Moreover, the Gamma integral representations can be interpreted as Laplace or Inverse Laplace transforms.
Finally, the main consequence of so-presented results is that all GHG functions of the Fox-Wright type can be represented as multiple (complex) integrals of three primitive special functions of orders , and respectively. This corroborates the findings of Kiryakova [9,10,17]. These multiple integrals can be denoted as generalized fractional differ-integrals; however, this line of representation is superfluous to the necessities of the numerical and physical modeling.
Acknowledgments
The work has been supported in part by a grants from Research Fund—Flanders (FWO), contract number VS.097.16N and the COST Association Action CA16212 INDEPTH.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A. Euler Integrals
The Gamma integral, i.e., the Euler integral of second kind is defined as
while for all
The complex representation for the reciprocal Gamma function is given by the Heine’s integral as
The contour is depicted in Figure A1. For non-integral arguments the branch cut is selected as the negative real axis.
The Beta integral (i.e., the Euler integral of first kind) is given as
The Beta function can be continued analytically along the self-intersecting Pochhammer contour as
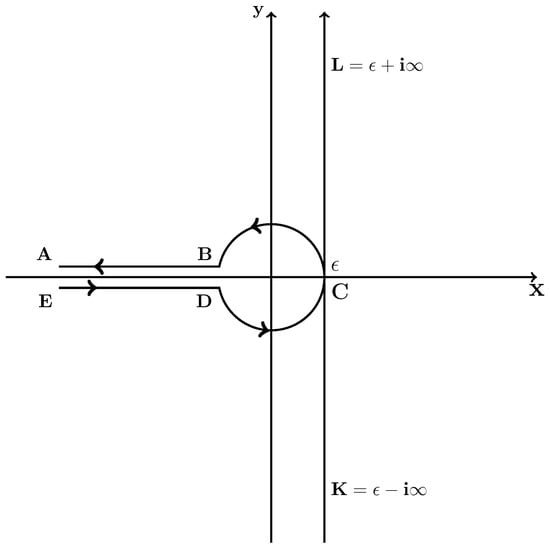
Figure A1.
The Hankel contour and the Bromwich contour .
Appendix B. The Wright Function
The function , named after E. M. Wright, is defined as the infinite series
is an entire function of z. The summation is carried out in steps where . The function is related to the Bessel functions and as
and is sometimes called generalized Bessel function. A recent survey about the properties of the function can be found in [5].
The integral representation of the Wright function is noteworthy because it can be used for numerical calculations
where denotes the Hankel contour in the complex -plane with a cut along the negative real semi-axis . The contour is depicted in Figure A1.
Furthermore,
The proof follows immediately from the integral representation by Azrelá’s theorem:
and formally the indefinite integral is
by the properties of anti-differentiation.
Appendix B.1. The M-Wright Function
Mainardi introduces a specialization of the Wright function, which is called here the M-Wright function, which is important in the applications to fractional transport problems [20].
Special cases of the M-Wright function are given in Table A1.

Table A1.
Special cases of the M-Wright function.
Table A1.
Special cases of the M-Wright function.
| ν | Mν(z) |
|---|---|
| 1/2 | |
| 1/3 |
References
- Kilbas, A.; Saigo, M.; Truijllo, J.J. On the generalized wright function. Fract. Calc. Appl. Anal. 2002, 5, 437–460. [Google Scholar]
- Haubold, H.J.; Mathai, A.M.; Saxena, R.K. Mittag-Leffler functions and their applications. J. Appl. Math. 2011, 2011, 298628. [Google Scholar] [CrossRef]
- Rogosin, S. The Role of the Mittag-Leffler Function in Fractional Modeling. Mathematics 2015, 3, 368–381. [Google Scholar] [CrossRef]
- Gorenflo, R.; Luchko, Y.; Mainardi, F. Wright functions as scale-invariant solutions of the diffusion-wave equation. J. Comput. Appl. Math. 2000, 118, 175–191. [Google Scholar] [CrossRef]
- Mainardi, F.; Mura, A.; Pagnini, G. The M-Wright function in time-fractional diffusion processes: A tutorial survey. Int. J. Differ. Equ. 2010, 2010, 1–29. [Google Scholar] [CrossRef]
- Oldham, K.; Spanier, J. The Fractional Calculus: Theory and Applications of Differentiation and Integration to Arbitrary Order; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Wright, E.M. The asymptotic expansion of the generalized hypergeometric function. J. Lond. Math. Soc. 1935, 1, 286–293. [Google Scholar] [CrossRef]
- Wright, E.M. The asymptotic expansion of integral functions defined by Taylor series. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 1940, 238, 423–451. [Google Scholar] [CrossRef]
- Kiryakova, V. All the special functions are fractional differintegrals of elementary functions. J. Phys. A Math. Gen. 1997, 30, 5085–5103. [Google Scholar] [CrossRef]
- Kiryakova, V. The special functions of fractional calculus as generalized fractional calculus operators of some basic functions. Comput. Math. Appl. 2010, 59, 1128–1141. [Google Scholar] [CrossRef]
- Prodanov, D. Regularized Integral Representations of the Reciprocal Gamma Function. Fractal Fract. 2019, 3, 1. [Google Scholar] [CrossRef]
- Pogány, T.K.; Srivastava, H.M. Some Mathieu-type Series Associated with the Fox-Wright Function. Comput. Math. Appl. 2009, 57, 127–140. [Google Scholar] [CrossRef]
- Mittag-Leffler, G.M. Sur la nouvelle fonction Ea(x). C. R. Acad. Sci. Paris 1903, 137, 554–558. [Google Scholar]
- Wiman, A. Über den Fundamentalsatz in der Teorie der Funktionen Ea(x). Acta Math. 1905, 29, 191–201. [Google Scholar] [CrossRef]
- Prabhakar, T.R. A singular equation with a generalized Mittag-Leffler function in the kernel. Yokohama Math. J. 1971, 19, 7–15. [Google Scholar]
- Samko, S.; Kilbas, A.; Marichev, O. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach: Yverdon, Switzerland, 1993. [Google Scholar]
- Kiryakova, V. Fractional calculus operators of special functions? The result is well predictable! Chaos Solitons Fractals 2017, 102, 2–15. [Google Scholar] [CrossRef]
- Luchko, Y. Algorithms for evaluation of the Wright function for the real arguments’ values. Fract. Calc. Appl. Anal. 2008, 11, 57–75. [Google Scholar]
- Dimovski, I. Operational calculus for a class of differential operators. C. R. Acad. Bulg. Sci. 1966, 19, 1111–1114. [Google Scholar]
- Mainardi, F.; Luchko, Y.; Pagnini, G. The fundamental solution of the space-time fractional diffusion equation. Fract. Calc. Appl. Anal. 2001, 4, 153–192. [Google Scholar]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).