Regularized Integral Representations of the Reciprocal Gamma Function

Abstract

This paper establishes a real integral representation of the reciprocal Gamma function in terms of a regularized hypersingular integral along the real line. A regularized complex representation along the Hankel path is derived. The equivalence with the Heine’s complex representation is demonstrated. For both real and complex integrals, the regularized representation can be expressed in terms of the two-parameter Mittag-Leffler function. Reference numerical implementations in the Computer Algebra System Maxima are provided.

1. Introduction

Applications of the Gamma function in fractional calculus and the special function theory are ubiquitous. For example, the function is indispensable in the theory of Laplace transforms. The history of the Gamma function is surveyed in [1], in which the author further states that “of the so-called ’higher mathematical functions’, the Gamma function is undoubtedly the most fundamental”. A classical reference on the Gamma function is given by Artin [2]. The Gamma function has numerous remarkable properties that are surveyed in [3]. For example, one of its classical applications is the formula for the volume of an n-dimensional ball.

The reciprocal Gamma function is a normalization constant in all of the classical fractional derivative operators: the Riemann–Liouville, Caputo, and Grünwald–Letnikov. The reciprocal Gamma function is also prominent in the analytic number theory and its various connections to other transcendental functions (for example, the Riemann zeta function). Therefore, methods for the fast computation of the reciprocal Gamma function for arbitrary arguments may be beneficial for numerical applications of fractional calculus.

In the special function theory, the Gamma function is used explicitly in the definitions of the Fox type and Fox–Wright type of special functions, which are related to actions of fractional differential operators [4].

In a previous work, I investigated an approach to regularize derivatives at points where the ordinary limit diverges [5]. This paper exploits the same approach for the purposes of numerical computation of singular integrals, such as the Euler $\Gamma$ integrals for negative arguments.

The present paper proves a real singular integral representation of the reciprocal $\Gamma$ function. The algorithm was implemented in the computer algebra system Maxima for reference and demonstration purposes.

As a second application, the paper provides an integral representation of the Gamma function for negative numbers related to the Cauchy–Saalschütz integral [6]. The algorithm was also implemented in Maxima. Finally, the paper demonstrates an equivalent regularized complex representation based on the regularization of the Heine integral. The regularization procedure can be expressed in terms of the two-parameter Mittag-Leffler function.

2. Preliminaries and Notation

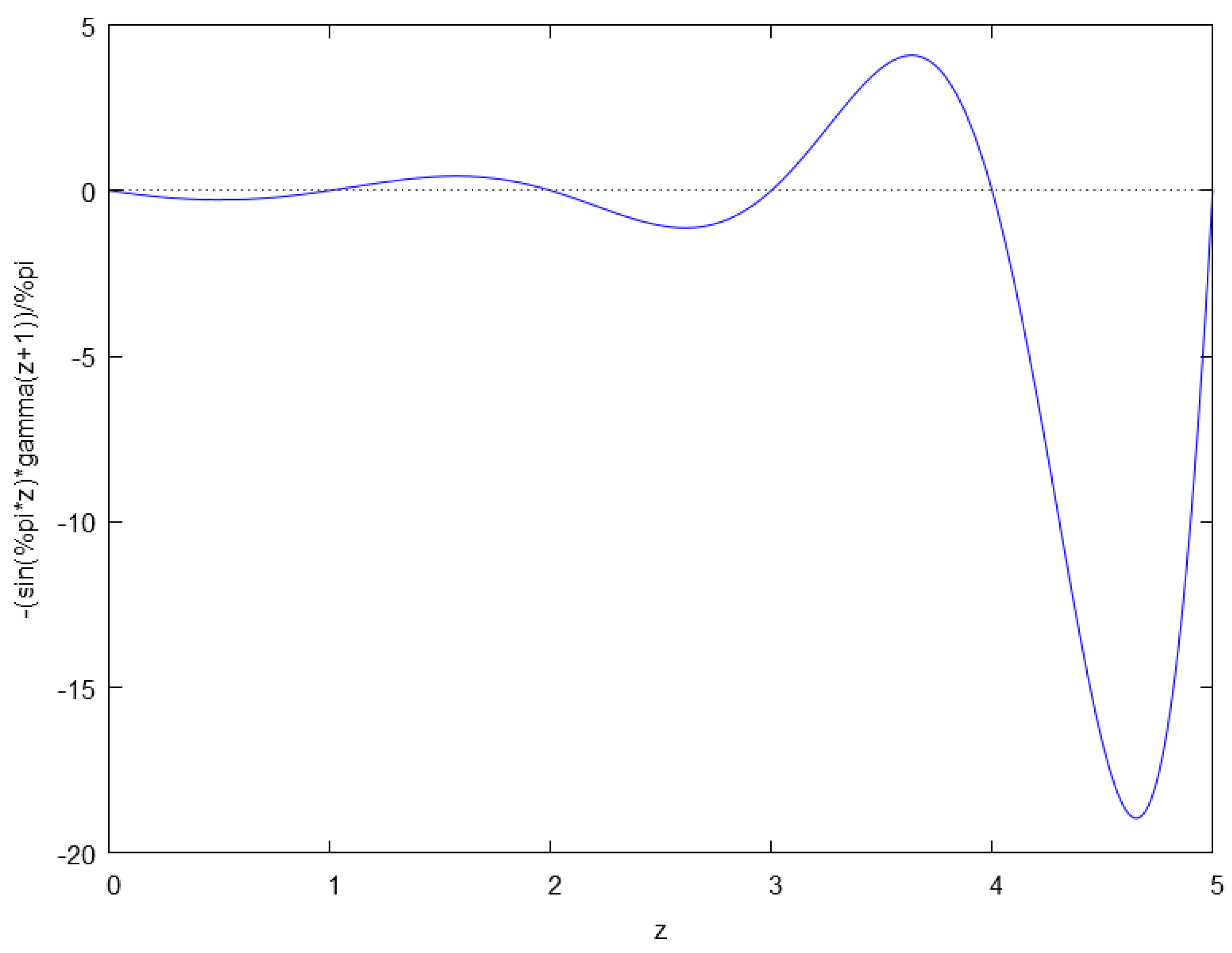
The reciprocal Gamma function is an entire function. Starting from the Euler’s infinite product definition, the reciprocal Gamma function can be defined by the infinite product:

$$\frac{1}{\Gamma \left(z\right)}:=\underset{n\to \infty }{lim}\frac{z\left(z+1\right)\dots \left(z+n\right)}{n^{z}n!}$$

Proceeding from the Euler’s reflection formula for negative arguments, the reciprocal Gamma function is simply

$$\frac{1}{\Gamma (-z)}=-\frac{sin\pi z}{\pi }\Gamma (z+1)$$

(1)

The plot of the above function is presented in Figure 1.

Figure 1. $1/\Gamma (-z)$ computed from Equation (1).

2.1. Real Representations

The Euler’s Gamma function integral representation is valid for real $z>0$ or complex numbers such that $Rez>0$

$$\Gamma \left(z\right)={\int }_0^{\infty }{e}^{-\tau }{\tau }^{z-1}d\tau$$

However, for negative z, the integral diverges. A less well-known integral representation for $Rez<0$ is the Cauchy–Saalschütz integral [7] (Chapter 3), also along the real line:

$$\Gamma (-z)={\int }_0^{\infty }\frac{e^{-\tau }-e_n(-\tau )}{{\tau }^{z+1}}d\tau$$

where $e_n\left(\right)$ is given by Definition 3.

2.2. Complex Representations

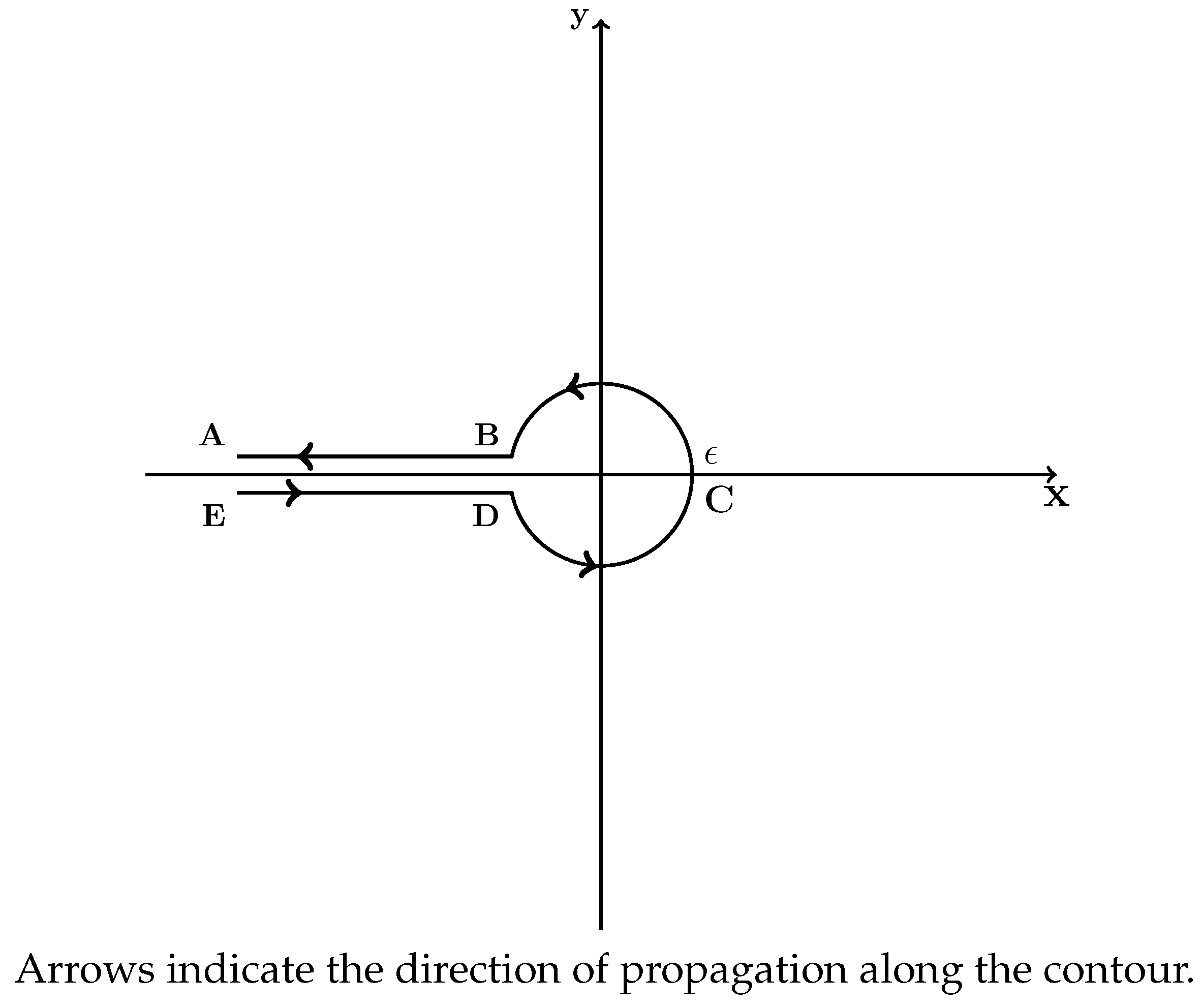
Hankel’s representation of the Gamma function is given as

$$\Gamma \left(z\right)=\frac{1}{2isin\left(\pi z\right)}{\int }_{H{a}^{-}}{e}^{\tau }{\tau }^{z-1}d\tau ,z\notin {\mathbb{Z}}^{}$$

Here, $H{a}^{-}$ denotes the Hankel contour in the complex $\zeta$-plane with a cut along the negative real semi-axis $arg\zeta =\pi$ and circulation in the positive direction. The contour is depicted in Figure 2.

Figure 2. The Hankel contour $H{a}^{-}$.

The Heine’s complex representation of the reciprocal Gamma function is well known and is given below [6] (p. 161):

$$\frac{1}{\Gamma \left(z\right)}=\frac{{(-1)}^{-z}}{2\pi i}{\int }_{H{a}^{+}}\frac{e^{-\tau }}{{\tau }^z}d\tau =\frac{1}{2\pi i}{\int }_{H{a}^{-}}\frac{e^{\tau }}{{\tau }^z}d\tau$$

$H{a}^{+}$ is the reflection of $H{a}^{-}$ across the origin. The integrand has a simple pole at $\tau =0$. The Hölder exponent at 0 can be computed in the closed interval $[0,ϵ]$ as

$$\underset{ϵ\to 0}{lim}\frac{log{e}^{ϵ}{ϵ}^{-z}}{logϵ}=-z+\underset{ϵ\to 0}{lim}\frac{ϵ}{logϵ}=-z$$

Therefore, for $k>\left[z\right]$, it holds that $\underset{ϵ\to 0}{lim}{ϵ}^k{e}^{ϵ}{ϵ}^{-z}=0$ and the order of the residue is the integer part $\left[z\right]$. This observation is indicative of the statement of the main result of the paper.

2.3. Auxiliary Notation

Definition 1.

For a real number z, the notation $\left[z\right]$ will mean the integral part of the number, while $\left\{z\right\}:=z-\left[z\right]$ will denote the non-integral remaining part.

Definition 2.

The falling factorial is defined as

$${\left(z\right)}_n:=\prod _{k=0}^{n-1}\left(z-k\right)$$

Definition 3.

Let

$$e_n\left(x\right):=\sum _{k=0}^n\frac{x^k}{k!}$$

be the truncated Taylor polynomial under the convention $e_{-1}\left(x\right)=0$.

3. Theoretical Results

Theorem 1 (Real Reciprocal Gamma Representation).

Let $z>0$, $z\notin {\mathbb{Z}}^{}$ and $n=\left[z\right]$. Then

$$\frac{1}{\Gamma \left(z\right)}=\frac{sin\pi z}{\pi }{\int }_0^{\infty }\frac{e^{-x}-e_{n-1}(-x)}{x^z}dx=Im\frac{1}{\pi }{\int }_{-\infty }^0\frac{e^x-e_{n-1}\left(x\right)}{x^z}dx$$

where the integrals are over the real axis.

Proof. 

First, we establish two preliminary results. Consider the following limit of the form $0/0$ and apply n times l’Hôpital’s rule:

$$L_z=\underset{x\to 0}{lim}\frac{e^x-e_n\left(x\right)}{x^z}=\frac{1}{{\left(z\right)}_n}\underset{x\to 0}{lim}\frac{e^x-1}{x^{z-n}}$$

Another application of l’Hôpital’s rule leads to

$$L_z=\frac{1}{{\left(z\right)}_n(z-n)}\underset{x\to 0}{lim}{e}^x{x}^{n+1-z}$$

Therefore,

$$L_z=\left\{\begin{array}{cc}0,\hfill & z<n+1\hfill \\ \frac{1}{\Gamma (n+1)},\hfill & z=n+1\hfill \\ \infty ,\hfill & z>n+1\hfill \end{array}\right.$$

Secondly, consider the limit

$$M_z=\underset{x\to -\infty }{lim}\frac{e^x-e_n\left(x\right)}{x^z}=M_z=\underset{x\to -\infty }{lim}\frac{e^x}{x^z}-\sum _{k=0}^n\underset{x\to -\infty }{lim}\frac{x^{k-z}}{\Gamma (k+1)}$$

Therefore,

$$M_z=\left\{\begin{array}{cc}\infty ,\hfill & z<n\hfill \\ \frac{1}{\Gamma (n+1)},\hfill & z=n\hfill \\ 0,\hfill & z>n\hfill \end{array}\right.$$

Therefore, in order for both limits to vanish simultaneously, $n<z<n+1$. Therefore, $n=\left[z\right]$. Let $\left\{z\right\}=z-\left[z\right]$.

In the following, we take $x^z$ as its principal value. Then,

$$\begin{array}{ccc}{I}_{n+1}(z+1)\hfill & =\hfill & {\int }_{-\infty }^0\frac{e^x-e_n\left(x\right)}{x^{z+1}}dx={\left.\frac{e^x-e_n\left(x\right)}{z{x}^z}\right|}_0^{\infty }+\frac{1}{z}{\int }_{-\infty }^0\frac{{\left(e^x-e_n\left(x\right)\right)}^{\prime }}{x^z}dx\hfill \\ & =\hfill & \frac{1}{z}{\int }_{-\infty }^0\frac{e^x-e_{n-1}\left(x\right)}{x^z}dx=\frac{1}{z}{I}_n\left(z\right)\hfill \end{array}$$

by the above results. Therefore, by reduction,

$$\begin{array}{ccc}{I}_{n+1}(z+1)\hfill & =\hfill & \frac{1}{{\left(z\right)}_n}{I}_0(z-n)=\frac{1}{{\left(z\right)}_n}{I}_0\left(\left\{z\right\}\right)=\frac{1}{{\left(z\right)}_n}{\int }_{-\infty }^0\frac{e^x}{x^{\left\{z\right\}}}dx\hfill \\ & =\hfill & \frac{1}{{\left(z\right)}_n}{\int }_0^{\infty }\frac{e^{-x}}{{(-x)}^{\left\{z\right\}}}dx=e^{-i\pi \left\{z\right\}}\frac{\Gamma (1-\{z\left\}\right)}{{\left(z\right)}_n}\hfill \end{array}$$

Therefore,

$$\begin{array}{ccc}\Gamma \left(\left\{z\right\}\right)I_{n+1}(z+1)\hfill & =\hfill & \frac{e^{-i\pi \left\{z\right\}}}{{\left(z\right)}_n}\Gamma (1-\left\{z\right\})\Gamma \left(\left\{z\right\}\right)\hfill \\ & =\hfill & e^{-i\pi \left\{z\right\}}\frac{\pi }{{\left(z\right)}_{n}sin\pi \left\{z\right\}}=\frac{\pi }{{\left(z\right)}_n}(cot\pi \left\{z\right\}-i)\hfill \end{array}$$

by Euler’s reflection formula. We take the imaginary part of the integral, since $\Gamma \left(\right\{z\left\}\right)$ is real and the middle expression is imaginary. Therefore,

$$\frac{1}{\Gamma (z+1)}=\frac{1}{{\left(z\right)}_n\Gamma \left(\left\{z\right\}\right)}=Im\frac{1}{\pi }{I}_{n+1}(z+1)$$

Therefore,

$$\frac{1}{\Gamma \left(z\right)}=Im\frac{1}{\pi }{\int }_{-\infty }^0\frac{e^x-e_{n-1}\left(x\right)}{x^z}dx$$

Finally, by change of variables $x\mapsto -x$,

$$\frac{1}{\Gamma \left(z\right)}=-Im\frac{1}{\pi }{\int }_{\infty }^0\frac{e^{-x}-e_{n-1}(-x)}{{(-x)}^z}dx=\frac{sin\pi z}{\pi }{\int }_0^{\infty }\frac{e^{-x}-e_{n-1}(-x)}{x^z}dx$$

□

Corollary 1.

By change of variables, it holds that

$$\frac{1}{\Gamma \left(z\right)}=\frac{sin\pi z}{\pi z}{\int }_0^{\infty }{u}^{\frac{1}{z}-2}\left(e^{-u^{\frac{1}{z}}}-\sum _{k=0}^{n-1}\frac{{\left(-1\right)}^k{u}^{\frac{k}{z}}}{k!}\right)du$$

The latter result can be useful for computations with large arguments of $\Gamma$.

Corollary 2 (Modified Euler Integral of the Second Kind).

By change of variables, it holds that, for $z>0$,

$$\frac{1}{\Gamma \left(z\right)}=\frac{sin\pi z}{\pi }{\int }_0^1\frac{1}{u{\left(logu\right)}^z}\left(u-\sum _{k=0}^{n-1}\frac{{(logu)}^k}{k!}\right)du=\frac{sin\pi z}{\pi }{\int }_0^1\frac{1-e_{n-1}\left(logu\right)/u}{{\left(log1/u\right)}^z}du$$

Finally, it is instructive to demonstrate the correspondence between the complex-analytical representation and the hypersingular representation.

Theorem 2 (Regularized Complex Reciprocal Gamma Representation).

For $Rez>0$, $z\notin {\mathbb{Z}}^{}$ and $n=\left[Rez\right]$,

$$\frac{1}{\Gamma \left(z\right)}=\frac{1}{2\pi i}{\int }_{H{a}^{-}}\frac{e^{\tau }-e_{n-1}\left(\tau \right)}{{\tau }^z}d\tau$$

where $\tau \in {\mathbb{C}}^{}$.

Proof. 

The proof technique follows [8]. We evaluate the line integral along the Hankel contour:

$$I_n\left(z\right)=\frac{1}{2\pi i}{\int }_{H{a}^{-}}\frac{e^{\tau }-e_{n-1}\left(\tau \right)}{{\tau }^z}d\tau$$

with kernel

$$Ker\left(\tau \right)=\frac{e^{\tau }-e_{n-1}\left(\tau \right)}{{\tau }^z},Rez>0$$

The contour is depicted in Figure 2. The integral can be split into three parts,

$${\int }_{Ha}Ker\left(\tau \right)d\tau ={\int }_{AB}Ker\left(\tau \right)d\tau +{\int }_{BCD}Ker\left(\tau \right)d\tau +{\int }_{DE}Ker\left(\tau \right)d\tau$$

along the rays AB, DE, and the arc BCD, respectively. Along the ray AB, where $\tau =r{e}^{i\delta }$, the kernel becomes

$$Ke{r}_A=\frac{1}{r^z}\left(e^{e^{i\delta }-i\delta zr}-\sum _{k=0}^{n-1}\frac{e^{i\delta k-i\delta z}{r}^k}{k!}\right)$$

Along the ray DE, where $\xi =r{e}^{-i\delta }$, the kernel becomes

$$Ke{r}_B=\frac{1}{r^z}\left(e^{e^{-i\delta }+i\delta zr}-\sum _{k=0}^{n-1}\frac{e^{-i\delta k+i\delta z}{r}^k}{k!}\right)$$

Therefore, changing the direction of DE, the rays can be added as

$$\begin{array}{ccc}{K}_{\delta }\hfill & =\hfill & Ke{r}_A{e}^{i\pi \delta }-Ke{r}_B{e}^{-i\pi \delta }\hfill \\ & =\hfill & \frac{e^{-i\delta }}{r^z}\left(-e^{i\delta z+e^{-i\delta }r}+\left(\sum _{k=0}^{n-1}\frac{e^{-i\delta k}{r}^k}{k!}\right)e^{i\delta z}-e^{2i\delta -i\delta z}\left(\sum _{k=0}^{n-1}\frac{e^{i\delta k}{r}^k}{k!}\right)+e^{e^{i\delta }r+2i\delta }\right)\hfill \end{array}$$

For $\delta =\pi$

$$K_{\pi }=\frac{2isin\left(\pi z\right)}{r^z}\left(e^{-r}-\sum _{k=0}^{n-1}\frac{{\left(-r\right)}^k}{k!}\right)$$

Therefore,

$$\underset{\delta \to \pi }{lim}\frac{1}{2\pi i}{\int }_0^{\infty }{K}_{\pi }dr=\frac{sin\left(\pi z\right)}{\pi }{\int }_0^{\infty }\frac{e^{-r}-e_{n-1}(-r)}{r^z}dr$$

by Azrelá’s theorem.

The integral on the (closure of the) arc BCD is given by the Cauchy Residue Theorem. By the above observation, the residue at $\tau =0$ is given by the limit

$$Res\left[Ker\right]\left(\tau \right)=\underset{\tau \to 0}{lim}{\tau }^{1-z}\left(e^{\tau }-e_{n-1}\left(\tau \right)\right)=\underset{\tau \to 0}{lim}\tau L_z=0,z\le n+1$$

since $L_z=0$. Therefore, in the limit where the arc closes to a circle,

$${\oint }_{BCD}Ker\left(\tau \right)d\tau =0$$

Furthermore, after integration by parts,

$$I_n\left(z\right)=-{\left.\frac{e^{\tau }-e_{n-1}\left(\tau \right)}{{\tau }^{z-1}}\right|}_{H{a}^{-}}+\frac{1}{2\pi i(z-1)}{\int }_{H{a}^{-}}\frac{e^{\tau }-e_{n-2}\left(\tau \right)}{{\tau }^{z-1}}d\tau =\frac{1}{z-1}{I}_{n-1}\left(z\right)$$

since $M_z=0$. Therefore, the claim follows by reduction to $n=0$ □.

Remark 1.

These results demonstrate that the regularized complex contour integral can be collapsed to an integral along the real line. The same principle can be used for the regularization of other nonlinear functions; for example, the Beta function or the Wright function [8].

It is interesting to note a connection to the Mittag-Leffler function.

Definition 4 (Mittag-Leffler function).

The two-parameter Mittag-Leffler function [9] under the present convention is denoted by

$$E_{a,b}\left(z\right):=\sum _{k=0}^{\infty }\frac{z^k}{\Gamma (ak+b)}$$

Notably, the regularizing kernel can be expressed in terms of the two-parameter Mittag-Leffler function of integer arguments. The basis for the computation is the following auxiliary result:

Proposition 1.

$$e^x-e_{n-1}\left(x\right)=x^n{E}_{1,n+1}\left(x\right)$$

Proof. 

By direct computation,

$$e^x-e_{n-1}\left(x\right)=\sum _{k=n}^{\infty }\frac{x^k}{\Gamma (k+1)}=\sum _{j=0}^{\infty }\frac{x^{j+n}}{\Gamma (j+n+1)}=x^n{E}_{1,n+1}\left(x\right)$$

□

Therefore, it directly follows that

Corollary 3.

For $Rez>0$, $z\notin {\mathbb{Z}}^{}$ and $n=\left[Rez\right]$,

$$\frac{1}{\Gamma \left(z\right)}=\frac{1}{2\pi i}{\int }_{H{a}^{-}}{\tau }^{n-z}{E}_{1,n+1}\left(\tau \right)d\tau =\frac{sin\pi z}{\pi }{\int }_0^{\infty }{x}^{n-z}{E}_{1,n+1}(-x)dx$$

where $\tau \in {\mathbb{C}}^{}$ and $x\in {\mathbb{R}}^{}$ in the last integral.

In a similar way, for an integer argument n, we have

Corollary 4.

For $n\in {\mathbb{N}}^{}$

$$\frac{1}{n!}=\frac{1}{\Gamma (n+1)}=\frac{1}{2\pi i}\oint \frac{e^{\tau }-e_{n-1}\left(\tau \right)}{{\tau }^{n+1}}d\tau =\frac{1}{2\pi i}\oint \frac{E_{1,n+1}\left(\tau \right)}{\tau }d\tau ,\tau \in {\mathbb{C}}^{}$$

where the circulation of the contour is counterclockwise around the origin.

Proof. 

The computation follows from the Cauchy formula for derivatives:

$$f^{\left(k\right)}\left(a\right)=\frac{k!}{2\pi i}{\oint }_{C_a}\frac{f\left(\tau \right)}{{\left(\tau -a\right)}^{k+1}}d\tau$$

Therefore, for $a=0$ and substitution $f\left(t\right)=e^t-e_{n-1}\left(t\right)$,

$$\frac{f^{\left(n\right)}\left(0\right)}{n!}=\frac{1}{n!}=\frac{1}{2\pi i}{\oint }_{C_0}\frac{f\left(\tau \right)}{{\tau }^{n+1}}d\tau =\frac{1}{2\pi i}\oint \frac{e^{\tau }-e_{n-1}\left(\tau \right)}{{\tau }^{n+1}}d\tau$$

For $n=1$, let $\tau =ϵe^{i\varphi }$. The integrand has the form $Q=i{e}^{ϵe^{i\varphi }}$. Therefore, in limit

$$\underset{ϵ\to 0}{lim}{\int }_{-\pi }^{\pi }i{e}^{ϵe^{i\varphi }}d\varphi ={\int }_{-\pi }^{\pi }id\varphi =2\pi i$$

Finally, we observe that

$$\frac{e^{\tau }-e_{n-1}\left(\tau \right)}{{\tau }^{n+1}}=\frac{E_{1,n+1}\left(\tau \right)}{\tau }$$

□

4. Applications

4.1. Laplace Transform Pairs

Consider the Laplace transform ${\mathcal{L}}_s:f\left(t\right)÷F\left(s\right)$. As a concrete application of Theorem 2, consider the pair

$$\begin{array}{cc}\hfill {\mathcal{L}}_s:t^k& ÷\frac{\Gamma (k+1)}{s^{k+1}},k>0\hfill \end{array}$$

The inverse Laplace transform can be calculated simply as

$$\begin{array}{c}{\mathcal{L}}_t^{-1}:\frac{\Gamma (k+1)}{s^{k+1}}÷\frac{1}{2\pi i}{\int }_{H{a}^{-}}\Gamma (k+1)\frac{e^{ts}-e_{\left[k\right]}\left(ts\right)}{s^{k+1}}ds=\frac{sin\pi (k+1)}{\pi i}\Gamma (k+1){\int }_{-\infty }^0\frac{e^{ts}-e_{\left[k\right]}\left(ts\right)}{s^{k+1}}ds=t^k\end{array}$$

by change of variables. The latter result can be used for numerical inversion of Laplace transforms.

4.2. Ratios of Gamma Functions

Secondly, the ratio of two Gamma functions can be represented as

Proposition 2.

Let $A,B>0$. Then,

$$\frac{\Gamma \left(A\right)}{\Gamma \left(B\right)}=\frac{1}{\pi }{\int }_0^1{\int }_0^1\frac{1-e_{n-1}\left(logu\right)/u}{{\left(logu\right)}^B}{\left(-logv\right)}^{A-1}dudv$$

where $n=\left[B\right]$.

Proof. 

$$\begin{array}{ccc}\frac{\Gamma (A+1)}{\Gamma \left(B\right)}\hfill & =\hfill & \frac{1}{\pi }{\int }_0^1\frac{1-e_{n-1}\left(logu\right)/u}{{\left(logu\right)}^B}du{\int }_0^1{\left(-logv\right)}^{A}dv\hfill \\ & =\hfill & \frac{1}{\pi }{\int }_0^1{\int }_0^1\frac{1-e_{n-1}\left(logu\right)/u}{{\left(logu\right)}^B}{\left(-logv\right)}^{A}dudv\hfill \end{array}$$

□

4.3. The Cauchy–Saalschütz Integral

Finally, for negative arguments:

Proposition 3.

For $z>0$, it holds that

$$\Gamma (-z)=-\frac{1}{z}{\int }_0^{\infty }\frac{e^{-x}-e_{n-1}(-x)}{x^z}dx$$

Proof. 

By the reflection formula,

$$\Gamma (1-z)\Gamma \left(z\right)=\frac{\pi }{sin\pi z}=-z\Gamma (-z)\Gamma \left(z\right)$$

Therefore,

$$\Gamma (-z)=-\frac{\pi }{zsin\pi z}\frac{1}{\Gamma \left(z\right)}=-\frac{1}{z}{\int }_0^{\infty }\frac{e^{-x}-e_{n-1}(-x)}{x^z}dx$$

□

Remark 2.

The latter result is equivalent to the classical Cauchy–Saalschütz integral representation [6] (p. 157), [7] (Chapter 3, p. 4). Indeed, by integration by parts,

$$\begin{array}{ccc}\Gamma (-z)\hfill & =\hfill & -\frac{1}{z}{\int }_0^{\infty }\frac{e^{-x}-e_{n-1}(-x)}{x^z}dx=\frac{1}{z}{\int }_0^{\infty }\frac{d(e^{-x}-e_n(-x))}{x^z}\hfill \\ & =\hfill & {\left.\frac{e^{-x}-e_n(-x)}{x^z}\right|}_0^{\infty }-\frac{-z}{z}{\int }_0^{\infty }\frac{e^{-x}-e_n(-x)}{x^{z+1}}dx={\int }_0^{\infty }\frac{e^{-x}-e_n(-x)}{x^{z+1}}dx\hfill \end{array}$$

which is the Cauchy–Saalschütz integral.

4.4. The Grünwald–Letnikov Derivative

The Grünwald–Letnikov derivative is defined [10] as

$${\mathbb{D}}_{\mp }^{q}f\left(x\right):=\underset{h\to 0}{lim}\frac{1}{h^q}\sum _{m=0}^{\left[\frac{x-a}{h}\right]}{(\pm 1)}^m\frac{\Gamma (q+1)}{\Gamma (m+1)\Gamma (q-m+1)}f(x\pm mh),h=\frac{x-a}{N},q>0$$

For numerical applications, the limit is approximated as the finite difference for some large $N\in {\mathbb{N}}^{}$. Therefore, Theorem 1 can be directly applied to compute the approximation for small m. For large m, on the other hand, the Stirling asymptotic formula can be used. Pursuing such application, however, goes beyond the scope of the present paper.

5. Numerical Implementation

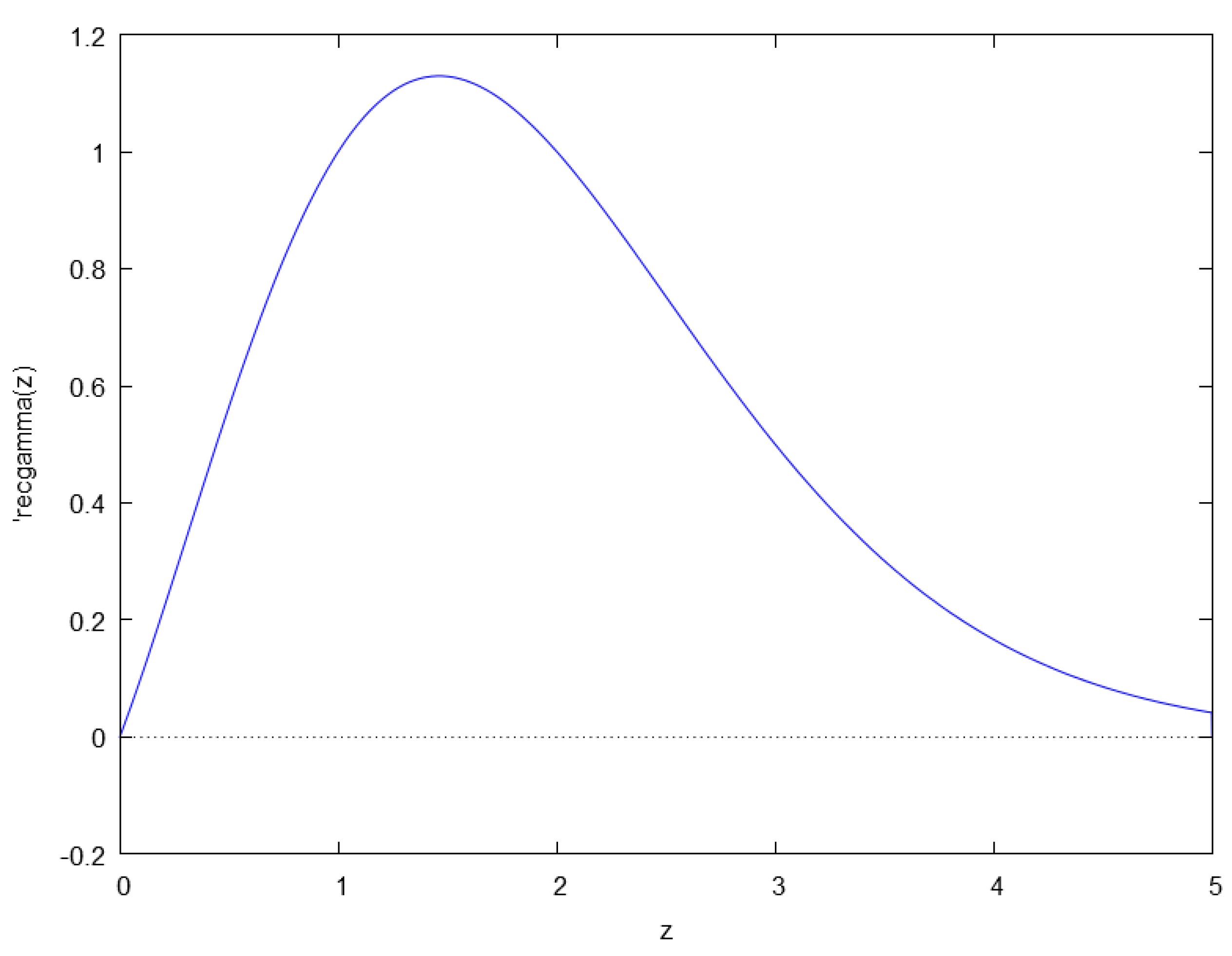
A reference implementation in the computer algebra system Maxima is given in Listings 1 and 2. The numerical integration code uses the library Quadpack, distributed with Maxima. The reference implementation given in this section uses a routine for semi-infinite interval integration with a tunable relative error of approximation (i.e., the epsrel parameter). A plot of the reciprocal $\Gamma$ function computed from Listing 1 is presented in Figure 3.

Figure 3. $1/\Gamma \left(z\right)$ computed from Theorem 1.

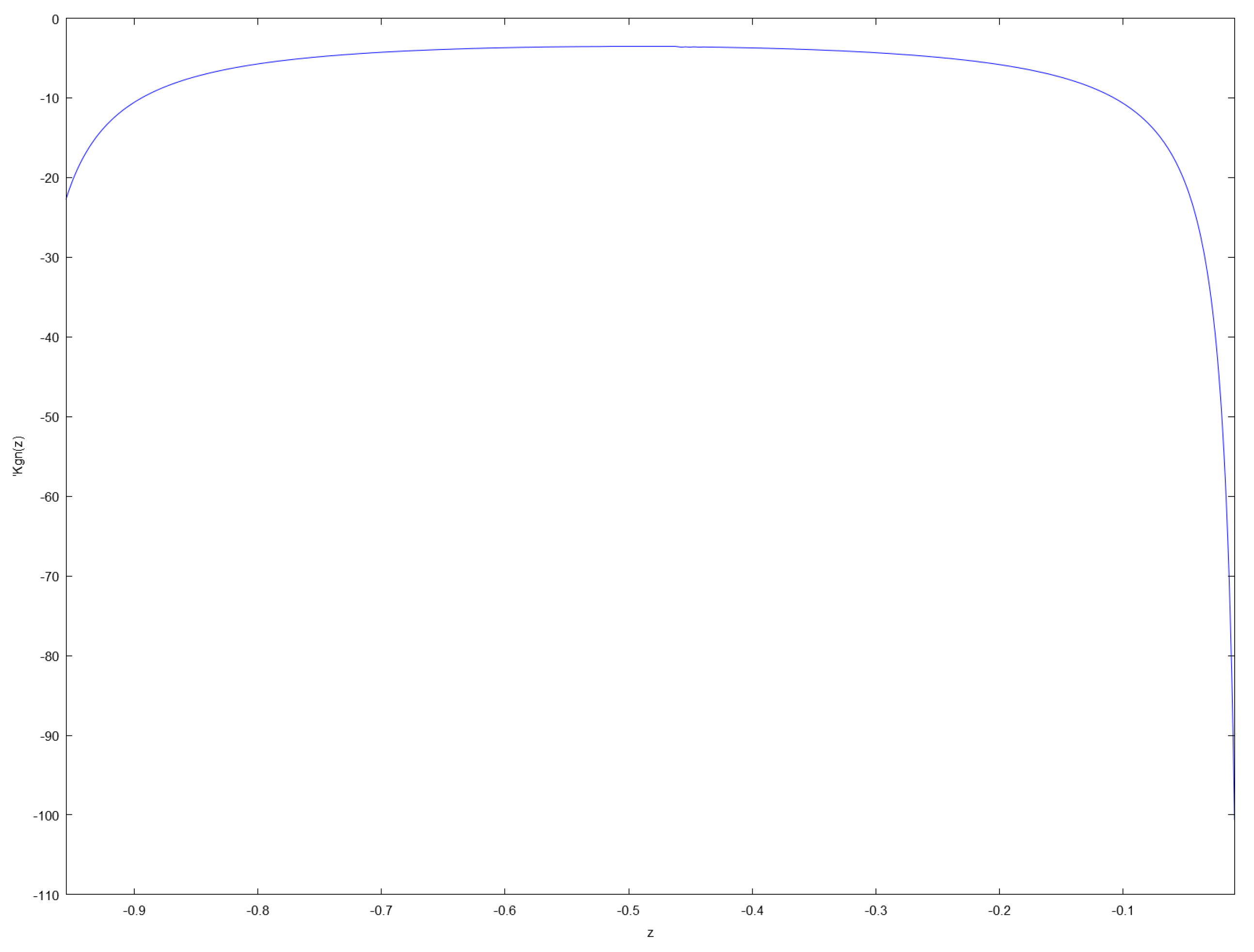
Figure 4 represents a plot of $\Gamma (-z)$ computed from Listing 1.

Figure 4. $\Gamma (-z)$ computed from Proposition 3.