Abstract
In the present study, the nonlinear vibration of a nanobeam resting on the fractional order viscoelastic Winkler–Pasternak foundation is studied using nonlocal elasticity theory. The D’Alembert principle is used to derive the governing equation and the associated boundary conditions. The approximate analytical solution is obtained by applying the multiple scales method. A detailed parametric study is conducted, and the effects of the variation of different parameters belonging to the application problems on the system are calculated numerically and depicted. We remark that the order and the coefficient of the fractional derivative have a significant effect on the natural frequency and the amplitude of vibrations.
1. Introduction
Due to the recent and rapid advances in nanomechanics, nanobeams have become the most important structures used extensively in technology such as nano-electromechanical systems (NEMs), opto-mechanical or nanoresonator devices. The exclusive properties of nanoscale beams are due to their size, and this size plays an important role in static and in dynamic analysis. In front of the difficulties of classical continuum mechanics in considering the size effect in modeling the behavior of this kind of structure, various size-dependent continuum theories have been developed. These theories include nonlocal continuum theory, strain gradient theory or a combination of both (nonlocal strain gradient theory), modified couple stress theory, micropolar theory and the surface elasticity theory. Among these theories, Eringen’s nonlocal elasticity theory [1,2] was utilized by a number of researchers to capture size-effects.
These kinds of structures can be modeled as a beam structure on a viscoelastic foundation. The beam can be modeled as a Timoshenko beam [3,4], or as a Rayleigh beam [5], or as a Euler–Bernouilli beam [6], and the foundation as a Winkler model [7,8,9], or as a Pasternak model, or a combination of both (Winkler–Pasternak model), or as a nonlinear elastic model and the fractional order viscoelastic model [10]. The Winkler model is a one-parameter model, namely the Winkler-type elastic foundation consists of a series of closely-spaced elastic springs. The Pasternak model is a two-parameter model, namely the Pasternak-type viscoelastic foundation consists of Winkler-type elastic springs and transverse shear deformation. The nonlinear model is a three parameter one in which the layer is indicated by the linear elastic spring, shear deformation and cubic nonlinearity elastic spring.The fractional order Winkler–Pasternak [10] has been well developed. This fractional order is due to the long memory effects of some kinds of viscoelastic materials. In vibration analysis of nanostructures, it is very important to evaluate the impact of the surrounding medium on the dynamic of beams. Niknam and Aghdam [11] proposed an analytical approach to study dynamic of nonlocal functionally graded beam resting on nonlinear elastic support. A meshless approach for free transverse vibration of single-walled carbon nanotube (SWCNT) was proposed by Kiani [12]. Eringens nonlocal theory and Timoshenko beam theory were used to make a buckling analysis of SWCNT on elastic medium [13,14]. Non-conservative dynamic of nonlocal cantilever carbon nanotubes (CNTs) on viscoelastic medium is proposed [15]. Mikhasev [16] researched localized modes of free vibrations of SWCNT. Mustapha and Zhong [17] studied the dynamics of non-prismatic SWCNT in a viscoelastic medium. Lee and Chang [18] studied the dynamics of a viscous fluid conveying SWCNT. Kiani [19,20] examined elastically-restrained double-walled carbon nanotube (DWCNT) and SWCNT for delivering nanoparticles. Instability analysis of CNT conveying fluid was conducted [21]. Yas and Samadi [22] examined CNT-reinforced composite on and elastic medium. A small scale effect in nonuniform CNT conveying fluid on the viscoelastic medium was examined [23]. Aydogdu [24] analyzed nanorods on an elastic medium. Dynamic analysis of nanotubes on elastic matrix was conducted by Wang [25]. Dynamics of curved SWCNT on a Pasternak elastic foundation was examined [26]. Aydogdu and Arda [27] researched the torsional dynamics of nonlocal DWCNTs. Necla [28] studied the nonlinear vibration of a nonlocal nanobeam resting on a Winkler-type foundation. The work of Anague [10] is based on the dynamics of Rayleigh beams resting on a fractional order viscoelastic Pasternak foundation subjected to moving loads.
Many time-space differential equations are very difficult to solve; sometimes, these equations are exactly impossible to solve. In front of these difficulties, a sophisticated analytical and numerical method to find approximated solutions is needed. Ozturk and Coskun [29] proposed the homotopy perturbation method. The multiple scale method was used to analyze the nonlinear vibration of CNT [30,31,32,33]. He’s variational method exhibited more advantages [12,34,35,36,37]. The direct iterative method was used in dynamical analysis of DWCNT [38]. The finite element method [21,23] and the differential quadrature method [13,22] also exhibited more advantages.
The above investigations clearly show that most of the studies presented in the literature are related to nonlocal and nonlinear structures, but studies on the nonlocal and nonlinear fractional order vibration are very limited. When it is observed in the field, the linear frequency amplitude and nonlinear frequency amplitude of beams are major topics, but dynamic analysis of beams embedded in a fractional order viscoelastic medium is very rare. The nonlinear free vibration of the nanotube with the damping effect was studied by using nonlocal elasticity theory [31]. To our knowledge, there is no published work on a fractional order nonlocal nonlinear vibration of a nanobeam resting on a viscoelastic foundation. The nonlinearity of the problem is obtained by considering the von Karman geometric nonlinearity, which introduces a cubic nonlinearity into the equations. In the present paper, we analyze the nonlinear vibration of a nanobeam resting on a fractional order viscoelastic Winkler–Pasternak foundation using Eringen’s nonlocal elasticity. Nonlinear fractional order frequency response and mode shapes are drawn for the nanobeam with different end conditions.
2. Preliminaries
2.1. Fractional Order Viscoelasticity
Fractional calculus is a part of mathematical analysis that has found many applications in nanomechanics. The role of fractional calculus is to study arbitrary real or complex order integrals and derivatives. There are many definitions of fractional order integrals and derivatives that have been given by different authors. However, in our study, we will consider only Riemann–Liouville’s definition of a fractional derivative as follows: If is an absolutely continuous function in and , then:
- The left Riemann–Liouville fractional derivative of order is of the form:
- The right Riemann–Liouville fractional derivative of order is of the form:
Fractional derivatives are used in the accurate modeling in rheology, as well as structural mechanics to model internal damping. In [39], it was shown that classical viscoelastic models failed to describe the damping of a viscoelastic solid and that improved fractional derivative-based models need to be considered. Such models have few advances. First, they are based on molecular theories [40]. Second, such models satisfy thermodynamic laws. At least, they need a few parameters to describe the viscoelastic behavior.
In the following, we give a constitutive relation of the fractional order viscoelastic Winkler–Pasternak foundation beam interaction force (per unit length of the beam’s axis), which is obtained including the fractional derivative term as [10]:
in which the deformed beam can be described by the transverse deflection , k and c are the foundation stiffness and damping coefficients and and are the foundation shear elastic and viscosity coefficients. is the fractional derivative with order .
2.2. Nonlocal Theory
In the nonlocal elasticity theory, the stress at a point x is a function of the strains at all other points of an elastic body. The integral form of the nonlocal constitutive relation for a three-dimensional structure is:
where is the nonlocal stress tensor, is the local or classical stress tensors at a point , denotes the attenuation function, which incorporates nonlocal effects into the constitutive equation, is the distance in the Euclidean norm and is a nonlocal parameter, where l is the external characteristic length (crack length or wave length), a is the internal characteristic length (lattice parameter, granular, etc.) and e0 is a material constant that can be determined from molecular dynamics simulations or by using the dispersive curve of the Born–Karman model of lattice dynamics. Later, Eringen [2] proposed a differential form of the constitutive relation with an appropriate kernel function as:
For the one-dimensional case, the local stress at a point can be explained according to Hooke’s law as:
where E denotes the elastic modulus and the strain. That yields the following differential form of the nonlocal constitutive equation for a one-dimensional elastic body:
where is the nonlocal parameter and is the nonlocal stress.
3. Governing Equation of the Nanobeam Resting on the Fractional Order Viscoelastic Foundation
This study is carried out on the basis of the nonlocal Euler–Bernouilli nanobeam of length L, cross-sectional area A, density and transverse deflection in the z direction. Two types of boundary conditions, which are simple-simple and clamped-clamped, are considered in this work and shown in Figure 1. We assume that the cross-sectional area is constant along the x coordinate and that the material of the nanobeam is homogeneous. The nanobeam is resting on a fractional order viscoelastic Winkler–Pasternak foundation in which k and c are the stiffness and damping coefficient and and are the foundation shear elastic and viscosity coefficients. We also consider that the nanobeam is under the influence of time varying axial load. According to Euler–Bernouilli beam theory, the displacement fields at any point of the beam can be expressed as:
where u and w are the axial and transverse displacements, respectively. By assuming the von Karman nonlinear strain displacement relation for the given displacement fields, we get:
where is the nonlinear extensional strain and is the bending strain. The von Karman nonlinear normal strain can be expressed as:
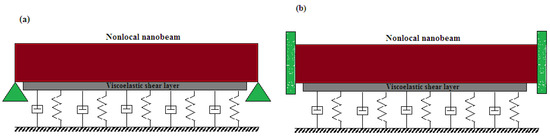
Figure 1.
Boundary conditions for different beam supports. (a) Simple-simple case and (b) clamped-clamped case.
By applying the D’Alembert principle to the infinitesimal element of the nanobeam, the equilibrium equation can be obtained as:
in which the stress resultant is defined as:
where Q, T and M are the transversal force, the axial force and the bending moment, respectively. and are the shear and normal stress components. The longitudinal inertia can be neglected based on the discussion about the nonlinear vibration of continuous systems [41,42], then the axial normal force T can be represented as:
Assuming that the axial force is periodic and time-dependent and combining Equations (7) and (11), the nonlinear vibration equation of motion for the nanobeam resting on the fractional order viscoelastic Pasternak-type foundation in terms of transversal displacements is obtained as follows:
where F is the amplitude of axial load and is the frequency of this load. The following non-dimensional quantities aim to study the problem in the general form as:
The non-dimensional Equations (14) and (15) can be expressed as:
in which K and C denote dimensionless stiffness and viscosity medium, and denote the dimensionless shear elastic and viscosity coefficient, represent the dimensionless amplitude of axial load and , and denote the nonlocal parameter, transversal displacement and time, respectively, in dimensionless form. The small bookkeeping parameter is used to emphasize the transversal deformation, viscosity coefficients and tension fluctuation compared to the other terms.
The non-dimensional form of boundary conditions can be expressed as
Simple-simple case:
Clamped-clamped case:
Solution of the Governing Equation
The dimensionless fractional order nonlinear partial differential equation, Equation (16), describes the transversal vibration of the nanobeam resting on a fractional order viscoelastic foundation under the influence of periodic axial load. In order to obtain the asymptotic approximate solution in the first order for the problem, the perturbation method of multiple scales will be employed. By applying the Galerkin method, we assume the asymptotic approximate solution in the following form:
in which is the unknown time function and is the linear mode shape determined from the boundary conditions. The linear mode shapes of Equations (17) and (18) are given by:
The boundary conditions are applied, and the constants and can be obtained. Mode shapes of the linear first frequency are plotted in Figure 2 and Figure 3.
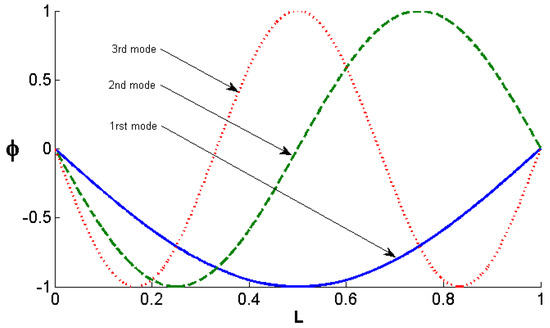
Figure 2.
First three vibration mode shapes for the simple-simple case boundary condition.
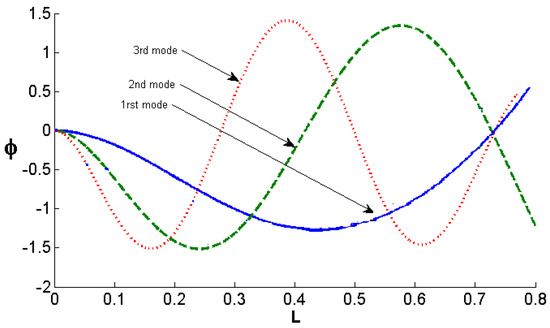
Figure 3.
First three vibration modes shapes for the clamped-clamped case boundary condition.
By introducing Equation (19) into Equation (16), multiplying the results by the linear mode shape function and then integrating them over the length of the nanobeam, we obtain a fractional order nonlinear ordinary differential equation expressed as:
where is the natural frequency for the linear system, and are normal damping ratio and shear damping ratio, is the reduced nonlinear stiffness and is the constant:
Equation (21) is a new form of parametrical; 7-excited Duffing differential equation due to the presence of the fractional order term. In order to determine the asymptotic approximate solution with combined effects of nonlinearity, parametric excitation and fractional order damping, we will apply the method of multiple scales. A straightforward asymptotic expansion can be introduced:
where and represent the fast and low timescale. The fast timescale is associated with the linear unperturbed system, while the slow timescale is characterized by the modulation of the amplitude and phase in the presence of possible resonance. Denoting , the ordinary time derivatives can be transformed into the partial derivative as:
Inserting Equations (23) and (24) into Equation (21), we obtain the following relation:
Fundamental frequencies are obtained by solving the first order of expansion, and the solvability condition is obtained by solving the second order of expansion. The solution of the first order equation is given as:
where , A is a complex function of slow timescale and is the complex conjugate. Excitation frequency is assumed close to one of the natural frequencies of the system; the dimensionless form of this excitation frequency can be written as:
where is a detuning parameter. Substituting Equation (26) into the second order of expansion and using the dimensionless form of excitation frequency yield:
where and represent the complex conjugate and the non-secular term, respectively. The solvability condition for Equation (28) is obtained as follows:
Taking into account the real amplitude a and phase , the complex amplitude A can be written as:
Then, the amplitude and phase modulation equations are:
in which is the new phase angle. In the steady-case, Equation (31) will be solved in a further section.
4. Numerical Results
Numerical examples of frequencies are presented in this section. The linear fundamental frequencies for different kinds of boundary conditions will be evaluated, and the fractional order nonlinear frequencies for free vibrations will also be evaluated in the case of the steady-state. To show the correctness of the presented study, we compared the obtained results to the results proposed by Mustapha and Zhong [17], Yokoyama [43] and Togun et al. [28]. A detailed parametric study was conducted to investigate the effects of system parameters such as stiffness, damping, the nonlocal parameter and fractional parameter on the dimensional fractional order nonlinear natural frequencies of the nanobeam with simple-simple boundary conditions and the frequency response curve obtained by the perturbation method. For free vibration , in the case of the steady-state, we obtain:
By introducing Equation (32) into Equation (31b), we get:
where and are the constants’ steady-state real amplitude and phase, which are determined from the initial conditions. Introducing the obtained results into Equation (26) gives the first order vibration response:
and hence, the fractional order nonlinear frequency is:
where is the nonlinear correction coefficient and the third term is a correction of the natural frequency due to the fractional order damping term. At the steady-state, and . The detuning parameter or the amplitude-frequency response is as follows:
Validation Study
Studies related to the nonlinear nonlocal nanobeam resting on a Winkler–Pasternak viscoelastic foundation in the literature are very limited. In order to validate the present analytical results for the amplitude-frequency response of the dynamical fractional order nonlinear nonlocal nano-beam with the simple-simple boundary condition, we compared the obtained results proposed by Mustapha and Zhong [17], Yokoyama [43] and Togun et al. [28]. Let us consider the case of free vibration and only the classical damping influence ; thus, the fractional order correction to the natural frequency is absent in Equations (35) and (36), and then, we recognize the common form of nonlinear frequency and the detuning parameter:
where is the nonlinear correction coefficient and the damping coefficient. The work of Mustapha and Zhong [17] studied the non-uniform SWCNT depending on a nonlocal Rayleigh beam resting on a Pasternak-type foundation. Yokoyama [43] studied the free transverse vibration of the classical Euler–Bernouilli beam resting on a Winkler–Pasternak foundation, and Togun et al. [28] studied the nonlinear vibration of a nonlocal nanobeam on a Winkler–Pasternak foundation using Euler–Bernouilli beam theory. A comparison study was performed to check the correctness of the present study. To this aim, the linear frequency of the local case of our nanobeam resting on a Winkler–Pasternak foundation for the simple-simple boundary condition was compared to those of the work of Mustapha and Zhong [17], Yokoyama [43] and Togun et al. [28]. It can be seen from Table 1 and Table 2 that there is good harmony among the four results.

Table 1.
The first five non-dimensional natural frequencies of a local Euler–Bernouilli beam resting on a Winkler–Pasternak foundation for the simple-simple boundary condition (, , , .

Table 2.
The first five non-dimensional natural frequencies of a local Euler–Bernouilli beam resting on a Winkler–Pasternak foundation for the simple-simple boundary condition (, , , .
Figure 4 shows the nonlocal parameter effect on the fractional nonlinear frequency; we observe that the natural frequency decreases when the nonlocal parameter increases. The variation of the fractional nonlinear frequency with the amplitude for the first three modes of vibration is shown in Figure 5; this figure shows that the fractional nonlinear frequencies increase with an increase in the mode number.
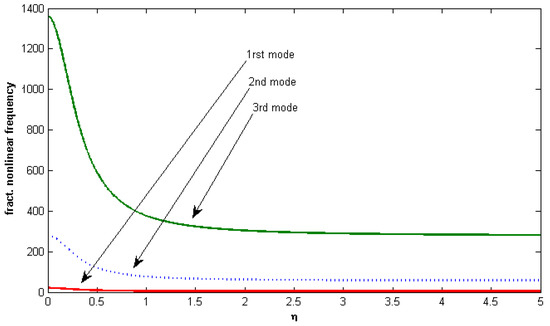
Figure 4.
First three modes of the fractional nonlinear frequency versus nonlocality (, , , ).
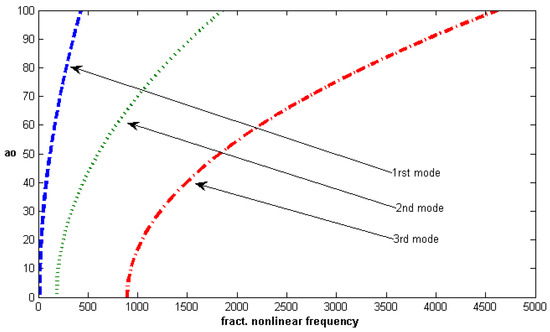
Figure 5.
First three modes of the fractional nonlinear frequency versus amplitude (, , , , ).
In Figure 6, Figure 7 and Figure 8, the fractional nonlinear frequency versus amplitude for different values of the system parameter are shown for the first mode of vibration. Figure 6 shows the effect of Pasternak parameter on the fractional nonlinear frequency versus amplitude curves, and we can observe in this figure that the fractional nonlinear frequency increases with an increase of . In Figure 7, the fractional nonlinear frequency also increases with an increase of Winkler stiffness parameter K. In Figure 8, the fractional nonlinear frequency versus amplitude for different values of fractional damping coefficient is drawn, and we can notice that the fractional nonlinear frequency increases slowly when the fractional damping coefficient increases. This is normal because the fractional nonlinear frequency has a direct relation to . Furthermore a hardening behavior can be observed in Figure 6, Figure 7 and Figure 8 because the fractional nonlinear frequency increases as the amplitude increases.
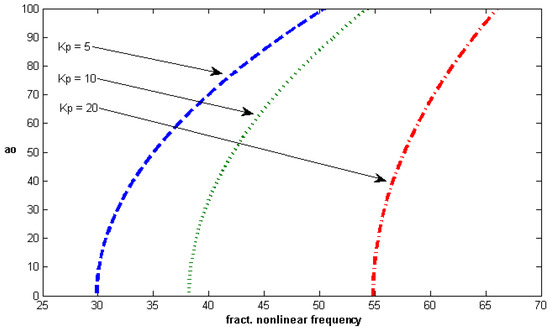
Figure 6.
Fractional nonlinear frequency versus amplitude for different values of (, , , ).
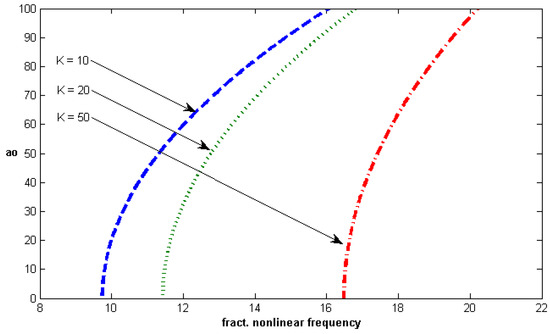
Figure 7.
Fractional nonlinear frequency versus amplitude for different values of K (, , , ).
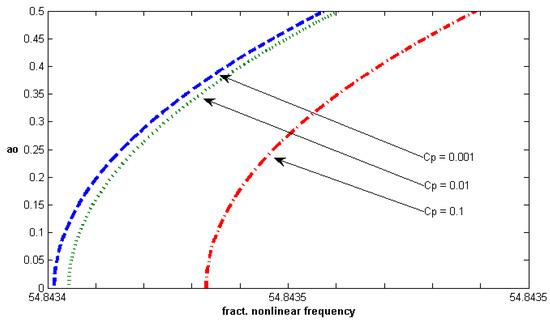
Figure 8.
Fractional nonlinear frequency versus amplitude for different values of (, , , ).
Frequency response curves are presented in Figure 9 for different values of the nondimensional nonlinear coefficient. In this figure, nonlinearity is actually observed. In Figure 10, Figure 11 and Figure 12, the fractional contribution frequency versus Winkler parameter K and nonlocal parameter for different values of fractional parameter are shown. It can be seen from Figure 10, Figure 11 and Figure 12 that the fractional contribution frequency increases and reaches the constant maximum value when the nonlocal parameter increases. For the small values of the nonlocal parameter, the fractional contribution increases quickly, but for the high values, this contribution is constant.
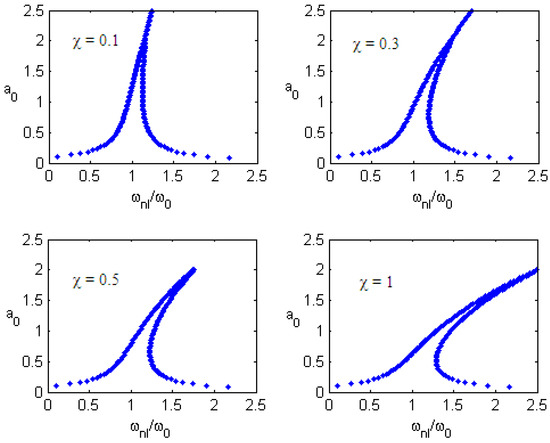
Figure 9.
Frequency-response curves versus amplitude for different values of (, , , , ).
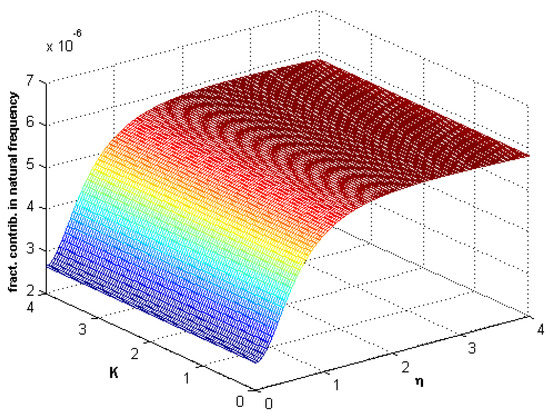
Figure 10.
Fractional contribution frequency versus stiffness K and nonlocality ().
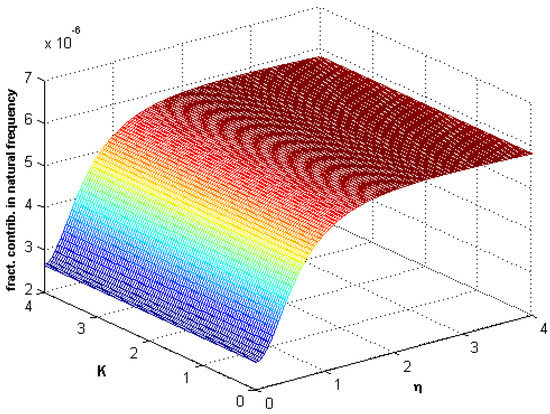
Figure 11.
Fractional contribution frequency versus stiffness K and nonlocality ().
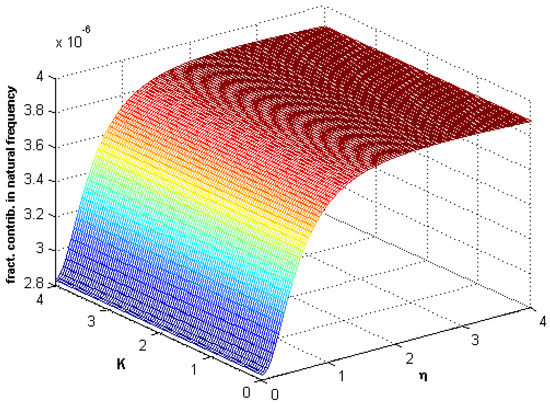
Figure 12.
Fractional contribution frequency versus stiffness K and nonlocality ().
In Figure 13 and Figure 14, the fractional contribution frequency versus Pasternak parameter and nonlocal parameter curves for different values of fractional parameter are drawn. It is observed that the variation of the fractional contribution depends on the interval of variation of the nonlocal parameter . For a small value of , the fractional contribution increases, but for a high value of , this fractional contribution decreases.
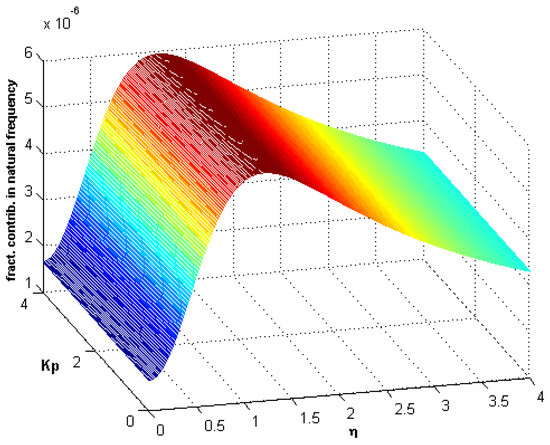
Figure 13.
Fractional contribution frequency versus stiffness and nonlocality ().
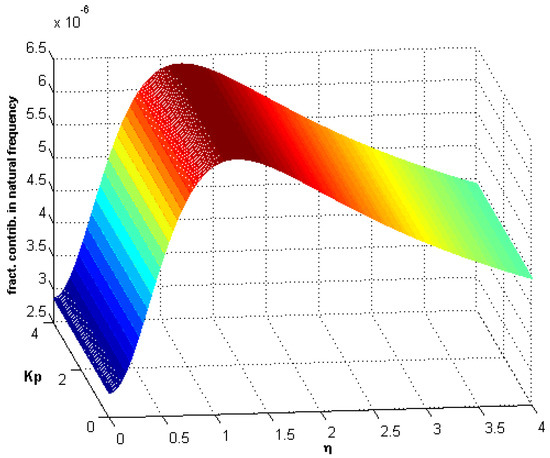
Figure 14.
Fractional contribution frequency versus stiffness and nonlocality ().
In Figure 15, Figure 16 and Figure 17, the fractional contribution frequency versus fractional damping coefficient and nonlocal parameter curves are shown for different values of fractional parameter . It can be seen that the fractional contribution increases when increases. In front of all these observations, it is normally easy to say that every system parameter has a significant effect on the natural frequency of the nanobeam, especially the fractional parameter and fractional damping coefficient.
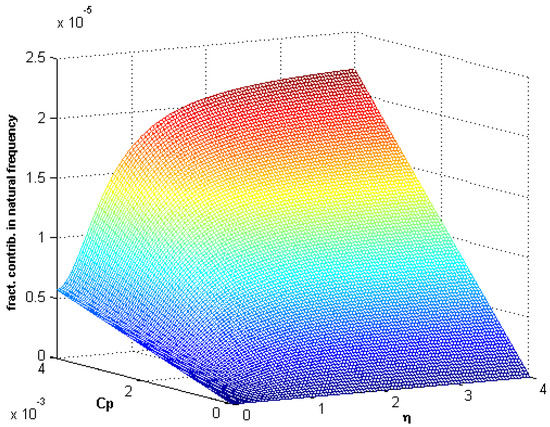
Figure 15.
Fractional contribution frequency versus fractional damping coefficient and nonlocality ().
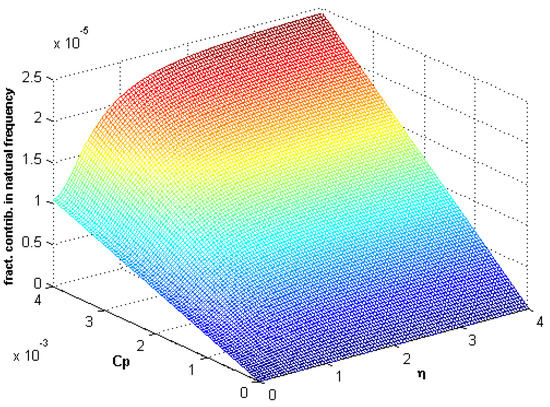
Figure 16.
Fractional contribution frequency versus fractional damping coefficient and nonlocality ().
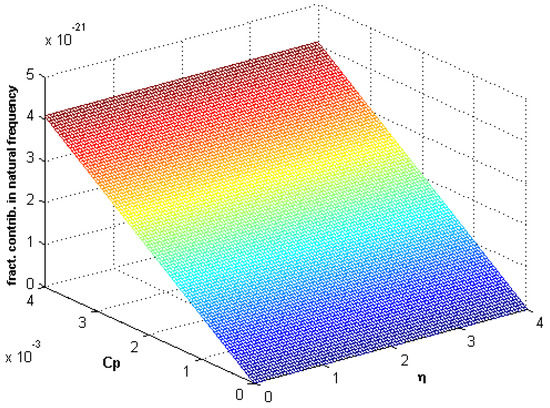
Figure 17.
Fractional contribution frequency versus fractional damping coefficient and nonlocality ().
5. Conclusions
In this study, using the fractional derivative, the nonlinear vibration of a nanobeam resting on a fractional order viscoelastic Winkler–Pasternak foundation is studied. For this purpose, Eringen’s nonlocal elasticity theory, the von Karman geometric nonlinearity and the Euler–Bernouilli beam theory are employed. The D’Alembert principle is used to derive the governing equation. In the solution procedure, using the Galerkin scheme, the fractional integro-partial differential governing equation is first simplified into the time-dependent fractional ordinary differential equation. This new equation is known as the fractional order nonlinear Duffing equation which is then solved by the multiple scales method. A detailed parametric study is conducted to get the effects of the system parameter such as the Winkler stiffness parameter, Pasternak stiffness parameter, nonlocal parameter, nonlinear coefficient, fractional damping coefficient and fractional parameter on the fractional nonlinear frequency of the nanobeam. It is found that fractional nonlinear frequency decreases when the nonlocal parameter increases. Furthermore, this fractional nonlinear frequency increases when the Winkler parameter, Pasternak parameter, mode, fractional damping coefficient and amplitude increase. It is further found that every parameter of the system has a significant effect on the fractional contribution frequency.
Author Contributions
All authors contributed extensively to the work presented in this paper. G.J.E. and B.G. obtained the equations, drew the figures and wrote the main paper. All authors discussed the results and implications and commented on the manuscript at all stages.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CNT | Carbon nanotube |
| SDCNT | Single-walled carbon nanotube |
| DWCNT | Double-walled carbon nanotube |
References
- Eringen, A.C. On differential equations of nonlocal elasticity and solution of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal Continuum Fields Theories; Springer: New York, NY, USA, 2002. [Google Scholar]
- Kargonovin, M.H.; Younesian, D.; Thompson, D.J.; Jones, C.J.C. Response of beams on the nonlinear viscoelastic foundations to harmonic moving loads. Comput. Struct. 2005, 83, 1865–1877. [Google Scholar] [CrossRef]
- Sapountzakis, E.J.; Kampitsis, A. Nonlinear response of shear deformable beams on tensionless nonlinear viscoelastic foundation under moving loads. J. Sound Vib. 2011, 330, 5410–5426. [Google Scholar] [CrossRef]
- Hryniewicz, Z. Dynamics of rayleigh beam on nonlinear foundation due to moving load using adomian decomposition and coiflet expansion. Soil Dyn. Earthq. Eng. 2011, 31, 1123–1131. [Google Scholar] [CrossRef]
- Ding, H.; Chen, Q.L.; Yang, S.P. Convergence of garlekin truncation for dynamic response of finite beams on nonlinear foundations under a moving load. J. Sound Vib. 2012, 331, 2426–2442. [Google Scholar] [CrossRef]
- Mathews, P.M. Vibrations of a beam on elastic foundation. J. Appl. Math. Mech. 1958, 38, 105–115. [Google Scholar] [CrossRef]
- Haitao, Y.; Yuan, Y. Analytical solution for an infinite euler-bernoulli beam on a visco-elastic foundation subjected to arbitrary dynamic loads. J. Eng. Mech. 2014, 140, 542–551. [Google Scholar]
- Achenbach, J.D.; Sun, C. Moving load on a flexibly supported timochenko beam. Int. J. Solids Struct. 1965, 1, 353–370. [Google Scholar] [CrossRef]
- Anague Tabejieu, L.M.; Nana Nbendjo, B.R.; Woafo, P. On the dynamics of rayleigh beams resting on fractional-order viscoelastic Pasternak foundations subjected to moving loads. Chaos Solitons Fract. 2016, 93, 39–47. [Google Scholar] [CrossRef]
- Niknam, H.; Aghdam, M.M. A semi analytical approach for large amplitude free vibration and buckling of nonlocal FG beams resting on elastic foundation. Compos. Struct. 2015, 119, 452–462. [Google Scholar] [CrossRef]
- Kiani, K. A meshless approach for free transverse vibration of embedded single walled nanotubes with arbitrary boundary conditions accounting for nonlocal effect. Int. J. Mech. Sci. 2010, 52, 1343–1356. [Google Scholar] [CrossRef]
- Murmu, T.; Pradhan, S.C. Buckling analysis of a single-walled carbon nanotube embedded in an elastic medium based on nonlocal elasticity and Timoshenko beam theory and using DQM. Physica E 2009, 41, 1232–1239. [Google Scholar] [CrossRef]
- Pradhan, S.C.; Reddy, G.K. Buckling analysis of single walled carbon nanotube on Winkler foundation using nonlocal elasticity theory and DTM. Comput. Mater. Sci. 2011, 50, 1052–1056. [Google Scholar] [CrossRef]
- Kazemi-Lari, M.A.; Fazelzadeh, S.A.; Ghavanloo, E. Non-conservative instability of cantilever carbon nanotubes resting on viscoelastic foundation. Physica E 2012, 44, 1623–1630. [Google Scholar] [CrossRef]
- Mikhasev, G. On localized modes of free vibrations of single-walled carbon nanotubes embedded in nonhomogeneous elastic medium. Z. Angew. Math. Mech. 2014, 94, 130–141. [Google Scholar] [CrossRef]
- Mustapha, K.B.; Zhong, Z.W. Free transverse vibration of an axially loaded non-prismatic single-walled carbon nanotube embedded in a two parameter elastic medium. Comput. Mater. Sci. 2010, 50, 742–751. [Google Scholar] [CrossRef]
- Lee, H.L.; Chang, W.J. Vibration analysis of a viscous-fluid-conveying single-walled carbon nanotube embedded in an elastic medium. Physica E 2009, 41, 529–532. [Google Scholar] [CrossRef]
- Kiani, K. Vibration analysis of elastically restrained double-walled carbon nanotubes on elastic foundation subject to axial load using nonlocal shear deformable beam theories. Int. J. Mech. Sci. 2013, 68, 16–34. [Google Scholar] [CrossRef]
- Kiani, K. Nonlinear vibrations of a single-walled carbon nanotube for delivering of nanoparticles. Nonlinear Dyn. 2014, 76, 1885–1903. [Google Scholar] [CrossRef]
- Ghavanloo, E.; Daneshmand, F.; Rafiei, M. Vibration and instability analysis of carbon nanotubes conveying fluid and resting on a linear viscoelastic Winkler foundation. Physica E 2010, 42, 2218–2224. [Google Scholar] [CrossRef]
- Yas, M.H.; Samadi, N. Free vibrations and buckling analysis of carbon nanotube-reinforced composite Timoshenko beams on elastic foundation. Int. J. Press Vessels Piping 2012, 98, 119–128. [Google Scholar] [CrossRef]
- Rafiei, M.; Mohebpour, S.R.; Daneshmand, F. Small-scale effect on the vibration of non-uniform carbon nanotubes conveying fluid and embedded in viscoelastic medium. Physica E 2012, 44, 1372–1379. [Google Scholar] [CrossRef]
- Aydogdu, M. Axial vibration analysis of nanorods (carbon nanotubes) embedded in an elastic medium using nonlocal elasticity. Mech. Res. Commun. 2012, 43, 34–40. [Google Scholar] [CrossRef]
- Wang, B.L.; Wang, K.F. Vibration analysis of embedded nanotubes using nonlocal continuum theory. Composites Part B Eng. 2013, 47, 96–101. [Google Scholar] [CrossRef]
- Mehdipour, I.; Barari, A.; Kimiaeifar, A.; Domairry, G. Vibrational analysis of curved single-walled carbon nanotube on a Pasternak elastic foundation. Adv. Eng. Softw. 2012, 48, 1–5. [Google Scholar] [CrossRef]
- Aydogdu, M.; Arda, M. Torsional vibration analysis of double walled carbon nanotubes using nonlocal elasticity. Int. J. Mech. Mater. Des. 2016, 12, 71–84. [Google Scholar] [CrossRef]
- Togun, N.; Bagdatli, S.M. Nonlinear vibration of a nanobeam on Pasternak elastic foundation based on nonlocal euler-bernoulli beam theory. Math. Comput. Appl. 2016, 21, 1–19. [Google Scholar]
- Ozturk, B.; Coskun, S.B. The homotopy perturbation method for free vibration analysis of beams on elastic foundation. Struct. Eng. Mech. 2011, 37, 415–425. [Google Scholar] [CrossRef]
- Yan, Y.; Wang, W.; Zhang, L. Applied multiscale method to analysis of nonlinear vibration for double-walled carbon nanotubes. Appl. Math. Model. 2011, 35, 2279–2289. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Li, F.M. Nonlinear free vibration of nanotube with small scale effects embedded in viscous matrix. Mech. Res. Commun. 2014, 60, 45–51. [Google Scholar] [CrossRef]
- Bagdatli, S.M. Nonlinear vibration of nanobeams with various boundary condition based on nonlocal elasticity theory. Composites Part B Eng. 2015, 80, 43–52. [Google Scholar] [CrossRef]
- Bagdatli, S.M. Non-linear transverse vibrations of tensioned nanobeams using nonlocal beam theory. Struct. Eng. Mech. 2015, 55, 281–298. [Google Scholar] [CrossRef]
- Simsek, M. Large amplitude free vibration of nanobeams with various boundary conditions based on the nonlocal elasticity theory. Composites Part B Eng. 2014, 56, 621–628. [Google Scholar] [CrossRef]
- Simsek, M. Nonlinear static and free vibration analysis of microbeams based on the nonlinear elastic foundation using modified couple stress theory and He’s variational method. Compos. Struct. 2014, 112, 264–272. [Google Scholar] [CrossRef]
- Fallah, A.; Aghdam, M.M. Nonlinear free vibration and post-buckling analysis of functionally graded beams on nonlinear elastic foundation. Eur. J. Mech. A Solids 2011, 30, 571–583. [Google Scholar] [CrossRef]
- Fallah, A.; Aghdam, M.M. Thermo-mechanical buckling and nonlinear free vibration analysis of functionally graded beams on nonlinear elastic foundation. Composites Part B Eng. 2012, 43, 1523–1530. [Google Scholar] [CrossRef]
- Ke, L.L.; Xiang, Y.; Yang, J.; Kitipornchai, S. Nonlinear free vibration of embedded double-walled carbon nanotubes based on nonlocal Timoshenko beam theory. Comput. Mater. Sci. 2009, 47, 409–417. [Google Scholar] [CrossRef]
- Pritz, T. Analysis of four parameter fractional derivative model of real solid materials. J. Sound Vib. 1996, 195, 103–115. [Google Scholar] [CrossRef]
- Koeller, R.C. Application of fractional calculus to the theory of viscoelasticity. ASME J. Appl. Mech. 1984, 51, 299–307. [Google Scholar] [CrossRef]
- Nayfeh, A.H. Introduction to Pertubation Techniques; John Wiley: New York, NY, USA, 1981. [Google Scholar]
- Nayfeh, A.H.; Mook, D.T. Nonlinear Oscillations; John Wiley: New York, NY, USA, 1979. [Google Scholar]
- Yokoyama, T. Vibrations and transient responses of timoshenko beams resting on elastic foundations. Arch. Appl. Mech. 1987, 57, 81–90. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).