Non-Gaussian Distributions to Random Walk in the Context of Memory Kernels

Abstract

The investigation of diffusive process in nature presents a complexity associated with memory effects. Thereby, it is necessary new mathematical models to involve memory concept in diffusion. In the following, I approach the continuous time random walks in the context of generalised diffusion equations. To do this, I investigate the diffusion equation with exponential and Mittag-Leffler memory-kernels in the context of Caputo-Fabrizio and Atangana-Baleanu fractional operators on Caputo sense. Thus, exact expressions for the probability distributions are obtained, in that non-Gaussian distributions emerge. I connect the distribution obtained with a rich class of diffusive behaviour. Moreover, I propose a generalised model to describe the random walk process with resetting on memory kernel context.

1. Introduction

The random walk formalism is a fundamental tool to approach fluctuations associated to atoms and molecules. In this sense, the random walk is essential on description of stochastic process in statistical physics. In the context of the random walk, the Brownian motion investigated by Einstein can be associated with stochastic process caused by molecules of fluid [1]; this hypothesis was also investigated by Smoluchowski [2] and Langevin [3], and confirmed by Jean Perin’s experiments [4,5]. In this framework, a class of random walkers that is Markovian and ergodic may be connected with Gaussian distribution and usual diffusion, i.e., $\langle {(\Delta x)}^2\rangle =2d\mathcal{D}t$, in which d spacial dimension and $\mathcal{D}$ is diffusion coefficient. In other words, the mean square displacement (MSD) assumes a linear behaviour in time; the anomalous diffusion defines the process in which occur the break of linear temporal behaviour to MSD. Recently, there are several investigations that reported the anomalous diffusion process in complex systems, e.g., we have anomalous diffusion in biological systems [6,7,8], and in fractal or disordered structures [9,10,11,12]. The anomalous diffusion implies a mean square displacement characterized by $\langle (x-\langle x\rangle )\rangle \propto t^{\alpha }$, in which it can be classified as super–diffusion to $\alpha >1$ and sub–diffusion to $\alpha <1$. In this scenario, a rich class of non-Gaussian distributions emerges. Thus, there are two types of ordinary formalisms that imply non-Gaussian distributions associated to anomalous spreading, the non-linear equations and fractional equations. The non-linear diffusion recovers the usual diffusion as a particular case. In this framework, the non-linear diffusion equation has been investigated in quantum random walk [13], random walks [14], and Fokker-Planck equation [15,16,17].

The fractional diffusion can be justified by fractional calculus which involves the non-integer order to derivative and integral [18]. These quantities are essentially defined by convolutions integrals with kernel of type power law functions that define the well-know Caputo, Riemann-Liouville and Riesz-Feller fractional operators, which are focus of recent mathematical applications [19,20,21,22,23,24,25,26]. Nowadays, a new family of kernels has been used to describe generalised diffusive models [27,28,29,30,31,32,33,34]. In this context, it is possible to define the generalised diffusion equation

$$\begin{array}{c}\hfill {\int }_0^{t}d{t}^{\prime }\mathcal{K}(t-t^{\prime })\frac{\partial \rho }{\partial t^{\prime }}=\mathcal{D}\frac{{\partial }^2\rho }{\partial x^2},-\infty <x<+\infty ,\end{array}$$

(1)

in which $\mathcal{D}$ is a generalised diffusion coefficient. Noting that $\mathcal{K}\left(t\right)=\delta \left(t\right)$ recovers the usual diffusion equation. Equation (1) describes a free diffusion (diffusion with memory kernel with conditions $\rho (\pm \infty ,t)=0$ and $\rho (x,0)=\phi \left(x\right)$. The choice of kernel $\mathcal{K}\left(t\right)$ defines the structure of temporal derivative. On the other hand, a recent theme on literature is searching the best way to include memory kernels in the diffusion equation [35,36,37]. The memory kernel as put on Equation (1) was considered on Fokker-Planck equation [38], the memory kernel in Laplacian term was considered in Ref. [36]. However, establishing the scenario which contains the exact solution to Equation (1) of some kernels is necessary.

The standard fractional form consider the singular power law kernel, as

$$\begin{array}{c}\hfill \mathcal{K}\left(t\right)=\frac{t^{-\alpha }}{\Gamma [1-\alpha ]},\alpha \in (0,1),\end{array}$$

(2)

in which Equation (1) incorporates the well-known Caputo fractional operator to temporal variable for $0<\alpha <1$. To consider these situations, two different forms of non-singular kernels $\mathcal{K}\left(t\right)$ are considered. The first one decays as a exponential form

$$\begin{array}{c}\hfill \mathcal{K}\left(t\right)=\frac{f}{\tau }exp\left[-\frac{t}{\tau }\right],\tau \in [0,+\infty ].\end{array}$$

(3)

in which f denotes a arbitrary constant. Assuming the particular choices $f=\frac{f_{\alpha }}{\alpha }$ and $\tau =\frac{1-\alpha }{\alpha }$, we obtain a special kernel which defines the fractional Caputo-Fabrizio derivative [32] in Equation (1) that, for simplicity, I denominate Caputo-Fabrizio diffusion.

The second one is

$$\begin{array}{c}\hfill \mathcal{K}\left(t\right)=\frac{b}{\tau }{E}_{\alpha ,1}\left[-\frac{t^{\alpha }}{\tau }\right],\alpha \in (0,1)\end{array}$$

(4)

$\tau \in [0,+\infty ]$, in which $E_{\alpha ,\gamma }(\cdots )$ denotes the Mittag-Leffler function for two parameters, i.e.,

$$\begin{array}{c}\hfill E_{\alpha ,\gamma }\left(z\right)=\sum _{l=0}^{\infty }\frac{z^l}{\Gamma [l\alpha +\gamma ]}.\end{array}$$

(5)

in which $E_{\alpha ,1}=E_{\alpha }$. To particular choice $b=\frac{b_{\alpha }}{\alpha }$ and $\tau =\frac{1-\alpha }{\alpha }$, Equation (4) assumes the kernel which defines the fractional Atangana-Baleanu derivative [31] in Equation (1). For simplicity, I denominate Atangana-Baleanu diffusion.

Equations (3) and (4) are non-singular forms (i.e., ${lim}_{x\to 0}\mathcal{K}\left(x\right)\ne +\infty$). Here, one question may be considered: how can the non-singular kernel in diffusion equation (Equation (1)) be linked with continuous time random walk (CTRW)? To answer this question, it is necessary to introduce stochastic quantities to random walkers. The CTRW is a formalism proposed by Montroll and Weiss in 1965 to describe a walk using joint distribution of jump length and waiting time $\mathsf{\Psi }(x,t)$ [39,40,41], in which $\psi \left(t\right)={\int }_{-\infty }^{+\infty }dx\mathsf{\Psi }(x,t)$ is the waiting time distribution of a walker between two successive jumps and $\lambda \left(x\right)={\int }_0^{+\infty }dt\mathsf{\Psi }(x,t)$ is the distribution of jump length. This formalism implies a class of fractional diffusion equation. The Montroll-Weiss equation has several consequences in temporal memory and non-local behaviour in transport system in disordered medium and complex system [42,43,44]. The appropriate choice for waiting time distribution describes systems such as integration-differential equation with chemical interaction [24,45,46], anomalous diffusion in expanding media [30] and diffusion of single metal atoms on a graphene oxide support [47].

The main objective of this work is to obtain the exact solutions to diffusion equation in generalised context for memory kernels and to present an applicability on the model of diffusion with stochastic resetting. Section 2 presentd the preliminary topics, including Montroll-Weiss equation on random walk movement with memory effects. Section 2.2 approaches how this memory kernel are connected with different versions of the diffusion equation. Consequently, in Section 3, I divide the results into four subsections: firstly, I consider the exponential kernel in Equation (1) and I obtain the exact solution by mean of Laplace-Fourier transforms. Secondly, I show the exact solution to diffusion equation under the presence of Mittag-Leffler memory kernel. The results imply non-Gaussian shapes due to memory effects. Thirdly, the anomalous relaxation processes associated with generalised random walks are discussed. Finally, I exemplify the efficiency of the methods proposed here, finding generalised solutions to the problem of diffusion with stochastic resetting. Section 4 presents the conclusions.

2. Preliminaries

We review some notions and concepts used throughout the paper.

2.1. Montroll-Weiss Formalism

The Montroll-Weiss equation establishes the distribution of probability in Laplace–Fourier space of random walks, as follows

$$\begin{array}{c}\hfill \rho (k,s)=\frac{1-\psi \left(s\right)}{s}\frac{\phi \left(k\right)}{1-\mathsf{\Psi }(k,s)},\end{array}$$

(6)

as defined in Ref. [43]. In the case the joint distribution of jump length and waiting time is separable, i.e., $\mathsf{\Psi }(k,s)=\psi \left(s\right)\lambda \left(k\right)$, the choice $\lambda \left(k\right)\sim 1-k^2\mathcal{D}\tau$, in that $\tau$ is a characteristic waiting time of the underlying continuous time random walk. It is important observe that the jump probability distribution is characterized by a Gaussian asymptotic behaviour, i.e., $\lambda \left(x\right)\sim e^{-\frac{x^2}{{\left(2\mathcal{D}\tau \right)}^2}}$, and it has a finite characteristic jump length. If $\psi \left(t\right)=\frac{e^{-\frac{t}{\tau }}}{\tau }$ (Poissonian distribution) ,we obtain the free diffusion (Brownian motion). For $\psi \left(t\right)\sim A_{\alpha }{(\tau /t)}^{1+\alpha }$, it is possible to write the diffusion equation with fractional Riemann-Liouville operator [48]. To include a generalised situation to waiting time, consider the next waiting time distribution in Laplace space

$$\begin{array}{c}\hfill \psi \left(s\right)=\frac{1}{\tau s{\mathcal{K}}_L\left(s\right)+1},\end{array}$$

(7)

as proposed in Ref. [38], in which $\mathcal{L}\left\{\mathcal{K}\left(t\right)\right\}={\int }_0^{\infty }{e}^{-st}\mathcal{K}\left(t\right)dt={\mathcal{K}}_L\left(s\right)$ denote the Laplace transform of memory kernel and $\tau$ is characteristic time. For $\mathcal{K}\left(t\right)=\delta \left(t\right)$, we recover the Brownian motion. The kernel implies a class of generalised diffusion random walks, therefore Equation (7) in Montroll-Weiss equation implies

$$\begin{array}{ccc}\rho (k,s)\hfill & =\hfill & {\displaystyle \frac{\tau s{\mathcal{K}}_L\left(s\right)}{s}}{\displaystyle \frac{\phi \left(k\right)}{\tau s{\mathcal{K}}_L\left(s\right)+1-(1-k^2\mathcal{D}\tau )}}\hfill \\ & =\hfill & {\displaystyle \frac{{\mathcal{K}}_L\left(s\right)\phi \left(k\right)}{s{\mathcal{K}}_L\left(s\right)+k^2\mathcal{D}}}.\hfill \end{array}$$

(8)

It is now necessary to emphasize two important points that are subtle and fundamental to the continuity of work. First, we approach the waiting time on Sandev sense [38]; there are alternative forms in the literature, as discussed in the Section 1. In fact, the choice of different forms to waiting time distribution change how the memory kernel appears on diffusion equation [49]. Second, it is important to find exact solutions to the generalised diffusion equation, which has attracted the attention of many researchers.

Equation (8) is a density distribution of walkers in Fourier–Laplace space, and includes the arbitrary kernel present waiting time distribution in CTRW formalism. Considering the kernel memory of Caputo operator in Laplace space, i.e., ${\mathcal{K}}_L\left(s\right)=s^{\alpha -1}$, waiting time distribution implies a particular form

$$\begin{array}{c}\hfill \psi \left(t\right)=\frac{t^{\alpha -1}}{\tau }{E}_{\alpha ,\alpha }\left[-\frac{t^{\alpha }}{\tau }\right].\end{array}$$

(9)

in which $\mathcal{L}\left\{t^{\gamma -1}{E}_{\alpha ,\gamma }(-\lambda t^{\alpha })\right\}=\frac{s^{\alpha -\gamma }}{\lambda +s^{\alpha }}$.

For standard fractional Caputo operator, i.e., ${\mathcal{K}}_L\left(s\right)=s^{\alpha -1}$, the Fourier–Laplace inversion implies the following solution

$$\begin{array}{c}\hfill \rho (x,t)={\int }_{-\infty }^{+\infty }d{x}^{\prime }\frac{\phi \left(x^{\prime }\right)}{\sqrt{4t^{\alpha }{\mathcal{D}}_{\alpha }}}{\mathrm{H}}_{1,1}^{1,0}\left[\frac{|x-x^{\prime }|}{{\mathcal{D}}_{\alpha }^{\frac{1}{2}}{t}^{\frac{\alpha }{2}}}{|}_{(0,1)}^{\left(1-\frac{\alpha }{2},\frac{\alpha }{2}\right)}\right],\end{array}$$

(10)

The $\mathrm{H}(\cdots )$ is Fox function. The Fox function consists in a type of Merlin integration [50]. This function is a characteristic type of solutions to fractional diffusion equations. Equation (10) has a non-Gaussian shape to $\alpha \ne 1$, which was investigated in the context of fractional dynamics by Metzler and Klafter in [43].

The Mittag-Leffler kernel in waiting time distribution reveals an intermediate behaviour between power law and stretched exponential functions. This case was discussed in References [36,49]. Equation (8) reports an important generalisation of the diffusion equation in fractional derivative context, which is the theme of the next subsection.

2.2. Generalised Diffusion Equation

The exponential and Mittag-Leffler kernels in Montroll-Weiss equation can imply other forms of the diffusion equation. These forms are relevant to conduction phenomena and transport process. The Equation (8) can be rewritten as follow

$$\begin{array}{c}\hfill s{\mathcal{K}}_L\left(s\right)\rho (k.s)-{\mathcal{K}}_L\left(s\right)\phi \left(k\right)=-{\mathcal{D}}_{\alpha }{k}^2\rho (k,s).\end{array}$$

(11)

It is important to notice that the inversion in Laplace–Fourier transforms imply the general diffusion in Equation (1). On the other hand, for the exponential kernel (Equation (3)) in Equation (11), we can rewrite an alternative expression

$$\begin{array}{c}\hfill \frac{\partial \rho }{\partial t}=\mathcal{D}\frac{{\partial }^2\rho }{\partial x^2}+{\mathcal{D}}_{\tau }\frac{{\partial }^3\rho }{\partial t\partial x^2},\end{array}$$

(12)

in which ${\mathcal{D}}_{\tau }=\tau \mathcal{D}$. This equation was investigated for the seepage of a homogeneous fluid in fissured rocks, by Barenblatt [51]. From the Mittag-Leffler kernel in (Equation (4)) in Equation (11), we obtain

$$\begin{array}{c}\hfill {}_0^C{D}_t^{\alpha }\rho =\mathcal{D}\frac{{\partial }^2\rho }{\partial x^2}{+}_0^{RL}{D}_t^{\alpha }{\mathcal{D}}_{\tau }\frac{{\partial }^2\rho }{\partial x^2}.\end{array}$$

(13)

This equation is a natural extension of Equation (12) for the fractional case. The fractional operators are defined by

$$\begin{array}{c}\hfill {}_0^C{D}_t^{\alpha }g\left(t\right)=\frac{1}{\Gamma [1-\alpha ]}{\int }_0^t{(t-t^{\prime })}^{-\alpha }\frac{dg}{d{t}^{\prime }},\end{array}$$

(14)

which is the Caputo fractional operator for $0<\alpha <1$ [18], and

$$\begin{array}{c}\hfill {}_0^{RL}{D}_t^{\alpha }g\left(t\right)=\frac{1}{\Gamma [1-\alpha ]}\frac{d}{dt}{\int }_0^t{(t-t^{\prime })}^{-\alpha }g\left(t^{\prime }\right),\end{array}$$

(15)

which is the Riemann-Liouville operator for $0<\alpha <1$ [18]. However, the memory effects in random walk context imply a class of generalised diffusion equation written in terms of Riemann-Liouville and Caputo operators. Equations (12) and (13) are formed by fractional derivative with singular kernels but are connected which non-singular representation, i.e., Equation (1). This analysis suggests that the Caputo and Riemann-Liouville fractional operator can represent a more general class of diffusive phenomena.

3. Main Results

In this section, the objective is to investigate formal solutions for the fractional diffusion in Equation (1) when the two different memory kernel are considered. The intention is to show that the memory functions in the diffusion equation imply a rich class of non-Gaussian forms to spatial distribution. These solutions are obtained by performing the inverse of Fourier and Laplace transforms of Montroll-Weiss equation, expressed by Equation (8). Performing the Fourier transform in the spatial variable, we obtain the general solution in terms of convolution form:

$$\begin{array}{c}\hfill \rho (x,s)={\int }_{-\infty }^{+\infty }d{x}^{\prime }\phi \left(x^{\prime }\right)\mathcal{G}(x-x^{\prime },s),\end{array}$$

(16)

in which the $\mathcal{G}$-function (Green function) is

$$\begin{array}{c}\hfill \mathcal{G}(x,s)=\sqrt{\frac{\mathcal{K}\left(s\right)}{4s{\mathcal{D}}_{\alpha }}}exp\left[-\sqrt{\frac{\mathcal{K}\left(s\right)s}{{\mathcal{D}}_{\alpha }}}\left|x\right|\right].\end{array}$$

(17)

Now, I separate into subsections to approach the solution in more details.

However, for non-singular operators acting in diffusion equation, the inversion of Laplace transform is not an easy task. Therefore, for the next Laplace–inverse transforms, the integrations are performed in s complex plane to find the non-Gaussian distributions. In addition, I establish the diffusive analysis approaching the anomalous diffusion behaviour that appears. Moreover, I generalise the diffusive green function, i.e., Equation (17), to the context of diffusion with stochastic resetting.

3.1. Exponential Memory-Kernel and Non-Gaussian Solutions

Assuming the exponential kernel. i.e., Equation (3), performing the Laplace transform, one obtains

$$\begin{array}{c}\hfill \mathcal{K}\left(s\right)=\frac{f}{\tau s+1},\tau \in [0,+\infty ].\end{array}$$

(18)

In context of fractional operator of Caputo-Fabrizio, we have

$$\begin{array}{c}\hfill f=\frac{f_{\alpha }}{\alpha }\mathrm{and}\tau =\frac{1-\alpha }{\alpha },\end{array}$$

(19)

in which $f_{\alpha }$ denotes a normalization constant and $\alpha \in (0,1)$. The Green function can be rewritten as

$$\begin{array}{c}\hfill \mathcal{G}(x,s)=-\frac{1}{2}\frac{\partial {\rm Y}}{\partial \left|x\right|},\end{array}$$

(20)

in which

$$\begin{array}{c}\hfill {\rm Y}(x,s)=\frac{1}{s}exp\left[-\frac{\left|x\right|}{\sqrt{\tau \mathcal{D}}}\sqrt{\frac{s}{s+\frac{1}{\tau }}}\right],\end{array}$$

(21)

taking the branch cuts associated with $\sqrt{s}$ and $\sqrt{s+\frac{1}{\tau }}$ along the negative real axis of s-plane (for more details, see [52]), the inversion is

$$\begin{array}{c}\hfill {\rm Y}(x,t)=1-\frac{2}{\pi }{\int }_0^{\infty }d\eta exp\left[-\frac{1}{\tau }\frac{t{\eta }^2}{{\eta }^2+1}\right]\frac{sin\left[\frac{\left|x\right|}{\sqrt{\tau \mathcal{D}{f}^{-1}}}\eta \right]}{\eta (1+{\eta }^2)}.\end{array}$$

(22)

However, using the definition in Equation (20), the $\mathcal{G}$-function corresponding to the kernel in Equation (3) is

$$\begin{array}{c}\hfill {\mathcal{G}}_1(x,t)=\frac{1}{\pi \sqrt{\tau \mathcal{D}{f}^{-1}}}{\int }_0^{\infty }d\eta exp\left[-\frac{1}{\tau }\frac{t{\eta }^2}{{\eta }^2+1}\right]\frac{cos\left[\eta \frac{\left|x\right|}{\sqrt{\tau \mathcal{D}{f}^{-1}}}\right]}{1+{\eta }^2}.\end{array}$$

(23)

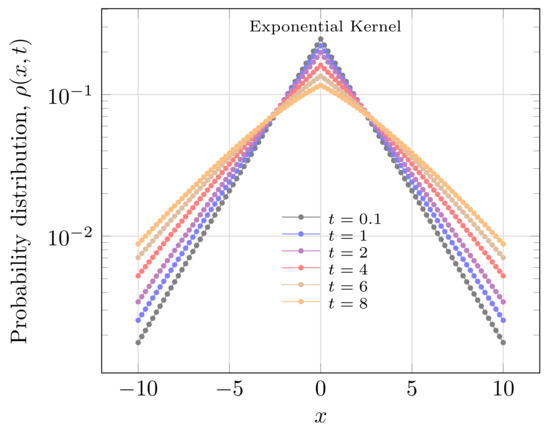
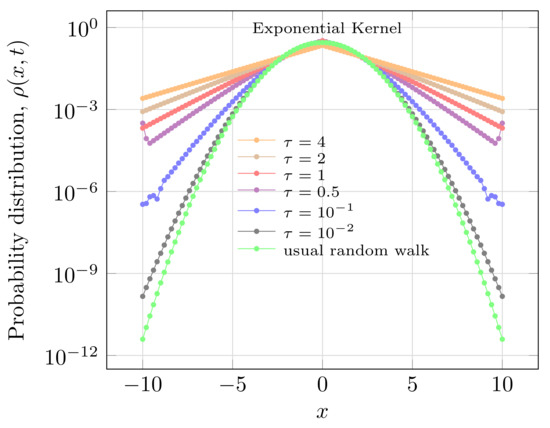
Equations (16) and (23) correspond to solution of diffusion equation with exponential kernel. In the case all walks are localized in a single point, i.e., $\rho (x,0)=\delta \left(x\right)$. It implies $\rho (x,t)$ that is governed by Equation (23); this distribution in space is illustrated in Figure 1 to a set of fractional index. Figure 2 exemplifies the temporal evolution of non-Gaussian distribution on time, to exponential memory. Moreover, the special situation in Equations (19) and (23) assumes the exact green function to solution of Caputo-Fabrizio diffusion.

3.2. Mittag-Leffler Memory–Kernel and Non-Gaussian Solutions

The Mittag-Leffler Kernel in Laplace space is represented by kernel

$$\begin{array}{c}\hfill {\mathcal{K}}_L\left(s\right)=\frac{b{s}^{\alpha -1}}{\tau s^{\alpha }+1},\mathrm{with}\alpha \in (0,1)\end{array}$$

(24)

in which $\mathcal{L}\left\{E_{\alpha }(-\lambda t^{\alpha })\right\}=\frac{s^{\alpha -1}}{\lambda +s^{\alpha }}$. The Atangana-Baleanu kernel is a special case ($b=\frac{b_{\alpha }}{\alpha }$ and $\tau =\frac{1-\alpha }{\alpha }$) of the solution which is obtained in this subsection.

For the general case presented in the kernel in Equation (24), the Green function is space $(x,s)$ can be represented by Equation (20), to the next ${\rm Y}(x,s)$ form

$$\begin{array}{c}\hfill {\rm Y}(x,s)=\frac{1}{s}exp\left[-\frac{\left|x\right|}{\sqrt{\tau {\mathcal{D}}_{\alpha }{b}^{-1}}}\sqrt{\frac{s^{\alpha }}{s^{\alpha }+\frac{1}{\tau }}}\right],\end{array}$$

(25)

solving the integration of branch cut associated with $s^{\alpha }$, the inverse obtained is

$$\begin{array}{ccc}{\rm Y}(x,t)\hfill & =\hfill & 1-{\displaystyle \frac{1}{\pi }}{\int }_0^{\infty }{e}^{-t\eta }exp\left\{-\left|x\right|\sqrt{{\displaystyle \frac{{\eta }^{\alpha }b}{\tau {\mathcal{D}}_{\alpha }{\gamma }_1}}}cos\left[{\displaystyle \frac{\alpha \pi -{\gamma }_2}{2}}\right]\right\}\hfill \\ & \times \hfill & sin\left\{\left|x\right|\sqrt{{\displaystyle \frac{b{\eta }^{\alpha }}{{\mathcal{D}}_{\alpha }{\gamma }_1}}}cos\left[{\displaystyle \frac{\alpha \pi -{\gamma }_2}{2}}\right]\right\}{\displaystyle \frac{d\eta }{\eta }},\hfill \end{array}$$

(26)

in that

$$\begin{array}{c}\hfill {\gamma }_1=\sqrt{{\eta }^{2\alpha }+{\left(\frac{1}{\tau }\right)}^2+2\left(\frac{1}{\tau }\right){\eta }^{\alpha }cos\left[\alpha \pi \right]},\end{array}$$

(27)

and

$$\begin{array}{c}\hfill {\gamma }_2=arctan\left[\frac{{\eta }^{\alpha }sin\left[\alpha \pi \right]}{{\eta }^{\alpha }cos\left[\alpha \pi \right]+\frac{1}{\tau }}\right].\end{array}$$

(28)

Using Equations (20) and (26), the $\mathcal{G}$-function to ML-memory is written as

$$\begin{array}{ccc}\hfill {\mathcal{G}}_2(x,t)& =& \frac{1}{2\pi }{\int }_0^{\infty }{e}^{-t\eta }exp\left\{-\left|x\right|\sqrt{\frac{b{\eta }^{\alpha }}{\tau {\mathcal{D}}_{\alpha }{\gamma }_1}}cos\left[\frac{\alpha \pi -{\gamma }_2}{2}\right]\right\}\sqrt{\frac{b{\eta }^{\alpha }}{\tau {\mathcal{D}}_{\alpha }{\gamma }_1}}\hfill \\ & \times & (cos\left[\frac{\alpha \pi -{\gamma }_2}{2}\right]sin\left\{\left|x\right|\sqrt{\frac{b{\eta }^{\alpha }}{\tau {\mathcal{D}}_{\alpha }{\gamma }_1}}sin\left[\frac{\alpha \pi -{\gamma }_2}{2}\right]\right\}\hfill \\ & +& sin\left[\frac{\alpha \pi -{\gamma }_2}{2}\right]cos\left\{\left|x\right|\sqrt{\frac{b{\eta }^{\alpha }}{\tau {\mathcal{D}}_{\alpha }{\gamma }_1}}sin\left[\frac{\alpha \pi -{\gamma }_2}{2}\right]\right\})\frac{d\eta }{\eta },\hfill \end{array}$$

(29)

which is the $\mathcal{G}$ function in $(x,t)$ space. If $\tau \to 0$ and $\alpha \to 1$, the Green function is rewritten as

$$\begin{array}{c}\hfill {\mathcal{G}}_2(x,t)={\int }_0^{\infty }\frac{e^{-t\eta }}{\sqrt{4{\pi }^2\mathcal{D}{b}^{-1}\eta }}cos\left[\frac{x\sqrt{b\eta }}{\sqrt{\mathcal{D}}}\right]d\eta ,\end{array}$$

(30)

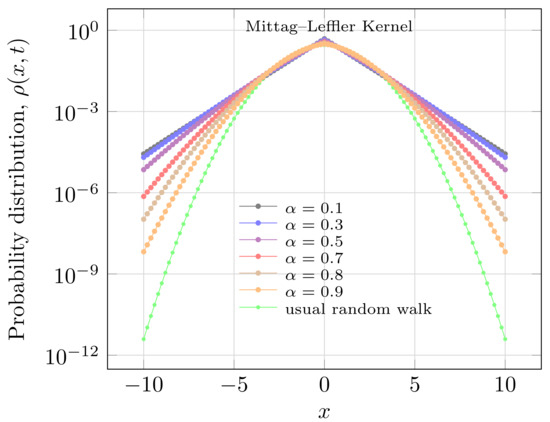
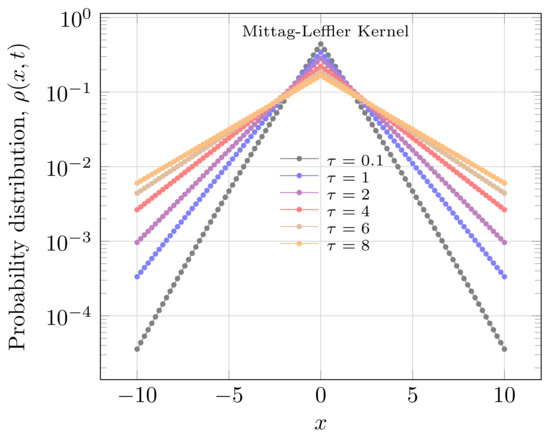
That implies a Gaussian form to $\mathcal{G}$-function of diffusion equation. Thereby, $\rho (x,t)$ correspondent to Einstein solution to Brownian motion [1]. Figure 3 and Figure 4 show the non-Gaussian distribution caused by different values to parameter $\alpha$ and $\tau$ in Mittag-Leffler kernel.

The non-Gaussian shapes obtained as consequence of non-singular operator in diffusion equations can imply a rich class of non-usual diffusive systems. In next section, this hypothesis is verified.

3.3. Diffusive Aspects of Non-Singular Diffusion Equations

Having established the CTRW formalism and distribution behaviours to the general situation presented here, it is relevant to obtain the temporal evolution to MSD; for symmetric distribution, we have $\langle {(x-\langle x\rangle )}^2\rangle =\langle x^2\rangle$. In CTRW formalism, the second moment is introduced as

$$\begin{array}{c}\hfill \langle x^2\rangle \left(t\right)=-{\mathcal{L}}^{-1}\left[\frac{{\partial }^2}{\partial k^2}\rho (k,s){|}_{k=0}\right].\end{array}$$

(31)

by use of Equation (8) to localized initial condition $\phi \left(k\right)=1$ (i.e., $\phi \left(x\right)=\delta \left(x\right)$), the general form to second moment can be written as

$$\begin{array}{c}\hfill \langle x^2\rangle \left(t\right)={\mathcal{L}}^{-1}\left[\frac{2{\mathcal{D}}_{\alpha }}{s^2{\mathcal{K}}_L\left(s\right)}\right].\end{array}$$

(32)

To constant kernel the second moment assume the linear time behaviour. To exponential kernel in the context of Caputo-Fabrizio diffusion, i.e., Equations (18) and (19), the inversion of Laplace transform

$$\begin{array}{c}\hfill \langle x^2\rangle =2{\mathcal{D}}_{\alpha }{f}_{\alpha }^{-1}(1-\alpha +\alpha t),\end{array}$$

(33)

to the asymptotic limit of long times, this MSD assumes the linear temporal behaviour, therefore, the usual diffusion. For $\alpha =1$, we recover the standard diffusion relation ($\langle x^2\rangle =2\mathcal{D}t$). In Ref. [37], the authors investigated the fractional CF operator on Riemann-Liouville sense applied on Laplacian term of the diffusion equation, the result for distribution and MSD are very different. Thereby, the side in which the non-singular operator is applied in diffusion equation implies in different influences on diffusive properties.

To Mittag-Leffler kernel, i.e., Equation (4), the MSD implies

$$\begin{array}{c}\hfill \langle x^2\rangle =2{\mathcal{D}}_{\alpha }\left(\tau +\frac{t^{\alpha }}{\Gamma [1+\alpha ]}\right).\end{array}$$

(34)

In the Atangana-Baleanu diffusion context, it is reduced to

$$\begin{array}{c}\hfill \langle x^2\rangle =2{\mathcal{D}}_{\alpha }{b}_{\alpha }^{-1}\left(1-\alpha +\alpha \frac{t^{\alpha }}{\Gamma [1+\alpha ]}\right),\end{array}$$

(35)

in which in short time the MSD of Equation (34) converges to same behaviour of MSD of Caputo-Fabrizio operator, i.e., $\langle x^2\rangle \propto 2\mathcal{D}{f}_{\alpha }^{-1}(1-\alpha )$. In long times, Equations (34) and (35) imply an anomalous behaviour, i.e., $\langle x^2\rangle \sim t^{\alpha }$. This long time behaviour occurs to Caputo and Riemann-Liouville operator [38,43]. For the appropriate limit of parameters $\tau$ and $\tau$ in Equation (34), to $\tau \to 0$, we obtain the standard fractional diffusion. The diffusive behaviour to CF and AB diffusion obtained in Equations (33) and (35) recover the usual diffusive process to $\alpha \to 1$.

3.4. Random Walk Process with Stochastic Resetting and Memory

In this subsection, I extend the results previously obtained in another scenario. The purpose is to show the applicability of non-Gaussian forms found previously.

Diffusion with resetting is an efficient mathematical model for describing search systems [53]. This model has been the focus of many studies [54,55,56]. The propose of the random walk process with resetting can be resumed by expression

$$\begin{array}{c}\hfill \frac{\partial \rho }{\partial t}=\mathcal{D}\frac{{\partial }^2\rho }{\partial x^2}-r\rho (x,t)+r\delta (x-x_0),\rho (x,0)=\delta (x-x_0),\end{array}$$

(36)

where r represents the rate of walker which are removed on system and restart in the initial condition. This idea can maximize the search for targets in a specific region. Some extensions of this model has been investigate on Levy flight context [57], coagulation–diffusion process [58] and others. The purpose is to generalise Equation (36) in the context of memory kernel, as follows

$$\begin{array}{c}\hfill {\int }_0^{t}d{t}^{\prime }\gamma (t-t^{\prime })\frac{\partial \rho }{\partial t^{\prime }}=\mathcal{D}\frac{{\partial }^2\rho }{\partial x^2}-r{\int }_0^{t}d{t}^{\prime }\gamma \left(t^{\prime }\right)\left(\rho (x,t-t^{\prime })-\delta (x-x_0)\right),\end{array}$$

(37)

with truncated memory kernel

$$\begin{array}{c}\hfill \gamma \left(t\right)=e^{-rt}\mathcal{K}\left(t\right),\end{array}$$

(38)

where $r=0$. Equation (37) recovers Equation (1). If $\mathcal{K}\left(t\right)=\delta \left(t\right)$, Equation (37) implies Equation (36). To solve the proposed model, I use the technique present in previous section, which implies on solution in Fourier–Laplace space, as

$$\begin{array}{ccc}\hfill \rho (k,s)& =& \frac{1}{s}\frac{{\mathcal{K}}_L(s+r)(s+r)e^{-ik{x}_0}}{(s+r){\mathcal{K}}_L(s+r)+k^2\mathcal{D}},\hfill \end{array}$$

(39)

where $\mathcal{L}\left\{\mathcal{K}\left(t\right)e^{-rt}\right\}={\mathcal{K}}_L(s+r)$, the systems have normalized number of walkers, i.e., ${\int }_{-\infty }^{+\infty }\rho (x,t)dx=1$. How ${lim}_{t\to \infty }\rho (k,t)={\mathcal{L}}^{-1}\left\{{lim}_{s\to 0}\rho (k,s)\right\}$, to kernels considered in this work, i.e., Equations (18)–(24), we have

$$\begin{array}{ccc}\hfill \rho (k,t)& =& \frac{{\mathcal{K}}_L\left(r\right)r{e}^{-ik{x}_0}}{r{\mathcal{K}}_L\left(r\right)+k^2\mathcal{D}},\hfill \end{array}$$

(40)

performing the inverse Fourier transform, we obtain the general stationary solution

$$\begin{array}{c}\hfill {\rho }_s\left(x\right)=\beta \frac{e^{-\beta |x-x_0|}}{2},\beta =\sqrt{\frac{r{\mathcal{K}}_L\left(r\right)}{\mathcal{D}}},\end{array}$$

(41)

in which ${\mathcal{K}}_L$ are functions presented in Section 3.1 and Section 3.2. To ${\mathcal{K}}_L\left(s\right)=1$, i.e., $\mathcal{K}\left(t\right)=\delta \left(t\right)$, we recover the usual case reported in Ref. [53].

The inverse transformations of Fourier and Laplace of Equation (39) to exponential kernel (Equation (3)) implies

$$\begin{array}{ccc}\rho (x,t)\hfill & =\hfill & {\mathcal{L}}^{-1}\left[\left(1+\frac{r}{s}\right)e^{-ik{x}_0}{\mathcal{G}}_1(k,s+r)\right]\hfill \\ & =\hfill & e^{-rt}{\mathcal{G}}_1(x-x_0,t)+r{\int }_0^{t}d{t}^{\prime }{e}^{-r{t}^{\prime }}{\mathcal{G}}_1(x-x_0,t^{\prime }),\hfill \end{array}$$

(42)

in which ${\mathcal{G}}_1$ was obtained in Equation (23). To diffusion resetting problem of random walks in the context of exponential kernel, the MSD can be written as follows

$$\begin{array}{ccc}\hfill \langle x^2\rangle \left(t\right)& =& 2\frac{\mathcal{D}}{f}\left(\tau -\frac{1}{r}\right)e^{-rt}+\frac{2\mathcal{D}}{rf},\hfill \end{array}$$

(43)

with $x_0=0$. To $r\to 0$, we obtain $\langle x^2\rangle \left(t\right)=2\mathcal{D}{f}^{-1}(\tau +t)$. It is clear that, for small time, we recover the initial behaviour to walkers present in Section 3.3. To long times in Equation (43), we obtain a constant MSD behaviour, which is justified by a stationary distribution (Equation (41)) that represents a delicate equilibrium between added and removed walkers.

On the other hand, to Mittag-Leffler kernel, i.e., Equation (4), we have the same mathematical structure of Equation (42), as follows

$$\begin{array}{c}\hfill \rho (x,t)=e^{-rt}{\mathcal{G}}_2(x-x_0,t)+r{\int }_0^{t}d{t}^{\prime }{e}^{-r{t}^{\prime }}{\mathcal{G}}_2(x-x_0,t^{\prime }),\end{array}$$

(44)

in which ${\mathcal{G}}_2$ was obtained in Equation (29). Performing the calculation of MSD to random walkers under effect of Mittag-Leffler kernel, we obtain

$$\begin{array}{ccc}\hfill \langle x^2\rangle \left(t\right)& =& 2\frac{\mathcal{D}}{b}\tau +2\mathcal{D}\frac{(\Gamma (\alpha )-\Gamma (\alpha ,rt\left)\right)}{b{r}^{\alpha }\Gamma \left(\alpha \right)},\hfill \end{array}$$

(45)

with $x_0=0$ and $\Gamma (\alpha ,z)={\int }_z^{\infty }dt{t}^{\alpha -1}{e}^{-t}$. Figure 5 illustrates the temporal evolution of Equation (45) for a set of different $\alpha$ parameters. The figure reveals a rich class of sub-diffusive behaviours to process. Equation (45) implies in an extensive class of behaviour associated with rate r of added and removed walkers.

The problem presented in this subsection makes clear that the non-Gaussian solutions found in Section 3.1 and Section 3.2 have an important degree of applicability. The next step is to apply the techniques presented in this work to investigate the effectiveness of search strategies for single and multiple targets, as investigated in Ref. [59]; thereby, the solutions found in this work can be very interesting for the investigation of other problems in mathematical models.

4. Conclusions

The fractional diffusion equations exhibit a very complex behaviour and its properties and anomalies are strongly influenced by memory effects or generalised waiting time distribution in Montroll-Weiss equation. In this sense, it is possible to write different forms of the diffusion equation. This work approaches the mathematical model expressed by Equation (1) and seeks to present this proposal generates compact solutions for walkers under memory effect. In Section 3, I present the exact solutions of the generalised diffusion equation and the time dependence of the mean square displacement to different memory kernels. The results reveal that memory kernels lead to non-Gaussian distributions (Section 3.1 and Section 3.2) and different diffusive regimes to MSD depending on the timescale (Section 3.3). For the Mittag-Leffler kernel, a crossover between two diffusive regimes occurs: constant for small times and sub-diffusive for long times, a feature observed in several empirical systems. In addition, I show the role of each of these kernels in the new forms of diffusion equations in the context of CF and AB fractional operators on Caputo sense. Moreover, in Section 3.4, I generalise the random walk process with stochastic resetting. The problem reveals a series of new consequences in relation to the usual case, including sub-diffusive process regimes ($\langle x^2\rangle \sim t^{\alpha }$ with $\alpha <1$) due to Mittag-Leffler kernel, and shows the applicability of the solutions obtained in the previous sections in another scenario.

The results and methods used in this work to approach non-singular kernels in diffusion equation suggest a simple way for incorporating the memory effects on description of dynamic behaviour with non-usual aspects. Thereby, this work reveals simple forms to solutions for generalised diffusion equation with memory kernels (exponential and Mittag-Leffler functions). Consequently, the solutions appear as a simple alternative to approach mathematical models associated with fractional operators of Caputo-Fabrizio and Atangana-Baleanu in diffusion problems. Moreover, this work presents possibilities for future investigations of diffusion in fractal systems, intermittent movement and reaction-diffusion systems, under influence of non-singular memory kernels.