Modeling of Heat Distribution in Porous Aluminum Using Fractional Differential Equation
Abstract
:1. Introduction
2. Fractional Heat Conduction Equation
3. Formulation of the Problem
4. Method of Solution
4.1. Solution of the Direct Problem
4.2. Minimum of the Functional
| minimized function, | |
| n | dimension (number of variables) |
| number of threads | |
| number of ants in population | |
| I | number of iterations |
| L | number of pheromone spots |
| parameters of the algorithm |
| Algorithm 1: Parallel Real ACO algorithm | |
| Initialization of the algorithm | |
| 1. | Setting input parameters of the algorithm L, M, I, , q, . |
| 2. | Randomly generate L pheromone spots (solutions) and assign them to set (starting archive). |
| 3. | Calculate values of the minimized function F for each pheromone spot and sort the archive from best to worst solution. |
| Iterative process | |
| 4. | Assigning probabilities to pheromone spots (solutions) according to the following formula:
|
| 5. | Ant chooses a random l-th solution with probability . |
| 6. | Ant transforms the j-th coordinate () of l-th solution by sampling proximity with the probability density function (Gaussian function)
|
| 7. | Repeat steps 5–6 for each ant. We obtain M new solutions (pheromone spots). |
| 8. | Divide new solutions on groups. Calculate values of minimized function F for each new solution (parallel computing). |
| 9. | Add to the archive new solutions, sort the archive by quality of solutions, remove M worst solution. |
| 10. | Repeat steps 4–9 I times. |
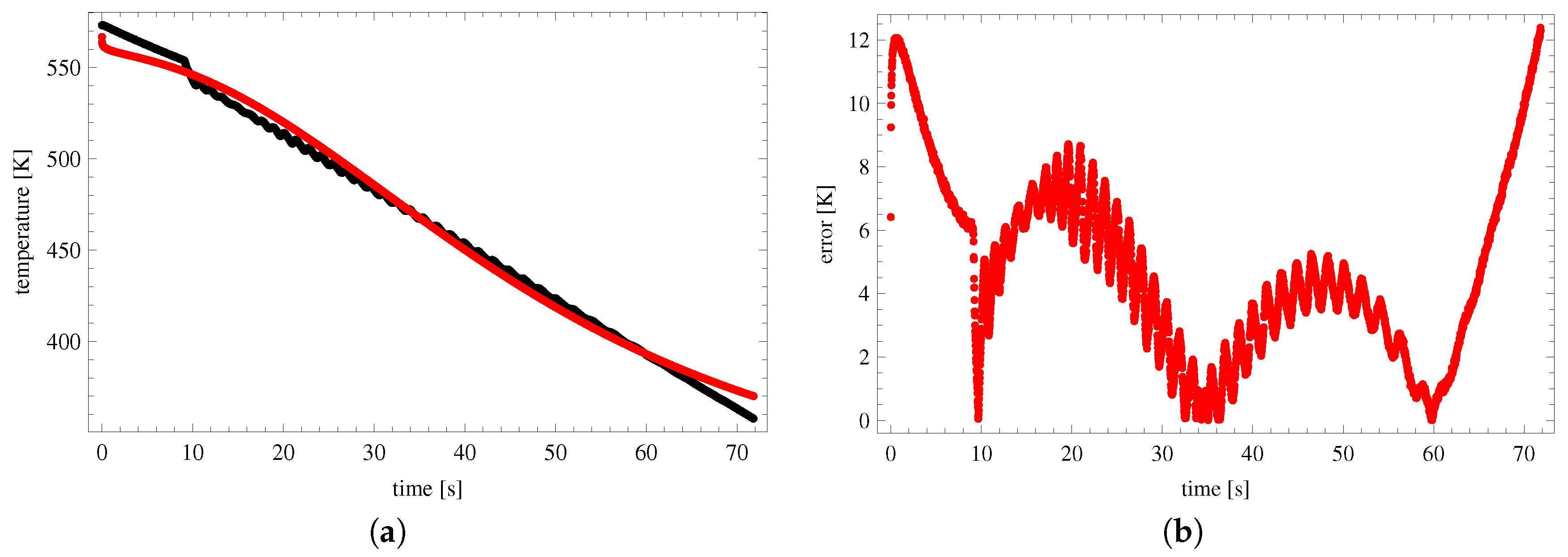
5. Results
- —modified thermal conductivity coefficient,
- —initial condition,
- —heat transfer coefficient,
- —order of derivative,
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Guo, B.; Pu, X.; Huang, F. Fractional Partial Differential Equations and Their Numerical Solutions; World Scientific: Singapore, 2015. [Google Scholar]
- Ortigueira, M.D. Fractional Calculus for Scientists and Engineers; Springer: Berlin, Germany, 2011. [Google Scholar]
- Das, S. Functional Fractional Calculus for System Identification and Controls; Springer: Berlin, Germany, 2008. [Google Scholar]
- Povstenko, Y.; Klekot, J. The Cauchy problem for the time-fractional advection diffusion equation in a layer. Tech. Sci. 2016, 19, 231–244. [Google Scholar]
- Abdeljawat, T. On conformable fractional calculus. J. Comput. Appl. Math. 2015, 279, 57–66. [Google Scholar] [CrossRef]
- Liu, H.Y.; He, J.H.; Li, Z.B. Fractional calculus for nanoscale flow and heat transfer. Int. J. Numer. Methods Heat Fluid Flow 2014, 24, 1227–1250. [Google Scholar] [CrossRef]
- Atangana, A. On the new fractional derivative and application to nonlinear Fisher’s reaction–diffusion equation. Appl. Math. Comput. 2016, 273, 948–956. [Google Scholar] [CrossRef]
- Freeborn, T.J.; Maundy, B.; Elwakil, A.S. Fractional-order models of supercapacitors, batteries and fuel cells: A survey. Mater. Renew. Sustain. Energy 2015, 4. [Google Scholar] [CrossRef]
- Błasik, M.; Klimek, M. Numerical solution of the one phase 1D fractional Stefan problem using the front fixing method. Math. Methods Appl. Sci. 2014, 38, 3214–3228. [Google Scholar] [CrossRef]
- Mitkowski, W.; Skruch, P. Fractional-order models of the supercapacitors in the form of RC ladder networks. J. Pol. Acad. Sci. 2013, 61, 581–587. [Google Scholar] [CrossRef]
- Matušů, R. Application of fractional order calculus to control theory. Int. J. Math. Models Methods Appl. Sci. 2011, 5, 1162–1169. [Google Scholar]
- Povstenko, Y.Z. Fractional heat conduction equation and associated thermal stress. J. Therm. Stresses 2004, 28, 83–102. [Google Scholar] [CrossRef]
- Yang, X.J.; Baleanu, D. Fractal heat conduction problem solved by local fractional variation iteration method. Therm. Sci. 2013, 17, 625–628. [Google Scholar] [CrossRef] [Green Version]
- Murio, D.A. Time fractional IHCP with Caputo fractional derivatives. Comput. Math. Appl. 2008, 56, 2371–2381. [Google Scholar] [CrossRef]
- Brociek, R.; Słota, D. Reconstruction of the boundary condition for the heat conduction equation of fractional order. Therm. Sci. 2015, 19, 35–42. [Google Scholar] [CrossRef]
- Murio, D.A. Implicit finite difference approximation for time fractional diffusion equations. Comput. Math. Appl. 2008, 56, 1138–1145. [Google Scholar] [CrossRef]
- Liu, J.J.; Yamamoto, M.; Yan, L.L. On the reconstruction of unknown time-dependent boundary sources for time fractional diffusion process by distributing measurement. Inverse Probl. 2016, 32. [Google Scholar] [CrossRef]
- Zhuag, Q.; Yu, B.; Jiang, X. An inverse problem of parameter estimation for time-fractional heat conduction in a composite medium using carbon–carbon experimental data. Physica B 2015, 456, 9–15. [Google Scholar] [CrossRef]
- Obrączka, A.; Kowalski, J. Modelowanie rozkładu ciepła w materiałach ceramicznych przy użyciu równań różniczkowych niecałkowitego rzędu. In Proceedings of the Materiały XV Jubileuszowego Sympozjum “Podstawowe Problemy Energoelektroniki, Elektromechaniki i Mechatroniki”, Gliwice, Poland, 11–13 December 2012; Volume 32. (In Polish). [Google Scholar]
- Brociek, R. Implicite finite difference metod for time fractional diffusion equations with mixed boundary conditions. Zesz. Naukowe Politech. Śląskiej 2014, 4, 73–87. (In Polish) [Google Scholar]
- Brociek, R.; Słota, D. Application of real ant colony optimization algorithm to solve space and time fractional heat conduction inverse problem. Inf. Technol. Control 2017, 46, 5–16. [Google Scholar] [CrossRef]
- Socha, K.; Dorigo, M. Ant Colony Optimization in continuous domains. Eur. J. Oper. Res. 2008, 185, 1155–1173. [Google Scholar] [CrossRef]
- Hetmaniok, E.; Hristov, J.; Słota, D.; Zielonka, A. Identification of the heat transfer coefficient in the two-dimensional model of binary alloy solidification. Heat Mass Transf. 2017, 53, 1657–1666. [Google Scholar] [CrossRef]
- Zielonka, A.; Hetmaniok, E.; Słota, D. Inverse alloy solidification problem including the material shrinkage phenomenon solved by using the bee algorithm. Int. Commun. Heat Mass Transf. 2017, 87, 295–301. [Google Scholar] [CrossRef]
- Zhang, B.; Qi, H.; Ren, Y.-T.; Sun, S.-C.; Ruan, L.-M. Application of homogenous continuous Ant Colony Optimization algorithm to inverse problem of one-dimensional coupled radiation and conduction heat transfer. Int. J. Heat Mass Transf. 2013, 66, 507–516. [Google Scholar] [CrossRef]
- Grysa, K.; Leśniewska, R. Different finite element approaches for inverse heat conduction problems. Inverse Probl. Sci. Eng. 2010, 18, 3–17. [Google Scholar] [CrossRef]
- Hristov, J. An inverse Stefan problem relevant to boilover: Heat balance integral solutions and analysis. Therm. Sci. 2007, 11, 141–160. [Google Scholar] [CrossRef]


| 100 × 1995 | 100 × 3990 | |||
|---|---|---|---|---|
| 300.00 | 69.74 | 237.91 | 67.78 | |
| 569.73 | 2.02 | 566.74 | 3.80 | |
| 1.63 | 0.40 | 1.52 | 2.20 | |
| 4.72 | 0.67 | 5.00 | 4.27 | |
| 198.02 | 46.05 | 178.05 | 51.73 | |
| 0.20 | 0.05 | 0.21 | 0.09 | |
| value of the functional | 246.98 | 352.88 | ||
| 100 × 1995 | 100 × 3990 | |
|---|---|---|
| 4.92 | 4.77 | |
| 11.04 | 12.38 | |
| 1.06 | 1.02 | |
| 3.08 | 3.46 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brociek, R.; Słota, D.; Król, M.; Matula, G.; Kwaśny, W. Modeling of Heat Distribution in Porous Aluminum Using Fractional Differential Equation. Fractal Fract. 2017, 1, 17. https://doi.org/10.3390/fractalfract1010017
Brociek R, Słota D, Król M, Matula G, Kwaśny W. Modeling of Heat Distribution in Porous Aluminum Using Fractional Differential Equation. Fractal and Fractional. 2017; 1(1):17. https://doi.org/10.3390/fractalfract1010017
Chicago/Turabian StyleBrociek, Rafał, Damian Słota, Mariusz Król, Grzegorz Matula, and Waldemar Kwaśny. 2017. "Modeling of Heat Distribution in Porous Aluminum Using Fractional Differential Equation" Fractal and Fractional 1, no. 1: 17. https://doi.org/10.3390/fractalfract1010017






