Abstract
Recently, fractional differential equations (FDEs) have attracted much more attention in modeling real-life problems. Since most FDEs do not have exact solutions, numerical solution methods are used commonly. Therefore, in this study, we have demonstrated a novel approximate-analytical solution method, which is called the Laplace homotopy analysis method (LHAM) using the Caputo–Fabrizio (CF) fractional derivative operator. The recommended method is obtained by combining Laplace transform (LT) and the homotopy analysis method (HAM). We have used the fractional operator suggested by Caputo and Fabrizio in 2015 based on the exponential kernel. We have considered the LHAM with this derivative in order to obtain the solutions of the fractional Black–Scholes equations (FBSEs) with the initial conditions. In addition to this, the convergence and stability analysis of the model have been constructed. According to the results of this study, it can be concluded that the LHAM in the sense of the CF fractional derivative is an effective and accurate method, which is computable in the series easily in a short time.
1. Introduction and Some Preliminaries
Modeling with fractional calculus has become increasingly important in recent years. During the last few decades especially, new fractional operators, methods and algorithms have been developed relating to mathematical modeling and simulation. Many studies have been undertaken in the last quarter of a century on new fractional derivative operators. Fractional calculus (FC) and numerical-approximate solution methods are extensively used in the solution of real-life problems, such as mathematical, engineering, financial, biological and physical problems.
For example, these techniques have been used to evaluate the performance of an electrical resistance inductance and capacitance (RLC) circuit using a new fractional operator with a local and nonlocal kernel [1], to price fractional European vanilla-type options [2,3], to analyze a new model of H1N1 spread [4], to model the population growth [5], to apply the homotopy analysis method [6], the Adomian decomposition method [7,8], the homotopy perturbation method [9,10], He’s variational iteration method in conformable derivative sense [11], the generalized differential transform method [12], the finite difference method [13] and the multivariate Padé approximation method [14]. Moreover, these proposed fractional techniques have been used to obtain the solution of the optimal control problem [15], the constrained optimization problem [16], the portfolio optimization problem [17], the diffusion-wave problem [18], etc.
In 2015, Caputo and Fabrizio developed a new fractional derivative operator built upon the exponential function to overcome the singular kernel problem [19]. Their fractional derivative has a smooth kernel, which takes on two different representations for the temporal and spatial variable. Atangana and Alkahtani [20] applied the CF derivative operator to the groundwater flowing within a confined aquifer. Singh et al. [21] analyzed the ENSO model in the global climate with the CF operator, and their simulations found out that when tends to one, the CF derivative shows more interesting behavior. Ali et al. [22] obtained the solution of the fractional model of Walters’-B fluid by using CF fractional derivative. In another study, Morales-Delgado et al. [23] compared the solutions obtained by using the CF derivative and the Liouville–Caputo derivative. Sheikh et al. [24] used the analysis of the Atangana–Baleanu (AB) and CF for generalized Casson fluid model. Atangana and Alkahtani [20] modeled the groundwater flowing within a confined aquifer by using the CF derivative. Koca and Atangana [25] solved the Cattaneo–Hristov model with CF and AB operators. Also in [26,27,28,29,30], the authors studied some interesting problems based on the CF fractional derivative.
Many powerful approximate-analytical methods have been presented in the finance literature, especially in modeling the European and American option prices. For example, [9,31,32] are relatively new approaches providing an analytical and numerical approximation to the Black–Scholes option pricing equation. The financial system can be viewed as money, capital and derivative markets (options, futures, forwards, swaps, etc.). Options are widely used in global financial markets. An option is a right, but not an obligation. The most important benefit of the option is the ability to invest in large amounts with a very small capital.
In 1973, Fisher Black and Myron Scholes [33] investigated in their study a model that can easily compute the prices of the options. This model also can evaluate the Greeks of the options and ratio of hedge. The Black–Scholes model that prices stock options has been applied to many different possessions and payments. This form of the pricing model is one of the most meaningful mathematical equations for a financial instrument. The Black–Scholes model with respect to an option can be considered as [34,35]:
where shows the vanilla-type option price at asset price S and time T represents the maturity time; is the risk-free interest rate; and is the volatility function of the underlying asset. In Equation (1), we observe that as and we can write payoff functions as: and where and show the value of the vanilla call and put options, respectively, and E is the exercise (strike) price. The closed form solution of Equation (1) can be obtained by using the heat equation. In order to obtain the FBSE, we make the following conversions:
This yields the equation:
with initial condition:
Equation (2) is called the Black–Scholes option pricing equation of fractional order. In Equation (2), we define , where k represents the balance between the interest rates’ and stock returns’ variability.
In addition to this, Cen and Le (2011) obtained the generalized fractional Black–Scholes equation [36] (GFBSE) by considering and in Equation (2):
with the initial condition:
When the market mechanism is given a full scope, it is concluded that the estimating effect of the fractional Black–Scholes model would be more effective than the traditional Black–Scholes model. For example, according to a special study [37] on China Merchants Bank, it was found that Fractional Black–Scholes (FBS) price is bigger than the Black–Scholes (BS) price. Additionally, FBS is better than BS, while the volatility is relatively larger (). We have aimed in this study to display the solution of fractional Black–Scholes Equations (2)–(5) using the proposed fractional derivative operator. Furthermore, we have aimed to determine the stability analysis of the method and the effectiveness of the CF operator using the results obtained.
Definition 1.
The usual Caputo time-fractional derivative of order α is given by [19]:
By changing the kernel with the function and with we obtain the following new fractional time derivative named the Caputo–Fabrizio time fractional derivative.
Definition 2.
The definition of the CF sense derivative is given by [19]:
where is a normalization function such that This definition can also be considered for functions that do not belong to , and the kernel has non-singularity for Equation (7) can be formulated also for and for any as:
Definition 3.
The Laplace transform of CF fractional derivative can be defined as follows [19]:
From Definition 3, we get the following special cases:
2. Description of the Method Using the Caputo–Fabrizio Fractional Operator
In this section of the study, we have demonstrated the solution method described by using the CF operator. Consider the following fractional PDE [5]:
where , with the initial conditions:
and the boundary conditions:
where and are known functions and is a real number and We define the method of solution for solving Problems (2)–(5). The LT of the CF derivative is satisfied as:
Now, we can construct the homotopy for Equation (15) as follows:
where and Furthermore, the Laplace transforms of the initial conditions are obtained as:
Then, the solution of Equation (16) can be represented as:
By comparing the coefficients of powers of we obtain the homotopies as follows:
When the we see that Equation (20) gives the approximate solution for the problems (15) and (16), and the solution is given by:
Furthermore, we will show the error rates of the solution with LHAM described above, by applying this method to the homogeneous fractional option pricing problem. If we define which is the first n-th sum of the series in the approximate solution of (22), the rate of absolute error is computed as:
3. Solution of the European Option Pricing Problem
In this part of the study, we have solved the fractional Black–Scholes equation and generalized fractional Black–Scholes equation (FBSE), which are two of the most important option pricing models. We have regarded this as the method LHAM, which is described with the Caputo–Fabrizio fractional derivative.
3.1. Fractional European Option Pricing Problem in the Sense of the Caputo–Fabrizio Derivative
Now, we consider the classical FBSE (2) with the initial condition (3). Firstly, we solve this equation by using the LHAM in the sense of the CF fractional derivative operator. Because the equation is homogeneous, we obtain the LT of the right side of the equation as zero, i.e., Now, we create the homotopies as follows:
By summing the iteration term up to n-th order, we obtain:
Getting the inverse LT of Equation (25), we have the approximate solution of Equation (2) with the initial condition Equation (3) when as follows:
Considering the special case of fractional parameter we have the exact solution of the problems (2) and (3) as
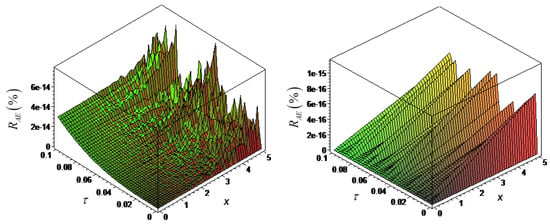
In Figure 1, the numerical computation of Equation (26) for special case and, in Figure 2, the simulation sketch for in the sense of the Caputo–Fabrizio fractional derivative are presented.
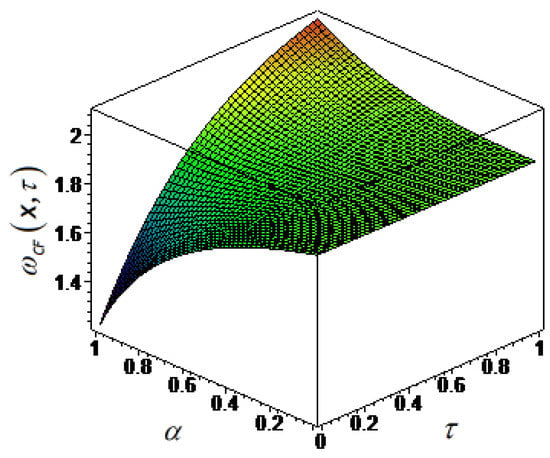
Figure 1.
The solution function of Equation (2) in the sense of Caputo–Fabrizio (CF) with respect to
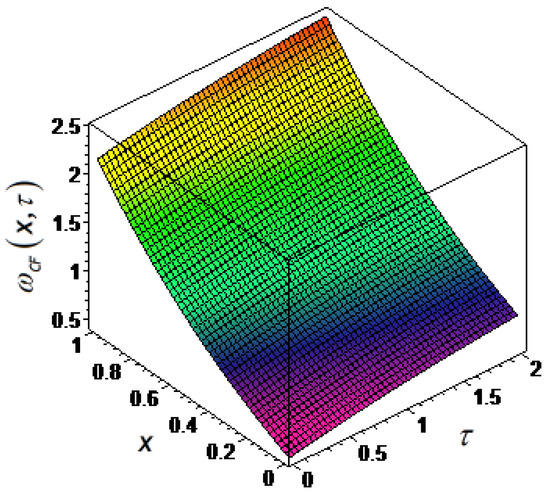
Figure 2.
Numerical simulation of Equation (26) in the sense of CF for
Figure 3 shows the European vanilla call option prices, which are given in Equation (1) with exercise price for fractional values and . According to Figure 3, we can say that the option has the lowest price in exercise time of the option , when As decreases, the payoff of the option increases. When , we observe that the option is overpriced [38].
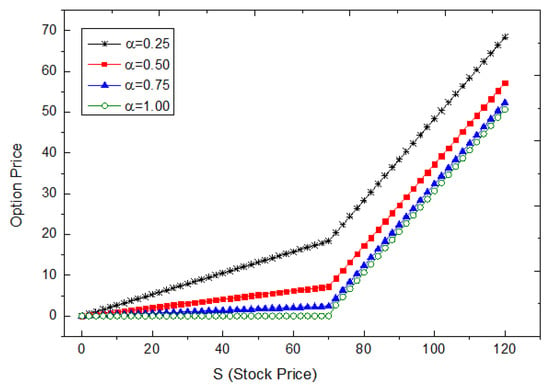
Figure 3.
Option prices with respect to underlying asset S for different values.
3.2. Fractional Generalized European Option Pricing Problem in the Sense of the Caputo–Fabrizio Derivative
Secondly, we solve the generalized version of the European vanilla option problems (4) and (5) by using the LHAM constructed in the Caputo–Fabrizio derivative sense. The Laplace transformation of the homogenous term is zero, i.e., Now, we obtain the homotopies according to the CF derivative as follows:
By building the n-th order approximate solution, we have:
Applying the inverse LT to Equation (28), when , we get the approximate solution of (4) and (5) as follows:
For the special case of fractional parameter we obtain the exact solution of the mentioned problem as , which is the same solution found in [8].
The numerical evaluation of Equation (29) is shown in Figure 4 regarding in the Caputo–Fabrizio fractional derivative sense. In addition, the numerical simulation of the solution function (29) for different distance values is represented in Figure 5.
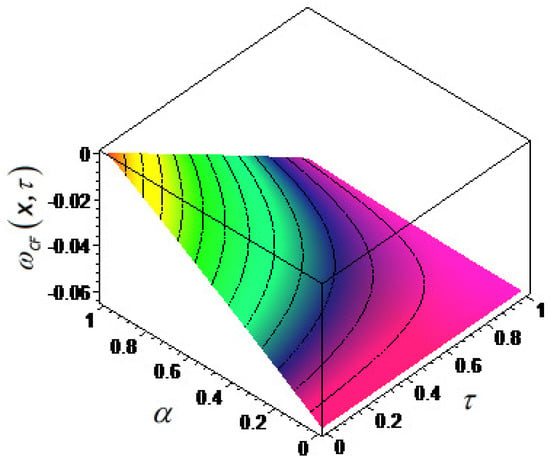
Figure 4.
The solution function of (4) in the CF derivative sense with respect to
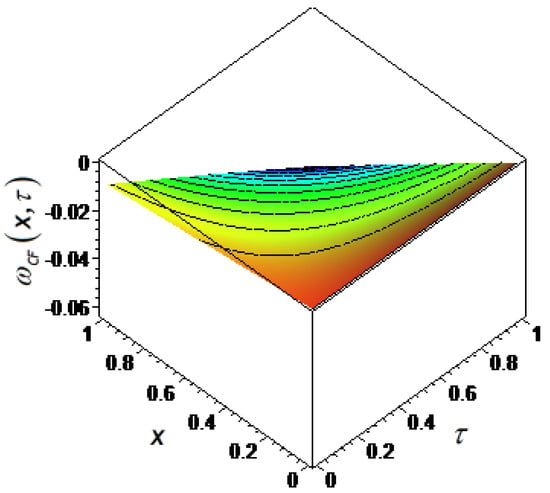
Figure 5.
Numerical simulation of (29) in the CF derivative sense for
4. Determining Stabilization and Convergence of Suggested Method
In this part of the study, we have explained the obtained values compatibility test by regarding them as the convergence and the stability of the suggested method. Because the series (25) and (28) converges, these series have to be the solution of initial value problems (2)–(5), respectively. In addition, the solution results represent that the suggested solution technique is convergent and stable. The mentioned method we used in this study provides a good convergence area of the solution. The numerical results found with LHAM are good settlements with the exact solutions. For the purpose of understanding the convergence and stability of the method defined by using the CF operator fractional derivative in Section 2, the amount of the absolute error for some values of x and has been presented. In Figure 6, we have also investigated the error rates based on the numerical and exact solution results. According to the results of this stability analysis, it can be concluded that the Caputo–Fabrizio LHAM is an effective and accurate method, for which the series is easily computable in a short time.
5. Conclusions
In this paper, we have employed approximate-analytical solutions by using a new numerical method, which is described with the Caputo–Fabrizio fractional derivative operator for linear PDEs of time-fractional order. This new fractional operator has a smooth kernel that takes on two different impressions for the spatial and temporal variable. Furthermore, the CF operator has been extremely popular in the last few years. We have demonstrated the efficiencies and accuracies of the suggested method by applying it to the FBS option pricing models with their initial conditions satisfied by the classical European vanilla option. By using the real market values from the finance literature, we can obtain how the option is priced for fractional cases of European call option pricing models. If we consider the European vanilla call option prices, which are given in Equation (1) with exercise price for special fractional values and in Figure 3, we have concluded that the option has the lowest price in exercise time of the option, when Moreover, as decreases, the payoff of the option increases. When , we observe that the option is overpriced [38]. The fractional model suggested in this study can model the price of different financial derivatives like swaps, warrant, etc. The successful applications of the proposed model prove that this model is in complete agreement with the corresponding exact solutions. Besides, in view of their usability, our method is applicable to many initial-boundary problems and fractional linear-nonlinear PDEs. Furthermore, the method is much easier than other homotopy methods, so the LT allows one in many positions to eliminate the inadequacy essentially caused by insufficient conditions, which take part in other approximate-analytical methods like homotopy perturbation method [39].
Acknowledgments
The authors are grateful to the referees for their improvements of the paper.
Author Contributions
Mehmet Yavuz conceived the manuscripts, designed the model and wrote the paper. Necati Özdemir analyzed the solution method and the stabilization; all authors read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| FDE | Fractional differential equation |
| LHAM | Laplace homotopy analysis method |
| CF | Caputo–Fabrizio |
| AB | Atangana–Baleanu |
| LT | Laplace transform |
| FC | Fractional calculus |
| ENSO | El Niño–Southern Oscillation |
| FBSE | Fractional Black–Scholes equation |
| GFBSE | Generalized fractional Black–Scholes equation |
References
- Gómez-Aguilar, J.F.; Morales-Delgado, V.F.; Taneco-Hernández, M.A.; Baleanu, D.; Escobar-Jiménez, R.F.; Al Qurashi, M.M. Analytical solutions of the electrical RLC circuit via Liouville–Caputo operators with local and non-local kernels. Entropy 2016, 18, 402. [Google Scholar] [CrossRef]
- Özdemir, N.; Yavuz, M. Numerical solution of fractional Black–Scholes equation by using the multivariate Padé approximation. Acta Phys. Pol. A. 2017, 132, 1050–1053. [Google Scholar] [CrossRef]
- Yavuz, M.; Özdemir, N.; Okur, Y.Y. Generalized differential transform method for fractional partial differential equation from finance. In Proceedings of the International Conference on Fractional Differentiation and its Applications, Novi Sad, Serbia, 18–20 July 2016; pp. 778–785. [Google Scholar]
- Alkahtani, B.S.T.; Koca, I.; Atangana, A. Analysis of a new model of H1N1 spread: Model obtained via Mittag-Leffler function. Adv. Mech. Eng. 2017, 9, 1–8. [Google Scholar] [CrossRef]
- Momani, S.; Qaralleh, R. Numerical approximations and Padé approximants for a fractional population growth model. App. Math. Model. 2007, 31, 1907–1914. [Google Scholar] [CrossRef]
- Hashim, I.; Abdulaziz, O.; Momani, S. Homotopy analysis method for fractional IVPs. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 674–684. [Google Scholar] [CrossRef]
- Evirgen, F.; Özdemir, N. Multistage Adomian decomposition method for solving NLP problems over a nonlinear fractional dynamical system. J. Comput. Nonlinear Dyn. 2011, 6. [Google Scholar] [CrossRef]
- Yavuz, M.; Özdemir, N. A quantitative approach to fractional option pricing problems with decomposition series. Konuralp J. Math. 2018, in press. [Google Scholar]
- Elbeleze, A.A.; Kılıçman, A.; Taib, B.M. Homotopy perturbation method for fractional Black–Scholes European option pricing equations using sumudu transform. Math. Prob. Eng. 2013, 2013, 1–7. [Google Scholar] [CrossRef]
- Yavuz, M. Novel solution methods for initial boundary value problems of fractional order with conformable differentiation. Int. J. Opt. Control Theor. Appl. 2018, 8, 1–7. [Google Scholar] [CrossRef]
- Yavuz, M.; Yaşkıran, B. Approximate-analytical solutions of cable equation using conformable fractional operator. New Trends Math. Sci. 2017, 5, 209–219. [Google Scholar] [CrossRef]
- Odibat, Z.; Momani, S.; Erturk, V.S. Generalized differential transform method: Application to differential equations of fractional order. App. Math. Comput. 2008, 197, 467–477. [Google Scholar] [CrossRef]
- Chen, W.; Wang, S. A finite difference method for pricing European and American options under a geometric Lévy process. Management 2015, 11, 241–264. [Google Scholar] [CrossRef]
- Turut, V.; Güzel, N. On solving partial differential equations of fractional order by using the variational iteration method and multivariate Padé approximations. Eur. J. Pure Appl. Math. 2013, 6, 147–171. [Google Scholar]
- Eroğlu, B.İ.; Avcı, D.; Özdemir, N. Optimal control problem for a conformable fractional heat conduction equation. Acta Phys. Pol. A. 2017, 132, 658–662. [Google Scholar] [CrossRef]
- Evirgen, F. Conformable fractional gradient based dynamic system for constrained optimization problem. Acta Phys. Pol. A. 2017, 132, 1066–1069. [Google Scholar] [CrossRef]
- Hu, Y.; Øksendal, B.; Sulem, A. Optimal consumption and portfolio in a Black–Scholes market driven by fractional Brownian motion. Infin. Dimens. Anal. Quantum Prob. Relat. Top. 2003, 6, 519–536. [Google Scholar] [CrossRef]
- Özdemir, N.; Agrawal, O.P.; Karadeniz, D.; Iskender, B.B. Analysis of an axis-symmetric fractional diffusion-wave problem. J. Phys. A Math. Theor. 2009, 42, 355208. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 1–13. [Google Scholar] [CrossRef]
- Atangana, A.; Alkahtani, B.S.T. New model of groundwater flowing within a confine aquifer: Application of Caputo–Fabrizio derivative. Arab. J. Geosci. 2016, 9, 1–8. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Nieto, J.J. Analysis of an El Nino-Southern Oscillation model with a new fractional derivative. Chaos Solitons Fractals 2017, 99, 109–115. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Nieto, J.J. Application of Caputo–Fabrizio derivatives to mhd free convection flow of generalized Walters’-B fluid model. Eur. Phys. J. Plus 2016, 131, 377. [Google Scholar] [CrossRef]
- Morales-Delgado, V.F.; Gómez-Aguilar, J.F.; Yépez-Martínez, H.; Baleanu, D.; Escobar-Jimenez, R.F.; Olivares-Peregrino, V.H. Laplace homotopy analysis method for solving linear partial differential equations using a fractional derivative with and without kernel singular. Adv. Differ. Equ. 2016, 2016, 164. [Google Scholar] [CrossRef]
- Sheikh, N.A.; Ali, F.; Saqib, M.; Khan, I.; Jan, S.A.A.; Alshomrani, A.S.; Alghamdi, M.S. Comparison and analysis of the Atangana–Baleanu and Caputo–Fabrizio fractional derivatives for generalized Casson fluid model with heat generation and chemical reaction. Res. Phys. 2017, 7, 789–800. [Google Scholar] [CrossRef]
- Koca, I.; Atangana, A. Solutions of Cattaneo–Hristov model of elastic heat diffusion with Caputo–Fabrizio and Atangana–Baleanu fractional derivatives. Therm. Sci. 2017, 21, 2299–2305. [Google Scholar] [CrossRef]
- Hristov, J. Steady-state heat conduction in a medium with spatial non-singular fading memory: Derivation of Caputo–Fabrizio space-fractional derivative with Jeffrey’s kernel and analytical solutions. Therm. Sci. 2017, 21, 827–839. [Google Scholar] [CrossRef]
- Alkahtani, B.S.T.; Atangana, A. Controlling the wave movement on the surface of shallow water with the Caputo–Fabrizio derivative with fractional order. Chaos Solitons Fractals 2016, 89, 539–546. [Google Scholar] [CrossRef]
- Alkahtani, B.S.T.; Atangana, A. Analysis of non-homogeneous heat model with new trend of derivative with fractional order. Chaos Solitons Fractals 2016, 89, 566–571. [Google Scholar] [CrossRef]
- Hristov, J. Transient heat diffusion with a non-singular fading memory: From the Cattaneo constitutive equation with Jeffrey’s kernel to the Caputo–Fabrizio time-fractional derivative. Therm. Sci. 2016, 20, 757–762. [Google Scholar] [CrossRef]
- Atangana, A.; Koca, I. On the new fractional derivative and application to nonlinear Baggs and Freedman model. J. Nonlinear Sci. Appl. 2016, 9, 2467–2480. [Google Scholar]
- Ghandehari, M.A.M.; Ranjbar, M. European option pricing of fractional Black–Scholes model with new Lagrange multipliers. Comput. Methods Differ. Equ. 2014, 2, 1–10. [Google Scholar]
- Yerlikaya-Özkurt, F.; Vardar-Acar, C.; Yolcu-Okur, Y.; Weber, G.W. Estimation of the Hurst parameter for fractional Brownian motion using the CMARS method. J. Comput. Appl. Math. 2014, 259, 843–850. [Google Scholar] [CrossRef]
- Black, F.; Scholes, M. The pricing of options and corporate liabilities. J. Political Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef]
- Wilmott, P.; Howison, S.; Dewynne, J. The Mathematics of Financial Derivatives: A Student Introduction; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Ahmed, E.; Abdusalam, H.A. On modified Black–Scholes equation. Chaos Solitons Fractals 2004, 22, 583–587. [Google Scholar] [CrossRef]
- Cen, Z.; Le, A. A robust and accurate finite difference method for a generalized Black–Scholes equation. J. Comput. Appl. Math. 2011, 235, 3728–3733. [Google Scholar] [CrossRef]
- Meng, L.; Wang, M. Comparison of Black–Scholes formula with fractional Black–Scholes formula in the foreign exchange option market with changing volatility. Asia-Pac. Finan Markets 2010, 17, 99–111. [Google Scholar] [CrossRef]
- Yavuz, M.; Özdemir, N. A different approach to the European option pricing model with new fractional operator. Math. Model. Nat. Phenom. 2018, in press. [Google Scholar] [CrossRef]
- Madani, M.; Fathizadeh, M.; Khan, Y.; Yildirim, A. On the coupling of the homotopy perturbation method and Laplace transformation. Math. Comput. Model. 2011, 53, 1937–1945. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).