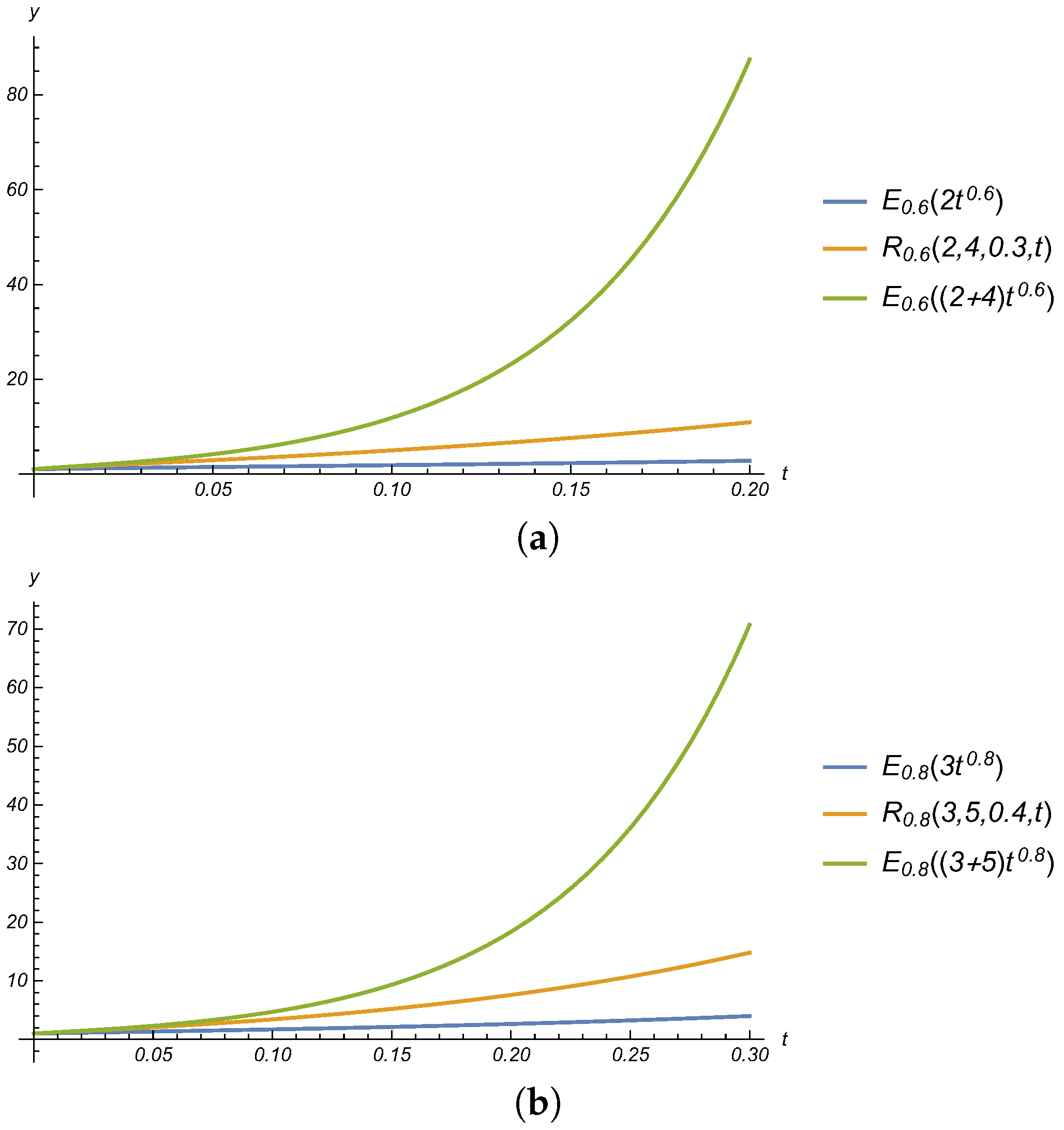Series Solution of the Pantograph Equation and Its Properties

Abstract

In this paper, we discuss the classical pantograph equation and its generalizations to include fractional order and the higher order case. The special functions are obtained from the series solution of these equations. We study different properties of these special functions and establish the relation with other functions. Further, we discuss some contiguous relations for these special functions.

1. Introduction

Ordinary differential equations (ODE) are widely used by researchers to model various natural systems. However, it is observed that such equations cannot model the actual behavior of the system. Since the ordinary derivative is a local operator, it cannot model the memory and hereditary properties in real-life phenomena. Such phenomena can be modeled in a more accurate way by introducing some nonlocal component, e.g., delay in it.

The characteristic equation of delay differential equations (DDE) is a transcendental equation in contrast with the polynomial in the case of ODE. Hence, the DDEs are difficult to analyze as compared with ODEs.

Various special functions viz. exponential, sine, cosine, hypergeometric, Mittag-Leffler and gamma are obtained from ODEs [1]. If the equations have variable coefficients, then we may get the Legendre polynomial, the Laguerre polynomial, Bessel functions, and so on [2]. However, there are vary few papers that are devoted to the special functions arising in DDEs [3]. This motivates us to work on the special functions emerging from the solution of DDE with proportional delay. We analyze different properties of such special functions and present the relationship with other functions.

2. Preliminaries

Definition 1

([4]). Gaussian binomial coefficients are defined by:

$${\left({\displaystyle \genfrac{}{}{0pt}{}{n}{r}}\right)}_q=\left\{\begin{array}{cc}\frac{(1-q^n)(1-q^{n-1})\cdots (1-q^{n-r+1})}{(1-q)(1-q^2)\cdots (1-q^r)}\hfill & ifr\le n\hfill \\ 0\hfill & ifr>n,\hfill \end{array}\right.$$

(1)

where with $\mid q\mid <1$.

Definition 2

([5]). The Riemann–Liouville integral of order $\mu ,\mu >0$ is given by:

$$I^{\mu }f(t)=\frac{1}{\Gamma (\mu )}{\int }_0^t{(t-\tau )}^{\mu -1}f(\tau )d\tau ,t>0.$$

(2)

Definition 3

([5]). The Caputo fractional derivative of f is defined as:

$$\begin{array}{ccc}\hfill D^{\mu }f(t)& =& \frac{d^m}{d{t}^m}f(t),\mu =m\hfill \\ & =& I^{m-\mu }\frac{d^m}{d{t}^m}f(t),m-1<\mu <m,m\in \mathbb{N}.\hfill \end{array}$$

(3)

Definition 4

([6]). Two special functions are said to be contiguous if their parameters differ by integers. The relations made by contiguous functions are said to be contiguous function relations.

Theorem 1

([7]). (Existence and uniqueness theorem)

Let X be a Banach space and $J=[0,T]$. If $f:J\times X\times X\to X$ is continuous and there exists a positive constant $L>0$, such that $\mid \mid f\left(t,u,x\right)-f\left(t,v,y\right)\mid \mid \le L\left(\mid \mid u-v\mid \mid +\mid \mid x-y\mid \mid \right)$, $t\in J$, $u,v,x,y\in X$ and if $\frac{4T^{\alpha }L}{\Gamma (\alpha +1)}<1$, then the fractional differential equation with proportional delay:

$$D^{\alpha }u(t)=f\left(u,u(t),u(qt)\right),u(0)=u_0,t\in [0,T]$$

where $0<\alpha \le 1$, $0<q<1$ has a unique solution.

3. Pantograph Equation

The pantograph is a current collection device, which is used in electric trains. The mathematical model of the pantograph is discussed by various researchers [8,9,10,11].

The differential equation:

$$y^{\prime }(t)=ay(t)+by(qt),y(0)=1,$$

(4)

with proportional delay modeling these phenomena is discussed by Ockendon and Tayler in [12]. Equation (4) is called the pantograph equation. Kato and McLeod [13] showed that the problem (4) is well-posed if $q<1$. Further, the authors discussed the asymptotic properties of this equation. The coefficients in the power series solution are obtained by using a recurrence relation.

In [14], Fox et al. showed that the solution of (4) is given by a power series:

$$\begin{array}{ccc}\hfill y(t)& =& 1+\sum _{n=1}^{\infty }\frac{t^n}{n!}\prod _{j=0}^{n-1}\left(a+b{q}^j\right).\hfill \end{array}$$

(5)

Iserles [15] considered a generalized pantograph equation $y^{\prime }(t)=Ay(t)+By(qt)+C{y}^{\prime }(qt),y(0)=y_0,$ where $q\in (0,1)$. The condition for the well-posedness of the problem is given in terms of $A,B$ and C. The solution of the problem is expressed in the form of the Dirichlet series. Further, the advanced pantograph equation $y^{(n)}(t)={\sum }_{j=0}^l{\sum }_{k=0}^{m-1}{a}_{j,k}{y}^{(k)}({\alpha }_{j}t),t\ge 0$, where $a_{j,k}\in \mathbb{C}$ and ${\alpha }_j>1$ for all $j=0,1,\dots ,l$, is also analyzed by Derfel and Iserles [16]. In [17], Patade and Bhalekar discussed the pantograph equation with incommensurate delay. Various properties of the series solution obtained are discussed.

In this paper, we write the solution (5) in the form of a special function and study its properties. We discuss the generalization of (4) to fractional order and the higher order case, as well.

4. Special Function Generated from the Pantograph Equation

We write solution (5) in the form of following special function:

$$\mathcal{R}(a,b,q,t)=1+\sum _{n=1}^{\infty }\frac{t^n}{n!}\prod _{j=0}^{n-1}\left(a+b{q}^j\right).$$

(6)

The notation $\mathcal{R}$ is used in memory of Ramanujan [18].

Theorem 2

([14]). If $q\in (0,1)$, then the power series:

$$\mathcal{R}(a,b,q,t)=1+\sum _{n=1}^{\infty }\frac{t^n}{n!}\prod _{j=0}^{n-1}\left(a+b{q}^j\right)$$

has an infinite radius of convergence.

Corollary 1.

The power series (6) is absolutely convergent for all t, and hence, it is uniformly convergent on any compact interval on $\mathbb{R}$.

Theorem 3.

For $m\in \mathbb{N}\cup \left\{0\right\}$, we have:

$$\frac{d}{dt}\mathcal{R}(a,b,q,q^{m}t)=a{q}^m\mathcal{R}(a,b,q,q^{m}t)+b{q}^m\mathcal{R}(a,b,q,q^{m+1}t).$$

Proof. 

Consider:

$$\begin{array}{ccc}\hfill \frac{d}{dt}\mathcal{R}(a,b,q,q^{m}t)& =& \frac{d}{dt}\left(1+\sum _{n=1}^{\infty }\frac{{(q^{m}t)}^n}{n!}\prod _{j=0}^{n-1}\left(a+b{q}^j\right)\right)\hfill \\ & =& q^m\sum _{n=1}^{\infty }\frac{{(q^{m}t)}^{n-1}}{(n-1)!}\prod _{j=0}^{n-1}\left(a+b{q}^j\right)\hfill \\ & =& q^m(a+b)+q^m\sum _{n=2}^{\infty }\frac{{(q^{m}t)}^{n-1}}{(n-1)!}\prod _{j=0}^{n-1}\left(a+b{q}^j\right)\hfill \\ & =& q^m(a+b)+q^m\sum _{n=1}^{\infty }\frac{{(q^{m}t)}^n}{n!}\prod _{j=0}^n\left(a+b{q}^j\right)\hfill \\ & =& q^m(a+b)+q^m\sum _{n=1}^{\infty }\frac{{(q^{m}t)}^n(a+b{q}^n)}{n!}\prod _{j=0}^{n-1}\left(a+b{q}^j\right)\hfill \\ & =& a{q}^m\left(1+\sum _{n=1}^{\infty }\frac{{(q^{m}t)}^n}{n!}\prod _{j=0}^{n-1}\left(a+b{q}^j\right)\right)\hfill \\ & & +b{q}^m\left(1+\sum _{n=1}^{\infty }\frac{{(q^{m+1}t)}^n}{n!}\prod _{j=0}^{n-1}\left(a+b{q}^j\right)\right)\hfill \\ \hfill \frac{d}{dt}\mathcal{R}(a,b,q,q^{m}t)& =& a{q}^m\mathcal{R}(a,b,q,q^{m}t)+b{q}^m\mathcal{R}(a,b,q,q^{m+1}t)\hfill \end{array}$$

Hence the proof. ☐

Theorem 4.

For $m\in \mathbb{N}$, we have:

$$\frac{d^m}{d{t}^m}\mathcal{R}(a,b,q,t)=\sum _{r=0}^m{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{r}{2}}\right)}{\left({\displaystyle \genfrac{}{}{0pt}{}{m}{r}}\right)}_q{a}^{m-r}{b}^r\mathcal{R}(a,b,q,q^{r}t).$$

Proof. 

We prove the result by using the induction hypothesis on m.

From Theorem 3, the result is true for $m=1$.

Suppose,

$$\frac{d^{m-1}}{d{t}^{m-1}}\mathcal{R}(a,b,q,t)=\sum _{r=0}^{m-1}{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{r}{2}}\right)}{\left({\displaystyle \genfrac{}{}{0pt}{}{m-1}{r}}\right)}_q{a}^{m-(r+1)}{b}^r\mathcal{R}(a,b,q,q^{r}t).$$

Consider,

$$\begin{array}{ccc}\hfill \frac{d^m}{d{t}^m}\mathcal{R}(a,b,q,t)& =& \frac{d}{dt}\left(\frac{d^{m-1}}{d{t}^{m-1}}\mathcal{R}(a,b,q,t)\right)\hfill \\ & =& \frac{d}{dt}\left(\sum _{r=0}^{m-1}{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{r}{2}}\right)}{\left({\displaystyle \genfrac{}{}{0pt}{}{m-1}{r}}\right)}_q{a}^{m-(r+1)}{b}^r\mathcal{R}(a,b,q,q^{r}t)\right)\hfill \\ & =& \sum _{r=0}^{m-1}{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{r}{2}}\right)}{\left({\displaystyle \genfrac{}{}{0pt}{}{m-1}{r}}\right)}_q{a}^{m-(r+1)}{b}^r\frac{d}{dt}\mathcal{R}(a,b,q,q^{r}t).\hfill \end{array}$$

Using Theorem 3, we have:

$$\begin{array}{ccc}\hfill \frac{d^m}{d{t}^m}\mathcal{R}(a,b,q,t)& =& \sum _{r=0}^{m-1}{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{r}{2}}\right)}{\left({\displaystyle \genfrac{}{}{0pt}{}{m-1}{r}}\right)}_q{a}^{m-(r+1)}{b}^r\hfill \\ & & \left(a{q}^r\mathcal{R}(a,b,q,q^{r}t)+b{q}^r\mathcal{R}(a,b,q,q^{r+1}t)\right)\hfill \\ & =& \sum _{r=0}^{m-1}{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{r}{2}}\right)}{q}^r{\left({\displaystyle \genfrac{}{}{0pt}{}{m-1}{r}}\right)}_q{a}^{m-r}{b}^r\mathcal{R}(a,b,q,q^{r}t)\hfill \\ & & +\sum _{k=0}^{m-1}{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{k}{2}}\right)}{q}^k{\left({\displaystyle \genfrac{}{}{0pt}{}{m-1}{k}}\right)}_q{a}^{m-(k+1)}{b}^{k+1}\mathcal{R}(a,b,q,q^{k+1}t)\hfill \\ & =& \sum _{r=0}^{m-1}{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{r}{2}}\right)}{q}^r{\left({\displaystyle \genfrac{}{}{0pt}{}{m-1}{r}}\right)}_q{a}^{m-r}{b}^r\mathcal{R}(a,b,q,q^{r}t)\hfill \\ & & +\sum _{k=1}^m{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{k}{2}}\right)}{\left({\displaystyle \genfrac{}{}{0pt}{}{m-1}{k-1}}\right)}_q{a}^{m-k}{b}^k\mathcal{R}(a,b,q,q^{k}t)\hfill \\ & =& \sum _{r=0}^m{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{r}{2}}\right)}{q}^r{\left({\displaystyle \genfrac{}{}{0pt}{}{m-1}{r}}\right)}_q{a}^{m-r}{b}^r\mathcal{R}(a,b,q,q^{r}t)\hfill \\ & & -q^{\left({\displaystyle \genfrac{}{}{0pt}{}{m}{2}}\right)}{q}^m{\left({\displaystyle \genfrac{}{}{0pt}{}{m-1}{m}}\right)}_q{b}^m\mathcal{R}(a,b,q,q^{m}t)\hfill \\ & & +\sum _{k=0}^m{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{k}{2}}\right)}{\left({\displaystyle \genfrac{}{}{0pt}{}{m-1}{k-1}}\right)}_q{a}^{m-k}{b}^k\mathcal{R}(a,b,q,q^{k}t)\hfill \\ & & -{\left({\displaystyle \genfrac{}{}{0pt}{}{m-1}{-1}}\right)}_q{a}^m\mathcal{R}(a,b,q,t)\hfill \\ & =& \sum _{r=0}^m{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{r}{2}}\right)}{q}^r{\left({\displaystyle \genfrac{}{}{0pt}{}{m-1}{r}}\right)}_q{a}^{m-r}{b}^r\mathcal{R}(a,b,q,q^{r}t)\hfill \\ & & +\sum _{k=0}^m{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{k}{2}}\right)}{\left({\displaystyle \genfrac{}{}{0pt}{}{m-1}{k-1}}\right)}_q{a}^{m-k}{b}^k{q}^r\mathcal{R}(a,b,q,q^{k}t)\hfill \\ & =& \sum _{r=0}^m{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{r}{2}}\right)}\left(q^r{\left({\displaystyle \genfrac{}{}{0pt}{}{m-1}{r}}\right)}_q+{\left({\displaystyle \genfrac{}{}{0pt}{}{m-1}{r-1}}\right)}_q\right)a^{m-r}{b}^r\mathcal{R}(a,b,q,q^{r}t).\hfill \\ \hfill \frac{d^m}{d{t}^m}\mathcal{R}(a,b,q,t)& =& \sum _{r=0}^m{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{r}{2}}\right)}{\left({\displaystyle \genfrac{}{}{0pt}{}{m}{r}}\right)}_q{a}^{m-r}{b}^r\mathcal{R}(a,b,q,q^{r}t),\hfill \end{array}$$

This completes the proof. ☐

Theorem 5.

For $q\in (0,1)$, we have:

$$\mathcal{R}(a,b,q,t)=1+\sum _{n=1}^{\infty }\sum _{r=0}^n{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{r}{2}}\right)}{\left({\displaystyle \genfrac{}{}{0pt}{}{n}{r}}\right)}_q{a}^{n-r}{b}^r\frac{t^n}{n!}.$$

Proof. 

We have:

$$\mathcal{R}(a,b,q,t)=1+\sum _{n=1}^{\infty }\frac{t^n}{n!}\prod _{j=0}^{n-1}\left(a+b{q}^j\right).$$

Using the q- binomial theorem:

$$\prod _{j=0}^{n-1}\left(a+b{q}^j\right)=\sum _{r=0}^n{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{r}{2}}\right)}{\left({\displaystyle \genfrac{}{}{0pt}{}{n}{r}}\right)}_q{a}^{n-r}{b}^r,$$

(7)

defined in [19], we obtain:

$$\begin{array}{ccc}\hfill \mathcal{R}(a,b,q,t)& =& 1+\sum _{n=1}^{\infty }\frac{t^n}{n!}\sum _{r=0}^n{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{r}{2}}\right)}{\left({\displaystyle \genfrac{}{}{0pt}{}{n}{r}}\right)}_q{a}^{n-r}{b}^r\hfill \\ \hfill \mathcal{R}(a,b,q,t)& =& 1+\sum _{n=1}^{\infty }\sum _{r=0}^n{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{r}{2}}\right)}{\left({\displaystyle \genfrac{}{}{0pt}{}{n}{r}}\right)}_q{a}^{n-r}{b}^r\frac{t^n}{n!}.\hfill \end{array}$$

Hence the proof. ☐

Theorem 6.

If $q\in (0,1)$, then we can express the integral of $e^{-t}\mathcal{R}$ in the following series containing $q-$binomial coefficients:

$${\int }_t^{\infty }{e}^{-t}\mathcal{R}(a,b,q,t)dt=\Gamma (1,t)\left(1+\sum _{n=1}^{\infty }\sum _{k=0}^n\sum _{r=0}^n{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{r}{2}}\right)}{\left({\displaystyle \genfrac{}{}{0pt}{}{n}{r}}\right)}_q{a}^{n-r}{b}^r\frac{t^k}{k!}\right).$$

Proof. 

Consider:

$$\begin{array}{ccc}\hfill {\int }_t^{\infty }{e}^{-t}\mathcal{R}(a,b,q,t)dt& =& {\int }_t^{\infty }{e}^{-t}+\sum _{n=1}^{\infty }\prod _{j=0}^{n-1}\frac{\left(a+b{q}^j\right)}{n!}{\int }_t^{\infty }{e}^{-t}{t}^{n}dt\hfill \\ & =& e^{-t}+\sum _{n=1}^{\infty }\sum _{k=0}^n\prod _{j=0}^{n-1}\frac{\left(a+b{q}^j\right)}{n!}\Gamma (n+1,t)\hfill \\ & =& e^{-t}+\sum _{n=1}^{\infty }\prod _{j=0}^{n-1}\frac{\left(a+b{q}^j\right)}{n!}n!e^{-t}\sum _{k=0}^n\frac{t^k}{k!}\hfill \\ & =& e^{-t}\left(1+\sum _{n=1}^{\infty }\sum _{r=0}^n{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{r}{2}}\right)}{\left({\displaystyle \genfrac{}{}{0pt}{}{n}{r}}\right)}_q{a}^{n-r}{b}^r\sum _{k=0}^n\frac{t^k}{k!}\right)\hfill \\ \hfill {\int }_t^{\infty }{e}^{-t}\mathcal{R}(a,b,q,t)dt& =& \Gamma (1,t)\left(1+\sum _{n=1}^{\infty }\sum _{k=0}^n\sum _{r=0}^n{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{r}{2}}\right)}{\left({\displaystyle \genfrac{}{}{0pt}{}{n}{r}}\right)}_q{a}^{n-r}{b}^r\frac{t^k}{k!}\right).\hfill \end{array}$$

 ☐

Theorem 7.

If $q\in (0,1)$, then we have the following relation:

$$\begin{array}{ccc}\hfill {\int }_0^t{e}^{-t}\mathcal{R}(a,b,q,t)dt& =& 1+\sum _{n=1}^{\infty }\sum _{r=0}^n{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{r}{2}}\right)}{\left({\displaystyle \genfrac{}{}{0pt}{}{n}{r}}\right)}_q{a}^{n-r}{b}^r\hfill \\ & & -\Gamma (1,t)\left(1+\sum _{n=1}^{\infty }\sum _{k=0}^n\sum _{r=0}^n{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{r}{2}}\right)}{\left({\displaystyle \genfrac{}{}{0pt}{}{n}{r}}\right)}_q{a}^{n-r}{b}^r\frac{t^k}{k!}\right).\hfill \end{array}$$

Proof. 

Consider:

$$\begin{array}{ccc}\hfill {\int }_0^t{e}^{-t}\mathcal{R}(a,b,q,t)dt& =& {\int }_0^t{e}^{-t}dt+\sum _{n=1}^{\infty }\prod _{j=0}^{n-1}\frac{\left(a+b{q}^j\right)}{n!}{\int }_0^t{e}^{-t}{t}^{n}dt\hfill \\ & =& 1-e^{-t}+\sum _{n=1}^{\infty }\prod _{j=0}^{n-1}\frac{\left(a+b{q}^j\right)}{n!}\gamma (n+1,t)\hfill \\ & =& 1-e^{-t}+\sum _{n=1}^{\infty }\prod _{j=0}^{n-1}\frac{\left(a+b{q}^j\right)}{n!}n!\left(1-e^{-t}\sum _{k=0}^n\frac{t^k}{k!}\right)\hfill \\ & =& 1+\sum _{n=1}^{\infty }\sum _{r=0}^n{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{r}{2}}\right)}{\left({\displaystyle \genfrac{}{}{0pt}{}{n}{r}}\right)}_q{a}^{n-r}{b}^r\hfill \\ & & -e^{-t}\left(1+\sum _{n=1}^{\infty }\sum _{k=0}^n\sum _{r=0}^n{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{r}{2}}\right)}{\left({\displaystyle \genfrac{}{}{0pt}{}{n}{r}}\right)}_q{a}^{n-r}{b}^r\frac{t^k}{k!}\right)(\mathrm{From}(7))\hfill \\ \hfill {\int }_0^t{e}^{-t}\mathcal{R}(a,b,q,t)dt& =& 1+\sum _{n=1}^{\infty }\sum _{r=0}^n{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{r}{2}}\right)}{\left({\displaystyle \genfrac{}{}{0pt}{}{n}{r}}\right)}_q{a}^{n-r}{b}^r\hfill \\ & & -\Gamma (1,t)\left(1+\sum _{n=1}^{\infty }\sum _{k=0}^n\sum _{r=0}^n{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{r}{2}}\right)}{\left({\displaystyle \genfrac{}{}{0pt}{}{n}{r}}\right)}_q{a}^{n-r}{b}^r\frac{t^k}{k!}\right).\hfill \end{array}$$

 ☐

Theorem 8.

The function $\mathcal{R}$ shows the following relationship with the lower incomplete gamma function γ:

$${\int }_0^t{e}^{-t}\mathcal{R}(a,b,q,\lambda t)dt=\gamma (1,t)+\lambda \sum _{n=1}^{\infty }\sum _{m=0}^{n+1}\prod _{j=0}^{n-1}\left(a+b{q}^j\right)\frac{{\lambda }^n}{n!}\frac{\gamma (n+m+1,t)}{m!}{(1-\lambda )}^m.$$

Proof. 

We have:

$$\begin{array}{ccc}\hfill {\int }_0^t{e}^{-t}\mathcal{R}(a,b,q,\lambda t)dt& =& 1-e^{-t}+\sum _{n=1}^{\infty }\prod _{j=0}^{n-1}\frac{\left(a+b{q}^j\right)}{n!}{\int }_0^t{e}^{-t}{(\lambda t)}^{n}dt\hfill \\ & =& \gamma (1,t)+\sum _{n=1}^{\infty }\prod _{j=0}^{n-1}\frac{\left(a+b{q}^j\right)}{n!}\gamma (n+1,\lambda t).\hfill \end{array}$$

By using the property [20]: $\gamma (n,\lambda t)={\lambda }^n{\sum }_{m=0}^n\frac{\gamma (n+m,t)}{m!}{(1-\lambda )}^m$, we get

$${\int }_0^t{e}^{-t}\mathcal{R}(a,b,q,\lambda t)dt=\gamma (1,t)+\lambda \sum _{n=1}^{\infty }\sum _{m=0}^{n+1}\prod _{j=0}^{n-1}\left(a+b{q}^j\right)\frac{{\lambda }^n}{n!}\frac{\gamma (n+m+1,t)}{m!}{(1-\lambda )}^m.$$

 ☐

Theorem 9.

The following integral gives the relation between the function $\mathcal{R}$ and the upper incomplete gamma function $\Gamma$:

$${\int }_t^{\infty }{e}^{-t}\mathcal{R}(a,b,q,\lambda t)dt=\Gamma (1,t)+\lambda \sum _{n=1}^{\infty }\sum _{m=0}^{n+1}\prod _{j=0}^{n-1}\left(a+b{q}^j\right)\frac{{\lambda }^n}{n!}\frac{\Gamma (n+m+1,t)}{m!}{(1-\lambda )}^m.$$

Proof. 

$$\begin{array}{ccc}\hfill {\int }_t^{\infty }{e}^{-t}\mathcal{R}(a,b,q,\lambda t)dt& =& e^{-t}+\sum _{n=1}^{\infty }\prod _{j=0}^{n-1}\frac{\left(a+b{q}^j\right)}{n!}{\int }_t^{\infty }{e}^{-t}{(\lambda t)}^{n}dt\hfill \\ & =& \Gamma (1,t)+\sum _{n=1}^{\infty }\prod _{j=0}^{n-1}\frac{\left(a+b{q}^j\right)}{n!}\Gamma (n+1,\lambda t).\hfill \end{array}$$

By using the property [20]: $\Gamma (n,\lambda t)={\lambda }^n{\sum }_{m=0}^n\frac{\Gamma (n+m,t)}{m!}{(1-\lambda )}^m$, we obtain

$${\int }_t^{\infty }{e}^{-t}\mathcal{R}(a,b,q,\lambda t)dt=\Gamma (1,t)+\lambda \sum _{n=1}^{\infty }\sum _{m=0}^{n+1}\prod _{j=0}^{n-1}\left(a+b{q}^j\right)\frac{{\lambda }^n}{n!}\frac{\Gamma (n+m+1,t)}{m!}{(1-\lambda )}^m.$$

 ☐

5. Properties, Relations and Identities of $\mathcal{R}(\mathit{a},\mathit{b},\mathit{q},\mathit{t})$

We state the following properties of $\mathcal{R}(a,b,q,t)$ without proof.

5.1. Properties of $\mathcal{R}(a,b,q,t)$

For $l,m\in \mathbb{N}$:

• $\mathcal{R}\left(0,\pm b^m,q,t\right)=\mathcal{R}\left(0,1,q,\pm b^{m}t\right)$.

  (a)

  $\mathcal{R}\left(0,\pm a^l{b}^{-m},q,t\right)=\mathcal{R}\left(0,1,q,\pm a^l{b}^{-m}t\right)$.

  (b)

  $\mathcal{R}\left(0,\pm b^{-m},q,t\right)=\mathcal{R}\left(0,1,q,\pm b^{-m}t\right)$.

• $\mathcal{R}\left(a^m,a^m,q,t\right)=\mathcal{R}\left(1,1,q,a^{m}t\right)$.

  (a)

  $\mathcal{R}\left(\pm a^{-m},\pm a^m,q,t\right)=\mathcal{R}\left(1,a^{2m},q,\pm a^{-m}t\right)$.

  (b)

  $\mathcal{R}\left(\pm a^m,\pm a^{-m},q,t\right)=\mathcal{R}\left(1,a^{-2m},q,\pm a^{m}t\right)$.

  (c)

  $\mathcal{R}\left(-a^m,a^{-m},q,t\right)=\mathcal{R}\left(1,-a^{-2m},q,-a^{m}t\right)$.

  (d)

  $\mathcal{R}\left(a^m,-a^{-m},q,t\right)=\mathcal{R}\left(1,-a^{-2m},q,a^{m}t\right)$.

  (e)

  $\mathcal{R}\left(-a^{-m},a^m,q,t\right)=\mathcal{R}\left(1,-a^{2m},q,-a^{-m}t\right)$.

  (f)

  $\mathcal{R}\left(a^{-m},-a^m,q,t\right)=\mathcal{R}\left(1,-a^{2m},q,a^{-m}t\right)$.

• $\mathcal{R}\left(a^l,b^m,q,t\right)=\mathcal{R}\left(1,a^{-l}{b}^m,q,a^{l}t\right)$.

  (a)

  $\mathcal{R}\left(a^l{b}^{-m},b^m,q,t\right)=\mathcal{R}\left(1,a^{-l}{b}^{2m},q,a^l{b}^{-m}t\right)$.

  (b)

  $\mathcal{R}\left(a^{-l}{b}^m,b^m,q,t\right)=\mathcal{R}\left(1,a^l,q,a^{-l}{b}^{m}t\right)$.

  (c)

  $\mathcal{R}\left(a^l{b}^{-m},a^m,q,t\right)=\mathcal{R}\left(1,a^{m-l}{b}^m,q,a^l{b}^{-m}t\right)$.

  (d)

  $\mathcal{R}\left(a^{-l}{b}^m,a^m,q,t\right)=\mathcal{R}\left(1,a^{l+m}{b}^{-m},q,a^{-l}{b}^{m}t\right)$.

5.2. Relation to Other Functions

• $\mathcal{R}(a,b,q,t)=1+{\sum }_{n=1}^{\infty }\frac{B(t,n,1)}{(n-1)!}{\prod }_{j=0}^{n-1}\left(a+b{q}^j\right)$.
• $\mathcal{R}(a,b,q,t)=1+{\sum }_{n=1}^{\infty }\frac{B(t,n,1)}{B(n,1)n!}{\prod }_{j=0}^{n-1}\left(a+b{q}^j\right)$.
• $\mathcal{R}(a,b,q,t)=1+{\sum }_{n=1}^{\infty }\frac{I_t(n,1)}{n!}{\prod }_{j=0}^{n-1}\left(a+b{q}^j\right)$,

where $B(t,n,1)$ and $I_t(n,1)$ are the incomplete beta function and regularized incomplete beta function [4].

5.3. Contiguous Relations of $\mathcal{R}(a,b,q,t)$

• $\mathcal{R}(a\pm 1,b,q,t)=\mathcal{R}(1,{(a\pm 1)}^{-1}b,q,(a\pm 1)t)$.
• $\mathcal{R}(a,b\pm 1,q,t)=\mathcal{R}(1,a^{-1}(b\pm 1),q,at)$.
• $\mathcal{R}(a\pm 1,,b\pm 1,q,t)=\mathcal{R}(1,{(a\pm 1)}^{-1}(b\pm 1),q,(a\pm 1)t)$.

6. Generalizations

6.1. Generalizations to Include the Fractional Order Derivative

Consider the fractional delay differential equation with proportional delay:

$$D^{\alpha }y(t)=ay(t)+by(qt),y(0)=1,$$

(8)

where $0<\alpha \le 1$, $q\in (0,1)$, $a\in \mathbb{R}$ and $b\in \mathbb{R}$.

The solution of (8) is:

$$y(t)=1+\sum _{n=1}^{\infty }\frac{t^{\alpha n}}{\Gamma (\alpha n+1)}\prod _{j=0}^{n-1}\left(a+b{q}^{\alpha j}\right).$$

(9)

We denote the series in (9) by:

$${\mathcal{R}}_{\alpha }(a,b,q,t)=1+\sum _{n=1}^{\infty }\frac{t^{\alpha n}}{\Gamma (\alpha n+1)}\prod _{j=0}^{n-1}\left(a+b{q}^{\alpha j}\right).$$

Theorem 10.

If $q\in (0,1)$, then the power series:

$${\mathcal{R}}_{\alpha }(a,b,q,t)=1+\sum _{n=1}^{\infty }\frac{t^{\alpha n}}{\Gamma (\alpha n+1)}\prod _{j=0}^{n-1}\left(a+b{q}^{\alpha j}\right),$$

is convergent for all finite values of t.

Theorem 11.

For $q\in (0,1)$, $a\ge 0$ and $b\ge 0$, the function ${\mathcal{R}}_{\alpha }(a,b,q,t)$ satisfies the following inequality:

$$E_{\alpha }(a{t}^{\alpha })\le {\mathcal{R}}_{\alpha }(a,b,q,t)\le E_{\alpha }((a+b)t^{\alpha }),0\le t<\infty .$$

Proof. 

Since $q\in (0,1)$, $a\ge 0$ and $b\ge 0$, we have:

$$\begin{array}{ccc}\hfill \prod _{j=0}^{n-1}\left(a+b{q}^{{}_{\alpha }j}\right)& \le & {(a+b)}^n\hfill \\ \hfill \Rightarrow \frac{t^{\alpha n}}{\Gamma (\alpha n+1)}\prod _{j=0}^{n-1}\left(a+b{q}^{\alpha j}\right)& \le & \frac{t^{\alpha n}{(a+b)}^n}{\Gamma (\alpha n+1)}.\hfill \end{array}$$

Taking summation over n, we get:

$$\begin{array}{ccc}\hfill {\mathcal{R}}_{\alpha }(a,b,q,t)& \le & E_{\alpha }((a+b)t^{\alpha }),0\le t<\infty .\hfill \end{array}$$

(10)

Similarly, we have:

$$\begin{array}{ccc}\hfill a^n& \le & \prod _{j=0}^{n-1}\left(a+b{q}^{{}_{\alpha }j}\right)\hfill \\ \hfill \Rightarrow E_{\alpha }(a{t}^{\alpha })& \le & {\mathcal{R}}_{\alpha }(a,b,q,t),0\le t<\infty .\hfill \end{array}$$

(11)

From (10) and (11), we get:

$$E_{\alpha }(a{t}^{\alpha })\le {\mathcal{R}}_{\alpha }(a,b,q,t)\le E_{\alpha }((a+b)t^{\alpha }),0\le t<\infty .$$

 ☐

The result is illustrated in Figure 1a,b.

Theorem 12.

For $k\in \mathbb{N}\cup \left\{0\right\}$, we have:

$$\begin{array}{ccc}\hfill \frac{d^k}{d{t}^k}{\mathcal{R}}_{\alpha }(a,b,q,t)& =& \sum _{n=1}^{\infty }\frac{t^{\alpha n-k}}{\Gamma (\alpha n-k+1)}\prod _{j=0}^{n-1}\left(a+b{q}^{\alpha j}\right).\hfill \end{array}$$

Theorem 13.

(Addition theorem)

$${\mathcal{R}}_{\alpha }(a,b,q,t+x)=\sum _{k=0}^{\infty }\frac{t^k}{k!}{\mathcal{R}}_{\alpha }^{(k)}(a,b,q,x),$$

where ${\mathcal{R}}_{\alpha }^{(k)}(a,b,q,x)=\frac{d^k}{d{t}^k}{\mathcal{R}}_{\alpha }(a,b,q,t)$

Proof. 

We have:

$$\begin{array}{ccc}\hfill {\mathcal{R}}_{\alpha }(a,b,q,t+x)& =& 1+\sum _{n=1}^{\infty }\frac{{(t+x)}^{\alpha n}}{\Gamma (\alpha n+1)}\prod _{j=0}^{n-1}\left(a+b{q}^{\alpha j}\right)\hfill \\ & =& 1+\sum _{n=1}^{\infty }\frac{1}{\Gamma (\alpha n+1)}\left(x^{\alpha n}+\sum _{k=1}^{\infty }\frac{\Gamma (\alpha n+1)t^k{x}^{\alpha n-k}}{k!\Gamma (\alpha n-k+1)}\right)\prod _{j=0}^{n-1}\left(a+b{q}^{\alpha j}\right)\hfill \\ & =& 1+\sum _{n=1}^{\infty }\frac{x^{\alpha n}}{\Gamma (\alpha n+1)}\prod _{j=0}^{n-1}\left(a+b{q}^{\alpha j}\right)\hfill \\ & & +\sum _{n=1}^{\infty }\sum _{k=1}^{\infty }\frac{t^k}{k!}\frac{x^{\alpha n-k}}{\Gamma (\alpha n-k+1)}\prod _{j=0}^{n-1}\left(a+b{q}^{\alpha j}\right)\hfill \\ & =& {\mathcal{R}}_{\alpha }(a,b,q,x)+\sum _{k=1}^{\infty }\sum _{n=1}^{\infty }\frac{t^k}{k!}\frac{x^{\alpha n-k}}{\Gamma (\alpha n-k+1)}\prod _{j=0}^{n-1}\left(a+b{q}^{\alpha j}\right)\hfill \\ & =& {\mathcal{R}}_{\alpha }(a,b,q,x)+\sum _{k=1}^{\infty }\frac{t^k}{k!}\sum _{n=1}^{\infty }\frac{x^{\alpha n-k}}{\Gamma (\alpha n-k+1)}\prod _{j=0}^{n-1}\left(a+b{q}^{\alpha j}\right)\hfill \\ & =& {\mathcal{R}}_{\alpha }(a,b,q,x)+\sum _{k=1}^{\infty }\frac{t^k}{k!}{\mathcal{R}}_{\alpha }^{(k)}(a,b,q,x)\hfill \\ \hfill {\mathcal{R}}_{\alpha }(a,b,q,t+x)& =& \sum _{k=0}^{\infty }\frac{t^k}{k!}{\mathcal{R}}_{\alpha }^{(k)}(a,b,q,x).\hfill \end{array}$$

 ☐

Properties and Relations of ${\mathcal{R}}_{\alpha }(a,b,q,t)$

We get the following analogous properties and relations as in Section 5, e.g.,

• ${\mathcal{R}}_{\alpha }\left(0,\pm b^{\alpha m},q,t\right)={\mathcal{R}}_{\alpha }\left(0,1,q,\pm b^{\alpha m}t\right)$.
• ${\mathcal{R}}_{\alpha }\left(a^{\alpha m},a^{\alpha m},q,t\right)={\mathcal{R}}_{\alpha }\left(1,1,q,a^{\alpha m}t\right)$.
• ${\mathcal{R}}_{\alpha }\left(a^{\alpha l},b^{\alpha m},q,t\right)={\mathcal{R}}_{\alpha }\left(1,a^{-\alpha m}{b}^{\alpha m},q,a^{\alpha l}t\right)$ and so on.

6.2. Generalizations to the Higher Order Case

Consider the system of delay differential equation with proportional delay:

$$Y^{\prime }(t)=AY(t)+BY(qt),Y(0)=Y_0,$$

(12)

where $q\in (0,1)$, $A={\left(a_{ij}\right)}_{n\times n}$, $B={\left(b_{ij}\right)}_{n\times n}$ and $Y=$ $\left[\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_n\end{array}\right].$

The solution of (12) is:

$$\overline{\mathcal{R}}(A,B,q,tI)=\left(I+\sum _{n=1}^{\infty }\frac{t^n}{n!}\prod _{j=1}^n\left(A+B{q}^{n-j}\right)\right)Y_0.$$

Theorem 14.

If $(A+B{q}^n)$ is invertible for each n, then the power series:

$$\overline{\mathcal{R}}(A,B,q,tI)=\left(I+\sum _{n=1}^{\infty }\frac{t^n}{n!}\prod _{j=1}^n\left(A+B{q}^{n-j}\right)\right)Y_0,$$

where $A\in M_{n\times n}$ and $B\in M_{n\times n}$ is convergent for $t\in \mathbb{R}$.

6.3. Properties and Relations of $\overline{\mathcal{R}}(A,B,q,tI)$

We get the following analogous properties and relations as in Section 5 under the condition that A, B, $A\pm I$ and $B\pm I$ are invertible.

6.3.1. Properties of $\overline{\mathcal{R}}(A,B,q,tI)$

• $\overline{\mathcal{R}}\left(0,\pm B^m,q,tI\right)=\overline{\mathcal{R}}\left(0,I,q,\pm B^{m}t\right)$.
• $\overline{\mathcal{R}}\left(A^m,A^m,q,tI\right)=\overline{\mathcal{R}}\left(I,I,q,A^{m}t\right)$, etc.

6.3.2. Contiguous Relations of $\overline{\mathcal{R}}(A,B,q,tI)$

• $\overline{\mathcal{R}}\left(A\pm I,B,q,tI\right)=\overline{\mathcal{R}}\left(I,{(A\pm I)}^{-1}B,q,(A\pm I)t\right)$.
• $\overline{\mathcal{R}}\left(A,B\pm I,q,tI\right)=\overline{\mathcal{R}}\left(I,A^{-1}(B\pm I),q,At\right)$.
• $\overline{\mathcal{R}}\left(A\pm I,,B\pm I,q,tI\right)=\overline{\mathcal{R}}\left(I,{(A\pm I)}^{-1}(B\pm I),q,(A\pm I)t\right)$.

7. Conclusions

In this article, we discussed the pantograph equation and its generalizations. The series solutions of these equations are treated as special functions. These special functions are different from hyper-geometric and other special functions because they are obtained as a solution of the delay differential equation. It is observed that the m-th derivative of $\mathcal{R}$ can be represented as a linear combination of $\mathcal{R}(a,b,q,q^{r}t)$ for $0\le r\le m$ with Gaussian binomial coefficients. The function ${\mathcal{R}}_{\alpha }$ is shown to be bounded by the Mittag-Leffler functions. We have studied different properties and discussed some relations of these special functions. We hope that our work will encourage researchers to dig for more properties of the special functions obtained from delay differential equations.