Abstract
The evolution of public opinion on social media affects societal security and stability. To effectively control the societal impact of public opinion evolution, it is essential to study its underlying mechanisms. Public opinion evolution on social media primarily involves two processes: information dissemination and opinion interaction. However, existing studies overlook the bidirectional coupling relationship between these two processes, with limitations such as weak coupling and insufficient consideration of individual heterogeneity. To address this, we propose the SIS-FJ model with a bidirectional coupling mechanism, which combines the strengths of the SIS (Susceptible–Infected–Susceptible) model in information dissemination and the FJ (Friedkin–Johnsen) model in opinion interaction. Specifically, the SIS model is used to describe information dissemination, while the FJ model is used to describe opinion interaction. In the computation of infection and recovery rates of the SIS model, we introduce the opinion differences between individuals and their observable neighbors from the FJ model. In the computation of opinion values in the FJ model, we introduce the node states from the SIS model, thus achieving bidirectional coupling between the two models. Moreover, the model considers individual heterogeneity from multiple aspects, including infection rate, recovery rate, and individual susceptibility. Through simulation experiments, we investigate the effects of initial opinion distribution, individual susceptibility, and network structure on public opinion evolution. Interestingly, neither initial opinion distribution, individual susceptibility, nor network structure exerts a significant influence on the proportion of disseminating and non-disseminating individuals at termination. Furthermore, we optimize the model by adjusting the functions for infection and recovery rates.
1. Introduction
Public opinion evolution refers to the process by which the collective attitudes or beliefs of a social group toward a specific issue or event change over time during a given period [1,2]. With the rapid development and widespread application of Internet technologies, social media is gradually replacing traditional media as the primary platform for public discourse [3]. The openness, real-time nature, high interactivity, and low cost of social media [4] allow users to quickly access content and express their opinions [5], leading to public opinion evolution. Public opinion evolution on social media can promote people’s thinking and discussions, thereby increasing attention to social issues [6], enhancing group cohesion [7], and forming collective intelligence [8]. However, it can also lead to the dissemination of false or incorrect information [9,10,11,12], disrupt public discussion order [13], exacerbate social biases [14,15,16], and even trigger collective events [17], posing significant challenges to governance of the online environment. Therefore, the evolution of public opinion on social media has a profound impact on the security and stability of society. Understanding the mechanisms of public opinion evolution is crucial for addressing the governance dilemmas in the online environment.
On social media, user interactions form a relational network [18]. Within this network, information spreads rapidly among users [19]. Additionally, users may modify their own opinions under the influence of others’ expressed viewpoints, leading to opinion interaction [20]. Therefore, the evolution of public opinion on social media primarily involves two processes: information dissemination and opinion interaction [1,21]. However, in real-world scenarios such as the outbreak of collective events, the formation of social trends, or the hot sale of products, these two processes do not occur independently [22]. Information dissemination between individuals influences their opinions, while opinion interactions also expand the scope of information dissemination. To study public opinion evolution on social media, dynamics models are practical tools for investigating its mechanisms. Among these, propagation dynamics models are commonly used to study information dissemination [23], while opinion dynamics models are frequently used to study opinion interactions [24]. Most existing studies consider information dissemination and opinion interaction separately. A few studies have simultaneously considered both processes, but have limitations, such as weak coupling between the two dynamics and a lack of individual heterogeneity. Therefore, this study integrates propagation dynamics and opinion dynamics models to explore the coupling mechanism between information dissemination and opinion interaction in the evolution of public opinion.
In propagation dynamics models, the SIS (Susceptible–Infected–Susceptible) model [25] can effectively and concisely simulate the information dissemination process caused by individuals repeatedly posting or withdrawing messages on social media. In opinion dynamics models, the FJ (Friedkin–Johnsen) model [26] can account for individual susceptibility to surrounding opinions and is convenient for introducing individual heterogeneity. In this paper, we propose a bidirectionally coupled SIS-FJ model by combining the SIS model and the FJ model to simulate public opinion evolution on social media. This study conducts modeling and simulation incorporating information dissemination and opinion interaction. The main contributions of this paper are as follows:
- We establish a bidirectional coupling mechanism between the SIS and FJ models. In the computation of infection rate and recovery rate in the SIS model, we incorporate the opinion difference between individuals and their observable neighbors in the FJ model. In the computation of opinion values in the FJ model, we incorporate the node states in the SIS model. This achieves bidirectional coupling between the SIS and FJ models. Moreover, the SIS-FJ model we constructed takes into account individual heterogeneity from multiple aspects, including infection rate, recovery rate, and individual susceptibility.
- We investigate the effects of various model elements on public opinion evolution, including initial opinion distribution, individual susceptibility, and network structure.
- We optimize the model by adjusting the infection rate and recovery rate functions, which enhance its generalizability.
2. Literature Review
Dynamics models represent a practical methodology for studying public opinion evolution. This paper reviews the relevant literature on public opinion evolution primarily from three primary aspects: information dissemination within propagation dynamics, opinion interaction within opinion dynamics, and the coupling of these two dynamics.
2.1. Propagation Dynamics Model
Propagation dynamics is a crucial area of research in communication and complex network studies, focusing on the processes and patterns of propagation in fields such as infectious diseases [27], behavior [28], and information [29]. Currently, the models of propagation dynamics are primarily divided into two categories: infectious disease models and influence propagation models. Infectious disease models include the classical SI (Susceptible–Infected) model [30], the SIS (Susceptible–Infected–Susceptible) model [25], and the SIR (Susceptible–Infected–Recovered) model [31], along with several variant models such as the SIRS (Susceptible–Infected–Recovered–Susceptible) model [32], the SEIR (Susceptible–Exposed–Infected–Recovered) model [33]. Influence propagation models mainly include the IC (Independent Cascade) model [34] and the LT (Linear Threshold) model [35].
Due to the similarity between information dissemination and infectious disease transmission, researchers have widely applied infectious disease models to study information dissemination [36]. Zhang and Chen [37] considered the effects of time lag, containment, and forgetting mechanisms during information dissemination and proposed the SETQR (Susceptible–Exposed–Trusted–Questioned–Recovered) model. Their study analyzed how these mechanisms influence the speed of information dissemination and the time required for the network to reach equilibrium. The study explains the reasons why the spread range of information varies in the network. Liu [38] considered the influence of news on the speed of emotion propagation among Internet users and proposed the SHIR (Susceptible–Hesitant–Infected–Removed) model. Furthermore, to account for the impact of different network structures on user propagation behavior, the author introduced an SLPR (Susceptible–Latent–Propagative–Removal) propagation model with network characteristics. By integrating the SHIR and SLPR models, this study investigated how public opinion affects the rate of emotional communication among individuals, as well as how network structure influences user behavior. This research is of great significance for effectively managing and guiding the spread of emotions on social media to create a healthier online environment. Zhou et al. [39] posited that individual emotions affect rumor spreading and proposed a SCIR (Spreader–Chord–Ignorant–Restorer) model. The study found that a higher proportion of individuals with high emotionality leads to a greater impact of rumor propagation. Govindankutty and Gopalan Padinjappurathu [40] incorporated exposed and doubter states, constructing a SEDIS (Susceptible–Exposed–Doubter–Infected–Susceptible) model. They discovered that sustained and effective interventions during the early stages of rumor spreading could prevent its dissemination within the network. Wang et al. [41] introduced a transitional state and described the recovery rate using a time-dependent function, establishing an ISRT (Ignorant–Spreader–Stifler–Transition) model. Their findings revealed that different influence mechanisms can more accurately identify the characteristic features of stage-specific changes in rumor propagation. The above three models have an effective role in suppressing the spread of rumors.
The studies above have expanded classical infectious disease models by improving the information dissemination mechanism and introducing factors that influence the spread of information in different scenarios. Additionally, the research perspective has gradually transitioned from the macro to the micro level.
2.2. Opinion Dynamics Model
Opinion dynamics represents a crucial aspect of sociophysics, investigating the processes and patterns of group opinion convergence across diverse fields such as marketing [42], public opinion management [24,43], political elections [44], and collective decision-making [45]. Based on the representation format of opinions, opinion dynamics models can be categorized into two major types: discrete and continuous. Discrete opinion dynamics models primarily consist of the Voter model [46], the Majority rule model [47], and the Sznajd model [48]. Continuous opinion dynamics mainly include averaging models and bounded confidence models. Among these, averaging models include the DeGroot model [49] and the FJ model [26], while bounded confidence models mainly include the DW (Deffuant–Weisbuch) model [50], the HK (Hegselmann–Krause) model [51], and the JA (Jager–Amblard) model [52].
Since opinions on the Internet typically evolve in a continuous manner, researchers have widely adopted continuous opinion dynamics models to study information dissemination processes [36]. Zhou et al. [53] introduced the concept of self-persistence into the DeGroot model to quantify the extent to which individuals adhere to their initial opinions. They proposed a new method for determining weights and employed three opinion control strategies to regulate the process of opinion formation. The above strategies have demonstrated certain effectiveness in the experimental simulation, but they still need to be verified in practical applications. Proskurnikov et al. [54] extended the FJ model by incorporating time-varying social network structures and analyzed the convergence speed of opinions in the resulting time-varying FJ model. This model can also be further extended to the case of multidimensional opinions. Chen et al. [55] introduced the concepts of a repulsion mechanism and cyclical opinions into the DW model, leading to spatiotemporal patterns in which all individuals maintain distinct opinions. The opinion dynamics of this model depend on bounded confidence and convergence speed. Jiang et al. [56], based on the DW model, proposed a set of inclusiveness functions that integrate the conflict and compromise mechanism, constructed the ISDW (Inclusiveness-degree-based Signed Deffuant–Weisbush) model, and analyzed the patterns of opinion interaction under varying conditions. This model considers communication and compromise between agents with opposing opinions, thereby improving the realism and practicality of the bounded confidence model. Xu et al. [57] incorporated media literacy into the HK model, finding that differences in individuals’ abilities to acquire, analyze, and produce information affected the effectiveness of opinion interactions between them. This study highlights the importance of enhancing citizens’ media literacy for maintaining a healthy public opinion ecosystem. Wang et al. [58] introduced individual stubbornness levels into the HK model, categorizing them into different types (e.g., expert-influenced, environment-influenced, and intrinsic) to simulate more complex real-world opinion interaction processes. This model approximates real-world scenarios more closely under certain conditions. Xu et al. [59] introduced the concept of public opinion atmosphere into the HK model, discovering that individuals’ opinions ultimately reached consensus under its influence. The results of this study can well explain the phenomenon of group polarization in current online societies and provide insights for online social services. Chen et al. [60] calculated similarity based on personal attributes, proposing the SSHK (Social–Similarity-based HK) model to investigate the combined effects of confidence bounds and social similarity. Their study shows that the social relationships between individuals have a non-negligible impact on opinion dynamics.
The studies above have expanded classical opinion dynamics models by improving the opinion interaction mechanism and introducing factors that influence the interaction of opinions in different scenarios.
2.3. Coupled Dynamics Model
The propagation dynamics model mainly consists of three elements: information, dissemination mechanism, and network structure. The research on public opinion evolution from this perspective mainly focuses on the dissemination mechanism of information and its unidirectional dissemination, and generally does not involve the mutual influence of multiple pieces of information [23]. The opinion dynamics model mainly consists of three elements: opinion, interaction mechanism, and network structure. The research on public opinion evolution from this perspective mainly focuses on the interaction mechanism of opinions and their bidirectional exchanges, and requires studying the mutual influence among various opinions [24], as shown in Figure 1.
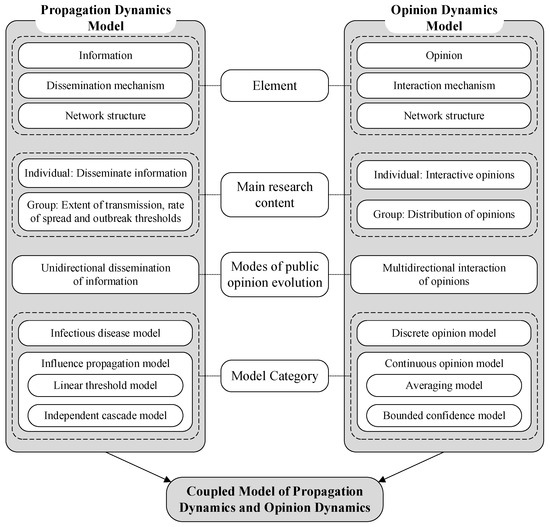
Figure 1.
A comparative overview of the propagation dynamics model and opinion dynamics model.
In many realistic scenarios, the processes of information dissemination and opinion interaction often occur simultaneously. Consequently, integrating a propagation dynamics model with an opinion dynamics model to investigate the coupling mechanisms between information dissemination and opinion interaction has become an emerging research focus. Li et al. [1] proposed the HK-SEIR model for public opinion evolution by integrating the HK model with the SEIR model and quantified key factors influencing opinion propagation, such as user influence, topic popularity, and topic interest. Experimental results demonstrated that the HK-SEIR model better captures the characteristics of public opinion evolution compared to the traditional SEIR model. Yuan et al. [61] constructed a model of online opinion polarization by integrating the SIR model with the JA model, taking into account dynamic network structures. They investigated the impacts of network adaptation, individual infection rates, and vaccination rates on public opinion evolution. Chen et al. [4] constructed a group polarization model by integrating the SIRS model with the JA model. They investigated how the immune recovery rate and relationship strength influence the evolution of public opinion. Yin et al. [62] integrated the SLFI model with the JA model, taking into account both internal (individual-level) and external (environmental-level) factors, to construct the SLFI-JA model. They found that this model exhibits strong robustness in capturing the complex dynamics of information dissemination and opinion interaction.
The studies above mainly employ the infectious disease model from propagation dynamics and the bounded confidence model from opinion dynamics when constructing coupled models. The propagation dynamics model is used to identify individuals whose states have changed, while the opinion dynamics model quantifies individual opinion values, thereby simulating the process of public opinion evolution.
Through the analysis of the current literature, it can be observed that research utilizing infectious disease models to study information dissemination and continuous opinion dynamics models to study opinion interaction has achieved substantial progress. Coupled models integrating propagation dynamics and opinion dynamics can simultaneously simulate both processes, offering greater comprehensiveness. However, although some scholars have conducted preliminary research in this area, the following limitations still persist. Firstly, in current coupled models, bounded confidence models are predominantly chosen for the opinion dynamics component. Within these models, the specific rules governing opinion interaction (assimilation rule, repulsion rule, and neutral rule) depend on the selection of threshold parameters. The values of threshold parameters often rely on manual settings, making it difficult to ensure their scientific validity. Secondly, current approaches in constructing coupled models typically first determine individuals undergoing state changes based on the propagation dynamics model and then quantify their opinion values using the opinion dynamics model. The two dynamics models have not achieved tight coupling. Thirdly, existing coupled models tend to operate at a macro level, with insufficient consideration given to individual heterogeneity at the micro level.
3. Methodology
This section constructs a coupled model of information dissemination and opinion interaction based on propagation dynamics and opinion dynamics. Individuals on social media are abstracted as nodes in a network, with their connections represented as edges. The SIS model is employed to characterize the mechanism of information dissemination, while the FJ model is used to describe the mechanism of opinion interaction. In this way, an SIS-FJ coupled model is established.
The model is implemented using the Python 3.12.7 programming language along with scientific computing libraries including NumPy 1.26.4 and NetworkX 3.3. All experiments are carried out on a machine with an Intel Core i9 processor and 16 GB of RAM, under the Windows 11 operating system.
3.1. SIS Model
In propagation dynamics models, the SIS model [25] can effectively and concisely simulate the process of information dissemination caused by individuals repeatedly posting or withdrawing messages on social media, which is highly consistent with the evolutionary characteristics of public opinion in such environments. Therefore, this study adopts the SIS model to formalize information dissemination during public opinion evolution processes.
In the SIS model, there are two node states: the susceptible state (S) and the infected state (I). During the information dissemination process, a susceptible node represents a non-disseminating individual who is unable to spread information to others, meaning the individual has not yet expressed an opinion or has previously expressed an opinion but has deleted it. An infected node represents a disseminating individual who is able to spread information to others, meaning the individual has currently expressed an opinion. The model leads to the differential Equation (1).
In Equation (1), represents the total population size; and represent the number of individuals in the non-disseminating and disseminating states, respectively; represents the infection rate; and represents the recovery rate.
3.2. FJ Model
In opinion dynamics models, the FJ model [26], as a type of averaging model, has a clear advantage over the bounded confidence model. In the bounded confidence model, the specific rules of opinion interaction depend on the selection of threshold parameters, which are typically set manually and may lack scientific justification. Averaging models do not face this issue. Furthermore, compared to another averaging model, the DeGroot model, the FJ model can take into account both an individual’s own opinion and the opinions of their neighbors, while the DeGroot model neglects the role of an individual’s original opinions. The individual susceptibility parameter in the FJ model not only regulates the influence of these two factors but also reflects individual heterogeneity. Therefore, this study adopts the FJ model to formalize opinion interaction during public opinion evolution processes.
In the FJ model, individual opinions are represented as continuous values with 1 indicating complete endorsement, 0 indicating neutral stance, and indicating complete opposition. The individual opinion value in this model consists of two components: its own intrinsic opinion and the opinions of its neighbors. The influence of these two components is determined by the individual susceptibility. A higher susceptibility indicates that the individual is more susceptible to the opinions of others, meaning that the neighbors’ opinions have a greater impact on the individual’s opinion update. Specifically, the opinion update mechanism for individual is formalized in Equation (2).
In Equation (2), represents the susceptibility of individual to the opinion of the neighboring individuals; represents the neighboring individuals of individual ; and represents the influence weight of individual on individual .
3.3. SIS-FJ Model
Public opinion evolution on social media often involves both information dissemination and opinion interaction. This study describes public opinion evolution by constructing an SIS-FJ model with a bidirectional coupling mechanism, as illustrated in Figure 2. In this model, an individual mainly has three attributes: node state , node opinion value , and the susceptibility of the node to the neighboring nodes. For individual , indicates that the individual is in the non-disseminating state (S) and indicates that the individual is in the disseminating state (I). The update method of the node opinion value is based on the above FJ model and introduces the states of neighboring nodes; only the neighboring nodes in the disseminating state can act on node . The specific update method is as shown in Equation (3).
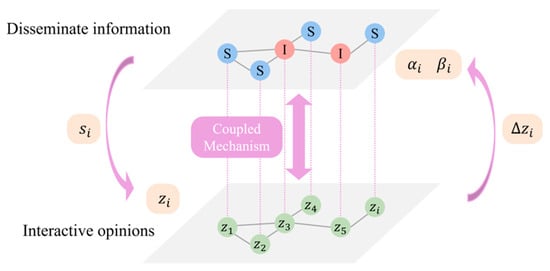
Figure 2.
The SIS-FJ model with a bidirectional coupling mechanism.
The edge weight is determined by the degree of the neighboring nodes of node , as shown in Equation (4). The larger is, the stronger the influence of node on node is.
During public opinion evolution on social media, for individuals in the non-disseminating state, the closer their opinion value is to those of their observable neighboring individuals, the stronger their willingness to express their own opinions, that is, the higher the likelihood of transitioning from the non-disseminating state to the disseminating state. Therefore, when calculating the infection rate , we extend the SIS model by incorporating the difference in opinion values between an individual and its observable neighboring nodes (the neighboring nodes in I state), denoted as , as shown in Equation (5).
The sigmoid function is widely used in the fields of statistics and artificial neurons and is often used as a cumulative distribution expression [63]. This function can smoothly map the input to a value within the interval [64], which aligns with the probabilistic nature of the infection rate. Additionally, the functional characteristic is consistent with the trend described earlier, where the infection rate varies with the difference between an individual opinion value and the opinions of observable neighboring nodes. Therefore, this study adjusts the sigmoid function to describe the relationship between the infection rate and , as shown in Equation (6).
Similarly, for individuals in the disseminating state during public opinion evolution, the greater the difference between their opinion value and the values of their observable neighboring individuals, the stronger their willingness to delete their currently expressed opinion, that is, the higher the likelihood of transitioning from the disseminating state to the non-disseminating state. Therefore, when calculating the recovery rate , the SIS model is similarly extended by incorporating . This study adjusts the sigmoid function to describe the relationship between the recovery rate and , as shown in Equation (7).
In the above process, by introducing the node state in the computation of individual opinion values and introducing the opinion difference between individuals and their observable neighbors in the computation of the infection rate and recovery rate, we achieve a bidirectional coupling between the SIS and FJ models and construct the SIS-FJ model for public opinion evolution. This model not only links the process of information dissemination and opinion interaction, but also fully considers individual heterogeneity.
4. Experimental Simulation
In this section, the evolution of public opinion on social media is simulated through experimental simulations based on the established SIS–FJ model. The main focus is to investigate the effects of initial opinion distribution, individual susceptibility, and network structure on the evolution trends. In the experimental setup, the number of nodes is set to 2000. To better observe the simulation outcomes, individual susceptibility heterogeneity is temporarily ignored, with all individuals assigned a susceptibility value of 0.5. Given that public opinion evolution on social media is often initiated by a small number of individuals spreading information in the early stage, 5% of the nodes are initialized as disseminating individuals (I), with their opinion values uniformly distributed in the interval . The remaining 95% are set as non-disseminating individuals (S), representing those who are currently uninformed, with their opinion values initialized at 0. Since the node degrees in social networks generally follow a power law distribution, the simulations are conducted on a BA (Barabás–Albert) network [4]. The specific algorithm steps are as follows (Algorithm 1). For a visual representation, refer to the flowchart in Figure 3.
| Algorithm 1: The SIS-FJ model with a bidirectional coupling mechanism |
| Input: |
| //Network structure |
| //Initial opinion values of nodes |
| //Initial states of nodes |
| //Susceptibilities of nodes |
| Output: |
| //Final opinion values of nodes |
| //Final states of nodes |
| Procedure: |
| For to : |
| For each node : |
| Compute //The opinion differences between node and its observable neighbors (the neighboring nodes in I state) |
| If : //Non-disseminating nodes (S state) |
| Compute infection rate |
| With probability , update //Node becomes a disseminating node (I state) |
| Else: //Disseminating nodes (I state) |
| Compute recovery rate |
| With probability , update . //Node becomes a non-disseminating node (S state) |
| Compute the weighted average opinion of the neighboring nodes of node |
| Return , |
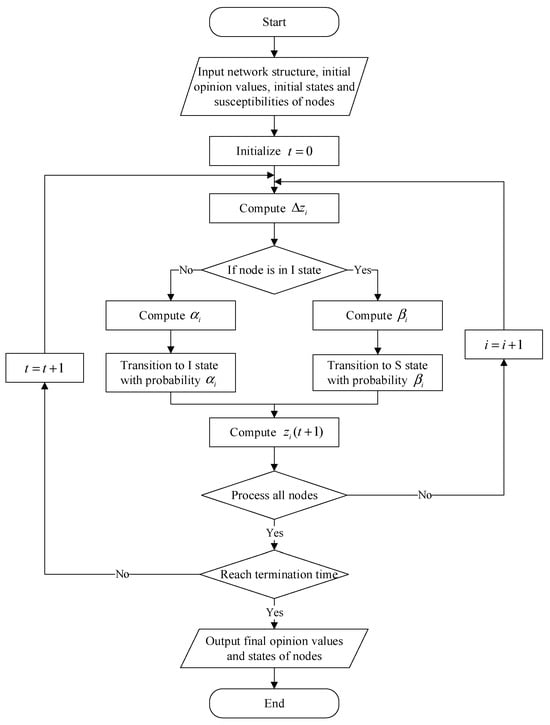
Figure 3.
Flowchart of the SIS-FJ model with a bidirectional coupling mechanism.
4.1. The Effect of Initial Opinion Distribution on Public Opinion Evolution
4.1.1. Proportion of Nodes in Different States
Change the proportion of disseminating nodes and non-disseminating nodes at the initial time. is the proportion of disseminating nodes at the initial time, and is the proportion of non-disseminating nodes. The results after 100 time steps of evolution are shown in Figure 4 and Figure 5 and Table 1.

Figure 4.
The node states during evolution under different

Figure 5.
Trends in opinion interaction under different (The different colored lines in the figures represent specific individuals, and the colors are assigned randomly. Same as the Figures 6–8 and 10).

Table 1.
The evolution results under different
To study the convergence speed of opinion under different initial opinion distributions, the moment when the variance of opinion began to be less than 0.001 is recorded during the experiment. It can be known from the evolution results that the larger is, that is, the more disseminating nodes at the initial time, the slower the opinion converges. Furthermore, we find that under this condition, after evolution at different , the variance of the opinion at the termination time can always be equal to 0, that is, the opinion can always be consistent. Furthermore, we find that the proportion of the final non-disseminating nodes and the disseminating nodes is not affected by the proportion of each state node at the initial time.
4.1.2. Distribution of Opinion Values
To investigate the effect of the magnitude and range of initial opinion distributions on public opinion evolution, the opinions of disseminating nodes at the initial stage are characterized by a normal distribution . During the experiment, the range of the opinion value is limited to . The results after evolving for 100 time steps are presented in Figure 6 and Table 2.
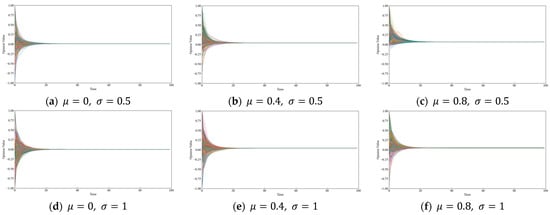
Figure 6.
Trends in opinion interaction under different opinion distributions of disseminating nodes at the initial stage.

Table 2.
The evolution results under different opinion distributions of disseminating nodes at the initial stage.
It can be known from the evolution results that the larger the is, that is, the greater the disseminating nodes’ opinions deviate from the mainstream opinion at the initial time, the slower the opinion converges, and the more the opinion values of all nodes deviate at the termination time. The larger is, that is, the larger the range of the disseminating nodes’ opinions at the initial time, the slower the opinion converges, and the less the opinion values of all nodes deviate at the termination time. In addition, we find that under this condition, after evolution under different initial opinion distributions of disseminating nodes at the initial stage, the variance of opinion at the termination time can always be equal to 0, indicating that opinion can always be consistent.
4.1.3. Bipolar Initial Opinions
When the initial opinions are bipolarized (only considering the initial disseminating nodes), we find that the opinion could always be consistent. However, for realistic scenarios such as political campaigns or marketing, the individuals who first spread information often play an important role in guiding public opinion and are not easily influenced by the surrounding public opinion. Therefore, the initial disseminating node is set as the stubborn node to simulate opinion leaders. Their state and opinion values are not affected by the neighboring nodes, and the opinion values are 1 or −1, respectively. The remaining nodes maintain an initial opinion value of 0 and a susceptibility of 0.5. Based on the above conditions, change the proportion of stubborn nodes of the two opinions at the initial time. Let denote the proportion of stubborn nodes with an opinion value of 1, and represent those with an opinion value of −1. The resulting opinion interaction trends are shown in Figure 7. It can be observed that the final opinion distribution tends to align with the dominant stubborn group. However, due to the presence of stubborn nodes on the opposing side, the system fails to reach a global consensus.
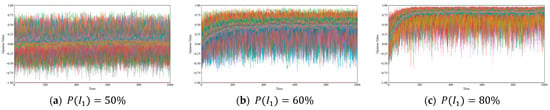
Figure 7.
Trends in opinion interaction under different
4.2. The Effect of Individual Susceptibility on Public Opinion Evolution
4.2.1. Distribution of Individual Susceptibility
To investigate the effect of the magnitude and range of individual susceptibility on public opinion evolution, the susceptibilities of all nodes are characterized by a normal distribution . The individual susceptibilities remain unchanged during the evolution. During the experiment, the range of individual susceptibility is limited to . The results after evolution are presented in Figure 8 and Table 3.
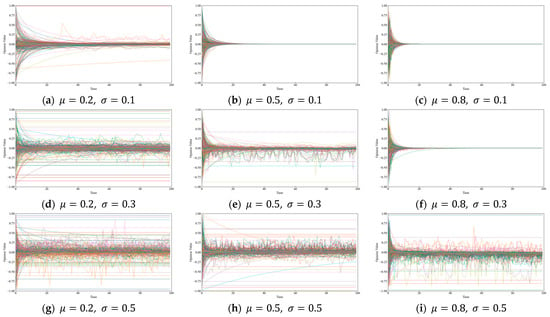
Figure 8.
Trends in opinion interaction under different distributions of individual susceptibility.

Table 3.
The evolution results under different distributions of individual susceptibility.
It can be known from the evolution results that the larger the is, that is, the greater the overall susceptibility, the smaller the opinion variance with the same evolution time, and the faster the opinion converges. This is because a higher susceptibility indicates that individuals are more likely to accept the opinions of their neighbors, thus leading to a faster rate of opinion change. The larger the is, that is, the larger the range of susceptibility, the greater the opinion variance with the same evolution time, and the slower the opinion converges, and it may even fail to converge. This is because a wider susceptibility range is more likely to produce extreme values. In particular, a susceptibility of 0 means that the individual is completely unaffected by the opinions of others. Considering that when using the normal distribution to describe the susceptibility of nodes, some extreme values generated will have an impact on the observation of the evolution process. Therefore, the node susceptibility is assigned deterministic values in the subsequent experiments.
4.2.2. Susceptibility and the Rate of Opinion Change
In realistic scenarios, such as changing the direction of public opinion, official accounts often release information to alter the public’s perception. To simulate this setting, we assume that the non-disseminating nodes at the initial stage follow a normal distribution , representing the negative cognition of the masses. The initial disseminating nodes are set as stubborn nodes, whose state and opinion values remain fixed throughout the evolution process, simulating the role of official accounts with an opinion value of 1. We conduct simulation experiments by systematically varying the susceptibility of all nodes except the stubborn nodes. We record the time at which the opinion variance first falls below 0.001 under different susceptibility levels. The results are shown in Figure 9. It can be observed that when the individual susceptibility tends to 0, the time required for the convergence of opinion is relatively long. With the increase in individual susceptibility, the time required for the convergence of opinion decreases exponentially.
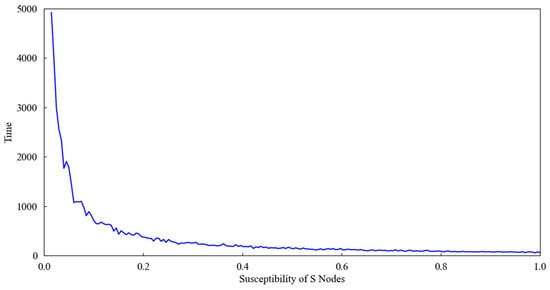
Figure 9.
The time when opinion variance stabilizes below 0.001 under different individual susceptibility.
4.3. The Effect of Network Structure on Public Opinion Evolution
Social media platforms host various types of relationship networks. The BA network and the WS (Watts–Strogatz) network (small-world network) can reflect their distinct topological structure characteristics. In this section, we select both the BA network and the WS network to investigate the effect of network structure on public opinion evolution.
4.3.1. BA Network
The BA network is formed based on the preference connection mechanism, and its important parameter is the number of edges when a new node is added. By changing the parameter , the results of evolving 100 time steps are shown in Figure 10 and Table 4. It can be observed that as increases, meaning the connection between nodes becomes denser, the opinion converges faster. This is because in a network with high-density links, each node has more neighbors to exchange opinions with, and more edges result in more pathways for information dissemination, thereby reducing the time delay of information dissemination. Additionally, under this condition, the variance of the opinion at the termination time can always be equal to 0, that is, the opinion can always be consistent.

Figure 10.
Trends in opinion interaction under different values in the BA network structure.

Table 4.
The evolution results under different values in the BA network structure.
4.3.2. WS Network
The WS network is formed by introducing the random reconnection edge mechanism into the regular network. The WS network’s important parameters are the number of neighbors of each node in the initial regular network and the reconnection edge probability of the edges. By changing parameters and , the evolution results are shown in Figure 11 and Table 5. It can be observed that as increases, meaning the connection between nodes becomes denser, the opinion converges faster. This behavior resembles that of BA networks, where each node has more neighbors for opinion interaction, and reduces the time delay of information dissemination. As increases, meaning the probability of reconnecting edges becomes greater, the opinion converges faster. This is because a higher reconnection edge probability implies that existing edges are more likely to be reconnected to other randomly selected nodes. With low reconnection edge probability, information dissemination and opinion interaction are mainly confined to local neighborhoods in the early stages. In contrast, a high reconnection edge probability breaks this limitation, allowing information dissemination and opinion interaction to rapidly spread across distant regions, effectively preventing the isolation of local opinions. Additionally, for networks with a small number of neighbors per node and a low reconnection edge probability, the convergence speed of opinion is very slow.
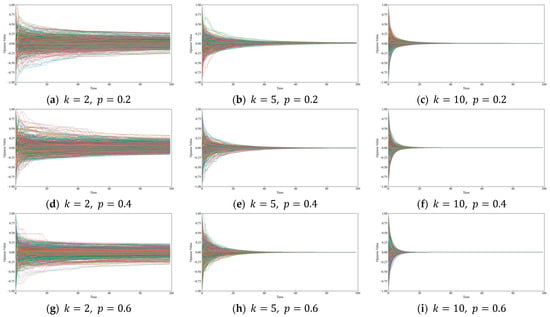
Figure 11.
Trends in opinion interaction under different and values in the WS network structure.

Table 5.
The evolution results under different and values in the WS network structure.
5. Model Optimization
After the above experiments, it can be found that different initial opinion distributions, individual susceptibilities, and network structures have no significant effect on the final proportions of disseminating and non-disseminating individuals. The possible reason is that during the evolution process, individuals constantly modify their own opinions based on the opinions of the neighboring nodes, and the difference in opinion values between an individual and its observable neighboring nodes gradually decreases. Following a sufficiently long evolution process, the values of most nodes tend toward 0, particularly when opinions reach convergence. As a result, the infection rate approaches , and the recovery rate approaches , driving the system toward a state of dynamic equilibrium. For Equation (1) in Section 3.1, when the system reaches the steady state ( and ), the proportion of individuals in the non-disseminating state and disseminating state is analytically derived as shown in Equation (8). When the infection rate and recovery rate are substituted into this expression, the resulting proportions align closely with those observed in the simulations at the end of the evolution process.
To further verify the above inference and optimize the model, we adjust the base parameters of the infection rate and recovery rate functions in the model, resulting in the updated formulations given in Equations (9) and (10). It is worth noting that to ensure that the S-shaped curve trend of the sigmoid does not change, it is necessary to limit and .
By changing the values of the base parameters and , the changes in infection rate and recovery rate with respect to are illustrated in Figure 12. Experiments are also conducted based on the initial conditions in Section 4, and the results are shown in Table 6. To verify the above inference, the inferred proportions of individuals in the non-disseminating state and disseminating state are listed, and the corresponding relative errors and are calculated separately as Equations (11) and (12).
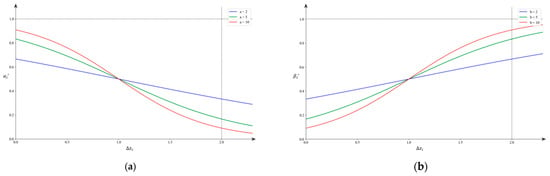
Figure 12.
Trend of or with at different values of or (The dashed line represents the upper bound of ). (a) Relationship between and under various settings (The dashed line represents the upper bound of the function value). (b) Relationship between and under various settings (The dashed line represents the upper bound of the function value).

Table 6.
The evolution results under different and values.
It can be observed that the relative error in all cases is less than 5%. This supports the conclusion that different initial opinion distributions, individual susceptibilities, and network structures have no significant effect on the final proportions of disseminating and non-disseminating individuals. The reason is that, after a sufficient evolution period, the values of most nodes tend toward 0, leading the infection and recovery rates to stabilize at fixed values, as described by Equation (8). As a result, the system reaches a steady-state distribution between disseminating and non-disseminating nodes. It is also observed that the speed of opinion convergence is independent of the parameters or , and under the above conditions, the opinion can always be consistent. Therefore, the improvement to the functions mainly refines the calculation of infection and recovery rates, allowing the model to more accurately characterize the difference in state distributions during public opinion evolution.
In summary, the optimization of the infection and recovery rate functions not only further validates the reason behind the stable proportions of disseminating and non-disseminating individuals at the end of the simulations but also enhances the model’s universality and applicability.
6. Conclusions
In this paper, we construct an SIS-FJ model with a bidirectional coupling mechanism based on the public opinion evolution on social media. Specifically, we use the SIS model from propagation dynamics to characterize information dissemination and the FJ model from opinion dynamics to characterize opinion interaction. When computing the infection rate and recovery rate in the SIS model, we introduce the opinion differences between individuals and their observable neighbors from the FJ model. When computing the opinion values in the FJ model, we introduce the node states from the SIS model. Thus, the bidirectional coupling of the SIS model and the FJ model has been achieved. Meanwhile, the model takes individual heterogeneity into account from multiple aspects, such as infection rate, recovery rate, and individual susceptibility. Based on this model, we investigated the effects of different elements on public opinion evolution. The main experiments and conclusions are as follows:
- We investigated the effect of initial opinion distribution on public opinion evolution. Under the conditions of our experiment, the more disseminating nodes at the initial time, the slower the convergence of the opinion. Additionally, the greater the disseminating nodes’ opinions deviate from the mainstream opinion at the initial time, the slower the opinion converges, and the more the opinion values of all nodes deviate at the termination time. The larger the range of the disseminating nodes’ opinions at the initial time, the slower the opinion converges, and the less the opinion values of all nodes deviate at the termination time. And under this condition, opinion can always be consistent. Furthermore, in realistic scenarios where opinions are bipolarized, such as political campaigns or marketing, it is found that the final distribution of opinion tends toward the stance held by the majority of stubborn nodes. However, due to the presence of opposing stubborn agents, global consensus could not be achieved.
- We investigated the effect of individual susceptibility on public opinion evolution. Under the conditions of our experiment, the greater the overall susceptibility and the smaller the range of susceptibility, the faster the opinion converges. And extreme values of susceptibility can lead to the failure of opinion to converge. Furthermore, in the realistic scenario of changing the direction of public opinion, as individual susceptibility increases, the time required for the opinion to converge decreases exponentially. When the individual susceptibility tends to 0, the time required for the convergence of opinion is relatively long.
- We investigated the effect of network structure on public opinion evolution. For the BA network, it is found that the denser the connection between nodes, the faster the opinion converges. Under this condition, opinion can always be consistent. For the WS network, it is found that the denser the connections between nodes and the greater the probability of reconnecting edges, the faster the opinion converges. Although under this condition, opinion can always be consistent, for the network structure with a small number of neighbors per node and a low reconnection edge probability, the convergence speed of opinion is very slow.
- We found that different initial viewpoint distributions, individual susceptibilities, and network structures have no significant effect on the final proportions of disseminating and non-disseminating individuals. Therefore, we optimized the model by adjusting the base parameters of the infection rate and recovery rate functions. This modification provides additional validation that the stability in the proportions of nodes in different states arises because, after a period of evolution, the opinion differences among most nodes and their neighbors approach 0, causing their infection and recovery rates to stabilize at fixed values, as described by Equation (8). As a result, the system reaches a steady-state distribution between disseminating and non-disseminating nodes. Moreover, this optimization also enhances the model’s universality and applicability.
7. Discussion
The SIS-FJ model with a bidirectional coupling mechanism constructed in this study provides a new perspective for simultaneously investigating information dissemination and opinion interaction in the process of public opinion evolution. We hope that this article can provide insights for scholars in this field and offer scientific references for governments or social media platforms in addressing current challenges in online environment governance. However, the main objective of this study is to propose the coupled model in the context of public opinion evolution on social media and to conduct a preliminary exploration of its properties. Therefore, this study still has certain limitations, which are as follows:
- The model constructed in this study takes into account individual heterogeneity in terms of infection rate, recovery rate, and individual susceptibility. However, individual behavioral mechanisms in reality are influenced by various psychological and social factors. Therefore, the model does not fully account for these complex influences.
- This study conducts experiments on static networks to ensure clear observation of the evolution outcomes. However, in realistic scenarios, social or communication networks may evolve over time, leading to structural adjustments that are not accounted for in the current model.
- This study conducts experiments based on simulation data using synthetic networks (BA and WS networks), and has not yet employed real-world data for empirical analysis. Therefore, the applicability of the model in realistic scenarios remains to be validated.
Given the limitations above, future studies may explore the following directions to improve the model’s theoretical foundation and practical applicability.
- Further incorporate comprehensive factors influencing public opinion evolution on social media into the model, such as individual historical behaviors and preference mechanisms, to make the model more reflective of individuals’ behavioral patterns in realistic social media environments.
- Set the network structure of the model as a dynamic network, and further study the characteristics of public opinion evolution when the network structure changes.
- Based on specific public opinion events on social media, real-world data can be collected to calibrate the model parameters and validate the model’s effectiveness. Thus, the model can be applied to the governance of public opinion on social media. The government can predict future public opinion trends based on the current public opinion during emergencies or the implementation of public policies, thereby formulating more targeted intervention strategies.
Author Contributions
Conceptualization, W.F., R.Z. and X.L. (Xin Lu); methodology, W.F. and B.L.; software, W.F. and X.L. (Xiang Lin); validation, X.L. (Xiang Lin); formal analysis, W.F.; data curation, W.F. and B.L.; writing—original draft preparation, W.F. and X.L. (Xiang Lin); writing—review and editing, R.Z., B.L. and X.L. (Xin Lu); visualization, W.F. and X.L. (Xiang Lin); supervision, R.Z.; funding acquisition, R.Z. and X.L. (Xin Lu). All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant numbers 72025405, 72421002, 92467302, and 72401289.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors would like to thank the reviewers for their valuable suggestions and comments.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Li, Q.; Du, Y.; Li, Z.; Hu, J.; Hu, R.; Lv, B.; Jia, P. HK–SEIR Model of Public Opinion Evolution Based on Communication Factors. Eng. Appl. Artif. Intell. 2021, 100, 104192. [Google Scholar] [CrossRef]
- Li, N. Analyzing the Complexity of Public Opinion Evolution on Weibo: A Super Network Model. J. Knowl. Econ. 2024, 16, 3404–3439. [Google Scholar] [CrossRef]
- Sun, J.; Gong, Z.; Song, H.; Xu, Y.; Forrest, J.Y. Multiple Criteria Decision Modeling in Social Networks: An Application to Identify Opinion Leaders in Online Public Opinion Events. Expert Syst. Appl. 2024, 249, 123591. [Google Scholar] [CrossRef]
- Chen, T.; Shi, J.; Yang, J.; Cong, G.; Li, G. Modeling Public Opinion Polarization in Group Behavior by Integrating SIRS-Based Information Diffusion Process. Complexity 2020, 2020, 4791527. [Google Scholar] [CrossRef]
- Kaplan, A.M.; Haenlein, M. Users of the World, Unite! The Challenges and Opportunities of Social Media. Bus. Horiz. 2010, 53, 59–68. [Google Scholar] [CrossRef]
- Lu, Z.; Gao, X. The Study on the Formation Mechanism and Guiding Strategies of Group Polarization in Social Media Platforms. Inf. Stud. Theory Appl. 2021, 8, 51–58. [Google Scholar] [CrossRef]
- El-Shinnawy, M.; Vinze, A.S. Polarization and Persuasive Argumentation: A Study of Decision Making in Group Settings. MIS Q. 1998, 22, 165. [Google Scholar] [CrossRef]
- Shi, F.; Teplitskiy, M.; Duede, E.; Evans, J.A. The Wisdom of Polarized Crowds. Nat. Hum. Behav. 2019, 3, 329–336. [Google Scholar] [CrossRef]
- Vicario, M.D.; Quattrociocchi, W.; Scala, A.; Zollo, F. Polarization and Fake News. ACM Trans. Web 2019, 13, 1–22. [Google Scholar] [CrossRef]
- Del Vicario, M.; Bessi, A.; Zollo, F.; Petroni, F.; Scala, A.; Caldarelli, G.; Stanley, H.E.; Quattrociocchi, W. The Spreading of Misinformation Online. Proc. Natl. Acad. Sci. USA 2016, 113, 554–559. [Google Scholar] [CrossRef]
- Tucker, J.; Guess, A.; Barbera, P.; Vaccari, C.; Siegel, A.; Sanovich, S.; Stukal, D.; Nyhan, B. Social Media, Political Polarization, and Political Disinformation: A Review of the Scientific Literature. SSRN Electron. J. 2018. [Google Scholar] [CrossRef]
- Maia, H.P.; Ferreira, S.C.; Martins, M.L. Controversy-Seeking Fuels Rumor-Telling Activity in Polarized Opinion Networks. Chaos Solitons Fractals 2023, 169, 113287. [Google Scholar] [CrossRef]
- Jiang, J.; Chen, E.; Yan, S.; Lerman, K.; Ferrara, E. Political Polarization Drives Online Conversations about COVID-19 in the United States. Hum. Behav. Emerg. Technol. 2020, 2, 200–211. [Google Scholar] [CrossRef] [PubMed]
- Sunstein, C.R. Republic.com; Princeton University Press: Princeton, NJ, USA, 2001; ISBN 9780691095899. [Google Scholar]
- Iyengar, S.; Lelkes, Y.; Levendusky, M.; Malhotra, N.; Westwood, S.J. The Origins and Consequences of Affective Polarization in the United States. Annu. Rev. Political Sci. 2019, 22, 129–146. [Google Scholar] [CrossRef]
- Kingzette, J.; Druckman, J.N.; Klar, S.; Krupnikov, Y.; Levendusky, M.; Ryan, J.B. How Affective Polarization Undermines Support for Democratic Norms. Public Opin. Q. 2021, 85, 663–677. [Google Scholar] [CrossRef]
- Xie, T.; Wei, Y.; Chen, W.; Huang, H. Parallel Evolution and Response Decision Method for Public Sentiment Based on System Dynamics. Eur. J. Oper. Res. 2020, 287, 1131–1148. [Google Scholar] [CrossRef]
- Luo, G.; Zhang, Z.; Diao, S. Empirical Analysis and Modelling Social Network User Interaction Behavior and Time Characteristics Based on Selection Preference. Inf. Sci. 2022, 608, 1202–1220. [Google Scholar] [CrossRef]
- Li, H.; Xia, C.; Wang, T.; Wen, S.; Chen, C.; Xiang, Y. Capturing Dynamics of Information Diffusion in SNS: A Survey of Methodology and Techniques. ACM Comput. Surv. 2021, 55, 1–51. [Google Scholar] [CrossRef]
- Geng, L.; Zheng, H.; Qiao, G.; Geng, L.; Wang, K. Online Public Opinion Dissemination Model and Simulation under Media Intervention from Different Perspectives. Chaos Solitons Fractals 2023, 166, 112959. [Google Scholar] [CrossRef]
- Liu, S.; Tian, Y.; Wu, X. Research on Opinion Diffusion and Evolution Model in Complex Network. IEEE Trans. Comput. Soc. Syst. 2024, 11, 7595–7607. [Google Scholar] [CrossRef]
- Wu, Y.; Li, L.; Yu, Q.; Gan, J.; Zhang, Y. Strategies for Reducing Polarization in Social Networks. Chaos Solitons Fractals 2023, 167, 113095. [Google Scholar] [CrossRef]
- Sun, L.; Rao, Y.; Wu, L.; Zhang, X.; Lan, Y.; Nazir, A. Fighting False Information from Propagation Process: A Survey. ACM Comput. Surv. 2023, 55, 1–38. [Google Scholar] [CrossRef]
- Dong, Y.; Zhan, M.; Kou, G.; Ding, Z.; Liang, H. A Survey on the Fusion Process in Opinion Dynamics. Inf. Fusion 2018, 43, 57–65. [Google Scholar] [CrossRef]
- Kermack, W.O.; McKendrick, A.G. Contributions to the Mathematical Theory of Epidemics. III. Further Studies of the Problem of Endemicity. Proc. R. Soc. A Math. Phys. Eng. Sci. 1933, 141, 94–122. [Google Scholar] [CrossRef]
- Friedkin, N.E.; Johnsen, E.C. Social Positions in Influence Networks. Soc. Netw. 1997, 19, 209–222. [Google Scholar] [CrossRef]
- Keeling, M.; Rohani, P.; Pourbohloul, B. Modeling Infectious Diseases in Humans and Animals: Modeling Infectious Diseases in Humans and Animals. Clin. Infect. Dis. 2008, 47, 864–865. [Google Scholar] [CrossRef]
- Centola, D. How Behavior Spreads: The Science of Complex Contagions; Princeton University Press: Princeton, NJ, USA, 2018. [Google Scholar]
- Wang, W.; Liu, Q.; Liang, J.; Hu, Y.; Zhou, T. Coevolution Spreading in Complex Networks. Phys. Rep. 2019, 820, 1–51. [Google Scholar] [CrossRef]
- Pugliese, A. Population Models for Diseases with No Recovery. J. Math. Biol. 1990, 28, 65–82. [Google Scholar] [CrossRef]
- Kermack, W.O.; McKendrick, A.G. A Contribution to the Mathematical Theory of Epidemics. Proc. R. Soc. A Math. Phys. Eng. Sci. 1927, 115, 700–721. [Google Scholar] [CrossRef]
- Cheng, Y.; Huang, L.; Ramlogan, R.; Li, X. Forecasting of Potential Impacts of Disruptive Technology in Promising Technological Areas: Elaborating the SIRS Epidemic Model in RFID Technology. Technol. Forecast. Soc. Change 2017, 117, 170–183. [Google Scholar] [CrossRef]
- Prem, K.; Liu, Y.; Russell, T.W.; Kucharski, A.J.; Eggo, R.M.; Davies, N.; Jit, M.; Klepac, P.; Flasche, S.; Clifford, S.; et al. The Effect of Control Strategies to Reduce Social Mixing on Outcomes of the COVID-19 Epidemic in Wuhan, China: A Modelling Study. Lancet Public Health 2020, 5, 261–270. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, A.V. A Simple Model of Herd Behavior. Q. J. Econ. 1992, 107, 797–817. [Google Scholar] [CrossRef]
- Granovetter, M. Threshold Models of Collective Behavior. Am. J. Sociol. 1978, 83, 1420–1443. [Google Scholar] [CrossRef]
- Yin, F.; Tang, X.; Liang, T.; Kuang, Q.; Wang, J.; Ma, R.; Miao, F.; Wu, J. Coupled Dynamics of Information Propagation and Emotion Influence: Emerging Emotion Clusters for Public Health Emergency Messages on the Chinese Sina Microblog. Phys. A Stat. Mech. Its Appl. 2024, 639, 129630. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Z. SETQR Propagation Model for Social Networks. IEEE Access 2019, 7, 127533–127543. [Google Scholar] [CrossRef]
- Liu, X. Social Network Influence Based on SHIR and SLPR Propagation Models. Heliyon 2024, 10, e36658. [Google Scholar] [CrossRef]
- Zhou, X.; Qiu, L.; Hao, T. SCIR Rumor Propagation Model with the Chord Mechanism in Social Networks. Int. J. Mod. Phys. C 2021, 33, 2250014. [Google Scholar] [CrossRef]
- Govindankutty, S.; Gopalan Padinjappurathu, S. SEDIS—A Rumor Propagation Model for Social Networks by Incorporating the Human Nature of Selection. Systems 2022, 11, 12. [Google Scholar] [CrossRef]
- Wang, H.; Qiu, L.; Sun, C. ISRT Rumor Spreading Model with Different Influence Mechanisms in Social Networks. Int. J. Mod. Phys. C 2022, 34, 2350003. [Google Scholar] [CrossRef]
- Chen, J.; Kou, G.; Wang, H.; Zhao, Y. Influence Identification of Opinion Leaders in Social Networks: An Agent-Based Simulation on Competing Advertisements. Inf. Fusion 2021, 76, 227–242. [Google Scholar] [CrossRef]
- Bashari, M.; Akbarzadeh-T, M.R. Controlling Opinions in Deffuant Model by Reconfiguring the Network Topology. Phys. A Stat. Mech. Its Appl. 2019, 544, 123462. [Google Scholar] [CrossRef]
- Di Guilmi, C.; Galanis, G. Convergence and Divergence in Dynamic Voting with Inequality. J. Econ. Behav. Organ. 2021, 187, 137–158. [Google Scholar] [CrossRef]
- Dong, J.; Hu, J.; Zhao, Y.; Peng, Y. Opinion Formation Analysis for Expressed and Private Opinions (EPOs) Models: Reasoning Private Opinions from Behaviors in Group Decision-Making Systems. Expert Syst. Appl. 2024, 236, 121292. [Google Scholar] [CrossRef]
- Holley, R.A.; Liggett, T.M. Ergodic Theorems for Weakly Interacting Infinite Systems and the Voter Model. Ann. Probab. 1975, 3, 643–663. [Google Scholar] [CrossRef]
- Galam, S. Minority Opinion Spreading in Random Geometry. Eur. Phys. J. B 2002, 25, 403–406. [Google Scholar] [CrossRef]
- Sznajd-Weron, K.; Sznajd, J. Opinion Evolution in Closed Community. Int. J. Mod. Phys. C 2000, 11, 1157–1165. [Google Scholar] [CrossRef]
- DeGroot, M.H. Reaching a Consensus. J. Am. Stat. Assoc. 1974, 69, 118–121. [Google Scholar] [CrossRef]
- Deffuant, G.; Neau, D.; Amblard, F.; Weisbuch, G. Mixing Beliefs among Interacting Agents. Adv. Complex Syst. 2000, 3, 87–98. [Google Scholar] [CrossRef]
- Hegselmann, R.; Krause, U. Opinion Dynamics and Bounded Confidence Models, Analysis and Simulation. RePEc Res. Pap. Econ. 2002, 5, 1–2. [Google Scholar]
- Jager, W.; Amblard, F. Uniformity, Bipolarization and Pluriformity Captured as Generic Stylized Behavior with an Agent-Based Simulation Model of Attitude Change. Comput. Math. Organ. Theory 2005, 10, 295–303. [Google Scholar] [CrossRef]
- Zhou, Q.; Wu, Z.; Altalhi, A.H.; Herrera, F. A Two-Step Communication Opinion Dynamics Model with Self-Persistence and Influence Index for Social Networks Based on the DeGroot Model. Inf. Sci. 2020, 519, 363–381. [Google Scholar] [CrossRef]
- Proskurnikov, A.V.; Tempo, R.; Cao, M.; Friedkin, N.E. Opinion Evolution in Time-Varying Social Influence Networks with Prejudiced Agents. IFAC-PapersOnLine 2017, 50, 11896–11901. [Google Scholar] [CrossRef]
- Chen, G.; Cheng, H.; Huang, C.; Han, W.; Dai, Q.; Li, H.; Yang, J. Deffuant Model on a Ring with Repelling Mechanism and Circular Opinions. Phys. Rev. E 2017, 95, 42118. [Google Scholar] [CrossRef] [PubMed]
- Jiang, B.; Zhao, Y.; Dong, J.; Hu, J. Analysis of the Influence of Trust in Opposing Opinions: An Inclusiveness-Degree Based Signed Deffuant–Weisbush Model. Inf. Fusion 2023, 104, 102173. [Google Scholar] [CrossRef]
- Xu, H.; Cai, H.; Wu, S.; Ai, K.; Xu, M. HKML: A Novel Opinion Dynamics Hegselmann-Krause Model with Media Literacy. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics (SMC), Toronto, ON, Canada, 11–14 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 52–57. [Google Scholar] [CrossRef]
- Wang, N.; Rong, Z.; Yang, W. Opinion Dynamics of Improved Hegselmann-Krause Model with Agent’s Stubbornness and Stubborn Agents. EPL (Europhys. Lett.) 2023, 143, 52001. [Google Scholar] [CrossRef]
- Xu, H.; Li, Z.; Guan, A.; Xu, M.; Wang, B. Opinion-Climate-Based Hegselmann-Krause Dynamics. Pattern Recognit. Lett. 2023, 167, 9–17. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, X.; Xie, Y.; Li, W. Opinion Dynamics of Social-Similarity-Based Hegselmann–Krause Model. Complexity 2017, 2017, 1–12. [Google Scholar] [CrossRef]
- Yuan, J.; Shi, J.; Wang, J.; Liu, W. Modelling Network Public Opinion Polarization Based on SIR Model Considering Dynamic Network Structure. Alex. Eng. J. 2022, 61, 4557–4571. [Google Scholar] [CrossRef]
- Yin, F.; She, Y.; Wang, J.; Wu, Y.; Wu, J. Modeling and Analyzing Information Propagation Evolution Integrating Internal and External Influences. Adv. Theory Simul. 2023, 7, 1820257. [Google Scholar] [CrossRef]
- Lian, Y.; Dong, X.; Liu, Y. Topological Evolution of the Internet Public Opinion. Phys. A Stat. Mech. Its Appl. 2017, 486, 567–578. [Google Scholar] [CrossRef]
- Dubey, S.R.; Singh, S.K.; Chaudhuri, B.B. Activation Functions in Deep Learning: A Comprehensive Survey and Benchmark. Neurocomputing 2022, 503, 92–108. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).