Research on a Crime Spatiotemporal Prediction Method Integrating Informer and ST-GCN: A Case Study of Four Crime Types in Chicago
Abstract
1. Introduction
- First, based on the locations and adjacent relationships of urban communities, a topological graph is constructed, and relevant historical crime, weather, and holiday data are stored.
- Second, ST-GCN is used to capture the complex spatiotemporal transition trends of crime, while the Informer method is utilized to evaluate the temporal crime trends.
- Finally, through Convolutional Neural Networks (CNNs), the spatiotemporal and temporal features are integrated to construct a powerful spatiotemporal crime prediction model. This model, rooted in detailed community topological graphs and robust organized crime data, provides solid theoretical and data support for crime prediction.
2. Materials and Methods
2.1. Data Description
- Addressing missing and abnormal data in the raw data;
- Generating non-obvious feature data based on existing data;
- Merging crime data with temperature data.
2.1.1. Data Collection
2.1.2. Data Processing
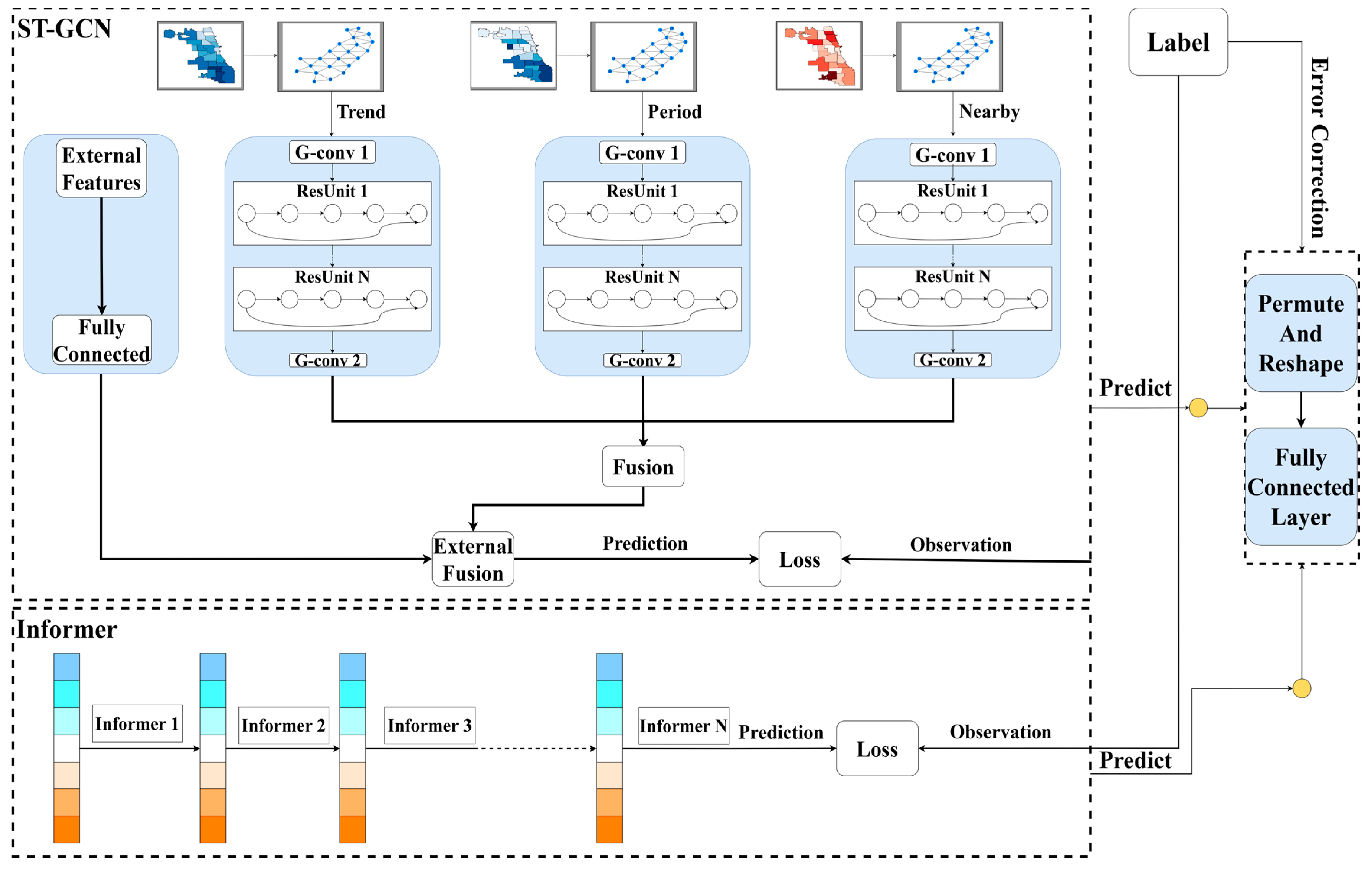
2.2. Methods
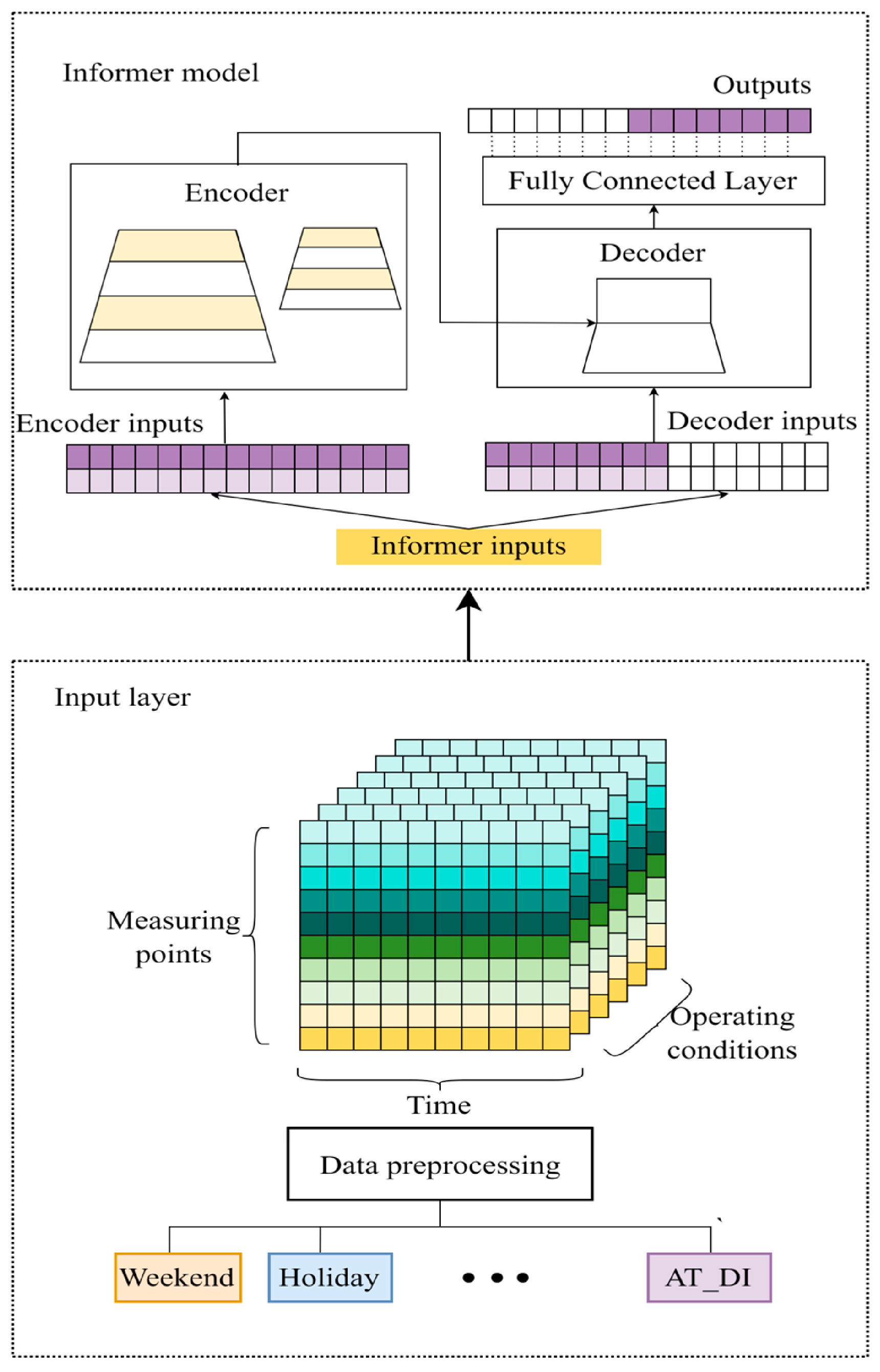
2.2.1. Informer Time Feature Extraction Module
2.2.2. The Spatiotemporal Feature Extraction Module
2.2.3. Evaluation
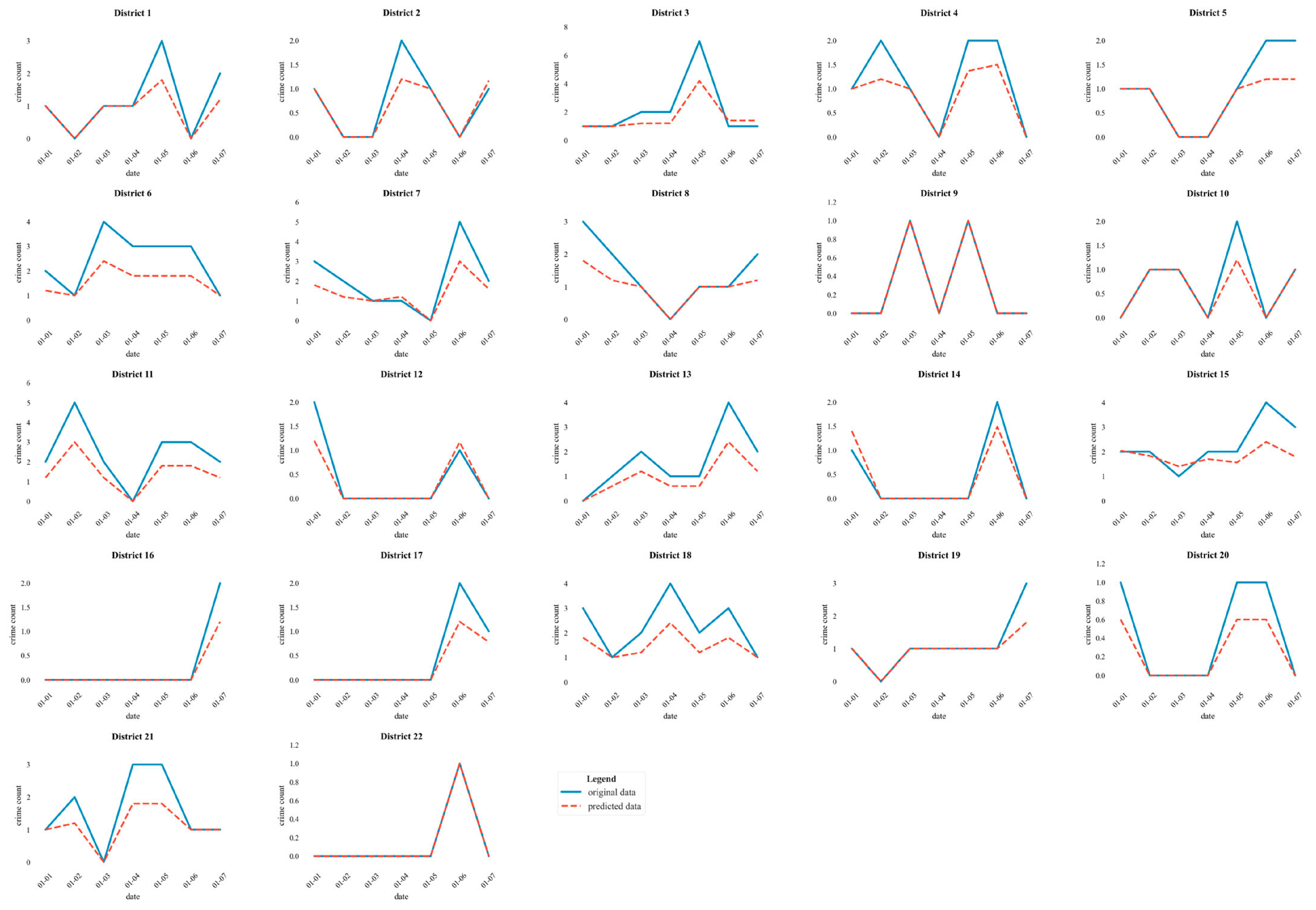
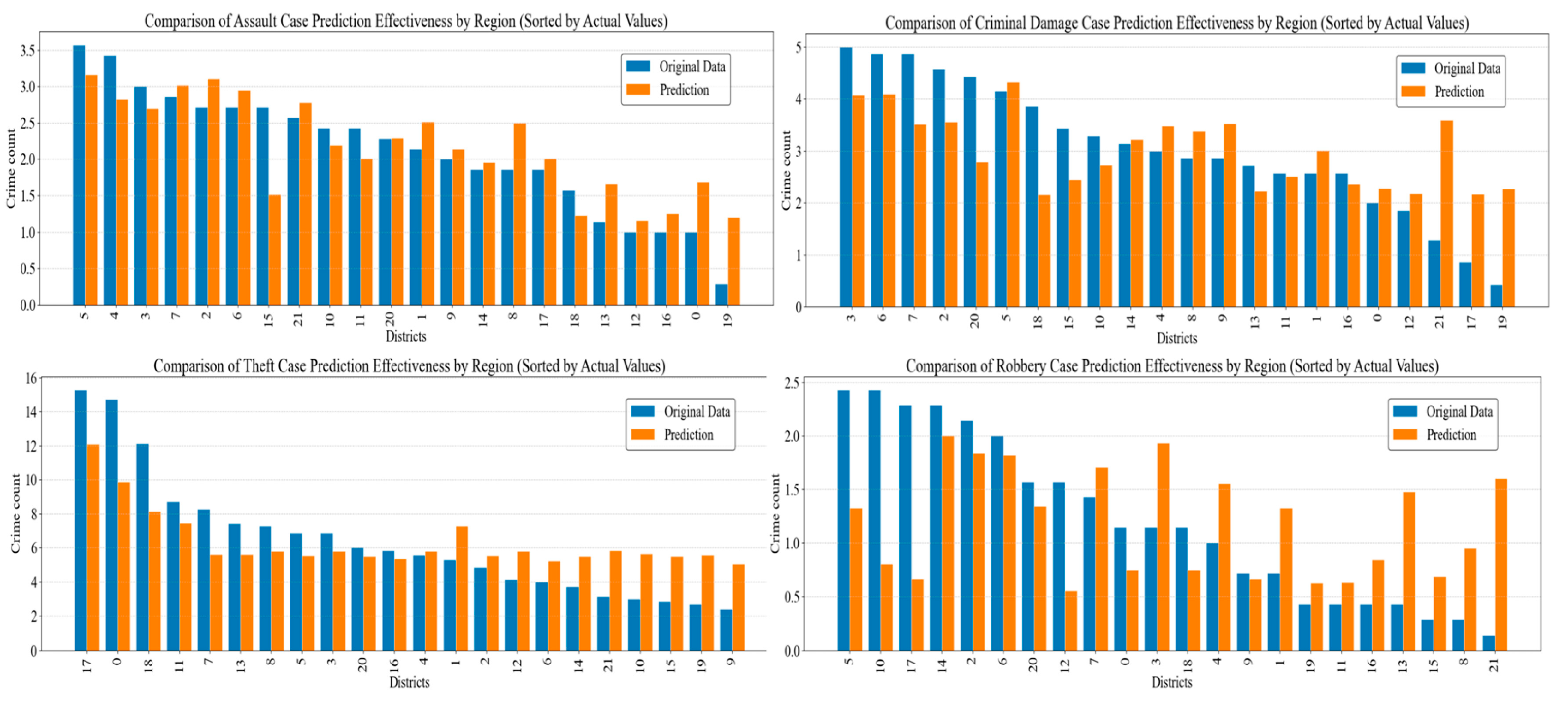
3. Results
4. Discussion
- Informer’s multi-head self-attention quantifies temporal contribution weights across different time windows and geographic zones, providing traceable temporal-spatial attribution for crime forecasts.
- ST-GCN’s graph attention networks reveal inter-regional influence patterns by learning adaptive edge weights between graph nodes, thereby elucidating complex spatial dependencies that conventional grid-based approaches overlook.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B


References
- Kornec, R. Ecological security of communities in polish cities. J. Plant Growth Regul. 2020, 16, 41–50. [Google Scholar] [CrossRef]
- Andresen, M.A.; Linning, S.J.; Malleson, N. Crime at places and spatial concentrations: Exploring the spatial stability of property crime in Vancouver BC, 2003–2013. J. Quant. Criminol. 2017, 33, 255–275. [Google Scholar] [CrossRef]
- Hegewald, S. Locality as a safe haven: Place-based resentment and political trust in local and national institutions. J. Eur. Public Policy 2023, 31, 1749–1774. [Google Scholar] [CrossRef]
- Chen, Y. Research on influencing factors of local epidemic prevention and control policy making: Based on the fuzzy set qualitative comparative analysis of 46 cities aiming at Chengdu’s epidemic prevention and control policies. In Proceedings of the 7th International Conference on Humanities and Social Science Research (ICHSSR 2021), Qingdao, China, 23–25 April 2021; pp. 140–143. [Google Scholar]
- Ravi Kumar, P.; Jayaram, A.; Somashekar, R. Assessment of the performance of different compost models to manage urban household organic solid wastes. Clean Technol. Environ. Policy 2009, 11, 473–484. [Google Scholar] [CrossRef]
- Vaccaro, A.; Popov, M.; Villacci, D.; Terzija, V. An integrated framework for smart microgrids modeling, monitoring, control, communication, and verification. Proc. IEEE 2010, 99, 119–132. [Google Scholar] [CrossRef]
- Liao, W.; Huang, X.; Van Coillie, F.; Gautama, S.; Pižurica, A.; Philips, W.; Liu, H.; Zhu, T.; Shimoni, M.; Moser, G.; et al. Processing of multiresolution thermal hyperspectral and digital color data: Outcome of the 2014 IEEE GRSS data fusion contest. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2984–2996. [Google Scholar] [CrossRef]
- Qiu, J.; Zhuang, L.; Zhou, Y.; Duan, Z. A standard cloud platform technology of traffic performance index based on multi-source data fusion. Open J. Trans. Technol. 2018, 7, 340–350. [Google Scholar] [CrossRef]
- Muchwanju, C.; Chelule, J.C.; Mung’Atu, J. Modelling crime rate using a mixed effects regression model. Am. J. Theor. Appl. Stat. 2015, 4, 496–503. [Google Scholar] [CrossRef]
- Cohen, L. Social change and crime rate trends: A routine activity approach. Am. Sociol. Rev. 1979, 44, 588–608. [Google Scholar] [CrossRef]
- Johnson, S.D.; Bowers, K.; Hirschfield, A. New insights into the spatial and temporal distribution of repeat victimization. Br. J. Criminol. 1997, 37, 224–241. [Google Scholar] [CrossRef]
- Eysenck, H.J.; Gudjonsson, G.H. Crime and personality. In The Causes and Cures of Criminality; Springer: New York, NY, USA, 1997; pp. 43–89. [Google Scholar]
- Clarke, R.V.G.; Felson, M. Routine Activity and Rational Choice; Routledge: Piscataway, NJ, USA, 1993. [Google Scholar]
- Hadzikadic, M.; Carmichael, T.; Curtin, C. Complex adaptive systems and game theory: An unlikely union. Complexity 2010, 16, 34–42. [Google Scholar] [CrossRef]
- Mohamad, A.M.; Hamin, Z.; Nor, M.Z.M.; Aziz, N.A. Selected theories on criminalisation of hacking. Int. J. Law Gov. Commun. 2021, 6, 168–178. [Google Scholar] [CrossRef]
- Tolulope, O.O. Students’ predisposition to being a victim of internet crime in tertiary institutions of Nigeria. Cult. Commun. Social. J. 2022, 3, 44–48. [Google Scholar] [CrossRef]
- Shiode, N.; Shiode, S.; Nishi, H.; Hino, K. Seasonal characteristics of crime: An empirical investigation of the temporal fluctuation of the different types of crime in London. Comput. Urban Sci. 2023, 3, 19. [Google Scholar] [CrossRef]
- Breetzke, G.D.; Cohn, E.G. Seasonal assault and neighborhood deprivation in South Africa: Some preliminary findings. Environ. Behav. 2012, 44, 641–667. [Google Scholar] [CrossRef]
- Tang, Y.; Zhu, X.; Guo, W.; Wu, L.; Fan, Y. Anisotropic diffusion for improved crime prediction in urban China. ISPRS Int. J. Geo-Inf. 2019, 8, 234. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, X. Analysis of burglary hot spots and near-repeat victimization in a large Chinese city. ISPRS Int. J. Geo-Inf. 2017, 6, 148. [Google Scholar] [CrossRef]
- Reid, A.A.; Frank, R.; Iwanski, N.; Dabbaghian, V.; Brantingham, P. Uncovering the spatial patterning of crimes: A criminal movement model (CriMM). J. Res. Crime Delinq. 2014, 51, 230–255. [Google Scholar] [CrossRef]
- Yang, M.; Chen, Z.; Zhou, M.; Liang, X.; Bai, Z. The impact of COVID-19 on crime: A spatial temporal analysis in Chicago. ISPRS Int. J. Geo-Inf. 2021, 10, 152. [Google Scholar] [CrossRef]
- Monish, N. Chicago crime analysis using r programming. Int. J. Sci. Res. Comput. Sci. Eng. Inform. Technol. 2019, 5, 937–944. [Google Scholar] [CrossRef]
- Shen, H.L.; Zhang, H.; Zhang, Y.F.; Zhang, Z.G.; Zhu, Y.M.; Cai, L. Prediction of burglary crime based on LSTM. J. Stat. Inform. 2019, 34, 107–115. [Google Scholar] [CrossRef]
- Zhuang, Y.; Almeida, M.; Morabito, M.; Ding, W. Crime hot spot forecasting: A recurrent model with spatial and temporal information. In Proceedings of the 2017 IEEE International Conference on Big Knowledge (ICBK), Hefei, China, 9–10 August 2017; pp. 143–150. [Google Scholar]
- Yan, S.; Xiong, Y.; Lin, D. Spatial temporal graph convolutional networks for skeleton-based action recognition. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; pp. 7444–7452. [Google Scholar]
- Gao, Z.; Yang, R.; Zhao, K.; Yu, W.; Liu, Z.; Liu, L. Hybrid convolutional neural network approaches for recognizing collaborative actions in human-robot assembly tasks. Sustainability 2024, 16, 139. [Google Scholar] [CrossRef]
- Zhao, D.; Du, P.; Liu, T.; Ling, Z.F. Spatio-temporal distribution prediction model of urban theft by fusing graph autoencoder and GRU. J. Geo-Inform. Sci. 2023, 25, 1448–1463. [Google Scholar] [CrossRef]
- Han, X.G.; Hu, X.F.; Wu, H.; Shen, B.; Wu, J. Risk prediction of theft crimes in urban communities: An integrated model of LSTM and ST-GCN. IEEE Access 2020, 8, 217222–217230. [Google Scholar] [CrossRef]
- Hu, J.M.; Hu, X.F.; Han, X.G.; Lin, Y.; Wu, H.; Shen, B. Exploring the correlation between temperature and crime: A case-crossover study of eight cities in America. J. Saf. Sci. Resil. 2024, 5, 13–36. [Google Scholar] [CrossRef]
- Pleshakova, E.; Osipov, A.; Gataullin, S.; Gataullin, T.; Vasilakos, A. Next gen cybersecurity paradigm towards artificial general intelligence: Russian market challenges and future global technological trends. J. Comput. Virol. Hack. Tech. 2024, 20, 429–440. [Google Scholar] [CrossRef]
- Kalai Selvan, A.; Sivakumaran, N. Crime detection and crime hot spot prediction using the BI-LSTM deep learning model. Int. J. Knowl.-Based Dev. 2024, 14, 57. [Google Scholar] [CrossRef]
- Fan, Q.; Xu, G. Real-time prediction model of public safety events driven by multi-source heterogeneous data. Front. Phys. 2025, 13, 1553640. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. arXiv 2020, arXiv:2012.07436. [Google Scholar] [CrossRef]
- Atero, F.J.; Vinagre, J.J.; Morgado, E.; Wilby, M.R. A low energy and adaptive architecture for efficient routing and robust mobility management in wireless sensor networks. In Proceedings of the 2011 31st International Conference on Distributed Computing Systems Workshops, Minneapolis, MN, USA, 20–24 June 2011; pp. 172–181. [Google Scholar]
- Ya, M.A.; Yaw, C.; Koh, S.; Tiong, S.; Chen, C.; Yusaf, T.; Abdalla, A.; Ali, K.; Raj, A. Detection of corona faults in switchgear by using 1D-CNN, LSTM, and 1D-CNN-LSTM methods. Sensors 2023, 23, 3108. [Google Scholar] [CrossRef]
- Xu, H.; Peng, Q.; Wang, Y.; Zhan, Z. Power-load forecasting model based on informer and its application. Energies 2023, 16, 3086. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, L.; Li, N.; Tian, J. Time series forecasting of motor bearing vibration based on informer. Sensors 2022, 22, 5858. [Google Scholar] [CrossRef] [PubMed]
- Jun, J.; Kim, H.K. Informer-based temperature prediction using observed and numerical weather prediction data. Sensors 2023, 23, 7047. [Google Scholar] [CrossRef] [PubMed]
- Davies, N.B.; Krebs, J.R.; West, S.A. An Introduction to Behavioural Ecology; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Zhang, J.; Zheng, Y.; Qi, D. Deep spatio-temporal residual networks for citywide crowd flows prediction. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; pp. 1655–1661. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Identity mappings in deep residual networks. In Proceedings of the Computer Vision-ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; pp. 630–645. [Google Scholar]


| Feature Name | Feature Value | Data Type |
|---|---|---|
| Date | The moment when the crime occurred | Date |
| Weekend | 1-Weekday, 0-Weekend | Boolean |
| Holiday | 1-Holiday, 0-Workday | Boolean |
| Weekday_avg | Average number of crime occurrences on weekdays | Float |
| Weekend_avg | Average number of crime occurrences on non-weekdays | Float |
| Month_avg | Average number of monthly crime occurrences | Float |
| Count_avg | Number at the previous moment | Int |
| T | Air temperature | Float |
| RH | Relative humidity | Float |
| V | Wind speed | Float |
| e | Water vapor pressure | Float |
| U | Relative humidity is indicated in the raw data | Float |
| Ff | Wind speed is indicated in the raw data | Float |
| Model | MAE | RMSE | |
|---|---|---|---|
| ARIMA | 3.42 | 3.98 | 0.43 |
| Ridge Regression | 3.13 | 3.61 | 0.45 |
| SVR | 2.91 | 3.43 | 0.48 |
| Random Forest | 2.42 | 2.89 | 0.54 |
| XGBoost | 2.46 | 2.95 | 0.53 |
| LSTM | 1.86 | 2.44 | 0.72 * |
| CNN | 1.44 | 1.76 | 0.76 * |
| Informer | 1.45 | 1.78 | 0.75 * |
| Conv-LSTM | 1.42 | 1.72 | 0.81 * |
| LSTM-STGCN | 1.38 | 1.68 | 0.82 * |
| Our Model | 1.36 | 1.65 | 0.83 * |
| Model | MAE | RMSE | |
|---|---|---|---|
| ARIMA | 1.83 | 2.24 | 0.45 |
| Ridge Regression | 1.56 | 1.97 | 0.49 |
| SVR | 1.42 | 1.91 | 0.50 |
| Random Forest | 1.37 | 1.68 | 0.51 |
| XGBoost | 1.29 | 1.63 | 0.54 |
| LSTM | 1.18 | 1.43 | 0.71 * |
| CNN | 0.93 | 1.13 | 0.78 * |
| Informer | 1.10 | 1.38 | 0.74 * |
| Conv-LSTM | 0.89 | 1.06 | 0.82 * |
| LSTM-STGCN | 0.82 | 0.94 | 0.83 * |
| Our Model | 0.73 | 0.89 | 0.86 * |
| Model | MAE | RMSE | |
|---|---|---|---|
| ARIMA | 2.47 | 3.04 | 0.44 |
| Ridge Regression | 2.13 | 2.62 | 0.47 |
| SVR | 2.07 | 2.51 | 0.49 |
| Random Forest | 1.84 | 2.35 | 0.54 |
| XGBoost | 1.81 | 2.28 | 0.55 |
| LSTM | 1.45 | 1.77 | 0.76 * |
| CNN | 1.26 | 1.49 | 0.78 * |
| Informer | 1.25 | 1.47 | 0.78 * |
| Conv-LSTM | 1.12 | 1.35 | 0.83 * |
| LSTM-STGCN | 1.06 | 1.22 | 0.84 * |
| Our Model | 1.03 | 1.17 | 0.84 * |
| Model | MAE | RMSE | |
|---|---|---|---|
| ARIMA | 2.65 | 3.15 | 0.45 |
| Ridge Regression | 2.46 | 2.87 | 0.48 |
| SVR | 2.28 | 2.66 | 0.49 |
| Random Forest | 1.73 | 2.02 | 0.58 |
| XGBoost | 1.74 | 2.05 | 0.58 |
| LSTM | 1.15 | 1.46 | 0.75 * |
| CNN | 1.12 | 1.39 | 0.78 * |
| Informer | 1.11 | 1.38 | 0.78 * |
| Conv-LSTM | 1.06 | 1.28 | 0.82 * |
| LSTM-STGCN | 1.04 | 1.22 | 0.83 * |
| Our Model | 1.05 | 1.24 | 0.83 * |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, Y.; Hu, X.; Hu, J. Research on a Crime Spatiotemporal Prediction Method Integrating Informer and ST-GCN: A Case Study of Four Crime Types in Chicago. Big Data Cogn. Comput. 2025, 9, 179. https://doi.org/10.3390/bdcc9070179
Fan Y, Hu X, Hu J. Research on a Crime Spatiotemporal Prediction Method Integrating Informer and ST-GCN: A Case Study of Four Crime Types in Chicago. Big Data and Cognitive Computing. 2025; 9(7):179. https://doi.org/10.3390/bdcc9070179
Chicago/Turabian StyleFan, Yuxiao, Xiaofeng Hu, and Jinming Hu. 2025. "Research on a Crime Spatiotemporal Prediction Method Integrating Informer and ST-GCN: A Case Study of Four Crime Types in Chicago" Big Data and Cognitive Computing 9, no. 7: 179. https://doi.org/10.3390/bdcc9070179
APA StyleFan, Y., Hu, X., & Hu, J. (2025). Research on a Crime Spatiotemporal Prediction Method Integrating Informer and ST-GCN: A Case Study of Four Crime Types in Chicago. Big Data and Cognitive Computing, 9(7), 179. https://doi.org/10.3390/bdcc9070179




