Evaluating Adversarial Robustness of No-Reference Image and Video Quality Assessment Models with Frequency-Masked Gradient Orthogonalization Adversarial Attack
Abstract
1. Introduction
- A novel white box attack for NR-IQA. We introduce FM-GOAT, an adversarial method that goes beyond simple norm constraints in favor of multiple, differentiable human-vision-inspired metrics. It jointly optimizes against these constraints using a novel gradient correction technique, yielding imperceptible perturbations, extends seamlessly to video via motion-compensated propagation, and outperforms existing attacks in pair-wise comparisons across different NR-IQA models.
- Comprehensive vulnerability evaluation. We test six different NR-IQA architectures, demonstrating that all are highly susceptible to the proposed attack with a fairly limited perturbation budget.
- Deep feature analysis. By comparing intermediate model activations on clean and attacked inputs, we reveal characteristic patterns of perturbation propagation within different target models—insights that could inform more robust detection and defense strategies.
- Defense assessment. We benchmark common image transformations as purification defenses against the attack and show they only partially mitigate its effect, often introducing new artifacts that degrade model performance on benign images.
2. Related Work
2.1. No-Reference Image Quality Assessment
2.2. Adversarial Attacks
2.3. Restricted Attacks
2.4. Unrestricted Attacks
2.4.1. Generative Methods
2.4.2. Adversarial Texture and Color Correction
2.4.3. Adversarial Deformations
2.5. Adversarial Attacks on IQA Models
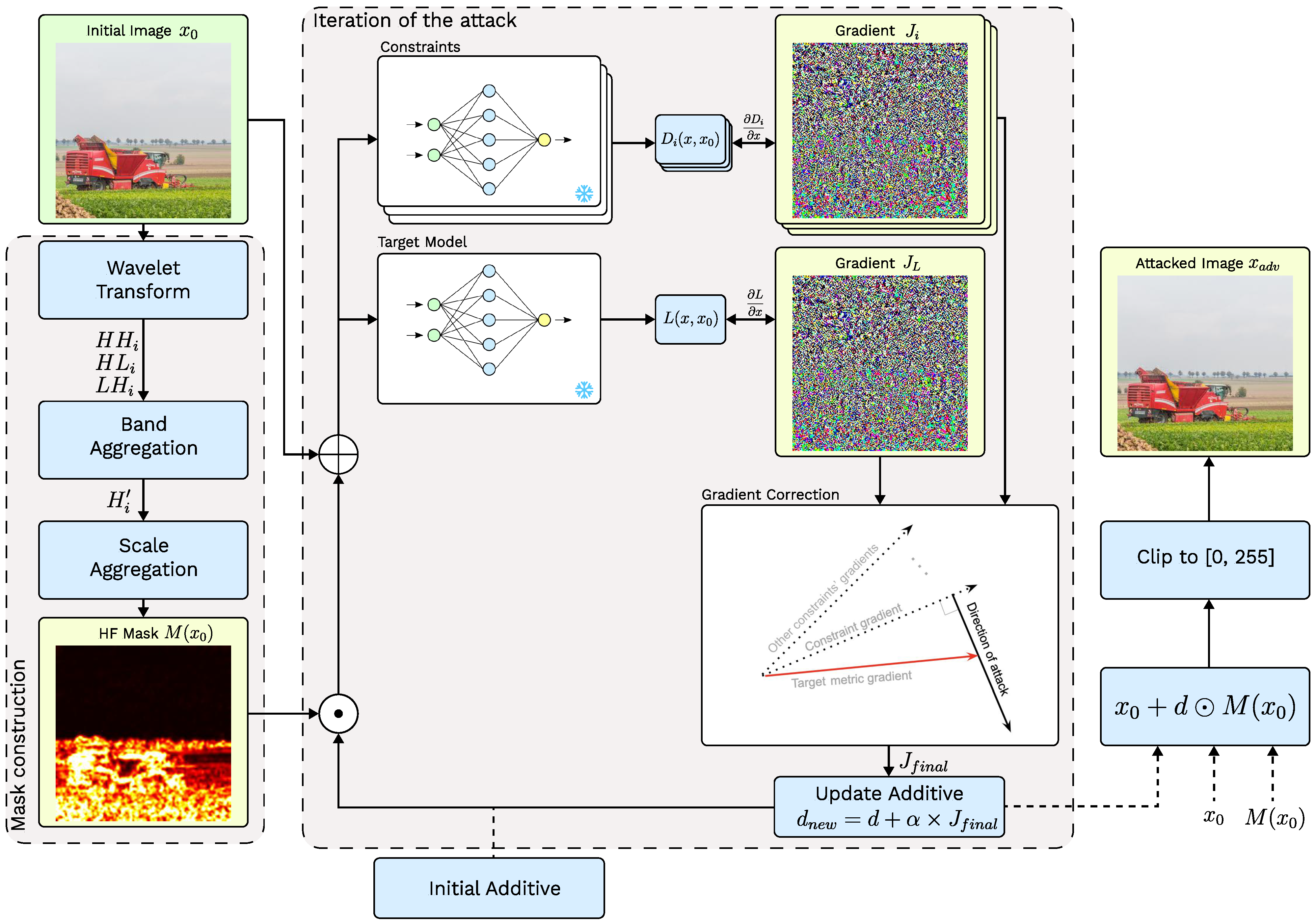
3. Proposed Method
3.1. Problem Formulation and Constraints Design
3.2. Optimization Method
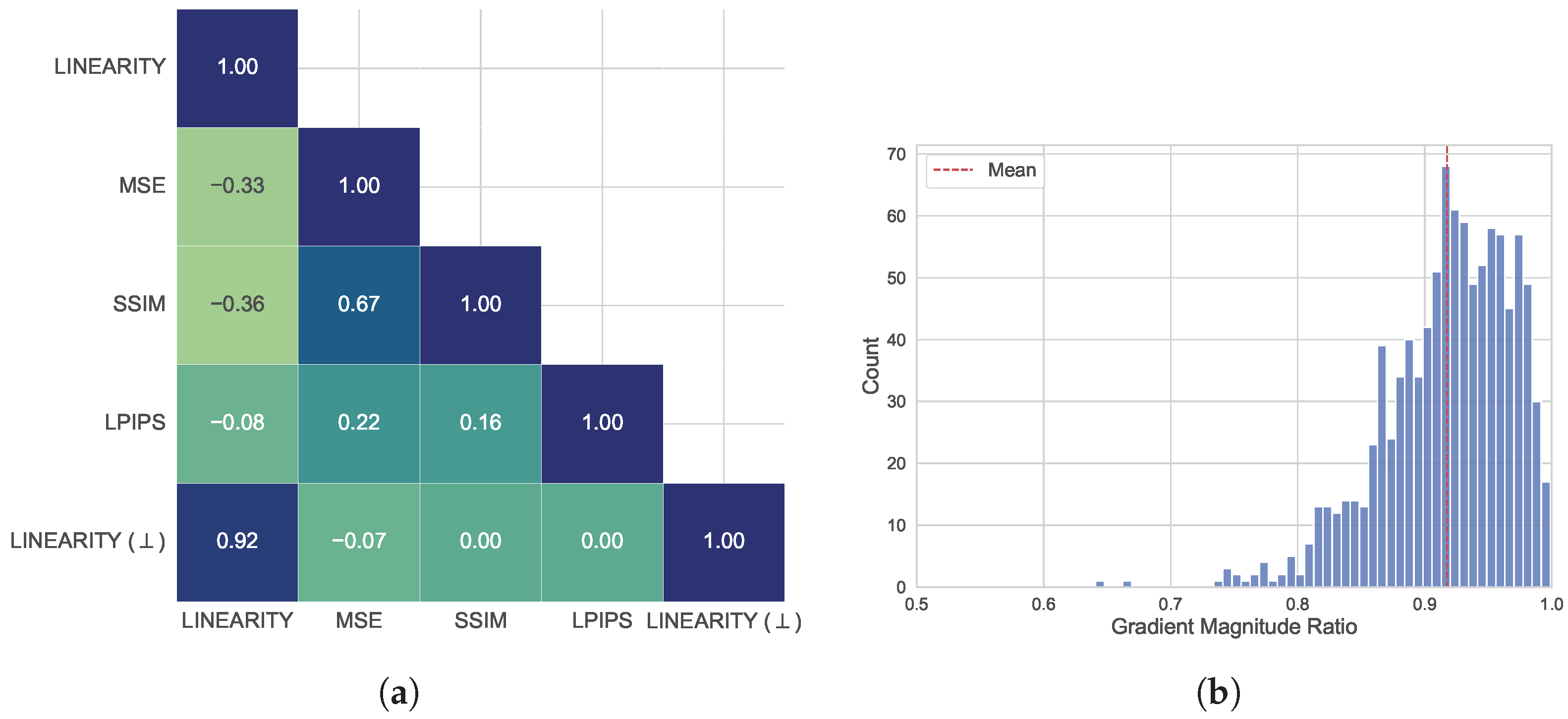
3.3. Reducing Attack Visibility
3.3.1. High-Frequency Masking
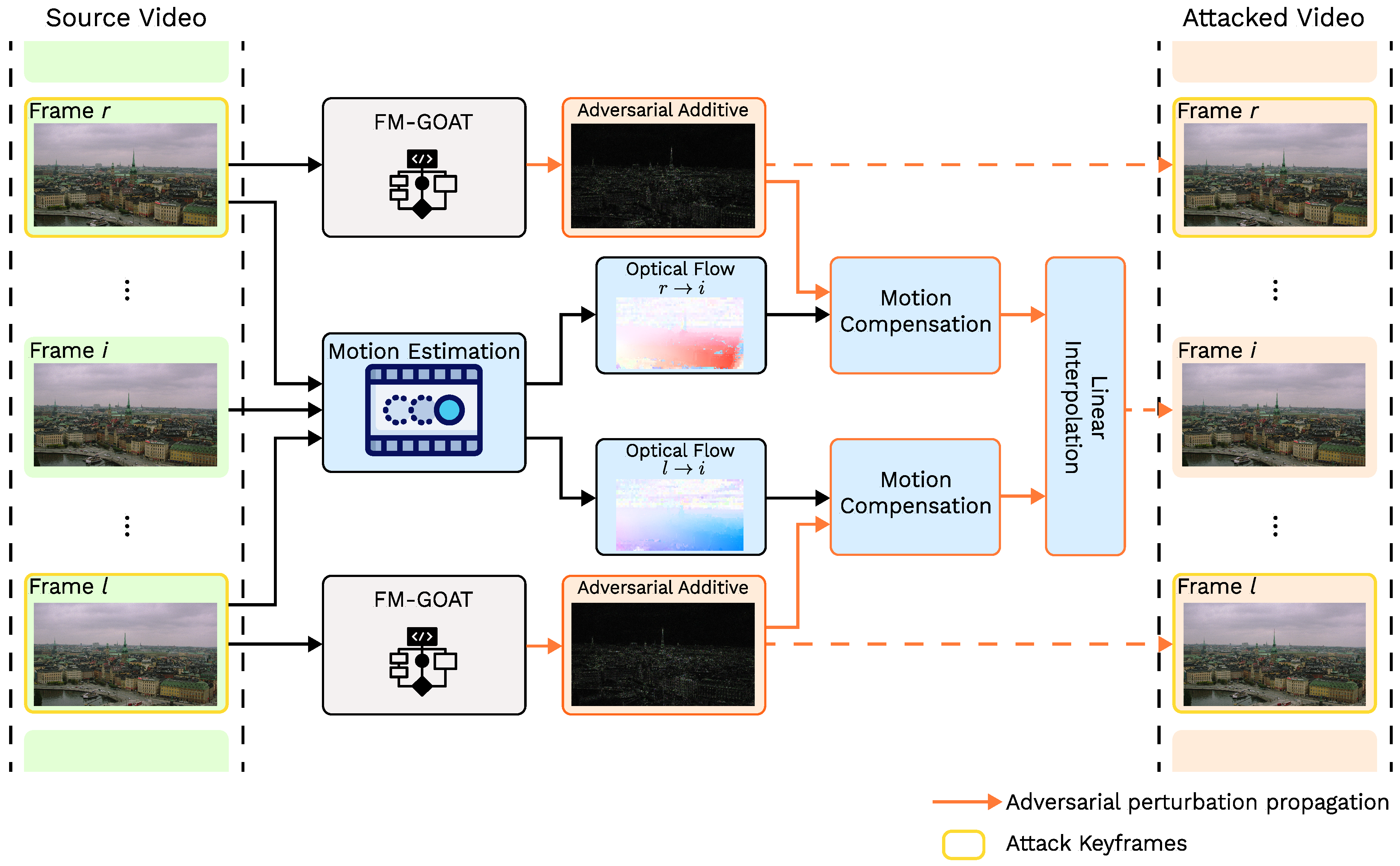
3.3.2. Propagating Adversarial Attacks on Videos
4. Experiments
4.1. Experimental Setup
- PaQ-2-PiQ [27]: CNN-based NR metric that predicts image quality by analyzing patches and pooling them in accordance with regions of interest (RoI Pooling) to assess the quality of the entire image. It underwent training on the eponymous PaQ-2-PiQ subjective-quality database and uses ResNet-18 as a feature-extraction backbone.
- Linearity [15]: A model that introduces a novel norm-in-norm loss for NR-IQA training, demonstrating up to faster convergence than traditional loss functions such as MAE and MSE. It is based on a ResNeXt-101 backbone.
- Hyper-IQA [28]: An IQA metric specifically designed for real-life images, utilizing a hyper convolutional network to predict weights for the last fully connected layers. Feature extraction is performed by using the ResNet-50 backbone.
- TReS [34]: A metric that incorporates a self-attention mechanism for computing nonlocal image features as well as a CNN (ResNet-50) for extracting local features. It also introduces a self-supervision loss calculated on reference and flipped images.
- MDTVSFA [30]: An improved version of the VSFA video quality assessment metric. It employs a ResNet-50 backbone for feature extraction and a GRU recurrent network for temporal feature aggregation. MDTVSFA enhances VSFA through multi-dataset training and a score mapping technique between predicted and dataset-specific ground-truth quality scores. According to benchmark [71], it delivers a state-of-the-art VQA performance. It handles images as well by treating them as one-frame videos.
- TOPIQ(NR) [33]: A no-reference version of the novel TOPIQ metric, which introduces the coarse-to-fine network (CFANet) to employ multiscale image features and effectively propagate semantic information to lower-level features. It is among the top-performing IQA models in terms of computational efficiency and correlation with subjective quality.
- CLIPIQA+ [39]: CLIPIQA+ is a popular metric that employs a pretrained Vision–Language model for NR-IQA. It utilizes pairs of positive and negative text prompts to assess different aspects of image quality and further adopts the CLIP model [72] to the IQA domain using trainable context tokens. It also utilizes the ViT [73] backbone in its vision branch.
4.2. Comparison with Other Attacks
4.2.1. Comparison Under Fixed Gains
4.2.2. Comparison Under Fixed Perceptual Losses
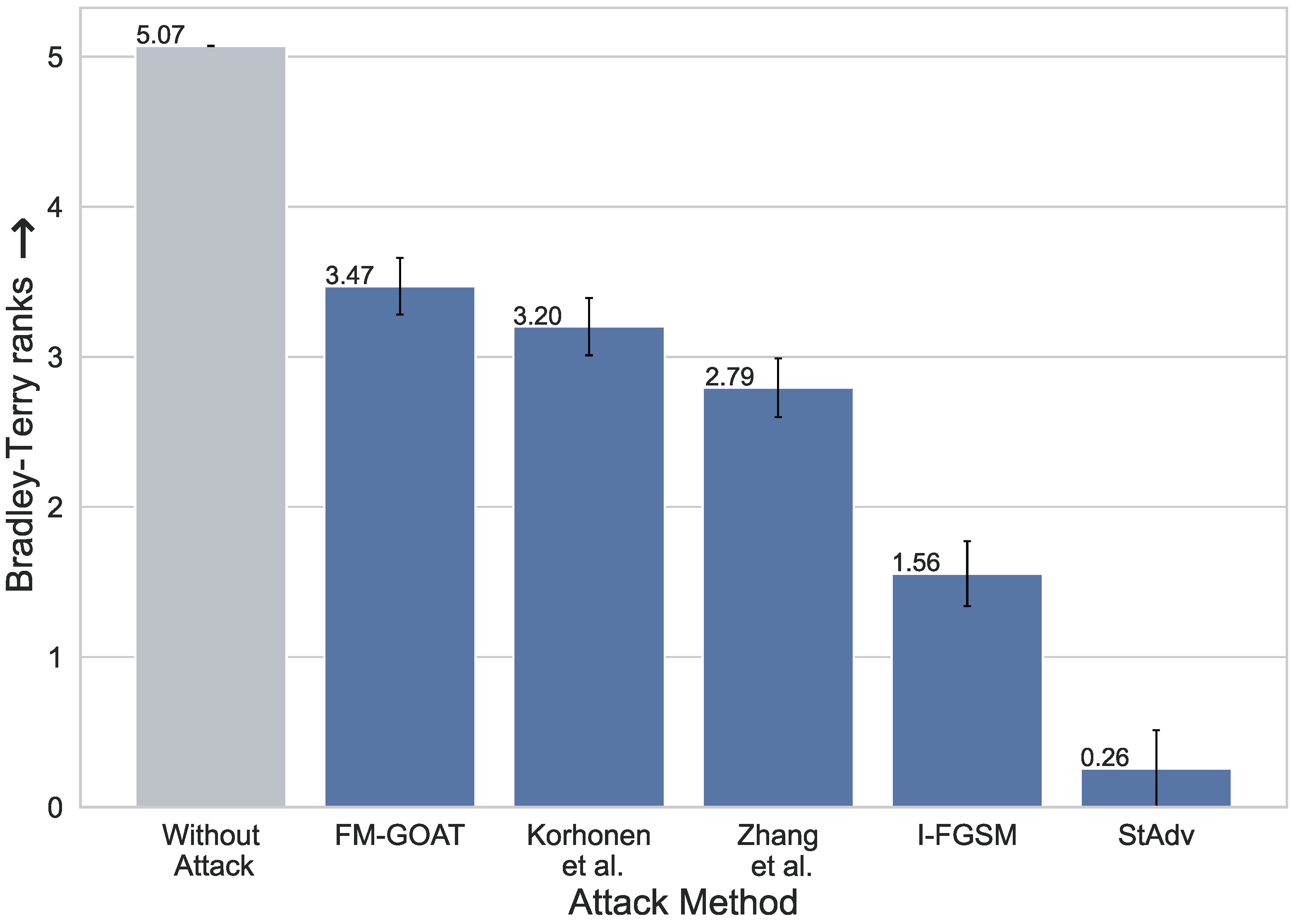
4.2.3. Subjective Study of Attack Perceptibility
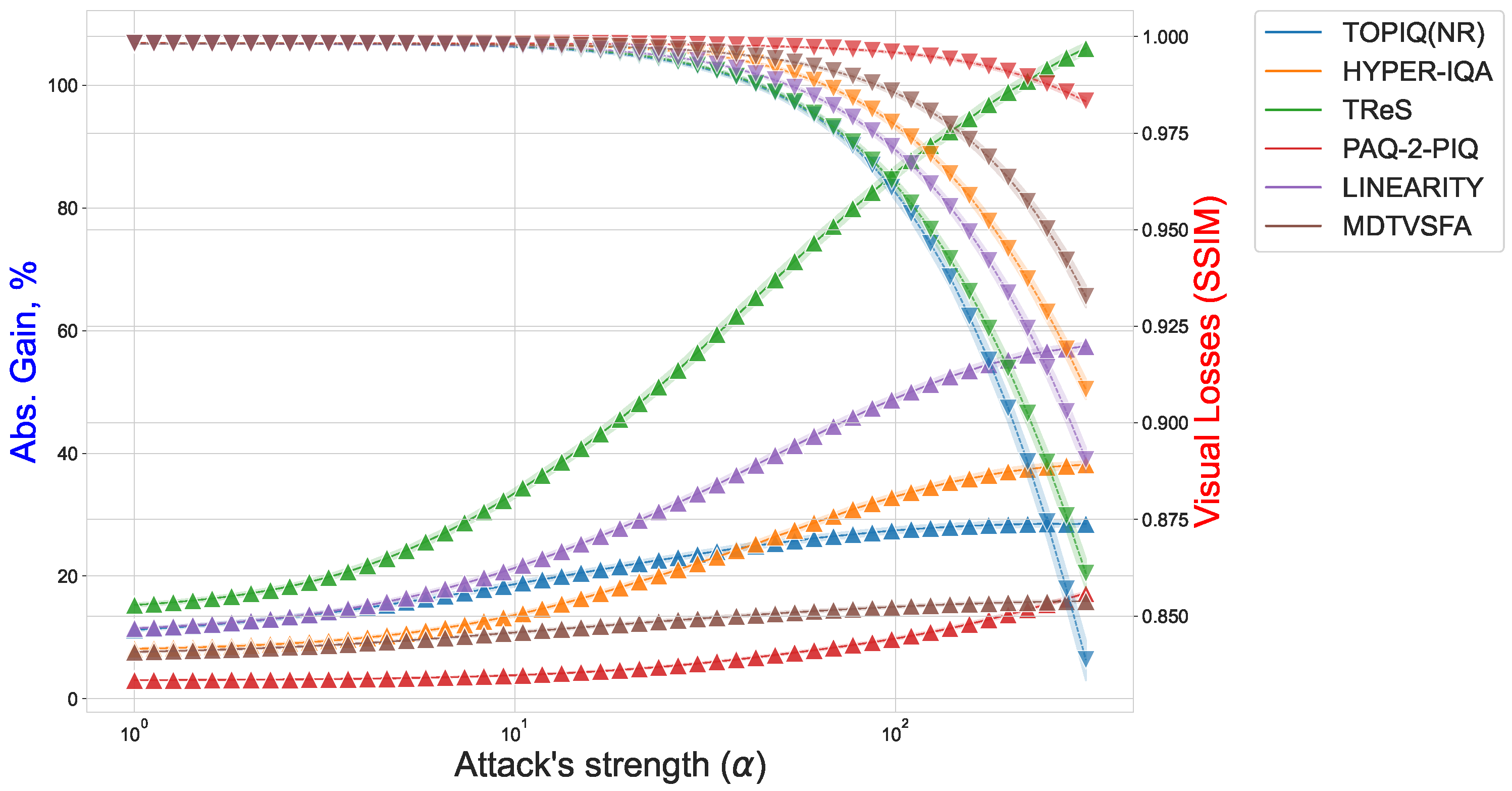
4.3. Evaluating the Robustness of Different NR-IQA Models
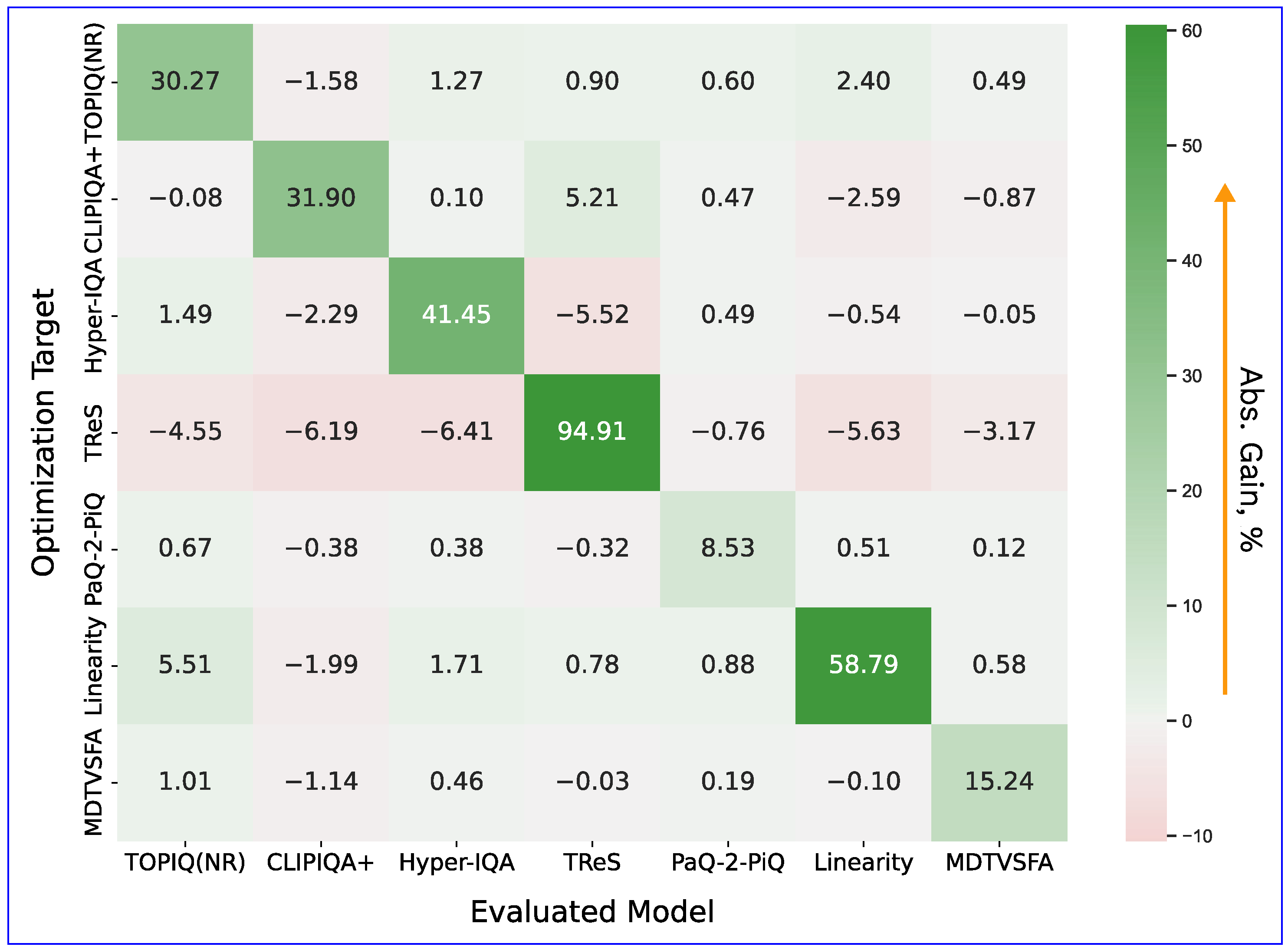
4.4. Transferability of Adversarial Examples
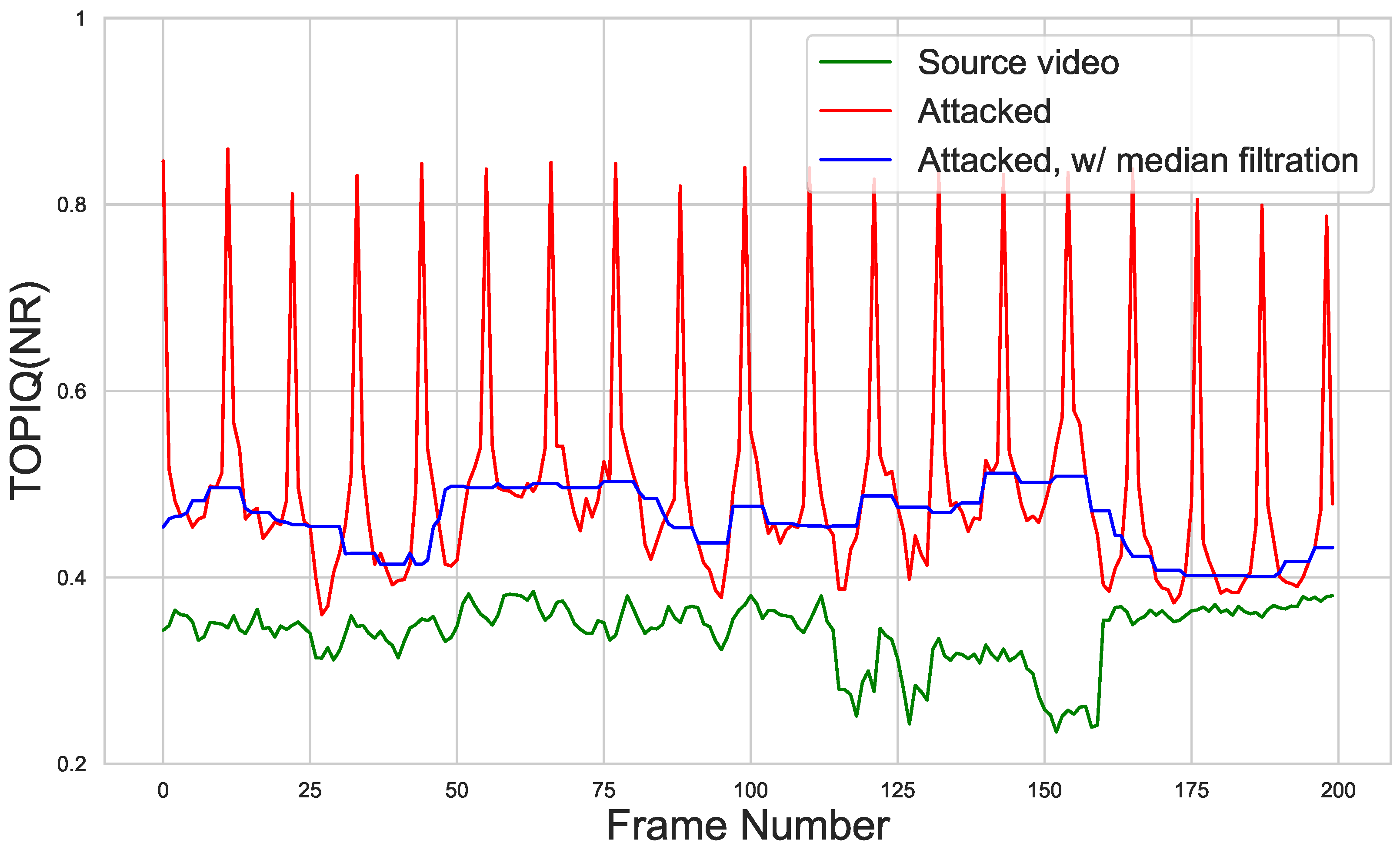
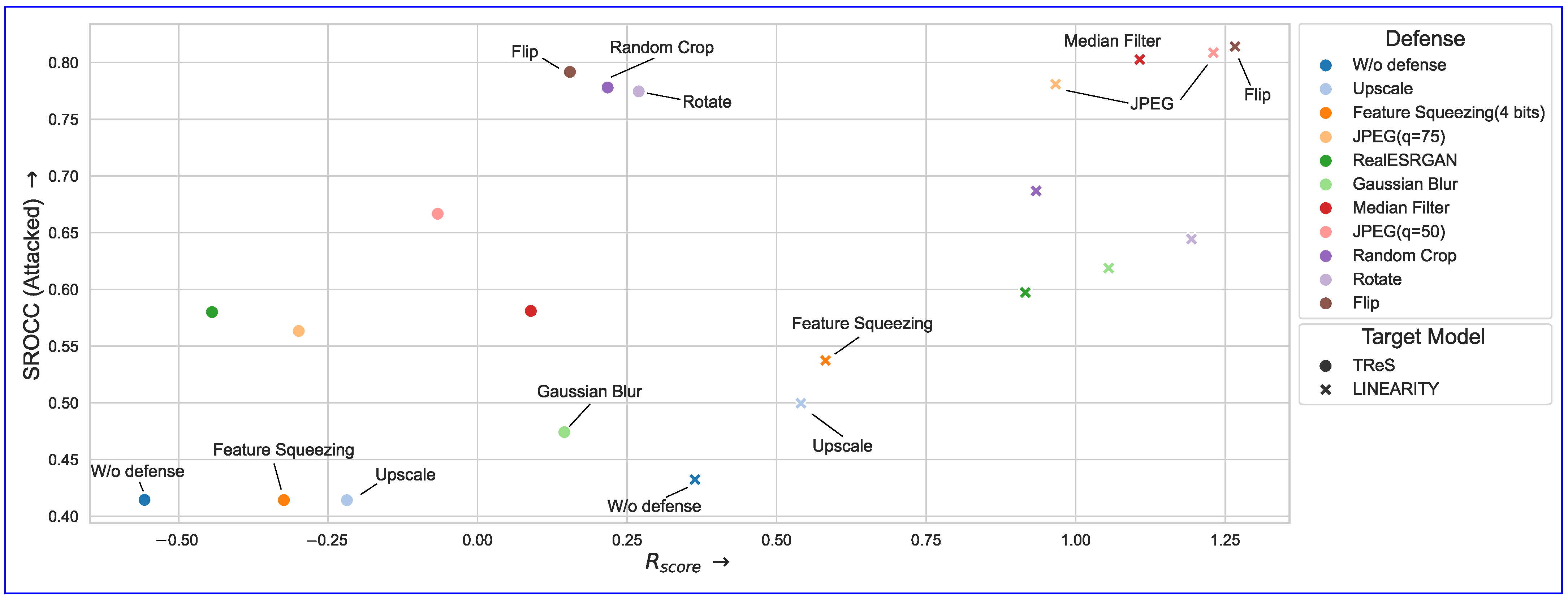
4.5. Defending NR-IQA Models with Input Transformations
4.6. Analyzing Attack Effectiveness
4.6.1. Attack Susceptibility and Initial Scores
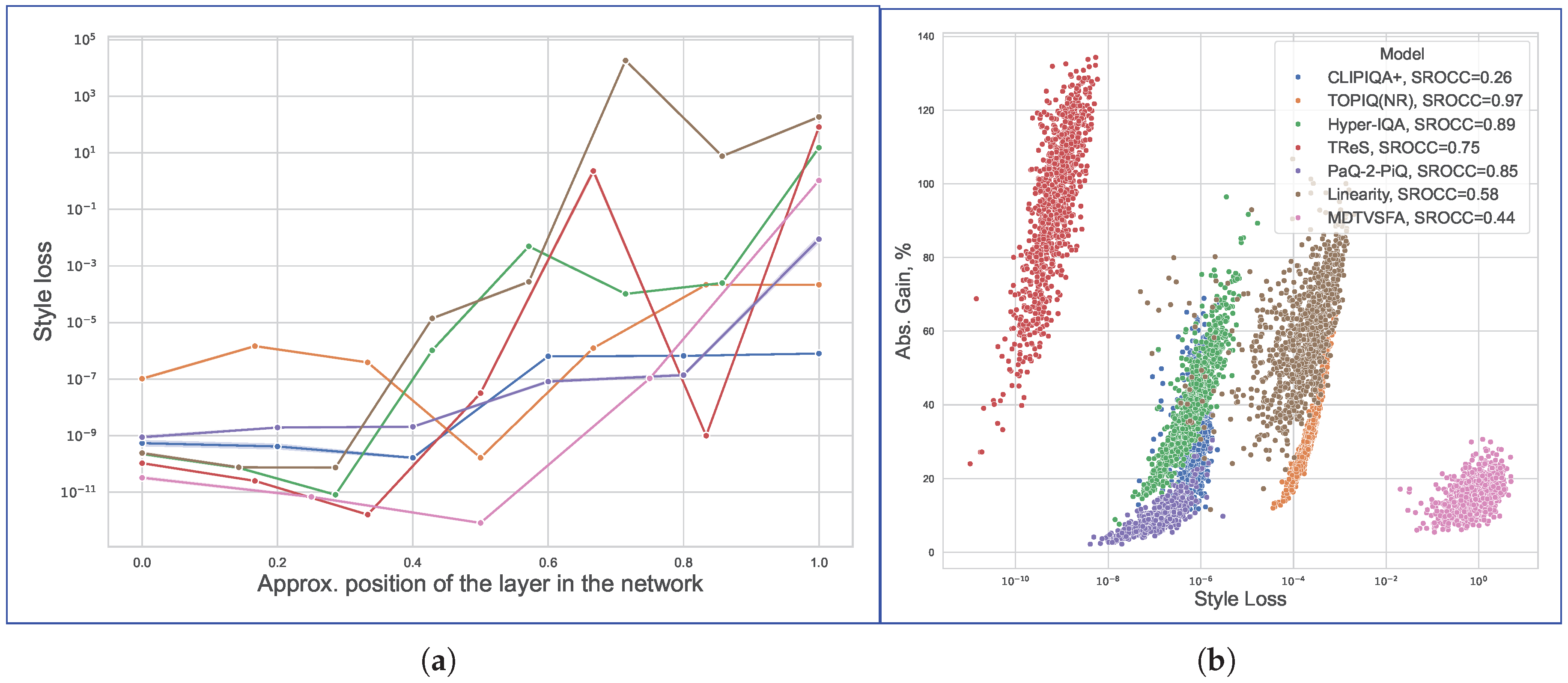
4.6.2. Perturbation Propagation in Feature Space
4.6.3. Activation Patterns and Attack Efficacy
5. Ablation Study
5.1. Effects of Gradient Correction
5.2. Comparing Video Propagation Methods
6. Discussion
6.1. Robustness of NR-IQA Models
6.2. Cross-Model Patterns
6.3. Defenses Evaluation
7. Conclusions
8. Future Work
8.1. Multitask Adversarial Scenarios
8.2. Interpretable Feature Defense
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Attack Algorithm
| Algorithm 1: FM-GOAT |
|
|
| Algorithm 2: |
|
Appendix B. Time Complexity Comparison
| Model | # of Iters | Attack | ||||
|---|---|---|---|---|---|---|
| FM-GOAT | Korhonen et al. | I-FGSM | Zhang et al. | StAdv | ||
| Hyper-IQA | 3 | 172 ± 6.17 ms | 105 ± 1.22 ms | 102 ± 1.76 ms | 156 ± 5.23 ms | 147 ± 5.19 ms |
| 10 | 486 ± 15.2 ms | 320 ± 3.57 ms | 321 ± 5.04 ms | 498 ± 7.13 ms | 480 ± 8.76 ms | |
| Linearity | 3 | 280 ± 7.23 ms | 214 ± 4.99 ms | 207 ± 3.01 ms | 261 ± 4.6 ms | 271 ± 8.67 ms |
| 10 | 851 ± 9.3 ms | 710 ± 16 ms | 690 ± 6.94 ms | 873 ± 18.1 ms | 885 ± 21.2 ms | |
| MDTVSFA | 3 | 156 ± 3.29 ms | 98.2 ± 2.58 ms | 92.2 ± 2.22 ms | 146 ± 3.42 ms | 13 ± 7.65 ms |
| 10 | 466 ± 5.03 ms | 295 ± 3.77 ms | 292 ± 4.71 ms | 469 ± 17.2 ms | 466 ± 9.96 ms | |
| PAQ-2-PIQ | 3 | 99.6 ± 5.28 ms | 47 ± 2 ms | 38.9 ± 0.7 ms | 95.4 ± 2.94 ms | 86.5 ± 4.8 ms |
| 10 | 294 ± 7.32 ms | 136 ± 2.8 ms | 127 ± 2.17 ms | 320 ± 15.8 ms | 271 ± 18 ms | |
| TOPIQ(NR) | 3 | 273 ± 7.24 ms | 204 ± 3.13 ms | 198 ± 5.68 ms | 253 ± 4.78 ms | 258 ± 12.9 ms |
| 10 | 777 ± 6.31 ms | 640 ± 19 ms | 608 ± 4.74 ms | 780 ± 7.51 ms | 795 ± 12.1 ms | |
| TReS | 3 | 236 ± 6.22 ms | 194 ± 3.75 ms | 188 ± 2.9 ms | 254 ± 5.17 ms | 210 ± 5.86 ms |
| 10 | 754 ± 11.7 ms | 591 ± 10.9 ms | 585 ± 13.1 ms | 857 ± 17.6 ms | 693 ± 23.8 ms | |
| Model | I-FGSM | StAdv | Korhonen et al. | Zhang et al. | FM-GOAT |
|---|---|---|---|---|---|
| Hyper-IQA | 2469.54 | 2467.65 | 2409.25 | 2689.00 | 2485.45 |
| Linearity | 1403.05 | 1403.05 | 1403.05 | 1533.07 | 1412.10 |
| MDTVSFA | 384.79 | 382.41 | 393.92 | 721.90 | 400.04 |
| PAQ-2-PIQ | 169.96 | 169.95 | 194.65 | 522.90 | 187.95 |
| TOPIQ(NR) | 646.94 | 641.76 | 665.90 | 994.72 | 668.73 |
| TReS | 1632.11 | 1628.14 | 1435.09 | 1687.89 | 1651.59 |
Appendix C. Additional Results
| (a) | ||||
|---|---|---|---|---|
| Score | Abs. Gain↓ | Rscore↑ | SROCC↑ (Attacked) | |
| Target Model | ||||
| TOPIQ(NR) | 32.87 ± 12.98% | 0.325 | 0.538 | |
| Hyper-IQA | 28.28 ± 10.98% | 0.390 | 0.551 | |
| TReS | 74.35 ± 19.88% | −0.701 | 0.395 | |
| PAQ-2-PIQ | 10.05 ± 5.76% | 0.921 | 0.395 | |
| Linearity | 39.32 ± 14.15% | 0.226 | 0.425 | |
| MDTVSFA | 14.57 ± 4.18% | 0.606 | 0.162 | |
| CLIPIQA+ | 38.60 ± 13.9 | 0.248 | 0.462 | |
| (b) | ||||
| Score | Abs. Gain↓ | Rscore↑ | SROCC↑ (Attacked) | |
| Target Model | ||||
| TOPIQ(NR) | 13.60 ± 5.95% | 0.734 | 0.845 | |
| Hyper-IQA | 6.17 ± 3.61% | 1.093 | 0.700 | |
| TReS | 24.35 ± 18.75% | −0.127 | 0.405 | |
| PAQ-2-PIQ | 13.41 ± 7.65% | 0.742 | 0.676 | |
| Linearity | 2.80 ± 3.37% | 1.415 | 0.983 | |
| MDTVSFA | 5.89 ± 3.13% | 1.029 | 0.644 | |
| CLIPIQA+ | 13.74 ± 7.6% | 0.762 | 0.778 | |
| Target Model Score | Linearity | TReS | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Defense | Abs. Gain↓ | Rscore↑ | SROCC↑ (Clear) | SROCC↑ (Attacked) | Abs. Gain↓ | Rscore↑ | SROCC↑ (Clear) | SROCC↑ (Attacked) | |
| W/o defense | 33.09 ± 0.33% | 0.363 | - | 0.432 | 56.80 ± 0.67% | −0.557 | - | 0.414 | |
| Upscale | 21.06 ± 0.28% | 0.541 | 0.941 | 0.500 | 44.54 ± 0.59% | −0.219 | 0.983 | 0.414 | |
| Feature squeezing (4 bits) | 18.78 ± 0.25% | 0.582 | 0.900 | 0.537 | 43.85 ± 0.63% | −0.324 | 0.974 | 0.414 | |
| RealESRGAN | 10.63 ± 0.19% | 0.916 | 0.886 | 0.597 | 30.92 ± 0.57% | −0.444 | 0.963 | 0.580 | |
| Random crop | 10.58 ± 0.23% | 0.934 | 0.968 | 0.687 | 13.92 ± 0.30% | 0.217 | 0.962 | 0.778 | |
| JPEG (q = 75) | 7.88 ± 0.13% | 0.967 | 0.921 | 0.781 | 33.34 ± 0.52% | −0.299 | 0.971 | 0.563 | |
| Rotate | 6.37 ± 0.24% | 1.194 | 0.877 | 0.644 | 12.90 ± 0.38% | 0.269 | 0.913 | 0.775 | |
| Median filter | 5.89 ± 0.10% | 1.107 | 0.875 | 0.803 | 25.03 ± 0.40% | 0.089 | 0.917 | 0.581 | |
| Gaussian blur | 5.55 ± 0.10% | 1.055 | 0.752 | 0.619 | 28.37 ± 0.44% | 0.145 | 0.929 | 0.474 | |
| Flip | 4.60 ± 0.10% | 1.266 | 0.886 | 0.814 | 12.41 ± 0.23% | 0.154 | 0.947 | 0.792 | |
| JPEG(q = 50) | 4.09 ± 0.08% | 1.230 | 0.849 | 0.809 | 23.89 ± 0.38% | -0.067 | 0.949 | 0.667 | |
References
- Wang, Z.; Bovik, A.; Sheikh, H.; Simoncelli, E. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Isola, P.; Efros, A.A.; Shechtman, E.; Wang, O. The Unreasonable Effectiveness of Deep Features as a Perceptual Metric. In Proceedings of the CVPR, Salt Lake City, UT, USA, 19-21 June 2018. [Google Scholar]
- Ding, K.; Ma, K.; Wang, S.; Simoncelli, E.P. Image Quality Assessment: Unifying Structure and Texture Similarity. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 2567–2581. [Google Scholar] [CrossRef]
- Startsev, V.; Ustyuzhanin, A.; Kirillov, A.; Baranchuk, D.; Kastryulin, S. Alchemist: Turning Public Text-to-Image Data into Generative Gold. arXiv 2025, arXiv:2505.19297. Available online: http://arxiv.org/abs/2505.19297 (accessed on 8 June 2025).
- V-Nova. FFmpeg with LCEVC. 2023. Available online: https://v-nova.com/press-releases/globo-deploys-lcevc-enhanced-stream-for-2023-brazilian-carnival/ (accessed on 1 May 2025).
- Phadikar, B.; Phadikar, A.; Thakur, S. A comprehensive assessment of content-based image retrieval using selected full reference image quality assessment algorithms. Multimed. Tools Appl. 2021, 80, 15619–15646. [Google Scholar] [CrossRef]
- Yang, Y.; Jiao, S.; He, J.; Xia, B.; Li, J.; Xiao, R. Image retrieval via learning content-based deep quality model towards big data. Future Gener. Comput. Syst. 2020, 112, 243–249. [Google Scholar] [CrossRef]
- Abud, K.; Lavrushkin, S.; Kirillov, A.; Vatolin, D. IQA-Adapter: Exploring Knowledge Transfer from Image Quality Assessment to Diffusion-based Generative Models. arXiv 2024, arXiv:2412.01794. Available online: http://arxiv.org/abs/2412.01794 (accessed on 8 June 2025).
- Zhu, H.; Li, L.; Wu, J.; Dong, W.; Shi, G. MetaIQA: Deep Meta-Learning for No-Reference Image Quality Assessment. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Virtual Conference, 16–18 June 2020; pp. 14143–14152. [Google Scholar]
- Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and harnessing adversarial examples. arXiv 2014, arXiv:1412.6572. [Google Scholar]
- Ma, W.; Li, Y.; Jia, X.; Xu, W. Transferable Adversarial Attack for Both Vision Transformers and Convolutional Networks via Momentum Integrated Gradients. In Proceedings of the 2023 IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 2–3 October 2023; pp. 4607–4616. [Google Scholar] [CrossRef]
- Bai, T.; Luo, J.; Zhao, J.; Wen, B.; Wang, Q. Recent Advances in Adversarial Training for Adversarial Robustness. In Proceedings of the Thirtieth International Joint Conference on Artificial Intelligence (IJCAI-21), Virtual Conference, 19–26 August 2021; pp. 4312–4321. [Google Scholar] [CrossRef]
- Papernot, N.; McDaniel, P.; Wu, X.; Jha, S.; Swami, A. Distillation as a Defense to Adversarial Perturbations Against Deep Neural Networks. In Proceedings of the Proceedings—2016 IEEE Symposium on Security and Privacy (SP 2016), San Jose, CA, USA, 23–25 May 2016; pp. 582–597. [Google Scholar] [CrossRef]
- Nie, W.; Guo, B.; Huang, Y.; Xiao, C.; Vahdat, A.; Anandkumar, A. Diffusion Models for Adversarial Purification. In Proceedings of the International Conference on Machine Learning (ICML), Honolulu, HI, USA, 23–29 July 2022. [Google Scholar]
- Li, D.; Jiang, T.; Jiang, M. Norm-in-norm loss with faster convergence and better performance for image quality assessment. In Proceedings of the 28th ACM International Conference on Multimedia, Seattle, WA, USA, 12–16 October 2020; pp. 789–797. [Google Scholar]
- Hosu, V.; Lin, H.; Szirányi, T.; Saupe, D. KonIQ-10k: An Ecologically Valid Database for Deep Learning of Blind Image Quality Assessment. IEEE Trans. Image Process. 2020, 29, 4041–4056. [Google Scholar] [CrossRef]
- Li, Z.; Aaron, A.; Katsavounidis, I.; Manohara, M. Toward A Practical Perceptual Video Quality Metric. 2016. Available online: https://netflixtechblog.com/toward-a-practical-perceptual-video-quality-metric-653f208b9652 (accessed on 1 May 2024).
- Kashkarov, E.; Chistov, E.; Molodetskikh, I.; Vatolin, D. Can No-Reference Quality-Assessment Methods Serve as Perceptual Losses for Super-Resolution? arXiv 2024, arXiv:eess.IV/2405.20392. Available online: http://arxiv.org/abs/2405.20392 (accessed on 23 April 2025).
- Chen, J.; Chen, H.; Chen, K.; Zhang, Y.; Zou, Z.; Shi, Z. Diffusion Models for Imperceptible and Transferable Adversarial Attack. IEEE Trans. Pattern Anal. Mach. Intell. 2025, 47, 961–977. [Google Scholar] [CrossRef]
- Dai, X.; Liang, K.; Xiao, B. AdvDiff: Generating Unrestricted Adversarial Examples using Diffusion Models. arXiv 2023, arXiv:2307.12499. [Google Scholar]
- Yang, X.; Li, F.; Zhang, W.; He, L. Blind Image Quality Assessment of Natural Scenes Based on Entropy Differences in the DCT Domain. Entropy 2018, 20, 885. [Google Scholar] [CrossRef] [PubMed]
- Oszust, M.; Piórkowski, A.; Obuchowicz, R. No-reference image quality assessment of magnetic resonance images with high-boost filtering and local features. Magn. Reson. Med. 2020, 84, 1648–1660. [Google Scholar] [CrossRef] [PubMed]
- Mittal, A.; Moorthy, A.K.; Bovik, A.C. No-Reference Image Quality Assessment in the Spatial Domain. IEEE Trans. Image Process. 2012, 21, 4695–4708. [Google Scholar] [CrossRef]
- Kang, L.; Ye, P.; Li, Y.; Doermann, D. Convolutional Neural Networks for No-Reference Image Quality Assessment. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition (CVPR ’14), Columbus, OH, USA, 24–27 June 2014; pp. 1733–1740. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Tan, M.; Le, Q.V. EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks. arXiv 2020, arXiv:cs.LG/1905.11946. Available online: http://arxiv.org/abs/1905.11946 (accessed on 25 April 2025).
- Ying, Z.a.; Niu, H.; Gupta, P.; Mahajan, D.; Ghadiyaram, D.; Bovik, A. From Patches to Pictures (PaQ-2-PiQ): Mapping the Perceptual Space of Picture Quality. arXiv 2019, arXiv:1912.10088. [Google Scholar]
- Su, S.; Yan, Q.; Zhu, Y.; Zhang, C.; Ge, X.; Sun, J.; Zhang, Y. Blindly assess image quality in the wild guided by a self-adaptive hyper network. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Virtual Conference, 16–18 June 2020; pp. 3667–3676. [Google Scholar]
- Li, D.; Jiang, T.; Jiang, M. Quality Assessment of In-the-Wild Videos. In Proceedings of the 27th ACM International Conference on Multimedia, Nice, France, 21–25 October 2019; pp. 2351–2359. [Google Scholar] [CrossRef]
- Li, D.; Jiang, T.; Jiang, M. Unified quality assessment of in-the-wild videos with mixed datasets training. Int. J. Comput. Vis. 2021, 129, 1238–1257. [Google Scholar] [CrossRef]
- Wu, H.; Chen, C.; Liao, L.; Hou, J.; Sun, W.; Yan, Q.; Gu, J.; Lin, W. Neighbourhood Representative Sampling for Efficient End-to-end Video Quality Assessment. arXiv 2022, arXiv:2210.05357. Available online: http://arxiv.org/abs/2210.05357 (accessed on 5 April 2025). [CrossRef]
- Wu, H.; Chen, C.; Hou, J.; Liao, L.; Wang, A.; Sun, W.; Yan, Q.; Lin, W. FAST-VQA: Efficient End-to-end Video Quality Assessment with Fragment Sampling. In Proceedings of the European Conference of Computer Vision (ECCV), Tel Aviv, Israel, 23–27 October 2022. [Google Scholar]
- Chen, C.; Mo, J.; Hou, J.; Wu, H.; Liao, L.; Sun, W.; Yan, Q.; Lin, W. TOPIQ: A Top-down Approach from Semantics to Distortions for Image Quality Assessment. arXiv 2023, arXiv:2308.03060. [Google Scholar] [CrossRef]
- Golestaneh, S.A.; Dadsetan, S.; Kitani, K.M. No-reference image quality assessment via transformers, relative ranking, and self-consistency. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 4–8 January 2022; pp. 1220–1230. [Google Scholar]
- Wu, H.; Zhang, Z.; Zhang, W.; Chen, C.; Li, C.; Liao, L.; Wang, A.; Zhang, E.; Sun, W.; Yan, Q.; et al. Q-Align: Teaching LMMs for Visual Scoring via Discrete Text-Defined Levels. arXiv 2023, arXiv:2312.17090. [Google Scholar]
- Miyata, T. ZEN-IQA: Zero-Shot Explainable and No-Reference Image Quality Assessment With Vision Language Model. IEEE Access 2024, 12, 70973–70983. [Google Scholar] [CrossRef]
- Varga, D. Comparative Evaluation of Multimodal Large Language Models for No-Reference Image Quality Assessment with Authentic Distortions: A Study of OpenAI and Claude.AI Models. Big Data Cogn. Comput. 2025, 9, 132. [Google Scholar] [CrossRef]
- Zhang, W.; Zhai, G.; Wei, Y.; Yang, X.; Ma, K. Blind Image Quality Assessment via Vision-Language Correspondence: A Multitask Learning Perspective. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2023; pp. 14071–14081. [Google Scholar]
- Wang, J.; Chan, K.C.; Loy, C.C. Exploring CLIP for Assessing the Look and Feel of Images. In Proceedings of the AAAI, Washington, DC, USA, 7–14 February 2023. [Google Scholar]
- Chen, C.; Yang, S.; Wu, H.; Liao, L.; Zhang, Z.; Wang, A.; Sun, W.; Yan, Q.; Lin, W. Q-Ground: Image Quality Grounding with Large Multi-modality Models. arXiv 2024, arXiv:cs.CV/2407.17035. Available online: http://arxiv.org/abs/2407.17035 (accessed on 23 April 2025).
- Chen, Z.; Wang, J.; Wang, W.; Xu, S.; Xiong, H.; Zeng, Y.; Guo, J.; Wang, S.; Yuan, C.; Li, B.; et al. SEAGULL: No-reference Image Quality Assessment for Regions of Interest via Vision-Language Instruction Tuning. arXiv 2024, arXiv:cs.CV/2411.10161. Available online: http://arxiv.org/abs/2411.10161 (accessed on 8 June 2025).
- Vassilev, A.; Oprea, A.; Fordyce, A.; Andersen, H. Adversarial Machine Learning: A Taxonomy and Terminology of Attacks and Mitigations. National Institute of Standards and Technology, Computer Security Resource Center, NIST AI 100-2 E2023, January 2024. Available online: https://nvlpubs.nist.gov/nistpubs/ai/NIST.AI.100-2e2023.pdf (accessed on 23 March 2025).
- Kurakin, A.; Goodfellow, I.J.; Bengio, S. Adversarial examples in the physical world. In Artificial Intelligence Safety and Security; Chapman and Hall/CRC: Boca Raton, FL, USA, 2018; pp. 99–112. [Google Scholar]
- Dong, Y.; Liao, F.; Pang, T.; Su, H.; Zhu, J.; Hu, X.; Li, J. Boosting adversarial attacks with momentum. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 19–21 June 2018; pp. 9185–9193. [Google Scholar]
- Shi, Y.; Han, Y.; Zhang, Q.; Kuang, X. Adaptive iterative attack towards explainable adversarial robustness. Pattern Recognit. 2020, 105, 107309. [Google Scholar] [CrossRef]
- Mittal, A.; Soundararajan, R.; Bovik, A. Making a “Completely Blind” Image Quality Analyzer. IEEE Signal Process. Lett. 2013, 20, 209–212. [Google Scholar] [CrossRef]
- Madry, A.; Makelov, A.; Schmidt, L.; Tsipras, D.; Vladu, A. Towards Deep Learning Models Resistant to Adversarial Attacks. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Carlini, N.; Wagner, D.A. Towards Evaluating the Robustness of Neural Networks. In Proceedings of the 2017 IEEE Symposium on Security and Privacy (SP), San Jose, CA, USA, 22–24 May 2016; pp. 39–57. [Google Scholar]
- Moosavi-Dezfooli, S.M.; Fawzi, A.; Frossard, P. DeepFool: A Simple and Accurate Method to Fool Deep Neural Networks. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016; pp. 2574–2582. [Google Scholar] [CrossRef]
- Yin, M.; Li, S.; Song, C.; Asif, M.S.; Roy-Chowdhury, A.K.; Krishnamurthy, S.V. ADC: Adversarial attacks against object Detection that evade Context consistency checks. In Proceedings of the 2022 IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 4–8 January 2022; pp. 2836–2845. [Google Scholar] [CrossRef]
- Xue, W.; Xia, X.; Wan, P.; Zhong, P.; Zheng, X. Adversarial Attack on Object Detection via Object Feature-Wise Attention and Perturbation Extraction. Tsinghua Sci. Technol. 2025, 30, 1174–1189. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhu, X.; Li, Y.; Chen, X.; Guo, Y. Adversarial Attacks on Monocular Depth Estimation. arXiv 2020, arXiv:cs.CV/2003.10315. Available online: http://arxiv.org/abs/2003.10315 (accessed on 22 March 2025).
- Kettunen, M.; Härkönen, E.; Lehtinen, J. E-lpips: Robust perceptual image similarity via random transformation ensembles. arXiv 2019, arXiv:1906.03973. [Google Scholar]
- Korhonen, J.; You, J. Adversarial Attacks against Blind Image Quality Assessment Models. In Proceedings of the QoEVMA 2022—Proceedings of the 2nd Workshop on Quality of Experience in Visual Multimedia Applications, Lisboa, Portugal, 14 October 2022. [Google Scholar] [CrossRef]
- Zhang, W.; Li, D.; Min, X.; Zhai, G.; Guo, G.; Yang, X.; Ma, K. Perceptual Attacks of No-Reference Image Quality Models with Human-in-the-Loop. In Proceedings of the Advances in Neural Information Processing Systems, New Orleans, LA, USA, 28 November–9 December 2022. [Google Scholar]
- Moosavi-Dezfooli, S.M.; Fawzi, A.; Fawzi, O.; Frossard, P. Universal Adversarial Perturbations. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 86–94. [Google Scholar] [CrossRef]
- Poursaeed, O.; Katsman, I.; Gao, B.; Belongie, S. Generative adversarial perturbations. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 19–21 June 2018; pp. 4422–4431. [Google Scholar] [CrossRef]
- Dhariwal, P.; Nichol, A. Diffusion models beat GANs on image synthesis. In Proceedings of the 35th International Conference on Neural Information Processing Systems (NIPS ’21), Red Hook, NY, USA, 6–14 December 2021. [Google Scholar]
- Bhattad, A.; Chong, M.J.; Liang, K.; Li, B.; Forsyth, D.A. Unrestricted Adversarial Examples via Semantic Manipulation. In Proceedings of the International Conference on Learning Representations, Virtual Conference, 26 April–1 May 2020. [Google Scholar]
- Alaifari, R.; Alberti, G.S.; Gauksson, T. ADef: An Iterative Algorithm to Construct Adversarial Deformations. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Xiao, C.; Zhu, J.Y.; Li, B.; He, W.; Liu, M.; Song, D. Spatially Transformed Adversarial Examples. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Wang, Z.; Simoncelli, E.P. Maximum differentiation (MAD) competition: A methodology for comparing computational models of perceptual quantities. J. Vis. 2008, 8, 8. [Google Scholar] [CrossRef]
- Ma, K.; Duanmu, Z.; Wang, Z.; Wu, Q.; Liu, W.; Yong, H.; Li, H.; Zhang, L. Group Maximum Differentiation Competition: Model Comparison with Few Samples. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 851–864. [Google Scholar] [CrossRef]
- Shumitskaya, E.; Antsiferova, A.; Vatolin, D. Fast Adversarial Cnn-Based Perturbation Attack on No-Reference Image Quality Metrics. In Proceedings of the First Tiny Papers Track at The Eleventh International Conference on Learning Representations, Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Mohammadi, P.; Ebrahimi-Moghadam, A.; Shirani, S. Subjective and Objective Quality Assessment of Image: A Survey. Majlesi J. Electr. Eng. 2015, 9, 55–83. [Google Scholar]
- Orthogonalization. Encyclopedia of Mathematics. Available online: http://encyclopediaofmath.org/index.php?title=Orthogonalization&oldid=52369 (accessed on 5 February 2025).
- Abello, A.A.; Hirata, R.; Wang, Z. Dissecting the High-Frequency Bias in Convolutional Neural Networks. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Virtual Conference, 19–25 June 2021; pp. 863–871. [Google Scholar] [CrossRef]
- Simonyan, K.; Grishin, S.; Vatolin, D.; Popov, D. Fast video super-resolution via classification. In Proceedings of the 15th IEEE International Conference on Image Processing, San Diego, CA, USA, 12–15 October 2008; pp. 349–352. [Google Scholar] [CrossRef]
- NIPS 2017: Adversarial Learning Development Set. 2017. Available online: https://www.kaggle.com/datasets/google-brain/nips-2017-adversarial-learning-development-set (accessed on 4 October 2024).
- Xiph.org Video Test Media [Derf’s Collection]. 2001. Available online: https://media.xiph.org/video/derf/ (accessed on 5 October 2024).
- Antsiferova, A.; Lavrushkin, S.; Smirnov, M.; Gushchin, A.; Vatolin, D.; Kulikov, D. Video compression dataset and benchmark of learning-based video-quality metrics. In Proceedings of the 36th International Conference on Neural Information Processing Systems, New Orleans, LA, USA, 28 November–9 December 2022; Volume 35, pp. 13814–13825. [Google Scholar]
- Radford, A.; Kim, J.W.; Hallacy, C.; Ramesh, A.; Goh, G.; Agarwal, S.; Sastry, G.; Askell, A.; Mishkin, P.; Clark, J.; et al. Learning Transferable Visual Models From Natural Language Supervision. arXiv 2021, arXiv:cs.CV/2103.00020. Available online: http://arxiv.org/abs/2103.00020 (accessed on 4 May 2025).
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. arXiv 2021, arXiv:cs.CV/2010.11929. Available online: http://arxiv.org/abs/2010.11929 (accessed on 8 June 2025).
- Prashnani, E.; Cai, H.; Mostofi, Y.; Sen, P. PieAPP: Perceptual Image-Error Assessment Through Pairwise Preference. In Proceedings of the The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 19–21 June 2018. [Google Scholar]
- Borisov, A.; Bogatyrev, E.; Kashkarov, E.; Vatolin, D. MSU Video Super-Resolution Quality Metrics Benchmark 2023. 2023. Available online: https://videoprocessing.ai/benchmarks/super-resolution-metrics.html (accessed on 9 June 2025).
- Subjectify.us Platform. Available online: https://www.subjectify.us/ (accessed on 8 June 2025).
- Bradley, R.A.; Terry, M.E. Rank Analysis of Incomplete Block Designs: I. The Method of Paired Comparisons. Biometrika 1952, 39, 324–345. [Google Scholar] [CrossRef]
- Wang, X.; Xie, L.; Dong, C.; Shan, Y. Real-ESRGAN: Training Real-World Blind Super-Resolution with Pure Synthetic Data. Proceeding of the 2021 IEEE/CVF International Conference on Computer Vision Workshops (ICCVW), Montreal, BC, Canada, 11–17 October 2021; pp. 1905–1914. [Google Scholar] [CrossRef]
- Xu, W.; Evans, D.; Qi, Y. Feature Squeezing: Detecting Adversarial Examples in Deep Neural Networks. Proceedings 2018 Network and Distributed System Security Symposium, San Diego, CA, USA, 18–21 February 2018. [Google Scholar] [CrossRef]
- Shin, R. JPEG-resistant Adversarial Images. 2017. Available online: https://machine-learning-and-security.github.io/papers/mlsec17_paper_54.pdf (accessed on 24 January 2025).
- Sanakoyeu, A.; Kotovenko, D.; Lang, S.; Ommer, B. A Style-Aware Content Loss for Real-time HD Style Transfer. In Proceedings of the 15th European Conference, Munich, Germany, 8–14 September 2018; Proceedings, Part VIII. pp. 715–731. [Google Scholar]
- Xu, X.; Liu, H.; Yao, M. Recent Progress of Anomaly Detection. Complexity 2019, 2019, 2686378. [Google Scholar] [CrossRef]
- Gushchin, A.; Abud, K.; Bychkov, G.; Shumitskaya, E.; Chistyakova, A.; Lavrushkin, S.; Rasheed, B.; Malyshev, K.; Vatolin, D.; Antsiferova, A. Guardians of Image Quality: Benchmarking Defenses Against Adversarial Attacks on Image Quality Metrics. arXiv 2024, arXiv:cs.CV/2408.01541. Available online: http://arxiv.org/abs/2408.01541 (accessed on 8 June 2025).
- Templeton, A.; Conerly, T.; Marcus, J.; Lindsey, J.; Bricken, T.; Chen, B.; Pearce, A.; Citro, C.; Ameisen, E.; Jones, A.; et al. Scaling Monosemanticity: Extracting Interpretable Features from Claude 3 Sonnet. Transform. Circuits Thread, 21 May 2024. Available online: https://transformer-circuits.pub/2024/scaling-monosemanticity/ (accessed on 12 April 2025).
- Lim, H.; Choi, J.; Choo, J.; Schneider, S. Sparse autoencoders reveal selective remapping of visual concepts during adaptation. In Proceedings of the Thirteenth International Conference on Learning Representations, Singapore, 24–28 April 2025. [Google Scholar]
- Kim, D.; Thomas, X.; Ghadiyaram, D. Revelio: Interpreting and leveraging semantic information in diffusion models. arXiv 2024, arXiv:cs.CV/2411.16725. Available online: http://arxiv.org/abs/2411.16725 (accessed on 24 January 2024).






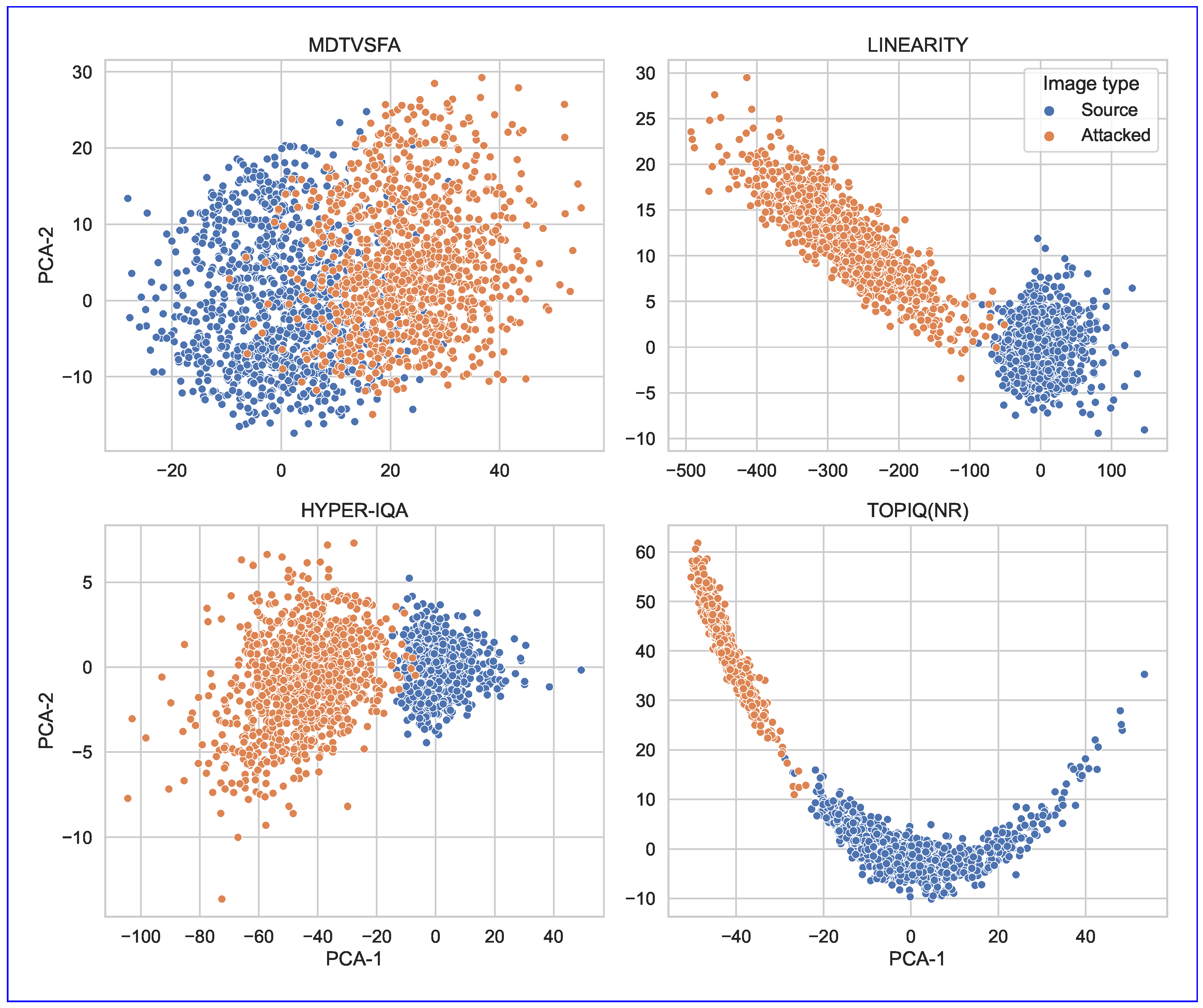
| FM-GOAT vs. | Korhonen et al. [54] | IFGSM [43] | Zhang et al. [55] | StAdv [61] | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Target Model | SSIM | LPIPS | DISTS | PIEAPP | SSIM | LPIPS | DISTS | PIEAPP | SSIM | LPIPS | DISTS | PIEAPP | SSIM | LPIPS | DISTS | PIEAPP | |
| TReS | 93.90% | 87.30% | 62.10% | 72.30% | 100.00% | 98.30% | 99.80% | 96.00% | 97.00% | 76.70% | 4.10% | 74.80% | 100.00% | 100.00% | 99.90% | 88.20% | |
| Hyper-IQA | 84.80% | 76.10% | 51.60% | 53.20% | 100.00% | 99.90% | 100.00% | 99.80% | 93.10% | 64.70% | 9.10% | 57.50% | 99.80% | 100.00% | 99.80% | 88.50% | |
| PAQ-2-PIQ | 98.00% | 95.80% | 56.70% | 66.00% | 100.00% | 83.10% | 84.40% | 76.60% | 100.00% | 96.40% | 49.10% | 75.10% | 100.00% | 98.60% | 98.60% | 84.00% | |
| MDTVSFA | 84.40% | 73.10% | 38.90% | 56.40% | 100.00% | 100.00% | 99.80% | 99.50% | 94.80% | 65.10% | 3.40% | 67.10% | 99.80% | 100.00% | 99.90% | 75.70% | |
| Linearity | 81.70% | 72.50% | 38.50% | 50.20% | 100.00% | 99.80% | 99.80% | 99.50% | 89.80% | 57.90% | 0.70% | 51.20% | 99.60% | 99.90% | 99.70% | 76.50% | |
| TOPIQ (NR) | 93.40% | 80.70% | 52.50% | 62.80% | 100.00% | 99.90% | 99.90% | 99.70% | 98.50% | 72.60% | 6.80% | 77.70% | 99.90% | 100.00% | 99.90% | 73.80% | |
| CLIPIQA+ | 98.40% | 85.00% | 80.10% | 83.00% | 100.00% | 99.90% | 100.00% | 99.70% | 99.40% | 88.00% | 34.60% | 90.70% | 97.70% | 98.40% | 96.70% | 74.00% | |
| FM-GOAT vs. | Korhonen et al. [54] | IFGSM [43] | Zhang et al. [55] | StAdv [61] | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Target Model | SSIM | LPIPS | DISTS | PIEAPP | SSIM | LPIPS | DISTS | PIEAPP | SSIM | LPIPS | DISTS | PIEAPP | SSIM | LPIPS | DISTS | PIEAPP | |
| TReS | 85.53% (±7.55%) | 41.29% (±5.40%) | 11.92% (±6.41%) | 51.63% (±8.98%) | 360.46% (±57.15%) | 173.91% (±40.96%) | 204.79% (±35.97%) | 192.14% (±35.49%) | 139.15% (±15.91%) | 40.03% (±5.88%) | −80.38% (±12.47%) | 68.51% (±9.56%) | 415.50% (±57.03%) | 389.97% (±53.61%) | 391.46% (±53.30%) | 232.51% (±38.29%) | |
| Hyper-IQA | 4.47% (±0.15%) | 2.56% (±0.15%) | 0.05% (±0.14%) | 0.58% (±0.16%) | 31.73% (±0.37%) | 25.49% (±0.35%) | 27.95% (±0.34%) | 26.40% (±0.34%) | 6.83% (±0.16%) | 1.27% (±0.15%) | −6.48% (±0.17%) | 0.88% (±0.16%) | 25.73% (±0.27%) | 24.71% (±0.29%) | 25.38% (±0.29%) | 16.57% (±0.31%) | |
| PAQ-2-PIQ | 2.24% (±0.05%) | 1.93% (±0.04%) | 0.26% (±0.04%) | 0.75% (±0.05%) | 4.58% (±0.14%) | 3.56% (±0.12%) | 3.85% (±0.12%) | 2.56% (±0.11%) | 5.55% (±0.06%) | 2.25% (±0.04%) | 0.12% (±0.06%) | 1.54% (±0.08%) | 10.77% (±0.16%) | 10.22% (±0.14%) | 9.73% (±0.13%) | 6.20% (±0.16%) | |
| MDTVSFA | 1.76% (±0.07%) | 0.83% (±0.06%) | −0.64% (±0.07%) | 0.44% (±0.08%) | 6.39% (±0.09%) | 5.77% (±0.09%) | 5.90% (±0.09%) | 5.77% (±0.09%) | 2.64% (±0.06%) | 0.45% (±0.06%) | −3.83% (±0.11%) | 0.91% (±0.07%) | 7.05% (±0.10%) | 6.99% (±0.11%) | 6.77% (±0.11%) | 4.55% (±0.12%) | |
| Linearity | 5.91% (±0.21%) | 3.15% (±0.19%) | −1.20% (±0.16%) | 0.96% (±0.22%) | 41.27% (±0.37%) | 30.94% (±0.39%) | 31.94% (±0.35%) | 32.06% (±0.38%) | 8.19% (±0.21%) | 1.07% (±0.20%) | −12.51% (±0.20%) | 1.26% (±0.23%) | 37.24% (±0.37%) | 37.91% (±0.35%) | 36.54% (±0.36%) | 23.45% (±0.50%) | |
| TOPIQ (NR) | 3.74% (±0.12%) | 2.33% (±0.12%) | 0.39% (±0.10%) | 2.37% (±0.18%) | 15.73% (±0.28%) | 13.72% (±0.26%) | 14.00% (±0.25%) | 14.04% (±0.25%) | 5.12% (±0.12%) | 1.84% (±0.11%) | −4.95% (±0.18%) | 3.31% (±0.17%) | 14.80% (±0.24%) | 16.16% (±0.29%) | 15.39% (±0.26%) | 11.87% (±0.34%) | |
| CLIPIQA+ | 5.43% (±0.15%) | 3.81% (±0.16%) | 3.04% (±0.15%) | 3.65% (±0.17%) | 13.28% (±0.34%) | 12.98% (±0.34%) | 13.08% (±0.33%) | 12.93% (±0.33%) | 5.70% (±0.15%) | 3.97% (±0.16%) | −0.12% (±0.20%) | 4.18% (±0.16%) | 21.04% (±0.50%) | 21.30% (±0.51%) | 20.95% (±0.51%) | 19.52% (±0.57%) | |
| Constraint Score | SSIM ≥ 0.99 | LPIPS ≤ 0.01 | DISTS ≤ 0.01 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Target Model | Abs. Gain↓ | Rscore↑ | SROCC↑ (Attacked) | Abs. Gain↓ | Rscore↑ | SROCC↑ (Attacked) | Abs. Gain↓ | Rscore↑ | SROCC↑ (Attacked) | |
| TReS | 65.04 ± 0.45% | −0.640 | 0.557 | 58.31 ± 0.37% | −0.593 | 0.706 | 30.08 ± 0.34% | −0.286 | 0.833 | |
| Hyper-IQA | 29.12 ± 0.20% | 0.399 | 0.550 | 27.96 ± 0.21% | 0.418 | 0.534 | 17.87 ± 0.18% | 0.622 | 0.695 | |
| PAQ-2-PIQ | 14.64 ± 0.11% | 0.724 | 0.457 | 12.93 ± 0.08% | 0.774 | 0.693 | 6.71 ± 0.06% | 1.072 | 0.842 | |
| MDTVSFA | 14.90 ± 0.12% | 0.603 | 0.353 | 14.83 ± 0.11% | 0.605 | 0.390 | 11.16 ± 0.11% | 0.734 | 0.595 | |
| Linearity | 39.79 ± 0.26% | 0.271 | 0.596 | 40.00 ± 0.26% | 0.268 | 0.617 | 21.42 ± 0.18% | 0.550 | 0.822 | |
| TOPIQ(NR) | 24.76 ± 0.21% | 0.459 | 0.703 | 25.54 ± 0.22% | 0.446 | 0.657 | 18.57 ± 0.16% | 0.588 | 0.763 | |
| CLIPIQA+ | 32.04 ± 0.31% | 0.344 | 0.388 | 32.08 ± 0.31% | 0.343 | 0.355 | 30.21 ± 0.30% | 0.371 | 0.417 | |
| Attack Score | Default Attack | + Flip | + Gaussian blur | + Rotate | + DiffJPEG(q = 50) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Defense | Abs. Gain↓ | SROCC↑ (Attacked) | SROCC↑ (Clear) | Abs. Gain↓ | SROCC↑ (Attacked) | Abs. Gain↓ | SROCC↑ (Attacked) | Abs. Gain↓ | SROCC↑ (Attacked) | Abs. Gain↓ | SROCC↑ (Attacked) | |
| W/o defense | 23.86 ± 0.27% | 0.343 | — | 20.16 ± 0.25% | 0.443 | 19.25 ± 0.24% | 0.527 | 20.99 ± 0.25% | 0.452 | 19.31 ± 0.25% | 0.491 | |
| Flip | 5.80 ± 0.15% | 0.785 | 0.909 | 22.10 ± 0.25% | 0.421 | 4.56 ± 0.12% | 0.838 | 6.94 ± 0.17% | 0.741 | 3.95 ± 0.11% | 0.842 | |
| JPEG (q = 50) | 3.16 ± 0.08% | 0.746 | 0.805 | 2.70 ± 0.06% | 0.769 | 4.11 ± 0.08% | 0.763 | 4.04 ± 0.09% | 0.739 | 2.72 ± 0.06% | 0.778 | |
| JPEG (q = 75) | 6.36 ± 0.13% | 0.788 | 0.899 | 5.23 ± 0.11% | 0.821 | 5.87 ± 0.11% | 0.829 | 7.27 ± 0.15% | 0.754 | 4.40 ± 0.09% | 0.847 | |
| Random rotate | 5.26 ± 0.20% | 0.678 | 0.891 | 4.80 ± 0.18% | 0.701 | 4.37 ± 0.18% | 0.718 | 9.30 ± 0.22% | 0.569 | 4.06 ± 0.19% | 0.718 | |
| Gaussian blur | 3.02 ± 0.07% | 0.392 | 0.524 | 2.52 ± 0.06% | 0.425 | 18.81 ± 0.21% | 0.326 | 3.61 ± 0.08% | 0.384 | 3.16 ± 0.07% | 0.418 | |
| Score | SSIM ↑ | LPIPS | DISTS | PIEAPP | Abs. Gain, % ↑ | |
|---|---|---|---|---|---|---|
| Constraints | ||||||
| Baseline (w/o constraints and mask) | 84.601 | 13.485 | 15.586 | 67.656 | 97.858 | |
| Baseline (w/o constraints) | 99.624 | 0.351 | 2.805 | 10.199 | 38.090 | |
| 99.756 (0.13%) | 0.191 (−45.49%) | 2.064 (−26.41%) | 7.391 (−27.53%) | 33.734 (−11.44%) | ||
| SSIM | 99.799 (0.18%) | 0.247 (−29.72%) | 2.168 (−22.71%) | 8.113 (−20.45%) | 33.577 (−11.85%) | |
| LPIPS | 99.633 (0.01%) | 0.168 (−52.21%) | 2.630 (−6.23%) | 9.522 (−6.64%) | 37.654 (−1.14%) | |
| SSIM, | 99.804 (0.18%) | 0.204 (−41.99%) | 2.009 (−28.37%) | 7.401 (−27.44%) | 32.714 (−14.11%) | |
| LPIPS, SSIM, | 99.803 (0.18%) | 0.162 (−53.79%) | 1.962 (−30.05%) | 7.178 (−29.62%) | 32.582 (−14.46%) | |
| DISTS, SSIM, | 99.801 (0.18%) | 0.213 (−39.42%) | 2.036 (−27.43%) | 7.610 (−25.38%) | 32.988 (−13.39%) | |
| PIEAPP, SSIM, | 99.804 (0.18%) | 0.204 (−41.91%) | 1.997 (−28.80%) | 7.906 (−22.48%) | 32.715 (−14.11%) | |
| DISTS, LPIPS, SSIM, | 99.801 (0.18%) | 0.165 (−52.86%) | 1.980 (−29.40%) | 7.338 (−28.05%) | 32.814 (−13.85%) | |
| DISTS, PIEAPP, LPIPS, SSIM, | 99.802 (0.18%) | 0.164 (−53.33%) | 1.977 (−29.51%) | 7.798 (−23.54%) | 32.793 (−13.91%) | |
| Score | Abs. Gain ↑ | SSIM ↑ | LPIPS ↓ | DISTS ↓ | Time, s/Frame ↓ | |
|---|---|---|---|---|---|---|
| Propagation Type | ||||||
| All frames attacked | 18.118 % (±5.420%) | 0.980 (±0.009) | 0.020 (±0.023) | 0.046 (±0.042) | 1.652 (±0.010) | |
| Interpolation + motion comp (proposed) | 5.641 % (±4.110%) | 0.982 (±0.009) | 0.011 (±0.014) | 0.026 (±0.033) | 0.580 (±0.049) | |
| Repeat + motion comp | 4.728 % (±4.128%) | 0.983 (±0.008) | 0.009 (±0.012) | 0.023 (±0.032) | 0.374 (±0.018) | |
| Only n-th frames attacked | 1.531 % (±1.789%) | 0.986 (±0.007) | 0.004 (±0.009) | 0.010 (±0.019) | 0.158 (±0.004) | |
| Repeat | 5.106 % (±4.821%) | 0.977 (±0.010) | 0.022 (±0.024) | 0.036 (±0.043) | 0.273 (±0.002) | |
| Interpolation | 5.219 % (±4.681%) | 0.979 (±0.009) | 0.016 (±0.019) | 0.033 (±0.042) | 0.314 (±0.003) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abud, K.; Lavrushkin, S.; Vatolin, D. Evaluating Adversarial Robustness of No-Reference Image and Video Quality Assessment Models with Frequency-Masked Gradient Orthogonalization Adversarial Attack. Big Data Cogn. Comput. 2025, 9, 166. https://doi.org/10.3390/bdcc9070166
Abud K, Lavrushkin S, Vatolin D. Evaluating Adversarial Robustness of No-Reference Image and Video Quality Assessment Models with Frequency-Masked Gradient Orthogonalization Adversarial Attack. Big Data and Cognitive Computing. 2025; 9(7):166. https://doi.org/10.3390/bdcc9070166
Chicago/Turabian StyleAbud, Khaled, Sergey Lavrushkin, and Dmitry Vatolin. 2025. "Evaluating Adversarial Robustness of No-Reference Image and Video Quality Assessment Models with Frequency-Masked Gradient Orthogonalization Adversarial Attack" Big Data and Cognitive Computing 9, no. 7: 166. https://doi.org/10.3390/bdcc9070166
APA StyleAbud, K., Lavrushkin, S., & Vatolin, D. (2025). Evaluating Adversarial Robustness of No-Reference Image and Video Quality Assessment Models with Frequency-Masked Gradient Orthogonalization Adversarial Attack. Big Data and Cognitive Computing, 9(7), 166. https://doi.org/10.3390/bdcc9070166







