Ship Typhoon Avoidance Route Planning Method Under Uncertain Typhoon Forecasts
Abstract
1. Introduction
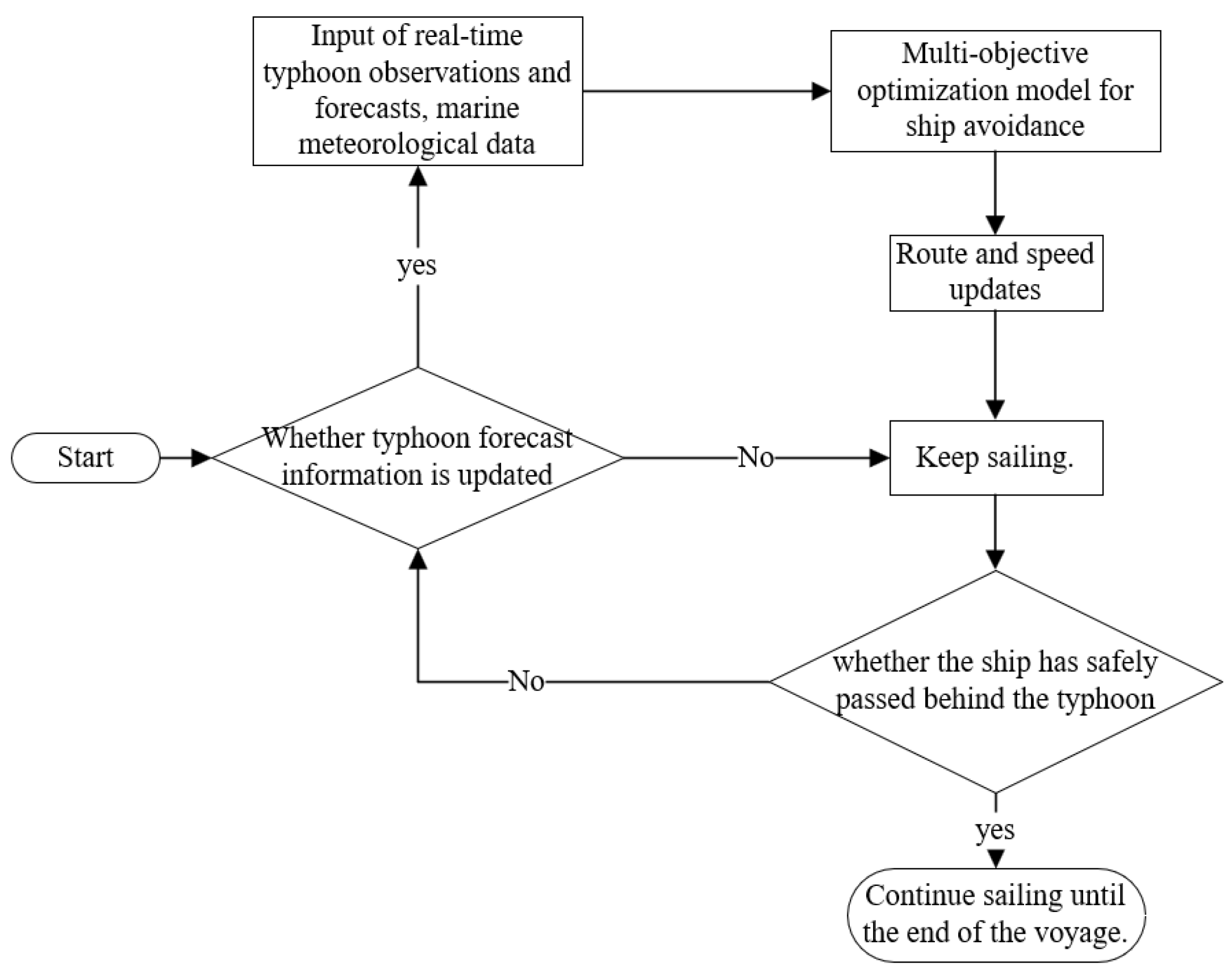
2. Problem Description
3. Probability Model for Ships Encountering Typhoons
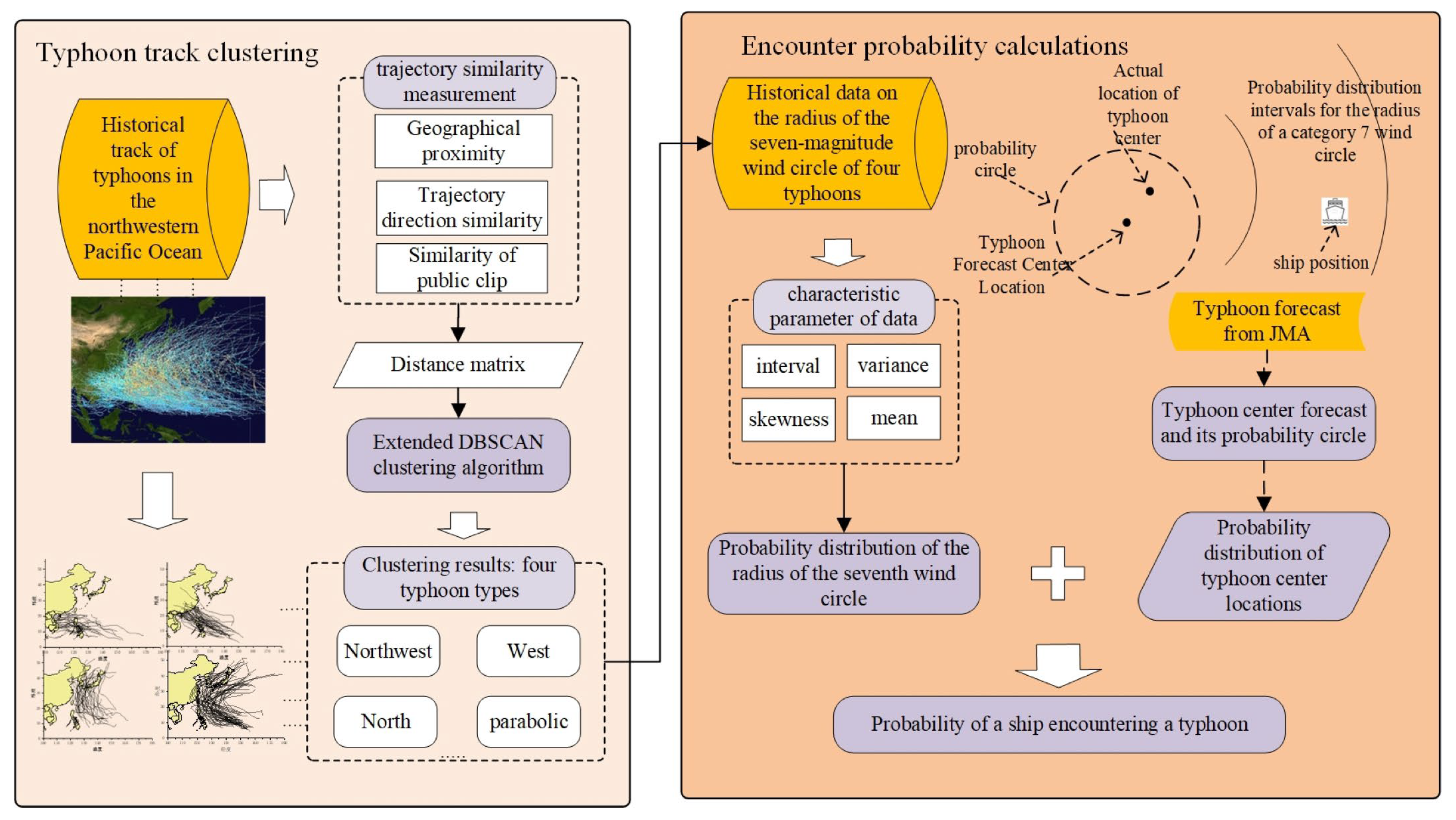
3.1. Typhoon Track Clustering
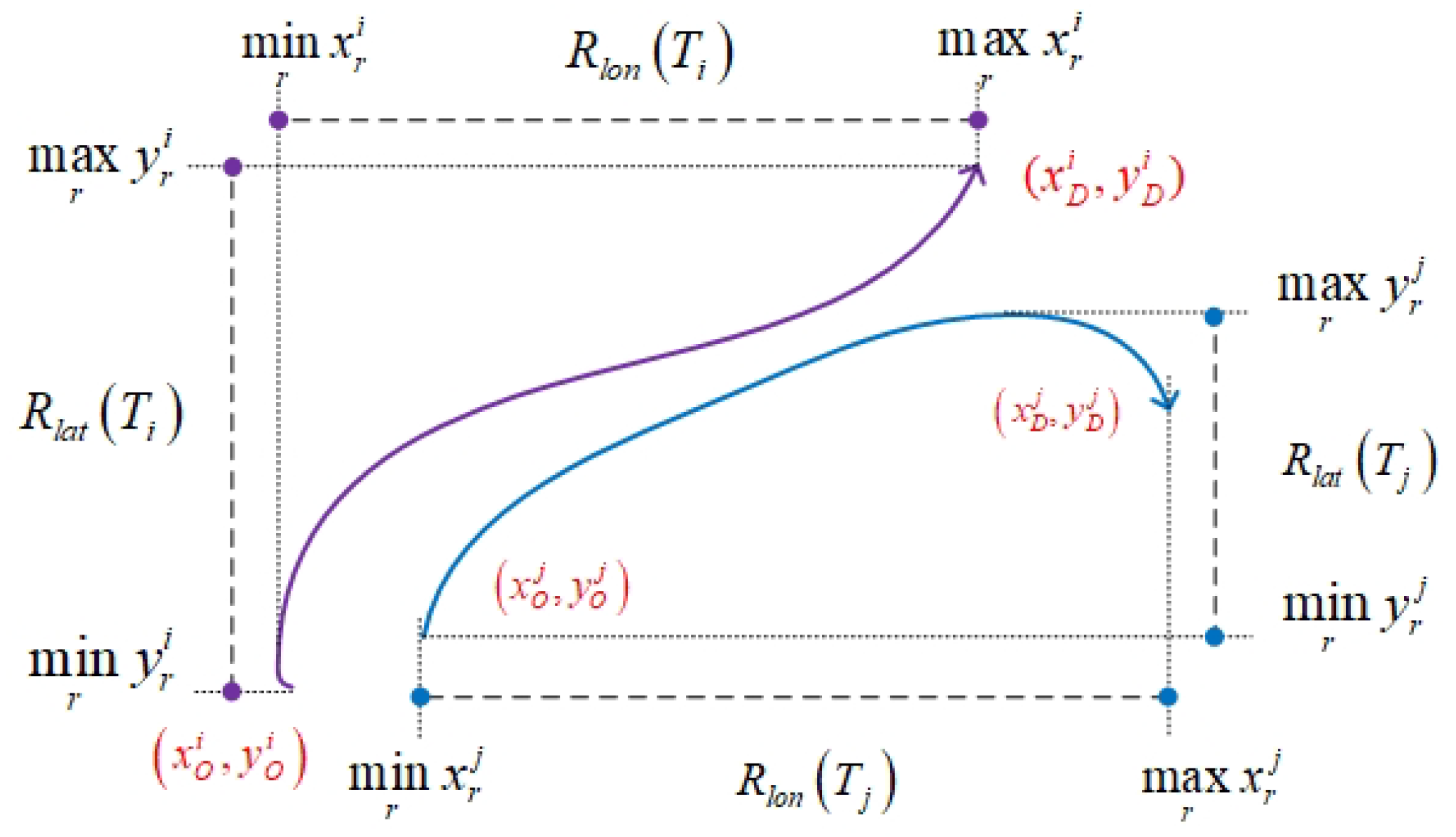
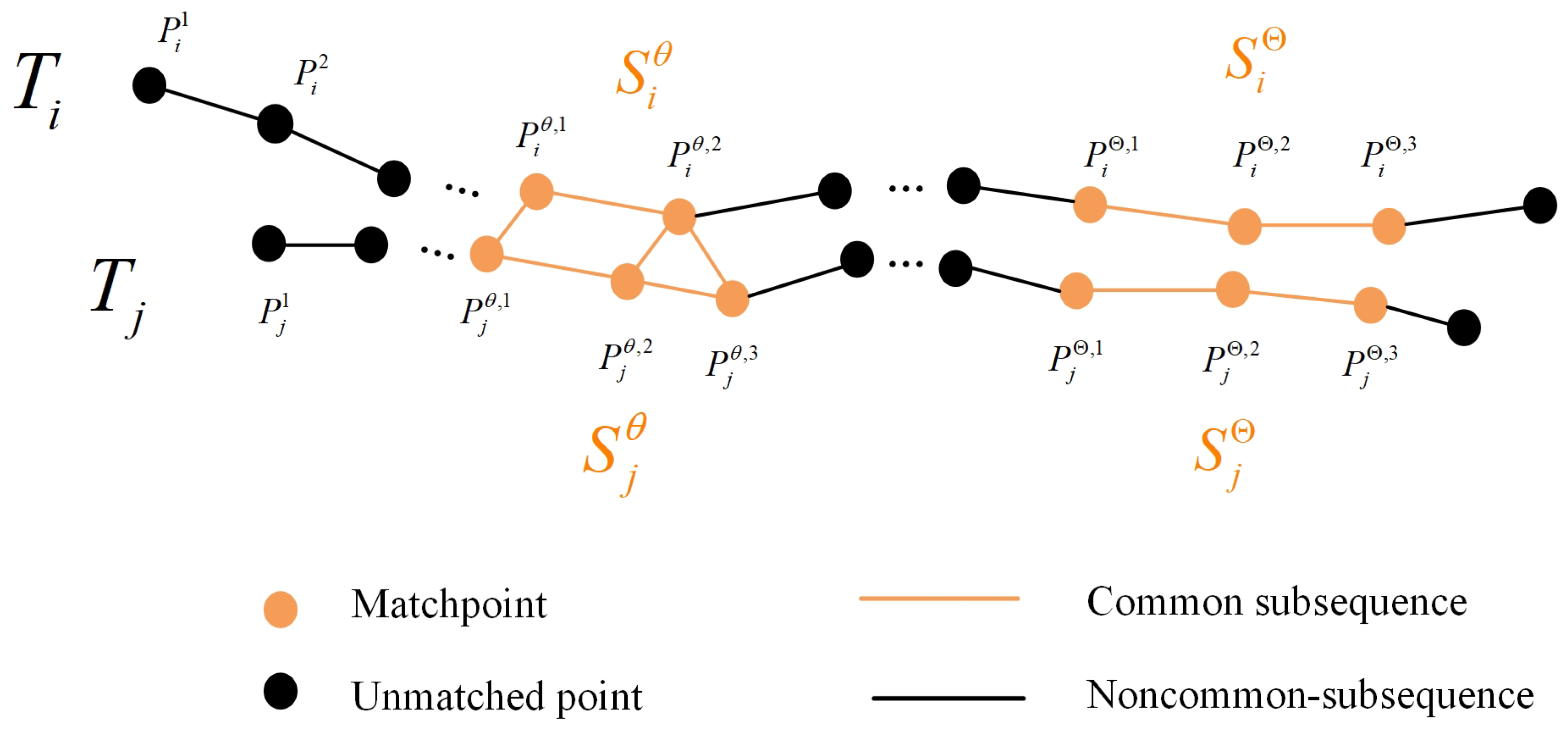
3.1.1. Trajectory Similarity Measurement
- (1)
- Geographical proximity
- (2)
- Trajectory direction similarity
- (3)
- Trajectory public segment similarity
3.1.2. Trajectory Clustering Extension to the DBSCAN Clustering Algorithm
- (1)
- The integrated domain of the trajectory is defined as follows:
- (2)
- On direct density reachability
- (3)
- Density up to
- (4)
- Density linked
| Algorithm 1 DBSCAN algorithm for fusing multi-featured trajectory similarity | |||
| Input: Trajectory clustering set ; Distance matrix ; Clustering parameter | |||
| Output: Cluster , and, | |||
| 1 set C //Initialization | |||
| 2 set all trajutories in as unvisited | |||
| 3 | if is not visited then | ||
| 4 | set as visited | ||
| 5 | get using | ||
| 6 | if then | ||
| 7 | set as noise | ||
| 8 | else | ||
| 9 | C C //Next cluster number | ||
| 10 | assign C to all trajectories in | ||
| 11 | insert into queue N | ||
| 12 | call | ||
| 13 | return C | ||
| 14 | |||
| 15 | while N is not empty, do | ||
| 16 | remove from top of the N | ||
| 17 | get using | ||
| 18 | if then | ||
| 19 | for in do | ||
| 20 | if is visited or noise then | ||
| 21 | assign C to | ||
| 22 | if is not visited then | ||
| 23 | insert into N | ||
3.1.3. Quality Assessment of Trajectory Clustering
3.1.4. Typhoon Cluster Results
3.2. Calculation of the Probability of a Ship Encountering a Typhoon
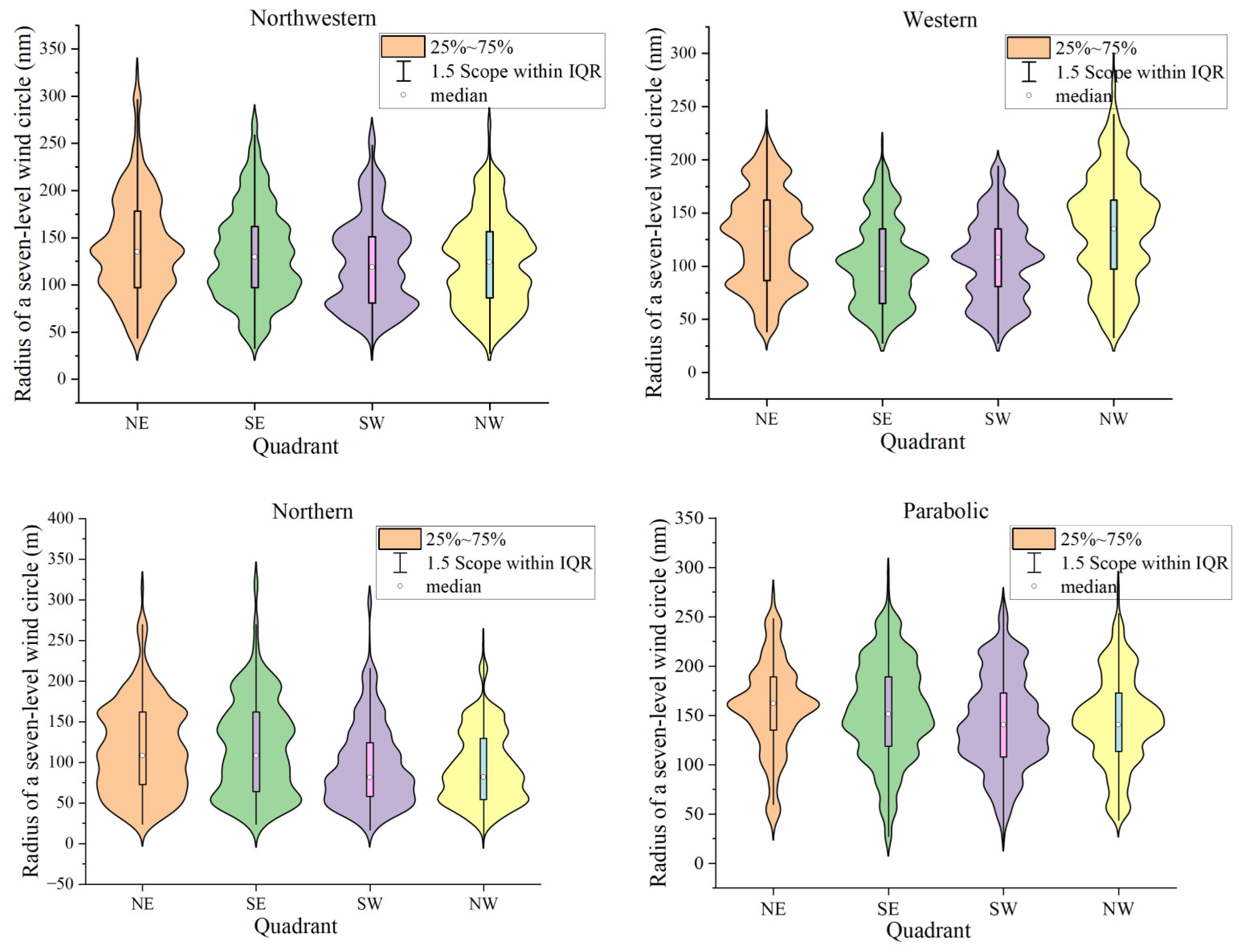
3.2.1. Probability Distribution of the Radius of the Seventh Wind Circle
3.2.2. Representation of Typhoon Center Location Probability
3.2.3. Calculation of the Conditional Probability of a Ship Encountering a Force 7 Wind Circle
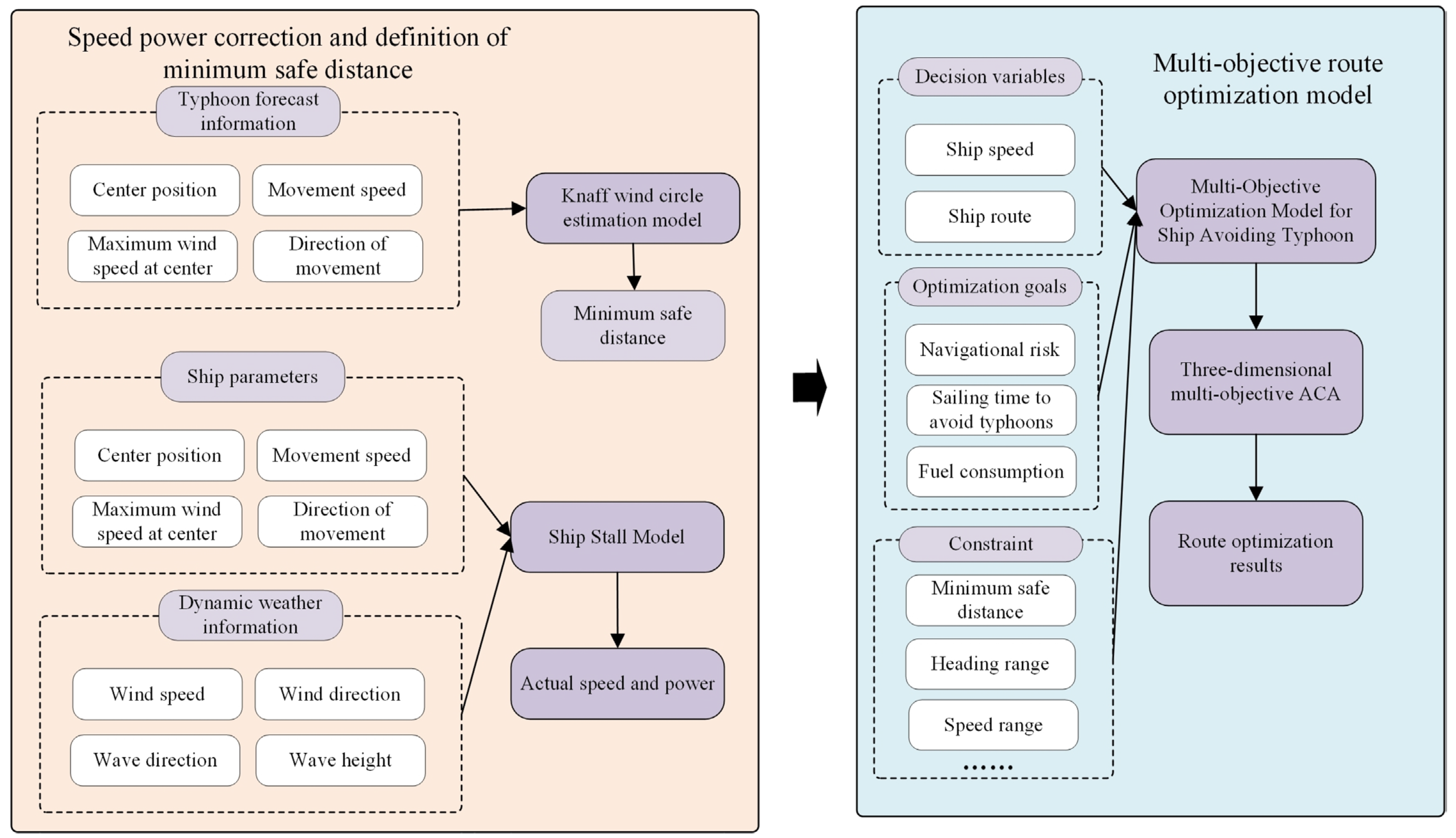
4. Optimization Methods and Models for Avoiding Platform Routes
4.1. Quantification of Minimum Safety Distances
4.2. Judgment Method for Whether a Ship Should Take Evasive Action
4.3. Ship Route Optimization Model for Avoiding Typhoons
4.3.1. Model Parameter Definition
4.3.2. Model Variable
4.3.3. Optimization Objectives
- (1)
- Sailing Time for Avoiding Typhoon
- (2)
- Fuel consumption
- (3)
- Typhoon risk to ships
4.3.4. Multi-Objective Optimization Modeling of Ship Avoidance Routes
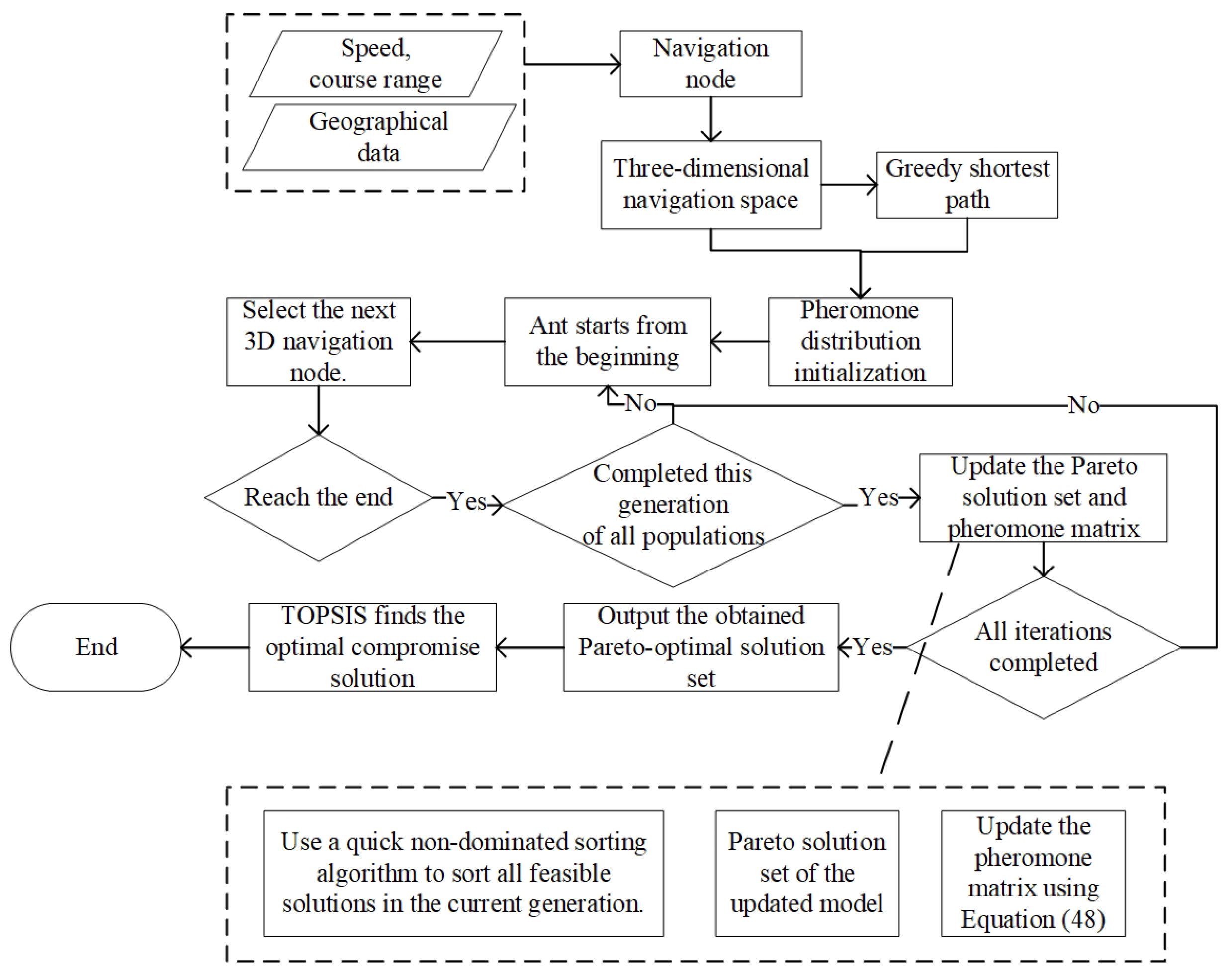
5. Solving Algorithm Design
5.1. Three-Dimensional Discretization of the Ship’s Navigation Space
5.2. Principles of Classical Ant Colony Algorithm
5.3. Three-Dimensional Discretization of the Ship’s Navigation Space
- (1)
- Greedy algorithm initializes pheromone distribution
- (2)
- Elite Strategy
5.4. Multi-Objective Ant Colony Algorithm Search Strategy
- (1)
- Comparison of feasible solutions based on fast nondominated sorting algorithms
- (2)
- Pheromone update based on nondominated ranking weights
- (3)
- TOPSIS for compromise optimal solution
- 1.
- Raw matrix normalization:
- 2.
- Obtain the solution vector after the virtual solution normalization:
- 3.
- Calculate the distance between the distance virtual solutions separately:
- 4.
- Calculate the distance between the distance virtual solutions separately:
6. Case Study
6.1. Background of the Example
6.1.1. Parameter Selection for Simulation Experiments
6.1.2. Typhoon Forecasting and Meteorological Data Acquisition
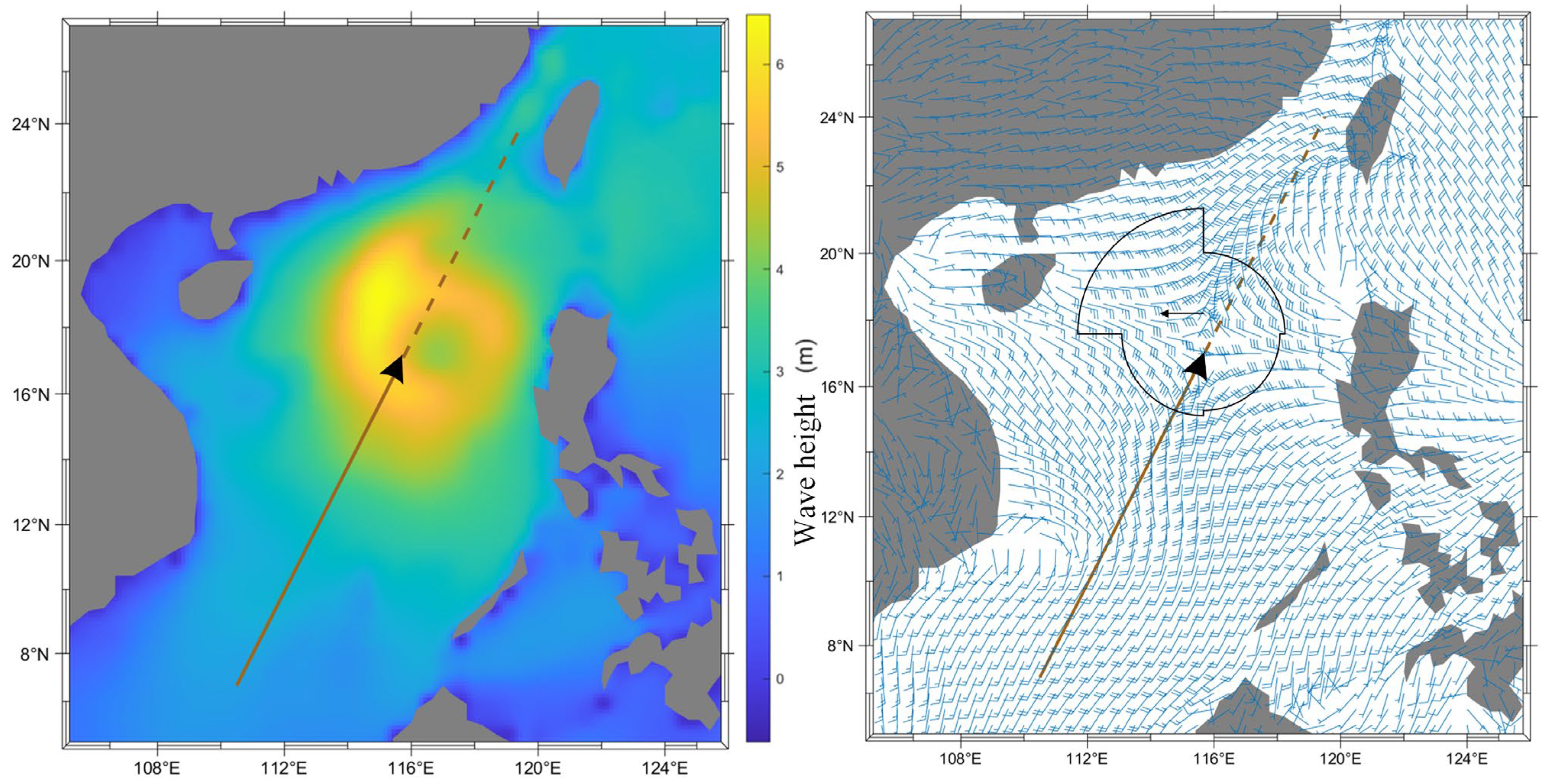
6.1.3. Planned Route Simulation Results
6.2. Design and Analysis of Platform Avoidance Routes
6.2.1. Design of Avoidance Routes
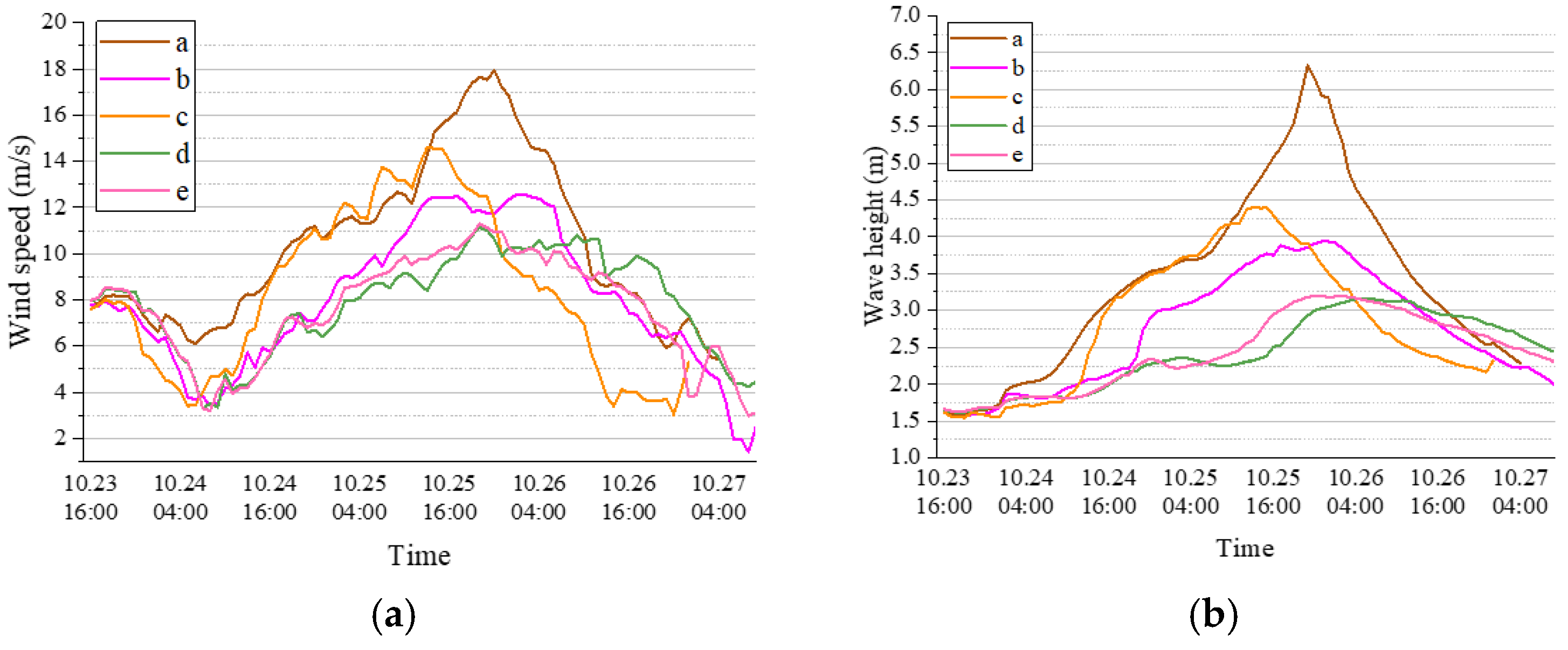
6.2.2. Analysis of Wind and Wave Results of the Typhoon Avoidance Route
6.2.3. Exhaust Emission Assessment
6.3. Comparison of the Effect of Improved Algorithms
6.4. Model Sensitivity Analysis
7. Conclusions
- (1)
- Refining the encounter scenario analysis and model construction: Systematically analyze the various encounter scenarios that may occur between the ship and the typhoon, such as face-to-face encounter, small-angle crossing, large-angle crossing, etc., and construct the decision-making model of avoiding the typhoon for the different encounter modes so as to enhance the adaptability and effectiveness of the avoidance solution.
- (2)
- Enhancing the scalability and adaptability of the model: Explore the extended application of the platform avoidance model in complex scenarios, such as large-scale multi-vessel collaborative path planning, platform avoidance strategies under double typhoon systems, etc., so as to enhance the applicability of the model in dynamic marine environments.
- (3)
- Integration of data-driven and intelligent methods: Introduce advanced data-driven techniques, such as deep learning, to adaptively optimize key parameters, such as the probability distribution function of typhoon tracks, to improve the model’s prediction accuracy and generalization ability under different meteorological conditions.
- (4)
- Exploring real-time applications through satellite data integration: Future work could incorporate satellite remote sensing, AIS vessel tracking, and real-time meteorological datasets to transform the current offline optimization approach into a real-time, adaptive decision-support system, greatly enhancing its value in operational maritime navigation.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Typhoon Type | Interval (a, b) | NE | SE | SW | NW |
|---|---|---|---|---|---|
| Northwestern | a | 43.19 | 32.39 | 26.99 | 26.99 |
| b | 323.97 | 269.97 | 259.18 | 269.97 | |
| western | a | 37.79 | 26.99 | 26.99 | 32.39 |
| b | 242.98 | 215.98 | 194.38 | 296.98 | |
| Northern | a | 23.32 | 23.32 | 21.59 | 26.23 |
| b | 269.97 | 269.97 | 215.98 | 215.98 | |
| parabolic | a | 32.39 | 43.19 | 26.99 | 26.99 |
| b | 242.98 | 242.98 | 215.98 | 269.97 |
| Typhoon Type | Value | NE | SE | SW | NW |
|---|---|---|---|---|---|
| Northwestern western | 0.68 | 0.53 | 0.53 | 0.36 | |
| 141.04 | 132.35 | 123.15 | 124.21 | ||
| 54.13 | 50.06 | 47.67 | 47.36 | ||
| Northern | 00.01 | 0.37 | 0.17 | 0.11 | |
| 126.57 | 102.80 | 104.92 | 135.55 | ||
| 43.98 | 39.36 | 38.58 | 50.80 | ||
| parabolic typhoon type | 0.54 | 0.57 | 1.02 | 0.72 | |
| 116.43 | 117.64 | 95.78 | 93.25 | ||
| 55.42 | 59.15 | 50.26 | 44.57 | ||
| Northwestern | −0.24 | 0.49 | 0.53 | 0.57 | |
| 128.48 | 132.17 | 109.44 | 114.67 | ||
| 48.89 | 52.52 | 49.09 | 56.33 |
References
- Jewson, S. Tropical Cyclones and Climate Change: Global Landfall Frequency Projections Derived from Knutson et al. Bull. Am. Meteorol. Soc. 2023, 104, E1085–E1104. [Google Scholar] [CrossRef]
- Shen, Z.; Xu, X.; Li, J.; Wang, S. Vulnerability of the maritime network to tropical cyclones in the northwest pacific and the northern indian ocean. Sustainability 2019, 11, 6176. [Google Scholar] [CrossRef]
- Ningsih, N.S.; Azhari, A.; Al-Khan, T.M. Wave climate characteristics and effects of tropical cyclones on high wave occurrences in Indonesian waters: Strengthening sea transportation safety management. Ocean. Coast. Manag. 2023, 243, 106738. [Google Scholar] [CrossRef]
- Szlapczynska, J. Multi-objective weather routing with customised criteria and constraints. J. Navig. 2015, 68, 338–354. [Google Scholar] [CrossRef]
- Wang, H.; Mao, W.; Eriksson, L. A Three-Dimensional Dijkstra’s algorithm for multi-objective ship voyage optimization. Ocean. Eng. 2019, 186, 106131. [Google Scholar] [CrossRef]
- Chen, A.; Chen, W.; Zheng, J. Arctic Route Planning and Navigation Strategy: The Perspective of Ship Fuel Costs and Carbon Emissions. J. Mar. Sci. Eng. 2023, 11, 1308. [Google Scholar] [CrossRef]
- Ma, D.; Ma, W.; Jin, S.; Ma, X. Method for simultaneously optimizing ship route and speed with emission control areas. Ocean. Eng. 2020, 202, 107170. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, H.; Zhao, W.; Guan, Z.; Li, P. Application of improved multi-objective ant colony optimization algorithm in ship weather routing. J. Ocean. Univ. China 2021, 20, 45–55. [Google Scholar] [CrossRef]
- Li, Y.; Cui, J.; Zhang, X.; Yang, X. A ship route planning method under the sailing time constraint. J. Mar. Sci. Eng. 2023, 11, 1242. [Google Scholar] [CrossRef]
- Zaccone, R.; Ottaviani, E.; Figari, M.; Altosole, M. Ship voyage optimization for safe and energy-efficient navigation: A dynamic programming approach. Ocean. Eng. 2018, 153, 215–224. [Google Scholar] [CrossRef]
- Bijlsma, S.J. On the applications of the principle of optimal evolution in ship routing. Navigation 2004, 51, 93–100. [Google Scholar] [CrossRef]
- Zhang, L.H.; Zhu, Q.; Liu, Y.C.; Li, S.J. A method for automatic routing based on ECDIS. J. Dalian Marit. Univ. 2007, 33, 109–112. [Google Scholar]
- Sasa, K.; Chen, C.; Fujimatsu, T.; Shoji, R.; Maki, A. Speed loss analysis and rough wave avoidance algorithms for optimal ship routing simulation of 28,000-DWT bulk carrier. Ocean. Eng. 2021, 228, 108800. [Google Scholar] [CrossRef]
- Lee, J.S.; Kim, T.H.; Park, Y.G. Maritime Transport Network in Korea: Spatial-Temporal Density and Path Planning. J. Mar. Sci. Eng. 2023, 11, 2364. [Google Scholar] [CrossRef]
- Wu, L.; Wen, Y.; Wu, D.; Zhang, J.; Xiao, C. Safe-economical route model of a ship to avoid tropical cyclones using dynamic forecast environment. Nat. Hazards Earth Syst. Sci. Discuss. 2014, 2, 4907–4945. [Google Scholar]
- Wu, L.; Wen, Y.; Peng, S.; Zhang, J.; Xiao, C. Optimizing the routing of ship’s tropical cyclone avoidance based on the numerical forecasts. Nat. Hazards 2013, 69, 781–792. [Google Scholar] [CrossRef]
- Wu, L.C.; Wen, Y.Q.; Wu, D.Y. Safe-economical route and its assessment model of a ship to avoid tropical cyclones using dynamic forecast environment. Nat. Hazards Earth Syst. Sci. Discuss. 2013, 1, 1857–1893. [Google Scholar]
- Xiao, Y.; Huang, Y.; Zhang, Y.; Wang, H. Local weather routing in avoidance of adverse sea conditions based on reachability theory. Ocean. Eng. 2025, 315, 119834. [Google Scholar] [CrossRef]
- Huang, Y.; Ding, X.; Zhang, Y.; Yan, L. T_GRASP: Optimization Algorithm of Ship Avoiding Typhoon Route. J. Quantum Comput. 2022, 4, 85–95. [Google Scholar] [CrossRef]
- Lee, J.-S.; Kim, M.-K.; Kim, B.-R.; Kim, T.-K.; Lee, C.-Y.; Park, Y.-G. Spatial-temporal big data analysis of ship avoidance patterns during typhoon approaches. Ocean. Eng. 2025, 320, 120316. [Google Scholar] [CrossRef]
- Sasmal, K.; Miratsu, R.; Kodaira, T.; Fukui, T.; Zhu, T.; Waseda, T. Statistical model representing storm avoidance by merchant ships in the North Atlantic Ocean. Ocean. Eng. 2021, 235, 109163. [Google Scholar] [CrossRef]
- Liu, L.; Feng, J.; Ma, L.; Yang, Y.; Wu, X.; Wang, C. Ensemble-based sensitivity analysis of track forecasts of typhoon In-fa (2021) without and with model errors in the ECMWF, NCEP, and CMA ensemble prediction systems. Atmos. Res. 2024, 309, 107596. [Google Scholar] [CrossRef]
- Guo, R.; Yu, R.; Yang, M.; Chen, G.; Chen, C.; Chen, P.; Huang, X.; Zhang, X. Analysis of characteristics and evaluation of forecast accuracy for Super Typhoon Doksuri (2023). Trop. Cyclone Res. Rev. 2024, 13, 219–229. [Google Scholar] [CrossRef]
- Ren, H.; Liu, H.; Zhang, C.; Sun, X.; Yang, J.; Ke, S. TC-SRNet: Reconstruction and prediction of typhoon high-resolution turbulent fields based on meteorological numerical forecast scale wind fields and deep learning method. J. Wind. Eng. Ind. Aerodyn. 2024, 254, 105885. [Google Scholar] [CrossRef]
- Zhang, H.; Li, W.; Shi, G.; Desrosiers, R.; Wang, X. A ship trajectory clustering algorithm based on segmentation direction. Ocean. Eng. 2024, 313, 119383. [Google Scholar] [CrossRef]
- Bai, X.; Xie, Z.; Xu, X.; Xiao, Y. An adaptive threshold fast DBSCAN algorithm with preserved trajectory feature points for vessel trajectory clustering. Ocean. Eng. 2023, 280, 114930. [Google Scholar] [CrossRef]
- Knaff, J.A.; Sampson, C.R.; DeMaria, M.; Marchok, T.P.; Gross, J.M.; McAdie, C.J. Statistical tropical cyclone wind radii prediction using climatology and persistence. Weather. Forecast. 2007, 22, 781–791. [Google Scholar] [CrossRef]
- Knaff, J.A.; Sampson, C.R.; Musgrave, K.D. Statistical tropical cyclone wind radii prediction using climatology and persistence: Updates for the western North Pacific. Weather. Forecast. 2018, 33, 1093–1098. [Google Scholar] [CrossRef]
- Scharfenaker, E.; Yang, J. Maximum entropy economics. Eur. Phys. J. Spec. Top. 2020, 229, 1577–1590. [Google Scholar] [CrossRef]
- YJ, K. Speed loss due to added resistance in wind and waves. Nav Arch. 2008, 3, 14–16. [Google Scholar]
- Lu, R.; Turan, O.; Boulougouris, E.; Banks, C.; Incecik, A. A semi-empirical ship operational performance prediction model for voyage optimization towards energy efficient shipping. Ocean. Eng. 2015, 110, 18–28. [Google Scholar] [CrossRef]
- Walther, L.; Rizvanolli, A.; Wendebourg, M.; Jahn, C. Modeling and optimization algorithms in ship weather routing. Int. J. e-Navig. Marit. Econ. 2016, 4, 31–45. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Gao, S.; Wang, Y.; Cheng, J.; Inazumi, Y.; Tang, Z. Ant colony optimization with clustering for solving the dynamic location routing problem. Appl. Math. Comput. 2016, 285, 149–173. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, D.; Zhang, M.; Zhang, J.; Mao, W. A three-dimensional ant colony algorithm for multi-objective ice routing of a ship in the Arctic area. Ocean. Eng. 2022, 266, 113241. [Google Scholar] [CrossRef]






| Clustering Method | Silhouette ↑ | DBI ↓ | CH ↑ |
|---|---|---|---|
| Expanded DBSCAN | 0.672 | 0.395 | 531.7 |
| K-means | 0.441 | 0.739 | 370.4 |
| TRACLUS | 0.528 | 0.602 | 413.9 |
| Type of Typhoon Track | Number |
|---|---|
| Northwestern | 58 |
| Western | 47 |
| Parabolic | 66 |
| Northern | 39 |
| Noise track | 11 |
| Total quantity | 221 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| −13.03 | 0.3151 | ||
| 0.8485 | 0.0038 | ||
| 1.0653 | −0.0022 | ||
| 4.2980 | 56.9200 | ||
| −0.1574 | −0.1541 | ||
| 0.0035 | 0.7372 | ||
| 0.1276 | -- | -- |
| Symbol | Interpretation |
|---|---|
| Total time of navigation avoiding typhoon/h | |
| Total fuel consumption for avoiding the typhoon/ton | |
| General risk of navigation | |
| Set of segments | |
| Drostatic speed of ship in the i-th leg/knots | |
| Actual speed of ship in the ith leg/knots | |
| Course of ship in the ith leg/degrees | |
| Daily fuel consumption/ton | |
| Leg length/nautical miles | |
| Wave height/(m) | |
| Wind speed/(m/s) | |
| The moment the ship takes action to avoid the typhoon | |
| The minimum safe distance at all times is determined by the bearing of the Ship at moment to the center of the typhoon and the formula of the physical model of a wind circle of force 7. | |
| Distance between the ship’s position and the typhoon center at moment | |
| The speed at moment is determined by the speed of the section of the waterway the ship is traveling through at moment. | |
| The position of the ship at moment is determined by the position of the ship at moment at the point on segment ith. | |
| Areas with static obstacles such as islands and shorelines | |
| Constant, the risk objective function multiplied by the probability of encountering a typhoon | |
| / | The minimum/maximum speed limit/knots during the voyage of the ship is determined by the actual performance of the ship. |
| Minimum speed limit during navigation/knots, determined by the actual situation of the route |
| Vessel Parameters | Parameter Value |
|---|---|
| Overall length of vessel/(m) | 332.95 |
| Width of vessel/(m) | 60 |
| Length of ship’s waterline/(m) | 332.6 |
| Length between ship drogue lines/(m) | 326.6 |
| squareness factor | 0.8026 |
| Ship’s auxiliary engine power/(kW) | 1440 |
| Ship design speed/(knots) | 14.1 |
| Basic Parameters | Parameter Value |
|---|---|
| Number of iterations | 50 |
| Number of ants | 30 |
| Pheromone importance factor | (1, 1, 1) |
| Heuristic factor importance coefficients | (7, 7, 5) |
| Pheromone evaporation factor | (0.3, 0.3, 0.3) |
| Information literacy enhancement factor | (500, 300, 200) |
| Business Strategy Pheromone Additional Enhancement Factor | (600, 300, 200) |
| Number of elite ants | 1 |
| Time/h | Geographical Coordinates/N,E | Probability Circle Radius/nm | Center Pressure/hPa | Direction of Travel | Movement Speed/kn |
|---|---|---|---|---|---|
| 0 | 16.1 N, 123.7 E | 0 | 985 | northwest | 12 |
| 12 | 17.4 N, 121.6 E | 40 | 985 | northwest | 10 |
| 24 | 16.4 N, 120.2 E | 57 | 990 | southwest | 8 |
| 48 | 17.4 N,117.1 E | 100 | 980 | northwest | 8 |
| 72 | 17.4 N, 113.1 E | 120 | 975 | west | 10 |
| 96 | 17.2 N, 110.5 E | 150 | 980 | west | 6 |
| 120 | 16.5 N, 109.8 E | 180 | 985 | west | 3 |
| Nearest Distance to the Wind Circle /nm | Time Spent on the Voyage /h | Fuel Consumption/tons | Total Distance /n mile | |
|---|---|---|---|---|
| Planned routes | −88.09 | 107.88 | 432.78 | 1144.06 |
| Multi-target routes | 49.19 | 90.44 | 515.28 | 1246.79 |
| Minimum sailing time routes | −6.02 | 82.05 | 586.14 | 1204.34 |
| Lowest Fuel Consumption Route | 199.10 | 180.41 | 271.58 | 1233.11 |
| Lowest risk routes | 248.62 | 134.48 | 345.47 | 1297.92 |
| CO2 Emissions/(tons) | SOX Emissions/(tons) | Total Emission | |
|---|---|---|---|
| Planned routes | 1373.21 | 20.99 | 1393.99 |
| Multi-target routes | 1634.98 | 24.99 | 1659.97 |
| Minimum sailing time routes | 1859.82 | 28.43 | 1888.25 |
| Lowest Fuel Consumption Route | 861.72 | 13.17 | 874.89 |
| Lowest risk routes | 1096.17 | 16.75 | 1112.92 |
| MOPSO | NSGA-II | 3D-ACO | |
|---|---|---|---|
| Length of route (nm) | 1277.61 | 1220.91 | 1246.79 |
| Closest distance to a category 7 wind circle (nm) | 15.46 | −19.72 | 49.19 |
| Maximum wind speed (m/s) | 16.62 | 18.92 | 12.82 |
| Maximum wave height (m) | 5.31 | 5.94 | 4.41 |
| Average calculation time (s) | 54.87 | 58.66 | 61.14 |
| convergent algebra | 46 | 51 | 33 |
| Deviation Direction | Min. Distance to Force 7 Wind Circle (nm) | Max. Wind Speed Encounterd (kn) | Max. Significant Wave Height (nm) | |
|---|---|---|---|---|
| Baseline | None | 49.19 | 12.82 | 4.41 |
| case 1 | East | 26.54 | 14.38 | 4.36 |
| case 2 | South | 32.87 | 14.21 | 3.98 |
| case 3 | West | 45.42 | 13.11 | 3.37 |
| case 4 | North | 19.35 | 15.34 | 4.19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Z.; Guo, J.; Ma, W.; Zhang, J. Ship Typhoon Avoidance Route Planning Method Under Uncertain Typhoon Forecasts. Big Data Cogn. Comput. 2025, 9, 143. https://doi.org/10.3390/bdcc9060143
He Z, Guo J, Ma W, Zhang J. Ship Typhoon Avoidance Route Planning Method Under Uncertain Typhoon Forecasts. Big Data and Cognitive Computing. 2025; 9(6):143. https://doi.org/10.3390/bdcc9060143
Chicago/Turabian StyleHe, Zhengwei, Junhong Guo, Weihao Ma, and Jinfeng Zhang. 2025. "Ship Typhoon Avoidance Route Planning Method Under Uncertain Typhoon Forecasts" Big Data and Cognitive Computing 9, no. 6: 143. https://doi.org/10.3390/bdcc9060143
APA StyleHe, Z., Guo, J., Ma, W., & Zhang, J. (2025). Ship Typhoon Avoidance Route Planning Method Under Uncertain Typhoon Forecasts. Big Data and Cognitive Computing, 9(6), 143. https://doi.org/10.3390/bdcc9060143






