From Accuracy to Vulnerability: Quantifying the Impact of Adversarial Perturbations on Healthcare AI Models
Abstract
1. Introduction
- is the loss function that evaluates the model’s performance.
- N represents the total number of samples in the dataset.
- is the true label for the i-th sample ().
- is the predicted probability for the i-th sample.
- represents a model’s parameters (e.g., weights and biases).
2. Related Works
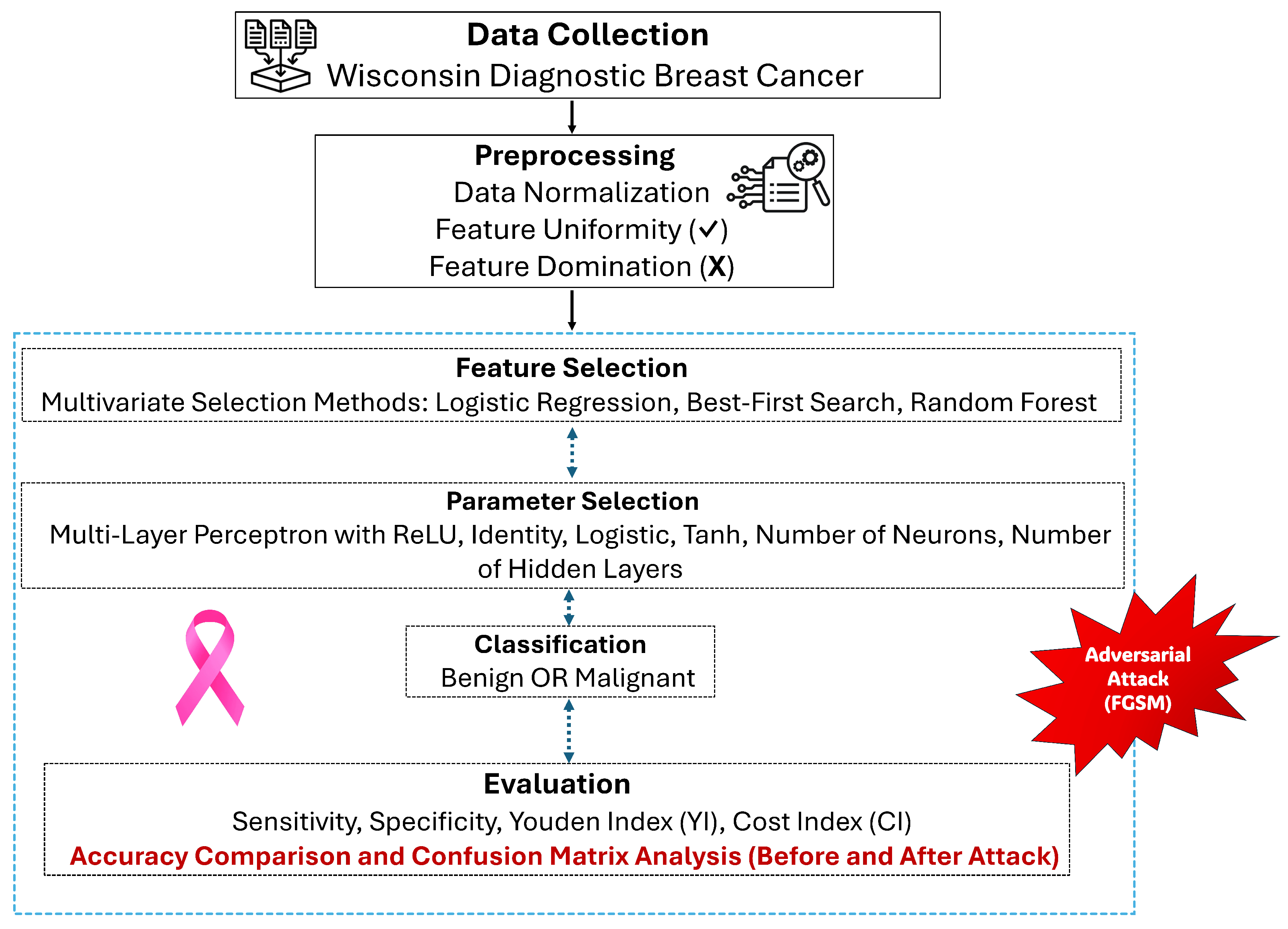
3. Materials and Methods
4. The Proposed Model
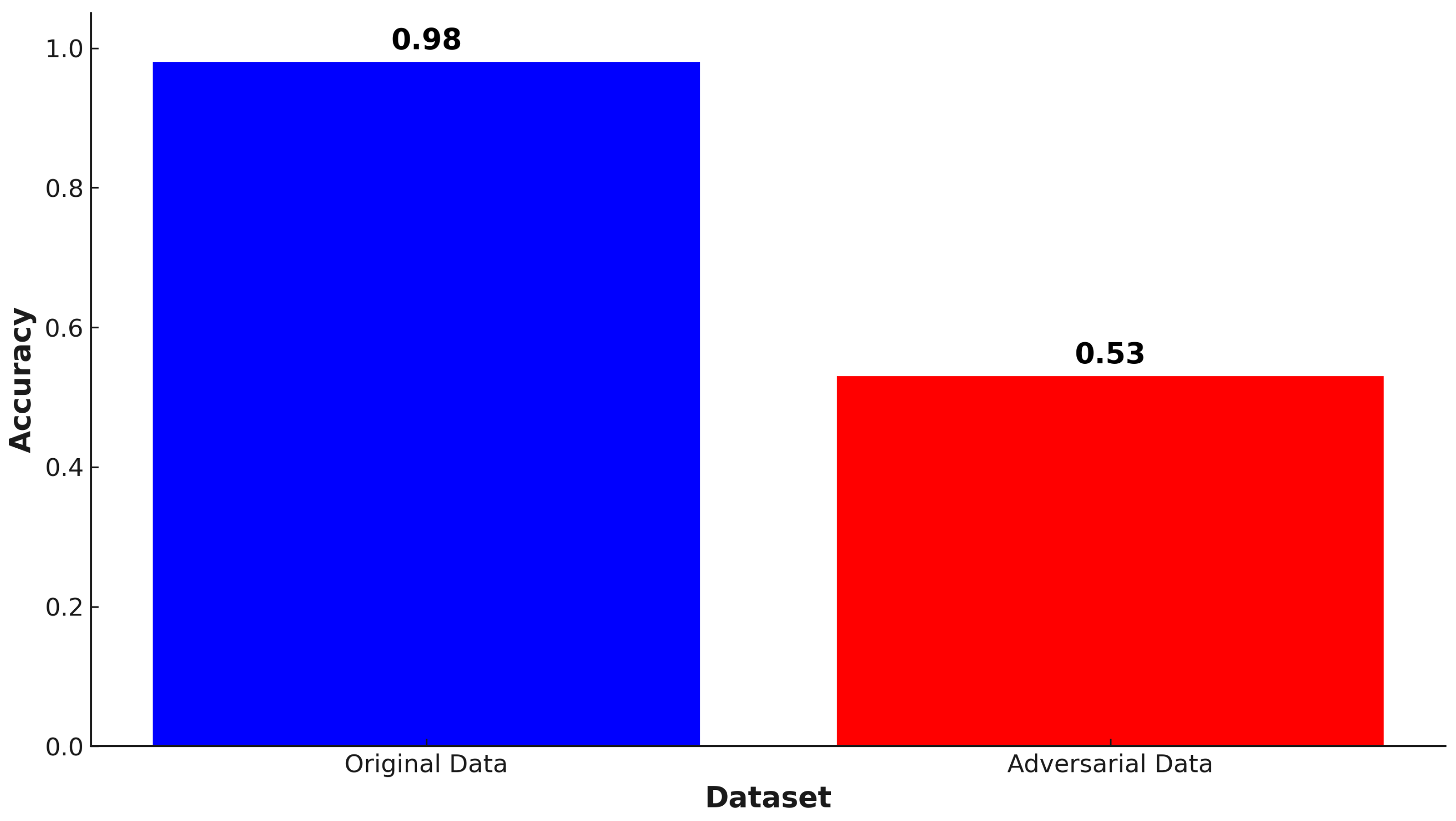
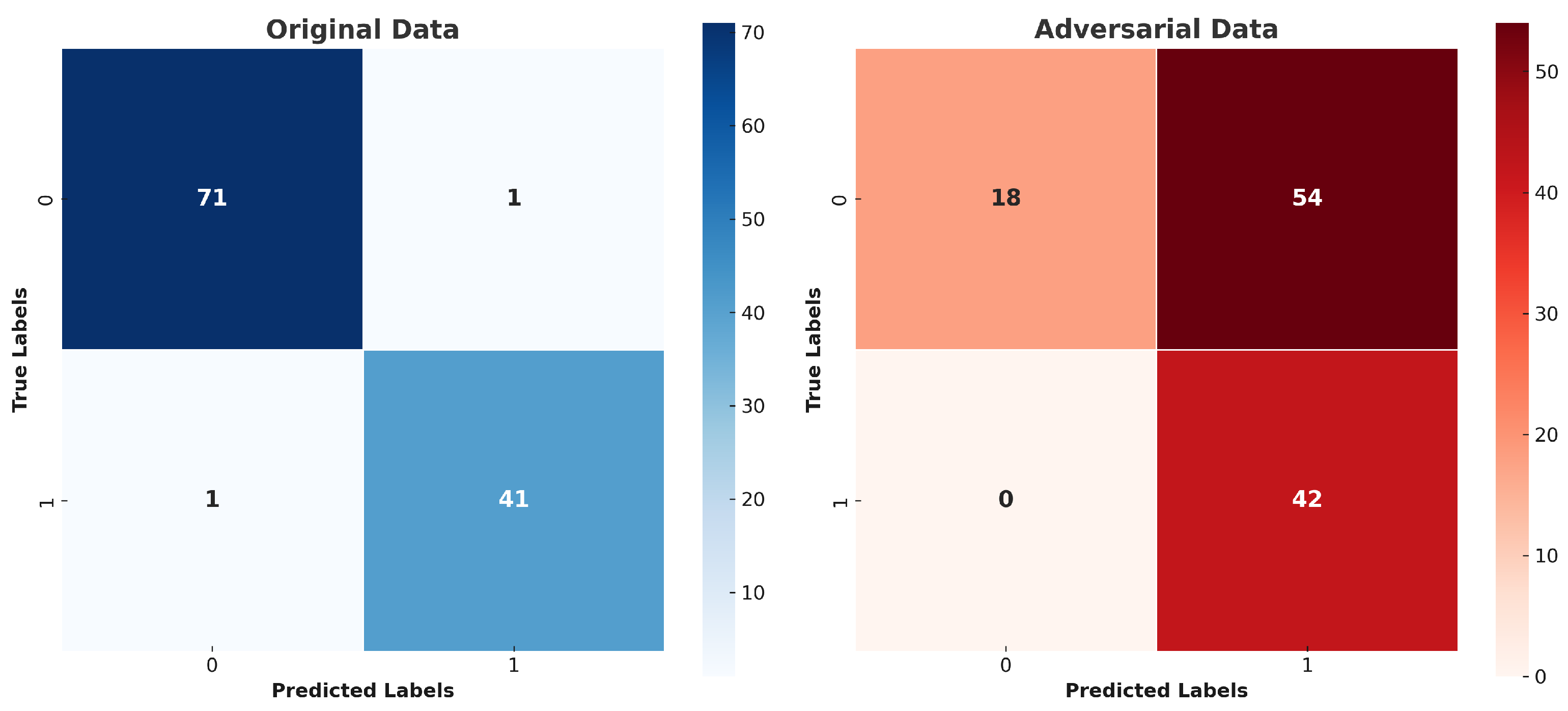
5. Results and Discussion
- x represents the original input.
- y denotes the true label.
- is the perturbation magnitude that controls the attack’s strength.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- WHO. Breast Cancer. 2024. Available online: https://www.who.int/news-room/fact-sheets/detail/breast-cancer (accessed on 21 June 2024).
- Hamid, R.; Brohi, S. A Review of Large Language Models in Healthcare: Taxonomy, Threats, Vulnerabilities, and Framework. Big Data Cogn. Comput. 2024, 8, 161. [Google Scholar] [CrossRef]
- Mastoi, Q.; Latif, S.; Brohi, S.; Ahmad, J.; Alqhatani, A.; Alshehri, M.S.; Al Mazroa, A.; Ullah, R. Explainable AI in medical imaging: An interpretable and collaborative federated learning model for brain tumor classification. Front. Oncol. 2025, 15, 1535478. [Google Scholar] [CrossRef]
- Kumar, V.; Chandrashekhara, K.T.; Jagini, N.P.; Rajkumar, K.V.; Godi, R.K.; Tumuluru, P. Enhanced breast cancer detection and classification via CAMR-Gabor filters and LSTM: A deep Learning-Based method. Egypt. Inform. J. 2025, 29, 100602. [Google Scholar] [CrossRef]
- Li, H.; Zhao, J.; Jiang, Z. Deep learning-based computer-aided detection of ultrasound in breast cancer diagnosis: A systematic review and meta-analysis. Clin. Radiol. 2024, 79, e1413. [Google Scholar] [CrossRef] [PubMed]
- Ernawan, F.; Fakhreldin, M.; Saryoko, A. Deep Learning Method Based for Breast Cancer Classification. In Proceedings of the 2023 International Conference on Information Technology Research and Innovation (ICITRI), Jakarta, Indonesia, 16 August 2023. [Google Scholar] [CrossRef]
- Goodfellow, I.; Shlens, J.; Szegedy, C. Explaining and harnessing adversarial examples. arXiv 2014, arXiv:1412.6572. [Google Scholar]
- Akhtar, N.; Mian, A. Threat of adversarial attacks on deep learning in computer vision: A survey. IEEE Access 2018, 6, 14410–14430. [Google Scholar] [CrossRef]
- Biggio, B.; Roli, F. Wild patterns: Ten years after the rise of adversarial machine learning. Pattern Recognit. 2018, 84, 317–331. [Google Scholar] [CrossRef]
- Veale, M.; Binns, R.; Edwards, L. Algorithms that remember: Model inversion attacks and data protection law. Philos. Trans. A Math. Phys. Eng. Sci. 2018, 376, 20180083. [Google Scholar] [CrossRef]
- Tsai, M.J.; Lin, P.Y.; Lee, M.E. Adversarial Attacks on Medical Image Classification. Cancers 2023, 15, 4228. [Google Scholar] [CrossRef]
- Muoka, G.W.; Yi, D.; Ukwuoma, C.C.; Mutale, A.; Ejiyi, C.J.; Mzee, A.K.; Gyarteng, E.S.A.; Alqahtani, A.; Al-antari, M.A. A Comprehensive Review and Analysis of Deep Learning-Based Medical Image Adversarial Attack and Defense. Mathematics 2023, 11, 4272. [Google Scholar] [CrossRef]
- Finlayson, S.G.; Bowers, J.D.; Ito, J.; Zittrain, J.L.; Beam, A.L.; Kohane, I.S. Adversarial attacks on medical machine learning. Science 2019, 363, 6433. [Google Scholar] [CrossRef] [PubMed]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Kurakin, A.; Goodfellow, I.; Bengio, S. Adversarial examples in the physical world. arXiv 2017, arXiv:1607.02533. [Google Scholar]
- Moosavi-Dezfooli, S.M.; Fawzi, A.; Frossard, P. DeepFool: A Simple and Accurate Method to Fool Deep Neural Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar] [CrossRef]
- Carlini, N.; Wagner, D. Towards Evaluating the Robustness of Neural Networks. In Proceedings of the IEEE Symposium on Security and Privacy (SP), San Jose, CA, USA, 22–26 May 2017. [Google Scholar] [CrossRef]
- Madry, A.; Makelov, A.; Schmidt, L.; Tsipras, D.; Vladu, A. Towards deep learning models resistant to adversarial attacks. arXiv 2019, arXiv:1706.06083. [Google Scholar]
- Su, J.; Vargas, D.V.; Sakurai, K. One pixel attack for fooling deep neural networks. IEEE Trans. Evol. Comput. 2019, 23, 828–841. [Google Scholar] [CrossRef]
- Xu, W.; Evans, D.; Qi, Y. Feature squeezing: Detecting adversarial examples in deep neural networks. arXiv 2017, arXiv:1704.01155. [Google Scholar]
- Yuan, X.; He, P.; Zhu, Q.; Li, X. Adversarial examples: Attacks and defenses for deep learning. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 2805–2824. [Google Scholar] [CrossRef]
- Koh, P.W.; Liang, P. Understanding black-box predictions via influence functions. arXiv 2020, arXiv:1703.04730. [Google Scholar]
- Fredrikson, M.; Jha, S.; Ristenpart, T. Model Inversion Attacks That Exploit Confidence Information and Basic Countermeasures. In Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security (CCS ’15), Denver, CO, USA, 12–16 October 2015. [Google Scholar] [CrossRef]
- Jagielski, M.; Oprea, A.; Biggio, B.; Liu, C.; Nita-Rotaru, C.; Li, B. Manipulating Machine Learning: Poisoning Attacks and Countermeasures for Regression Learning. In Proceedings of the IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 20–24 May 2018. [Google Scholar] [CrossRef]
- Dwork, C.; Roth, A. The algorithmic foundations of differential privacy. Found. Trends Theor. Comput. Sci. 2014, 9, 211–407. [Google Scholar] [CrossRef]
- Song, S.; Chaudhuri, K.; Sarwate, A.D. Stochastic Gradient Descent with Differentially Private Updates. In Proceedings of the 2013 IEEE Global Conference on Signal and Information Processing, Austin, TX, USA, 3–5 December 2013. [Google Scholar] [CrossRef]
- Tramer, F.; Zhang, F.; Juels, A.; Reiter, M.K.; Ristenpart, T. Stealing Machine Learning Models via Prediction APIs. In Proceedings of the USENIX Security Symposium, Austin, TX, USA, 10–12 August 2016. [Google Scholar]
- Orekondy, T.; Schiele, B.; Fritz, M. Knockoff Nets: Stealing Functionality of Black-Box Models. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar] [CrossRef]
- Papernot, N.; McDaniel, P.; Wu, X.; Jha, S.; Swami, A. Distillation as a Defense to Adversarial Perturbations Against Deep Neural Networks. In Proceedings of the 2016 IEEE Symposium on Security and Privacy (SP), San Jose, CA, USA, 22–26 May 2016. [Google Scholar] [CrossRef]
- Zhang, H.; Yu, Y.; Jiao, J.; Xing, E.; Ghaoui, L.E.; Jordan, M. Theoretically principled trade-off between robustness and accuracy. arXiv 2019, arXiv:1901.08573. [Google Scholar]
- Szegedy, C.; Zaremba, W.; Sutskever, I.; Bruna, J.; Erhan, D.; Goodfellow, I.; Fergus, R. Intriguing properties of neural networks. arXiv 2014, arXiv:1312.6199. [Google Scholar]
- Wolberg, W.; Mangasarian, O.; Street, W. Breast Cancer Wisconsin (Diagnostic). 1995. Available online: https://archive.ics.uci.edu/dataset/17/breast+cancer+wisconsin+diagnostic (accessed on 8 March 2024).
- Street, W.N.; Wolberg, W.H.; Mangasarian, O.L. Nuclear feature extraction for breast tumor diagnosis. Biomed. Image Process. Biomed. Vis. 1993, 1905, 861–870. [Google Scholar] [CrossRef]
- Athalye, A.; Carlini, N.; Wagner, D. Obfuscated gradients give a false sense of security: Circumventing defenses to adversarial examples. arXiv 2018, arXiv:1802.00420. [Google Scholar]
- Shafahi, A.; Najibi, M.; Goldstein, T. Adversarial training for free! arXiv 2019, arXiv:1904.12843. [Google Scholar]


| No. | Feature | Mean | SD | LR | BF | RF | Count |
|---|---|---|---|---|---|---|---|
| 1 | radius_mean | 14.13 | 3.52 | Yes | Yes | Yes | 3 |
| 2 | texture_mean | 19.29 | 4.30 | Yes | Yes | Yes | 3 |
| 3 | perimeter_mean | 91.97 | 24.30 | Yes | Yes | Yes | 3 |
| 4 | area_mean | 654.89 | 351.91 | No | Yes | Yes | 2 |
| 5 | smoothness_mean | 0.10 | 0.01 | Yes | No | No | 1 |
| 6 | compactness_mean | 0.10 | 0.05 | No | No | No | 0 |
| 7 | concavity_mean | 0.09 | 0.08 | Yes | Yes | Yes | 3 |
| 8 | concave points_mean | 0.05 | 0.04 | Yes | No | Yes | 2 |
| 9 | symmetry_mean | 0.18 | 0.03 | Yes | No | No | 1 |
| 10 | fractal_dimension_mean | 0.06 | 0.01 | No | No | No | 0 |
| 11 | radius_se | 0.41 | 0.28 | No | Yes | No | 1 |
| 12 | texture_se | 1.22 | 0.55 | Yes | No | No | 1 |
| 13 | perimeter_se | 2.87 | 2.02 | No | Yes | No | 1 |
| 14 | area_se | 40.34 | 45.49 | No | Yes | Yes | 2 |
| 15 | smoothness_se | 0.01 | 0.00 | No | No | No | 0 |
| 16 | compactness_se | 0.03 | 0.02 | No | No | No | 0 |
| 17 | concavity_se | 0.03 | 0.03 | No | No | No | 0 |
| 18 | concave points_se | 0.01 | 0.01 | No | No | Yes | 1 |
| 19 | symmetry_se | 0.02 | 0.01 | No | No | No | 0 |
| 20 | fractal_dimension_se | 0.00 | 0.00 | No | No | No | 0 |
| 21 | radius_worst | 16.27 | 4.83 | Yes | Yes | Yes | 3 |
| 22 | texture_worst | 25.68 | 6.15 | Yes | Yes | Yes | 3 |
| 23 | perimeter_worst | 107.26 | 33.60 | No | Yes | Yes | 2 |
| 24 | area_worst | 880.58 | 569.36 | No | Yes | Yes | 2 |
| 25 | smoothness_worst | 0.13 | 0.02 | Yes | No | Yes | 2 |
| 26 | compactness_worst | 0.25 | 0.16 | No | Yes | No | 1 |
| 27 | concavity_worst | 0.27 | 0.21 | Yes | Yes | Yes | 3 |
| 28 | concave points_worst | 0.11 | 0.07 | Yes | Yes | Yes | 3 |
| 29 | symmetry_worst | 0.29 | 0.06 | Yes | No | No | 1 |
| 30 | fractal_dimension_worst | 0.08 | 0.02 | Yes | No | No | 1 |
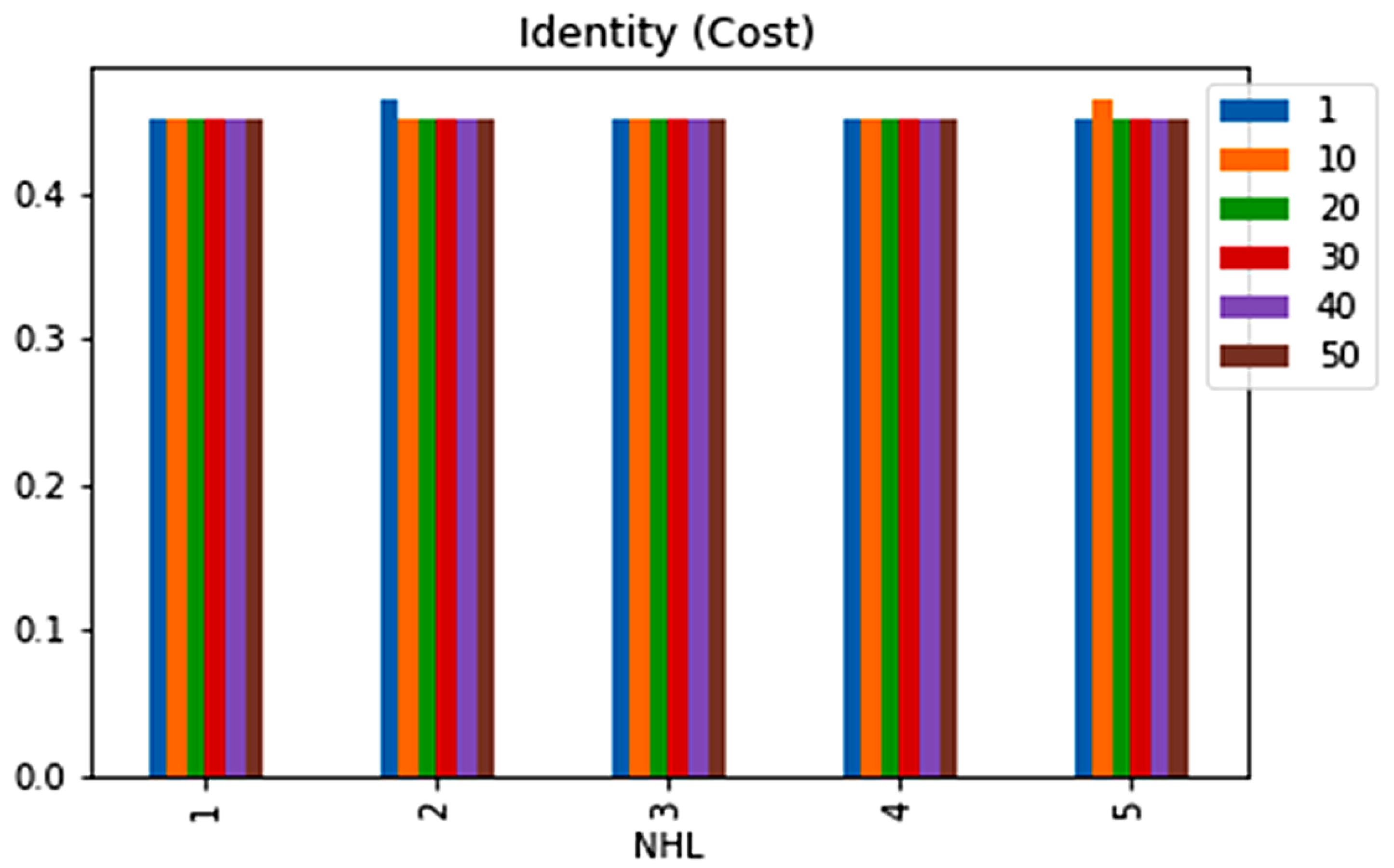
| NHL | NN | Accuracy | Sensitivity | Specificity | YI | CI |
|---|---|---|---|---|---|---|
| 1 | 1 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 1 | 10 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 1 | 20 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 1 | 30 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 1 | 40 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 1 | 50 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 2 | 1 | 0.9737 | 0.9706 | 0.9783 | 0.9489 | 0.465122829 |
| 2 | 10 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 2 | 20 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 2 | 30 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 2 | 40 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 2 | 50 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 3 | 1 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 3 | 10 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 3 | 20 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 3 | 30 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 3 | 40 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 3 | 50 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 4 | 1 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 4 | 10 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 4 | 20 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 4 | 30 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 4 | 40 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 4 | 50 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 5 | 1 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 5 | 10 | 0.9737 | 0.9706 | 0.9783 | 0.9489 | 0.465122829 |
| 5 | 20 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 5 | 30 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 5 | 40 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 5 | 50 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
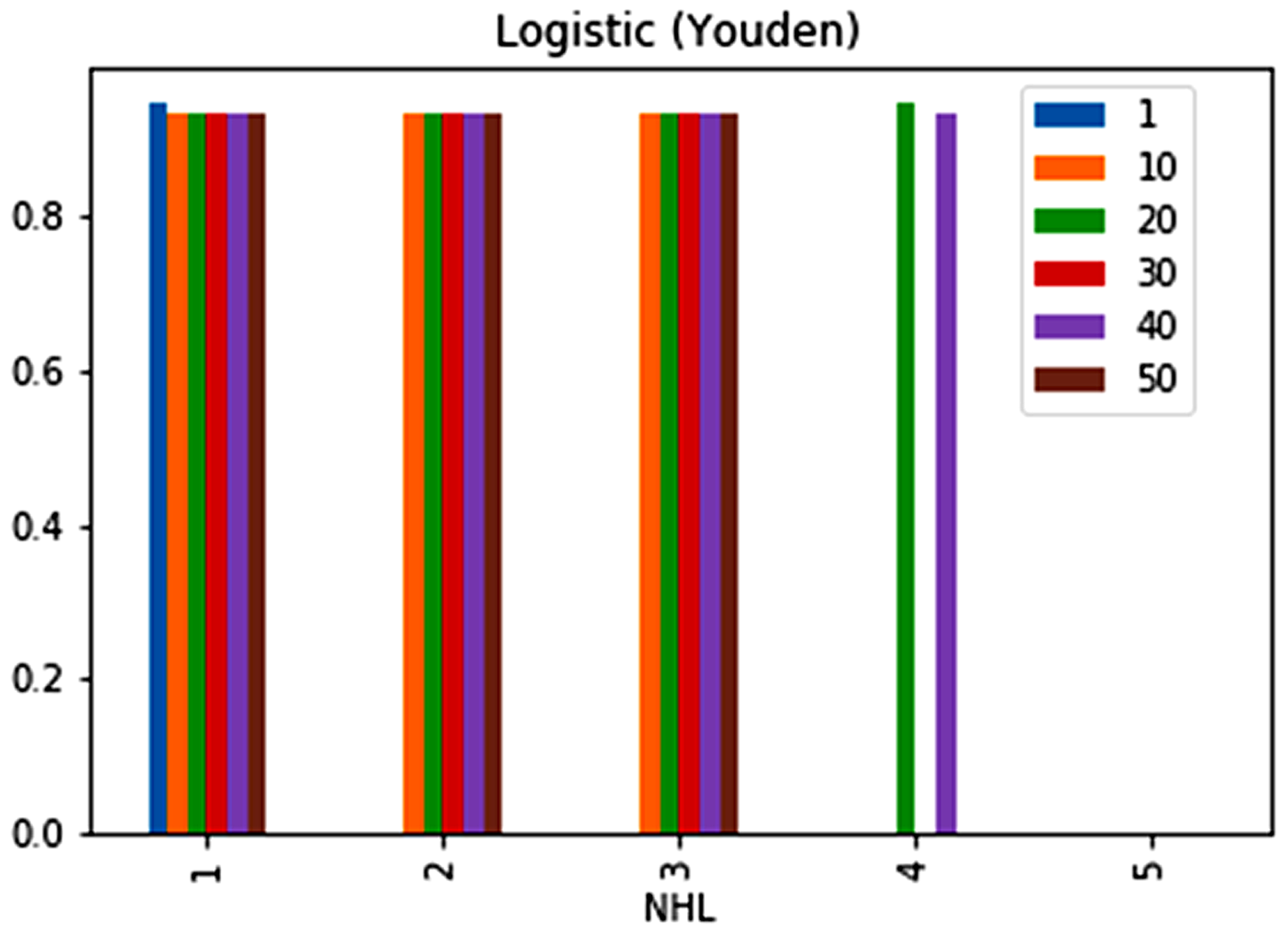
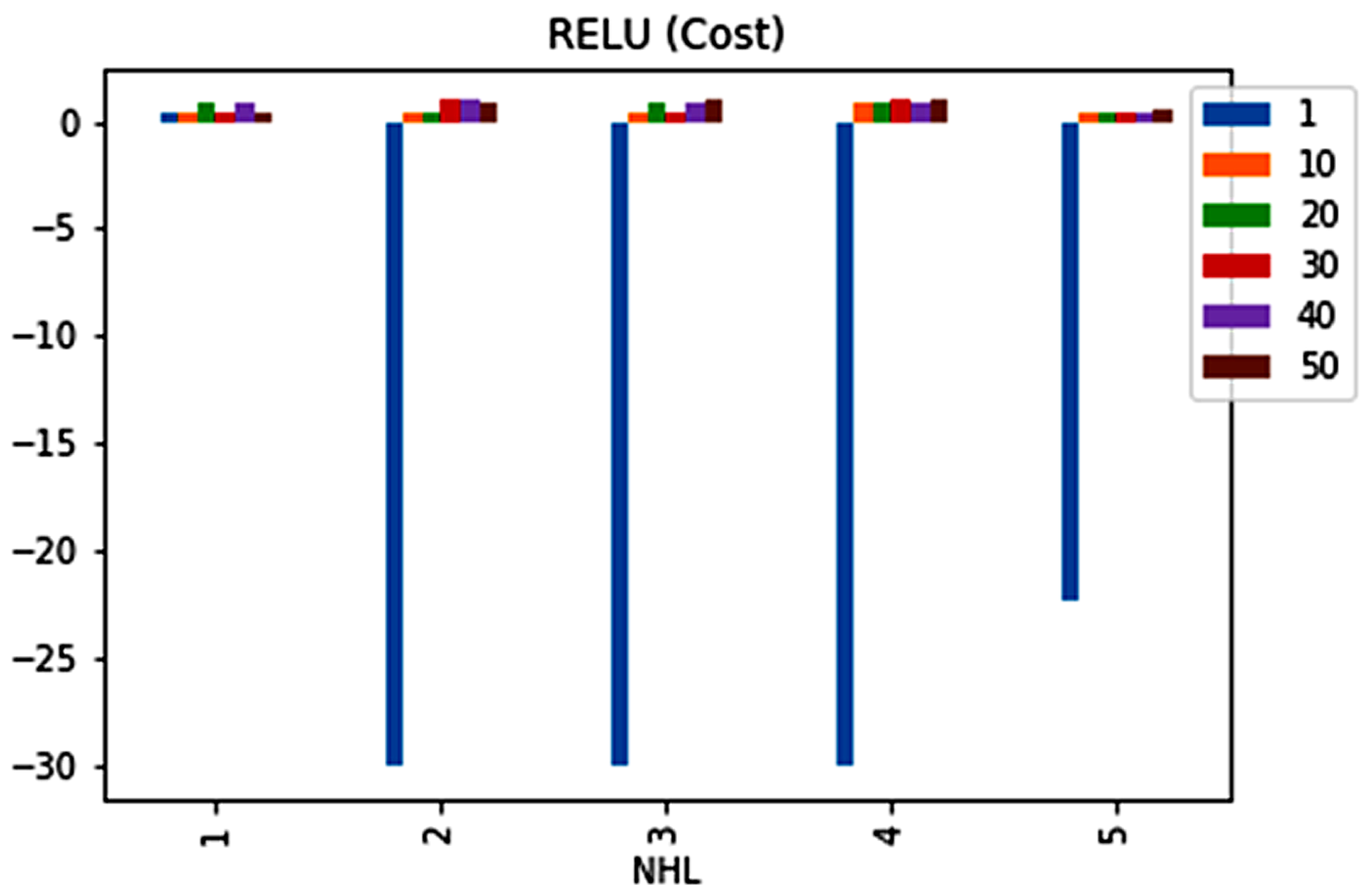
| NHL | NN | Accuracy | Sensitivity | Specificity | YI | CI |
|---|---|---|---|---|---|---|
| 1 | 1 | 0.9737 | 0.9706 | 0.9783 | 0.9489 | 0.465122829 |
| 1 | 10 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 1 | 20 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 1 | 30 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 1 | 40 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 1 | 50 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 2 | 1 | 0.5965 | 1 | 0 | 0 | −22.29387884 |
| 2 | 10 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 2 | 20 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 2 | 30 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 2 | 40 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 2 | 50 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 3 | 1 | 0.5965 | 1 | 0 | 0 | −22.29387884 |
| 3 | 10 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 3 | 20 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 3 | 30 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 3 | 40 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 3 | 50 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 4 | 1 | 0.5965 | 1 | 0 | 0 | −22.29387884 |
| 4 | 10 | 0.5965 | 1 | 0 | 0 | −22.29387884 |
| 4 | 20 | 0.9737 | 0.9706 | 0.9783 | 0.9489 | 0.465122829 |
| 4 | 30 | 0.5965 | 1 | 0 | 0 | −22.29387884 |
| 4 | 40 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 4 | 50 | 0.5965 | 1 | 0 | 0 | −22.29387884 |
| 5 | 1 | 0.5965 | 1 | 0 | 0 | −22.29387884 |
| 5 | 10 | 0.5965 | 1 | 0 | 0 | −22.29387884 |
| 5 | 20 | 0.5965 | 1 | 0 | 0 | −22.29387884 |
| 5 | 30 | 0.5965 | 1 | 0 | 0 | −22.29387884 |
| 5 | 40 | 0.5965 | 1 | 0 | 0 | −22.29387884 |
| 5 | 50 | 0.5965 | 1 | 0 | 0 | −22.29387884 |
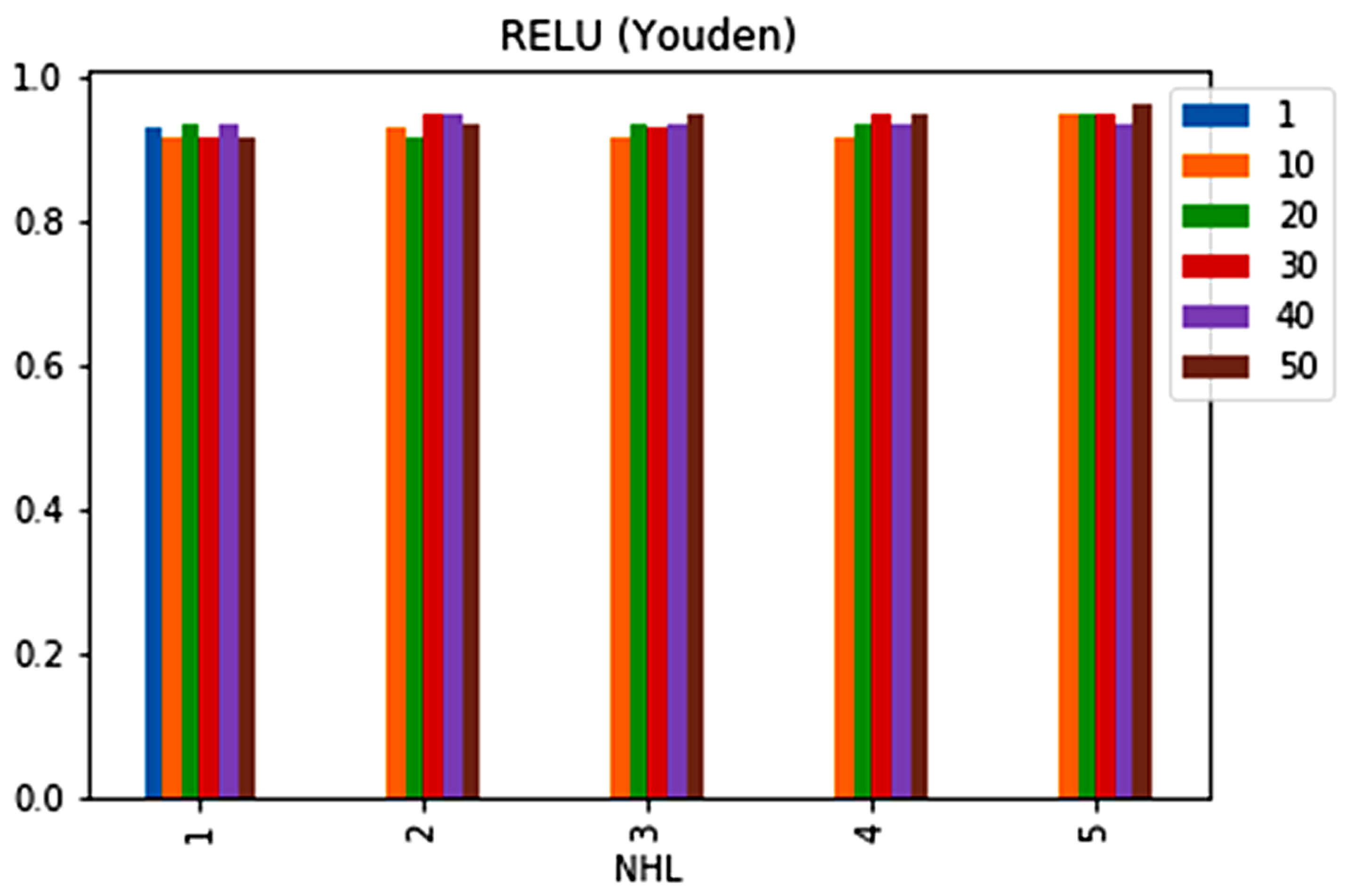
| NHL | NN | Accuracy | Sensitivity | Specificity | YI | CI |
|---|---|---|---|---|---|---|
| 1 | 1 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 1 | 10 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 1 | 20 | 0.9737 | 0.9706 | 0.9783 | 0.9489 | 0.465122829 |
| 1 | 30 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 1 | 40 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 1 | 50 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 2 | 1 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 2 | 10 | 0.9737 | 0.9706 | 0.9783 | 0.9489 | 0.465122829 |
| 2 | 20 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 2 | 30 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 2 | 40 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 2 | 50 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 3 | 1 | 0.9737 | 0.9706 | 0.9783 | 0.9489 | 0.465122829 |
| 3 | 10 | 0.9737 | 0.9706 | 0.9783 | 0.9489 | 0.465122829 |
| 3 | 20 | 0.9737 | 0.9706 | 0.9783 | 0.9489 | 0.465122829 |
| 3 | 30 | 0.9737 | 0.9706 | 0.9783 | 0.9489 | 0.465122829 |
| 3 | 40 | 0.9737 | 0.9706 | 0.9783 | 0.9489 | 0.465122829 |
| 3 | 50 | 0.9737 | 0.9706 | 0.9783 | 0.9489 | 0.465122829 |
| 4 | 1 | 0.9737 | 0.9706 | 0.9783 | 0.9489 | 0.465122829 |
| 4 | 10 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 4 | 20 | 0.9737 | 0.9706 | 0.9783 | 0.9489 | 0.465122829 |
| 4 | 30 | 0.9737 | 0.9706 | 0.9783 | 0.9489 | 0.465122829 |
| 4 | 40 | 0.9737 | 0.9706 | 0.9783 | 0.9489 | 0.465122829 |
| 4 | 50 | 0.9737 | 0.9706 | 0.9783 | 0.9489 | 0.465122829 |
| 5 | 1 | 0.9737 | 0.9706 | 0.9783 | 0.9489 | 0.465122829 |
| 5 | 10 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 5 | 20 | 0.9737 | 0.9706 | 0.9783 | 0.9489 | 0.465122829 |
| 5 | 30 | 0.9737 | 0.9706 | 0.9783 | 0.9489 | 0.465122829 |
| 5 | 40 | 0.9825 | 0.9853 | 0.9783 | 0.9636 | 0.479822829 |
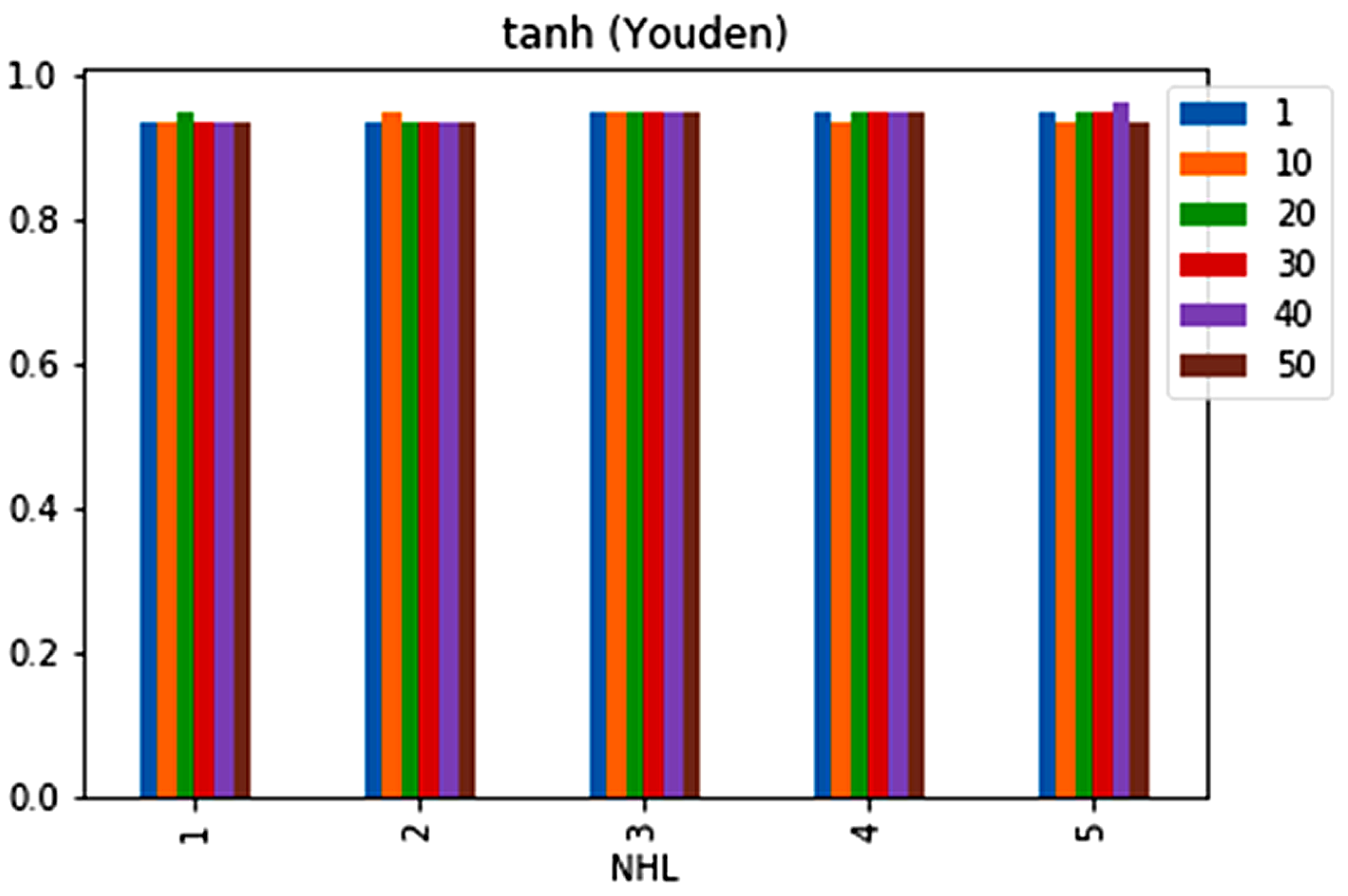
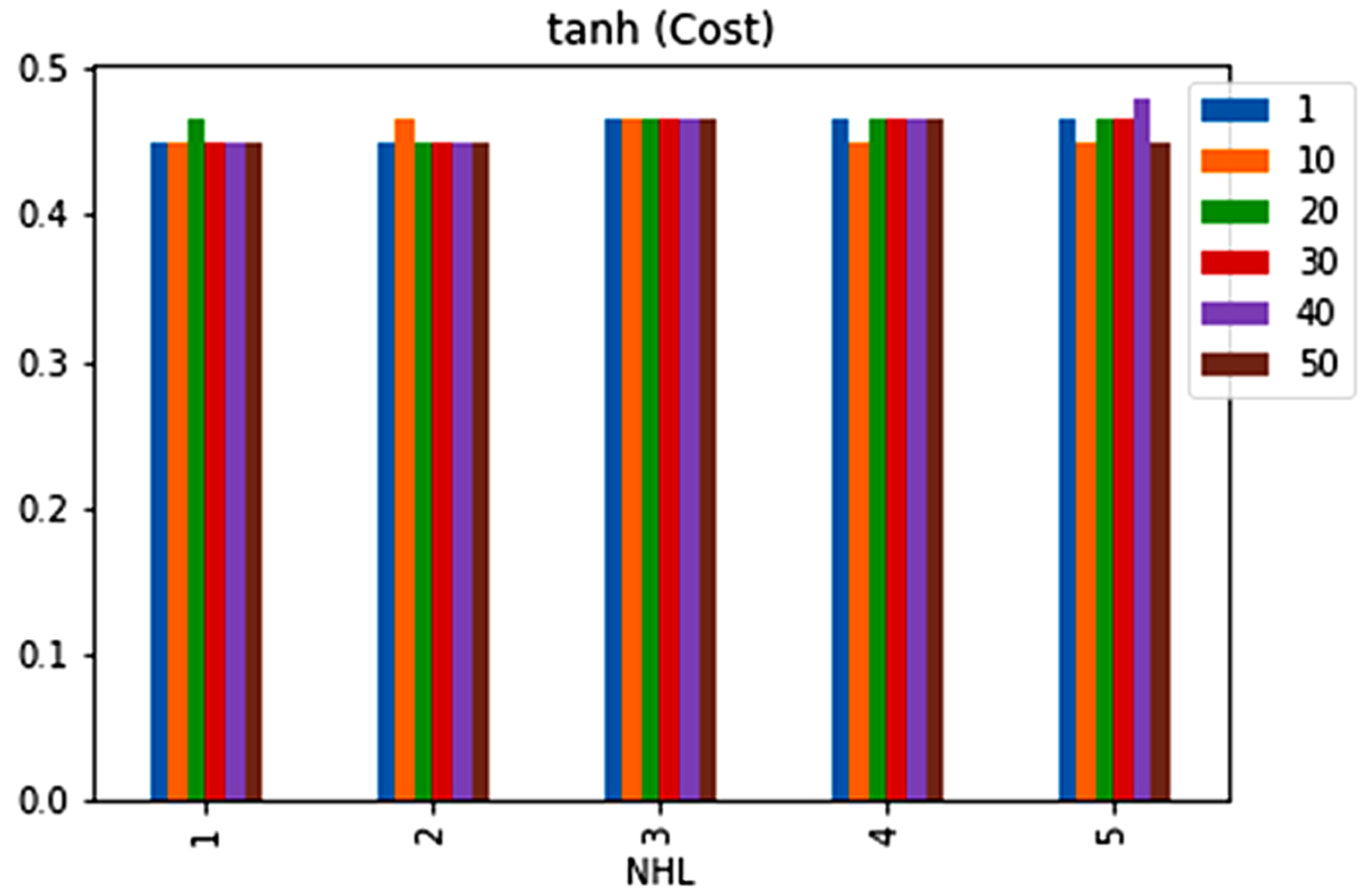
| NHL | NN | Accuracy | Sensitivity | Specificity | YI | CI |
|---|---|---|---|---|---|---|
| 1 | 1 | 0.9649 | 0.95 | 0.9815 | 0.9315 | 0.376666747 |
| 1 | 10 | 0.9561 | 0.9333 | 0.9815 | 0.9148 | 0.359966747 |
| 1 | 20 | 0.9649 | 0.9333 | 1 | 0.9333 | 0.9333 |
| 1 | 30 | 0.9561 | 0.9333 | 0.9815 | 0.9148 | 0.359966747 |
| 1 | 40 | 0.9649 | 0.9333 | 1 | 0.9333 | 0.9333 |
| 1 | 50 | 0.9561 | 0.9333 | 0.9815 | 0.9148 | 0.359966747 |
| 2 | 1 | 0.5263 | 1 | 0 | 0 | −29.99098664 |
| 2 | 10 | 0.9649 | 0.95 | 0.9815 | 0.9315 | 0.376666747 |
| 2 | 20 | 0.9561 | 0.9333 | 0.9815 | 0.9148 | 0.359966747 |
| 2 | 30 | 0.9737 | 0.95 | 1 | 0.95 | 0.95 |
| 2 | 40 | 0.9737 | 0.95 | 1 | 0.95 | 0.95 |
| 2 | 50 | 0.9649 | 0.9333 | 1 | 0.9333 | 0.9333 |
| 3 | 1 | 0.5263 | 1 | 0 | 0 | −29.99098664 |
| 3 | 10 | 0.9561 | 0.9333 | 0.9815 | 0.9148 | 0.359966747 |
| 3 | 20 | 0.9649 | 0.9333 | 1 | 0.9333 | 0.9333 |
| 3 | 30 | 0.9649 | 0.95 | 0.9815 | 0.9315 | 0.376666747 |
| 3 | 40 | 0.9649 | 0.9333 | 1 | 0.9333 | 0.9333 |
| 3 | 50 | 0.9737 | 0.95 | 1 | 0.95 | 0.95 |
| 4 | 1 | 0.5263 | 1 | 0 | 0 | −29.99098664 |
| 4 | 10 | 0.9561 | 0.9167 | 1 | 0.9167 | 0.9167 |
| 4 | 20 | 0.9649 | 0.9333 | 1 | 0.9333 | 0.9333 |
| 4 | 30 | 0.9737 | 0.95 | 1 | 0.95 | 0.95 |
| 4 | 40 | 0.9649 | 0.9333 | 1 | 0.9333 | 0.9333 |
| 4 | 50 | 0.9737 | 0.95 | 1 | 0.95 | 0.95 |
| 5 | 1 | 0.5965 | 1 | 0 | 0 | −22.29387884 |
| 5 | 10 | 0.9737 | 0.9706 | 0.9783 | 0.9489 | 0.465122829 |
| 5 | 20 | 0.9737 | 0.9706 | 0.9783 | 0.9489 | 0.465122829 |
| 5 | 30 | 0.9737 | 0.9706 | 0.9783 | 0.9489 | 0.465122829 |
| 5 | 40 | 0.9649 | 0.9559 | 0.9783 | 0.9342 | 0.450422829 |
| 5 | 50 | 0.9825 | 0.9853 | 0.9783 | 0.9636 | 0.479822829 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brohi, S.; Mastoi, Q.-u.-a. From Accuracy to Vulnerability: Quantifying the Impact of Adversarial Perturbations on Healthcare AI Models. Big Data Cogn. Comput. 2025, 9, 114. https://doi.org/10.3390/bdcc9050114
Brohi S, Mastoi Q-u-a. From Accuracy to Vulnerability: Quantifying the Impact of Adversarial Perturbations on Healthcare AI Models. Big Data and Cognitive Computing. 2025; 9(5):114. https://doi.org/10.3390/bdcc9050114
Chicago/Turabian StyleBrohi, Sarfraz, and Qurat-ul-ain Mastoi. 2025. "From Accuracy to Vulnerability: Quantifying the Impact of Adversarial Perturbations on Healthcare AI Models" Big Data and Cognitive Computing 9, no. 5: 114. https://doi.org/10.3390/bdcc9050114
APA StyleBrohi, S., & Mastoi, Q.-u.-a. (2025). From Accuracy to Vulnerability: Quantifying the Impact of Adversarial Perturbations on Healthcare AI Models. Big Data and Cognitive Computing, 9(5), 114. https://doi.org/10.3390/bdcc9050114










