Exploring How Phonotactic Knowledge Can Be Represented in Cognitive Networks

Abstract

In Linguistics and Psycholinguistics, phonotactics refers to the constraints on individual sounds in a given language that restrict how those sounds can be ordered to form words in that language. Previous empirical work in Psycholinguistics demonstrated that phonotactic knowledge influenced how quickly and accurately listeners retrieved words from that part of memory known as the mental lexicon. In the present study, we used three computer simulations to explore how three different cognitive network architectures could account for the previously observed effects of phonotactics on processing. The results of Simulation 1 showed that some—but not all—effects of phonotactics could be accounted for in a network where nodes represent words and edges connect words that are phonologically related to each other. In Simulation 2, a different network architecture was used to again account for some—but not all—effects of phonotactics and phonological neighborhood density. A bipartite network was used in Simulation 3 to account for many of the previously observed effects of phonotactic knowledge on spoken word recognition. The value of using computer simulations to explore different network architectures is discussed.

1. Introduction

In Linguistics and Psycholinguistics, phonotactics refers to the individual sounds (known as phonemes) that are used in a given language, as well as the constraints on how those sounds can be ordered to form words in that language [1,2,3]. For example, Arabic uses a glottal stop /Ɂ/, but English does not. (Characters or sequences of characters placed between angled lines (i.e., //) are symbols from the International Phonetic Alphabet (IPA), which are used to represent the sounds found in the languages of the world.) Similarly, the sequence /br/ is permissible at the ends of words in Arabic, but is not permissible at the beginning of words. The opposite is true for the sequence /br/ in English.

Speakers of a given language are not only aware of which phonemes and sequences of phonemes are used in the language(s) they speak, but they are also implicitly aware that certain phonemes and sequences are more common than other phonemes and sequences in the language. The variability in the frequency with which phonemes and sequences occur in a language is referred to as phonotactic probability. For example, in English words the phoneme /p/ and the sequence /pæv/ (“pav”) occurs often in words, and would be said to have high phonotactic probability. In contrast, the phoneme /ʒ/ and the sequence /ðeʒ/ (“thayzh”) occurs less often in English words and would be said to have low phonotactic probability.

Research in Linguistics and Psycholinguistics has shown that by 9-months of age children prefer to listen to nonwords containing high—rather than low—probability phonemes and sequences of phonemes, demonstrating that sensitivity to the sounds of one’s native language occurs early in life [4]. Additional research has found that listeners rely on phonotactic probability to segment individual words from the stream of fluent speech [5], to recognize words in speech [1,2], and to learn new words [6]. For a review of research on how phonotactic probability influences spoken word recognition and other language processes see [7].

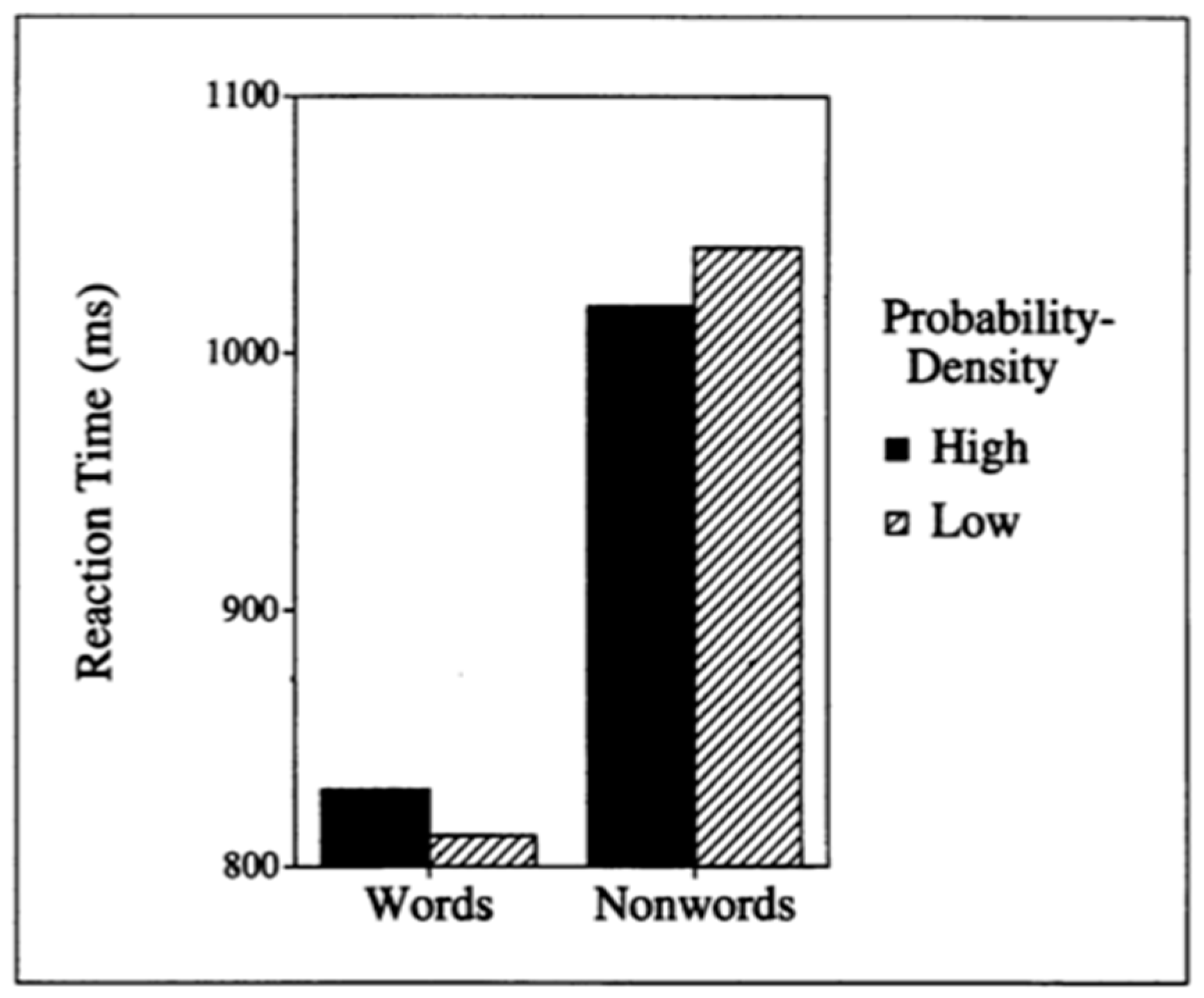
Seminal work was conducted by [1,2] on how phonotactic probability influences spoken word recognition. They found that when participants were asked to repeat the words and nonwords that they heard (in a psycholinguistic task known as an auditory naming task), participants responded differentially as a function of the phonotactic probability of the words that naturally varied in phonotactic probability and the nonwords that were specially created to vary in phonotactic probability (such as the examples /pæv/ and /ðeʒ/ described above). As shown in Figure 1, participants responded more quickly and accurately to words with low phonotactic probability than to words with high phonotactic probability. For the nonwords, however, participants responded more quickly and accurately to nonwords with high phonotactic probability than to nonwords with low phonotactic probability.

These results were interpreted by [1,2] as indicative that listeners represented in the mental lexicon (i.e., that part of memory that stores linguistic knowledge) not only information about the words they knew, but also information about the phonemes and sequences of phonemes that occur in the language. When the representations of phonemes and sequences of phonemes (so called, “sub-lexical representations”) were used to process the spoken input, one could expect to see stimuli with high phonotactic probability being responded to more quickly and accurately than stimuli with low phonotactic probability. Enhanced performance to stimuli that are common in the environment are common in many domains of perceptual and cognitive processing [8], and may give rise to the processing advantage observed for stimuli with high phonotactic probability.

However, when representations of words (so called, “lexical representations”) were used to process the spoken input, one could expect to see stimuli with low phonotactic probability being responded to more quickly and accurately than stimuli with high phonotactic probability. This is because words with high phonotactic probability, like cat, are confusable with many words in the language (e.g., rat, fat, mat, sat, hat, cut, kit, cap, can, calf, etc.), and words with low phonotactic probability, like dog, are confusable with fewer words in the language (e.g., log, hog, dig, doll). A word that is confusable with many words (e.g., cat) is said to have high neighborhood density, whereas a word that is confusable with fewer words (e.g., dog) is said to have low neighborhood density. Numerous studies have demonstrated that when there are many confusable words to discriminate among, spoken word recognition occurs slowly and less accurately (for reviews see [9,10,11]).

Participants can be induced to use lexical representations by presenting them with real words in a psycholinguistic task, or by asking them to engage in a task, such as a lexical decision task, that requires them to discriminate whether a stimulus is a real word or a nonword. In tasks that induce the listener to use lexical representations, one would expect to find that words with high neighborhood density (e.g., cat) are responded to slower and less accurately than words with low neighborhood density (e.g., dog).

Participants can be induced to use sub-lexical representations by presenting them with nonwords and by asking them to engage in a task, such as the auditory naming task, that does not require them to discriminate among words (i.e., they simply need to repeat what they hear, whether it is a word or not). Participants can also be induced to use sub-lexical representations to process real words when a small number of real words are embedded with many nonwords in a task that does not require them to discriminate among words, such as a same-different decision of two sequentially presented stimuli [12]. In tasks that induce the listener to use sub-lexical representations, words may be treated as if they are nonwords, so we would expect to find that nonwords and words with high phonotactic probability are responded to more quickly and accurately than nonwords and words with low phonotactic probability.

To account for these effects, [2] appealed to a type of artificial neural network called adaptive resonance theory (ART; [13]), because it included sub-lexical representations that were sensitive to how common they occurred in the environment (i.e., producing enhanced performance for more common items), and lexical representations that were sensitive to how many other similar sounding words they could be confused with (i.e., a word that is confusable with few other words is responded to quickly and accurately). Subsequent computer simulations by [14] formally confirmed that an ART network could account for the results observed by [1,2]. Note that the ART network and other types of artificial neural networks (e.g., Kohonen neural networks, recurrent neural networks, etc.) differ from the cognitive networks used in the present simulations. In the present simulations, we explored if a different type of network—namely, cognitive networks—could represent phonotactic information in some way to also account for the results observed by [1,2]. The term “cognitive network” has emerged recently [15] to describe applications of the mathematical tools of network science to questions commonly studied by cognitive psychologists and cognitive scientists [15,16]). Broadly speaking, artificial neural networks such as ART attempt to model cognitive processing, whereas cognitive networks attempt to capture how representations are organized in memory. It is important in the cognitive network approach to understand how representations are organized in memory because that structure can make cognitive processes more or less efficient.

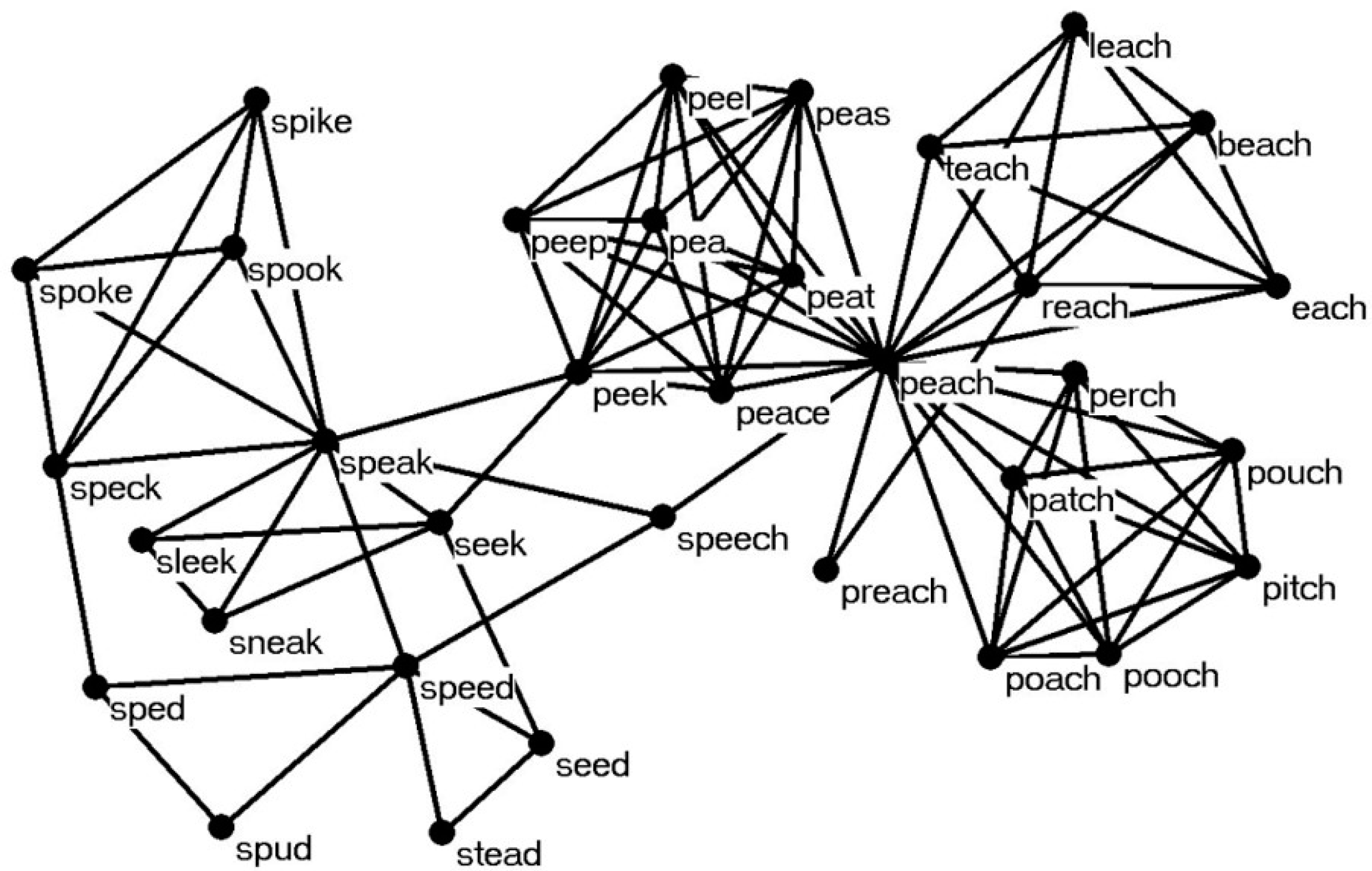
An example of a cognitive network is illustrated in Figure 2, where nodes represent words in the mental lexicon, and edges connect words that are phonologically related [17]. Cognitive networks can also be constructed of words that are semantically related [18], and, as in the simulations reported below, of sub-lexical representations instead of whole words.

In what follows we report the results of several computer simulations that explored how three different cognitive network architectures might account for the effects of phonotactic probability and neighborhood density on words and nonwords that were observed by [1,2]. The advantages and disadvantages of each cognitive network architecture are also discussed.

2. Simulation 1: Lexical Network

In the first simulation, we used the phonological network first examined by [17]. In that network, nodes represent 19,340 words in the mental lexicon, and edges connect words if the addition, deletion, or substitution of a phoneme in one word formed the other word (as in Figure 2). For example, deleting the /s/ in the word speech produces the phonologically related word peach.

Note that there are no sublexical representations—neither individual phonemes nor biphones—explicitly represented in this network. We were motivated to examine the extent to which a cognitive network containing only words could account for the effects of phonotactic probability and neighborhood density by two interesting findings.

First, [19] showed that phonotactic knowledge could emerge from lexical representations in their TRACE model of spoken word recognition. In this artificial neural network, it was found that phonotactic knowledge emerged as a result of a conspiracy effect among lexical representations. That is, the TRACE model would “know” that /tl-/ was not a legal sequence of word-initial phonemes in English, but that /tr-/ was a legal sequence of word-initial phonemes in English simply because there were several lexical representations that started with /tr--/, but none that started with /tl--/. The model did not explicitly represent information related to the legality or probability of sequences of phonemes, but such knowledge could emerge from the lexical representations.

Second, [20] used the Louvain method with a resolution of 0.2 to examine the community structure of the cognitive network of words examined by [17]. A modularity value, Q, of 0.655 was found, indicating a reasonably robust community structure. Further analysis of the communities, or sub-groups of words that were more likely to be connected to each other than to other words in the network, revealed that the words in a community tended to share common phonemes and sequences of phonemes. For example, one of the communities of words observed by [20] contained the biphones /ŋk/, /Iŋ/ and /rI/, which were found in the words rink, bring, drink and wrinkle that populated that community. It was suggested that if cognitive processing focused on the individual word node, one would observe the neighborhood density effects typically observed in other studies (e.g., [9]). However, if cognitive processing was distributed across multiple word nodes, perhaps considering the overall activation of a community, one might observe the sub-lexical effects reported in [1,2]. In the present simulation we used an R package called spreadr [21] to diffuse activation across the lexical network of [17] for several time-steps. Although there are other R packages that implement diffusion mechanisms in networks (e.g., [22]), spreadr implements the diffusion of activation in a way that is consistent with how it is commonly discussed and used in the cognitive sciences. In this context, activation is viewed as a limited cognitive resource that can spread to and activate the information in connected nodes (e.g., [23]).

The real words varying in neighborhood density and phonotactic probability that were used as stimuli in [2] were presented to the network model. To examine cognitive processing of the individual word, we examined the activation level of those stimulus words at the end of five time-steps during which activation had diffused across the network. To examine cognitive processing that was distributed across multiple word nodes, we considered the sum of the activation levels of all of the other words in the network that had been partially activated at the end of five time-steps. Note that the sum of the activation of all the words that had been activated after five time-steps results in processing that is more distributed than simply considering the activation levels of the other words in a given community. We elected to use all of the partially activated words rather than just the words in the community to which the stimulus word belonged in order to strike a balance between the idea from [20] of distributed processing, and the idea from [19] of conspiracy effects emerging from all of the words in the lexicon.

If [20] is correct, then when we examine the activation of the individual stimulus words, we should find that words that are low in neighborhood density/phonotactic probability will have higher activation levels (corresponding to faster and more accurate performance in humans) than words that are high in neighborhood density/phonotactic probability. Recall that words with high phonotactic probability tend to have high neighborhood density (and words with low phonotactic probability tend to have low neighborhood density). Henceforth, we will use the terms neighborhood density/phonotactic probability to emphasize effects driven by lexical representations, and phonotactic probability/neighborhood density to emphasize effects driven by sub-lexical representations. This result would replicate the effects observed by [1,2] for words that had been processed with lexical representations.

Further, when we examine the sum of the activation levels of all of the other words in the network that had been partially activated at the end of five time-steps, we should now find that words that are high in phonotactic probability/neighborhood density will have higher activation levels (corresponding to faster and more accurate performance in humans) than words that are low in phonotactic probability/neighborhood density. This result would replicate the effects observed by [12] for words that had been processed using sub-lexical representations.

2.1. Materials and Methods of Simulation 1

The network used in the present simulation consisted of the 19,340 words in the phonological network examined in [17]. Edges were placed between word nodes if the addition, deletion, or substitution of a single phoneme in one word resulted in the other word. The 140 real words from [2] were presented to spreadr ([21]; version 0.2.0) with the following settings for the various parameters in the model. An initial activation value of 20 units was used for each stimulus word in the present simulation. Our decision to use an initial activation value of 20 is arbitrary, and qualitatively similar results would be obtained using other initial activation values (e.g., [24]).

Decay (d) refers to the proportion of activation lost at each time step. This parameter ranges from 0 to 1, and was set to 0 in the simulations reported here to be consistent with the parameter settings used in previous simulations (e.g., [24,25]).

Retention (r) refers to the proportion of activation retained in a given node when it diffused activation evenly to the other nodes connected to it. This value ranges from 0 to 1, and was set to 0.5 in the simulations reported here. In [24] values ranged from 0.1 to 0.9 in increments of 0.1. Because the various retention values in [24] produced comparable results across retention values, we selected in the present simulation a single, mid-range value (0.5) for the retention parameter in order to reduce the computational burden, thereby accelerating data collection.

The suppress (s) parameter in spreadr forces nodes with activation values lower than a selected value to activation = 0. It was suggested in [21] that when this parameter is used a very small value (e.g., <0.001) should be used. In the present simulations suppress = 0 in order to be consistent with the parameter settings used in previous simulations (e.g., [24,25]).

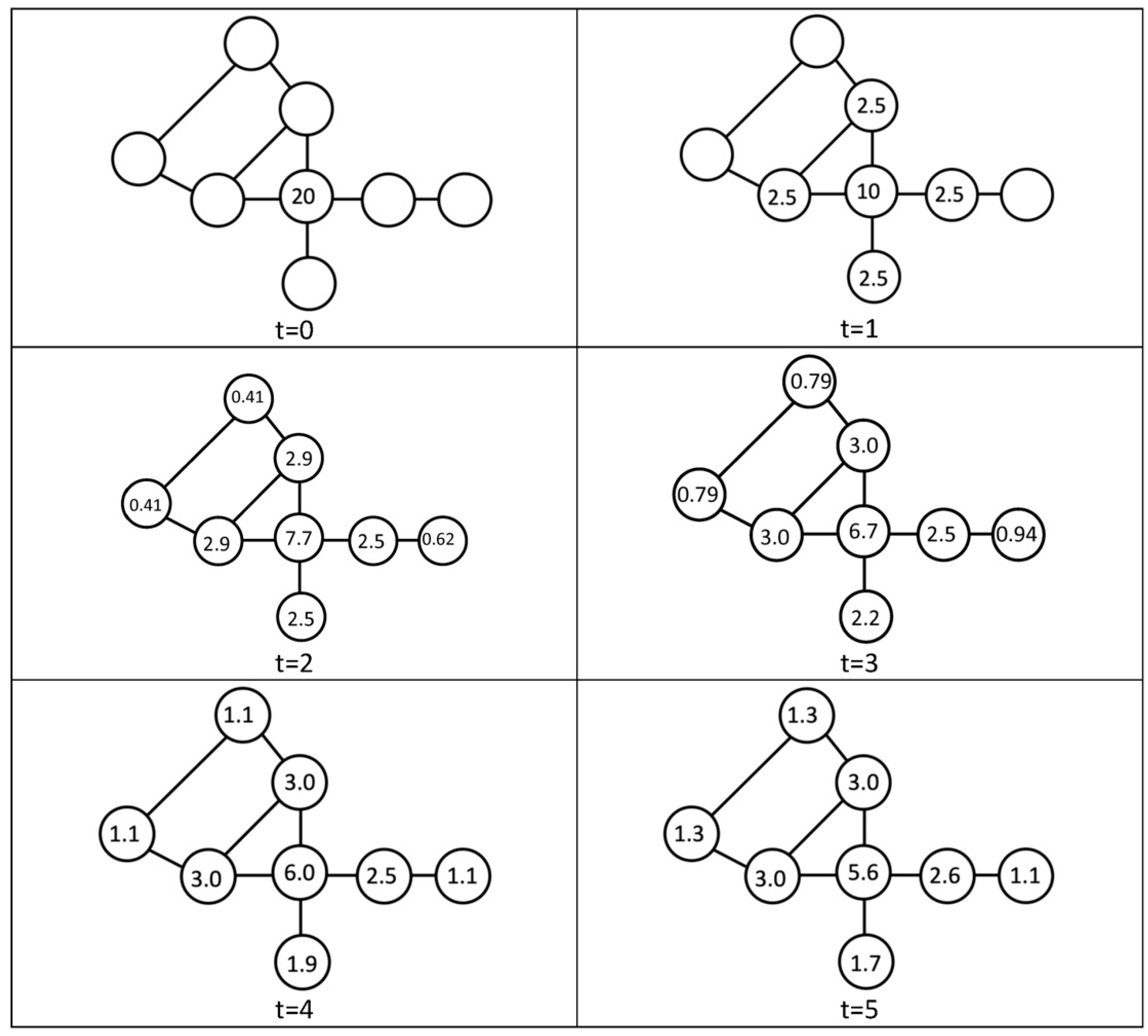
Time (t) refers to the number of time steps that activation diffuses or spreads across the network. In the present simulations t = 5. This value was selected because as shown in Figure 3 of [21], activation values reach asymptote in approximately five time-steps. Furthermore, as shown in the hop-plot depicted in Figure 2 of [26] approximately 50% of the network has been reached by traversing on average five connections (i.e., hops) in every direction from a given node, suggesting that the network has been sufficiently saturated. This value for the time parameter (t = 5) enabled us to reduce the computational burden, thereby accelerating data collection. At the end of five timesteps we documented the activation level of each of the stimulus words, and summed the activation of all the other words that had been partially activated.

Details about the words and nonwords used in the present simulations can be found in [1,2], but we provide here a few key characteristics of the stimuli. The 140 real words and 240 nonwords were monosyllabic, both had a consonant–vowel–consonant syllable structure. Phonotactic probability was calculated as in [27,28] taking in to account the frequency of occurrence of the segments and the biphones in the words and the nonwords. A median split was used to categorize the words and nonwords into the high and low phonotactic probability categories used in [1,2] and in the present simulations. A similar procedure (i.e., median split) was used to categorize the words and nonwords in to high and low neighborhood density categories. The words in the high categories were matched to words in the low categories on a number of factors including the initial phonemes of the words, stimulus duration, and frequency of occurrence in English. The nonwords in the high categories were matched to the nonwords in the low categories in a comparable manner.

2.2. Results of Simulation 1

In [1,2] words with low neighborhood density/phonotactic probability like dog were responded to more quickly and accurately than words with high neighborhood density/phonotactic probability like cat. In the cognitive network model implemented on spreadr, we found when looking at the activation values of the stimulus words that words with low neighborhood density/phonotactic probability had higher activation levels (mean = 1.23 units; sd = 0.31) indicating that they were responded to more quickly and accurately than words with high neighborhood density/phonotactic probability (mean = 1.14 units; sd = 0.14). Similar to the analyses used in [1,2], an independent samples t-test, a statistic that is robust to various assumption violations [29], was used [30] and indicated that this difference was statistically significant (t (138) = −2.29, p < 0.05). This result qualitatively replicates the results of [1,2].

As described above participants in [12] were induced to respond to words using sub-lexical representations, resulting in words with high phonotactic probability/neighborhood density being responded to more quickly and accurately than words with low phonotactic probability/neighborhood density. In the cognitive network model implemented on spreadr, we found when looking at the sum of the activation values of all of the other words in the network that had been partially activated at the end of five time-steps that words in the high phonotactic probability/neighborhood density condition had higher activation levels (mean = 18.86 units; sd = 0.14) indicating they were responded to more quickly and accurately than words with low phonotactic probability/neighborhood density (mean = 18.77 units; sd = 0.31). An independent samples t-test indicated that this difference was statistically significant (t (138) = 2.29, p < 0.05). This result qualitatively replicates the results of [12].

2.3. Discussion of Simulation 1

Based on the ideas of [19,20], see also [31], that phonotactic knowledge can emerge from lexical representations, we examined if a cognitive network that contained only words might be able to exhibit knowledge of phonotactic information. Previous attempts to account for the representation of phonotactic information have typically appealed to the explicit representation of words (i.e., lexical representations) and phonemes and biphones (i.e., sub-lexical representations). To examine if phonotactic knowledge could emerge from a cognitive network of only words we simulated the retrieval of the words from [1,2] in the phonological network of [17].

We predicted that when we examined the activation of the individual stimulus words, we should find that words that are low in neighborhood density/phonotactic probability will have higher activation levels (corresponding to faster and more accurate performance in humans) than words that are high in neighborhood density/phonotactic probability as observed in [1,2]. We further predicted that when we examined the sum of the activation levels of all of the other words in the network that had been partially activated at the end of five time-steps, we should find that words in the high phonotactic probability/neighborhood density condition will have higher activation levels (corresponding to faster and more accurate performance in humans) than words in the low phonotactic probability/neighborhood density condition, as observed by [12] for words that had been processed using sub-lexical representations. The results of Simulation 1 confirmed those predictions and provide some credence to the idea that phonotactic knowledge can emerge from lexical representations.

The results of Simulation 1 also demonstrate that some forms of phonotactic knowledge can be represented using the cognitive network science approach. This is an important demonstration because in order for the cognitive network approach to be a useful approach it should be able to account for a wide range of linguistic phenomena. The results of Simulation 1, therefore, represent an important step in that direction.

It is also important to acknowledge the limitations of the present simulation. Although lexical representations are typically used during spoken word recognition [1,2], there are other language processes that rely on sub-lexical representations, such as segmenting individual words from the stream of fluent speech [5], and learning new words [6]. Given that there are only words in the cognitive network used in the present simulation, there is no way to examine how these other linguistic phenomena might be accounted for by the cognitive network approach with the present network architecture. Indeed, there is also no way to examine the processing of the nonwords used by [1,2], because, by definition, nonwords are not represented in the lexicon. Therefore, in the simulations that follow, we explored different cognitive network architectures that included biphones (Simulation 2) and phonemes (Simulation 3).

3. Simulation 2: Network of Words Connected via Shared Biphones

Recall that the network used in Simulation 1 contained words that were connected based on the addition, deletion, or substitution of a single phoneme [17]. For example, the words cat (/kæt/) and cut (/kʌt/) were connected because substitution of the medial phoneme resulted in the other word. Even though the network did not have explicit knowledge of phonemes and biphones, the results of Simulation 1 showed that phonotactic knowledge could emerge from the lexicon. In the present simulation, we used a different network architecture to explicitly include knowledge of biphones in the cognitive network.

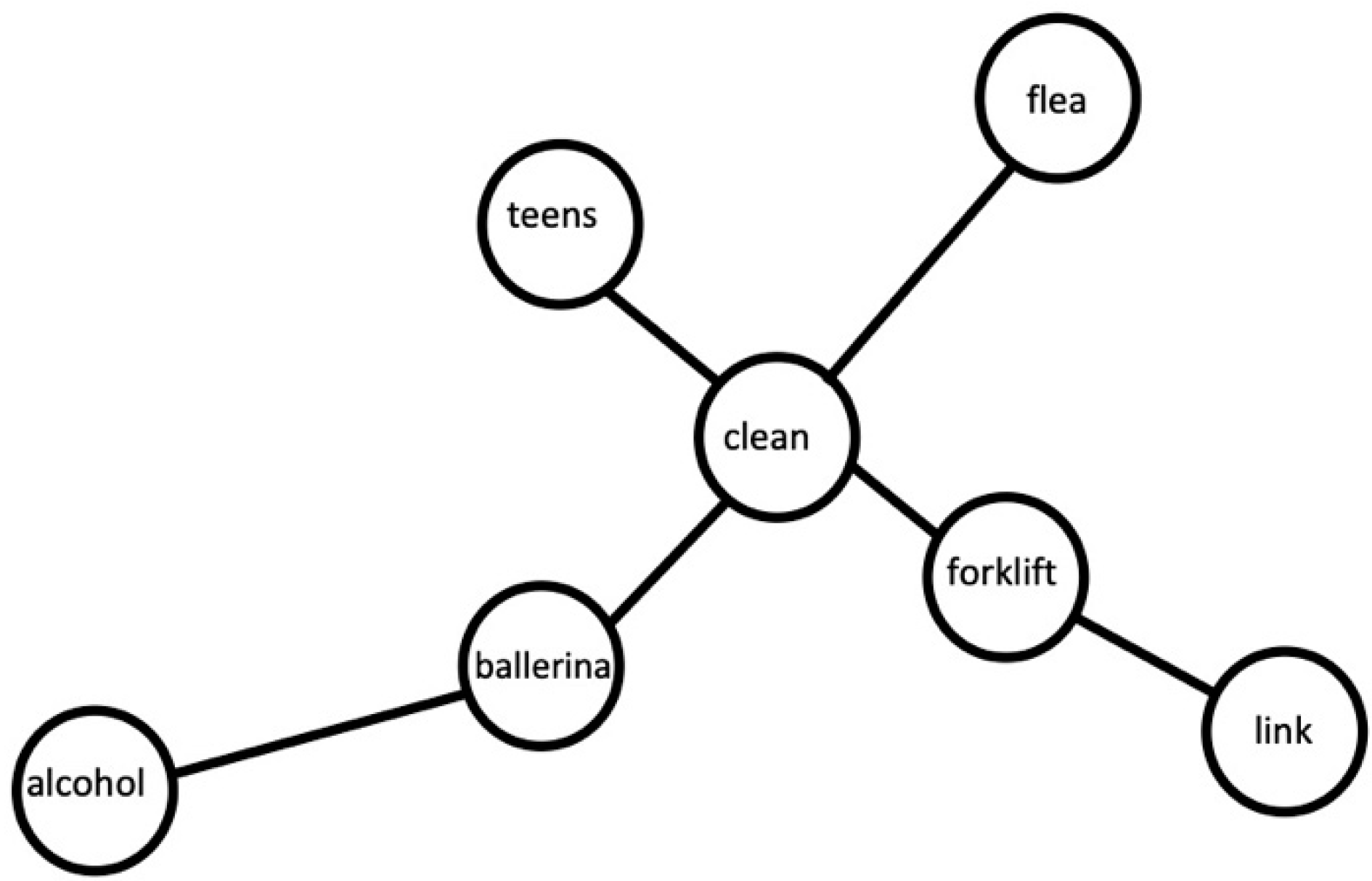
In the network used in the present simulation, nodes again represented the 19,340 words from the network used in Simulation 1. In this case, however, edges connected words if they contained one or more shared biphones (see [32] for networks constructed using a similar approach). As shown in Figure 4, for example, the word clean (/klin/) contains the biphones /kl/, /li/, and /in/. Edges in the present network would connect clean to all the other words that contain at least one of those biphones, such as flea (/fli/), teens (/tinz/), forklift (/fɔklɪft/) and ballerina (/baləɹinə/). The word clean (/klin/) would not be connected to words that merely contain some of the same phonemes, such as link (/lInk/) or alcohol (/ælkəhɑl/), both of which contain /k/ and /l/, but not the specific biphone /kl/. Although the words cat (/kæt/) and cut (/kʌt/) were connected in the network used in Simulation 1 [17], these words share no biphones, and are therefore not connected in the present network.

As in Simulation 1, the R package spreadr [21] was again used to diffuse activation across the network (using the same parameters as in Simulation 1). This allowed us to examine how a cognitive network with a different architecture might account for the effects of phonotactic probability and neighborhood density on the words originally tested in psycholinguistic experiments by [1,2].

3.1. Materials and Methods for Simulation 2

The network used in the present simulation contained the same 19,340 words used in Simulation 1 [17]. In Simulation 1, words were connected based on the addition, deletion or substitution of a single phoneme. In the present case, words were connected if they had one or more biphones in common. The networks used in the present simulation and in Simulation 3 were generated in R version 4.1.0 [33] using the following libraries: igraph version 1.2.6 [34], and tidyverse [35].

Although the present simulation used a new method by which to connect words, the degree (which corresponds to neighborhood density) of the words in the present network is qualitatively similar to the degree of the words in the network used in Simulation 1. For the network in Simulation 1, the words with high neighborhood density/phonotactic probability had a mean degree of 26.9 words (sd = 5.9), and the words with low neighborhood density/phonotactic probability had a mean degree of 20.0 words (sd = 7.0). For the network in Simulation 2 the words with high neighborhood density/phonotactic probability had a mean degree of 565.8 words (sd = 329.7), and the words with low neighborhood density/phonotactic probability had a mean degree of 258.6 words (sd = 182.9). A Pearson’s correlation shows that the measure of degree from the network used in Simulation 1 is correlated with the measure of degree from the network used in Simulation 2 (r (138) = 0.47, p < 0.001), suggesting that the two ways of placing edges between words in the two networks are similar. The R package spreadr [21] was again used to diffuse activation across the network. The same parameters used in Simulation 1 (decay = 0, retention = 0.5, suppress = 0, t = 5) were also used in the present simulation.

As in Simulation 1, the 140 real words varying in neighborhood density/phonotactic probability from [2] were again presented to the network. We again examined the activation value of each word at the end of five time-steps.

3.2. Results of Simulation 2

In [1,2] words with low neighborhood density/phonotactic probability were responded to more quickly and accurately than words with high neighborhood density/ phonotactic probability. In the cognitive network model implemented on spreadr with words connected because they shared biphones, we found when looking at the activation values of the stimulus words that words with low neighborhood density/phonotactic probability had higher activation levels (mean = 0.638 units; sd = 0.009) indicating that they were responded to more quickly and accurately than words with high neighborhood density/phonotactic probability (mean = 0.632 units; sd = 0.003). An independent samples t-test indicated that this difference was statistically significant (t (138) = −5.32, p < 0.001). This result qualitatively replicates the results of [1,2] and of Simulation 1 using a different way to represent phonotactic knowledge in the cognitive network architecture.

As in Simulation 1, we sought in the present simulation to examine the ideas of [19,20,31] that phonotactic knowledge can emerge from lexical representations. We again examined if the sum of the other activated words in the network would capture how words are processed if sublexical representations were used.

We found when looking at the sum of the activation values of all of the other words in the network that had been partially activated at the end of five time-steps that words in the high phonotactic probability/neighborhood density condition had higher activation levels (mean = 19.368 units; sd = 0.003) indicating they were responded to more quickly and accurately than words with low phonotactic probability/neighborhood density (mean = 19.362 units; sd = 0.009). An independent samples t-test indicated that this difference was statistically significant (t (138) = 5.32, p < 0.001), which qualitatively replicates the results of [12]. The different architecture for the cognitive network used in the present simulation also allows us to assess how the number of phonological neighbors affects processing using a different definition of phonological similarity. Recall that the number of phonologically related words is often determined by counting the number of words that are similar to a given word based on the addition, deletion, or substitution of a phoneme in one word to form another word [9,17]. However, phonological similarity has been defined in other ways as well [9,10].

In the present simulation, we can assess how the number of phonological neighbors influences processing using a different measure of phonological neighbor, namely the degree of each word, which in the present network indicates that two words share one or more biphones. A Pearson’s correlation shows a significant relationship between the number of neighbors a word has (i.e., degree based on sharing at least one biphone) and the activation value of the word after five time-steps (r (138) = −0.566, p < 0.001). That is, words with few neighbors had higher activation values indicating they were responded to more quickly and accurately than words with many neighbors. This result replicates previous findings about the influence of the number of neighbors on spoken word recognition that used different ways to define phonological similarity [9,10].

3.3. Discussion of Simulation 2

In the present simulation we used a different architecture to represent phonotactic information in the cognitive network. Specifically, word nodes were connected if they shared one or more biphones, thereby explicitly encoding phonotactic knowledge in the cognitive network in the edges between word nodes. This representational scheme differs from the architecture used in Simulation 1, where a word node was connected to another word node if the addition, deletion, or substitution of a single phoneme produced the other word. Despite using a different network architecture in the present simulation, we were still able to qualitatively replicate the results of [1,2]. That is, real English words with low neighborhood density/phonotactic probability were responded to more quickly and accurately than words with high neighborhood density/phonotactic probability. Further, when, as in Simulation 1, we summed the activation of the other partially activated words to assess the emergence of phonotactic effects from lexical representations we found that real English words with high phonotactic probability/neighborhood density were responded to more quickly and accurately than words with low phonotactic probability/neighborhood density, qualitatively replicating the results of [12].This new representational scheme also provided a different way to define phonological similarity among words, one that differs from the one-phoneme metric often used to define the phonological neighborhood [9]. Despite phonological similarity now being defined by the sharing of biphones, we also replicated the influence of phonological neighborhood density in spoken word recognition. Specifically, words with few phonological neighbors (i.e., low neighborhood density, or low degree in the network) are responded to more quickly and accurately than words with many phonological neighbors (i.e., high neighborhood density, or high degree in the network).

Although phonotactic knowledge was now explicitly encoded in the cognitive network via the edges between words, we, like in Simulation 1, were still not able to test how the cognitive network performs on the nonword stimuli used in [1,2]. The influence of sub-lexical representations such as phonemes and biphones appears limited in spoken word recognition [1,2]. However, there are other language processes that do rely on sub-lexical representations, such as segmenting individual words from the stream of fluent speech [5], and learning new words [6]. Further, [1,2] observed differences in performance in response to the nonwords that they constructed to vary in phonotactic probability. To more fully examine if the cognitive network approach can account for the influence of phonotactic knowledge on spoken word recognition and perhaps other language processes, we used yet another network architecture in Simulation 3. This new architecture will allow us to attempt to replicate via computer simulation the results observed by [1,2] for the real word as well as the nonword stimuli.

4. Simulation 3: Network Containing Phonemes and Words

In Simulations 1 and 2 the cognitive network contained only lexical nodes (i.e., they were one mode networks). In Simulation 1, phonologically similar word nodes were connected based on a one-phoneme metric. Thus, phonotactic knowledge was not explicitly encoded in the network, but, as suggested by [19,20], phonotactic knowledge can emerge from subsets of words in the lexicon. In Simulation 2, phonologically similar word nodes were connected if they shared one or more biphones. In that representational scheme, which was a one mode projection of a bipartite network containing biphones and word nodes, some phonotactic knowledge was explicitly encoded in the edges between nodes in the network.

In the present simulation we wished to encode phonotactic knowledge by including both phoneme nodes and word nodes in the network. However, in contrast to the one-mode projection used in Simulation 2, in the present simulation we retained the bipartite structure. Thus, word nodes were not directly connected to each other, and phoneme nodes were not directly connected to each other. Rather phoneme nodes connected to word nodes if the word contained that phoneme.

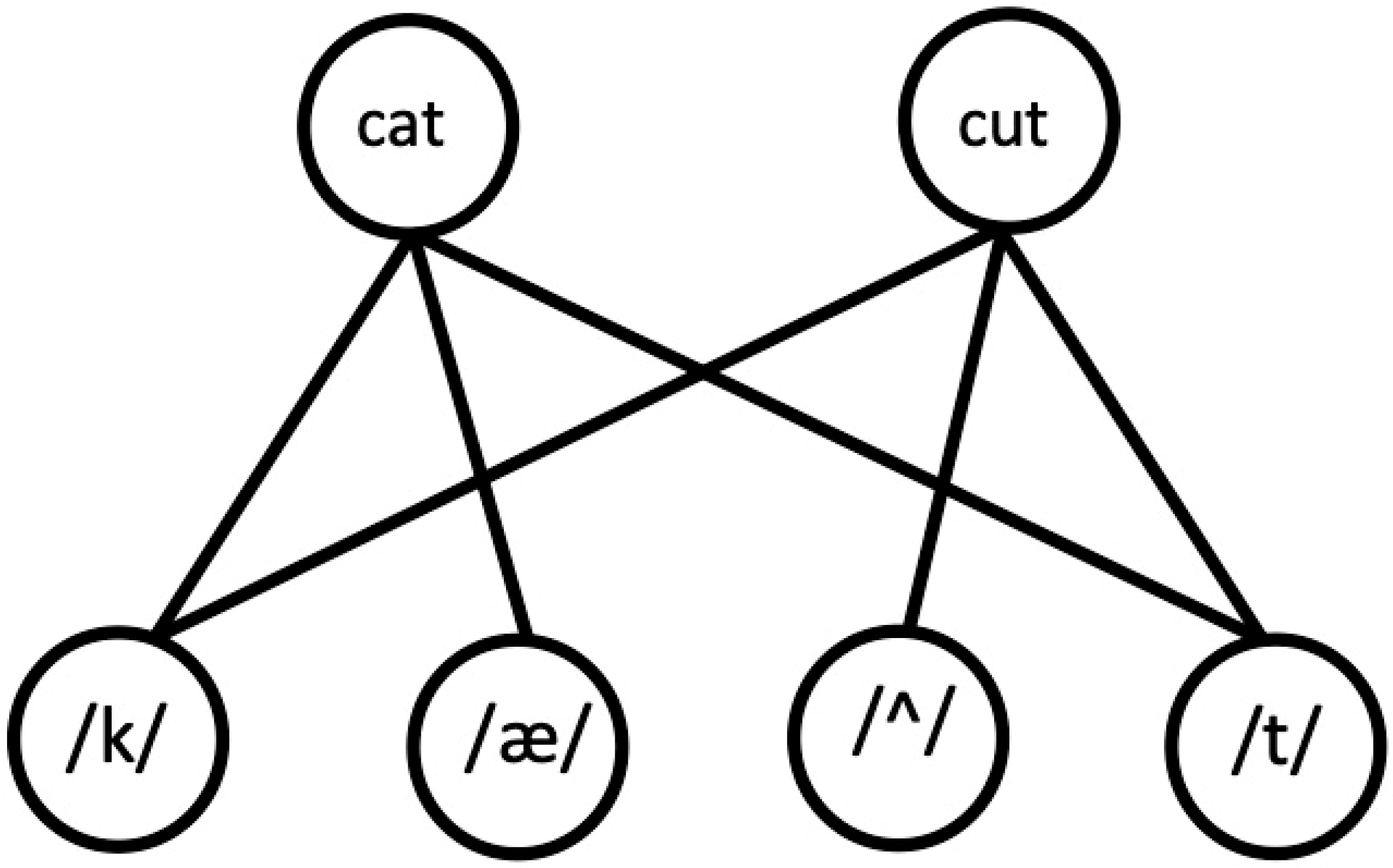
Consider the word nodes for cat (/kæt/) and cut (/kʌt/) as shown in Figure 5. In the network architecture used in Simulation 1, those word nodes would be connected by an edge, because of a single phoneme substitution of the medial segment. In the network architecture used in Simulation 2, those word nodes would not be connected by an edge, because those two words do not share a common biphone. In the bipartite network used in the present simulation cat and cut would again not be directly connected by an edge. Instead, nodes for the phonemes /k/ and /t/ would connect to the cat and cut nodes. Only the node for the phoneme /æ/ would connect to the node for cat, and only the node for the phoneme /ʌ/ would connect to the node for cut.

This bipartite network architecture allowed us to examine processing when lexical representations were used to respond to real words (as in Simulations 1 and 2) by considering the final activation levels of the word nodes. This network architecture also allowed us to examine processing when sublexical representations were used to respond to both real words [12] and nonwords [1,2] by considering the sum of the final activation levels of the phoneme nodes.

4.1. Materials and Methods of Simulation 3

The word nodes in the network used in the present simulation were the same 19,340 words used in Simulations 1 and 2 [17]. The phoneme nodes in the present bipartite network were the 45 phonemes used to transcribe the words. Word nodes were not directly connected to each other, and phoneme nodes were not directly connected to each other. Rather, edges appeared between phoneme nodes and word nodes if the word contained those phonemes, thereby forming a bipartite network.

The R package spreadr [21] was again used to diffuse activation across the network. The same parameters used in Simulations 1 and 2 were also used in the present simulation, except that activation was allowed to spread over twice as many time-steps given the increased distance between lexical representations resulting from the bipartite architecture of the network (decay = 0, retention = 0.5, suppress = 0, t = 10). To examine cognitive processing that uses lexical representations, activation started at the word node corresponding to the target word, and diffused across the network. After 10 time-steps, activation values in the nodes corresponding to the target words were then recorded and analyzed. To examine cognitive processing that uses sublexical representations, activation started at the phoneme nodes that were constituents of the target word or target nonword, and diffused across the network. After 10 time-steps, activation values in the constituent phoneme nodes were then recorded and the sum of those values were analyzed.

As in Simulations 1 and 2, the 140 real words varying in phonotactic probability and neighborhood density from [2] were presented to the network. This time, however, we also used the 240 nonwords (120 were designated high phonotactic probability/neighborhood density, and 120 were designated low phonotactic probability/neighborhood density) from [1,2].

4.2. Results of Simulation 3

In [1,2], when lexical representations were used to process the real English words, words with low neighborhood density/phonotactic probability were responded to more quickly and accurately than words with high neighborhood density/phonotactic probability. In the bipartite network model containing nodes for phonemes and words, we examined the activation values after 10 time-steps at the word nodes to simulate the use of lexical representations to process the words.

We found when looking at the activation values of the stimulus words that words with low neighborhood density/phonotactic probability had higher activation levels (mean = 0.021 units; sd = 0.0005086) indicating they were responded to more quickly and accurately than words with high neighborhood density/phonotactic probability (mean = 0.020 units; sd = 0.0002767). An independent samples t-test indicated that this difference was statistically significant (t (138) = −5.43, p < 0.001). This result qualitatively replicates the results of [1,2] and of Simulations 1 and 2 using a different way of representing phonotactic knowledge in the cognitive network.

In [12], when sublexical representations were used to process the real English words, words with high phonotactic probability/neighborhood density were now responded to more quickly and accurately than words with low phonotactic probability/neighborhood density, similar to the pattern typically seen for nonwords. In the bipartite network model containing nodes for phonemes and words, we examined the sum of the activation values after 10 time-steps at the phoneme nodes to simulate the use of sublexical representations to process the words.

We found when looking at the sum of the activation values of the phoneme nodes corresponding to the stimulus word that words with high phonotactic probability/neighborhood density had higher activation levels (mean = 4.190 units; sd = 0.682) indicating they were responded to more quickly and accurately than words with low phonotactic probability/neighborhood density (mean = 3.516 units; sd = 0.727). An independent samples t-test indicated that this difference was statistically significant (t (138) = 5.66, p < 0.001). This result qualitatively replicates the results of [12].

We now consider the results for the nonwords. In [1,2], when sublexical representations were used to process the nonwords, nonwords with high phonotactic probability/neighborhood density were responded to more quickly and accurately than words with low phonotactic probability/neighborhood density. In the bipartite network model containing nodes for phonemes and words, we examined the sum of the activation values after 10 time-steps at the phoneme nodes to simulate the use of sublexical representations to process the nonwords.

We found when looking at the sum of the activation values of the phoneme nodes that were found in the nonword that nonwords with high phonotactic probability/neighborhood density had higher activation levels (mean = 3.708 units; sd = 0.607) indicating they were responded to more quickly and accurately than nonwords with low phonotactic probability/neighborhood density (mean = 2.150 units; sd = 0.372). An independent samples t-test indicated that this difference was statistically significant (t (238) = 23.97, p < 0.001). This result qualitatively replicates the results of [1,2].

4.3. Discussion of Simulation 3

In the present simulation we used a bipartite network containing nodes for phonemes and words. Phoneme nodes were not connected to each other, and word nodes were not connected to each other (in contrast to the word nodes in the networks used in Simulations 1 and 2). Rather, phoneme nodes connected to word nodes if that phoneme was a constituent of that word. This network architecture enabled us to simulate the use of lexical representations to process real words by considering the activation values at the word nodes after 10 time-steps.

Rather than looking at the emergence of phonotactic effects from a conspiracy of lexical representations as we did in Simulations 1 and 2, we were able in the present simulation using a different network architecture to examine the use of sublexical representations to process the real words and nonwords by considering the sum of the activation values at the phoneme nodes after 10 time-steps. The results of the present simulation using this bipartite representational scheme replicated the results for the words and nonwords observed in [1,2], and for the real words observed in [12].

5. Conclusions

We reported the results of computer simulations using three different network architectures to explore how the cognitive network approach might be used to represent phonotactic knowledge. Previous attempts to account for the processing of phonotactic information relied on artificial neural networks with lexical and sub-lexical representations [14]. However, more recent accounts have suggested that phonotactic knowledge could emerge just from lexical representations [20]. Therefore, in Simulation 1 we tested whether phonotactic information could emerge from a cognitive network of phonologically related words that did not have phonotactic information explicitly encoded in it, and did not have a separate layer of sub-lexical representations.

The simulation of lexical retrieval from the network of phonologically related words qualitatively replicated the results for real words observed by [1,2]. That is, when specific lexical representations were used to process the input, words with low neighborhood density/phonotactic probability had higher activation levels (indicating faster and more accurate responses) than words with high neighborhood density/phonotactic probability.

To examine the emergence of phonotactic information from collections of partially activated words in the lexicon we analyzed the sum of the activation levels of all of the other words in the network that had been partially activated at the end of five time-steps. In that analysis we found that words in the high phonotactic probability/neighborhood density condition had higher activation levels (corresponding to faster and more accurate performance in humans) than words in the low phonotactic probability/neighborhood density condition, as observed by [12] for words that had been processed using sub-lexical representations. The results of this simulation lend credence to the idea that phonotactic knowledge can emerge solely from lexical representations. However, this network architecture which lacked sub-lexical representations (and of course did not, by definition, include nodes for nonwords in the lexicon) did not allow us to examine the effects observed by [1,2] for nonwords varying in phonotactic probability, prompting us to explore different network architectures in Simulations 2 and 3.

In Simulation 2 we explicitly modeled phonotactic knowledge in the network by connecting word nodes if they shared one or more biphones. Using this network architecture, we again found that words with low neighborhood density/phonotactic probability had higher activation levels (indicating faster and more accurate responses) than words with high neighborhood density/phonotactic probability, as observed by [1,2].

This network architecture also provided us with an alternative way to define phonological similarity that differed from the one-phoneme metric used to define phonological similarity among words in the network that was used in Simulation 1. Using this alterative definition of phonological similarity, we found that words with few phonological neighbors (i.e., low neighborhood density, or low degree in the network) were responded to more quickly and accurately than words with many phonological neighbors (i.e., high neighborhood density, or high degree in the network), replicating the often-observed effects of neighborhood density in spoken word recognition [9,10].

Finally, in Simulation 3 we used a bipartite network containing nodes for words and nodes for phonemes in order to explicitly represent phonotactic information with sub-lexical representations. This network architecture also allowed us to test whether the cognitive network approach could also account for the results observed by [1,2] for specially constructed nonwords in their psycholinguistic experiments. The results of the simulation using the bipartite representational scheme replicated the results for the words and nonwords observed in [1,2], and for the real words observed in [12], demonstrating that with the right network architecture the cognitive network approach can be used to account for the previously observed effects of phonotactic probability and neighborhood density on spoken word recognition. Future simulations could explore how these network architectures might account for the influence of phonotactic probability and neighborhood density in other language processes. The present set of simulations illustrates the value of using computer simulations to explore how different cognitive network architectures might or might not account for previously studied phenomena. For example, Simulations 1 and 2 contained lexical representations, but not sublexical representations. The network architectures in Simulations 1 and 2 allowed us to explore lexical effects (i.e., neighborhood density), and the idea that phonotactic information may emerge from a conspiracy of lexical representations. However, without sublexical representations in the networks used in Simulations 1 and 2, we were not able to directly examine some of the phonotactic probability effects that had been previously observed, especially those effects obtained with nonword stimuli (which by definition are not represented in the lexicon). The present work therefore highlights how important the network architecture is for accounting for a wide range of psycholinguistic phenomena.

For other demonstrations of cognitive networks accounting for other phenomena related to language and memory see [21]. We believe it is important for new approaches, such as cognitive networks, to be able to account for previous findings in new ways, as well as generate new ideas for future research.

The present exploration of alternative network architectures suggests that future work using cognitive networks may need to consider network architectures that are more complex in order to examine other types of linguistic phenomena. Those more complex network architectures may incorporate multiple layers of representation, like the bipartite network used in Simulation 3, or may take the form of multiplex networks. In multiplex networks there may be a network of phonologically related words connected to another network layer in which the words are connected by edges if they are semantically related. Such networks have been used to examine a number of language phenomena, including the word-finding difficulties of people with aphasia (e.g., [36]).

Another approach may be to employ feature-rich networks [37], which are networks that include additional information (e.g., temporal or probabilistic information) to complement the topological information inherent in the network itself. One type of feature-rich network is a node-attributed network, which adds categorical or numerical information to the nodes. In the case of cognitive networks representing the mental lexicon, one might include information regarding the part of speech, length of the word, frequency of occurrence, or age of acquisition of the word nodes. Work on community detection algorithms in node-attribute networks has been able to successfully detect important modules that could not be detected by topological or homophilic clustering criteria alone [38], highlighting the insight that network science approaches might provide to language researchers. In addition to feature-rich networks, it might be worth exploring networks that grow over time. Such networks have been used to explore word learning and changes in the lexicon with age (e.g., [39]). Much research has examined how phonotactic information influences word learning (e.g., [6,40]). Exploring how phonotactic knowledge is represented in various types of cognitive networks that grow over time might be a productive way to further examine typical language development as well as atypical language development (e.g., [41]). We believe the cognitive network approach offers Psychology (and other related disciplines) a simple yet powerful way to model how knowledge is represented in memory, and how the structure of that knowledge might influence cognitive processing.