1. Introduction
Face verification is one of the main computer vision challenges that has been intensively researched for more than twenty years [
1,
2,
3,
4]. Face verification is not only considered for its various applications, such as passport control at airport terminals and system access control, but also for face search problems in large galleries. In face verification, two face images are given, with the aim to decide whether they relate to the same individual or not. Most of the face verification and recognition techniques yield acceptable results on a set of pictures that are captured in constrained environments. However, face images of the same person seem to be very contrastive when captured in various illuminations, poses, expressions, occlusions, and aging. Different identities could also look very similar, like the case of twins or father and his son. Accordingly, inter-personal differences magnification and intra-personal variation reduction are becoming an active research topic in face verification. Generally, recent face verification methodologies use Convolutional Neural Network (CNN) [
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15] to process each one of a pair of faces independently. This implies the need for a large dataset for training. Siamese neural networks process images in pairs and focus on learning embedding in deep hidden layers, which results in more accurately determining the distance between faces. Two images are handled in parallel, following a stepwise interlaced manner that allows for identifying similarities and differences more precisely, even when the available training dataset size is limited. Hence, similar faces are clustered together more efficiently. When several face classes in a dataset have only a few training instances, a traditional Deep Convolutional Neural Network (DCNN), which is the state of art in face recognition, will most likely fail to learn seldom observed face classes during training as their pairwise dissimilarity with other classes is not accurately expressed. Hence, Siamese NN outperforms DCNN in face verification when only a few training samples are available for a person.
The goal of this research is to design a deep Hybrid Siamese network for face verification that has high precision, is highly optimized in run-time performance, uses a small dataset, and affordable computing resources, when compared to other similar systems reported in the literature [
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15].
We were encouraged to further use these features to enhance the performance of the face clustering problem due to the achieved success in learning efficient face features using the proposed Hybrid Siamese network. Clustering large sets of untagged face pictures by identity are significant in speeding up face recognition, which is an important issue in real-time security systems. Face clustering is used as a preparation for manual/automatic examination of a set of pictures in surveillance systems, public security, and other applications. In many clustering scenarios [
16,
17,
18], the labels of the face images may be provided, but most likely they are either noisy or deficient. Some face images may be incorrectly labelled. In most clustering situations, the number of personalities that appear in a dataset is expected to be enormous and unknown. A challenging aspect in clustering face pictures is that the outcomes rely not just on the selection of clustering technique, yet in addition to the face representation and metric used. There is no generally approved face representation or distance metric.
In this study, a single neural network (NN) based on Hybrid Siamese model architecture is proposed for face verification. A face clustering system is developed, which uses the features extracted by the proposed Hybrid Siamese face verifier. The proposed architecture utilizes a small dataset (0.5 million images) and it was still able to achieve significant verification accuracies when tested on the Labeled Faces in the Wild (LFW) benchmark [
19] and Arabian faces dataset [
20]. These accuracy levels were achieved by other systems [
5,
6,
7,
8,
9,
10,
11,
12,
14] but via training using datasets that are (2–10) times bigger than ours or using multiple NNs. The proposed architecture decreases the neural network training time from days to a few hours on a single GPU. The proposed clustering system is based on a modified DBSCAN and using a novel post-processing optimization procedure, which enhances the recall and F1-measure.
This paper is organized, as follows: in
Section 2, some related works are briefly reviewed. The Hybrid Siamese model architecture used to find similar/dissimilar face images and the proposed post-clustering optimization procedure are described in
Section 3. The details of used datasets and the experimental verification/clustering results are provided and discussed in
Section 4. Finally, the paper is concluded in
Section 5.
2. Literature Review
Face recognition is a comprehensive topic that incorporates face identification and face authentication/verification. Face identification is the process of recognizing a person relied on an image of the face. This face image is compared to a face database to answer “Who is this person?” question. Face verification is the process of confirming a supposed identity relied on face images. Two face images are matched to decide whether they are of the same identity or not. Nowadays, superior face recognition techniques [
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
14,
20,
21,
22,
23,
24,
25] depend on DCNNs. The majority of these techniques have surprisingly outperformed humans on the LFW [
19] dataset. Google’s FaceNet [
6], Facebook’s DeepFace [
4], Baidu [
11], and DeepVisage [
12] models achieved the most remarkable accuracies. Nevertheless, these models use personal datasets for training, comprising millions of social media pictures that are bigger than any obtainable research dataset. FaceNet [
6] applied the inception CNN architecture [
26] to the problem of face recognition. This network was trained using a large scale private dataset of more than 200 million identities. A deep network coupled with 3D alignment is used by Deep-Face [
4] in order to normalize facial pose by warping facial landmarks to a canonical view before encoding. Their best performance on LFW is obtained from a combination of three networks while using different alignments and color channels. A Siamese [
27] Deep-Face network was also experimented in [
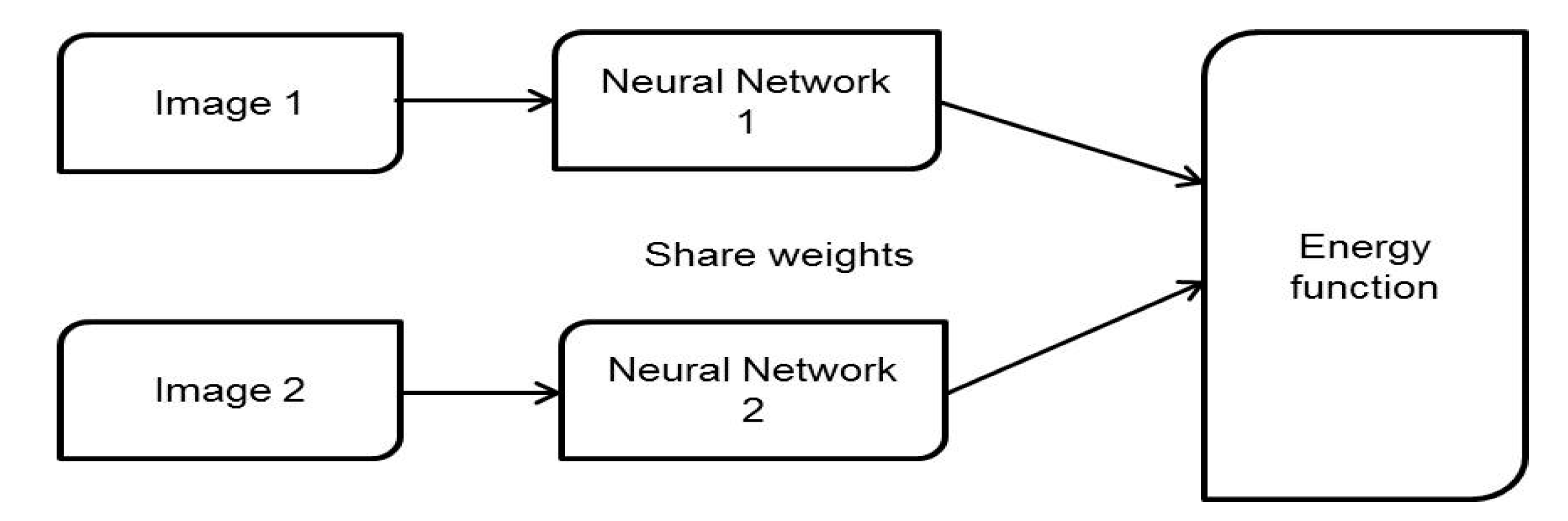
4], where the L1-distance between two facial features was optimized. Deep-Face models were trained on about 4 M face pictures captured for 4000 people. A traditional Siamese neural network comprises two identical networks where a different input vector is given to each network. The two networks are connected by an energy function at the topmost. This energy function calculates some metrics between the highest-level representations of each branch (
Figure 1). The two network’s weights are shared. By weight sharing, two similar images guarantee to be mapped by their particular networks to very near positions in the feature space as each branch of the Siamese network calculates the same metric. DeepID2 [
5] introduce 25 networks, each network process a different face region. Subsequently, 50 (regular and flipped) responses are merged for their performance in the LFW dataset. DeepID3 [
7] extended the inception architecture to train the network for the joint identification-verification task. Parkhi et al. [
10] introduced a large face dataset, called VGG-Face, and proposed the VGG model for face recognition. The VGG-Face database consists of 2.6 M face pictures of 2622 celebrities with manual filtering. The network consists of five convolution blocks (each of them has two or three convolutional layers and max-pooling layers) trailed by three fully connected layers. It was trained using their proposed dataset only, which is much smaller than the training datasets utilized by other methods like [
4,
6,
12].
Chen et al. [
3] trained a DCNN utilizing a relatively small face dataset that has 494,414 face images of 10,575 subjects. Subsequently, the joint Bayesian metric is computed utilizing the deep features and the training dataset. The data is augmented with horizontally flipped face images. Given a pair of test pictures, the similarity is computed dependent on their deep features and the learned metric. Their network was fine-tuned on the training splits, at a significant computational cost. The verification cost was not taken into consideration; Their DCNN is trained for around nine days utilizing NVidia Tesla K40. DeepVisage [
12] proposed a single DCNN based method. The DCNN model consists of 27 convolutional layers and one fully connected layer, which incorporates the residual learning framework. In addition, it applied a batch normalization approach for feature descriptor normalization prior to utilizing the softmax loss. They gather the training pictures from the cleaned version of the MS-Celeb-1 M dataset, which consists of 4.47 M pictures of 62.5 K characters. The proposed DCNN model is trained utilizing only the identity label of each face picture.
In [
14], an L2-constraint is added to the basic softmax loss in order to train a face verification system. The proposed constraint forces the extracted features to lie on a hypersphere of a particular radius. It can be easily implemented utilizing existing deep learning systems. Experiments showed that incorporating this simple constraint in the training pipeline provides a significant improvement in face verification performance for the LFW dataset. In [
25], a generic pyramid-based scale-invariant (PSI) CNN was presented that utilized the additionally extracted untrained feature maps from multiple picture resolutions in order to improve matching accuracy in low-resolution pictures. It permits the network to be scale-independent. In [
2], a single DCNN was introduced and a Bayesian probabilistic model was utilized in the embedding space, which efficiently corresponds to a linear transform. A comprehensive review of the literature and classifications of the face verification methodologies can be found in [
24].
The clustering problem has been intensively studied in pattern recognition and machine learning literature. A brief review of some face clustering techniques and some general clustering methods are given in this section. The most widely used clustering techniques are K-Means [
28] and spectral [
29]. The main drawback of K-Means is its sensitivity to the initialization and difficulty to deal with clusters of size, density, and shape variations. Spectral clustering, on the other hand, has the ability [
16,
29] to deal with the inhomogeneous distributions effectively; however, it has high complexity and it typically works inadequately with the presence of outliers and noises. In addition, K-Means and spectral clustering techniques need to determine the cluster’s number at the beginning, which is unsuitable for a wide range of practical applications. Agglomerative hierarchical clustering algorithms [
30,
31,
32] do not need to define the number of clusters a priori. Beginning with every sample as a cluster, in each iteration nearest cluster pairs that fulfil some similarity/distance measure are joined until no cluster pair fulfils the join criteria. The only distinction among these algorithms is their diverse similarity/distance criteria for joining. DBSCAN [
30] considers adequately high-density areas as clusters and finds out clusters of random shapes in datasets with noise. A cluster is outlined as a maximal set of density-connected data samples according to density-reachability. DBSCAN differs from K-means and spectral, as it does not require determining the clusters’ count at the beginning. It outperforms K-Means at clustering non-spherical data. In addition, it can detect a cluster that is wholly surrounded by a different cluster, but not linked to it.
In face clustering, a joint subspace learning and clustering approach is developed by Vidal and Favaro [
33]. The method is evaluated on the extended Yale-B database. A semi-supervised method for organizing face datasets for improved retrieval speed via hierarchical clustering is developed by Bhattarai et al. [
17]. In [
34], a personal images clustering approach utilizes a diversity of contextual data involving clustering based on time, and the likelihood that faces of certain persons appear together in images, with identity estimations being obtained via a two-dimensional (2D)-Hidden Markov Model, and hierarchical clustering outcomes relies on the detection of the body structure. The algorithm is tested utilizing a dataset of 1,500 face pictures of eight persons. A semi-automatic tool for image annotation is proposed in [
35], which applies clustering as an initial step for sorting out pictures. The recognized face is utilized to obtain Local Binary Pattern (LBP) features, and the recognized body structure is used in order to obtain texture and colour features. Spectral clustering is applied, and the clustering outcomes are manually adjusted by an individual. Assessment is completed on a dataset of four hundred pictures of five persons. Moreover, Tian et al. [
16] suggest tagging faces with partial clustering and repetitive labelling that includes a “junk” cluster, permitting the proposed procedure to ignore clusters that have loosely-coupled data samples. To accomplish high precision, most of the faces are not clustered and the sizes of the created clusters are small. As a result, numerous manual activities are needed to name these faces. In [
36], hierarchical clustering is applied that is dependent on rank-order distance. The computed distance depends on the rankings of a face images pair according to each face’s closest neighbours. A Deep Closed-Form Subspace Clustering (DCFSC) was introduced in [
18] to learn non-linear mapping. DCFSC utilized the implicit data-driven self-expressive layer derived from closed-form shallow auto-encoder. The model was evaluated on face clustering, utilizing the extended Yale B and ORL face datasets. The good clustering results of private gallery utilizing a deep learning-based face representation are reported in [
4]. Following recent advancement in unconstrained face verification, the face clustering difficulty can be overcome if distinctive features are used. The clustering system that was proposed in this paper uses features extracted from a hybrid Siamese network coupled with an updated version of DBSCAN. The update is partially inspired by Dynamic Method DBSCAN (DMDBSCAN) [
37]. Although DBSCAN [
30] is an old classical clustering technique, it has been efficiently updated using a Dynamic Method to develop DMDBSCAN [
37], which can automatically calculate system parameters, hence improving the performance. This improvement in performance inspired us to attempt to further update DBSCAN. Our update includes using a hybrid Siamese network-based face verifier and the K-distance Plot idea suggested in DMDBSCAN in addition to a post-clustering optimization procedure.
Three main contributions are proposed in this paper. Firstly, an effective deep Hybrid Siamese neural net architecture was developed for face verification based on Deep Convolutional Neural Network (DCNN). The proposed method reached near human-performance in the LFW benchmark and when tested on Arabian faces dataset [
20], using a small training dataset and simple architecture. Secondly, the neural network training time was reduced according to the proposed architecture from days to a few hours on a single GPU. Thirdly, a novel post-clustering optimization procedure coupled with an updated version of the DBSCAN clustering algorithm is proposed. It improves the recall of the clusters generated and enhances the F1-measure on the LFW and Arabian faces datasets.
3. Proposed Method
Although face verification is a two-image matching problem, most of the current face verification techniques use methods borrowed from face recognition. These methods process each of the face images independently, which is counter-intuitive. Verification should inspire parallel processing techniques. For instance, given two face images, verifying whether both face images are of the same person is performed by running each of them separately through a face detector trained on images of that person, and then combine the detector’s outputs. This is different from utilizing a verification classifier that takes a pair of face images as input and classifies them jointly as being both of the same person or not. The latter classifier would be trained on similar/different person pairs, which is more distinctive for face similarity and dissimilarity. Given a collection of images, the Siamese Network attempts to discover how comparable two given images are. The proposed approach aims to build a face verification end to end trainable system. It accepts the face image pair as input and runs them simultaneously. It nonlinearly maps the raw face images into points in a low-dimensional feature space where the distance between features vectors of the same person images is small and large otherwise. The goal is to learn a general similarity metric for face image pairs by training a deep hybrid Siamese network. Under this setting, different tasks can be performed utilizing few or unlabelled data. In the Siamese networks, each of the identical networks maps the face image to high-level features. These high-level features of the two face images are joined by a similarity metric. Hence, they benefit from relationships between faces, easily label face pairs as similar/dissimilar pairs, and it is also capable of generalizing to new unseen inputs and output.
The main design consideration is a system that provides high accuracy accompanied by low training time and prediction time. In general, the main problem of DCNN training in computer vision is to find a large, reliable dataset appropriate for a particular task. Training a DCNN requires a lot of data. As small training datasets are available for research, the proposed system will benefit from the concept of transfer learning [
38]. It is a popular approach in deep learning, where pre-trained models on a specific problem are used as the starting point in another problem. Inspired by the ongoing accomplishment in image classification, the FaceNet pre-trained model is used as a prime component of the proposed network. The architecture of the FaceNet pre-trained model [
39] pursues the Inception ResNet-v1 architecture depicted by Szegedy et al. [
40].
3.1. Proposed Face Verification Method
The proposed system is trained utilizing 100 K coloured face images of 500 celebrities from FaceScrub dataset [
41] (the images for which face alignment was carried out effectively). First, the data was divided into 80% and 20% for training and validation, respectively.
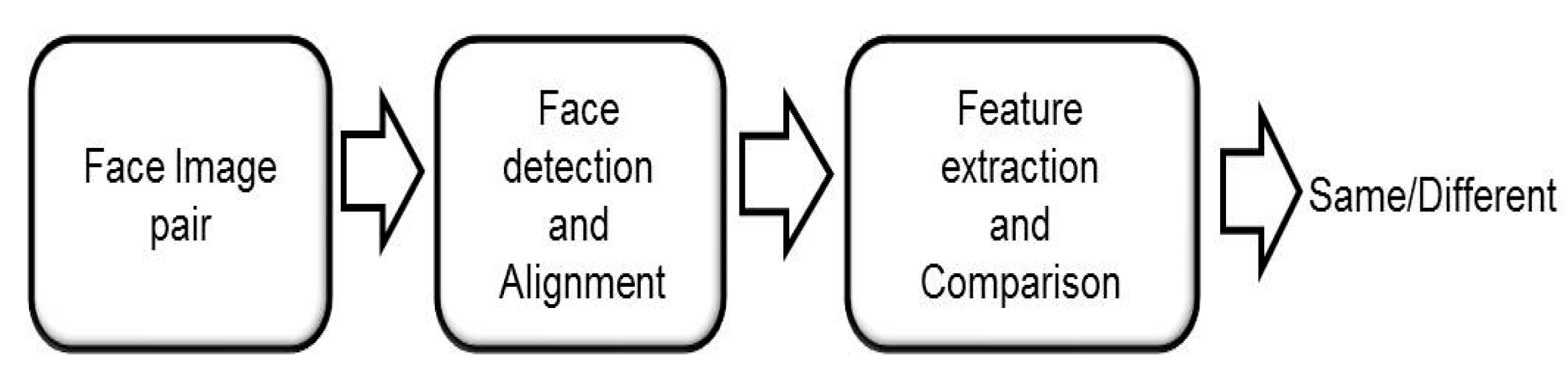
Figure 2 depicts the pipeline of the proposed face verification approach.
3.1.1. Pre-Processing
Pre-processing is an important step before training the proposed hybrid Siamese network. As a start, joint face detection and alignment using Multi-task Cascaded Convolutional Networks (MTCNN) developed by Zhang et al. [
42] is applied in order to find out facial landmarks to localize each face. A deep cascaded multitask procedure is introduced that applies the inherent correlation for performance improvement. The CNN framework comprises of three phases: the first phase quickly creates candidate windows through a shallow CNN. Subsequently, the subsequent phase refines the windows by dismissing all non-face windows via a more complicated CNN. The last phase utilizes a more robust CNN to refine the outcomes and yield facial landmark positions. Afterwards, face alignment is applied to each detected face. In particular, the alignment pre-process is important for lessening problem fluctuation and, thereby, both the needed training set size is decreased, and the precision of the classifier is enhanced. After alignment, the face image is scaled to 160 × 160 pixels. A pre-whitening method is employed in order to process the face images to increase training efficiency in spite of the image’s illumination conditions. The average is subtracted from the pixels in order to normalize the range of the pixel values of input face images, which will ease the training.
3.1.2. Network Architecture
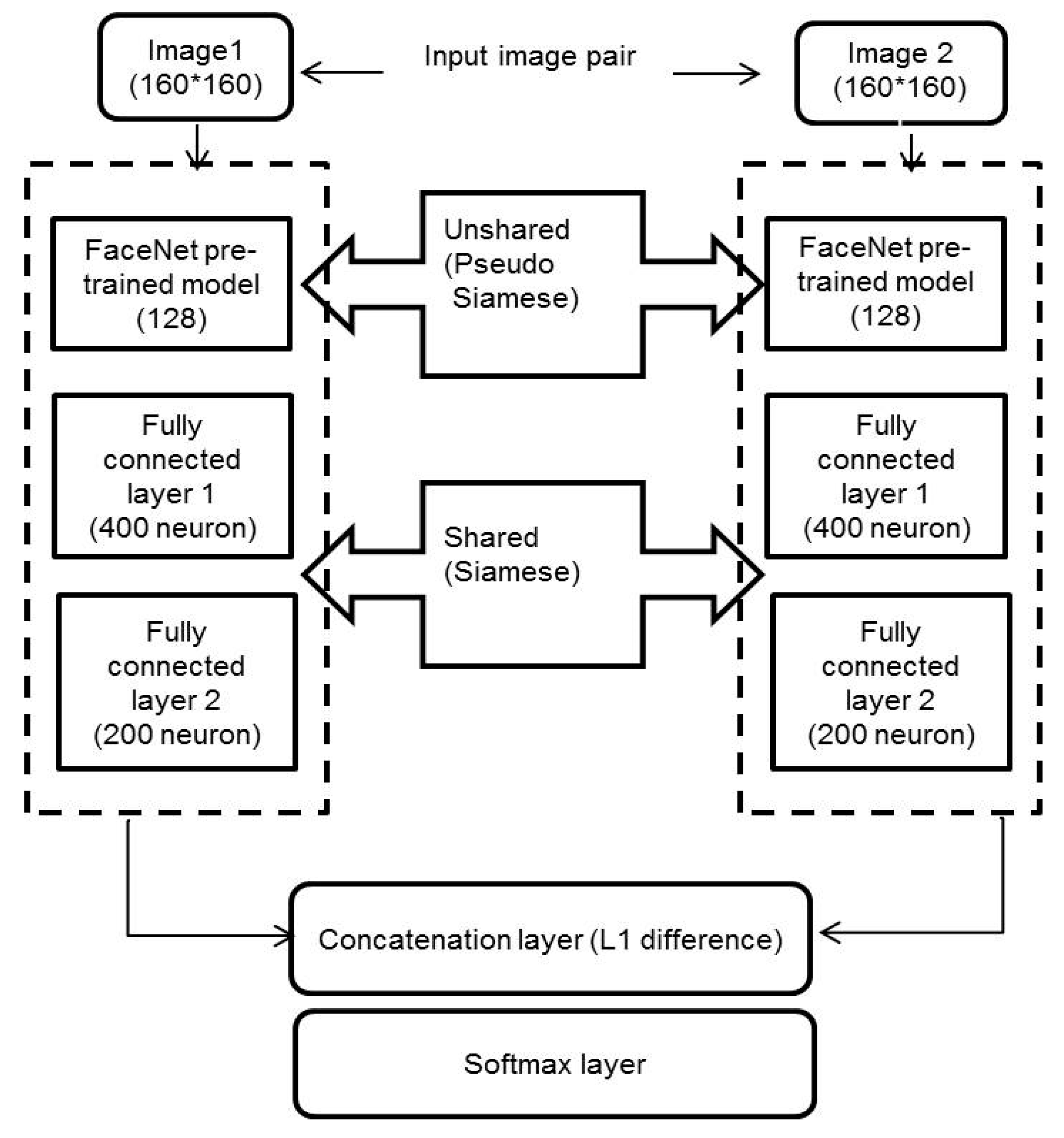
A hybrid Siamese network is proposed instead of the traditional Siamese network to avoid overfitting. The proposed hybrid Siamese network is implemented utilizing the open-source TensorFlow [
43] library. A lot of trials are performed to choose the parameters utilized in each layer, like the number of neurons. This subsection introduces the specifics of the best deep hybrid Siamese neural network that accomplishes the highest verification results. It comprises of two branches. Each branch has a part that shares the parameters and another part that does not share the parameters. Each branch processes a single face image and, thus, the hybrid Siamese network receives two face images as input, as depicted in
Figure 3. Each input image is a 2D aligned RGB face image. Subsequently, each image is mapped to a 200-dimensional feature vector utilizing the corresponding Siamese branch. Each Siamese branch consists of a FaceNet pre-trained model. Two fully-connected layers follow the pre-trained model output.
3.1.3. Learning
The proposed Hybrid Siamese neural network’s main training target is to deduce the likelihood that a face image pair belongs to the same person. If the face images pair belongs to the same person, the proposed network has to yield 1; or else, it has to yield 0. The fully connected layer output can be calculated while using the following equation:
where j = 1, 2 for the first and second fully-connected layers, respectively, h
i is the output of the previous layer, and W
j is the interconnection weights matrix between the previous layer output and the fully-connected layer, b
j is the layer bias, and
(.) is the activation function. A Rectified Linear Unit (ReLU) activation function follows the first fully connected layer. The concatenation layer takes the (200D) generated deep features as input in order to calculate the distance metric between each Siamese branch. The L1 distance between the two feature vectors is calculated. This L1 distance metric is fed into a softmax layer of two neurons (similar, different). A cross-entropy loss function is imposed on the binary classifier. For every mini-batch, the loss function is presented, as follows:
where m is the mini-batch size, y is the correct label, x
1 and x
2 are the face signatures (200D) for image 1 and image 2, respectively, and
p(x
1, x
2) is defined as:
where σ is the softmax function output and j is the last fully connected layer neurons count. The update is accomplished based on a mini-batch. The mini-batch update is cheaper than the whole dataset update, as it calculates for a small subset of training samples. The proposed network is trained to employ the conventional back-propagation method, where the gradient is additive across the twin networks due to shared weights. It guarantees that if the input pictures are similar to each other; their high-level features will be mapped to near locations in the feature space. Adam [
44] (Adaptive moment) optimization algorithm is used to minimize the L1 distance between the target and the hybrid Siamese network output. It is an extension of Stochastic Gradient Descent (SGD) [
45]. SGD has a single learning rate for the update of all weights and it is fixed throughout the training. Adam calculates an adaptive learning rate for each parameter estimated from the first and second moments of the gradients. The Nth moment of a random variable is depicted as the expected value of that random variable to the power of
n.
The gradient of the neural network cost function can be considered to be a random variable because it is commonly evaluated on a mini-batch of data. Mean is the first moment and variance is the second moment (mean is not deducted throughout calculation of the variance). In order to estimate the first and second moments, exponentially moving averages are used by Adam, which are calculated on the gradient assessed on the current mini-batch:
where m and v are moving averages, g is the gradient on current mini-batch, and β
1 and β
2 are Adam hyper-parameters. Hyper-parameters default values are 0.9 and 0.999, respectively. Equations (5) and (6) represent bias correction of first and second moment estimates. The estimator final equations are outlined as:
These moving averages are utilized to scale learning rate independently for each parameter. Adam weight update rule is outlined, as follows:
where w is network weights and η is the learning rate. The learning rate for Adam optimizer is 1 × 10
−3. A standard batch size of 100 is used for the training phase.
The two fully connected layer’s weights were initialized while using a normal distribution of zero-mean and a standard deviation of 0.1. The biases of the two fully connected layers were initialized to zero. For overfitting avoidance, training is enabled only for the two topmost fully connected layers and dropout [
46] is introduced after the second fully connected layer. During training, 80% of the second fully connected layer outputs are kept as-is and the remaining 20% are randomly settled to zero (dropped out).
Generally, a supervised methodology is applied to learn face image representations via a Hybrid Siamese neural network, and then this network’s features are reused for face clustering and search. For this domain, a deep Hybrid Siamese convolutional neural network is utilized, where (a) a competitive methodology that does not rely on domain-specific information but instead takes the advantage of deep learning approaches is provided, and (b) standard optimization techniques are easily utilized for training on pairs sampled from the dataset. If the proposed network is efficiently trained to discriminate between similar and different images, it can generalize to new pairs from unseen classes.
The end-to-end learning capability of the entire system is the most crucial characteristic of the proposed methodology. The proposed Hybrid Siamese network is trained on one of the biggest datasets accessible for research, which is smaller than FaceNet by two orders of magnitude and smaller than DeepFace by one order of magnitude, the progressive private datasets that have been revealed. Although the utilized training dataset is small, the performance results showed competitive accuracy on the LFW verification benchmark. Utilizing the proposed Siamese network, semantic similarity can be learned which is different from classification Loss where the network is rewarded only when it makes the classes linearly separable. This makes its embedding more powerful in various generic scenarios, such as picture search applications. The proposed Siamese network can be thought of as a generic feature extractor.
3.2. Proposed Face Clustering Method
Faces captured under unconstrained conditions have to be clustered, as in the case presented in this paper. Only the 200D second fully connected layer output is used as a face signature in the clustering experiments. A modified version of DBSCAN is proposed. DBSCAN is a standard algorithm for density-based data clustering that includes a lot of noise and outliers. Noise points are outliers to the data points being compared and fail to join any of the clusters formed.
DBSCAN has the main parameter named Epsilon (Eps or ε), which is a radial distance extending from a data point to find its neighbours. Traditional DBSCAN cannot estimate optimal Eps value. A modified version of DBSCAN inspired by DMDBSCAN [
37] is used to determine optimal Eps value automatically using the idea of a K-distance plot. Computing the distance between each point and its k nearest neighbor’s points is the main idea of the K distance plot. These distances are plotted in ascending order and appropriate values of Eps are chosen where an “elbow” point is found in the plot. The main idea depends on the fact that points locate in the same cluster roughly have their k
th nearest neighbors at a similar separation distance. The noise points have their k
th nearest neighbor at far away distance. Specifying the “elbow” is the target, as it corresponds to the ideal Eps value. In this study, the LFW face images are clustered by resolving the ideal DBSCAN Eps. The benefit of this approach is that the ideal Eps value can be automatically resolved. The K-distance plot pseudo-code is outlined in
Algorithm 1, as follows:
| Algorithm 1 K-distance plot
|
| 1: For i = 1 to n |
| 2: For j = 1 to n
|
| 3: D (i, j) = calculate distance (xi, xj)
|
| 4: Specify minimum distance values to nearest k
|
| 5: End for
|
| 6: End for
|
| 7: Sort distances in an ascending order and plot them to find Eps value
|
As DBSCAN cannot cluster some face images and consider it as outliers, a novel post-clustering optimization procedure is proposed. Outlier face images are handled by placing it in the correct cluster by applying the minimum distance rule between the 200D feature vector of the outlier face image and the cluster representative. A cluster representative is calculated for each generated cluster. The cluster representative is described as the mean of the 200D feature vector of all pictures in this cluster, as follows:
where Z
ji depicts the feature vector (200D) of ith picture in cluster
j and
Nj is the total number of pictures in cluster
j. The correct cluster index (CI) for each outlier face image is defined via the minimum distance method as:
where x
i denotes the ith image in the outlier’s images, CR
j denotes the cluster representative for jth cluster, and D is the l1 norm distance defined as:
where n is the vector length.
3.3. Clustering Evaluation
Precision, recall, and F1-measure are computed over pairs of points to evaluate clustering quality based on identity labels. Precision is characterized as the portion of pairs (taking into consideration all attainable pairs) that are put correctly in the same cluster.
where TP (True Positive) is when identical points are assigned to the same cluster and FP (False Positive) is when non- identical points are assigned to the same cluster. In
Figure 4, (X
1, X
2) is an identical pair (TP), (X
1, Y
2), and (X
4, Y
2) are non-identical pairs (FP). The Recall is characterized as the portion of identical class pairs (taking into consideration all attainable pairs) that are correctly put in one cluster, over the whole number of identical class pairs in the dataset.
where TP (True Positive) is when identical points are assigned to the same cluster and FN (False Negative) is when identical points are assigned to different clusters. In
Figure 4, (X
1, X
4) is an identical class pair in the same cluster (TP), whereas (X
3, X
4) is an identical class pair in different clusters (FN).
These measures can face two types of error:
Low recall, but high precision results from a clustering method that puts all points as individual clusters.
Low precision, but high recall results from a clustering method that puts all points in the same cluster.
These two measures can be summed up utilizing their harmonic mean (F1-measure), in order to give a good combination of the two. F1-measure is outlined as:
It has its best value when it reaches 1 and the worst value when it reaches 0.
4. Experimental Results and Discussion
Firstly, the used datasets in the experiments are introduced. Secondly, the proposed hybrid Siamese neural network is assessed on verification tasks. Thirdly, the performance of the learned face similarities/dissimilarities is evaluated on clustering tasks and its generalization ability is evaluated under transfer learning scenarios. For the experiments that are presented in this section, a system with a 64-bit, i7 core processor, Nvidia GeForce 960 M GPU, and 16 GB RAM, which run Linux Ubuntu 16.04.
4.1. Datasets
Face verification and clustering experiments use three publicly available datasets. The FaceScrub dataset [
41] is used for training. The LFW [
19] and the Arabian faces [
20] datasets are used for verification/clustering evaluation.
4.1.1. The FaceScrub Dataset
The FaceScrub dataset [
41] is available online and includes 106,863 images of 530 celebrities. The images are taken within real-world scenarios. The FaceScrub dataset has an equal number of female and male characters (52,076 images of 265 females and 55,742 images of 265 males) with about 200 images per person. It contains a huge variety across images of the same person. Although FaceScrub is labeled, it is known to contain noise.
Figure 5 presents examples of FaceScrub images.
4.1.2. The LFW Dataset
The LFW dataset [
19], released in 2007, is the most popular academic dataset for face verification because of the availability of detailed evaluation standards and the diversity of evaluation protocols. The LFW dataset contains 13,233 pictures of 5749 different persons, 4069 of them have just one face image, with massive variations in expressions, illuminations, and poses. All of the images are gathered from the internet.
Figure 6 presents examples of LFW images.
Two training approaches have been proposed by the LFW dataset:
The restricted training approach where just a small number of determined pairs are available for training.
The unrestricted approach where the formation of extra training pairs is allowed by combining images in LFW.
Lately, new approaches were developed to keep up equitable comparisons among methods that start to use additional training data from outside LFW for the sake of performance improvement. The proposed model is evaluated while using the standard unrestricted approach with labeled outside data protocol that includes 3000 positive pairs and 3000 negative pairs. The standard unrestricted approach divides pairs into ten disjoint subsets for cross-validation. In every subset, the identities are mutually exclusive, 300 positive, and 300 negative pairs are provided in every subset (examples are shown in
Figure 7). Ten-fold cross-validation is applied for performance evaluation.
4.1.3. The Arabian Faces Dataset
The Arabian faces dataset [
20] contains 18,000 images of 100 celebrities (79 males, 21 females) collected from the recorded Arabic TV media. It is collected for a project funded by the National Telecom Regulatory Authority (NTRA).
Figure 8 presents examples of Arabian face images.
4.2. Verification Experiment
In the verification experiment, the proposed model is evaluated on two different datasets. The hybrid Siamese deep neural network is trained following the image pre-processing method and the network structure that is described in
Section 3.
4.2.1. Labelled Face in the Wild
In this subsection, the proposed approach results on the LFW benchmark are presented. The proposed model is evaluated pursuing the standard protocol of unrestricted with labelled outside data. The provided 6000 pairs of data and 10-fold validation are used in the evaluation. The accuracy is outlined as the percentage of correctly verified faces:
where TP (True Positive) represents the number of similar faces that were verified as similar, TN (True Negative) represents the number of dissimilar faces that were verified as dissimilar, FP (False Positive) rep-resents the number of dissimilar faces that were verified as similar, and FN (False Negative) represents the number of similar faces that were verified as dissimilar. Along with the mean accuracy over the 10-fold, the number of images and networks used by the other methods for their overall training are also compared.
Table 1 presents the experimental results.
The majority of current face verification methodologies achieve high performance either with massive training data or complex model architecture of multiple networks. From the results in
Table 1, the following remarks are noticed. Our results were higher than that of DeepFace [
4] by(+1.6%), DeepID2 [
5] single network by (+3.52%), Li et al. [
21] by (+1.22%), Wang et al. [
22] single network by (+1.5%), Chen et al. [
3] by (+1.5%), OpenFace [
23] by (+6.03%), PSI-CNN [
25] by (+0.08%), Zhao et al. [
2] by (+0.55%), and CNN-3DMM estimation [
47] by (+6.6%).
Although only the FaceScrub outside data and CASIA-WebFace dataset (used by the pre-trained model) are used for training the proposed system, it outperforms DeepFace-Siamese [
4] accuracy by (+2.78%), while DeepFace uses approximately 9x larger training dataset. It achieves comparable results to the innovative, deep learning-based methodologies, such as DeepVisage, FaceNet, and Parkhi et al. [
10]. These methods use private outside data with millions of data samples for training. In other words, the proposed model required much less training data for the face-verification task.
While using simple network architecture (a smaller number of parameters to train), the proposed system performs better (+0.72%) than Wang et al. [
22], which uses seven networks. In contrast, Baidu uses 10 networks and had only about a 0.82% improvement. DeepID3 has a much more complicated model (50 networks), but it achieved only 0.58% higher than the proposed model. Note that, DeepID3 results are for the test set with label errors corrected, which has not been done by any other method. Although the proposed model has only one simple network, it still accomplished a steady performance for LFW.
4.2.2. The Arabian Faces Dataset
The dataset contains 18,000 face images: 13,000 face images are utilized for training and the other 5000 face images for testing. The Siamese network is trained with similar and dissimilar pairs. Therefore, the training set is formed by picking a random pair from the training set. Assign a corresponding new label to 1 if the images of the pair are of the same person or to 0 if the images are of different persons. In the training, face images with some degree of variations are used in order to construct a verification model that can generalize to unseen face images under unconstrained conditions. The proposed model is assessed on 6000 pairs. It reaches 99.1% accuracy on the Arabian faces dataset. The results are very promising given that the Siamese network has not seen any of these images through the training phase.
4.3. Clustering Experiment
Once the proposed Siamese network has been optimized to master the unconstrained face verification task, the difficulty of the face clustering problem is ready to be alleviated by using the proposed hybrid Siamese network-based face representation. The evaluation of face clustering by identity will be presented using two different experiments. The inputs to the clustering algorithm are aligned face images. In addition to F1-measure, a set of Precision-Recall (PR) characteristics will be presented. It can better clarify the success of the proposed algorithm in improving recall and making a fair balance between precision and recall. An experiment with different Eps values is conducted to demonstrate the effectiveness of the automatically chosen clustering parameter Eps.
4.3.1. First Experiment
The first experiment uses a fixed number of images (44,850 pairs) and a varying number of characters (clusters) from 30 and up to 100 random selected identities from the LFW and Arabian faces datasets. The experimental results are presented in
Table 2 and
Table 3 for the LFW and Arabian faces datasets, respectively. It is noted from
Table 2 and
Table 3 that K-Means and spectral performance, given the correct number of clusters, is relatively poor. These clustering techniques necessitate determining the true number of clusters at the beginning which is inapplicable for various practical scenarios. It is also noted that, for DBSCAN as character (cluster) count increases, the precision increases. This is natural, as a larger number of clusters diminishes the size of the cluster and refines the purity of the cluster. Obvious improvement can be observed on recall and F1-measure when applying proposed modified DBSCAN as compared to the traditional K-Means, spectral, and DBSCAN algorithms. In
Figure 9, four face clusters generated by the proposed clustering algorithm in experiment 1 (LFW dataset) are shown. As seen, the same character faces of massive variances can be properly gathered.
4.3.2. Second Experiment
The second experiment uses a certain number of characters (clusters) and a varying number of images per character ranging from four images/character (4950 pairs) and up to 12 images/character (44,850 pairs) on 25 randomly selected identities from the LFW and Arabian faces datasets. The experimental results are provided in
Table 4 and
Table 5, respectively. It is noticed that the proposed approach has the ability to properly cluster images of the randomly selected identities. Although the numbers of images per identity change, the results present the ability of the proposed methodology to handle the variations and keep the accuracy. The F1-measure is remarkably higher than the K-Means and spectral clustering outcomes.
4.3.3. Effect of Automatically Estimate the Ideal Eps Value
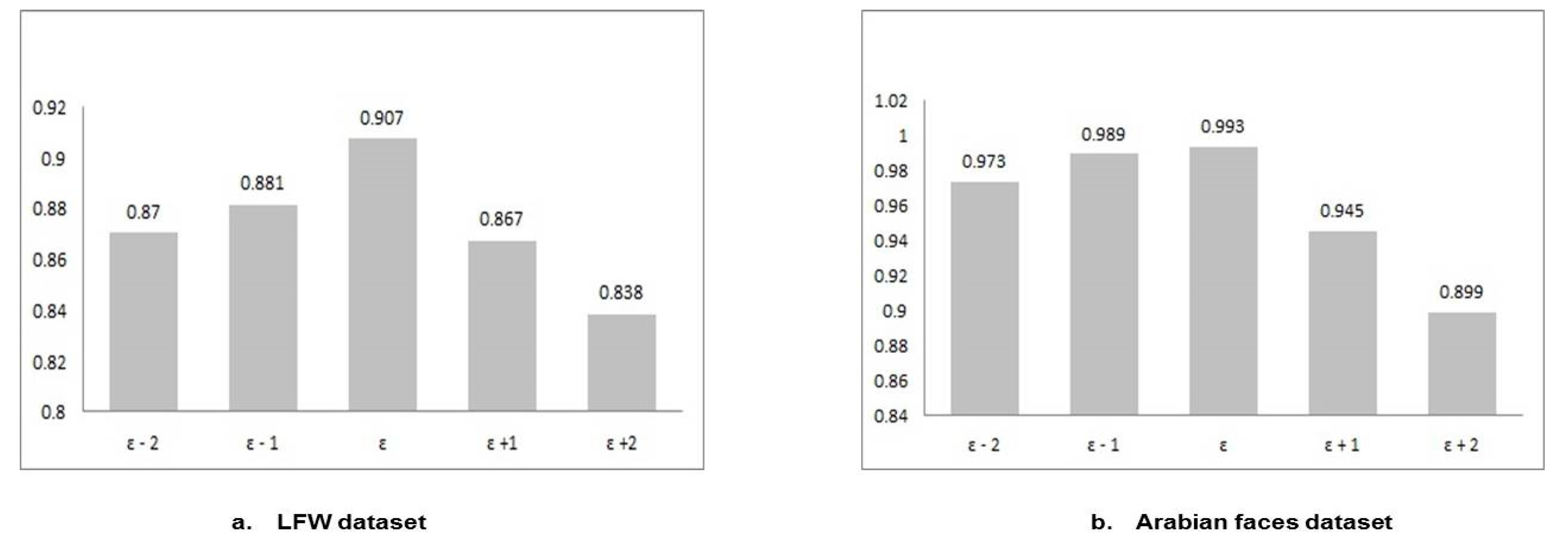
Eps is the main parameter in the proposed clustering procedure. An experiment with different Eps values is conducted in order to verify the sensitivity of the automatically chosen Eps on clustering performance. Twenty individuals (15 images for each) in both LFW and Arabian faces datasets are clustered with variations within the same individual in both datasets. In addition to visual comparison, clustering is also assessed in terms of precision, recall, and F1-measure on both datasets to assess the effect of Eps.
Figure 10 shows the clustering F1-measures on both LFW and Arabian faces datasets. Eps varies from the automatically chosen one by ± 1, 2.
One can observe that the automatically chosen Eps value is the optimal Eps value. It is observed that larger Eps leads to a lower number of clusters, as it merges similar individuals together. In
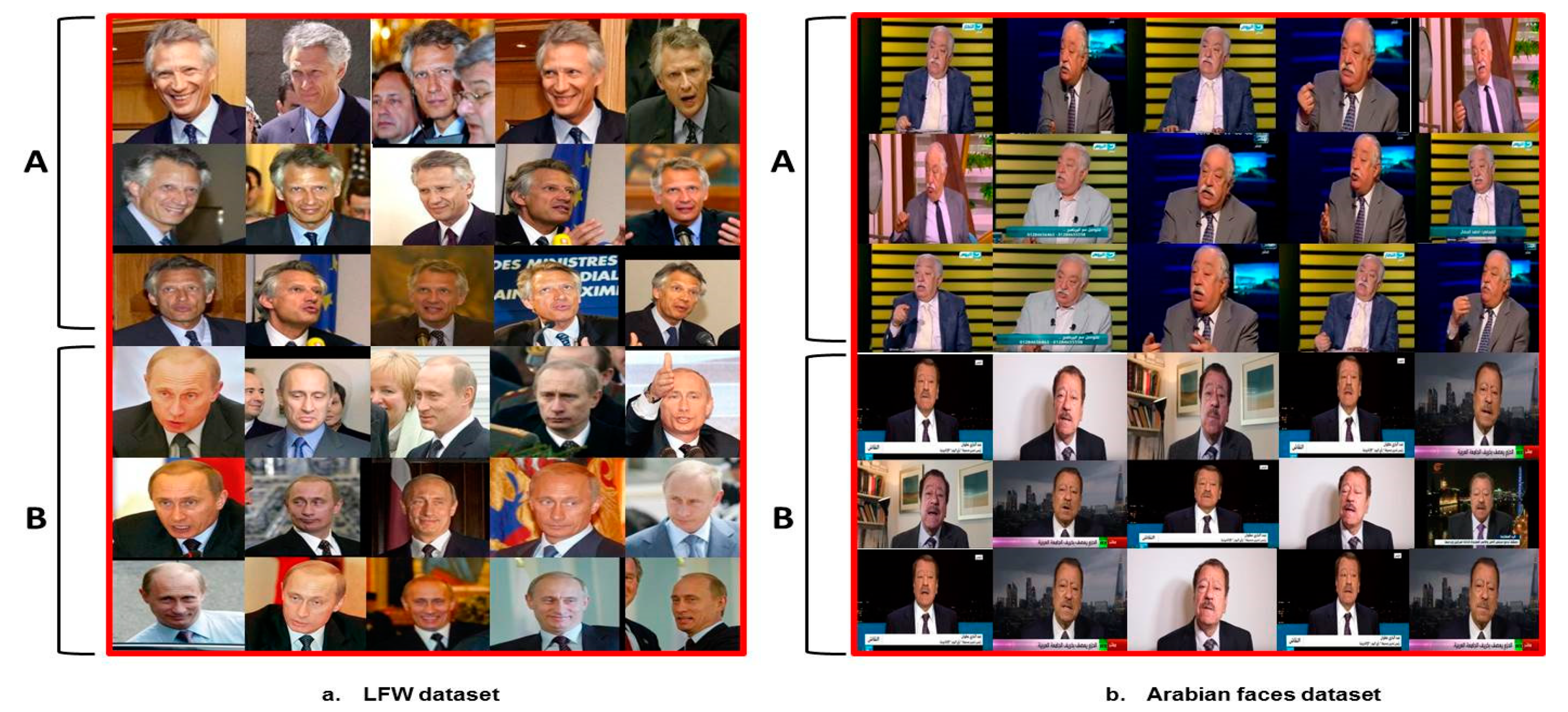
Figure 11a, two distinct LFW individuals A and B are merged into one cluster.
Figure 11b visualizes two distinct Arabian individuals A and B merged together into one cluster. It is also observed that smaller Eps leads to a large number of clusters, as it separates similar individuals into separate classes, as it cannot handle variations within the same individual. An example of the same individual separated into two different clusters is depicted in
Figure 12a for the LFW dataset and in
Figure 12b for Arabian faces dataset.
4.4. Generalization/Transfer Learning Experiment
Taking into consideration the good performance of the proposed end-to-end face verifier, this experiment evaluates its generalization ability under transfer learning scenarios. Knowledge transfer from the source classes to the new unseen classes is the main aim of this experiment. For transfer learning, the proposed hybrid Siamese network is trained on Arabian faces dataset, which contains 100 classes and 18 K images. Subsequently, it is validated on the LFW dataset, and thus does not use any auxiliary knowledge. The unseen LFW classes have high variations as well as a high level of similarity. The proposed approach achieves 93.9% mean accuracy on 6000 pairs provided in 10-fold cross-validation protocol.
4.5. Computational Cost
The proposed hybrid Siamese deep neural network training process took only 6 h while using a single Nvidia GTX 960 M GPU. It was noticed that the training time is reasonable (compared to other methods which take days [
3,
4,
6] for training the networks) for several applications, as face verification/clustering can be performed off-line.
5. Conclusions
In this paper, a new face verification system dependent on a deep hybrid Siamese neural network has been proposed. The proposed network proved to be very efficient in learning discriminative features. The verification accuracy increased using a training dataset of relatively smaller size, fewer computation requirements, and less training time. The results on both the LFW and the Arabian faces benchmarks are reasonably competitive (reaching 98.95% overall accuracy on the standard LFW protocol and 99.1% on the Arabian faces dataset). In the face clustering experiment, it is shown that the proposed approach can improve recall and make a good balance between precision and recall. The overall F1-measure of the proposed clustering approach outperforms popular traditional clustering techniques, such as K-Means, spectral, and DBSCAN. Additionally, the proposed approach has shown promising results when generalized to cross-dataset evaluation, which is much more challenging than in-dataset evaluation.
In the future, we are planning to improve the deep model architecture by utilizing more complicated loss functions as a supervisory signal or combining different loss functions as a multi-loss function. We are also interested in examining the performance of the proposed Siamese network on different races, such as Chinese faces. Although deeper Siamese networks would be more effective in such cases, these networks suffer overfitting problems. We are interested in investigating the performance of deeper Siamese networks.