Breast Cancer Diagnosis System Based on Semantic Analysis and Choquet Integral Feature Selection for High Risk Subjects
Abstract
:1. Introduction
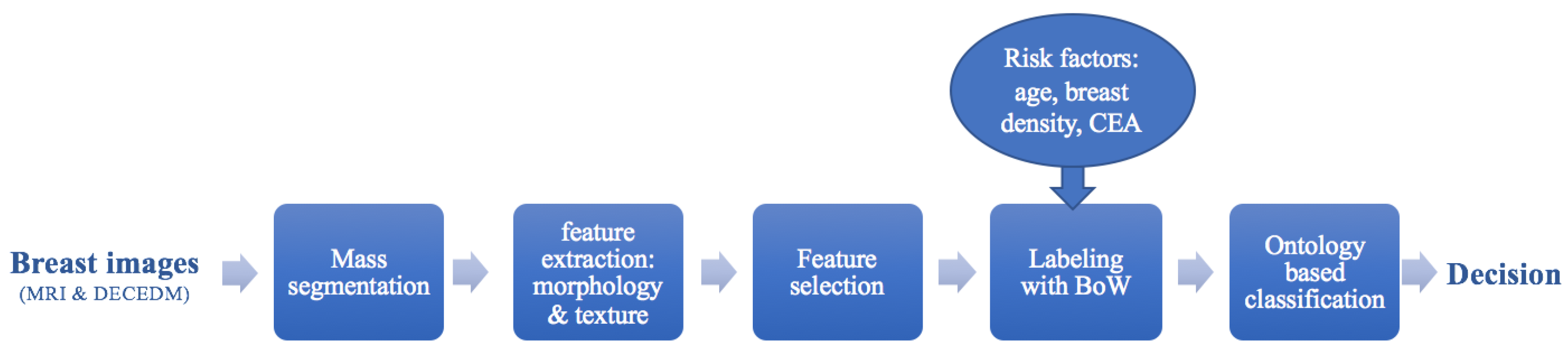
2. Material and Methods
2.1. Mass Segmentation
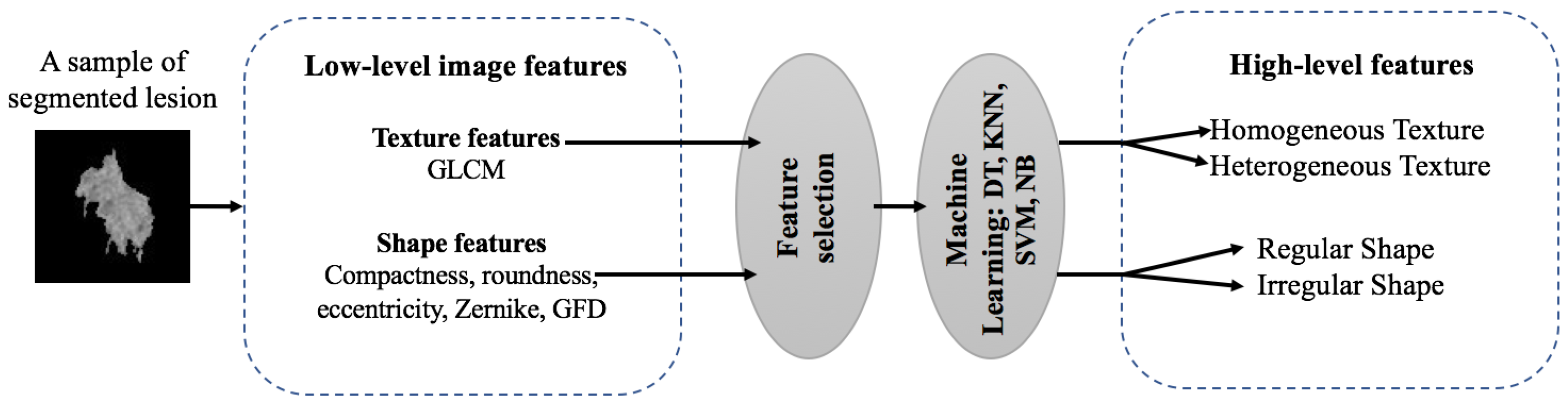
2.2. Feature Extraction
- Compactness is used to quantify the connection between portions of a region. A highly non-convex lesion (malignant) have a high compactness index, whereas benign lesions have a low compactness value index.
- Roundness is a measure of the similarity of an object shape to a circle. Shape with a roundness index closer to 1 indicates that the mass is approximately round so it is rather benign.
- Eccentricity is the measure of aspect ratio of a region. It is defined by the ratio of the major axis to the minor axis. A shape with an eccentricity index too close to 1 is almost a circle.
- Zernike moments are used as an object descriptor in several pattern recognition systems, edge detection and image retrieval applications with significant results. It allows us to represent image properties without redundancy and overlap of information between the moments thanks to complex kernel functions based on Zernike polynomials orthogonal to each other. The discrete form of the Zernike moments of an image size N × N is defined as follows:where , and is a normalization factor. The transformed distance and the phase at the pixel of (x,y) are given by:
- GFD extracted from spectral domain by applying 2D Fourier transform on polar raster sampled shape image. It allows multi-resolution feature analysis in both radial and angular directions. The GFD, based on the polar Fourier (PF), is defined as:where m and n are the radial and angular frequencies and is the 1st order moment. Here we choose m= 4 and n= 9.
2.3. Feature Selection
2.3.1. Choquet Integral Selection
2.3.2. Learning Step
2.3.3. Extraction Step
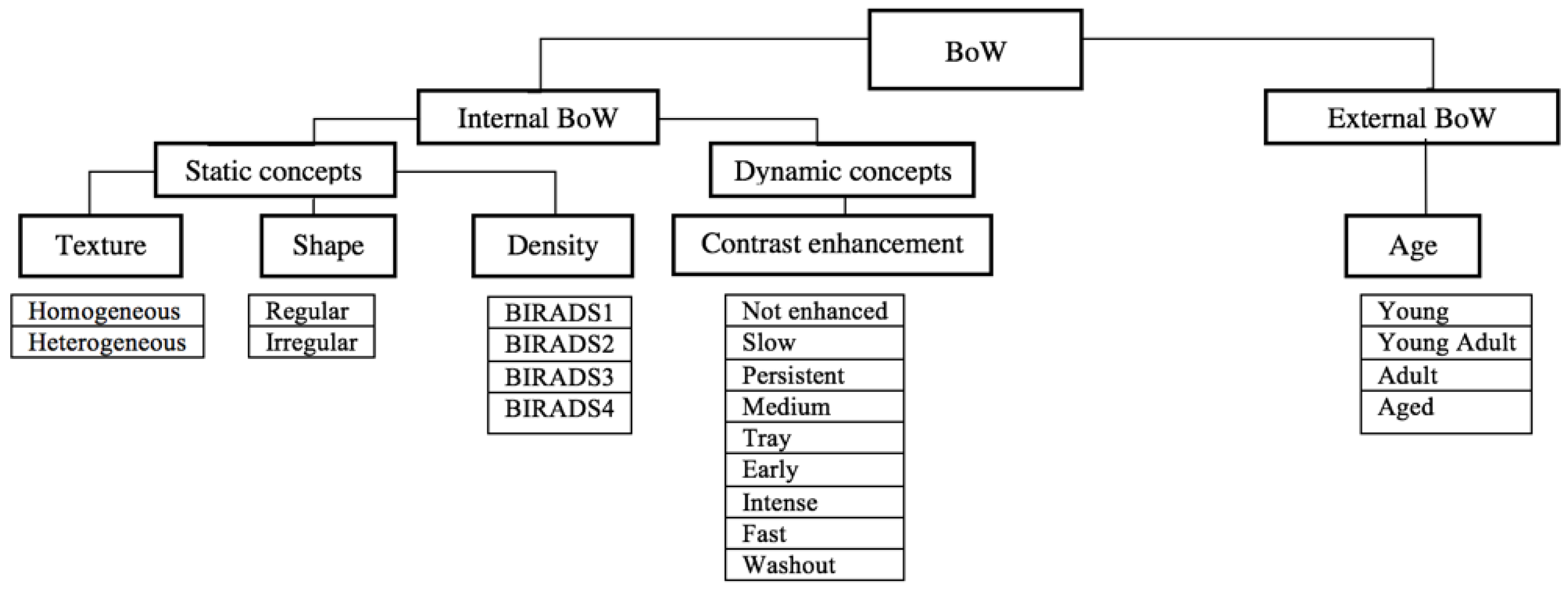
2.4. Bag of Words Modeling
2.5. Image Annotation
3. Results and Discussion
3.1. Database
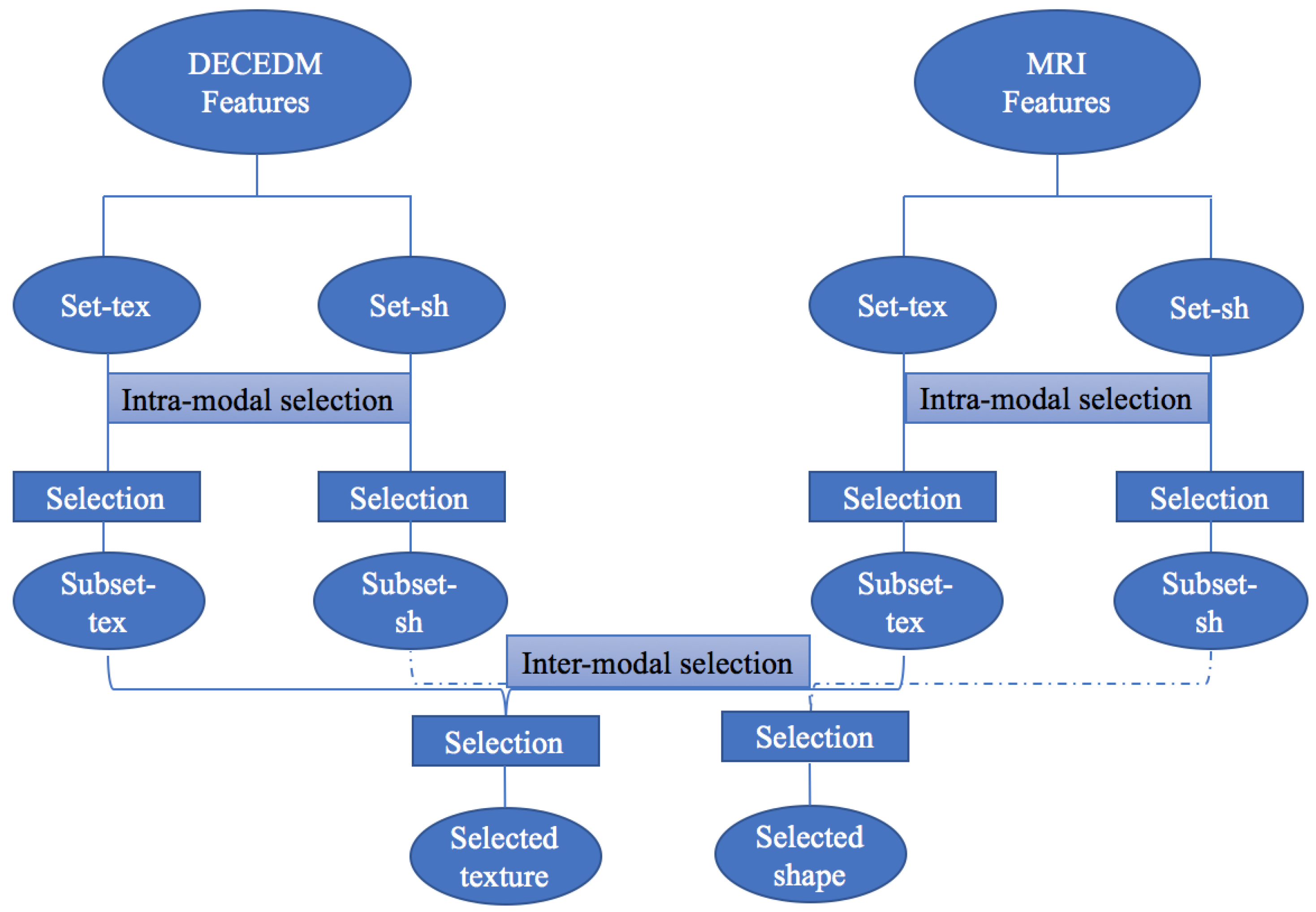
3.2. Feature Selection
3.3. A Comparison between Choquet Intagral for Feature Selection and Other Selection Method
3.3.1. Structural Selection
3.3.2. Inter-Modal Selection
3.4. Labeling Results
3.4.1. Performance Metrics
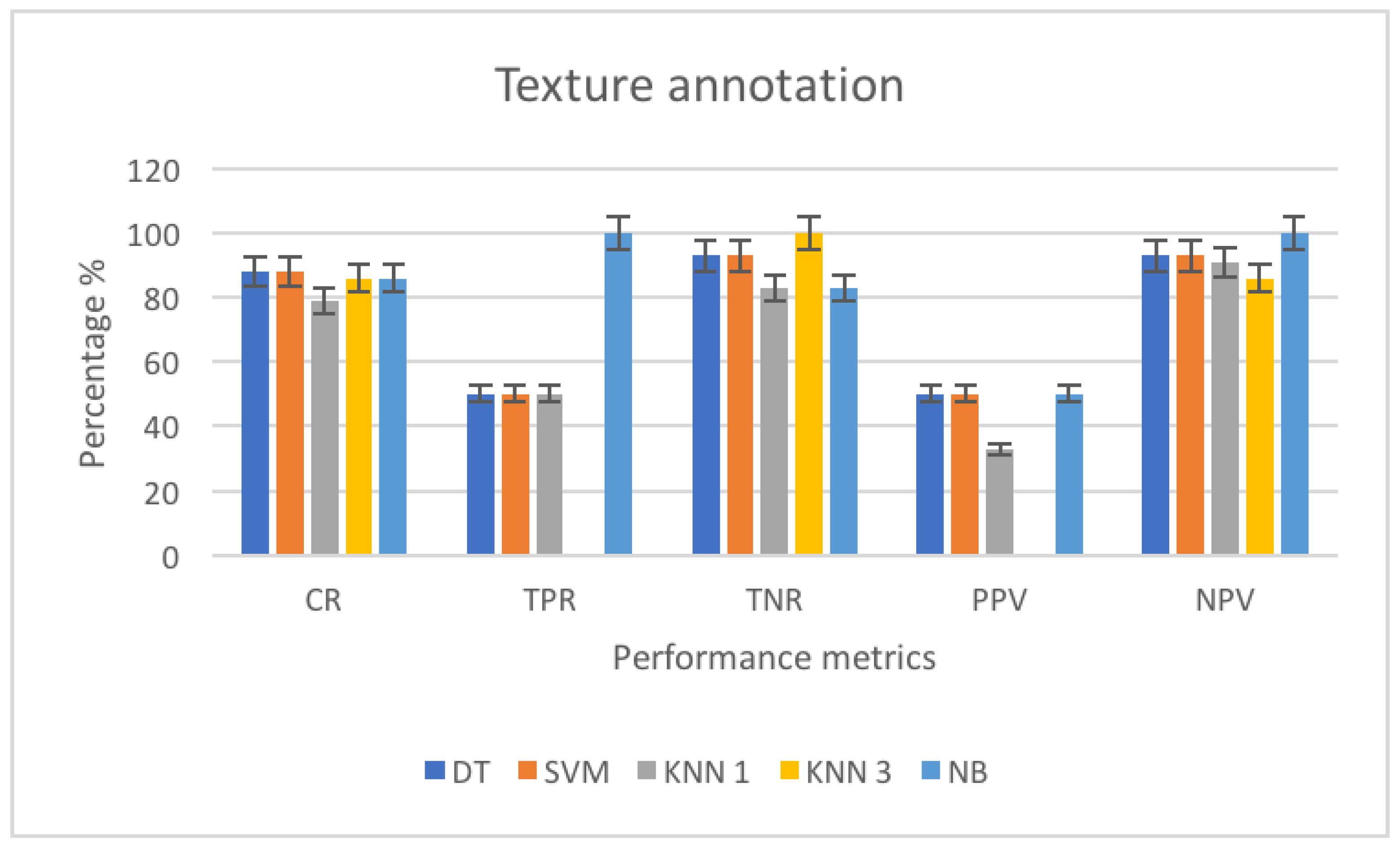
3.4.2. Texture Annotation
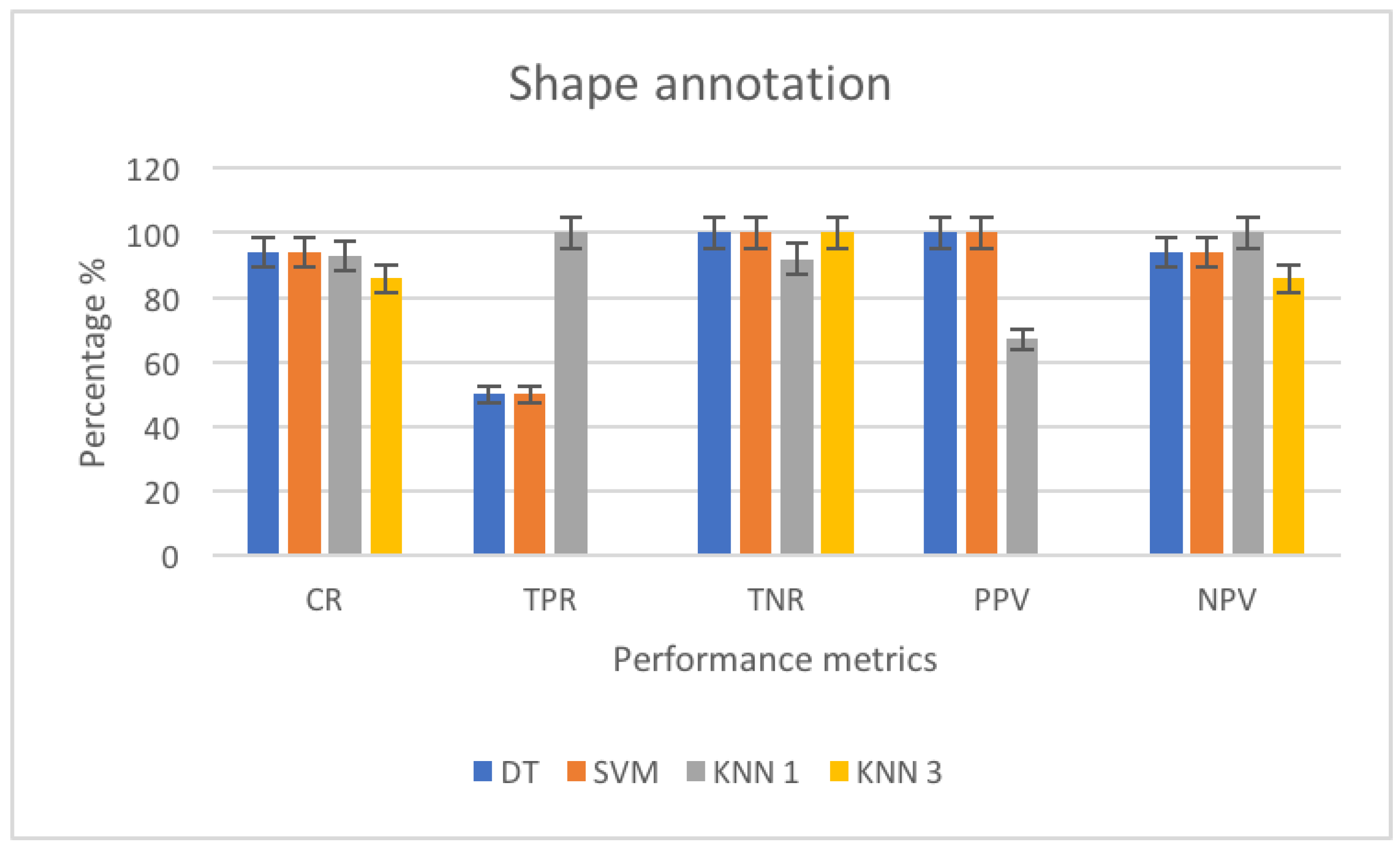
3.4.3. Shape Annotation
3.5. Decision Making and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MRI | Magnetic resonance imaging |
| DECEDM | Dual energy contrast enhanced digital mammography |
| CAD | Computer aided diagnosis |
| BoW | Bag of words |
| KBS | Knowledge-based systems |
| FCM | Fuzzy C-means clustering |
| DRLSE | Distance regularized level set evolution |
| LSF | Level set function |
| GLCM | Gray level co-occurrence matrix |
| GFD | Generic Fourier descriptor |
| ZM | Zernike moments |
| OWA | Ordered weighted average |
| SWA | Simple weighted average |
| QAM | Quasi arithmetic means |
| CEA | Contrast enhancement agent |
| BIRADS | Breast imaging reporting and data system |
| ACR | American college of radiology |
| DT | Decision tree |
| KNN | K-nearest neighbors |
| SVM | Support vector machine |
| NB | Naive Bayes |
| SMO | Sequential minimal optimization |
| SFFS | Sequential floating forward selection |
| SFS | Sequential forward selection |
| SBS | Sequential backward selection |
| SFBS | Sequential floating backward selection |
| CCR | Correct classification rate |
| ROC | Receiver operating characteristics |
| AUC | Area under the curve |
| TPR | True positive rate |
| TNR | True negative rate |
| PPV | Positive predictive value |
| NPV | Negative predictive value |
| ANN | Artificial neural network |
References
- Trabelsi, S.B.A.; Cloppet, F.; Wendling, L.; Sellami, D. Detection and Analysis of Breast Masses from MRIs and Dual Energy Contrast Enhanced Mammography; IPAS: Hammamet, Tunisia, 2016. [Google Scholar]
- Cheng, H.D.; Shi, X.J.; Min, R.; Hu, L.M.; Cai, X.P.; Du, H.N. Approaches for automated detection and classification of masses in mammograms. Pattern Recogn. 2006, 39, 646–668. [Google Scholar] [CrossRef]
- Gubern-Merida, A.; Marti, R.; Melendez, J.; Hauth, J.L.; Mann, R.M.; Karssemeijer, N.; Platel, B. Automated localization of breast cancer in DCE-MRI. Med. Image Anal. 2015, 20, 265–274. [Google Scholar] [CrossRef] [PubMed]
- Swiderski, B.; Osowski, S.; Kurek, J.; Kruk, M.; Lugowska, I.; Rutkowski, P.; Barhoumi, W. Novel methods of image description and ensemble of classifiers in application to mammogram analysis. Expert Syst. Appl. 2017, 81, 67–78. [Google Scholar] [CrossRef]
- Ramos-Pollan, R.; Guevara-Lopez, M.; Suarez-Ortega, C.; Diaz-Herrero, G.; Franco-Valiente, J.; Rubio-del-Solar, M.; de Posada Gonzalez, N.; Vaz, M.; Loureiro, J.; Ramos, I. Discovering mammography-based machine learning classifiers for breast cancer diagnosis. J. Med. Syst. 2011, 36, 2259–2269. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.C.; Huang, Y.H.; Huang, C.S.; Chen, J.H.; Huang, G.Y.; Chang, Y.C.; Chang, R.F. Computer-aided diagnosis of breast DCE-MRI using pharmacokinetic model and 3-D morphology analysis. J. Magn. Reson. Imaging 2014, 32, 197–205. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Y.; Giger, M.L.; Hui, L.; Neha, B.; Sennett, C.A. Multimodality computer-aided breast cancer diagnosis with FFDM and DCE-MRI. Acad. Radiol. 2010, 32, 1158–1167. [Google Scholar] [CrossRef] [PubMed]
- Amin, M.E.; Abdrabou, L.; Salem, M.A. A breast cancer classifier based on a combination of case-based reasoning and ontology approach. In Proceedings of the International Multiconference on Computer Science and Information Technology, Wisla, Poland, 18–20 October 2010; pp. 3–10. [Google Scholar]
- Yang, C.; Dong, M.; Hua, J. Region-based image annotation using asymmetrical support vector machine-based multiple-instance learning. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR ’06), New York, NY, USA, 17–22 June 2006. [Google Scholar]
- Vailaya, A.; Figueiredo, M.A.T.; Jain, A.K.; Zhang, H.J. Image classification for content-based indexing. IEEE Trans. Image Process. 2001, 10, 117–130. [Google Scholar] [CrossRef] [Green Version]
- Sethi, I.K.; Coman, I.L.; Stan, D. Mining association rules between low-level image features and high-level concepts. In Proceedings of the Aerospace/Defense Sensing, Simulation, and Controls, Orlando, FL, USA, 16–20 April 2001. [Google Scholar]
- Town, C.; Sinclair, D. Content Based Image Retrieval Using Semantic Visual Categories; TR2000-14; AT and T Labs Cambridge: Cambridge, UK, 2000. [Google Scholar]
- Patil, M.P.; Kolhe, S.R. Automatic image categorization and annotation using k-nn for corel dataset. Adv. Comput. Res. 2012, 4, 108–112. [Google Scholar]
- Venkatesh, N.M.; Subhransu, M.; Manmatha, R. Automatic image annotation using deep learning representations. In Proceedings of the ICMR ’15, Shanghai, China, 23–26 June 2015. [Google Scholar]
- Wu, J.; Yu, Y.; Huang, C.; Yu, K. Deep multiple instance learning for image classification and auto-annotation. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Colace, F.; De Santo, M.; Moscato, V.; Picariello, A.; Schreiber, A.F.; Tanca, L. Data Management in Pervasive Systems; Springer: Cham, Switzerland, 2015; p. 299. [Google Scholar]
- Abdel-Nasser, M.; Moreno, A.; Rashwan, A.H.; Puig, D. Analyzing the evolution of breast tumors through flow fields and strain tensors. Pattern Recogn. Lett. 2017, 93, 162–171. [Google Scholar] [CrossRef]
- Tabakov, M.; Kozak, P. Segmentation of histopathology HER2/neu images with fuzzy decision tree and Takagi–Sugeno reasoning. Comput. Biol. Med. 2014, 49, 19–29. [Google Scholar] [CrossRef]
- Liney, G.P.; Sreenvias, M.; Garcia-Alvarez, R.; Turnbull, L.W. Breast lesion analysis of shape technique: Semi-automated vs. manual morphological description. J. Magn. Reson. Imaging 2006, 23, 493–498. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Giger, M.L.; Bick, U. A fuzzy C-means FCM-based approach for computerized segmentation of breast lesions in dynamic contrast-enhanced MR images. Acad. Radiol. 2006, 13, 63–72. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Giger, M.L.; Lan, L.; Bick, U. Computerized interpretation of breast MRI: Investigation of enhancement-variance dynamics. Med. Phys. 2004, 31, 1076–1082. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Kao, C.Y.; Gore, J.C.; Ding, Z. Minimization of region scalable fitting energy for image segmentation. IEEE Trans. Image Process. 2008, 17, 1940–1949. [Google Scholar] [PubMed]
- Li, C.; Huang, R.; Ding, Z.; Gatenby, J.C.; Metaxas, D.N.; Gore, J.C. A level set method for image segmentation in the presence of intensity in-homogeneities with application to MRI. IEEE Trans. Image Process. 2011, 20, 2007–2016. [Google Scholar] [PubMed]
- Gomes, J.; Faugeras, O. Reconciling distance functions and level sets. J. Vis. Commun. Image Represent 2000, 11, 209–223. [Google Scholar] [CrossRef]
- Weber, M.; Blake, A.; Cipolla, R. Sparse finite elements for geodesic contours with level-sets. In Computer Vision—ECCV 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 391–404. [Google Scholar]
- Li, C.; Xu, C.; Gui, C.; Fox, D.M. Distance Regularized Level Set Evolution and its Application to Image Segmentation. IEEE Trans. Image Process. 2010, 19, 3234–3254. [Google Scholar]
- Nie, K. Quantitative analysis of lesion morphology and texture features for diagnostic prediction in breast MRI. Acad. Radiol. 2008, 15, 1513–1525. [Google Scholar] [CrossRef] [PubMed]
- Thibault, G.; Tudorica, A.; Afzal, A.; Chui, S.Y.; Naik, A.; Troxell, M.L.; Kemmer, K.A.; Oh, K.Y.; Roy, N.; Jafarian, N.; et al. DCE-MRI texture features for early prediction of breast cancer therapy response. Tomography 2017, 3, 23–32. [Google Scholar]
- Liu, H.; Tan, T.; van Zelst, J.; Mann, R.; Karssemeijer, N.; Platel, B. Incorporating texture features in a computer-aided breast lesion diagnosis system for automated three-dimensional breast ultrasound. J. Med. Imaging 2014, 1, 024501. [Google Scholar] [CrossRef]
- Prakasa, E. Texture Feature Extraction by Using Local Binary Pattern. INKOM 2015, 9, 45–48. [Google Scholar] [CrossRef]
- Nanni, L.; Lumini, A.; Brahnam, S. Survey on LBP based texture descriptors for image classification. Expert Syst. Appl. 2012, 39, 3634–3641. [Google Scholar] [CrossRef]
- Oliver, A.; Llado, X.; Freixenet, J.; Marti, J. False positive reduction in mammographic mass detection using local binary patterns. In Medical Image Computing and Computer-Assisted Intervention (MICCAI); Lecture Notes in Computer Science 4791; Springer: Brisbane, Australia, 2007; Volume 1, pp. 286–293. [Google Scholar]
- Keramidas, E.G.; Iakovidis, D.K.; Maroulis, D.; Dimitropoulos, N. Thyroid texture representation via noise resistant image features. In Proceedings of the 21st IEEE International Symposium on Computer-Based Medical Systems (CBMS 2008), Jyvaskyla, Finland, 17–19 June 2008. [Google Scholar]
- Harb, H.M.; Desuky, A.S.; Mohammed, A.; Jennane, R. Histogram of oriented gradients and texture features for bone texture characterization. Int. J. Comput. Appl. 2017, 165, 23–28. [Google Scholar]
- Pomponiu, V.; Hariharan, H.; Zheng, B.; Gur, D. Improving breast mass detection using histogram of oriented gradients. In Proceedings of the SPIE Medical Imaging, San Diego, CA, USA, 15–20 February 2014. [Google Scholar]
- Dalal, N.; Triggs, B. Histograms of Oriented Gradients for Human Detection. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, 20–26 June 2005; Volume 1, pp. 886–893. [Google Scholar]
- Liu, X.; Xu, X.; Liu, J.; Tang, J. Mass classification with level set segmentation and shape analysis for breast cancer diagnosis using mammography. In Proceedings of the International Conference on Intelligent Computing, Zhengzhou, China, 11–14 August 2011. [Google Scholar]
- Shen, L.; Rangayyan, R.M.; Desautels, J.E.L. Application of shape analysis to mammographic calcifications. IEEE Trans. Med. Imaging 1994, 13, 263–274. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.W.; Zhang, C.; Zhuang, J. An application of classifier combination methods in hand gesture recognition. Math. Problems Eng. 2012. [Google Scholar] [CrossRef]
- Ruta, D.; Gabrys, B. An overview of classifier fusion methods. Comput. Inform. Syst. 2000, 7, 1–10. [Google Scholar]
- Gader, P.D.; Mohamed, M.A.; Keller, J.M. Fusion of handwritten word classifiers. Pattern Recogn. Lett. 1996, 17, 577–584. [Google Scholar] [CrossRef]
- Salama, G.I.; Abdelhalim, M.; Zeid, M.A. Breast Cancer Diagnosis on Three Different Datasets Using Multi-Classifiers Breast Cancer. Int. J. Comput. Appl. Inf. Tech. 2012, 1, 36–43. [Google Scholar]
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Liu, H.; Yu, L. Toward integrating feature selection algorithms for classification and clustering. IEEE Trans. Knowl. Data Eng. 2005, 17, 491–502. [Google Scholar] [Green Version]
- Saeys, Y.; Inza, I.; Larranaga, P. A review of feature selection techniques in bioinformatics. Bioinformatics 2007, 23, 2507–2517. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jovic, A.; Brkic, K.; Bogunovic, N. A review of feature selection methods with applications. In Proceedings of the 38th International Convention on Information and Communication Technology, Electronics and Microelectronics, Opatija, Croatia, 25–29 May 2015. [Google Scholar]
- Choi, Y.S.; Kim, D. Relevance feedback for content-based image retrieval using the Choquet integral. In Proceedings of the 2000 IEEE International Conference on Multimedia and Expo, ICME2000, Latest Advances in the Fast Changing World of Multimedia (Cat. No.00TH8532), New York, NY, USA, 30 July–2 August 2004; pp. 1185–1199. [Google Scholar]
- Stejic, Z.; Takama, Y.; Hirota, K. Mathematical aggregation operators in image retrieval: Effect on retrieval performance and role in relevance feedback. Signal Process. 2005, 85, 297–324. [Google Scholar] [CrossRef]
- Chang, S.; Greenberg, S. Application of fuzzy integration based multiple information aggregation in automatic speech recognition. In Intelligent Sensory Evaluation; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Lim, J.S.; Oh, Y.S.; Lim, D.H. Bagging support vector machine for improving breast cancer classification. J. Health Inf. Stat. 2014, 39, 15–25. [Google Scholar]
- Liying, Y.; Liu, Z.; Yuan, X.; Wei, J.; Zhang, J. Random subspace aggregation for cancer prediction with gene expression profiles. BioMed Res. Int. 2016. [Google Scholar] [CrossRef]
- Datta, S. Classification of breast cancer versus normal samples from mass spectrometry profiles using linear discriminant analysis of important features selected by random forest. Stat. Appl. Genet. Mol. Biol. 2008, 7. [Google Scholar] [CrossRef] [PubMed]
- Thongkam, J.; Xu, G.; Zhang, Y.; Huang, F. Breast cancer survivability via AdaBoost algorithms. In Proceedings of the Second Australasian Workshop on Health Data and Knowledge Management HDKM ’08, Wollongong, NSW, Australia, 1 January 2008; pp. 55–64. [Google Scholar]
- Kontos, K.; Maragoudakis, M. Breast cancer detection in mammogram medical images with data mining techniques. In Artificial Intelligence Applications and Innovations; Springer: Berlin/Heidelberg, Germany, 2013; pp. 336–347. [Google Scholar]
- Wu, Y.; Wang, C.; Ng, S.G.; Madabhushi, A.; Zhong, Y. Breast Cancer Diagnosis Using Neural-Based Linear Fusion Strategies. In Neural Information Processing; Springer: Berlin/Heidelberg, Germany, 2006; pp. 165–175. [Google Scholar]
- Mohammed, E.A.; Naugler, C.T.; Far, B.H. Breast tumor classification using a new OWA operator. Expert Syst. Appl. 2016, 61, 302–313. [Google Scholar] [CrossRef]
- Krishnan, A.R.; Kasim, M.M.; Abu Bakar, E.M.N.E. Ashort survey on the usage of choquet integral and its associated fuzzy measure in multiple attribute analysis. Proc. Comput. Sci. 2015, 59, 427–434. [Google Scholar] [CrossRef]
- Grabisch, M. OWA operators and nonadditive integrals. In Recent Developments in the Ordered Weighted Averaging Operators: Theory and Practice; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Iourinski, D.; Modave, F. Qualitative multicriteria decision making based on the Sugeno integral. In Proceedings of the 22nd International Conference of the North American Fuzzy Information Processing Society IEEE, Chicago, IL, USA, 24–26 July 2003. [Google Scholar]
- Martinez, G.E.; Mendoza, O.; Castro, J.R.; Rodriguez-Diaz, A.; Melin, P.; Castillo, O. Comparison between Choquet and Sugeno integrals as aggregation operators for pattern recognition. In Proceedings of the Annual Conference of the North American Fuzzy Information Processing Society (NAFIPS), El Paso, TX, USA, 31 October–4 November 2016. [Google Scholar]
- Sugeno, M. Theory of Fuzzy Integrals and Its Applications. Ph.D. Thesis, Tokyo Institute of Technology, Tokyo, Japan, 1974. [Google Scholar]
- Choquet, G. Theory of capacities. Ann. Inst. Four. 1953, 5, 131–295. [Google Scholar] [CrossRef]
- Grabisch, M. The application of fuzzy integrals in multi-criteria decision making. Eur. J. Oper. Res. 1996, 89, 445–456. [Google Scholar] [CrossRef]
- Rendek, J.; Wendling, L. On determining suitable subsets of decision rules using Choquet integral. Int. J. Pattern Recogn. Artif. Intell. 2008, 22, 207–232. [Google Scholar] [CrossRef]
- Shapley, L.S. A Value for n-Person Games. In Contributions to the Theory of Games II, Annals of Mathematics Studies; Kuhn, H.W., Tucker, A.W., Eds.; Princeton University Press: Princeton, NJ, USA, 1953; Volume 28, pp. 307–317. [Google Scholar]
- Murofushi, T.; Soneda, S. Techniques for reading fuzzy measures (iii): Interaction index. In Proceedings of the 9th Fuzzy System Symp, Sapporo, Japan, 19–21 May 1993; pp. 693–696. [Google Scholar]
- Murofushi, T.; Sugeno, M. A theory of fuzzy measures: Representations, the Choquet integral, and null sets. Math. Anal. Appl. 2014, 159, 532–549. [Google Scholar] [CrossRef]
- Ververidis, D.; Kotropoulos, C. Fast and accurate sequential floating forward feature selection with the Bayes classifier applied to speech emotion recognition. J. Signal Process. Arch. 2008, 88, 2956–2970. [Google Scholar] [CrossRef]
- Otoum, S.; Kantarci, B.; Mouftah, H.T. On the feasibility of deep learning in sensor network intrusion detection. IEEE Netw. Lett. 2019, 1, 68–71. [Google Scholar] [CrossRef]
- Otoum, S.; Kantarci, B.; Mouftah, H.T. Detection of known and unknown intrusive sensor behavior in critical applications. IEEE Sens. Lett. 2017, 1, 1–4. [Google Scholar] [CrossRef]
- Aloqaily, M.; Otoum, S.; Al Ridhawi, I.; Jararweh, Y. An intrusion detection system for connected vehicles in smart cities. Ad Hoc Netw. 2019, 90. [Google Scholar] [CrossRef]
- Aloqaily, M.; Kantarci, B.; Mouftah, H.T. On the impact of quality of experience (QoE) in a vehicular cloud with various providers. In Proceedings of the 2014 11th Annual High Capacity Optical Networks and Emerging/Enabling Technologies (Photonics for Energy), Charlotte, NC, USA, 15–17 December 2014; pp. 94–98. [Google Scholar]

| Lesion | Class | ||
|---|---|---|---|
| L1 | 0.76 | 0.61 | B |
| L2 | 0.61 | 0.82 | M |
| L3 | 0.74 | 0.72 | B |
| L4 | 0.62 | 0.62 | M |
| L5 | 0.58 | 0.63 | M |
| L6 | 0.79 | 0.67 | B |
| L7 | 0.49 | 0.79 | M |
| L8 | 0.54 | 0.82 | M |
| L9 | 0.63 | 0.76 | M |
| L10 | 0.66 | 0.82 | M |
| L11 | 0.54 | 0.80 | M |
| L12 | 0.54 | 0.81 | M |
| L13 | 0.57 | 0.81 | M |
| Shapley Values | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cr | Ep | MP | Ds | Hg | Eg | CS | Vr | CP | Ac | HOG | LBP | Ct | 13 features |
| 0.069 | 0.072 | 0.072 | 0.076 | 0.076 | 0.076 | 0.076 | 0.077 | 0.077 | 0.079 | 0.079 | 0.080 | 0.090 | 0.077 |
| Interaction Values | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ct | Cr | Eg | Hg | Ep | Ac | CP | CS | Ds | MP | Vr | |
| Ct | - | 7.56× 10 | −1.42× 10 | −2.19× 10 | −7.37× 10 | 1.24× 10 | −2.96× 10 | −1.19× 10 | 3.03× 10 | 7.60× 10 | 1.91× 10 |
| Cr | 7.56× 10 | - | 1.49× 10 | 4.69× 10 | 1.93× 10 | −5.29× 10 | −2.17× 10 | −1.12× 10 | 1.67× 10 | 1.25× 10 | 7.51× 10 |
| Eg | −1.42× 10 | 1.49× 10 | - | −2.80× 10 | −1.26× 10 | −5.78× 10 | −2.14× 10 | −8.45× 10 | 7.90× 10 | −2.55× 10 | 3.30× 10 |
| Hg | −2.19× 10 | 4.69× 10 | −2.80× 10 | - | 3.88× 10 | 1.16× 10 | −1.42× 10 | −1.48× 10 | 1.15× 10 | 7.51× 10 | 1.81× 10 |
| Ep | −7.37× 10 | 1.93× 10 | −1.26× 10 | 3.88× 10 | - | 2.09× 10 | 4.43× 10 | 4.06× 10 | −1.54× 10 | −1.89× 10 | −2.43× 10 |
| Ac | 1.24× 10 | −5.29× 10 | −5.78× 10 | 1.16× 10 | 2.09× 10 | - | −1.97× 10 | −2.24× 10 | −1.52× 10 | 2.08× 10 | −1.94× 10 |
| CP | −2.96× 10 | −2.17× 10 | −2.14× 10 | −1.42× 10 | 4.43× 10 | −1.97× 10 | - | 5.93× 10 | 2.27× 10 | 1.32× 10 | 5.83× 10 |
| CS | −1.19× 10 | −1.12× 10 | −8.45× 10 | −1.48× 10 | 4.06× 10 | −2.24× 10 | 5.93× 10 | - | 4.50× 10 | 2.95× 10 | 2.90× 10 |
| Ds | 3.03× 10 | 1.67× 10 | 7.90× 10 | 1.15× 10 | −1.54× 10 | −1.52× 10 | 2.27× 10 | 4.50× 10 | - | −2.11× 10 | −1.55× 10 |
| MP | 7.60× 10 | 1.25× 10 | −2.55× 10 | 7.51× 10 | −1.89× 10 | 2.08× 10 | 1.32× 10 | 2.95× 10 | −2.11× 10 | - | −1.89× 10 |
| Vr | 1.91× 10 | 7.51× 10 | 3.30× 10 | 1.81× 10 | −2.43× 10 | −1.94× 10 | 5.83× 10 | 2.90× 10 | −1.55× 10 | −1.89× 10 | - |
| LBP | 8.31× 10 | −5.73× 10 | 2.82× 10 | 1.38× 10 | 5.76× 10 | 1.16× 10 | 7.44× 10 | −3.78× 10 | −1.57× 10 | −1.82× 10 | −1.18× 10 |
| HOG | −5.02× 10 | −1.50× 10 | 2.59× 10 | 5.43× 10 | 1.06× 10 | 1.18× 10 | 7.69× 10 | −4.35× 10 | −1.35× 10 | 7.12× 10 | −3.71× 10 |
| LBP | HOG | ||||||||||
| Ct | 8.31× 10 | −5.02× 10 | |||||||||
| Cr | −5.73× 10 | −1.50× 10 | |||||||||
| Eg | 2.82× 10 | 2.59× 10 | |||||||||
| Hg | 1.38× 10 | 5.43× 10 | |||||||||
| Ep | 5.76× 10 | 1.06× 10 | |||||||||
| Ac | 1.16× 10 | 1.18× 10 | |||||||||
| CP | 7.44× 10 | 7.69× 10 | |||||||||
| CS | −3.78× 10 | −4.35× 10 | |||||||||
| Ds | −1.57× 10 | −1.35× 10 | |||||||||
| MP | −1.82× 10 | 7.12× 10 | |||||||||
| Vr | −1.18× 10 | −3.71× 10 | |||||||||
| LBP | - | 2.17× 10 | |||||||||
| HOG | 2.17× 10 | - | |||||||||
| Selection Method | CCR |
|---|---|
| SFS | 0.92 |
| SFFS | 0.93 |
| SBS | 0.89 |
| SFBS | 0.86 |
| Choquet | 0.99 |
| Ite | N | F | CCR | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ct | Cr | Eg | Hg | Ep | Ac | CP | CS | Ds | MP | Vr | LBP | HOG | |||
| 1 | 13 | 0.85 | |||||||||||||
| 1 | 12 | X | 0.85 | ||||||||||||
| 2 | 11 | X | X | 0.85 | |||||||||||
| 3 | 10 | X | X | X | 0.85 | ||||||||||
| 4 | 9 | X | X | X | X | 0.85 | |||||||||
| 5 | 8 | X | X | X | X | X | 0.85 | ||||||||
| 6 | 7 | X | X | X | X | X | X | 0.92 | |||||||
| 7 | 6 | X | X | X | X | X | X | X | 0.92 | ||||||
| 8 | 5 | X | X | X | X | X | X | X | X | 0.92 | |||||
| 9 | 4 | X | X | X | X | X | X | X | X | X | 0.92 | ||||
| Ite | N | F | CCR | ||||
|---|---|---|---|---|---|---|---|
| Rd | Cp | Ec | ZM | GFD | |||
| 1 | 5 | 0.92 | |||||
| 2 | 4 | X | 0.92 | ||||
| 3 | 2 | X | X | X | 0.92 | ||
| Ite | N | F | CCR | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ct | Cr | Eg | Hg | Ep | Ac | CP | CS | Ds | MP | Vr | LBP | HOG | |||
| 1 | 13 | 0.85 | |||||||||||||
| 1 | 12 | X | 0.85 | ||||||||||||
| 2 | 11 | X | X | 0.85 | |||||||||||
| 3 | 10 | X | X | X | 0.85 | ||||||||||
| 4 | 9 | X | X | X | X | 0.85 | |||||||||
| 5 | 8 | X | X | X | X | X | 0.85 | ||||||||
| 6 | 7 | X | X | X | X | X | X | 0.92 | |||||||
| 7 | 6 | X | X | X | X | X | X | X | 0.92 | ||||||
| 8 | 5 | X | X | X | X | X | X | X | X | 0.92 | |||||
| 9 | 4 | X | X | X | X | X | X | X | X | X | 0.92 | ||||
| Ite | N | F | CCR | ||||
|---|---|---|---|---|---|---|---|
| Rd | Cp | Ec | ZM | GFD | |||
| 1 | 5 | 0.92 | |||||
| 2 | 4 | X | 0.92 | ||||
| 3 | 2 | X | X | X | X | 0.92 | |
| Ite | N | F | CCR | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Ct1 | Hg1 | LBP1 | HOG1 | Ct2 | Ac2 | LBP2 | HOG2 | |||
| 1 | 8 | 0.92 | ||||||||
| 2 | 6 | X | X | 0.92 | ||||||
| 3 | 5 | X | X | X | 0.92 | |||||
| Shapley Values | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Ite | Ct1 | Hg1 | LBP1 | HOG1 | Ct2 | Ac2 | LBP2 | HOG2 | 1/N |
| 1 | 0.121 | 0.127 | 0.130 | 0.129 | 0.121 | 0.122 | 0.125 | 0.125 | 0.125 |
| 2 | - | 0.165 | 0.171 | 0.171 | - | 0.160 | 0.166 | 0.167 | 0.167 |
| 3 | - | 0.200 | 0.200 | 0.200 | - | - | 0.200 | 0.200 | 0.200 |
| KNN | ANN | SVM | DT | ||
|---|---|---|---|---|---|
| BoW | CCR | 93% | 97% | 99% | 99% |
| p-value | 0.02 | - |
| KNN | ANN | SVM | DT | |
|---|---|---|---|---|
| Texture and shape without selection | 93% | 90% | 93% | 87% |
| Texture and shape selected | 93% | 96.7% | 99% | 93% |
| BoW | 93% | 97% | 99% | 99% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trabelsi Ben Ameur, S.; Sellami, D.; Wendling, L.; Cloppet, F. Breast Cancer Diagnosis System Based on Semantic Analysis and Choquet Integral Feature Selection for High Risk Subjects. Big Data Cogn. Comput. 2019, 3, 41. https://doi.org/10.3390/bdcc3030041
Trabelsi Ben Ameur S, Sellami D, Wendling L, Cloppet F. Breast Cancer Diagnosis System Based on Semantic Analysis and Choquet Integral Feature Selection for High Risk Subjects. Big Data and Cognitive Computing. 2019; 3(3):41. https://doi.org/10.3390/bdcc3030041
Chicago/Turabian StyleTrabelsi Ben Ameur, Soumaya, Dorra Sellami, Laurent Wendling, and Florence Cloppet. 2019. "Breast Cancer Diagnosis System Based on Semantic Analysis and Choquet Integral Feature Selection for High Risk Subjects" Big Data and Cognitive Computing 3, no. 3: 41. https://doi.org/10.3390/bdcc3030041





