Pruning Fuzzy Neural Network Applied to the Construction of Expert Systems to Aid in the Diagnosis of the Treatment of Cryotherapy and Immunotherapy
Abstract
1. Introduction
2. Literature Review
2.1. Human Papillomavirus Concepts
2.2. Artificial Intelligence, Artificial Neural Networks and Fuzzy Systems
2.3. Related Works
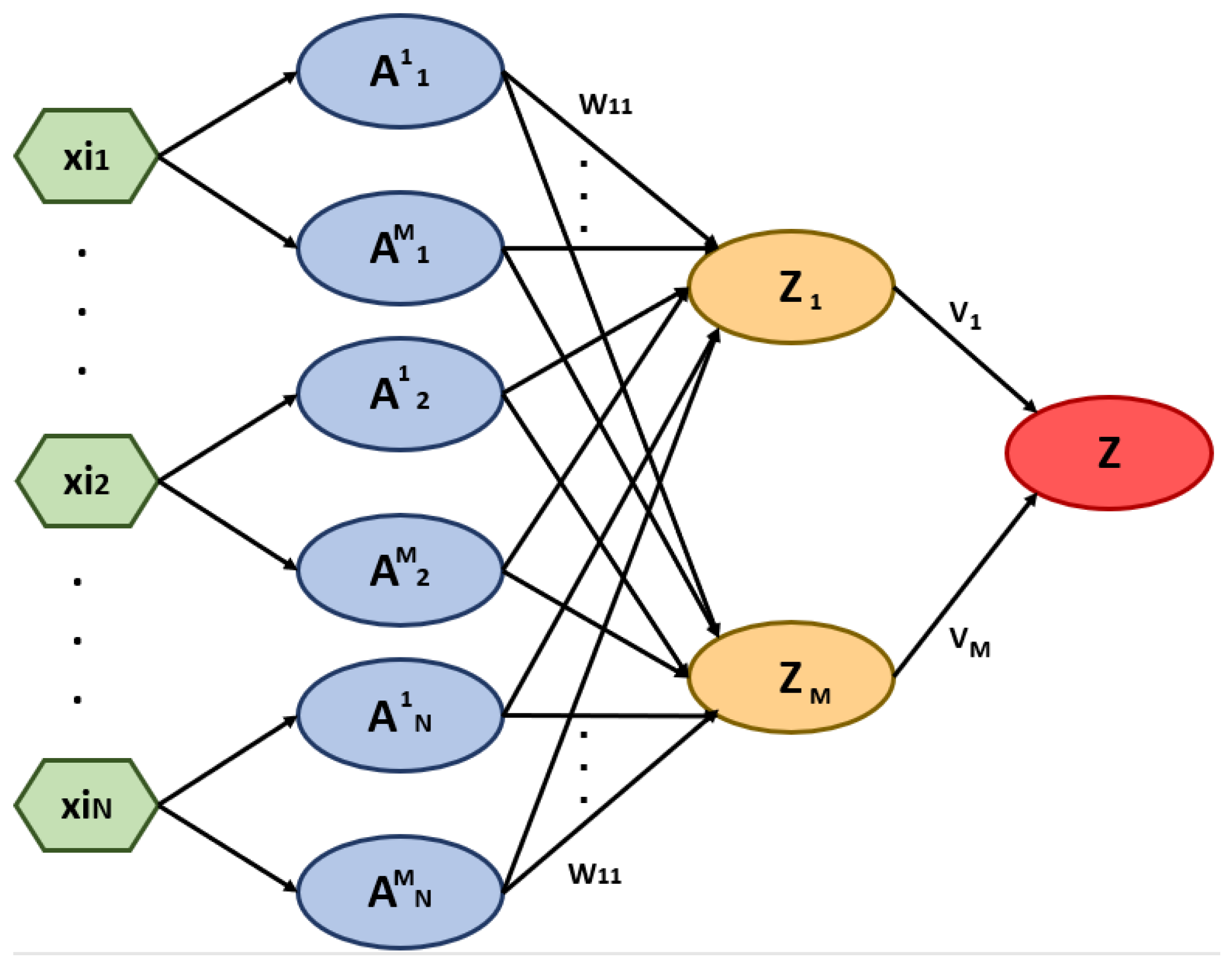
2.4. Fuzzy Neural Network
3. Pruning Fuzzy Neural Network Applied to Problems of Cryotherapy and Immunotherapy
3.1. First Layer
3.2. Second Layer
- each pair (, ) is transformed into a single value = h(, )
- calculate the unified aggregation of the transformed values U (), where n is the number of inputs.
3.3. Third Layer
- the number of membership functions, M
- the type of fuzzy logic neuron, unineuron
| Algorithm 1: Fuzzy neural network for detection of immunotherapy and cryotherapy treatments—fuzzy neural network (FNN) training. |
| (1) Define the number os membership functions, M. (2) Calculate M neurons for each characteristic in the first layer using ANFIS. (3) Construct L fuzzy neurons with Gaussian membership functions constructed with center and values derived from ANFIS. (4) Define the weights and bias of the fuzzy neurons randomly. (5) Construct L fuzzy logical neurons with random weights and bias on the second layer of the network by welding the L fuzzy neurons of the first layer. (6) Use f-scores to define the most significant neurons to the problem (). (7) For all K input do (7.1) Calculate the mapping using logical neurons (8) Estimate the weights of the output layer using Equation (7). (9) Calculate output y using Equation (5). |
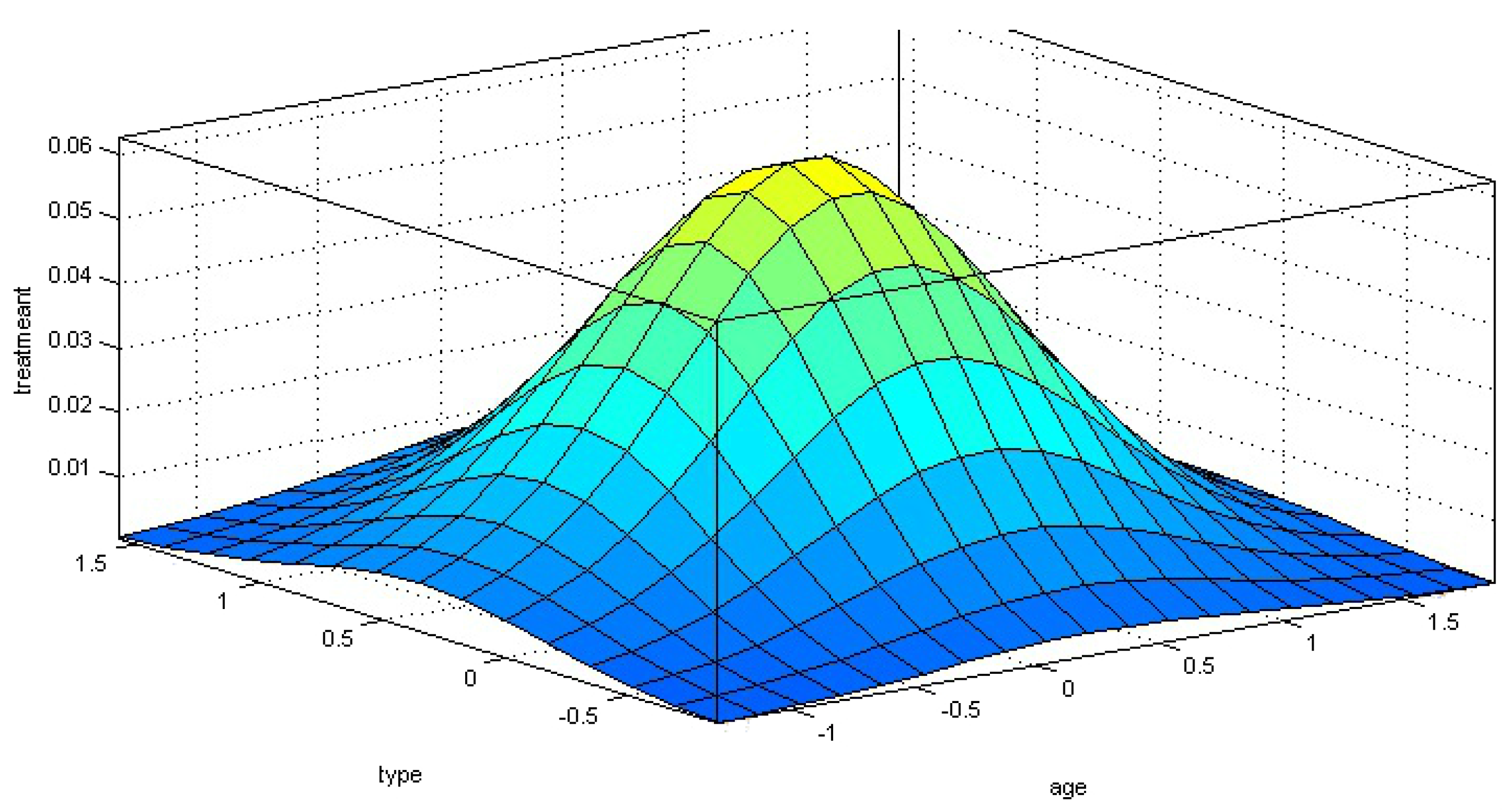
4. Results
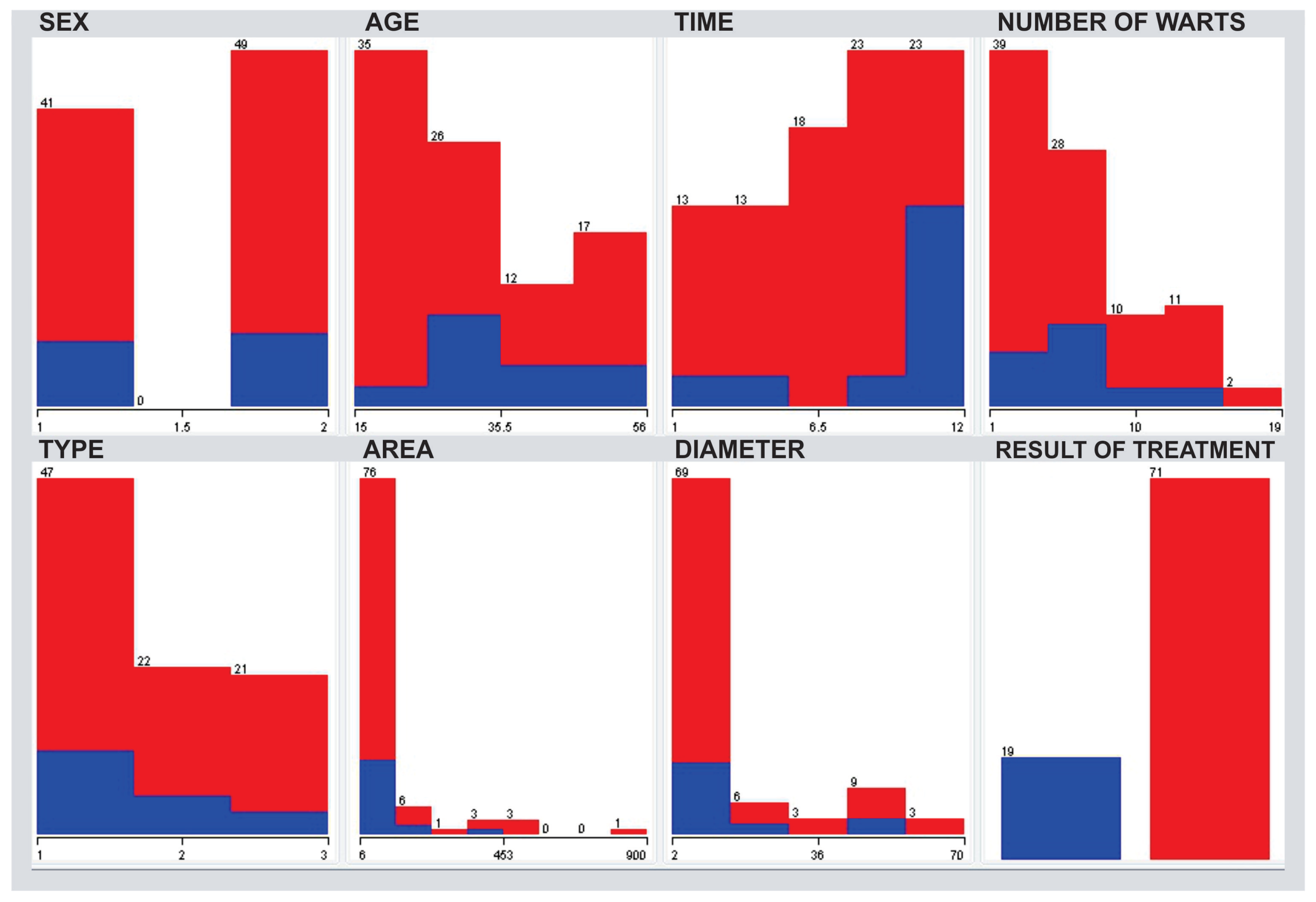
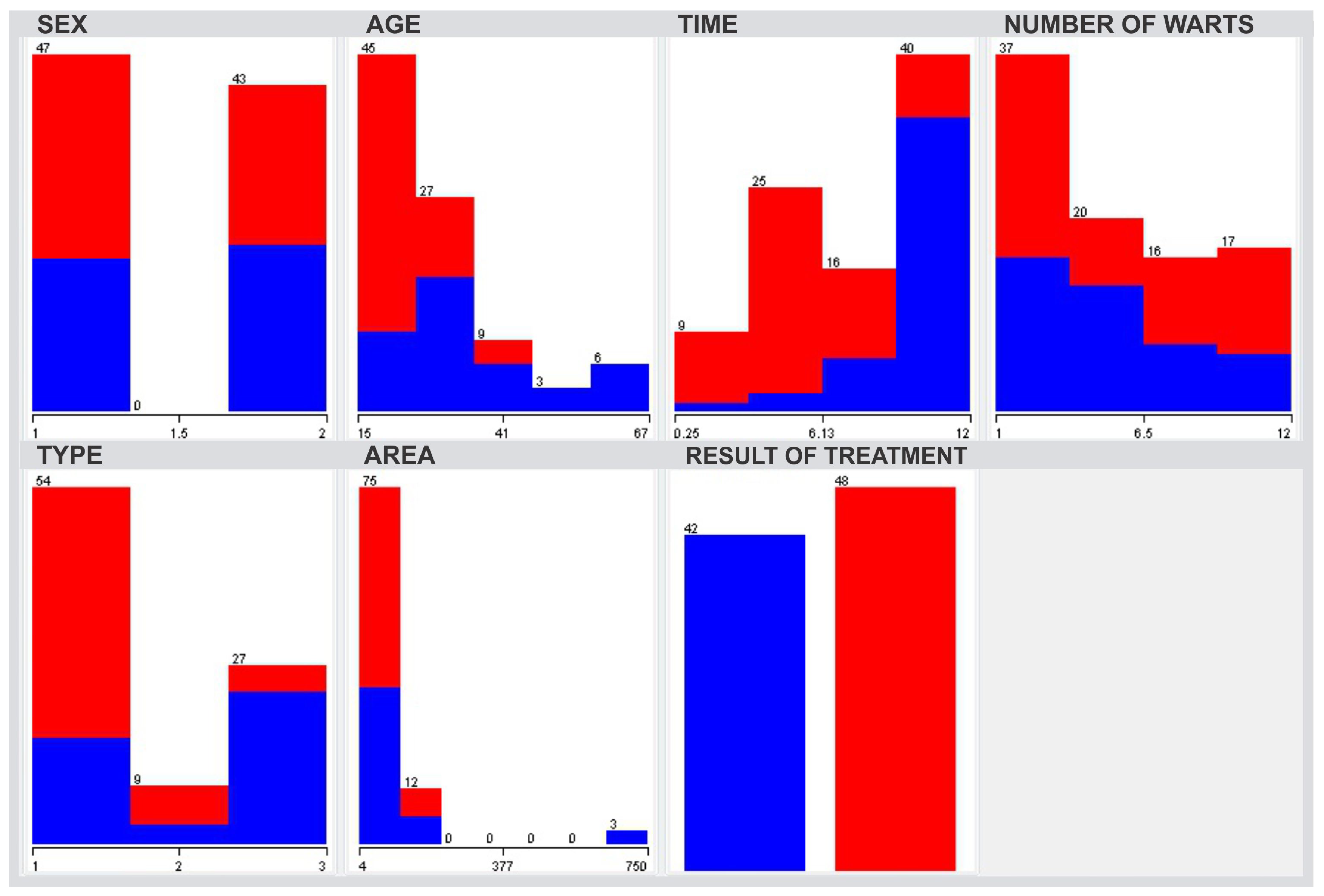
4.1. Database Used in the Test
- Sex (41 male (1), and 49 female (2));
- Age (minimum of 15 years and a maximum of 56 years with mean in 31.04 years and standard deviation of 12.23);
- Time (minimum of one and maximum of 12-time units with a mean of 7.23 and a standard deviation of 3.09);
- Number of warts (minimum one and maximum of 19 warts with a mean of 6.14 and a standard deviation of 4.21);
- Type (type (1) in 47 people, type (2) in 22 people and type (3) in 21 people);
- Area (minimum of 6 and maximum of 900 measurements with the mean of 95.7 and standard deviation of 136.61);
- Induration diameter (only in immunotherapy database) (minimum of two and maximum of 70 measurements with a mean of 14.3 and a standard deviation of 17.21);
- The outcome of the treatment (19 people who did not give (0) and 71 people that the treatment was effective (1) for immunotherapy and 48 has effective (1), and 42 have not been successful in the treatment of warts in cryotherapy treatment).
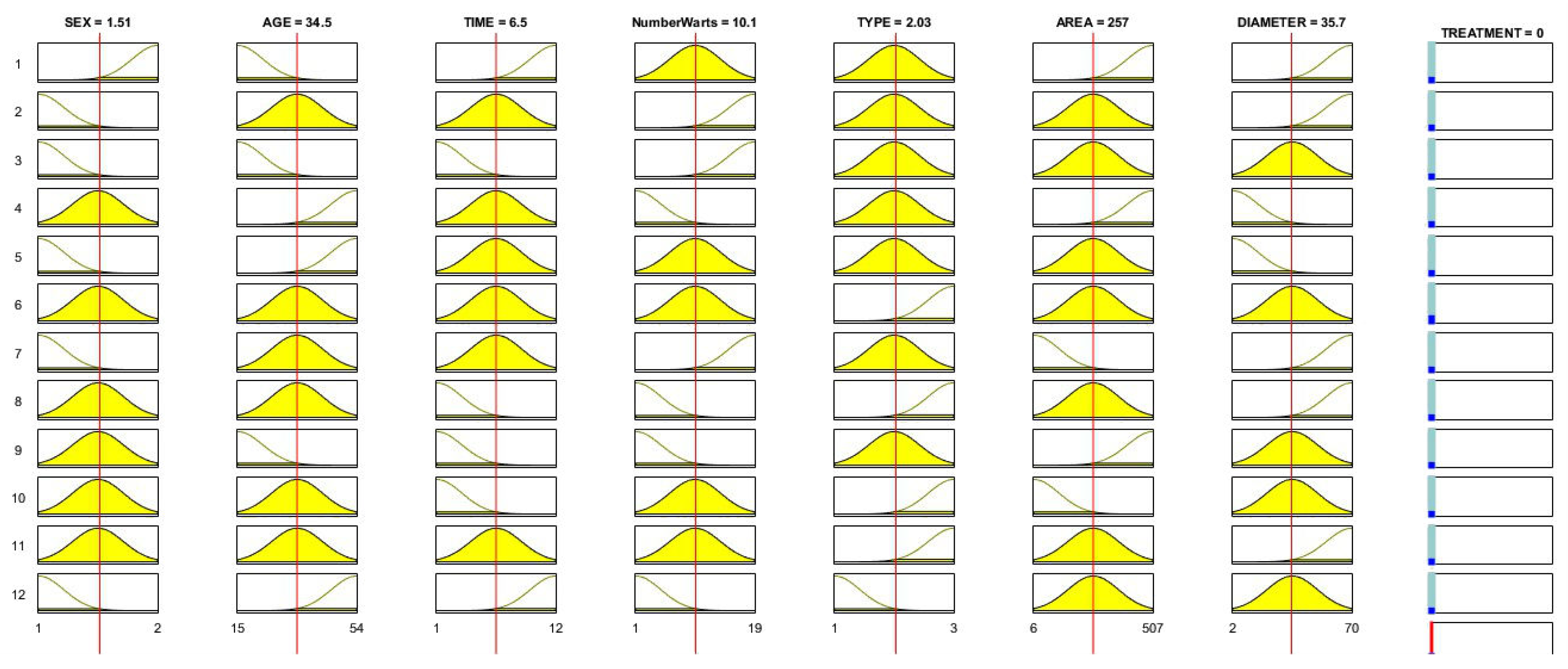
4.2. Test Settings
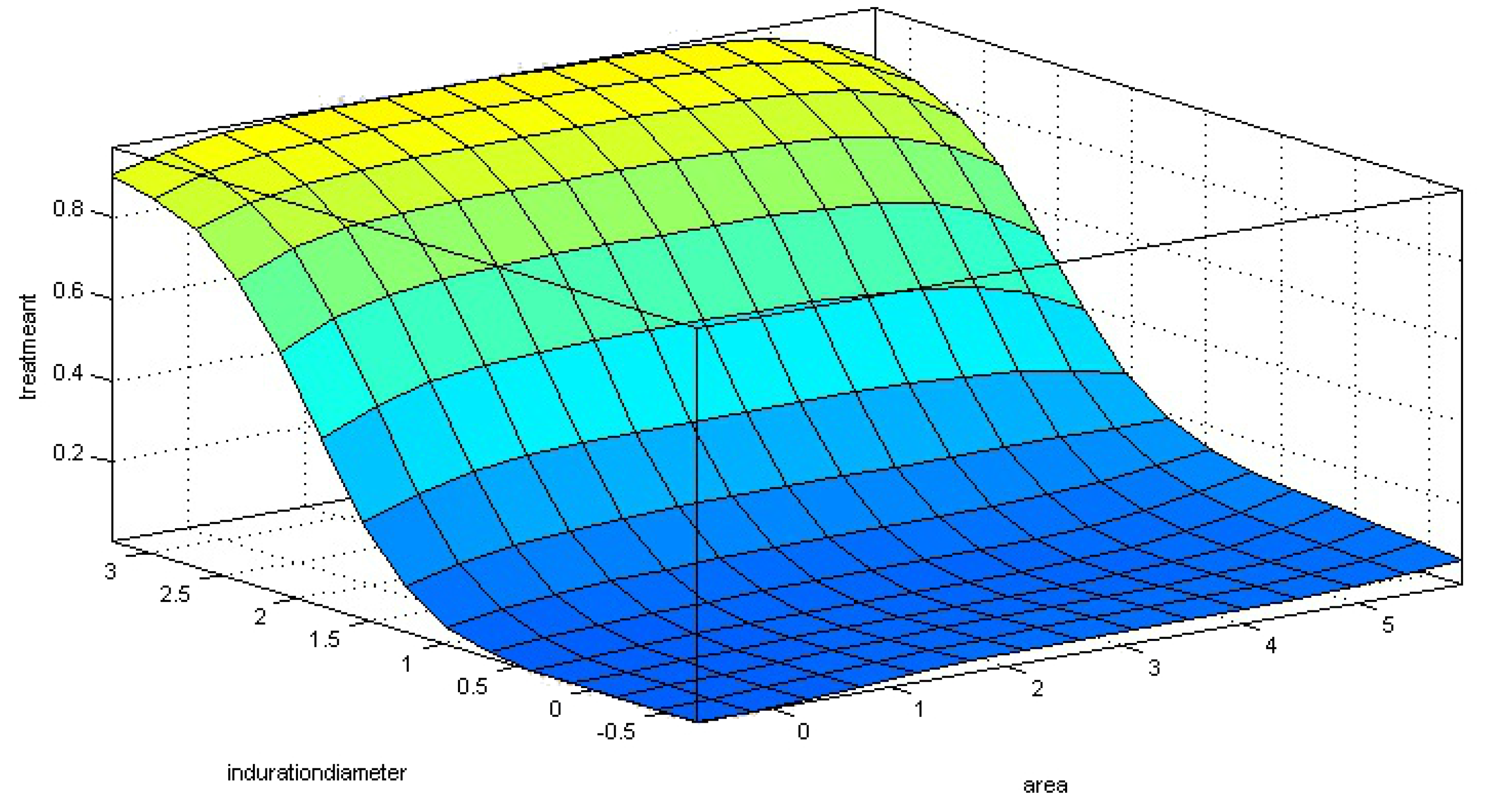
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| HPV | Human papillomavirus |
| WHO | World Health Organization |
| FNN | Fuzzy neural network |
| ELM | Extreme learning machine |
References
- Muñoz, N.; Bosch, F.X.; De Sanjosé, S.; Herrero, R.; Castellsagué, X.; Shah, K.V.; Snijders, P.J.; Meijer, C.J. Epidemiologic classification of human papillomavirus types associated with cervical cancer. N. Engl. J. Med. 2003, 348, 518–527. [Google Scholar] [CrossRef] [PubMed]
- Scheinfeld, N.; Lehman, D.S. An evidence-based review of medical and surgical treatments of genital warts. Dermatol. Online J. 2006, 12, 5. [Google Scholar]
- Khozeimeh, F.; Alizadehsani, R.; Roshanzamir, M.; Khosravi, A.; Layegh, P.; Nahavandi, S. An expert system for selecting wart treatment method. Comput. Biol. Med. 2017, 81, 167–175. [Google Scholar] [CrossRef]
- Lin, C.T.; Yeh, C.M.; Liang, S.F.; Chung, J.F.; Kumar, N. Support-vector-based fuzzy neural network for pattern classification. IEEE Trans. Fuzzy Syst. 2006, 14, 31–41. [Google Scholar]
- Souza, P.V.C. Regularized fuzzy neural networks for pattern classification problems. Int. J. Appl. Eng. Res. 2018, 13, 2985–2991. [Google Scholar]
- De Campos Souza, P.V.; de Oliveira, P.F.A. Regularized fuzzy neural networks based on nullneurons for problems of classification of patterns. In Proceedings of the 2018 IEEE Symposium on Computer Applications & Industrial Electronics (ISCAIE), Penang, Malaysia, 28–29 April 2018; pp. 25–30. [Google Scholar]
- De Campos Souza, P.V.; Torres, L.C.B.; Guimaraes, A.J.; Araujo, V.S.; Araujo, V.J.S.; Rezende, T.S. Data density-based clustering for regularized fuzzy neural networks based on nullneurons and robust activation function. In Soft Computing; Springer: Berlin, Germany, 2019; pp. 1–15. [Google Scholar]
- De Campos Souza, P.V.; Nunes, C.F.G.; Guimares, A.J.; Rezende, T.S.; Araujo, V.S.; Arajuo, V.J.S. Self-organized direction aware for regularized fuzzy neural networks. In Evolving Systems; Springer: Berlin, Germany, 2019; pp. 1–15. [Google Scholar]
- De Campos Souza, P.V.; Guimaraes, A.J.; Araújo, V.S.; Rezende, T.S.; Araújo, V.J.S. Fuzzy neural networks based on fuzzy logic neurons regularized by resampling techniques and regularization theory for regression problems. Intel. Artif. 2018, 21, 114–133. [Google Scholar] [CrossRef][Green Version]
- De Campos Souza, P.V.; Torres, L.C.B. Regularized fuzzy neural network based on or neuron for time series forecasting. In North American Fuzzy Information Processing Society Annual Conference; Springer: Berlin, Germany, 2018; pp. 13–23. [Google Scholar]
- Chang, P.C.; Liu, C.H.; Fan, C.Y. Data clustering and fuzzy neural network for sales forecasting: A case study in printed circuit board industry. Knowl. Based Syst. 2009, 22, 344–355. [Google Scholar] [CrossRef]
- Özbay, Y.; Ceylan, R.; Karlik, B. A fuzzy clustering neural network architecture for classification of ECG arrhythmias. Comput. Biol. Med. 2006, 36, 376–388. [Google Scholar] [CrossRef]
- Osowski, S.; Linh, T.H. ECG beat recognition using fuzzy hybrid neural network. IEEE Trans. Biomed. Eng. 2001, 48, 1265–1271. [Google Scholar] [CrossRef] [PubMed]
- Ceylan, R.; Özbay, Y.; Karlik, B. A novel approach for classification of ECG arrhythmias: Type-2 fuzzy clustering neural network. Expert Syst. Appl. 2009, 36, 6721–6726. [Google Scholar] [CrossRef]
- De Campos Souza, P.V.; Guimaraes, A.J. Using fuzzy neural networks for improving the prediction of children with autism through mobile devices. In Proceedings of the 2018 IEEE Symposium on Computers and Communications (ISCC), Bern, Switzerland, 25–28 June 2018; pp. 01086–01089. [Google Scholar]
- Vinicius, J.; Araújo, L.; de Oliveira, B.; Paulo, V.C.S.; Araújo, V.; Thiago Silva Rezende, A.J.G. Using fuzzy neural networks to improve prediction of expert systems for detection of breast cancer. An. Encontro Nac. Intel. Artif. Comput. (ENIAC) 2018, 15, 799–810. [Google Scholar] [CrossRef]
- Silva Araújo, V.J.; Guimarães, A.J.; de Campos Souza, P.V.; Silva Rezende, T.; Souza Araújo, V. Using resistin, glucose, age and BMI and pruning fuzzy neural network for the construction of expert systems in the prediction of breast cancer. Mach. Learn. Knowl. Extr. 2019, 1, 466–482. [Google Scholar] [CrossRef]
- Souza, P.V.d.C.; Guimaraes, A.J.; Araujo, V.S.; Rezende, T.S.; Araujo, V.J.S. Regularized fuzzy neural networks to aid effort forecasting in the construction and software development. arXiv, 2018; arXiv:1812.01351. [Google Scholar]
- De Campos Souza, P.V.; Guimaraes, A.J.; Araujo, V.S.; Rezende, T.S.; Araujo, V.J.S. Incremental regularized data density-based clustering neural networks to aid in the construction of effort forecasting systems in software development. In Applied Intelligence; Springer: Berlin, Germany, 2019. [Google Scholar] [CrossRef]
- Guimarães, A.J.; Araujo, V.J.S.; de Campos Souza, P.V.; Araujo, V.S.; Rezende, T.S. Using fuzzy neural networks to the prediction of improvement in expert systems for treatment of immunotherapy. In Ibero-American Conference on Artificial Intelligence; Springer: Berlin, Germany, 2018; pp. 229–240. [Google Scholar]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Vitor de Campos Souza, P. Pruning fuzzy neural networks based on unineuron for problems of classification of patterns. J. Intell. Fuzzy Syst. 2018, 2, 1–9. [Google Scholar]
- Bruni, L.; Barrionuevo-Rosas, L.; Albero, G.; Aldea, M.; Serrano, B.; Valencia, S.; Brotons, M.; Mena, M.; Cosano, R.; Muñoz, J.; et al. ICO information centre on HPV and cancer (HPV information centre). In Human Papillomavirus and Related Diseases in India; Summary Report; Institut Català dOncologia: Barcelona, Spain, 2015; pp. 12–23. [Google Scholar]
- World Health Organization. Cervical Cancer, Human Papillomavirus (HPV) and HPV Vaccines: Key Points for Policy-Makers and Health Professionals; WHO: Geneva, Switzerland, 2008. [Google Scholar]
- Walboomers, J.M.; Jacobs, M.V.; Manos, M.M.; Bosch, F.X.; Kummer, J.A.; Shah, K.V.; Snijders, P.J.; Peto, J.; Meijer, C.J.; Muñoz, N. Human papillomavirus is a necessary cause of invasive cervical cancer worldwide. J. Pathol. 1999, 189, 12–19. [Google Scholar] [CrossRef]
- Stone, K.; Becker, T.; Hadgu, A.; Kraus, S. Treatment of external genital warts: A randomised clinical trial comparing podophyllin, cryotherapy, and electrodesiccation. Sex. Transm. Infect. 1990, 66, 16–19. [Google Scholar] [CrossRef]
- Brandt, H.R.C.; Fernandes, J.D.; Patriota, R.C.R.; Criado, P.R.; Belda Junior, W. Treatment of human papillomavirus in childhood with imiquimod 5% cream. An. Bras. Dermatol. 2010, 85, 549–553. [Google Scholar] [CrossRef]
- Eggermont, A.M.; Kroemer, G.; Zitvogel, L. Immunotherapy and the concept of a clinical cure. Eur. J. Cancer 2013, 49, 2965–2967. [Google Scholar] [CrossRef]
- Josephs, D.H.; Spicer, J.F.; Karagiannis, P.; Gould, H.J.; Karagiannis, S.N. IgE Immunotherapy: A Novel Concept with Promise for the Treatment of Cancer; Taylor & Francis: Didcot, UK, 2014; Volume 6, pp. 54–72. [Google Scholar]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice Hall: Upper Saddle River, NJ, USA, 1994. [Google Scholar]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Braga, A.D.P.; Carvalho, A.; Ludermir, T.B. Redes Neurais Artificiais: Teoria e Aplicações; LTC-Livros Técnicos e Científicos Editora: Rio de Janeiro, Brazil, 2000. [Google Scholar]
- Riedmiller, M.; Braun, H. A direct adaptive method for faster backpropagation learning: The RPROP algorithm. In Proceedings of the IEEE International Conference on Neural Networks, San Francisco, CA, USA, 28 March–1 April 1993; pp. 586–591. [Google Scholar]
- Coello, C.A.C.; Lamont, G.B.; Van Veldhuizen, D.A. Evolutionary Algorithms for Solving Multi-Objective Problems; Springer: Berlin, Germany, 2007; Volume 5. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms; Pearson Education: Tharamani, India, 2006. [Google Scholar]
- Zadeh, L.A. Information and control. Fuzzy Sets 1965, 8, 338–353. [Google Scholar]
- Pedrycz, W.; Gomide, F. An Introduction to Fuzzy Sets: Analysis and Design; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Shah, S.C.; Kusiak, A.; O’Donnell, M.A. Patient-recognition data-mining model for BCG-plus interferon immunotherapy bladder cancer treatment. Comput. Biol. Med. 2006, 36, 634–655. [Google Scholar] [CrossRef] [PubMed]
- Basarslan, M.; Kayaalp, F. A hybrid classification example in the diagnosis of skin disease with cryotherapy and immunotherapy treatment. In Proceedings of the 2nd International Symposium on Multidisciplinary Studies and Innovative Technologies (ISMSIT), Ankara, Turkey, 19–21 October 2018; pp. 1–5. [Google Scholar]
- Jain, R.; Sawhney, R.; Mathur, P. Feature selection for cryotherapy and immunotherapy treatment methods based on gravitational search algorithm. In Proceedings of the 2018 International Conference on Current Trends towards Converging Technologies (ICCTCT), Coimbatore, India, 1–3 March 2018; pp. 1–7. [Google Scholar]
- Platzman, I.; Janiesch, J.W.; Matić, J.; Spatz, J.P. Artificial antigen-presenting interfaces in the service of immunology. Isr. J. Chem. 2013, 53, 655–669. [Google Scholar] [CrossRef]
- Akben, S.B. Predicting the success of wart treatment methods using decision tree based fuzzy informative images. Biocybern. Biomed. Eng. 2018, 38, 819–827. [Google Scholar] [CrossRef]
- CÜvitoğlu, A.; Işik, Z. Evaluation machine-learning approaches for classification of cryotherapy and immunotherapy datasets. Age 2018, 15, 15–56. [Google Scholar]
- Khatri, S.; Arora, D.; Kumar, A. Enhancing decision tree classification accuracy through genetically programmed attributes for wart treatment method identification. Proc. Comput. Sci. 2018, 132, 1685–1694. [Google Scholar] [CrossRef]
- Khozeimeh, F.; Jabbari Azad, F.; Mahboubi Oskouei, Y.; Jafari, M.; Tehranian, S.; Alizadehsani, R.; Layegh, P. Intralesional immunotherapy compared to cryotherapy in the treatment of warts. Int. J. Dermatol. 2017, 56, 474–478. [Google Scholar] [CrossRef] [PubMed]
- Mirandola, L.; Timsah, Z.; Nguyen, D.D.T.; Bresalier, R.; Daver, N.G.; Chiriva-Internati, M. Phase I/II study of BSK01, an artificial intelligence-driven, peptide-pulsed, mature DC immunotherapy for solid and hematological malignancies. J. Clin. Oncol. 2018, 36. [Google Scholar] [CrossRef]
- Houy, N.; Le Grand, F. Optimizing immune cell therapies with artificial intelligence. J. Theor. Biol. 2019, 461, 34–40. [Google Scholar] [CrossRef] [PubMed]
- Ajili, F.; Issam, B.M.; Kourda, N.; Darouiche, A.; Chebil, M. Prognostic value of artificial neural network in predicting bladder cancer recurrence after BCG immunotherapy. J. Cytol. Histol. 2014, 5, 226. [Google Scholar] [CrossRef]
- Suberi, A.A.M.; Zakaria, W.N.W.; Tomari, R. Dendritic cell recognition in computer aided system for cancer immunotherapy. Proc. Comput. Sci. 2017, 105, 177–182. [Google Scholar] [CrossRef]
- Ngufor, C.; Wojtusiak, J.; Hooker, A.; Oz, T.; Hadley, J. Extreme logistic regression: A large scale learning algorithm with application to prostate cancer mortality prediction. In Proceedings of the FLAIRS Conference, Pensacola Beach, FL, USA, 21–23 May 2014. [Google Scholar]
- Fulcher, J. Computational intelligence: An introduction. In Computational Intelligence: A Compendium; Springer: Berlin, Gemarny, 2008; pp. 3–78. [Google Scholar]
- Cordón, O.; Gomide, F.; Herrera, F.; Hoffmann, F.; Magdalena, L. Ten years of genetic fuzzy systems: Current framework and new trends. Fuzzy Sets Syst. 2004, 141, 5–31. [Google Scholar] [CrossRef]
- Pedrycz, W. Fuzzy neural networks and neurocomputations. Fuzzy Sets Syst. 1993, 56, 1–28. [Google Scholar] [CrossRef]
- Amjady, N. Day-ahead price forecasting of electricity markets by a new fuzzy neural network. IEEE Trans. Power Syst. 2006, 21, 887–896. [Google Scholar] [CrossRef]
- Cheng, M.Y.; Tsai, H.C.; Sudjono, E. Conceptual cost estimates using evolutionary fuzzy hybrid neural network for projects in construction industry. Expert Syst. Appl. 2010, 37, 4224–4231. [Google Scholar] [CrossRef]
- Chatterjee, A.; Pulasinghe, K.; Watanabe, K.; Izumi, K. A particle-swarm-optimized fuzzy-neural network for voice-controlled robot systems. IEEE Trans. Ind. Electron. 2005, 52, 1478–1489. [Google Scholar] [CrossRef]
- Wai, R.J.; Liu, C.M. Design of dynamic petri recurrent fuzzy neural network and its application to path-tracking control of nonholonomic mobile robot. IEEE Trans. Ind. Electron. 2009, 56, 2667–2683. [Google Scholar]
- He, W.; Dong, Y. Adaptive fuzzy neural network control for a constrained robot using impedance learning. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 1174–1186. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Zhao, Y.; Liu, M. Self-learning interval type-2 fuzzy neural network controllers for trajectory control of a delta parallel robot. Neurocomputing 2018, 283, 107–119. [Google Scholar] [CrossRef]
- Lin, J.W.; Hwang, M.I.; Becker, J.D. A fuzzy neural network for assessing the risk of fraudulent financial reporting. Manag. Audit. J. 2003, 18, 657–665. [Google Scholar] [CrossRef]
- García, F.; Guijarro, F.; Oliver, J.; Tamošiūnienė, R. Hybrid fuzzy neural network to predict price direction in the German DAX-30 index. Technol. Econ. Dev. Econ. 2018, 24, 2161–2178. [Google Scholar] [CrossRef]
- Hu, H.; Tang, L.; Zhang, S.; Wang, H. Predicting the direction of stock markets using optimized neural networks with Google Trends. Neurocomputing 2018, 285, 188–195. [Google Scholar] [CrossRef]
- De Campos Souza, P.V.; Torres, L.C.B.; Guimarães, A.J.; Araujo, V.S. Pulsar detection for wavelets SODA and regularized fuzzy neural networks based on andneuron and robust activation function. Int. J. Artif. Intell. Tools 2019, 28, 1950003. [Google Scholar] [CrossRef]
- Zhang, J.; Morris, J. Process modelling and fault diagnosis using fuzzy neural networks. Fuzzy Sets Syst. 1996, 79, 127–140. [Google Scholar] [CrossRef]
- Zhou, G.; Mao, C.; Tian, M. Spindle fault prediction based on improved fuzzy neural network algorithm. In International Conference on Applications and Techniques in Cyber Security and Intelligence; Springer: Berlin, Germany, 2018; pp. 1240–1248. [Google Scholar]
- Zhao, T.; Li, P.; Cao, J. Soft sensor modeling of chemical process based on self-organizing recurrent interval type-2 fuzzy neural network. In ISA Transactions; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Gai, J.; Hu, Y. Research on fault diagnosis based on singular value decomposition and fuzzy neural network. Shock Vib. 2018, 2018. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, Y.S.; Thakor, N.V.; Xu, Y.H. A short-time multifractal approach for arrhythmia detection based on fuzzy neural network. IEEE Trans. Biomed. Eng. 2001, 48, 989–995. [Google Scholar] [CrossRef] [PubMed]
- Cheng, H.; Cui, M. Mass lesion detection with a fuzzy neural network. Pattern Recognit. 2004, 37, 1189–1200. [Google Scholar] [CrossRef]
- Ushida, Y.; Kato, R.; Niwa, K.; Tanimura, D.; Izawa, H.; Yasui, K.; Takase, T.; Yoshida, Y.; Kawase, M.; Yoshida, T.; et al. Combinational risk factors of metabolic syndrome identified by fuzzy neural network analysis of health-check data. BMC Med. Inform. Decis. Mak. 2012, 12, 80. [Google Scholar] [CrossRef]
- Tan, T.Z.; Quek, C.; Ng, G.S.; Razvi, K. Ovarian cancer diagnosis with complementary learning fuzzy neural network. Artif. Intell. Med. 2008, 43, 207–222. [Google Scholar] [CrossRef]
- Plawiak, P.; Tadeusiewicz, R. Approximation of phenol concentration using novel hybrid computational intelligence methods. Int. J. Appl. Math. Comput. Sci. 2014, 24, 165–181. [Google Scholar] [CrossRef]
- Pławiak, P.; Maziarz, W. Classification of tea specimens using novel hybrid artificial intelligence methods. Sens. Actuators B Chem. 2014, 192, 117–125. [Google Scholar] [CrossRef]
- Pławiak, P.; Rzecki, K. Approximation of phenol concentration using computational intelligence methods based on signals from the metal-oxide sensor array. IEEE Sens. J. 2015, 15, 1770–1783. [Google Scholar]
- Plawiak, P.; Maziarz, W. Comparison of artificial intelligence methods on the example of tea classification based on signals from E-nose sensors. Adv. Signal Process. 2013, 1, 19–32. [Google Scholar]
- Jang, J.S. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Yager, R.R.; Rybalov, A. Uninorm aggregation operators. Fuzzy Sets Syst. 1996, 80, 111–120. [Google Scholar] [CrossRef]
- Pedrycz, W. Logic-based fuzzy neurocomputing with unineurons. IEEE Trans. Fuzzy Syst. 2006, 14, 860–873. [Google Scholar] [CrossRef]
- Lemos, A.; Caminhas, W.; Gomide, F. New uninorm-based neuron model and fuzzy neural networks. In Proceedings of the IEEE 2010 Annual Meeting of the North American Fuzzy Information Processing Society (NAFIPS), Toronto, ON, Canada, 12–14 July 2010; pp. 1–6. [Google Scholar]
- Lemos, A.P.; Caminhas, W.; Gomide, F. A fast learning algorithm for uninorm-based fuzzy neural networks. In Proceedings of the IEEE 2012 Annual Meeting of the North American Fuzzy Information Processing Society (NAFIPS), Berkeley, CA, USA, 6–8 August 2012; pp. 1–6. [Google Scholar]
- Albert, A. Regression and the Moore-Penrose Pseudoinverse; Elsevier: Amsterdam, The Netherlands, 1972. [Google Scholar]
- Hecht-Nielsen, R. Theory of the backpropagation neural network. In Neural Networks for Perception; Elsevier: Amsterdam, The Netherlands, 1992; pp. 65–93. [Google Scholar]
- Gao, J.; Wang, Z.; Yang, Y.; Zhang, W.; Tao, C.; Guan, J.; Rao, N. A novel approach for lie detection based on F-score and extreme learning machine. PLoS ONE 2013, 8, e64704. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.W.; Lin, C.J. Combining SVMs with various feature selection strategies. In Feature Extraction; Springer: Berlin, Germany, 2006; pp. 315–324. [Google Scholar]
- Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I.H. The WEKA data mining software: An update. ACM SIGKDD Explor. Newslett. 2009, 11, 10–18. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Patil, T.R.; Sherekar, S. Performance analysis of Naive Bayes and J48 classification algorithm for data classification. Int. J. Comput. Sci. Appl. 2013, 6, 256–261. [Google Scholar]
- Langley, P.; Iba, W.; Thompson, K. An analysis of Bayesian classifiers. Aaai 1992, 90, 223–228. [Google Scholar]
- Witten, I.H.; Frank, E.; Trigg, L.E.; Hall, M.A.; Holmes, G.; Cunningham, S.J. Weka: Practical Machine Learning Tools and Techniques with Java Implementations; Working paper 99/11; University of Waikato: Hamilton, New Zealand, 1999. [Google Scholar]
- Aldous, D. The continuum random tree. I. Ann. Probab. 1991, 21, 1–28. [Google Scholar] [CrossRef]

| Models | Accuracy | AUC | Sens. | Spec. | Time |
|---|---|---|---|---|---|
| This paper | 84.32 (5.21) | 0.69 (0.01) | 0.41 (0.12) | 0.97 (0.03) | 1.11 (0.06) |
| FNN | 81.91 (7.64) | 0.65 (0.01) | 0.36 (0.24) | 0.94 (0.02) | 17.39 (1.03) |
| MLP | 78.02 (7.44) | 0.74 (0.12) | 0.60 (0.21) | 0.88 (0.10) | 1.18 (0.08) |
| J48 | 83.92 (4.69) | 0.71 (0.03) | 0.52 (0.20) | 0.91 (0.03) | 0.01 (0.00) |
| NB | 76.67 (6.55) | 0.69 (0.13) | 0.51 (0.18) | 0.87 (0.13) | 0.01 (0.00) |
| ZR | 79.13 (1.42) | 0.50 (0.00) | 0.50 (0.00) | 0.50 (0.00) | 0.01 (0.00) |
| RT | 81.24 (7.56) | 0.74 (0.10) | 0.54 (0.07) | 0.94 (0.06) | 0.21 (0.01) |
| Models | Accuracy | AUC | Sens. | Spec. | Time |
|---|---|---|---|---|---|
| This paper | 88.64 (5.83) | 0.89 (0.05) | 0.93 (0.08) | 0.86 (0.08) | 1.04 (0.08) |
| FNN | 85.75 (8.08) | 0.85 (0.05) | 0.90 (0.16) | 0.80 (0.11) | 22.78 (2.11) |
| MLP | 86.17 (7.91) | 0.91 (0.05) | 0.92 (0.06) | 0.90 (0.05) | 1.05 (0.02) |
| J48 | 85.91 (6.42) | 0.89 (0.05) | 0.90 (0.09) | 0.88 (0.02) | 0.02 (0.01) |
| NB | 85.67 (6.18) | 0.95 (0.05) | 0.90 (0.08) | 1.00 (0.00) | 0.52 (0.06) |
| ZR | 53.64 (1.33) | 0.50 (0.00) | 0.50 (0.00) | 0.50 (0.00) | 0.05 (0.00) |
| RT | 87.27 (7.98) | 0.87 (0.01) | 0.84 (0.02) | 0.90 (0.01) | 0.21 (0.01) |
| 1. If (SEX is lndifferent) and (AGE is New) and (TIME is Righ) and (NumberWarts is Medium) and |
| (TYPE is Two) and (AREA is Big) and (DIAMETER is Hard) then (TREATMENT is effective)(1) |
| 2. If (SEX is Male) and (AGE is Medium) and (TIME is Medium) and (NumberWarts is Elevated) and |
| (TYPE is Two) and (AREA is Medium) and (DIAMETER is Hard) then (TREATMENT is non-effective) (1) |
| 3. If (SEX is Male) and (AGE is New) and (TIME is Little) and (NumberWarts is Elevated) and |
| (TYPE is Two) and (AREA is Medium) and (DIAMETER is Medium) then (TREATMENT is non-effective) (1) |
| 4. If (SEX is Female) and (AGE is Old) and (TIME is Medium) and (NumberWarts is Few) and |
| (TYPE is Two) and (AREA is Big) and (DIAMETER is Small) then (TREATMENT is effective)(1) |
| 5. If (SEX is Male) and (AGE is Old) and (TIME is Medium) and (NumberWarts is Medium) and |
| (TYPE is Two) and (AREA is Medium) and (DIAMETER is Small) then (TREATMENT is effective)(1)) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Junio Guimarães, A.; Vitor de Campos Souza, P.; Jonathan Silva Araújo, V.; Silva Rezende, T.; Souza Araújo, V. Pruning Fuzzy Neural Network Applied to the Construction of Expert Systems to Aid in the Diagnosis of the Treatment of Cryotherapy and Immunotherapy. Big Data Cogn. Comput. 2019, 3, 22. https://doi.org/10.3390/bdcc3020022
Junio Guimarães A, Vitor de Campos Souza P, Jonathan Silva Araújo V, Silva Rezende T, Souza Araújo V. Pruning Fuzzy Neural Network Applied to the Construction of Expert Systems to Aid in the Diagnosis of the Treatment of Cryotherapy and Immunotherapy. Big Data and Cognitive Computing. 2019; 3(2):22. https://doi.org/10.3390/bdcc3020022
Chicago/Turabian StyleJunio Guimarães, Augusto, Paulo Vitor de Campos Souza, Vinícius Jonathan Silva Araújo, Thiago Silva Rezende, and Vanessa Souza Araújo. 2019. "Pruning Fuzzy Neural Network Applied to the Construction of Expert Systems to Aid in the Diagnosis of the Treatment of Cryotherapy and Immunotherapy" Big Data and Cognitive Computing 3, no. 2: 22. https://doi.org/10.3390/bdcc3020022
APA StyleJunio Guimarães, A., Vitor de Campos Souza, P., Jonathan Silva Araújo, V., Silva Rezende, T., & Souza Araújo, V. (2019). Pruning Fuzzy Neural Network Applied to the Construction of Expert Systems to Aid in the Diagnosis of the Treatment of Cryotherapy and Immunotherapy. Big Data and Cognitive Computing, 3(2), 22. https://doi.org/10.3390/bdcc3020022






