Numerical Investigation of the Excitation Characteristics of Contaminated Nozzle Rings ^†

Abstract

The deposition of combustion residues in the nozzle ring (NR) of a turbocharger turbine stage changes the NR geometry significantly in a random manner. The resultant complex and highly asymmetric geometry induces low engine order (LEO) excitation, which may lead to resonance excitation of rotor blades and high cycle fatigue (HCF) failure. Therefore, a suitable prediction workflow is of great importance for the design and validation phases. The prediction of LEO excitation is, however, computationally expensive as high-fidelity, full annulus CFD models are required. Previous investigations showed that a steady-state computational model consisting of the volute, the NR, and a radial extension is suitable to reduce the computational costs massively and to qualitatively predict the level of LEO forced response. In the current paper, the aerodynamic excitation of 69 real contaminated NRs is analyzed using this simplified approach. The results obtained by the simplified simulation model are used to select 13 contaminated NR geometries, which are then simulated with a model of the entire turbine stage, including the rotor, in a transient time-marching manner to provide high-fidelity simulation results for the verification of the simplified approach. Furthermore, two contamination patterns are analyzed in a more detailed manner regarding their aerodynamic excitation. It is found that the simplified model can be used to identify and classify contamination patterns that lead to high blade vibration amplitudes. In cases where transient effects occurring in the rotor alter the harmonic pressure field significantly, the ability of the simplified approach to predict the LEO excitation is not sufficient.

1. Introduction

Forced response blade vibrations can be excited due to the rotation of the rotor blades through a spatially varying flow field. The movement through such a flow field leads to dynamic blade loading and, thus, aerodynamic excitation. In the case of a turbine stage, the geometry of an upstream NR plays an important role as the rotor rotates through its outflow field. In the case of a cyclic-symmetric NR geometry, the flow field is spatially periodic. The resulting forced response blade vibrations are called blade-passing forced response, as they are mainly excited by the blade-passing frequency (BPF) and its higher harmonics. Since the NR geometry normally has a high number of vanes, the BPF is high and thus excites higher structural modes [1,2,3]. In reality, the NR geometry is never perfectly cyclic-symmetric, e.g., due to manufacturing tolerances, wear, or damage [1,4]. According to Bréard et al. [1], any loss of symmetry can lead to forced response blade vibrations excited by so-called low engine orders (LEO). These low engine order harmonics have frequencies that are usually much lower than the BPF and excite mostly low structural modes. This type of forced response blade vibrations are called low-engine order forced response according to their excitation source [1,2,3]. In the following, a brief literature review on the aforementioned topic is given.

Many researchers studied the effect of small geometric mistuning in the NR on the aerodynamic excitation, e.g., caused by manufacturing tolerances. The effect of individual blade parameters, such as throat width or stagger angle variation, on LEO excitation is often investigated. Elliot et al. [5] and Vahdati et al. [6] studied the influence of generic throat width patterns in a high-pressure axial turbine. Both concluded that throat width variation can cause a significant LEO-forced response. Bréard et al. [1] analyzed the effect of the variation of the NR throat width and flow exit angle as well as blocked burner and cooling flow non-uniformities in a high-pressure axial turbine individually and concurrently. The investigation showed that the influence of the individual effects cannot be linearly superimposed to obtain the influence of the combined effects. Kovachev et al. [3] addressed the effect of tolerance-induced mistuning by investigating a specific NR throat width variation in a radial turbine stage. It is reported that a small amount of geometrical mistuning may lead to significant blade vibration amplitudes. Figaschewski et al. [7] studied stagger angle and throat width variation using a 2D model in an axial turbine stage. In the following paper, Figaschewski et al. [8] investigated the stagger angle variation, considering structural mistuning probabilistically using a normally distributed stagger angle variation. The investigation showed that LEO excitation in combination with structural mistuning can lead to significant blade vibration amplitudes. Gambitta et al. [9] studied the influence of geometrical uncertainties due to the manufacturing process on LEO forced response probabilistically in an axial compressor. A parameterized model was created from optical surface scans. The investigations were carried out using a simplified numerical approach on the basis of a single-passage CFD model in combination with a reconstruction algorithm. The strongest scattering was found in the LEOs. However, the researchers pointed out that the accuracy of the model needs to be increased. Aschenbruck et al. [10] studied the effect of typical regeneration-induced variations of NR vanes in an axial turbine. Small changes in stagger angle, trailing edge thickness, and blending at the trailing edge of the NR vanes are investigated numerically using a uni-directional fluid-structure interaction approach. The influence of each variable was investigated individually using a generic pattern where every second blade is changed identically. It was found that the stagger angle has the largest influence on the LEO forced response. The influence of NR vane damage on the LEO forced response was investigated numerically by Di Mare et al. [4] and Meyer et al. [11]. Di Mare et al. [4] showed that the LEO excitation can be up to eight times higher due to NR blade damage.

During the operation of combustion engines with critical fuels such as heavy fuel oil and medium fuel oil, the turbocharger turbine stage, especially the NR, may get contaminated by combustion residues. Since the main chemical, non-burnable components of the combustion residues have a melting point in the range of the exhaust gas temperature, these combustion residues deposit in the turbine stage, where flow channels of the NR can get partially or completely clogged [12]. The resulting change in geometry is heavily asymmetrical and leads to LEO excitation, which may lead to resonance excitation of rotor blades and potentially HCF failure. The resulting uncertainty should be considered in the design process to prevent component failure during operation. For this purpose, quantifying the HCF damage potential of different contamination patterns due to LEO excitation is of paramount importance.

In a previously published study [13], the influence of contamination and the resulting blockage on LEO excitation in a radial turbocharger turbine stage was numerically investigated. Two deteriorated NRs, a generic one having one flow channel blocked by 90% and a digital replica of a real contaminated NR were analyzed, and the results were validated against blade vibration test data. It was found that geometrical mistuning due to contamination as well as partially blocking of one flow channel in a symmetric NR induces substantial LEO excitation. A simplified steady-state CFD simulation model consisting of the volute, the NR, and a radial extension was developed to assess LEO excitation. The spatially Fourier-decomposed NR outflow field is used to quantify the aerodynamic excitation. It was shown that the simplified model is suitable to qualitatively rank the LEO excitation induced by different contamination patterns and to drastically reduce the computational costs. In the current study, the same simplified model is used to investigate 69 3D-scanned real contaminated NRs with respect to their aerodynamic excitation numerically. A total of 13 NRs are also calculated with a full-annulus, high-fidelity CFD model including the rotor to extend the verification of the simplified model through further validation cases and to analyze the limitations of the model.

2. Real Contamination Patterns

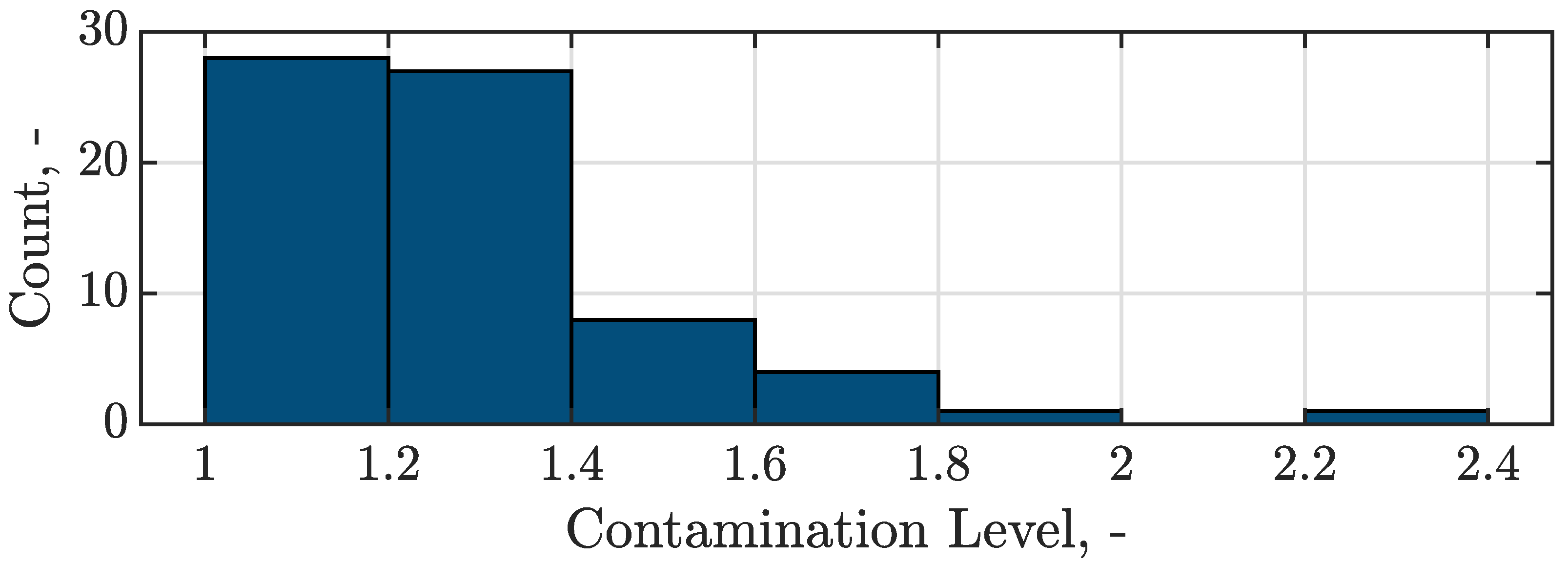
A total of 69 contaminated NRs of different sizes taken from real applications are measured by means of an optical measurement system. All NRs are scaled to the same size in order to have a sufficiently large data set that represents reality as accurately as possible. The intensity of the contamination is represented by the ratio of the volume of all contaminated vanes ($V_{contaminated}$) to the volume of all tuned vanes ($V_{tuned}$),

$$\mathrm{Contamination}\mathrm{Level}=\frac{V_{contaminated}}{V_{tuned}}.$$

(1)

Figure 1 shows the distribution of the contamination level for the 69 measured NRs. A large portion of the NRs have only a low level of contamination. Only a few NRs are heavily contaminated. A total of 18 of the NRs have a partially blocked flow channel, and 2 of them have completely blocked flow channels. 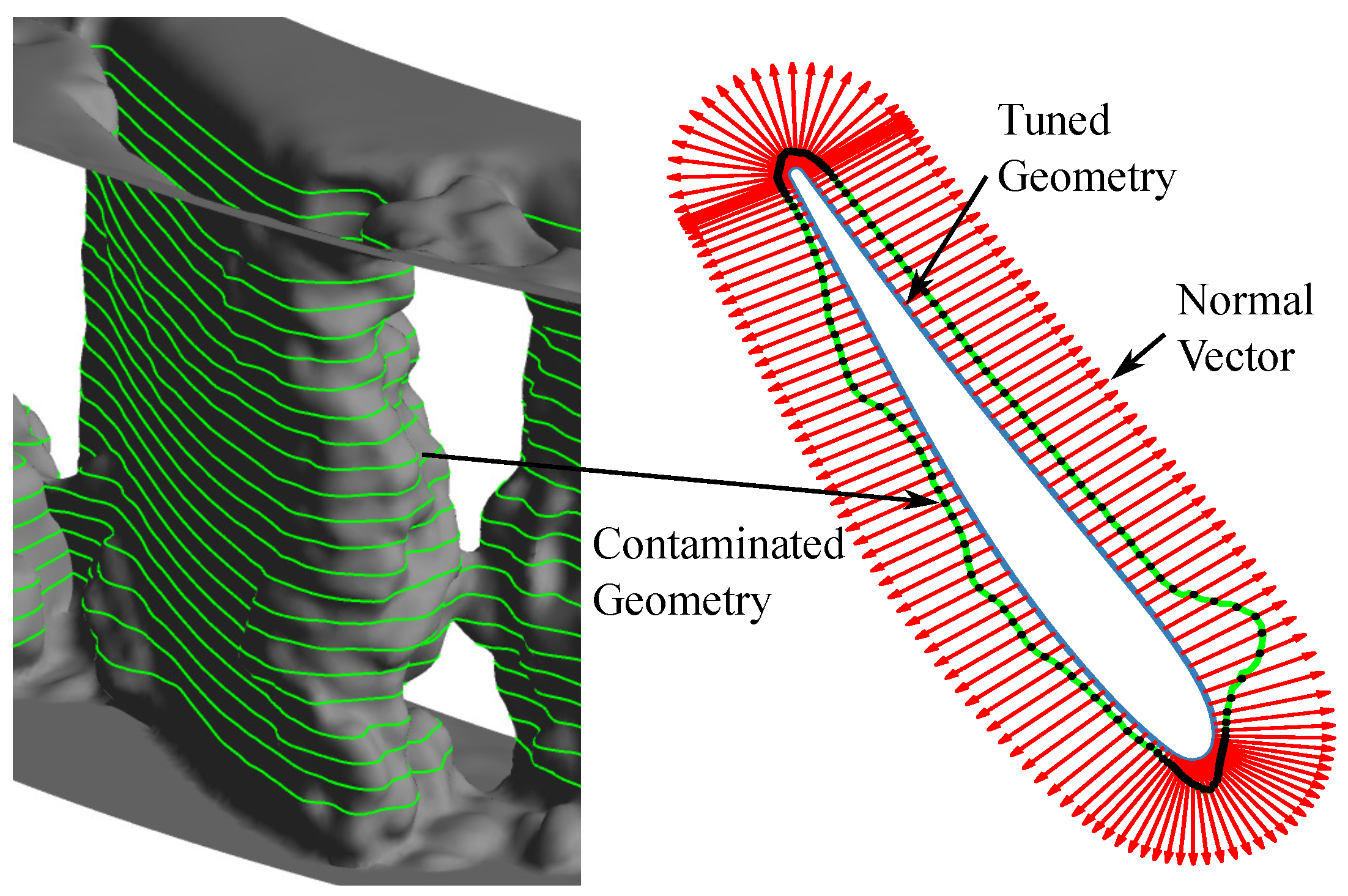To represent the measured NR geometry, 21 equidistant spanwise sections for each vane are created from the 3D scanned geometry, ranging from 8% to 92% blade height, see Figure 2. The fillet regions at the hub and shroud are neglected. The tuned vane profile is fitted into the determined contaminated vane profile; see Figure 2. Effects such as trailing edge bending and erosion are not considered to analyze the effect of the contamination on the LEO excitation individually. The deviation between the tuned and contaminated vane profiles is determined by means of normal vectors; see Figure 2. A vane profile is defined by 152 points, with a higher point density in the leading and trailing edge areas. A total of 76,608 variables is therefore used to represent the whole contaminated NR geometry.

Figure 3 depicts the averaged contamination pattern derived from all measured NR vanes, represented by the normal offset to the tuned geometry. The vane is shown in an unwrapped way, starting from the leading edge (LE) via the pressure side (PS) to the trailing edge (TE) and finally from the TE via the suction side (SS) back to the LE. It is apparent that the strongest changes are near the TE on the PS and near the LE on the SS, especially in the upper and lower blade areas. This indicates that the throat area in particular is affected by the contamination and that the combustion residuals do not deposit evenly in a spanwise direction.

3. Investigation Methodology

In the present study, the excitation characteristics of digital replicas of real contaminated NRs are numerically investigated on a radial turbocharger turbine stage for marine applications. An illustration of the whole radial turbine stage can be found in [13]. The stage consists of a double-entry volute, an NR with 24 vanes, and a rotor with 11 blades. A validated simplified steady-state CFD simulation model as described in [13] is used for the numerical investigations, as the accurate prediction of LEO excitation is computationally intensive due to the asymmetrical and complex NR geometry as well as the large number of simulations. The experimental and numerical investigation of a contaminated and blocked NR geometry showed that the contamination of the NR and the resulting blockage can lead to LEO excitation [13]. During tests, a LEO excitation of the lowest eigenmode 1 (M1) at the fifth nodal diameter (N5) excited by engine order six (EO6) occurred at a rotational speed of around 70% of the maximum speed [13]. This LEO excitation is used in the study presented herein. The investigations described in this paper are divided into three parts.

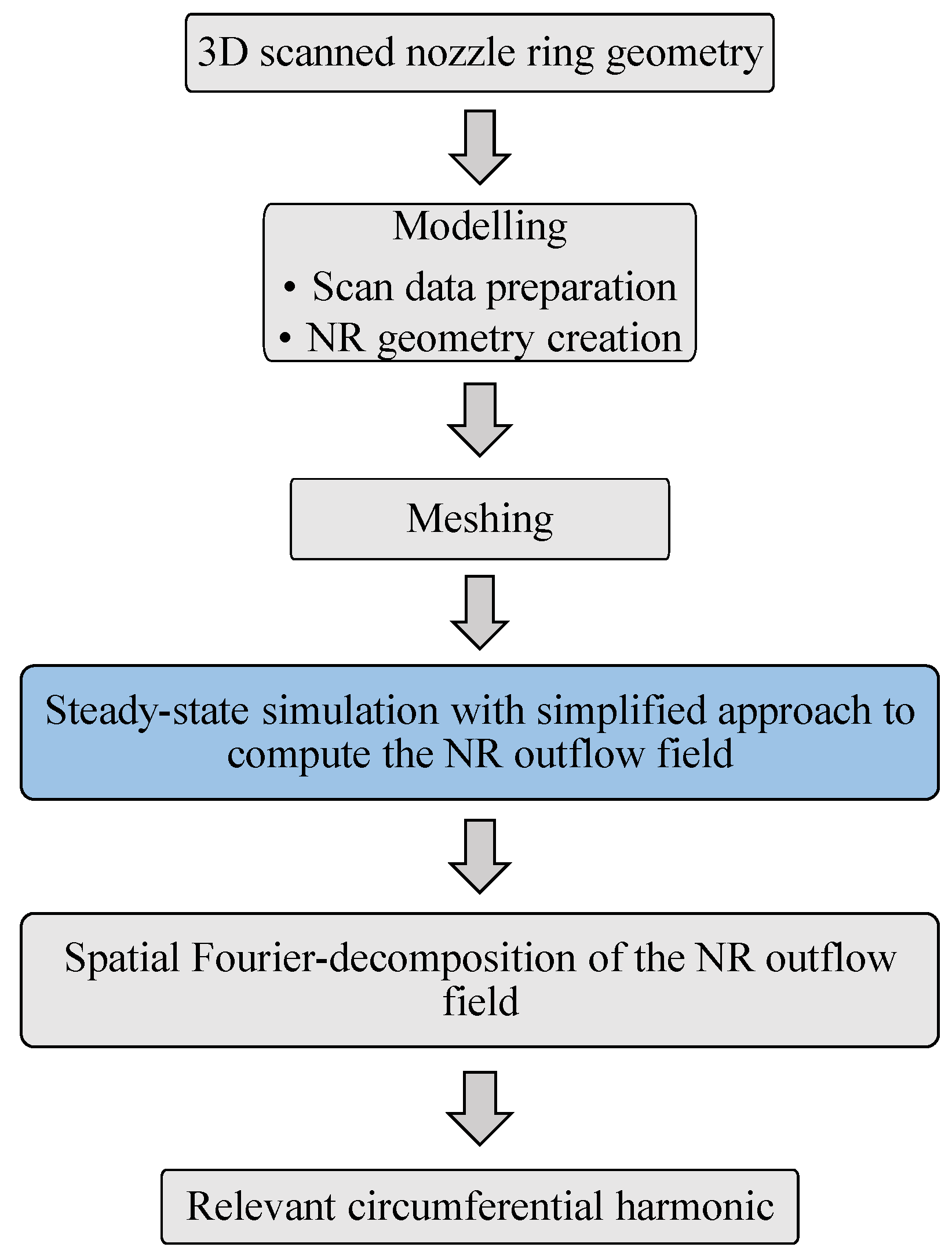
In the first part, 69 digital replicas of real contaminated NRs are investigated using an automated calculation process quantifying the LEO excitation potential bases on a simplified steady-state CFD model. The workflow of the calculation process is depicted in Figure 4. The first step in the process is to create the contaminated NR geometry from the 3D geometry scan data, as described in the previous section. Afterwards, the created NR geometry is meshed. In the third step, the NR outflow field is computed using a simplified steady-state CFD model, which is suitable to qualitatively rank the LEO excitation induced through different contamination patterns [13]. Then, the calculated NR outflow field is spatially Fourier-decomposed, and finally, the relevant circumferential harmonic (CH), CH6 in the case of the investigated operating point M1 ND5 EO6, is obtained to compare different contamination patterns regarding their aerodynamic excitation. Details about the last four steps are provided in the following sections.

In the second part, 13 selected contaminated NR geometries are numerically investigated using full annulus time-marching (TM) CFD simulations, which can predict the LEO excitation sufficiently accurately [13], employing the generalized force (GF) approach. The GF value is directly proportional to the blade vibration amplitude when assuming constant damping [2]. Therefore, the GF can be used to compare different contamination patterns in terms of their aerodynamic excitation. The results of the TM CFD simulations are used to extend the verification of the simplified approach with further validation cases.

In the third part, two contamination patterns are analyzed in a more detailed manner regarding their aerodynamic excitation. Both contamination patterns produce a high dynamic pressure amplitude at the relevant CH at the NR outflow field. Thus, the simplified model predicts a high excitation potential for both cases. The TM model showed that only one of the two produced high excitation. This is analyzed more in detail by evaluating the transient rotor flow field.

4. CFD Analysis

All CFD simulations are carried out using the commercial software ANSYS CFX v.20.1. In all CFD simulations, the fluid is modeled as an ideal gas, whereas turbulence is modeled by means of the SST turbulence model. All endwalls are treated as adiabatic, featuring no-slip boundary conditions. Two different CFD models are used to assess the aerodynamic excitation. Both models are described in a more detailed manner in the following.

4.1. Isolated Nozzle Ring (INR) Model

The numerical CFD model for the INR simulation is illustrated in Figure 5. The model consists of the volute, the corresponding contaminated NR, and a radial extension downstream of the NR. The contaminated NRs are meshed with unstructured grids in ANSYS ICEM CFD. The meshes consist of tetrahedral elements in the inner core region and prism layers in the wall region to capture boundary layer flow details. All 69 NRs are meshed automatically with the same mesh parameters to ensure comparability. The resulting mesh size depends strongly on the contamination pattern and can vary from under 7 million elements to over 17 million elements. The mass flow rate is imposed as a boundary condition at the inlet and the averaged static pressure at the outlet. The same mass flow rate and static pressure value are used for all investigated cases. Test data are available from [13] for one contamination pattern and one nozzle ring geometry, where one flow channel is blocked by 90%. These two cases are used to determine the mass flow boundary condition at the inlet as well as the static pressure boundary condition at the extension outlet. Convergence is continuously monitored by means of an online evaluation of the relevant CH. The simulation is stopped when the coefficient of variation of the mean value evaluated for a certain period falls below a predefined limit.

4.2. Time-Marching (TM) Simulation

A full-annulus numerical CFD model from [13] is used for the TM simulations. The model consists of the double-entry volute, the corresponding NR, the rotor, and an axial extension at the outlet to avoid numerical reflections [14]. The scallop and back wheel cavities are neglected. An illustration of the numerical CFD model can be found in [13] as well as detailed information on the volute and rotor mesh. The transient rotor-stator interface of CFX is applied in the time-marching simulations, while one rotor revolution is discretized into 360 time steps. This corresponds to 60 time steps per EO6 feature. The chosen time step is the result of an extensive convergence study. Total pressure and total temperature are imposed as boundary conditions at the inlet and averaged static pressure at the outlet. The total conditions at the inlet are obtained from the INR model and the averaged static pressure from a full-stage, full-annulus steady-state CFD model, where total conditions are imposed at the inlet and mass flow at the outlet. Convergence is assessed by means of an online evaluation of the GF.

5. Generalized Force

The GF can be derived from the equation of motion. Equation (2) shows the basic equation of motion

$$\mathit{M}\ddot{x}\left(t\right)+\mathit{D}\dot{x}\left(t\right)+\mathit{K}x\left(t\right)=F\left(t\right)$$

(2)

with M being the mass matrix, D the damping matrix, K the stiffness matrix, F the force vector, and x the displacement in physical coordinates. Under the assumption of harmonic displacement $x\left(t\right)=\widehat{x}{e}^{i\omega t}$ and harmonic forcing $F\left(t\right)=\widehat{F}{e}^{i\omega t}$, Equation (2) can be rewritten to the harmonic equation of motion in physical coordinates

$$(-{\omega }^2\mathit{M}+i\omega \mathit{D}+\mathit{K})\widehat{x}=\widehat{F}.$$

(3)

By transforming the complex physical coordinates $\widehat{x}$ into complex modal coordinates $\widehat{q}$ ($\widehat{x}=\mathit{\varphi }\widehat{q}$), Equation (3) can be rewritten as

$$(-{\omega }^2{\mathit{\varphi }}^T\mathit{M}\mathit{\varphi }+i\omega {\mathit{\varphi }}^T\mathit{D}\mathit{\varphi }+{\mathit{\varphi }}^T\mathit{K}\mathit{\varphi })\widehat{q}={\mathit{\varphi }}^T\widehat{F}$$

(4)

$$(-{\omega }^2\tilde{\mathit{M}}+i\omega \tilde{\mathit{D}}+\tilde{\mathit{K}})\widehat{q}={\mathit{\varphi }}^T\widehat{F}.$$

(5)

Thereby, $\mathit{\Phi }$ is the transformation matrix containing the mass normalized eigenvectors obtained by solving the eigenvalue problem. The right-hand side of Equation (4) and Equation (5) represents the modal or generalized force. If the GF is calculated for a certain resonance crossing where just one eigenmode is responding, the calculation can be simplified to the scalar product of the eigenmode with the harmonic forcing field, and the GF is directly proportional to the vibration amplitude when assuming constant damping [2,3]. Therefore, it is a suitable criterion to compare different contamination patterns regarding their aerodynamic excitation.

6. Results and Discussion

The results of the numerical study, which are divided into three parts, are described and discussed below. The excitation predicted with both numerical models is normalized to the value of a reference geometry (NR 0) in order to ensure comparability between the numerical models. The normalized values are referred to as the excitation potential. The reference geometry is a tuned NR geometry where one flow channel is blocked by 90%. For this purpose, a plate is attached to the leading edges of two neighboring blades.

6.1. Influence of Contamination on Aerodynamic Excitation

This section covers the investigation of differences in aerodynamic excitation between the 69 investigated contamination patterns using the results of the INR simulations. For this purpose, the NR outflow field at the interface position between the NR and rotor is spatially Fourier-decomposed at different spanwise positions from 0% to 100% in steps of 1%. An averaged amplitude spectrum is created from the individual amplitude spectra. 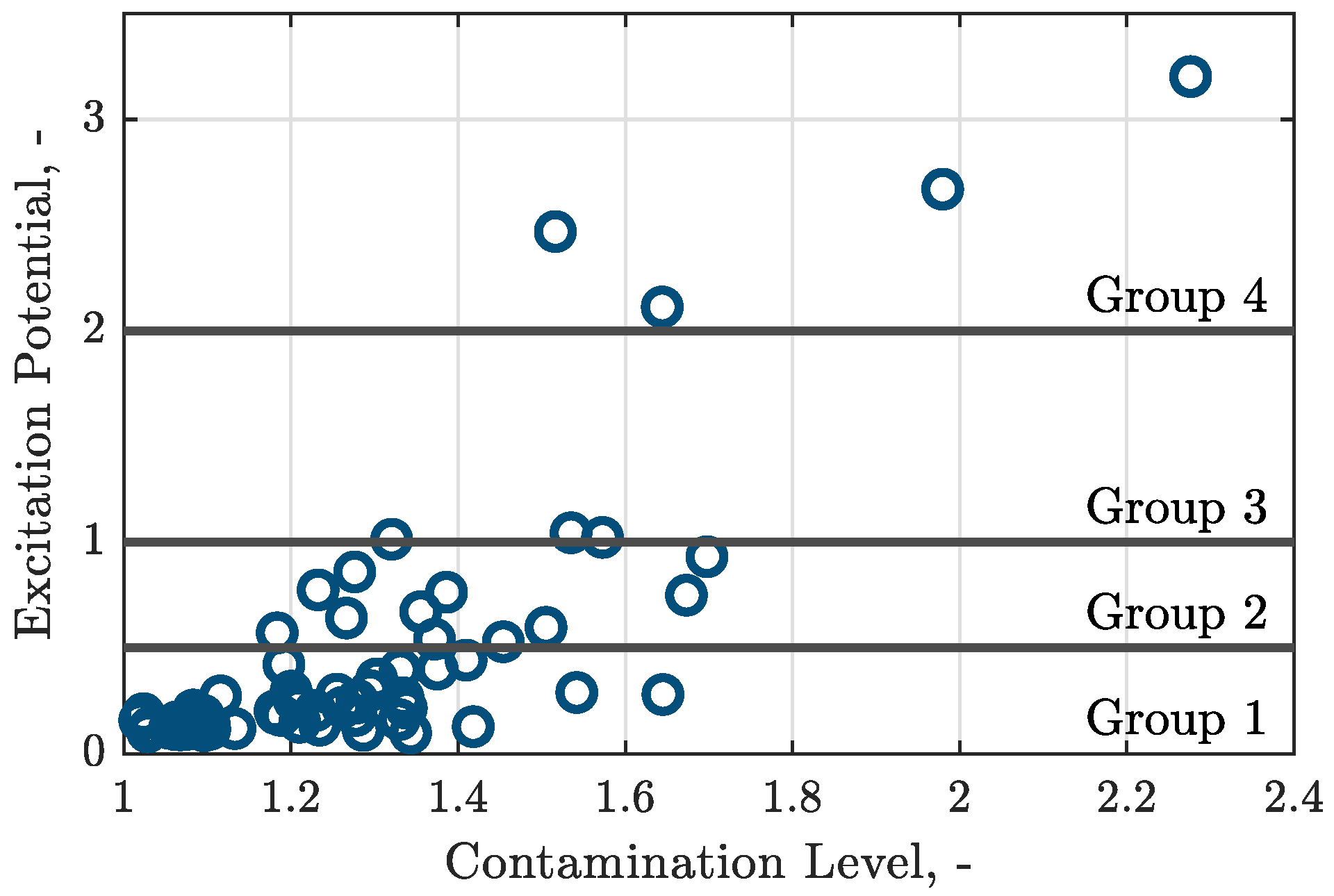Dynamic pressure in combination with arithmetic averaging was used as it gave the most accurate results when developing the simplified model [13]. The obtained normalized dynamic pressure amplitude, referred to as excitation potential, for CH6 is shown in Figure 6. The NRs are divided into four groups:

• Group 1: $\mathrm{Excitation}\mathrm{Potential}\le 0.5$
• Group 2: $0.5<\mathrm{Excitation}\mathrm{Potential}\le 1$
• Group 3: $1<\mathrm{Excitation}\mathrm{Potential}\le 2$
• Group 4: $\mathrm{Excitation}\mathrm{Potential}\ge 2$.

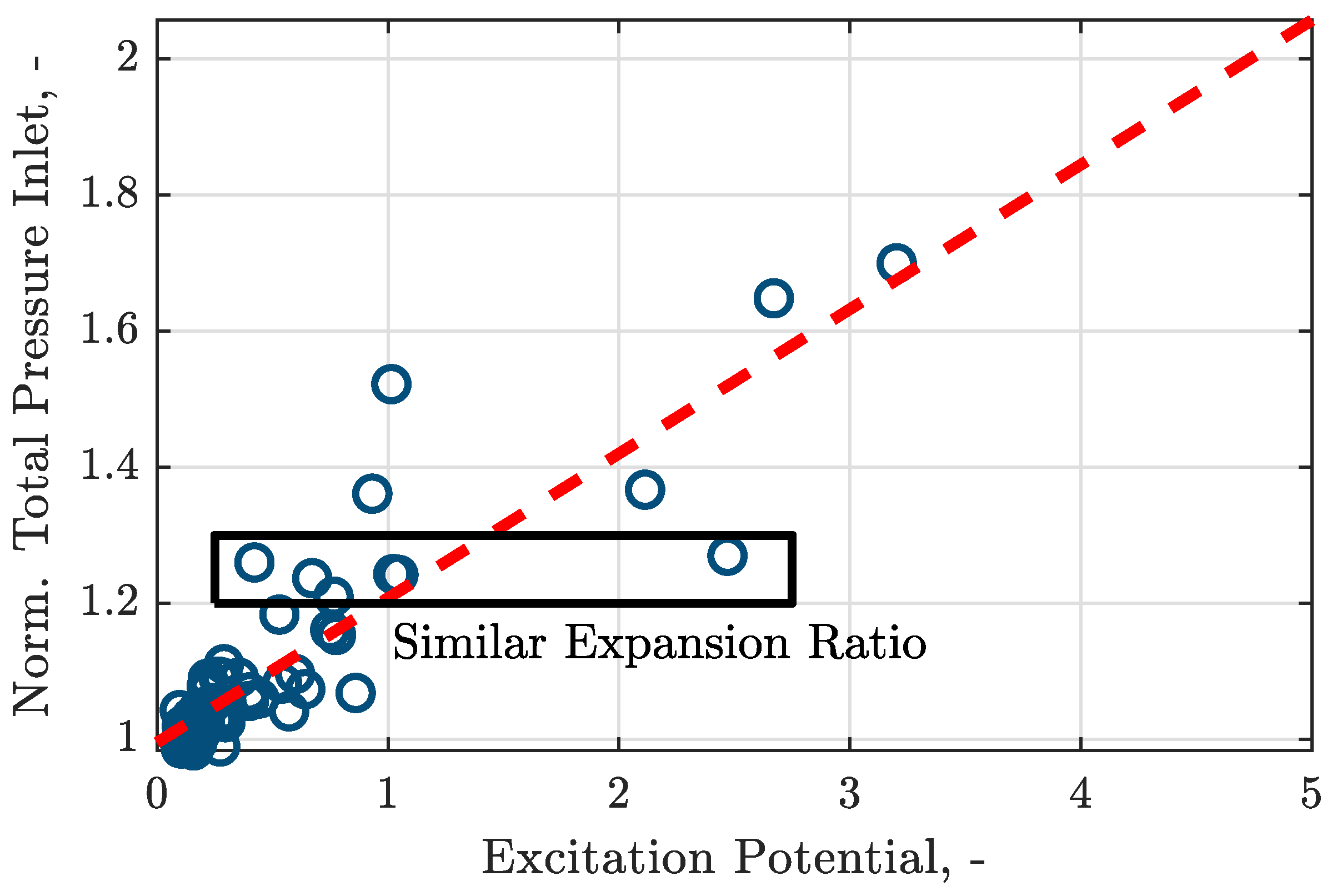
According to the simplified calculation model, the majority of the investigated contamination patterns have less than half the excitation of the reference NR. Only seven NRs (about 10%) have a higher excitation than the reference NR, and more than twice the excitation is predicted for four NRs (about 6%). Figure 6 shows that a high contamination level is often related to a high excitation potential. However, it must be considered that, due to the selected mass flow boundary condition at the inlet, a higher contamination level also means a higher pressure at the inlet and thus a higher expansion ratio, resulting in a higher level of outlet kinetic energy. The change in excitation is therefore not only the result of the contamination but also a result of the change in operating point. Figure 7 depicts the normalized total pressure at the inlet plotted against the excitation potential. The total pressure values are normalized by the inlet total pressure of NR 0. The data suggest a linear relationship between the excitation potential and the averaged total pressure at the inlet as shown by the red line in Figure 7. The excitation potential increases with increasing total pressure at the inlet and, thus, with increasing expansion ratio. The linear trend does not, however, exactly explain the excitation. There are NRs that have a similar averaged total pressure at the inlet but nevertheless show clearly different excitation potentials; see box in Figure 7. This scatter shows that the contamination pattern can have a similar influence on the aerodynamic excitation as the operating point. It can be concluded that, according to the simplified model, the majority of the investigated NRs cause a low aerodynamic excitation compared to the reference NR (NR 0). Only a few cause a very high aerodynamic excitation. The change in excitation is not only due to the contamination pattern but also to the change in operating point.

6.2. Verification of the Isolated Nozzle Ring Model

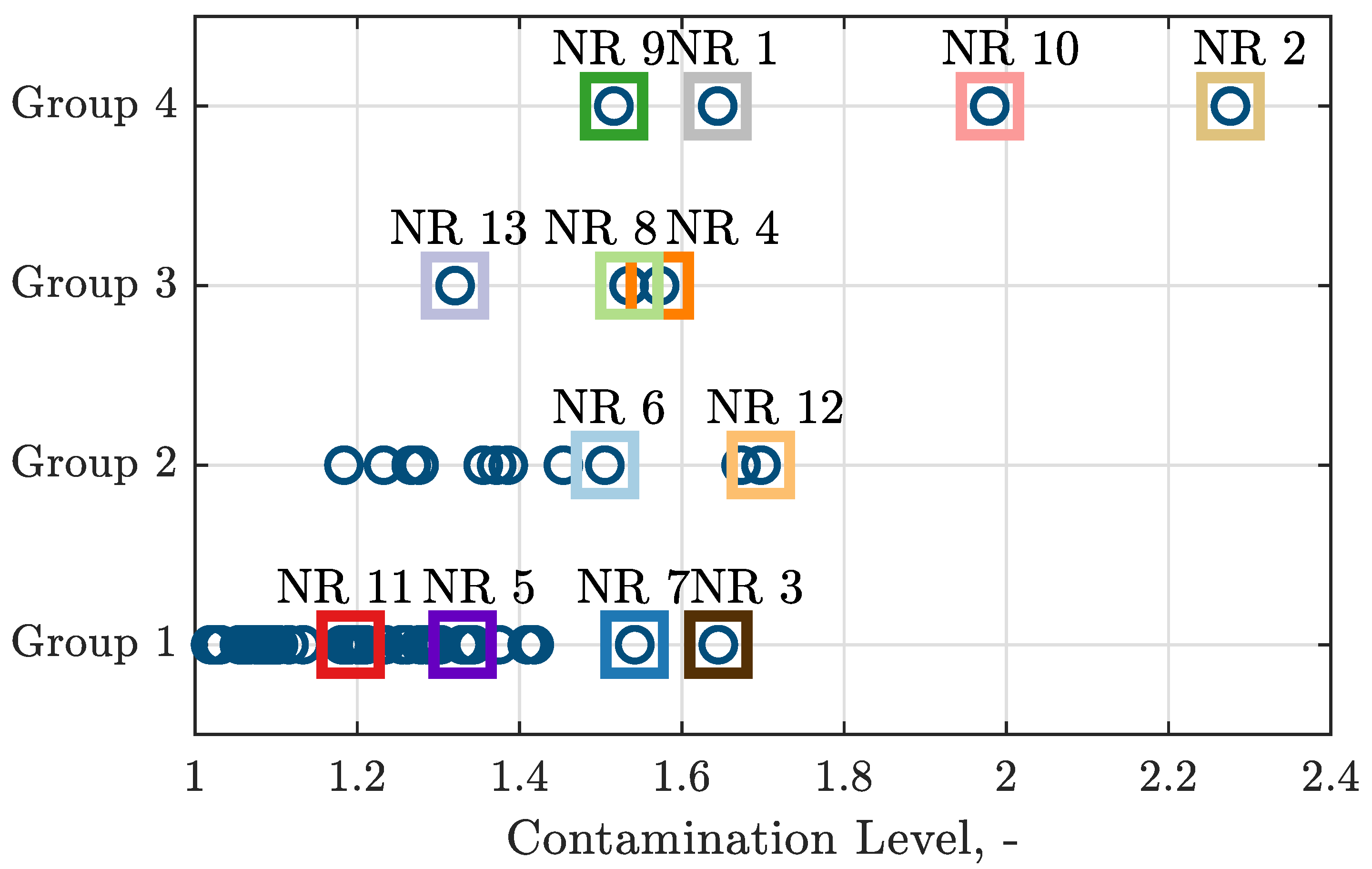
All 13 selected contaminated NRs are calculated using TM simulations to extend the verification of the INR model through further validation cases and to evaluate the constrains of the model. The selected NRs are numbered consecutively and are highlighted in Figure 8. The selection was made as follows:

• All NRs from group 4 and 3: NRs with the highest predicted excitation (NR 9, NR 1, NR 10, NR 2 & NR 13, NR 8, NR 4)
• NRs with similar contamination level but clearly different excitation potential (NR 9, NR 8/NR 4, NR 6, NR 7 & NR 1, NR 12, NR 3 & NR 13, NR 5)
• Two NRs with a similar contamination level and predicted excitation potential (NR 8, NR 4)
• NR with low contamination level and low predicted excitation potential (NR 11).

The simplified model is verified in two steps. In the first step, the accuracy of the amplitude prediction at CH6 at the interface position between the NR and rotor is evaluated using the time-averaged transient NR outflow field obtained with the TM model. In a second step, the GF approach is used to evaluate the suitability of the simplified model to quantitatively predict the actual level of LEO excitation.

Figure 9 shows the relative deviation between the dynamic pressure amplitude of the first CHs obtained with the INR model and those calculated with the TM model. The amplitudes from CH3 to CH6 obtained with the simplified model agree well with the ones calculated by the transient model for all 13 investigated cases. The greatest differences can be observed at CH4. The amplitude values of CH1 and CH2 cannot be adequately predicted with the simplified model. The CH6 is analyzed more in detail as it is relevant for the excitation of the investigated operating point (M1 ND5 EO6) and therefore focused in Figure 9. The amplitude can be predicted well for most of the investigated cases with the INR model. The absolute amount of the relative deviation is smaller than 10%. The largest deviation of about −17% occurs at NR 11. The smallest deviations occur with NRs at significantly different contamination levels. Therefore, a correlation between the model quality and the contamination level cannot be found. In summary, the applied INR model is able to predict the amplitude of CH6 with sufficient accuracy.

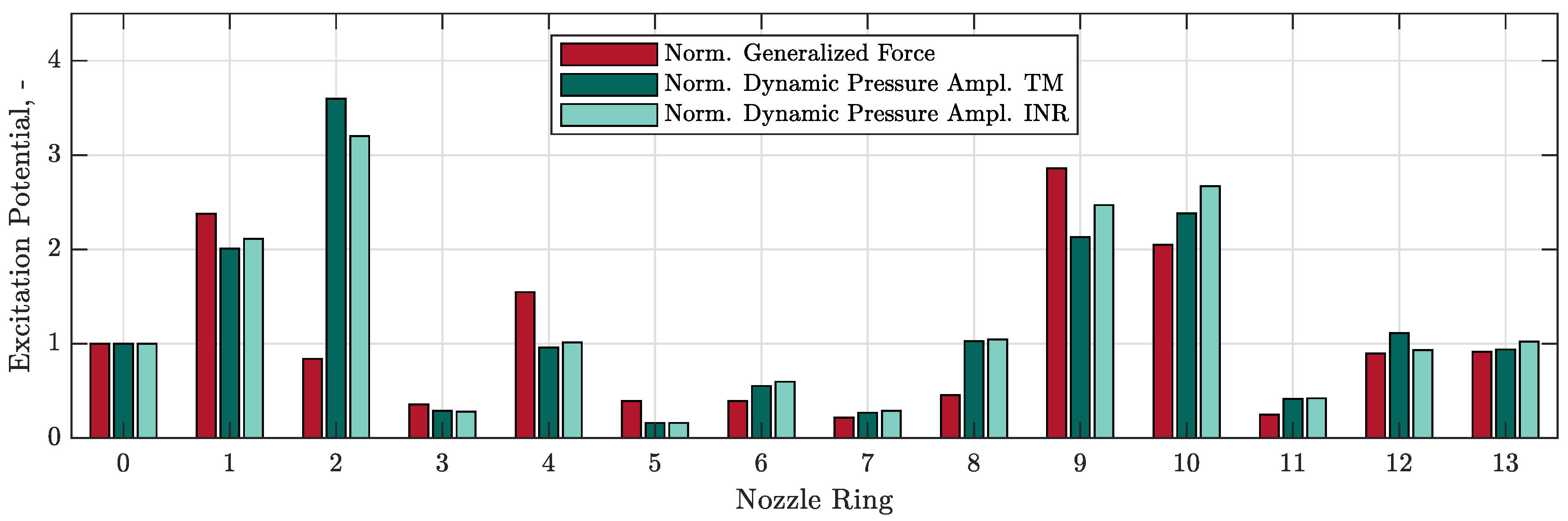
In the second step, the GF approach is used to investigate whether the simplified model is suitable for evaluating LEO excitation. For this purpose, the GF value is calculated for all 13 selected NRs for the resonance crossing of EO6 with mode 1. As stated above, the GF is directly proportional to the vibration amplitude due to the assumption of constant damping. The determined GFs are normalized with respect to the GF of NR 0 to ensure a comparison with the simplified model. This value as well as the normalized dynamic pressure amplitude determined from the INR model and from the TM model are depicted in Figure 10 for all 13 investigated NRs. It confirms that the INR model delivers results at an acceptable level of accuracy, taking the TM model as a reference. In most cases, it can be estimated whether the NR causes a high or low aerodynamic excitation. An exact prediction of the vibration amplitude is, however, not possible in all cases.

The limitations of the INR model are analyzed more in detail using two tables.

Table 1. Ranking at similar contamination level.

INR	NR 9 > NR 8/NR 4 > NR 6 > NR 7
Norm. GF	2.86 > 0.46/1.54 > 0.39 > 0.22
INR	NR 1 > NR 12 > NR 3
Norm. GF	2.34 > 0.9 > 0.36
INR	NR 13 > NR 5
Norm. GF	0.91 > 0.4

lists three groups, each containing NRs with a similar contamination level. The respective NRs are ordered according to their excitation potential predicted with the INR model. The respective normalized GF value for each NR is listed in the line below. The table shows that the simplified model ranks all NRs correctly.

Table 2. Assignment to groups of different excitation potential (high numbers indicate high excitation potential).

NR	Group as Derived from INR Model Based on Spatial FFT	Group as Derived from TM Model Based on GF
1	4	4
2	4	2
3	1	1
4	3	3
5	1	1
6	1	1
7	1	1
8	2	1
9	4	4
10	4	4
11	1	1
12	2	2
13	3	2

shows if the simplified model can assign the NRs to the correct excitation potential group. All NRs except three are assigned to the correct group. The excitation potential of two NRs (NR 2 and NR 8) is greatly overestimated by the simplified model. One NR (NR 13) is incorrectly assigned since the excitation potential is close to the group boundary. The two NRs 8 and 4 with similar contamination levels are assigned to the same group by the INR model. This could not be confirmed on the basis of the GF value; see Figure 10. While the INR model was able to assign NR 11 to the correct excitation potential group, it failed to predict the exact excitation potential level. These observations suggest that the simplified model is suitable for classifying NRs into groups according to their aerodynamic excitation potential. However, when it comes to predicting the exact vibration levels, the simplified model falls short in certain cases. Apparently, there are effects that cannot be captured by a steady simulation, as addressed in the next section.

6.3. Influence of Transient Effects in the Rotor Domain on the Aerodynamic Excitation

This section covers the investigation of two contamination patterns (NR 1 and NR 2) regarding their aerodynamic excitation in a more detailed manner. Both NRs have a high dynamic pressure amplitude at CH6 in the NR outflow field, several completely clogged flow channels, and a high contamination level; see Figure 8 and Figure 10. However, this only leads to a high vibration amplitude for NR 1 according to the TM model; see Table 2. The INR model predicts a high excitation potential for both NRs; see Figure 10, as only the amplitude of the CH6 of the NR outflow field is used for the evaluation.

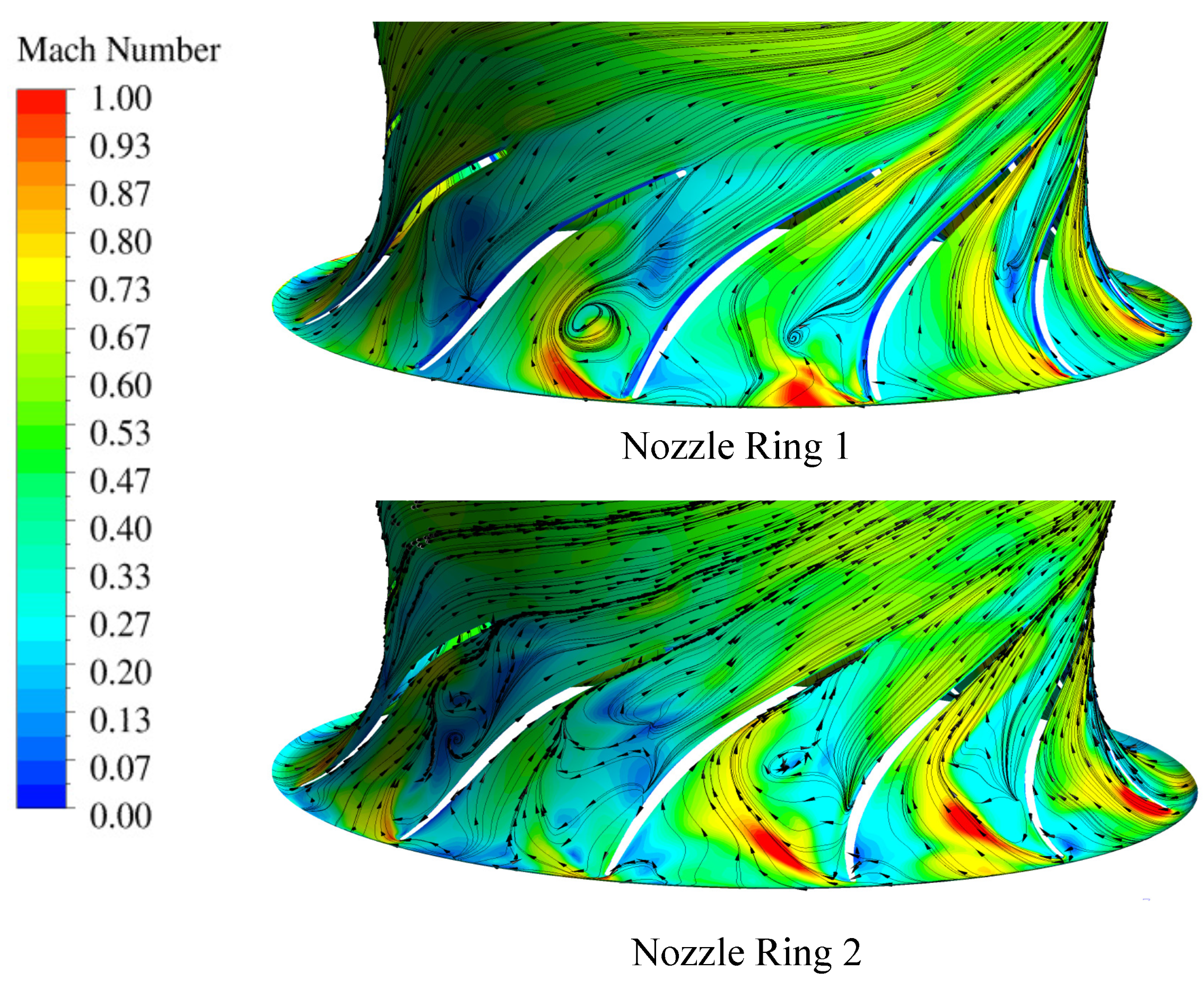
Figure 11 shows the Mach number distribution with streamlines for both cases at one time step at 90% span. In both cases, flow separation occurs on the SS and PS due to incidence, resulting in a complex three-dimensional flow field. These flow separations lead to a narrowing of the flow channel and, thus, an increase in speed, resulting in transonic flow speeds in both cases. Figure 12 depicts the standard deviation from the mean pressure value at 90% span, calculated from one rotor revolution. The standard deviation is used to identify large pressure perturbations as an indication of significant transient effects. In both NRs, the highest values occur in the area near the LE. In the case of NR 2, significantly higher values occur in this area, indicating a strongly varying flow field within one rotor revolution. In the rotor channel between SS and PS, the values for NR 2 also tend to be higher. 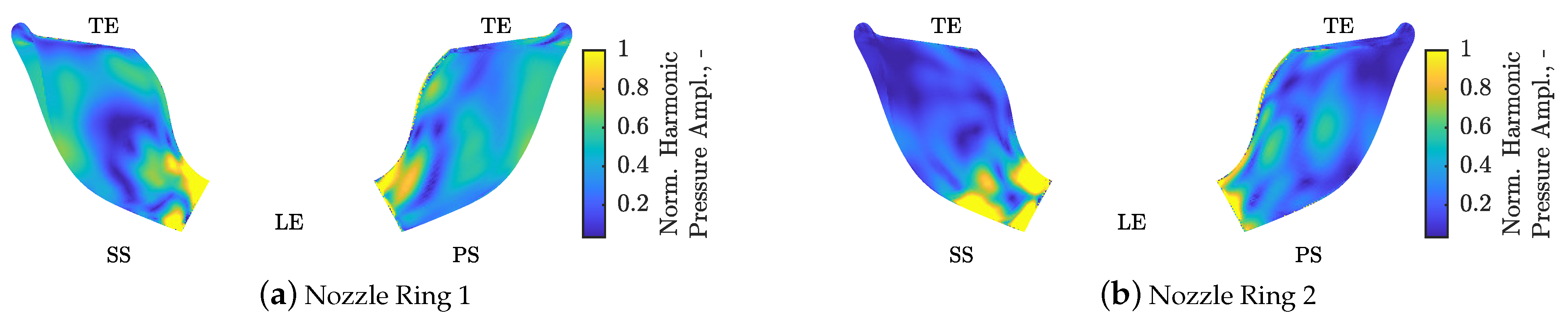The effect of these transient phenomena on the harmonic pressure field at EO6 at 90% span is shown in Figure 13. In both cases, the highest values occur near the LE on the SS, where the highest standard deviations also occur. In the case of NR 2, the values decrease significantly towards the TE. In the aft of the passage, the harmonic pressure amplitudes are small compared to those occurring near the LE. In the case of NR 1, higher harmonic amplitudes occur in this region near the PS as well as in the center portion of the passage compared to NR 2.

Figure 14 compares the harmonic pressure on the rotor blade and Figure 15 the modal pressure between the two cases. Similar observations can be made as above; the highest values occur in the LE area on SS and PS. For both NRs, the values decrease toward the TE. Whereas NR 2 shows smaller values in the aft part of the blade compared to NR 1, especially on the SS near the blade tip. This is also the region in which the investigated first eigenmode has its largest displacements, yielding the maximum modal pressure amplitude. NR 1 has significantly higher harmonic pressure and thus modal pressure amplitudes in this area, which leads to a higher GF value and thus to higher vibration amplitudes. These observations suggest that transient effects occurring in the rotor can alter the harmonic pressure field originating from the upstream components significantly. In the case of modes, which have their highest displacements in the aft part of the blade, this can lead to a significant over- or underestimation of the vibration amplitude when employing the INR model, as this model neglects all transient effects in the rotor.

7. Conclusions

In this numerical study, 69 digital replicas of real contaminated NRs were investigated with respect to their aerodynamic excitation. For this purpose, a simplified simulation approach was used to reduce computational costs and identify critical contamination patterns. Based on the results of the simplified simulation model, 13 NRs were selected and analyzed using transient time-marching simulations with a model of the entire stage, including the rotor. The results of the 13 investigated NRs were used to extend the verification of the simplified model with further validation cases. The prediction accuracy of the simplified approach is limited in some cases. For example, the trend for the excitation potential is well captured for NR 1, whereas the opposite trend is predicted for NR 2. In order to better understand the limitations of the model, these two NRs were analyzed in a more detailed manner regarding their aerodynamic excitation. The main findings of the numerical study are:

• The aerodynamic excitation is influenced both by the asymmetries induced by the contamination itself as well as by the resulting change in expansion ratio under the assumption of a constant mass flow rate. The order of magnitude of both effects is similar.
• Only a small number of the investigated contamination patterns cause a higher aerodynamic excitation compared to the reference geometry featuring one blocked channel. Most feature lower aerodynamic excitation.
• The simplified model is suitable to classify contamination patterns into groups according to their excitation potential.
• The simplified model is suitable to rank different contamination patterns regarding their aerodynamic excitation if the contamination patterns feature sufficiently large differences.
• Transient effects in the rotor, which the simplified model does not consider, can have a non-negligible influence on the aerodynamic excitation.
• The simplified model is not suitable to predict the aerodynamic excitation with sufficient accuracy if transient effects in the rotor domain alter the harmonic pressure field originating from the upstream NR significantly.

Considering the low computational effort, the simplified model is nevertheless suitable to identify critical contamination patterns, rank different contamination patterns, and classify them into groups. High-fidelity, full annulus CFD models, including the rotor, should be used for an accurate analysis of the LEO excitation.