State of the Art on Two-Phase Non-Miscible Liquid/Gas Flow Transport Analysis in Radial Centrifugal Pumps Part C: CFD Approaches with Emphasis on Improved Models
Abstract
1. Introduction
2. Review of CFD Methods for Multiphase Flow in Pumps
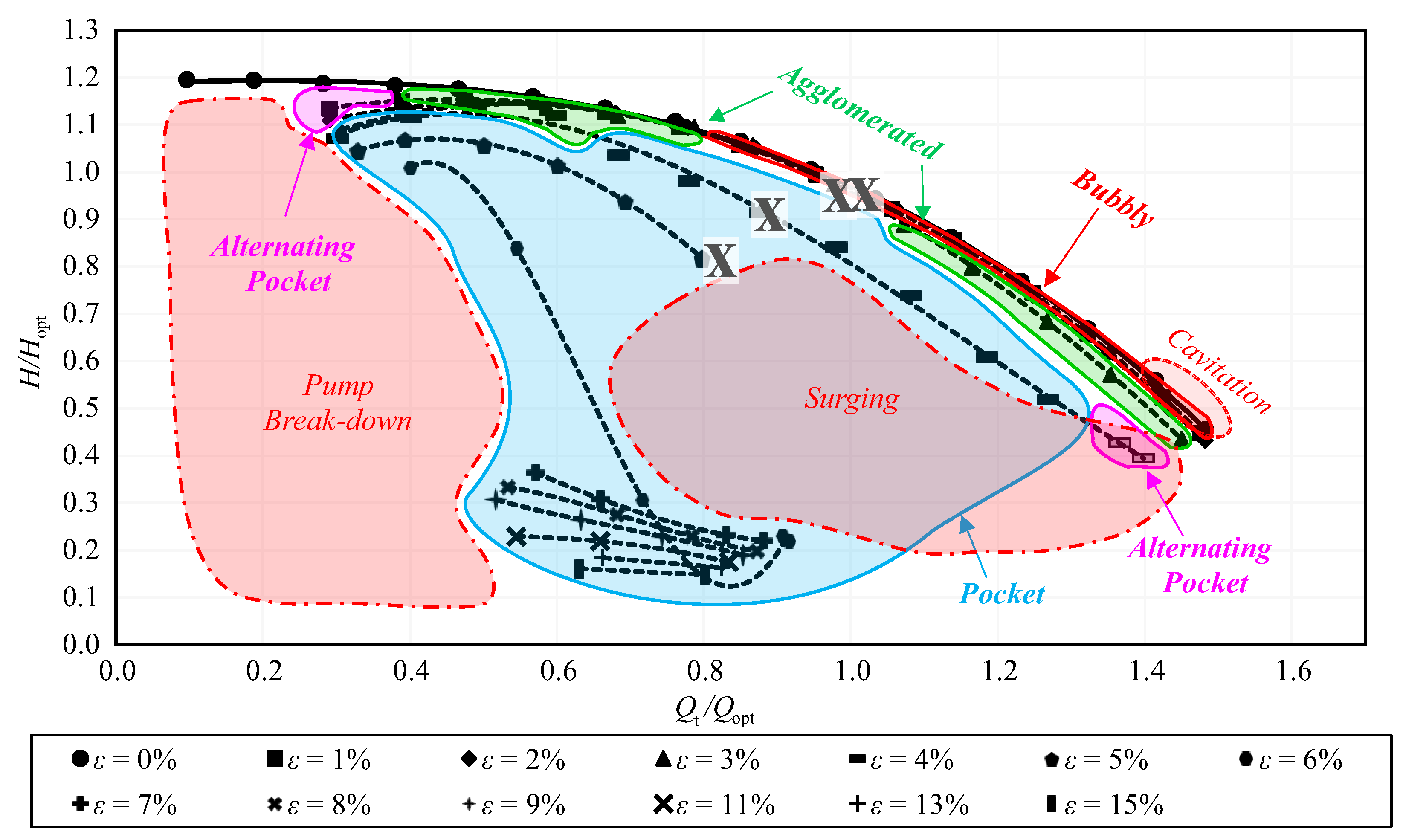
2.1. Physical Reasoning
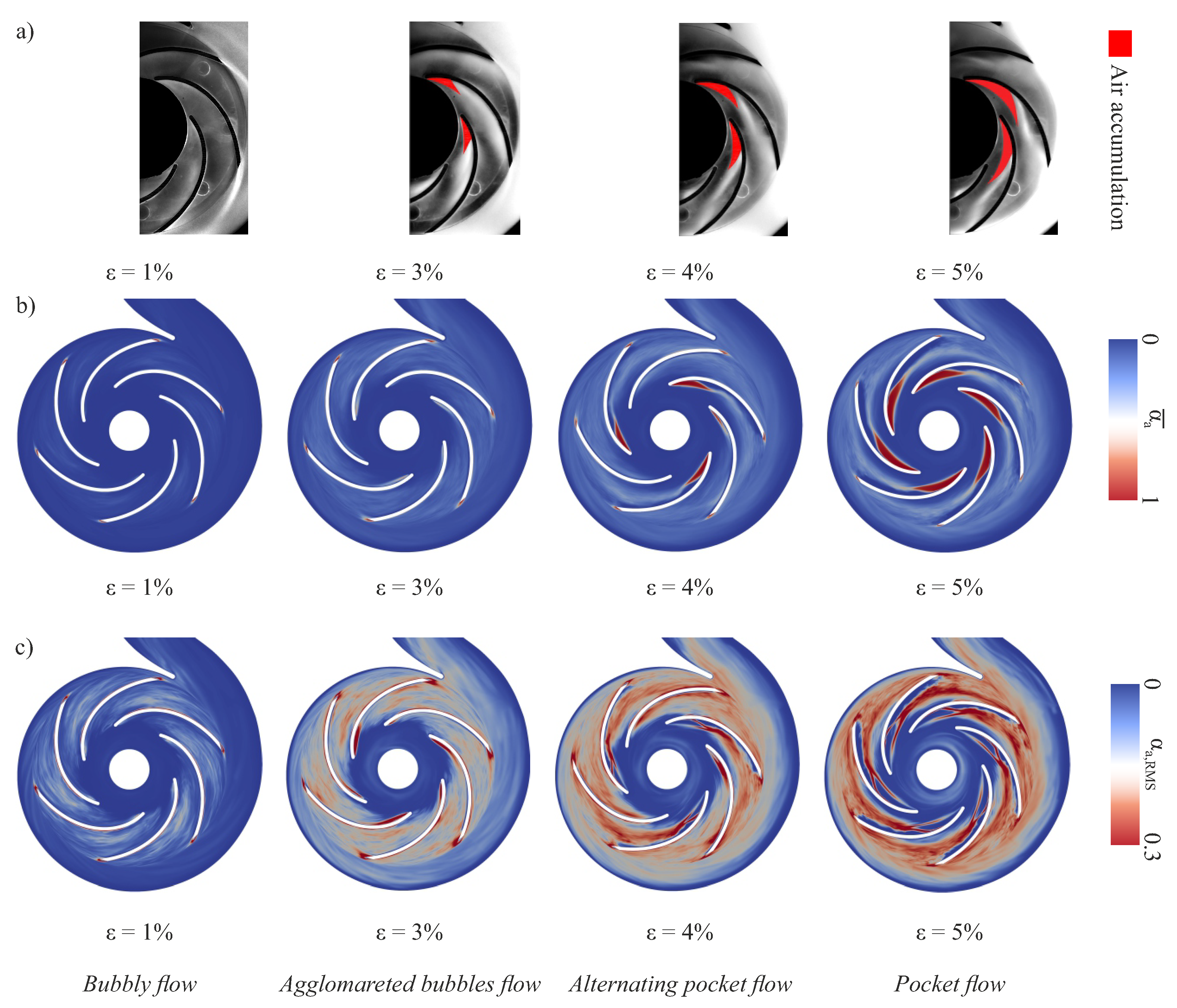
- Bubbly flow: the air bubbles are dispersed everywhere in the impeller.
- Agglomerated bubbles flow: air bubbles start to accumulate in small bubble clusters.
- Alternating pocket flow: highly unsteady air pockets, with strongly variable sizes and locations, appear at the impeller blades but are not located at each blade.
- Pocket flow: stable and steady air pockets are located at the suction side of each blade.
2.2. Euler–Euler Two-Fluid (EE2F) Approach
2.3. Volume-of-Fluid (VoF) Approach
2.4. Hybrid Two-Phase (H2P) Approach
2.5. Turbulence-Scale Resolving Approach and Scale-Adaptive Simulations (SASs)
3. Recent Enhancement of CFD Methods
3.1. Summary of State-of-the-Art Method Algorithms
3.2. Hybrid Two-Phase (H2P) Approach
3.3. Population Balance Model (PBM)
3.4. Simulation Method
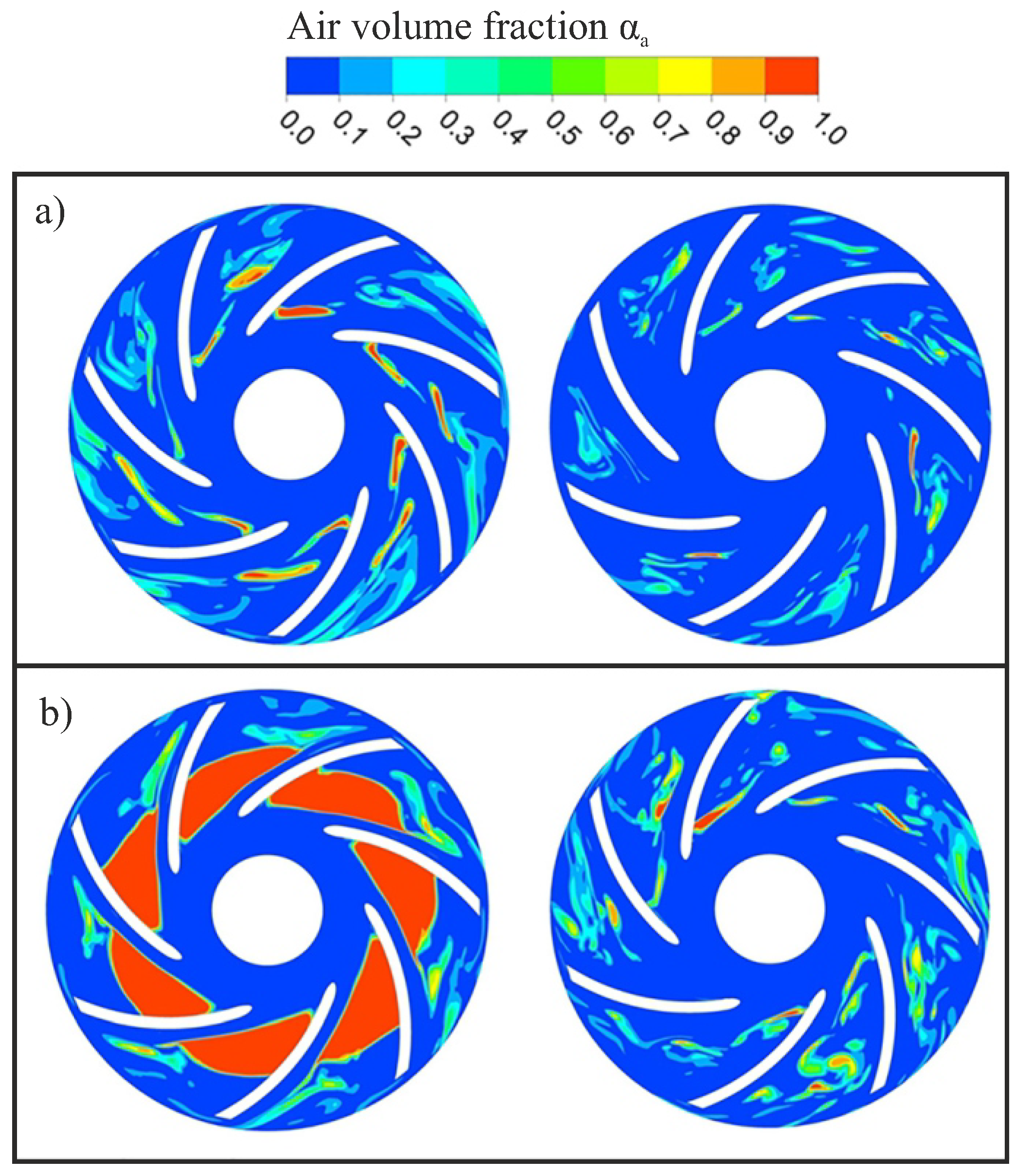
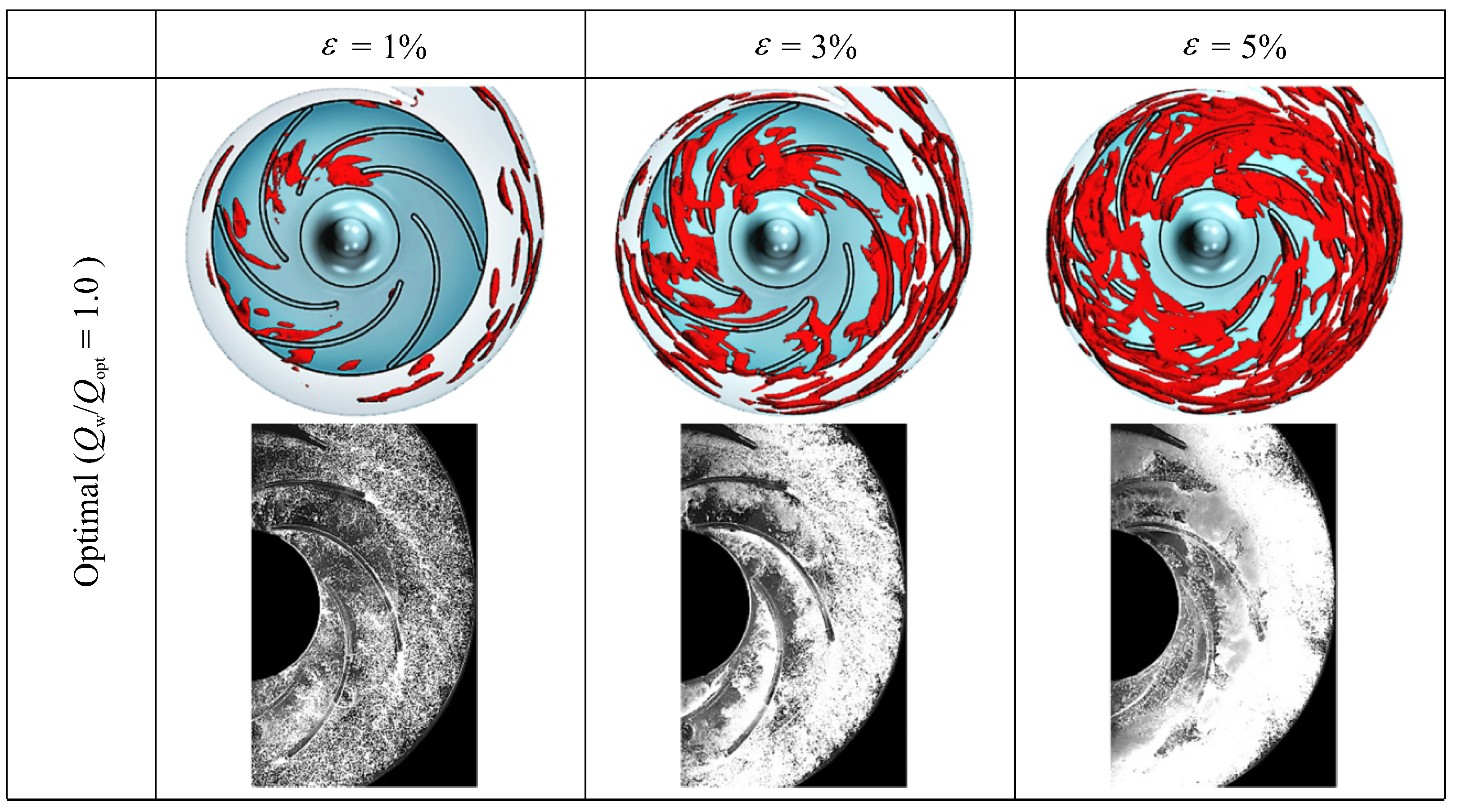
4. Example Application of The Hybrid Two-Phase (H2P) Model
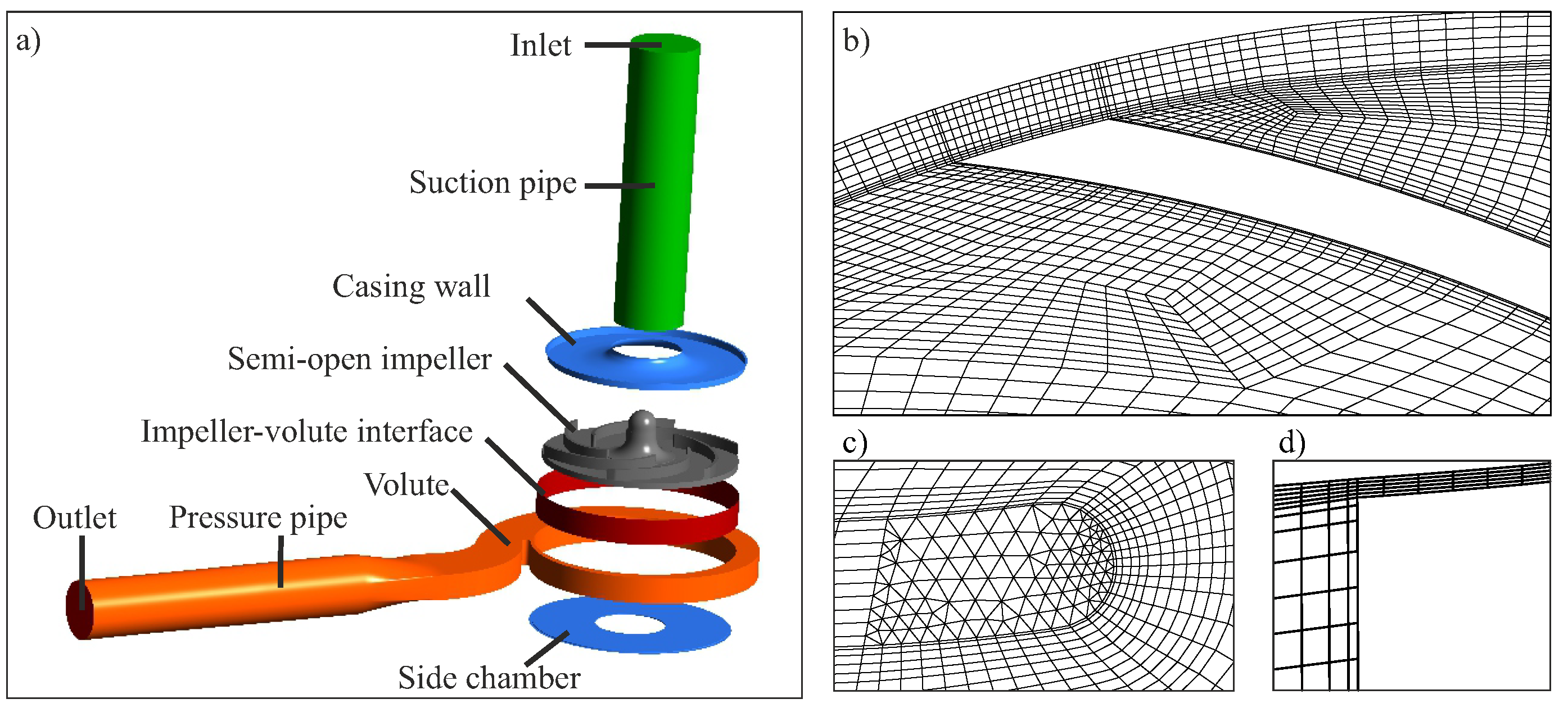
4.1. Test Case and Simulation Setup
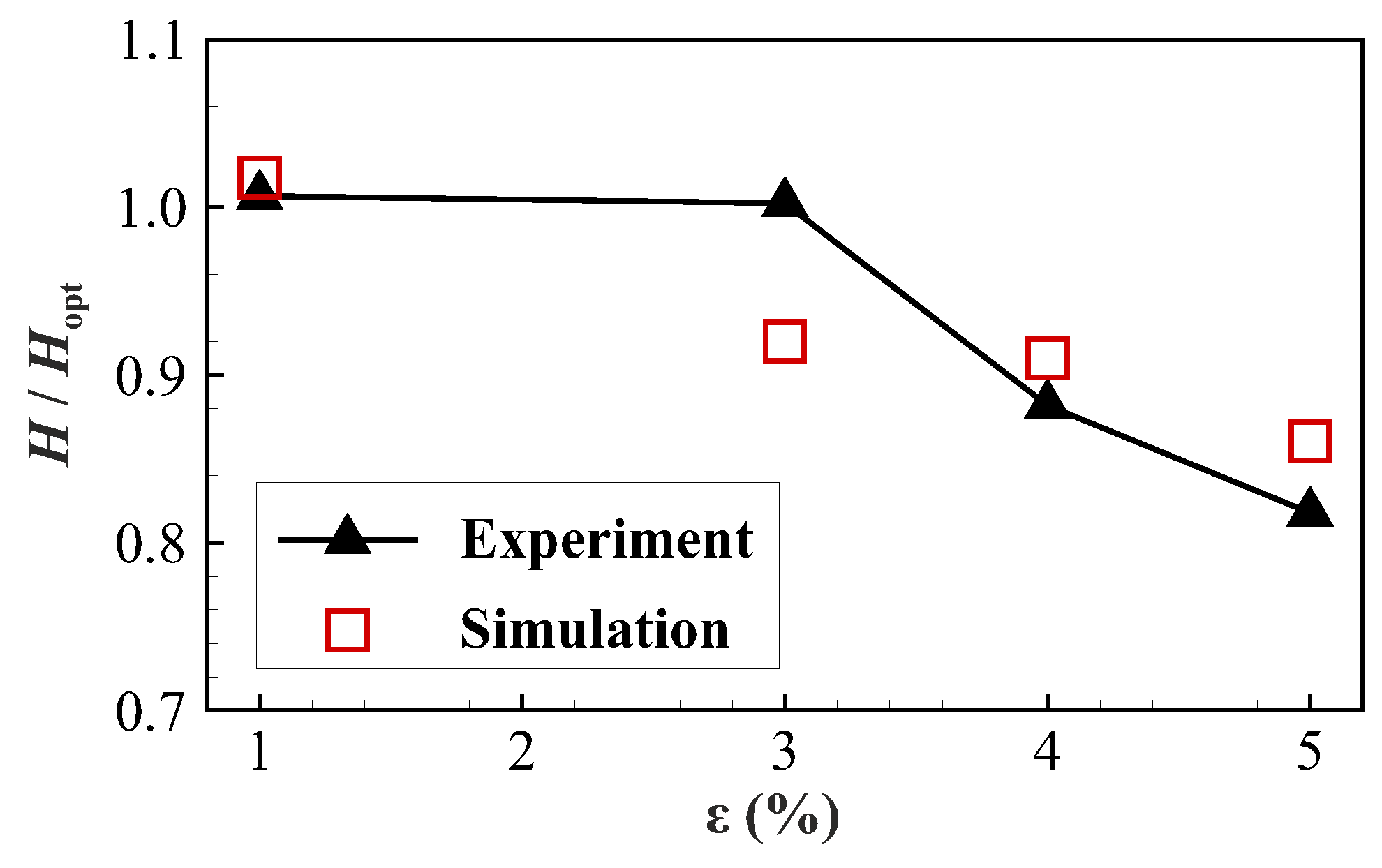
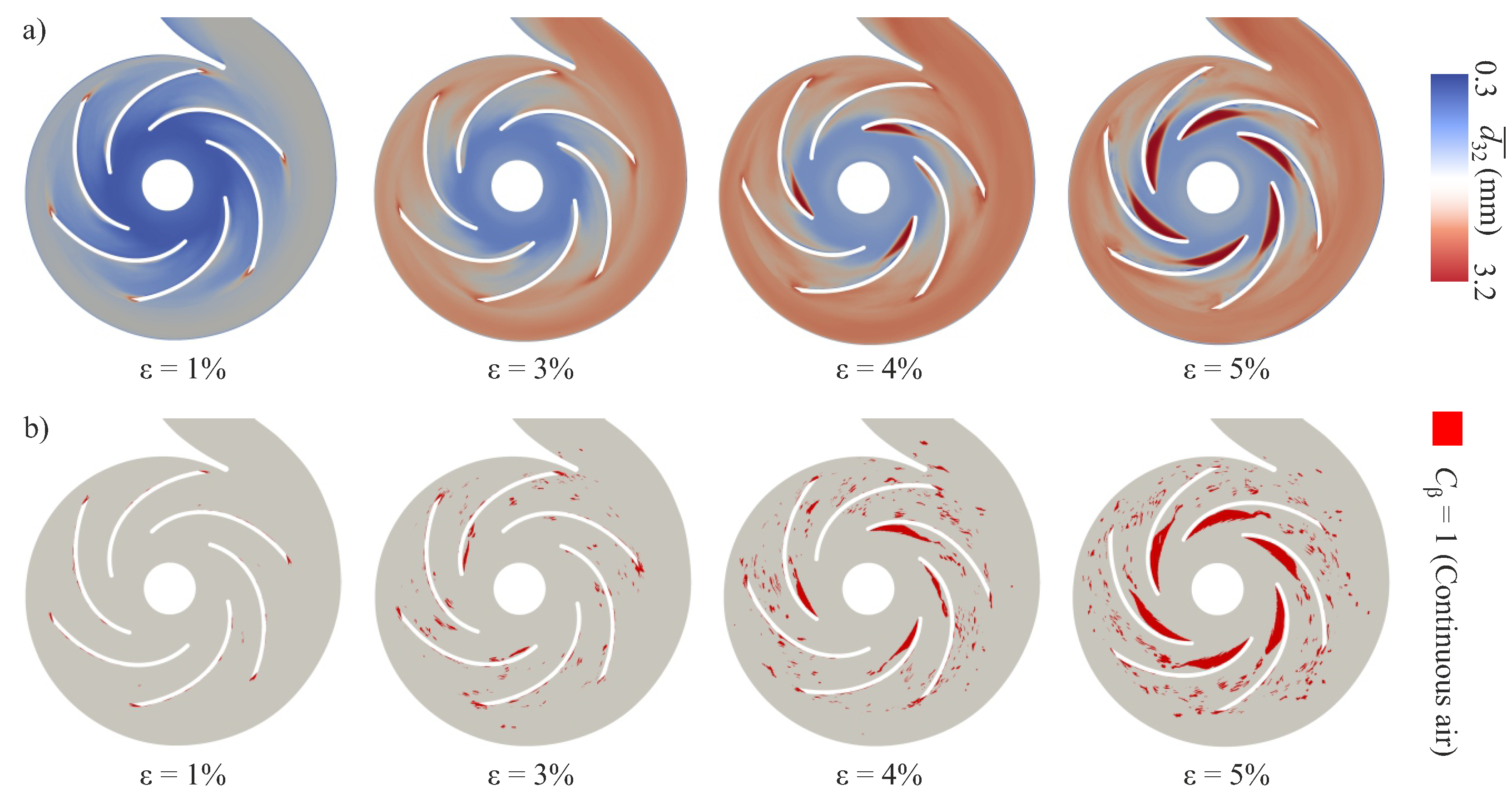
4.2. Selected Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature and Abbreviations
| Roman characters | ||
| Model constants for | (-) | |
| Model constants for | (-) | |
| Velocity vector | (m/s) | |
| & | Blending functions | (-) |
| Drag coefficient | (-) | |
| Pressure increment coefficient | (-) | |
| d | Diameter | (m) |
| Sauter mean diameter | (m) | |
| H | Pump head | (m) |
| k | Turbulence kinetic energy | (m2/s2) |
| M | Momentum transfer terms | (kg m/s2) |
| Surface tension force | (kg m/s2) | |
| n | Rotational speed | (1/s) |
| Bubble number density function | (1/m3) | |
| p | Pressure | (Pa) |
| Q | Volume flow rate | (m3/s) |
| Effective stress tensor | (kg m/s2) | |
| Cell volume | (m3) | |
| Greek characters | ||
| Volume fraction | (-) | |
| Temporal derivative | (1/s) | |
| Difference | (-) | |
| Inlet gas volume fraction | (-) | |
| Curvature | (1/m) | |
| Inlet gas volume fraction | (-) | |
| ∇ | Divergence operator | (1/m) |
| Specific dissipation | (1/s) | |
| Flow coefficient | (-) | |
| Density | (kg/m3) | |
| Surface tension factor | (-) | |
| Stage pressure coefficient | (-) | |
| Constant | (-) | |
| Subscripts | ||
| a | Air | |
| B | Bubble | |
| Exp | Experimental result | |
| m | Mixture | |
| opt | Optimal | |
| RMS | Standard deviation | |
| Sim | Simulation result | |
| t | Total | |
| w | Water | |
| Arbitrary phase | ||
| 3D | Three-dimensional |
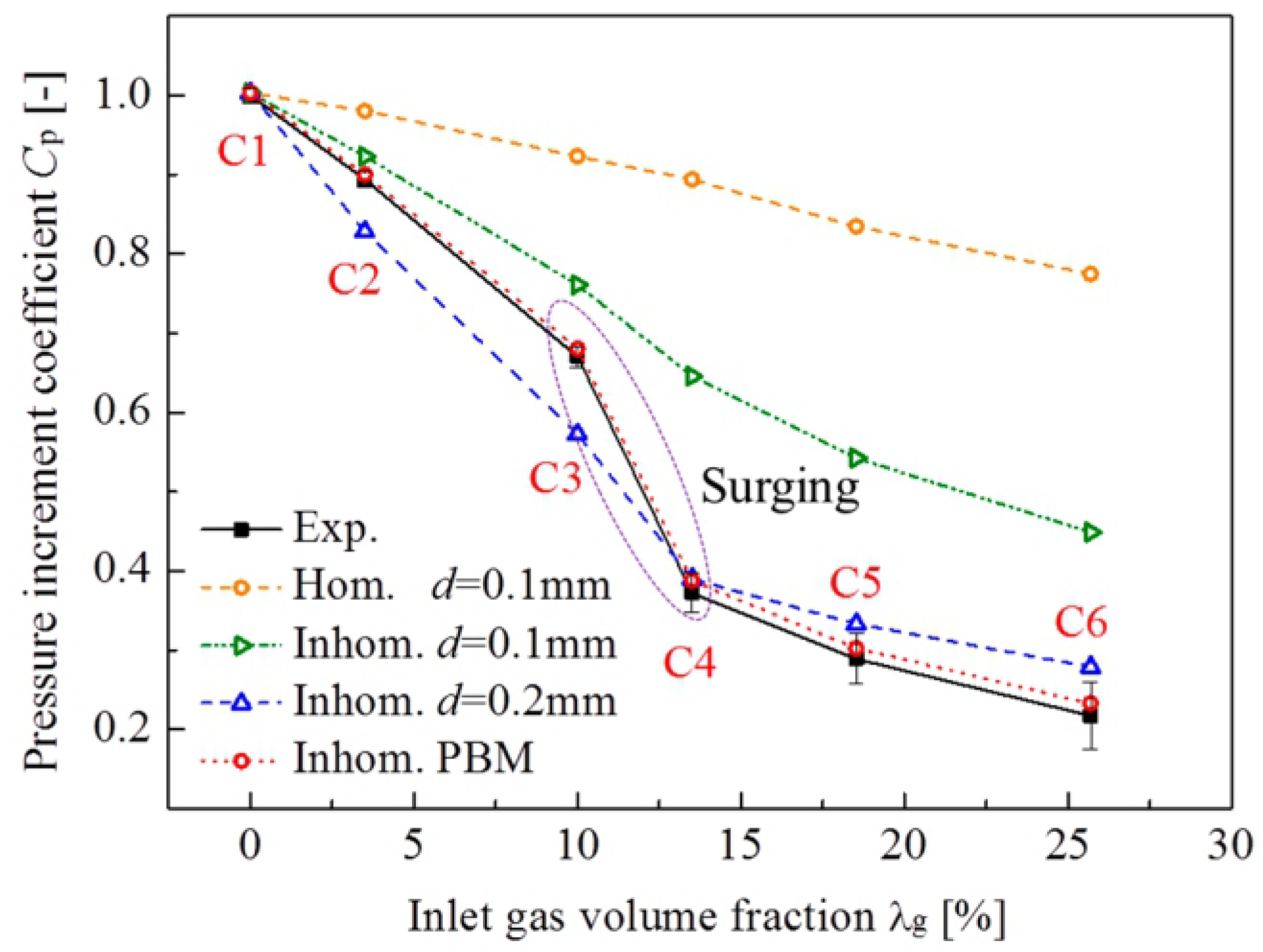
| C1 to C6 | Operation points in the study of Yan et al. [60] |
| CFD | Computational fluid dynamics |
| DES | Detached eddy simulation |
| DDES | Delayed DES |
| EE2F | Euler–Euler Two-Fluid |
| ESP | Electrical submersible pump |
| GEMMA | Generalized multiphase modeling approach |
| H2P | Hybrid Two-Phase |
| Hom. | Homogeneous |
| Inhom. | Inhomogeneous |
| LES | Large-eddy simulation |
| MUSIG | Multi-size group |
| PANS | Partially-averaged Navier–Stokes |
| PBM | Population balance modeling |
| PIMPLE | Combination of PISO and SIMPLE algorithm |
| PISO | Pressure Implicit with Splitting of Operators |
| PITM | Partially-integrated transport model |
| SIMPLE | Semi-Implicit Pressure Method for Pressure Linked Equations |
| SAS | Scale-adaptive simulation |
| SST | Shear Stress transport |
| TVD | Total variation diminishing |
| URANS | Unsteady Reynolds-averaged Navier Stokes |
| VoF | Volume-of-Fluid |
References
- Chan, A.; Kawaji, M.; Nakamura, H.; Kukita, Y. Experimental study of two-phase pump performance using a full size nuclear reactor pump. Nucl. Eng. Des. 1999, 193, 159–172. [Google Scholar] [CrossRef]
- Amoresano, A.; Langella, G.; Niola, V.; Quaremba, G. Advanced Image Analysis of Two-Phase Flow inside a Centrifugal Pump. Adv. Mech. Eng. 2014, 6. [Google Scholar] [CrossRef]
- Cappelino, C.A.; Roll, D.R.; Wilson, G. Design considerations and application guidelines for pumping liquids with entrained gas using open impeller centrifugal pump. In Proceedings of the 9th International Pump User Symposium, Houston, TX, USA, 24–27 September 2012; pp. 51–60. [Google Scholar] [CrossRef]
- Monte Verde, W.; Biazussi, J.L.; Sassim, N.A.; Bannwart, A.C. Experimental study of gas-liquid two-phase flow patterns within centrifugal pumps impellers. Exp. Therm. Fluid Sci. 2017, 85, 37–51. [Google Scholar] [CrossRef]
- Murakami, M.; Minemura, K. Effects of Entrained Air on the Performance of a Centrifugal Pump: 1st Report, Performance and Flow Conditions. Bull. JSME 1974, 17, 1047–1055. [Google Scholar] [CrossRef]
- Murakami, M.; Minemura, K.; Suehiro, H. Effects of entrained air on the performance of centrifugal and axial flow pumps. Mem. Fac. Eng. Kyushu Univ. 1971, 124–133. [Google Scholar]
- Furukawa, A.; Togoe, T.; Sato, S.; Takamatsu, Y. Fundamental studies on a tandem bladed impeller of gas/liquid two-phase flow centrifugal pump. Mem. Fac. Eng. Kyushu Univ. 1988, 48, 231–240. [Google Scholar] [CrossRef]
- Tillack, P. Förderverhalten von Kreiselpumpen bei viskosem, gasbeladenem Fördermedium. Ph.D. Thesis, Technical University Kaiserslautern, Kaiserslautern, Germany, 1998. [Google Scholar]
- Gülich, J.F. Centrifugal Pumps; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Sato, S.; Furukawa, A.; Takamatsu, Y. Air-water two-phase flow performance of centrifugal pump impellers with various blade angles. JSME Int. J., Ser. B 1996, 39, 223–229. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, H.Q. A Review of Experiments and Modeling of Gas-Liquid Flow in Electrical Submersible Pumps. Energies 2018, 11, 180. [Google Scholar] [CrossRef]
- Iben, U.; Wolf, F.; Freudigmann, H.A.; Fröhlich, J.; Heller, W. Optical measurements of gas bubbles in oil behind a cavitating micro-orifice flow. Exp. Fluids 2015, 56, 114. [Google Scholar] [CrossRef]
- Freudigmann, H.A.; Iben, U.; Pelz, P.F. Air release measurements of V-oil 1404 downstream of a micro orifice at choked flow conditions. J. Phys. Conf. Ser. 2015, 656, 12113. [Google Scholar] [CrossRef]
- Freudigmann, H.A.; Dörr, A.; Iben, U.; Pelz, P.F. Modeling of Cavitation-Induced Air Release Phenomena in Micro-Orifice Flows. ASME J. Fluids Eng. 2017, 139, 111301. [Google Scholar] [CrossRef]
- Kowalski, K.; Pollak, S.; Skoda, R.; Hussong, J. Experimental Study on Cavitation-Induced Air Release in Orifice Flows. ASME J. Fluids Eng. 2018, 140, 61201. [Google Scholar] [CrossRef]
- Frobenius, M.; Schilling, R.; Friedrichs, J.; Kosyna, G. Numerical and Experimental Investigations of the Cavitating Flow in a Centrifugal Pump Impeller. In Proceedings of the 2002 ASME Joint U.S.-European Fluids Engineering Conference, Montreal, QC, Canada, 14–18 July 2002; Rohatgi, U.S., Ed.; American Society of Mechanical Engineers: New York, NY, USA, 2002; pp. 361–368. [Google Scholar] [CrossRef]
- Limbach, P.; Kimoto, M.; Deimel, C.; Skoda, R. Numerical 3D Simulation of the Cavitating Flow in a Centrifugal Pump With Low Specific Speed and Evaluation of the Suction Head. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014. [Google Scholar] [CrossRef]
- Limbach, P.; Müller, T.; Blume, M.; Skoda, R. Numerical and Experimental Investigation of the Cavitating Flow in a Low Specific Speed Centrifugal Pump and Assessment of the Influence of Surface Roughness on Head Prediction. In Proceedings of the International Symposium on Transport Phenomena and Dynamics (ISROMAC), Honululu, HI, USA, 10–15 April 2016. [Google Scholar]
- Limbach, P.; Skoda, R. Numerical and Experimental Analysis of Cavitating Flow in a Low Specific Speed Centrifugal Pump With Different Surface Roughness. ASME J. Fluids Eng. 2017, 139, 101201. [Google Scholar] [CrossRef]
- Liu, H.l.; Wang, J.; Wang, Y.; Zhang, H.; Huang, H. Influence of the empirical coefficients of cavitation model on predicting cavitating flow in the centrifugal pump. Int. J. Nav. Archit. Ocean Eng. 2014, 6, 119–131. [Google Scholar] [CrossRef]
- Shi, W.; Wang, C.; Wang, W.; Pei, B. Numerical Calculation on Cavitation Pressure Pulsation in Centrifugal Pump. Adv. Mech. Eng. 2014, 6, 367631. [Google Scholar] [CrossRef]
- Zhang, D.; Shi, W.; Pan, D.; Dubuisson, M. Numerical and Experimental Investigation of Tip Leakage Vortex Cavitation Patterns and Mechanisms in an Axial Flow Pump. ASME J. Fluids Eng. 2015, 137, 121103. [Google Scholar] [CrossRef]
- Mousmoulis, G.; Karlsen-Davies, N.; Aggidis, G.; Anagnostopoulos, J.; Papantonis, D. Experimental analysis of the onset and development of cavitation in a centrifugal pump. J. Phys. Conf. Ser. 2017, 813, 12044. [Google Scholar] [CrossRef]
- Mansour, M.; Wunderlich, B.; Thévenin, D. Effect of tip clearance gap and inducer on the transport of two-phase air-water flows by centrifugal pumps. Exp. Therm. Fluid Sci. 2018, 99, 487–509. [Google Scholar] [CrossRef]
- Mansour, M.; Wunderlich, B.; Thévenin, D. Experimental Study of Two-Phase Air/Water Flow in a Centrifugal Pump Working With a Closed or a Semi-Open Impeller. In Proceedings of the ASME Turbo Expo 2018: Turbine Technical Conference and Exposition, Oslo, Norway, 11–15 June 2018; The American Society of Mechanical Engineers: New York, NY, USA, 2018. [Google Scholar] [CrossRef]
- Mansour, M.; Parikh, T.; Thévenin, D. Influence of the shape of the impeller blade trailing edge on single and two-phase air water flows in a centrifugal pump. In Proceedings of the Turbomachinery & Pump Symposia, Houston, TX, USA, 13–16 December 2020. [Google Scholar]
- Mansour, M.; Kopparthy, S.; Thévenin, D. Investigations on the effect of rotational speed on the transport of air-water two-phase flows by centrifugal pumps. Int. J. Heat Fluid Flow 2022, 94, 108939. [Google Scholar] [CrossRef]
- Bieberle, A.; Schäfer, T.; Neumann, M.; Hampel, U. Validation of high-resolution gamma-ray computed tomography for quantitative gas holdup measurements in centrifugal pumps. Meas. Sci. Technol. 2015, 26, 95304. [Google Scholar] [CrossRef]
- Schäfer, T.; Bieberle, A.; Neumann, M.; Hampel, U. Application of gamma-ray computed tomography for the analysis of gas holdup distributions in centrifugal pumps. Flow Meas. Instrum. 2015, 46, 262–267. [Google Scholar] [CrossRef]
- Neumann, M.; Schäfer, T.; Bieberle, A.; Hampel, U. An Experimental Study on the Gas Entrainment in Horizontally and Vertically Installed Centrifugal Pumps. ASME J. Fluids Eng. 2016, 138, 12–19. [Google Scholar] [CrossRef]
- Schäfer, T.; Neumann, M.; Bieberle, A.; Hampel, U. Experimental investigations on a common centrifugal pump operating under gas entrainment conditions. Nucl. Eng. Des. 2017, 316, 1–8. [Google Scholar] [CrossRef]
- Schäfer, T.; Neumann-Kipping, M.; Bieberle, A.; Bieberle, M.; Hampel, U. Ultrafast X-Ray Computed Tomography Imaging for Hydrodynamic Investigations of Gas–Liquid Two-Phase Flow in Centrifugal Pumps. ASME J. Fluids Eng. 2020, 142, 41502. [Google Scholar] [CrossRef]
- Gambao, J.; Prado, M.G. Visualization study of performance breakdown in two-phase performance of an electrical submersible pump. In Proceedings of the Twenty-Sixth International Pump User Symposium, Houston, TX, USA, 26–28 September 2010. [Google Scholar] [CrossRef]
- Barrios, L.; Prado, M.G. Experimental Visualization of Two-Phase Flow Inside an Electrical Submersible Pump Stage. J. Energy Resour. Technol. 2011, 133, 42901. [Google Scholar] [CrossRef]
- Trevisan, F.E.; Prado, M. Experimental Investigation of the Viscous Effect on Two-Phase-Flow Patterns and Hydraulic Performance of Electrical Submersible Pumps. J. Can. Pet. Technol. 2011, 50, 45–52. [Google Scholar] [CrossRef]
- Shao, C.; Li, C.; Zhou, J. Experimental investigation of flow patterns and external performance of a centrifugal pump that transports gas-liquid two-phase mixtures. Int. J. Heat Fluid Flow 2018, 71, 460–469. [Google Scholar] [CrossRef]
- Stel, H.; Ofuchi, E.M.; Alves, R.F.; Chiva, S.; Morales, R.E.M. Experimental Analysis of Gas–Liquid Flows in a Centrifugal Rotor. ASME J. Fluids Eng. 2020, 142, 31101. [Google Scholar] [CrossRef]
- Zhao, L.; Chang, Z.; Zhang, Z.; Huang, R.; He, D. Visualization of gas-liquid flow pattern in a centrifugal pump impeller and its influence on the pump performance. Meas. Sensors 2021, 13, 100033. [Google Scholar] [CrossRef]
- Mansour, M.; Parikh, T.; Thévenin, D. Influence of Blade Pitch and Number of Blades of a Pump Inducer on Single and Two-Phase Flow Performance. In Proceedings of the ASME Turbo Expo 2020; Volume 9: Oil and Gas Applications; Organic Rankine Cycle Power Systems; Steam Turbine; The American Society of Mechanical Engineers: New York, NY, USA, 2020. [Google Scholar] [CrossRef]
- Si, Q.; Bois, G.; Zhang, K.; Yuan, J. Air-water two-phase flow experimental and numerical analysis in a low specific speed centrifugal pump. In Proceedings of the 12th European Turbomachinery Conference on Turbomachinery Fluid Dynamics & Thermodynamics, Stockholm, Sweden, 3–7 April 2017. [Google Scholar] [CrossRef]
- Si, Q.; Bois, G.; Jiang, Q.; He, W.; Ali, A.; Yuan, S. Investigation on the Handling Ability of Centrifugal Pumps under Air–Water Two-Phase Inflow: Model and Experimental Validation. Energies 2018, 11, 48. [Google Scholar] [CrossRef]
- Si, Q.; Bois, G.; Liao, M.; Zhang, H.; Cui, Q.; Yuan, S. A Comparative Study on Centrifugal Pump Designs and Two-Phase Flow Characteristic under Inlet Gas Entrainment Conditions. Energies 2020, 13, 65. [Google Scholar] [CrossRef]
- Si, Q.; Liao, M.; Fan, M.; Yuan, S.; Cui, Q.; Bois, G. Experimental study on flow behavior of unshrouded impeller centrifugal pumps under inlet air entrainment condition. In Proceedings of the 14th European Turbomachinery Conference on Turbomachinery Fluid Dynamics & Thermodynamics, Gdansk, Poland, 12–16 April 2021. [Google Scholar]
- Liao, M.; Si, Q.; Fan, M.; Wang, P.; Liu, Z.; Yuan, S.; Cui, Q.; Bois, G. Experimental Study on Flow Behavior of Unshrouded Impeller Centrifugal Pumps under Inlet Air Entrainment Condition. Int. J. Turbomach. Propuls. Power 2021, 6, 31. [Google Scholar] [CrossRef]
- Wan, Y.; Peters, N. Scaling of Spray Penetration with Evaporation. Atomiz. Spr. 1999, 9, 111–132. [Google Scholar] [CrossRef]
- Pak, E.T.; Lee, J.C. Performance and pressure distribution changes in a centrifugal pump under two-phase flow. Proc. Inst. Mech. Eng. A: J. Power Energy 1998, 212, 165–171. [Google Scholar] [CrossRef]
- Minemura, K.; Uchiyama, T. Prediction of Pump Performance Under Air-Water Two-Phase Flow Based on a Bubbly Flow Model. ASME J. Fluids Eng. 1993, 115, 781–783. [Google Scholar] [CrossRef]
- Müller, T.; Limbach, P.; Skoda, R. Numerical 3D RANS Simulation of Gas-Liquid Flow in a Centrifugal Pump with an Euler-Euler Two-Phase Model and a Dispersed Phase Distribution. In Proceedings of the 11th European Conference on Turbomachinery Fluid Dynamics & Thermodynamics, Madrid, Spain, 23–27 March 2015. [Google Scholar]
- Minemura, K.; Uchiyama, T. Three-Dimensional Calculation of Air-Water Two-Phase Flow in Centrifugal Pump Impeller Based on a Bubbly Flow Model. ASME J. Fluids Eng. 1993, 115, 766–771. [Google Scholar] [CrossRef]
- Caridad, J.; Asuaje, M.; Kenyery, F.; Tremante, A.; Aguillon, O. Characterization of a centrifugal pump impeller under two-phase flow conditions. J. Pet. Sci. Eng. 2008, 63, 18–22. [Google Scholar] [CrossRef]
- Yu, Z.Y.; Zhang, Q.Z.; Huang, R.; Cao, S.L. Numerical analysis of gas-liquid mixed transport process in a multiphase rotodynamic pump. IOP Conf. Ser. Earth Environ. Sci. 2012, 15, 32062. [Google Scholar] [CrossRef]
- Müller, T.; Limbach, P.; Skoda, R. Influence of Geometry Simplifications and Numerical Parameters in 3D URANS Liquid-Gas Flow Simulations of a Radial Pump with an Eulerian Mono-Dispersed Two-Phase Model. In Proceedings of the International Symposium on Transport Phenomena and Dynamics (ISROMAC), Honululu, HI, USA, 10–15 April 2016. [Google Scholar]
- Wang, B.; Zhang, H.; Deng, F.; Wang, C.; Si, Q. Effect of Short Blade Circumferential Position Arrangement on Gas-Liquid Two-Phase Flow Performance of Centrifugal Pump. Processes 2020, 8, 1317. [Google Scholar] [CrossRef]
- Zhou, L.; Han, Y.; Lv, W.; Yang, Y.; Zhu, Y.; Song, X. Numerical Calculation of Energy Performance and Transient Characteristics of Centrifugal Pump under Gas-Liquid Two-Phase Condition. Micromachines 2020, 11, 728. [Google Scholar] [CrossRef]
- Zhong, G.; Shao, C.; Cheng, W.; Zhao, Z. Numerical simulation and experimental study on gas–liquid two-phase unsteady flow in a centrifugal pump during the transition process. Proc. Inst. Mech. Eng. C: J. Mech. Eng. Sci. 2022, 236, 2224–2241. [Google Scholar] [CrossRef]
- Hundshagen, M.; Mansour, M.; Thévenin, D.; Skoda, R. Numerical investigation of two-phase air-water flow in a centrifugal pump with closed or semi-open impeller. In Proceedings of the 13th European Turbomachinery Conference on Turbomachinery Fluid Dynamics & Thermodynamics, Lausanne, Switzerland, 8–12 April 2019. [Google Scholar] [CrossRef]
- Hundshagen, M.; Mansour, M.; Thévenin, D.; Skoda, R. Experimental investigation and 3D-CFD simulation of centrifugal pumps for gasladen liquids with closed and semi-open impellers. In Proceedings of the 4th International Rotating Equipment Conference, Wiesbaden, Germany, 24–25 September 2019. [Google Scholar]
- Hundshagen, M.; Mansour, M.; Thévenin, D.; Skoda, R. 3D Simulation of Gas-Laden Liquid Flows in Centrifugal Pumps and the Assessment of Two-Fluid CFD Methods. Exp. Comput. Multiph. Flow 2021, 3, 186–207. [Google Scholar] [CrossRef]
- He, D.; Ge, Z.; Bai, B.; Guo, P.; Luo, X. Gas–Liquid Two-Phase Performance of Centrifugal Pump Under Bubble Inflow Based on Computational Fluid Dynamics–Population Balance Model Coupling Model. ASME J. Fluids Eng. 2020, 142, 81402. [Google Scholar] [CrossRef]
- Yan, S.; Sun, S.; Luo, X.; Chen, S.; Li, C.; Feng, J. Numerical Investigation on Bubble Distribution of a Multistage Centrifugal Pump Based on a Population Balance Model. Energies 2020, 13, 908. [Google Scholar] [CrossRef]
- Stel, H.; Ofuchi, E.M.; Chiva, S.; Morales, R.E. Numerical simulation of gas-liquid flows in a centrifugal rotor. Chem. Eng. Sci. 2020, 221, 115692. [Google Scholar] [CrossRef]
- Stel, H.; Ofuchi, E.M.; Chiva, S.; Morales, R.E.M. Numerical assessment of performance characteristics and two-phase flow dynamics of a centrifugal rotor operating under gas entrainment condition. Exp. Comput. Multiph. Flow 2021, 17, 221–240. [Google Scholar] [CrossRef]
- Zhang, F.; Zhu, L.; Chen, K.; Yan, W.; Appiah, D.; Hu, B. Numerical Simulation of Gas–Liquid Two-Phase Flow Characteristics of Centrifugal Pump Based on the CFD–PBM. Mathematics 2020, 8, 769. [Google Scholar] [CrossRef]
- Chen, Y.; Patil, A.; Chen, Y.; Bai, C.; Wang, Y.; Morrison, G. Numerical Study on the First Stage Head Degradation in an Electrical Submersible Pump With Population Balance Model. J. Energy Resour. Technol. 2019, 141. [Google Scholar] [CrossRef]
- Si, Q.; Asad, A.; Wang, B.; Wang, P.; Bois, G.; Jianping, Y.; Kubar, A.A. Numerical Study on Gas-Liquid Two Phase Flow Characteristic of Multistage Electrical Submersible Pump by Using a Novel Multiple-Size Group (MUSIG) Model. Phys. Fluids 2022, 34, 063311. [Google Scholar] [CrossRef]
- Mansour, M.; Kováts, P.; Wunderlich, B.; Thévenin, D. Experimental investigations of a two-phase gas/liquid flow in a diverging horizontal channel. Exp. Therm. Fluid Sci. 2018, 93, 210–217. [Google Scholar] [CrossRef]
- Kopparthy, S.; Mansour, M.; Janiga, G.; Thévenin, D. Numerical investigations of turbulent single-phase and two-phase flows in a diffuser. Int. J. Multiphase Flow 2020, 130, 103333. [Google Scholar] [CrossRef]
- Parikh, T.; Mansour, M.; Thévenin, D. Maximizing the performance of pump inducers using CFD-based multi-objective optimization. Struct. Multidisc. Optim. 2022, 65, 9. [Google Scholar] [CrossRef]
- Parikh, T.; Mansour, M.; Thévenin, D. Investigations on the effect of tip clearance gap and inducer on the transport of air-water two-phase flow by centrifugal pumps. Chem. Eng. Sci. 2020, 218, 115554. [Google Scholar] [CrossRef]
- Pineda, H.; Biazussi, J.; López, F.; Oliveira, B.; Carvalho, R.D.; Bannwart, A.C.; Ratkovich, N. Phase distribution analysis in an Electrical Submersible Pump (ESP) inlet handling water–air two-phase flow using Computational Fluid Dynamics (CFD). J. Pet. Sci. Eng. 2016, 139, 49–61. [Google Scholar] [CrossRef]
- Zhu, J.; Zhu, H.; Zhang, J.; Zhang, H.Q. A numerical study on flow patterns inside an electrical submersible pump (ESP) and comparison with visualization experiments. J. Pet. Sci. Eng. 2019, 173, 339–350. [Google Scholar] [CrossRef]
- Mansour, M.; Parikh, T.; Engel, S.; Thévenin, D. Numerical Investigations of Gas/Liquid Two-Phase Flow in a Pump Inducer. ASME J. Fluids Eng. 2020, 142, 21302. [Google Scholar] [CrossRef]
- de Santis, A.; Colombo, M.; Hanson, B.C.; Fairweather, M. A generalized multiphase modelling approach for multiscale flows. J. Comput. Phys. 2021, 436, 110321. [Google Scholar] [CrossRef]
- Hundshagen, M.; Rave, K.; Mansour, M.; Thévenin, D.; Skoda, R. Assessment of multi-phase CFD methods for gas-laden liquid flows in centrifugal pumps with particular emphasis on the change of flow morphology. In Proceedings of the 14th European Turbomachinery Conference on Turbomachinery Fluid Dynamics & Thermodynamics, Gdansk, Poland, 12–16 April 2021. [Google Scholar] [CrossRef]
- Marschall, H. Towards the Numerical Simulation of Multi-Scale Two-Phase Flows. Ph.D. Thesis, Technische Universität München, München, Germany, 2011. [Google Scholar]
- Hundshagen, M.; Rave, K.; Nguyen, B.D.; Popp, S.; Hasse, C.; Mansour, M.; Thévenin, D.; Skoda, R. Two-Phase Flow Simulations of Liquid/Gas Transport in Radial Centrifugal Pumps With Special Emphasis on the Transition From Bubbles to Adherent Gas Accumulations. ASME J. Fluids Eng. 2022, 144, 101202. [Google Scholar] [CrossRef]
- Hänsch, S.; Lucas, D.; Krepper, E.; Höhne, T. A multi-field two-fluid concept for transitions between different scales of interfacial structures. Int. J. Multiphase Flow 2012, 47, 171–182. [Google Scholar] [CrossRef]
- Hänsch, S.; Lucas, D.; Höhne, T.; Krepper, E. Application of a new concept for multi-scale interfacial structures to the dam-break case with an obstacle. Nucl. Eng. Des. 2014, 279, 171–181. [Google Scholar] [CrossRef]
- Meller, R.; Schlegel, F.; Lucas, D. Basic verification of a numerical framework applied to a morphology adaptive multifield two–fluid model considering bubble motions. Int. J. Numer. Meth. Fluids 2021, 93, 748–773. [Google Scholar] [CrossRef]
- Yin, J.; Zhang, T.; Krull, B.; Meller, R.; Schlegel, F.; Lucas, D.; Wang, D.; Liao, Y. A CFD approach for the flow regime transition in a vane-type gas-liquid separator. Int. J. Multiphase Flow 2023, 159, 104320. [Google Scholar] [CrossRef]
- Frederix, E.; Dovizio, D.; Mathur, A.; Komen, E. All-regime two-phase flow modeling using a novel four-field large interface simulation approach. Int. J. Multiphase Flow 2021, 145. [Google Scholar] [CrossRef]
- Wardle, K.E.; Weller, H.G. Hybrid Multiphase CFD Solver for Coupled Dispersed/Segregated Flows in Liquid-Liquid Extraction. Int. J. Chem. Eng. 2013, 2013, 128936. [Google Scholar] [CrossRef]
- Shonibare, O.Y.; Wardle, K.E. Numerical Investigation of Vertical Plunging Jet Using a Hybrid Multifluid–VOF Multiphase CFD Solver. Int. J. Chem. Eng. 2015, 2015, 925639. [Google Scholar] [CrossRef]
- Mathur, A.; Dovizio, D.; Frederix, E.; Komen, E. A Hybrid Dispersed-Large Interface Solver for multi-scale two-phase flow modelling. Nucl. Eng. Des. 2019, 344, 69–82. [Google Scholar] [CrossRef]
- Byskov, R.K.; Jacobsen, C.B.; Pedersen, N. Flow in a Centrifugal Pump Impeller at Design and Off-Design Conditions—Part II: Large Eddy Simulations. ASME J. Fluids Eng. 2003, 125, 73–83. [Google Scholar] [CrossRef]
- Kato, C.; Mukai, H.; Manabe, A. Large-Eddy Simulation of Unsteady Flow in a Mixed-Flow Pump. Int. J. Rotating Mach. 2003, 9, 345–351. [Google Scholar] [CrossRef]
- Tang, X.; Wang, F.; Wu, Y. An improved large eddy simulation of two-phase flows in a pump impeller. Acta Mech. Sin. 2007, 23, 635–643. [Google Scholar] [CrossRef]
- Tokyay, T.E.; Constantinescu, S.G. Validation of a Large-Eddy Simulation Model to Simulate Flow in Pump Intakes of Realistic Geometry. J. Hydraul. Eng. 2006, 132, 1303–1315. [Google Scholar] [CrossRef]
- Zhang, W.; Yu, Y.; Chen, H. Numerical Simulation of Unsteady Flow in Centrifugal Pump Impeller at Off-Design Condition by Hybrid RANS/LES Approaches. In High Performance Computing and Applications; Hutchison, D., Kanade, T., Kittler, J., Kleinberg, J.M., Mattern, F., Mitchell, J.C., Naor, M., Nierstrasz, O., Pandu Rangan, C., Steffen, B., et al., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 5938, pp. 571–578. [Google Scholar] [CrossRef]
- Wang, W.; Wang, Y. Analysis of inner flow in low specific speed centrifugal pump based on LES. J. Mech. Sci. Technol. 2013, 27, 1619–1626. [Google Scholar] [CrossRef]
- Posa, A.; Lippolis, A.; Verzicco, R.; Balaras, E. Large-eddy simulations in mixed-flow pumps using an immersed-boundary method. Comput. Fluids 2011, 47, 33–43. [Google Scholar] [CrossRef]
- Posa, A.; Lippolis, A.; Balaras, E. Large-Eddy Simulation of a Mixed-Flow Pump at Off-Design Conditions. ASME J. Fluids Eng. 2015, 137, 49. [Google Scholar] [CrossRef]
- Si, Q.; Yuan, J.; Yuan, S.; Wang, W.; Zhu, L.; Bois, G. Numerical Investigation of Pressure Fluctuation in Centrifugal Pump Volute Based on SAS Model and Experimental Validation. Adv. Mech. Eng. 2014, 6, 972081. [Google Scholar] [CrossRef]
- Cui, B.; Zhang, C.; Zhang, Y.; Zhu, Z. Influence of Cutting Angle of Blade Trailing Edge on Unsteady Flow in a Centrifugal Pump Under Off-Design Conditions. Appl. Sci. 2020, 10, 580. [Google Scholar] [CrossRef]
- Shen, J.F.; Li, Y.J.; Liu, Z.Q.; Tang, X.L. Turbulent flow and pressure fluctuation prediction of the impeller in an axial-flow pump based on LES. IOP Conf. Ser.: Mater. Sci. Eng. 2013, 52, 032015. [Google Scholar] [CrossRef]
- Posa, A.; Lippolis, A.; Balaras, E. Investigation of Separation Phenomena in a Radial Pump at Reduced Flow Rate by Large-Eddy Simulation. ASME J. Fluids Eng. 2016, 138, 121101. [Google Scholar] [CrossRef]
- Posa, A.; Lippolis, A. A LES investigation of off-design performance of a centrifugal pump with variable-geometry diffuser. Int. J. Heat Fluid Flow 2018, 70, 299–314. [Google Scholar] [CrossRef]
- Posa, A.; Lippolis, A. Effect of working conditions and diffuser setting angle on pressure fluctuations within a centrifugal pump. Int. J. Heat Fluid Flow 2019, 75, 44–60. [Google Scholar] [CrossRef]
- Posa, A. LES investigation on the dependence of the flow through a centrifugal pump on the diffuser geometry. Int. J. Heat Fluid Flow 2021, 87, 108750. [Google Scholar] [CrossRef]
- Posa, A. LES study on the influence of the diffuser inlet angle of a centrifugal pump on pressure fluctuations. Int. J. Heat Fluid Flow 2021, 89, 108804. [Google Scholar] [CrossRef]
- Kye, B.; Park, K.; Choi, H.; Lee, M.; Kim, J.H. Flow characteristics in a volute-type centrifugal pump using large eddy simulation. Int. J. Heat Fluid Flow 2018, 72, 52–60. [Google Scholar] [CrossRef]
- Pacot, O.; Kato, C.; Guo, Y.; Yamade, Y.; Avellan, F. Large Eddy Simulation of the Rotating Stall in a Pump-Turbine Operated in Pumping Mode at a Part-Load Condition. ASME J. Fluids Eng. 2016, 138. [Google Scholar] [CrossRef]
- Zhang, N.; Liu, X.; Gao, B.; Wang, X.; Xia, B. Effects of modifying the blade trailing edge profile on unsteady pressure pulsations and flow structures in a centrifugal pump. Int. J. Heat Fluid Flow 2019, 75, 227–238. [Google Scholar] [CrossRef]
- Zhang, T.; Wu, D.; Qiu, S.; Zhou, P.; Ren, Y.; Mou, J. LES Analysis of the Unsteady Flow Characteristics of a Centrifugal Pump Impeller. Fluid Dyn. Mater. Process. 2022, 18, 1349–1361. [Google Scholar] [CrossRef]
- Zhou, P.; Dai, J.; Yan, C.; Zheng, S.; Ye, C.; Zhang, X. Effect of Stall Cells on Pressure Fluctuations Characteristics in a Centrifugal Pump. Symmetry 2019, 11, 1116. [Google Scholar] [CrossRef]
- Sorguven, E.; Incir, S.; Highgate, J. Understanding loss generation mechanisms in a centrifugal pump using large eddy simulation. Int. J. Heat Fluid Flow 2022, 96, 108994. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar] [CrossRef]
- Fröhlich, J.; Mellen, C.P.; Rodi, W.; Temmermann, L.; Leschziner, M.A. Highly resolved large-eddy simulation of separated flow in a channel with streamwise periodic constrictions. J. Fluid Mech. 2005, 526, 19–66. [Google Scholar] [CrossRef]
- Kim, D.; Choi, H. Immersed boundary method for flow around an arbitrarily moving body. J. Comp. Phys. 2006, 212, 662–680. [Google Scholar] [CrossRef]
- Spalart, P.R.; Jou, W.H.; Strelets, M. Comments on the Feasibility of LES for Wings and on a Hybrid RANS/LES Approach. In Advances in DNS/LES; Liu, C., Liu, Z., Sakell, L., Eds.; Greyden Press: Columbus, OH, USA, 1997. [Google Scholar]
- Spalart, P.R. Detached-Eddy Simulation. Annu. Rev. Fluid Mech. 2009, 41, 181–202. [Google Scholar] [CrossRef]
- Spalart, P.R.; Deck, S.; Shur, M.L.; Squires, K.D.; Strelets, M.K.; Travin, A. A New Version of Detached-eddy Simulation, Resistant to Ambiguous Grid Densities. Theoret. Comput. Fluid Dynamics 2006, 20, 181–195. [Google Scholar] [CrossRef]
- Speziale, C.G. Turbulence Modeling for Time-Dependent RANS and VLES: A Review. AIAA J. 1998, 36, 173–184. [Google Scholar] [CrossRef]
- Basara, B.; Krajnovic, S.; Girimaji, S.; Pavlovic, Z. Near-Wall Formulation of the Partially Averaged Navier Stokes Turbulence Model. AIAA J. 2011, 49, 2627–2636. [Google Scholar] [CrossRef]
- Girimaji, S.S. Partially-Averaged Navier-Stokes Model for Turbulence: A Reynolds-Averaged Navier-Stokes to Direct Numerical Simulation Bridging Method. J. Appl. Mech. 2006, 73, 413–421. [Google Scholar] [CrossRef]
- Chaouat, B.; Schiestel, R. A new partially integrated transport model for subgrid-scale stresses and dissipation rate for turbulent developing flows. Phys. Fluids 2005, 17, 065106. [Google Scholar] [CrossRef]
- Xin, T.; Zhili, L.; Meng, Z.; Haotian, Y.; Wei, J.; Yuchuan, W.; Diyi, C. Analysis of Unsteady Flow Characteristics of Centrifugal Pump under Part Load Based on DDES Turbulence Model. Shock Vib. 2021, 2021, 1–11. [Google Scholar] [CrossRef]
- Zhang, N.; Liu, X.; Gao, B.; Xia, B. DDES analysis of the unsteady wake flow and its evolution of a centrifugal pump. Renew. Energy 2019, 141, 570–582. [Google Scholar] [CrossRef]
- Strelets, M. Detached eddy simulation of massively separated flows. In Proceedings of the 39th Aerospace Sciences Meeting and Exhibit; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2001. [Google Scholar] [CrossRef]
- Menter, F.; Carregal Ferreira, J.; Esch, T.; Konno, B. The SST Turbulence Model with Improved Wall Treatment for Heat Transfer Predictions in Gas Turbines. In Proceedings of the International Gas Turbine Congress, Tokyo, Japan, 2–7 November 2003. [Google Scholar]
- Gritskevich, M.S.; Garbaruk, A.V.; Schütze, J.; Menter, F.R. Development of DDES and IDDES Formulations for the k-$∖omega$ Shear Stress Transport Model. Flow Turbul. Combust. 2012, 88, 431–449. [Google Scholar] [CrossRef]
- Menter, F.; Hüppe, A.; Matyushenko, A.; Kolmogorov, D. An Overview of Hybrid RANS–LES Models Developed for Industrial CFD. Appl. Sci. 2021, 11, 2459. [Google Scholar] [CrossRef]
- Rotta, J.C. Turbulente Strömungen: Eine Einführung in die Theorie und ihre Anwendung; Vieweg+Teubner Verlag: Wiesbaden, Germany, 1972; Volume 15. [Google Scholar] [CrossRef]
- Fröhlich, J.; von Terzi, D. Hybrid LES/RANS methods for the simulation of turbulent flows. Prog. Aerosp. Sci. 2008, 44, 349–377. [Google Scholar] [CrossRef]
- Jakirlić, S.; Bopp, M.; Chang, C.Y.; Köhler, F.; Krumbein, B.; Kutej, L.; Kütemeier, D.; Maden, I.; Maduta, R.; Ullrich, M.; et al. RANS-based Sub-scale Modelling in Eddy-resolving Simulation Methods. ERCOFTAC Bull. 2019, 121, 5–16. [Google Scholar]
- Egorov, Y.; Menter, F. Development and Application of SST-SAS Turbulence Model in the DESIDER Project. In Advances in Hybrid RANS-LES Modelling; Peng, S.H., Haase, W., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 97, pp. 261–270. [Google Scholar] [CrossRef]
- Menter, F. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Menter, F.; Egorov, Y. The Scale-Adaptive Simulation Method for Unsteady Turbulent Flow Predictions. Part 1: Theory and Model Description. Flow Turbul. Combust. 2010, 85, 113–138. [Google Scholar] [CrossRef]
- Lucius, A.; Brenner, G. Unsteady CFD simulations of a pump in part load conditions using scale-adaptive simulation. Int. J. Heat Fluid Flow 2010, 31, 1113–1118. [Google Scholar] [CrossRef]
- Schiffer-Rosenberger, J.; Bodner, C.; Jaberg, H. Performance analysis of a single-blade impeller pump based on unsteady 3D numerical simulation. In Proceedings of the 3rd International Rotating Equipment Conference, Düsseldorf, Germany, 14–15 September 2016; pp. 193–203. [Google Scholar]
- Pavesi, G.; Dazin, A.; Cavazzini, G.; Caignaert, G.; Bois, G.; Ardizzon, G. Experimental and numerical investigation of unforced unsteadiness in a vaneless radial diffuser. In Proceedings of the 9th European Conference on Turbomachinery Fluid Dynamics & Thermodynamics, Istanbul, Turkey, 21–25 March 2011. [Google Scholar]
- Zhao, X.; Luo, Y.; Wang, Z.; Xiao, Y.; Avellan, F. Unsteady Flow Numerical Simulations on Internal Energy Dissipation for a Low-Head Centrifugal Pump at Part-Load Operating Conditions. Energies 2019, 12, 13. [Google Scholar] [CrossRef]
- Hundshagen, M.; Casimir, N.; Pesch, A.; Falsafi, S.; Skoda, R. Assessment of scale-adaptive turbulence models for volute-type centrifugal pumps at part load operation. Int. J. Heat Fluid Flow 2020, 85, 108621. [Google Scholar] [CrossRef]
- Rave, K.; Lehmenkühler, M.; Wirz, D.; Bart, H.J.; Skoda, R. 3D flow simulation of a baffled stirred tank for an assessment of geometry simplifications and a scale-adaptive turbulence model. Chem. Eng. Sci. 2021, 231, 116262. [Google Scholar] [CrossRef]
- Müller, T.; Limbach, P.; Skoda, R. 3D Liquid-Gas Flow Simulations of a Radial Pump with an Eulerian Mono-Dispersed Two-Phase Model. In Proceedings of the 3rd International Rotating Equipment Conference, Düsseldorf, Germany, 14–15 September 2016. [Google Scholar]
- Schiller, L.; Naumann, A. Über die grundlegenden Berechnungen bei Schwerkraftaufbereitung. Z. Des Vereines Dtsch. Ingenieure 1933, 77, 318–320. [Google Scholar]
- Auton, T.R.; Hunt, J.C.R.; Prud’Homme, M. The force exerted on a body in inviscid unsteady non-uniform rotational flow. J. Fluid Mech. 1988, 197, 241–257. [Google Scholar] [CrossRef]
- Rzehak, R.; Krepper, E.; Liao, Y.; Ziegenhein, T.; Kriebitzsch, S.; Lucas, D. Baseline Model for the Simulation of Bubbly Flows. Chem. Eng. Technol. 2015, 38, 1972–1978. [Google Scholar] [CrossRef]
- Brackbill, J.; Kothe, D.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Nguyen, B.D.; Popp, S.; Hundshagen, M.; Skoda, R.; Mansour, M.; Thévenin, D.; Hasse, C. Large Eddy Simulations of Turbulent Gas-Liquid Flows in a Diverging Horizontal Channel Using a Hybrid Multiphase Approach. ASME J. Fluids Eng. 2023, 145, 31501. [Google Scholar] [CrossRef]
- Blume, M.; Schwarz, P.; Rusche, H.; Weiß, L.; Wensing, M.; Skoda, R. 3D Simulation of Turbulent and Cavitating Flow for the Analysis of Primary Breakup Mechanisms in Realistic Diesel Injection Processes. Atomiz. Spr. 2019, 29, 861–893. [Google Scholar] [CrossRef]
- Ansys Inc. ANSYS CFX-Solver Theory Guide, Release 18.0; ANSYS, Inc.: Canonsburg, PA, USA, 2017. [Google Scholar]
- De Santis, A.; Hanson, B.C.; Fairweather, M. Hydrodynamics of annular centrifugal contactors: A CFD analysis using a novel multiphase flow modelling approach. Chem. Eng. Sci. 2021, 242, 116729. [Google Scholar] [CrossRef]
- Colombo, M.; de Santis, A.; Hanson, B.C.; Fairweather, M. Prediction of Horizontal Gas–Liquid Segregated Flow Regimes with an All Flow Regime Multifluid Model. Processes 2022, 10, 920. [Google Scholar] [CrossRef]
- Štrubelj, L.; Ťiselj, I. Two-fluid model with interface sharpening. Int. J. Numer. Meth. Eng. 2011, 85, 575–590. [Google Scholar] [CrossRef]
- Lo, S. Application of the MUSIG model to bubbly flows. In Proceedings of the AEAT-1096, AEA Technology, Carlsbad, CA, USA, June 1996. [Google Scholar]
- Krepper, E.; Frank, T.; Lucas, D.; Prasser, H.M.; Zwart, P. Inhomogeneous MUSIG model—A population balance approach for poly-dispersed bubbly flow. In Proceedings of the 6th International Conference on Multiphase Flow, Leipzig, Germany, 9–13 July 2007. [Google Scholar]
- Lehnigk, R.; Bainbridge, W.; Liao, Y.; Lucas, D.; Niemi, T.; Peltola, J.; Schlegel, F. An open–source population balance modeling framework for the simulation of polydisperse multiphase flows. AIChE J. 2022, 68, e17539. [Google Scholar] [CrossRef]
- Kumar, S.; Ramkrishna, D. On the solution of population balance equations by discretization—I. A fixed pivot technique. Chem. Eng. Sci. 1996, 51, 1311–1332. [Google Scholar] [CrossRef]
- Krepper, E.; Lucas, D.; Frank, T.; Prasser, H.M.; Zwart, P.J. The inhomogeneous MUSIG model for the simulation of polydispersed flows. Nucl. Eng. Des. 2008, 238, 1690–1702. [Google Scholar] [CrossRef]
- Prince, M.J.; Blanch, H.W. Bubble coalescence and break-up in air-sparged bubble columns. AIChE J. 1990, 36, 1485–1499. [Google Scholar] [CrossRef]
- Luo, H.; Svendsen, H.F. Theoretical model for drop and bubble breakup in turbulent dispersions. AIChE J. 1996, 42, 1225–1233. [Google Scholar] [CrossRef]
- Liao, Y.; Rzehak, R.; Lucas, D.; Krepper, E. Baseline closure model for dispersed bubbly flow: Bubble coalescence and breakup. Chem. Eng. Sci. 2015, 122, 336–349. [Google Scholar] [CrossRef]
- Rave, K.; Hermes, M.; Wirz, D.; Hundshagen, M.; Friebel, A.; von Harbou, E.; Bart, H.J.; Skoda, R. Experiments and fully transient coupled CFD-PBM 3D flow simulations of disperse liquid-liquid flow in a baffled stirred tank. Chem. Eng. Sci. 2022, 253, 117518. [Google Scholar] [CrossRef]
- Jasak, H. Error Analysis and Estimation for the Finite Volume Method with Applications to Fluid Flows. Ph.D. Thesis, Imperial College of Science, Technology and Medicine, London, UK, 1996. [Google Scholar]
- Patankar, S.; Spalding, D. A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows. Int. J. Heat Mass Transfer 1972, 15, 1787–1806. [Google Scholar] [CrossRef]
- Farrell, P.E.; Maddison, J.R. Conservative interpolation between volume meshes by local Galerkin projection. Comput. Methods Appl. Mech. Eng. 2011, 200, 89–100. [Google Scholar] [CrossRef]
- Černe, G.; Petelin, S.; Ťiselj, I. Coupling of the Interface Tracking and the Two-Fluid Models for the Simulation of Incompressible Two-Phase Flow. J. Comp. Phys. 2001, 171, 776–804. [Google Scholar] [CrossRef]
- Noroozi, M.M.; Maddahian, R.; Ramezani, M.H.; Ansari, M.R. An LES-Like Multiscale Multiphase Flow Model Based on Break-up and Coalescence Phenomena. J. Appl. Fluid Mech. 2022, 15, 1073–1085. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Hundshagen, M.; Skoda, R. State of the Art on Two-Phase Non-Miscible Liquid/Gas Flow Transport Analysis in Radial Centrifugal Pumps Part C: CFD Approaches with Emphasis on Improved Models. Int. J. Turbomach. Propuls. Power 2023, 8, 15. https://doi.org/10.3390/ijtpp8020015
Hundshagen M, Skoda R. State of the Art on Two-Phase Non-Miscible Liquid/Gas Flow Transport Analysis in Radial Centrifugal Pumps Part C: CFD Approaches with Emphasis on Improved Models. International Journal of Turbomachinery, Propulsion and Power. 2023; 8(2):15. https://doi.org/10.3390/ijtpp8020015
Chicago/Turabian StyleHundshagen, Markus, and Romuald Skoda. 2023. "State of the Art on Two-Phase Non-Miscible Liquid/Gas Flow Transport Analysis in Radial Centrifugal Pumps Part C: CFD Approaches with Emphasis on Improved Models" International Journal of Turbomachinery, Propulsion and Power 8, no. 2: 15. https://doi.org/10.3390/ijtpp8020015
APA StyleHundshagen, M., & Skoda, R. (2023). State of the Art on Two-Phase Non-Miscible Liquid/Gas Flow Transport Analysis in Radial Centrifugal Pumps Part C: CFD Approaches with Emphasis on Improved Models. International Journal of Turbomachinery, Propulsion and Power, 8(2), 15. https://doi.org/10.3390/ijtpp8020015