Forcing Pulsations by Means of a Siren for Gas Turbine Applications
Abstract
1. Introduction
2. Solutions for Flow Modulation, Noise Emissions, or both Simultaneously
2.1. Passive and Active Control
2.2. Active Control for Combustion in Continuous Flow Machines
2.3. The Siren
2.4. Evolution of a Pulsator of Siren Type
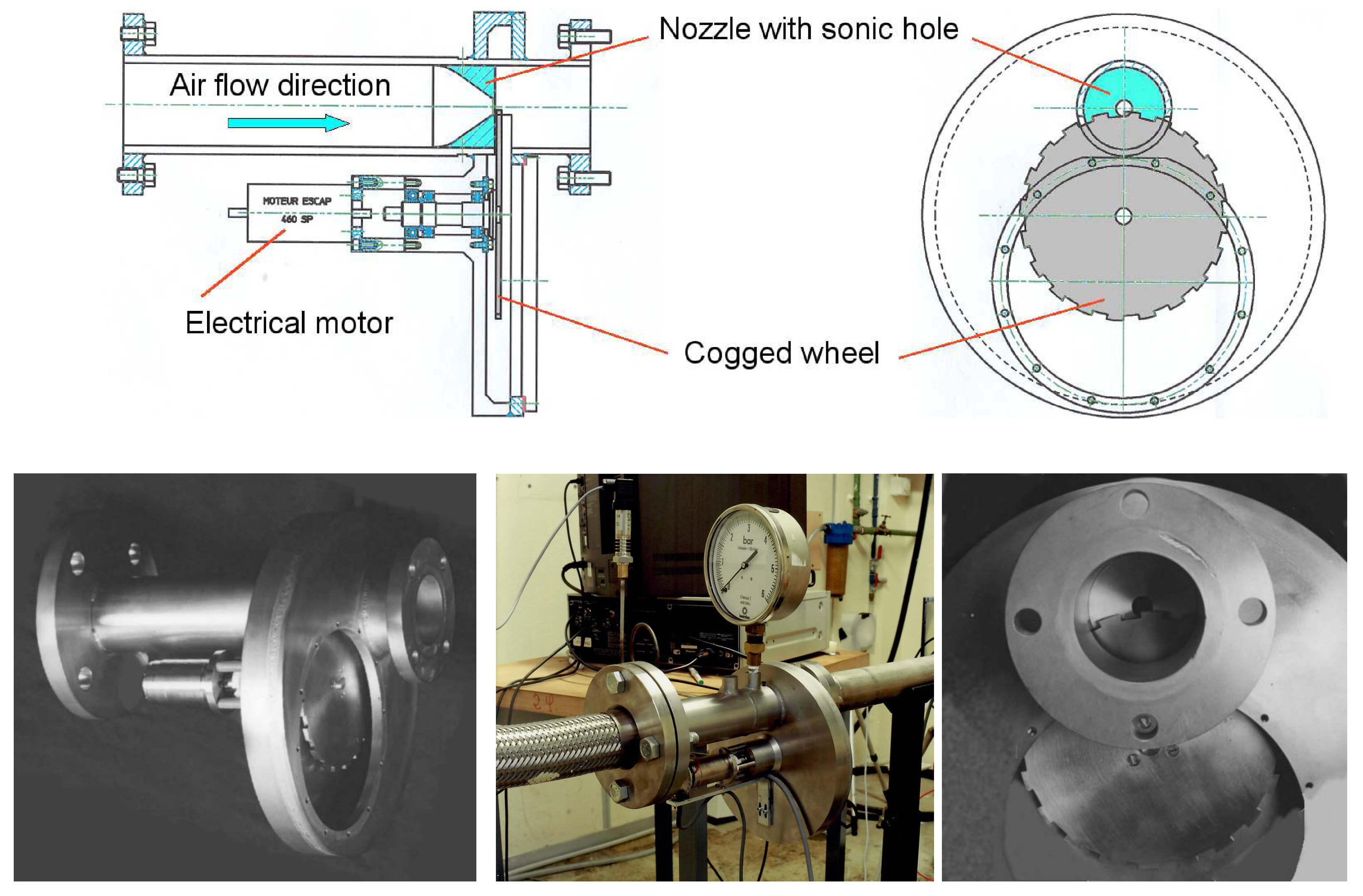
2.4.1. The ONERA Siren
2.4.2. TU Graz Siren
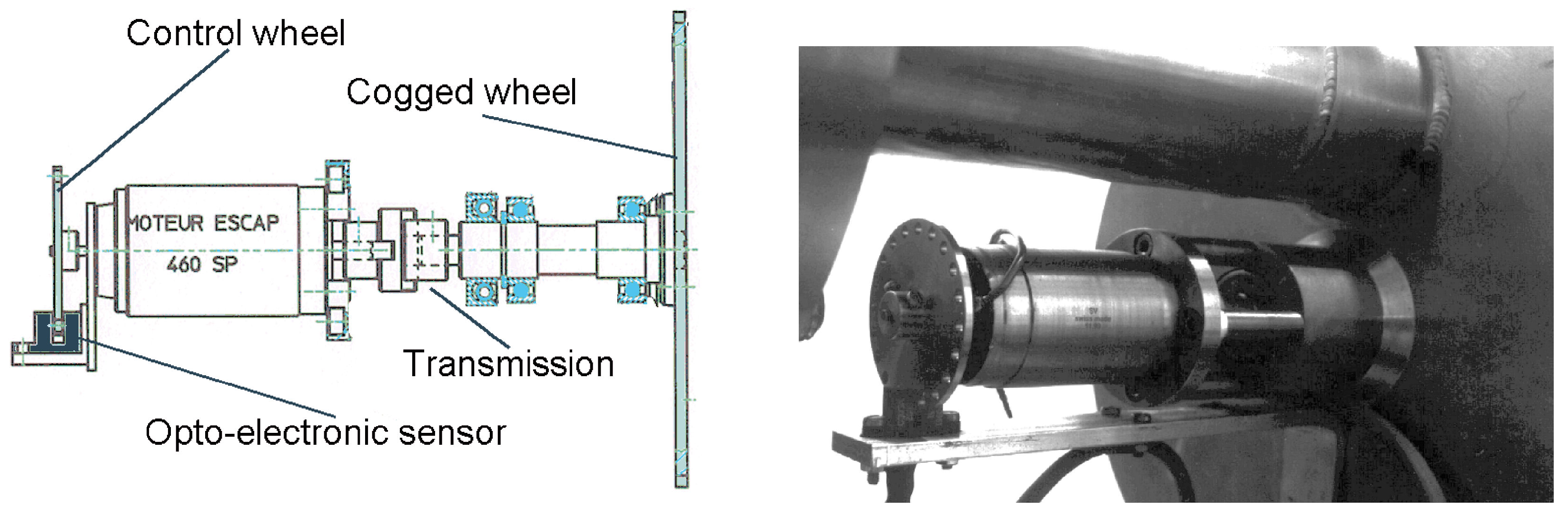
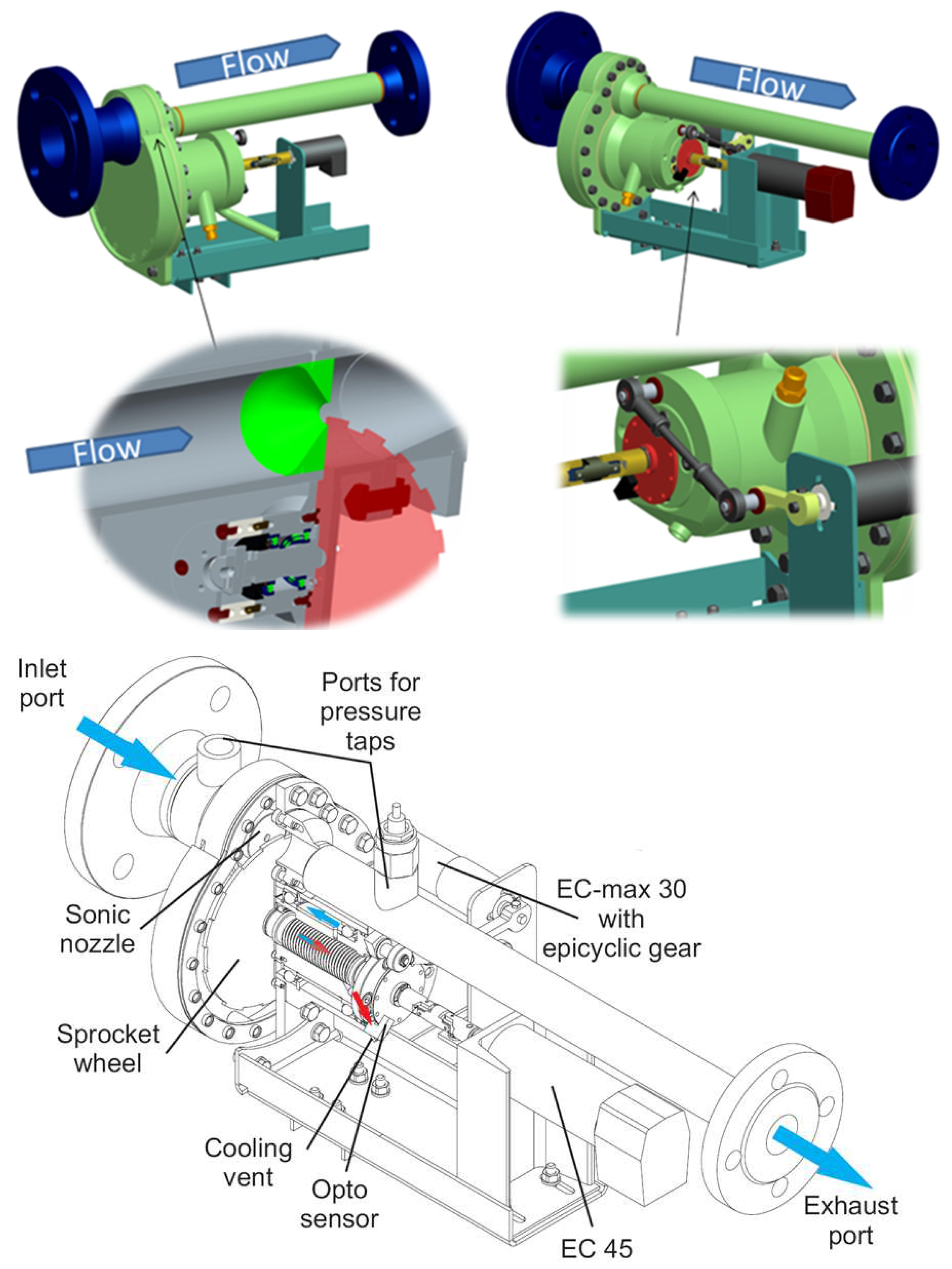
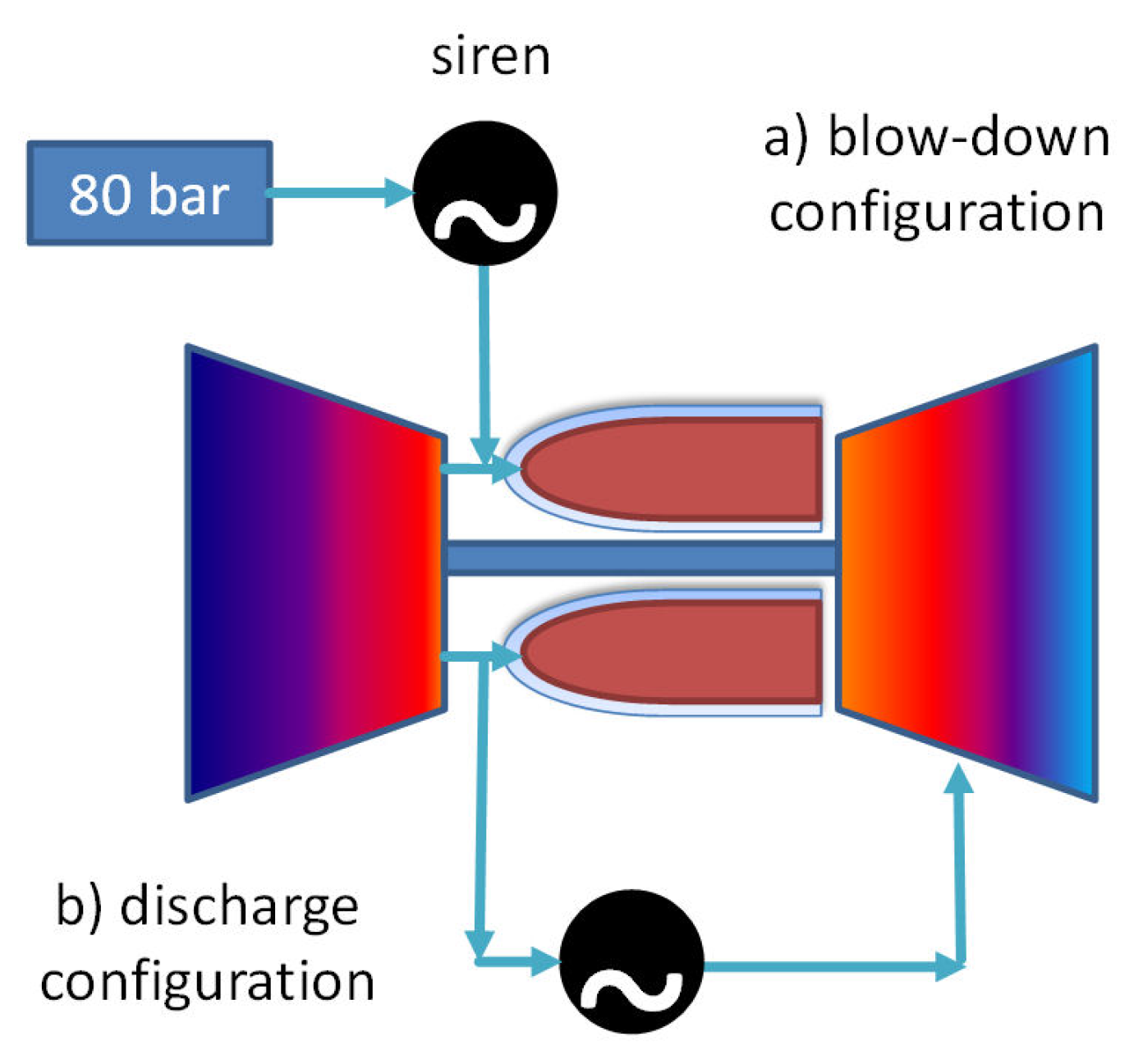
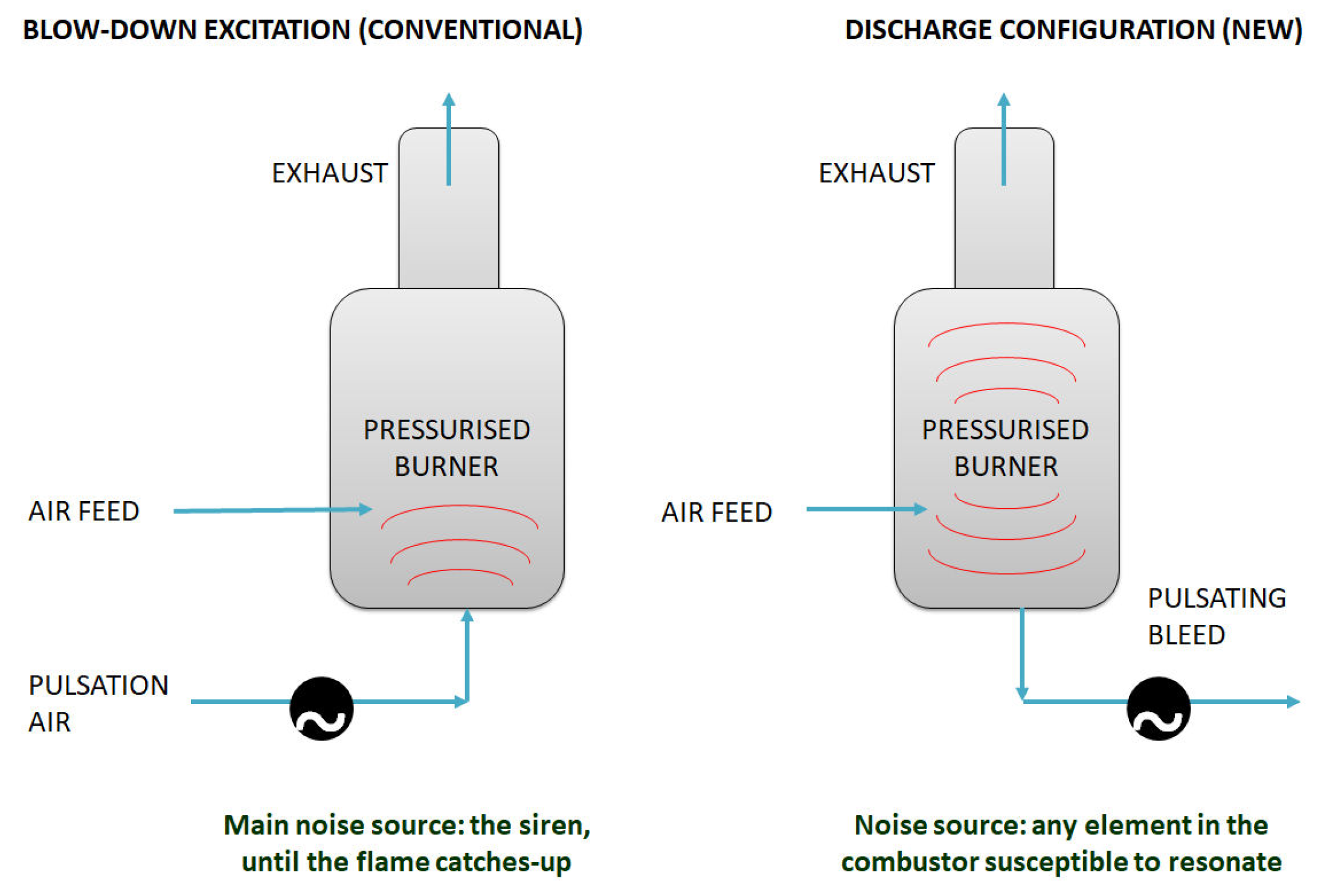
2.4.3. Combustion Bay One (CBOne)’s Siren
3. Elements of Design
3.1. Mass Flow
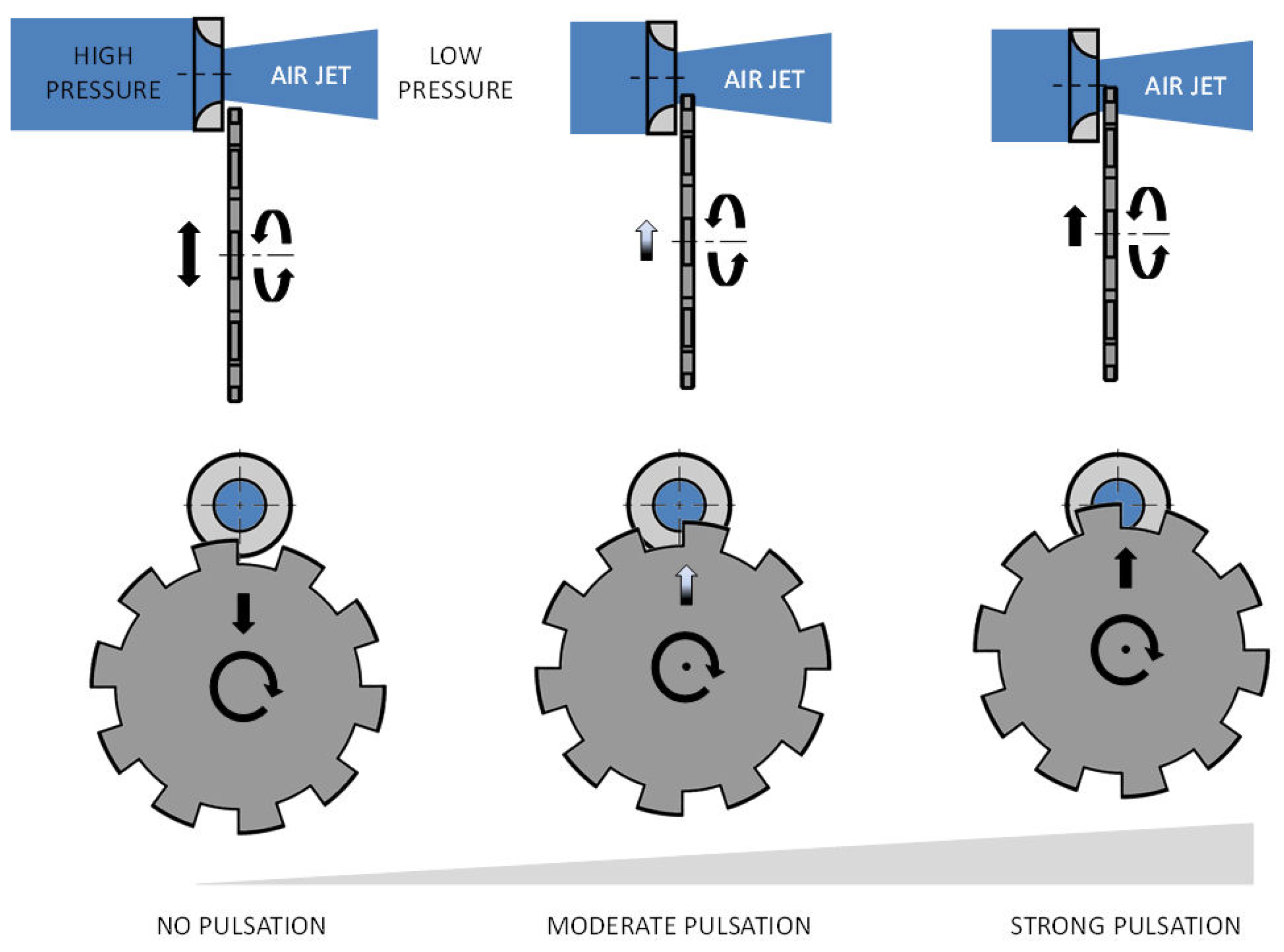
3.2. Technical Solution to Achieve Elevated Frequencies
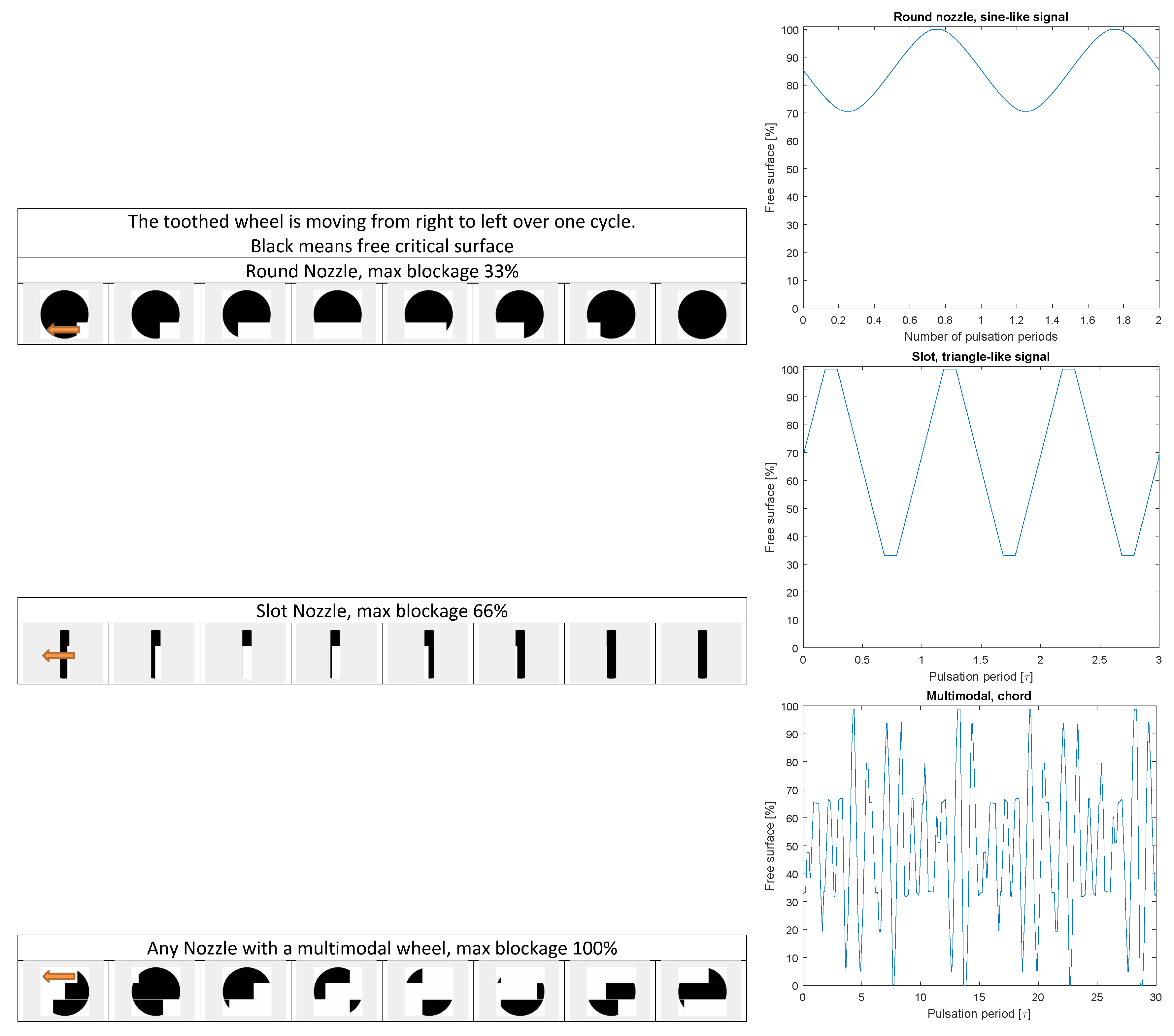
3.3. Multimodal Excitation
3.4. Nozzle Free Surface Calculation and Pulsed Flow Prediction Tools
3.5. Siren Performance
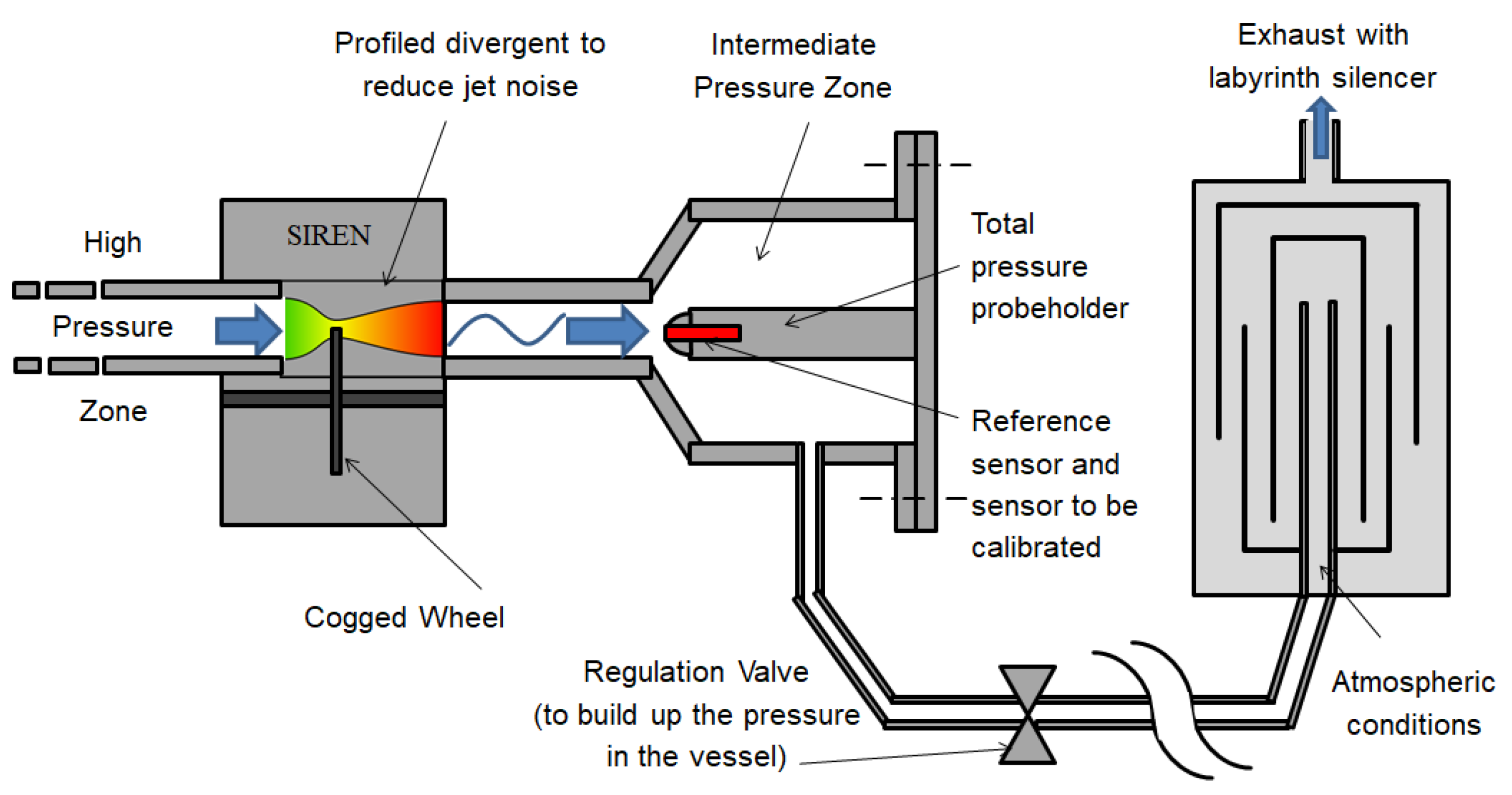
4. Calibration of Dynamic Sensors and Acoustic Characterisation of the Hot Core
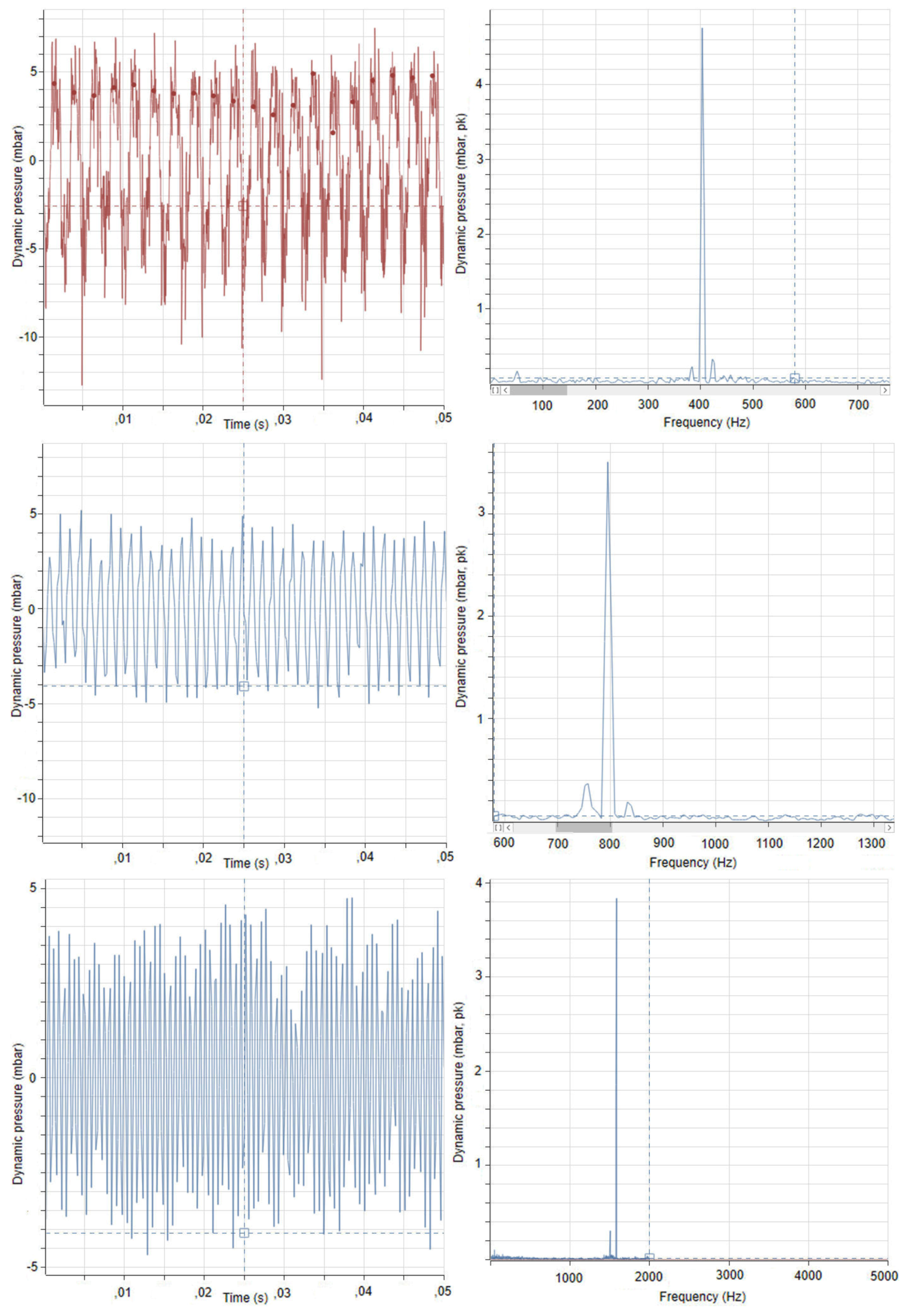
4.1. Calibration of Dynamic Sensors
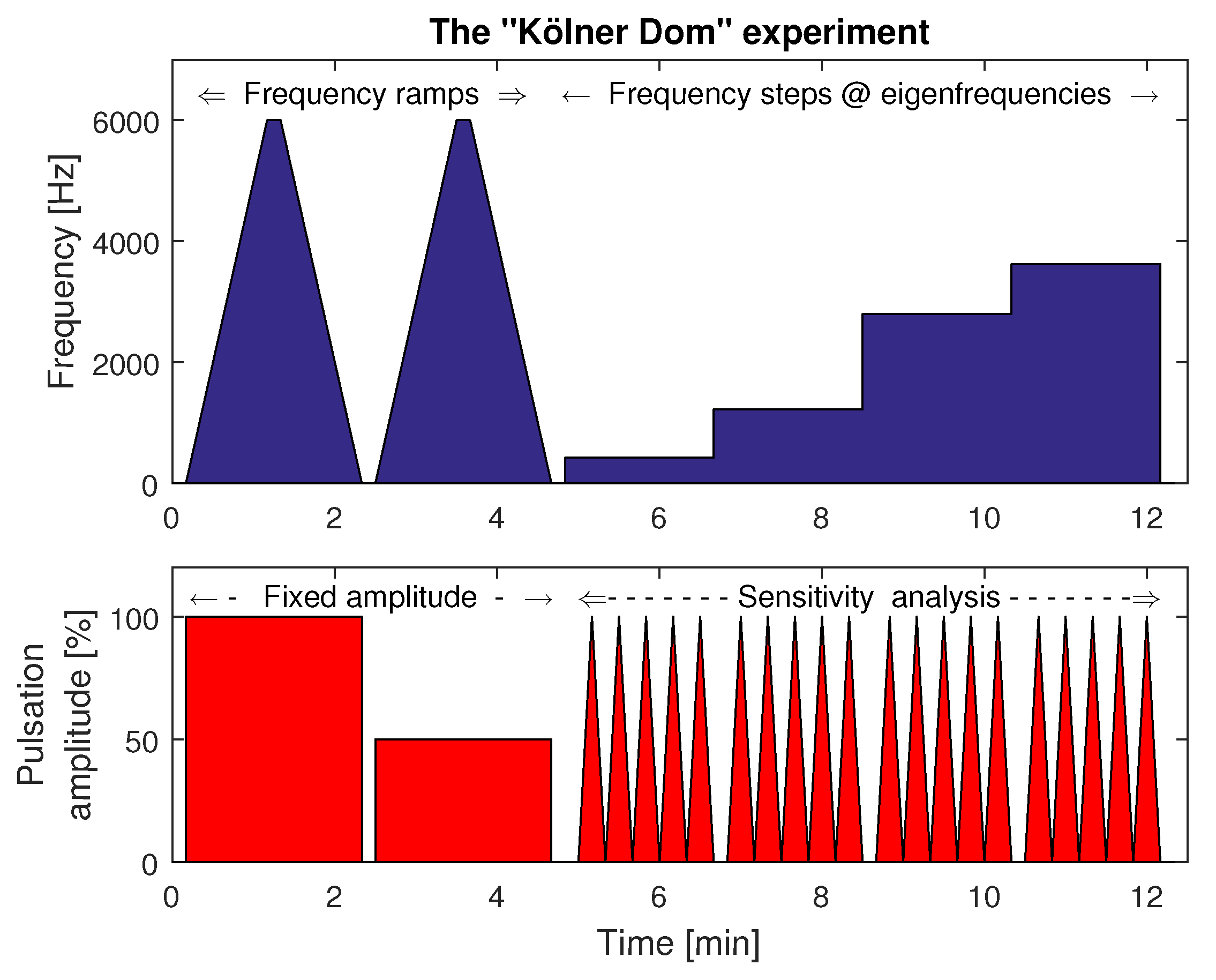
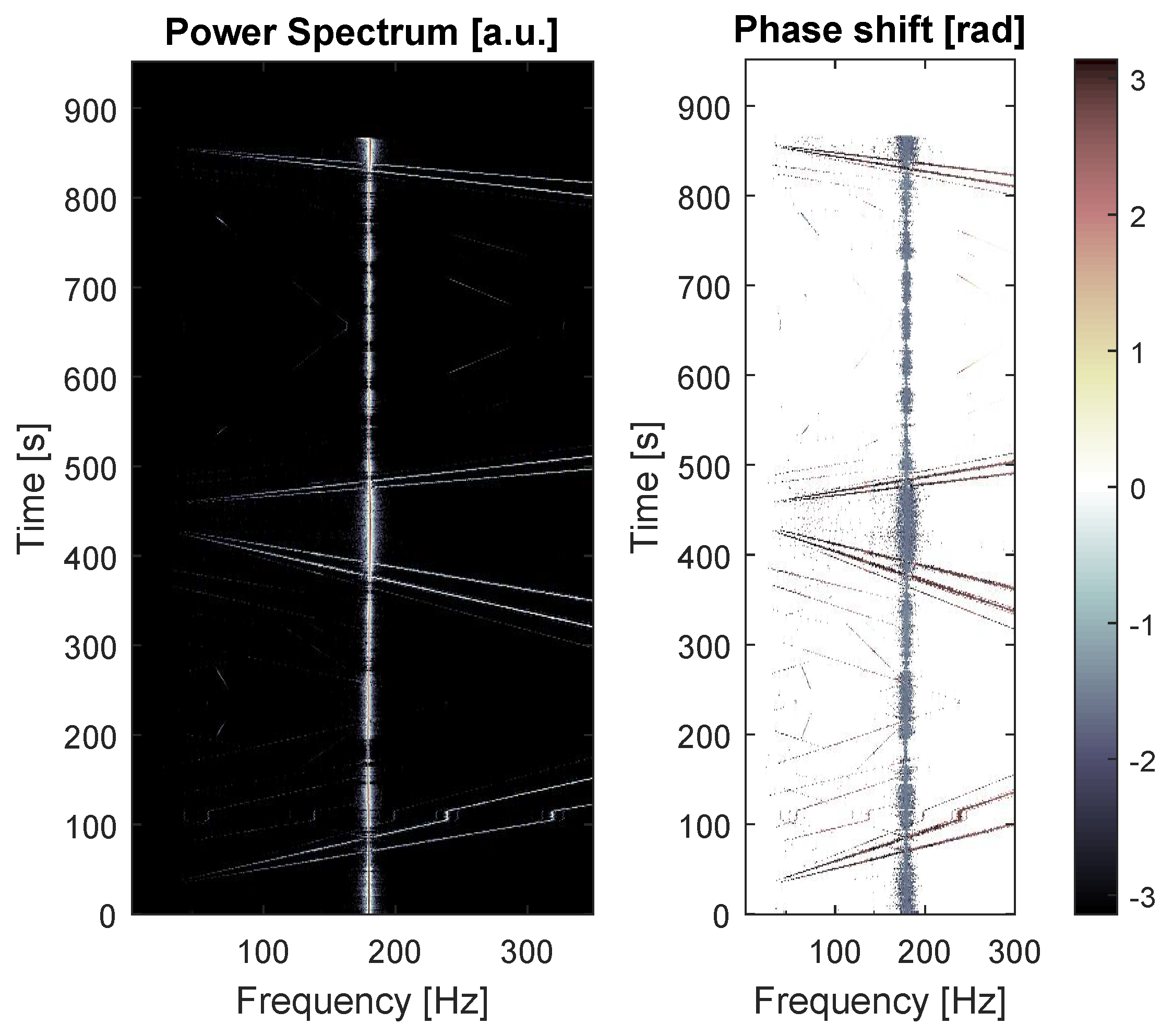
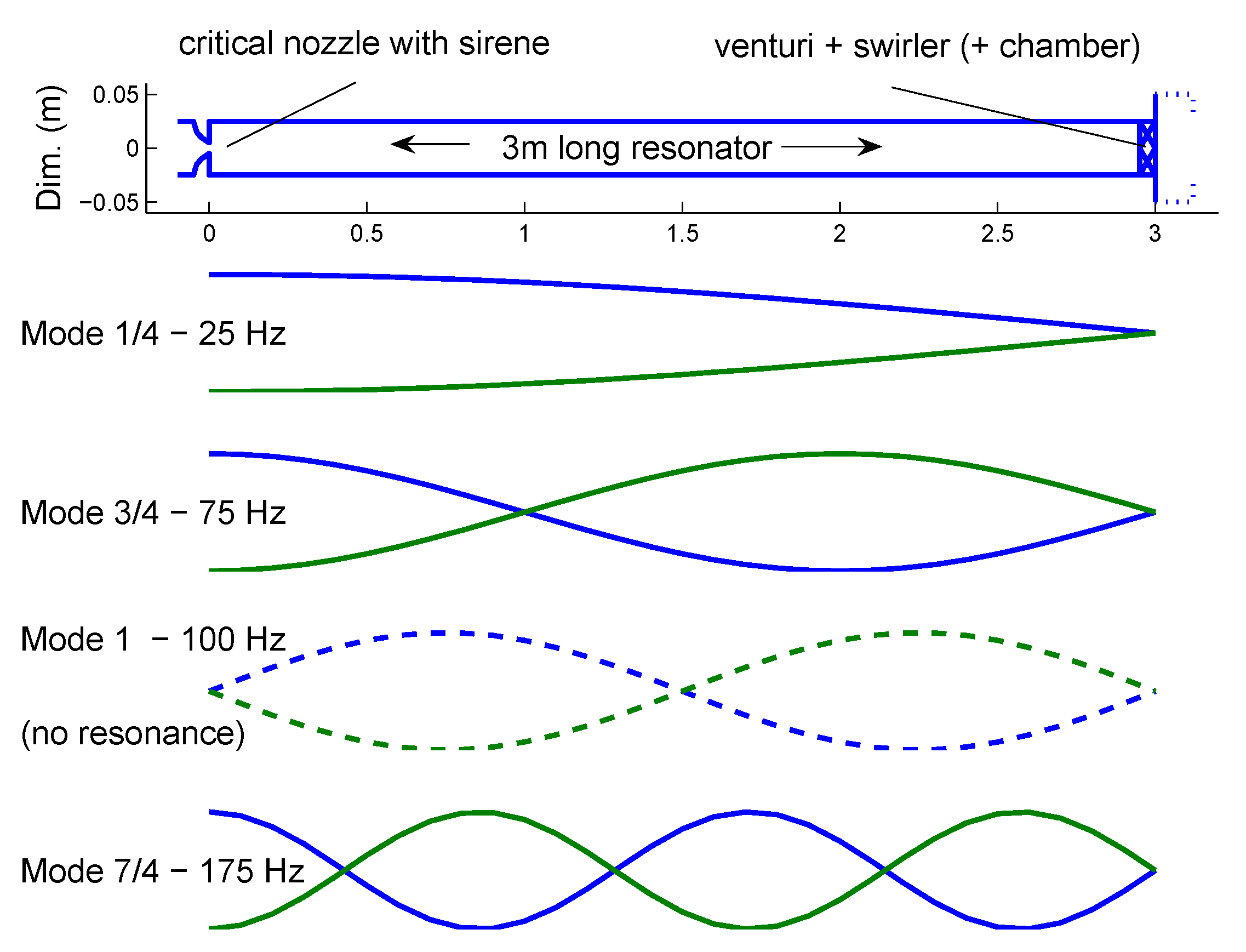
4.2. Determination of the Eigenfrequencies and Related Time Lags in the Combustor
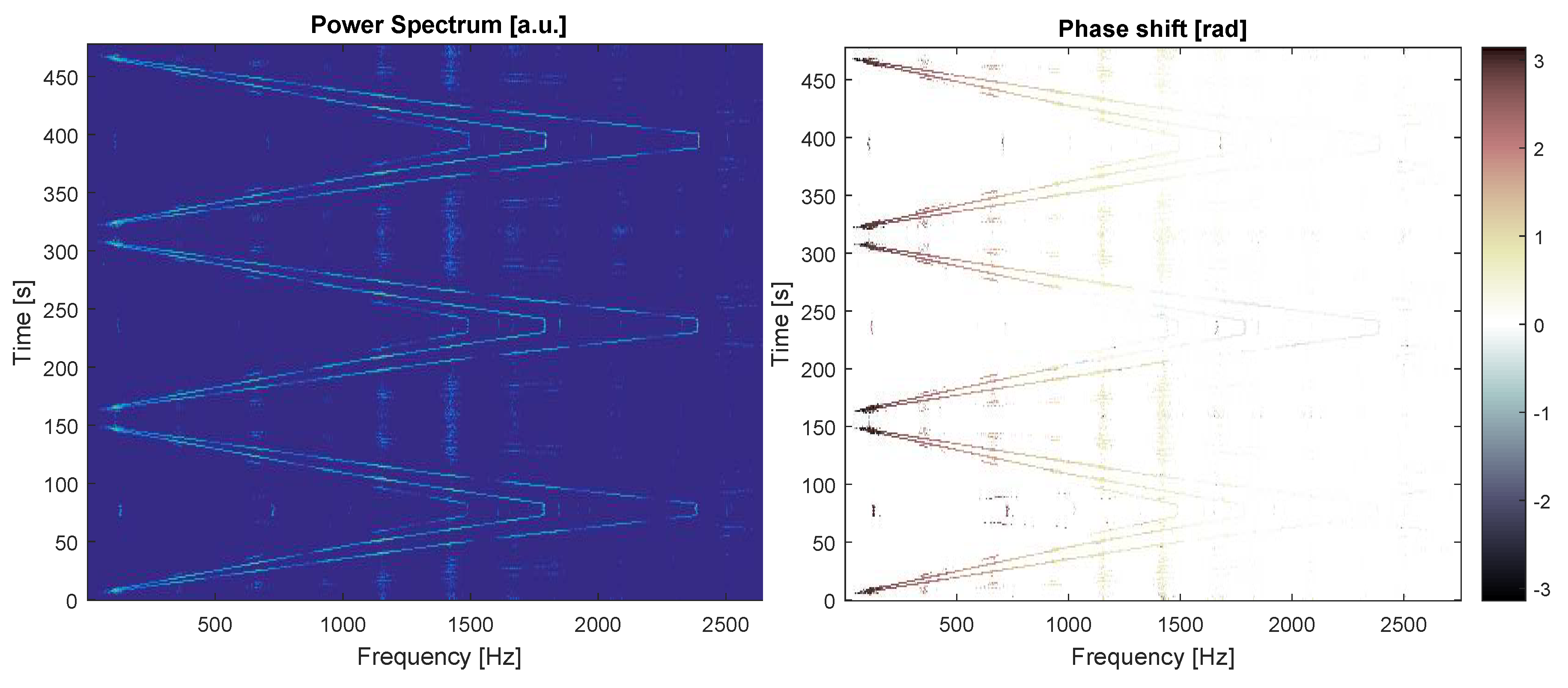
4.3. Modal Analysis: Measurement of the Phase Shifts or Time Lags in Relationship to Standing or Transported Waves
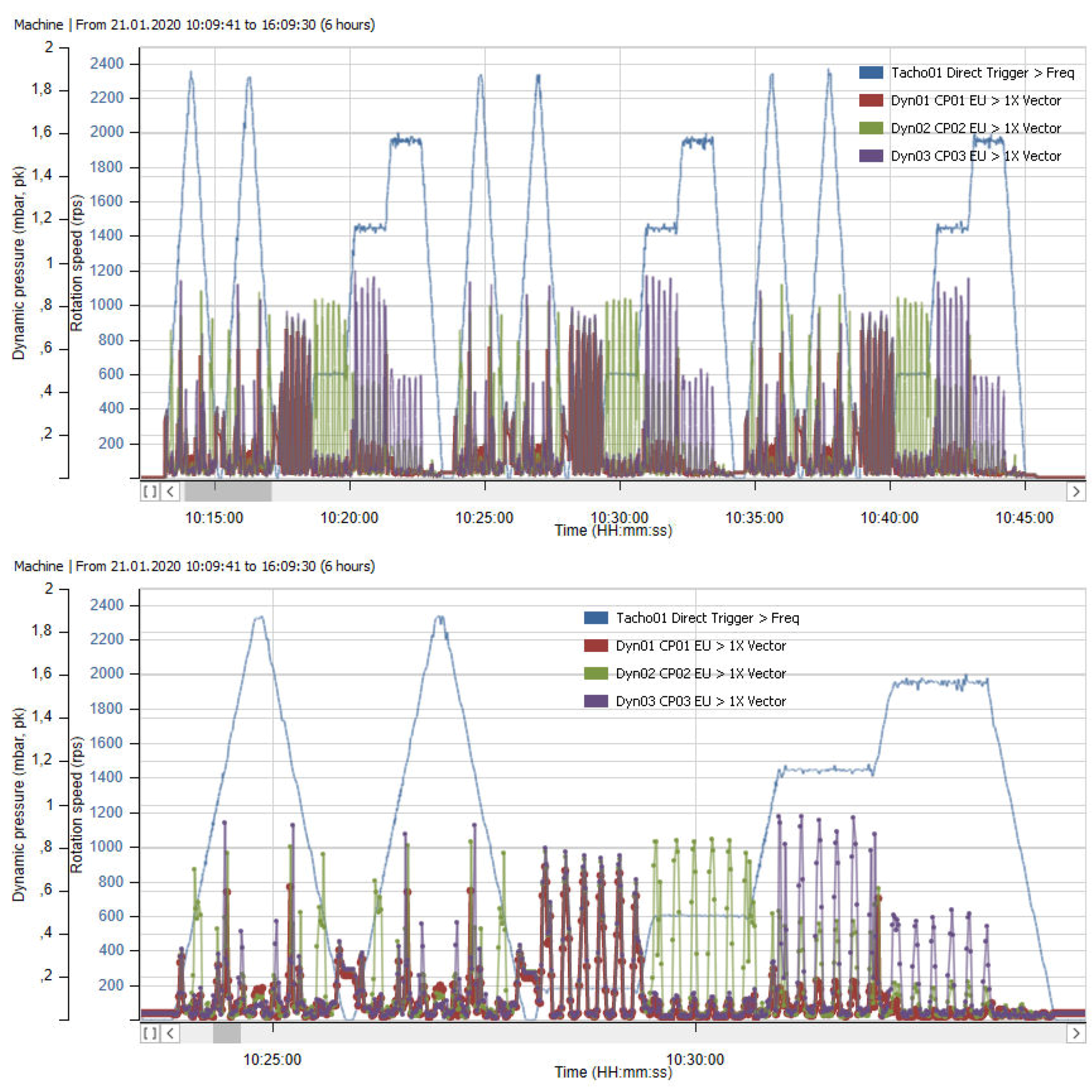
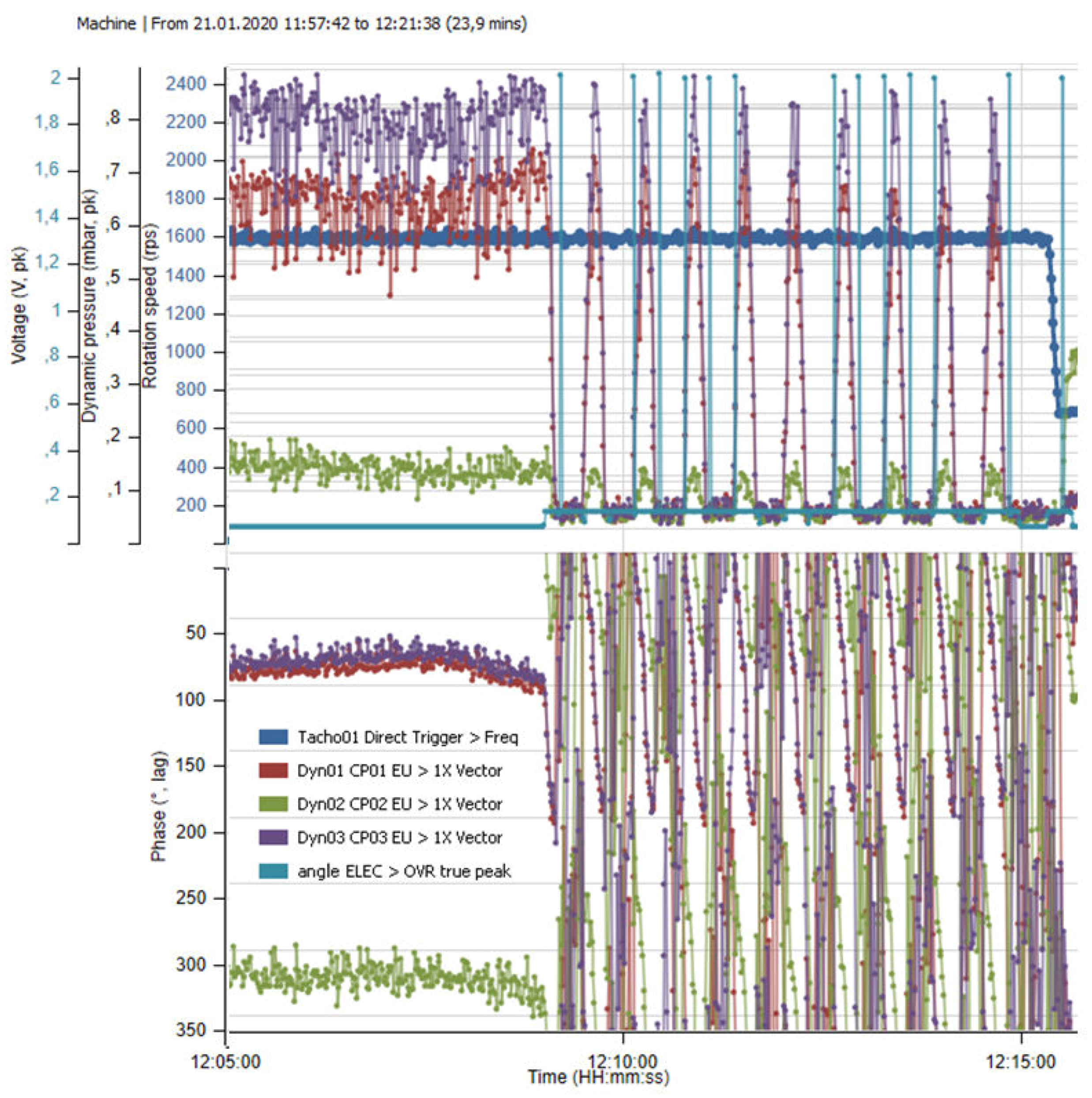
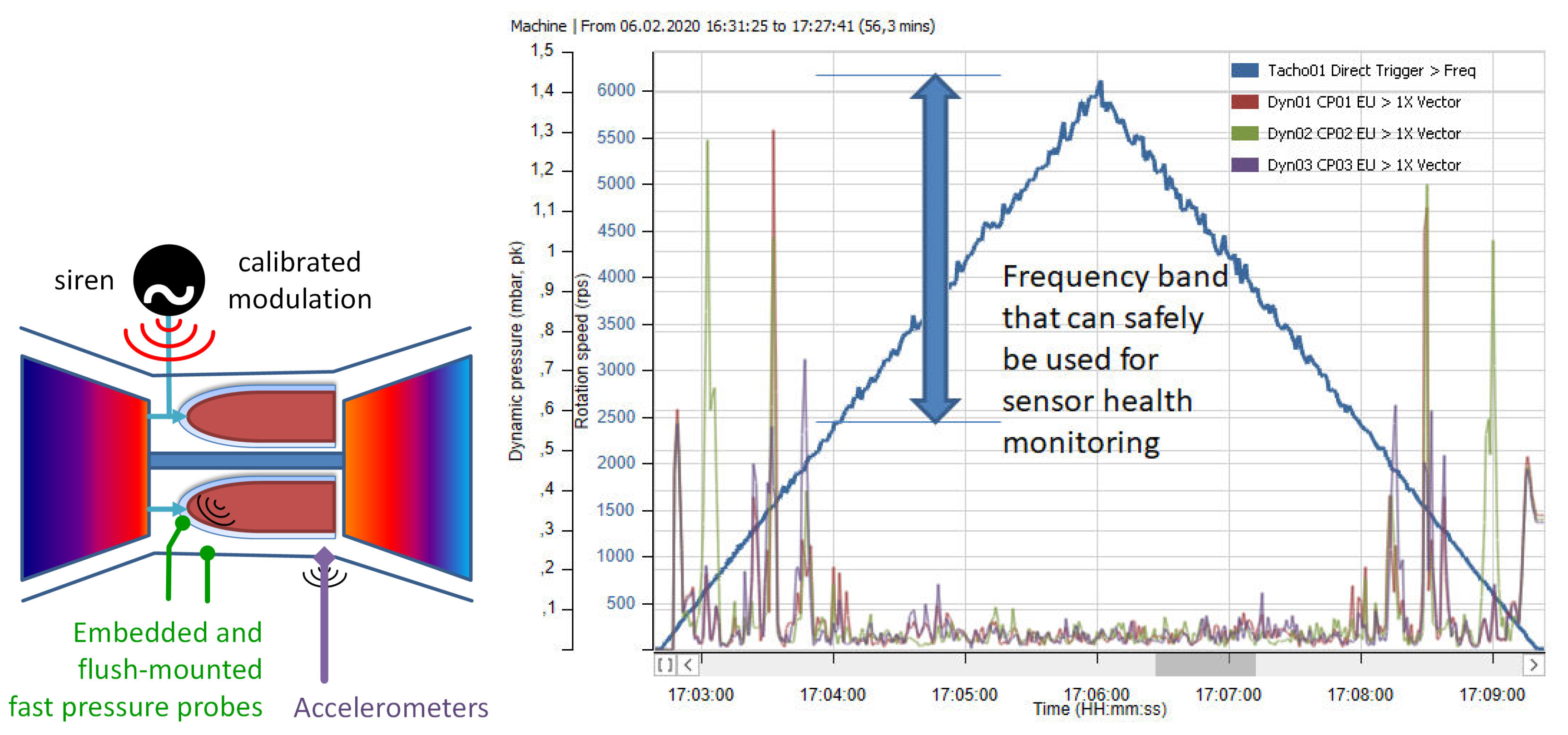
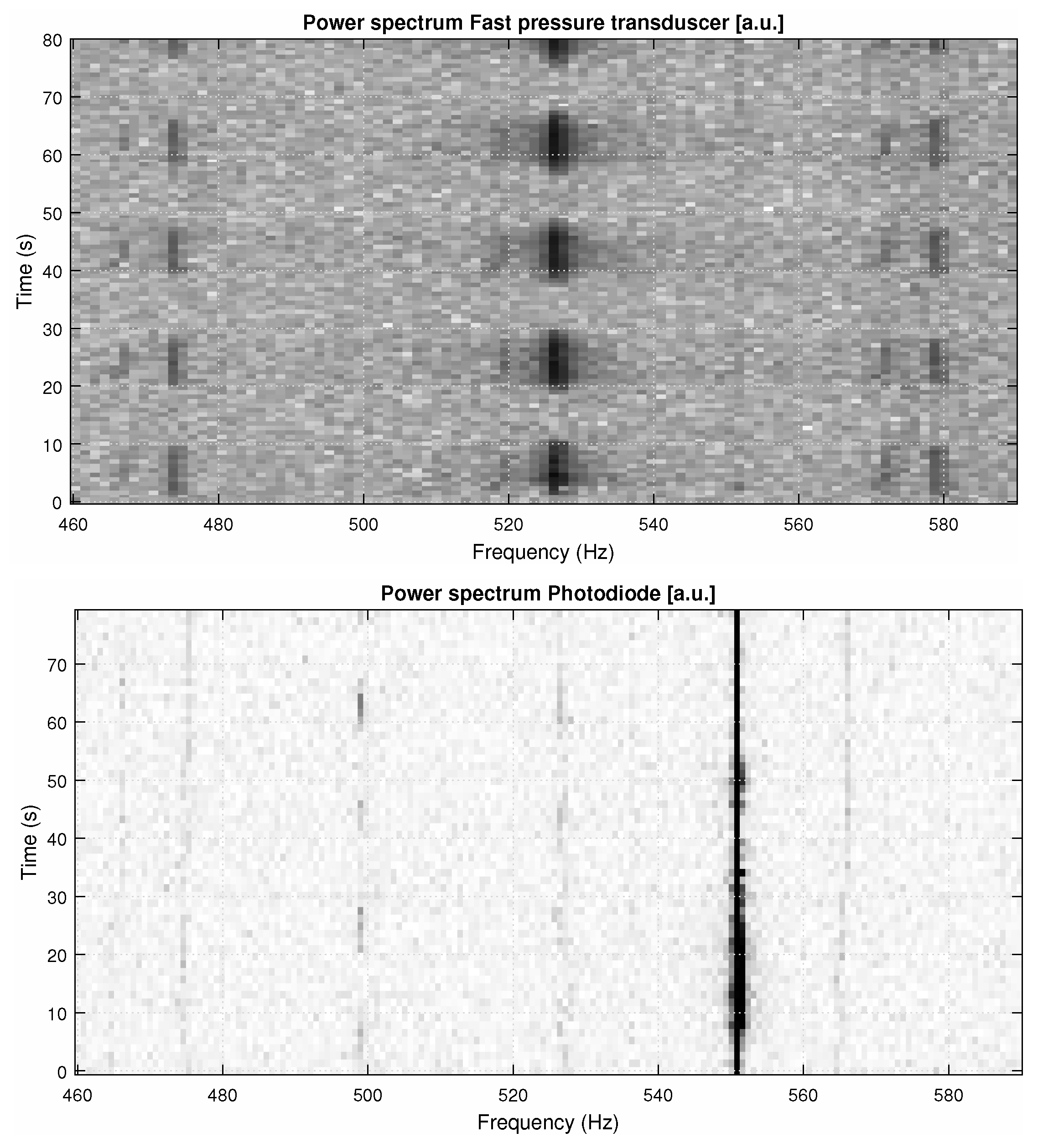
4.4. Health Diagnostic of Fast Pressure Sensors and Accelerometers during Operation
4.5. Modal Analysis Using the Multimodal Excitation
5. Combustor Flow Control and Flame Forcing
5.1. Effective Flow Control in the Combustor of a Gas Turbine: Possible Siren Placements
5.2. Analysis of a Pulse Jet
5.3. Modal Control of a Pulse Flame
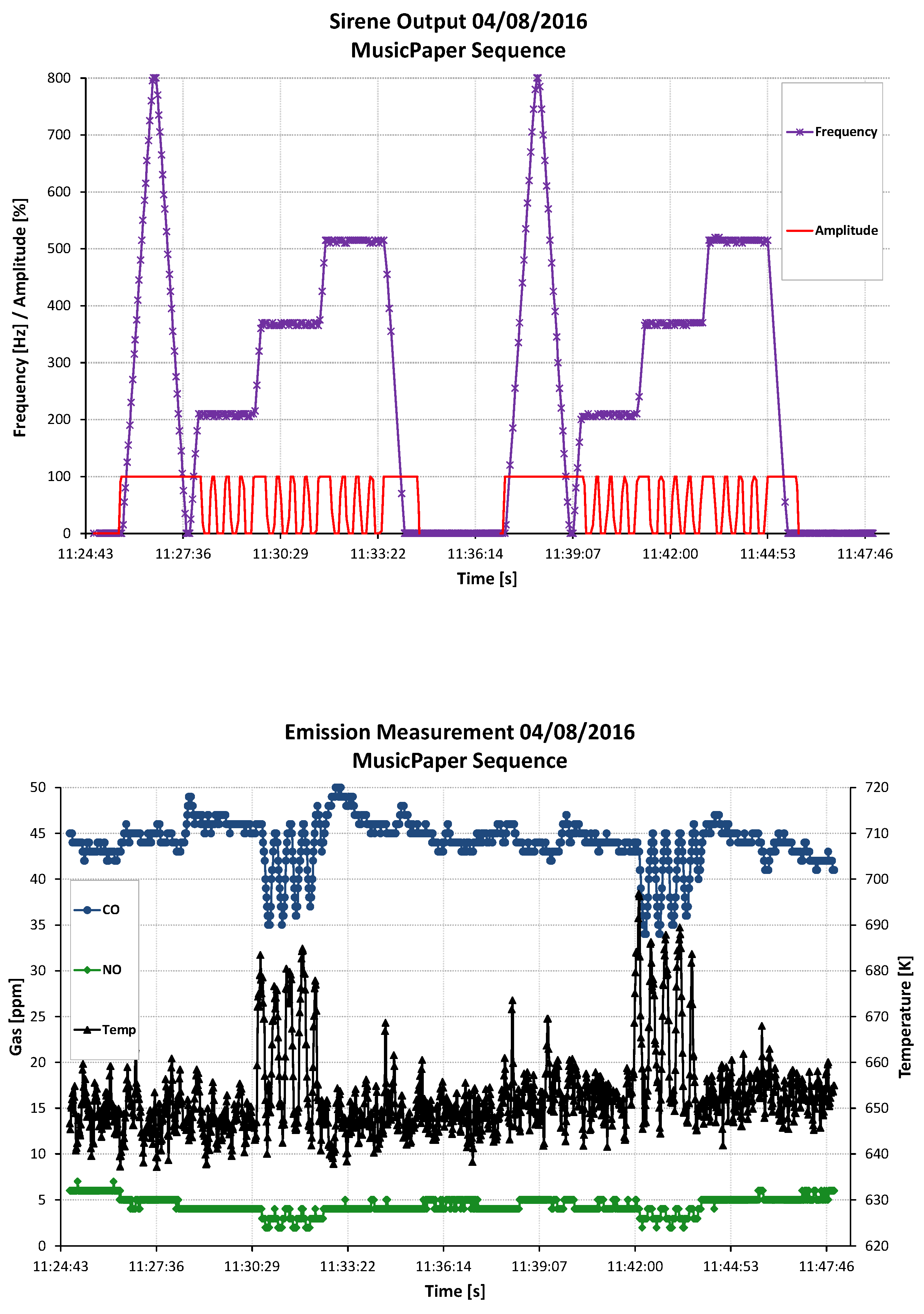
5.4. Improvement of the Combustion Performance Using Forcing
6. Future Developments: A More Powerful Siren
7. Conclusions
8. Patents
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CBOne | Combustion Bay One e.U. | |
| CBO4 | Name of the burner described in Reference [39] | |
| d | (mm) | Nozzle diameter (round) or reference diameter (slot) |
| DN | (mm) | Nominal pipe size (from diamètre nominal) according to standard ISO 6708 |
| emootion | Project acronym, stands for “engine health monitoring and refined combustion control based on optical diagnostic techniques embedded in the combustor” | |
| f | (Hz) | Frequency |
| (Hz) | Resonant frequency in an Helmholtz resonator | |
| LDA | Laser Doppler Anemometer | |
| (kg/s) | Air mass flow | |
| n | A given number, number of teeth | |
| r | (J/kg/K) | Air constant, r = 286 J/kg/K |
| OPR | Operating pressure ratio | |
| PIV | Particle image velocimetry | |
| (Pa,K) | Generating pressure and temperature upstream of the chocked nozzle | |
| S | (mm) | Area of the critical section |
| USP | Unique selling proposition | |
| x | Variable | |
| w | (m) | Width of the slot |
| (rad) | Angle deciding the opening of the nozzle’s slot | |
| (-) | Heat capacity ratio of air | |
| (rpm) | Spool rotating speed |
References
- Hirschberg, A.; Rienstra, S. Elements of Aero-Acoustics; Applied Aero-Acoustics, LS 1994-04; Von Karman Institute for Fluid Dynamics: Brussels, Belgium, 1994. [Google Scholar]
- Culick, F. Dynamics of Combustion Systems, Fundamentals, Acoustics and Control; Active Control of Engine Dynamics; RTO AVT-VKI Special Course: Brussels, Belgium, 2001. [Google Scholar]
- Hermann, J. Application of Active Instability Control to Heavy Duty Gas Turbines; Active Control of Engine Dynamics, RTO-EN-020; RTO AVT-VKI Special Course: Brussels, Belgium, 2001; pp. 287–302. [Google Scholar]
- Kokanovic, S.; Guidati, G.; Torchalla, S.; Schuermans, B. Active Combustion Control System for Reduction of NOx and Pulsation Levels in Gas Turbines. In Proceedings of the ASME Turbo Expo: Power for Land, Sea, and Air, Barcelona, Spain, 8–11 May 2006; Volume 1, pp. 673–682. Available online: https://asmedigitalcollection.asme.org/GT/proceedings-pdf/GT2006/42363/673/4564907/673_1.pdf (accessed on 12 May 2020).
- Lieuwen, T.C.; Yang, V. Gas Turbine Emissions; Cambridge Aerospace Series; Cambridge University Press: Cambridge, MA, USA, 2013; Volume 38. [Google Scholar]
- Apeloig, J.M.; d”Herbigny, F.X.; Simon, F.; Gajan, P.; Orain, M.; Roux, S. Liquid-Fuel Behavior in an Aeronautical Injector Submitted to Thermoacoustic Instabilities. J. Propuls. Power 2015, 31, 309–319. [Google Scholar] [CrossRef]
- Renaud, A.; Ducruix, S.; Zimmer, L. Bistable behaviour and thermo-acoustic instability triggering in a gas turbine model combustor. Proc. Combust. Inst. 2016. [Google Scholar] [CrossRef]
- Yu, K.; Wilson, K. Scale-Up Experiments on Liquid-Fueled Active Combustion Control. J. Propuls. Power 2002, 18, 53–60. [Google Scholar] [CrossRef]
- Dowling, A.P.; Stow, S.R. Acoustic analysis of gas turbine combustors. J. Propuls. Power 2003, 19, 751–764. [Google Scholar] [CrossRef]
- Zinn, B. Pulse combustion applications: Past, Present and Future. In Unsteady Combustion; Kluwer Academic Publishers: Berlin, Germany, 1996; pp. 113–137. [Google Scholar]
- Putnam, A.; Belles, F.; Kentfield, J. Pulse combustion. Prog. Energy Combust. Sci. 1986, 12, 43–79. [Google Scholar] [CrossRef]
- Boudy, F.; Durox, D.; Schuller, T.; Jomaas, G.; Candel, S. Describing Function Analysis of Limit Cycles in a Multiple Flame Combustor. J. Eng. Gas Turbines Power 2011, 133, 061502. [Google Scholar] [CrossRef]
- Der Reichsminister der Luftfahrt und Oberbefehlshaber der Luftwaffe, Vorwald. FZG 76, Gerätehandbuch, Detailierte Konstruktions-, Wartungs- und Serviceanleitung. Teil 3: Triebwerk; Fieseler Fi-103. D. (Luft) T.2076, g. Kdos.: Flensburg, Germany, 1944. [Google Scholar]
- Reynst, F.H. Pulsating Combustion: The Collected Works of FH Reynst; Pergamon Press: Oxford, UK, 1961. [Google Scholar]
- Meng, X.; de Jong, W.; Kudra, T. A state-of-the-art review of pulse combustion: Principles, modeling, applications and R&D issues. Renew. Sustain. Energy Rev. 2016, 55, 73–114. [Google Scholar] [CrossRef]
- Dowling, A.; Morgans, A. Feedback control of combustion oscillations. Annu. Rev. Fluid Mech. 2005, 37, 151–182. [Google Scholar] [CrossRef]
- Leitgeb, T.; Schuller, T.; Durox, D.; Giuliani, F.; Koeberl, S.; Woisetschlaeger, J. Interferometric determination of heat release rate in a pulsated flame. Combust. Flame 2013, 160, 589–600. [Google Scholar] [CrossRef]
- Lückoff, F.; Sieber, M.; Paschereit, C.O.; Oberleithner, K. Phase-Opposition Control of the Precessing Vortex Core in Turbulent Swirl Flames for Investigation of Mixing and Flame Stability. J. Eng. Gas Turbines Power 2019, 141, 111008. [Google Scholar] [CrossRef]
- Giuliani, F.; Gajan, P.; Diers, O.; Ledoux, M. Influence of pulsed entries on a spray generated by an air-blast injection device-An experimental analysis on combustion instability processes in aeroengines. Proc. Combust. Inst. 2002, 29, 91–98. [Google Scholar] [CrossRef]
- Choudhury, P.; Gerstein, M.; Mojardy, R. A novel feedback concept for combustion instabilities in ramjet. In Proceedings of the 22rd JANNAF Combustion Meeting, Johns Hopkins Univ, Baltimore, MD, USA, 7–10 October 1985. [Google Scholar]
- Parikh, P.G.; Moffat, R.J. Resonant entrainment of a confined pulsed jet. J. Fulid Eng. 1982, 104, 482–488. [Google Scholar] [CrossRef]
- Yu, K.; Wilson, K.; Parr, T.; Smith, R.; Schadow, K. Characterization of pulsating spray droplets and their interaction with vortical structures. In Proceedings of the 34th Aerospace Sciences Meeting and Exhibit, AIAA 96-0083, Reno, NV, USA, 15–18 January 1996. [Google Scholar]
- Burnel, S.; Thomas, J. Influence de la forme d’entrée sur un écoulement pulsé en canalisation cylindrique. J. Mécanique Appliquée 1978, 2, 399–417. [Google Scholar]
- Cheung, W.; Sims, G.; Copplestone, R.; Tilston, J.; Wilson, C.; Stow, S.R.; Dowling, A.P. Measurement and analysis of flame transfer function in a sector combustor under high pressure conditions. In Proceedings of the ASME Turbo Expo 2003, Collocated with the 2003 International Joint Power Generation Conference. American Society of Mechanical Engineers, GT2003-38219, Atlanta, GA, USA, 16–19 June 2003; pp. 187–194. [Google Scholar]
- Eckstein, J.; Freitag, E.; Hirsch, C.; Sattelmayer, T.; von der Bank, R.; Schilling, T. Forced Low-Frequency Spray Characteristics of a Generic Airblast Swirl Diffusion Burner. J. Eng. Gas Turbines Power 2005, 127, 301–306. [Google Scholar] [CrossRef]
- Giuliani, F.; Lang, A.; Gradl, K.J.; Siebenhofer, P.; Fritzer, J. Air flow modulation for refined control of the combustion dynamics using a novel actuator. J. Eng. Gas Turbine Power 2012. [Google Scholar] [CrossRef]
- Gajan, P.; Strzelecki, A.; Platet, B.; Lecourt, R.; Giuliani, F. Experimental Investigation of Spray Behavior Downstream of an Aeroengine Injector with Acoustic Excitation. J. Propuls. Power 2007, 23, 390–397. [Google Scholar] [CrossRef]
- Giuliani, F.; Wagner, B.; Woisetschläger, J.; Heitmeir, F. Laser Vibrometry for Real-Time Combustion Stability Diagnostic. In Proceedings of the ASME Turbo Expo 2006: Power for Land, Sea and Air, GT2006-90413, Barcelona, Spain, 8–11 May 2006. [Google Scholar]
- Lang, A.; Leitgeb, T.; Woisetschläger, J.; Strzelecki, A.; Gajan, P.; Giuliani, F. Analysis of a pulsed flame at intermediate pressure. In Proceedings of the ISFV13-13th International Symposium on Flow Visualization/FLUVISU12-12th French Congress on Visualization in Fluid Mechanics, Nice, France, 1–4 July 2008. [Google Scholar]
- Giuliani, F.; Leitgeb, T.; Lang, A.; Woisetschlaeger, J. Mapping the density fluctuations in a pulsed air-methane flame using laser-vibrometry. J. Eng. Gas Turbines Power 2010, 132. [Google Scholar] [CrossRef]
- Renaud, A.; Ducruix, S.; Scouflaire, P.; Zimmer, L. Experimental study of the interactions between air flow rate modulations and PVC in a swirl-stabilised liquid fuel burner. In Proceedings of the ASME Turbo Expo, GT2015-42775, Montreal, QC, Canada, 15–19 June 2015. [Google Scholar]
- Renaud, A.; Ducruix, S.; Zimmer, L. Experimental Study of the Precessing Vortex Core Impact on the Liquid Fuel Spray in a Gas Turbine Model Combustor. J. Eng. Gas Turbines Power 2019, 141. [Google Scholar] [CrossRef]
- Ghirardo, G.; Juniper, M.P. Azimuthal instabilities in annular combustors: Standing and spinning modes. Proc. R. Soc. A: Math. Phys. Eng. Sci. 2013, 469. [Google Scholar] [CrossRef]
- Giuliani, F.; Paulitsch, N.; Cozzi, D.; Görtler, M.; Andracher, L. An assessment on the benefits of additive manufacturing regarding new swirler geometries for gas turbine burners. In Proceedings of the ASME Turbo Expo 2018: Turbomachinery Technical Conference and Exposition. American Society of Mechanical Engineers, GT2018-75165, Oslo, Norway, 11–15 June 2018. [Google Scholar]
- Lang, A. Unsteady Combustion Phenomena in Current and Future Aero Engines. Ph.D. Thesis, TU Graz, Graz, Austria, 2011. [Google Scholar]
- Giuliani, F.; Pfefferkorn, L.; Kraft, G.E. Improvement of impaired combustion conditions at some off-design operation by driving a precisely controlled modulation of the burner air feed. In Proceedings of the ASME Turbo Expo, GT2017-64429, Charlotte, CA, USA, 26–30 June 2017. [Google Scholar]
- Giuliani, F.; Reiss, H.; Stuetz, M.; Moosbrugger, V.; Silbergasser, A. Readings on specific gas turbine flame behaviours using an industrial combustion monitoring system. In Proceedings of the ASME Turbo Expo, GT2016-56166, Seoul, Korea, 13–17 June 2016. [Google Scholar]
- Andracher, L.; Giuliani, F.; Paulitsch, N.; Moosbrugger, V. Progress on Combined Optic-Acoustic Monitoring of Combustion in a Gas Turbine. In Proceedings of the ASME Turbo Expo 2020, Turbomachinery Technical Conference & Exposition, GT2020-16007, London, UK, 22 June 2020. [Google Scholar]
- Moosbrugger, V.; Giuliani, F.; Paulitsch, N.; Andracher, L. Progress in burner design using additive manufacturing with a monolithic approach and added features. In Proceedings of the Turbomachinery Technical Conference & Exposition, ASME Turbo Expo 2019, GT2019-90720, Phoenix, AZ, USA, 17–21 June 2019. [Google Scholar]
- Giuliani, F.; Andracher, L.; Moosbrugger, V.; Paulitsch, N.; Hofer, A. Combined Optic-Acoustic Monitoring of Combustion in a Gas Turbine. Int. J. Turbomach. Propulsion Power 2020. Submitted, under revision. [Google Scholar]
- Seybert, A.; Ross, D. Experimental determination of acoustic properties using a two-microphone random-excitation technique. J. Acoust. Soc. Am. 1977, 61, 1362–1370. [Google Scholar] [CrossRef]
- Padois, T.; Berry, A.; Gauthier, P.A.; Joshi, N. Beamforming matrix regularization and inverse problem for sound source localization: Application to aero-engine noise. In Proceedings of the 19th AIAA/CEAS Aeroacoustics Conference, Berlin, Germany, 27–29 May 2013; p. 2212. [Google Scholar]
- Giuliani, F.; Moosbrugger, V.; Stuetz, M.; Leitgeb-Simandl, T. Optimisation of support fuel consumption burning low heat value gas using controlled combustion oscillations. In Proceedings of the ASME Turbo Expo, GT2015-42377, Montreal, QC, Canada, 15–19 June 2015. [Google Scholar]
- Kraft, G.E.; Giuliani, F.; Pfefferkorn, L.; Paulitsch, N.; Andracher, L. Heat resistant probe combining optic and acoustic sensors for advanced combustion monitoring including detection of flame instabilities. In Proceedings of the ASME Turbo Expo, GT2017-63626, Charlotte, CA, USA, 26–30 June 2017. [Google Scholar]
- Jeong, J.; Hussain, F. On the identification of a vortex. J. Fluid Mech. 1995, 285, 69–94. [Google Scholar] [CrossRef]


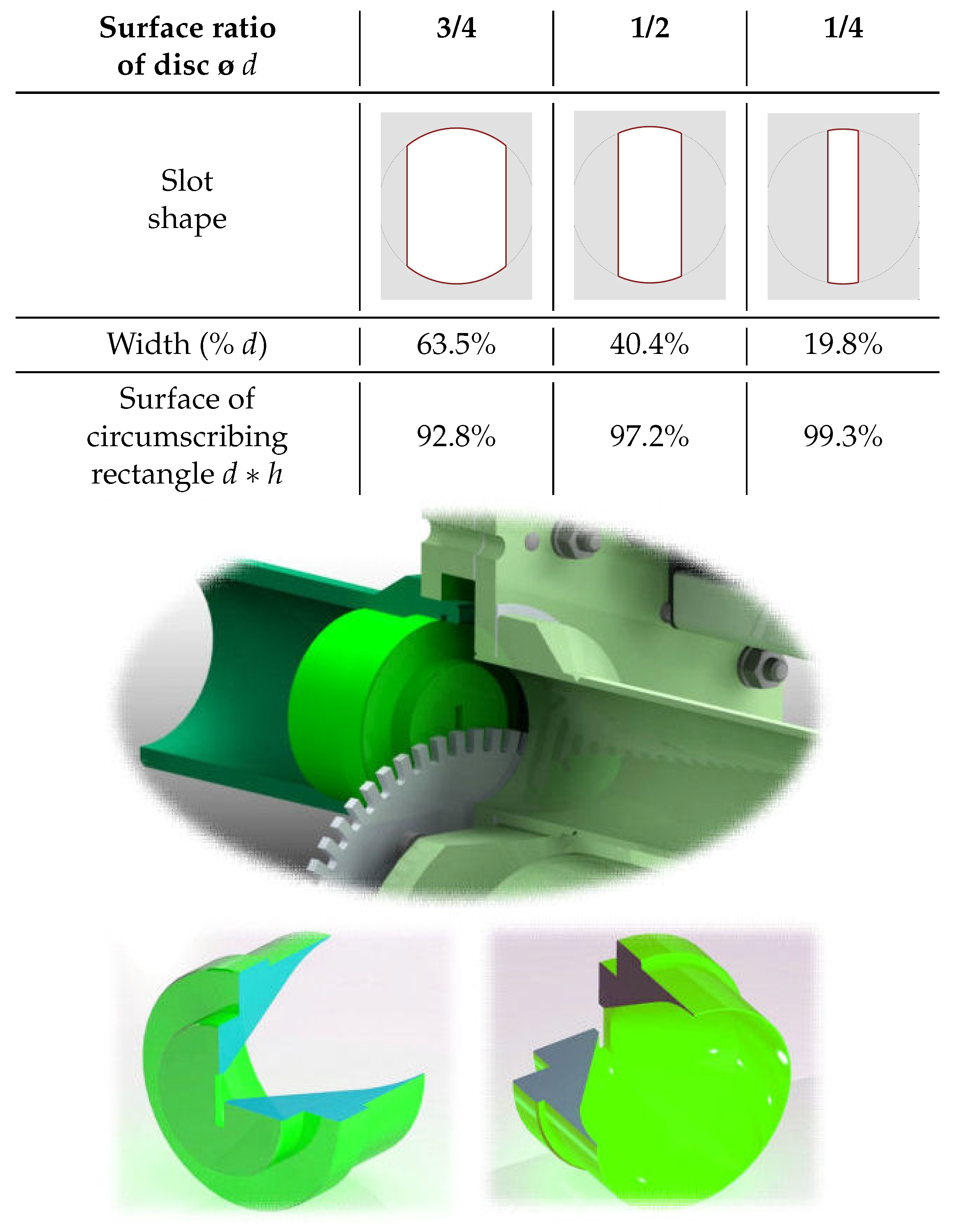
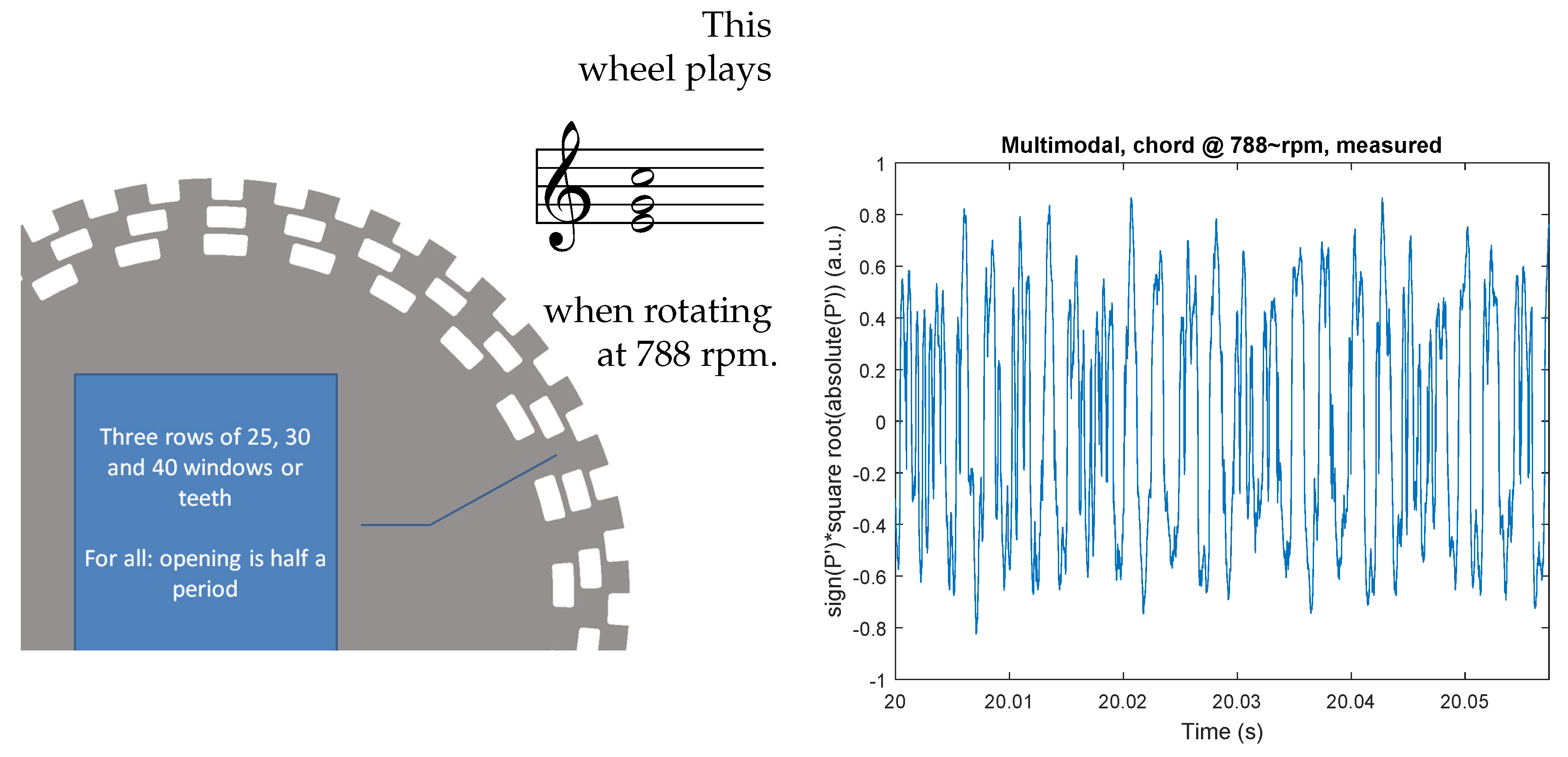
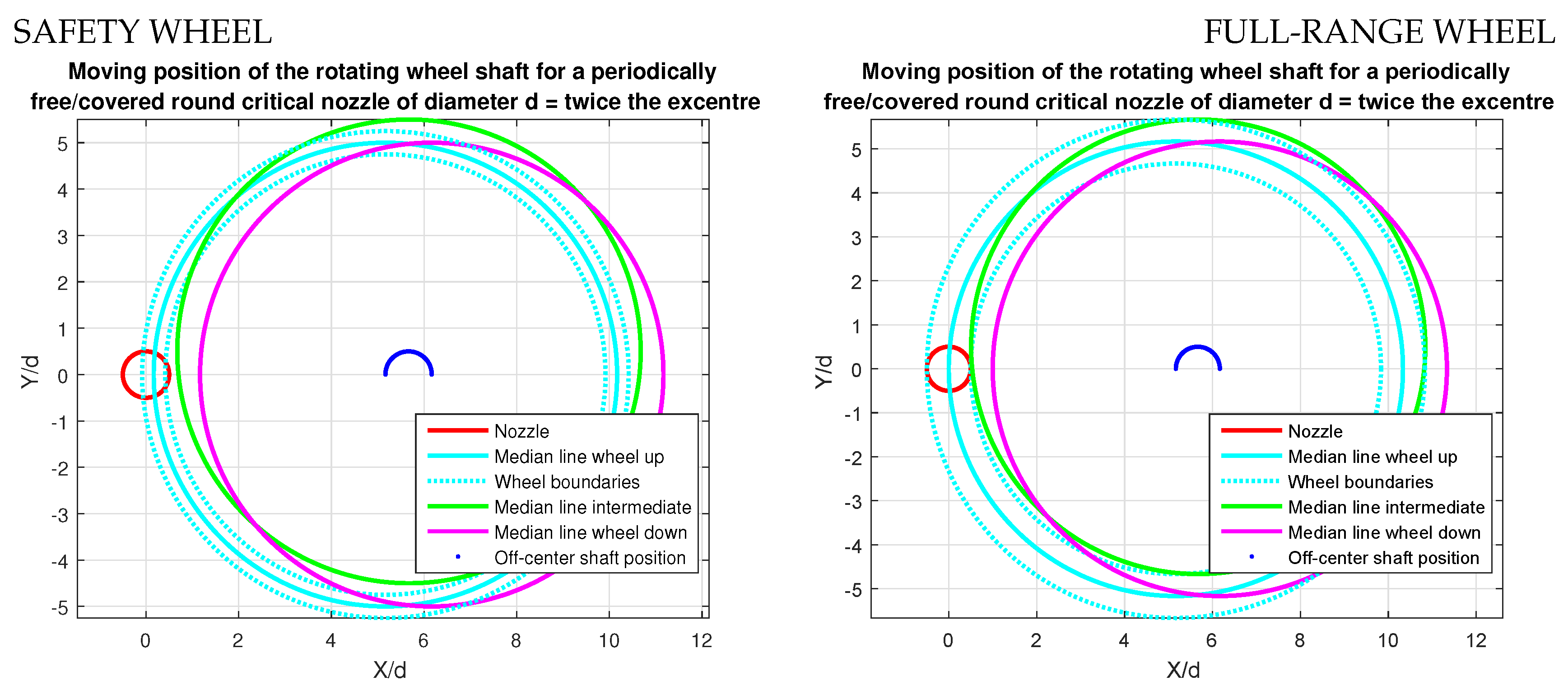
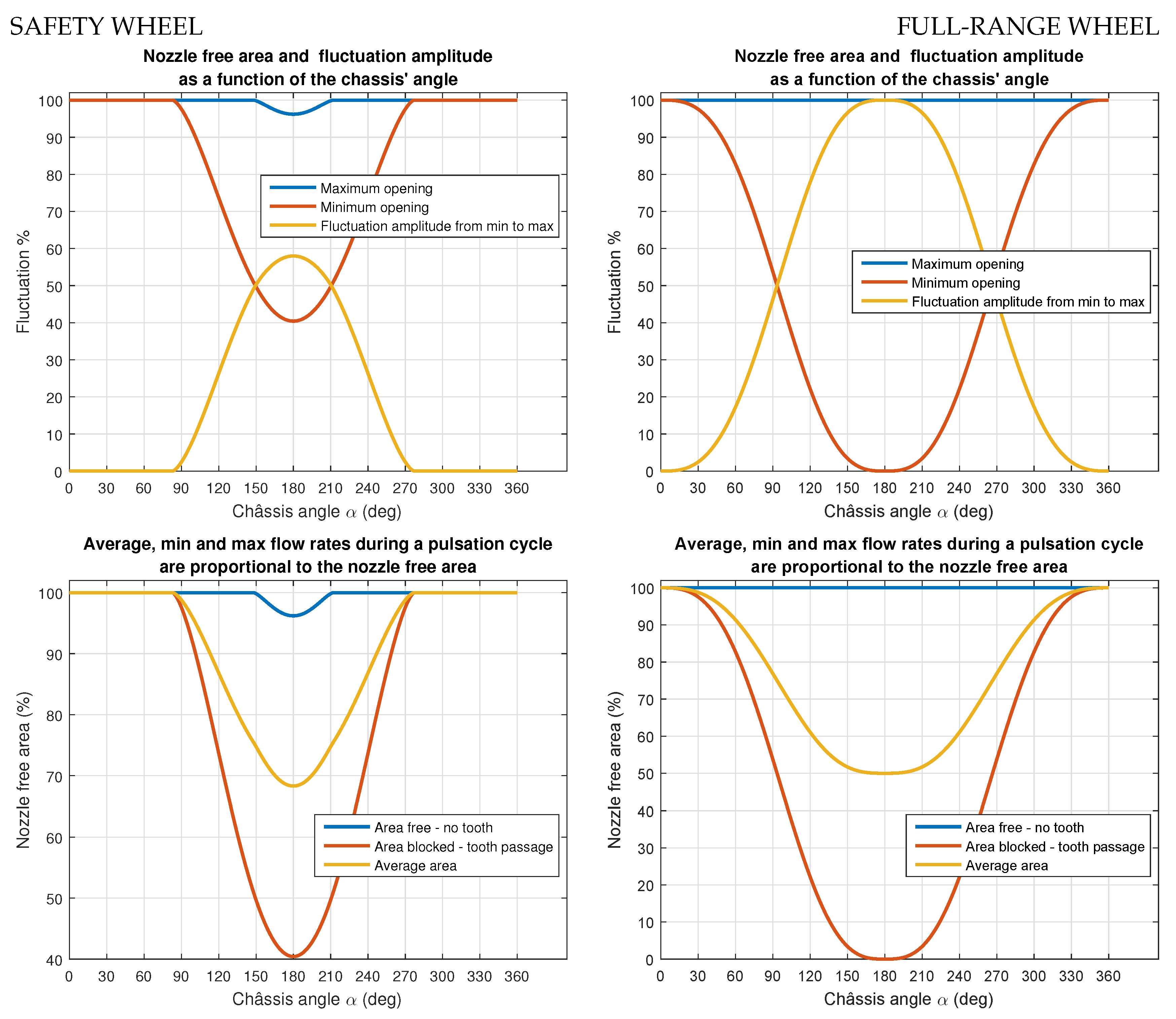
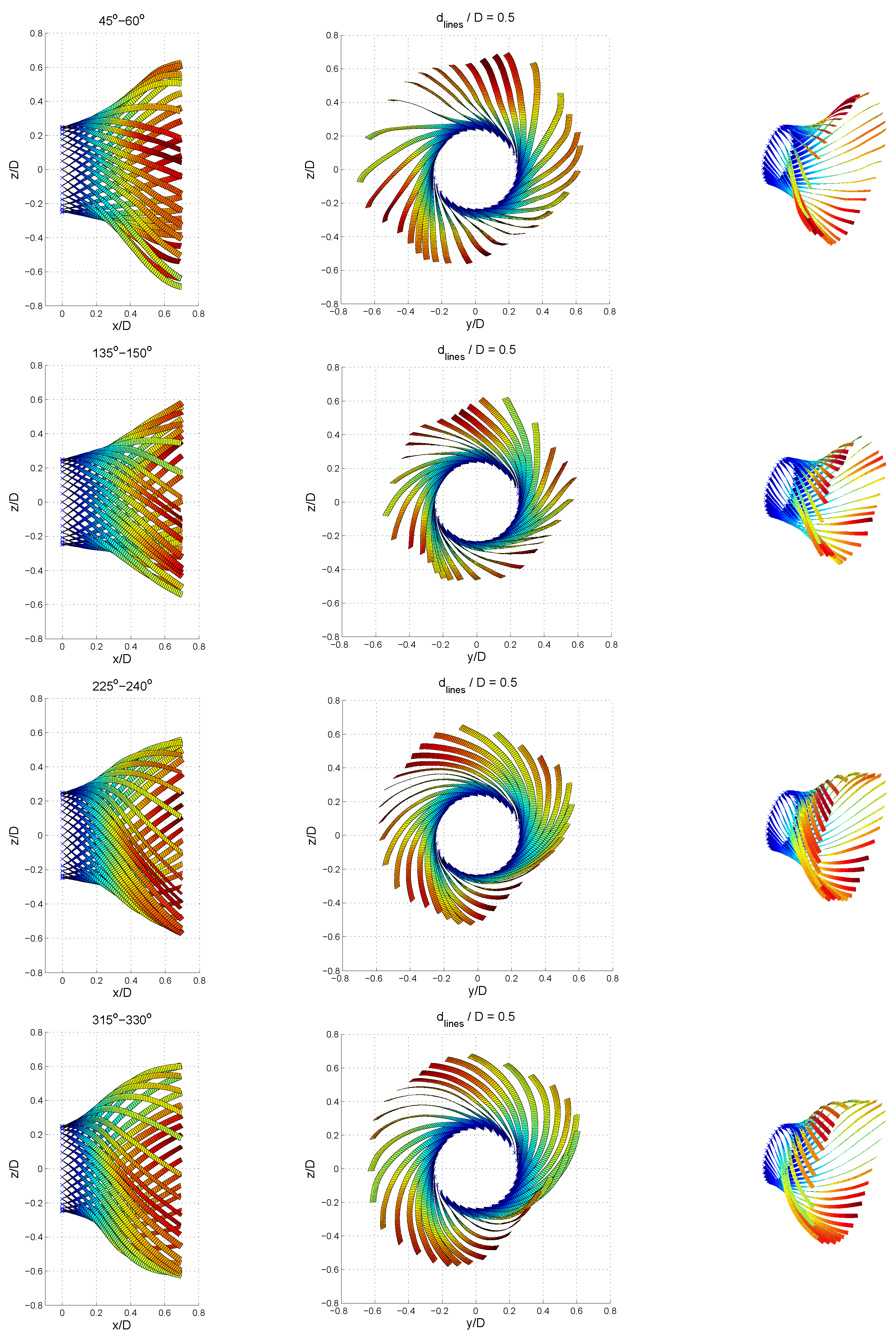


| Parameter | Lower | Design | Full Load | |
|---|---|---|---|---|
| Frequency range | (Hz) | 0–500 | 0–1000 | 0–6000 |
| Number of teeth n | – | 5 | 10 | 60 |
| Pulsation | (%) | 0 | 30 | 100 |
| Nozzle critical surface | (mm) | 20 | 50 | 120 |
| Free flowing mass flow at room temperature | (g/s) of dry air | 10 | 50 | 500 (120) |
| Maximum admissible pulsation level | (%) | 100 | 100 | 5 |
| Corresponding SPL at outlet stagnation point under atmospheric conditions | (dB SPL) | 113 | 146 | 155 (150 forced resonance [36]) |
| Open/close Periodicity | (%/%) of cycle | 20/80 | 50/50 | 80/20 |
| High pressure side | (bar abs) | 2 | 4 | 20 (12) |
| Low pressure side | (bar abs) | 1 | 2 | 10 (6) |
| Flow temperature | (K) | 223 (dry) | 293 | 550 |
| Accelerations/decelerations | (Hz/s) | 1 | 30 | 60 |
| Amplitude change rate | (%/s) of full scale | 1 | 2 | 4 |
| Frequency uncertainty | (%) | ± 1 | ± 1 | ± 1 |
| Average amplitude uncertainty | (%) of full scale | ± 3 | ± 3 | ± 3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (http://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Giuliani, F.; Stütz, M.; Paulitsch, N.; Andracher, L. Forcing Pulsations by Means of a Siren for Gas Turbine Applications. Int. J. Turbomach. Propuls. Power 2020, 5, 9. https://doi.org/10.3390/ijtpp5020009
Giuliani F, Stütz M, Paulitsch N, Andracher L. Forcing Pulsations by Means of a Siren for Gas Turbine Applications. International Journal of Turbomachinery, Propulsion and Power. 2020; 5(2):9. https://doi.org/10.3390/ijtpp5020009
Chicago/Turabian StyleGiuliani, Fabrice, Markus Stütz, Nina Paulitsch, and Lukas Andracher. 2020. "Forcing Pulsations by Means of a Siren for Gas Turbine Applications" International Journal of Turbomachinery, Propulsion and Power 5, no. 2: 9. https://doi.org/10.3390/ijtpp5020009
APA StyleGiuliani, F., Stütz, M., Paulitsch, N., & Andracher, L. (2020). Forcing Pulsations by Means of a Siren for Gas Turbine Applications. International Journal of Turbomachinery, Propulsion and Power, 5(2), 9. https://doi.org/10.3390/ijtpp5020009







